DOI:10.32604/cmc.2021.015102
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015102 | |
| Article |
Minimum Error Entropy Based EKF for GPS Code Tracking Loop
1Department of Communications, Navigation and Control Engineering, National Taiwan Ocean University, 202301, Taiwan
2Chunghwa Precision Test Tech. Co., Ltd., Taoyuan City, 324, Taiwan
*Corresponding Author: Dah-Jing Jwo. Email: djjwo@mail.ntou.edu.tw.
Received: 06 November 2020; Accepted: 31 December 2020
Abstract: This paper investigates the minimum error entropy based extended Kalman filter (MEEKF) for multipath parameter estimation of the Global Positioning System (GPS). The extended Kalman filter (EKF) is designed to give a preliminary estimation of the state. The scheme is designed by introducing an additional term, which is tuned according to the higher order moment of the estimation error. The minimum error entropy criterion is introduced for updating the entropy of the innovation at each time step. According to the stochastic information gradient method, an optimal filer gain matrix is obtained. The mean square error criterion is limited to the assumption of linearity and Gaussianity. However, non-Gaussian noise is often encountered in many practical environments and their performances degrade dramatically in non-Gaussian cases. Most of the existing multipath estimation algorithms are usually designed for Gaussian noise. The I (in-phase) and Q (quadrature) accumulator outputs from the GPS correlators are used as the observational measurements of the EKF to estimate the multipath parameters such as amplitude, code delay, phase, and carrier Doppler. One reasonable way to obtain an optimal estimation is based on the minimum error entropy criterion. The MEEKF algorithm provides better estimation accuracy since the error entropy involved can characterize all the randomness of the residual. Performance assessment is presented to evaluate the effectivity of the system designs for GPS code tracking loop with multipath parameter estimation using the minimum error entropy based extended Kalman filter.
Keywords: Entropy; extended Kalman filter; multipath; global positioning system; tracking loop
Multipath [1–4] is known as one of the dominant error sources in high accuracy GNSS (global navigation satellite system) positioning systems, such as the Global Positioning System (GPS) [1,2]. Multipath effects occur when GPS signals arrive at a receiver site via multiple paths due to reflections from nearby objects, such as the ground and water surfaces, buildings, vehicles, hills, trees, etc. Many estimation algorithms have been studied to eliminate the positioning error caused by multipath. Since multipath errors are among uncorrelated errors that are not cancelled out during observation differencing, the performance of high precision GPS receivers are mostly limited by the multipath induced errors. One of the most important issues in GPS system performance improvement is the interference suppression techniques.
Traditional GPS receivers track signals from different satellites independently. Each tracking channel measures the pseudorange and pseudorange rate, respectively, and then sends the measurements to the navigation processor, which solves for the user’s position, velocity, clock bias and clock drift. Most of the conventional approach for code synchronization process employs the delay-locked-loop (DLL) structure, which employs a discriminator function constructed with a specific combination of its early, prompt, and late correlator to detect code tracking error. Jee et al. [4] proposed the design of GPS receiver tracking loop using the extended Kalman filter (EKF), extracting and estimates parameters of the direct satellite signal component from the multipath corrupted signal for the loss lock problem in receiver tracking loop. The EKF can suitably combine multiple correlator branches for better code tracking as well as the other signal parameters, so as to estimate the multipath components for mitigating the multipath errors. Extended work had been carried out using the unscented Kalman filer by Jwo and Chang [5]. The in-phase (I) and quadrature (Q) correlator accumulator outputs are used as measurements in the filter estimation process [1,2,4,5].
The well-known Kalman filter (KF) [6] provides optimal (minimum mean square error) estimate of the system state vector and has been recognized as one of the most powerful state estimation techniques. KF is one of the most useful tools to observe linear dynamic systems and provide the estimation with minimum error variance. The EKF is a nonlinear version of the KF and has been widely employed as the GPS navigation processor. The fact that EKF highly depends on a predefined dynamics model forms a major drawback. For achieving good filtering results, the designers are required to have the complete a priori knowledge on both the dynamic process and measurement models, in addition to the assumption that both the process and measurement are corrupted by zero-mean Gaussian white sequences. In addition, the calculation of the Jacobian matrices makes it difficult to implement, especially for the non-differentiable function. Moreover, the mean square error criterion is limited to the assumption of linearity and Gaussianity.
Most of the existing multipath mitigation algorithms are designed for Gaussian noise. However, non-Gaussian noise is often encountered in many practical environments and their performances degrade dramatically in non-Gaussian cases. To solve the performance degradation problem in heavy-tailed (or impulsive) non-Gaussian noises, some robust Kalman filters have been developed by using certain non- minimum mean square error (MMSE) principle as the optimality criterion. As a unified probabilistic measure of uncertainty quantification, entropy has been widely used in information theory. Some efforts have been made to employ the entropy as the performance index in the filter design for general non-Gaussian stochastic systems. The minimum error entropy (MEE) criterion [7–14] and maximum correntropy criterion (MCC) [15–17] are information theoretic learning (ITL) [13] approaches, which have been successfully applied in robust regression, classification, system identification and adaptive filtering. Maximizing the mutual information between a state and the estimate is equivalent to minimizing the entropy of the estimation error.
Having been successfully applied to estimation technique, MEE aims to minimize the Renyi’s entropy of the estimation error information to improve the robustness against impulsive noises. The corresponding minimum error entropy algorithm can be employed and the probability density function (pdf) of estimation error was formulated in terms of the noise pdf and the filter gain matrix. Using the entropy based performance index, a recursive optimal filtering algorithm was put forward such that the hybrid entropy of the estimation error was minimized and the local stability of the error dynamics was guaranteed as well. The EKF assisted by the MEE criterion, referred to as the minimum error entropy EKF (MEEKF) uses the MEE as the optimality criterion. The EKF is designed to give a preliminary estimation of the state. The algorithm uses the propagation equations to obtain the prior estimates of the state and covariance matrix, and a fixed-point algorithm to update the posterior estimates and covariance matrix, recursively and online. In this paper, the MEEKF based DLL tracking loop with better multipath mitigation capability is presented. Simulation work is carried out to verify the feasibility of this method.
The remainder of this paper is organized as follows. In Section 2, preliminary background on the multipath interference and estimator based code tracking loops of the GPS receiver are reviewed. The minimum entropy based nonlinear filters are introduced in Section 4. In Section 5, some related information for estimation of the line-of-sight (LOS) and multipath parameters is discussed; application of the proposed method into the tracking loop of the GPS navigation filter design is discussed. Conclusion is given in Section 6.
2 Multipath Interference and the Estimator Based Code Tracking Loop
Multipath interference and non-line-of-sight reception are major error sources for GPS in an urban environment. Unlike other error sources, multipath cannot be mitigated through differential processing, since it decorrelates spatially rapidly. It is one of the dominant error sources for high accuracy positioning systems due to the irrelevancy between different instants and the occurrence uncertainty along the observation period. These multipath effects on the code phase measurements are most crucial, and the error can reach up to a few tens of meters, or a couple of hundred. The pseudorange errors caused by the multipath interference can be significantly mitigated through carefully designed antenna, such as antenna siting, choke-ring antenna design.
A typical functional diagram of the GPS receiver is shown as in Fig. 1. GPS receivers utilize an omni-directional antenna to receive the GPS signals. These are passed through a band-pass filter and low noise amplifier before being down-converted to an intermediate frequency (IF) by a mixer. Many GPS receivers use two down-conversions to reach baseband, where the analog signal is sampled and converted into digital in-phase and quadrature channels by multiplication by sine and cosine versions of the local oscillator (mixing) frequency. Some receivers sample at an intermediate frequency, before down-converting to baseband.
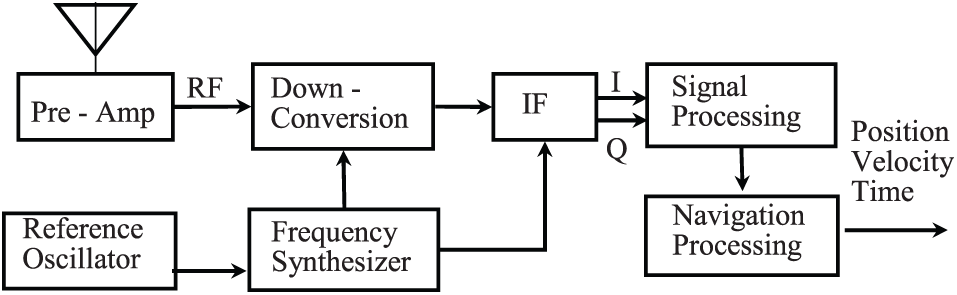
Figure 1: Global Positioning System (GPS) receiver functional diagram
The purpose of code tracking loop is to estimate the delay time between satellite and user, commonly referred to as the DLL, which compares the incoming spreading code with three different phase versions of the code (early, prompt, and late). Most of the conventional approach for code synchronization process employs the DLL structure. Receiver-based multipath mitigation techniques use modified discriminator designs, often with additional correlators, to improve the resolution of the signal correlation process. The conventional DLL loop uses a discriminator function constructed with a specific combination of its early, prompt, and late correlator to detect code tracking error. As a better nonlinear estimation approach, the EKF can suitably combine multiple correlator branches for better code tracking as well as the other signal parameters, so as to estimate the multipath components for mitigating the multipath errors.
The estimator based code tracking loop is shown as in Fig. 2. The structure of the tracking loop is comprised of several branches of correlators followed by accumulator, a nonlinear filter, and a loop filter. These branch outputs are fed into an estimator, which jointly estimates the various signal parameters: Amplitude, phase and delay for all of the signal components, and the estimation error is fed back to the loop filter, enabling the loop to accurately track the parameters of the signal. The outputs of the correlator branches are samples of the autocorrelation function of the spreading pseudorandom noise sequence and sinc function of Doppler frequency and phase error. The structure resembles the classical DLL in that it uses various early-late correlators. The EKF based DLL tracking loop with multipath mitigation capability has been proposed [4], where the tracking loop using the EKF with multiple correlator structure was involved.
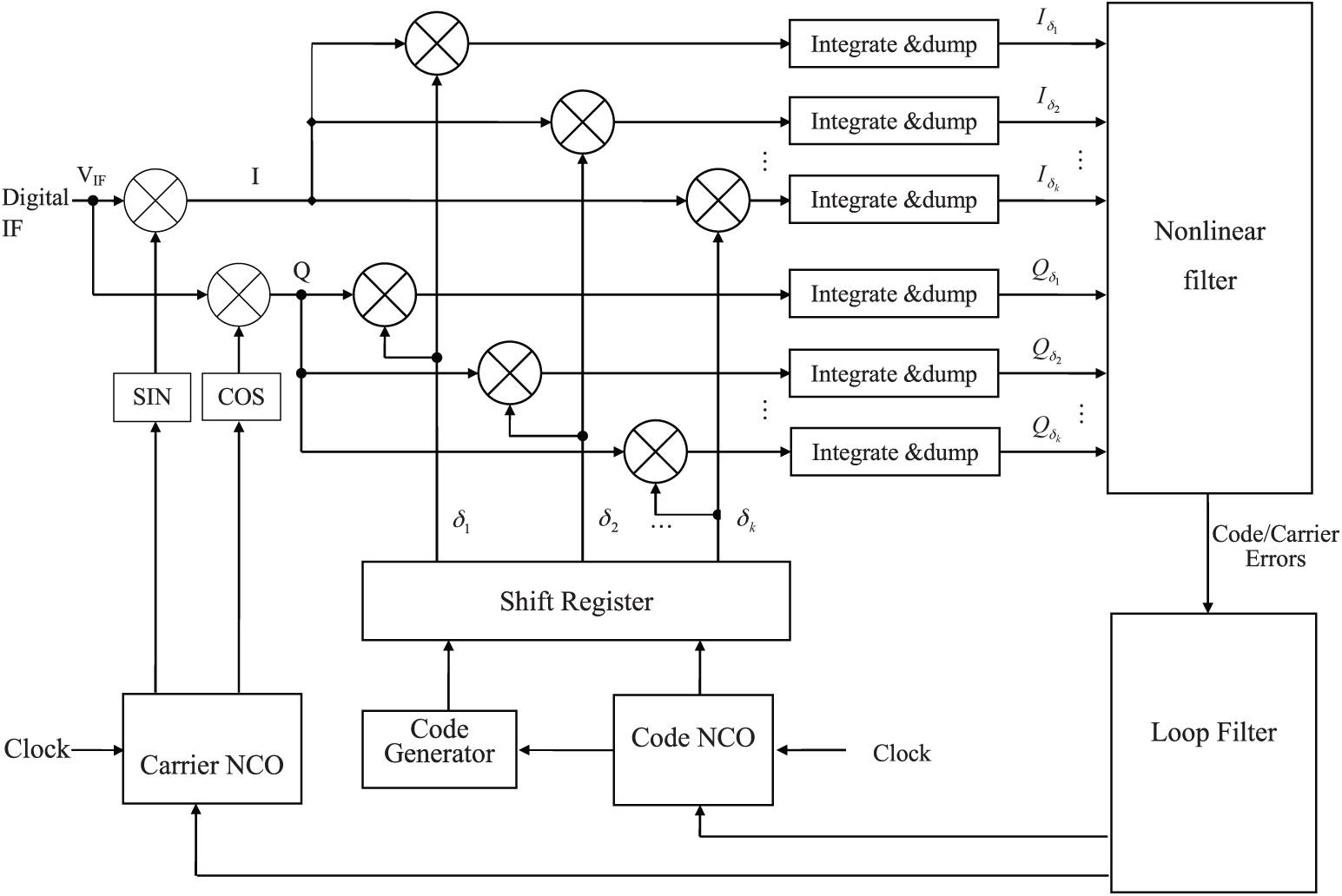
Figure 2: The estimator based code tracking loop with nonlinear filters
To estimate the multipath components multiple samples of C/A code autocorrelation function are required and multiple correlators are involved. Instead of subtracting the two early-late branches, several correlator branches are employed. The following assumptions are made: (1) The received signal is comprised of a single multipath component; (2) The signal parameters are modeled as a random walk sequence during the sampling time interval; (3) The noise processes are Gaussian with zero mean and variance to be defined in the sequel; (4) The processing gain is high enough so that the autocorrelation function of the CA code can be approximated by a triangle function. Under these assumptions, the received GPS signal can then be written as:
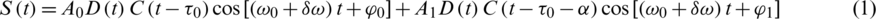
The j-th branch correlator accumulator output can be written by
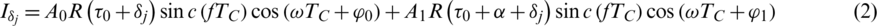
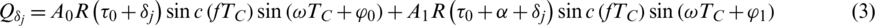
There are mainly seven parameters involved, including four LOS parameters and three multipath parameters, namely A0: the amplitude,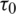 
: the code delay, f : the Doppler frequency, 
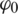: the carrier phase, A1: the amplitude of the multipath affect, 
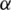: the multipath parameter, 
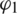: the carrier phase by multipath affect. Furthermore, 
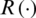denotes the autocorrelation function of the PRN sequences with correlator spacing given as
The idealized correlation function between local prompt code and the received spreading code is shown in Fig. 3.
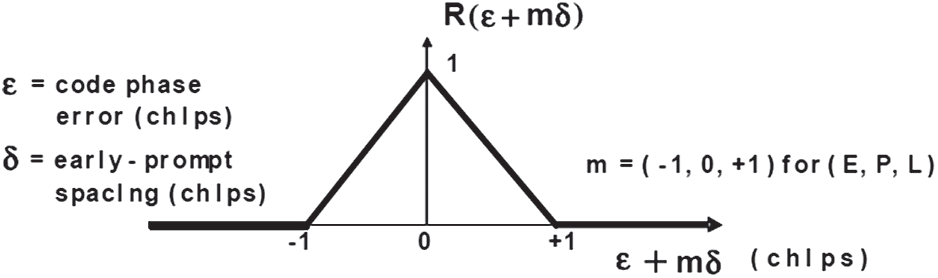
Figure 3: Idealized correlation function
3 The Minimum Error Entropy Based Extended Kalman Filter
The nonlinear filters deal with the case governed by the nonlinear stochastic difference equations:
where the state vector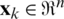 
, process noise vector 
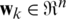, measurement vector 
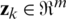, and measurement noise vector 
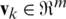. Both the vectors 
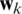and 
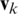are zero mean Gaussian white sequences having zero cross-correlation with each other:
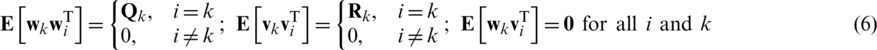
where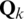 
is the process noise covariance matrix, and 
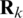is the measurement noise covariance matrix.
3.1 The Extended Kalman Filter
The discrete-time EKF algorithm is summarized as follows:
(1) Initialize state vector and state covariance matrix: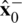 
and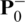 
(2) Compute Kalman gain matrix:
(3) Update state vector:
(4) Update error covariance
(5) Predict new state vector and state covariance matrix
where the linear approximation equations for system and measurement matrices are obtained through the relations
Eqs. (7)–(9) are the measurement update equations. These equations incorporate a measurement value into a priori estimation to obtain an improved a posteriori estimation. Eqs. (10), (11) are the time update equations of the algorithm from k to step k + 1 . In the above equations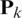 
is the error covariance matrix defined by 
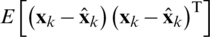, in which 
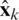is an estimation of the system state vector 
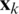. Further detailed discussion can be referred to Brown et al. [6].
3.2 Minimum Entropy Based Extended Kalman Filter
In information theory, entropy is a measure of the uncertainty associated with random variables. ITL is a framework to non-parametrically adapt systems based on entropy and divergence. Originally presented by Shannon in 1948, many definitions of entropy have been introduced for various purposes, such as Shannon entropy and Renyi’s entropy. Renyi’s entropy is usually used for quantifying the diversity, uncertainty or randomness of a random variable. Renyi’s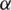 
-order entropy of a random variable X is defined by
The base of the logarithm is not as important since it only contributes to a constant coefficient and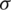 
the kernel size. When 
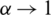, the Renyi’s 
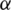-order entropy approaches Shannon entropy. For 
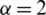(quadratic entropy), the quadratic Renyi’s entropy can be obtained and has the form
There are numerous methods to estimate the probability density. The kernel density estimation (KDE) has wide applicability and is closely related to the Renyi’s entropy. Kernel density estimation, also referred to as the Parzen window method, is a nonparametric method to estimate the pdf of a random process. When the KDE is used to estimate the pdf from the samples, it can be expressed as
where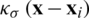 
is the Parzen window, and 
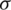represents the bandwidth. The first requirement ensures that the Parzen window method results in a pdf, while the second one guarantees the expectation of the process keep unchanged. There are various kernel functions that can be used. Examples are uniform, triangular, and Gaussian, etc. The most commonly used one is the Gaussian kernel with the following form
where the Gaussian function is defined as
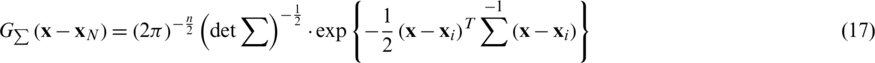
Using the KDE, the Renyi’s quadratic entropy can be formulated with the form
From the estimation equation
where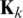 
is the Kalman filter gain matrix to be determined; 
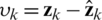is the innovation. The randomness uncertainty can be remarkably mitigated when employing the minimum error entropy criterion given by:
The adaptive filter based on the optimization learning algorithm is shown as in Fig. 4 [14].
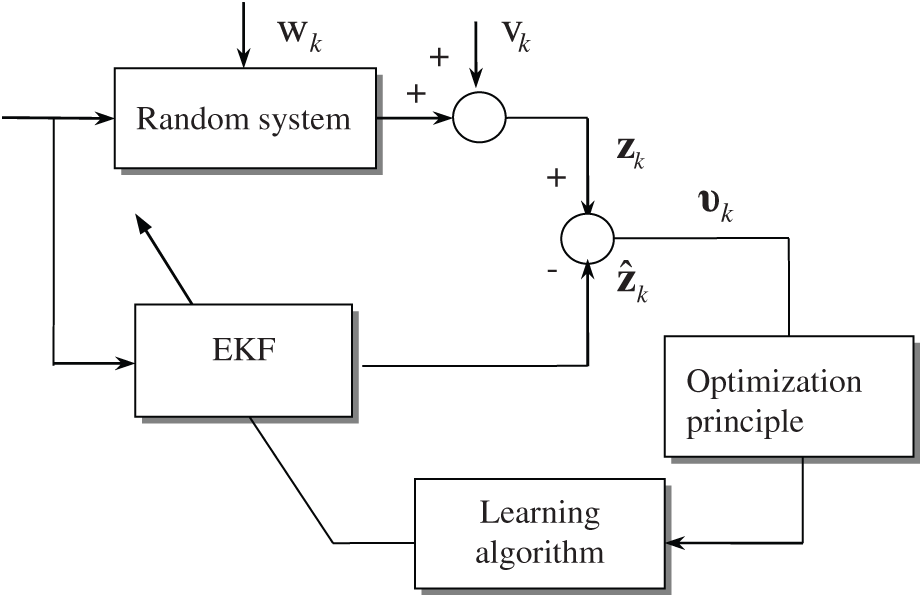
Figure 4: Adaptive filter algorithm based on the optimization learning algorithm
The argument of the logarithm in quadratic Renyi’s entropy is called the information potential expressed as follows
where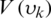 
is the informational potential (IP) of 
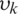. The minimization of the entropy can be replaced with the maximization of the information potential,
The locally optimal weight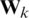 
can be obtained by
There are a set of samples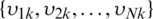 
for epoch k. Using Gaussian kernel method for non-parametric estimation:
where
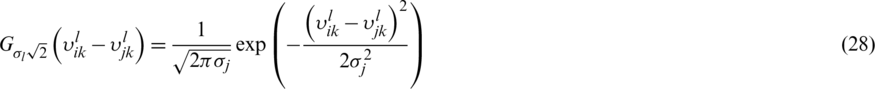
Employing the gradient descent method, the adaptive law can be written as
where 
is the learning rate, and the potential information of the pseudo-innovation at time step can be calculated as
For further formulations, the gradient of the information potential 
is given as
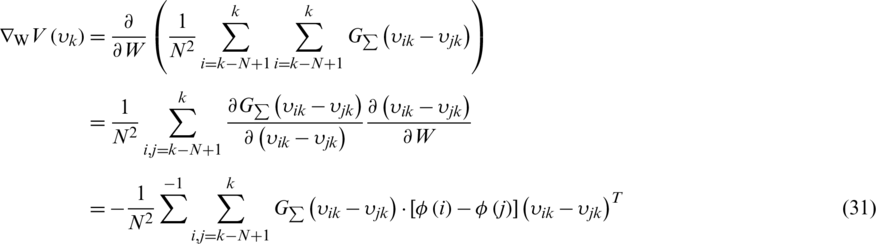
Numerical experiments have been carried out to evaluate the estimation performance for the MEEKF approach in comparison with the EKF approach. The MEEKF based DLL tracking loop with multipath parameter estimation and mitigation capability is demonstrated. The computer codes were developed using the Matlab® software. The commercial software Satellite Navigation (SATNAV) toolbox by GPSsoft LLC [18] was employed for generating the satellite constellation and the pseudorange observables. To evaluate the estimation performance using the MEEKF algorithm in comparison with those of EKF approach, illustrative examples are presented for demonstrating the effectiveness under two types of noise environments.
The received signal assumed for simulation is a two-path channel model, which consists of a direct and one multipath signal component. The amplitude, delay and phase of the direct (LOS) and the reflected (multipath) signals components are estimated by the filter. When the LOS and multipath components of signals are involved, the state vector is defined as
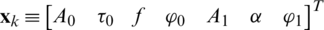
The initial state for the signal is given by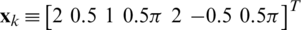 
. The dynamics of the signal parameters is assumed to take a linear system model, while the correlator accumulator measurements are nonlinear. Therefore, a nonlinear filter needs to be employed. As was shown in Fig. 1, the proposed tracking loop consists of multiple correlators and an EKF. The received signal is multiplied by the I and Q carrier replicas in separate channels. The resulting signals in each channel are then multiplied by each replica of the code. In this work, since a linear system equation is used, we have 
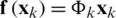, with
The measurements are the outputs of the I and Q correlator accumulator: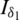 
, 
and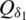 
, 
, which form the measurement vector: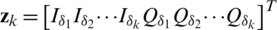 
. They are nonlinear functions of the carrier frequency, carrier phase and code phase. Since I and Q measurements are outputs of the correlator, the nonlinear functions contain non-smoothing terms. The function need to be linearized in order to use it in the EKF. The EKF can separate LOS components from the multipath components by modeling and estimating the parameters of each signal component, which is employed to estimate both the LOS and multipath signal components. The Jacobian matrix of the measurement for the EKF is given by
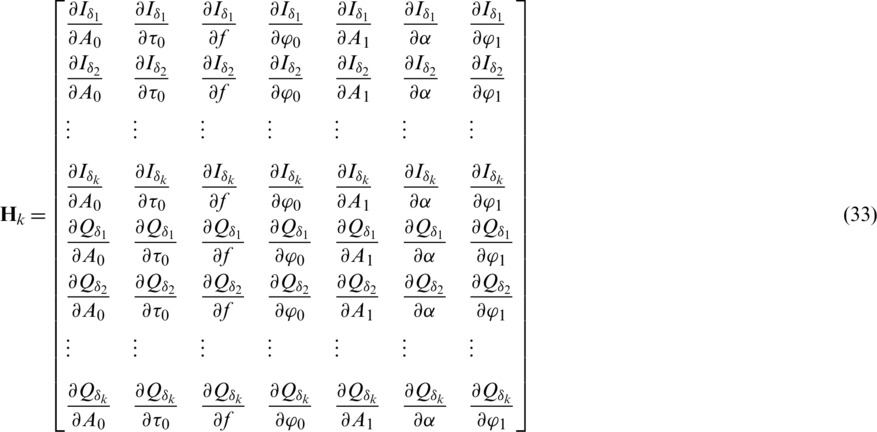
The complete derivatives for the measurement Jacobian matrix are shown in Appendix A.
In the first scenario, it is assumed that the observation errors possess the Gaussian distribution, while the Gaussian mixture errors in the observation are assumed for the second scenario. For the first scenario, the noise pdf of the Gaussian noise is given as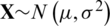 
, representing the Gaussian random variable with mean 
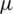and standard deviation 
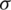, where the parameter settings are given as: 
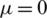and 
(in unit of meter), respectively. Comparison of the estimation results for the LOS signal components A0, 
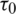, f and 
, using the MEEKF as compared to those of EKF is shown in Figs. 5, 6; comparison of the estimation results for the multipath components A1, 
and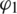 
, is shown in Figs. 7, 8. The MEEKF demonstrate overall improved estimation accuracy as compared to the EKF method, with more impact on the multipath parameters than the LOS parameters.
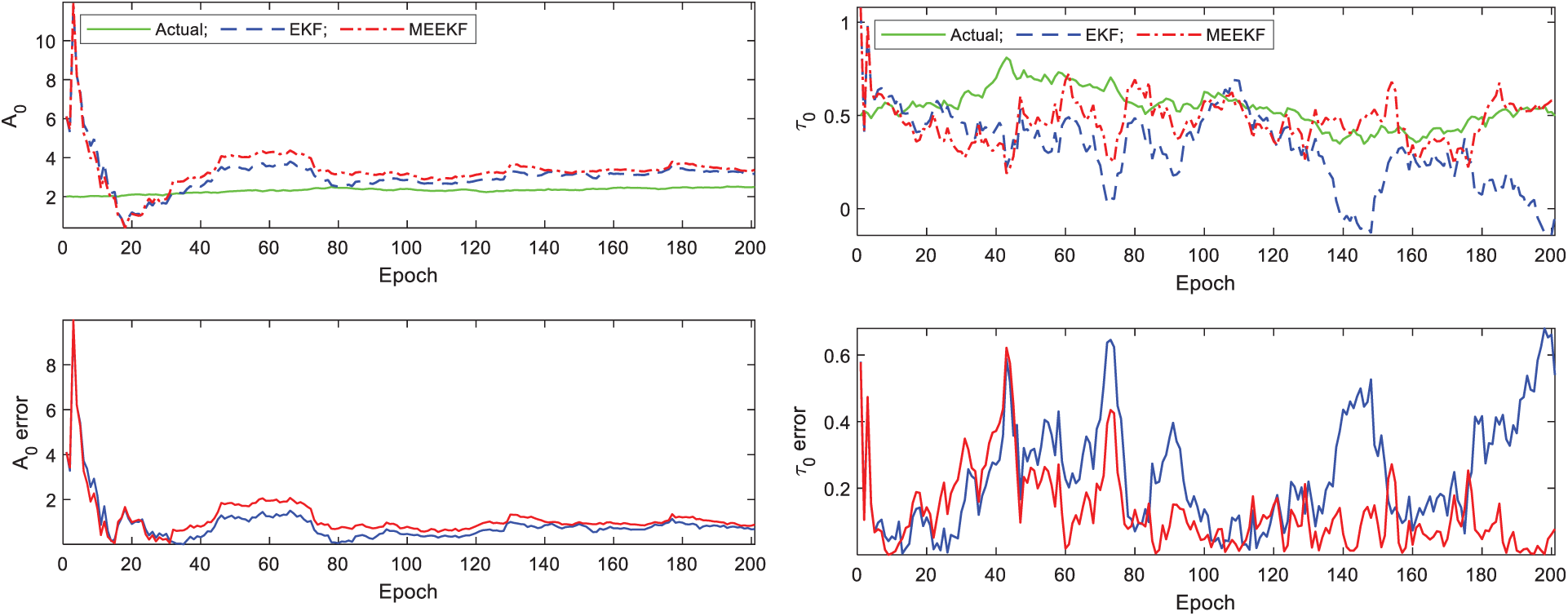
Figure 5: Tracking performance for LOS amplitude A0 and code 
-Gaussian multipath errors
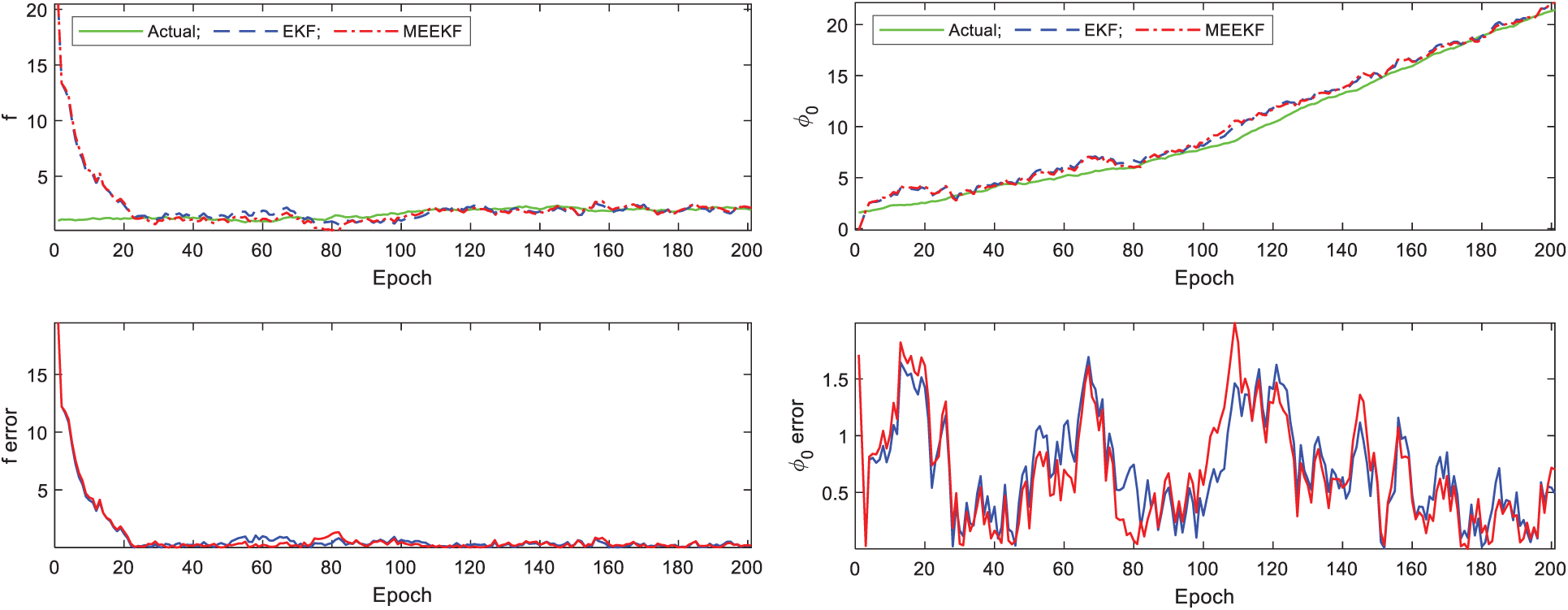
Figure 6: Tracking performance for LOS frequency f and phase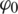 
-Gaussian multipath errors
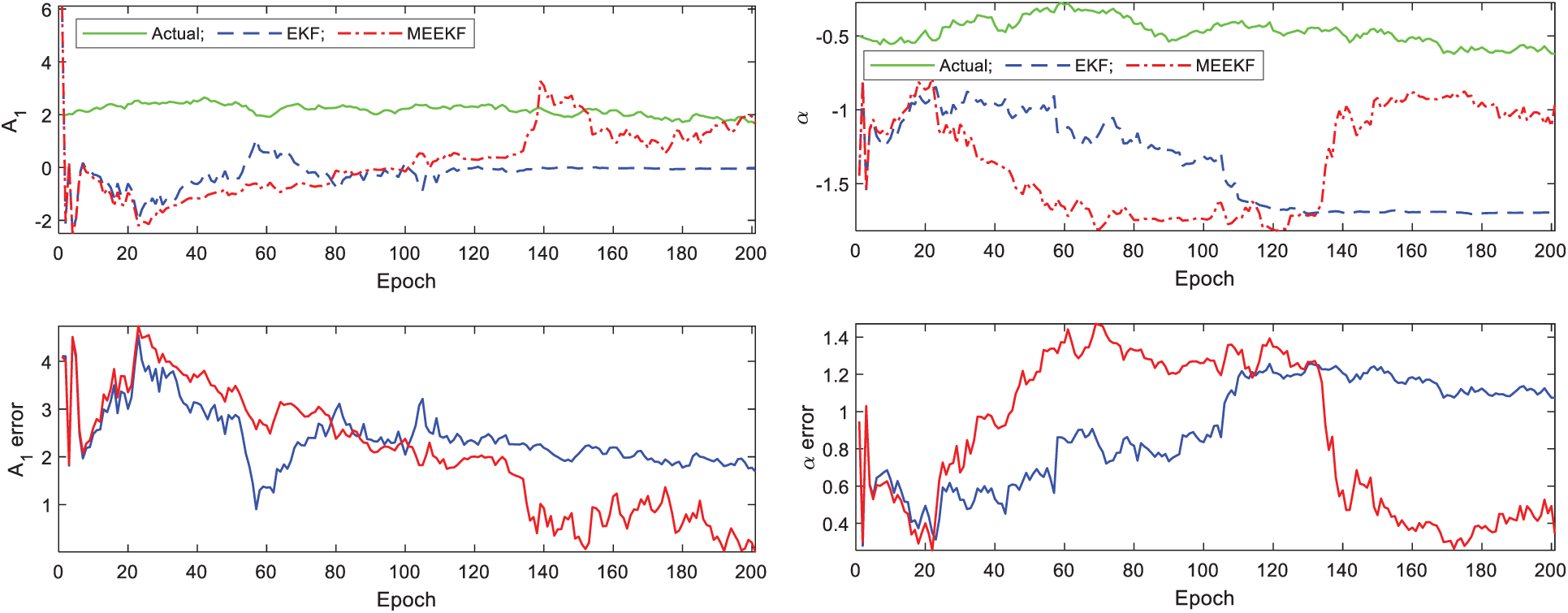
Figure 7: Tracking performance for multipath parameters, A1 and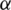 
-Gaussian multipath errors
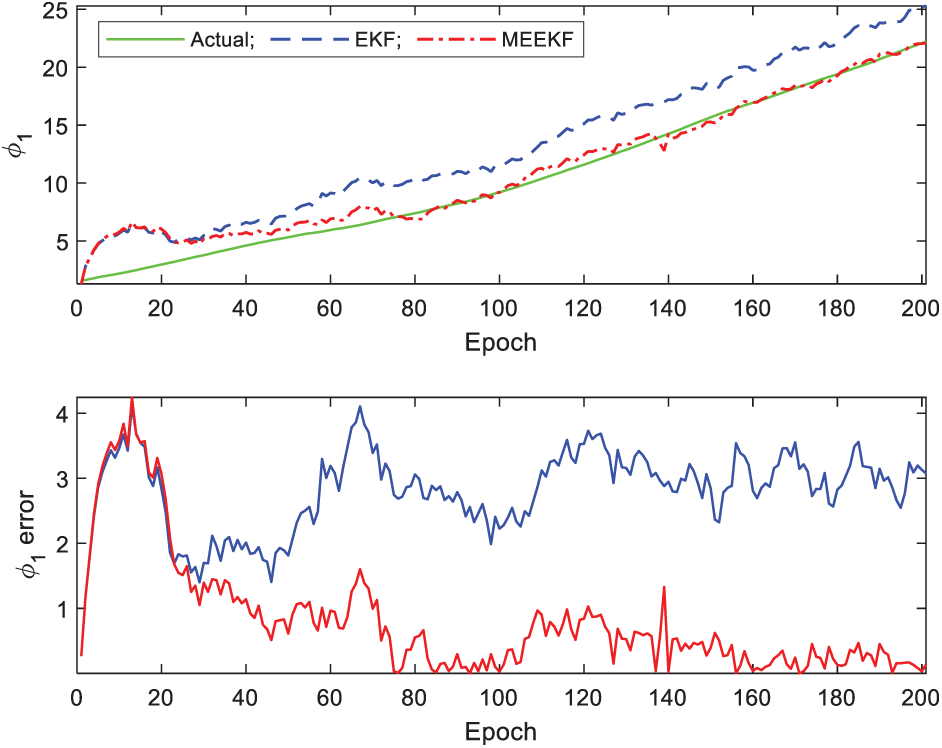
Figure 8: Tracking performance for multipath parameter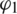 
-Gaussian multipath errors
As for the second scenario, it is assumed that the multipath errors follow the Gaussian mixture distribution, defined by the pdf of the form
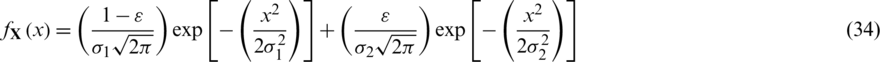
where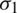 
and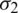 
are the standard deviations of the individual Gaussian distributions, and 
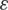is a perturbing parameter that represents error model contamination. The noise pdf for the Gaussian mixture noise can be represented as 
, or equivalently by 
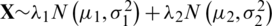. In this scenario, the parameter settings are given as 
, 
, 
, 
, 
, 
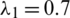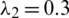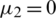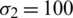, respectively. Namely, the perturbed conditions 
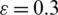(i.e., with 30% contamination due to multipath effects), and 
(m) were assumed. Fig. 9 shows the pdf’s and the corresponding cumulative distribution functions, for the individual Gaussian and the resulting Gaussian mixture model employed to generate the multipath errors. Comparison of the estimation results for the LOS signal components A0, 
, f and 
, using the MEEKF as compared to those of EKF is shown in Figs. 10, 11; Comparison of the estimation results for the multipath components A1, 
and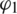 
, is shown in Figs. 12, 13. It can be seen that MEEKF based tracking loop demonstrates improved performance as compared to those of EKF based tracking loop. The MEEKF has more impact on the estimation accuracy improvement on the multipath parameters, for both scenarios.
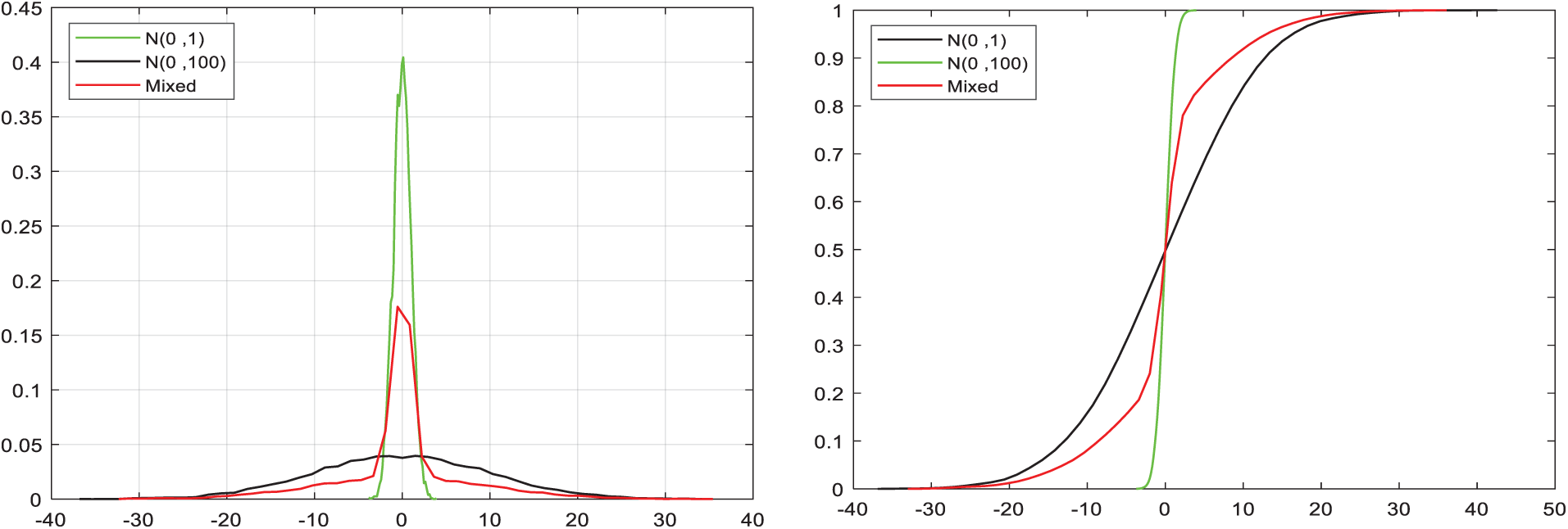
Figure 9: Probability density functions and the corresponding cumulative distribution functions, for the individual Gaussian and the resulting Gaussian mixture model
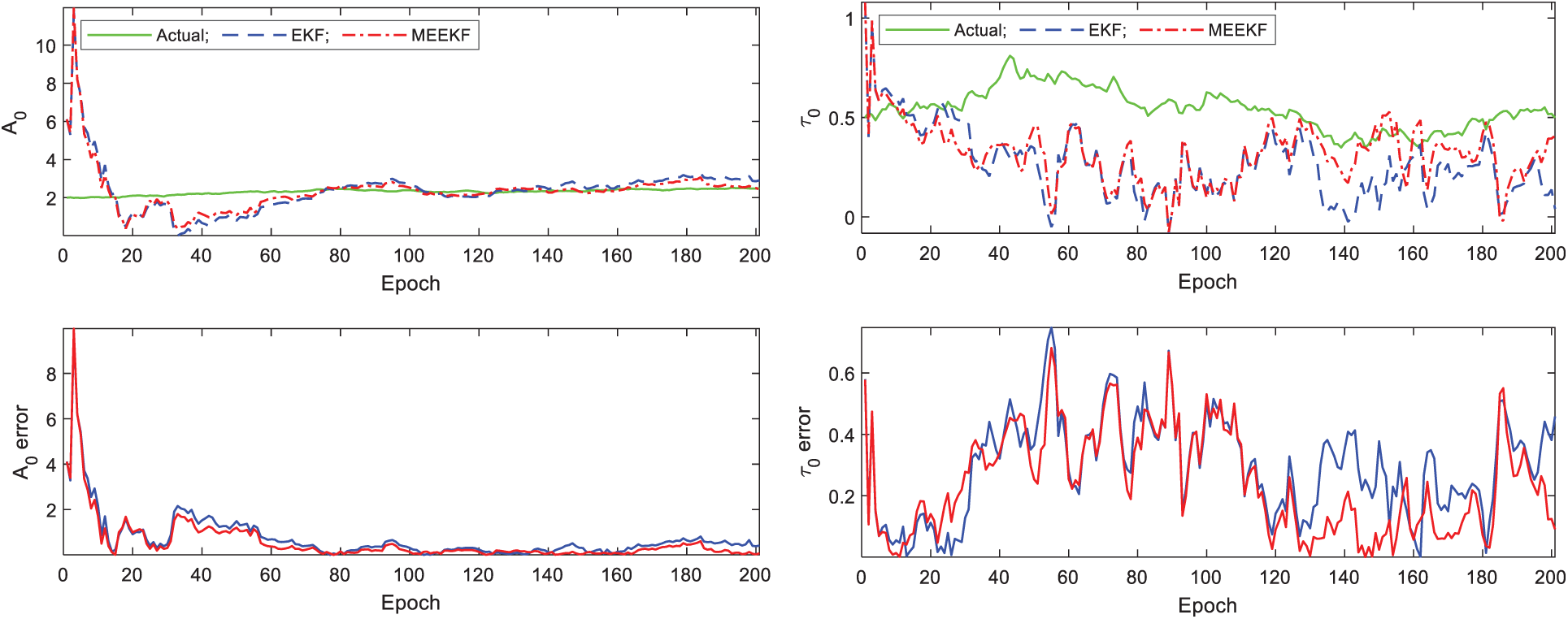
Figure 10: Tracking performance for LOS amplitude A0 and code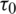 
-Gaussian mixture errors
Figure 11: Tracking performance for LOS frequency f and phase 
-Gaussian mixture errors
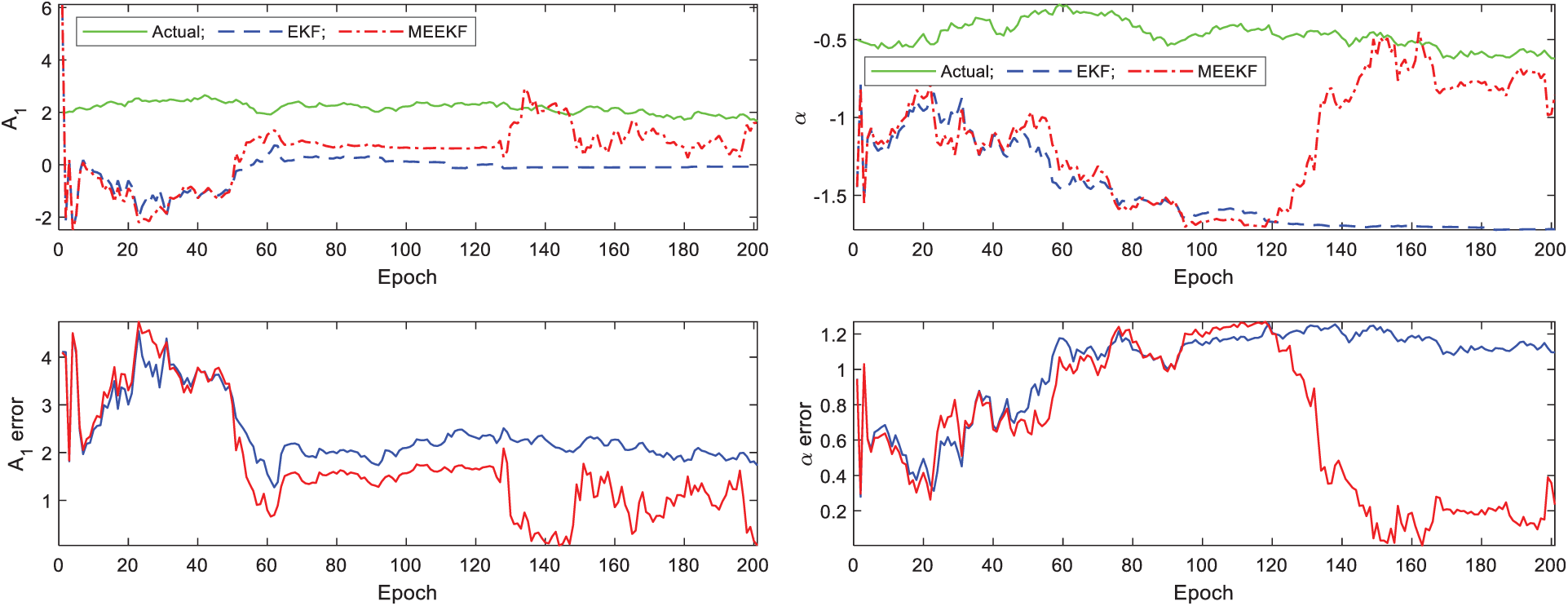
Figure 12: Tracking performance for multipath parameters, A1 and 
-Gaussian mixture errors
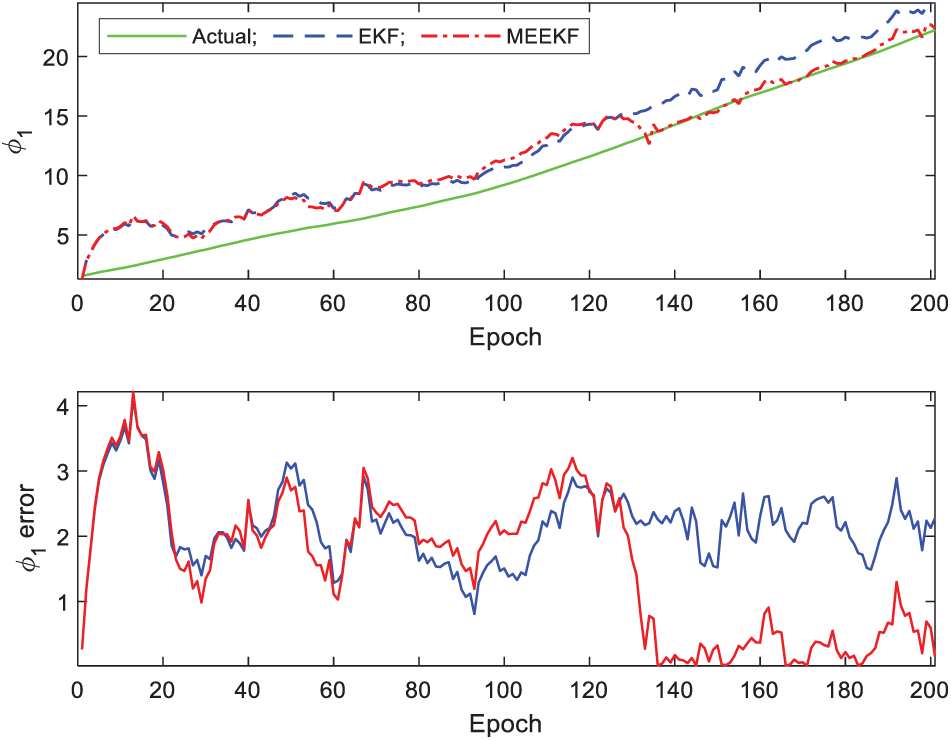
Figure 13: Tracking performance for multipath parameter 
-Gaussian mixture errors
Multipath parameter estimation is crucial for multipath mitigation and subsequently accuracy improvement for the GPS positioning. Conventional DLL tracking loop in GPS receiver suffers from performance degradation due to multipath errors. The estimation-based approach for multipath mitigation utilizes the nonlinear filter to estimate multipath component and extract the direct signal component. However, the conventional EKF does not possess sufficiently good capability to monitor the change of parameters due to changes in measurement model.
This paper has presented a potentially useful approach for GPS multipath parameter estimation in the code tracking loop, where the minimum error entropy based extended Kalman filter was used as the GPS code tracking loop, in which the multipath parameter estimation was carried out. A multipath estimation algorithm was based on kernel minimum error entropy filter, where the MEE optimality criterion was employed. The proposed filter uses the propagation equations to obtain the prior estimates of the state and covariance matrix, and a fixed-point algorithm to update the posterior estimates and covariance matrix, recursively and online. The estimation performance has been remarkably improved once the MEE criterion is incorporated into the EKF, which leads to the MEEKF.
To assess the estimation performance, numerical experiments were conducted for evaluation. Two scenarios of observation noise environments, including Gaussian and non-Gaussian cases, respectively, are presented for demonstrating the effectiveness. Simulation results show that the MEEKF algorithm possesses noticeable improvement on tracking accuracy as compared to that of conventional EKF method and thus demonstrates good potential as the alternative as the GPS code tracking loop with multipath parameter estimation, especially in the case of nonlinear and/or non-Gaussian observables.
Funding Statement: This work has been partially supported by the Ministry of Science and Technology, Taiwan [Grant Numbers MOST 107-2221-E-019-025 and MOST 108-2221-E-019-013].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. W. Parkinson, J. J. Spilker, P. Axelrad and P. Enge. (1996). Global Positioning System: Theory and Applications. Washington, DC, USA: American Institute of Aeronautics and Astronautics, Inc. [Google Scholar]
2. B. Hofmann-Wellenhof, H. Lichtenegger and E. Wasle. (2008). Global Navigation Satellite Systems, GPS, GLONASS, Galileo, and More. New York, NY, USA: Springer. [Google Scholar]
3. R. A. Iltis. (1990). “Joint estimation of PN code delay and multipath using the extended Kalman filter,” IEEE Transactions on Communications, vol. 38, no. 10, pp. 1677–1685. [Google Scholar]
4. G. I. Jee, H. S. Kim, Y. J. Lee and C. G. Park. (2002). “A GPS C/A code tracking loop based on extended Kalman filter with multipath mitigation,” in Proc. ION GPS 2002, Portland, OR, USA, pp. 446–451. [Google Scholar]
5. D. J. Jwo and Y. J. Chang. (2009). “GPS receiver code tracking loop designs using the unscented Kalman filtering approach,” in Proc. GPS/GNSS 2009, Jeju, Korea. [Google Scholar]
6. R. G. Brown and P. Y. C. Hwang. (1997). Introduction to Random Signals and Applied Kalman Filtering. New York, NY, USA: John Wiley & Sons. [Google Scholar]
7. L. Guo and H. Wang. (2006). “Minimum entropy filtering for multivariate stochastic systems with non-Gaussian noises,” IEEE Transactions on Automatic Control, vol. 51, no. 4, pp. 695–700. [Google Scholar]
8. M. Janzura, T. Koski and A. Otahal. (1994). “Minimum entropy of error principle in estimation,” Information Science, vol. 79, no. 1–2, pp. 123–144. [Google Scholar]
9. H. Wang. (2002). “Minimum entropy control of non-Gaussian dynamic stochastic systems,” IEEE Transactions on Automatic Control, vol. 47, no. 2, pp. 398–403. [Google Scholar]
10. D. Erdogmus, K. E. Hild and J. C. Principe. (2003). “Online entropy manipulation: Stochastic information gradient,” IEEE Signal Processing Letter, vol. 10, no. 8, pp. 242–245. [Google Scholar]
11. L. Guo and H. Wang. (2006). “Minimum entropy filtering for multivariate stochastic systems with non-Gaussian noises,” IEEE Transactions on Automatic Control, vol. 51, no. 4, pp. 695–700. [Google Scholar]
12. B. Chen, Z. J. Yuan, N. N. Zheng and J. C. Principe. (2013). “Kernel minimum error entropy algorithm,” Neurocomputing, vol. 121, pp. 160–169. [Google Scholar]
13. J. C. Principe. (2010). Information Theoretic Learning, Renyi’s Entropy and Kernel Perspectives. New York, NY, USA: Springer. [Google Scholar]
14. Y. Liu, H. Wang and C. H. Hou. (2013). “UKF based nonlinear filtering using minimum entropy criterion,” IEEE Transactions on Signal Processing, vol. 61, no. 20, pp. 4988–4999. [Google Scholar]
15. W. Liu, P. P. Pokharel and J. C. Principe. (2007). “Correntropy: Properties and applications in non-Gaussian signal processing,” IEEE Transactions on Signal Processing, vol. 55, no. 11, pp. 5286–5298. [Google Scholar]
16. B. Chen, X. Liu, H. Zhao and J. C. Principe. (2017). “Maximum correntropy Kalman filter,” Automatica, vol. 76, pp. 70–77. [Google Scholar]
17. S. Hernández, A. Baldomir, J. Díaz and F. Pereira. (2012). “An enhanced formulation of the maximum entropy method for structural optimization,” Computers Materials & Continua, vol. 32, no. 3, pp. 219–239. [Google Scholar]
18. GPSoft LLC., Satellite Navigation ToolBox 3.0 User’s Guide, Athens, OH, USA. [Google Scholar]
Appendix A. Derivatives in the Measurement Matrix
(1) Derivatives that related to the j-th branch of I correlator accumulator outputs:
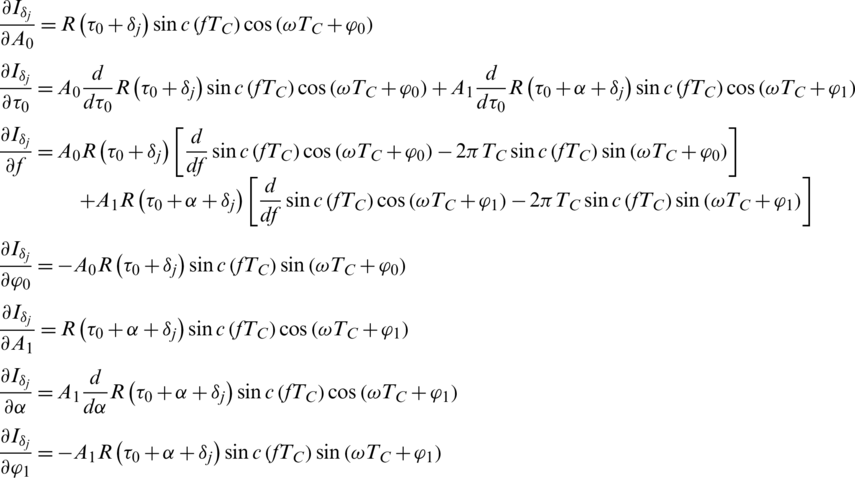
(2) Derivatives that related to the j-th branch of Q correlator accumulator outputs:
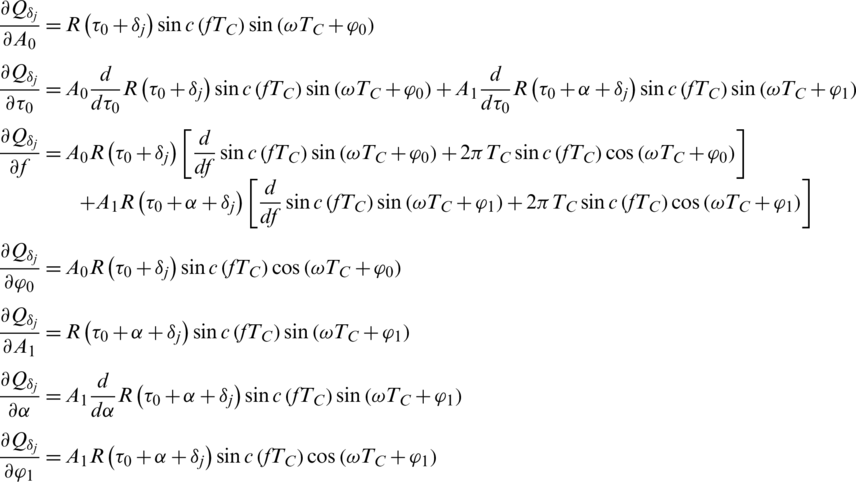
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |