DOI:10.32604/cmc.2021.015161
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015161 | |
| Article |
Optimal and Memristor-Based Control of A Nonlinear Fractional Tumor-Immune Model
1Department of Mathematics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, 44519, Egypt
3Department of Physics and Engineering Mathematics, Faculty of Electronic engineering, Menoufia University, Menouf, 32952, Egypt
4Department of Mathematics, Faculty of Science, Al-Azher University, Nasr City, 11884, Egypt
*Corresponding Author: Amr M. S. Mahdy. Email: amattaya@tu.edu.sa
Received: 08 November 2020; Accepted: 05 January 2021
Abstract: In this article, the reduced differential transform method is introduced to solve the nonlinear fractional model of Tumor-Immune. The fractional derivatives are described in the Caputo sense. The solutions derived using this method are easy and very accurate. The model is given by its signal flow diagram. Moreover, a simulation of the system by the Simulink of MATLAB is given. The disease-free equilibrium and stability of the equilibrium point are calculated. Formulation of a fractional optimal control for the cancer model is calculated. In addition, to control the system, we propose a novel modification of its model. This modification is based on converting the model to a memristive one, which is a first time in the literature that such idea is used to control this type of diseases. Also, we study the system’s stability via the Lyapunov exponents and Poincare maps before and after control. Fractional order differential equations (FDEs) are commonly utilized to model systems that have memory, and exist in several physical phenomena, models in thermoelasticity field, and biological paradigms. FDEs have been utilized to model the realistic biphasic decline manner of elastic systems and infection of diseases with a slower rate of change. FDEs are more useful than integer-order in modeling sophisticated models that contain physical phenomena.
Keywords: RDTM; tumor-immune; optimal control; caputo derivative; signal flow; simulink; disease-free equilibrium; stability; memristive; lyapunov exponents; poincare map
Delayed ordinary differential equations have been utilized in modeling cancer diseases [1–10]. Fractional order differential equations (FDEs) are commonly utilized to model systems that have memory that exists in several physical phenomena, models in thermoelasticity field and biological paradigms. In [1], a system of FDEs was applied for modeling the interactions in the cancer-immune system. The model comprises double immune effectors: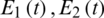 
(as an example for natural killer cells and cytotoxic T cells), interactive ?? against the cancer cells, 
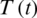, with a type III’s Holling function. A type III’s Holling function represents a case where the number of victims wasted per each predator at start increases slowly as the density of victim increases, but then levels decrease with further increase in victim density. That means the response of predators to the victim is decreased at low victim density, then levels decrease with further increase in victim density.
The form of the model is (see [11]):
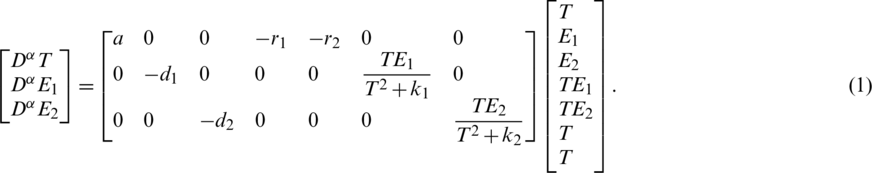
where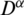 
is Caputo fractional derivative operator ( [12–15]) with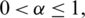 
, 
, 
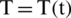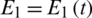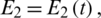and 
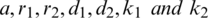are positive constants.
Using a signal flow graph for representing the dynamical systems is very useful (see for example [16,17]).
The signal flow graph is a graph tool that can be used to show the interrelation between the system states and enable us to use the graph theoretic tools to discover new features of the system.
The above system Eq. (1) can be represented by the signal flow graph 
as shown in Fig. 1. The signal flow diagram of the calculated system Eq. (1) has the following adjacency matrix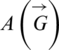 
. Where each state variable is modeled by a vertex and there is an edge about two states (a, b) if the state a affects directly the state b according to Eq. (1).
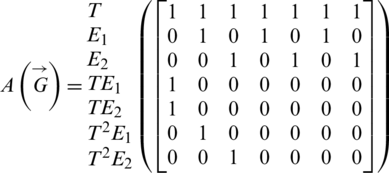
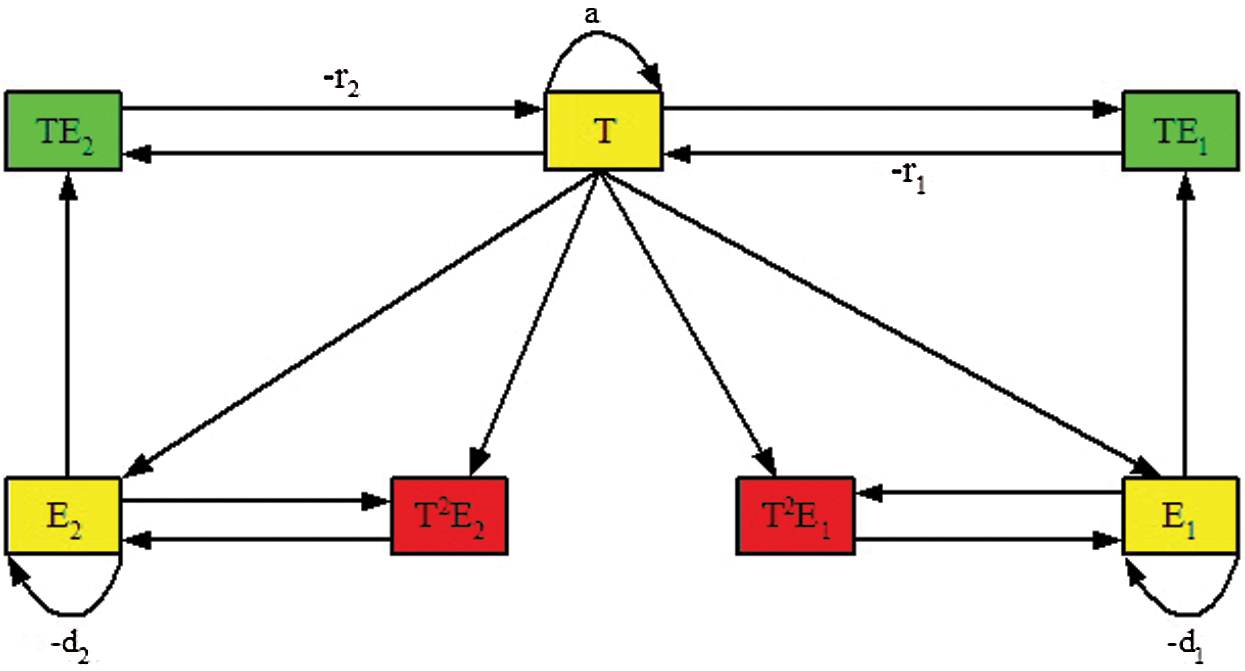
Figure 1: The signal flow graph of the studied system (Eq. (1))
For more details about signal flow graph and theoretical graph theory, see for example ([16,18–20]) and the references therein.
In this work, the reduced differential transform method is introduced for solving the nonlinear fractional model of Tumor-Immune. The fractional derivatives are described in the Caputo sense. The solutions derived using this method are easy and very accurate. The model is given by its signal flow diagram. Moreover, a simulation of the system using the Simulink of MATLAB is given. The disease-free equilibrium and stability of the equilibrium point are calculated. Formulation of a fractional optimal control for the cancer model is calculated. In addition, To control the system, we proposed a novel modification of this model utilizing the method of converting it to be a memristive system which is the first time in the literature to use such idea to control this type of diseases. Also, we study the system’s stability via the Lyapunov exponent and Poincare map before and after control. FDEs have been utilized to model the realistic biphasic decline manner of elastic systems and infection of diseases but at a slower rate of change. FDEs are more useful than integer-order in modeling sophisticated models that contain physical phenomena.
The paper is structured in eight sections. In Section 2, the basic definitions of fractional calculus are presented. In Section 3, the formulation of a fractional optimal control of the cancer model is studied. In Section 4, we describe the Reduced differential transform method (RDTM) with illustration examples. In Section 5, fixed points and the stability of the system are investigated. In Section 6, the Cancer model is simulated using Simulink
Matlab and campared with the RDTM. In Section 7, we propose a novel method to control the system based on the idea of the memristor. Also, the equilibrium point and stability of nonlinear fractional memristor-based cancer model are studied. In addition, we study the system’s stability via the Lyapunov exponent and Poincare map before and after control. Conclusions are given in Section 8.
2 Basic Definitions of Fractional Calculus
In this section, we present the basic definitions and properties of the fractional calculus theory, which are used in this paper.
Definition 1 Areal function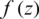 
, z > 0, is said to be in the space 
, 
, if there exists a real number 
such that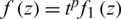 
where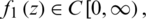 
and it is said to be in the space 
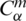if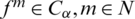 
.
Definition 2 The Riemann–Liouville integral operator of order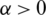 
with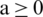 
is defined as ([21–29]):
Definition 3 The Caputo fractional derivative operator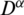 
of order 
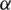is defined in the following form ([11–14,23–30]):
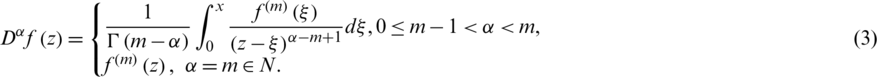
3 Formulation of Fractional Optimal Control of Cancer Model
Consider the state system given in Eq. (1), in R3, with the set of admissible control functions:
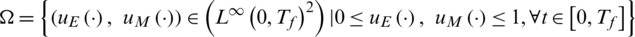
where Tfis the final time, 
are the control functions.
The objective function is defined as follows (quadratic is the control variable).
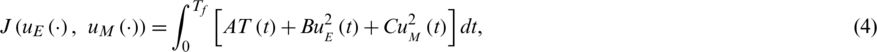
Wherever both immune effectors coexist, the non biological inner solution is measured by A, B and C.
Minimizing the following objective function is the main aim in FOCPs by finding the optimal controls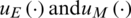 
:
subjected to the constraints
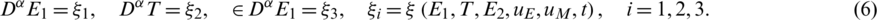
The following inital conditions are satisfied:
In order to give a definition of the FOCP, define a modified objective (cost) function as:
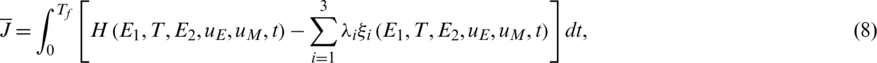
where we can define the Hamiltonian of the objective function (8) and the cancer immune system (1) as follows:
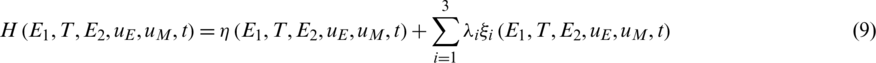
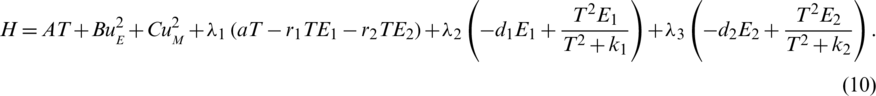
From (8) and (10), the necessary and sufficient conditions of FOPC can be derived as follows.
where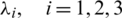 
are the Lagrange multipliers. Eqs. (12) and (13) produce the necessary conditions in terms of a Hamiltonian of the FOPC. We arrive at the following theorem.
Theorem 1.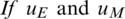 
are optimal controls with corresponding state 
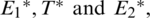then there are adjoint elements, 
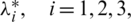satisfy the following conditions.
(i) Co-state equations (adjoint equations)
(ii) Transversal cases
(iii) Optimality conditions
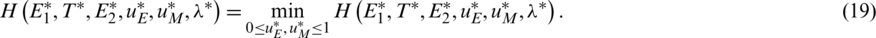
Moreover, the controlling functions 
are presented by
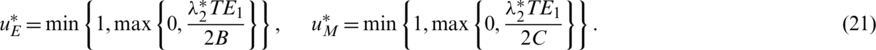
For more details about problem optimal control, see for example [31–34].
4 Applications of Reduced Differential Transform Method (RDTM)
To clarify the efficiency of our proposed method [34–41], we shall apply it to a special case of fractional-order biological systems that presented in [11]. The symbolic calculus software MatLab is used to calculate all of the results given here. Recently, there is some growth in the area of numerical study as well as their applications ([42–55]).
Example 4.1 Take into account the cancer fractional model (1) (c.f [11]):
Applying RDTM Eq. (22), we get:
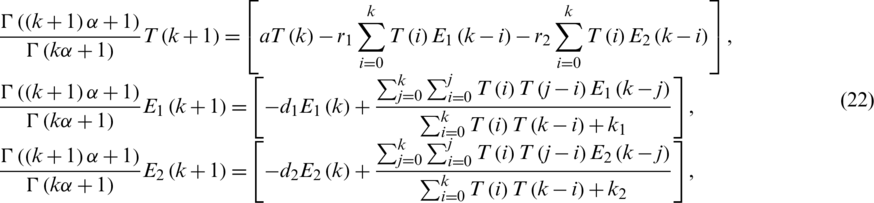
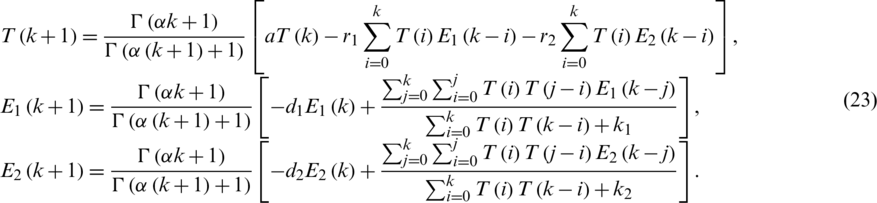
By substituting Eq. (1) in Eq. (23).
The series solution of the system (1.1) can be calculated via applying the differential inverse transform, where a = r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and different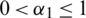 
and get it as:
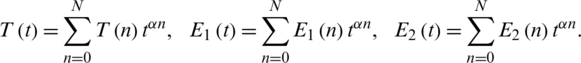
We get the solution as a series (for illustration see Figs. 2–4):
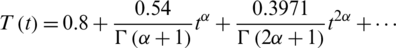
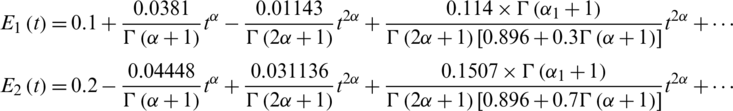
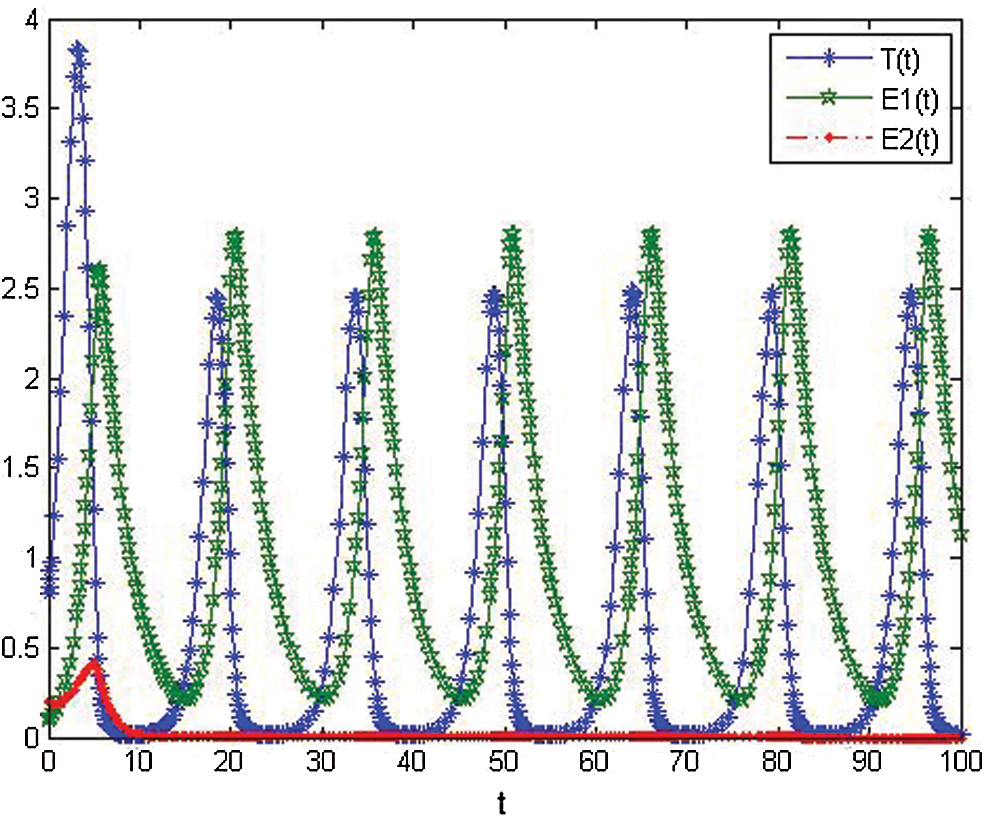
Figure 2: The numerical simulations T, E1 and E2 of model cancer at 
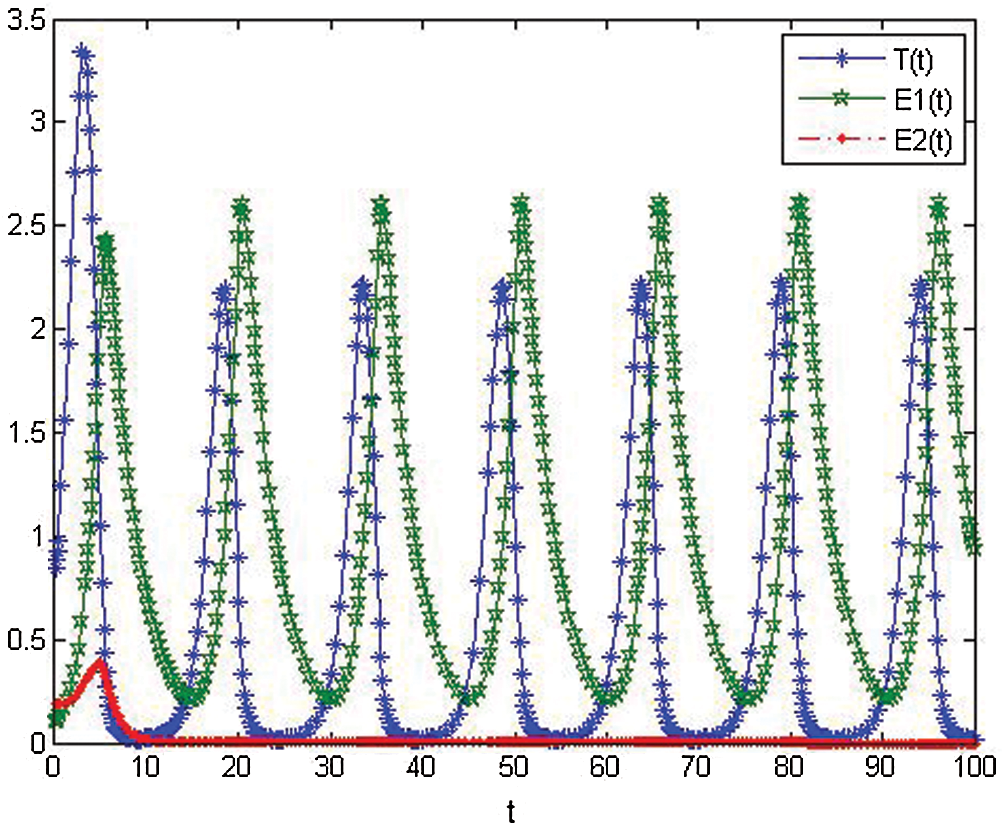
Figure 3: The numerical simulations of T, E1 and E2 model cancer at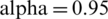 
Figure 4: The numerical simulations T, E1 and E2 of model cancer at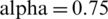 
From model (1) the numerical results are given in Figs. 2–4. Where in Figs. 2–4, we present the behavior of numerical simulations of T, E1 and E2 model cancer with different values of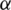 
.
5 Fixed Point and the Stability of The System
To compute the fixed points, equate all right hand sides of (1) to zero.
We calculate the Jacobian matrix as:
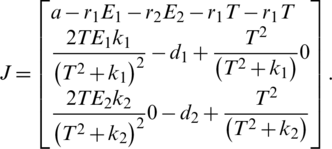
Stability of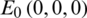 
:
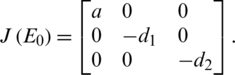
To calculate the Eigen-values, we write:
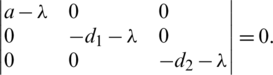
Then we have: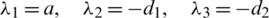 
.
Stability of all fixed points using Lyapunov exponents and poincare map satisfy the behavior of the uncontrolled system, see Figs. 5–8.
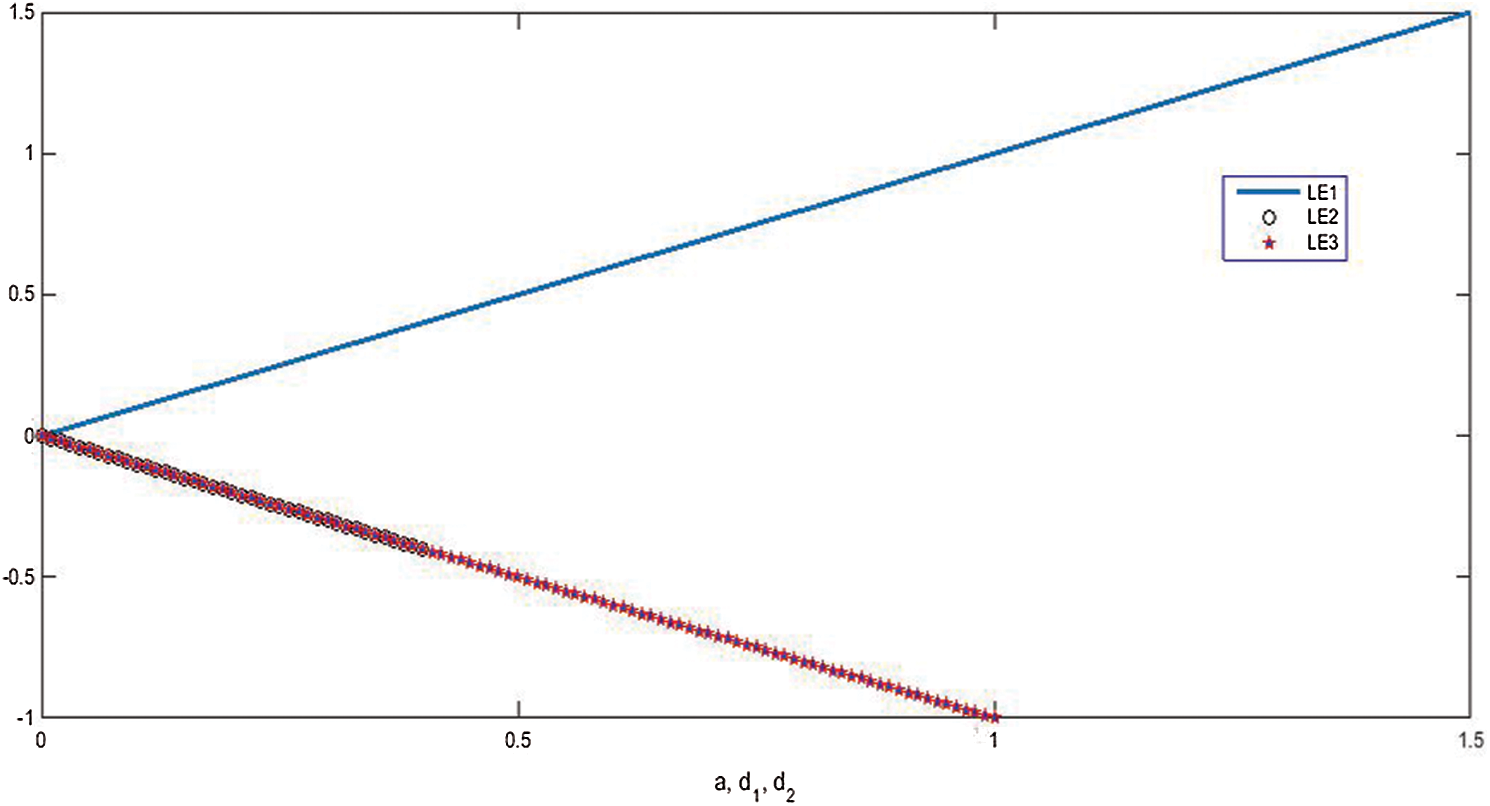
Figure 5: The dependency of Lyapunov exponents on the system parameters
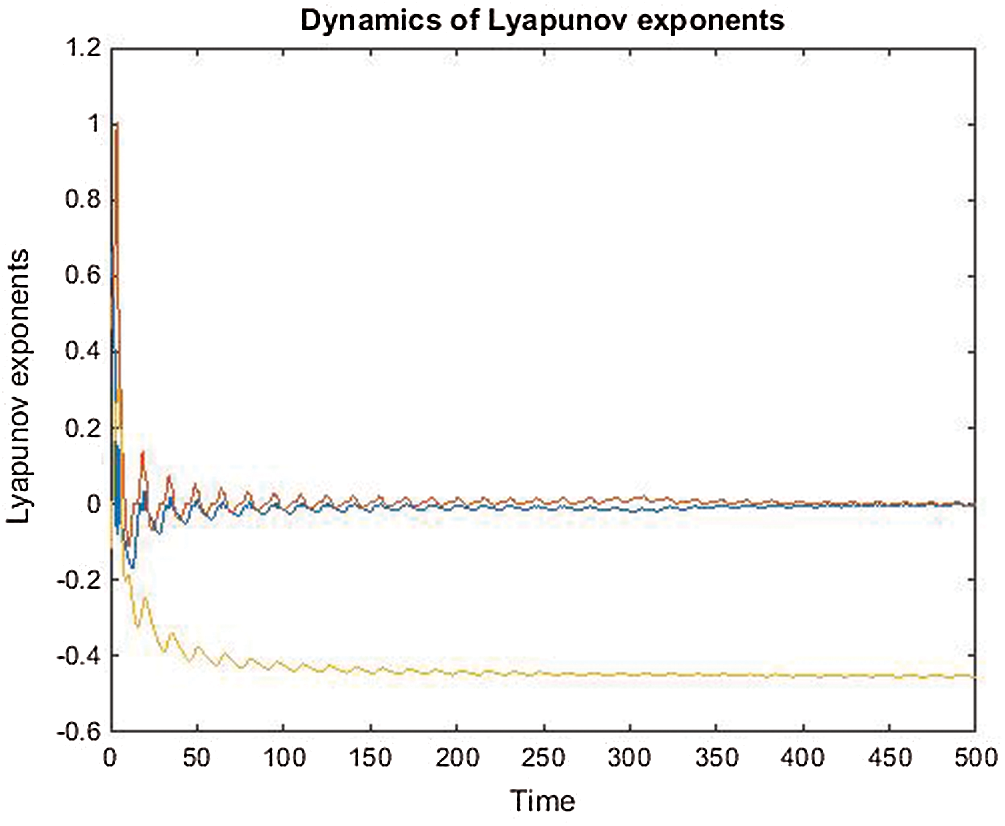
Figure 6: The behavior of Lyapunov exponenets vs. time of the uncontrolled system where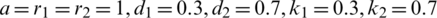 
and 
Figure 7: Poincere map of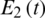 
vs. 
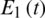of the uncontrolled system where 
and 
Figure 8: Poincere map of 
vs. 
of the uncontrolled system where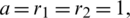 
d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and 
In this section, in Fig. 9, we ready a simulation of the system by Simulink of MATLAB. From which, as shown in Figs. 10–12, it is clear that the solutions of the system by the proposed method are the same as it from the Simulink. In addition, the diagram of the Simulink shows the dependency of the system components on each other.
Figure 9: System simulation by MATLAB
Simulink
Figure 10: T(t) of cancer model at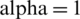 
Figure 11: E1(t) of cancer model at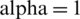 
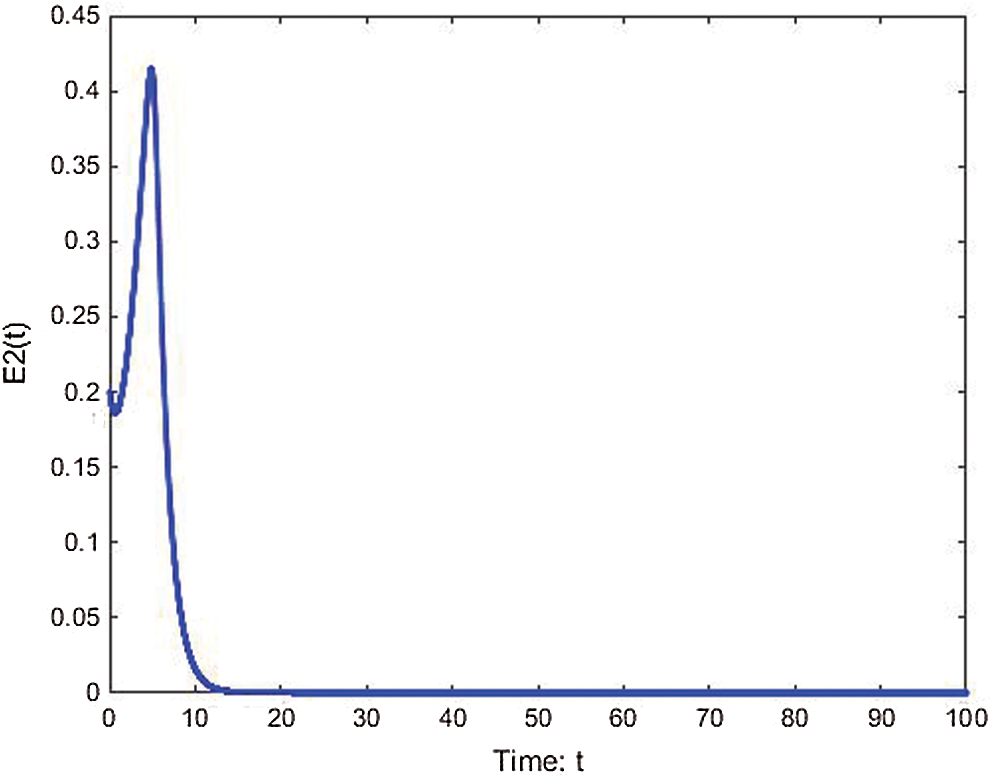
Figure 12: E2(t) of cancer model at 
The following Figs. 10–12, show the simulation responses that completely agree with the analytical solution. Figs. 13–15, represents the phase spaces.
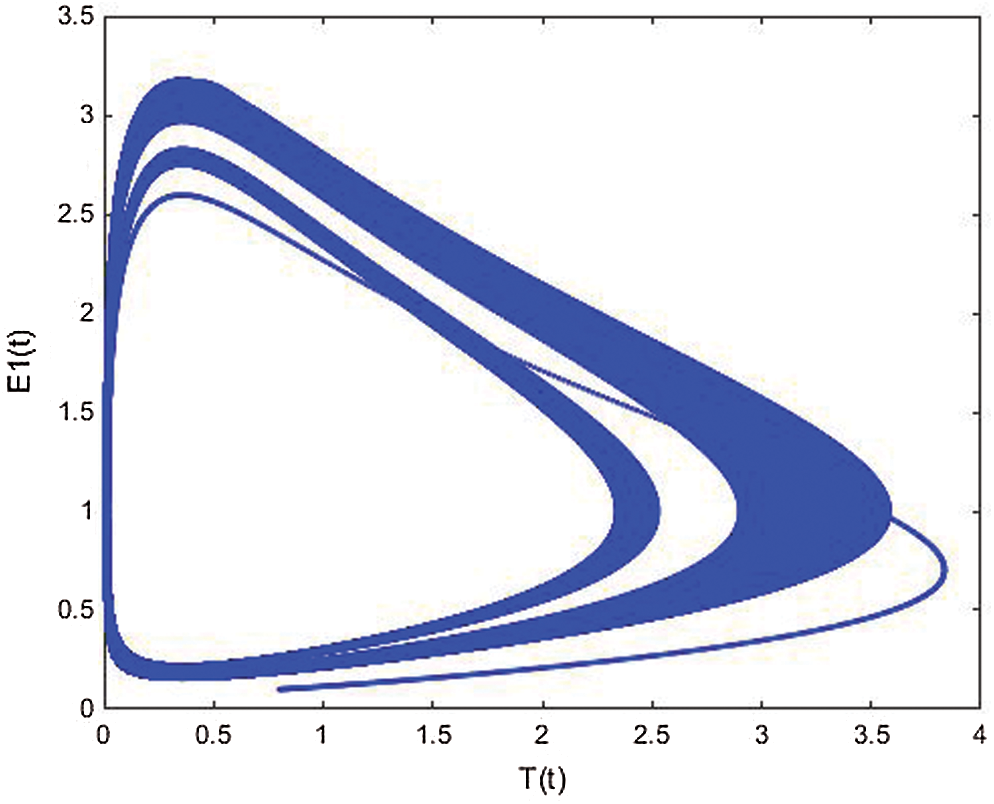
Figure 13: E1(t) vs. T(t) space from Simulink simulation of the cancer model
Figure 14: E2(t) vs. T(t) space from Simulink simulation of the cancer model
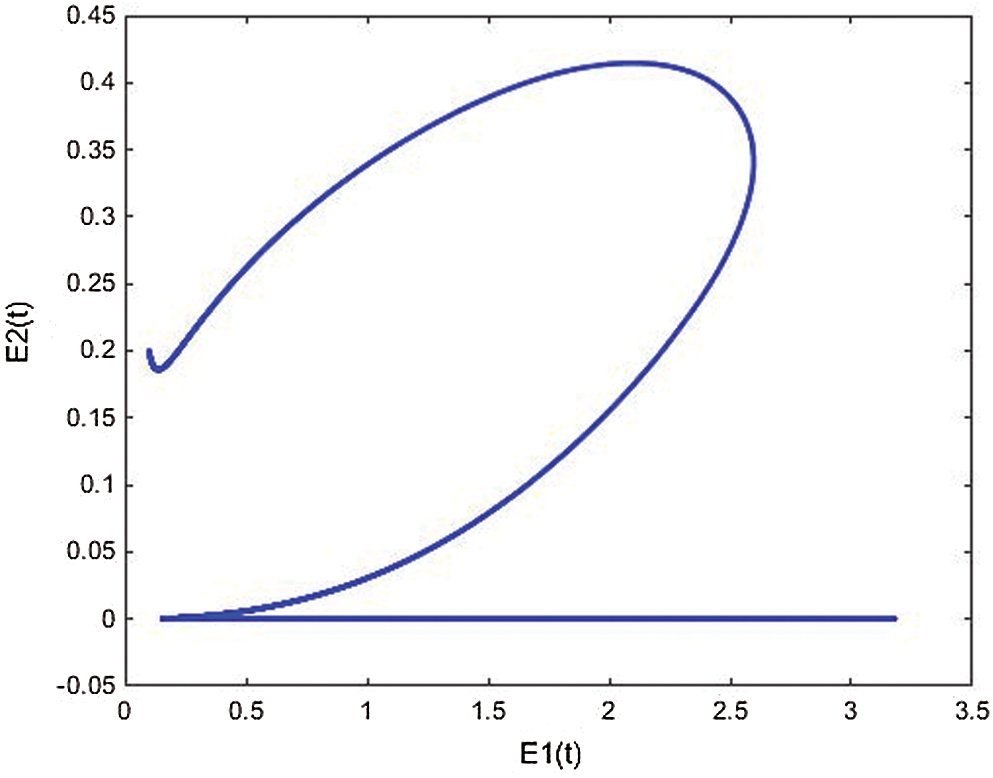
Figure 15: E2(t) vs. E1(t) space from Simulink simulation of the cancer model
7 The Memristor-Based Conrelled Cancer Model
The memristive system is the system that has a memristor. The memristor is a variable that store the history of a selected state variable. Converting systems to be memristive means using the history of the system to improve and control the dynamics of the system.
Considering the symmetry of the cancer model (1), we modified this model to become a memristive system via the method of adding a memristor effect to the first equation. In this work, we use the memristor that has a quadratic nonlinearity for flux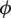 
and the electric charge q .
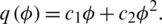
So, the memductance is given by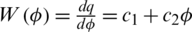 
where c1 and c2 are two memristor parameters with positive values (for more details about types of memristors and its applications see for example [35]). We suggest to add a memristor effect as the feedback term on the first equation of the original system T(t) and use the second equation as the internal state equation of memristor, then a 3-dimensional memristive controlled cancer system can be constructed:
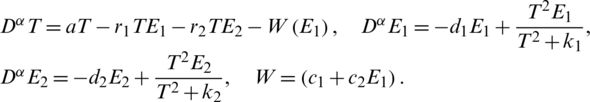
In the following, we study the fixed point and the stability of the proposed memristive controlled cancer system.
I Fixed Points of the Proposed Memristive Controlled Cancer System
To compute the fixed points solve the following system:
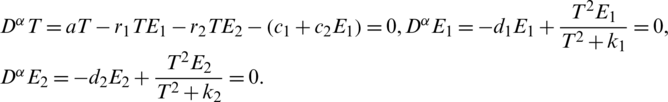
II Studying the Stability:
We calculate the Jacobian matrix as: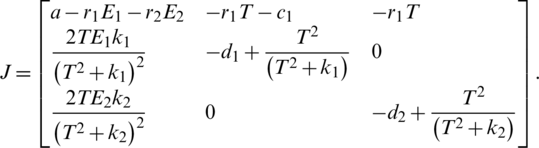 
Stability of E0 :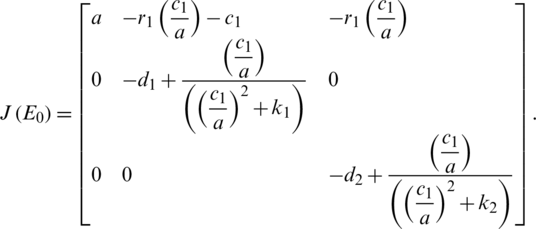 
That has the following Eigen-values:
The above system has solved numerically using Rung–Kuta method where a = r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7, c1 = 0.0005, c2 = 0.005 and the initial conditions are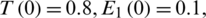 
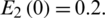The solution of the memristive cancer model is shown in Figs. 16–18. The proposed memristive cancer model is well controlled as shown in its time response see Figs. 19–21. The stability of the equilibrium points are shown by the behavior of Lyapunov exponents and Poincere maps see Figs. 22–27.
Figure 16: T(t) of the proposed memristive cancer model is well controlled
Figure 17: E1(t) of the proposed memristive cancer model is well controlled
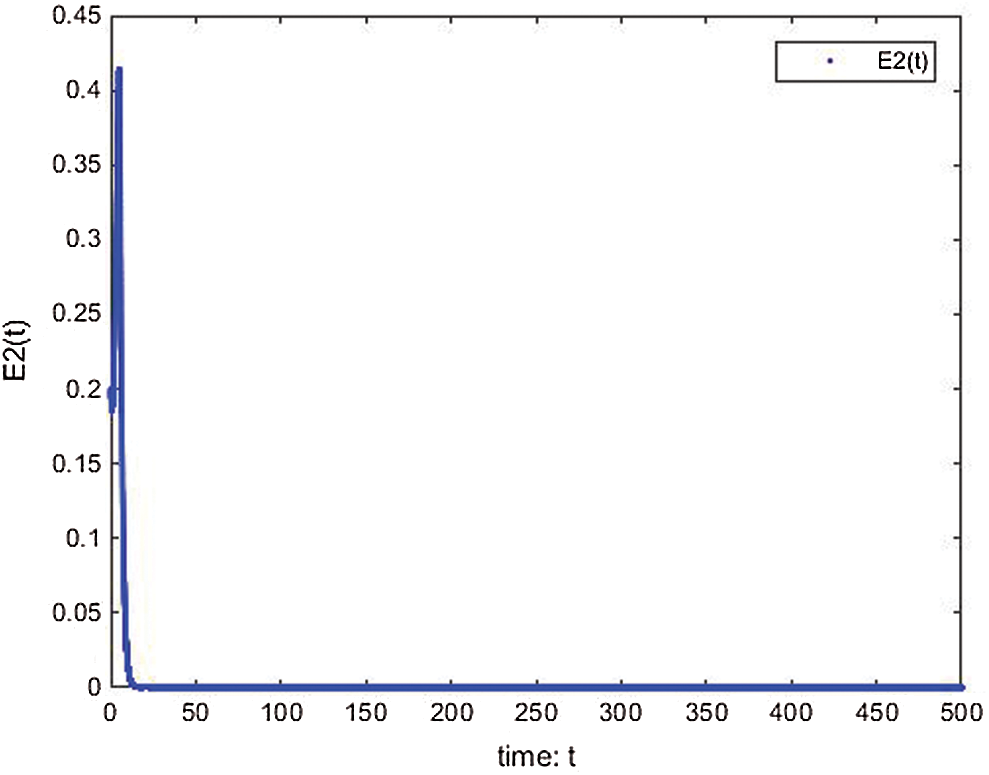
Figure 18: E2(t) of the proposed memristive cancer model is well controlled
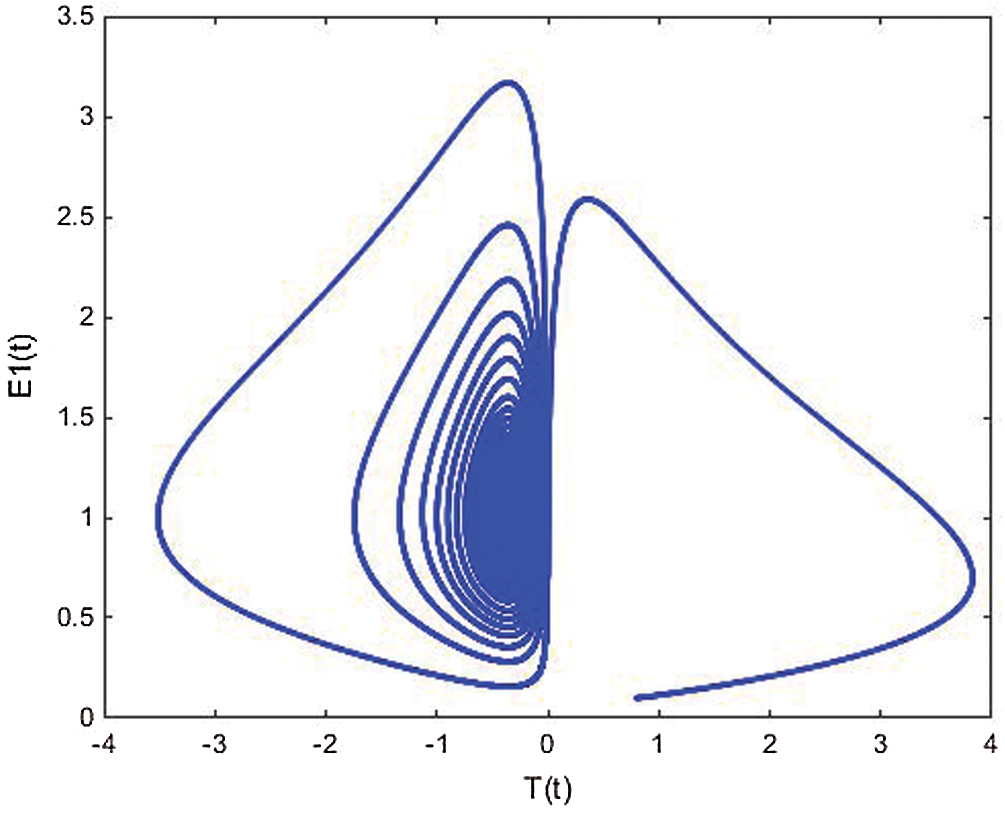
Figure 19: The phase plane E1(t) vs. T(t) of the memristive controlled cancer model
The phase planes of the memristive canser model are shown in Figs. 19–21.
Figure 20: The phase plane E2(t) vs. T(t) of the memristive controlled cancer model
Figure 21: The phase plane E2(t) vs. E1(t) of the memristive controlled cancer model
Figure 22: The behavior of Lyapunov exponenets vs. time of the controlled system where 
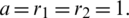
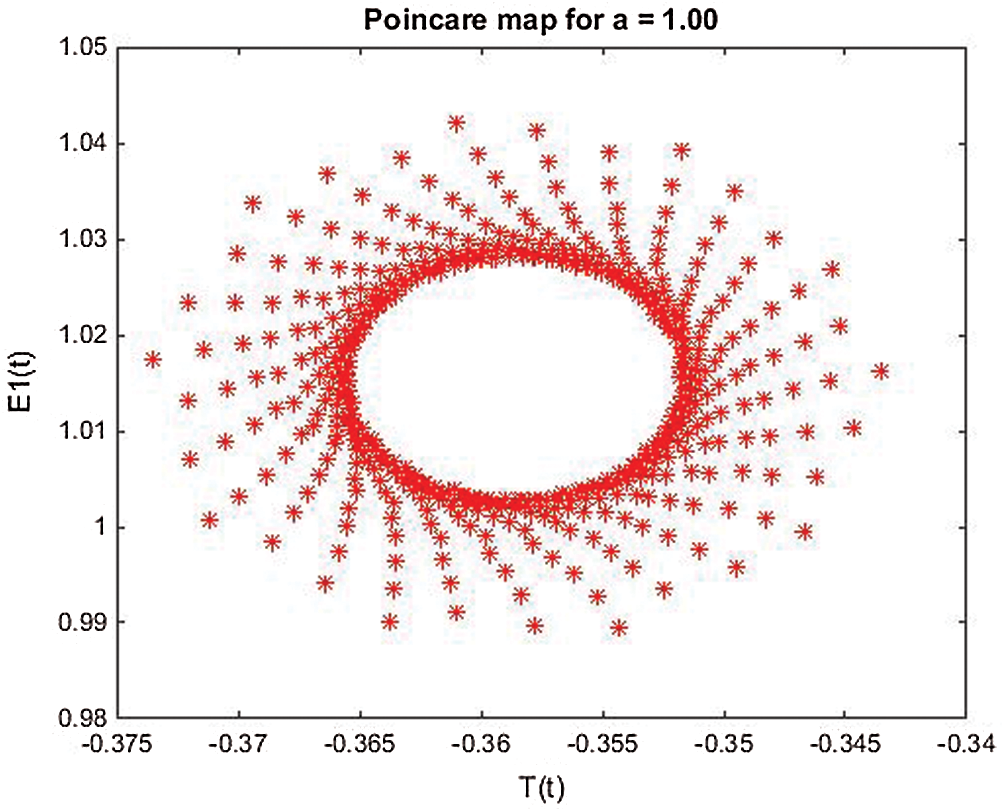
Figure 23: Poincere map of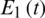 
vs.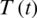 
of the controlled system where 
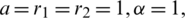d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7
Figure 24: Poincere map of 
vs. 
of the controlled system where a = 3 , r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and 
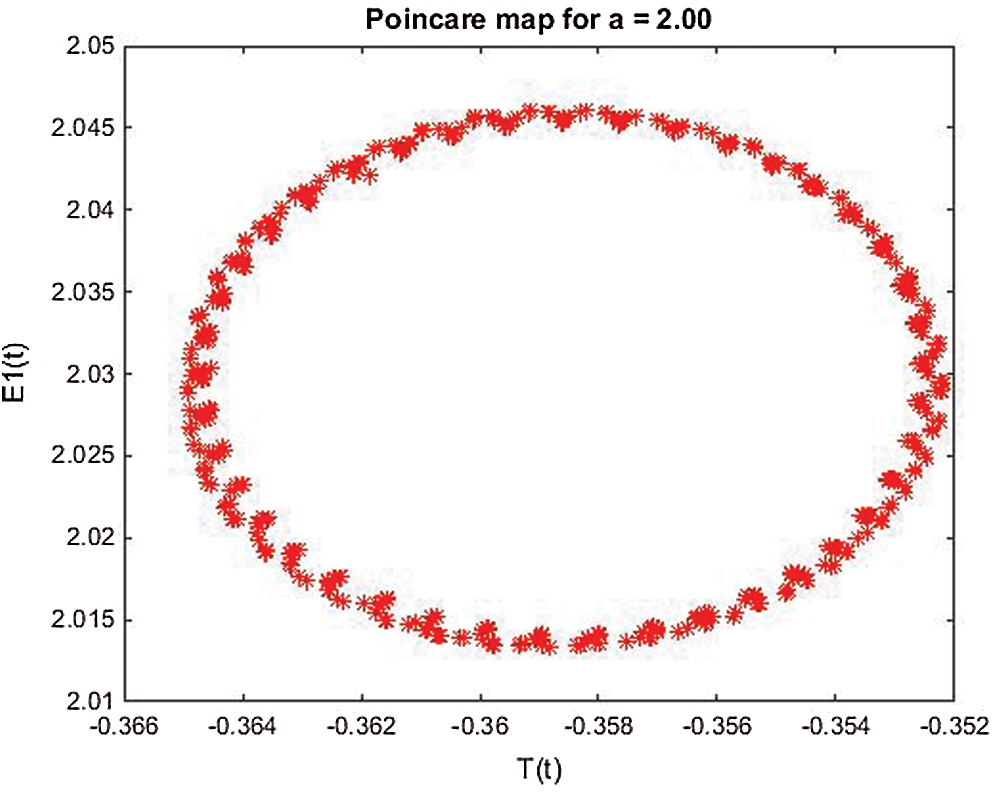
Figure 25: Poincere map of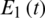 
vs.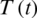 
of the controlled system where a = 2 , r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and 
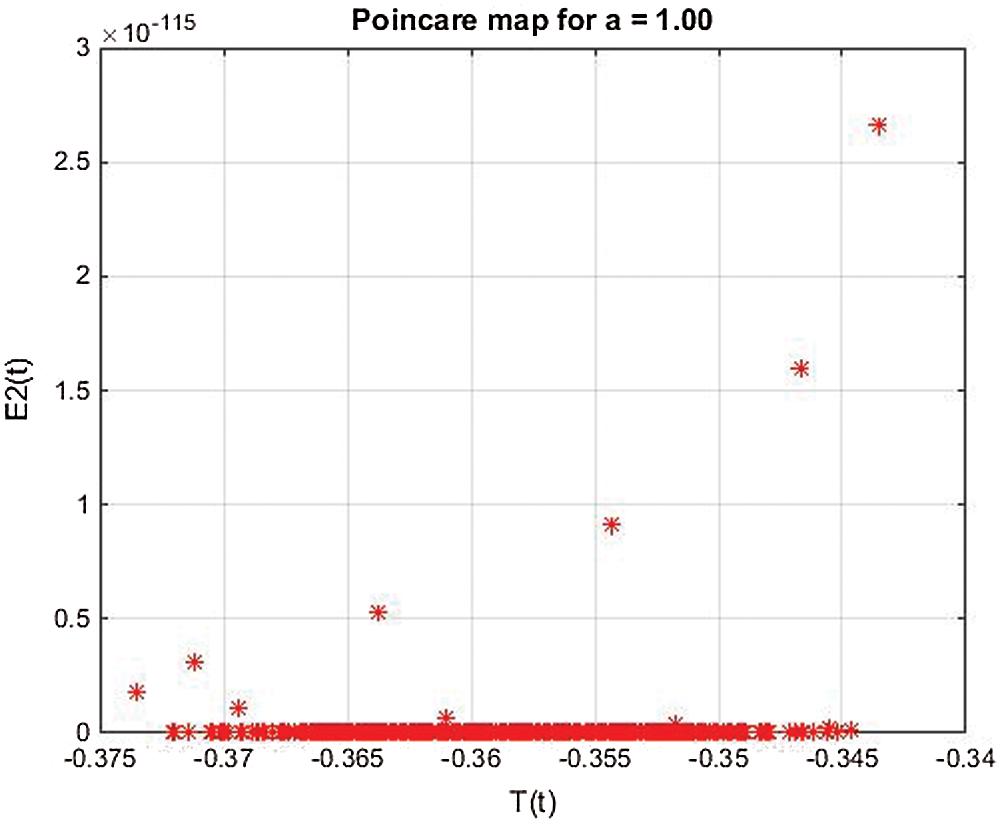
Figure 26: Poincere map of 
vs.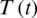 
of the controlled system where a = 1 , r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and 
Figure 27: Poincere map of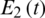 
vs.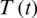 
of the controlled system where a = 3 , r1 = r2 = 1, d1 = 0.3, d2 = 0.7, k1 = 0.3, k2 = 0.7 and 
In this paper, a nonlinear cancer fractional model of the Tumor-Immune problem has been calculated which plays a necessary role in applied sciences. The fractional derivatives have been described in the Caputo sense. Also, RDTM has been applied to get the approximate solutions of this model. A signal flow diagram of the calculated system has been proposed and disscussed. The free disease equilibrium (FDE) and stability of equilibrium point have been studied. A simulation of the system using Simulink of MATLAB has been presesnted. The phase space has been displayed. To control the nonlinear fractional model of the Tumor-Immune, we have proposed a novel modification of this model via converting it to be a memristive system. It is the first time in the literature to convert such models to be memristive. Also, we have studied the system’s stability via Lyapunov exponents and Poincare maps before and after control. The numerical simulations are very consistent with the analytical ones.
Acknowledgement: The authors are thankful of the Taif University. Taif University researchers supporting project number (TURSP-2020/160), Taif University, Taif, Saudi Arabia.
Funding Statement: This paper was funded by “Taif University Researchers Supporting Project number (TURSP-2020/160), Taif University, Taif, Saudi Arabia”.
Conflicts of interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. Ahmed, A. Hashish and F. A. Rihan. (2012). “On fractional order cancer model,” Journal of Fractional Calculus and Applied Analysis, vol. 3, no. 2, pp. 1–6. [Google Scholar]
2. A. A. M. Arafa, S. Z. Rida and M. Khalil. (2012). “Fractional modeling dynamics of HIV and CD4+ T-cells during primary infection,” Nonlinear Biomedical Physics, vol. 6, no. 1, pp. 73. [Google Scholar]
3. K. S. Cole. (1993). “Electric conductance of biological systems,” in Cold Spring Harbor Symposia on Quantitative Biology, NY, USA, pp. 107–116. [Google Scholar]
4. A. M. A. El-Sayed, A. E. M. El-Mesiry and H. A. A. El-Saka. (2007). “On the fractional-order logistic equation,” Applied Mathematics Letters, vol. 20, no. 7, pp. 817–823. [Google Scholar]
5. H. Xu. (2009). “Analytical approximations for a population growth model with fractional order,” Communications in Nonlinear Science and Numerical Simulation, vol. 14, no. 5, pp. 1978–1983. [Google Scholar]
6. N. Bellomo, A. Bellouquid, J. Nieto and J. Soler. (2010). “Multiscale biological tissue models and flux-limited chemotaxis for multicellular growing systems,” Mathematical Models & Methods in Applied Sciences, vol. 20, no. 7, pp. 1179–1207. [Google Scholar]
7. A. Gokdogan, A. Yildirim and M. Merdan. (2011). “Solving a fractional ordermodel of HIV infection of CD+ Tcells,” Mathematical and Computer Modelling, vol. 54, no. 9–10, pp. 2132–2138. [Google Scholar]
8. D. Kirschner and J. C. Panetta. (1998). “Modeling immunotherapy of the tumor-immune interaction,” Journal of Mathematical Biology, vol. 37, no. 3, pp. 235–252. [Google Scholar]
9. F. A. Rihan, M. Safan, M. A. Abdeen and D. Abdel Rahman. (2012). “Qualitative and computational analysis of a mathematical model for tumor-immune interactions,” Journal of Applied Mathematics, vol. 2012, no. 4, pp. 1–19. [Google Scholar]
10. R. Yafia. (2007). “Hopf bifurcation in differential equations with delay for tumor-immune system competition model,” SIAM Journal on Applied Mathematics, vol. 67, no. 6, pp. 1693–1703. [Google Scholar]
11. F. A. Rihan. (2013). “Numerical modeling of fractional-order biological systems,” Abstract and Applied Analysis, vol. 2013, no. 2, pp. 1–13. [Google Scholar]
12. A. M. A. El-Sayed and S. M. Salman. (2013). “On a discretization process of fractional order Riccati’s differential equation,” Journal of Fractional Calculus and Applications, vol. 4, pp. 251–259. [Google Scholar]
13. R. P. Agarwal, A. M. A. El-Sayed and S. M. Salman. (2013). “Fractional-order Chua’s system discretization, bifurcation and chaos,” Advances in Difference Equations, vol. 2013, pp. 1–13. [Google Scholar]
14. A. A. Elsadany and A. E. Matouk. (2015). “Dynamical behaviors of fractional-order Lotka-Voltera predator-prey model and its discretization,” Applied Mathematics and Computation, vol. 49, pp. 269–283. [Google Scholar]
15. M. El-Shahed, J. J. Nieto, A. M. Ahmed and I. M. E. Abdelstar. (2013). “Fractional-order model for biocontrol of the lesser date moth in palm trees and its discretization,” Advances in Difference Equations, vol. 2013, pp. 1–16. [Google Scholar]
16. H. Schmid and A. Huber. (2018). “Analysis of switched-capacitor circuits using driving-point signal-flowgraphs,” Analog Integrated Circuits and Signal Processing, vol. 96, pp. 495–507. [Google Scholar]
17. E. E. Mahmoud, M. Higazy and T. M. Al-Harthi. (2019). “A new nine-dimensional chaotic Lorenz system with quaternion variables: Complicated dynamics electronic circuit design, anti-anticipating synchronization, and Chaotic masking communication application,” Mathematics, vol. 7, no. 877, pp. 1–26. [Google Scholar]
18. A. M. S. Mahdy, N. H. Sweilam and M. Higazy. (2020). “Approximate solutions for solving nonlinear fractional order smoking model,” Alexandria Engineering Journal, vol. 59, no. 2, pp. 739–752. [Google Scholar]
19. A. M. S. Mahdy and M. Higazy. (2019). “Numerical different methods for solving the nonlinear biochemical reaction model,” International Journal of Applied and Computational Mathematics, vol. 5, no. 6, pp. 1–17. [Google Scholar]
20. M. Higazy. (2020). “Orthogonal double covers of circulant graphs by corona product of certain infinite graph classes,” Indian Journal of Pure and Applied Mathematics, vol. 51, pp. 1573–1585. [Google Scholar]
21. J. Sabatier, O. P. Agrawal and M. J. A. Tenreiro. (2007). “Advances in fractional calculus, theoretical developments and applications,” in Physics and Engineering, Dordrecht, The Netherlands: Springer. [Google Scholar]
22. K. B. Oldham and J. Spanier. (1974). The Fractional Calculus. New York, NY, USA: Academic Press. [Google Scholar]
23. Y. A. Amer, A. M. S. Mahdy and E. S. M. Youssef. (2018). “Solving fractional integro-differential equations by using sumudu transform method and Hermite spectral collocation method,” Computers Materials & Continua, vol. 54, no. 2, pp. 161–180. [Google Scholar]
24. M. M. Khader, N. H. Sweilam and A. M. S. Mahdy. (2015). “Two computational algorithms for the numerical solution for system of fractional,” Arab Journal of Mathematical Sciences, vol. 21, no. 1, pp. 39–52. [Google Scholar]
25. A. M. S. Mahdy. (2018). “Numerical studies for solving fractional integro-differential equations,” Journal of Ocean Engineering and Science, vol. 3, no. 2, pp. 127–132. [Google Scholar]
26. K. A. Gepreel, A. M. S. Mahdy, M. S. Mohamed and A. Al-Amiri. (2019). “Reduced differential transform method for solving nonlinear biomathematics models,” Computers, Materials & Continua, vol. 61, no. 3, pp. 979–994. [Google Scholar]
27. M. M. Khader, N. H. Sweilam, A. M. S. Mahdy and N. K. Abdel Moniem. (2014). “Numerical simulation for the fractional SIRC model and influenza a,” Applied Mathematics & Information Sciences, vol. 8, no. 3, pp. 1–8. [Google Scholar]
28. Y. A. Amer, A. M. S. Mahdy and E. S. M. Youssef. (2017). “Solving systems of fractional differential equations using Sumudu transform method,” Asian Research J. of Mathematics, vol. 7, no. 2, pp. 1–15. [Google Scholar]
29. A. M. S. Mahdy, A. S. Mohamed and A. A. H. Mtawa. (2015). “Implementation of the homotopy perturbation sumudu transform method for solving Klein-gordon equation,” Applied Mathematics, vol. 6, no. 3, pp. 617–628. [Google Scholar]
30. K. A. Gepreel, M. S. Mohamed, H. Alotaibi1 and A. M. S. Mahdy. (2021). “Dynamical behaviors of nonlinear coronavirus (COVID-19) model with numerical studies,” Computers Materials & Continua, vol. 67, no. 1, pp. 675–686. [Google Scholar]
31. N. H. Sweilam and S. M. Al-Mekhlafi. (2018). “Optimal control for a nonlinear mathematical model of tumor under immune suppression a numerical approach,” Optimal Control Applications and Methods, vol. 39, no. 5, pp. 1581–1596. [Google Scholar]
32. N. H. Sweilam, S. M. Al-Mekhlafi and D. Baleanu. (2019). “Optimal control for a fractional tuberculosis infection model including the impact of diabetes and resistant strains,” Journal of Advanced Research, vol. 17, no. 3–4, pp. 125–137. [Google Scholar]
33. N. H. Sweilam, O. M. Saad and D. G. Mohamed. (2019). “Fractional optimal control in transmission dynamics of west nile model with state and control time delay a numerical approach,” Advances in Difference Equations, vol. 2019, no. 210, pp. 1–25. [Google Scholar]
34. N. H. Sweilam, O. M. Saad and D. G. Mohamed. (2019). “Numerical treatments of the tranmission dynamics of west nile virus and it’s optimal control,” Electonic Journal of Mathematical Analysis and Applications, vol. 7, no. 2, pp. 9–38. [Google Scholar]
35. L. Xiong, L. Yanjun, Y. Zhang and X. Zhang. (2019). “A novel memductor-based chaotic system and its applications in circuit design and experimental validation,” Complexity, vol. 2019, no. 18, article 180502, pp. 1–17. [Google Scholar]
36. M. Garg, P. Manohar and S. L. Kalla. (2011). “Generalized differential transform method to space-time fractional telegraph equation,” International Journal of Differential Equations, vol. 2011, no. 1, pp. 1–9.
37. Y. Keskin and G. Oturanc. (2010). “Reduced differential transform method for solving linear and nonlinear wave equations,” Iranian Journal of Science and Technology, Transaction A, vol. 34, no. A2, pp. 113–122.
38. Y. Keskin. (2010). “Ph.D. Thesis (in turkishSelcuk University.
39. Y. Keskin and G. Oturanc. (2010). “Reduced differential transform method for fractional partial differential equations,” Nonlinear Science Letters A, vol. 1, no. 2, pp. 207–217.
40. Y. Keskin and G. Oturanc. (2009). “Reduced differential transform method for partial differential equations,” International Journal of Nonlinear Sciences and Numerical Simulation, vol. 10, no. 6, pp. 741–749.
41. M. I. A. Othman and A. M. S. Mahdy. (2010). “Differential transformation method and variation iteration method for Cauchy reaction-diffusion problems,” Journal of Mathematics and Computer Science, vol. 1, no. 2, pp. 61–75. [Google Scholar]
42. M. Higazy and M. AhmedAlyami. (2020). “New caputo-fabrizio fractional order SEIASQEQHR model for covid-19 epidemic transmission with genetic algorithm based control strategy,” Alexandria Engineering Journal, vol. 59, no. 6, pp. 4719–4736. [Google Scholar]
43. M. Higazy. (2020). “Novel fractional order SIDARTHE mathematical model of COVID -19 pandemic,” Chaos Solitons and Fractals, vol. 138, no. 110007, pp. 1–19. [Google Scholar]
44. E. E. Mahmoud, M. Higazy and M. Turkiah Al-Harthi. (2020). “Signal flow graph and control of realizable autonomous nonlinear Chen model with quaternion variables,” Alexandria Engineering Journal, vol. 59, no. 3, pp. 1287–1305. [Google Scholar]
45. S. Kumar, A. Ahmadian, R. Kumar, D. Kumar, J. Singh et al. (2020). , “An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets,” Mathematics, vol. 9, no. 558, pp. 558. [Google Scholar]
46. A. M. S. Mahdy, Kh. Lotfy, M. H. Ahmed, A. El-Bary and E. A. Ismail. (2020). “Electromagnetic hall current effect and fractional heat order for micro temperature photo-excited semiconductor medium with laser pulses,” Results in Physics, vol. 17, pp. 1–9. [Google Scholar]
47. A. M. S. Mahdy, Kh. Lotfy, E. A. Ismail, A. El-Baryd, M. Ahmed et al. (2020). , “Analytical solutions of time-fractional heat order for a magneto-photothermal semiconductor medium with Thomson effects and initial stress,” Results in Physics, vol. 18, pp. 1–11. [Google Scholar]
48. Kh. Lotfy. (2019). “A novel model for photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field,” Scientific Reports, vol. 9, no. 1, pp. 3319. [Google Scholar]
49. M. I. A. Othman and Kh. Lotfy. (2015). “The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation,” Journal of Computational and Theoretical Nanoscience, vol. 12, no. 9, pp. 2587–2600. [Google Scholar]
50. A. M. S. Mahdy, M. S. Mohamed, K. A. Gepreel, A. AL-Amiri and M. Higazy. (2020). “Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model,” Chaos, Solitons & Fractals, vol. 141, pp. 1–13. [Google Scholar]
51. A. M. S. Mahdy. (2020). “Numerical solutions for solving model time-fractional Fokker–Planck equation,” Numerical Methods for Partial Differential Equations, pp. 1–16. [Google Scholar]
52. K. A. Gepreel, M. Higazy and A. M. S. Mahdy. (2020). “Optimal control, signal flow graph, and system electronic circuit realization for nonlinear Anopheles mosquito model,” International Journal of Modern Physics C, vol. 31, no. 9, pp. 1–18. [Google Scholar]
53. A. M. S. Mahdy, H. Higazy, K. A. Gepreel and A. A. A. El-dahdouh. (2020). “Optimal control and bifurcation diagram for a model nonlinear fractional SIRC,” Alexandria Engineering Journal, vol. 59, no. 5, pp. 1–21. [Google Scholar]
54. M. S. Mohamed and K. A. Gepreel. (2017). “Reduced differential transform method for nonlinear integral member of Kadomtsev-Petviashvili hierarchy differential equations,” Journal of the Egyptian Mathematical Society, vol. 25, no. 1, pp. 1–7. [Google Scholar]
55. I. H. Abdel-Halim Hassan, M. I. A. Othman and A. M. S. Mahdy. (2009). “Variational iteration method for solving: Twelve order boundary value problems,” International Journal of Mathematical Analysis, vol. 3, no. 13–16, pp. 719–730. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |