DOI:10.32604/cmc.2021.015409
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015409 | |
| Article |
A Heuristics-Based Cost Model for Scientific Workflow Scheduling in Cloud
1Department of Transport and Planning, Faculty of Civil Engineering and Geosciences (CiTG), Delft University of Technology, Delft, Netherlands
2Faculty of Computer Science and Information Technology, University of Malaya, Kuala Lumpur, Malaysia
3Department of Computer Science, COMSATS University Islamabad (CUI), Islamabad, Pakistan
4Faculty of Computing and Digital Technology, HELP University, Kuala Lumpur, Malaysia
5Al-Nahrain Nanorenewable Energy Research Centre, Al-Nahrain University, Baghdad, Iraq
6Department Multi-Actor Systems, Faculty of Technology, Policy and Management (TPM), Delft University of Technology, Delft, Netherlands
*Corresponding Author: Ehab Nabiel Al-Khanak. Email: E.N.M.Al-Khannaq@tudelft.nl
Received: 19 November 2020; Accepted: 10 January 2021
Abstract: Scientific Workflow Applications (SWFAs) can deliver collaborative tools useful to researchers in executing large and complex scientific processes. Particularly, Scientific Workflow Scheduling (SWFS) accelerates the computational procedures between the available computational resources and the dependent workflow jobs based on the researchers’ requirements. However, cost optimization is one of the SWFS challenges in handling massive and complicated tasks and requires determining an approximate (near-optimal) solution within polynomial computational time. Motivated by this, current work proposes a novel SWFS cost optimization model effective in solving this challenge. The proposed model contains three main stages: (i) scientific workflow application, (ii) targeted computational environment, and (iii) cost optimization criteria. The model has been used to optimize completion time (makespan) and overall computational cost of SWFS in cloud computing for all considered scenarios in this research context. This will ultimately reduce the cost for service consumers. At the same time, reducing the cost has a positive impact on the profitability of service providers towards utilizing all computational resources to achieve a competitive advantage over other cloud service providers. To evaluate the effectiveness of this proposed model, an empirical comparison was conducted by employing three core types of heuristic approaches, including Single-based (i.e., Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Invasive Weed Optimization (IWO)), Hybrid-based (i.e., Hybrid-based Heuristics Algorithms (HIWO)), and Hyper-based (i.e., Dynamic Hyper-Heuristic Algorithm (DHHA)). Additionally, a simulation-based implementation was used for SIPHT SWFA by considering three different sizes of datasets. The proposed model provides an efficient platform to optimally schedule workflow tasks by handling data-intensiveness and computational-intensiveness of SWFAs. The results reveal that the proposed cost optimization model attained an optimal Job completion time (makespan) and total computational cost for small and large sizes of the considered dataset. In contrast, hybrid and hyper-based approaches consistently achieved better results for the medium-sized dataset.
Keywords: Scientific workflow scheduling; empirical comparison; cost optimization model; heuristic approach; cloud computing
Effective management of Scientific Workflow Scheduling (SWFS) processes in a cloud environment remains a challenging task when dealing with large and complex Scientific Workflow Applications (SWFAs). The SWFA is the first stage of the Scientific Workflow Scheduling (SWFS) process and requires users (i.e., scientists) to specify the nature of their data. In other words, the SWFA receives user preferences regarding the task execution order that is carried out in the computational environment stage. Users’ preferences include the precedence constraints of tasks, job completion time, and Total Computational Cost (TCC). A number of inputs are also required from users to successfully perform SWFS. These main inputs are inter-dependent tasks (e.g., programs) associated with their input data (e.g., images), along with the scripts, catalogs, and Application Program Interface (API) written using various programming languages to represent the dependencies of the submitted workflow tasks. The expected outcome of SWFS (from the users’ view) is the statistical and analytical data obtained from executing the workflow tasks. Thus, SWFAs present several advantages to users, such as simplifying the process for scientists to reuse similar workflows. Ultimately, SWFAs provide scientists with a supportive (i.e., easy-to-use) environment in which to track and virtually share obtained optimization results. The second major stage of the SWFS process is the Workflow Management System (WfMS) stage. Generally, IT staff manually execute the workflow tasks, which requires prior knowledge about two core elements: (i) available resources and (ii) estimated starting time of each workflow task [1–3]. However, manual task execution introduces many challenges, including longer processing time, staff unavailability, impact on quality due to limitations in staff skills, and high probability of failure.
To overcome the above-mentioned challenges, this paper aims to propose a cost optimization model for SWFS that mainly focuses on managing the execution processes of the given dependent workflow tasks (also referred to as precedence constraints) of SWFAs. The model then schedules the submitted tasks onto the targeted shared computational resources, that is, Virtual Machines (VMs). At the same time, this model addresses optimizing the job completion time and TCC. The model contains three main components: (i) scientific workflow application (type and size of SWFA), (ii) targeted computational environment (number of VMs), and (iii) cost optimization criteria. The model is beneficial in mapping and scheduling processes of workflow tasks by considering the scheduling stages along with completion time and total computational cost parameters. Generally speaking, to propose a cost-optimal solution for a given SWFS problem, the completion time (makespan) and total computational cost of workflow tasks need to be simultaneously minimized as much as possible.
Current reports on cost optimization tasks of SWFS used a number of approaches, including ones that are heuristic and meta-heuristic based. Yet, these contemporary SWFS approaches lack in providing an empirical evaluation primarily based on the variants of heuristic approaches. Thus, to comprehensively develop and evaluate the performance of any cost optimization approach of SWFS in a cloud computing environment, three types of heuristic approaches, Single-based, Hybrid-based, and Hyper-based, have been considered in this research context. The evaluation for the proposed approach is conducted through a WorkflowSim simulator. The simulation-based environment easily determines different scenarios (e.g., size of a given SWFA and number of available VMs) to allow for a full investigation of the performance of the proposed model.
The major contributions of this research work are:
• A proposed novel cost optimization model that contains three main stages: (i) scientific workflow application, (ii) targeted computational environment, and (iii) cost optimization criteria and that classifies the cost parameters into the categories of pre-scheduling, during scheduling, and post-scheduling.
• An empirical comparison based on the different types of heuristic approaches, Single-based, Hybrid-based, and Hyper-based, that considers a number of VMs and various sizes of SWFA.
• An extensive review and analysis of the existing approaches based on several perspectives, including the types of existing experimental cloud environments, number of computational resources, types of computational resources, types of SWFAs, and the average size of the considered SWFA datasets.
This paper is structured as follows: Section 2 provides related works. Section 3 presents the proposed cost optimization model of SWFS as well as it describes the conducted empirical comparison based on the considered heuristic approaches. After that Section 4 explicitly discusses the results and evaluation using a simulation-based experimentation environment. Finally, the conclusion and future work is outlined in Section 5.
In order to assess the quality of the proposed model (i.e., cost optimization of SWFS in a cloud environment), relevant studies were reviewed to identify parameter values for each defined attribute and to construct a comparative table. The main identified attributes were the tool environment, environment type, number and type of computational resources, and size and type of SWFA tasks. Note that the Amazon instance specification is regarded as the standard [4] in this research context. Prior work has used various types of computational resources (i.e., VMs, and supercomputers), depending on the selected computational and tool environments.
Tab. 1 provides a mapping between the extracted attributes and the relevant parameters and presents the obtained comparative results from the chosen approaches. It is evident that the majority of the researchers have focused on a simulation-based environment rather than the real-world environment. This is mainly due to the wide availability of the standard dataset supporting the simulation-based environment. A significant number of SWFS approaches, supporting cost optimization, have used a larger size of computational resources. Additionally, the four main types of SWFA that have been used are Montage, CyberShake, Inspiral, and SIPHT.
Table 1: Qualitative comparison results of cost optimisation SWFS approaches
Most of the considered SWFAs have different types of task dependencies. The main types are pipeline, data distribution and redistribution, process, and data aggregation. Hence, it is important to accurately measure the data-intensiveness and computational-intensiveness related to the performance of the various SWFS approaches. To achieve this, there is a high demand to compare various sizes of SWFA tasks. For more reviews in the area of SWFS, please refer to the previously conducted work of the authors [14–17].
3 Proposed Cost Optimization Model of SWFS
To propose a cost-optimal solution for a given SWFS problem, the completion time (makespan) and total computational cost of workflow tasks need to be simultaneously minimized as much as possible. Therefore, there is a need to apply a Pareto-optimal solution method, which considers many solutions in the feasible region rather than focusing on just one. Based on the nature of the optimization problem, there are two main types of objectives: minimizing or maximizing the optimization problem [18–27]. In this research context, minimizing the completion time of the submitted workflow tasks and the overall execution cost has been considered as an optimization problem and is applied to the given workflow tasks for different workflow scenarios [28–31].
Furthermore, the proposed model has classified the cost parameters into three categories: (i) pre-scheduling, (ii) during the scheduling, and (iii) post-scheduling. At the Pre-Scheduling stage, the main responsibility of the scheduler is to check whether the given SWFS tasks are schedulable, based on a set of attributes. During the Scheduling stage, it is of vital importance to check the ready time parameter. Notice that the ready time is the time by which all of the data required by the tasks have reached the scheduled virtual machine (VM), that is, the computational site. Finally, at the Post-Scheduling stage, once all of the given tasks have been scheduled on the available virtual machines, the time between the startTime and endTime can be computed, grounded on the allocated time frame for task execution.
In the subsequent sections, the details of each element of the proposed model are provided.
3.1 Scientific Workflow Applications
SWFAs are regarded as data and computationally intensive workflow applications, which broadly speaking, process, and execute data flows collectively with task execution. They consist of a couple of tasks required to successfully accomplish a specific workflow. The aspects of these tasks can be any executable elements (e.g., load sets, document sets, data, and programs) with distinct structural dependencies, such as process, pipeline, records distribution, facts aggregation, and data redistribution. SWFAs include a number of input scripts, such as scientific software along with their structured data. Notice that the input scripts are used to generate, analyze, and visualize the obtained results (Fig. 1). Moreover, SWFAs have to deal with large size of workflow tasks (e.g., earthquake prediction, biomedical applications, and astrophysics applications).
Figure 1: Cost optimization model of SWFS
The output of SWFAs presents interactive tools that assist service consumers to better execute the given workflows. Moreover, it also supports in visualizing the obtained results in a legitimate time. Also, of note is that SWFAs streamline the execution procedures for scientists, which is useful in reusing identical workflows. Furthermore, SWFAs present a highly usable environment for tuning and sharing outcomes in a virtual environment. Conversely, a high level of dependency between the workflow duties remains a distinct mission of SWFAs. This mainly occurs because of the task’s precedence related limitations. Thus, SWFAs need extra computational resources to effectively determine an optimum SWFS solution for large statistics and complex tasks. Due to the complex nature of SWFAs, a structural illustration is required to simplify the submitted workflow tasks. Hence, it is essential to operate the modeling for the submitted jobs, along with their precedence constraints, using preferred notations. In the literature, numerous variants of structural illustration strategies have been adopted to represent the tasks’ dependency on an SWFA. One of the popular strategies is a Direct Acyclic Graph (DAG), as it can handle highly complex SWFA tasks. In essence, the DAG highlights the workflow’s estimated execution cost, keeping in view available resources and remaining solely grounded on the historical statistics of the WfMS. It also shows the verbal exchange between the estimated resources.
3.2 Targeted Computational Environment
Mapping is required between the submitted set of tasks and the available set of homogeneous/heterogeneous computational resources that help in successfully executing the workflow tasks using a cloud-computing requirement. Generally, the computational resources are regarded as a set of available Virtual Machines (VMs) in the cloud computing context.
3.3 Cost Optimization Criteria
In order to recommend a cost-optimal solution for the SWFS problem, the completion time (makespan) and the total computational fee of workflow tasks have been regarded to be minimized. The cost optimization of SWFS can be accomplished by means statically and simultaneously minimizing the execution time and execution cost. Thus, there is a need to apply a Pareto-optimal method. The underlying concept of the Pareto-optimal approach is to think about many options in the possible area rather than focusing on a single solution. Based on the nature of the optimization problem, there are two kinds of objectives, which are minimizing or maximizing the optimization problem. In this research, minimizing the completion time (makespan) of the submitted workflow tasks and total execution cost of workflow tasks has been viewed as an optimization problem. As shown in Fig. 2, the cost parameters of the proposed model have been classified into three categories: pre-scheduling, during scheduling, and post-scheduling.
Figure 2: The considered cost-optimization parameters
The scheduler in this stage initially focuses on determining whether the given SWFS tasks are schedulable or not. Suppose, if the given tasks are schedulable, then the scheduler performs a selection grounded on a set of parameters. The parameters are (i) types of in-hand processors, (ii) available processors, (iii) busy processors, (iv) title of the computational site, and (v) estimated tasks execution time. To conduct optimal scheduling, the scheduler performs the crucial decisions based on the historical data and the available computational resources. Thus, there is a need to keep the historical data, which is necessary to estimate the feasible execution time.
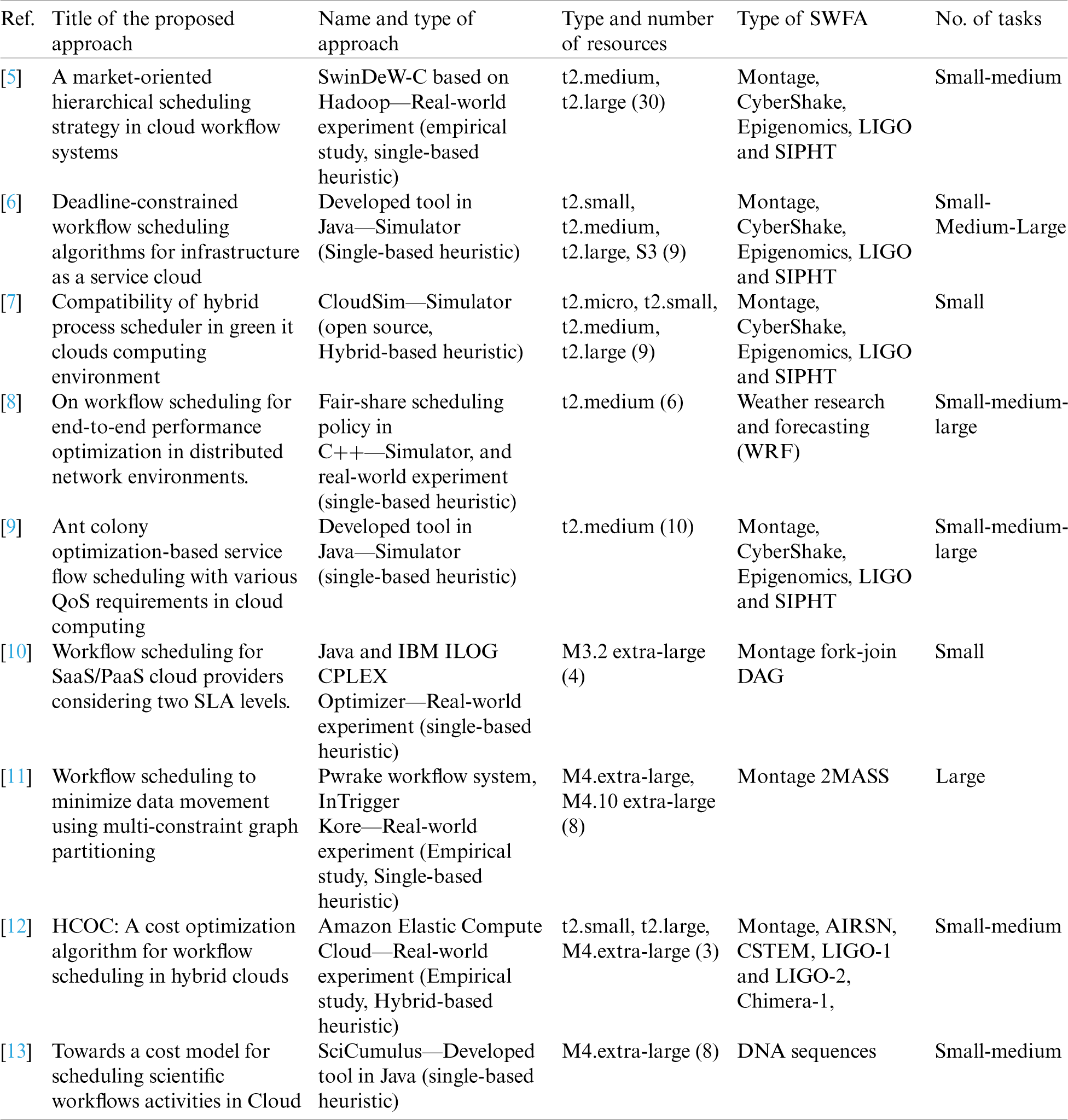
It is important to devise a mechanism for assigning every computational challenge to each of the available virtual computational devices for each estimated cost weight. Motivated by this, the scheduler uses a computational cost matrix (w) having facets 
where VM is employed to focus on a given challenge (ti) and assign to the suitable virtual computing device (VMk) based on the estimated cost weight (
). Notice that the average computational cost is labeled to each of the submitted workflow tasks at the pre-scheduling stage. Eq. (1) describes the average computational cost for a given workflow task ti:
Likewise, a communication cost matrix (
) of size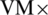 
is used, where VM refers to the stored data transfer charges between the virtual machines (
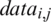). A VM-dimensional vector (L) holds the communication startup charges between the VMs. The communication cost (c) of an edge (i, j) represents the data switch charge from a source task ti (arranged on VMm) to a mission task tj (arranged on VMn) and is formally defined as in Eq. (2):
Suppose there is a scenario in which the scheduler maps (schedules) both tasks, say ti and tj, onto the same VM. In this situation, the communication cost (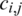
) becomes zero. This is mainly because the inter-process communication cost of the VM is negligible, and this cost is generally ignored. The communication cost of an edge (i, j) is represented in Eq. (3) [14–17]:
where L′ and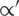 
denotes the communication startup time and the standard transfer charge between the VMs located at a particular host site, respectively. Notice that the researchers have considered the obtained average value to support the decision process of the employed heuristic.
Based on the historical information, and to correctly begin the scheduling processes, it is integral to reflect on the Earliest Start Time (EST) and Earliest Finish Time (EFT) of the execution processes. The EST is described as the earliest time to provoke the challenge execution on the available VM. However, it remains a difficult task to determine the EST, especially in a heterogeneous environment. This is mainly due to the fact that a task computational time of a specific cloud differs inside each available VM. On the other hand, a challenge requires a specific amount of time; thus, it cannot be scheduled before the EST and must be finished on the EFT. The formal representation of EST for each of the unscheduled workflows tasks is given as follows in Eqs. (4) and (5) [14–17]:
Note that the start of the workflow is indicated by the task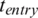 
.
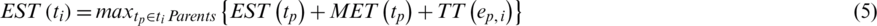
where ti refers to a workflow Task,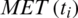 
is the Minimal Execution Time for an available computational Resource 
that requires the minimal Execution Time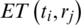 
from all of the available computational resources.
ET and TT respectively represent the estimated Execution Time and Transfer Time of a workflow task ti. In contrast, tp refers to the parent task, while 
denotes the connection (known as an edge) between the father node and a task ti in the DAG.
EFT refers to the Earliest Finish Time, during which the earliest computation of every unscheduled task ti can be finished. Hence, it is essential to compute the EST and MET, and next determine the EFT for each of the unscheduled SWFS tasks before assigning to the available computational resource. The EFT computational process is formally denoted using Eq. (6) [14–17]:
It is important to check the ready time parameter in this scheduling stage. The ready time is the time by which all the data needed by the tasks have reached (after the parent(s) node has/have been executed) the scheduled virtual machine (computational site).
In comparison to EST, ready time is the earliest time required for the first workflow task to be accomplished. The first task (assignment) is solely selected based on the parent workflow tasks. The ready time is formally calculated using Eq. (7):
where ti refers to an individual task having the set of parents (father or mother) workflow tasks pi, and endTime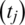 
represents the deadline in order to stop the task execution tj.
Generally, a workflow task ti scheduled on a particular VM VMk does have the same estimated and actual start and end time. In other words, the EST and EFT of a task execution are generally equal to the actual begin and finish time respectively. The allotted time frame is the amount of time between the start time and end time that is permissible for task execution on a virtual machine. However, the overall workflow completion time needs to include a set of serial and parallel constraints that may occur during the start and end time.
Once the submitted tasks are scheduled, the start time of the parent task will be used as a deadline for different dependent tasks. At this point, the scheduling algorithm considers two main possibilities for the workflow task. The first scenario presumes that the workflow start time is the EST that is known prior to its scheduling. The second scenario assumes that the actual start time can only be calculated once the tasks are scheduled on a virtual machine. The actual finish time represents the time that has been used to whole the execution of the submitted workflow task. In other words, after all the tasks are scheduled, the scheduling size (completion time) is represented as the actual end time of the exit texit. If there are a couple of exit tasks, the completion time of the scheduling (makespan) is considered the most real-time of the exit task.
3.4 Empirical Comparison Based on the Heuristic Approaches
The traditional population-based meta-heuristic approaches have shown good performance for the optimization problem, having a large search space. This is because the traditional meta-heuristics do not exhaustively search the scheduling problem space. They use different underlying strategies to find the desired solution based on defined fitness criteria. Therefore, population-based (e.g., random-guided) methods take less computational effort than single-based ones and can often find good solutions. However, each type of approach has some strengths and limitations, which affect the scheduling operation of SWFS.
In contrast, the hybrid meta-heuristic uses the best features of two or more traditional meta-heuristics in each iteration to provide a better optimal solution compared to the traditional heuristics. However, in some cases, and due to the complexity of the hybrid method, a longer convergence time may be needed at each iteration process than with the traditional meta-heuristics. Furthermore, hybrid approaches could require a longer scheduling time.
In this research, an empirical comparison has been conducted based on three types of heuristic approaches, Single-based, Hybrid-based, and Hyper-based, to evaluate the effectiveness of the proposed cost optimization model.
3.4.1 Single-Based Heuristics Algorithms
After conducting an extensive literature review, the authors have considered three well-known single-optimization-based (population-oriented) heuristic techniques: (i) Genetic Algorithm (GA), (ii) Particle Swarm Optimization (PSO), and (iii) Invasive Weed Optimization (IWO) [14–17]. The underlying working mechanism of each of these considered heuristic techniques is presented in this section.
3.4.2 Hybrid-Based Heuristics Algorithms (HIWO)
In total, five core phases of HIWO have been proposed: (i) initialization, (ii) reproduction (duplication), (iii) mutation, (iv) spatial dispersal, and (v) competitive exclusion. Algorithm-3 presents the core phases of HIWO.
Initialization Phase:
This phase accepts the main inputs of population size and the problem size. As previously discussed, the population size and problem size refer to the set of schedulable workflow tasks and set of VMs respectively. In this research context, each weed represents a scheduling solution, which is encoded using a pair of one-dimensional strings. Each string represents an ordered task listing to be scheduled using an available VM. So, a population of initial weeds represents one single scheduling effort from the random positions covering a one-dimensional large problem space.
Reproduction Phase:
This phase aims at computing the attained fitness price that is attained completion time, grounded on the fitness function of the generated weeds. Each of the generated weeds is regarded as a single solution. So, the HIWO works on the sub-simulation (i.e., local solution) in order to find the minimal value with respect to the completed cost and time.
Mutation Operation Phase:
This stage aims at enhancing the colony range by artificially improving (and replacing) a single weed with the best solution, which is regarded as NewSeeds in this research context. This operation helps in avoiding premature convergence and the probability of skipping the global-optimum cost for multi-dimensional problems. Importantly, the mutation operation assists in speeding up the searching operation, crucial to finding the best solution.
Spatial Distribution Phase:
This stage focuses on randomly dispensing the generated NewSeeds (regarded as children) over d-dimensional problem search space grounded on the conventional random numbers’ distribution. It is important to minimize the iterations range during the searching process based on the initial price (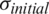
) to a final price (
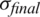). For this purpose, this phase uses the standard deviation (
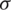) of the random feature. The calculation process for each time step is represented as:
where itermax and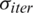 
respectively represent the maximum allowed iterations range and standard deviation of the existing time step. Notice that the non-linear modulation index represented as n is normally set to 2.
Competitive Exclusion Phase:
This phase mainly aims at excluding an unwanted plant based on the attained bad (low) fitness. This economical mechanism permits searching for a good (fitter) flower in order to intimate the additional seeds, and this continues until the defined stooping standard has been met. Finally, the plant with good time and cost (compared to others) is picked and yields as a better solution.
3.4.3 Hyper-Based Heuristics Algorithms
In the current research work, the authors have employed a Dynamic Hyper-Heuristic Algorithm (DHHA) regarded as a hyper-heuristic technique, motivated from their prior work. Complete details on the DHHA approach can be found in our previous work [14–17].
The evaluation of any approach using the simulation environment allows researchers to compare application configurations under controlled conditions. Several types of simulation tools have been utilized by researchers to evaluate the cost optimization of SWFS approaches in cloud computing (e.g., CloudSim [32], and EMUSIM [33]). However, only WorkflowSim [34] is considered the standard workflow execution model. It is an open-access programming tool for developing and simulating WfMS implemented in a parallel and distributed environment and contains a workflow mapper, workflow engine, workflow scheduler, clustering engine, provenance collector, and workflow partitioner.
The extensive evaluation in the current study was conducted through WorkflowSim by setting it up on an eclipse editor. The data collected from executing the actual SWFA was used to generate synthetic workflows resembling those used by real-world scientific applications. The simulation-based environment helped in clearly understanding the scheduling process. At the same time, it determined different scenarios (i.e., the number of VMs and size of SWFA) to fully investigate the performance of the proposed model.
Using the simulation experimentation environment, the proposed cost optimization model was evaluated using SWFA datasets (i.e., SIPHT). For each of these SWFAs, three dataset sizes were considered to evaluate the data intensiveness and computational intensiveness of the proposed approach. Different types of statistical analysis were conducted for the collected results. The details of the evaluation are provided in the remainder of this section.
4.1 Scientific Workflow Applications
As already defined, SWFAs consist of multiple tasks necessary to accomplish the given workflow. Note that the main elements of the tasks are some of the executable instances, such as data, programs, load sets, and reports sets. The other correlation in a scientific workflow application is the relationship between the tasks/jobs and their data dependencies. There are five main types of these relationships: Process, pipeline, data distribution, data aggregation, and data redistribution.
Additionally, in the clustering stage of WorkflowSim, the tasks with the same type of process can be represented as a job. In this way, similar tasks can be executed one time instead of repeating the same execution several times. Tab. 2 represents the settings (i.e., application size and the number of considered tasks) of the SWFAs used for the extensive assessment of the proposed approach.
Table 2: Completion time and total computational cost comparison for SIPHT SWFA
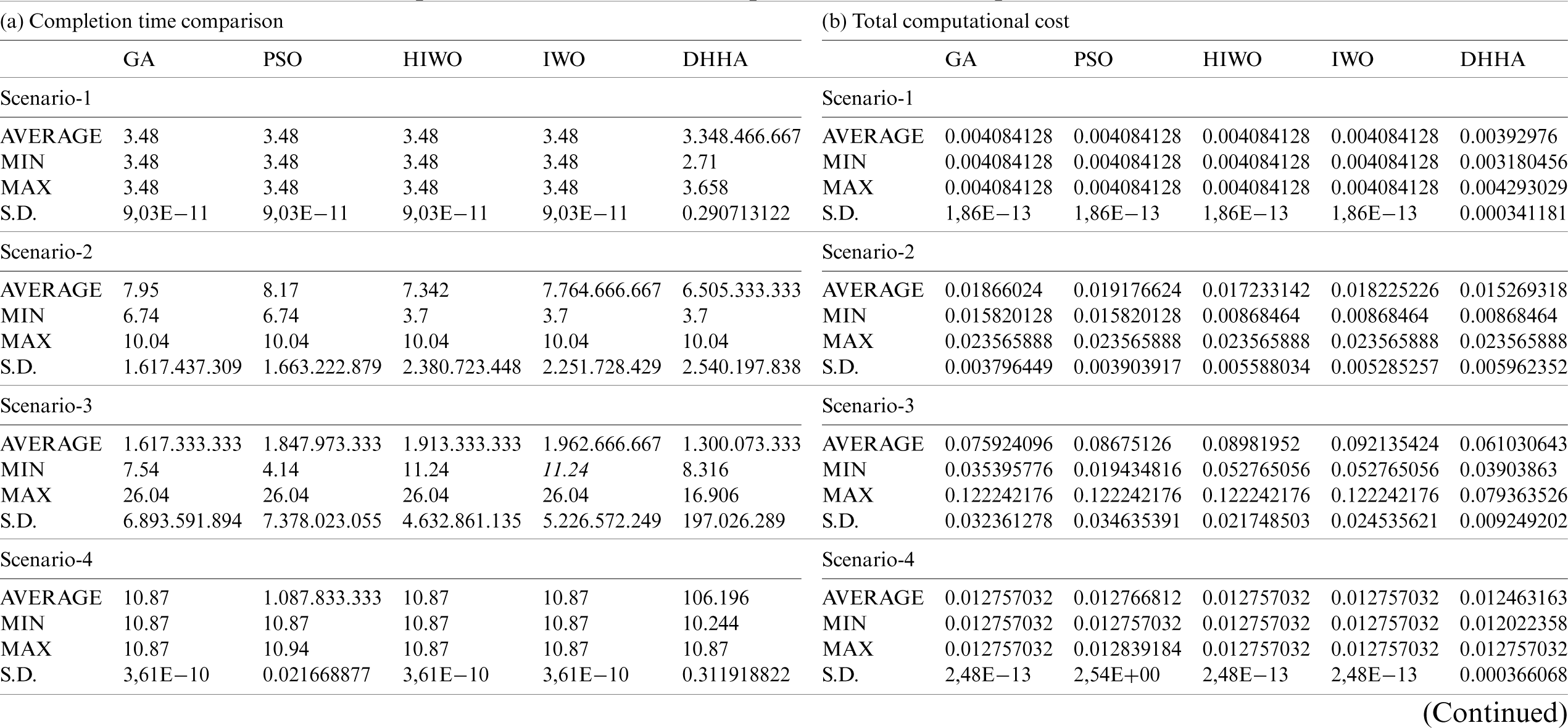
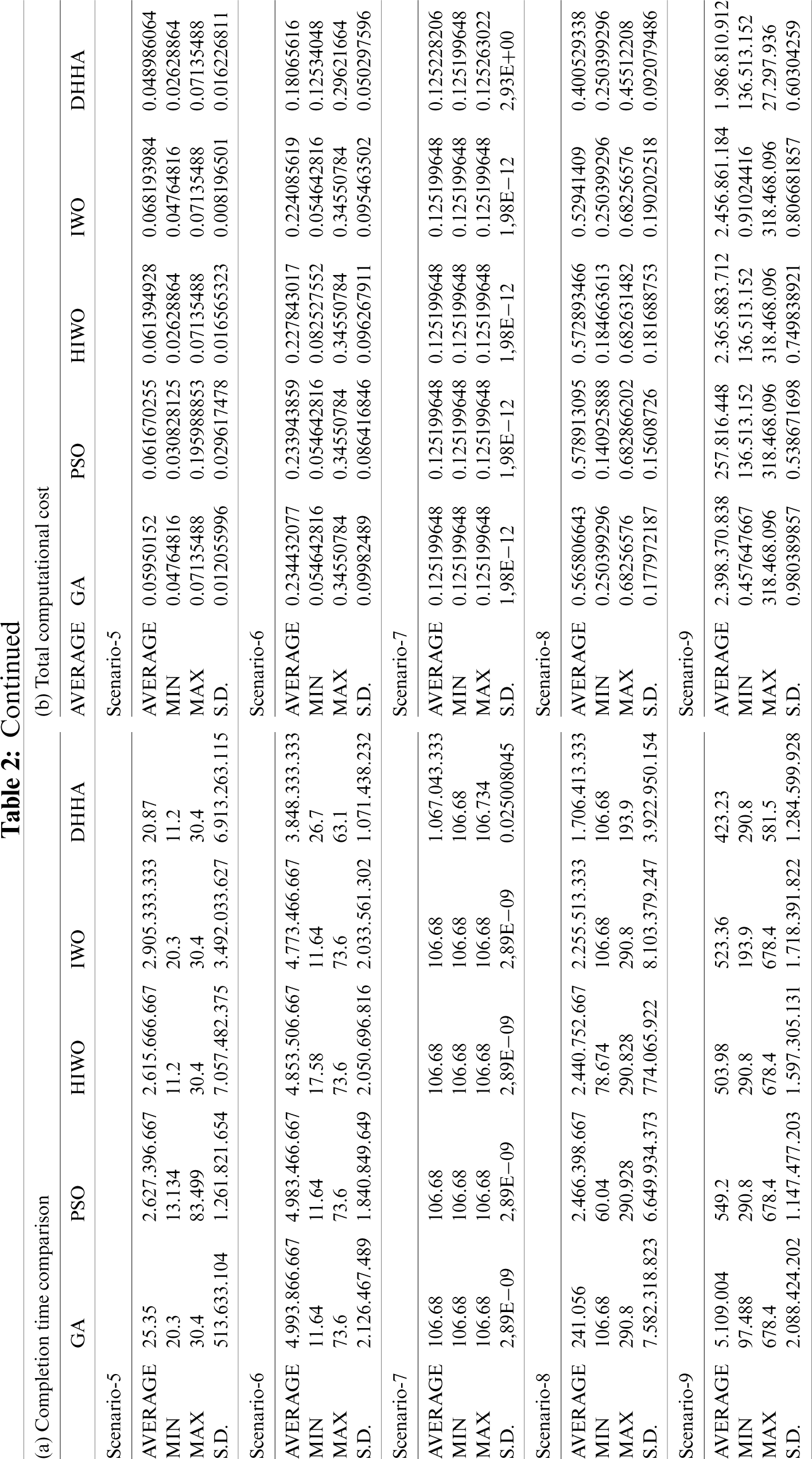
SIPHT-search for sRNAs Workflow Application: The bioinformatics project at Harvard University is conducting a wide search for small untranslated Ribonucleic Acids (sRNAs) that regulate several processes, such as secretion or virulence in bacteria. The SIPHT workflow is composed of small (30), medium (100), and large (1000) tasks.
For running the simulation experiments, a PC with the following specifications was used: operating system: Windows 10 Pro (64 bit); processor: Intel(R) Core (TM) i7-3770 CPU@3.40 GHz; and memory (RAM): 12.0 GB. As WorkflowSim is programmed using Java, Eclipse, an integrated development environment, was used to run the WorkflowSim codes and to implement the proposed approach. The code for WorkflowSim (Version 1.0) is directly imported from the GitHub website [34]. After performing the necessary modifications to the directories of code, existing provided examples of the simulator were successfully run.
It is worth noting that the prices of VM are based on the EC2 pricing list. In this research, the type of available computational resources (i.e., VMs) has been selected based on the comprehensive study of the existing approaches discussed in Section 2 and based on the WorkflowSim, where the considered VM instance is equivalent to t2.small instance of the Amazon EC2 website [4].
In order to substantially analyze the collected data from experimentation, four kinds of widely used descriptive statistical analysis were performed: minimum, maximum, standard deviation (S.D), and average. The total required time to finish executing the submitted workflow tasks is calculated as the completion time. Moreover, due to the static submitting criteria, the total computational cost is calculated by multiplying the task completion time with the number of considered virtual machines together with the cost of each virtual machine. In this section, the descriptive statistical analysis of the experimental results is presented and discussed for each of the considered SWFAs (i.e., SIPHT-search for sRNAs SWFAs).
Based on the workflow tasks (datasets size), the first three scenarios are considered the smallest (30 tasks, with 2, 4, 8 VMs) datasets scenarios, while the last three are the largest (1000 tasks, with 2, 4, 8 VMs).
Tab. 2a presents the descriptive statistical analysis for completion time results for the SIPHT SWFA for all nine considered scenarios. The average completion time values for all of the approaches are very close for most of the scenarios. This could be due to the SIPHT SWFA having a lower number of dependencies between their tasks, which gives smaller search space for the employed Lower-Level Heuristic algorithms to find an optimal solution, especially when the number of VMs is lower (scenarios 1, 4, and 6). However, in scenario 7 the average values for the completion time of the IWO approach are slightly lower than the DHHA approach, due to strong dependencies between the tasks of the SIPHT SWFA. This allowed the IWO approach to find the optimal solution with a shorter convergence time.
Fig. 3 depicts the average completion time attained by the various approaches for the Insprial SWFA and for the considered scenarios. It can be clearly observed from Fig. 3 that GA, HIWO, and DHHA approaches obtained the lowest average completion time for most of the scenarios. Interestingly, for scenarios 1 to 7, all approaches attained similar average completion times. In contrast, Fig. 4 shows the average computational cost ($/hour) for all of the approaches and for each of the considered scenarios. It is evident that the results for the accumulated computational cost depend on the average completion values, which are ultimately influenced by the sizes of the datasets of the submitted SWFA as well as the number of available VMs. Furthermore, it can be observed that the Single-based (GA), Hybrid-based (HIWO) and Hyper-based (DHHA) approaches had the lowest total computational cost for all scenarios, and especially for scenarios 8 and 9. Furthermore, the average completion time (in second) of the proposed DHHA approach is more optimal for all considered scenarios. However, the other considered meta-heuristic algorithms always attained very similar or closer values to each other, especially for scenarios one to seven.
Figure 3: Average completion time
Figure 4: Average total computational
4.3.2 Total Computational Cost Results
Tab. 2b presents the total computational cost descriptive statistical analysis results for the SIPHT SWFA. It can be clearly seen that the DHHA approach attained much better results with regard to total computational cost for most of the considered scenarios. This is mainly because the hybrid and hyper-heuristic approaches always select the most suitable LLH algorithm on each iteration, which helps in finding the most optimal solution. Furthermore, DHHA approach attains most optimal average total computational cost results for all considered scenarios and especially scenarios seven, eight and nine, where the number of tasks is high (1000 tasks). This shows the optimal performance of the proposed CHDHH with different types, complexities, and sizes of SWFAs.
This research work has proposed a novel cost optimization model that contains the three main stages of scientific workflow application, targeted computational environment, and cost optimization criteria, and the three cost parameters categories of pre-scheduling, during scheduling, and post-scheduling. An empirical comparison of Single-based, Hybrid-based, and Hyper-based heuristic approaches has been provided while considering different numbers of VMs and different sizes of SWFAs.
Statistical analysis has been applied to the collected data by running the heuristic approaches aimed at supporting the proposed SWFS based cost optimization model in a WorkflowSim experimentation environment. SIPHT scientific workflow application with different sizes of datasets was executed to determine completion time (makespan) and total computational cost. For completion time results, it is concluded that the Single-based heuristic approaches lack in achieving good results compared to the Hybrid-based and Hyper-based approaches. This is due to the nature of the solution proposed by these algorithms, which have limitations in considering a more optimal solution. In some cases, the S.D. values of these algorithms were equal to zero because there was no variation to be measured. Besides this, the SIPHT SWFA has a longer completion time (makespan) compared to the other SWFA for all sizes of datasets. This is because the size of tasks is large compared to the other SWFAs and the data dependencies (precedence constraints) between the SIPHT SWFA tasks are more complex than in the other SWFA. For total computational cost results, similar to the completion time results, the Hybrid-based and Hyper-based approaches showed lower computational cost than the Single-based approaches. In the future, implementing the proposed model in the real-world using a hybrid cloud environment would be an interesting direction in this research domain. Finally, the authors plan to consider other cost parameters such as the cost of storage and communication cost.
Funding Statement: This work has been sponsored by the NWO/TTW project Multi-scale integrated Traffic Observatory for Large Road Networks (MiRRORS) under Grant Number 16270.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Dutta and D. VanderMeer. (2011). “Cost-based decision-making in middleware virtualization environments,” European Journal of Operational Research, vol. 210, no. 4, pp. 344–357. [Google Scholar]
2. T. Miu and P. Missier. (2012). “Predicting the execution time of workflow activities based on their input features,” in Proc. SC Companion, Salt Lake City, UT, USA, pp. 64–72. [Google Scholar]
3. D. Yuan, Y. Yang, X. Liu and J. Chen. (2010). “A cost-effective strategy for intermediate data storage in scientific cloud workflow systems,” in Proc. IPDPS, Atlanta, GA, USA, pp. 1–12. [Google Scholar]
4. S. Khatua and N. Mukherjee. (2020). “Application-centric resource provisioning for amazon ec2 spot instances,” in European Conf. on Parallel Processing, Berlin, Heidelberg: Springer, vol. 8097, pp. 267–278. [Google Scholar]
5. W. Zhangjun, L. Ziao, N. Zhiwei, Y. Dong and Y. Yun. (2013). “A market-oriented hierarchical scheduling strategy in cloud workflow systems,” Journal of Supercomputing, vol. 63, no. 1, pp. 256–293. [Google Scholar]
6. S. Abrishami, M. Naghibzadeh and D. H. Epema. (2013). “Deadline-constrained workflow scheduling algorithms for infrastructure as a service clouds,” Future Generation Computer Systems, vol. 29, no. 1, pp. 158–169. [Google Scholar]
7. K. Giridas and A. S. Nargunam. (2012). “Compatibility of hybrid process scheduler in green it cloud computing environment,” International Journal of Computer Applications, vol. 55, no. 5, pp. 27–33. [Google Scholar]
8. Q. Wu, D. Yun, X. Lin, Y. Gu, W. Lin et al. (2012). , “On workflow scheduling for end-to-end performance optimization in distributed network environments,” in Proc. JSSPP, LNCS, Berlin, Heidelberg: Springer, vol. 7698, pp. 76–95. [Google Scholar]
9. H. Liu, D. Xu and H. K. Miao. (2011). “Ant colony optimization based service flow scheduling with various QoS requirements in cloud computing,” in Proc. ISSNE, Seoul, South Korea, pp. 53–58. [Google Scholar]
10. T. A. Genez, L. F. Bittencourt and E. R. Madeira. (2012). “Workflow scheduling for SaaS/PaaS cloud providers considering two SLA levels,” in Proc. NOMS, Maui, HI, USA, pp. 906–912. [Google Scholar]
11. M. Tanaka and O. Tatebe. (2012). “Workflow scheduling to minimize data movement using multi-constraint graph partitioning,” in Proc. CCGRID, Ottawa, ON, Canada, pp. 65–72. [Google Scholar]
12. L. F. Bittencourt and E. R. M. Madeira. (2011). “HCOC: A cost optimization algorithm for workflow scheduling in hybrid clouds,” Journal of Internet Services and Applications, vol. 2, no. 3, pp. 207–227. [Google Scholar]
13. V. Viana, D. d. Oliveira and M. Mattoso. (2011). “Towards a cost model for scheduling scientific workflows activities in cloud environments,” in Proc. SERVICES, Washington, DC, USA, pp. 216–219. [Google Scholar]
14. E. N. Alkhanak, S. U. R. Khan, A. Verbareck and H. V. Lint. (2020). “A conceptual framework supporting pattern design selection for scientific workflow applications in cloud computing,” in Proc. CLOSER, Prague, Czech Republic, pp. 229–236. [Google Scholar]
15. E. N. Alkhanak and S. P. Lee. (2018). “A hyper-heuristic cost optimisation approach for scientific workflow scheduling in cloud computing,” Future Generation Computer Systems, vol. 86, pp. 480–506. [Google Scholar]
16. E. N. Alkhanak, S. P. Lee and T. Ling. (2015). “A hyper-heuristic approach using a prioritized selection strategy for workflow scheduling in cloud computing,” in Proc. ICCSCM, Kuala Lumpur, MAS, pp. 601–608. [Google Scholar]
17. K. Dowlatshah, M. Alizadeh, M. A. Raji and E. N. Alkhanak. (2020). “A secure and robust smart card-based remote user authentication scheme,” International Journal of Internet Technology and Secured Transactions, vol. 10, pp. 255–267. [Google Scholar]
18. S. K. Prasad, J. Rachna, O. I. Khalaf and D. N. Le. (2020). “Map matching algorithm: Real time location tracking for smart security application,” Telecommunications and Radio Engineering, vol. 79, no. 13, pp. 1189–1203. [Google Scholar]
19. O. I. Khalaf, G. M. Abdulsahib, H. D. Kasmaei and K. A. Ogudo. (2020). “A new algorithm on application of blockchain technology in live stream video transmissions and telecommunications,” International Journal of e-Collaboration, vol. 16, no. 1, pp. 16–32. [Google Scholar]
20. K. A. Ogudo, D. M. J. Muwawa, O. I. Khalaf and H. A. D. Kasmaei. (2019). “Device performance and data analytics concept for smartphones,” IoT Services and Machine-Type Communication in Cellular Networks, vol. 11, no. 4, pp. 1–15. [Google Scholar]
21. O. I. Khalaf and B. M. Sabbar. (2019). “An overview on wireless sensor networks and finding optimal location of nodes,” Periodicals of Engineering and Natural Sciences, vol. 7, no. 3, pp. 1096–1101. [Google Scholar]
22. A. M. Ghaida and O. I. Khalaf. (2018). “An improved algorithm to fire detection in forest by using wireless sensor networks,” International Journal of Civil Engineering and Technology, vol. 9, no. 11, pp. 369–377. [Google Scholar]
23. A. F. Subahi, Y. Alotaibi, O. I. Khalaf and F. Ajesh. (2020). “Packet drop battling mechanism for energy aware detection in wireless networks,” Computers, Materials and Continua, vol. 66, no. 2, pp. 2077–2086. [Google Scholar]
24. X. Xiang, Q. Li, S. Khan and O. I. Khalaf. (2021). “Urban water resource management for sustainable environment planning using artificial intelligence techniques,” Environmental Impact Assessment Review, vol. 86, pp. 106515. [Google Scholar]
25. O. I. Khalaf and G. M. Abdulsahib. (2020). “Energy efficient routing and reliable data transmission protocol in WSN,” International Journal of Advances in Soft Computing and its Application, vol. 12, no. 3, pp. 45–53. [Google Scholar]
26. O. I. Khalaf, G. M. Abdulsahib and B. M. Sabbar. (2020). “Optimization of wireless sensor network coverage using the Bee algorithm,” Journal of Information Science Engineering, vol. 36, no. 2, pp. 377–386. [Google Scholar]
27. A. Dawood, O. I. Khalaf and G. M. Abdulsahib. (2019). “An adaptive intelligent alarm system for wireless sensor network,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 15, no. 1, pp. 142–147. [Google Scholar]
28. O. I. Khalaf and G. M. Abdulsahib. (2019). “Frequency estimation by the method of minimum mean squared error and P-value distributed in the wireless sensor network,” Journal of Information Science and Engineering, vol. 35, no. 5, pp. 1099–1112. [Google Scholar]
29. O. I. Khalaf, G. M. Abdulsahib and M. Sadik. (2018). “A modified algorithm for improving lifetime WSN,” Journal of Engineering and Applied Sciences, vol. 13, pp. 9277–9282. [Google Scholar]
30. N. Sulaiman, G. M. Abdulsahib, O. I. Khalaf and M. N. Mohammed. (2014). “Effect of using different propagations on performance of OLSR and DSDV routing protocols,” in Proc. ISMS, Langkawi, Malaysia, pp. 540–545. [Google Scholar]
31. G. M. Abdulsahib and O. I. Khalaf. (2018). “Comparison and evaluation of cloud processing models in cloud-based networks,” International Journal of Simulation–Systems, Science & Technology, vol. 19, no. 5, pp. 26.1–26.6. [Google Scholar]
32. R. N. Calheiros, R. Ranjan, A. Beloglazov, C. A. F. De Rose and R. Buyya. (2011). “CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms,” Software: Practice and Experience, vol. 41, no. 1, pp. 23–50. [Google Scholar]
33. R. N. Calheiros, M. A. S. Netto, C. A. F. De Rose and R. Buyya. (2013). “EMUSIM: An integrated emulation and simulation environment for modeling, evaluation, and validation of performance of cloud computing applications,” Software: Practice and Experience, vol. 43, no. 5, pp. 595–612. [Google Scholar]
34. W. Chen and E. Deelman. (2012). “Workflowsim: A toolkit for simulating scientific workflows in distributed environments,” in Proc. e-Science, Chicago, IL, USA, pp. 1–8. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |