DOI:10.32604/cmc.2021.015790

| Computers, Materials & Continua DOI:10.32604/cmc.2021.015790 |  |
| Article |
On Network Designs with Coding Error Detection and Correction Application
1Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Physics and Engineering Mathematics, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
*Corresponding Author: Mahmoud Higazy. Email: m.higazy@tu.edu.sa
Received: 07 December 2020; Accepted: 07 January 2021
Abstract: The detection of error and its correction is an important area of mathematics that is vastly constructed in all communication systems. Furthermore, combinatorial design theory has several applications like detecting or correcting errors in communication systems. Network (graph) designs (GDs) are introduced as a generalization of the symmetric balanced incomplete block designs (BIBDs) that are utilized directly in the above mentioned application. The networks (graphs) have been represented by vectors whose entries are the labels of the vertices related to the lengths of edges linked to it. Here, a general method is proposed and applied to construct new networks designs. This method of networks representation has simplified the method of constructing the network designs. In this paper, a novel representation of networks is introduced and used as a technique of constructing the group generated network designs of the complete bipartite networks and certain circulants. A technique of constructing the group generated network designs of the circulants is given with group generated graph designs (GDs) of certain circulants. In addition, the GDs are transformed into an incidence matrices, the rows and the columns of these matrices can be both viewed as a binary nonlinear code. A novel coding error detection and correction application is proposed and examined.
Keywords: Network decomposition; network designs; network edge covering; circulant graphs
Graph (Network) designs are introduced as a generalization of symmetric balanced incomplete block designs (BIBDs) (see, e.g., [1,2]) which are decompositions of complete graphs (networks) to subgraphs (subnetworks) satisfying certain conditions (see [1]). There are several research papers on the subject of graph decompositions; for more details see [3]. Through the paper we use the word (graph) to mean (network).
As defined in [1], a symmetric graph design, or SGD, with parameters 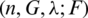 , where n,
, where n, 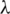 are positive integers and G and F are graphs with n vertices, is a set
are positive integers and G and F are graphs with n vertices, is a set  of spanning subgraphs of the complete graph Kn such that
of spanning subgraphs of the complete graph Kn such that
a) Gi 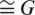 for
for 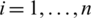 ;
;
b) any edge of Kn is contained in exactly 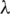 subgraphs Gi, and
subgraphs Gi, and
c) 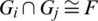 for
for 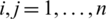 ,
, 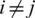 .
.
In [4], Dalibor Fronček and Alex Rosa determined all graphs F and all orders for which there exists an 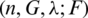 -SGD where
-SGD where 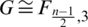 , the friendship graph on n vertices.
, the friendship graph on n vertices.
In this paper, a generalization of symmetric BIBDs is investigated and we introduce a new graph representation that will help in constructing new graph designs (GDs).
Definition 1.1 Let H be a r-regular Cayley graph of order n and B be a non-empty set of spanning subgraphs of H. 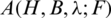 -GD (Graph Design, GD) is a collection
-GD (Graph Design, GD) is a collection 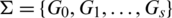 of spanning subgraphs of H such that
of spanning subgraphs of H such that
1. all graphs G in B have the same size 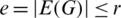 ,
,
2. any graph of 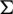 is isomorphic to one graph of B,
is isomorphic to one graph of B,
3. every edge of H belongs to exactly 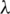 elements of
elements of 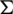 ,
,
4. for any two different subgraphs Gi and Gj of 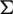 , we have
, we have 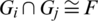 .
.
If 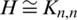 ,
, 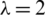 ,
, 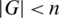 and
and 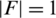 or 0, then the
or 0, then the  -GD is equivalent to the sub-orthogonal double covers (SODCs) of the complete bipartite graph by G. SODC’s have been studied by many authors (for SODCs of Kn, n by G, see [5–7] and for SODCs of Kn by G, see, [8–10]. The
-GD is equivalent to the sub-orthogonal double covers (SODCs) of the complete bipartite graph by G. SODC’s have been studied by many authors (for SODCs of Kn, n by G, see [5–7] and for SODCs of Kn by G, see, [8–10]. The 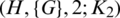 -GD with
-GD with  is equivalent to the orthogonal double covers (ODCs) of Cayley graphs which have been studied in [11]. Also, the
is equivalent to the orthogonal double covers (ODCs) of Cayley graphs which have been studied in [11]. Also, the 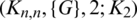 -GD with
-GD with 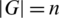 is equivalent to ODCs of Kn, n by G that have been investigated by many authors (see, e.g., [12–15]). Studying the case when
is equivalent to ODCs of Kn, n by G that have been investigated by many authors (see, e.g., [12–15]). Studying the case when 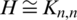 ,
, 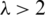 ,
, 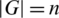 and
and  is equivalent to studying the mutually orthogonal graph squares which have been studied by many authors (see, e.g., [7,16–19]) and for more details see the survey [20]. Since SODCs and ODCs can be considered as graph designs, its construction tools can be used to construct new graph designs as will be done in this work.
is equivalent to studying the mutually orthogonal graph squares which have been studied by many authors (see, e.g., [7,16–19]) and for more details see the survey [20]. Since SODCs and ODCs can be considered as graph designs, its construction tools can be used to construct new graph designs as will be done in this work.
Here, all graphs are assumed to be finite, simple and with non-empty edge set. We use the usual notations: 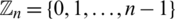 for the group of all residual classes modulo n,
for the group of all residual classes modulo n, 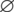 for the empty set, Kn, n for the complete bipartite graphs, Kn for the complete graph, Pn+1 for the path graph with n edges, Sn for the star of size n, En the empty graph of order n, the circulant graph
for the empty set, Kn, n for the complete bipartite graphs, Kn for the complete graph, Pn+1 for the path graph with n edges, Sn for the star of size n, En the empty graph of order n, the circulant graph 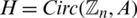 is defined by
is defined by 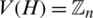 and
and 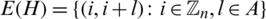 , see [21].
, see [21].
In our current study, we concentrate on the case when 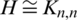 or
or 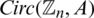 and
and 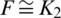 or
or 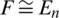 . Note that, if
. Note that, if  , then
, then 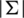 > n.
> n.
From now on, all addition and subtraction shall be done modulo n.
The vertices of Kn, n shall be labeled by the elements of 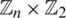 . Namely, for
. Namely, for  we shall write vi for the corresponding vertex and define
we shall write vi for the corresponding vertex and define 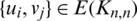 if and only if
if and only if 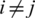 , for all
, for all 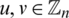 and
and 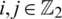 . To avoid ambiguity, the edge
. To avoid ambiguity, the edge 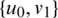 shall be written as (u, v).
shall be written as (u, v).
All designs can be represented by a corresponding incidence matrix [22]. Following the method produced in [23], the incidence matrices can be used in coding error detection and corrections. Here, the suggested codes are not linear codes.
The arrangement of our paper is as follows: In Section 2, a new representation of graphs is introduced. In Section 3, a technique of constructing the group generated graph designs of Kn, n is studied. In Section 4, detection of error and its correction is suggested as an application of the codes generated by the constructed graph designs. In Section 5, we construct new group generated graph designs of Kn, n. In Section 6, a technique of constructing the group generated graph designs of the circulants is given with group generated graph designs of certain circulants. The conclusion shall be in Section 7.
2 New Representation of Graphs
In this section, we introduce a new representation of graphs following the method that has been introduced in [13]. In [13], the graphs have been represented by a vector whose entries are the labels of the vertices related to the lengths of edges linked to it. This method of graph representation has simplified the method of constructing the graph designs. Here, a general method is proposed and applied to construct new graph designs.
Let G be a spanning subgraph of H and let 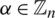 . Then the graph G with
. Then the graph G with
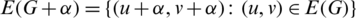
is called the 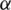 -translate of G. The length of an edge
-translate of G. The length of an edge 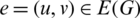 is defined by l(e) = v − u.
is defined by l(e) = v − u.
For any subgraph G of Kn, n, let 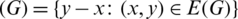
be the multiset containing the length of every edge in G. For any two subgraphs G1 and G2 of H, let
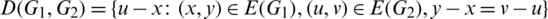
be the multiset containing the distance of every pair of equal length edges in G1 and G2. Note that the distance set D(G, G) means the set of distances between the different edges in G which have the same lengths. For any collection of graph 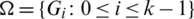 , we define rd-matrix as a
, we define rd-matrix as a  matrix whose entries are
matrix whose entries are 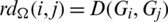 for
for 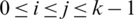 .
.
Let G be a graph of order n and its vertices are the elements of  , G can be represented by a map
, G can be represented by a map 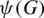 from
from  to its power set (i.e.,
to its power set (i.e., 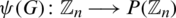 ) where for all
) where for all  ,
, 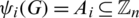 such that for all
such that for all 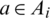 , the edge
, the edge 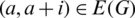 .
. 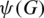 can be written in the form of n-tuple where
can be written in the form of n-tuple where
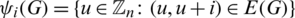
for all  (a vector whose ith entry is a set of vertices, from
(a vector whose ith entry is a set of vertices, from  , incident to the edges with length equal i). Then the following are clear.
, incident to the edges with length equal i). Then the following are clear.
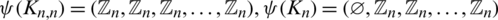
and for all  ,
, 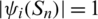 and
and 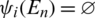 .
.
Let 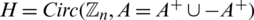 where
where 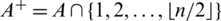 . Then
. Then
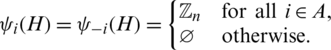
Let G and H be two spanning subgraphs of Kn, n, G and H are said to be orthogonal if they share at most one edge (i.e., 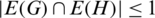 ), see [8,10] or [24]. Then the collection
), see [8,10] or [24]. Then the collection  is mutually orthogonal if and only if all cells of
is mutually orthogonal if and only if all cells of 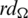 matrix are sets.
matrix are sets.
For H = r-regular 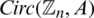 , the existence of (
, the existence of (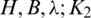 )-GD immediately implies the following two necessary conditions that is recorded as
)-GD immediately implies the following two necessary conditions that is recorded as
Lemma 2.1 Let 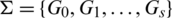 be a
be a 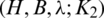 -GD and e is the size of any element of B. Then
-GD and e is the size of any element of B. Then
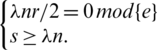
Proof. From Definition 1.1 of the (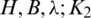 )-GD, we have
)-GD, we have
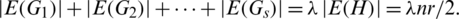
Since all elements of 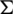 are isomorphic to one element of B and all elements of B have the same size e, this implies that
are isomorphic to one element of B and all elements of B have the same size e, this implies that 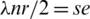 . Also, we have
. Also, we have 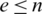 by Definition 1.1, which imply that
by Definition 1.1, which imply that 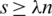 .
.
3 Group Generated Graph Designs of 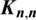
Definition 3.1 Let  be a collection of spanning subgraphs of Kn, n. We call
be a collection of spanning subgraphs of Kn, n. We call  a
a 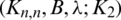 -GD generator if it satisfies the following conditions:
-GD generator if it satisfies the following conditions:
1. Every element of  appears exactly
appears exactly 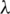 times in the sum of the multisets
times in the sum of the multisets
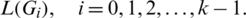
2. For all pairs i, j with 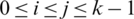 , the cells of the
, the cells of the 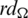 matrix are sets, that is D(Gi, Gj) are all sets.
matrix are sets, that is D(Gi, Gj) are all sets.
The elements of the generator  are called
are called 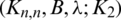 -GD pre-starters graphs.
-GD pre-starters graphs.
Theorem 3.2 Let 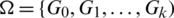 be a
be a 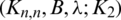 -GD generator. Then for all
-GD generator. Then for all 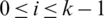 , the collection of all the translates of
, the collection of all the translates of  for all
for all 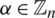 , forms a
, forms a 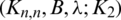 -GD by B.
-GD by B.
Proof. It is clear that the collection of all translates covers every edge of Kn, n exactly  times. Now, It is to show that the collection of all translates are mutually orthogonal, that is any two graphs of the collection of all translates share at most one edge. Consider two translates
times. Now, It is to show that the collection of all translates are mutually orthogonal, that is any two graphs of the collection of all translates share at most one edge. Consider two translates 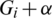 and
and 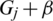 where
where 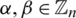 and assume that they share two edges e1 = (x, y) with length l1 = y − x and e2 = (u, v) with length l2 = v − u. Then the two edges
and assume that they share two edges e1 = (x, y) with length l1 = y − x and e2 = (u, v) with length l2 = v − u. Then the two edges 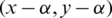 ,
, 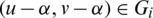 with lengths l1, l2 respectively and
with lengths l1, l2 respectively and  ,
, 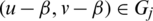 with lengths l1, l2 respectively. Then the distance between the two edges with length l1 in Gi and Gj is
with lengths l1, l2 respectively. Then the distance between the two edges with length l1 in Gi and Gj is  , and also the distance between the two edges with length l2 in Gi and Gj is
, and also the distance between the two edges with length l2 in Gi and Gj is  and then D(Gi, Gj) is not a set. This is a contradiction of the second condition in the Definition 3.1 of the
and then D(Gi, Gj) is not a set. This is a contradiction of the second condition in the Definition 3.1 of the 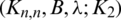 -GD generator. Consequently, all subgraphs in the collection of all translates of GD-generator are mutually orthogonal, that is a
-GD generator. Consequently, all subgraphs in the collection of all translates of GD-generator are mutually orthogonal, that is a 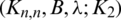 -GD.
-GD.
Lemma 3.3 Let 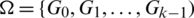 be a
be a 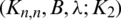 -GD generator, then
-GD generator, then
i) the number of pre-starters in 
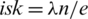 .
.
ii) For all 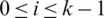 , if
, if 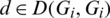 then
then 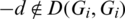 ,
,
iii) For all 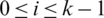 , if n is even then
, if n is even then 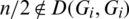 .
.
Proof. (i) 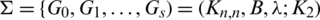 -GD. Since s = kn then
-GD. Since s = kn then 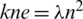 and hence
and hence  .
.
(ii) Let D(Gi, Gi) contains 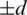 . then Gi contains four edges each pair of them has the same length l1 and l2, that is (x, x + l1), (x + d, x + d + l1),
. then Gi contains four edges each pair of them has the same length l1 and l2, that is (x, x + l1), (x + d, x + d + l1), 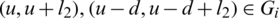 .
.
Then Gi + d contains (x + d, x + d + l1), (x + 2d, x + 2d + l1), (u + d, u + d + l2), (u, u + l2) which imply that 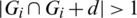 which is a contradiction. Hence, for all
which is a contradiction. Hence, for all 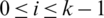 , if
, if 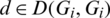 then
then 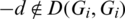 .
.
(iii) For any 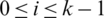 , let
, let 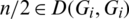 .
.
So there exist two edges e1 = (x, x + l), e2 = (x + n/2, x + n/2+l) belong to E(Gi) with the same length l and D(e1, e2) = n/2.
Then Gi + n/2 contains also e1 = (x, x + l), e2 = (x + n/2, x + n/2+l) that means 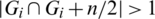 which is a contradiction. Hence, for all
which is a contradiction. Hence, for all  , if n is even then
, if n is even then 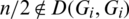 .
.
Therefore, 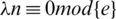 is a necessary condition of the existence of the
is a necessary condition of the existence of the 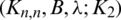 -GD generator.
-GD generator.
Lemma 3.4 Let 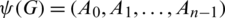 is a pre-starter of
is a pre-starter of 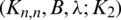 -GD and
-GD and
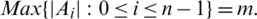
Then
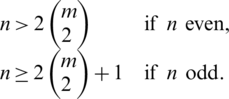
Proof. Case 1. For n is even; for 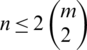 , then
, then 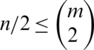 (the number of differences of the edges of length i), then D(G, G) is a multiset set. This is a contradiction, then
(the number of differences of the edges of length i), then D(G, G) is a multiset set. This is a contradiction, then 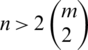 .
.
Case 2. For n is odd; for 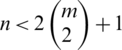 , then
, then 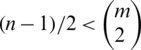 (the number of differences of the edges of length i), then D(G, G) is a multiset set. This is a contradiction, then
(the number of differences of the edges of length i), then D(G, G) is a multiset set. This is a contradiction, then  .
.
Proposition 3.5 Let 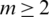 and
and 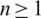 be any integers, B is a set of graphs of size e. If there exists a
be any integers, B is a set of graphs of size e. If there exists a 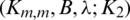 -GD generator of Km, m by B, then there exists a
-GD generator of Km, m by B, then there exists a  -GD generator of Kmn, mn by B.
-GD generator of Kmn, mn by B.
Proof. Here, the element 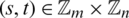 is written as st. Let
is written as st. Let 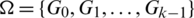 be a
be a  -GD generator of Km, m by B with respect to
-GD generator of Km, m by B with respect to 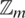 that is every edge in Km, m appears
that is every edge in Km, m appears 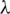 times in
times in  and D(Gp, Gq) for all
and D(Gp, Gq) for all 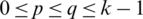 , are sets, and
, are sets, and 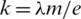 .
.
For all  and
and 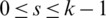 , let
, let  is a pre-starter graph
is a pre-starter graph 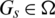 , that is
, that is 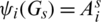 and
and 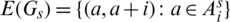 .
.
Let the set D(Gp, Gp) = D1 and the set D(Gp, Gq) = D2 and 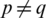 .
.
For all  , and for all
, and for all 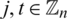 , define
, define 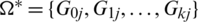 by
by
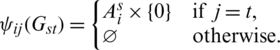
Then 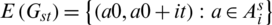 . Then every edge in Kmn, mn (its vertices are
. Then every edge in Kmn, mn (its vertices are  ) appears
) appears 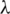 times in
times in 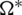 . For any two graphs
. For any two graphs 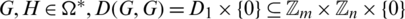 which is a set and
which is a set and 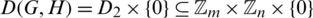 which is a set then
which is a set then 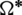 is a
is a 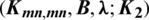 -GD generator of
-GD generator of 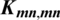 by
by 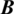 with respect to
with respect to 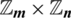 .
.
4 Coding Error Detection and Correction Application
The rows or columns of the incedence matrix of the GDs can be used as binary codes because all of its entries are 0 or 1. Let us define the GD’s Incedence matrix 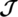 as follows.
as follows.
For the 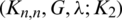 -GD, since Kn, n has n2 edges and we have s blocks (GD subgraphs), define
-GD, since Kn, n has n2 edges and we have s blocks (GD subgraphs), define 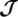 as
as 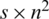 integer matrix where its elements are 0 or 1 and displays the relation between the edges and the blocks where every row corresponds to a block (GD subgraph Gi) and every column corresponds to an edge (ej) in the graph Kn, n.
integer matrix where its elements are 0 or 1 and displays the relation between the edges and the blocks where every row corresponds to a block (GD subgraph Gi) and every column corresponds to an edge (ej) in the graph Kn, n.
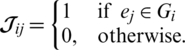
GD Incidence Matrix has the following properties:
As the incidence matrix 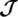 of a
of a 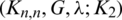 -GD has the following properties.
-GD has the following properties.
1. Every row has n number of 1s,
2. Every column has 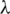 number of 1s,
number of 1s,
3. Two distinct columns both have 1s in at most 1 rows.
For illustration, the following example is produced.
The blocks of (K3, 3, S3, 2; K2)-GD is constructed as:
where ab is an edge between vertex a0 and vertex b1, see Fig. 1. The incedence matrix of this GD is

Figure 1: (K3, 3, S3, 2; K2)-GD
When a GD is transformed into an incidence matrix, the rows and the columns can be both viewed as a binary nonlinear code. The binary codes formed from the row denoted as  and binary codes from the column will be referred as
and binary codes from the column will be referred as  . As mentioned previously, by conversion of GD to incidence matrix, the incidence matrix of a GD retains certain properties that are inherited from GD. Using these properties, results can be obtained to evaluate the minimum Hamming distance (number of different bits in two codes) between codes from
. As mentioned previously, by conversion of GD to incidence matrix, the incidence matrix of a GD retains certain properties that are inherited from GD. Using these properties, results can be obtained to evaluate the minimum Hamming distance (number of different bits in two codes) between codes from  or
or 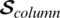 . Where
. Where
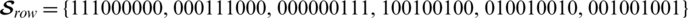
and
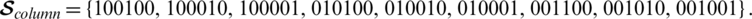
The minimum Hamming distance 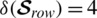 and
and 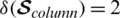 .
.
Distance in binary codes detects the number of errors a code can detect or correct [25]. As proved in [26], we have
• a binary code 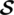 can be detected up to q errors iff the minimum distance
can be detected up to q errors iff the minimum distance 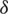 is greater or equivalent to q + 1.
is greater or equivalent to q + 1.
• a binary code 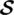 can be corrected up to q errors iff the minimum distance
can be corrected up to q errors iff the minimum distance 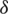 is greater or equivalent to 2q + 1.
is greater or equivalent to 2q + 1.
Then for our example 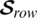 can detect upto 3 errors and correct upto one error.
can detect upto 3 errors and correct upto one error.
Efficiency factor E is the the quality estimation of the design efficiency. The efficiency factor E is a numerical value lies between 0 and 1. The quality of a design is “good” if E is greater than 0.75 The efficiency of the 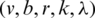 -BIBD design codes [27] is calculated as
-BIBD design codes [27] is calculated as 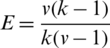 which can be simplified for our graph design as
which can be simplified for our graph design as  (put v = n2, the size of Kn, n and k = n, the size of G) which will be always greater than 0.75 where n is the size of the GD blocks. Then the efficiency of the codes from the GDs are very good and can be safely used in coding processes. For more details about the design efficiency, see [27]. For more applications of networks, see [28–30].
(put v = n2, the size of Kn, n and k = n, the size of G) which will be always greater than 0.75 where n is the size of the GD blocks. Then the efficiency of the codes from the GDs are very good and can be safely used in coding processes. For more details about the design efficiency, see [27]. For more applications of networks, see [28–30].
To clear the proposed application, we use the above 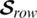 for coding the following words shown in Tab. 1 and assuming that there is a possibility of occurring an error in at most two positions. From the structure of the corresponding GD, the number of ones must be 3 in any code.
for coding the following words shown in Tab. 1 and assuming that there is a possibility of occurring an error in at most two positions. From the structure of the corresponding GD, the number of ones must be 3 in any code.
If the code 111100001 is received. Since number of ones must be 3, the error is detected. To correct the error, the code with the minimum Hamming distance from the received one can be chosen that is 111000000. Then the message is “go,” and so on.
Here, we use the above representation of graphs to construct 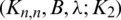 -GD for
-GD for 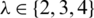 by certain graph classes B.
by certain graph classes B.
Lemma 5.1 Let 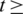 1 be a positive integer. There exists
1 be a positive integer. There exists 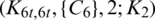 -GD.
-GD.
Proof. For n = 6, define 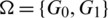 by
by
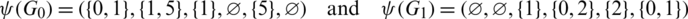
Then all graphs in  are isomorphic to C6 and
are isomorphic to C6 and
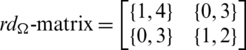
Since every cell of the 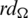 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 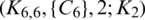 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.2 Let 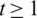 be a positive integer. There exists
be a positive integer. There exists 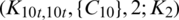 -GD.
-GD.
Proof. For n = 10, define 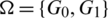 by
by
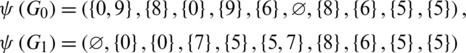
Then all graphs in  are isomorphic to C10 and
are isomorphic to C10 and
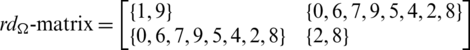
Since every cell of the 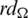 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 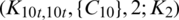 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
The existence of 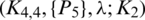 -GD still open for
-GD still open for 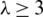 . Nevertheless, we can record the following result as:
. Nevertheless, we can record the following result as:
Lemma 5.3 For 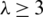 . There is no
. There is no 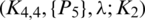 -GD generator.
-GD generator.
Proof. Let P5 is a spanning subgraph of K4, 4. Then the following vectors and all of its translates are the all possible pre-starter vectors of P5 shown in Tab. 2. By careful inspection, we find that there are no 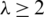 mutually orthogonal pre-starter vectors inside this collection, then the proof is complete.
mutually orthogonal pre-starter vectors inside this collection, then the proof is complete.
Table 2: All possible pre-starter vectors of P5


Proposition 5.4 Let 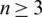 be a positive integer. There exists a
be a positive integer. There exists a 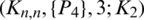 -GD.
-GD.
Proof. Define 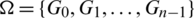 as follows.
as follows.
For all 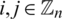 .
.
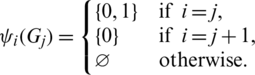
Then all graphs in  are isomorphic to P4 and
are isomorphic to P4 and 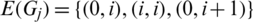 , and
, and
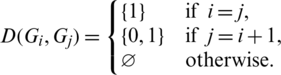
Since every cell of the 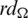 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 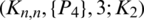 -GD generator.
-GD generator. 
Lemma 5.5 Let 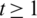 be a positive integer. There exists a
be a positive integer. There exists a 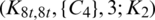 -GD.
-GD.
Proof. For n = 8, define 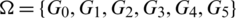 as.
as.
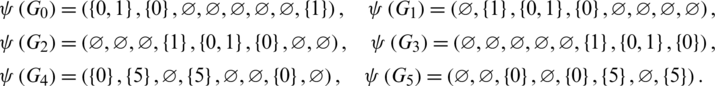
Then all graphs in  are isomorphic to C4 and
are isomorphic to C4 and

Since every cell of the 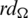 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 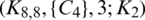 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.6 Let 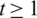 be a positive integer. There exists
be a positive integer. There exists  -GD.
-GD.
Proof. For n = 6, define 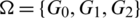 as.
as.
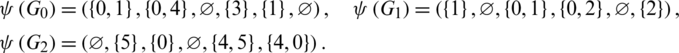
Then all graphs in  are isomorphic to P7 and
are isomorphic to P7 and
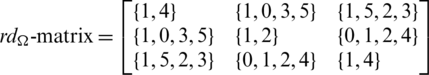
Since every cell of the 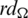 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 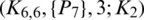 -GD generator, Applying Proposition 3.5 completes the proof.
-GD generator, Applying Proposition 3.5 completes the proof. 
Lemma 5.7 Let 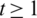 be a positive integer. There exists a
be a positive integer. There exists a 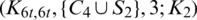 -GD.
-GD.
Proof. For n = 6, define 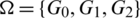 by
by
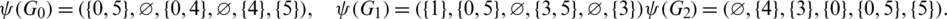
Then all graphs in  are isomorphic to
are isomorphic to 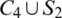 and
and
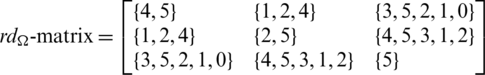
Since every cell of the 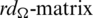 is a set satisfying Lemma 3.3, then
is a set satisfying Lemma 3.3, then  is a
is a  -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.8 Let 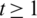 be a positive integer. There exists a
be a positive integer. There exists a  -GD.
-GD.
Proof. For n = 6, define 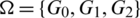 by
by

Then 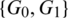 are isomorphic to C6, G2 is isomorphic to
are isomorphic to C6, G2 is isomorphic to 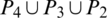 and
and
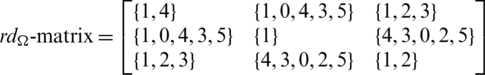
Since every cell of the 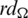 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 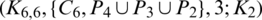 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof.
Lemma 5.9 Let  be a positive integer. There exists a
be a positive integer. There exists a 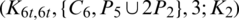 -GD.
-GD.
Proof. For n = 6, define 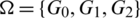 by
by
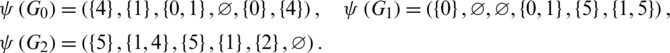
Then  are isomorphic to C6, G2 is isomorphic to
are isomorphic to C6, G2 is isomorphic to 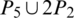 and
and
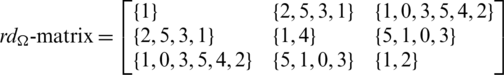
Since every cell of the 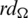 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 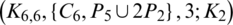 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.10 Let 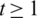 be a positive integer and G is the class of the spanning sub-graphs isomorphic to the graph with vertices
be a positive integer and G is the class of the spanning sub-graphs isomorphic to the graph with vertices 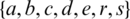 and the 6 edges
and the 6 edges 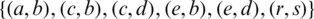 . There exists a
. There exists a 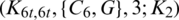 -GD.
-GD.
Proof. For n = 6, define 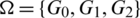 by
by
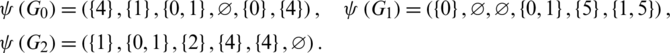
Then 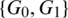 are isomorphic to C6, G2 is isomorphic to G and
are isomorphic to C6, G2 is isomorphic to G and
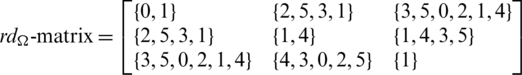
Since every cell of the 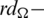 matrix is a set satisfying Lemma 3.3, then
matrix is a set satisfying Lemma 3.3, then  is a
is a 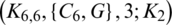 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.11 Let 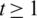 be a positive integer. There exists a
be a positive integer. There exists a 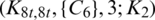 -GD.
-GD.
Proof. For n = 8, define 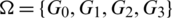 as.
as.
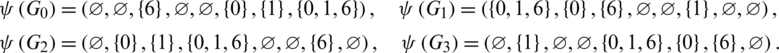
Then all graphs in  are isomorphic to C6 and
are isomorphic to C6 and

Since every cell of the 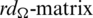 is a set satisfying Lemma 3.3, then
is a set satisfying Lemma 3.3, then  is a
is a 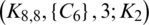 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.12 Let 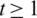 be a positive integer and G is a graph containing a cycle C4 in addition to an edge K2such that they share a vertex. There exists
be a positive integer and G is a graph containing a cycle C4 in addition to an edge K2such that they share a vertex. There exists 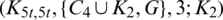 -GD.
-GD.
Proof. For n = 5, define 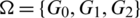 as:
as:
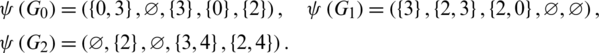
Then 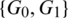 are isomorphic to C4, G2 is isomorphic to G and
are isomorphic to C4, G2 is isomorphic to G and

Since every cell of the 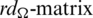 is a set satisfying Lemma 3.3, then
is a set satisfying Lemma 3.3, then  is a
is a 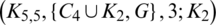 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.13 Let 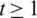 be a positive integer. There exists a
be a positive integer. There exists a 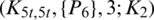 -GD.
-GD.
Proof. For n = 5, define 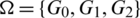 as:
as:

Then all graphs in  are isomorphic to P6 and
are isomorphic to P6 and
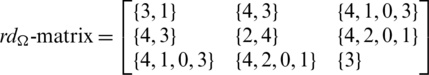
Since every cell of the 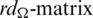 is a set satisfying Lemma 3.3, then
is a set satisfying Lemma 3.3, then  is a
is a 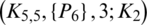 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof.
Lemma 5.14 Let  be a positive integer. There exists a
be a positive integer. There exists a 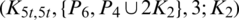 -GD.
-GD.
Proof. For n = 5, define 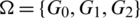 as.
as.
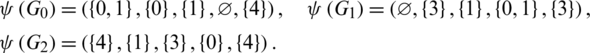
Then 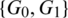 are isomorphic to P6, G2 is isomorphic to
are isomorphic to P6, G2 is isomorphic to 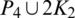 and
and
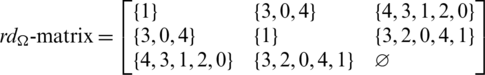
Since every cell of the 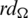 -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a  -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.15 Let 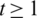 be a positive integer. There exists a
be a positive integer. There exists a 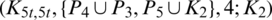 -GD.
-GD.
Proof. For n = 5, define 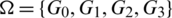 as:
as:
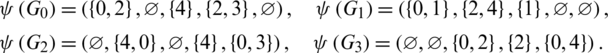
Then 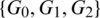 are isomorphic to
are isomorphic to 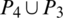 , G3 is isomorphic to
, G3 is isomorphic to 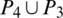 and
and

Since every cell of the  -matrix is a set satisfying Lemma 3.3, then
-matrix is a set satisfying Lemma 3.3, then  is a
is a 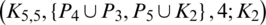 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Lemma 5.16 Let 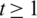 be a positive integer. There exists a
be a positive integer. There exists a  -GD.
-GD.
Proof. For n = 5, define 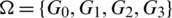 as:
as:
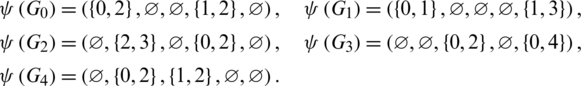
Then all graphs in  are isomorphic to
are isomorphic to  and
and

Since every cell of the 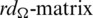 is a set satisfying Lemma 3.3, then
is a set satisfying Lemma 3.3, then  is a
is a 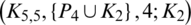 -GD generator. Applying Proposition 3.5 completes the proof.
-GD generator. Applying Proposition 3.5 completes the proof. 
Definition 6.1 Let 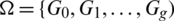 be a collection of spanning subgraphs of H = r-regular
be a collection of spanning subgraphs of H = r-regular 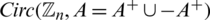 where
where 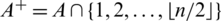 . We call
. We call  a
a 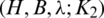 -GD generator if it satisfies the following conditions:
-GD generator if it satisfies the following conditions:
1. Every element of A+ appears exactly  times in the sum of the multisets L(Gi),
times in the sum of the multisets L(Gi), 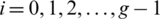 .
.
2. For all pairs i, j with 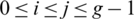 , the cells of the
, the cells of the 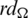 matrix are sets, that is D(Gi, Gj) are all sets.
matrix are sets, that is D(Gi, Gj) are all sets.
The elements of the generator  are called
are called 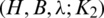 -GD pre-starters graphs.
-GD pre-starters graphs.
Theorem 6.2 Let 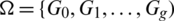 be a
be a 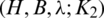 -GD generator. Then for all
-GD generator. Then for all 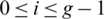 , the collection of all the translates of
, the collection of all the translates of 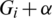 for all
for all  , forms a
, forms a  -GD by B.
-GD by B.
Proof. It is clear that the collection of all translates covers every edge of H exactly 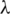 times. Now, It is to show that the collection of all translates are mutually orthogonal, that is any two graphs of the collection of all translates share at most one edge. Consider two translates
times. Now, It is to show that the collection of all translates are mutually orthogonal, that is any two graphs of the collection of all translates share at most one edge. Consider two translates 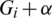 and
and 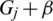 where
where 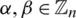 and assume that they share two edges e1 = (x, y) with length l1 = y − x and e2 = (u, v) with length l2 = v − u. Then the two edges
and assume that they share two edges e1 = (x, y) with length l1 = y − x and e2 = (u, v) with length l2 = v − u. Then the two edges 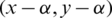 ,
, 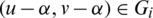 with lengths l1, l2 respectively and
with lengths l1, l2 respectively and 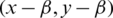 ,
, 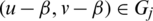 with lengths l1, l2 respectively. Then the distance between the two edges with length l1 in Gi and Gj is
with lengths l1, l2 respectively. Then the distance between the two edges with length l1 in Gi and Gj is  , and also the distance between the two edges with length l1 in Gi and Gj is
, and also the distance between the two edges with length l1 in Gi and Gj is  and then D(Gi, Gj) is not a set. This is a contradiction of the second condition in the Definition 6.1 of the
and then D(Gi, Gj) is not a set. This is a contradiction of the second condition in the Definition 6.1 of the 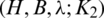 -GD generator. Consequently, all subgraphs in the collection of all translates of GD-generator are mutually orthogonal, that is a
-GD generator. Consequently, all subgraphs in the collection of all translates of GD-generator are mutually orthogonal, that is a 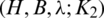 -GD.
-GD. 
Lemma 6.3 Let 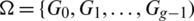 be a
be a 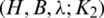 -GD generator, then
-GD generator, then
i) the number of pre-starters in 
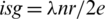 ,
,
ii) For all 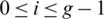 , if
, if 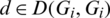
 ,
,
iii) For all  , if n is even then
, if n is even then 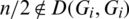 .
.
Proof. (i) 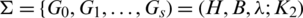 -GD. Since the s = gn then
-GD. Since the s = gn then 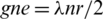 and hence
and hence 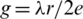 .
.
(ii) Let D(Gi, Gi) contains 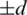 then Gi contains four edges each pair of them has the same length l1 and l2, that is (x, x + l1), (x + d, x + d + l1), (u, u + l2),
then Gi contains four edges each pair of them has the same length l1 and l2, that is (x, x + l1), (x + d, x + d + l1), (u, u + l2), 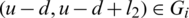 .
.
Then Gi + d contains (x + d, x + d + l1), (x + 2d, x + 2d + l1), (u + d, u + d + l2), (u, u + l2) which imply that 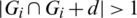 which is a contradiction. Hence, for all
which is a contradiction. Hence, for all 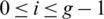 , if
, if  then
then 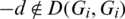
(iii) For any 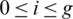 , let
, let  .
.
So there exist two edges e1 = (x, x + l), e2 = (x + n/2, x + n/2+l) belong to E(Gi) with the same length l and D(e1, e2) = n/2.
Then Gi + n/2 contains also e1 = (x, x + l), e2 = (x + n/2, x + n/2+l) that means 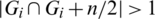 which is a contradiction. Hence, for all
which is a contradiction. Hence, for all 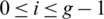 , if n is even then
, if n is even then 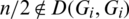 .
.
Therefore, 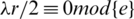 is a necessary condition of the existence of the
is a necessary condition of the existence of the 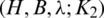 -GD generator.
-GD generator. 
Proposition 6.4 Let 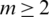 and
and 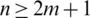 be integers and let H = 2m-regular
be integers and let H = 2m-regular 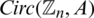 where
where
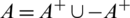
where 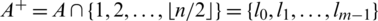 . Then there exists
. Then there exists 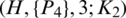 -GD.
-GD.
Proof. Define 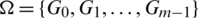 as:
as:
For all 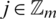 and for all
and for all 
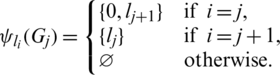
Then all graphs in  are isomorphic to P4 and
are isomorphic to P4 and
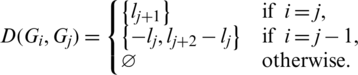
Since every cell of the 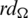 -matrix is a set satisfying Lemma 6.3, then
-matrix is a set satisfying Lemma 6.3, then  is a
is a  -GD generator.
-GD generator. 
Proposition 6.5 Let 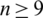 be an integer and let H = 8 -regular
be an integer and let H = 8 -regular 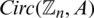 where
where 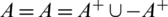 where
where  . Then there exists
. Then there exists 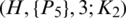 -GD.
-GD.
Proof. Define 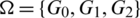 as:
as:
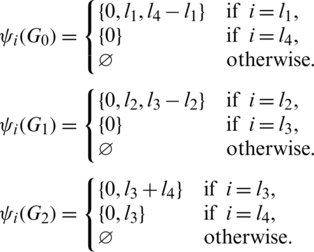
Then all graphs in  are isomorphic to P5 and
are isomorphic to P5 and

Since every cell of the 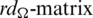 is a set satisfying Lemma 6.3, then
is a set satisfying Lemma 6.3, then  is a
is a 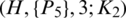 -GD generator.
-GD generator. 
Proposition 6.6 Let  be a positive integer and H be 4-regular
be a positive integer and H be 4-regular 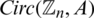 where
where 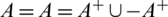 where
where 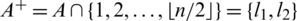 such that
such that 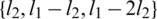 ,
, 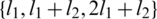 ,
,  ,
, 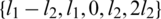 and
and 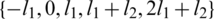 are all sets (i.e., all have different elements).Then there exists
are all sets (i.e., all have different elements).Then there exists 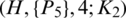 -GD.
-GD.
Proof. Define 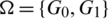 as
as
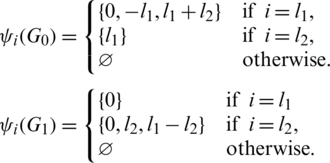
Since 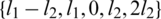 and
and 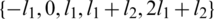 are sets then all graphs in
are sets then all graphs in  are isomorphic to P5 and
are isomorphic to P5 and
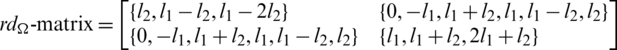
Since every cell of the 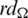 -matrix is a set satisfying Lemma 6.3, then
-matrix is a set satisfying Lemma 6.3, then  is a
is a 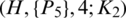 -GD generator. For illustration, at n = 7 take l1 = 1 and l2 = 3.
-GD generator. For illustration, at n = 7 take l1 = 1 and l2 = 3.
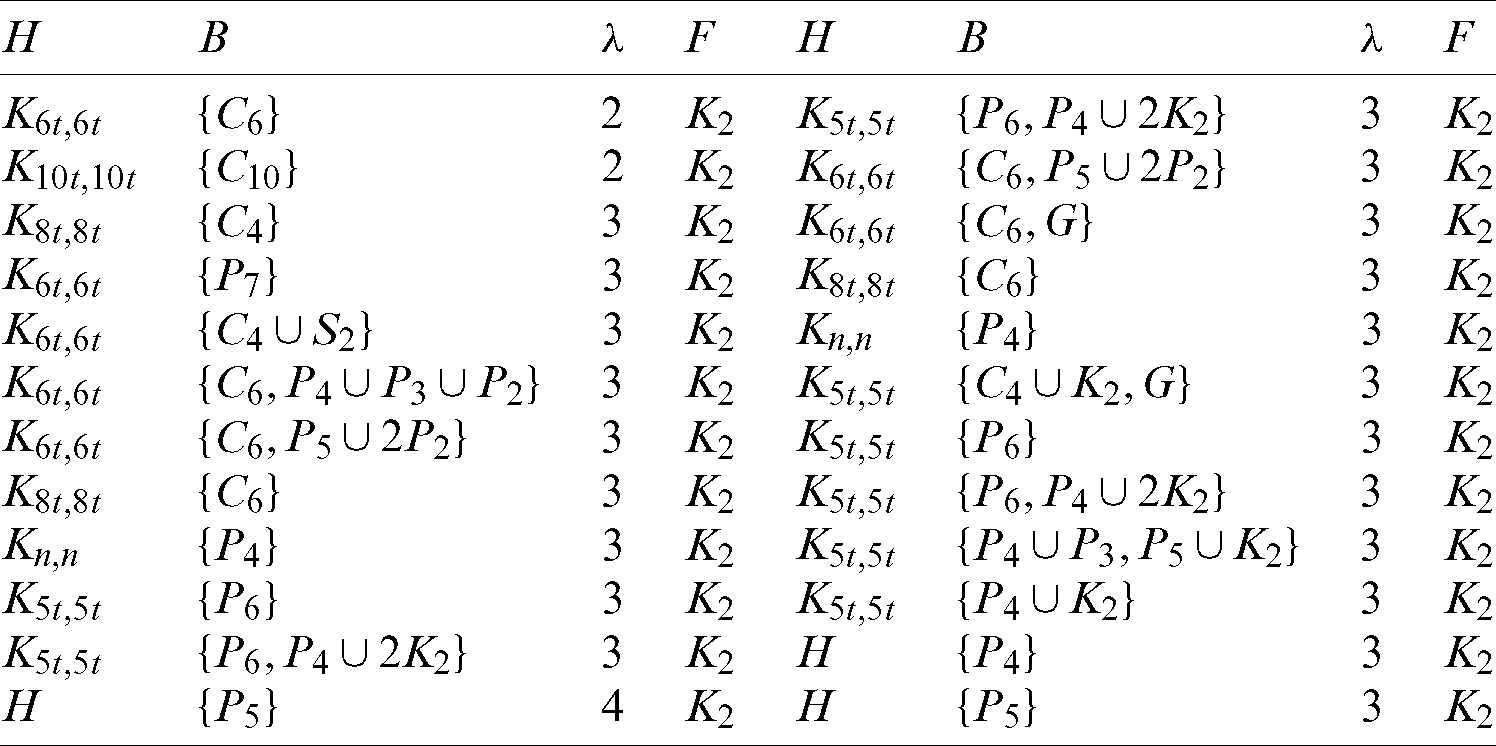
In this paper, we have studied the group generated graph designs. A new representation of graphs has been proposed that help in constructing new graph designs  -GD that can be summerized in Tab. 3. Where H is certain circulant graph. In addition, an efficient coding method has been proposed using the constructed graph designs which may open a new door to produce more research in this area. Finally, we can state that the constructed GD’s can be efficiently used to generate a code set.
-GD that can be summerized in Tab. 3. Where H is certain circulant graph. In addition, an efficient coding method has been proposed using the constructed graph designs which may open a new door to produce more research in this area. Finally, we can state that the constructed GD’s can be efficiently used to generate a code set.
Acknowledgement: The authors are thankful of the Taif University. Taif University researchers supporting project number (TURSP-2020/031), Taif University, Taif, Saudi Arabia.
Funding Statement: The authors received financial support from Taif University Researchers Supporting Project Number (TURSP-2020/031), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. D. O. F. Gronau, R. C. Mullin, A. Rosa and P. J. Schellenberg. (2000). “Symmetric graph designs,” Graphs and Combinatorics, vol. 16, no. 1, pp. 93–102. [Google Scholar]
2. P. Hell and A. Rosa. (1972). “Graph decompositions, handcuffed prisoners and balanced P-designs,” Discrete Mathematics, vol. 2, no. 3, pp. 229–252. [Google Scholar]
3. J. Bosák. (1990). Decomposition of graphs. London: Kluwer. [Google Scholar]
4. D. Fronček and A. Rosa. (2000). “Symmetric graph designs on friendship graphs,” Journal of Combinatorial Designs, vol. 8, pp. 201–206. [Google Scholar]
5. M. Higazy and R. Scapellato. (2015). “Orthogonal double covers of complete bipartite graphs by paths and cycles,” Advances and Applications in Discrete Mathematics, vol. 15, no. 1, pp. 9–20. [Google Scholar]
6. M. Higazy. (2015). “Suborthogonal double covers of the complete bipartite graphs by all bipartite subgraphs with five edges over finite fields,” Far East Journal of Applied Mathematics, vol. 91, no. 1, pp. 63–80. [Google Scholar]
7. R. El-Shanawany. (2002). “Orthogonal double covers of complete bipartite graphs,” Ph.D. dissertation, University of Rostock, Germany. [Google Scholar]
8. S. Hartmann. (1999). “A symptotic results on suborthogonal G-decompositions of complete digraphs,” Discrete Applied Mathematics, vol. 95, pp. 311–320. [Google Scholar]
9. S. Hartmann and U. Shumacher. (2000). “Suborthogonal double covers of complete graphs,” Congressus Numerantium, vol. 147, pp. 33–40. [Google Scholar]
10. U. Shumacher. (1999). “Suborthogonal double covers of complete graphs by stars,” Discrete Applied Mathematics, vol. 95, no. 1–3, pp. 439–444. [Google Scholar]
11. R. Scapellato, R. El Shanawany and M. Higazy. (2009). “Orthogonal double covers of Cayley graphs,” Discrete Applied Mathematics, vol. 157, no. 14, pp. 3111–3118. [Google Scholar]
12. R. Sampathkumar and S. Srinivasan. (2011). “Cyclic orthogonal double covers of 4-regular circulant graphs,” Discrete Mathematics, vol. 311, no. 21, pp. 2417–2422. [Google Scholar]
13. R. El-Shanawany, H. D. O. F. Gronau and M. Grüttmüller. (2004). “Orthogonal double covers of Kn, n by small graphs,” Discrete Applied Mathematics, vol. 138, pp. 47–63. [Google Scholar]
14. R. El-Shanawany and M. Higazy. (2008). “Orthogonal double covers of complete graphs by certain spanning subgraphs,” Australasian Journal of Combinatorics, vol. 42, pp. 223–228. [Google Scholar]
15. R. A. El-Shanawany, M. Higazy and R. Scapellato. (2009). “Orthogonal double covers of complete bipartite graphs by the union of a cycle and a star,” Australasian Journal of Combinatorics, vol. 43, pp. 281–293. [Google Scholar]
16. R. Sampathkumar and S. Srinivasan. (2009). “Mutually orthogonal graph squares,” Journal of Combinatorial Designs, vol. 17, no. 5, pp. 369–373. [Google Scholar]
17. R. El-Shanawany and A. El-Mesady. (2017). “On cyclic orthogonal double covers of circulant graphs by special infinite graphs,” AKCE International Journal of Graphs and Combinatorics, vol. 14, no. 3, pp. 269–276. [Google Scholar]
18. R. El-Shanawany. (2016). “On mutually orthogonal disjoint copies of graph squares,” Note di Matematica, vol. 36, no. 2, pp. 89–98. [Google Scholar]
19. R. El-Shanawany. (2016). “On mutually orthogonal graph-path squares,” Open Journal of Discrete Mathematics, vol. 6, no. 1, pp. 7–12. [Google Scholar]
20. H. D. O. F. Gronau, S. Hartmann, M. Grüttmüller, U. Leck and V. Leck. (2002). “On orthogonal double covers of graphs,” Designs Codes and Cryptography, vol. 27, no. 1/2, pp. 49–91. [Google Scholar]
21. J. Lauri and R. Scapellato. (2003). Topics in Graph Automorphisms and Reconstruction. London Mathematical Society S.T. 54, London: Cambridge University Press, . https://doi.org/10.1017/CBO9781316669846. [Google Scholar]
22. A. Boua, L. Oukhtite, A. Raji and O. A. Zemzami. (2014). “An algorithm to construct error correcting codes from planar near-rings,” International Journal of Mathematical Engineering and Science, vol. 3, no. 1, pp. 14–23. [Google Scholar]
23. S. Joon and M. Hwang. (2016). “Application of balanced incomplete block designs in error detection and correction,” . [Online]. Available: https://www.researchgate.net/publication/319621339. [Google Scholar]
24. H. D. O. F. Gronau, S. Hartman, M. Grüttmüller, U. Leck and V. Leck. (2002). “On orthogonal double covers of graphs,” Designs Codes and Cryptography, vol. 27, no. 1/2, pp. 49–91. [Google Scholar]
25. R. Merris. (2003). “Codes and designs,” in Combinatorics. 2nd ed., Hoboken, NJ: John Wiley, vol. 464. [Google Scholar]
26. K. H. Rosen, “Coding theory, AT&T laboratories: 7,” Accessed 14 October 2015. [Google Scholar]
27. R. Lidl and G. Pilz. (1984). “Further applications of fields and groups,” in Applied Abstract Algebra. 1st ed., New York: Springer-Verlag, vol. 256. [Google Scholar]
28. Q. Wu. (2020). “Computer image processing and neural network technology for boiler thermal energy diagnosis,” Thermal Science, vol. 24, no. 5, pp. 3059–3068. [Google Scholar]
29. J. Zhang. (2020). “Computer image processing and neural network technology for thermal energy diagnosis of boiler plants,” Thermal Science, vol. 24, no. 5, pp. 3221–3228. [Google Scholar]
30. G. Yu, J. Sang and Y. Sun. (2020). “Thermal energy diagnosis of boiler plant by computer image processing and neural network technology,” Thermal Science, vol. 24, no. 5, pp. 3367–3374. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |