Computers, Materials & Continua DOI:10.32604/cmc.2021.015371
Article

Analytical Comparison of Resource Search Algorithms in Non-DHT Mobile Peer-to-Peer Networks

Ajay Arunachalam1,*, Vinayakumar Ravi2, Moez Krichen3, Roobaea Alroobaea4 and Jehad Saad Alqurni5

1Centre for Applied Autonomous Sensor Systems (AASS), Örebro University, Örebro, Sweden
2Center for Artificial Intelligence, Prince Mohammad Bin Fahd University, Khobar, Saudi Arabia
3Faculty of CSIT, Al-Baha University, Saudi Arabia ReDCAD Laboratory, University of Sfax, Tunisia
4Department of Computer Science, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia
5Department of Education Technologies, College of Education, Imam Abdulrahman Bin Faisal University, Saudi Arabia
*Corresponding Author: Ajay Arunachalam. Email: ajay.arunachalam08@gmail.com
Received: 17 November 2020; Accepted: 08 January 2021

Abstract: One of the key challenges in ad-hoc networks is the resource discovery problem. How efficiently & quickly the queried resource/object can be resolved in such a highly dynamic self-evolving network is the underlying question? Broadcasting is a basic technique in the Mobile Ad-hoc Networks (MANETs), and it refers to sending a packet from one node to every other node within the transmission range. Flooding is a type of broadcast where the received packet is retransmitted once by every node. The naive flooding technique floods the network with query messages, while the random walk scheme operates by contacting subsets of each node’s neighbors at every step, thereby restricting the search space. Many earlier works have mainly focused on the simulation-based analysis of flooding technique, and its variants, in a wired network scenario. Although, there have been some empirical studies in peer-to-peer (P2P) networks, the analytical results are still lacking, especially in the context of mobile P2P networks. In this article, we mathematically model different widely used existing search techniques, and compare with the proposed improved random walk method, a simple lightweight approach suitable for the non-DHT architecture. We provide analytical expressions to measure the performance of the different flooding-based search techniques, and our proposed technique. We analytically derive 3 relevant key performance measures, i.e., the avg. number of steps needed to find a resource, the probability of locating a resource, and the avg. number of messages generated during the entire search process.

Keywords: Mathematical model; MANET; P2P networks; P2P MANET; unstructured; search algorithms; Peer-to-Peer; ad-hoc; flooding; random walk; resource discovery; content discovery; mobile peer-to-peer; broadcast; peer

1  Introduction

MANETs are dynamic mobile ad-hoc wireless networks that use multi-hop routing. The nodes in such networks are capable of communicating using layer-3 routing in case they are not connected at layer-2 directly. The resource discovery process is very challenging in such networks as there is a continuous movement of nodes. Previously, traditional search techniques like random walk and flooding were extensively employed for the resource discovery process. In flooding, the source node transmits the packet to all the other nodes in the network. Contrary to this, the packet is randomly transmitted to a few nodes in the network in the random walk approach. Although both approaches have some disadvantages, they are used in MANETs as it suits the self-organizing nature of the network. Several previous research works have studied the effectiveness of peer-to-peer (P2P) resource discovery approaches for wired networks. The effectiveness of several content searching techniques is tested for the P2P network. But, due to problems related to energy consumption, mobility, infrastructure deficiency, and churn, their performance is not validated against MANETs.

Noor et al. [1] studied the effectiveness of the random walk approach for MANETs and they have discussed its issues like unicast transmission disadvantage, valid termination check parameter, next-hop selection criteria, etc. P2P networks are very common, and they constitute a majority of internet traffic [2]. P2P networks are known for their flexibility and distributive network properties and P2P based systems are employed over the internet for services like video conferencing applications, torrent applications, information retrieval systems, telephony, file sharing, etc. Based on the architecture design, the P2P networks are categorized into 2 types. One is the structured type, where the peers are strictly well-organized with each peer maintaining a DHT index. Some of the cases that belong to this type are Tapestry, Pastry, Chord, CAN, etc. In this type, since the involved peer positions are structured, the query searches are more effective. But these systems have major shortcomings in a mobile ecosystem mainly due to peer churn. Due to rapid movement, index pointer is required to be altered constantly which increases overhead and complexity. Contrary to this, there are no strict rules for forming topology and placement of the peers in the unstructured type. Further, there is no need for any central indexing and nodes join arbitrarily. Some of the cases that belong to this type are Freenet, Random walk, Kazaa, Fastrack, Gnutella, etc. In a fully distributed P2P system, every peer has an equivalent role in the network. Centralized architecture is used for most mobile communication even today and the bottleneck issue created by them can be overcome by employing the P2P platform [3]. This P2P based approach suits wired and wireless networks including MANETs.

Combining P2P network properties in mobile ad-hoc networks is coined as P2P MANETs or Mobile P2P networks. Due to similarities in P2P and MANETs, a P2P overlay can run over Mobile Ad-hoc Network. An overlay network is formed by communication between the peers wherein each link of overlay corresponds to a path in an underlay physical network. But, at the same time, their direct combination also poses difficulties due to differences in the operating layer, transmission mechanism, and rapid mobility in MANETs.

In such a distributed environment, resource discovery is a key issue. Unstructured P2P networks mostly rely on flooding and random walk techniques for searching. As a preliminary study, we evaluated the unstructured P2P searching techniques over MANET [4,5]. According to our study, the pure random walk approach under MANETs consumes more battery power, increases network overhead, has high search latency, and lowered hit rate when compared to other unstructured protocols. To overcome this, we proposed a resource discovery protocol based on the cross-layered architecture to suit better and work well under P2P-MANETs as shown in Fig. 1. It is essential to take the topology of the underlying physical links into consideration when developing an efficient search strategy for such dynamic evolving networks [6–8]. For the same, we proposed an alternate technique for discovering the neighbor nodes and extracting the node density information for P2P applications running over MANET as given in Algorithm 1, whose source code is publicly available in SourceForge1 and the complete P2P network resource discovery simulation over mobile ad-hoc network with our proposed neighbor node discovery method is publicly available in GitHub.2

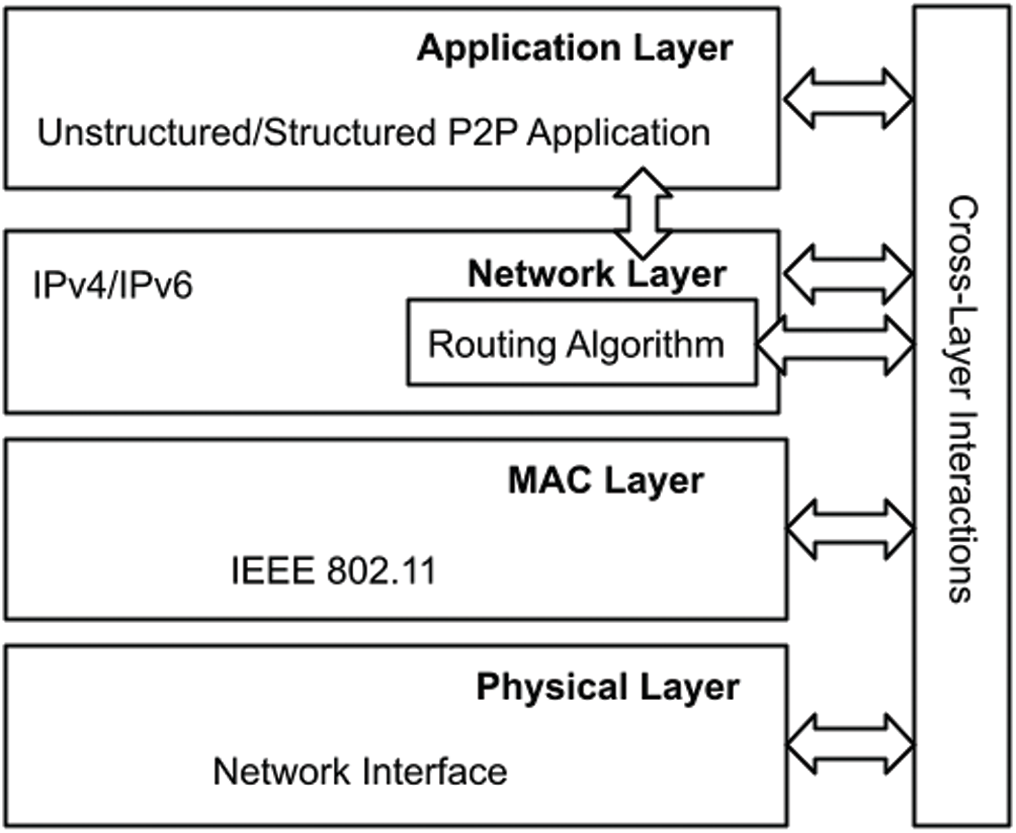
Figure 1: Proposed addressed cross-layered architecture

The rest of this paper is structured as follows. In Section 2, we review the existing work related to analytical based analysis for P2P and MANETs. Section 3 discusses the problem statement of modeling the physical situation. Analysis of flooding-based search procedures and our proposed scheme are introduced in Section 4, and their performance measures are derived. In Section 5, we summarize our results, and finally, Section 6 concludes the paper.

2  Related Works

In this section, we discuss the various relevant works that estimate the performance of resource discovery protocols analytically. Although there are many empirical studies and simulation-based analyses of flooding-based schemes and its variants, the mathematical results are still lacking especially in the context of P2P networks over MANET. Efficiently and quickly locating a resource is a major issue in unstructured networks. Techniques such as probabilistic forwarding, random walk, and flooding are extensively used in such unstructured architecture. Barjini et al. [9] analytically review many search techniques that are based on a flooding approach for an unstructured P2P network. They measure the coverage growth rate and traffic loads for each scheme. They introduce a metric, i.e., the critical value which is the ratio of the amount of redundant messages over the coverage growth rate. According to their study and simulation results, the probabilistic limit-based flooding schemes (i.e., teeming, modified breadth-first search, random walk, etc.) have better performance than the TTL limit based flooding schemes (such as local indices, expanding ring, iterative deepening, etc.). Bisnik et al. [10] present an analytical expression to measure the performance metrics of random walk protocol in unstructured P2P networks in terms of TTL of walkers, count of walkers, and demand of the resource. Their work focuses on a wired P2P network. Dimakopoulos et al. [11] study the performance of teeming, random path, and flooding search schemes, in P2P systems. Their study considers two scenarios, i.e., resource requests in the presence of popular and unpopular resources. Further, they assume that a cache is used to store the details of the resources and their corresponding resource providers at each node. To overcome the drawbacks observed in flooding and random walk techniques, Lin et al. [12] propose a technique that is the combination of both schemes. Depending on the search context, it performs flooding for a short-term search and follows the random walk technique for a long-term search. They use Newman’s work [13] for the random graph and adopt generating functions to model distribution degrees. An alternative to the flooding scheme is the gossip protocol, where every node transmits the message to a subset of its neighbors in a random fashion based on some probability. In [14], costs of Gnutella’s flooding-based broadcasting and the classic gossip protocol are studied by varying network size and the average number of neighbors. Further, they calculate the bandwidth required for each node in the flooding mechanism. They propose a deterministic gossip-based protocol and compare their performance with the flooding technique. Ferretti [15] proposes a mathematical model for the gossip-based resource discovery protocol in unstructured P2P overlay networks. Their analysis is based on complex network theory. They analyze and evaluate the count of nodes receiving the query and the amount of query hits. Specific work to model and optimize random walk protocol over MANET is presented in [16]. They modeled their method using a queuing system called G-network which has positive and negative kinds of customers. Further, they used the gradient descent method to optimize their method which uses 3 parameters such as consumption of energy, response time, and hit rate as part of the cost function. Most of the aforementioned works are evaluated over a wired and fixed layout like the internet. Further, in the case of analysis and evaluation of P2P content searching techniques under MANET, there is a lack of empirical study that considers the underlay network topology. A game theory-based resource search algorithm is proposed in [17]. In their work, a Rock-Paper-Scissors-Game-Based (RPSGB) strategy is deployed for resource discovery to complement mobile P2P networks. We apply the probability and queuing theory concepts to model the unstructured search techniques over MANET.

3  Problem Specification, and Analytical Modeling

An Overlay Graph OG=(V,E) is used to represent a P2P overlay network, where V is the count of nodes, and E is the count of links. The vertices and the edges of this graph represent the participating peers and virtual links respectively. Therefore, OG can be explicitly defined as, OG=(V,E) where |V|=p and link(i,j)∈E if i is a neighbour of j, and vice versa, and p is the count of peers. The underlay structure is formed by ad-hoc and peer nodes. Under MANETs, the P2P platform is implemented as an overlay network at the application layer, formed by communications between the peers wherein each link of the overlay is supported by a path in the underlay physical network. In our analysis, the underlay structure is considered as a connected graph CG=(V,E) where |V|=WN and link(i,j)∈E if and only if Dij≤Tx where WN is the count of wireless nodes, and Dij is the Euclidean distance between them. If the Euclidean distance between 2 nodes is less than Tx (transmission range of the node), then it means that they are in the transmission range of each other. Fig. 2 depicts the above explanation, where each virtual link of the overlay network is supported by a path in the underlying physical network.

:

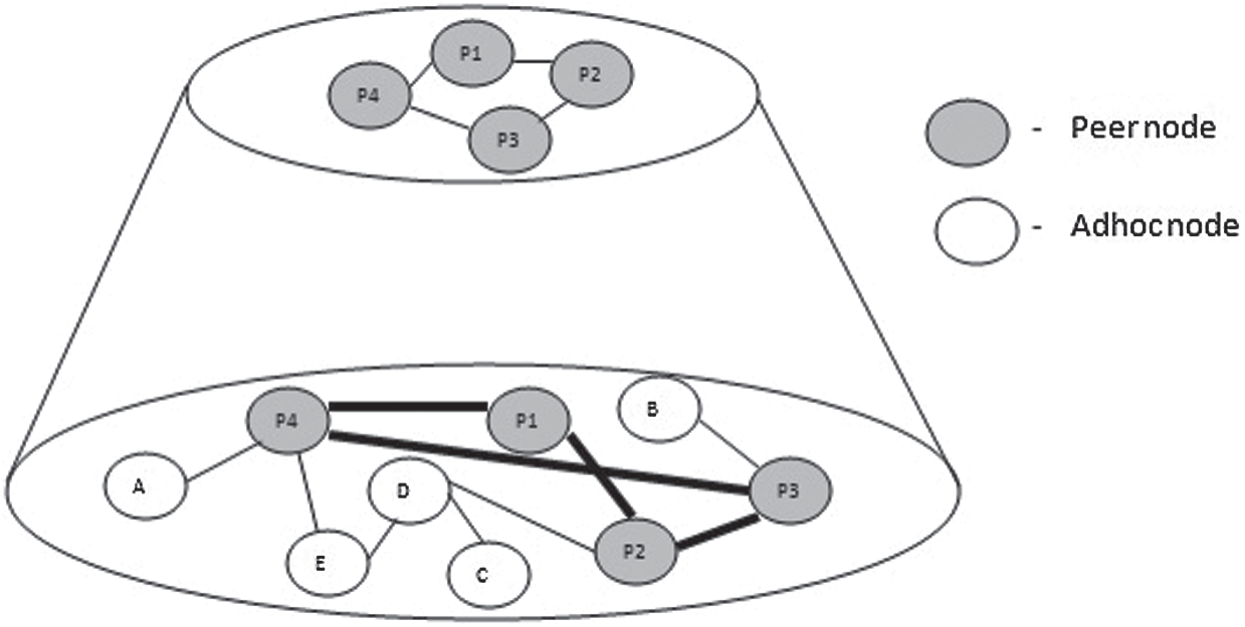
Figure 2: P2P Overlay running on MANET

Smart resource discovery is the heart of the P2P system. In ad-hoc networks, routing is expensive, so it requires a more effective resource discovery process. In such resultant networks, resource discovery is the key challenge due to frequent network dynamics. So, how the search query can be resolved quickly and efficiently while lowering the message overhead is the aim of our proposed scheme, validated further with analytical modeling.

We preliminarily assume a random network topology of N mobile nodes where only one node provides the resource x, and there is a single node S searching for that resource. Each node knows its d neighbors. We use the work done in [11] as the basis for our further analysis. Tab. 1 contains the summary of the notations used in the model along with their descriptions.

Table 1: Notations used and derived.

To limit the broadcast storm, the search is bounded to the maximum t number of steps (i.e., TTL value). Let us assume that F is the probability of resource x being known to a specific node. A node can know a resource only when it holds that resource.

F=1-P[the node doesn’t hold x]

Let nx be the count of nodes offering the resource “x”. Since a resource x is offered by only one node, we have nx = 1.

P [ node holds x ]=nxN=1N(1)

F=1-[1-(nxN)]=1-[N-nxN]=1-[a],wherea=N-nxN (2)

Let a be the probability that a node is not aware of the resource. So, a = 1 − F. Let Qt be the probability of finding a resource within t steps. We assume that within t steps, a resource can be located. Hence, the mean of steps needed to find the resource x is given as,

St¯=t-1Qt∑i=0t-1Qi(3)

The derivation of Eq. (3) is given at the end of the section. In the equation, Qt depends on the searching strategy. We consider flooding, random walk and our proposed addressed random walk methods which are depicted as a d-ary tree that unfolds as the search progresses, shown in Fig. 3. A tree representation may not be perfect for representing such wireless network topology as many nodes may overlap each other’s range and, multiple nodes may communicate with a single node. Yet, the tree representation can visualize the search scenario pictorially.

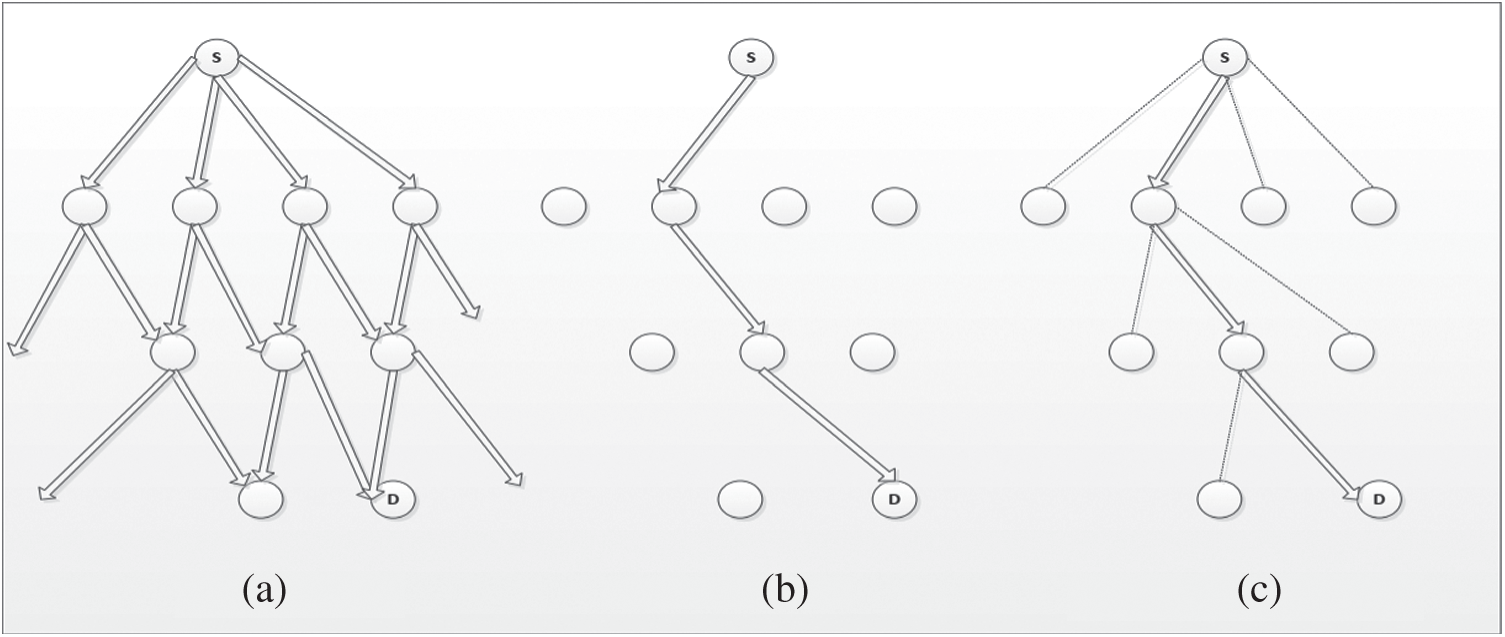
Figure 3: Comparison of different flooding-based search strategies and our proposed scheme. (a) Flooding, (b) random walk (c) addressed random walk

The focus of this article is on several decentralized resource discovery schemes. In flooding, when a resource is required by a node, it will communicate with its neighboring nodes and further, those nodes will communicate with their neighbors. This process will be repeated until every node in the network is communicated as shown in Fig. 3a. The flooding method can find a resource without any hierarchy or prior specific information about the system, thus an ideal candidate in such dynamically evolving networks. One of the disadvantages of this pure flooding method is that it increases the network traffic exponentially. Therefore, another variation of flooding called random walk is considered. This method restricts the search space by restricting the node to communicate only with one of its neighbors in a random fashion as presented in Fig. 3b. The limitation of this method is that it takes more steps to find a resource. Both the above-discussed schemes have their drawbacks and limitations. From our preliminary study [4,5], we observe that the random walk scheme under MANET increases the network overhead, battery power consumption, bandwidth usage, search latency, etc. And, further has a low success ratio. To overcome these issues, we propose a simple and lightweight resource discovery technique to suit well under MANET where the node propagates the inquiring message to exactly one of their neighbors at each hop, but at the same time end up unfolding different virtual paths concurrently, as shown in Fig. 3c. So, it will lower the network traffic even without restricting the search space.

Derivation of Eq. (3): Let si is the probability of finding a resource in ith step exactly. The probability of finding it within t≥1 steps is formulated as:

Qt=∑i=0tsi

This implies that st = Qt − Qt −1. Under the assumption that within t steps, the resource is found, the probability of finding it in ith step exactly is given by siQt and the mean of steps is given by:

St¯=1Qt∑i=1tisi=1Qt(Qt-1St-1¯+tst)

Substituting for st, we obtain:

QtSt¯=Qt-1St-1¯+tQt-tQt-1

Let gt=QtSt¯, the recurrence takes the following form:

gt = gt −1 +tQt − tQt −1, with the boundary of g0 = S0Q0 = 0

Evaluating gt we get,

gt=∑i=1tiQi-∑i=1tiQi-1=tQt-∑i=0t-1Qi

Since, gt=QtSt¯, Eq. (3). follows,

St¯=t-1Qt∑i=0t-1Qi

4  Performance Analysis

4.1 Flooding Algorithm

In flooding, a node that requires the resource will flood the message to its neighbors which in turn retransmits it to their neighbors. This will continue until the node that is holding the required resource is found or the TTL expires. For better understanding, the nodes in the network are represented as a d-ary tree. To visualize the situation, refer to Fig. 4, where the resource requesting node S is the root and node D holds the resource being searched. Fig. 4a shows a sample network where flooding technique is used while its corresponding rough d-ary tree representation is shown in Fig. 4b. Within consecutive search steps, the tree will contact at most di different nodes in the ith level.

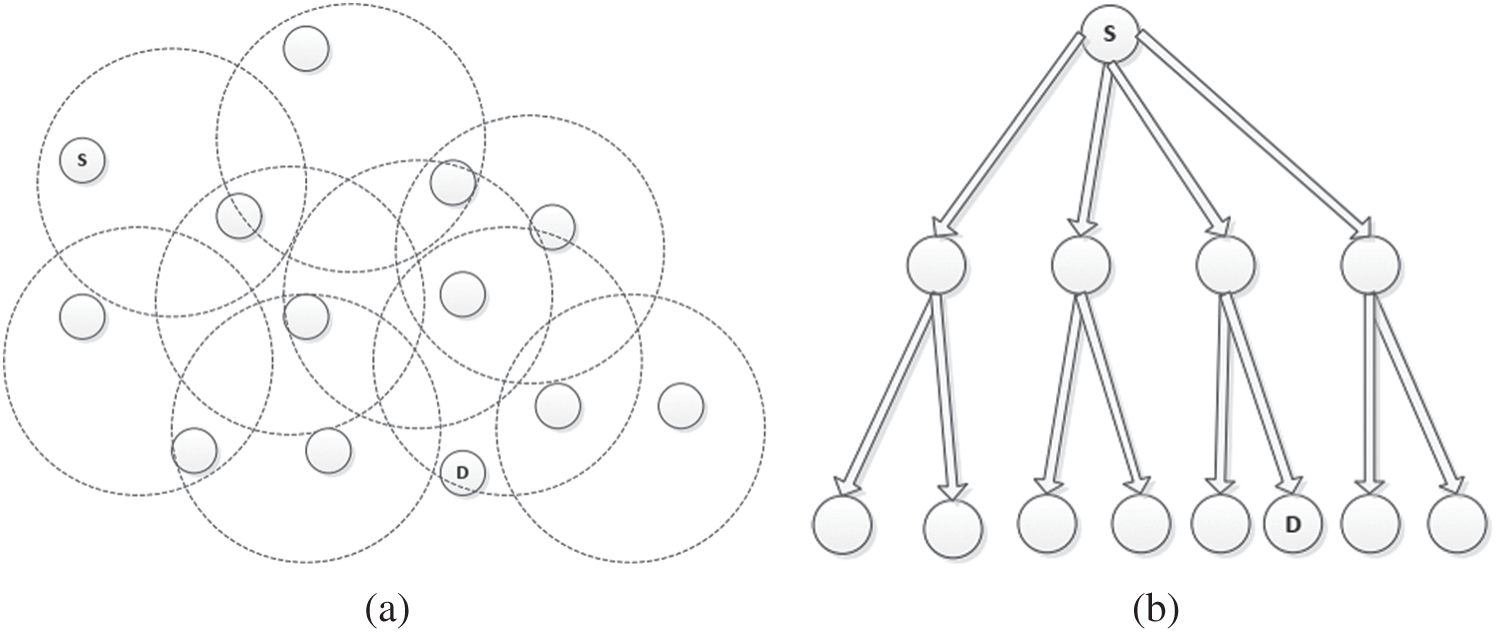
Figure 4: Searching using naive flooding technique (a) searching using broadcast by flooding technique (b) d-ary tree representation

Let Qt(F) be the probability to find the resource x within t steps for the flooding algorithm. F is the probability that a resource is known to a node and ‘a’ is the probability that a resource is not known to a node. Hence, a = 1 − F.

At ‘0’ step, the probability of not locating the resource x is given as,

Q0(F)=1-a=F (4)

1-Q0(F)=a (5)

1-Q1(F)=Probability of not locating the resource within “1” step

1-Q1(F)=Probability of not locating in 0 step * Probability of not finding in Step 1

1-Q1(F)=a*(1-Q0(F))d

Similarly,

1-Q2(F)=Probability of not locating in 0 steps * Probability of not locating in Step 1 *

Probability of not locating in Step 2

1-Q2(F)=a*(1-Q0(F))d*(1-Q1(F))d

Continuing this way, if we unfold the subsequent inquiring node’s neighbors until the t steps, then the probability of not locating resource x is generated as,

1-Qt(F)=a*(1-Qt-1(F))d(6)

From Eq. (4), it is clear than the initial boundary condition is Q0(F)=1-a=F. The probability Qt −1 occurs only if it finds the required resource until the t −1 levels of the subtree.

Therefore,

Qt(F)=1-a*(1-Qt-1(F))d(7)

Now replace 1-Qt(F) as qt, so Eq. (6) becomes, qt=a*(qt-1)d. Solving further we get,

qt=adt+1-1d-1

Now evaluating for different values of t,

q0=aq1=ad+1q2=a(ad+1)d=ad(d+1)+1q3=a(ad(d+1)+1)d=a(d+1)(d2+1)q4=a(d2+1)(d+1)(d+1)

Therefore, generalized as, qt=adt+1-1d-1

Hence Eq. (7) becomes,

Qt(F)=1-adt+1-1d-1(8)

Next, we determine the average number of steps required to locate the resource. In general, the average steps needed are given as in Eq. (3). Now substituting Eqs. (8) in (3), we get the average number of steps required to find the resource within t steps for the flooding algorithm for t≥1.

(9) St(F)¯=t-1Qt(F)*∑i=1t-1Qi(F)St(F)¯=t-1Qt(F)*∑i=1t-1(1-adi+1-1d-1)St(F)¯=t-1Qt(F)*(∑i=1t-11-∑i=1t-1adi+1-1d-1)St(F)¯=t-tQt(F)+∑i=0t-1adi+1-1d-1

St(F)¯=t-tQt(F)+1Qt(F)∑i=1tadi-1d-1 (10)

We now compute the average number of messages that will be generated for the flooding technique. In flooding, the messages are flooded through the network. A 1-hop broadcast with the message will be transmitted by the node S. Once the message is received by the 1-hop neighbors, the processed messages list will be updated with the newly received message’s sequence ID. This is done to avoid retransmitting the same message again in case if the message is received again through a different path. Now, if the required resource is held by a neighboring node D, an exclusive multi-hop reply will be transmitted by node D through the path resolved by routing protocol to the source S. However, even after the transmission of the resource reply message, the request message may be forwarded meaninglessly by all the other nodes that have received the request until every node in the network is reached. So, under MANETs, “d” messages will be generated by “d” neighboring nodes of the root, plus for the internal subtrees of those neighboring nodes. Thus,

Mt(F)¯=a(d+dm(t-1))(11)

where, m(t-1) denotes the transmission along the subtree T with (t-1) levels. In a subtree T, if the resource x is located at the root, a response will be sent to the querying node or else d messages will be generated by the child nodes plus the generated messages internally for each respective child subtrees T with (t-2) levels.

Symbolically it means,

m(t-1)=F+(d+dm(t-2))*(1-F)m(t-1)=1-a+ad+adm(t-2)

which has initial boundary condition of m(0)=1. After evaluating the recurrence, we get,

m(t-1)=(ad)t-1+(ad)t-1-1ad-1(ad+1-a)(12)

Now substituting Eqs. (12) in (11) and evaluating further we have,

Mt(F)¯=a+(ct-1)(2c-a)c-1,c=ad,t≥1(13)

4.2 Random Walk Algorithm

In the random walk algorithm under MANET, the querying node transmits the message to a specific neighboring node n that is selected in a random fashion from a list of neighbors resolved from the routing layer information over a unicast transmission. For such a random walk scenario, there will be p randomly unfolding paths to reach the destination, i.e., the node sends the request to p≥1 of its neighboring nodes and each of those neighboring nodes will unfold a random path of which one possibility is shown in Fig. 5.

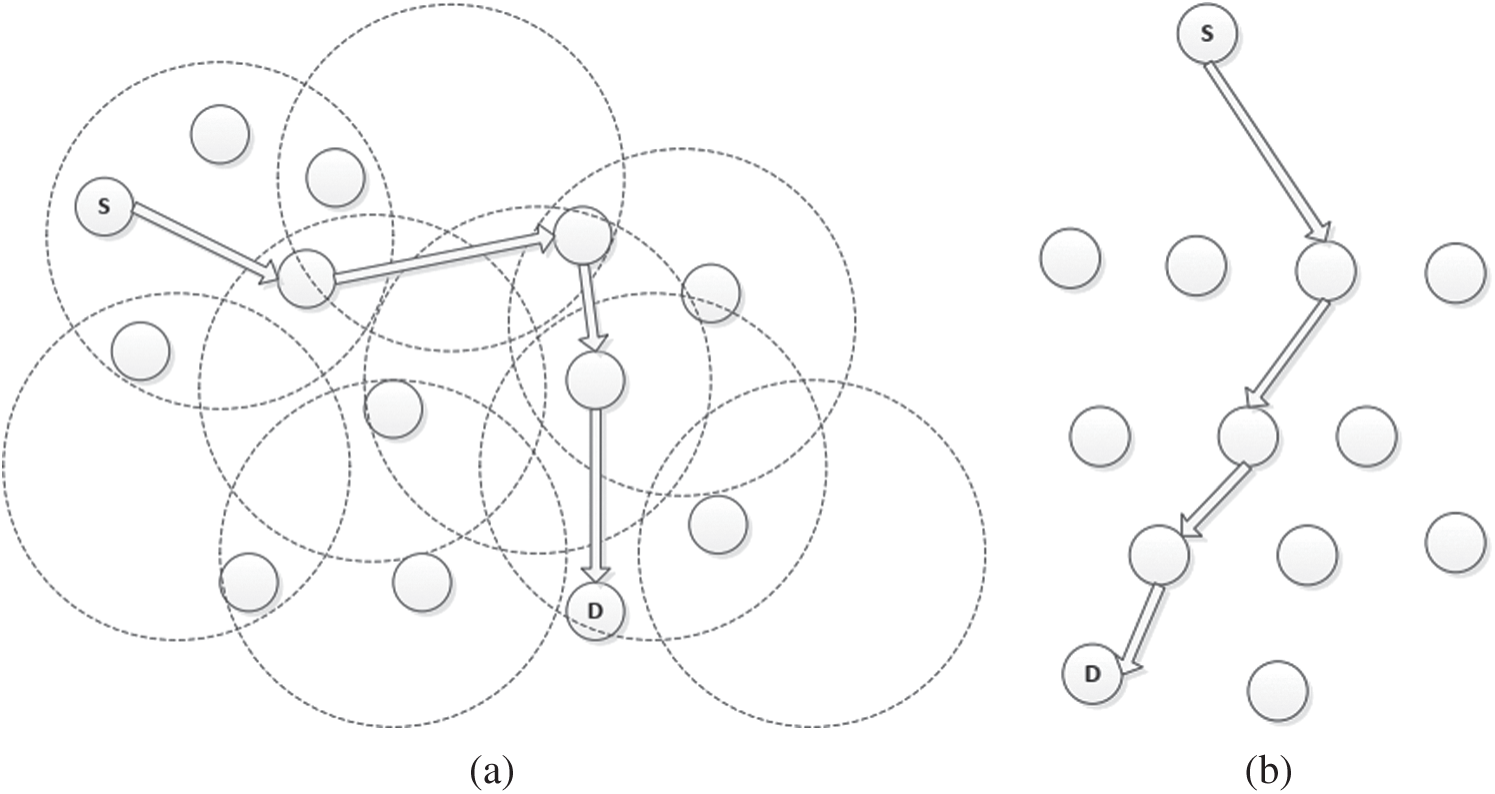
Figure 5: Searching using simple random walk technique (a) searching the network using classic random walk protocol (b) d-ary tree representation

Let Qt(p) be the probability of finding a resource within t steps for the random walk algorithm where p is one of the randomly unfolding paths of length t −1. F is the probability that a resource is known to a node and a is a probability that a resource is not known to a node. Hence, a = 1 − F. At “0”, step the probability of not locating x is given as,

1-Q0(p)=1-F=a

1-Qt(p)= Probability(‘x’ is not occur in ‘t’ step)

1-Qt(p)= Probability(‘x’ is not occur in ‘0’ step) and Probability(‘x’ is not occur in ‘1’ to ‘t’ step)

1-Qt(p)=(1-F)(1-qt-1)p(14)

where (1-F) is the probability that a resource is not known to a given node and (1-qt-1) is the probability of not finding the resource in one of the “p” randomly unfolding paths of length t −1.

After further evaluation we get,

Qt(p)=1-apt+1(15)

The average number of steps needed in general to locate the resource x is given in Eq. (3). Now substituting Eqs. (15) in (3) we get the average number of steps needed to find a resource within t steps for the random walk algorithm for p≥1, t≥1.

St(p)¯=t-1Qt(p)∑i=0t-11-api+1 which further is evaluated to,

St(p)¯=a-(1+t-tap)apt+1(1-ap)(1-apt+1)(16)

Finally, we compute the avg. generated messages in the random walk scheme under MANET which is different from that as in the wired network. The unicast transmission uses the routing layer information in a standard random walk algorithm under MANET. But the issue is that the nodes move continuously in MANETs. Therefore, there will be a rapid change of neighbors of all nodes over time. So, such transmission may often lead to failure since the topology of the network changes rapidly. Also, this leads to frequent re-route discovery which increases the message overhead. Hence, the overall message generated will be much more than the normal for each path due to the failure thereby incurring frequent re-route discovery at every hop. In such a dynamic scenario, there will be p messages generated by d neighbors for every p of its children, plus the messages generated in each of the p paths.

Mt(p)¯=(1-F)(dp+dpm(t-1))(17)

where, m(t-1) denotes the transmissions that take place along a path p of t −1 nodes.

For such a path p, the reply will be unicasted through the path resolved by the routing protocol if resource x is located at the root node. Further, the query will be terminated at that moment since the received message also contains the address S and the process will get terminated or else a message will be generated while forwarding to next node of the path plus the message generated inside the subpath p′ with t −2 nodes rooted at the next node. This gives the recurrence relation:

m(t-1)=1*F+(1+m(t-2))*(1-F)=am(t-2)+1 where, m(0)=1. On solving the recurrence relation, we get:

m(t-1)=at-1a-1(18)

Now substituting Eqs. (18) in (17) it gives:

Mt(p)¯=adp+adp(at-1a-1)(19)

4.3 Addressed Broadcast Random Walk (ABRW) Algorithm

To reduce the overhead in the classic random walk protocol, we proposed an improved random walk algorithm [7]. Our technique is based on the addressed broadcast transmission mechanism in which the querying node will pass the request to a particular random node over a 1-hop addressed broadcast transmission, i.e., the request is forwarded to that node, while the neighboring nodes within the hop range will overhear the request, but only the addressed node will process the request further and continue the resource discovery. So, in short, every neighbor node will receive the message at its application layer, but inside the message, there will be the nodeID for which that message is actually addressed to. The P2P agent at the application layer will process it differently based on the message content. So, the addressed node will only try to forward the message again. For our addressed random walk algorithm also, there will be a p randomly unfolding paths that can be followed to reach the destination. Our scheme is different from the standard random walk protocol as even the d overhearing neighbors can also see or receive the message, and hence there is a high probability of reaching the destination as the intermediate nodes can also reply if they have the resource x along the path p. And only p messages will be generated for its p children, as the addressed node will only continue with the resource discovery process further, i.e., the node transmits the message to p≥1 of its neighbors where each such neighbor unfolds a sub-tree with d neighbors of length t −1 where every d neighbors can also overhear the message. Let Qtdp be the probability of locating a resource within t steps for our proposed scheme where p is one of the randomly unfolding paths and for every such p children it unfolds a sub-tree of length t −1 with their d neighbors shown in Fig. 6.

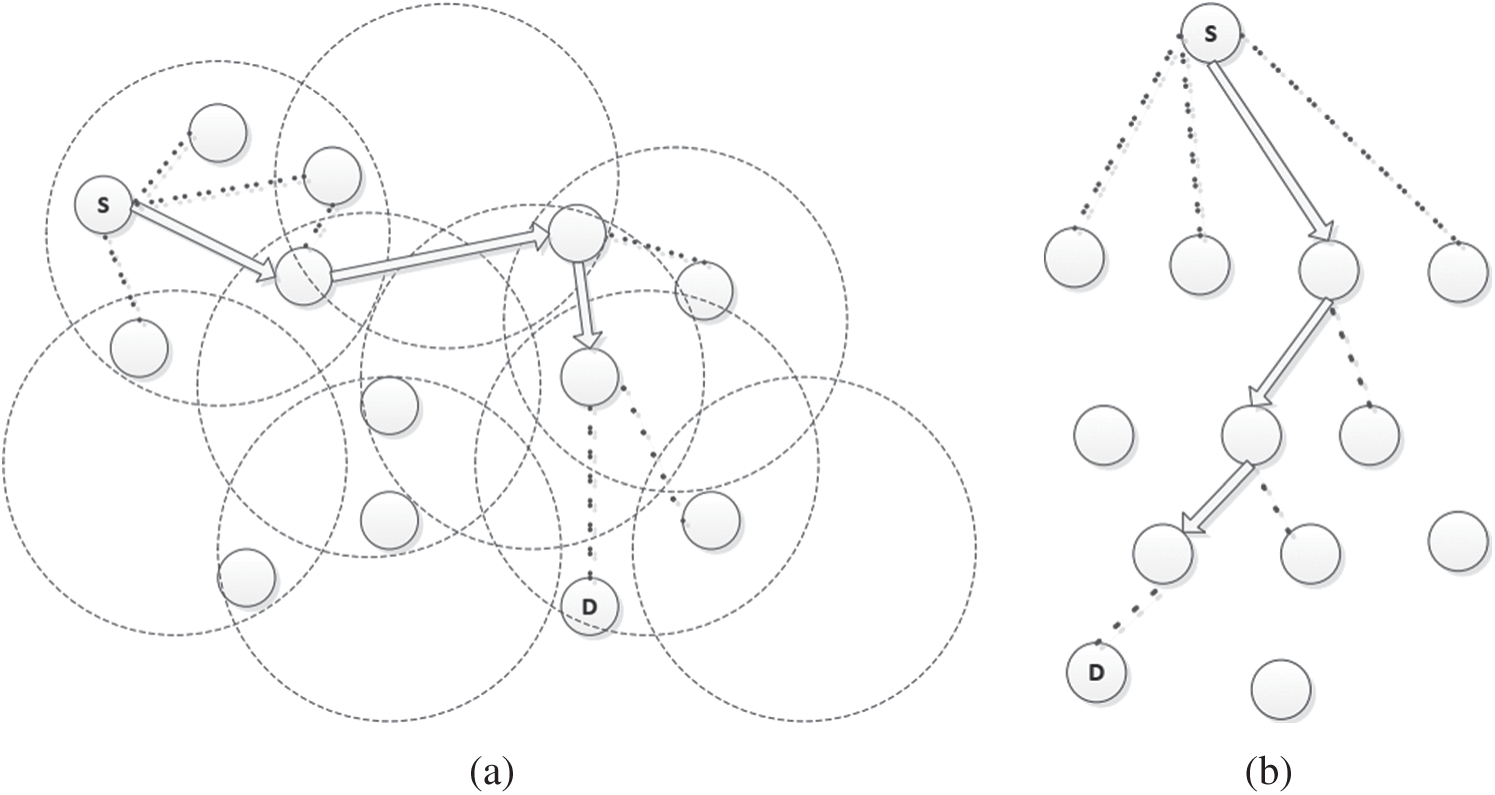
Figure 6: Searching using addressed broadcast random walk technique (a) searching the network using addressed broadcast random walk technique (b) d-ary tree representation

Let F be the probability that a resource is known to a node, and a is the probability that a resource is not known to a node. Hence, a = 1 − F. At step “0”, the probability of not locating x is given as,

1-Q0(dp)=1-F=a

Now,

1-Qt(dp)=Probability that ‘x’ is not found in ‘t’ step

1-Qt(dp)=(Probability that ‘x’ is not found in ‘0’ step) * (Probability that ‘x’ is not occur in ‘1’ to ‘t’ step)

1-Qt(dp)=(1-F)(1-Pt-1)p(20)

where, 1 − Pt −1 is the probability of not locating the resource in one of p randomly unfolding sub-tree of length t −1 with d neighbors.

1-Pt-1=a(1-Pt-2)dPt-1=1-adt-1d-11-Pt-1=adt-1d-1(21)

Now substituting Eqs. (21) in (20) we have,

1-Qt(dp)=(1-F)*ap(dt-1d-1)1-Qt(dp)=a*ap(dt-1d-1)1-Qt(dp)=ap(dt-1d-1)+1

Hence,

Qt(dp)=1-ap(dt-1d-1)+1(22)

In our proposed random walk technique, the probability of finding x is high at each p children along the path, as even the d neighbors can respond immediately. Hence, the number of steps required to find the resource will be minimal when compared to the other discussed techniques.

The average number of steps needed to find the resource “x” can be found using Eq. (3), now substituting Eqs. (22) in (3) we have,

St(dp)¯=t-1Qt(dp)∑i=1t-1Qi(dp) which further evaluates to,

St(dp)¯=t-1Qt(dp)∑i=0t-1(1-ap((di-1d-1)+1))(23)

Next, we compute the average number of generated messages for our proposed algorithm. In our resource discovery scenario, the nodes reply directly to the querying node. If x is not offered by the addressed node then there will be one fixed message generated while forwarding to every addressed child node and the message generated in each of the p paths.

Mt¯(dp)=(1-F)(1+pm(t-1))(24)

where, m(t-1) are the transmission occurring along the path p of t −1 nodes.

For such a path p, if resource x is found in its addressed node or any of its d neighbors of the broadcasting node then it will generate a reply to the querying node which is unicasted back using the path resolved by the routing protocol, and the query gets terminated only if the reply was from the addressed node or else a message will be generated while forwarding to next addressed node of the path plus the message generated inside the subpath p′ with t −2 nodes rooted at the next node. This gives the recurrence relation:

m(t-1)=1*F+(1+m(t-2))*(1-F)=am(t-2)+1 where, m(0)=1, since the last node receiving the message will always reply to the querying node whether it knows x or not. On solving the recurrence relation, we get:

m(t-1)=at-1a-1(25)

Now substituting Eqs. (25) in (24) it gives:

Mt¯(dp)=a+ap(at-1a-1)(26)

5  Theoretical Analysis

We compare the three search strategies analytically with the following settings. The network consists of N = 100 nodes, and nx = 1 (as only one node holds the resource “x”). We consider for two different node degrees, i.e., sparse (d = 4) and dense (d = 6) scenarios. We evaluate with p = 1 and p = 4 paths for both the random walk protocol and our proposed method. We measure the probability of not finding the resource within “t” steps (1 − Qt), the average number of steps required (St¯), and the number of messages generated within “t” steps (Mt¯) for each of the algorithms. The results are shown in Fig. 7.

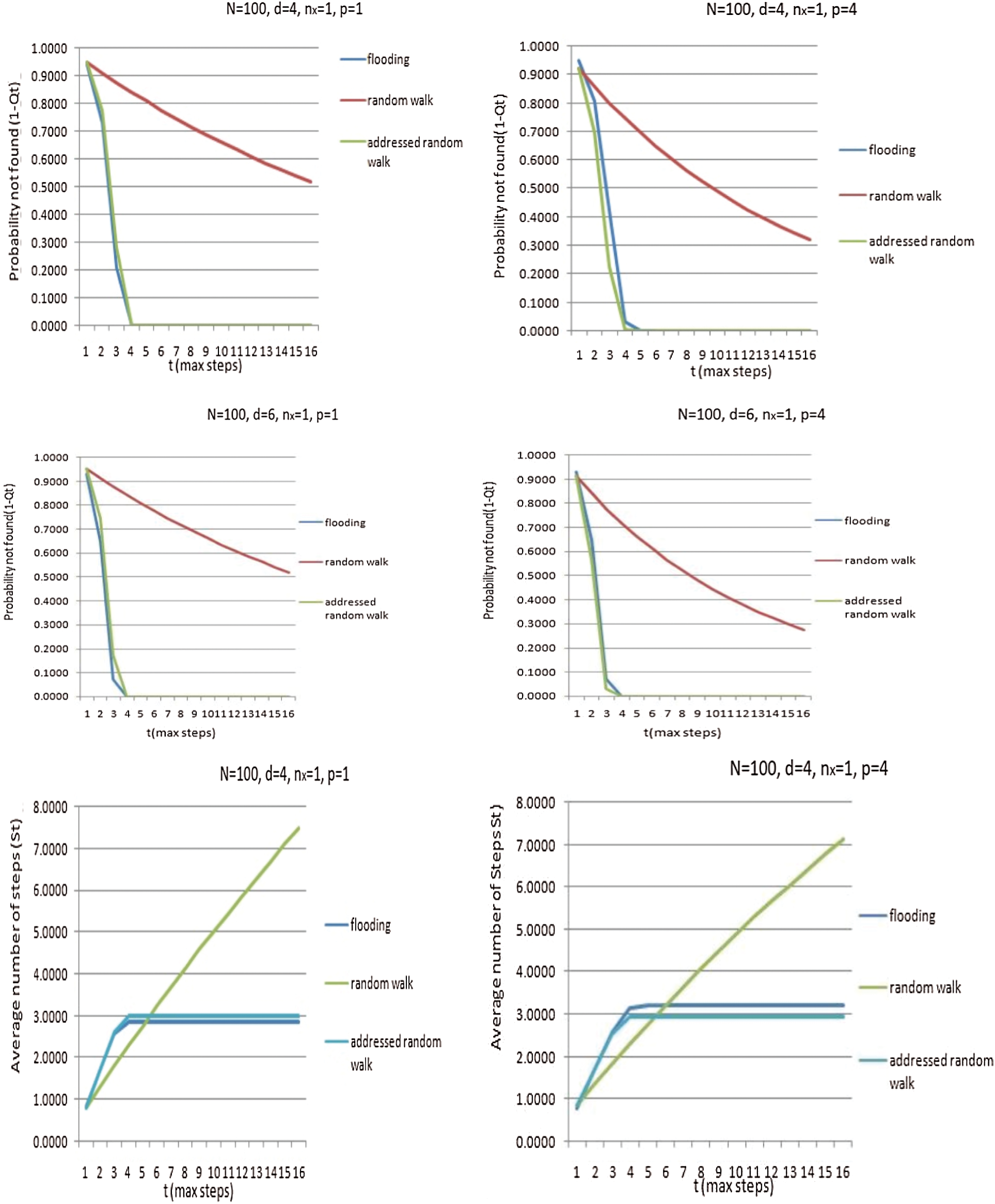
Figure 7: Comparisons of different search techniques using the metrics: Probability of not finding the resource, average number of steps needed to locate the resource, and average number of messages generated during the search process

The mathematical results are summarized in Tab. 2. for each of the search techniques.

Table 2: Search algo. evaluation performance metrics (t≥1,p≥1,Q0=1-a)

6  Conclusion

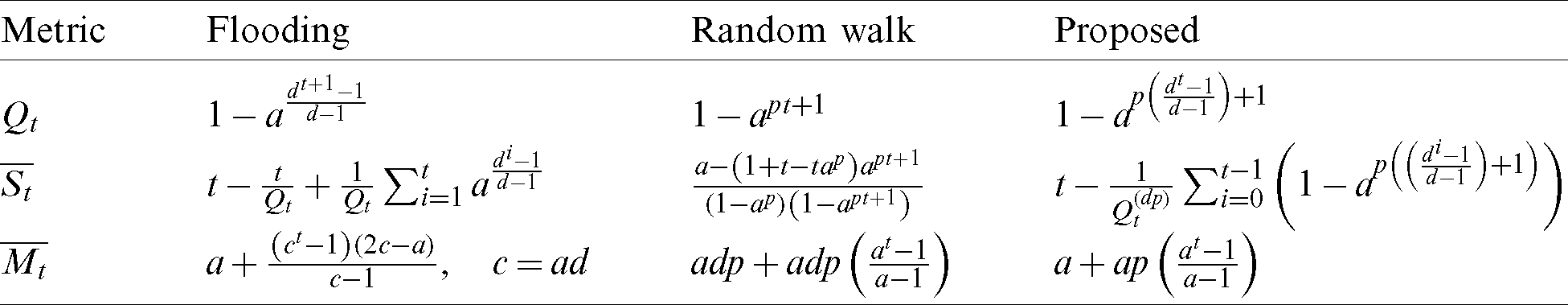
In this work, the focus is on the general issues of resource discovery under a highly dynamic mobile P2P network. Specifically, the performance of random walk and flooding techniques related to this problem are studied. Flooding tries to locate the resource in an aggressive manner by visiting almost all the nodes and it has a scalability issue as it leads to the generation of an enormous quantity of queries. Even though random walk searches conservatively, but under MANETs, it also generates huge message overhead at each hop, and further, it takes longer search time. To overcome the above issues, we introduce a cross-layered addressed random walk scheme for MANETs which is a hybrid of random walk and flooding method that is designed considering the physical network aimed to suit such a highly evolving network. The contribution of the article is two-fold. (1) Theoretical modeling of the search algorithms, and deriving analytical measures evaluating their performances. (2) Mathematical modeling of the proposed resource discovery protocol to optimize random walk algorithm over MANETs. Such, evaluation in context to P2P MANETs is not done before. This paper focuses on improving the performance of the random walk method by lowering the message overhead, and increasing the query hit rate while lowering the query delay. We present an analytical model to estimate the performance of each studied search strategy based on the metrics including the probability of finding a resource, the mean of steps needed to find a resource, and the mean of messages generated while finding a resource. The derived parameters are one of the most important performance metrics in MANET. As future work, we decide to validate the theoretical results through simulation experiments. We further also plan to model our game theory-based resource discovery algorithm.

Acknowledgement: We are thankful to all the collaborating partners in the presented study.

https://sourceforge.net/projects/neighbordiscovery/

https://github.com/ajayarunachalam/Neighbor-Discovery

Funding Statement: Taif University Researchers Supporting Project Number (TURSP-2020/36), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the presented study.

References

 1.  M. A. Noor, R. Beraldi and R. Baldoni. (2010). “Identifying open problems in random walk based service discovery in mobile,” in Proc. I2CS, Bonn, NW, Germany, pp. 91–102. [Google Scholar]

 2.  R. Schollmeier, I. Gruber and F. Niethammer. (2003). “Protocol for peer-to-peer networking in mobile environments,” in Proc. ICCN, Dallas, TX, USA, pp. 121–127. [Google Scholar]

 3.  Y. Chawathe, S. Ratnasamy, L. Breslau, N. Lanham and S. Shenker. (2003). “Making gnutella-like P2P systems scalable,” in Proc. ATAPCC, Karlsruhe, BW, Germany, pp. 407–418. [Google Scholar]

 4.  A. Arunachalam and O. Sornil. (2015). “An analysis of the overhead and energy consumption in flooding, random walk and gossip based resource discovery protocols in MP2P networks,” in Proc. ICACC, Haryana, HR, India, pp. 292–297. [Google Scholar]

 5.  A. Arunachalam and O. Sornil. (2015). “Issues of implementing random walk and gossip based resource discovery protocols in P2P MANETs & suggestions for improvement,” in Proc. ICRTC, Delhi, India, pp. 509–518. [Google Scholar]

 6.  A. Arunachalam and O. Sornil. (2017). “A broadcast based random query gossip algorithm for resource search in non-DHT mobile peer-to-peer networks,” Journal of Computers, vol. 28, no. 1, pp. 209–223. [Google Scholar]

 7.  A. Arunachalam and O. Sornil. (2016). “Reducing routing overhead in random walk protocol under MP2P network,” International Journal of Electrical & Computer Engineering, vol. 6, no. 6, pp. 3121–3130. [Google Scholar]

 8.  A. Arunachalam and O. Sornil. (2016). “Minimizing redundant messages and improving search efficiency under highly dynamic mobile P2P network,” Journal of Engineering Science & Technology Review, vol. 9, no. 1, pp. 23–35. [Google Scholar]

 9.  H. Barjini, M. Othman, H. Ibrahim and I. N. Udzir. (2012). “Shortcoming, problems and analytical comparison for flooding-based search techniques in unstructured P2P networks,” Peer-to-Peer Networking and Applications, vol. 5, no. 1, pp. 1–13. [Google Scholar]

10. N. Bisnik and A. A. Abouzeid. (2007). “Optimizing random walk search algorithms in P2P networks,” Computer Networks, vol. 51, no. 6, pp. 1499–1514. [Google Scholar]

11. V. Dimakopoulos and E. Pitoura. (2006). “On the performance of flooding-based resource discovery,” IEEE Transactions on Parallel and Distributed Systems, vol. 17, no. 11, pp. 1242–1252. [Google Scholar]

12. T. Lin, P. Lin, H. Wang and C. Chen. (2008). “Dynamic search algorithm in unstructured peer-to-peer networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 20, no. 5, pp. 654–666. [Google Scholar]

13. M. E. Newman, S. H. Strogatz and D. J. Watts. (2001). “Random graphs with arbitrary degree distributions and their applications,” Physical Review, vol. 64, no. 2, pp. 1–17. [Google Scholar]

14. M. Portmann and A. Seneviratne. (2003). “Cost-effective broadcast for fully decentralized peer-to-peer networks,” Computer Communications, vol. 26, no. 11, pp. 1159–1167. [Google Scholar]

15. S. Ferretti. (2014). “Searching in unstructured overlays using local knowledge and gossip,” in Proc. Complex Networks V, Bologna BO, Italy, pp. 63–74. [Google Scholar]

16. H. Babaei, M. Fathy and M. Romoozi. (2014). “Modeling and optimizing random walk content discovery protocol over mobile ad-hoc networks,” Performance Evaluation, vol. 74, no. 2, pp. 18–29. [Google Scholar]

17. A. Arunachalam. (2020). “Rock, Paper, Scissors game based model for content discovery in P2P MANETs,” Wireless Personal Communications, vol. 113, no. 1, pp. 1–16. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.