DOI:10.32604/cmc.2021.014709

| Computers, Materials & Continua DOI:10.32604/cmc.2021.014709 |  |
| Article |
A Genetic Based Leader Election Algorithm for IoT Cloud Data Processing
1Department of Computer Science, University of Engineering and Technology, Taxila, 47050, Pakistan
2School of Intelligent Mechatronics Engineering, Sejong University, Seoul, Korea
3School of Electrical and Computer Engineering, Department of Information and Communication Technology, Xiamen University Malaysia, Sepang, 43900, Malaysia
*Corresponding Author: Kamran Siddique. Email: kamran.siddique@xmu.edu.my
Received: 11 October 2020; Accepted: 14 November 2020
Abstract: In IoT networks, nodes communicate with each other for computational services, data processing, and resource sharing. Most of the time huge data is generated at the network edge due to extensive communication between IoT devices. So, this tidal data is transferred to the cloud data center (CDC) for efficient processing and effective data storage. In CDC, leader nodes are responsible for higher performance, reliability, deadlock handling, reduced latency, and to provide cost-effective computational services to the users. However, the optimal leader selection is a computationally hard problem as several factors like memory, CPU MIPS, and bandwidth, etc., are needed to be considered while selecting a leader amongst the set of available nodes. The existing approaches for leader selection are monolithic, as they identify the leader nodes without taking the optimal approach for leader resources. Therefore, for optimal leader node selection, a genetic algorithm (GA) based leader election (GLEA) approach is presented in this paper. The proposed GLEA uses the available resources to evaluate the candidate nodes during the leader election process. In the first phase of the algorithm, the cost of individual nodes, and overall cluster cost is computed on the bases of available resources. In the second phase, the best computational nodes are selected as the leader nodes by applying the genetic operations against a cost function by considering the available resources. The GLEA procedure is then compared against the Bees Life Algorithm (BLA). The experimental results show that the proposed scheme outperforms BLA in terms of execution time, SLA Violation, and their utilization with state-of-the-art schemes.
Keywords: IoT; cloud computing; datacenter; leader election algorithm; machine learning; genetic algorithm
The Internet of Things (IoT) is defined as the immense number of devices connected. Recent research [1] predicts that by 2020, more than 50 billion of the devices will communicate online which shows that number of persons on the globe is far less than that. However, a huge amount of data will be generated by these traditional computing devices like PCs, cellphones, and smart sensing devices, etc. According to another study [2,3] IoT devices will produce 1.6 Zettabytes of IoT data by 2020. Therefore, in this digital era, data is declared as the “new oil” [4,5] which needs to be processed to extract meaningful information. The efficient processing of data requires a lot of resources, however, with the advancement of internet technologies and cloud computing (CC), information processing resources have become less expensive. Cloud computing provides different resources e.g., memory, storage, processing cores, etc., to the hosted applications as per their data processing requirements. Cloud computing provides benefits like lower data storage [6] and processing cost, pay-per-use, fast deployment of applications, flexibility, and scalability of the hardware architecture. In cloud computing, the data center is the combination of multiple network servers and nodes, and they collaborate with each other in form of a cluster to share the resources. Cluster leaders are responsible to manage the communication and synchronization of the nodes for resource sharing. Therefore, selection of an optimal node as a leader is a fundamental requirement to prevent the network to go in an unpredictable state.
In the data center, the leader election to select the best node is a challenging problem, as leaders are responsible to manage the segregated data, share the resources amongst nodes, and to overcome the latency. The leaders are responsible for parallel and distributed processing, which is a primary activity performed in a data center; hence, communication amongst the nodes cannot occur effectively without the leader/master nodes, therefore, the leader selection cannot be compromised. As nodes are directly associated with the leader, therefore, the leader ensures that deadlock may never occur amongst the network nodes, and tasks can be processed efficiently. [7–10] and algorithms [11–16] have been proposed in the distributed IoT networks and cloud computing research for effective leader election. In [17–21] bully algorithm was proposed for leader election. In the bully algorithm, leader nodes were dynamically generated based on the node ID criteria. In [22,23], the ring algorithm was proposed. In the ring algorithm, every node shares its ID with all other nodes and maintains a list of IDs. From this list, the algorithm picks one node as a leader on the bases of priority. In [24–28] node IDs have been randomly generated and a priority number was assigned to each node. The node with the highest priority number was then selected as the leader node. In [29–32] message-passing approach has been considered for leader election. The message passing approach introduces latency due to higher message passing rate and slower node response. The main drawback of all these approaches is that the resource profile of the nodes is 56 always overlooked. Due to which, the selection of the weaker nodes becomes equally probable. The weak leader crash in high load scenarios, thus, leader elections are needed to be reoccurred that slows 58 down the overall processing and delays the task execution over the network nodes. Therefore, during the leader election phase, node resources must be considered to ensure the task processing occurs efficiently, and to bring stability in the network.
In this paper, a genetic algorithm (GA) based Leader Election (GLEA) approach is presented for IoT data processing on cloud computing. Our algorithm [16] selects the node with the most available resources as a leader and ensures the communication amongst the nodes occurs effectively. Moreover, we also ensure that the resources are efficiently shared amongst the nodes and minimum delay occurs during the task execution. Our algorithm utilizes the meta-information i.e., tasks, VMs, and servers available in the data centers and compute the resource score for different servers based on the available server resources i.e., MIPS, memory, bandwidth, and throughput, etc. This information is utilized to generate the initial chromosome population for the GA. Chromosome comprises of multiple tasks on different servers as genes. The length of the chromosome depends on the number of tasks in a cluster. To elect the leader node from each cluster, we find the server that has the maximum value against the fitness function. The fitness value is calculated after performing the crossover and mutation. Crossover in our case is the swapping of multiple tasks amongst different servers in each cluster, whereas a mutation is the swapping of individual tasks on different servers. Fitness value depends on following four factors i.e., CPU-MIPS, memory, throughput, and bandwidth. This leader node selection approach is important to use in a centralized manner to select the leader in an efficient manner. The successful an election in a cluster to select the best node as a leader reliably reduces the communication delay between the nodes. In contrast to the message passing approaches that suffer from communication delays, our approach efficiently performs the leader election without suffering from this vulnerability. To justify the significance of our approach, we compare the proposed GLEA with modified Bees Life Algorithm (BLA) for leader election. The reason to compare GLEA with BLA is that both approaches are based on GA, hence, fare comparison is possible. Therefore, encapsulated the whole contribution of this work is as follows:
• A novel technique is presented by employing a genetic algorithm (GA) based Leader Election (GLEA) approach for IoT data processing on cloud computing.
• The presented framework provides efficient data processing and effective data storage due to optimal leader selection through the GLEA.
• Our work is robust to task execution time; SLA violation and memory utilization as compared to latest approaches.
The rest of the paper is organized as follows: In Section 2, the state-of-the-art in leader election is presented. In Section 3, the proposed GA-based leader election approach is described. In Section 4, experiments and the results are presented, and finally, we conclude our work in Section 5.
In the literature, there are frequent leader election protocols and algorithms that are discussed in the literature. Ktari et al. [33] have proposed an agent-based election algorithm for a dynamic tree. The important focus of the author is to sustain a forest of trees or the root node is taken as the leader node in the tree. The selection of the leader node is based on the highest ID value that is generated randomly and without considering any resources during the election process of the leader. Authors present an algorithm of leader election for a probabilistic investigation of traffic lights in [14]. In [16] proposed a new leader election algorithm for IoT network which is based on the tree routing protocol. During the process of leader election, each node forwards the value and the best value node is elected as a leader.
In [34], the Old algorithm of the ring considers a unidirectional interface that links the entire hubs or nodes. This algorithm has been presumed that a procedure is successfully running on every hub or node. In this system, each node is generated a unique priority number randomly. Now, that node is considered as a leader who has a maximum priority number. If the leader hub fails, then initiating the whole election process for the selection of a new leader. The method of leader hub election requires a total of 2(
Bounceur et al. [37] proposed an algorithm for a leader is WBS (Wait-Before-Starting) for IoT networks. The node which will wait for the least before starting the execution of the process is called the leader node in the network. The leader node is the first node that starts the execution by sending the message to the other nodes in the network. After electing the leader node, other nodes will start the processing of their programs. In [29,38] modify the recent bully election algorithm procedure for cloud computing systems, where the election of a leader is on the bases of a Super Node (SN). This algorithm increases the election speed and the complexity of the message is reduce in O(n2/k) to O(n2), where n is the number of hubs or nodes, and k is the district. Another algorithm for the elect a leader was proposed for ring topology which was bidirectional with the
Shindo et al. [41], Biswas et al. [11] proposed a multi-leader algorithm to decrease communication delay and reduce the latency among the leaders. Three experiential tactics are used in a unified way for computing the appropriate status of leaders in a polynomial period. A probabilistic grounded model for elected a leader is proposed in MANETs [26]. The authors have exposed enhancements on the consumption of energy and the consistency problem of channel communication. There are other more than a few algorithms such as; leader election in a peer-to-peer network [42], elect a leader in a distributed network via software mediators to rise the election process speed, saving energy [42,43], and negotiate some more protocol for fault-tolerant election in asynchronous distributed systems [44]. The authors introduce two new mobility conscious algorithms for leader election in ad-hoc network systems [23,45]. These algorithms confirm that every connected node in the topology has just a single leader. These two new algorithms depend on a temporarily ordered routing algorithm called TORA. Most of the current election algorithms are based on the unique Id or priority numbers that are randomly generated by the system. They have not carefully considered the topology of the network and do not properly take care of real-time resources in the process of leader election [28,46–48].
In the Internet of Mobile Things (IOMT) devices are considered as a smart mobility device. Mobile-Hub (M-Hub) is known as a middleware in IoT that collects information from the edge of network devices. M-Hub is run on devices and monitors these devices independently without considering the neighbor M-Hubs. According to this situation, Silva et al. [49] introduced Neighborhood-aware M-Hub (NAM-Hub) to elect a leader to integrate with the neighbor M-Hub for efficient computation without any delay or interaction. Lei et al. [50] proposed a Groupchain method for block-chain structure, appropriate for computing services in IoT. Groupchain method applied to the leader group to cooperatively execute blocks for better transaction productivity and introduced the efficient method to supervise the performance of participants in the leader group.
After a literature review, we analyze that present algorithms for leader election based on the unique number of id that system generates randomly. Most of the algorithms only consider a random id’s for leader election do not consider the topological changes. The problem of Leader election is more challenging with the complexity increase in cloud computing. To overcome this problem, many leader election algorithms are designed, but still, these algorithms do not consider maximum resources due to increased complexity. We are proposing a novel technique for the leader election algorithm by using Genetic algorithms as they are used to solving NP-hard problems, which consider maximum resources and cover more aspects like synchronization, communication, and resource sharing for leader election.
Consider a data center Dc with
3.1 Genetic Leader Election Algorithm (GLEA)
GA (Genetic Algorithm) is a bio-inspired algorithm and based on the Theory of Evolution and Genetics. The genetic algorithm belongs to the Evolutionary Algorithm. Theory of Evolution demonstrates the process of evolution, individuals who have a higher survival probability and environment adaptable. In Genetic Algorithm indicates the gene, that genes make chromosome, for the new individual perform crossover on chromosome and mutation on a gene. The primary operators of GA involve selection, crossover, mutation. The purpose of the selection of GA in our methodology is to select the best node (individual) with a higher probability for the leader. GA operator plays a very important role in achieving the best and optimal solution.
In our proposed algorithm GLEA, we take a server Si that contains three tasks
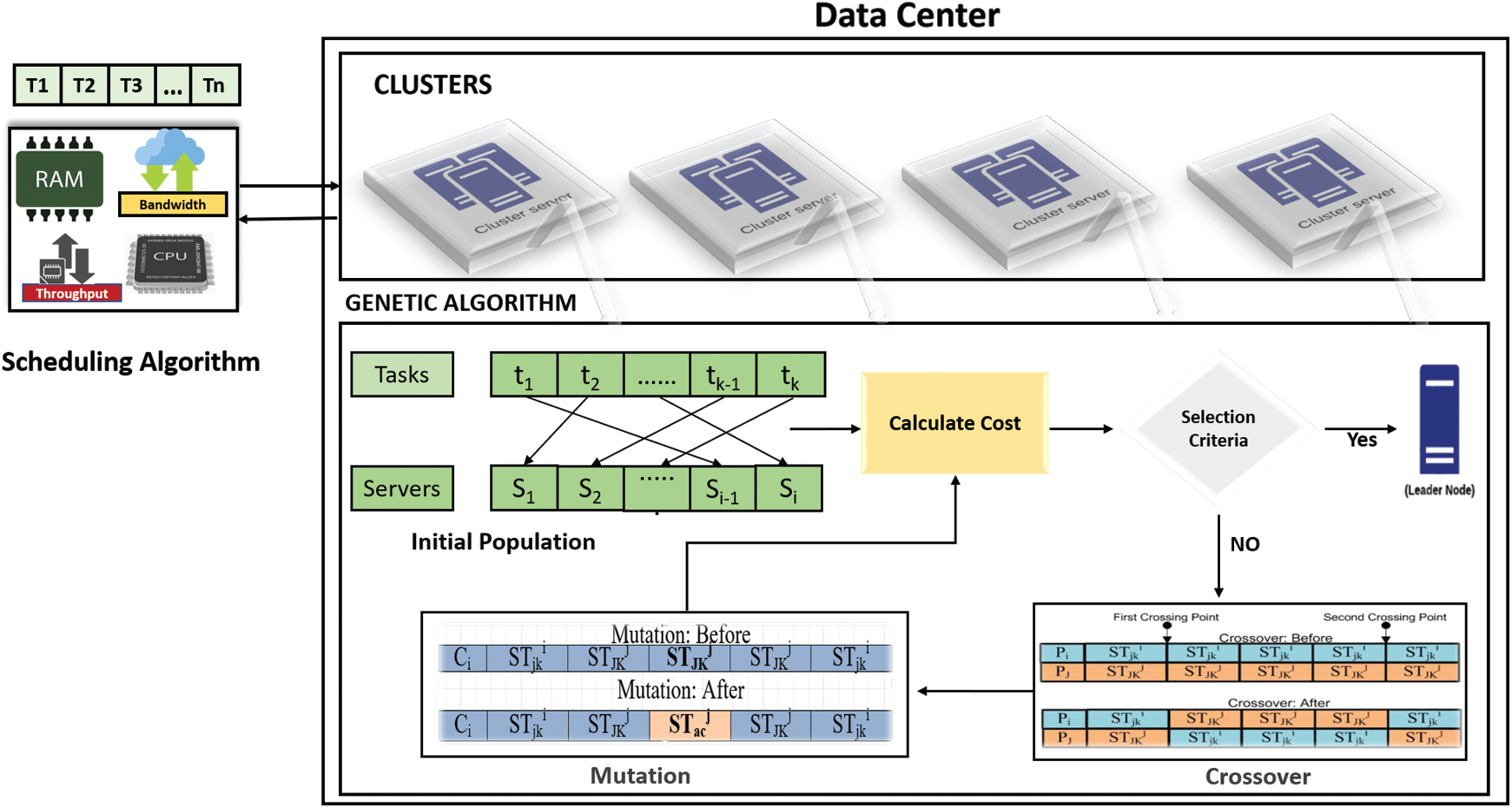
Figure 1: Proposed model of the genetic based leader election algorithm
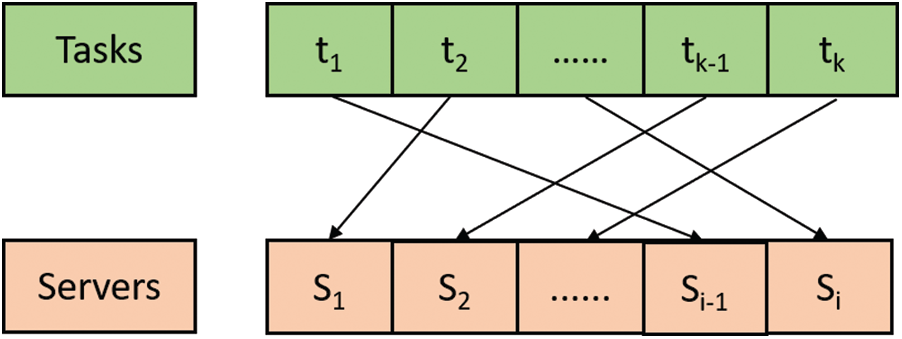
Figure 2: Chromosome set of GLEA
The procedure of crossover is applied to two population individuals called chromosomes which are the Server Si, and a Task tk. There are some crossover strategies, we use a two-point crossover strategy as shown in Fig. 3. Where, Q1 and Q2 two selected chromosome which have the highest fitness values, randomly selected
Whereas,
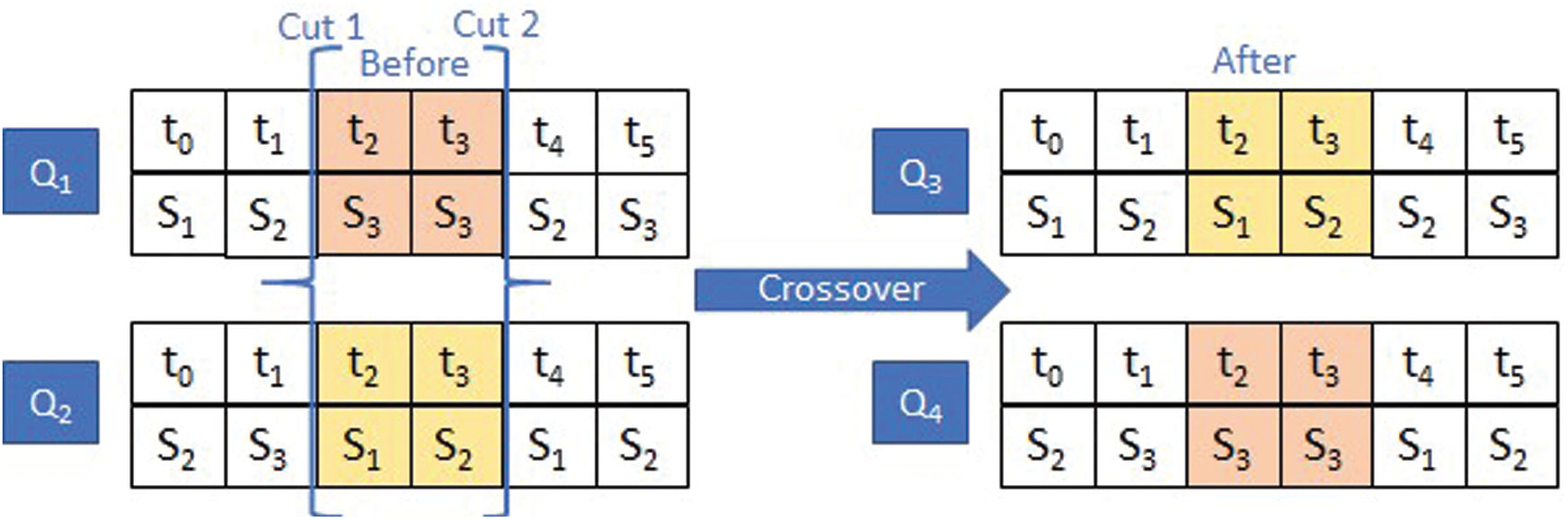
Figure 3: Crossover
The operation of Mutation is a urinary which introduces the changes into the features of the offspring, which is coming about from the process of crossover. These deviations are minor according to the probability of mutation. Generally selected a very slight value. So, the innovative server or offspring will not be reformed from the previous and unique or original one. In our scheme, we use the substitution process of mutation. In this, we select a position from the population and substitute the values, shown in Fig. 4.
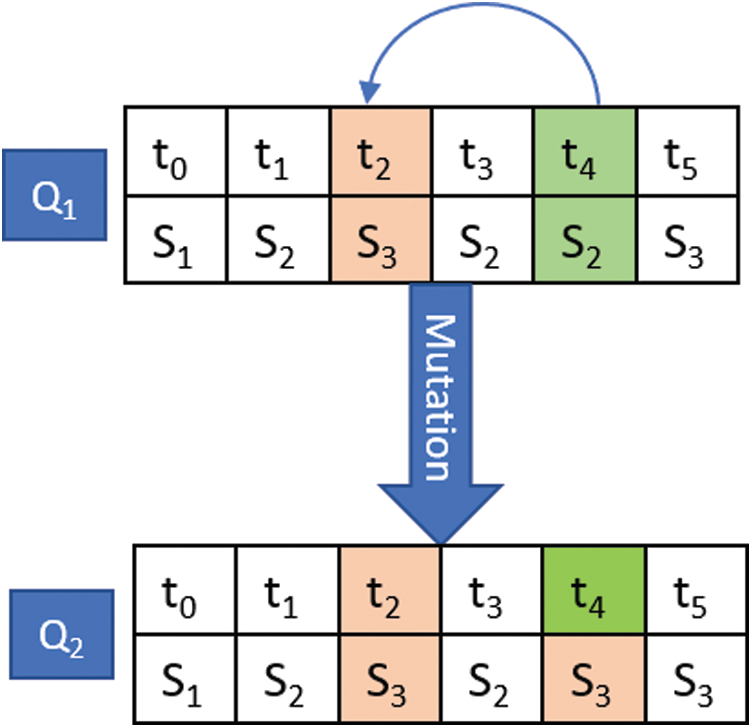
Figure 4: Mutation
We evaluate the quality of our solution by using the fitness function. We will evaluate all solutions by this function. A solution with the greatest fitness value will be the most optimal solution. Following the system, parameters are used in the fitness function, and the weight of these parameters changes according to user SLA (Service Level Agreement) using the knapsack algorithm. For example, if the user wants to give 10% weightage to CPU MIPS, 30% to RAM, 20% to Bandwidth, and 40% to throughput, then weights of system parameters are shown in Tab. 1 [51]. We have assigned weights to these parameters. The parameter with greater weight will have a greater impact on fitness value. So, our fitness value Fv from Eq. (2).
where Fs is the fitness of the server and calculate using Eq. (3).
As we aim to find a solution with the maximum available resources, we will select the leader with the maximum value of the server.

There are a few selection approaches such as tournament, sorting, and roulette selection. Tournament selection is the method of choosing an individual from a randomly generated population and the individual which has the highest fitness value will be selected. In the sorting selection method, firstly calculate the fitness value of every individual. After sorting the individual according, the fitness value and assigned a probability to a solution will be a selected solution. The third method is the roulette method, used in this technique. Roulette selection is also called a Fitness proportionate selection, selects the useful individuals for recombination. In roulette selection, the fitness function assigns a fitness value to a possible chromosome. Calculate the probability of each chromosome. if fa is the fitness of everyone ‘ a ’ in the population, its probability is being calculated through Eq. (4). Where b is the number of individuals in the population.
In this algorithm, we have two phases first is the task allocation phase and the second is the Selection phase.
In this phase, we aim to allocate tasks to different servers. When a new task is submitted, the first step will choose the best leader LB from the set of nodes. A leader LB can be chosen from the subsequent Eq. (5).
where RL is the resources of the leader. The following Eq. (6) can find RL.
In the second step selected leader will assign the task to a server ‘
In this phase, choose leaders L from the set of clusters C in a datacenter DC. We will use the genetic algorithm to choose the leader in each cluster. The genetic algorithm will return us an optimal server from each cluster, and we will choose it as a leader. After each time interval, our system will run this phase to optimize a leader.

Several experiments are conducted to evaluate the performance of the proposed method by comparing it against the state-of-art BLA algorithm. Detail experiment analyses are described in the subsections.
To elaborate on the performance of the proposed method, a set of extensive experiments are performed using Cloudsim Plus [20] simulator that is based on Cloudsim [21]. Cloudsim is a framework for modeling and simulating cloud data centers. The Cloudsim Plus is an extension of Cloudsim to simulate the more realistic scenarios. For simulation used multiple set of heterogeneous servers (MIPS range 1000–4,000), for processing used AMD-Ryzen 5 2500, and Python library to generate the graph. The proposed method performance is evaluated, based on performance parameters like execution time, SLA Violation, and Utilization of memory. Execution time is the time in which the servers finished the tasks. Utilization is defined as the ratio of the allocated MIPS from the total MIPS of the server during the time interval. An SLA violation is a violation when the task or job is not completely executed in the given time frame. To evaluate the performance randomly generates the graphs of the experiment using the input parameter shown in Tab. 2.

In this section, we explain the details about how to perform experiments. Experiments were used to compare the efficiency and performance of the proposed GLEA algorithm with the traditional BLA algorithm. In experiments using the system parameter like CPU MIPS, RAM, Bandwidth, and throughput. The weightage is given to these system parameters according to the requirement of users shown in Tab. 3.
Table 3: System parameters weights

4.2.1 Experiment 1; Evaluation Through the Increment of Host
In the first conduct experiment, the efficiency of the proposed GLEA is compared with the BLA algorithm based on execution time, SLA violation, and memory utilization. In this scenario, evaluated the performance by incrementing the number of hosts/servers but used the fixed number of tasks. The range of hosts is 20–100 with an increment of 20, and the tasks range is fixed to 1000. In this simulation, the number of hosts is not fixed (increment by 20) and the task number is fixed. Fig. 5, shows that the proposed GLEA performance is better than BLA in terms of execution time. GLEA takes minimum time to complete a task as compared to the BLA algorithm. Fig. 6 shows SLA violation, the GLE algorithm remains to perform better as compared to the BLA algorithm with the fixed number of tasks. Fig. 7 shows the utilization of resources for both GLEA and BLA algorithms. Utilization is the same because algorithms schedule VMs to hosts is the same. Utilization is shown in the range of 0 to 1. Results validate that the GLEA performance is better and improved the efficiency with the increment of servers in terms of performance parameters like execution time and SLA violation.
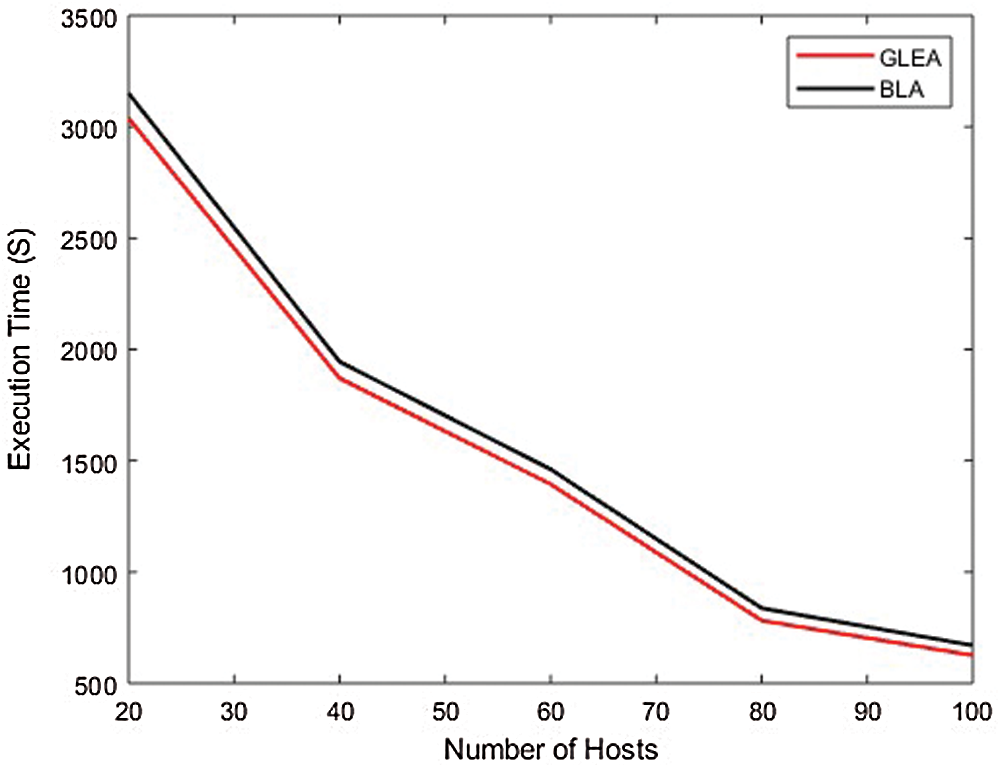
Figure 5: Execution time
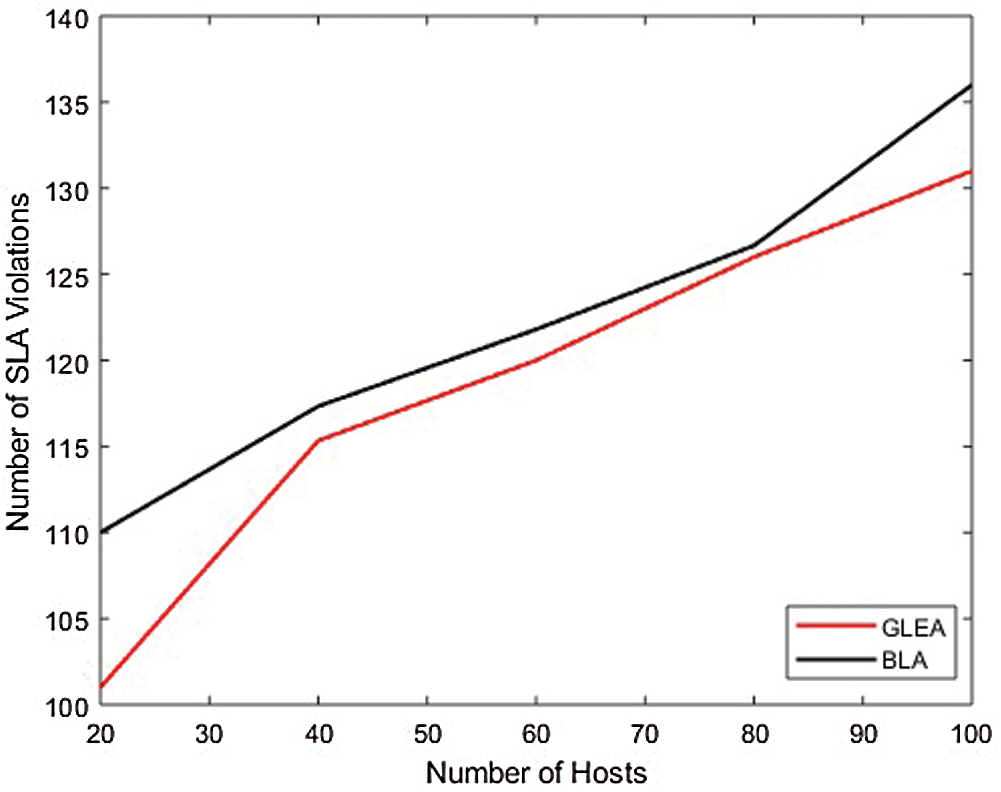
Figure 6: SLA violation
Figure 7: Memory utilization
4.2.2 Experiment 2; Evaluation Through the Increment of Task
In the second experiment, to evaluate the performance and efficiency by incrementing task and the number of hosts is fixed. The range of tasks from 100 to 10,000 with an increment of 100. In this experimental set-up, the number of hosts is 50. Fig. 8 equate the time to completely execute the assigned tasks or jobs. In this scenario validate the performance parameter like execution time by incrementing the number of tasks and the number of hosts is fixed. The BLA algorithm is less performed in the execution of a task to complete than the GLEA algorithm. It is the efficiency of the GLEA that takes less time to complete the job execution. Fig. 9 shows the GLEA reduces the SLA violation as in comparison to the BLA algorithm during the execution of a workflow.
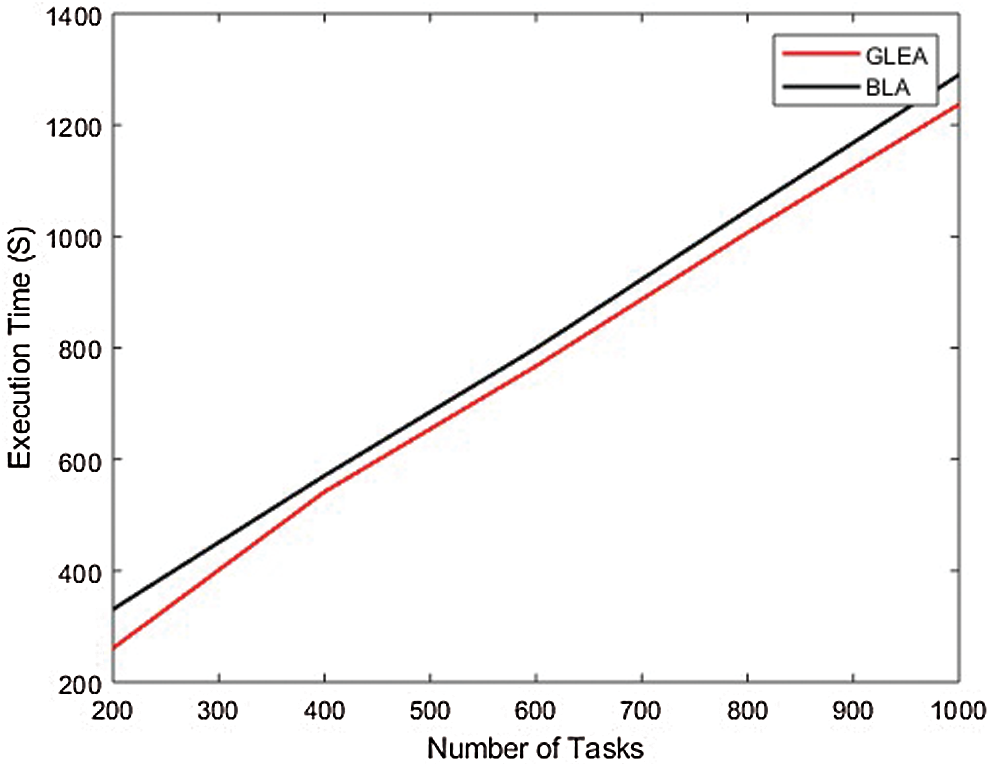
Figure 8: Execution time
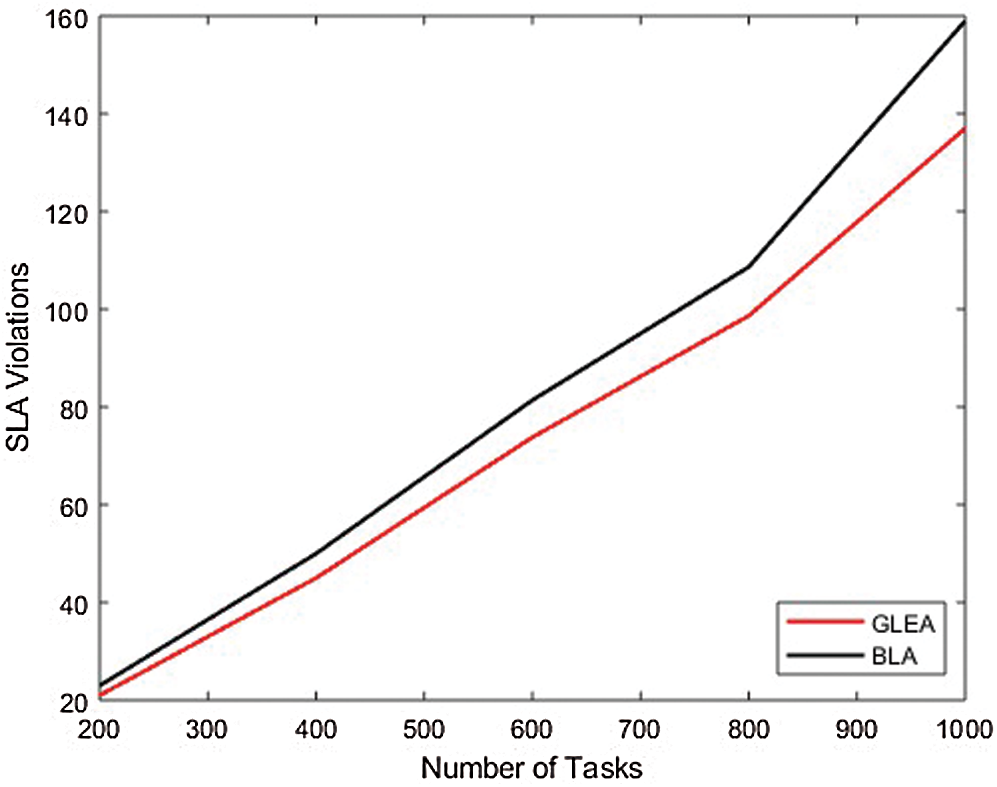
Figure 9: SLA violation
4.2.3 Experiment 3; Evaluation Through Different Weightage
In this simulation, changed the weightage of parameters to evaluate the performance of the GLEA algorithm with the BLA algorithm. We used two different scenarios, in each simulation to give different weightage to parameters shown in Tab. 4. Using this distinct weightage of parameters analyze the execution time and SLA violation of both GLEA and BLA algorithms. In scenarios 1, the number of tasks is increasing by 1000, and the number of hosts is not increasing that is fixed. The range of hosts is the same, that is 50 but the weightage of resources is different. The weightage of the parameter in scenario 1 is CPU 10%, RAM 60%, Bandwidth 20%, and Throughput 10% shown in the above table. To ensure the validity of the GLEA algorithm in terms of execution time and SLA violation. Fig. 10 shows the GLEA algorithm again performs better in time to complete the task or job execution. When the number of hosts is increased then SLA violation is decreased because greater resources are accessible to complete the execution of the tasks. This experiment results prove that the GLEA algorithm substantial performance and improved efficiency in terms of performance metrics. In scenario 2, the number of hosts and the number of tasks or jobs is the same as scenario 1. The weightage of system parameters is changed. The weightage of CPU 10%, RAM 10%, Bandwidth 70%, and Throughput 10% in scenario 2. Fig. 11 shows the execution time and SLA violation is better by experimenting with the GLEA as compared to the BLA algorithm. As a result, prove by performing these experiments the GLEA algorithm achieves better performance in terms of performance parameters when compared with the BLA algorithm.
Table 4: System parameter’s weightage for different scenarios
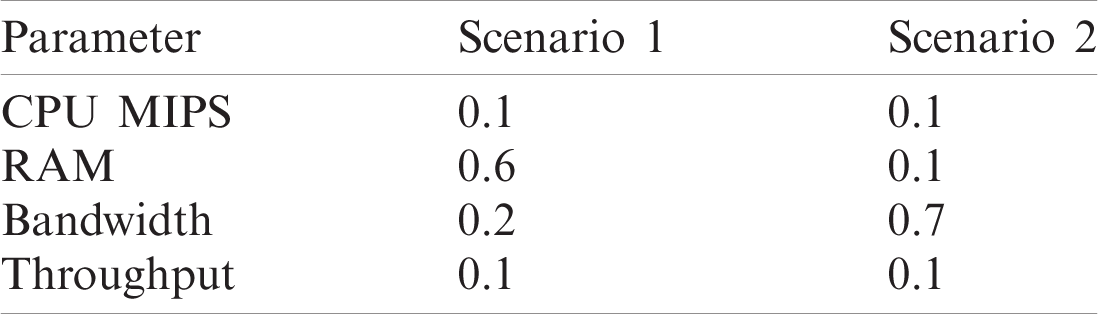
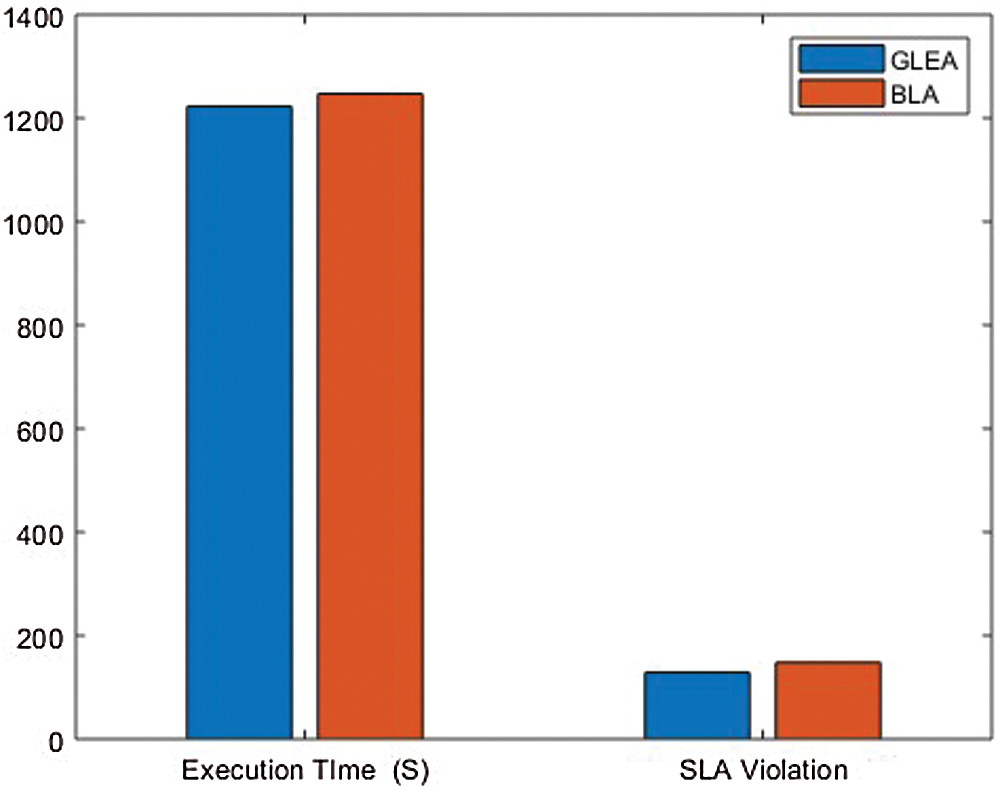
Figure 10: Scenario 1
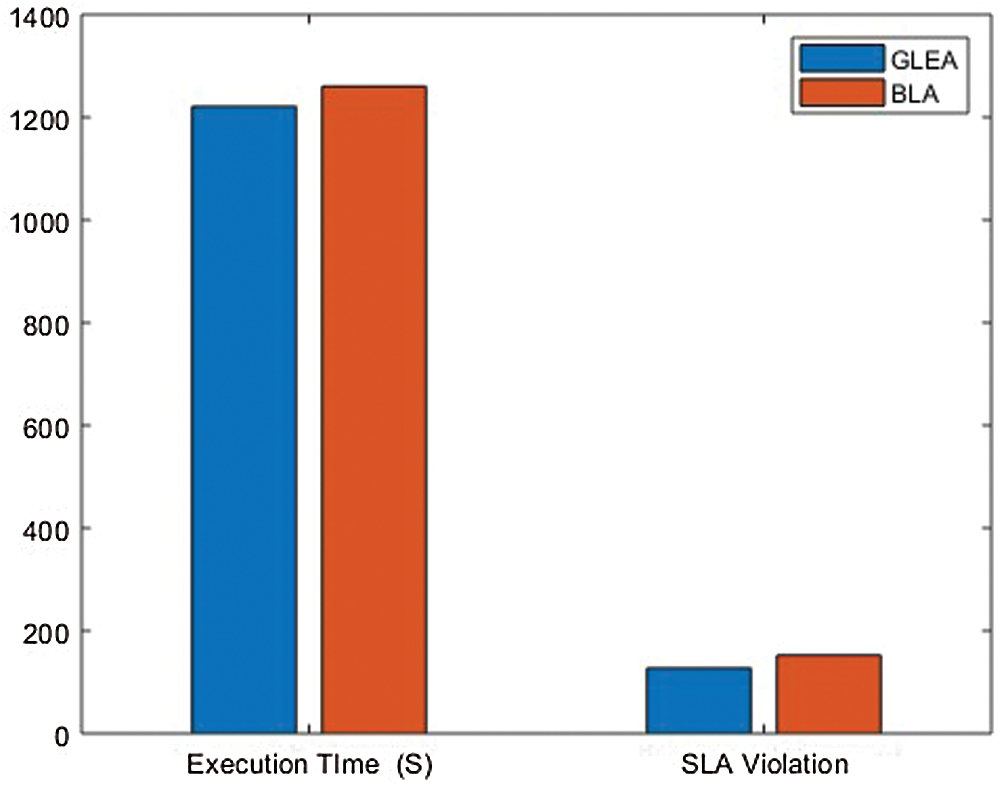
Figure 11: Scenario 2
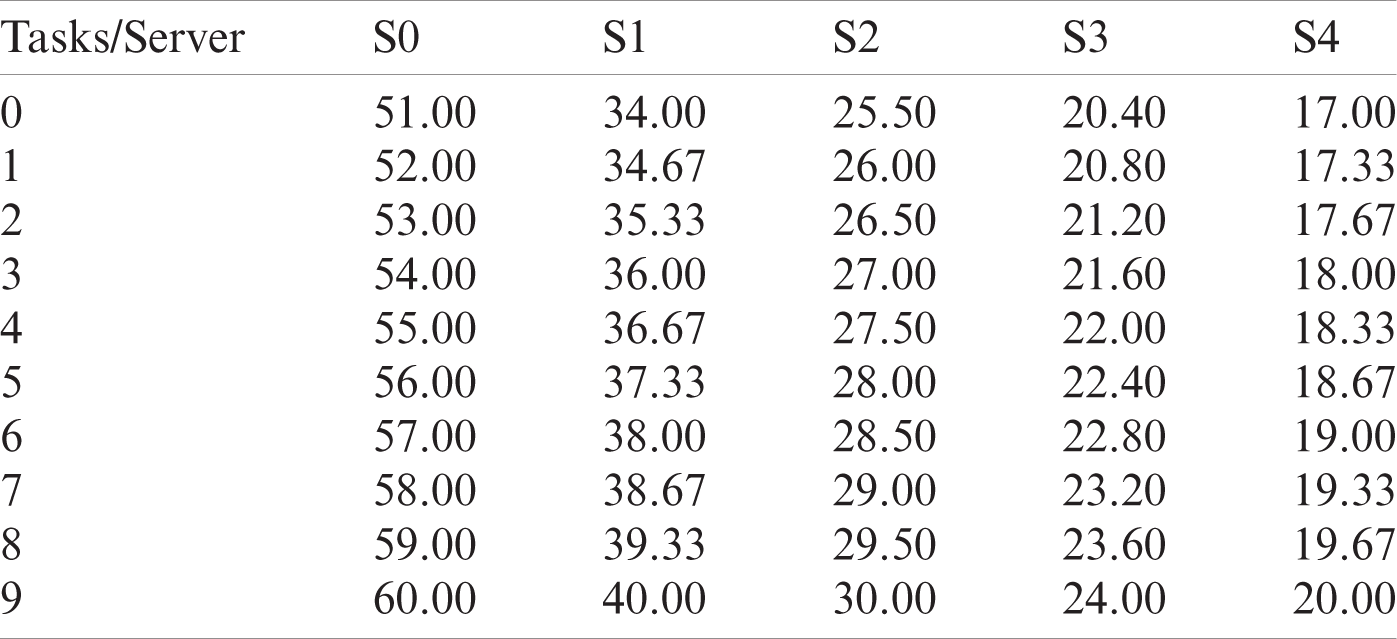
4.2.4 Tasks Scheduling Comparison
Now we compare the performance of the GLEA Algorithm with the conventional algorithm BLA. In this simulation, ten tasks are randomly generated, and the length of each task is (51000–60000). Then, the execution time of each server can be calculated as shown in Tab. 5. Fig. 12 represents the assignments of tasks by the BLA algorithm and Fig. 13 shows the execution time of tasks on different sever after applying the GLEA algorithm. GLEA schedules the tasks on those servers which meet the requirement of tasks and efficiently execute it with the minimum time. Through GLEA, T9 executes on S2 with minimum time as compared to BLA execute T9 on S3, so GLEA efficiently executes the tasks as compared to BLE.
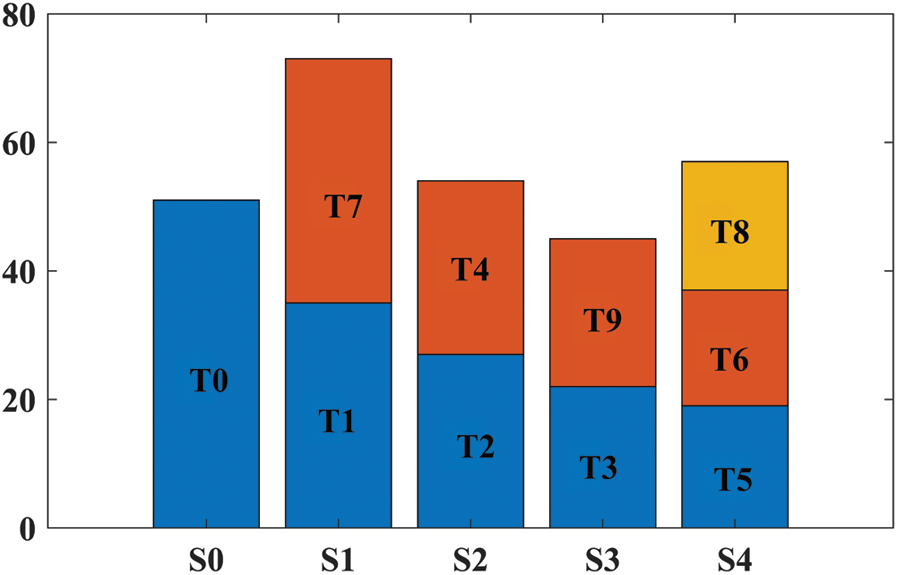
Figure 12: Execution time through BLA
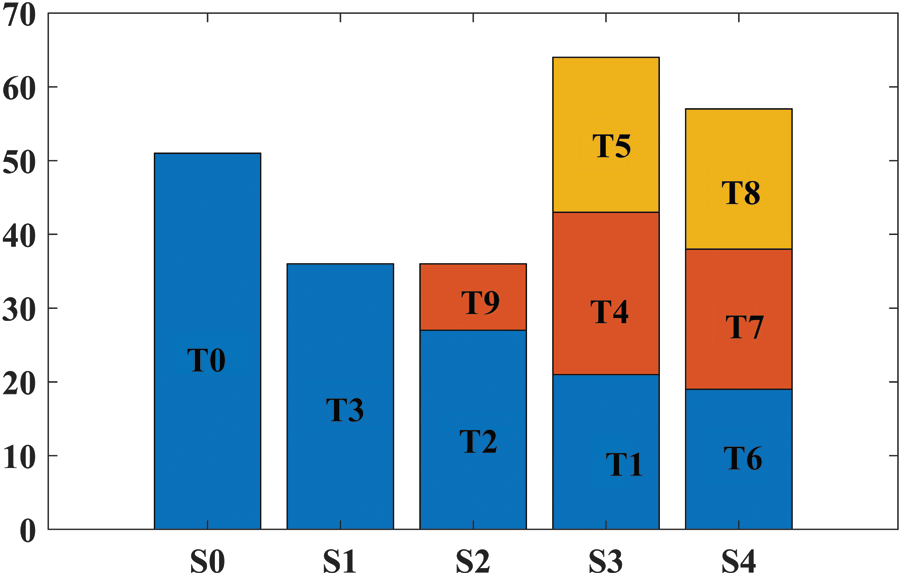
Figure 13: Execution time through GLEA
In our work, we centered on the issues of leader election in an IoT environment, through cloud data centers to ensure that the task is executed efficiently with well-organized services and satisfy the user requirements. Leader election is a challenging task in the cloud computing environments due to the occurrence of deadlock and node failures in resource sharing. To overcome the aforementioned challenges, we have proposed an optimized algorithm called the GLEA algorithm, motivated by the genetic processes that occur in nature. The presented GLEA algorithm utilizes the available resources to analyze the candidate nodes during the LE process. Initially, the fittest value of individual nodes and overall cluster cost is calculated based on available resources. Secondly, the optimal nodes are selected as the leader nodes by employing the GA against a cost function by considering the useable resources. To analyze the efficiency and reliability of our algorithm, we performed a simulation of the GLEA algorithm and compared the results against the BLA method. Our findings suggest that the GLEA algorithm is more efficient in terms of execution time, memory utilization, and SLA violation. In the future, we plan to extend our work to fog and mobile computing.
Funding Statement: This research was supported by the Research Management Center, Xiamen University Malaysia under XMUM Research Program Cycle 3 (Grant No: XMUMRF/2019-C3/IECE/0006).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Evans, “The internet of things: How the next evolution of the internet is changing everything,” CISCO White Paper, vol. 1, pp. 1–11, 2011. [Google Scholar]
2. Schooler, E. Zage, D. Sedayao, J. Moustafa, H. Brown et al., “An architectural vision for a data-centeric IoT: Rethinking things, trust and clouds,” in IEEE 37th Int. Conf. on Distributed Computing System, Atlanta, GA, USA, pp. 1717–1728, 2017. [Google Scholar]
3. K. H. N. Bui and J. J. Jung, “Computional negatiation-based edge analytics for smart objects,” Information Sciences, vol. 480, no. 2, pp. 222–236, 2019. [Google Scholar]
4. M. Loi and P. O. Dehaye, “If data is the new oil, when is the extraction of value from data unjust?,” Filosofia e Questioni Pubbliche, vol. 7, no. 2, pp. 137–178, 2017. [Google Scholar]
5. J. M. Nolin, “Data as oil, infrastructure or asset? Three metaphors of data as economic value,” Journal of Information, Communication and Ethics in Society, vol. 18, no. 1, pp. 28–43, 2019. [Google Scholar]
6. B. Assiri, “Leader election and blockchain algorithm in cloud environment for e-health,” in 2nd Int. Conf. on New Trends in Computing Sciences, Amman, Jordan, pp. 1–6, 2019. [Google Scholar]
7. D. Becker, F. Junqueira and M. Serafini, “Leader election for replicated services using application scores,” in ACM/IFIP/USENIX Int. Conf. on Distributed Systems Platforms and Open Distributed Processing, Lisbon, Portugal, pp. 289–308, 2013. [Google Scholar]
8. T. Koponen, K. Amidon, B. Peter, M. Casado, C. Anupam et al., “Network virtualization in multi-tenant datacenters,” in 11th Symp. on Networked Systems Design and Implementation, Seattle, WA, pp. 203–216, 2014. [Google Scholar]
9. A. Mostafa and A. E. Youssef, “A leader replacement protocol based on early discovery of battery power failure in MANETs,” in Int. Conf. on IT Convergence and Security, Macao, China, pp. 1–4, 2013. [Google Scholar]
10. Quttoum and A. Nahar, “Interconnection structure, management and routing challenges in cloud-service data center networks: A survey,” International Journal of Interactive Mobile Technologies, vol. 12, no. 1, pp. 36–60, 2018. [Google Scholar]
11. T. Biswas, R. Bhardwaj, A. K. Ray and P. Kuila, “A novel leader election algorithm based on resources for ring networks,” International Journal of Communication Systems, vol. 31, no. 10, pp. 3583–3596, 2018. [Google Scholar]
12. R. Ingram, T. Radeva, P. Shields, S. Viqar, J. E. Walter et al., “A leader election algorithm for dynamic networks with causal clocks,” Distributed Computing, vol. 26, no. 2, pp. 75–97, 2013. [Google Scholar]
13. M. Ranwa, P. Sharma and G. Mehrotra, “Novel leader election algorithm using buffer,” in 2nd Int. Conf. on Telecommunication and Networks, Noida, India, pp. 1–4, 2017. [Google Scholar]
14. N. Fathollahnejad, R. Barbosa and J. Karlsson, “A probabilistic analysis of a leader election protocol for virtual traffic lights,” in IEEE 22nd Pacific Rim Int. Symp. on Dependable Computing, Christchurch, New Zealand, pp. 311–320, 2017. [Google Scholar]
15. B. Zhang, G. Liu and B. Hu, “The coordination of nodes in the internet of things,” in 2010 Int. Conf. on Information, Networking and Automation, Kunming, China, pp. 299–302, 2010. [Google Scholar]
16. N. Kadjouh, A. Bounceur, M. Bezoui, M. E. Khanouche, R. Euler et al., “A dominating tree based leader election algorithm for smart cities IoT infrastructure,” Mobile Networks and Applications, vol. 56, no. 10, pp. 1–14, 2020. [Google Scholar]
17. S. H. Lee and H. Choi, “The fast bully algorithm for electing a coordinator process in distributed systems,” in Int. Conf. on Information Networking, Island, Korea, pp. 609–622, 2002. [Google Scholar]
18. M. G. Murshed and A. R. Allen, “Enhanced bully algorithm for leader node election in synchronous distributed systems,” Computers, vol. 1, no. 1, pp. 3–23, 2012. [Google Scholar]
19. M. Méndez, F. G. Tinetti, A. M. Duran, D. A. Obon and N. G. Bartolome, “Distributed algorithms on IoT devices bully leader election,” in Int. Conf. on Computational Science and Computational Intelligence, Las Vegas, NU, USA, pp. 1351–1355, 2017. [Google Scholar]
20. M. S. Kordafshari, M. Gholipour, M. Mosakhani, A. T. Haghighat and M. Dehghan, “Modified bully election algorithm in distributed systems,” WSEAS Transactions on Information Science and Applications, vol. 2, no. 8, pp. 1189–1194, 2005. [Google Scholar]
21. M. Abdullah, I. Al-Kohali and M. Othman, “An adaptive bully algorithm for leader elections in distributed systems,” in Int. Conf. on Parallel Computing Technologies, Almaty, Kazakhstan, pp. 373–384, 2019. [Google Scholar]
22. I. Abraham, D. Dolev and J. Y. Halpern, “Distributed protocols for leader election: A game-theoretic perspective,” ACM Transactions on Economics and Computation, vol. 7, no. 1, pp. 1–26, 2019. [Google Scholar]
23. N. Malpani, J. L. Welch and N. Vaidya, “Leader election algorithms for mobile ad hoc networks,” in Proc. of the 4th Int. Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, Boston, MA, USA, pp. 96–103, 2000. [Google Scholar]
24. M. U. Rahman, “Leader election in the internet of things challenges and opportunities,” arXiv preprint arXiv: 1911.00759, 2019. https://arxiv.org/abs/1911.00759. [Google Scholar]
25. G. Yu, L. Hua, L. Yuanping, L. bowei, W. Xianrong et al., “Using TLA+ to specify leader election of RAFT algorithm with consideration of leadership transfer in multi controllers,” in IEEE 19th Int. Conf. on Softwear Quality, Realibality and Security Companion, Sofia, Bulgaria, Bulgaria, pp. 219–226, 2011. [Google Scholar]
26. X. Guo and Z. Yang, “Analyzing leader election protocol by probabilistic model checking,” in 7th IEEE Int. Conf. on Software Engineering and Service Science, Beijing, China, pp. 564–567, 2016. [Google Scholar]
27. R. Franklin, “On an improved algorithm for decentralized extrema finding in circular configurations of processors,” Communications of the ACM, vol. 25, no. 5, pp. 336–337, 1982. [Google Scholar]
28. K. Altisen, A. K. Datta, S. Devismes, A. Durand and L. L. Larmore, “Leader election in asymmetric labeled unidirectional rings,” in IEEE Int. Parallel and Distributed Processing Sympo., Orlando, FL, USA, pp. 182–191, 2017. [Google Scholar]
29. E. Chang and R. Roberts, “An improved algorithm for decentralized extrema-finding in circular configurations of processes,” Communications of the ACM, vol. 22, no. 5, pp. 281–283, 1979. [Google Scholar]
30. A. Biswas, A. K. Maurya, A. K. Tripathi and S. Aknine, “FRLLE: A failure rate and load-based leader election algorithm for a bidirectional ring in distributed systems,” Journal of Supercomputing, vol. 77, pp. 1–29, 2020. [Google Scholar]
31. R. Ingram, T. Radeva, P. Shields, J. E. Walter and J. L. Welch, “An asynchronous leader election algorithm for dynamic networks without perfect clocks,” in The Proc. of the Int. Symp. on Parallel and Distributed Processing, Rome, Italy, vol. 10, 2009. [Google Scholar]
32. S. Tucci-Piergiovanni and R. Baldoni, “Eventual leader election in infinite arrival message-passing system model with bounded concurrency,” in European Dependable Computing Conf., Valencia, Spain, pp. 127–134, 2010. [Google Scholar]
33. M. Ktari, M. Mosbah and A. H. Kacem, “Electing a leader in dynamic networks using mobile agents and local computations,” Procedia Computer Science, vol. 109, no. 2, pp. 351–358, 2017. [Google Scholar]
34. H. Garcia-Molina, “Elections in a distributed computing system,” IEEE Transactions on Computers, vol. 31, no. 1, pp. 48–59, 1982. [Google Scholar]
35. M. EffatParvar, N. Yazdani, M. EffatParvar, A. Dadlani and A. Khonsari, “Improved algorithms for leader election in distributed systems,” in 2nd Int. Conf. on Computer Engineering and Technology, Chengdu, China, pp. 6–10, 2010. [Google Scholar]
36. G. Antonoiu and P. K. Srimani, “A self-stabilizing leader election algorithm for tree graphs,” Journal of Parallel and Distributed Computing, vol. 34, no. 2, pp. 227–232, 1996. [Google Scholar]
37. A. Bounceur, M. Bezoui, R. Euler and F. Lalem, “A wait-before-starting algorithm for fast, fault-tolerant and low energy leader election in WSNs dedicated to smart-cities and IoT,” in IEEE Sensors, Glasgow, UK, pp. 1–3, 2017. [Google Scholar]
38. J. Surolia and M. M. Bundele, “Design and analysis of modified bully algorithm for leader election in distributed system,” in Int. Conf. on Artificial Intelligence: Advances and Applications, Singapore, pp. 337–347, 2020. [Google Scholar]
39. S. Sivasubramaniam, T. Kulkarni and J. Augustine, “Leader election in sparse dynamic networks with churn,” Internet Mathematics, vol. 12, no. 6, pp. 402–418, 2016. [Google Scholar]
40. P. Chaparala, A. R. Atmakuri and S. S. S. Rao, “3-phase leader election algorithm for distributed systems,” in 3rd Int. Conf. on Computing Methodologies and Communication, Erode, India, pp. 898–904, 2019. [Google Scholar]
41. H. Shindo, H. Kobayashi, G. Ishigaki and N. Shinomiya, “Multi-leader election in a clustered graph for distributed network control,” in IEEE 31st Int. Conf. on Advanced Information Networking and Applications, Taipei, Taiwan, pp. 342–346, 2017. [Google Scholar]
42. C. Newport, “Leader election in a smartphone peer-to-peer network,” in IEEE Int. Parallel and Distributed Processing Symp., Orlando, FL, USA, pp. 172–181, 2017. [Google Scholar]
43. E. Amiri, H. Keshavarz, A. S. Fahleyani, H. Moradzadeh and S. Komaki, “New algorithm for leader election in distributed WSN with software agents,” in IEEE Int. Conf. on Space Science and Communication, Melaka, Malaysia, pp. 290–295, 2013. [Google Scholar]
44. S. H. Park, S. G. Lee and S. C. Yu, “Notice of violation of IEEE publication principles a fault tolerant election protocol in asynchronous distributed systems with fail-stop model,” in 12th Int. Conf. on Information Technology-New Generations, Las Vegas, NU, USA, pp. 44–48, 2015. [Google Scholar]
45. H. Bagheri, M. J. Salehi, B. H. Khalaj and M. Katz, “An energy-efficient leader selection algorithm for cooperative mobile clouds,” in IFIP Wireless Days, Valencia, Spain, pp. 1–4, 2013. [Google Scholar]
46. C. Yu, X. Gou, C. Zhang and Y. Ji, “Supernode election algorithm in P2P network based upon district partition,” International Journal of Digital Content Technology and Its Applications, vol. 5, no. 1, pp. 186–194, 2011. [Google Scholar]
47. L. Xu and P. Jeavons, “Led by nature distributed leader election in anonymous networks,” in 10th Int. Conf. on Natural Computation, Xiamen, China, pp. 445–450, 2014. [Google Scholar]
48. K. Fitch and N. E. Leonard, “Information centrality and optimal leader selection in noisy networks,” in 52nd IEEE Conf. on Decision and Control, Florence, Italy, pp. 7510–7515, 2013. [Google Scholar]
49. M. Silva, A. Teles, R. Lopes, F. Silva, D. Viana et al., “Neighborhood-aware mobile hub: An edge gateway with leader election mechanism for internet of mobile things,” Mobile Networks and Applications, pp. 1–14, 2020. https://link.springer.com/article/10.1007/s11036-020-01630-3. [Google Scholar]
50. K. Lei, M. Du, J. Huang and T. Jin, “Groupchain: Towards a scalable public blockchain in fog computing of IoT services computing,” IEEE Transactions on Services Computing, vol. 13, no. 2, pp. 252–262, 2020. [Google Scholar]
51. F. T. Lin, “Solving the knapsack problem with imprecise weight coefficients using genetic algorithms,” European Journal of Operational Research, vol. 185, no. 1, pp. 133–145, 2008. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |