DOI:10.32604/cmc.2021.016047

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016047 |  |
| Article |
A New Medical Image Enhancement Algorithm Based on Fractional Calculus
1Faculty of Computer Science and Information Technology, University Malaya, Kuala Lumpur, 50603, Malaysia
2Nonlinear Dynamics Research Center (NDRC), Ajman University, Ajman, 346, UAE
3College of Medicine, Al-Nahrain University, Baghdad, 10001, Iraq
4Department of Computer Science, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, Riyadh, 84428, Saudi Arabia
5Department of Mathematics, Cankaya University, Balgat, Ankara, 06530, Turkey
6Institute of Space Sciences, Magurele-Bucharest, R76900, Romania
7Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
*Corresponding Author: Hamid A. Jalab. Email: hamidjalab@um.edu.my
Received: 20 December 2020; Accepted: 20 January 2021
Abstract: The enhancement of medical images is a challenging research task due to the unforeseeable variation in the quality of the captured images. The captured images may present with low contrast and low visibility, which might influence the accuracy of the diagnosis process. To overcome this problem, this paper presents a new fractional integral entropy (FITE) that estimates the unforeseeable probabilities of image pixels, posing as the main contribution of the paper. The proposed model dynamically enhances the image based on the image contents. The main advantage of FITE lies in its capability to enhance the low contrast intensities through pixels’ probability. Initially, the pixel probability of the fractional power is utilized to extract the illumination value from the pixels of the image. Next, the contrast of the image is then adjusted to enhance the regions with low visibility. Finally, the fractional integral entropy approach is implemented to enhance the low visibility contents from the input image. Tests were conducted on brain MRI, lungs CT, and kidney MRI scans datasets of different image qualities to show that the proposed model is robust and can withstand dramatic variations in quality. The obtained comparative results show that the proposed image enhancement model achieves the best BRISQUE and NIQE scores. Overall, this model improves the details of brain MRI, lungs CT, and kidney MRI scans, and could therefore potentially help the medical staff during the diagnosis process.
Keywords: Fractional calculus; image enhancement; brain MRI; lungs CT; kidney MRI
Medical imaging plays a detrimental role in the early-stage identification and treatment monitoring of several diseases due to its ability to represent the anatomical features as clinically useful information [1]. The imaging techniques employed in the medical setting might sometimes produce images with poor contrast and artifacts, which degrade the quality of the captured information [2]. Therefore, efforts have been made to improve the quality of medical images to improve the performance of the whole imaging system, and provide valuable information for diagnosis and treatment. Generally, the image enhancement methods aim to improve the image quality by increasing the contrast and reducing the loss of information so that the enhanced image presents better details for observers [3]. It is thus evident that the contrast enhancement step is crucial in image processing since it controls the amount of details that an image could have, subsequently influencing the interpretation of the image [4]. In this study, we present a new fractional integral entropy (FITE) based model for enhancing the different medical images. The performance of FITE has been assessed using two relevant image quality metrics, and compared with state-of-the-art of image enhancement techniques. The key contribution of the proposed study is the fractional integral entropy approach for enhancing the image low visibility contents which is the novelty of the proposed study. It can be concluded that the proposed FITE model can enhance the contrast of images with different quality accurately and efficiently. Due to its performance, the model has the potential to help radiologists obtain satisfactory results faster. Moreover, the FITE can be applied as an efficient pre-processing step for any image processing approach.
Most image enhancement algorithms are based on spatial processes implemented on image pixels to produce more appropriate images compared to the input image. Wong et al. [5] proposed a new histogram equalization (HE) algorithm to maximize the information content inside the input colored images. To provide images with richer details for radiologists, Subramani et al. [6] developed HE algorithm for medical image enhancement based on a fuzzy gray level difference that is used with MRI brain scans. The proposed algorithm improved the fine details in MRI brain scans. The HE is a common image enhancement method developed to uniformly redistribute the image gray level based on density function. However, the HE is not able to maintain the image’s mean brightness. Recently, a few image enhancement algorithms based on the concept of fractional calculus have been proposed. The fractional operators have the ability to keep the high frequency contour features, besides improving the low-frequency texture details. Roy et al. [3] proposed a new fractional calculus enhancement algorithm obtained by Laplacian operations. The method was proposed to remove the generated Laplacian noise from text inside video frames. Similarly, Raghunandan et al. [7] proposed a low contrast license plate image enhancement model based on Riesz fractional operator. The model achieved good results for the text images only. Another fractional based model for kidney images enhancement was developed by Al-Shamasneh et al. [4]. The proposed model developed based on the pixel probability of the neighboring pixels. This method was tested on their own MRI kidney dataset and attempted to enhance the contrast of the whole MRI image. In a similar approach, Chandra et al. [8] proposed a novel linear fractional mesh-free partial differential equation based method for images enhancement. The proposed enhancement model is able to preserve fine details in smooth areas, as well as non-linearly increase high frequency information. However, this method was applied on clear, cropped brain MRI images, which made them an easy target for enhancement. Additionally, the authors did not study the issue of overlapping contour of the brain region in the MRI scans. Another approach of image enhancement is the one based on the optimization of image quality. Anoop et al. [9] proposed a bilateral image filter to remove speckle noise from MRI images using an enhanced grass hopper optimization algorithm to optimize the image quality measure as a fitness value. However, this method focused on removing the speckle noise rather than improving the contrast quality of images. Alternatively, [10] proposed a tuned single-scale Retinex algorithm for improving the dynamic range of MRI scans. The proposed enhancement model is able to improve the brightness and contrast of the input MRI scans, but the preservation of fine details was not achieved. For poorly illuminated images, [11] proposed the fusion-based image enhancement method by applying different techniques to adjust the image illumination. This approach effectively improved the images illumination. However, the aim of the method is restricted to weakly illuminated images but not for images that suffer from degradations, and poor quality. In the same way, Zhang et al. [12] proposed an automatic image exposure correction method by using dual illumination estimation. In this method, the multi-exposure image fusion technique is employed to improve the input image with both under and over exposed regions into a globally well-exposed image. Despite the good results of this method, it was not shown to be able to preserve the fine details of medical images, which is required for the diagnosis process. Likewise, more image enhancements methods have been proposed based on nonlinear optimization with several constraints. Zhou et al. [13] proposed a new optimization algorithm based on the world cup optimization for controlling the Gamma value to enhance the image contrast. The enhancement process is performed using a traditional gamma correction. As a result, the computational complexity of this technique becomes large by applying several optimization constraints. Rundo et al. [1] proposed, a novel MRI enhancement using genetic algorithms and a bimodal intensity histogram. This method depends on image intensity histogram, which possibly suffered from over-enhancement. Alternatively, deep learning-based approaches have achieved a remarkable role in image enhancement, but they are still unable to enhance images well when there is a lack of training data, in addition to hardware limitations. Jiang et al. [14] proposed a deep learning approach to enhance dark images. This approach operated well without any paired training data for low-light enhancement jobs. The experimental results on various low light datasets show the effectiveness of this method. Moreover, Shi et al. [15] proposed a deep neural network for enhancing rainy images with low illumination. The goal of this study was to improve the image captured by low illumination. Kuang et al. [16] developed a deep learning optimization framework to remove background noise in infrared images. This method produced interesting visual results with good contrast enhancement compared to other network designs. Li et al. [17] proposed a trainable convolutional neural network for enhancing images with low illumination based on Retinex model without over or under enhancing the image’s regions. The enhanced results of this method significantly relied on the Retinex model, which is applied in many image enhancement approaches to improve the image brightness. The above mentioned methods explored different approaches for enhancing images. These methods work well in improving the whole image, but not for the sub-regions enhancement. Moreover, a limited number of enhancement methods were developed based on fractional calculus operators. Therefore, in this study, we propose a new fractional integral entropy (FITE) based model for enhancing different medical images by enhancing the dark area and maintaining the bright area of the input image.
Inspired by the fact that fractional integral has the ability to find solutions to complex problems like non-linear complexities [18], we explore new fractional integral entropy to enhance and preserve the fine details of the medical image boundaries. The fractional integral (local fractional integral) is one of the significant approaches of fractional analysis, which is utilized to measure the fractional structures of data, such as images. It includes a formal approach to give a fractional dimension (
Definition 1.1
For a function
Note that
By simulating Tsallis entropy under the fractional integral, and letting
where
By applying the properties of the fractional integral, we have the following proposition:
Proposition 1.2
For a function
i)
ii)
iii)
iv)
v)
vi)
Remark 1.3
In image processing context, we translate Eq. (2) into a discrete formula as follows:
where
Moreover, the inverse of (5) can be acted again on
By using 2-D image information, the formula is Eq. (6) can be expressed as follows
where m and n are the image dimension. The fractional parameter
The steps of the proposed model are as follow:
1. Calculate the image intensity occurrences number.
2. Calculate the probability of each intensity occurrences number.
3. Calculate the upper (
4. Calculate the sum of all pixels’ probability.
5. Calculate cumulative sum of the elements of Eq. (7).
6. Display the enhanced image
The output of the proposed FITE for a sample low contrast image is shown in Fig. 1. By looking at the input images in Fig. 1a, one cannot directly notice the lack of details in these images. However, when comparing them to the results of the proposed FITE as shown in Fig. 1c, the lack of details becomes more evident as weakly illuminated objects become brighter with well-defined details following the enhancement. The enhancement of the low visibility regions in the input images is attributed to the ability of FITE to extract illumination value from input image pixels. The histogram analyses of the input and the enhanced images are shown in Figs. 1b, 1d respectively. As seen from Fig. 1b, the gray level distribution for the input image looks dense, while after enhancement by proposed FITE, the gray level distribution looks more uniformed, as reflected by the enhanced contrast boundaries of the input images. The histogram analysis illustrates the variations in the features of the input and the enhanced images. The logic behind using fractional calculus in image enhancement is the capability of FITE to capture high frequency details efficiently, regardless of image system noise. The proposed enhancement model is able to preserve fine details in smooth areas, as well as non-linearly increase high frequency information.
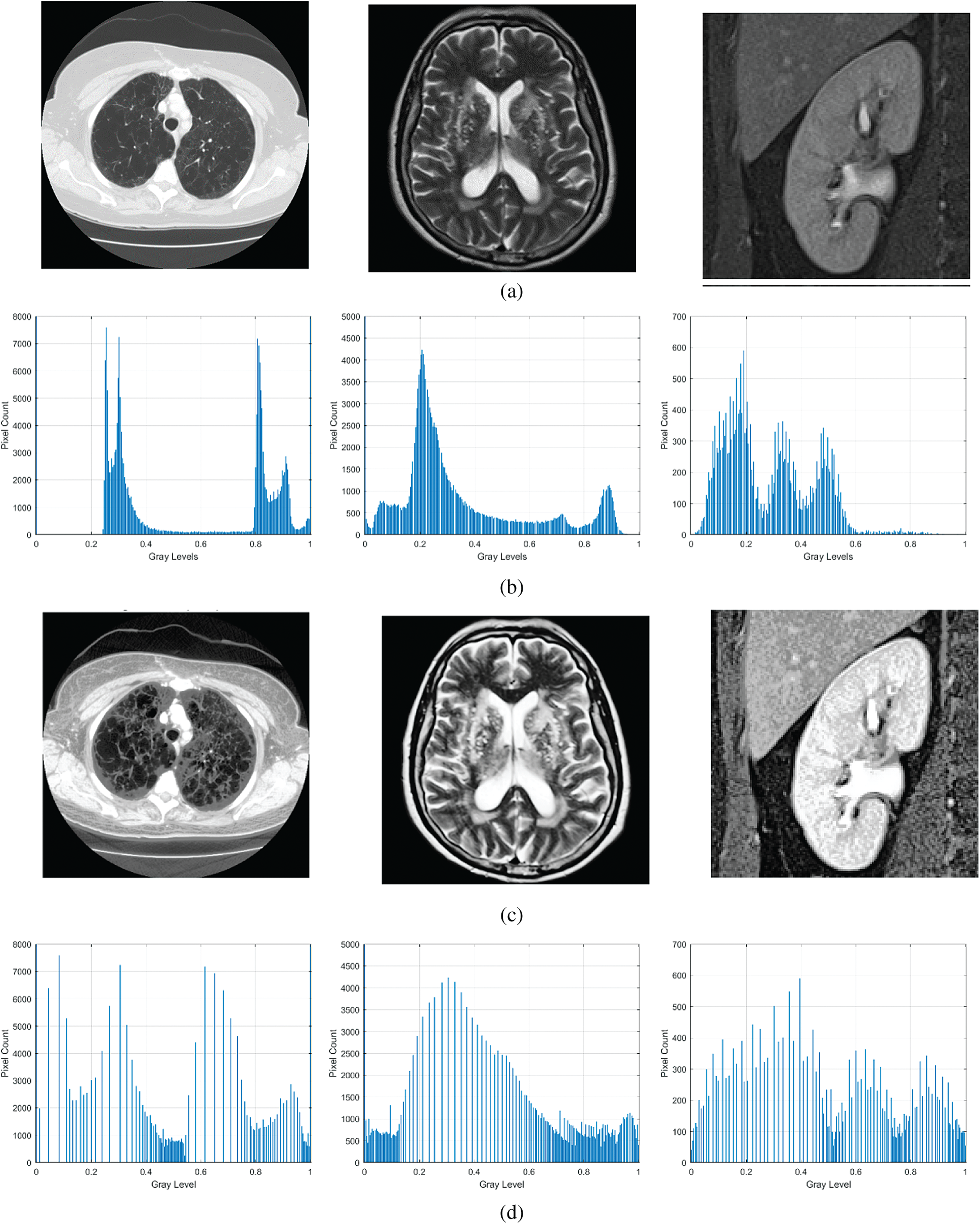
Figure 1: Sample output of the proposed algorithm along with histogram analysis. (a) Input image, (b) histogram detail of input image, (c) enhanced image, (d) histogram detail of enhanced image
The proposed method is evaluated using the following images datasets:
1. The lung CT scan dataset created by Italian Society of Medical and Interventional Radiology, which is named as COVID-19 DATABASE dataset [21].
2. Brain MRI dataset, comprising 154 MRI brain images [22].
3. Kidney MRI dataset of 230 images [23].
To evaluate the performance of the proposed image enhancement model, we employ the following standard metrics:
A) Two no-reference image quality assessment, which are: “the blind reference less image spatial quality evaluator (BRISQUE),” which calculates the perceptual quality of images, and “the naturalness image quality evaluator(NIQE),” which calculates the image quality affected by arbitrary distortion. It is noted that the low scores of BRISQUE and NIQE indicate better quality of the enhanced images.
B) Two histogram based metrics which quantify the flatness (HF), and the spread (HS) of the image histogram. These two metrics help differentiate between the low and high contrast images. Moreover. The HF, and the HS are defined as:
The histogram quartiles represent the amount of data spread. The value of the quartile distance is the difference between the 3rd quartile and the 1st quartile of the extracted image histogram. Both the HF, and HS depend on the intensity values of the histogram and on the histogram bin positions.
The code of proposed image enhancement algorithm was developed using MATLAB 2019b, while Matlab and Python have been used to conduct the comparative analysis with other methods. To show that the proposed model is effective as a medical image enhancement tool, we implemented the following existing methods for the comparative study: The histogram equalization (HE) method. The fractional entropy based enhancement method of kidney images by Al-Shamasneh et al. [4]. The image enhancement method for license plate by Raghunandan et al. [7] that is based on the Riesz fractional operator. The MRI brain images enhancement method by Al-Ameen et al. [10]. The fusion-based enhancement method of poorly illuminated images by Fu et al. [11]. The CNN-based image enhancement method by Li et al. [17] for weakly illuminated images. And finally, the automatic exposure correction method by Zhang et al. [12]. All of the aforementioned methods were executed on the same machine (Windows 10 64-bit, Intel Core i7, SSD storage, and 8 GB of RAM) for consistency.
In the proposed enhancement model, the fractional parameter (
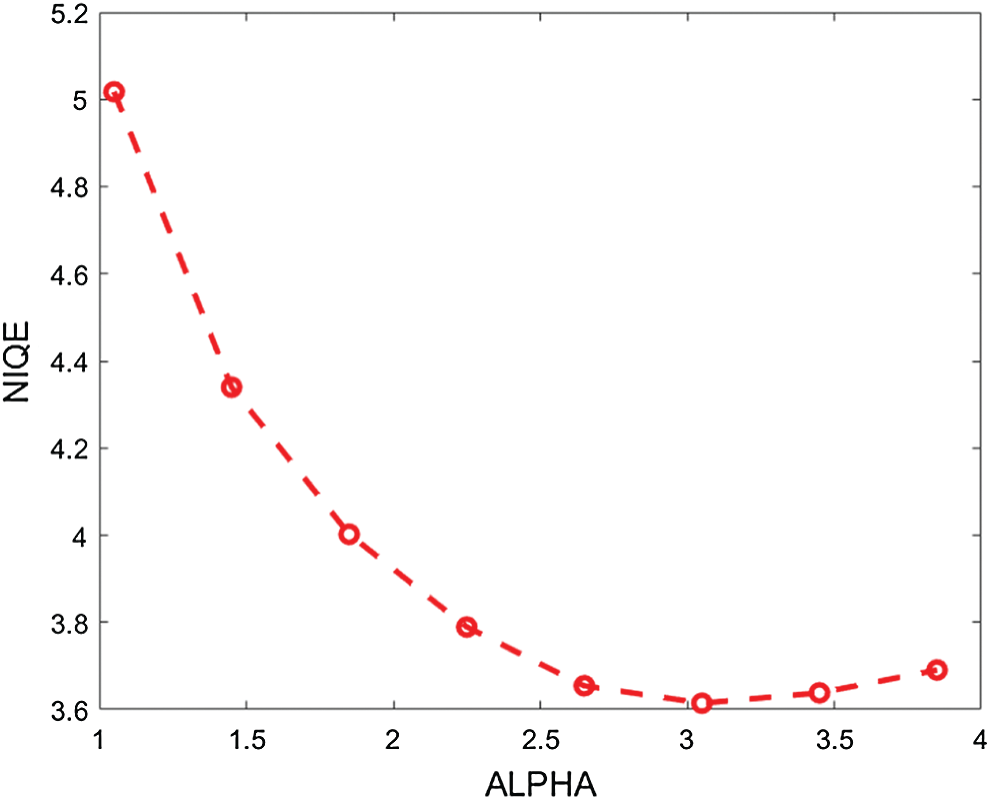
Figure 2: The average NIQE measure for different values of the fractional parameter (
The qualitative results are illustrated in Fig. 3 for brain MRI; in Fig. 4 for lung CT, and in Fig. 5 for kidney MRI. As shown in the figures, all of the images have different trends with the dark and bright areas. It could be seen that the Histogram Equalization (b), Fu et al. [11] (f), and Zhang et al. [12] (h) methods produce over-enhanced images, while the proposed method produces natural appearance by enhancing the dark areas and maintaining the bright areas of input images. Overall, when we look at the input images and its enhanced images, the brightness of the fine details increases compared to the input images, irrespective of the content and application of the image. The brightening caused by the proposed FITE model makes the structures of the medical images well-defined and clear. The proposed FITE method introduces fair visual results for the weakly illuminated images. This is the contribution of fractional integral entropy in this study.
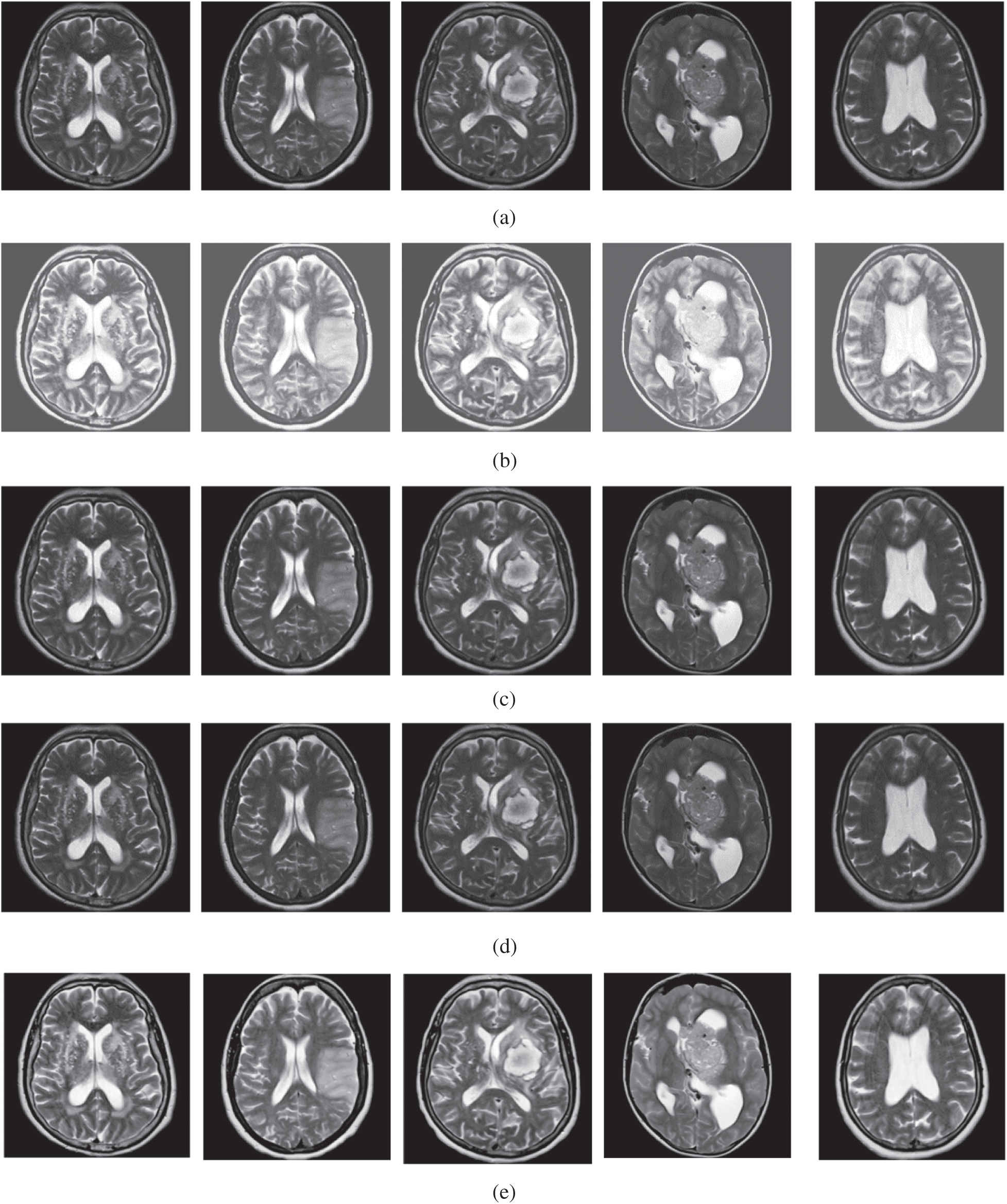
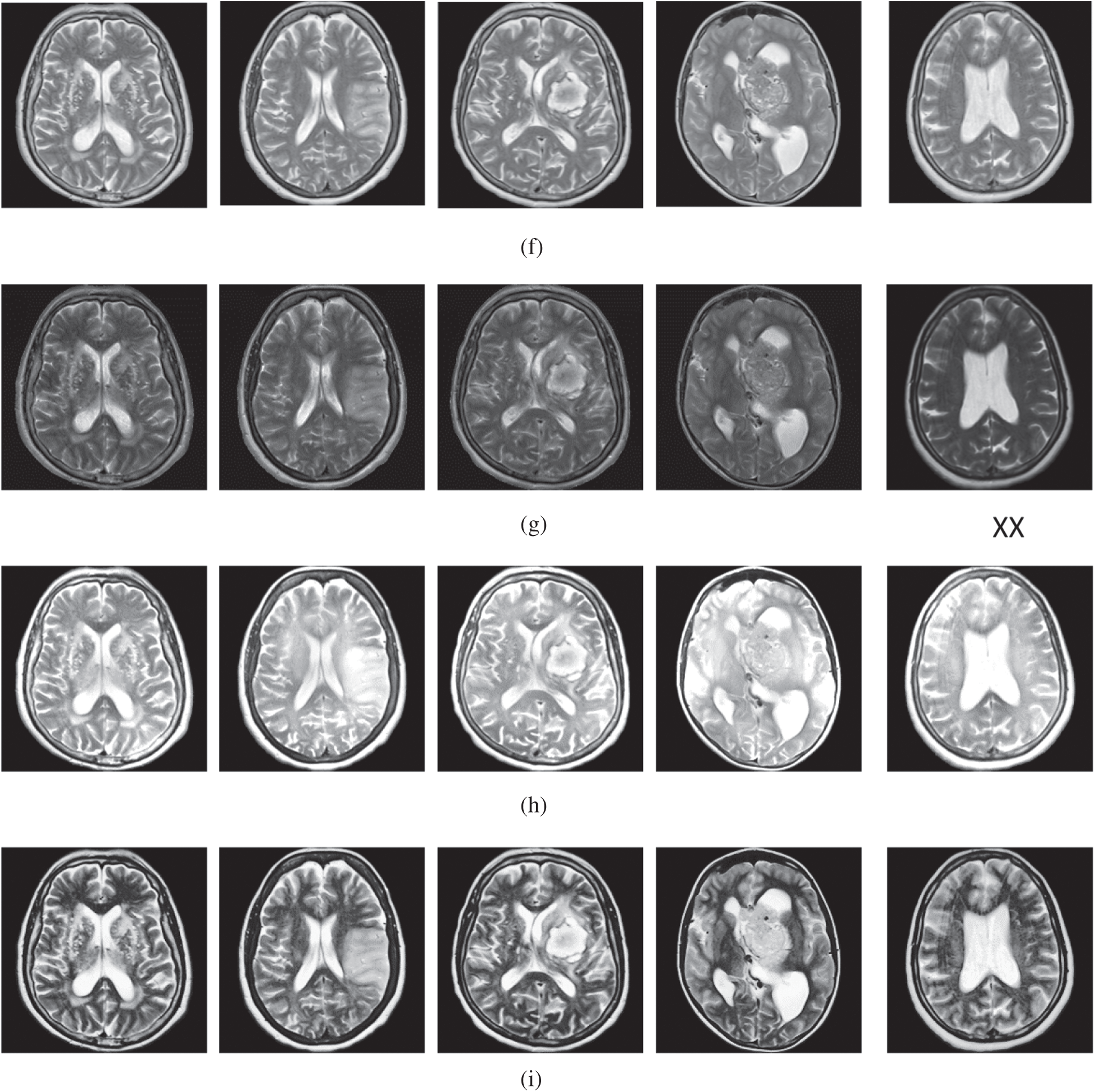
Figure 3: The brain MRI enhancement results of the proposed and existing enhancement models. (a) Input image, (b) histogram equalization, (c) Al-Shamasneh et al. [4], (d) Raghunandan et al. [7], (e) Al-Ameen et al. [10], (f) Fu et al. [11], (g) Li et al. [17], (h) Zhang et al. [12], (i) proposed FITE
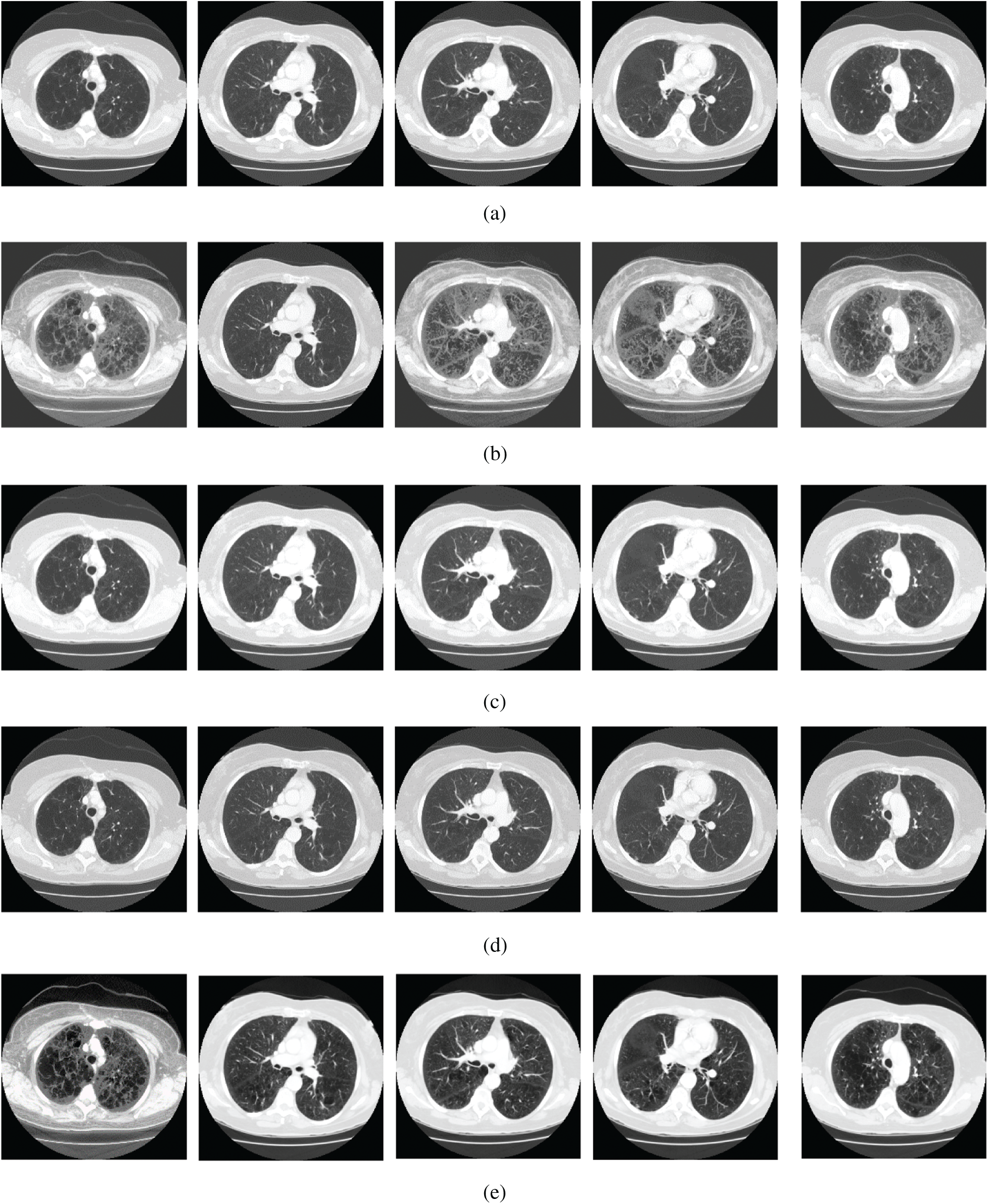
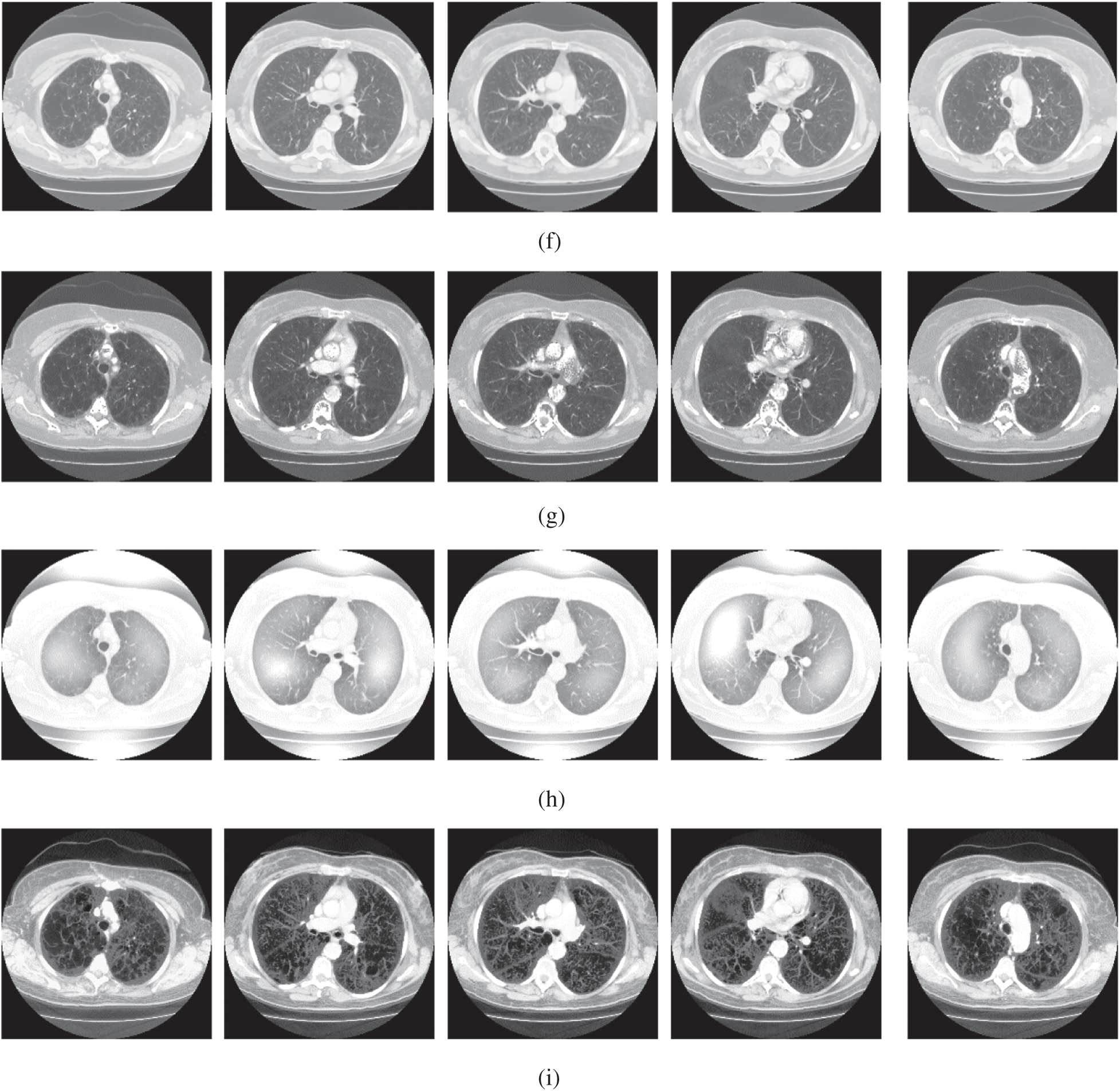
Figure 4: The lung CT enhancement results of the proposed and existing enhancement models. (a) Input Image, (b) histogram equalization, (c) Al-Shamasneh et al. [4], (d) Raghunandan et al. [7], (e) Al-Ameen et al. [10], (f) Fu et al. [11], (g) Li et al. [17], (h) Zhang et al. [12], (i) proposed FITE
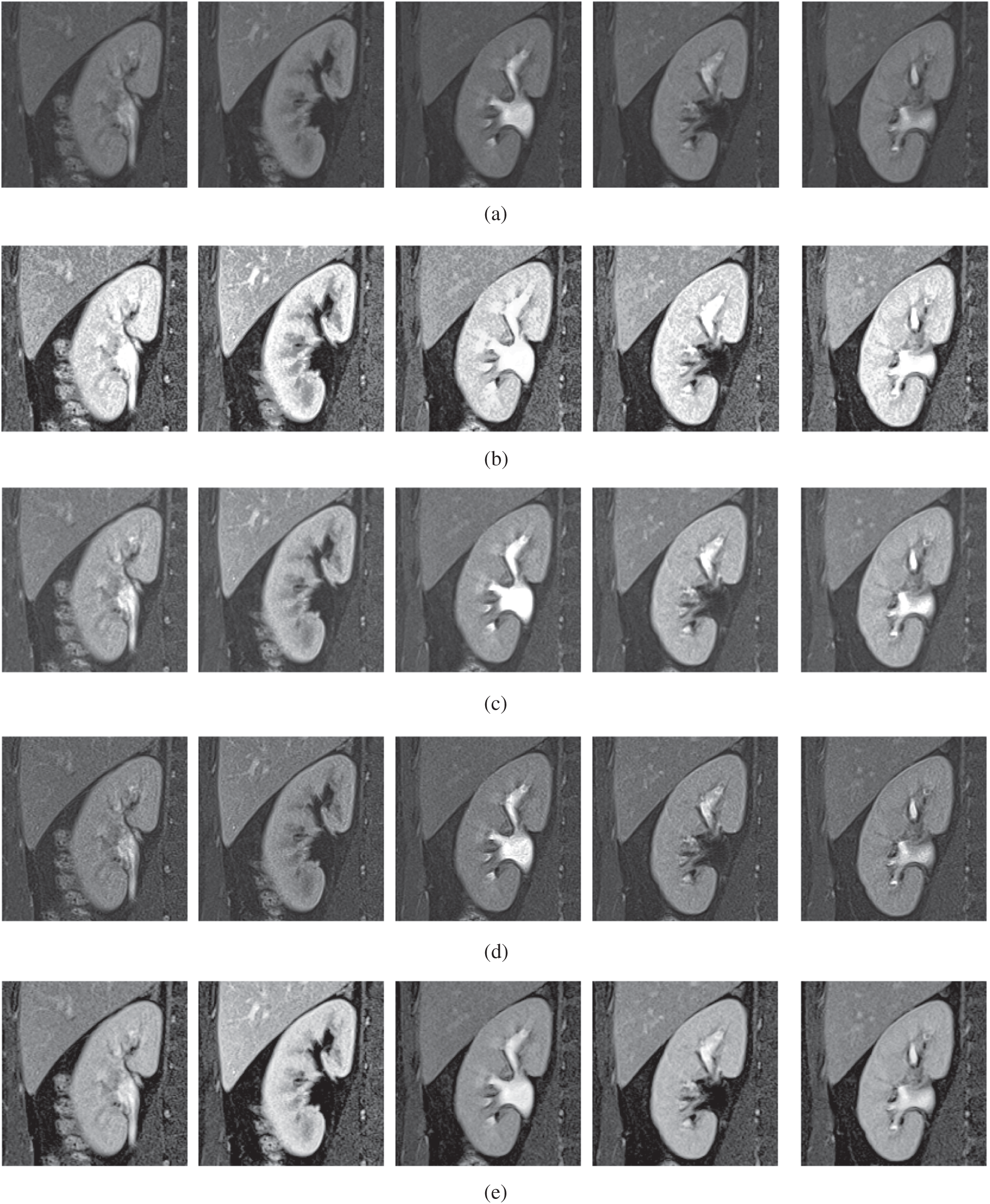
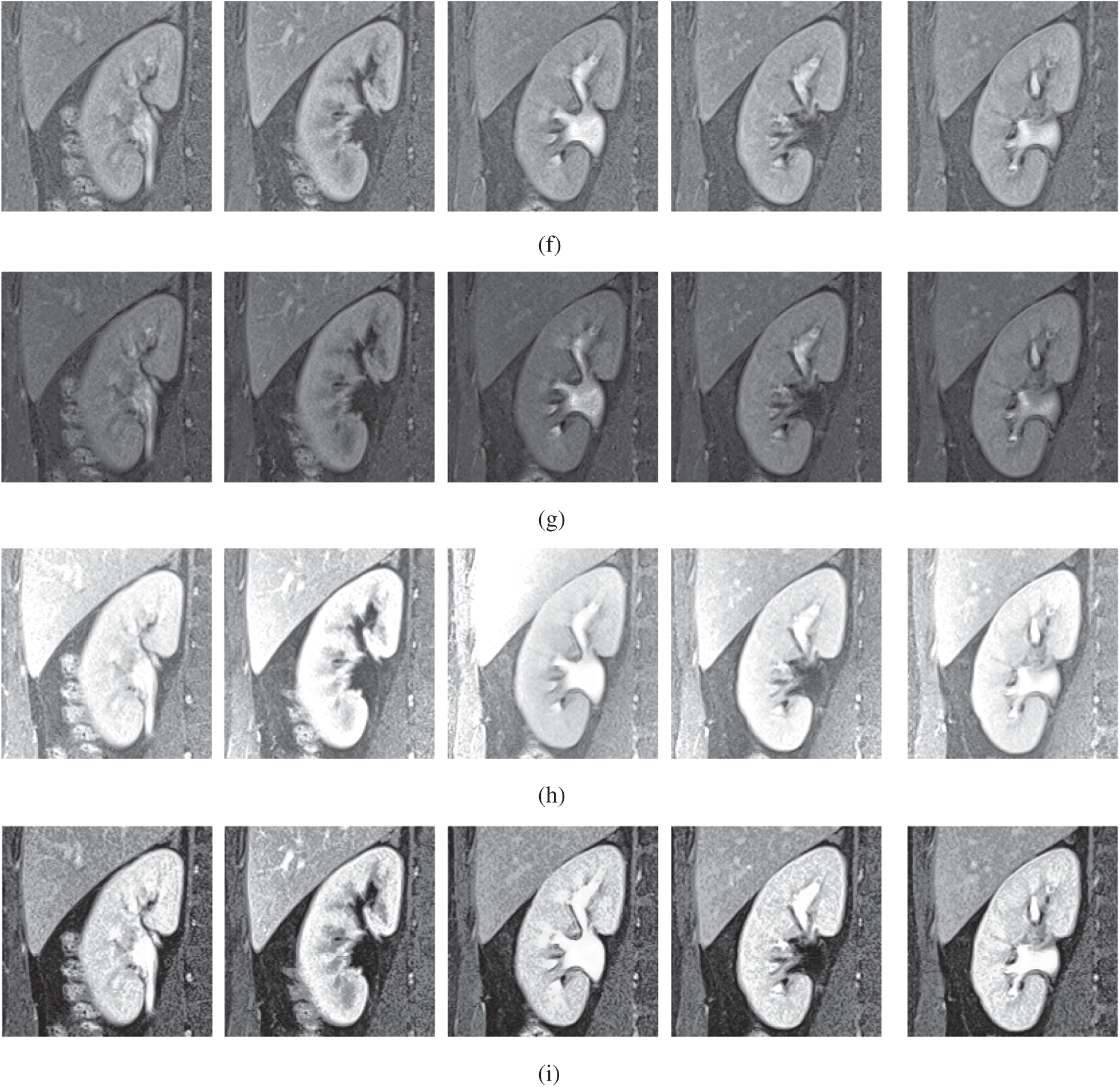
Figure 5: The kidney MRI enhancement results of the proposed and existing enhancement models. (a) Input image, (b) histogram equalization, (c) Al-Shamasneh et al. [4], (d) Raghunandan et al. [7], (e) Al-Ameen et al. [10], (f) Fu et al. [11], (g) Li et al. [17], (h) Zhang et al. [12], (i) proposed FITE
The achieved quantitative results of FITE and the existing image enhancement models are stated in Tabs. 1 and 2. Most of the image enhancement methods reported in the literature use the no-reference image quality metrics, therefore, the BRISQUE and NIQE scores have been used for the quantitative comparisons as presented in Tab. 1. The proposed method achieves the best BRISQUE and NIQE for almost all of the images from the three datasets. However, for the brain MRI images, the performance of the proposed FITE method degrades slightly compared to the Zhang et al [12] method. This might be caused by the increased complexity of the said images compared to the ones found in the other two datasets, and might constitute a primary limitation of the present work. Overall, the proposed FITE method achieves the best of BRISQUE and NIQE scores (lower is better), regardless of dataset and content. When considering the general goal of image enhancement, it can be said that the proposed method is the best compared to the rest of the mentioned methods due to its consistent results across the different datasets. However, some existing methods may produce better results when used under particular conditions since they were designed with a specific application in mind.
Table 1: Assessment of various image enhacnement methods and the proposed model against the three images datasets
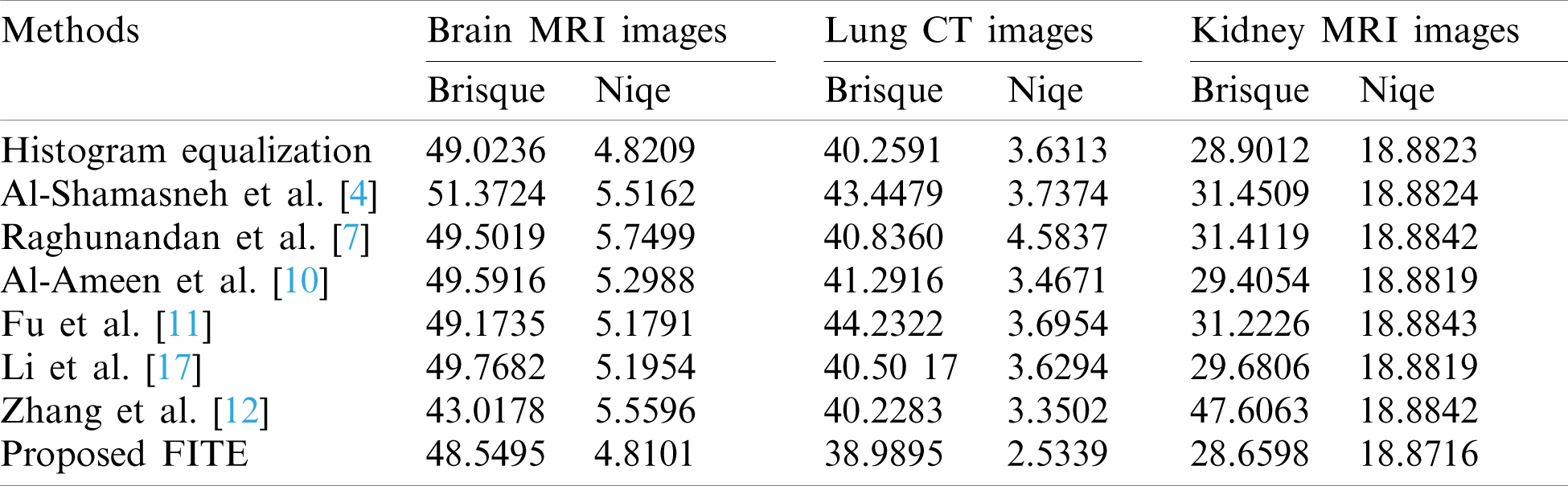
Table 2: The histogram flatness (HF), and the histogram spread (HS) measures
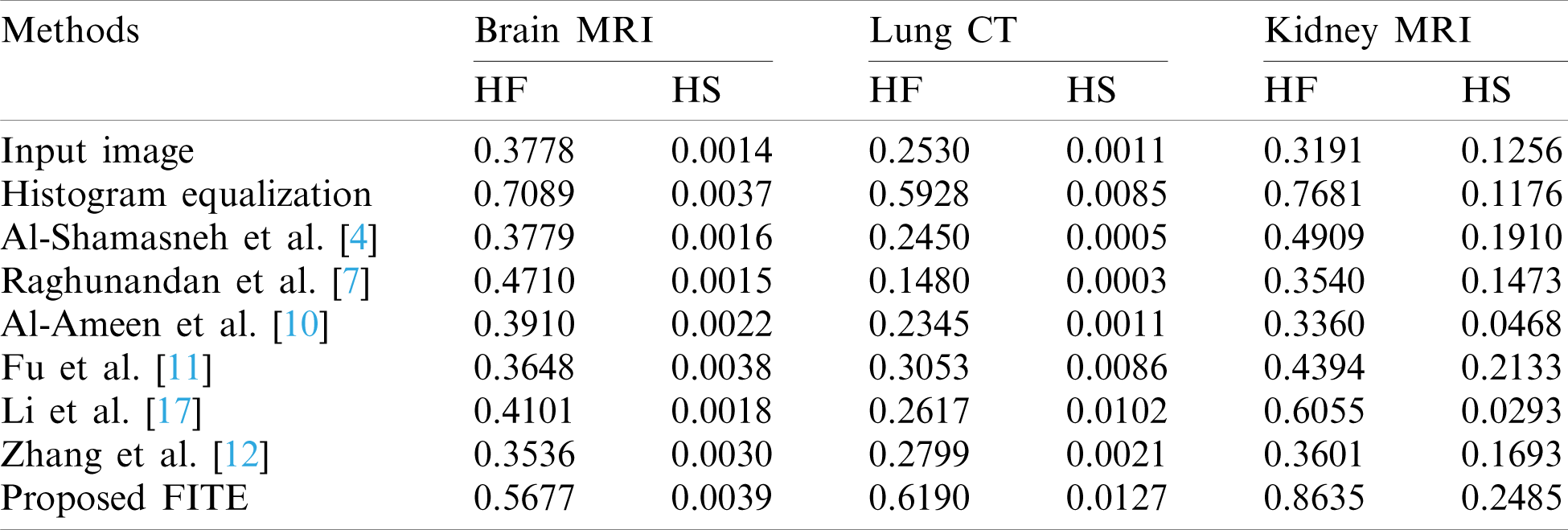
In Tab. 2, the histogram flatness (HF), and the histogram spread (HS) measures have been used as another quantitative comparison. The results in Tab. 2 show that the proposed FITE method achieves the best scores (high score) for different kinds of weakly illuminated images. It could be concluded that the scalability of the proposed FITE model is the best compared to the other image enhancement methods. This further consolidates the point mentioned above regarding the ability of the proposed model to perform well under general settings, compared to specialized methods.
In order to preserve the fine structures of images, irrespectively of the pixel’s contrast, we have introduced in this study a novel image enhancement model involving fractional integral entropy (FITE). This model integrates the properties of fractional integral and entropy, which can solve the problem of non-linear complexity of image enhancement. The proposed FITE dynamically enhances fine details of different medical images based on the image contents. Experimental results on three medical image datasets indicated that the proposed FITE approach outperforms the existing methods under the general application of image enhancement. It is noteworthy that some of the methods used for comparison may yield better results under certain conditions since they were specifically designed to handle the images produced under such conditions. This gives the proposed model the advantage of being more scalable for the general purpose of image enhancement than the existing methods. Thus, the proposed model could be utilized under a wider range of settings, such as under the clinical setting to aid the medical staff during the diagnosis process, or as a preprocessing setup for further imaging applications. Future works may adapt the present model for specific applications to attain maximum enhancement benefit.
Funding Statement: This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-track Research Funding Program.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. Rundo, A. Tangherloni, M. S. Nobile, C. Militello, D. Besozzi et al., “MedGA: A novel evolutionary method for image enhancement in medical imaging systems,” Expert Systems with Applications, vol. 119, no. 13, pp. 387–399, 2019. [Google Scholar]
2. F. Verdun, D. Racine, J. Ott, M. Tapiovaara, P. Toroi et al., “Image quality in CT: From physical measurements to model observers,” Physica Medica, vol. 31, no. 8, pp. 823–843, 2015. [Google Scholar]
3. S. Roy, P. Shivakumara, H. A. Jalab, W. I. Ibrahim, U. Pal et al., “Fractional Poisson enhancement model for text detection and recognition in video frames,” Pattern Recognition, vol. 52, pp. 433–447, 2016. [Google Scholar]
4. A. A. R. Al-Shamasneh, H. A. Jalab, P. Palaiahnakote, U. H. Obaidellah and W. I. Ibrahim, “A new local fractional entropy-based model for kidney MRI image enhancement,” Entropy, vol. 20, no. 5, pp. 344, 2018. [Google Scholar]
5. C. Y. Wong, S. Liu, S. C. Liu, M. A. Rahman, S. C. Lin et al., “Image contrast enhancement using histogram equalization with maximum intensity coverage,” Journal of Modern Optics, vol. 63, no. 16, pp. 1618–1629, 2016. [Google Scholar]
6. B. Subramani and M. Veluchamy, “Fuzzy gray level difference histogram equalization for medical image enhancement,” Journal of Medical Systems, vol. 44, no. 6, pp. 1–10, 2020. [Google Scholar]
7. K. Raghunandan, P. Shivakumara, H. A. Jalab, W. I. Ibrahim, G. H. Kumar et al., “Riesz fractional based model for enhancing license plate detection and recognition,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 28, no. 9, pp. 2276–2288, 2017. [Google Scholar]
8. S. K. Chandra and M. K. Bajpai, “Fractional mesh-free linear diffusion method for image enhancement and segmentation for automatic tumor classification,” Biomedical Signal Processing and Control, vol. 58, no. 101841, pp. 1–9, 2020. [Google Scholar]
9. V. Anoop and P. R. Bipin, “Medical image enhancement by a bilateral filter using optimization technique,” Journal of Medical Systems, vol. 43, no. 8, pp. 240, 2019. [Google Scholar]
10. Z. Al-Ameen and G. Sulong, “Ameliorating the dynamic range of magnetic resonance images using a tuned single-scale retinex algorithm,” International Journal of Signal Processing, Image Processing and Pattern Recognition, vol. 9, no. 7, pp. 285–292, 2016. [Google Scholar]
11. X. Fu, D. Zeng, Y. Huang, Y. Liao, X. Ding et al., “A fusion-based enhancing method for weakly illuminated images,” Signal Processing, vol. 129, no. 12, pp. 82–96, 2019. [Google Scholar]
12. Q. Zhang, Y. Nie and W. Zheng, “Dual illumination estimation for robust exposure correction,” ArXiv, vol. 1910.13688, pp. 1–10, 2019. [Google Scholar]
13. Y. Zhou, C. Shi, B. Lai and G. Jimenez, “Contrast enhancement of medical images using a new version of the world cup optimization algorithm,” Quantitative Imaging in Medicine and Surgery, vol. 9, no. 9, pp. 1528–1547, 2019. [Google Scholar]
14. Y. Jiang, X. Gong, D. Liu, Y. Cheng, C. Fang et al., “Enlightengan: Deep light enhancement without paired supervision,” ArXiv, vol. 1906-06972, pp. 1–10, 2019. [Google Scholar]
15. Z. Shi, Y. Feng, M. Zhao and L. He, “A joint deep neural networks-based method for single nighttime rainy image enhancement,” Neural Computing and Applications, vol. 32, no. 7, pp. 1913–1926, 2020. [Google Scholar]
16. X. Kuang, X. Sui, Y. Liu, Q. Chen and G. Gu, “Single infrared image enhancement using a deep convolutional neural network,” Neurocomputing, vol. 332, no. 4, pp. 119–128, 2019. [Google Scholar]
17. C. Li, J. Guo, F. Porikli and Y. Pang, “LightenNet: A convolutional neural network for weakly illuminated image enhancement,” Pattern Recognition Letters, vol. 104, pp. 15–22, 2018. [Google Scholar]
18. H. A. Jalab, R. W. Ibrahim and A. Ahmed, “Image denoising algorithm based on the convolution of fractional Tsallis entropy with the Riesz fractional derivative,” Neural Computing and Applications, vol. 28, no. 1, pp. 217–223, 2017. [Google Scholar]
19. C. Tsallis, “Possible generalization of Boltzmann-Gibbs statistics,” Journal of Statistical Physics, vol. 52, no. 1–2, pp. 479–487, 1988. [Google Scholar]
20. X. J. Yang, D. Baleanu and H. M. Srivastava, Local Fractional Integral Transforms and Their Applications. USA: Academic Press, United State, 2015. [Google Scholar]
21. COVID-19 images dataset. Italian Society of Medical and Interventional Radiology. [Online]. Available: https://www.sirm.org/category/senza-categoria/covid-19/ [Accessed on November 2020]. [Google Scholar]
22. A. M. Hasan, H. A. Jalab, R. W. Ibrahim, F. Meziane, A. R. Al-Shamasneh et al., “MRI brain classification using the quantum entropy LBP and deep-learning-based features,” Entropy, vol. 22, no. 9, pp. 1–15, 2020. [Google Scholar]
23. A. A. R. Al-Shamasneh, H. A. Jalab, P. Shivakumara, R. W. Ibrahim and A. U. H. Obaidellah, “Kidney segmentation in MR images using active contour model driven by fractional based energy minimization,” Signal, Image and Video Processing, vol. 14, no. 7, pp. 1361–1368, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |