Computers, Materials & Continua DOI:10.32604/cmc.2021.016960
Article

A Practical Quantum Network Coding Protocol Based on Non-Maximally Entangled State

Zhen-Zhen Li1, Zi-Chen Li1,*, Xiu-Bo Chen2, Zhiguo Qu3, Xiaojun Wang4 and Haizhu Pan5

1School of Information Engineering, Beijing Institute of Graphic Communication, Beijing, 102600, China
2Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
3Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing, 210044, China
4School of Electronic Engineering, Dublin City University, Dublin, 9, Ireland
5College of Computer and Control Engineering, Qiqihar University, Qiqihar, 161006, China
*Corresponding Author: Zi-Chen Li. Email: lizichen@bigc.edu.cn
Received: 10 January 2021; Accepted: 16 February 2021

Abstract: In many earlier works, perfect quantum state transmission over the butterfly network can be achieved via quantum network coding protocols with the assist of maximally entangled states. However, in actual quantum networks, a maximally entangled state as auxiliary resource is hard to be obtained or easily turned into a non-maximally entangled state subject to all kinds of environmental noises. Therefore, we propose a more practical quantum network coding scheme with the assist of non-maximally entangled states. In this paper, a practical quantum network coding protocol over grail network is proposed, in which the non-maximally entangled resource is assisted and even the desired quantum state can be perfectly transmitted. The achievable rate region, security and practicability of the proposed protocol are discussed and analyzed. This practical quantum network coding protocol proposed over the grail network can be regarded as a useful attempt to help move the theory of quantum network coding towards practicability.

Keywords: Quantum network coding; non-maximally entangled state; quantum grail network; practical protocol

1  Introduction

Classical network coding (CNC) [1], with many years of development, has made significant advances in classical network communications [2–4]. As a breakthrough technology, CNC can effectively improve the network communication efficiency since it can achieve the maximum flow network communication and reduce the bandwidth resource consumption. In 2007, Hayashi et al. [5] first introduced this idea into quantum networks, creating a new technology called quantum network coding (QNC). QNC has now become an important research direction related to the field of quantum communication and quantum information processes. Just like the CNC, QNC can solve the transmission congestion over quantum networks, gaining higher quantum communication efficiency [6–8] and achieving larger quantum network throughput [9–11] than the traditional technology of routing.

In Hayashi et al. foundation work [5] of QNC, it is proved that quantum states can not be perfectly transmitted through the network without the assistance of auxiliary resources. Thus, in recent years, there have been more researches on the perfect QNC assisted with auxiliary resources. In general, the representative resources introduced into the QNC schemes mainly include prior entanglement [12–14] and classical communication [15–17]. For the prior entanglement, in 2007, Hayashi [18] first introduced this kind of auxiliary resources into the QNC scheme over the butterfly network. Afterwards, several different kinds of perfect QNC schemes assisted with prior entanglement were proposed in [19,20]. For classical communication, in 2009, Kobayashi et al. [21] first explored the perfect QNC scheme assisted with this kind of auxiliary resources, based on the linear CNC. Subsequently, various QNC schemes assisted with classical communication have been proposed in [22,23] to achieve perfect transmission of quantum states. In 2019, Li et al. [24] proposed an efficient quantum state transmission scheme via perfect quantum network coding, in which auxiliary resources of both maximally entangled state and classical communication are assisted. Through the analysis of the amounts of the introduced auxiliary resources including prior entanglement and classical communication, the QNC scheme in [24] reached the highest level of quantum communication efficiency so far.

However, on the one hand, the network models including butterfly network and quantum k-pair network studied in [18–24] are homogeneous, since the quantum k-pair network is virtually extended from the butterfly network. On the other hand, in the QNC schemes of [18–20,24], the ideal situation was considered, where the maximally entangled state was introduced as the auxiliary entanglement resource. Hence, we have been trying to propose a more practical QNC scheme without reducing quantum communication efficiency. It is well known, as a kind of general entanglement with representation, non-maximally entangled state is more common in practice and hard to be distinguished. Therefore, it is reasonable to believe that non-maximally entangled state is contributed to improving the availability and security of the QNC.

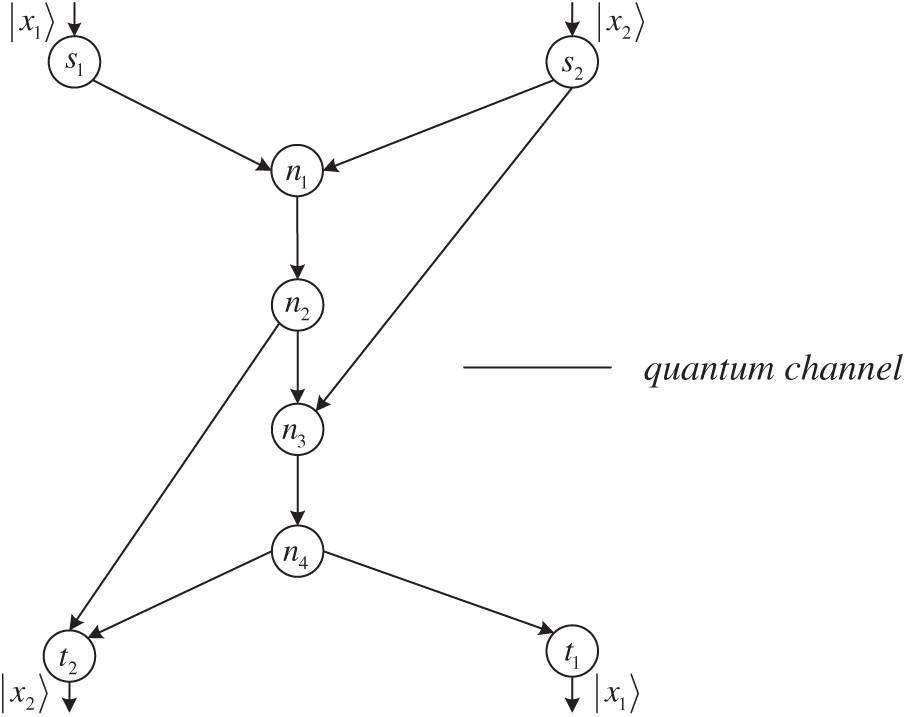
Figure 1: Quantum grail network

This work emphasizes on the proposal of a practical QNC scheme over the quantum grail network illustrated in Fig. 1 with the assist of non-maximally entangled state and classical communication. From the network model, the quantum grail network we considered is rarely studied but fairly imperative since it is another fundamental primitive network [25]. From the non-maximally entangled state, it is a kind of entanglement resource that can be more easily obtained in practice, which helps our QNC scheme better suited to applications. Besides, by the use of our proposed QNC scheme, the desired quantum states can be perfectly transmitted through the network, helping to expand the existed theory of QNC.

2  A Practical QNC Protocol Based on Non-Maximally Entangled State

In [25], grail network is viewed as a fundamental primitive network for CNC like butterfly network. Also like “butterfly network,” the network is named “grail network” because the network model is shaped like a “grail.” A typical communication task for CNC over grail network can be treated as the bottleneck problem like butterfly network. Applying that analogy to quantum network, the quantum communication task for QNC over quantum grail network can be treated as the quantum bottleneck problem. The specific quantum network model is illustrated in Fig. 1. It can be considered as a directed acyclic network (DAN). This DAN consists of a directed acyclic graph (DAG) G=(V,E) and the edge quantum capacity function c:E→ℤ+, where V is the set of nodes while E is the set of edges that connect pairs of nodes in V. Herein, we discuss the practical QNC scheme over this quantum grail network on d-dimension Hilbert space H=ℂd directly. According to the communication task of QNC, two source nodes s1, s2 needs to transmit two arbitrary qudit state |x1 < rangle >, |x2〉∈H to the sink nodes t1, t2 simultaneously and respectively through the network under the condition that c(e)≡1, e∈E, i.e., each edge of the network can transmit no more than one qudit state over H.

Suppose in the quantum grail network, for i∈{1,2}, each of the source nodes si possesses one quantum register Si while each of the sink nodes ti possesses one quantum register Ti. Quantum register Si can be considered to be received from a virtual incoming edge and Ti can be considered to be transmitted to a virtual outcoming edge. Before proposing our QNC protocol, the auxiliary entanglement resources of two identical non-maximally entangled states are formed as

|ϕ〉N1N2=∑m∈ℤdβm|m,m〉N1N2|ϕ〉N3N4=∑n∈ℤdγn|n,n〉N3N4(1)

are pre-shared between the intermediate nodes n1 and n2 (n3 and n4) respectively, where the βm (γn) are unequal complex numbers such that ∑m∈ℤdβm=1 (∑n∈ℤdγn=1), and the N1,N2,N3,N4 represent the four quantum registers introduced at the corresponding nodes. Besides, for convenience, the two arbitrary qudit states initially possessed at the two source nodes can be written as an entire quantum system formed as

|Ψ〉S=∑x1, x2∈Zdαx1, x2|x1x2〉S1S2,(2)

where the coefficients αx1,x2 are complex numbers such that ∑x1,x2∈ℤd|αx1,x2|2=1. Then, the initial state over the whole network before the transmission can be written as

|Ψ〉0=∑m, n∈ℤdβmγn|Ψ〉S⊗|m,m〉N1, N2⊗|n,n〉N3N4.(3)

Next, we will describe the specific processes of the practical QNC protocol based on the non-maximally entangled state over the quantum grail network in detail. The corresponding QNC model over the grail network is illustrated in Fig. 2.

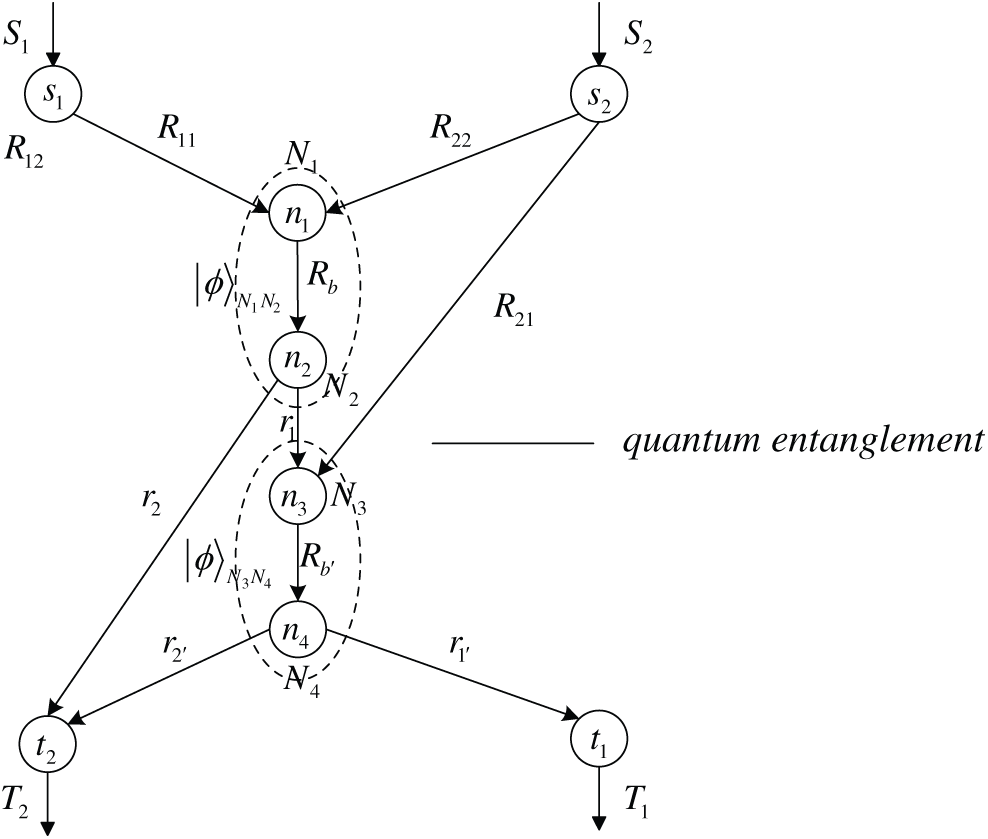
Figure 2: QNC model over quantum grail network

2.1 Encoding

In this process, the object is to make the particles in the quantum registers mutually entangled in the network topological order. Here, the quantum circuit of encoding is shown in Fig. 3 and the detailed steps are given below.

Figure 3: Quantum circuit of encoding

(S1) For i,j∈{1,2}, quantum registers Rij, each initialized to |0H〉, are introduced at each source node si, and then the operator CX̃Si→Rii is applied to the registers Si and Rii, operator CR̃Si→Rij is applied to the registers Si and Rij(j≠i). Here, quantum operator CX̃A→B is defined as CX̃A→B:=∑i∈ℤd|i〉〈i|A⊗XBi, where X|i〉=|i⊕1modd〉 is an analogue on qudits of the unitary Pauli operator σx on qubits [26]. Quantum operator CR̃A→B is defined as CR̃A→B:=∑i∈ℤd|i〉〈i|A⊗RBi, where R|i〉=|i-1modd〉 is the reverse transformation of X on qudits. Thus, the whole quantum system state becomes

|Ψ〉1=∑x1, x2, m, n∈ℤdαx1, x2βmγn|m,m,n,n〉N1N2N3N4⊗i,j=1,j≠i2|xi〉Si|xi〉Rii|−xi〉Rij.(4)

Then, quantum registers Rii are sent from each node si to the intermediate node n1, register R21 is sent to the intermediate node n3, register R12 is kept at node s1, and registers Si are kept at node si. Meanwhile, ancillary register Rb initialized to |0H〉 is introduced at node n1.

(S2) For i∈{1,2}, applying CX̃Rii→N1 on the registers Rii and N1, then CX̃N1→Rb on the registers N1 and Rb at the intermediate node n1, we have the quantum state

|Ψ〉2=∑x1,x2,m,n∈ℤdαx1,x2βmγn|X¯〉N1,Rb,N2|n,n〉N3N4⊗2i,j=1,j≠i|xi〉Si|xi〉Rii|−xi〉Rij,(5)

where |X¯〉N1,Rb,N2=|x1⊕x2⊕m,x1⊕x2⊕m,m〉N1,Rb,N2. Then, quantum register Rb is sent from the node n1 to n2, registers Rii and N1 are kept at n1.

(S3) At the intermediate node n2, quantum registers ri(i=1,2), each initialized to |0H〉, are introduced; then the quantum operator CX̃Rb→ri is applied to the registers Rb and ri, and CR̃N2→ri is applied to the registers N2 and ri. Thus, the quantum state becomes

|Ψ〉3=∑x1,x2,m,n∈ℤdαx1,x2βmγn|X¯〉N1,Rb,N2|n,n〉N3N4⊗i,j=1,j≠i2|x1⊕x2〉ri|xi〉Si|xi〉Rii|−xi〉Rij.(6)

Then, quantum register r1,r2 are transmitted from the node n2 to node n3 and to the sink node t2 respectively, the registers Rb,N2 are maintained at n2.

(S4) At the intermediate node n3, quantum registers Rb′ initialized to |0H〉 is introduced. Applying quantum operator CX̃r1→N3 and CX̃R21→N3 on the registers r1, R21 and N3, and then CX̃N3→Rb′ on the registers N3 and Rb′, we have the quantum state

|Ψ〉4=∑x1,x2,m, n∈ℤdαx1,x2βmγn|X¯〉N1,Rb,N2|Y¯〉N3,Rb′,N4⊗i,j=1,j≠i2|x1⊕x2〉ri|xi〉Si|xi〉Rii|−xi〉Rij,(7)

where |Y¯〉N3,Rb′,N4=|x1⊕n,x1⊕n,n〉N3,Rb′,N4. Then, quantum register Rb′ is sent from the node n3 to n4, registers r1, N3 and R21 are kept at n3.

(S5) At the intermediate node n4, quantum registers ri′(i∈{1,2}), each initialized to |0H〉, are introduced; then the quantum operator CX̃rb′→ri′ and CR̃N4→ri′ is applied to the registers rb′, N4 and r1′. Thus, the quantum state becomes

|Ψ〉5=∑x1, x2, m, n∈ℤdαx1, x2βmγn|X¯〉N1, Rb, N2|Y¯〉N3, Rb′, N4⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Si|xi〉Rii|−xi〉Rij.(8)

Then, quantum register r1′,r2′ are transmitted from the node n4 to the sink node t1 and t2 respectively, the registers Rb′,N4 are maintained at n4.

(S6) For each sink node (i∈{1,2}), the quantum register Ti initialized to |0H〉 is introduced. Remembering that t2 has received register r2 in step (S3) and register r2′ in step (S5), the quantum operator CX̃r2→T2 is applied to r2 and T2, CR̃r2′→T2 is applied to r2′ and T2 at the sink node t2. Simultaneously, the quantum operator CX̃r1′→T1 is applied to r1′ and T1 at the sink node t1.

Hence, the resulting state becomes

|Ψ〉6=∑x1,x2,m,n∈ℤdαx1,x2βmγn|X¯〉N1,Rb,N2|Y¯〉N3,Rb′,N4⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Si|xi〉Rii|−xi〉Rij.(9)

2.2 Decoding

In this process, the object is to remove all the entangled particles in the network topological order. Here, the quantum circuit of decoding is shown in Fig. 4 and the detailed steps are given as below.

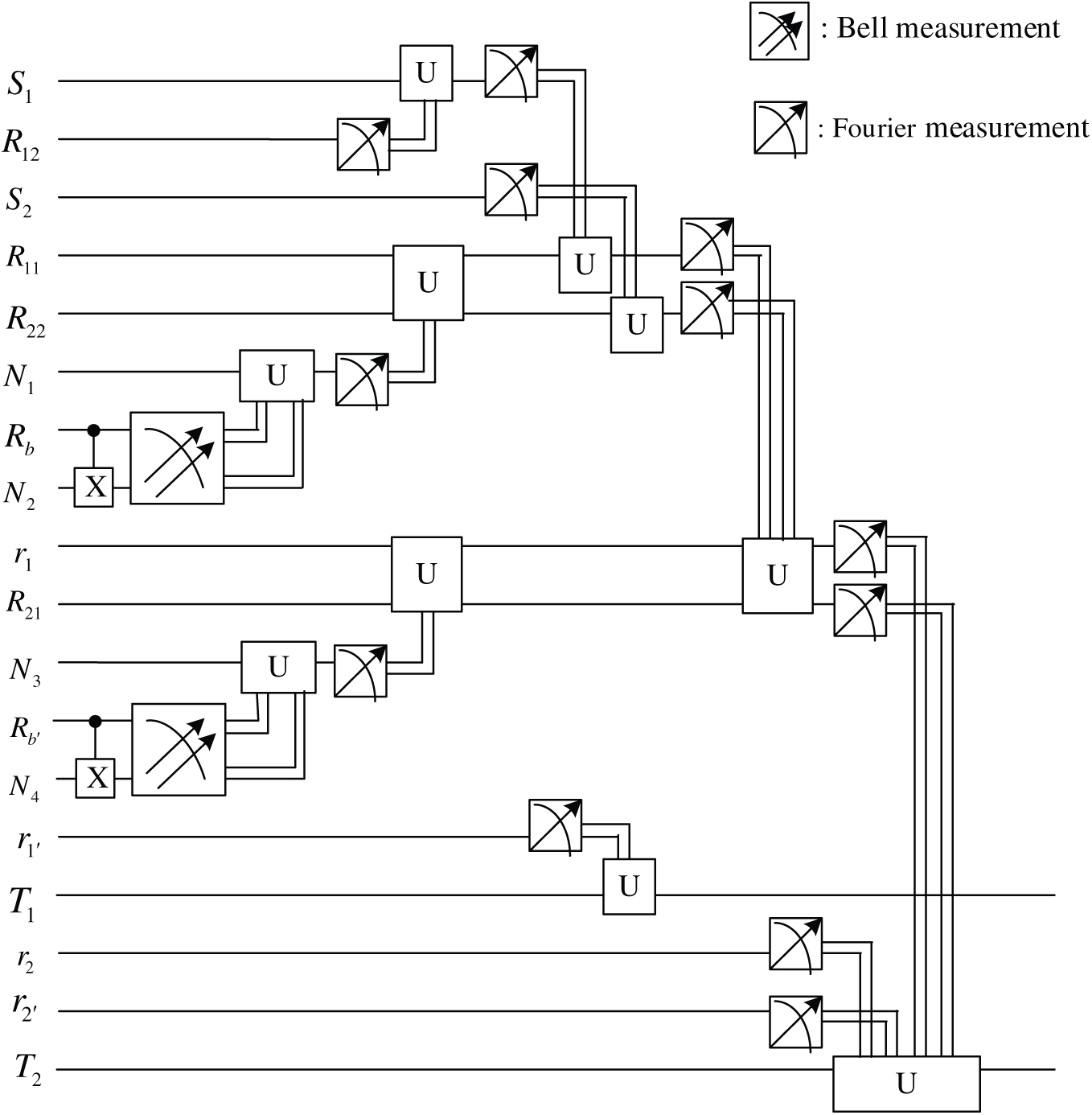
Figure 4: Quantum circuit of decoding

(T1) Considering the owned registers Rb′,N4, the intermediate node n4 performs the quantum operation CX̃Rb′→N4, followed by the Bell measurement on the two qudits, providing the measurement result u1u2. Here, it is worth mentioning that in the quantum system H=ℂd, the Bell states are represented as follows:

|ϕ(u1,u2)〉=1d∑j=0d-1e2πιju1/d|j,j⊕u2〉,u1,u2∈ℤd,whereι2=-1.(10)

Then, the basis states {|ϕ(u1,u2)<rangle>}u1,u2∈ℤd are called the Bell basis, and the quantum measurement in the Bell basis is called the Bell measurement.

Hence after the Bell measurement, we obtain the quantum state

|Ψ〉7=∑x1,x2,m∈ℤdαx1,x2βme-2πι(x1⊕u2)u1/d|X¯〉N1,Rb,N2|x1⊕u2〉N3i, j= 1, j≠i⊗2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Si⊗|xi〉Rii|-xi〉Rij(11)

Then, classical information u1u2 are transmitted from the node n4 to n3 through the bottleneck channel.

(T2) Upon receiving the information u1u2, the node n3 applies the quantum unitary operator on its register N3, mapping the state |x < rangle > to e2πιu1x/d|x-u2〉 for each x∈ℤd. Thus, the phase resulting from the Bell measurement in (T1) is corrected. Next, quantum Fourier measurement is performed on N3, providing the measurement result l. Here, it is worth mentioning that in the quantum system H=ℂd, quantum Fourier transform F is a unitary transformation that transforms the computing basis states {|k<rangle>}k∈ℤd to the Fourier basis as follows:

|wk〉=F|k〉=1d∑l=0d-1e2πιkl/d|l〉,whereι2=-1.(12)

Thus the basis states {|wk<rangle>}k∈ℤd are called the quantum Fourier basis, and the quantum measurement in the Fourier basis is called the quantum Fourier measurement. Hence after the quantum Fourier measurement, we obtain the quantum state

|Ψ〉8=∑x1, x2, m∈ℤdαx1, x2βme−2πιx1l/d|X¯〉N1, Rb, N2⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Si|xi〉Rii|−xi〉Rij.(13)

Then, the phase introduced is corrected as followings: the node n3 applies the unitary operator on its registers r1 and R21, mapping the state |x1⊕x2,-x2〉 to the state e2πιlx1/d|x1⊕x2,-x2〉 for any x₁, x₂ ∈ ℤ_d. Consequently, the state then becomes

|Ψ〉8=∑x1x2, m∈ℤdαx1, x2βm|X¯〉N1, Rb, N2⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Si|xi〉Rii|−xi〉Rij.(14)

(T3) The intermediate node n2 performs the quantum operation CX̃Rb→N2, followed by the Bell measurement on the two qudits, providing the measurement result u1′u2′. Thus, we obtain the quantum state

|Ψ〉9=∑x1,x2∈ℤdαx1,x2e-2πι(x1⊕x2⊕u2′)u1′/d|x1⊕x2⊕u2′〉N1i, j= 1, j≠i⊗2|x1⊕x2〉ri|x1〉ri′|xi〉Ti⊗|xi〉Si|xi〉Rii|-xi〉Rij.(15)

Then, classical information u1′u2′ are transmitted from the node n2 to n1 through the bottleneck channel.

(T4) Once receiving the information u1′u2′, node n1 applies the quantum unitary operator on its register N1, mapping the state |x < rangle > to e2πιu1′x/d|x-u2′〉 for each x∈ℤd. Then, quantum Fourier measurement is performed on registers and N1, producing the measurement result l′. Hereafter, The phase introduced is corrected as followings: the node n1 applies the unitary operator on its registers Rii(i=1,2), mapping the state |x1,x2〉 to the state e2πι(x1⊕x2)l′/d|x1,x2〉. Then, the resulting state becomes

|Ψ〉10=∑x1, x2∈ℤdαx1, x2⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Si|xi〉Rii|−xi〉Rij.(16)

(T5) At the source node s1, first the quantum Fourier measurement is applied to register R12, and then the phase introduced is corrected at the register S1. Afterwards, quantum Fourier measurements are simultaneously applied to the registers Si(i=1,2), returning the measurement results hi. As result, the whole quantum state becomes

|Ψ〉11=∑x1, x2∈ℤdαx1, x2∏i=12e−2πιhixi/d⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|xi〉Rii|−x2〉R21.(17)

Then, hi are transmitted from the node si to n1 respectively.

(T6) Upon receiving hi, the intermediate node n1 corrects the phase by performing the quantum unitary operator mapping on its register Rii, wherein the state |xi < rangle > is mapped to e^{2πιh_ix_i/d|x_i〉} for each xi∈ℤd. Hereafter, quantum Fourier measurements are applied to the registers Rii respectively, thereby producing the measurement results gi. Thus the state then becomes

|Ψ〉12=∑x1, x2∈ℤdαx1, x2∏i=12e−2πιgixi/d⊗i,j=1,j≠i2|x1⊕x2〉ri|x1〉ri′|xi〉Ti|−x2〉R21.(18)

Then, gi are transmitted from the node n1 to n3 past n2 respectively.

(T7) At the intermediate node n3, to correct the phase produced by the measurements, it applies the unitary operator on its register r1 and R21, mapping the state |x1⊕x2,-x2〉 to the state e2πι[g1(x1⊕x2)-(g1-g2)x2]/d|x1⊕x2,-x2〉. Hereafter, quantum Fourier measurements are applied to the registers r1 and R21 respectively, then after the measurement results’ transmission, the sink node t2 correct the introduced phase. Afterwards, the sink node t1 and t2 applies quantum Fourier measurements on the registers r1′ and r2,r2′ respectively. Finally, the introduced phases are corrected at the two sink node. Thus, the final quantum state becomes the desired state, as follows:

|Ψ〉13=∑x1,x2∈ℤdαx1, x2|x1x2〉T1T2.(19)

That is, the state of the quantum system over every source node is perfectly transmitted to the corresponding sink node through the quantum grail network.

3  Protocol Analysis

3.1 Correctness

The correctness of the proposed QNC protocol can be verified by the specific encoding and decoding steps. From Section 2, in the encoding process, the particles at every network node are entangled to the whole quantum system by applying relevant quantum operators on them. The resulting quantum state after the entanglement of each time is presented in the ending of every encoding steps. In the decoding process, by applying relevant quantum measurements, all the unnecessary particles are disentangled from the whole quantum system and leave alone the certain particles on the two sink nodes. The resulting quantum state after the disentanglement of each time is presented in the ending of every decoding steps. Thus, after all the encoding and decoding steps, the final quantum state at the two sink nodes formed |Ψ〉13=∑x1,x2∈Zdαx1,x2|x1x2〉T1T2 is exactly equal to the initial source state |Ψ〉S=∑x1,x2∈Zdαx1,x2|x1x2〉S1S2 at the two source nodes. Therefore, according to all the calculating procedure and numerical results, the correctness of the proposed QNC protocol is verified.

3.2 Achievable Rate Region

It is known that the communication rate [25] between si and ti in n network uses is defined as ri(n)=1nlog|Hi|, where Hi denotes the Hilbert space of the transmitted quantum state owned by si, and |⋅| denotes the dimension of the Hilbert space. Also, an edge capacity constraint [27], i.e., log|H(u,v)|≤n⋅c((u,v)), exists when the quantum state is transmitted with the fidelity of one over the edge (u,v)∈E in n uses.

Accordingly, in our protocol presented above, the perfect transmission of the quantum state over the quantum grail network can be achieved in one use of the network, which means that the 1-flow [25] value reaches

r1(1)+r2(1)=log|H1|+log|H2|≤∑i=12c((u,v))=∑i=121=2,(20)

under the condition that the capacity c((u,v)) of each edge (u,v) always remains equal to 1 according to the quantum grail network model. In fact, the 1-max flow is the supremum of 1-flow over all achievable rate. Hence, 1-max flow of value 2 is achievable through our PQNC protocol, and then the achievable rate region [25,28] can be written as {(r1,r2)|r1+r2≤2}.

3.3 Security

As is well known, the non-maximally entangled state is a kind of generalized entangled state, and is hard to be distinguished [29–31]. In the actual quantum communications, it is difficult for adversaries to launch attacks by forging the non-maximally entangled state. Therefore, the non-maximally entangled states which are pre-shared over the network can effectively improve the security of the whole quantum network communications.

3.4 Practicability

In terms of the network model, the quantum grail network we considered is rarely studied but fairly imperative since it is also a fundamental primitive network [25] like butterfly network. And the proposed protocol over quantum grail network can also be applied to the butterfly network. Thus, it is applicable to the communication scenarios of practically complex quantum networks. On the other hand, in terms of the non-maximally entangled state, it is a kind of entanglement resource that can be more easily obtained in practice, which helps our QNC scheme better suited to applications.

4  Protocol Comparison

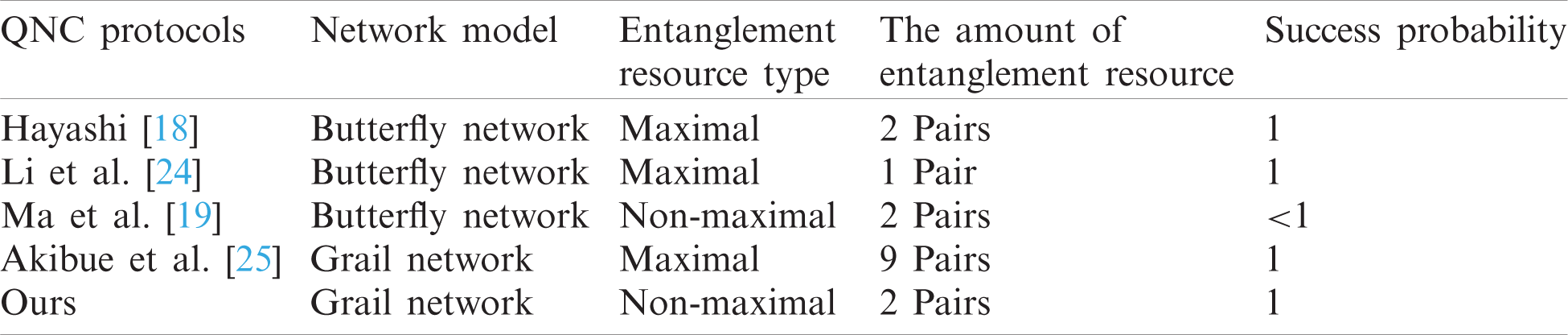
In this section, our proposed QNC protocol is compared with the existed QNC protocols [18,19,24,25] from the network model, the entanglement resource type, the amount of entanglement resource, and the success probability. The comparison result is shown in Tab. 1 as below.

From the comparison result, it can be seen that for butterfly network, Hayashi’s protocol [18] and Li et al. [24] protocol show that maximally entangled states can be used as the assisted resource to obtain the perfect quantum state transmission with success probability 1. Ma et al. [19] protocol shows the success probability of which assisted by non-maximally entangled states is less than 1. For grail network, Akibue et al. [25] protocol shows that maximally entangled states also can be assisted to obtain the perfect quantum state transmission with success probability 1 but consumed more. However, our protocol shows that non-maximally entangled states can also be assisted to obtain the perfect quantum state transmission with success probability 1, and even the resource consumption is lower. Therefore, compared with the existed protocols, our protocol expresses a certain advantage.

Table 1: Comparison result of different QNC protocols

5  Conclusions

In this paper, we propose a practical QNC scheme with the assist of the non-maximally entangled state over the grail network. Firstly, in terms of the network model, the grail network is another fundamental primitive network [25]. The research on the QNC scheme over grail network can effectively enrich the existing theory of QNC. Secondly, our proposed QNC scheme with the assist of non-maximally entangled state can also achieve the perfect quantum state transmission and 1-max flow quantum communications. Moreover, due to the security and practicability of the non-maximally entangled state, our QNC scheme is more applicable for actual quantum network communications.

Acknowledgement: We express our heartfelt thanks to the Beijing Institute of Graphic Communication for funding this study, as well as to the State Key Laboratory of Networking and Switching Technology for offering technical support.

Funding Statement: This work is supported by the National Natural Science Foundation of China (Grant Nos. 61671087, 92046001, 61962009, 61003287, 61370188, 61373131), the Scientific Research Common Program of Beijing Municipal Commission of Education (KM202010015009, KM201610015002), the Joint Funding Project of Beijing Municipal Commission of Education and Beijing Natural Science Fund Committee (KZ201710015010), the Initial Funding for the Doctoral Program of BIGC (27170120003/020), the Fok Ying Tung Education Foundation (Grant No. 131067), the Fundamental Research Funds for the Central Universities (Grant No. 2019XD-A02), the Fundamental Research Funds in Heilongjiang Provincial Universities (135509116), the Major Scientific and Technological Special Project of Guizhou Province (20183001), Huawei Technologies Co. Ltd. (No. YBN2020085019), PAPD and CICAEET funds.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Ahlswede, N. Cai, S. Y. R. Li and R. W. Yeung, “Network information flow,” IEEE Transactions on Information Theory, vol. 46, no. 4, pp. 1204–1216, 2000. [Google Scholar]

 2.  S. Y. R. Li, R. W. Yeung and N. Cai, “Linear network coding,” IEEE Transactions on Information Theory, vol. 49, no. 2, pp. 371–381, 2003. [Google Scholar]

 3.  Q. T. Sun, S. R. Li and C. Chan, “Matroidal characterization of optimal linear network codes over cyclic networks,” IEEE Communications Letters, vol. 17, no. 10, pp. 1992–1995, 2013. [Google Scholar]

 4.  A. A. Hady, “Duty cycling centralized hierarchical routing protocol with content analysis duty cycling mechanism for wireless sensor networks,” Computer Systems Science and Engineering, vol. 35, no. 5, pp. 347–355, 2020. [Google Scholar]

 5.  M. Hayashi, K. Iwama and H. Nishimura, “Quantum network coding,” Proc. Symp. Theoretical Aspects of Computer Science, Lecture Notes in Computer Science, vol. 4393, pp. 610–621, 2007. [Google Scholar]

 6.  N. Gisin and R. Thew, “Quantum communication,” Nature Photon, vol. 1, no. 3, pp. 165–171, 2007. [Google Scholar]

 7.  S. Wengerowsky, S. K. Joshi, F. Steinlechner, H. Hübel and R. Ursin, “An entanglement-based wavelength-multiplexed quantum communication network,” Nature, vol. 564, no. 7735, pp. 225–228, 2018. [Google Scholar]

 8.  S. Pirandola, “End-to-end capacities of a quantum communication network,” Communications Physics, vol. 2, no. 1, pp. 1–10, 2019. [Google Scholar]

 9.  W. J. Munro, K. A. Harrison, A. M. Stephens, S. J. Devitt and K. Nemoto, “From quantum multiplexing to high-performance quantum networking,” Nature Photonics, vol. 4, no. 11, pp. 792–796, 2010. [Google Scholar]

10. Z. Z. Li, G. Xu, X. B. Chen, X. Sun and Y. Yang, “Multi-user quantum wireless network communication based on multi-qubit GHZ state,” IEEE Communications Letters, vol. 20, no. 12, pp. 2470–2473, 2016. [Google Scholar]

11. T. Shang, R. Liu, J. Liu and Y. Hou, “Continuous-variable quantum network coding based on quantum discord,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1629–1645, 2020. [Google Scholar]

12. Z. G. Qu, S. Y. Wu, W. J. Liu and X. J. Wang, “Analysis and improvement of steganography protocol based on bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624, 2019. [Google Scholar]

13. P. Pathumsoot, T. Matsuo, T. Satoh, M. Hajdušek, S. Suwanna et al., “Modeling of measurement-based quantum network coding on a superconducting quantum processor,” Physical Review A, vol. 101, no. 5, pp. 52301, 2020. [Google Scholar]

14. Z. X. Zhang and Z. G. Qu, “Anti-noise quantum network coding protocol based on Bell states and butterfly network model,” Journal of Quantum Computing, vol. 1, no. 2, pp. 89–109, 2019. [Google Scholar]

15. H. Kobayashi, F. Le Gall, H. Nishimura and M. Rötteler, “Perfect quantum network communication protocol based on classical network coding,” in IEEE Int. Sym. on Information Theory, Austin, TX, USA, IEEE, pp. 2686–2690, 2010. [Google Scholar]

16. H. Lu, Z. D. Li, X. F. Yin, R. Zhang, X. X. Fang et al., “Experimental quantum network coding,” NPJ Quantum Information, vol. 5, no. 1, pp. 1–5, 2019. [Google Scholar]

17. Z. G. Qu, S. Y. Chen and X. J. Wang, “A secure controlled quantum image steganography algorithm,” Quantum Information Processing, vol. 19, no. 380, pp. 1–25, 2020. [Google Scholar]

18. M. Hayashi, “Prior entanglement between senders enables perfect quantum network coding with modification,” Physical Review A, vol. 76, no. 4, pp. 40301(R2007. [Google Scholar]

19. S. Y. Ma, X. B. Chen, M. X. Luo, X. X. Niu and Y. X. Yang, “Probabilistic quantum network coding of M-qudit states over the butterfly network,” Optics Communications, vol. 283, no. 3, pp. 497–501, 2010. [Google Scholar]

20. T. Satoh, F. Le Gall and H. Imai, “Quantum network coding for quantum repeaters,” Physical Review A, vol. 86, no. 3, pp. 32331, 2012. [Google Scholar]

21. H. Kobayashi, F. Le Gall, H. Nishimura and M. Roetteler, “General scheme for perfect quantum network coding with free classical communication,” in Proc. of the 36th Int. Colloquium on Automata, Languages and Programming, Lecture Note in Computer Science, Rhodes, Greece, pp. 622–633, 2009. [Google Scholar]

22. H. Kobayashi, F. Le Gall, H. Nishimura and M. Roetteler, “Constructing quantum network coding schemes from classical nonlinear protocols,” in Proc. of the 2011 IEEE Int. Symp. Information Theory, St. Petersburg, Russia, pp. 109–113, 2011. [Google Scholar]

23. J. Li, X. B. Chen, G. Xu, Y. X. Yang and Z. P. Li, “Perfect quantum network coding independent of classical network solutions,” IEEE Communications Letters, vol. 19, no. 3, pp. 115–118, 2015. [Google Scholar]

24. Z. Z. Li, G. Xu, X. B. Chen, Z. Qu, X. X. Niu et al., “Efficient quantum state transmission via perfect quantum network coding,” Science China Information Science, vol. 62, no. 1, pp. 1–14, 2019. [Google Scholar]

25. S. Akibue and M. Murao, “Network coding for distributed quantum computation over cluster and butterfly networks,” IEEE Transactions on Information Theory, vol. 62, no. 11, pp. 6620–6637, 2016. [Google Scholar]

26. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information. Cambridge: Cambridge University Press, 2000. [Google Scholar]

27. A. Jain, M. Franceschetti and D. A. Meyer, “On quantum network coding,” Journal of Mathematical Physics, vol. 52, no. 3, pp. 32201, 2011. [Google Scholar]

28. H. Nishimura, “Quantum network coding-how can network coding be applied to quantum information?,” in Proc. of the 2013 IEEE Int. Symp. on Network Coding, Calgary, AB, Canada, pp. 1–5, 2013. [Google Scholar]

29. A. G. White, D. F. James, P. H. Eberhard and P. G. Kwiat, “Non-maximally entangled states: Production, characterization, and utilization,” Physical Review Letters, vol. 83, no. 16, pp. 3103–3107, 1999. [Google Scholar]

30. H. Fan, “Distinguishability and indistinguishability by local operations and classical communication,” Physical Review Letters, vol. 92, no. 17, pp. 177905, 2004. [Google Scholar]

31. G. Xu, K. Xiao, Z. Li, X. Niu and M. Ryan, “Controlled secure direct communication protocol via the three-qubit partially entangled set of states,” Computers, Materials & Continua, vol. 58, no. 3, pp. 809–827, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.