Computers, Materials & Continua DOI:10.32604/cmc.2021.017216
Article

Verifiable Identity-Based Encryption with Keyword Search for IoT from Lattice

Lin Mei1, Chungen Xu1,*, Lei Xu1, Xiaoling Yu2 and Cong Zuo3

1School of Science, Nanjing University of Science and Technology, Nanjing, 210094, China
2College of Data Science, Taiyuan University of Technology, Taiyuan, 030000, China
3Faculty of Information Technology, Monash University, Clayton, 3800, Australia
*Corresponding Author: Chungen Xu. Email: xuchung@njust.edu.cn
Received: 19 January 2021; Accepted: 24 February 2021

Abstract: Internet of Things (IoT), which provides the solution of connecting things and devices, has increasingly developed as vital tools to realize intelligent life. Generally, source-limited IoT sensors outsource their data to the cloud, which arises the concerns that the transmission of IoT data is happening without appropriate consideration of the profound security challenges involved. Though encryption technology can guarantee the confidentiality of private data, it hinders the usability of data. Searchable encryption (SE) has been proposed to achieve secure data sharing and searching. However, most of existing SE schemes are designed under conventional hardness assumptions and may be vulnerable to the adversary with quantum computers. Moreover, the untrusted cloud server may perform an unfaithful search execution. To address these problems, in this paper, we propose the first verifiable identity-based keyword search (VIBKS) scheme from lattice. In particular, a lattice-based delegation algorithm is adopted to help the data user to verify both the correctness and the integrity of the search results. Besides, in order to reduce the communication overhead, we refer to the identity-based mechanism. We conduct rigorous proof to demonstrate that the proposed VIBKS scheme is ciphertext indistinguishable secure against the semi-honest-but-curious adversary. In addition, we give the detailed computation and communication complexity of our VIBKS and conduct a series of experiments to validate its efficiency performance.

Keywords: Internet of Things; verifiable; lattice; searchable encryption

1  Introduction

Internet of Things (IoT) has developed as one of the most popular and exciting technologies in information and communications [1,2]. Recent years’ studies have witnessed a broader range of applications in IoT networks, e.g., intelligent traffic, household appliances and medical devices. By 2025, forecasts suggest that there will be more than 75 billion Internet of Things (IoT) connected devices in use. A large number of devices produce tens of zettabytes of data in IoT makes the data storage and processing become a major challenger. Fortunately, cloud storage provides a solution that helps the IoT devices store and process data. However, due to the personal nature of the information collected in IoT networks, consumers are concerned about the sharing of information that reveals their personal habits. Therefore, sensitive private data needs to be encrypted before outsourced to the IoT cloud [3].

Along with data privacy, data utility is indispensable as well. Take the intelligent traffic as an example, the sensor (i.e., the data owner) transmits its data to the cloud server every day for subsequent maintenance and dispatch tasks. However, as mentioned, the above data is encrypted which may incur many practical issues. The primary problem is that how can the data owner get the desired data from such a large amount of encrypted dataset for data analytics. The naïve decrypt to search approach involves very expensive computation and communication overhead, and thus promotes the study of efficient and practical retrieval over the encrypted data.

Searchable symmetric encryption (SSE) [4] is such a promising paradigm proposed to address aforementioned encrypted retrieval problem. Despite SSE translates encrypted retrieval into reality, this mechanism is with limits in achieving practical data-sharing principle guarantee. As known, in SSE, the data owner and the data user are required to be the same one, but the above data analyst (user) are always experts from many different areas. To fill the gap, public key encryption with keyword search (PEKS) scheme is proposed [5]. In PEKS, a data owner first encrypts keywords with the public key of a designated data user and then uploads them to the cloud together with encrypted data. Afterwards, when the data user wants to retrieve data containing a specific keyword, he generates a search token for the keyword with his secret key and sends it to the cloud server. Once the cloud server receives the above search token, it performs well-designed search algorithm to check if the data containing the expected keywords and returns the matched data to the user.

To date, PEKS make considerable progress in strengthening security, enriching functionality, and facilitating efficiency [6–8]. Nevertheless, most of these PEKS constructions are built under the traditional hardness assumptions like discrete logarithm problem. As pointed out in [9], the quantum computers of the near future hold a high potential to invalidate these schemes. More urgently, researchers have made breakthrough progress in quantum computers [10]. Most recently, some initial efforts have been made from lattice [11–14], opening a direction to designing quantum secure encrypted search schemes. Following this way, in this paper, we will focus on the investigation of quantum secure encrypted search schemes and develop a new PEKS scheme with better performance in security and efficiency.

1.1 Our Motivation

The first problem we aim to address is the integrity of the search result. Note that, the real-world cloud server is always semi-honest-but-curious [15], it may intentionally return partial search or even unmatched results to the user for saving its cost. This is not a new problem in traditional PEKS, many researchers propose to use verifiable PEKS to solve this problem. Specifically, a verification block is adopted and will be sent to the user, together with the search result. The user can use this block to verify if the search result is integral. However, to the best of our knowledge, few lattice-based verifiable searchable encryption schemes have been known before. For this concern, our first effort is to design a verifiable PEKS from lattice. Our key idea is to design a verification algorithm, which can be imposed on existing lattice-based PEKS schemes directly. To achieve this goal, we introduce a lattice-based delegation algorithm, which can flexibly generate the verification block under the circumstance of semi-honest-but-curious server.

Based on the above result, our second problem is how to deploy the above verifiable PEKS scheme to an IoT system. Observe that, in a public-key cryptosystem, before encrypting the data, a user always needs to verify the authenticity of a public-key. However, the public key in a lattice-based encryption scheme is usually made up of some high-dimension matrices, transmitting these matrices through source-limited sensors is infeasible. Inspired by Zhang et al.’s ideal [13], we deal with this problem by introducing the identity-based encryption mechanism, where a small size identity-tag is used to denote the public key of the user. In particular, when a user enrolls, he registers the system with his individual identity and gets a credential from the central authority as his secret key. After that, he uses this identity and corresponding secret key to perform encryption and verification operations.

1.2 Our Contributions

In light of the above observations, our contributions can be summarized as follows:

1.    We propose the first verifiable PEKS scheme from lattice to check the result integrity of a quantum secure search scheme.

2.    We introduce the philosophy of identity-based encryption mechanism and use it to mitigate the heavy communication cost in public key authentication.

3.    We compare our scheme with some closely-related works, and the results demonstrate that our scheme performs better than prior arts in efficiency.

Organizations. The rest of this paper is organized as follows. In Section 2, we introduce some related work. The proposed system overview, corresponding threat model and design goals are presented in Section 3. In Section 4, we first introduce preliminaries, including the lattice-based knowledge, the hardness problem and some algorithms. Then we define the VIBKS scheme with the security model. In Section 5, we show the construction of our lattice-based VIBKS scheme, as well as its correctness and verifiability proof. In Section 6, we provide the security proof of our scheme. The theoretical comparison and performance analysis are presented in Section 7. Finally, we give a short conclusion in Section 8.

2  Related Work

With the rapid increase of data volume from quantities of IoT devices, cloud storage technology plays an increasingly crucial role in IoT. In terms of data confidentiality, it becomes prevalent to use cloud storage data encryption services. To achieve the goal of searching over encrypted data outsourced to the cloud server without leaking information about the messages shared by the data sender, searchable encryption (SE) is one of the essential approaches. SE is divided into symmetry searchable encryption and asymmetric searchable encryption. The SSE scheme was firstly introduced in [4]. Although the SSE scheme is with relatively high computational efficiency, it is only suitable for a single user model, but could not be well applied in multi-user model.

PEKS based on conventional hardness assumption. The first PEKS scheme was proposed to enable one to search over encrypted data generated by public key system [5]. Following with Boneh et al.’s work [5], a multitude of PEKS schemes that achieve various kinds of functionality are proposed [6–8]. Park et al. [6] considered the need for conjunctive keyword query and proposed the first public key encryption with conjunctive field keyword search scheme. To fill the gap in the area of fuzzy search on encrypted data, a PEKS scheme supporting fuzzy keyword query was proposed by Xu et al. [7]. Besides, schemes support proxy re-encryption with keyword search under the assistance of the proxy were proposed in [8]. However, the mentioned schemes above are all fragile to the attack from quantum computers.

PEKS based on lattice assumption. Lattice has been widely used to construct cryptosystems that can resist the near future quantum computer. The first PEKS built for quantum security is proposed by Gu et al. [11], whose security can be reduced to LWE assumption in the standard model. To further pursue the practicability, several lattice-based works have been proposed to support fine-grained access control [12], proxy-oriented search [13], conjunctive keyword search [14], verifiable search [15]. In addition to extending the functionality, researches on resisting varieties of attack methods have been sufficiently developed. In order to ensure the security when the scheme suffers from key-exposure problems, Zhang et al. [16] constructed a scheme satisfying the forward security in the quantum security level. Besides, keyword guessing attack is practical in PEKS as the keywords in real-life are with inherently low entropy. To prevent inside KGA, Yu et al. [17] employed the preimage sample algorithm on a random bit and a part of ciphertext, which prevents the malicious server from forging a valid ciphertext.

Verifiable searchable encryption. The verifiable search has been substantially developed in the plaintext retrieval using special data structures (e.g., signature and merkle tree) in case a malicious cloud server returns false results or conceals data loss incidents. For example, in 2010, Benabbas et al. [18] presented the first practical verifiable computation scheme for high degree polynomial functions. In the encrypted data search scenario, Zheng et al. [19] utilized bloom filter and signature algorithm to verify whether the cloud has faithfully executed the search operations, and proposed two different schemes, i.e., KP-ABKS and CP-ABKS. Sun et al. [15] proposed a scheme to enable authenticity check over the returned search result in the multi-user multi-data-contributor search scenario. Miao et al. [20] constructed the Verifiable SE Framework (VSEF), which can withstand the inside KGA and achieve verifiable searchability. Wu et al. [21] presented a new authenticated data structure based on homomorphic encryption, and shows how to apply it to verify the correctness and completeness of search results. However, the verification proof in their scheme is generated by the cloud server, who can forge the proof to pass the verification when it is viewed as an adversary. In summary, the above verifiable searchable encryption schemes seldom consider how to ensure the integrity of returned data when the cloud server is semi-honest-but-curious and equipmented with quantum computers.

3  Problem Statement

In this section, we will first give a high-level description of our proposed scheme and introduce the role of each participant involved in. Then, to explicitly show the capability of each party, we define the threat model.

3.1 System Overview

As shown in Fig. 1, we illustrate the architecture of the proposed VIBKS in an IoT system. The designed scheme is consisted of four entities: central authority (CA), cloud server (CS), IoT sensor (IoTs) and data receiver (DR).

•    CA: CA is assumed full responsibility for key generation and public parameters generation.

•    IoTs: IoTs is the sensor deployed in an IoT system, who holds the duty that transmits data to CS over the Internet. Specifically, the transmitted data requires to be encrypted before sent to CS. To further pursue the goal of data verification, a verification block is attached.

•    DR: DR is authorized by IoTs, it holds the ability of keyword retrieval and result verification. The former is realized by submitting search token, while the latter is due to the verification block generated by IoTs.

•    CS: CS is mainly responsible for two aspects of work in the system, the first is to store the encrypted data with keyword ciphertexts and verification block, the second is to perform test operation.

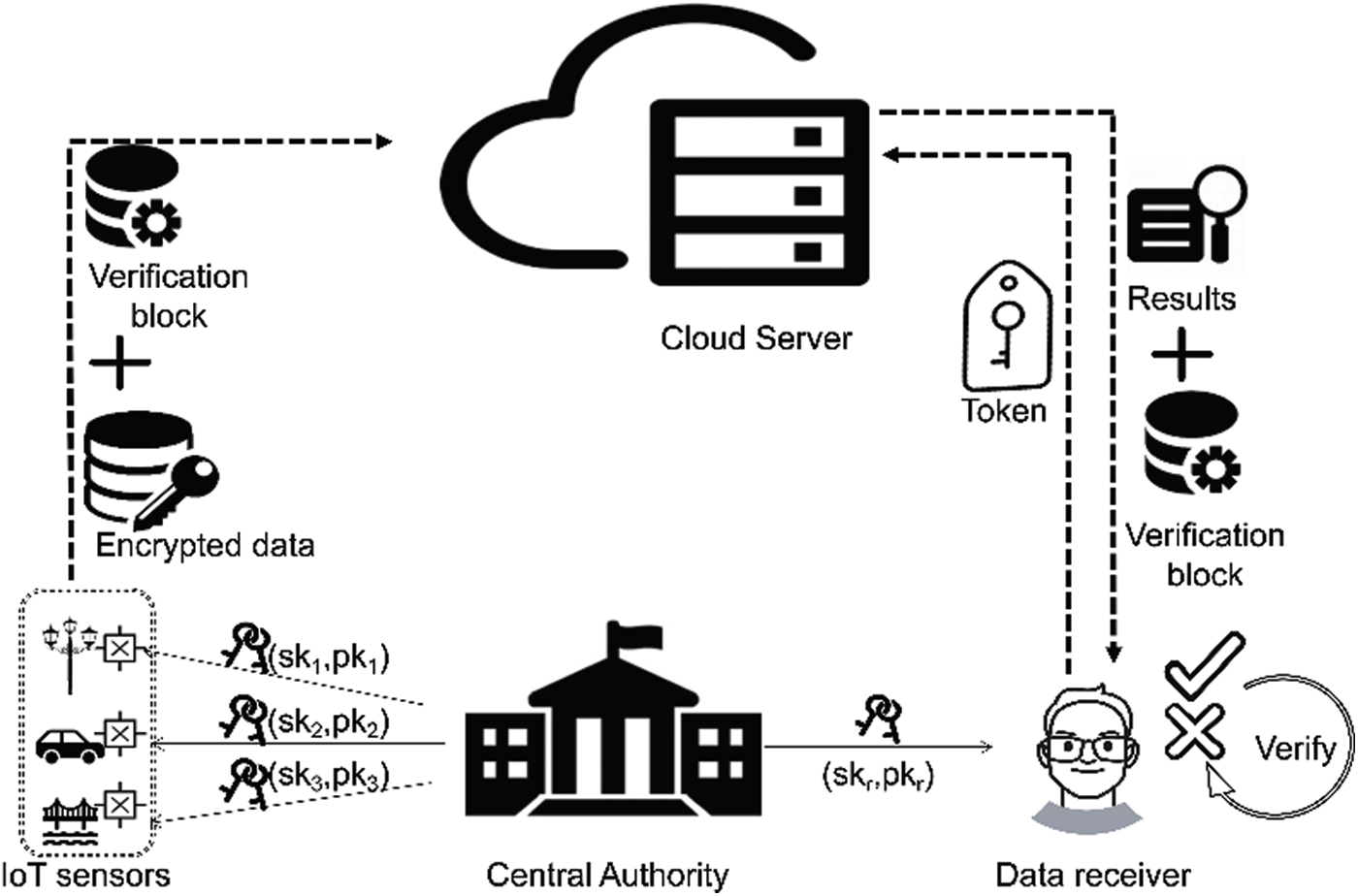
Figure 1: System overview

Overview. Here we elaborate on the implementation process of the proposed scheme with Fig. 1. First of all, the CA generates the system public parameters and the master secret key, with which it generates the corresponding identity secret key according to the tag submitted by other entities later. After obtaining tags of IoTs and DR, CA sends the public and secret key pairs to each entity. IoTs generates the keyword ciphertexts to allow the DR visit its data and compute the verification block for integrity check, which are sent with the encrypted data to CS. When DR wants to obtain ciphertexts corresponding to a keyword, the secret key will be used to create a keyword-oriented token, which is transmitted to the CS subsequently. Then, by testing whether the token and keyword ciphertexts match, the corresponding results (including encrypted data, data identity sets and verification blocks) are returned. Finally, DR decrypts the encrypted data and detects the correctness and integrity of results.

3.2 Threat Model

First of all, CA is supposed to be completely trusted in our model, who knows the secret key of the whole system but never launch an attack on the system. Then, we primarily stress that the server in our model behaves entirely in a “semi-honest-but-curious” fashion, as described in some previous literature. We assume that the server will not honestly follow the algorithm we set up and possibly returns a fraction of results or unrelated files. Lastly, in our model, IoTs with plaintexts and DR with search capability are both considered reliable, which means they are not considered the outside adversary.

To prove the security of VIBEKS under the above threat model, we follow the security definition of ciphertext indistinguishability. Details will be provided in Section 4.2.

3.3 Design Goals

In order to achieve secure and efficient searchable encryption over IoT data, we design our scheme to accomplish the following objects:

a)    Efficiency. It may involve some operations with high computational cost when designing a lattice-based SE scheme, e.g., matrix inverse operation. In order to gain higher efficiency, considering constructing the scheme in which the matrix inverse operation need to be performed only once.

b)    Security. Our scheme should achieve ciphertext indistinguishability under selective-ID attacks. The quantum computer cannot violate the privacy of outsourced data as it does for some SE schemes based on traditional hardness problems. Lattice-based tools are deployed in our scheme and the security of our scheme is based on the LWE problems, which has been proved to be secure under the attack from quantum computer.

c)    Functionality. Our scheme also aims to enable verifiable search on encrypted outsourced data. Verifiable search is more practical than the common encrypted search, since quantities of deceptions occur every day. The lattice-based delegation algorithm applied in the proposed scheme makes sure that any cheated behavior of server can be recognized by the user.

4  Preliminaries

4.1 Lattice and Hardness Problem

Now, we first give some notations applied in our scheme and definitions about lattice-based cryptography as follows.

Notation ℤ denotes the set of integers. The bold font denotes vector. ∥Ã∥ denotes the Gram-Schmidt norm of matrix A, where à is the Gram-Schmidt orthogonalization of A.

Definition 4.1 Given two random variables x and y on a countable set S, there is a defined function δ(x,y)=12∑s∈S|Pr[x=s]-Pr[y=s]| as statistical distance. If the distance d(λ)=δ(x(λ),y(λ)) is negligible in λ, we say x and y are statistically close.

Definition 4.2 Let bi∈Rm for i∈{1,…,n} be some linearly independent vectors and B={b1,…,bn}. The m-dimensional lattice Λ generated by the above vectors is Λ(B)={Σi=1nxibi∣xi∈ℤ}. Here m is the dimension and n is the rank. When n = m, the lattice is full-rank. The basis of the lattice Λ is {b1,…,bn}.

Definition 4.3 [8] Given a matrix A∈ℤqn×m, a vector u∈ℤqn and a prime q, define:

1.    Λq⊥(A):={e∈ℤm∣Ae=0modq},

2.    Λqu(A):={e∈ℤm∣Ae=umodq},

3.    Λq(A):={μ∈ℤqm∣∃s∈ℤqn,μ=ATsmodq}.

The ciphertext indistinguishability of VIBKS can be reduced to the learning with errors (LWE) problem. We introduce the LWE problem as follows.

Definition 4.4 [22] Given a prime q, a positive integer n, and a Guassian noise distribution χ over ℤq, for a vector s∈ℤqn, the LWE problem is to distinguish the distribution between the following two distributions:

1.    LWE distribution: samples are in the form of (v,u)=(v,vTs+e), where v is a random vector chosen from ℤqn, e is a sample drawn from distribution χ.

2.    Uniform distribution: samples are uniformly chosen from ℤqn×ℤq.

Then, we introduce the TrapGen algorithm and preimage sampleable algorithm SamplePre, which are utilized in Setup, Encrypt and TokGen of the proposed scheme.

Definition 4.5 [23] The probabilistic polynomial-time (PPT) algorithm TrapGen(q,n) generates a uniformly random matrix A∈ℤqn×m together with a short basis TA∈ℤqm×m for Λq⊥(A), satisfying ∥T̃A∥≤O(n log q), and ∥TA∥≤O(n log q) with all but negligible probability in n.

Definition 4.6 [24] Given a matrix A∈ℤqn×m with basis TA∈ℤqm×m of Λq⊥(A), a vector μ∈ℤqn, m≥2n⌈logq⌉, and a parameter σ≥∥T̃A∥⋅ω(log m) as inputs, the PPT algorithm SamplePre(A,TA,μ,σ) generates a vector t∈ℤqm sampled from a distribution statistically close to DΛq(A)μ,σ, such that At=μmodq.

Then we give the definition of the lattice basis delegation BasisDel [25], which is used in the private key derivation in our VIBKS scheme.

Definition 4.7 [25] Given a matrix A∈ℤqn×m with a short basis TA∈ℤqm×m of Λq⊥(A), a ℤq-invertible matrix R sampled from Dm×m, and a parameter δ≥∥T̃A∥⋅δRmω(log3/2m) as inputs, where δR=n log q⋅ω(log m), the PPT algorithm BasisDel(A,TA,R,δ) generates a random short lattice basis TB of Λq⊥(B), where B = AR−1.

Finally, to prove the ciphertext indistinguishability of our scheme, we introduce a PPT algorithm SampleR, referring to [24], to sample matrices from a distribution statistically close to Dm×m over ℤqm×m. Moreover, we employ a PPT algorithm SampleRwithBasis to simulate a random short lattice basis, which is defined as follows.

Definition 4.8 [25] Given a prime q > 2, m≥2n⌈logq⌉, a matrix A∈ℤqn×m as inputs, the PPT algorithm SampleRwithBasis(A) generates a low-form matrix R which is statistically close to Dm×m over ℤqm×m, and a random short lattice basis TB of Λq⊥(B), where B = AR−1, such that ∥T̃B∥≤δR/ω(log m) with an overwhelming probability.

4.2 VIBKS and Security Definition

A formal definition of VIBKS is given in the following part.

Definition 4.9 VIBKS consists of the following six algorithms.

1.    Setup (1n): This probabilistic algorithm is run by the CA to setup the system. It inputs a security parameter n and returns the public parameter PP, the master secret key MSK.

2.    KeyDerive (PP, MSK, τ): This probabilistic algorithm is run by the CA to derive keys for users. It inputs the public parameter SP, the master secret key MSK and the user’s tag τ, and returns the private key skτ and public key pkτ for the user.

3.    Encrypt (PP, τ, w, F, KS): This probabilistic algorithm is run by the IoTs to generate the keyword ciphertexts tuple set and the verification tuple set. It inputs the public parameter PP, the tag τ of data receiver, the keyword w, the file set F and the keyword set KS, and returns the keyword ciphertext tuple set CT and verification tuple set VT.

4.    TokGen (PP, τ, skτ, w*): This probabilistic algorithm is run by the receiver whenever he wants to search for some files containing the keyword w*. It inputs the keyword w*, the user’s private key skτ and the public parameter PP, and returns the search token STw *.

5.    Test (CT, STw*): This algorithm is run by the cloud server to search for the matched files containing the keyword w*. It inputs the search token STw * and the keyword ciphertext tuple set CT and verification tuple set VT, and returns the corresponding file set R with its verification block V, otherwise returns nothing.

6.    Verify (R, V): This algorithm is run by the data receiver to verify if the cloud server returns the correct and complete results.

The formal definition given above shows that our proposed VIBKS scheme provides the function of result verification, i.e., data receiver can check if the cloud server honestly performs the test operation and returns complete results. For security, we introduce a security game to define the security model of our proposed scheme.

Definition 4.10 Given the security parameter n, the game is carried out between an adversary A and a challenger C.

Setup: Take the security parameter n as input, C outputs the system public parameters PP and sends it to A. A submits a target identity idr* to C, and then it adaptively queries the following oracles.

KeyDerive oracle: Upon receiving the KeyDerive query on id from A, where the only restriction is id≠idr*, C generates the private key skid and returns it to A.

TokGen oracle: Upon receiving the TokGen query on w from A, C generates the search token stw and returns it to A.

Challenge phase: After finishing the above queries, A sends (idr*,w0*,w1*) to C, where w0*,w1* are two different randomly chosen keywords that have never been queried in the above oracles, idr* is the target identity. C randomly chooses a bit b∈{0,1}, and returns a random searchable ciphertext tuple C*=(c0*,c1*) to A.

A continues to query the TokGen oracle as above, the only restriction is that neither w0* nor w1* can be queried to obtain its search token.

Guess: Finally, A outputs a bit b′∈{0,1}. It wins the game if and only if b′=b.

The probability of A winning the above game is defined as AdvA(n)=|Pr[b′=b]-1/2|.

Definition 4.11 We say that our VIBKS scheme achieves ciphertext indistinguishability under the selective-ID attack if AdvA(n) is negligible for any PPT adversary A.

5  Our Construction

As introduced in Section 3, our scheme is composed of six algorithms, which will be described one by one in this section. Note that, we adopt a symmetric encryption scheme SE=(KeyGen,Enc,Dec) to encrypt data files.

5.1 Intuition Behind Our Construction

After we noticed that the existing lattice-based SE schemes only consider the server is honest-but-curious, we began to think about efficient lattice-based SE scheme that can thwart the server perform lazy search (i.e., search only a fraction of data or fooling users with previous search results) or return unfaithful result. Bloom filter can achieve this, but we want to avoid its false positive rate. We notice that we can solve this by adopting signature technique. The idea is to combine an efficient hash function with a lattice-based delegation algorithm to make sure that the verification result is deterministic, which implies that the user can check the completeness and correctness with 100% accuracy.

5.2 Construction

Now we describe the construction details of our lattice-based VIBKS scheme. It is composed of the following six polynomial-time algorithms.

Setup: Taking as input a security parameter n, CA generates the system public parameters q,m,σ,α,s, where q is prime, s is the gaussian parameter. Then CA performs the following steps:

1.    Set two secure hash function H1:{0,1}l1→ℤqm×m, H2:{0,1}l2→ℤqn, H3:{0,1}*→ℤqn, where the outputs of H1 are distributed in Dm×m.

2.    Invoke TrapGen(q,n) to generate a uniformly random matrix A0∈ℤqn×m together with a short basis TA0∈ℤqm×m for Λq⊥(A0).

3.    Select a uniformly random vector t∈ℤqn.

Finally, CA outputs the system public parameters PP and master secret key MSK given by MSK=TA0, PP=(q,m,n,l1,l2,σ,α,s,t,A0,H1,H2,H3).

KeyDerive: Taking as inputs the system public parameters PP, the master secret key MSK and a tag τ∈{0,1}l1, CA generates the public and secret key pair for the tag-belonged IoTs as follows:

1.    Compute the tag-matrix Rτ=H1(τ)∈ℤqm×m.

2.    Run skτ←BasisDel(A0,Rτ,TA0,s) to obtain a short random basis for Λq⊥(pkτ), where pkτ=A0Rτ-1.

Finally, CA sends the private key skτ and the public key pkτ to the IoTs whose tag is τ.

Encrypt: Taking as inputs the system public parameters PP, the file set F={F1,…,Fh}, the keyword set KS={w1,…,wu}, the IoTs’s key pair (sko,pko), the receiver’s tag τ∈{0,1}l1, the IoTs generates the keyword ciphertext tuple and the verification tuple as follows:

1.    For each file Fi in F, generate the symmetric key sk=SE⋅KeyGen(1n) and encrypt the file with it to get the ciphertext Ci=SE⋅Enc(sk,Fi).

2.    For each keyword wij∈{0,1}l2 in file Fi, first compute the tag-matrix Rτ=H1(τ)∈ℤqm×m and set Fτ=A0Rτ-1∈ℤqn×m, then compute the keyword-vector Gwij=t+H2(wij)∈ℤqn, finally compute the keyword ciphertexts cij=(cij0=GwijTr+x,cij1=FτTr+y), where r is a uniformly random vector from ℤqn, x∈ℤq and y∈ℤqm are noise vectors chosen from Ψ¯α and Ψ¯αm respectively.

3.    Let CTi=(Ci,{cij|wij∈Fi}) be the keyword ciphertext tuple of Fi.

4.    For each keyword wk∈KS, first generate the keyword ciphertext ck as in step 2, then compute hwk=H3(id1∥…∥idz∥wk)∈ℤqn, where {id1,…,idz} is the identity set of files containing the keyword wk, finally evaluate the verification block Vk←SamplePre(pks,sks,hwk,σ). Note that Vk⋅pks=hwk∈ℤqn, and the verification block is distributed in DΛq(pks)hwk,σ.

5.    Let VTk=(ck,Vk) be the verification tuple of keyword wk.

Finally, the IoTs outsources the keyword ciphertext tuple set CT={CTi}(i∈{1,…,h}) and the verification tuple set VT={VTk}(k∈{1,…,u}) to the cloud server.

TokGen: Taking as inputs the system public parameters PP, the receiver’s tag τ∈{0,1}l1, the keyword w*∈{0,1}l2 and the secret key skτ∈ℤqm×m, the data receiver computes the search token for searching as follows:

1.    Compute the tag-matrix Rτ=H1(τ)∈ℤqm×m and set Fτ=A0Rτ-1∈ℤqn×m.

2.    Compute the keyword-vector Gw*=t+H2(w*)∈ℤqn.

3.    Set stw*←SamplePre(Fτ,skτ,Gw*,σ). Note that Fτstw*=Gw*∈ℤqn, and the search token is distributed in DΛq(F(τ))G(w*),σ.

The data receiver sends the search token stw* to the cloud server.

Test: Taking as inputs the keyword ciphertext tuple set CT, the verification tuple set VT and the search token stw*, the cloud server searches for the matched files and the verification block as follows:

1.    For each keyword ciphertext tuple CTi∈CT, check if the file Fi contains the same keyword as stw*. To achieve this goal, for all cij∈CTi, compute γij=cij0-stw*Tcij1, if there exist γij, such that |γij|≤⌊q/4⌋, add the corresponding encrypted file Ci to the result set R. Otherwise, the cloud server aborts.

2.    For each verification tuple VTk∈VT, compute γk=ck0-stw*Tck1, if |γk|≤⌊q/4⌋, return the verification block Vk. Otherwise, the cloud server aborts.

The cloud server returns the result set R and the verification block Vk to the data receiver.

Verify: Taking as inputs the result set R and the verification block Vk, the data receiver verifies if the cloud server returns the integral results as follows:

1.    Decrypt the returning ciphertexts Fi=SE.Dec(sk,Ci).

2.    Compute hw=H3(id1∥…∥idh∥w*)∈ℤqn, where w* is the queried keyword, {id1,…,idh} is the identity set of the returned files.

3.    Check whether the equation pkoVk=hw* holds, and whether Vk is distributed in DΛq(pko)hw,σ. If they hold, it implies that the cloud server has faithfully returned all results. Otherwise, the cloud server behaviors dishonestly.

5.3 Correctness of VIBKS

Let (skτ,pkτ) be the data receiver’s key pair, w be the keyword contained in CTw and w* be that in stw*. In Test, take the token stw* as the input, the cloud server can compute γ as follows:

γ=c0-stw*Tc1=GwTr+x-stw*T(FτTr+y)=GwTr+x-Gw*Tr-stw*Ty.

When w = w*, γ=x-stwTy, as discussed in [23], |γ|≤⌊q/4⌋. When w≠w*, as γ≠x-stwTy, |γ|>⌊q/4⌋, thus we conclude that the ciphertext CTw and the token contain different keyword.

5.4 Verifiability of VIBKS

Let {id1,…,idh} be the identity set of decrypted files, V be the verification block, pko be the public key of data owner. In Verify, the data receiver computes hw=H3(id1∥…∥idh∥w*) and pkoVk. When the identity set of decrypted files is the same as the file identity set IDw that the data owner embeds in the verification block, the equation pkoVk=hw* holds from the definition of algorithm SamplePre. Thus, we come to the conclusion that the cloud server has returned the correct and complete results. Otherwise, we consider that the cloud server performs unfaithfully.

6  Security

In this section, we will give the security proof of our proposed scheme.

Theorem 6.1 VIBKS from lattice achieves ciphertext indistinguishability under the selective-ID attack in the random oracle model, provided that the hardness assumption of decisional-LWE problem holds.

Proof. Let A be an adversary, which breaks the ciphertext indistinguishability under the selective-ID attack with a non-negligible probability ε in the random oracle model. We construct a challenger C with a non-negligible probability solving the hardness assumption of LWE problem.

Setup: C requests from LWE oracle O for m + 1 times to obtain fresh pair (uk,vk)∈ℤqn×ℤq, where k=0,1,…,m. Then sets two lists L1, L2, L3, and let qHi be the maximum number of A’s queries to Hi, where i = 1, 2, 3. Finally, C prepares the system public parameters PP for A as follows.

1.    C samples a random matrix R*←Dm×m by running SampleR.

2.    C constructs a random matrix F*←ℤqn×m from m of the given LWE samples, where the k-th column of F* be the vector uk∈ℤqn for all k=1,…,m.

3.    C sets A0 = F*R*, where A0 is uniform in ℤqn×m since R*∈ℤqm×m are invertible modulo q and F* is uniform in ℤqn×m. C also let t=u0, and finally sets PP=(A0,t,H1,H2,H3) and sends it to A. Ahead of time, the target identity is idr* submitted by A.

Note that, regardless when A performs the KeyDrive oracle query, it has made all relevant H1 queries before. Now, A performs the following queries.

H1 query: For the l-th query, where l=1,2,…,qH1, A queries to H1 on any identity id adaptively. If l=I1*, such that id=idr*, C sets H1(id)=R* and returns it to A. Otherwise, C runs SampleRwithBasis(A0) to obtain a random matrix Rid∈ℤqm×m and a short random lattice basis Tid∈ℤqm×m for Λq⊥(A0Rid-1). Then C adds (id,A0Rid-1,Rid,Tid) to list L1, and returns Rid to A.

H2 query: For the l-th query, where l=1,2,…,qH2, A queries to H2 on any keyword w adaptively. If l = qH2, such that w = w*, C sets H2(w)=t0-t=t0-u0 and adds it to list L2, then returns it to A. Otherwise, C sets H2(w)=t0, where t0←ℤqn and adds it to list L2, then returns it to A.

KeyDerive oracle: Upon receiving the KeyDerive query on id from A, where the only restriction is id≠idr*, C checks the list L1 to find (id,A0Rid-1,Rid,Tid), if it is found, C returns Tid to A. Otherwise, C performs the same operation as H1 query on id, obtains (id,A0Rid-1,Rid,Tid) and returns Tid to A.

TokenGen oracle: Upon receiving the TokenGen query on w from A, where the only restriction is id≠idr*, C finds (id,A0Rid-1,Rid,Tid) in list L1 and t0 in list L2, it they are found, C computes Gw=t+t0 and runs SamplePre(A0Rid-1,Tid,Gw,σ) to obtain stw. Finally, C returns stw to A.

Challenge phase: A sends (idr*,w0*,w1*) to C, where w0*,w1* are two different keywords that have never been queried before, idr* is the challenge identity. C randomly chooses a bit b∈{0,1}, if b = 0, C returns a random searchable ciphertext C*=(c0*,c1*) to A. Otherwise, C performs as follows:

For each k=0,1,…,m, retrieve vk∈ℤq from LWE instance, set v*=(v1,v2,…,vm)T∈ℤqm, and set c0*=v0,c1*=v*. Finally, C returns the searchable ciphertext C*=(c0*,c1*) to A.

Guess: At last, A outputs its guess b′∈{0,1}.

The goal of A is to decide which keyword is contained in the challenged ciphertext C*, since the challenger C returns the searchable ciphertext which is associated with each keyword with probability 1/2. Now, we evaluate the probability of A in breaking the ciphertext indistinguishability under the selective-ID attack in the random oracle model. With the system public parameters PP, we have t+H2(w0*)=t+t0-t=t0, A0Rid-1=F*R*H1(id)-1=F*R*R*-1=F*, and c0*=v0=t0Tr*+x*c1*=v*=F*Tr*+y* for some random values x*∈ℤq and vectors r*∈ℤqn and y*∈ℤqm with Gaussian distribution. Therefore, c0*,c1* have the correct ciphertext form. We assume that A can successfully guess the keyword w0* is associated with the ciphertext C* with the probability ε, where the keyword w0* is the qH2-th H2 query when w0*=w* with the probability 1/qH2. When idr* is the I1*-th H1 query, it occurs with the probability 1/qH1. Thus, if A breaks the ciphertext indistinguishability under the selective-ID attack with a non-negligible probability ε in the random oracle model, C can solve the hardness assumption of decisional-LWE problem with the non-negligible probability ε′=ε/(2qH1qH2), which is contradictory. Consequently, AdvA(n) is negligible, and VIBKS achieves ciphertext indistinguishability under the selective-ID attack in the random oracle model.

7  Performance Analysis

7.1 Theoretical Analysis

In this section, we show a theoretical performance comparison of our proposed scheme and some other searchable encryption schemes [13,16,20]. First, we give the theoretical analysis of the computation overhead of keyword encryption, token generation, test operation, and verification process. Moreover, we describe the hardness problems on which the security models of each scheme are based. Finally, with regard to the functionalities, we describe the verifiability and post-quantum security.

Now, we specify some notations used in the comparison below. In particular, m denotes the number of results, E denotes the modular exponentiation operation, h denotes the hash operation which maps the arbitrary string into G, P denotes the bilinear pairing operation, H denotes the hash operation which maps the arbitrary string into a matrix. I denotes the matrix inversion operation, M denotes the matrix multiplication operation, BD denotes the BasisDel, SP denotes the SamplePre. The performance comparison is listed in Tab. 1.

Table 1: Performance comparison

7.2 Experiment Analysis

In this section, we conduct experiments of our proposed scheme in a laptop using Matlab R2017a. The environment is Windows 10 Ultimate (x64) with an Intel (R) Core (TM) i7-10750H CPU@2.60 GHz. We set the parameters m≥6nlogq. The security level of [13,16] is set to l = 10, as it utilized in their experiments. Under the above parameters, the time cost of SamplePre, hash operation and matrix multiplication are about 0.326574 s, 0.13221 s, and 0.028051 s respectively, which are far less than 183.067383 s required for matrix inverse operation. Therefore, we can only pay attention to the time cost of matrix inverse when considering the performance of algorithms that involves matrix inverse.

As shown in Tab. 1, although the theoretical computation cost of Encrypt in both [13,16] and our scheme contains matrix inverse operation, we found that the efficiency of our scheme is much higher than that of [13,16] in experiments. The advantage is due to that in our scheme, inverse matrix is only related to the user’s identity. It indicates that the matrix inverse operation can be done before the Encrypt process and keep it locally for the next Encrypt process. In [13,16], the keyword-related matrix needs to be inversed, so that the matrix inverse operation must be conducted once the keyword updates, which brings huge computation overhead. For the same reason, the efficiency of TokGen in our scheme is superior to that of [13,16]. Indeed, our scheme enjoys a greater advantage in TokGen because of the additional BasisDel overhead in [13,16].

Fig. 2 provides the comparison of test time with the increasing of the number of keywords. The left graph of Fig. 3 proves that our scheme and the scheme in [13] spend less time to complete the test no matter what the number of keywords is. The scheme in [20] involves time-consuming operation (i.e., bilinear pairing) when matching the token and encrypted keywords. We can observe that Test in [20] consumes around 9 times more computation time than that in [16] with the same number of keywords. Then, we consider the test time comparison of our scheme and [13,16], which are all constructed based on lattice hardness assumptions. From the left figure of Fig. 2, we can also see that the test time of [16] and our scheme is almost the same, far less than that in [13]. In order to further explore the relationship of time cost in [16] and our scheme, we list them in the right figure of Fig. 2. When the number of keywords is 100, we observe that our scheme and [16] take about 0.126 ms and 0.333 ms, respectively. The results again confirm the superiority of our scheme.

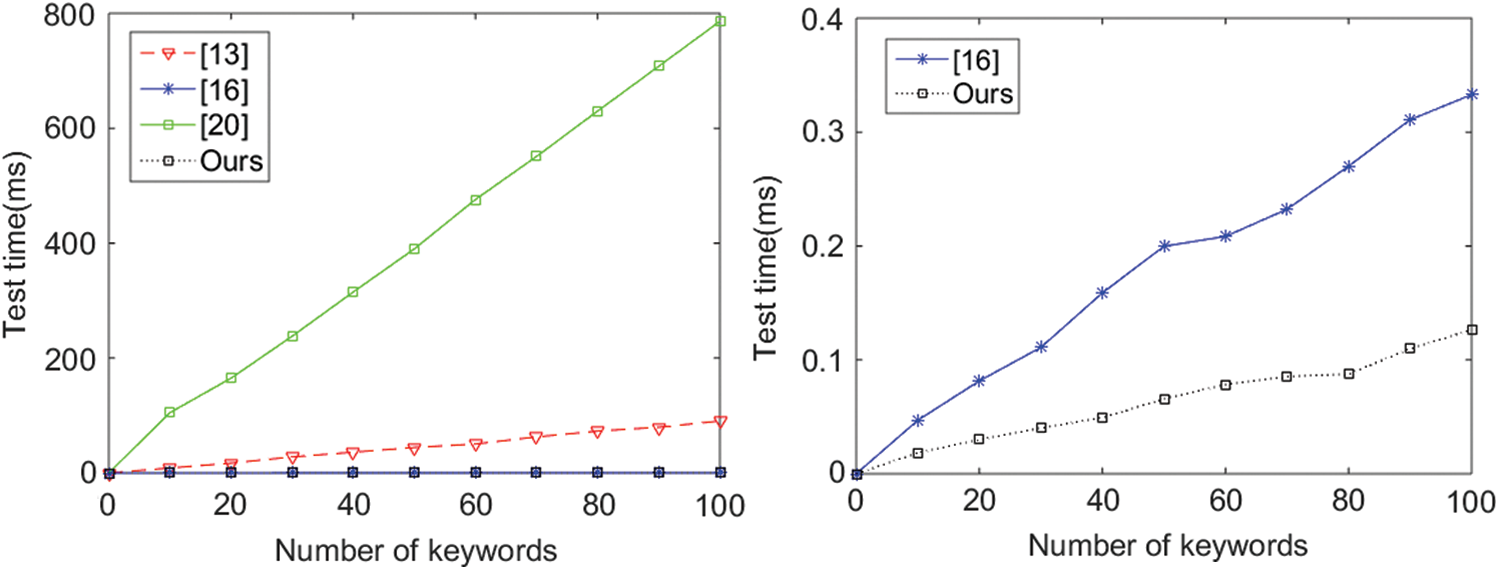
Figure 2: Comparison of Test

With respect to Verify, we implement the experiments to compare the verification time of our scheme and the basic scheme in [20]. As the basic scheme in [20] supports multi-keyword search, we set the number of keywords in one query to 1 to facilitate comparison. Furthermore, from Tab. 1, we can see that the performance of [20] in Verify depends on the number of results. In Fig. 3, we set the number of results to 1, which is the optimal case for [20]. Under the above setting, we notice that the performance of our scheme is significantly better than [20] as the verification times increases. It costs only 0.106 s to finish 100 times verification in our scheme, while it costs 2.899 s in [20]. The reason is that the scheme in [20] adopts time-consuming operations such as bilinear pairing and modular exponentiation, while our proposed scheme only involves in efficient matrix multiplication and hash operations.

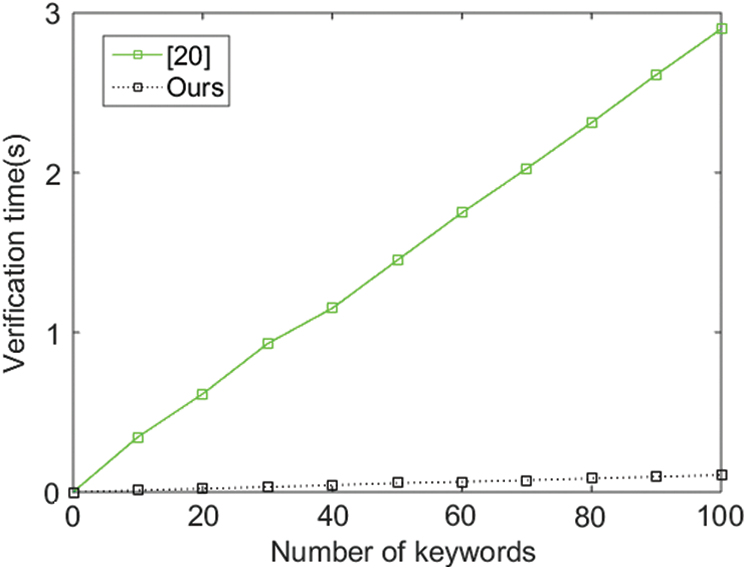
Figure 3: Comparison of Verify

8  Conclusion

Due to the booming of post-quantum cryptography, in this paper, we have constructed a lattice-based identity-based encryption with keyword search which can protect against quantum computer attacks. This paper proposes a lattice-based VIBKS scheme that can detect the misbehavior of cloud server and resist quantum computing attack. In the scheme, we use the preimage sample algorithm to generate a verification block for keyword ciphertext, which can be utilized by users to verify if the server returns correct and complete results. Then, we prove that our proposed scheme is secure under the selective-ID attack, and achieves both correctness and verifiability. Finally, we give theoretical and experimental comparisons with other searchable encryption schemes. The results demonstrate that our scheme achieves a better balance in efficiency and security. As future works, we consider the construction of lattice-based PEKS schemes with rich query functions.

Funding Statement: This work is supported by the National Natural Science Foundation of China (No: 62072240) and the National Key Research and Development Program of China (No. 2020YFB1804604).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Ashton, “That internet of things thing,” RFID Journal, vol. 22, no. 7, pp. 97–114, 2009. [Google Scholar]

 2.  J. Gubbi, R. Buyya, S. Marusic and M. Palaniswami, “Internet of Things (IoTA vision, architectural elements, and future directions,” Future Generation Computer Systems, vol. 29, no. 7, pp. 1645–1660, 2013. [Google Scholar]

 3.  L. Xu, C. G. Xu, Z. Y. Liu, Y. L. Wang and J. F. Wang, “Enabling comparable search over encrypted data for IoT with privacy-preserving,” Computers, Materials & Continua, vol. 60, no. 2, pp. 675–690, 2019. [Google Scholar]

 4.  D. X. Song, D. A. Wagner and A. Perrig, “Practical techniques for searches on encrypted data,” in Proc. S&P, Berkeley, California, USA, pp. 44–55, 2000. [Google Scholar]

 5.  D. Boneh, G. D. Crescenzo, R. Ostrovsky and G. Persiano, “Public key encryption with keyword search,” in Proc. EUROCRYPT, Interlaken, Switzerland, pp. 506–522, 2004. [Google Scholar]

 6.  D. J. Park, K. Kim and P. J. Lee, “Public key encryption with conjunctive field keyword search,” in Proc. WISA, Jeju Island, Korea, pp. 73–86, 2004. [Google Scholar]

 7.  P. Xu, H. Jin, Q. H. Wu and W. Wang, “Public-key encryption with fuzzy keyword search: A provably secure scheme under keyword guessing attack,” IEEE Transactions on Computers, vol. 62, no. 11, pp. 2266–2277, 2013. [Google Scholar]

 8.  J. Shao, Z. F. Cao, X. H. Liang and H. Lin, “Proxy re-encryption with keyword search,” Information Sciences, vol. 180, no. 13, pp. 2576–2587, 2010. [Google Scholar]

 9.  P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proc. FOCS, Santa Fe, New Mexico, USA, pp. 124–134, 1994. [Google Scholar]

10. F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, no. 7779, pp. 505–510, 2019. [Google Scholar]

11. C. X. Gu, Y. H. Zheng, F. Kang and D. Xin, “Keyword search over encrypted data in cloud computing from lattices in the standard model,” in Proc. Cloud Computing and Big Data, Huangshan, China, pp. 335–343, 2015. [Google Scholar]

12. L. Xu, X. L. Yuan, R. Steinfeld, C. Wang and C. G. Xu, “Multi-writer searchable encryption: An LWE-based realization and implementation,” in Proc. Asia CCS, Auckland, New Zealand, pp. 122–133, 2019. [Google Scholar]

13. X. J. Zhang, Y. Tang, H. X. Wang, C. X. Xu, Y. B. Miao et al., “Lattice-based proxy-oriented identity-based encryption with keyword search for cloud storage,” Information Sciences, vol. 494, no. 3, pp. 193–207, 2019. [Google Scholar]

14. Y. J. Mao, X. B. Fu, C. Guo and G. H. Wu, “Public key encryption with conjunctive keyword search secure against keyword guessing attack from lattices,” Transactions on Emerging Telecommunications Technologies, vol. 30, no. 11, pp. 789, 2019. [Google Scholar]

15. W. Sun, S. Yu, W. Lou, Y. T. Hou and H. Li, “Protecting your right: Verifiable attribute-based keyword search with fine-grained owner enforced search authorization in the cloud,” IEEE Transactions on Parallel and Distributed Systems, vol. 27, no. 4, pp. 1187–1198, 2016. [Google Scholar]

16. X. J. Zhang, C. X. Xu, H. X. Wang, Y. Zhang and S. X. Wang, “FS-PEKS: Lattice-based forward secure public-key encryption with keyword search for cloud-assisted industrial internet of things,” IEEE Transactions on Dependable and Secure Computing, 2019. https://doi.org/10.1109/TDSC.2019.2914117. [Google Scholar]

17. X. L. Yu, C. G. Xu, L. Xu and Y. T. Wang, “Lattice-based searchable encryption scheme against inside keywords guessing attack,” Computers, Materials & Continua, vol. 64, no. 2, pp. 1107–1125, 2020. [Google Scholar]

18. S. Benabbas, R. Gennaro and Y. Vahlis, “Verifiable delegation of computation over large datasets,” in Proc. CRYPTO, Santa Barbara, CA, USA, pp. 111–131, 2011. [Google Scholar]

19. Q. J. Zheng, S. H. Xu and G. Ateniese, “VABKS: Verifiable attribute-based keyword search over outsourced encrypted data,” in Proc. InfoCom., Toronto, Canada, pp. 522–530, 2014. [Google Scholar]

20. Y. B. Miao, Q. Y. Tong, R. H. Deng, K. R. Choo, X. M. Liu et al., “Verifiable searchable encryption framework against insider keyword-guessing attack in cloud storage,” IEEE Transactions on Cloud Computing, 2020. https://doi.org/10.1109/TCC.2020.2989296. [Google Scholar]

21. D. N. Wu, Q. Q. Gan and X. M. Wang, “Verifiable public key encryption with keyword search based on homomorphic encryption in multi-user setting,” IEEE Access, vol. 6, pp. 42445–42453, 2018. [Google Scholar]

22. O. Regev, “On lattices, learning with errors, random linear codes, and cryptography,” Journal of the ACM, vol. 56, no. 6, pp. 34:1–34:40, 2009. [Google Scholar]

23. J. Alwen and C. Peikert, “Generating shorter bases for hard random lattices,” Theory of Computing Systems, vol. 48, no. 3, pp. 535–553, 2011. [Google Scholar]

24. C. Gentry, C. Peikert and V. Vaikuntanathan, “Trapdoors for hard lattices and new cryptographic constructions,” in Proc. STOC, Victoria, British Columbia, Canada, pp. 197–206, 2008. [Google Scholar]

25. S. Agrawal, D. Boneh and X. Boyen, “Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE,” in Proc. CRYPTO, Santa Barbara, CA, USA, pp. 98–115, 2010. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.