Computers, Materials & Continua DOI:10.32604/cmc.2021.016021
Article

Numerical Solution of a Problem of Thermal Stresses of a Magnetothermoelastic Cylinder with Rotation by Finite-Difference Method

F. S. Bayones1, A. M. Abd-Alla2 and A. M. Farhan*,3,4

1Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, Faculty of Science, Sohag University, Egypt
3Physics Department, Faculty of Science, Jazan University, Jazan, Saudi Arabia
4Physics Department, Faculty of Science, Zagazig University, Zagazig, Egypt
*Corresponding Author: A. M. Farhan. Email: afarhan_afarhan@yahoo.com
Received: 19 December 2020; Accepted: 22 January 2021

Abstract: The present article deals with the investigation thermal stress of a magnetothermoelastic cylinder subjected to rotation, open or closed circuit, thermal and mechanical boundary conditions. The outer and inner surfaces of the cylinder are subjected to both mechanical and thermal boundary conditions. A The transient coupled thermoelasticity in an infinite cylinder with its base abruptly exposed to a heat flux of a decaying exponential function of time is devised solve by the finite-difference method. The fundamental equations’ system is solved by utilizing an implicit finite-difference method. This current method is a second-order accurate in time and space; it is also unconditionally stable. To illustrate the present model’s efficiency, we consider a suitable material and acquire the numerical solution of temperature, displacement components, and the components of stresses with time t and through the radial of an infinite cylinder. The results indicate that the effect of coupled thermoelasticity, magnetic field, and rotation on the temperature, stresses, and displacement is quite pronounced. In order to illustrate and verify the analytical developments, the numerical solution of partial differential equations, stress components, displacement components and temperature is carried out and computer simulated results are presented graphically. This study is helpful in the development of piezoelectric devices.

Keywords: Thermoelasticity; thermal stress; finite-difference method; non-homogeneous material; rotation; magnetic field

1  Introduction

Thermoelasticity’s dynamic problem has received quite the attention in literature through the past decade. Recently, numerous thermoelastic structures interact among strain and temperature harnessed the attention of many researchers due to extensive uses in diving-related fields, i.e., geophysics for to better understand Earth’s magnetic field effect on seismic waves, acoustic waves being dampened in magnetic fields, electromagnetic radiation emissions from nuclear devices, development of highly sensitive superconducting magnetometer, optics, electrical power engineering, etc. Bagri et al. [1] studied the unified generalized thermoelasticity, offering a solution for spheres and cylinders. Aziz et al. [2] gave further foundation to various concepts and applications of thermal stresses in a hollow cylinder subjected to convective boundary conditions. Propagation of Rayleigh waves in an elastic medum of orthotropic body was discussed by Abd-Alla [3]. Cherechukin et al. [4] analyzed the shape memory effect due to magnetic field-induced thermoelastic martensitic transformation in a polycrystalline. The problem of the rotational effect on the propagation of surface waves in magneto-thermoelastic materials with voids was discussed by Farhan et al. [5]. Ding et al. [6] Found the solution of the inhomogeneity orthotropic cylindrical shell for an axisymmetric plane strain. Abd-Elaziz et al. [7] discovered the effect of the Thomson parameter and inclined loads in an electro-magneto-thermoelastic solid with voids. Bayones et al. [8] discussed the eigenvalue approaches to coupled magneto-thermoelasticity structures in a rotating isotropic material. Bayones et al. [9] presented an analytical method for obtaining the wave propagation of a thermoelastic in a medium of a homogeneous isotropic material with effect of rotation and initial stress. Sheriff et al. [10] investigated propagation characteristics of discontinuities in electro-magneto generalized thermoelasticity in a cylindrical region. Abd-Elsalam et al. [11] found the numerical solution of the magneto-thermoelastic medium in an inhomogeneity isotropic cylinder via the finite-difference model. Othman et al. [12] considered the effect of magnetic field on a piezothermoelastic half-space with three theories. Othman et al. [13] studied the magnetic field, gravity field and rotation effects on a fiber-reinforced thermoelastic under three theories. Higuchi et al. [14] established the magneto-thermoelastic stresses induced by a magnetic field in a conducting solid cylinder. Abo-Dahab et al. [15] considered the effect of thermal stresses and magnetic fields in a thermoelastic medium without energy dissipation. Khader et al. [16] studied the uniform laser pulse for a solid cylinder via utilizing various theories of magneto-thermoelasticity. Said [17] investigated the influence of mechanical load on a magneto-micropolar thermoelastic half-space. Said et al. [18] studied the two-temperature rotating-micropolar thermoelastic medium while being affected by a magnetic field. Mukhopadhyay et al.[19] found the solution to the problem of generalized thermoelasticity of a cylinder with inhomogeneity material characteristics a finite-difference model. Wang et al. [20] investigated the magneto-mechanical stress and change of magnetic field vectors in an inhomogeneity thermoelastic cylinder. Ahire et al. [21] considered the behavior of thermoelastic a thin and a hollow cylinder using an internal moving heat source. From the extensive literature on the topic, we can mention some interesting investigations in [22–32].

The present paper aims to study the behaviors of thermal stresses. Another attempt is made to describe certain physical properties theoretically and graphically. This paper focuses on the thermal stresses in an inhomogeneity generalized thermoelastic cylinder under a magnetic field. The magnetic field plays a big role in studying the thermal stresses in an isotropic medium. The problem is treated in the finite-difference model of the governing equations of thermal stresses of a magnetothermoelastic cylinder are transformed into a system of differential equations and the numerical solution for the field variables inside the cylinder for Cobalt material are obtained directly in the space-time domain. The variations of temperature, displacement, and stresses we reacquired numerically and analyzed graphically.

2  Formulations of the Problem

Let us consider a cylindrical coordinate system (r, θ, z), with the z-axis coinciding with the cylinder’s axis. To consider the strains’ symmetry about the z-axis, we have only the radial displacement ur = u, uθ=0, uz = 0, which are independent of θ and z.

The Maxwell equations [20]

j→=∇∧h→,-μe∂h→∂t=∇∧e→,∇⋅h→,h→=∇→∧(u→∧H→)(1)

Here, h→ is the perturbed magnetic field, H0 is the initial magnetic field, μe is the magnetic permeability, e→ is the electric field vector, and j→ is the electric current density. Applying magnetic field vector H→=(0,0,H0) in cylindrical polar coordinates (r,θ,z),

The heat conduction equation is

∂2T′∂r2+1r∂T′∂r=1k1(∂∂t+τ∂2∂t2)T+γT0(∂∂t+τ∂2∂t2)[ur+∂u∂r](2)

And the equation of motion is

∂σrr∂r+1r(σrr+σθθ)+fr+ρΩ2u=ρ∂2u∂t2.(3)

where

fr=μe(j→∧H→)=μeH02∂∂r(∂u∂r+ur).(4)

The nonzero stress components are

σrr=c11∂u∂r+c12ur-β1(T′+τṪ′),σθθ=c11∂u∂r+c22ur-β2(T′+τṪ′),(5)

where σrr and σθθ are the mechanical stress, u→ is the mechanical displacement vector, ρ is the density, c11,c12, c22 are elastic constants, T′ is the temperature, Ω is the uniform angular velocity, T0 is the reference temperature solid, k is the thermal conductivity of the material, and γ=(β11+2β12). We define the quantities, c11,c12, c22 and ρ of the inhomogeneous body by

c11=β11r2m,c12=β12r2m,c22=β22r2m,ρ=ρ0r2m,γ=γ0r2mandμe=μ0r2m.(6)

where β11, β12, β22, ρ0, and μ0 are constants (values c11,c12c22, ρ and μe are inhomogeneous matter). Upon introducing the Eq. (6) in the Eq. (5), we obtain

σrr=r2m[β11∂u∂r+β12ur-β1′(T′+τṪ′)],σθθ=r2m[β11∂u∂r+β22ur-β2′(T′+τṪ′)].(7)

Now using Eq. (7) in the Eq. (3), we get

∂2u∂r2+1r(β11+μ0H02)(2M+1)(β11+μ0H02)∂u∂r-1r2[(β22-2mβ12)+(1-2m)μ0H02+ρ0Ω2](β11+μ0H02)u-[β1(β11+μ0H02)∂T∂r+(β1(2m+1)-β2)r(β11+μ0H02)(T+τṪ)+β1τ(β11+μ0H02)∂2T∂r∂t]=ρ0(β11+μ0H02)∂2u∂t2(8)

The following non-dimensional scheme is a convenience to be considered:

b(U,R)=(u,r),t′=bμ0t,T′=T0T,(9)

where T0 is a reference temperature, v is the dimension of velocity. Introduced Eq. (9) in Eq. (2) and (8), we have:

∂2T′∂R2+1R∂T′∂R=α(∂∂t+τ∂2∂t2)T+ε(∂∂t+τ∂2∂t2)(∂U∂R+1RU), (10)

∂2U∂R2+α1R∂U∂r-α2R2U-[α3∂T∂R+α4R(T+τṪ)+α5∂2T∂R∂t]=α6∂2U∂t2. (11)

Stress–displacement and temperature relations in the non-dimensional variables are given as

σRR=(bR)2m[β11∂U∂R+β12UR-ε(T+τṪ), (12)

σθθ=(bR)2m[β12∂U∂R+β22UR-ε(T+τṪ). (13)

where

α1=(β11+μ0H02)(2M+1)(β11+μ0H02),α2=[(β22-2mβ12)+(1-2m)μ0H02+ρ0Ω2](β11+μ0H02),α3=β1(β11+μ0H02),α4=(β1(2m+1)-β2)(β11+μ0H02),α5=β1τ(β11+μ0H02),α6=ρ0(β11+μ0H02),α=μ0bk,ε=γ0T0,

3  Boundary Conditions

The initial conditions as follows:

T=0att=0, (14)

U=0,∂U∂t=0.att=0. (15)

For the cylindrical problem, the boundary conditions as follows:

∂U∂R=0,T=1,atR=ab, (16)

U=0,∂U∂R=0.atR=1. (17)

4  Solution of the Problem

The governing equations obtained in the last section are partial differential equations that will be solved by an implicit finite-difference method described by Mukhopadhyay et al. [18]. The solution domain a≤R≤b, 0≤t≤τ is replaced by a grid illustrated by the node points (Ri,tn), in which Ri = 1+ih, i=0,1,2,…,N and tn = nk, n=0,1,2,…,K. Therefore, h=b-aN is taken as a mesh width and δt=τK is assumed to be the time step. We use the notation uin instead of u(Ri,tn).

The functions T(R, t) and U(R, t) may be at any nodal location:

T(Ri,tn)=Tin, (18)

U(R,tn)=Uin. (19)

By Applying an implicit finite-difference technique, finite-difference equations corresponding to Eqs. (10) and (11) are as follows:

Tin+1=Tin+ρa(Ti+1n-2Tin+Ti-1n+ρ(hb(a+ibh))(Ti+1n-Tin))-ε2h(Ui+1n+1-2Ui+1n+Ui+1n-1-Ui-1n+1+2Ui-1n-Ui-1n-1)-εR(Uin+1-2Uin+Uin-1),(20)

(ρ4−ρ3)Ui−1n+1+(1+2ρ3+ρ5)Uin+1−(ρ3+ρ4)Ui+1n+1=2Uin−Uin−1−α4(Δt)2Riα6−[α3α6(Ti+`1n−Ti−1n2h+α4Riα6(Tin+τTin+1−Tin−12Δt)+α5α6(Ti+1n+1−Ti−1n+1−Ti+1n−1+Ti−1n−1)4hΔt.(21)

where Uin, Tin is the approximate U(1+ih,nδt) and T(1+ih,nδt), respectively, and

ρ=δth2,ρ1=(δt)βh22,ρ2=(δt)22βhRi,ρ3=(δt)2α6h2,ρ4=(δt)2α12α6hRi,ρ5=(δt)2α2α6Ri.

The finite-difference form of the initial conditions (14) and (15) are

Tin=0att=0,Uin=Uin+1-Uin-12δtatt=0(22)

The finite-difference form of the boundary conditions (16) and (17) are

Ui+1n-Ui-1n2h=0,Tin=1atRi=ab,Uin=Ui+1n-Ui-1n2h=0,atRi=1(23)

5  Numerical Results and Discussion

The material chosen for the purpose of numerical calculation is Cobalt material, which is isotropic material. The physical data for Cobalt material is given [6]

T0=2000∘C,M=2,τ=0.02,β11=17.075GPa,β22=6.757GPa,β12=7.289GPa,k=1.14cal/s2,ρ0=8.93g/cm3.

Results are presented for a = 0.1 and b = 1. The variations are shown in Figs. 1–10, respectively.

We assessed the non-homogeneous scenario by considering that m = 0.5. We illustrated the numerical outcomes via graphs.

Fig. 1 demonstrates temperature T variation for various times t in the non-homogeneous case (m=0.5), temperature diminishes along side the surging R in all three modes, fulfilling the boundary conditions for the cylinder problem.

Fig. 2 demonstrates radial displacement U compared to R different values of magnetic field H0 and time t in the non-homogeneous case (m=0.5); displacement diminishes with surging R and it accumulates with increasing t.

Fig. 3 illustrates the variations of the radial stress σRR according to R across various values of time t and the magnetic field in the non-homogeneous case (m=0.5); radial stress surges with the increase of magnetic field in the range 0.1≤R≤0.5, while it diminishes with the increase of time. Also, it decreases with the increase of the magnetic field in the interval 0.5≤R≤1, while it surges with the increase of time in the same interval, increasing with the increase of R-the axis with the increase of time t.

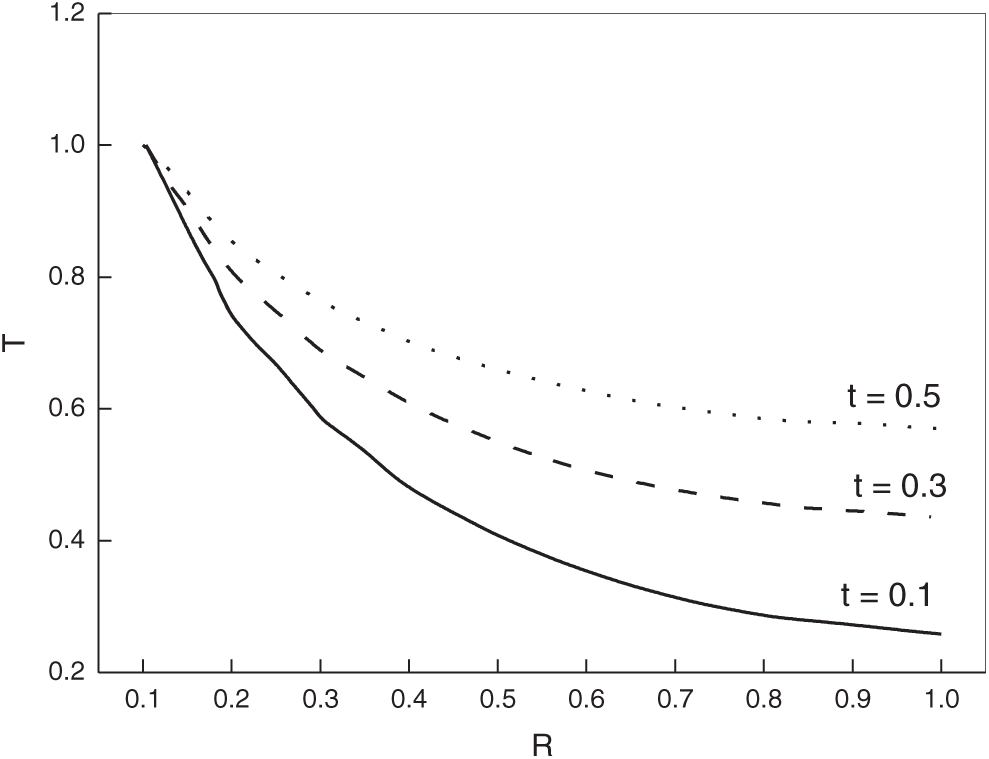
Figure 1: Variations of temperature with distance 0≤R≤1 for varying values of time t at m = 0.5 , Ω=0.5, H0 = 0.5

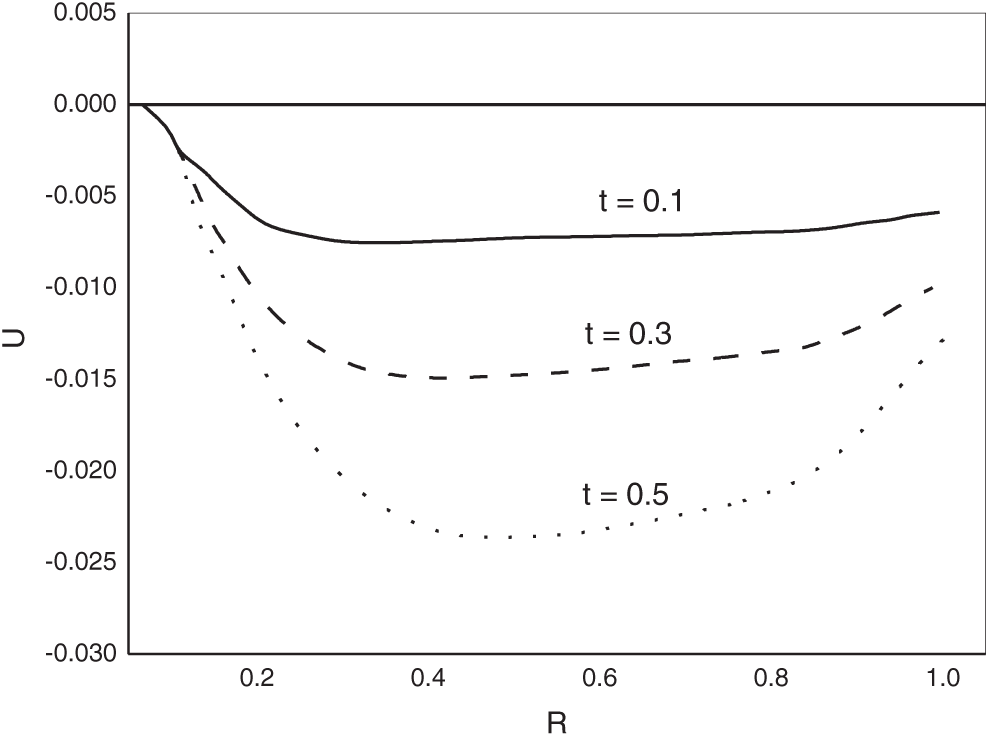
Figure 2: Variations of radial displacement with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0.5 , Ω=0.5…H0=.2×102, _ _ _ H0=0.5×102, –—H0=.8×102

Fig. 4 demonstrates tangential stress σθθ variations according to R across various values of magnetic field and time t in the non-homogeneous case (m=0.5); radial stress surges with the increase of magnetic field in the interval 0.1≤R≤0.9 while it diminishes with the increase of time and surges with the increase of R-the axis.

Fig. 5 represents radial displacement variations according to R across various values of magnetic field and time t in the homogeneous case (m=0). It is observed that the radial displacement increases with the increase of the magnetic field, while it decreases with the increase of time and it decreases and increases with the increase of R-the axis.

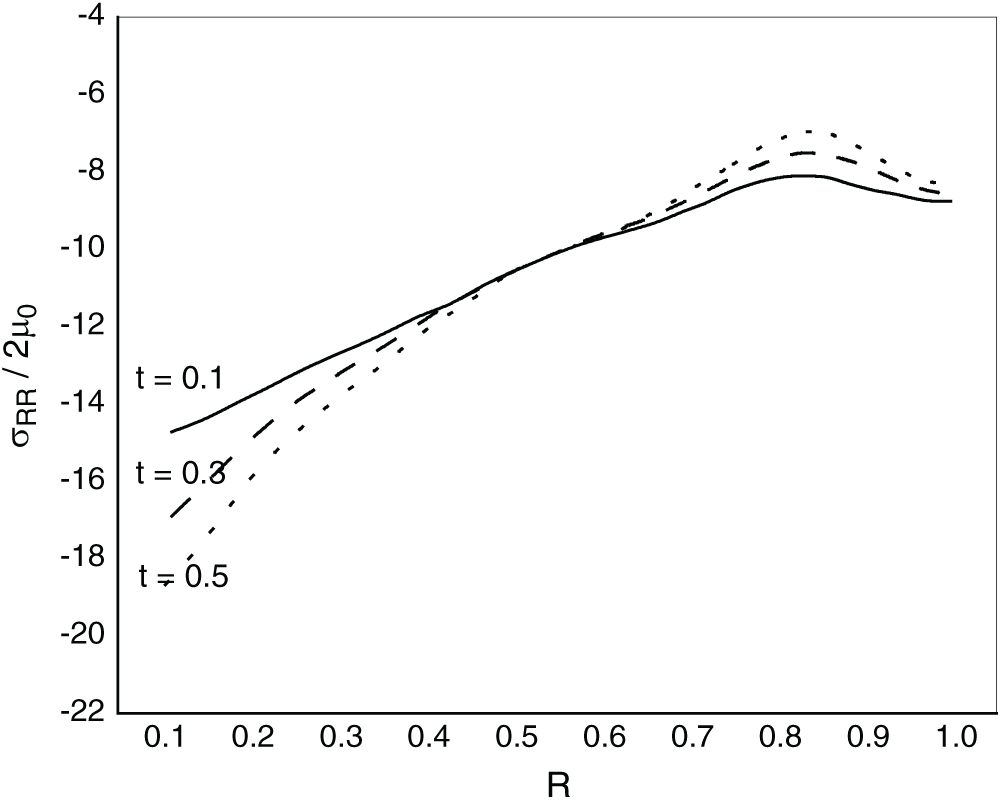
Figure 3: Variations of radial stress with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0.5 , Ω=0.5,…,H0=.2×102, _ _ _ H0=.5×102, –—H0=.8×102

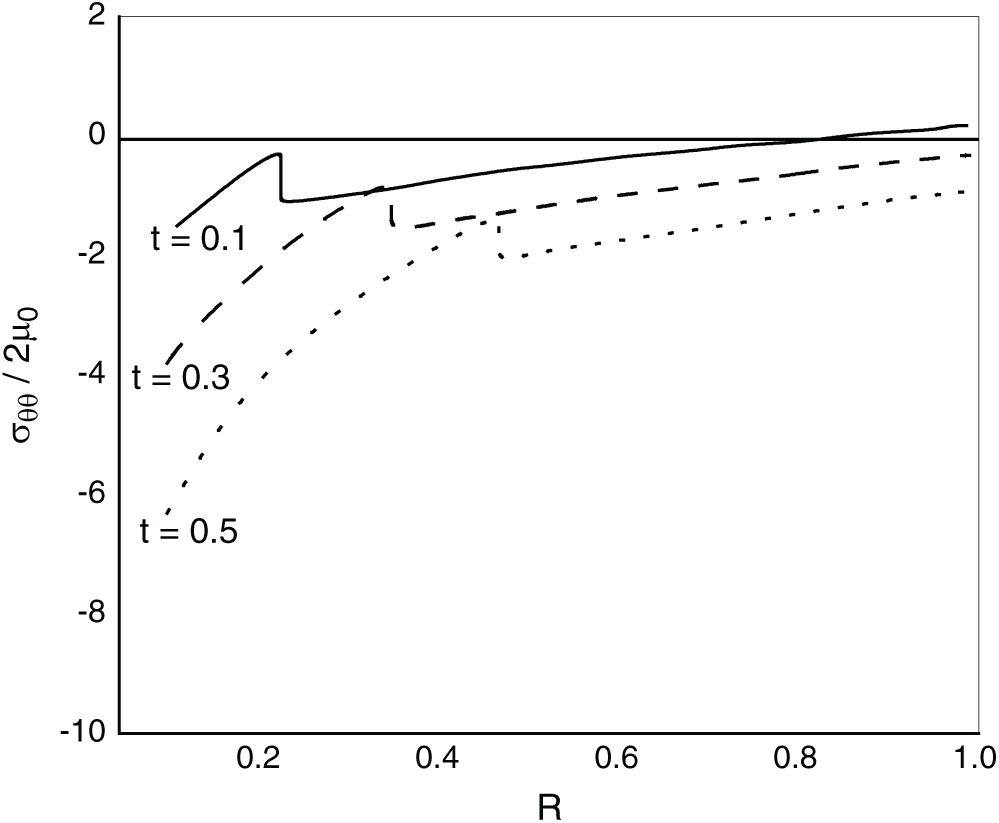
Figure 4: Variations of tangential stress with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0.5, Ω=0.5…H0=.2×102, _ _ _ H0=.5×102, –—H0=.8×102

Figs. 6 and 7 represent radial displacement variations according to R across various values of magnetic field and time t in the homogeneous case (m=0); radial stress surges with the increase of the magnetic field while it diminishes with the increase of time.

Fig. 8 illustrates radial displacement variations according to R across various values of rotation Ω and time t in the non-homogeneous case m = 0.5 ; radial displacement surges with the increase of rotation and time while it increases and decreases with the increase of R-axis.

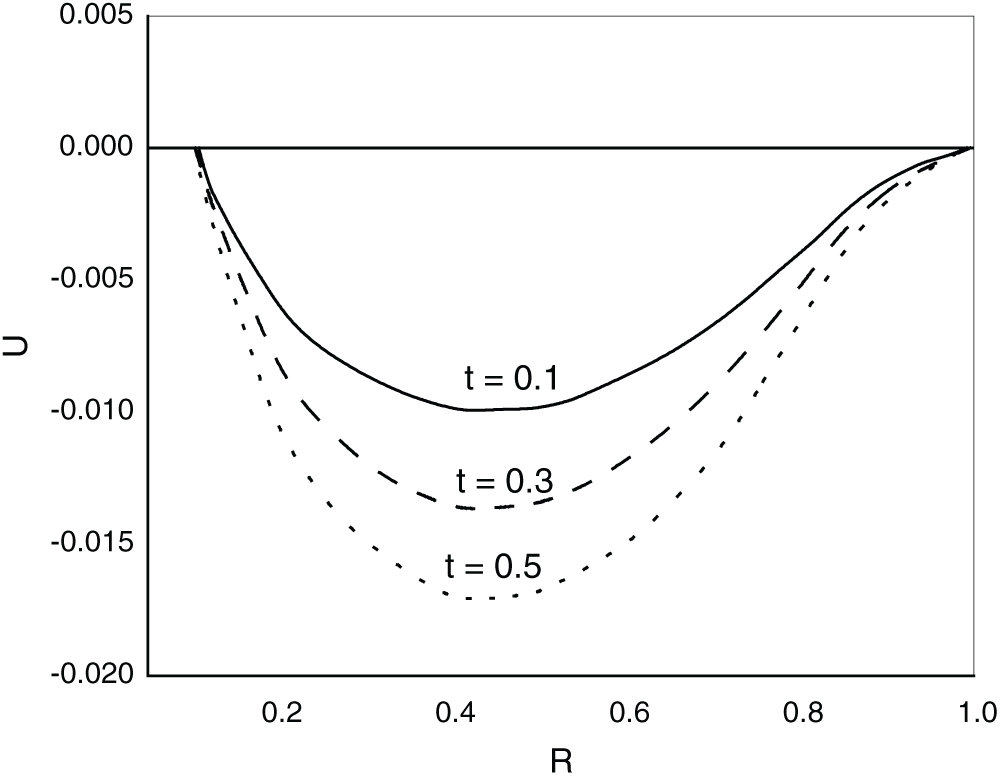
Figure 5: Variations of radial displacement with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0, Ω=0.5…H0=.2×102, _ _ _ H0=.5×102, –—H0=.8×102

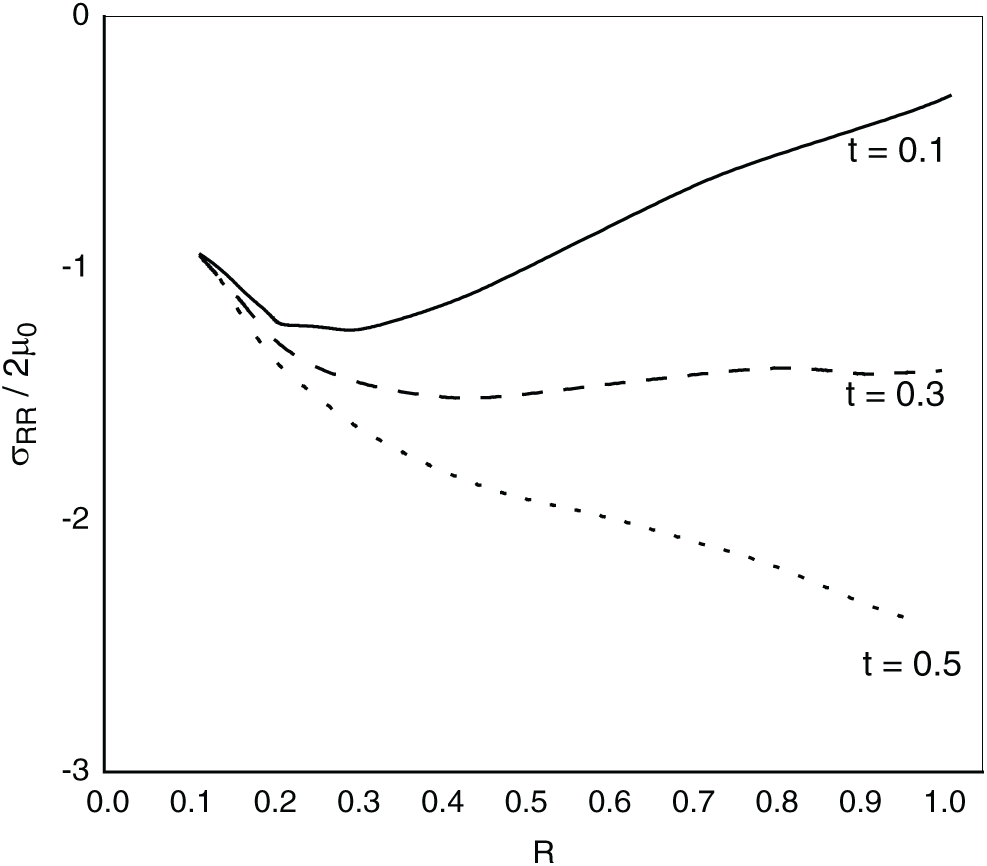
Figure 6: Variations of radial stress with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0, Ω=0.5…H0=.2×102, _ _ _ H0=.5×102, –—H0=0.8×102

Fig. 9 exhibits radial stress variations according to R for various values of rotation Ω and time t in the non-homogeneous case m = 0.5. It was evident that the radial stress surged with the increase of rotation and time in the interval 0.1≤R≤0.5 while it diminished with the increase of rotation and time in the interval 0.1≤R≤0.5 and decreased and increased with the increase of R-axis.

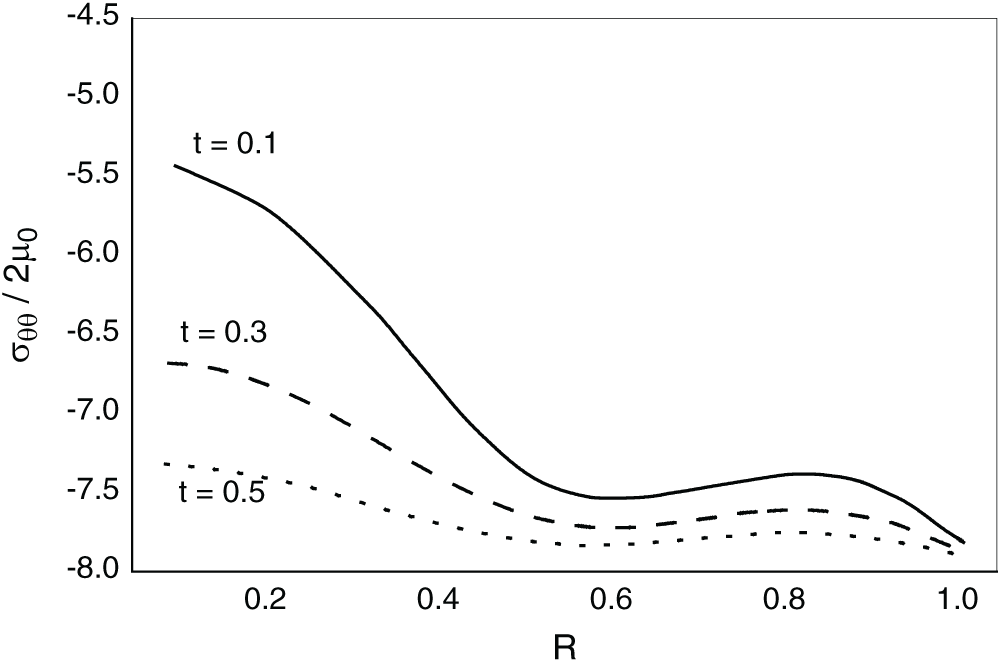
Figure 7: Variations of tangential stress with distance 0≤R≤1 for varying values of the magnetic field and time at m = 0, Ω=0.5,…,H0=.2×102, _ _ _ H0=.5×102, H0=.8×102

Figure 8: Variations of radial displacement with distance 0≤R≤1 for varying values of rotation Ω and time t at m = 0.5, H0=.2×102

Fig. 10 illustrates the tangential stress variations according to R across different values of rotation Ω and time t in the non-homogeneous case m = 0.5. It was evident that the tangential stress surged with the increase of time while diminishing with the increase of rotation. Also, it decreased and increased with the increase of R-the axis.

Figure 9: Variations of radial stress with distance 0≤R≤1 for varying values of rotation Ω and time t at m = 0.5, H0=.2×102

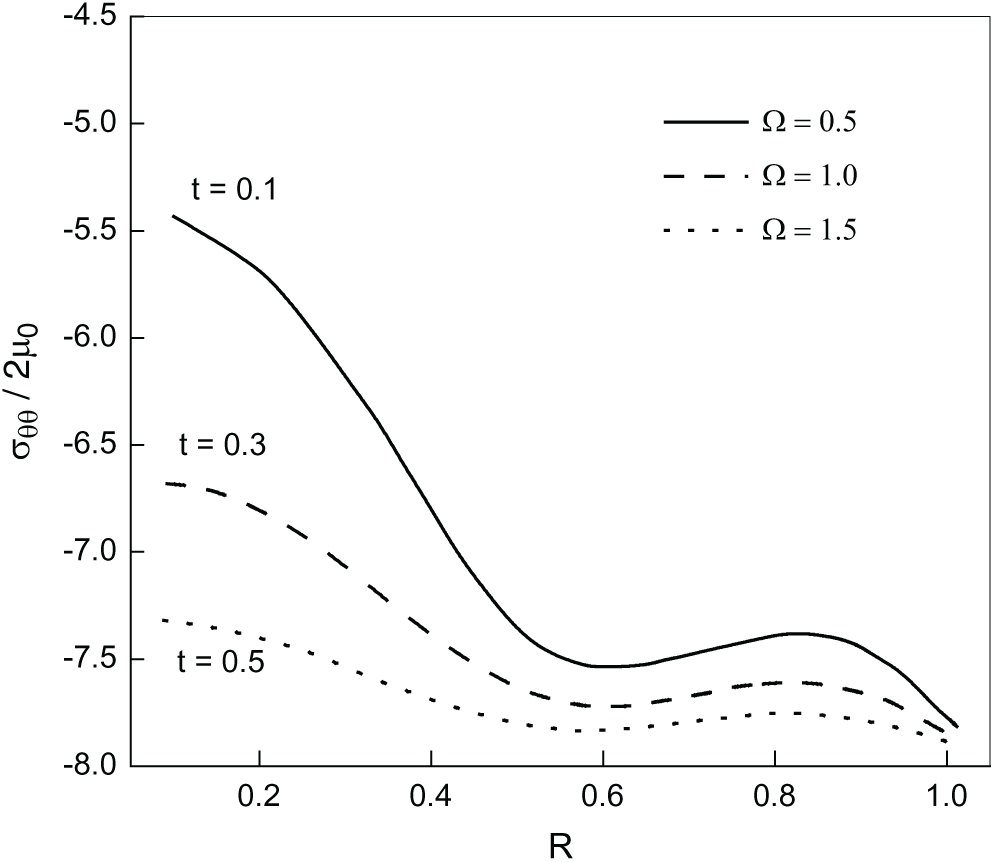
Figure 10: Variations of tangential stress with distance 0≤R≤1 for varying values of rotation Ω and time t at m = 0.5, H0=.2×102

From the graphical results, the following is surmised:

1.    Propagate of heat wave with a finite velocity in the body through space and time.

2.    This does not entail of thermoelasticity theory, propagation of heat wave with an infinite velocity is inherent.

3.    Therefore, generalized heat mechanism, essentially, drastically vary from the classic theory. In the thermoelasticity theory, propagates of heat wave with finite velocity rather than the infinite speed in the body.

4.    The results are given to the problem considered, but other problems may have different direction because of the dependence of the results on the properties of the material.

5.    The quantities of temperature, displacement, and stresses change due to the effect of rotation and magnetic field.

6  Conclusions

The analysis of graphs yields the following conclusions:

•   The medium deforms due to thermal point source with magnetic field and rotation., which turns out the coupled effects of the magneto-thermoelastic with radial R on physical domain.

•   The magnetic field and rotation play an influential role in the physical quantities.

•   The outcomes should incite investigations focusing on thermoelastic medium as a new class of applications as thermoelastic solids. The method in the article is widely applicable to different problems in thermodynamics and thermoelasticity.

Acknowledgement: Taif University Researchers Supporting Project Number (TURSP-2020/164), Taif University, Taif, Saudi Arabia.

Funding Statement: The author(s) received no specific funding for this study.

Conflicts of Interest: The authors declare that there are no conflicts of interest to report regarding the present study.

References

 1.  A. Bagri and M. R. Eslami, “A unified generalized thermoelasticity; Solution for cylinders and spheres,” International Journal of Mechanical Sciences, vol. 49, no. 12, pp. 1325–1335, 2007. [Google Scholar]

 2.  A. Aziz and M. Torabi, “Thermal stresses in a hollow cylinder with convective boundary conditions on the inside and outside surfaces,” Journal of Thermal Stresses, vol. 36, no. 10, pp. 1096– 1111, 2013. [Google Scholar]

 3.  A. M. Abd-Alla, “Propagation of Rayleigh waves in an elastic half-space of orthotropic material,” Applied Mathematics and Computation, vol. 99, no. 1, pp. 61–69, 1999. [Google Scholar]

 4.  A. A. Cherechukin, I. E. Dikshtein, D. I. Ermakov and T. Takagi, “Shape memory effect due to magnetic field-induced thermoelastic martensitic transformation in polycrystalline Ni–Mn–Fe–Ga alloy,” Physics Letters A, vol. 291, no. 2, 3, pp. 175–183, 2001. [Google Scholar]

 5.  A. M. Farhan and A. M. Abd-Alla, “Effect of rotation on the surface wave propagation in magneto-thermoelastic materials with voids,” Journal of Ocean Engineering and Science, vol. 3, pp. 334–342, 2018. [Google Scholar]

 6.  D. J. Ding, H. M.Wang and W. Q. Chen, “A solution of a non-homogeneous orthotropic cylindrical shell for axisymmetric plane strain dynamic thermoelastic problem,” Journal of Sound Vibration, vol. 263, no. 4, pp. 815–829, 2003. [Google Scholar]

 7.  E. M. Abd-Elaziz and M. I. M. Hilal, “The influence of Thomson effect and inclined loads in an electro-magneto-thermoelastic solid with voids under green-Naghdi theories,” Journal of Ocean Engineering and Science, vol. 3, no. 3, pp. 253–264, 2018. [Google Scholar]

 8.  F. S. Bayones and A. M. Abd-Alla, “Eigenvalue approach to two dimensional coupled magneto-thermoelasticity in a rotating isotropic medium,” Results in Physics, vol. 7, pp. 2941–2949, 2017. [Google Scholar]

 9.  F. S. Bayones, A. Abd-Alla, R. Alfatta and H. Al-Nefaie, “Propagation of a thermoelastic wave in a half-space of a homogeneous isotropic material Subjected to the effect of rotation and initial stress,” Computers, Materials & Continua, vol. 62, no. 2, pp. 551–567, 2020. [Google Scholar]

10. H. H. Sherief and S. E. Khader, “Propagation of discontinuities in electromagneto generalized thermoelasticity in cylindrical regions,” Meccanica, vol. 48, pp. 2511–2523, 2013. [Google Scholar]

11. M. R. Abd-Elsalam, A. M. Abd-Alla and H. A. Hosham, “Numerical solution of magneto-thermoelastic problem in non-homogeneous isotropic cylinder by the finite-difference method,” Applied Mathematical Modeling, vol. 31, no. 8, pp. 1662–1670, 2007. [Google Scholar]

12. M. I. A. Othman, Y. D. Elmaklizi and E. A. A. Ahmed, “Effect of magnetic field on piezo-thermoelastic medium with three theories,” Results in Physics, vol. 7, pp. 3361–3368, 2017. [Google Scholar]

13. M. I. A. Othman and K. Lotfy, “The effect of magnetic field and rotation of the 2-D problem of a fiber-reinforced thermoelastic under three theories with influence of gravity,” Mechanics of Materials, vol. 60, no. 5, pp. 129–143, 2013. [Google Scholar]

14. M. Higuchi, R. Kawamura and Y. Tanigawa, “Magneto-thermo-elastic stresses induced by a transient magnetic field in a conducting solid circular cylinder,” International Journal of Solids and Structures, vol. 44, no. 16, pp. 5316–5335, 2007. [Google Scholar]

15. S. M. Abo-Dahab, A. M. Abd-Alla and A. H. Alotaibi, “On an influence of thermal stresses and magnetic field in thermoelastic half-space without energy dissipation,” Journal of Thermal Stresses, vol. 40, no. 3, pp. 267–280, 2017. [Google Scholar]

16. S. Khader and M. Khedr, “A uniform laser pulse for a solid cylinder by using different theories of magneto-thermo elasticity,” Arab Journal of Nuclear Sciences and Applications, vol. 52, no. 3, pp. 121–130, 2019. [Google Scholar]

17. S. M. Said, “The effect of mechanical strip load on a magneto-micropolar thermoelastic medium: Comparison of four different theories,” Mechanics Research Communications, vol. 107, pp. 103–115, 2020. [Google Scholar]

18. S. M. Said, Y. D. Elmaklizi and M. I. A. Othman, “A two-temperature rotating-micropolar thermoelastic medium under influence of magnetic field,” Chaos, Solitons & Fractals, vol. 97, pp. 75–83, 2017. [Google Scholar]

19. S. Mukhopadhyay and R. Kumar, “Solution of a problem of generalized thermoelasticity of an annular cylinder with variable material properties by finite difference method,” Computational Method in Science and Technology, vol. 15, no. 2, pp. 169–176, 2009. [Google Scholar]

20. X. Wang and K. Dong, “Magnetothermodynamic stress and perturbation of magnetic field vector in a non-homogeneous thermoelastic cylinder,” European Journal of Mechanics A/Solids, vol. 25, no. 1, pp. 98–109, 2006. [Google Scholar]

21. Y. M. Ahire, K. P. Ghadle and A. A. Hamoud, “Thermoelastic behavior in thin hollow cylinder using internal moving heat source,” International Journal of Innovative Technology and Exploring Engineering, vol. 9, no. 2, pp. 2578–2583, 2019. [Google Scholar]

22. K. K. Żur, M. Arefi, J. Kim and J. N. Reddy, “Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory,” Composites Part B: Engineering, vol. 182, no. 1, pp. 107601, 2020. [Google Scholar]

23. M. Arefi and T. Rabczuk, “A nonlocal higher order shear deformation theory for electro-elastic analysis of a piezoelectric doubly curved nano shell,” Composites Part B: Engineering, vol. 168, no. 1, pp. 496–510, 2019. [Google Scholar]

24. A. Loghman, M. Nasr and M. Arefi, “Non-symmetric thermomechanical analysis of a functionally graded cylinder subjected to mechanical, thermal, and magnetic loads,” Journal of Thermal Stresses, vol. 40, no. 6, pp. 765–782, 2017. [Google Scholar]

25. M. Arefi, M. Nasr and A. Loghman, “Creep analysis of the FG cylinders: Time-dependent non-axisymmetric behavior,” Steel and Composite Structures, vol. 28, no. 3, pp. 331–347, 2018. [Google Scholar]

26. M. Arefi, G. H. Rahimi and M. J. Khoshgoftar, “Optimized design of a cylinder under mechanical, magnetic and thermal loads as a sensor or actuator using a functionally graded piezomagnetic material,” International Journal of Physical Sciences, vol. 6, no. 27, pp. 6315–6322, 2011. [Google Scholar]

27. M. Arefi, G. H. Rahimi and M. J. Khoshgoftar, “Exact solution of a thick walled functionally graded piezoelectric cylinder under mechanical, thermal and electrical loads in the magnetic field,” Smart Structures and Systems, vol. 9, no. 5, pp. 427–439, 2012. [Google Scholar]

28. M. J. Khoshgoftar, G. H. Rahimi and M. Arefi, “Exact solution of functionally graded thick cylinder with finite length under longitudinally non-uniform pressure,” Mechanics Research Communications, vol. 51, no. 5, pp. 61–66, 2013. [Google Scholar]

29. M. Arefi and M. Amabili, “A comprehensive electro-magneto-elastic buckling and bending analyses of three-layered doubly curved nanoshell, based on nonlocal three-dimensional theory,” Composite Structures, vol. 257, no. 1, pp. 113100, 2021. [Google Scholar]

30. H. Ren, X. Zhuang and T. Rabczuk, “Nonlocal operator method with numerical integration for gradient solid,” Computers & Structures, vol. 233, no. 1, pp. 106235, 2020. [Google Scholar]

31. H. Ren, X. Zhuang and T. Rabczuk, “A nonlocal operator method for solving partial differential equations,” Computer Methods in Applied Mechanics and Engineering, vol. 358, no. 1, pp. 112621, 2020. [Google Scholar]

32. T. Rabczuk, H. Ren and X. Zhuang, “A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem,” Computers, Materials & Continua, vol. 59, no. 1, pp. 31–55, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.