Computers, Materials & Continua DOI:10.32604/cmc.2021.016481
Article

Image-to-Image Style Transfer Based on the Ghost Module

Yan Jiang1, Xinrui Jia1, Liguo Zhang1,2,*, Ye Yuan1, Lei Chen3 and Guisheng Yin1

1College of Computer Science and Technology, Harbin Engineering University, Harbin, 150001, China
2Heilongjiang Hengxun Technology Co., Ltd., Harbin, 150001, China
3College of Engineering and Information Technology, Georgia Southern University, Statesboro, 30458, GA, USA
*Corresponding Author: Liguo Zhang. Email: zhangliguo@hrbeu.edu.cn
Received: 03 January 2021; Accepted: 17 March 2021

Abstract: The technology for image-to-image style transfer (a prevalent image processing task) has developed rapidly. The purpose of style transfer is to extract a texture from the source image domain and transfer it to the target image domain using a deep neural network. However, the existing methods typically have a large computational cost. To achieve efficient style transfer, we introduce a novel Ghost module into the GANILLA architecture to produce more feature maps from cheap operations. Then we utilize an attention mechanism to transform images with various styles. We optimize the original generative adversarial network (GAN) by using more efficient calculation methods for image-to-illustration translation. The experimental results show that our proposed method is similar to human vision and still maintains the quality of the image. Moreover, our proposed method overcomes the high computational cost and high computational resource consumption for style transfer. By comparing the results of subjective and objective evaluation indicators, our proposed method has shown superior performance over existing methods.

Keywords: Style transfer; generative adversarial networks; ghost module; attention mechanism; human visual habits

1  Introduction

Deep learning has shown excellent performance in various image processing tasks, e.g., image generation [1], object detection [2] and tracking [3], image classification [4], scene text recognition [5], and style transfer. Generally, the goal of style transfer is to learn and extract the styles of the source image, and then apply the extracted styles to the target image. In early style transfer research, a supervised learning strategy was mainly adopted to complete the style transfer. The style transfer based on supervised learning needs to acquire the paired training data, i.e., the source image and corresponding target image with the same image content and the different image styles. However, obtaining a large amount of paired data is a time-consuming and costly operation. Hence, semi-supervised or unsupervised learning-based methods have been proposed by researchers for style transfer to solve the above problems.

Zhu et al. [6] proposed a cycle-consistent adversarial network (CycleGAN) for cross-domain image style transfer. It breaks the strict requirement that supervised learning-based methods require paired training data. CycleGAN can use unpaired training data to complete the style transfer, and the image contents do not need to be the same. Since unpaired data can be used in style transfer, time is saved when obtaining data. A number of methods based on unpaired data have been proposed. For instance, the dual generative adversarial network (DualGAN) [7] was proposed to achieve style transfer based on unpaired training data. Chen et al. [8] proposed a novel framework named CartoonGAN, based on the GAN, for the cartoonization of photos using unpaired training data. Unlike the CycleGAN, CartoonGAN introduced a semantic content loss and an edge-promoting adversarial loss for coping with the abundant style variation within photos and cartoons and preserving clear edges, respectively. Both CycleGAN and DualGAN can effectively transfer the different styles of images. However, they cannot transfer the style and content of the image simultaneously. To address this problem, Hicsonmez et al. [9] proposed a GAN architecture (named GANILLA) for image-to-illustration translation. However, the above methods have a common shortcoming: a large computational cost. Besides the computational cost problem, the generated image’s quality, the number of parameters, and the number of floating-point operations (FLOPS) also need to be considered.

To achieve efficient style transfer by using unpaired training data, we utilized the GANILLA, which uses low-level features to retain content while transforming styles. Then, we made the following improvements. 1) We redesigned the convolutional module of Residual Neural {Network-18} (ResNet-18) [10], where a cheap linear model transformation (i.e., the convolution operation of GhostNet [11]) was used to build a lightweight network architecture. This improvement can reduce the number of parameters and FLOPs. 2) The attention mechanism was introduced into our proposed network. By adding an attention layer from the second layer to the fourth layer in our proposed network, we enhanced the useful features and suppressed the less useful features. Current style transfer was mainly employed to compare oil painting style results. In this paper, we present several different styles of generated images. e.g., seasonal style transfer, stick figure style transfer, and cartoon style transfer; these are shown in Fig. 1. The rest of this paper is organized as follows. In Section 2, related work is described, and in Section 3, we introduce the ghost module, attention mechanism, network architecture of our proposed method, and the loss function used. In Section 4, the complexity analysis and implementation details are described, and the results of various generated different styles images are demonstrated, and, in Section 5, we adopt two evaluation indicators, i.e., subjective evaluation and objective evaluation, to evaluate the results of our method and comparison method. Finally, in Section 6 conclusions are presented and future research discussed.

Figure 1: Sample with different styles obtained by our proposed method

2  Related Work

In recent years, the GAN [12] has been widely employed in the field of deep learning [13], and it consists of a generator and a discriminator. The purpose of the generator is to learn the feature distribution of the training data. The discriminator is employed as a classifier to classify the data, i.e., whether the data is generated by the generator or real samples. Hence, the training process of the GAN can be regarded as an adversarial game. The adversarial training process is complete once the generator can output the data the distribution of which is the same as that of real data. i.e., the discriminator cannot distinguish between the correctly generated data and real data. Benefiting from its strong generating ability, the GAN has also been employed in style transfer [14].

Style transfer is a hot topic in computer vision. The existing methods can be divided into two strategies according to the training data used: paired training data or unpaired training data. Style transfer based on supervised learning method needs to use paired training data directly. For example, Isola et al. [15] explored a GAN suitable for image-to-image translation tasks; their method is called Pix2Pix. Pix2Pix is different from prior works in its generator and discriminator architectures. The U-Net and PatchGAN classifiers are employed as the generator and the discriminator of Pix2Pix, respectively. To solve the unstable training and the generated image quality being unsatisfactory faced by Pix2Pix, Wang et al. [16] proposed Pix2PixHD. They used a coarse-to-fine generator and a multi-scale discriminator architecture, and modified the adversarial loss to achieve style transfer. Experimental results indicated that Pix2PixHD could effectively generate high-resolution images. Although the above methods can effectively transfer different styles, obtaining paired data is very difficult, time-consuming, and laborious. Compared with paired data, unpaired data is easier to obtain. Hence, researchers have proposed many methods based on unpaired data.

CycleGAN is a pioneering method that uses unpaired image style transfer based on the idea of unsupervised learning. Besides the adversarial loss of the original GAN, CycleGAN also utilizes the cycle consistency loss, which consists of the forward cycle consistency and the backward cycle consistency. By combining adversarial loss and cycle consistency loss, CycleGAN has achieved good performance on several tasks, e.g., the collection style transfer, photo enhancement, season transfer, and object transfiguration. However, the CycleGAN faces problems with poor quality, mapping ambiguity, and model sensitivity. Li et al. [17] proposed an asymmetric GAN (AsymGAN) to solve these problems. AsymGAN uses an auxiliary variable, which can provide more information when transferring images from an information-rich domain to an information-poor domain. AsymGAN can generate better quality images and mitigate the sensitivity convergence problem. After the CycleGAN was proposed, several style transfer methods based on the GAN and using unpaired data were proposed. For instance, CartoonGAN made the GAN’s architecture simpler and more effective. Moreover, two novel loss functions were designed, i.e., the semantic content loss and marginal promotion loss. The CartoonGAN can train the photos and cartoon images directly, and hence is simple to use. This method not only constructs sparse regularization in the VGG network [18] and realizes the conversion between photos and cartoons, but it also makes the photos clearer. Later, a unified quality-aware GAN (QGAN) [19] was designed to solve the data underrepresentation problem. The QGAN uses a multi-precision quantization based on the expectation-maximization algorithm, which provides the optimal number of bits configuration with the quality loss. Emami et al. [20] proposed a spatial attention GAN (SPAGAN) model that introduced the attention mechanism to the GAN architecture. SPAGAN used the attention mechanism to assist the generator in paying attention to the most discriminative regions between the source and target domains.

Although the above style transfer methods show significant progress, they still cannot solve the complex trade-off between image style and content. CycleGAN is very successful in transferring style, but it is not as successful in transferring content; CartoonGAN is successful in preserving image content, but it has shortcomings in delivering style. To this end, Hicsonmez et al. developed GANILLA, which can produce obvious styles but still retain content. By migrating the style of a given illustration, the transition from natural images to painting style illustrations can be achieved. Furthermore, the low-level and high-level features are merged by using skip connections and up-sampling. Overall, GANILLA is a relatively successful example of the style transfer methods using unpaired data. It overcomes the shortcomings of earlier methods and can maintain content while transferring the style. However, the style transfer process of GANILLA needs a large number of parameters and FLOPs. Therefore, we employed the Ghost module to construct a lightweight style transfer network that can reduce the number of parameters and FLOPs.

3  Proposed Method

3.1 Ghost Module for More Features

A well-trained convolutional neural network (CNN) usually includes rich feature maps to ensure a superior semantic understanding of the input data. We referenced the convolution operation in GhostNet to generate more feature maps with fewer parameters, as shown in Fig. 2. The number of ordinary convolution layers needs to be strictly controlled. We used a series of simple linear operations to produce more feature maps according to the inherent feature map of the ordinary convolution layers. The linear operation is a depthwise convolution [11]. Unlike the ordinary convolution operation, depthwise convolution performs its operation on each channel separately. Hence, the number of filters is the same as the number of channels. However, in the ordinary convolution operation, each filter operates in each channel of the input image simultaneously. The new channels’ feature maps are obtained after completing the convolution operation in each channel. Then we perform a standard 1×1 cross-channel convolution operation on the new batch of channel feature maps. Utilizing the depthwise convolution can effectively reduce the number of parameters and computational complexities without changing the size of the output feature maps.

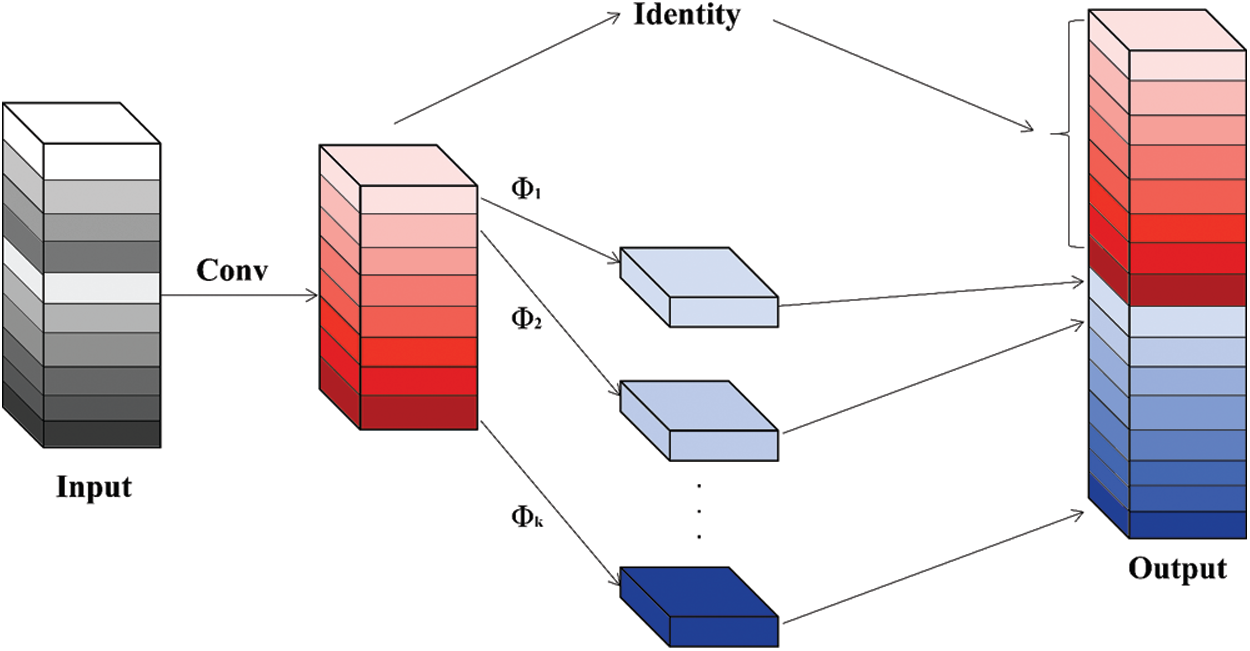
Figure 2: An illustration of the Ghost module

Let X∈Rc×h×w be the input feature maps, where c denotes its number of input channels, and h and w denote the maps’ height and width, respectively. The following formula is adopted to illustrate that the convolution generates n feature maps:

Y=X∗f+b, (1)

where Y∈Rn×h′×w′ represents the output feature maps with n channels, and f∈Rc×k×k×n refers to the convolution filters of the current layer, b is a bias term, and ∗ represents a convolution operation. Additionally, the width and height of the output feature maps are represented by h′ and w′, respectively, while k×k stands for the kernel size of the convolution filter. In such a convolution process, the number of FLOPs is described as n×h′×w′×c×k×k. The number of FLOPs is usually prodigious in that the number of filters n and the number of channels c are typically immense.

As indicated by the above formula, it can be clearly established that the number of parameters (in f and b) is actually dominated by the dimension of the input and output feature maps. There is usually significant redundancy in the output feature maps, which would lead to a decrease in computational efficiency. After some cheap transformations, the output feature maps are similar to those produced by the Ghost model of intrinsic feature mapping. The mapping of these intrinsic features is mostly generated by ordinary convolution filters, and thus they are relatively small. Specifically, the primary convolution generates m intrinsic feature maps Y′∈Rm×h′×w′:

Y′=X∗f′, (2)

where f′∈Rc×k×k×m is the filter used, m≤n, and the bias terms are omitted for simplicity. To keep the spatial size of the output feature maps consistent, the hyper-parameters (e.g., filter kernel size, stride, and padding) are similar to those in the ordinary convolution during the convolution process. To acquire the required n feature maps, we employ cheap linear operations on each intrinsic feature in Y′ to obtain s Ghost feature maps:

yij=Φi,j(yi′),∀i=1,…m,j=1,…,s, (3)

where yi′ represents the i-th intrinsic feature maps in Y′, and Φi,j is the j-th (except the last) linear operation to generate the j-th Ghost feature maps yij. In other words, there can be one or more Ghost feature maps {yij}j=1s. The last Φi,s denotes the identity maps used to hold the intrinsic feature maps, as shown in Fig. 2. From Eq. (3), we can obtain n=m×s feature maps Y=[y11,y12,…,yms] as the output of the Ghost module; this is also shown in Fig. 2. Note that the cost of performing linear operation Φ on every channel is significantly lower than that of the ordinary convolution.

3.2 Network Architecture

For the entire generator network, we used the same architecture as GANILLA to merge low-level features with high-level features while transforming styles. The model consists of two stages: down-sampling and up-sampling, and the down-sampling stage used a modified {ResNet-18} network. However, the parameters and calculations of the ResNet-18 network are extensive. To address this problem, some approaches have been proposed to compress the deep neural network (DNN), e.g., network pruning [21,22], low-bit quantization [23,24], and knowledge distillation [25,26]. Redesigning an efficient network architecture is also an effective solution. Recently, there has been some considerable success on redesigning networks with MobileNet [27,28], ShuffleNet [29], and GhostNet. Inspired by GhostNet, our networks apply the Ghost module to style transfer, thereby redesigning the convolution module of ResNet-18. In this way, a lightweight network architecture is built.

As shown in Fig. 3, the down-sampling stage starts with a Ghost module layer, followed by an instance norm (IN) [30], rectified linear unit (ReLU), and max-pooling layers. Each of these four layers contains two residual blocks (RBs). In Layer-I, each RB initiates with one Ghost module layer, followed by the IN and ReLU. Next are a Ghost module and an instance normalization layer. In Layers-II–IV, a SELayer is added after each RB. Finally, these concatenated feature maps are fed to the last convolution and ReLU.

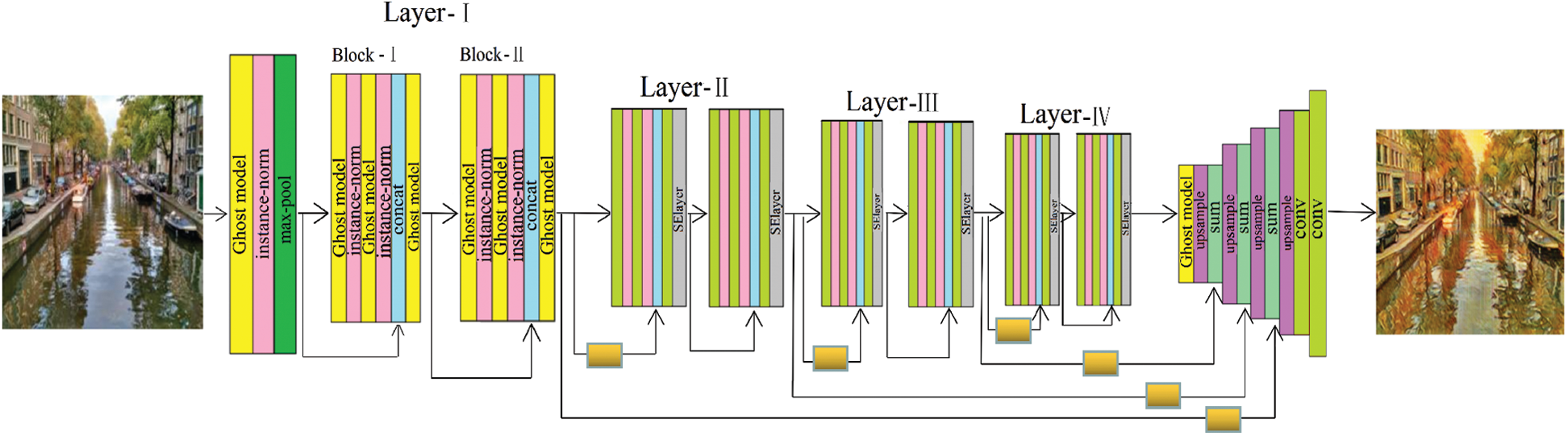
Figure 3: The generator architecture network of our proposed method

Our proposed method first performs down-sampling to extract the structural features, and then up-sampling to generate the image. Among them, the down-sampling is based on the modified Resnet-18 network, and the up-sampling combines low-and high-level features through the skip connections. In each layer of down-sampling, it is necessary to connect the features of the previous layers to integrate low-level features. The bottom layer can ensure that the output image contains the input’s content, i.e., morphological features, edges, shapes, and other information. In the up-sampling stage, the outputs of each layer in the down-sampling are used to feed the lower-level features to the summation layers. Different from down-sampling, up-sampling is conducted on the output of Layer-IV by long and skip connections to add lower-level features from the down-sampling; these connections contribute to the content of the generated image. Finally, the output of the network is a stylized image with three channels. All filters in the up-sampling have a 1×1 kernel. Eventually, the 3-channel translated image is output by a convolution layer with 7×7 kernels. Our method uses a 70×70 PatchGAN [15] as the discriminator, which is comprised of three blocks. For the first block, the kernel size is set as 64. For each consecutive block, the kernel size is set as 128.

3.3 Attention Mechanism

We introduced squeeze-and-excitation networks (SENet) [31] to each residual block of the second, third, and fourth layers in down-sampling. We improved network performance by explicitly modeling the interdependence between the feature channels. However, explicit modeling does not result in a novel spatial dimension for the fusion of the feature channels. Hence, we utilized a new feature recalibration strategy. Through this learning strategy, we can obtain each feature channel automatically and thus promote useful features and suppress useless features.

Fig. 4 is a schematic diagram of the SE module. Given an input X∈RC′×H′×W′, C′ is the number of feature channels. After general transformations such as convolution (Ftr), the feature maps U∈RC×H×W are obtained. The SE module is different from that in the traditional CNN in that we recalibrate the previously obtained features through three operations. The first operation is the squeeze. We apply feature compression along the spatial dimensions, and then transform every two-dimensional feature channel (H×W) into a real number. This real number provides a global receptive field to a certain extent, and its output dimension matches the number of input feature channels. It describes the global distribution of the feature channel, which is very useful in style transfer. The second operation is excitation, which is similar to the self-gating operation of the recurrent neural network (RNN) [32]. The parameter w is applied to each feature channel to generate weights, and is learned to explicitly model the correlation between the feature channels. Finally, there is a reweighting procedure. We regarded the weight of the output of excitation as the importance of every feature channel. The normalized weights for each channel feature are weighted simultaneously by multiplying the weight coefficients channel by channel to introduce the attention mechanism.

3.4 Loss Function

We next optimized the generator and discriminator of our proposed method. Our loss function is similar to that of GANILLA, and consists of two components: adversarial loss and cycle consistency loss. These losses are first applied in CycleGAN to achieve the transformation between domain X and domain Y, as shown in Fig. 5.

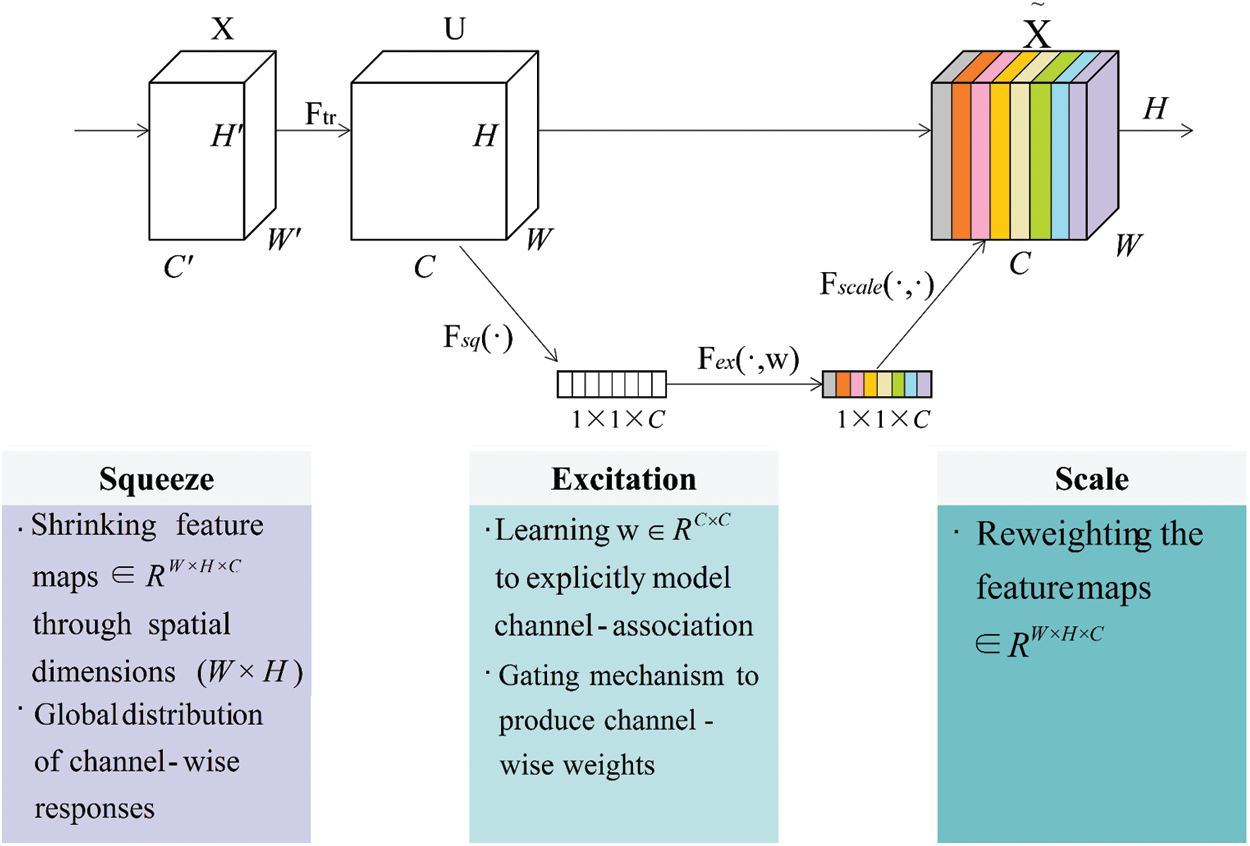
Figure 4: Squeeze and excitation block

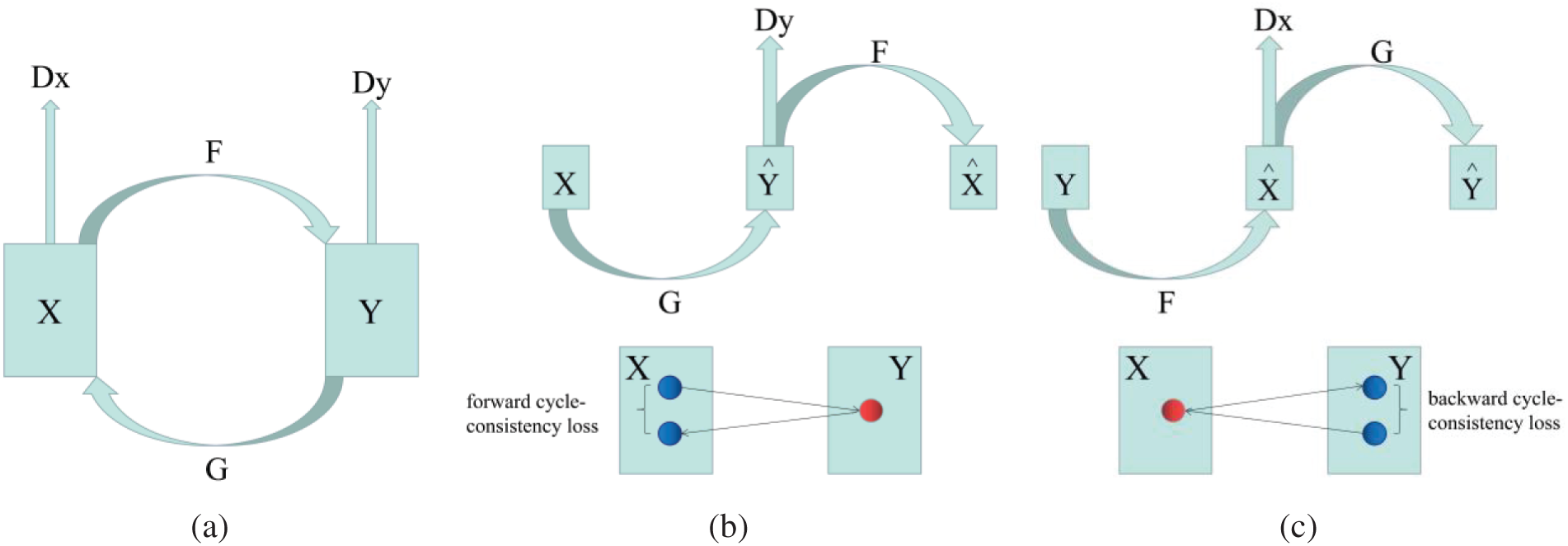
Figure 5: Structure diagram for CycleGAN

1) CycleGAN contains two mapping functions G:X→Y, F:Y→X, and the corresponding discriminator (DY and DX). DY excites G to convert X to the target domain Y. Similarly, DX stimulates F to transform Y into the X domain. CycleGAN introduces cycle consistency loss to normalize the mapping. Therefore, after the images X and Y are converted from the source domain to the target domain, they can be returned from the target domain to the source domain.

2) Forward cycle consistency loss: X→G(X)→F(G(X))≈X

3) Backward cycle consistency loss: Y→F(Y)→G(F(X))≈Y

In CycleGAN, the adversarial loss is used to match the data distribution of the generated image and the object images. The cycle consistency loss is used to prevent conflict of learning mappings G and F. In our experiments, we not only used the above-described adversarial loss and cycle consistency loss, but also the identity loss and L1 distance function. We aim to minimize the sum of these four loss functions.

4  Experiment

4.1 Complexity Analysis

To decrease the computation costs, we used the Ghost module to replace the ordinary convolutional layer and thus obtain the same number of feature maps. Hence, the Ghost module can be combined into current network architectures. This cuts back on memory usage and speeds up operation, i.e., there is one identity mapping and m×(s−1)=ns×(s−1) linear operations. The average kernel size of each linear operation is equivalent to d×d. We use linear operations of the same size (e.g., 3×3 or 5×5) to ensure the efficient implementation in a single Ghost module. The speed-up ratio of the upgrading ordinary convolution by the Ghost module is as shown below:

rs=n×h′×w′×c×k×kns×h′×w′×c×k×k+(s−1)×ns×h′×w′×d×d=c×k×k1s×c×k×k+(s−1)s×d×d≈s×cs+c−1≈s (4)

where d×d has a similar magnitude as k×k, and s≤c. Similarly, the compression ratio can be expressed as

rc=n×c×k×kns×c×k×k+(s−1)×ns×d×d≈s×cs+c−1≈s, (5)

which is equal to that of the speed-up ratio by utilizing the Ghost module.

Table 1: Experimental environment configuration

4.2 Implementation Details

We used the content data set and oil painting data set from the CycleGAN training dataset. The oil painting data set had more than 8000 images and included four artist styles: Monet, Ukiyoe, Van Gogh, and Cezanne. The cartoon data set was also from CartoonGAN. We collected stick figure images from the internet and books. In our experiment, we used CartoonGAN, CycleGAN, and GANILLA as comparison methods. We compared different styles of images generated by these three generator models with those generated by our proposed method. The size of all images for training (i.e., natural images and style images) was set to 256 × 256 pixels. We trained our models for 200 epochs and employ the Adam optimizer [33]. The learning rate was set to be 0.0002 for the whole training process. PyTorch [34] was employed to implement our proposed method. The experimental environment configuration is shown in Tab. 1.

Table 2: Comparison in terms of the number of parameters and FLOPs

5  Experimental Results

5.1 Style Transfer Results

To prove the effectiveness of our proposed method, we compared the number of parameters and the total FLOPs of the generator and discriminator for different generative models. We compared CartoonGAN, CycleGAN, and GANILLA with our proposed method. As shown in Tab. 2, our proposed method has the lowest values in both evaluation indexes. This phenomenon shows that our proposed generative model can efficiently save computational costs. This benefit is due to the use of the Ghost module as a conversion network to generate more feature maps. Furthermore, since we utilized the attention mechanism to allow the network to learn more useful features, the network is efficient and lightweight.

Fig. 6 shows the oil painting style results generated by CycleGAN, GANILLA, and our proposed method. Fig. 7 shows the generated images of cartoon style for the three methods. We found that most of the results generated by our proposed method captured content and style successfully.

Figure 6: Oil painting style results generated by CycleGAN, GANILLA, and our proposed method

Figure 7: Cartoon style results generated by CartoonGAN, GANILLA, and our proposed method

We selected the Cezanne style for testing, and trained for 200 epochs. Fig. 8 shows the image generated by the proposed model in different training periods. From left to right are the original images, and then the generated image at 5, 50, 100, 150 and 200 epochs. These experimental results indicate that this range can achieve the best results between 50 and 100 epochs. This range not only retains the content information but also transfers the style.

Figure 8: Cezanne style results by our proposed method in different training periods

Based on the above styles transfer results, we carried out a series of experiments on three additional styles: animation, stick figure, and season. We compare our proposed method with GANILLA in terms of generated images in Fig. 9.

5.2 Evaluation

We adopted two evaluation indicators in the assessment of style transfer. One is the subjective evaluation, which determines whether the image is generated well or not by personal cognition and aesthetics. The other is an objective evaluation, but since there is no clear objective evaluation standard for style transfer, most researchers compare their generated results with other experimental results as an evaluation method; we also adopt this approach.

5.2.1 Subjective Evaluation

The main factors affecting subjective evaluation are personal aesthetics and preferences. To this end, we designed a questionnaire. The questionnaire was sent to 200 participants, all of whom were computer graduate students with a foundation in drawing processing. The questionnaire focused on the point of view of aesthetics and the similarity between the generated image and the original image. We listed the different images generated by CycleGAN, GANILLA, CartoonGAN, and our proposed method, and then let the participants choose which one they thought was the best. Tabs. 3–5 show that our model was evaluated as producing the best images. However, for cartoon style transfer, our model is not as good as CartoonGAN in visual aesthetics.

Figure 9: Different style results: (a) animation, (b) autumn, (c) winter, and (d) stick figure

5.2.2 Objective Evaluation

So far, there is no clear objective evaluation standard for style transfer because it is difficult to obtain quantitative data as an evaluation indicator of image style transfer. To evaluate the generated image more objectively, we apply the peak signal-to-noise ratio (PSNR) value to compare the generated image to the original image. The PSNR value is a common index for evaluating images and can measure the similarity between original images and generated images. Usually, we need to use the mean square error (MSE) to calculate the PSNR. The MSE can be expressed as follows:

MSE(X,Y)=1mn∑i=0m−1∑j=0n−1[Y(i,j)−X(i,j)]2, (6)

where Y and X denote the generated and the original images with the size m×n, respectively. X(i,j) and Y(i,j) are the pixel values of X and Y, respectively. The calculation of PSNR is given as

PSNR(X,Y)=10log10(MAXY2MSE(X,Y))=20log10(MAXYMSE(X,Y)), (7)

where MAXI represents the maximum pixel value of the images that need to be calculated; smaller MSE values (i.e., bigger PSNR values) indicate better image quality.

We use the structural similarity (SSIM) [35] as another evaluation index to measure the similarity of two digital images. Compared with PSNR, SSIM can be more in line with human judgments of image quality. SSIM is expressed as follows:

SSIM(X,Y)=(2μXμY+c1)(2σXY+c2)(μX2+μY2+c1)(σX2+σY2+c2), (8)

where μX and μY are the mean values of X and Y, respectively. σX2 and σY2 are the variance values of X and Y, respectively. σXY denotes the covariance between X and Y. c1 and c2 are two small constants to ensure stability when the denominator becomes zero.

Table 3: Questionnaire results on oil painting style transfer

Table 4: Questionnaire results on cartoon style transfer

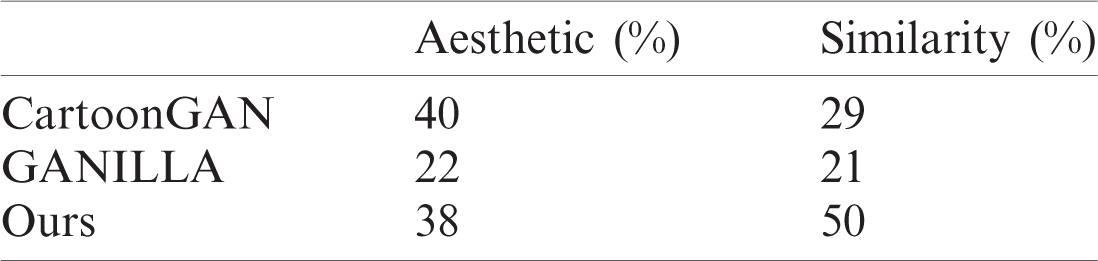
Table 5: Participants’ voting results for seasonal style transfer and stick figure style transfer

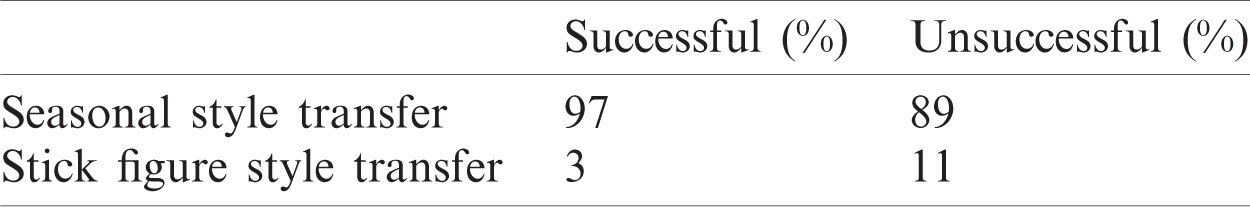
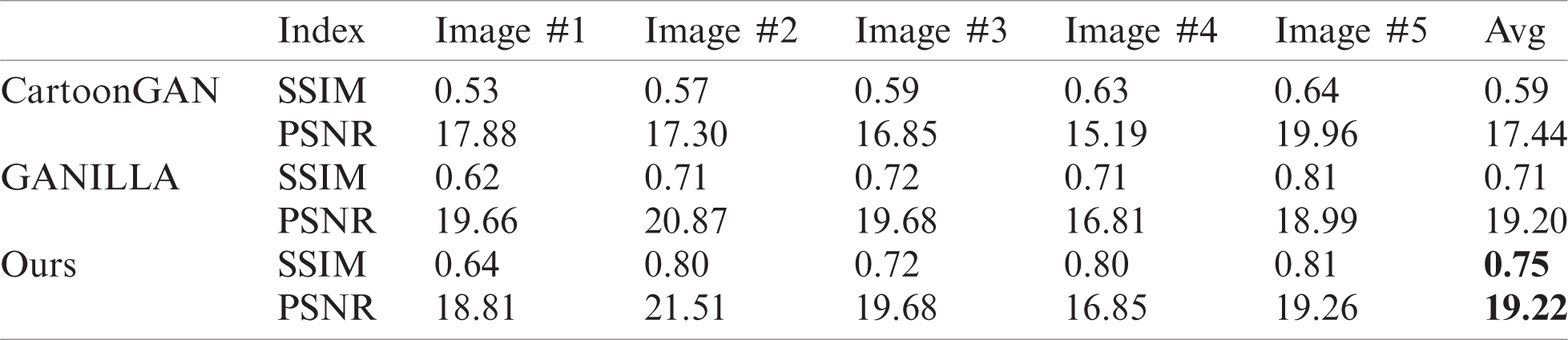
From Tabs. 6 and 7, we can see that our proposed method has the largest SSIM and PSNR values. Hence, our proposed method is better than the other methods. These results clearly illustrate that the images generated by our proposed method have lower distortion and better image quality.

Table 6: Quantitative results for oil painting style transfer

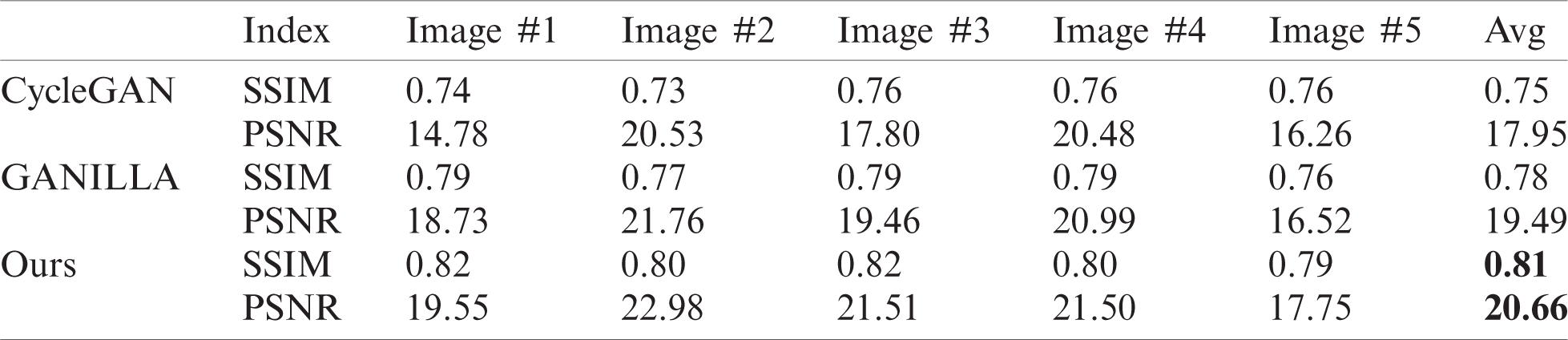
Table 7: Quantitative results for cartoon style transfer

6  Conclusion

In this paper, we proposed a lightweight style transfer network based on the Ghost module, which can reduce the number of parameters and FLOPs while ensuring the quality of generated images. We also introduced an attention mechanism into our proposed model to focus on more important content during the transfer process. The experimental results show that our proposed method has a comparable performance to other methods. Moreover, in terms of both efficiency and accuracy, our proposed method outperforms state-of-the-art lightweight neural architectures. Therefore, employing our architecture would significantly improve method performance in practical applications. In the future, we believe that designing a universal and efficient generator architecture for in image processing is worthy of study.

Funding Statement: This work was funded by the China Postdoctoral Science Foundation (No. 2019M661319), Heilongjiang Postdoctoral Scientific Research Developmental Foundation (No. LBH-Q17042), Fundamental Research Funds for the Central Universities (3072020CFQ0602, 3072020CF0604, 3072020CFP0601), and 2019 Industrial Internet Innovation and Development Engineering (KY1060020002, KY10600200008).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Hu and J. Wang, “Deep learning for distinguishing computer generated images and natural images: A survey,” Journal of Information Hiding and Privacy Protection, vol. 2, no. 2, pp. 37–47, 2020. [Google Scholar]

 2.  C. Song, X. Cheng, Y. X. Gu, B. J. Chen and Z. J. Fu, “A review of object detectors in deep learning,” Journal on Artificial Intelligence, vol. 2, no. 2, pp. 59–77, 2020. [Google Scholar]

 3.  F. Bi, X. Ma, W. Chen, W. Fang, H. Chen et al., “Review on video object tracking based on deep learning,” Journal of New Media, vol. 1, no. 2, pp. 63–74, 2019. [Google Scholar]

 4.  H. Wu, Q. Liu and X. Liu, “A review on deep learning approaches to image classification and object segmentation,” Computers, Materials & Continua, vol. 60, no. 2, pp. 575–597, 2019. [Google Scholar]

 5.  M. Wang, S. Niu and Z. Gao, “A novel scene text recognition method based on deep learning,” Computers, Materials & Continua, vol. 60, no. 2, pp. 781–794, 2019. [Google Scholar]

 6.  J. Zhu, T. Park, P. Isola and A. A. Efros, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, pp. 2242–2251, 2017. [Google Scholar]

 7.  Z. Yi, H. Zhang, P. Tan and M. Gong, “DualGAN: Unsupervised dual learning for image-to-image translation,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, pp. 2868–2876, 2017. [Google Scholar]

 8.  Y. Chen, Y. Lai and Y. Liu, “CartoonGAN: Generative adversarial networks for photo cartoonization,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, pp. 9465–9474, 2018. [Google Scholar]

 9.  S. Hicsonmez, N. Samet, E. Akbas and P. Duygulu, “GANILLA: Generative adversarial networks for image to illustration translation,” Image and Vision Computing, vol. 95, pp. 103886, 2020. [Google Scholar]

10. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, United states, pp. 770–778, 2016. [Google Scholar]

11. K. Han, Y. Wang, Q. Tian, J. Guo, C. Xu et al., “GhostNet: More features from cheap operations,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 1577–1586, 2020. [Google Scholar]

12. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley et al., “Generative adversarial nets,” in Proc. Advances in Neural Information Processing Systems, Cambridge, MA, USA, vol. 77, pp. 2672–2680, 2014. [Google Scholar]

13. Z. Wang, Q. She and T. E. Ward, “Generative adversarial networks in computer vision: A survey and taxonomy,” ArXiv, vol. abs/10.1145/3439723, pp. 1–41, 2021. [Google Scholar]

14. A. Alotaibi, “Deep generative adversarial networks for image-to-image translation: A review,” Symmetry, vol. 12, no. 10, pp. 1705, 2020. [Google Scholar]

15. P. Isola, J. Zhu, T. Zhou and A. A. Efros, “Image-to-image translation with conditional adversarial networks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, pp. 5967–5976, 2017. [Google Scholar]

16. T. Wang, M. Liu, J. Zhu, A. Tao, J. Kautz et al., “High-resolution image synthesis and semantic manipulation with conditional GANs,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, pp. 8798–8807, 2018. [Google Scholar]

17. Y. Li, S. Tang, R. Zhang, Y. Zhang, J. Li et al., “Asymmetric GAN for unpaired image-to-image translation,” IEEE Transactions on Image Processing, vol. 28, no. 12, pp. 5881–5896, 2019. [Google Scholar]

18. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. on Learning Representations, San Diego, CA, US, 2014. [Google Scholar]

19. L. Chen, L. Wu, Z. Hu and M. Wang, “Quality-aware unpaired image-to-image translation,” IEEE Transactions on Multimedia, vol. 21, no. 10, pp. 2664–2674, 2019. [Google Scholar]

20. H. Emami, M. M. Aliabadi, M. Dong and R. B. Chinnam, “SPA-GAN: Spatial attention GAN for image-to-image translation,” IEEE Transactions on Multimedia, vol. 23, pp. 391–401, 2021. [Google Scholar]

21. S. Han, H. Mao and W. J. Dally, “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding,” in Proc. Int. Conf. on Learning Representations, San Juan, Puerto rico, 2016. [Google Scholar]

22. J. Luo, J. Wu and W. Lin, “ThiNet: A filter level pruning method for deep neural network compression,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, pp. 5068–5076, 2017. [Google Scholar]

23. M. Rastegari, V. Ordonez, J. Redmon and A. Farhadi, “XNOR-Net: ImageNet classification using binary convolutional neural networks,” in Proc. European Conf. on Computer Vision, Scottsdale, AZ, United states, pp. 525–542, 2016. [Google Scholar]

24. B. Jacob, S. Kligys, B. Chen, M. Zhu, M. Tang et al., “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, pp. 2704–2713, 2018. [Google Scholar]

25. G. Hinton, O. Vinyals and J. Dean, “Distilling the knowledge in a neural network,” ArXiv, vol. abs/1503.02531, pp. 1–9, 2015. [Google Scholar]

26. S. You, C. Xu, C. Xu and D. Tao, “Learning from multiple teacher networks,” in Proc. ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Halifax, NS, Canada, pp. 1285–1294, 2017. [Google Scholar]

27. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang et al., “MobileNets: Efficient convolutional neural networks for mobile vision applications,” ArXiv, vol. abs/1704.04861, pp. 1–9, 2017. [Google Scholar]

28. M. Sandler, A. Howard, M. Zhu, A. Zhmoginov and L. Chen, “MobileNetV2: Inverted residuals and linear bottlenecks,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, pp. 4510–4520, 2018. [Google Scholar]

29. X. Zhang, X. Zhou, M. Lin and J. Sun, “ShuffleNet: An extremely efficient convolutional neural network for mobile devices,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, pp. 6848–6856, 2018. [Google Scholar]

30. D. Ulyanov, A. Vedaldi and V. Lempitsky, “Instance normalization: The missing ingredient for fast stylization,” ArXiv, vol. abs/1607.08022, pp. 1–6, 2016. [Google Scholar]

31. J. Hu, L. Shen, S. Albanie, G. Sun and E. Wu, “Squeeze-and-excitation networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 8, pp. 2011–2023, 2020. [Google Scholar]

32. V. Mnih, N. Heess and A. Graves, “Recurrent models of visual attention,” in Proc. Advances in Neural Information Processing Systems, Cambridge, MA, USA, vol. 27, pp. 2204–2212, 2014. [Google Scholar]

33. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” ArXiv, vol. abs/1412.6980, pp. 1–15, 2014. [Google Scholar]

34. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury et al., “Pytorch: An imperative style, high-performance deep learning library,” in Proc. Advances in Neural Information Processing Systems, Vancouver, BC, Canada, pp. 8026–8037, 2019. [Google Scholar]

35. W. Zhou, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.