DOI:10.32604/cmc.2021.016682

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016682 |  |
| Article |
Distributed Trusted Computing for Blockchain-Based Crowdsourcing
Department of Electrical and Computer Engineering, Inha University, Incheon, 22212, Korea
*Corresponding Author: Byeong-Seok Shin. Email: bsshin@inha.ac.kr
Received: 08 January 2021; Accepted: 01 March 2021
Abstract: A centralized trusted execution environment (TEE) has been extensively studied to provide secure and trusted computing. However, a TEE might become a throughput bottleneck if it is used to evaluate data quality when collecting large-scale data in a crowdsourcing system. It may also have security problems compromised by attackers. Here, we propose a scheme, named dTEE, for building a platform for providing distributed trusted computing by leveraging TEEs. The platform is used as an infrastructure of trusted computations for blockchain-based crowdsourcing systems, especially to securely evaluate data quality and manage remuneration: these operations are handled by a TEE group. First, dTEE uses a public blockchain with smart contracts to manage TEEs without reliance on any trusted third parties. Second, to update TEE registration information and rule out zombie TEEs, dTEE uses a reporting mechanism. To attract TEE owners to join in and provide service of trusted computations, it uses a fair monetary incentive mechanism. Third, to account for malicious attackers, we design a model with Byzantine fault tolerance, not limited to a crash-failure model. Finally, we conduct an extensive evaluation of our design on a local cluster. The results show that dTEE finishes evaluating 10,000 images within one minute and achieves about 65 tps throughput when evaluating Sudoku solution data with collective signatures both in a group of 120 TEEs.
Keywords: Crowdsourcing; blockchain; distributed trusted execution environment; Byzantine fault tolerance
A trusted execution environment (TEE) [1] has been used in many applications [2–4] to provide secure and trusted computing. It is widely used to be a secure component to address the performance issues of blockchain-based systems [4–8], in which a common architecture adopted by the systems is to decouple the TEE from the blockchain to provide off-chain trusted computing. Its design extends trust from the blockchain to the TEE to improve system performance. The same concept using the off-chain TEE can be applied to a blockchain-based crowdsourcing system [9,10], especially to evaluate data quality and manage remuneration securely.
However, if one or several TEEs under a centralized architecture are used to evaluate data quality when collecting large-scale data in a crowdsourcing system, the centralized TEE system might become a throughput bottleneck. It can also suffer single-point failures, causing service availability problems and even the loss of workers’ data and remuneration. A centralized TEE also has security problems if attackers attack the TEE specifically. Its security may be compromised because of implementation vulnerabilities and congenital defects, such as side-channel attacks [5] and rollback attacks [11]. Therefore, applying a centralized TEE to a blockchain-based system is a tradeoff between system security and efficiency.
To address those problems, we propose a blockchain-based distributed trusted computing scheme via TEEs for crowdsourcing applications, named dTEE, aiming at being used to collect large-scale data with security and high availability. dTEE is designed according to its special responsibilities in crowdsourcing, especially to evaluate the quality of sourcing data and to manage remuneration. It has the following properties:
1. Scalability. The data evaluation and remuneration management of a crowdsourcing task are handled by a specified TEE group. The more TEEs join in, the more groups exist to provide services of trusted computations. It uses a group of TEEs rather than a single one to handle a task, thereby guaranteeing availability. More importantly, it significantly reduces management overhead by keeping TEE registration information transparent and consistent by storing it in the blockchain, which gives all TEEs the same view. This means the same grouping result can be calculated locally without the need for communication across groups nor reliance on a centralized management service.
2. Self-government. dTEE is blockchain-based without reliance on any trusted third parties. To update the TEE registration information and rule out zombie TEEs, it uses smart contracts [12] with a reporting mechanism. To attract TEE owners to offer their computing services, dTEE uses a fair monetary incentive mechanism.
3. Byzantine fault tolerance. A crowdsourcing task is handled by a group. It uses m-of-n signatures [13,14] to manage the remuneration, which means the remuneration is available even when some TEEs within the group are not functioning. The remuneration is also safe when some TEEs are compromised by attackers. To ensure that the results are honestly generated based on the actual quality of the sourcing data, dTEE evaluates the data repeatedly using k different TEEs within the group (called k-repeated evaluation), accepting only the result produced by the majority of the k number of TEEs.
dTEE is suitable for blockchain-based crowdsourcing applications that need to collect large-scale data with a security guarantee. On the one hand, keeping unauthorized people from getting access to the sourcing data is highly desirable because the data may contain sensitive information about workers, and the data is an asset to the requester; On the other hand, the requester requires integrity guarantee of the program that evaluates data quality in remote servers. By using a group of TEEs for a crowdsourcing task, the TEEs work parallelly to collect and evaluate large-scale data submitted by workers. This also overcomes problems of single-point failures and improves system availability. In summary, dTEE can be used in crowdsourcing systems to collect large-scale data with security and high availability.
This paper makes the following contributions:
1. We propose a novel scheme for building a platform for distributed trusted computing via TEEs. The platform aims at being infrastructure of trusted computing for blockchain-based crowdsourcing systems to collect large-scale data with high availability.
2. dTEE’s design has three novel characteristics: (1) Self-government without relying on trusted third parties through a reporting mechanism for self-updates, as well as a fair monetary incentive mechanism to attract TEEs to join. (2) Security with Byzantine fault tolerance, not limited to crash fault tolerance. (3) Scalability and availability.
The remainder of this paper is structured as follows. In Section 2, we present related work. In Section 3, we provide the system overview, including workflow and architecture. In Section 4, we present our proposal in detail. In Section 5, we describe the implementation and experiments. Finally, Section 6 concludes the paper.
Blockchain-Based Crowdsourcing. A few existing works [10,14–18] have used blockchains [19] to replace the role of trusted third parties in crowdsourcing applications [20] to address issues of fairness, privacy preservation [21], and service availability. An essential operation in a crowdsourcing system is to evaluate the sourcing data uploaded by workers to confirm the data meet the requester’s requirements. The protocols of these works [10,16–18] evaluate the quality of sourcing data using smart contracts [22]. Although Zebralancer [15] uses smart contracts to verify the zero-knowledge proofs generated by requesters rather than to evaluate sourcing data, it still requires workers to submit the encrypted sourcing data to the blockchain. This causes significant overheads when propagating large-scale sourcing data over the peer-to-peer blockchain network.
TEE and Blockchains. A TEE is a tamper-resistant processing environment that runs on a separation kernel. It guarantees the authenticity of the executed code, the integrity of the runtime states (e.g., CPU registers, memory, and sensitive I/O), and the confidentiality of the code, data, and runtime states stored in persistent memory. Besides, it provides remote attestation of its trustworthiness to third parties. The content of the TEE is not static; it can be securely updated [23]. There are several existing TEE implementations, such as TrustZone [24], Sanctum [25], and Intel Software Guard Extensions (SGX) [1].
To improve the blockchain’s performance and guarantee its security, previous works [4–7] have used a TEE as an off-chain component, decoupling from the blockchain to provide efficient computation and eventually persisting the state data in the blockchain. Matetic et al. [5] presented an approach that protects the privacy of light clients in Bitcoin by leveraging TEEs. Fastkitten [4] leverages the power of TEEs to efficiently execute arbitrarily complex smart contracts at a low cost over distributed cryptocurrencies (e.g., Bitcoin) designed to support only simple transactions. Yan et al. [3] use TEEs to execute smart contracts for consortium blockchains to address confidentiality and efficiency problems, while Ekiden [8] combines blockchains with TEEs and separates consensus from execution by executing smart contracts inside TEE enclaves, which addresses the problems of lack of confidentiality and poor performance of smart contracts in current blockchain systems. Those systems use a common design concept that decouples the TEE from the blockchain to provide efficient off-chain computation without losing security. This paper adopts this design concept and applies it to crowdsourcing applications. However, a centralized TEE module could result in a throughput bottleneck for the system and is vulnerable to single-point failures, implementation bugs, and targeted attacks.
In this section, we first present the workflow overview of our system. Then we present the architecture, as well as the consideration of system security, availability, and efficiency. It is noteworthy that in this paper we only focus on the construction and management of distributed TEEs, which are used as an infrastructure of trusted computing for blockchain-based crowdsourcing. Therefore, our goal is to design robust distributed TEEs with properties of security and high availability. Designing a protocol of blockchain-based crowdsourcing is outside the scope of this paper.
We present the system architecture in Fig. 1a and the workflow overview in Fig. 1b, which is described as follows: (1) A TEE registers the platform via the blockchain for providing trusted computations. A smart contract is responsible for verifying the TEE’s eligibility before joining in. (2) A requester downloads all registration information of TEEs from the blockchain and calculates the target TEE group locally. Then, the requester publishes a task smart contract (TSC) on the blockchain, including a deposit and parameters for selecting the group. (3) The requester sends codetask and auxiliary data to the TEEs in the target group to set up the crowdsourcing task, where codetask is a program created by the requester and used to evaluate the quality of sourcing data. The program’s digest is stored on TSC. (4) The TEEs also download all the registration information from the blockchain and calculate the target group locally to confirm whether the TEEs themselves belong to the group. Then they confirm if the TSC and the deposit are accepted by the blockchain. If all the confirmations pass, the TEEs install codetask and initialize the program to be ready to provide trusted computation for the task. (5) During the crowdsourcing task, the group securely evaluates the quality of sourcing data and manages remuneration inside enclaves. (6) Finally, the group can publish a transaction with the remuneration records on the blockchain to get the remuneration or to transfer money.
Based on the workflow described above, dTEE is responsible for two main operations: to manage remuneration and to evaluate the quality of sourcing data. We use m-of-n signatures for remuneration management and k-repeated evaluation (see Section 4.2) to evaluate the sourcing data. We specifically cluster all TEEs based on their registration information and group the TEEs in each cluster (Fig. 1a), such that requests of m-of-n signatures and k-repeated evaluation can be processed by a specified group. Moreover, grouping the TEEs enables efficient and clear calculation of the service fee in a fine-grained way and enables system scalability.
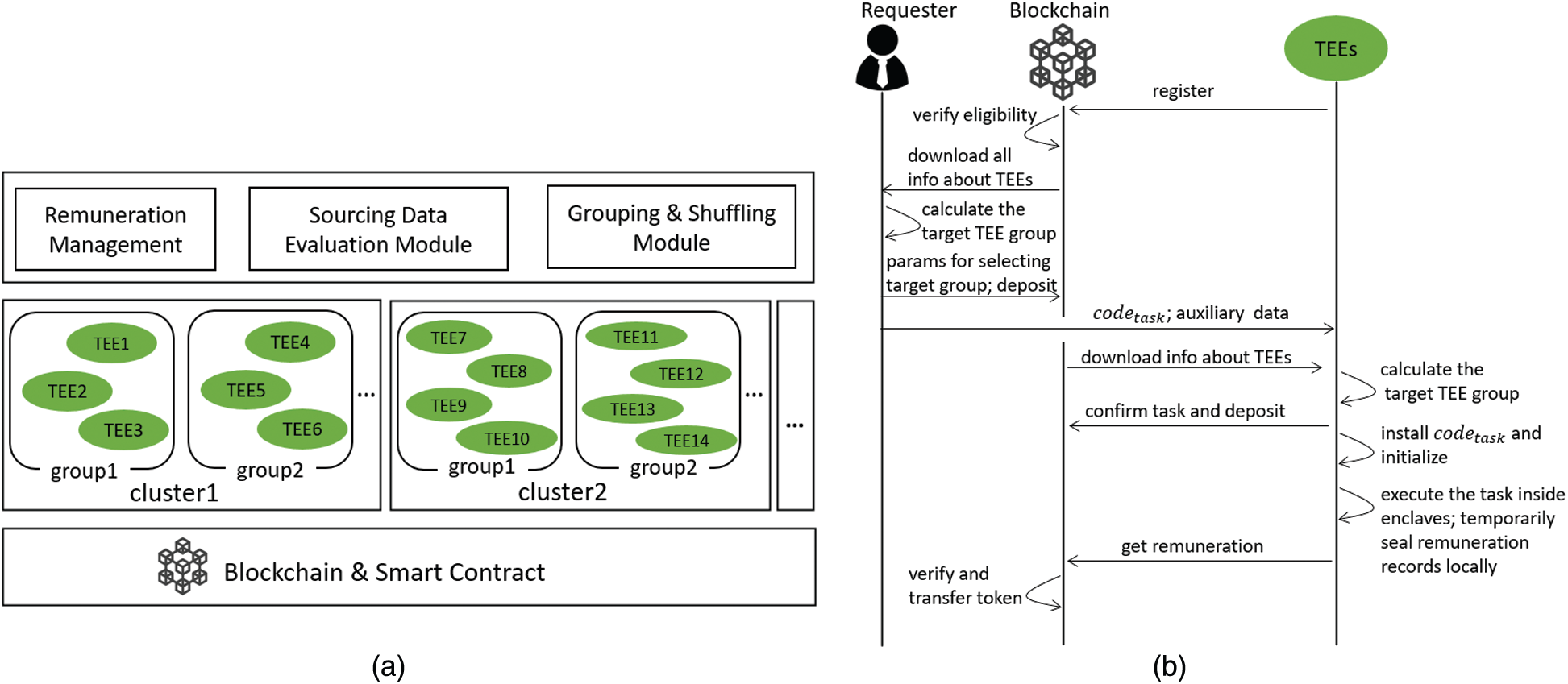
Figure 1: (a) System architecture, (b) operation sequences of our proposal
To address the possibility that attackers may adaptively compromise and corrupt the majority of TEEs within a group, making the group insecure, we shuffle and regroup all TEEs at the end of each epoch. One epoch is a system parameter that can be set as one day or one week. To avoid chaos or allowing a specified group to serve a worker across multiple epochs, the following two operations need to be finished. First, at the end of each epoch before shuffling, each TEE needs to calculate its total service remuneration and ask all its group members to sign it. The collective signature acts as proof, allowing the TEE to receive its remuneration via the blockchain. Second, after shuffling, any TEE that moves to another group should send all its state data back to the TEE taking its place. Thus, intuitively, we shuffle the TEEs rather than the state data stored in those TEEs. Thus, we can find state data in the same group index before and after shuffling.
We use a reporting mechanism to punish zombie TEEs that stop working before the promised time. We qualify some TEEs to be challengers and report zombie TEEs. A challenger publishes a challenge transaction to the blockchain, and the zombie TEE must respond to the challenge to prove it is alive. If the challenger succeeds, they can take the deposit of the zombie TEE. This process will also trigger a function of a TEE Committee smart Contract (TCC) to mark the information registered by the zombie TEE as invalid, such that in the next epoch, this zombie TEE will not belong to any group.
Grouping does not require communication among TEEs because all the registration information is transparent in the blockchain. Each TEE can locally perform group operations based on preset parameters contained in the registration information, obtaining the same result. To achieve that, all TEEs use the last block’s hash value of the previous epoch as a seed to re-group all TEEs. The seed is a random number used to generate a random permutation [26]. Parties that use the same seed and the same permutation generator will obtain the same permutation.
We assume that an attacker can gain full control of a TEE and assume the integrity and confidentiality of a TEE can be compromised, but this requires significant computational resources and time from attackers because the TEE itself is a hardware security environment. Therefore, the attacker can only compromise a very small fraction of all TEEs. Moreover, a group becomes insecure only the security of the majority of TEEs is compromised. Our system shuffles the group periodically to prevent the majority of TEEs within a group from being compromised. Furthermore, attackers can choose which TEE to corrupt (e.g., stop or restart the TEE; modify, reorder or delay network messages arbitrarily). We assume the attacker can only corrupt no more than half of TEEs in a group. Thus, by selecting a larger group, the requester has a securer guarantee but needs to spend more fees, which is a trade-off decided by the requester.
Our system is built on a blockchain. Thus, it also has the security assumptions made by the underlying blockchain system. A (possibly adversarial) host application facilitates all communications between enclaves and the blockchain. Thus, the host application might isolate the TEE and trick it into verifying a fake transaction on an easily minable forked chain. We assume the blockchain is capable of producing proof of publication to let the TEE confirm a specified transaction is accepted by the blockchain if the proof passes the verification. Practically in Ethereum for instance, the TEE can use Simple Payment Verification [27] or Flyclient [28] to verify the proof of publication produced by a set of full nodes, at least one of which is honest.
4 dTEE: Distributed Trusted Computing Scheme
In this section, we first present how a new TEE joins the platform and then explain why an m-of-n signature and k-repeated evaluation are used, as well as why we group TEEs. Next, we present how to associate a group with a crowdsourcing task and the details of group shuffling. We describe details of Byzantine fault tolerance and the calculation of TEE service remuneration. Finally, we explain the reporting mechanism.
Individuals and organizations with eligible TEE machines can join the platform by registering some information via a shared TCC. The registration information includes
4.2 M-of-n Signature & k-Repeated Evaluation & Grouping
An m-of-n signature is a collective signature that requires any m keys from a set of n keys to sign a transaction. Workers store their remuneration within a group temporarily and use an m-of-n signature to spend the remuneration. Using 1-of-1 signatures is insecure because some TEEs could be compromised by attackers and behave maliciously. Also, if a TEE stops working, the workers cannot spend the remuneration and may even lose them forever. In contrast, when an m-of-n signature is used, workers can still spend their remuneration even if (n–m) TEEs stop working, while even if (m −1) TEEs are compromised, attackers still cannot steal the money.
A requester may require workers to repeat the evaluation of data quality in k number of TEEs because some TEEs could be compromised. The k-repeated evaluation results are compared, and the requester accepts only the majority one as the final result. This gives the requester more confidence that the sourcing data has been evaluated by honest TEEs. The value k is specified by the requester when she publishes a TSC in the blockchain. A greater k provides greater confidence for the requester, but greater expenses for the services of trusted computing.
We divide the TEEs into various sizes of groups to handle the m-of-n signatures and k-repeated evaluations specifically for the following two reasons: (1) By grouping the TEEs, we achieve fine-grained management of the m-of-n signature and k-repeated evaluation processes. Grouping makes the platform scalable and the management of many TEEs more efficient. (2) A worker needs to pay only the TEEs in the group that provides a service rather than TEEs in other groups. Thus, grouping makes calculating the TEE service fees clearer and more efficient.
All TEEs in a group store the same state data and are responsible for providing collective signatures. The group size is equal to n of the m-of-n signature. A requester can specify a specified group size corresponding to the number n of the m-of-n signature, while workers can select m to spend their remuneration while registering the task.
dTEE uses an efficient function groupingAll to group all TEEs presented in Algorithm 2. This process does not require communication among TEEs, and each TEE calculates the same grouping result. Specifically, each TEE gets all valid registration information from the TCC, i.e.,
4.3 Associate a Group with a Task
A requester publishes a TSC and specifies some parameters to select a group, such as Z, the maximum TEE service price the requester can afford, and the parameter k. Each TEE locally calculates all candidate groups that meet the requester’s requirements, sorts the candidate groups and stores them in an array, and finally calculates the index of the target group within the array by
Using
Some TEEs in a group might be compromised by attackers. The group becomes insecure if the majority of its TEEs are compromised or corrupted. To address this problem, we shuffle the groups within a cluster to distribute the compromised TEEs evenly across the groups [2].
We present the details of how groups within a cluster are shuffled in Algorithm 1, as well as how all groups are shuffled in Algorithm 2. All TEEs within a cluster (and group), as mentioned, have the same RSE,
The


The process of group shuffling creates a new issue, which is that some TEEs and their state data are in different groups after shuffling, making it chaotic for workers to track the TEEs that have provided the services in previous epochs. This also creates difficulties in calculating service fees for those TEEs. Our approach intends to keep state data always with the same group index, even when the TEEs that store this state data move to other groups. Thus, a TEE na that changes to another group must send the state data back to the TEE nb that is currently in the old position of na. For example, as shown in Fig. 2a, TEE2 is in the old position of TEE6, so TEE6 must send its state data to TEE2. A TEE that changes position within the same group does not need to synchronize state data with others. Moreover, some TEEs might stop working or crash, causing the failure of the state data synchronization in two cases: (1) if the receiver crashes, the sender simply ignores the synchronization; (2) if the sender crashes, the receiver contacts a previous group member of the sender to get the state data. For example, as shown in Fig. 2a, TEE2 cannot receive state data from TEE6 because TEE6 has crashed already. TEE2 can ask TEE4, which was in the same group as TEE6 in epoch 1, to synchronize the state data. After shuffling and state synchronization, the TEEs can delete state data that belongs to other groups.
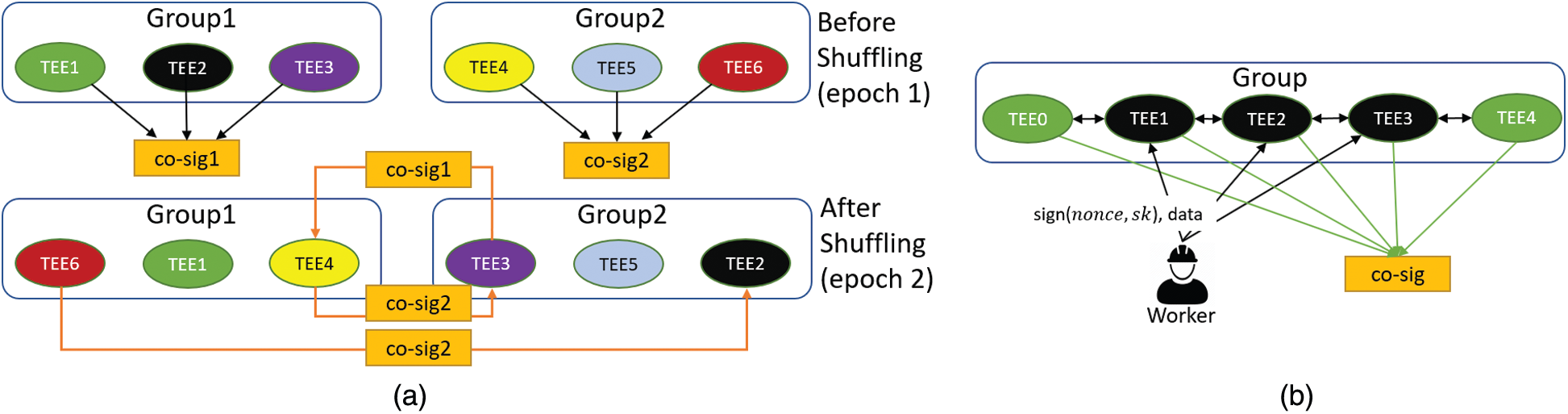
Figure 2: (a) Collective signatures are needed within a group before shuffling occurs. After shuffling, TEEs that move to another group, send the state data to the TEE in its previous position. (b) A worker submits the same sourcing data to three TEEs for instance. Those TEEs evaluate the data quality and ask the other four TEEs to sign the evaluation results
A TEE might be compromised by attackers. It might maliciously send tampered state data to other TEEs during state synchronization. Thus, a way for the receiver to verify whether state data has been tampered with is required. To address this issue, our approach intends for the receiver never to trust an individual but to trust that the majority of TEEs in a group are honest. A TEE needs to generate proof of honesty by obtaining a collective signature from its group. Specifically, the sender asks all its group members to collectively sign the state data using their msk and get a collective signature (co-sign), then send this co-sign to the receiver. The receiver verifies the co-sign using those signers’ mpk. The sender’s group members will refuse to sign the state data if the data is different from that stored in their local enclaves. For example, as shown in Fig. 2a, co-sig2 is the collective signature on the state data of epoch 1 signed by the TEEs in Group2. TEE4 and TEE6 send co-sig2 to TEE3 and TEE2, respectively. It is noteworthy that the TEEs need not communicate with others while verifying the co-sign, because all TEEs have the same view of the registration information.
In a group, only the k number of TEEs that evaluate sourcing data can gain the service fee. It is necessary to let all TEEs within the group know which k TEEs are selected. Otherwise, if a TEE, which is not within the k-selected TEEs, is compromised by attackers, it could use results from those k-selected TEEs and maliciously broadcast it to other group members to earn the service fee deceitfully. A strawman solution is to always select the k first TEEs within the group. This solution is simple but creates a load imbalance problem. Our solution is that, before submitting sourcing data, the worker signs a nonce using their secret key sk and calculates the first TEE index by
Security analysis. First, A compromised TEE that is not the k-selected TEE cannot trick the group to obtain the service fee for data evaluation. This is because all TEEs in the group can verify the worker’s signature. Second, if the compromised TEE is the k-selected TEE, it cannot gain the service fee by generating an arbitrary evaluation result because the group accepts only the result in the majority. The worker might sign a specific nonce on purpose. But the worker cannot gain any extra benefits. Moreover, if nonce is selected randomly, each TEE within the group has the same probability of evaluating the sourcing data, so the group is load-balanced. In summary, the operation of k-repeated evaluation is secure if the majority of k number of TEEs in the group are honest.
4.6 Calculate TEE Service Remuneration
dTEE uses a monetary incentive to attract TEE owners to join and provide computation services. The more service that a TEE provides, the greater remuneration the TEE can gain. At the end of each epoch before the group shuffle, each TEE needs to calculate and update its total service remuneration.
A TEE can get remuneration by providing two kinds of services. The first is to manage remuneration by participating in producing a collective signature to transfer the remuneration via the blockchain based on state data stored in the enclaves; the second is to evaluate the data quality. A worker submits the data to k TEEs within a group (Fig. 2b) for k-repeated evaluation, and each TEE sends the evaluation result to other members. The group members store the state data (amnt, epoch, receiver) in enclaves, where amnt is the remuneration that the TEE gains for this quality evaluation service and receiver is the TEE whose evaluation result is in the majority. Based on the state data, the group can transfer a specified amount of coins to the receiver via the blockchain. All TEEs within a group store the same state data.
To calculate the value of amnt, we assume there is a function (
A TEE also needs to store its total service remuneration proof (TSRP) in the form of a collective signature to prove its total remuneration. Different TEEs might gain various service remunerations depending on their service time,

At the end of each epoch, TEEs need to liquidate and update their TSRP to the current epoch. We present the details in Algorithm 3, which is executed in a TEE e that needs to update its TSRP. Specifically,
4.7 Exit TEE Committee and Reporting Mechanism
Much management cost and many difficulties will be introduced if TEEs can arbitrarily stop working or exit, which also leads to zombie TEEs and ruins the availability guarantee. Thus, a TEE can exit or stop working only after the amount of time the TEE has promised (i.e., until
dTEE encourages users to report and challenge potential zombie TEE nz but needs to prevent excessive reporting. Therefore, dTEE allows only the TEE whose group size is greater than a threshold
Our system uses a group of TEEs to handle a crowdsourcing task. The group size is specified by the crowdsourcing requester, wherein the trade-off between security and cost is decided by the requester. The group specifically is used to evaluate data quality and manage remuneration. It uses the way of k-repeated evaluation for data evaluation while using m-of-n signatures for the remuneration management. Both need group signatures, and the parameters n and k are decided by the requester, while parameter m is decided by the workers. The group signatures guarantee security and availability even if some TEEs crash or are compromised. Attackers might compromise the security of the majority of TEEs within a group to make the group insecure. Our system shuffles the group periodically to present such attacks based on the assumption presented in Section 3.2.
5 Implementation and Performance Evaluation
We use Ethereum as the blockchain and create a smart contract as a TCC to provide the functions that allow TEEs to register for the platform and store their registration information. A newly registered TEE transfers its deposit to the address of the TCC. A requester who publishes a new crowdsourcing task creates a smart contract as a TSC and also transfers the deposit to the address of the TSC. The workers then register the task by calling a function of the TSC if they want to participate in the task.
A requester’s deposit is associated with a group index, which means only the specified group can spend it. If the majority of TEEs in a group are compromised by attackers, the deposit could be stolen, but the deposits associated with other groups are still safe. We achieve this using a function in the TCC to verify the group index before a group spends its deposit. Moreover, before a group’s RSE becomes zero, the deposit associated with that group should be liquidated: the worker and the TEEs should be paid, and the rest money should be returned to the requester.
Within a group, we do not specifically select one of the TEEs to be the leader but make the TEE that receives the client’s request be responsible for replying to the client. First, if the request is for getting remuneration, the TEE needs to broadcast the request to other members, create a payment transaction with a collective signature, publish the transaction in the blockchain, and finally reply to the client. The client can select another TEE in the group if the previous TEE does not respond. Second, if the request is to evaluate the sourcing data, the TEE, which receives the request, evaluates the data inside its enclave, broadcasts the result to its group members, collects replies from the members, and responds to the worker. In our implementation, the worker directly submits the sourcing data to k number of TEEs, rather than submitting the data only to one TEE and having this TEE forward the data to others because in this case, the receiver could be malicious and tamper with the data before forwarding it.
Our experimental platform consists of six physical computers located in one room, each equipped with Intel Core 3 GHz CPUs and 32 GB RAM and running on a Windows 10 operating system. We use Intel’s SGX as the TEE implementation and run codeeval inside enclaves. Since SGX is not available for all these machines, we configured the software development kit (SDK) to run in simulation mode. We measured the latency of each SGX operation, running under Windows 10 on an Intel Core i5-8500 CPU clocked at 3.00 GHz with 32.0 GB RAM and SGX-enabled BIOS support, and injected it into the simulation. The network latency between two of the six machines is less than 1 ms, and each machine executes 20 virtual TEEs. Thus, we insert 10 ms network latency into the simulation so that each virtual TEE has about 10 ms network latency to communicate with the others.
Measuring blockchain access times is orthogonal to our approach because blockchain writing latency depends on parameters inherent to its implementation, such as about 13 s for Ethereum to create a block.
TEES stores state data for workers and themselves. This state data contains rewards of the workers and the service remuneration of the TEEs. After a TEE receives a request for getting rewards from a worker, the TEE broadcasts it to all group members for verification of the request; each member then creates a signature based on the state data stored locally. The TEE, which received the request, is responsible for collecting the signatures from its group members, and creating a payment transaction with the collective signature, and publishing it in the blockchain. Fig. 3a shows the throughput of the operation get rewards with various group sizes. It shows that dTEE achieves about 65 tps throughput when the group size is 120. The throughput value does not decrease much when the group size increases. This is because all TEEs within the group work in parallel. The latency of this operation is less than 50 ms within a group of 120, as shown in Fig. 3b.
To prove the remunerations owned by a TEE, the TEE must send its previous TSRP to its group members and ask them to generate a newly updated TSRP (i.e., a collective signature) at the end of each epoch before group shuffling. Each group member must verify the previous TSRP and sign the new TSRP. We evaluate the throughput of generating TSRP with various group sizes, finding that the throughput decreases, and the latency increases with greater group size (Fig. 3). This is because, in our experiment, a TSRP contains simply the signatures of each group member, meaning that TSRP size increases with greater group size. In the future, we will attempt to use Schnorr multi signatures [30] to merge the signatures in a TSRP to reduce its size and accelerate the verification process.
To evaluate the throughput and latency of evaluating the quality of sourcing data, we use two different sizes of sourcing data in the scenario that a request buys a lot of sourcing data via dTEE in a crowdsourcing task. The first dataset is classic Sudoku solution data; a Sudoku solution is a nine-by-nine matrix containing 81 integers. The second dataset is from the Modified National Institute of Standards and Technology (MNIST) [31] and consists of 10 classes of 28 by 28 grayscale images. The MNIST test set consists of 10,000 images, while the training set consists of 60,000 images. To recognize objects in the images and evaluate whether an image submitted by the worker meets the requirements, we built a convolutional neural network (CNN) model to be the codetask executed inside the enclave. The CNN model consists of about 1,240 lines of C++ code and contains five layers, including two convolutional layers, two pool layers, and one output layer. We trained the CNN model using the training set and tested it using the test set, achieving about 97% accuracy.
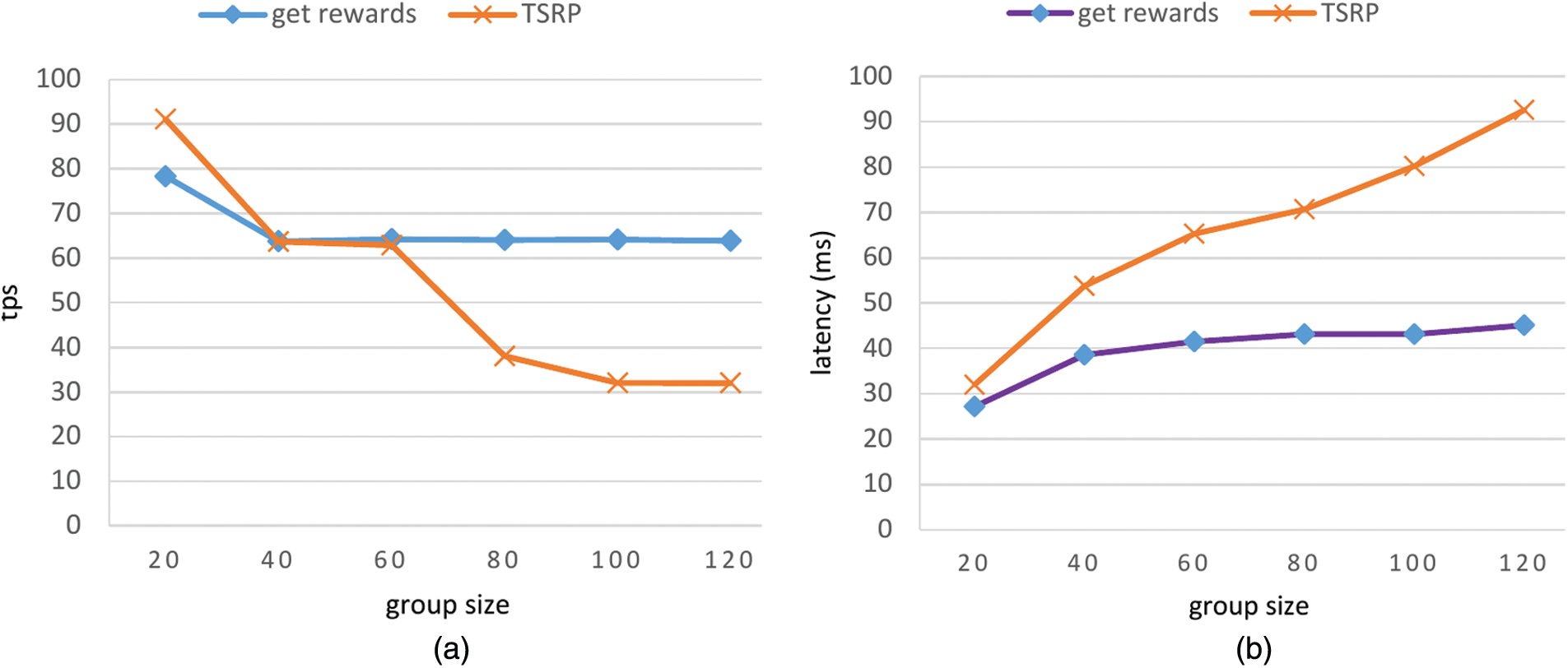
Figure 3: Evaluation results of TEEs’ ability to get rewards and generate a new TSRP in terms of (a) throughput and (b) latency
In the experiment, each time the client submits a Sudoku solution to k number of TEEs in a group. The k TEEs perform the same evaluation process and generate k evaluation results, then broadcast the results to all group members. The group members verify the signature over each result and generate a response message with their signatures. Fig. 4 shows the throughput and the latency of the process of evaluating a Sudoku solution with various group sizes. When we only use one TEE (k = 1) within the group to evaluate the data, the throughput is about 65 tps, and the latency is less than 50 ms when both groups are of 120. When we set k = 5, the throughput is about 12 tps and the latency is about 110 ms with a group of 120.
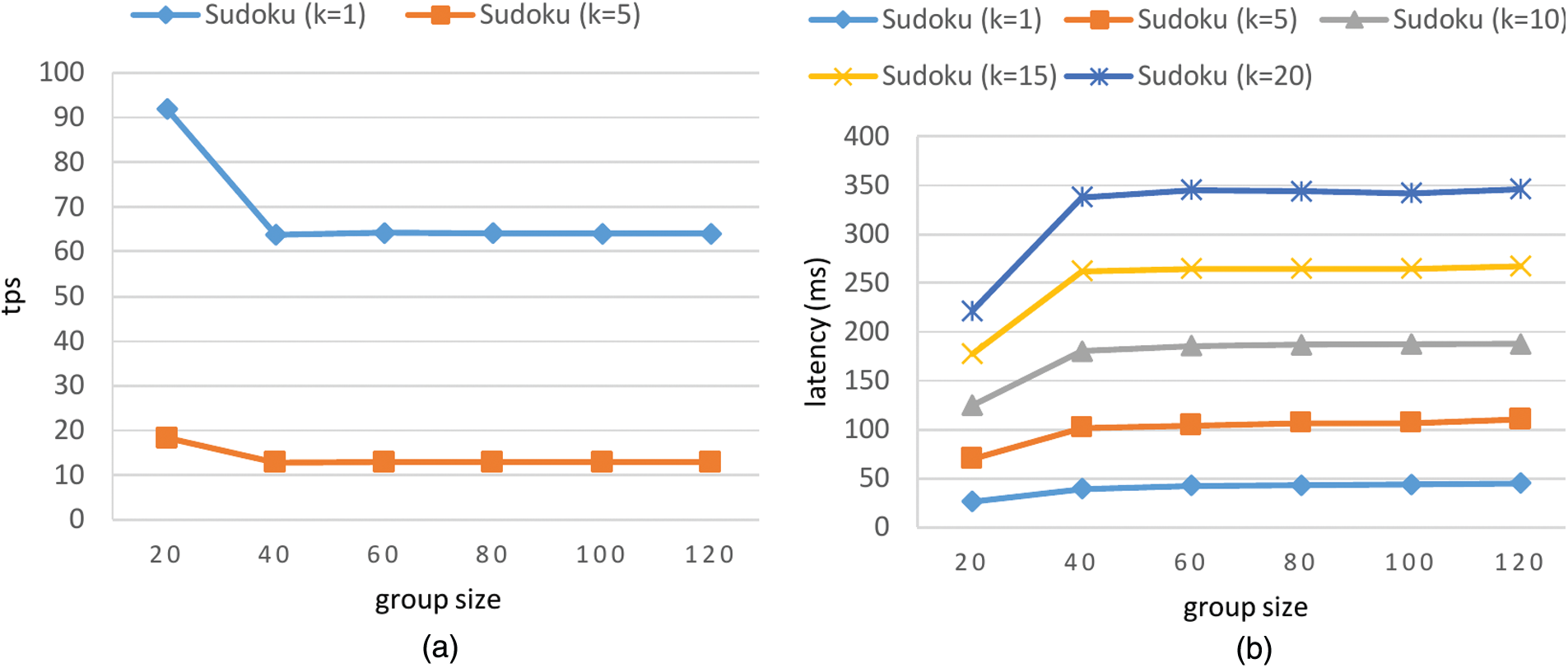
Figure 4: Results of evaluating Sudoku solution data in terms of (a) throughput and (b) latency
In Fig. 5a, we show the quality evaluation latency of submission with 50 images with various group sizes and various k values for k-repeated evaluation. In Fig. 5b, we show the processing time of evaluating the quality of MNIST images using k = 5 TEEs with various group sizes. Each time, the client submits 50 images to 5 TEEs for k-repeated evaluation. The client repeats the submission until the total image number is 2,000, 4,000, 6,000, 8,000 or 10,000. The evaluation results show that dTEE can finish evaluating 10,000 images in less than one minute. Moreover, the processing time does not change much even when the group size increases.
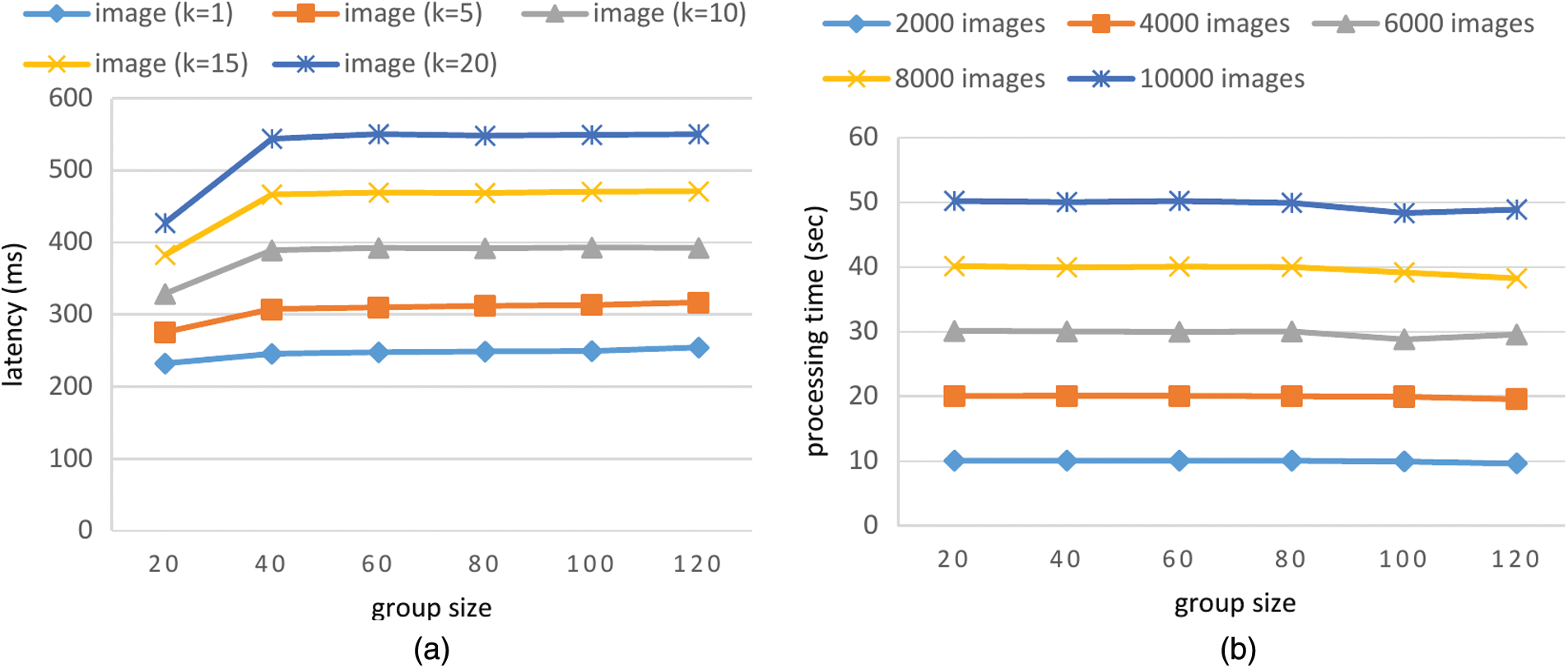
Figure 5: (a) Quality evaluation latency of submission with 50 images with various group sizes and various k values for k-repeated evaluation; (b) processing time to evaluate images with k = 5 and various group sizes
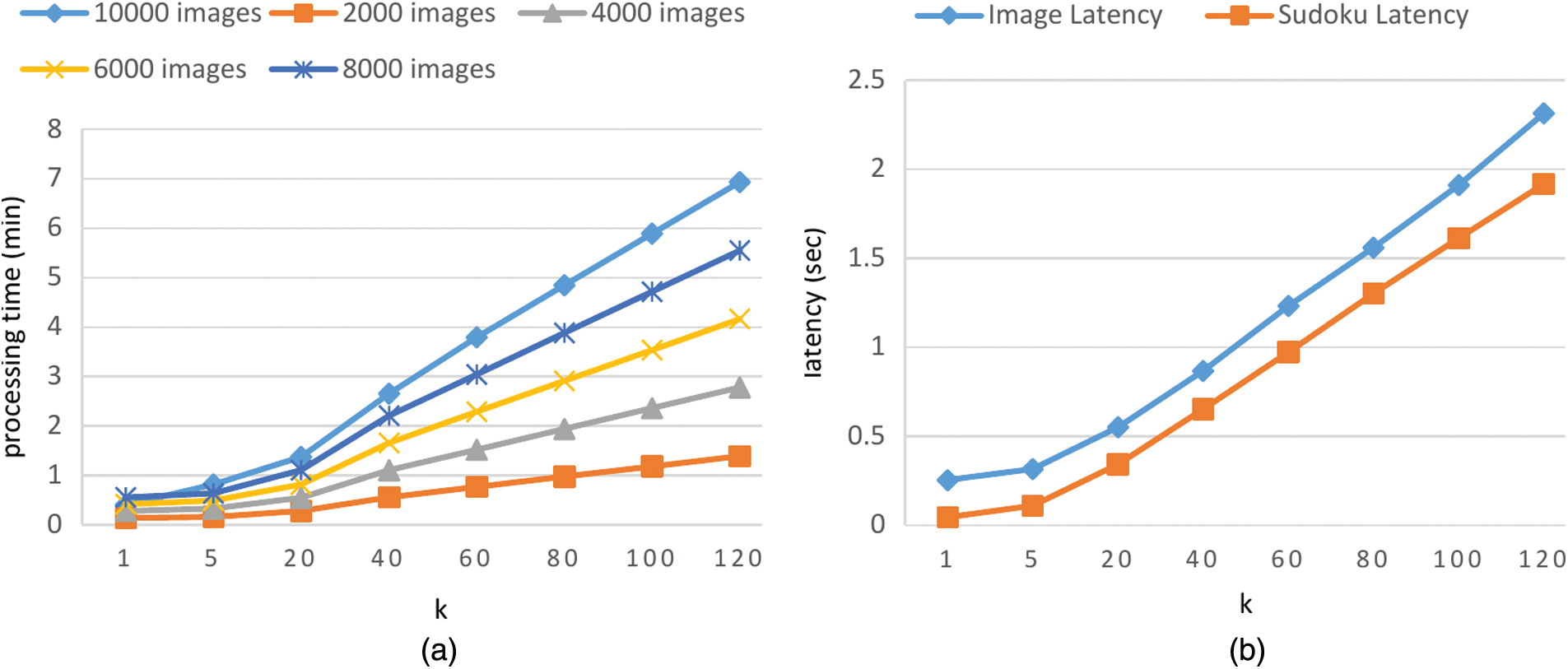
Figure 6: (a) Results of evaluating image quality with group size 120 and various k values for k-repeated evaluation; (b) The quality evaluation latency of submission with 50 images once, as well as a submission with 1 Sudoku solution, with various k values for k-repeated evaluation
To evaluate the effect of various k values for k-repeated evaluation on dTEE performance, we fix the group size to 120 and calculate the processing time for evaluating images and the latency of submission with 50 images or one Sudoku solution, using various k TEEs for k-repeated evaluation (Fig. 6). The results show that the processing time increases with a greater k value. However, practically speaking, it is rarely necessary to perform a k-repeated evaluation with a big k value. This is a tradeoff between security and speed (or cost) determined by the crowdsourcing requesters.
In this paper, we proposed dTEE, for building a platform for distributed trusted computing via TEEs. It aims at being infrastructure of trusted computing for blockchain-based crowdsourcing applications to collect large-scale sourcing data with high availability. It is Byzantine fault-tolerant and self-governing without reliance on any trusted third parties.
Funding Statement: This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (No. NRF-2019R1A2C1090713).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. C. Victor and S. Devadas, “Intel SGX explained,” International Association for Cryptologic Research ePrint Arch, vol. 2016, no. 86, pp. 1–118, 2016. [Google Scholar]
2. H. Dang, T. Dinh, D. Loghin, E. Chang, Q. Lin et al., “Towards scaling blockchain systems via sharding,” in Proc. of the 2019 Int. Conf. on Management of Data, New York City, NY, USA, pp. 123–140, 2019. [Google Scholar]
3. Y. Yan, C. Wei, X. Guo, X. Lu, X. Zheng et al., “Confidentiality support over financial grade consortium blockchain,” in Proc. of the 2020 ACM SIGMOD Int. Conf. on Management of Data, Portland City, OR, USA, pp. 2227–2240, 2020. [Google Scholar]
4. P. Das, L. Eckey, T. Frassetto, D. Gens, K. Hostáková et al., “Fastkitten: Practical smart contracts on bitcoin,” in 28th USENIX Security Symp., Santa Clara City, CA, USA, pp. 801–818, 2019. [Google Scholar]
5. S. Matetic, K. Wüst, M. Schneider, K. Kostiainen, G. Karame et al., “BITE: Bitcoin lightweight client privacy using trusted execution,” in 28th USENIX Security Symp., Santa Clara City, CA, USA, pp. 783–800, 2019. [Google Scholar]
6. H. Duan, Y. Zheng, Y. Du, A. Zhou, C. Wang et al., “Aggregating crowd wisdom via blockchain: A private, correct, and robust realization,” in 2019 IEEE Int. Conf. on Pervasive Computing and Communications, Kyoto City, Japan, pp. 1–10, 2019. [Google Scholar]
7. W. Dai, C. Dai, K. Choo, C. Cui, D. Zou et al., “SDTE: A secure blockchain-based data trading ecosystem,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 725–737, 2020. [Google Scholar]
8. R. Cheng, F. Zhang, J. Kos, W. He, N. Hynes et al., “Ekiden: A platform for confidentiality-preserving, trustworthy, and performant smart contracts,” in IEEE European Symp. on Security and Privacy, Stockholm City, Sweden, pp. 185–200, 2019. [Google Scholar]
9. A. Chittilappilly, L. Chen and S. Amer-Yahia, “A survey of general-purpose crowdsourcing techniques,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, no. 9, pp. 2246–2266, 2016. [Google Scholar]
10. M. Li, J. Weng, A. Yang, W. Lu, Y. Zhang et al., “Crowdbc: A blockchain-based distributed framework for crowdsourcing,” IEEE Transactions on Parallel and Distributed Systems, vol. 30, no. 6, pp. 1251–1266, 2018. [Google Scholar]
11. S. Matetic, M. Ahmed, K. Kostiainen, A. Dhar, D. Sommer et al., “ROTE: Rollback protection for trusted execution,” in 26th USENIX Security Symp., Vancouver City, BC, Canada, pp. 1289–1306, 2017. [Google Scholar]
12. N. Szabo, “Formalizing and securing relationships on public networks,” First Monday, vol. 2, no. 9, 1997. [Online]. Available: https://firstmonday.org/ojs/index.php/fm/article/view/548. [Google Scholar]
13. M-of-n standard transactions, “Bitcoin Improvement Proposal,” 2011. [Online]. Available: https://github.com/bitcoin/bips/blob/master/bip-0011.mediawiki. [Google Scholar]
14. G. Maxwell, A. Poelstra, Y. Seurin and P. Wuille, “Simple schnorr multi-signatures with applications to bitcoin,” Designs Codes and Cryptography, vol. 87, no. 9, pp. 2139–2164, 2019. [Google Scholar]
15. Y. Lu, T. Qiang and W. Guiling, “Zebralancer: Private and anonymous crowdsourcing system atop open blockchain,” in IEEE 38th Int. Conf. on Distributed Computing Systems, Vienna City, Austria, pp. 853–865, 2018. [Google Scholar]
16. Y. Liang, Y. Li and B. Shin, “FairCs—blockchain-based fair crowdsensing scheme using trusted execution environment,” Sensors, vol. 20, no. 11, pp. 3172, 2020. [Google Scholar]
17. B. Jia, T. Zhou, W. Li, Z. Liu and J. Zhang, “A blockchain-based location privacy protection incentive mechanism in crowd sensing networks,” Sensors, vol. 18, no. 11, pp. 3894, 2018. [Google Scholar]
18. J. Wang, M. Li, Y. He, H. Li, K. Xiao et al., “A blockchain based privacy-preserving incentive mechanism in crowdsensing applications,” IEEE Access, vol. 6, pp. 17545–17556, 2018. [Google Scholar]
19. Y. Sung and J. Park, “Future trends of blockchain and crypto currency: Challenges, opportunities, and solutions,” Journal of Information Processing Systems, vol. 15, no. 3, pp. 457–463, 2019. [Google Scholar]
20. M. Rad, A. Rahmani, A. Sahafi and N. Qader, “Social internet of things: Vision, challenges, and trends,” Human-Centric Computing and Information Sciences, vol. 10, no. 1, pp. 1–40, 2020. [Google Scholar]
21. X. Feng and Z. Chiping, “Local differential privacy for unbalanced multivariate nominal attributes,” Human-Centric Computing and Information Sciences, vol. 10, no. 1, pp. 1–21, 2020. [Google Scholar]
22. Y. Wang, D. Kim and D. Jeong, “A survey of the application of blockchain in multiple fields of financial services,” Journal of Information Processing Systems, vol. 16, no. 4, pp. 35–958, 2020. [Google Scholar]
23. M. Sabt, M. Achemlal and A. Bouabdallah, “Trusted execution environment: What it is, and what it is not,” IEEE Trustcom/BigDataSE/ISPA, vol. 1, pp. 57–64, 2015. [Google Scholar]
24. T. Alves and D. Felton, “Trustzone: Integrated hardware and software security,” White paper, 2004. [Online]. Available: http://docplayer.net/51242536-Trustzone-integrated-hardware-and-software-security-enabling-trusted-computing-in-embedded-systems.html. [Google Scholar]
25. V. Costan, L. Ilia and D. Srinivas, “Sanctum: Minimal hardware extensions for strong software isolation,” in 25th USENIX Security Symp., Austin City, Texas, USA, pp. 857–874, 2016. [Google Scholar]
26. P. Diaconis and M. Shahshahani, “Generating a random permutation with random transpositions,” Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, vol. 57, no. 2, pp. 159–179, 1981. [Google Scholar]
27. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” 2008. [Online]. Available: https://git.dhimmel.com/bitcoin-whitepaper. [Google Scholar]
28. B. Bünz, L. Kiffer, L. Luu and M. Zamani, “FlyClient: Super-light clients for cryptocurrencies,” in 2020 IEEE Symp. on Security and Privacy, San Francisco, CA, USA, pp. 928–946, 2020. [Google Scholar]
29. “A next-generation smart contract and decentralized application platform,” White paper, 2014. [Online]. Available: https://cryptorating.eu/whitepapers/Ethereum/Ethereum_white_paper.pdf. [Google Scholar]
30. E. Syta, I. Tamas, D. Visher, D. Wolinsky, P. Jovanovic et al., “Keeping authorities with decentralized witness cosigning,” in IEEE Symp. on Security and Privacy, San Jose City, California, USA, pp. 526–545, 2016. [Google Scholar]
31. Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |