Computers, Materials & Continua DOI:10.32604/cmc.2021.017094
Article

A Secure Rotation Invariant LBP Feature Computation in Cloud Environment

Shiqi Wang1, Mingfang Jiang*,2, Jiaohua Qin1, Hengfu Yang2 and Zhichen Gao3

1College of Computer Science and Information Technology, Central South University of Forestry and Technology, Changsha, 410004, China
2Department of Information Science and Engineering, Hunan First Normal University, Changsha, 410205, China
3Department of Applied Mathematics and Statistics, College of Engineering and Applied Sciences, Stony Brook University, NY, 11794, USA
*Corresponding Author: Mingfang Jiang. Email: bingyuejiang@126.com
Received: 20 January 2021; Accepted: 04 March 2021

Abstract: In the era of big data, outsourcing massive data to a remote cloud server is a promising approach. Outsourcing storage and computation services can reduce storage costs and computational burdens. However, public cloud storage brings about new privacy and security concerns since the cloud servers can be shared by multiple users. Privacy-preserving feature extraction techniques are an effective solution to this issue. Because the Rotation Invariant Local Binary Pattern (RILBP) has been widely used in various image processing fields, we propose a new privacy-preserving outsourcing computation of RILBP over encrypted images in this paper (called PPRILBP). To protect image content, original images are encrypted using block scrambling, pixel circular shift, and pixel diffusion when uploaded to the cloud server. It is proved that RILBP features remain unchanged before and after encryption. Moreover, the server can directly extract RILBP features from encrypted images. Analyses and experiments confirm that the proposed scheme is secure and effective, and outperforms previous secure LBP feature computing methods.

Keywords: Privacy-preserving; rotation invariant local binary pattern; cloud computing; image encryption

1  Introduction

With the rapid development of new information techniques such as big data, cloud computing, and the Internet of Things, users and companies are more willing to store their massive multimedia data on remote cloud servers. Cloud storage services have many advantages, including accessibility, convenience, and low storage expenditure, but massive multimedia data in the cloud servers contain some personal sensitive information needing to be protected. With the popularity of data outsourcing services, there is an increasing need for data security [1,2] and privacy protection in cloud computing. Privacy-preserving outsourcing protocol provides an effective way to cope with this problem [3].

So far, many privacy-preserving data outsourcing schemes have been developed. Previous privacy-preserving outsourcing works mainly focus on text documents. Song et al. [4] proposed practical cryptographic schemes supporting search on encrypted data by employing Boolean operators and phrase searches. Brinkman et al. [5] presented an efficient search method over encrypted data using secure multi-party computation in which XML elements are translated to polynomials. It prevented the server from revealing private content about the data or the query by splitting each polynomial into two parts. Boneh et al. [6] constructed a public key encryption mechanism that enables keyword search over encrypted email. User Alice provided a key to the gateway and tested whether the query word is a keyword in the email without revealing anything information about the email. Swaminathan et al. [7] designed a rank-ordered search framework over encrypted text documents. The scheme can return documents in the order of their relevance to the query term. Elmehdwi et al. proposed a secure k-nearest neighbor (kNN) protocol [8]. The secure kNN search scheme supports the kNN query, while the confidentiality of the data, the user’s input query, and data access patterns. Analysis results indicate that the presented retrieval protocol on encrypted data is secure and efficient. However, common cloud servers in practice may be owned by multiple users rather than only one user. In [9], a privacy–preserving ranked multi-keyword search of encrypted data suitable for the multi-owner model was introduced. Recently, the study on privacy-preserving data outsourcing services has been drawn to multimedia data [10–14]. The Scale-Invariant Feature Transform (SIFT) is a popular method in the field of image processing. It is widely used in computer vision such as object recognition and tracking, and image matching. Hsu et al. [15] first proposed a privacy-preserving SIFT feature representation and extraction approach using the Paillier cryptosystem. It enables us to perform feature extraction in the encrypted domain. Hu et al. [16] focused on privacy–preserving computation outsourcing protocol for SIFT feature over massive encrypted image data and presented a secure SIFT feature extraction scheme. it achieved efficiency and security requirements simultaneously by preserving its key characteristics and designed two protocols for secure multiplication and comparison by randomly splitting original image data. To achieve good efficiency and security, Jiang et al. [17] proposed an effective privacy-preserving SIFT scheme for encrypted images. It devised leveled homomorphic encryption using a new encoding method, homomorphic comparison, division, and derivative encryption. Wang et al. [18] aimed at Speeded-up Robust Features (SURF) and proposed a privacy-preserving SURF computation scheme. it can preserve the distinctiveness and robustness of SURFs while enabling secure multiplication and comparison by leveraging somewhat homomorphic encryption (SHE) and single-instruction multiple-data (SIMD). Jiang et al. [19] first proposed a secure searchable image encryption algorithm for Block Truncation Coding (BTC) compressed images by encrypting the bit plane and two quantization levels of each subblock using the Henon chaotic map. Features based on BTC can be directly computed from encrypted images. Qin et al. [20] proposed a secure Harris feature extraction method for encrypted image retrieval that uses the improved Harris method, SURF, and the Bag of Words model to form the feature vectors. A privacy-preserving BTC feature extraction (PPBTC) is reported in [21]. First, all images are uploaded to the cloud after encryption. The privacy-preserving image encryption process consists of block permutation, pixel diffusion, and a bit-plane random shift. BTC features remain unchanged after encryption and the cloud server can directly extract BTC features from the encrypted images. Some analyses and experimental results demonstrate that the proposed privacy-preserving feature extraction scheme for BTC-compressed images is efficient and secure, and it can be used to secure image computation applications in cloud computing. A local sensitive hash algorithm was employed to produce the searchable index because of the wide application of image hash [22] in image retrieval. The chaotic encryption approach was used to protect the security of images and indexes. Sultana et al. [23] proposed privacy-preserving Local Binary Patterns computation outsourcing scheme that can extract LBP features from encrypted images, in which image encryption was applied only on the MSB (Most Significant Bit) plane of an image. All operations were performed on encrypted images without revealing any information to cloud servers. However, its image scrambling degree is not good. Aiming at secure online data storage services in the Industrial Internet of Things (IIoT), Xia et al. [24] proposed a secure image LBP feature computation scheme. It can directly extract LBP based features from the encrypted images without revealing the private content in the images.

Rotation invariant LBP (RILBP) is an excellent operator and has been widely applied in texture description. Privacy-preserving RILBP feature computation will gain wide application in secure cloud computing. To achieve direct RILBP-based feature representation and computation in the encrypted domain and preserve the privacy of images stored in remote servers, we proposed a privacy-preserving RILBP (PPRILBP) features computation outsourcing scheme in this paper.

The main contributions of this paper are as follows.

1.    This paper proposed a novel secure feature computation algorithm by combining block scrambling, pixel circular shift, and pixel diffusion. Since the feature extraction does not need to decrypt the encrypted data, the new encryption strategy enables direct calculation of RILBP features from encrypted images without revealing private information in images.

2.    The correctness of RILBP feature extraction in the encrypted domain has been proved. Meanwhile, only one server is needed for direct feature computation from encrypted images. Our PPRILBP scheme can find good applications in privacy-preserving image retrieval in cloud environment.

3.    Compared with existing secure LBP feature computation schemes, the new PPRILBP scheme has shown better robustness against common signal processing manipulations, including slight geometric attacks. It can achieve better retrieval accuracy.

The remainder of this paper is organized as follows. In Section 2, a rotation invariant local binary pattern is briefly introduced. Section 3 describes the proposed PPRILBP algorithm in detail. The experiment results and analyses are given in Section 4. Section 5 analyzes the correctness of feature extraction. Finally, the conclusion is made in Section 6.

2  Rotation Invariant Local Binary Pattern

The Local Binary Pattern (LBP) technique was first introduced by Ojala et al. [25]. As a well-defined texture descriptor, it has been widely used in various image processing fields such as image retrieval, image recognition, and image authentication. The original LBP operator assigns pixel value differences of each pixel with its 3×3 neighboring pixels as a binary number. The neighbor is marked as ‘1’ if the corresponding pixel value is greater than the center pixel value and 0 otherwise.

The circular LBP is an extension of the basic LBP operator. It can deal with the texture description of different sizes. Let the notation (P,R) denote the neighbor set with P sampling points on a circle of radius R. The pixel values are bilinearly interpolated when the sampling point does not fall at integer coordinates. Given the center pixel (xc,yc) with pixel value Ic, the LBP number for the center pixel is calculated as follows.

LBPP,R(xc,yc)=∑p=0P-1s(Ip-Ic)2p(1)

where Ip is the pixel value of the neighbor pixel (xp,yp), and s(x) is the sign function.

{xp=xc+Rcos(2πpP)yp=yc-Rsin(2πpP) (2)

s(x)={1x≥00x<0 (3)

To remove the effect of rotation, the LBP operator is further extended to the so-called rotation invariant LBP operator, denoted as LBPP,Rri.

LBPP,Rri= min{ROR(LBPP,R,i)|i=0,1,…,P-1}(4)

where ROR(x,i) performs a right circular i-bit shift on each bit pattern and the function min(z) returns the minimum value of the array z.

For example, the linear permutation 111100002, 11100012, and 110000112 are different rotation versions of the same local pattern, and they all correspond to the same circular permutation with a minimum value 000011112. Let P = 8 and R = 1, Fig. 1 shows an example of the RILBP operator with a circular neighbor set (8,1)

Figure 1: The RILBP operator with a circular neighbor set (8, 1)

3  Proposed PPRILBP Scheme

In this section, the proposed secure outsourcing scheme for RILBP features is described in detail. All images will be encrypted using block scrambling, pixel circular shift, and pixel diffusion before uploaded into the remote server. The cloud server can directly compute the RILBP based features from encrypted images without decrypting them. The block diagram of the proposed method is illustrated in Fig. 2.

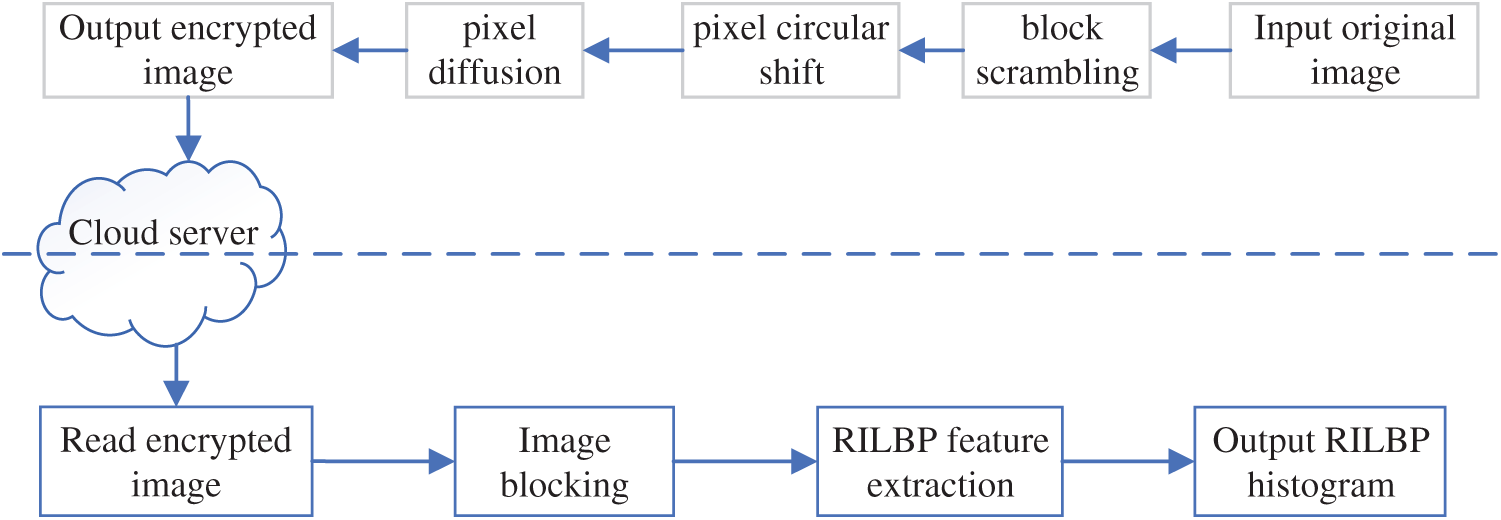
Figure 2: The block diagram of the proposed PPRILBP scheme

3.1 Image Encryption

In the image encryption phase, the original image is divided into 3 × 3 nonoverlapping blocks. Each subblock will undergo three processes: block scrambling, pixel circular shift, and pixel diffusion.

The secret key key1 is used to produce pseudo-random permutations from the interval [0,1,…,Nb-1] during block scrambling, where Nb is the number of nonoverlapped blocks.

Nb=m×nBs×Bs=m×n3×3(5)

Then use secret key key2 to generate a pseudo-random sequence ns for performing pixel shift on the neighbor pixels sequence Neb. The pixel shift operation does not change the RILBP feature since the minimum of the LBP feature remains unchanged before and after pixel circular shifting. Finally, secret key key3 is used to generate random sequences for performing pixel diffusion onto a circular shifted neighbor sequence Nec to further remove the correlation of the adjacent pixel. In order not to change the sign of the difference between the center pixel and the neighbor pixels, we adopt the following strategy,

Ned(k)={Inb2(Nec(k)-xc+1)ifNec(k)≥xcInb1(Nec(k)+1)else,k=0,1,…,P-1(6)

where Ned is the sequence of diffused neighbor pixels, xc is the center pixel, Inb1 and Inb2 are the pseudo-random sequence less than xc and greater than or equal to xc, respectively.

The detailed steps for image encryption are described in Algorithm 1.

The encrypted image E is produced when all image blocks are processed.

Image decryption is the inverse process of the encryption process. Given the same secret keys and image block size, users can recover the original images from encrypted images.

3.2 RILBP Feature Extraction From Encrypted Image

The proposed image encryption does not change the RILBP features of each block. The RILBP features can be directly computed in the encrypted domain without decryption. The main procedures of secure feature extraction are shown in Fig. 2, and a more detailed description of the proposed RILBP feature extraction method is illustrated in Algorithm 2.

4  The Correctness of RILBP Histogram Features Extraction

Definition 1 (Identical), two sequences are identical if and only if they contain the same elements in the same order. For example, these two sequences (5,6,23,9,3) and (5,6,23,9,3) should be considered identical.

Definition 2 (Equivalent), two sequences are equivalent if and only if they are different permutations of all elements from the same set, where ordering does not matter. For instance, these two sequences (3,5,6,9,23) and (5,6,23,9,3) should be considered equivalent.

We consider the original image signal sequence F. The signal is subdivided into blocks with a size of Bs. Let Bi be a subblock of the original image, i.e., F=(Bi)0Nb-1. We denote S as the block scrambling transform,

S(F)=F′(7)

where F′ is the scrambled image, F′=(Bi′)0Nb-1.

Hence, we have

Theorem 1. The sequence F and corresponding scrambled sequence F′ are equivalent, denoted as F≅F′.

Proof. Since the block scrambling transforms S only changes the position of an image subblock, the two sequences F and F′ contain the same image subblock except that only ordering of the subblock in the sequences is different. Therefore, the two sequences F and F′ are equivalent according to Definition 2.

For any subblock B′∈F′, the center pixel xc and the neighbor sequence Neb are got at first. The definition of the circular pixel shift operator ℂ is as follows.

Definition 3. The circular pixel shift operator ℂ(Neb,x) performs right circular x-pixel shift on the neighbor sequence Neb and produces a new sequence Nec,

ℂ(Neb,x)=Nec(8)

The sequence Neb and its circular shifted sequence Nec are rotation invariant, denoted as Neb=RiNec.

Denote the pixel diffusion strategy as D, according to Eq. (6), we have

D(Nec)=Ned(9)

Besides, then the following lemma can be concluded.

Lemma 1. Pixel diffusion strategy D does not change the sign of the difference between the center pixel and the neighboring pixels, i.e., sign(Nec-xc)=sign(Ned-xc).

Proof.∀k∈{0,1,…,P-1}ifNec(k)-xc≥0Ned(k)-xc=Inb2(Nec(k)-xc+1)-xc∵Inb2(Nec(k)-xc+1)≥xc∴Ned(k)-xc≥xc-xc=0elseNed(k)-xc=Inb1(Nec(k)+1)-xc∵Inb1(Nec(k)+1)<xc∴Ned(k)-xc<xc-xc=0

Therefore, the sign of the difference between the center pixel and the neighbor pixels remains unchanged before and after pixel diffusion, i.e., sign(Nec-xc)=sign(Ned-xc).

Let Bc′, Bd′ be the circularly shifted subblock and the pixel diffused subblock of any subblock B′, respectively. Let LBP(⋅), RILBP(⋅) be the LBP and RILBP operators, respectively. Let E be the encrypted image signal sequence. Then, we have

Theorem 2. RILBP(F′)=RILBP(E).

Proof. ∀B′∈F′,∀Bd′∈E,

Neb, Nec, Ned are neighbor sequences derived from subblocks B′,Bc′,Bd′, respectively.

According to Lemma 1, we have sign(Nec-xc)=sign(Ned-xc).

So, LBP(Bc′)=LBP(Bd′)

∵Neb=RiNec

∴RILBP(B′)=RILBP(Bd′)

Thus, RILBP(F′)=RILBP(E) since B′, Bd′ are any subblocks of sequences F′, E, respectively.

Finally, the following theorem be proved

Theorem 3. The histogram of RILBP features computed from the original image and encrypted images are the same,

Proof.

We have F≅F′ according to Theorem 1.

So, RILBP(F)≅RILBP(F′)

Also, because RILBP(F′)=RILBP(E) according to Theorem 2.

We have RILBP(F)≅RILBP(E).

Since the histogram feature does not consider the ordering of elements, we can conclude that the same RILBP histogram features can be computed from the original image and encrypted image, respectively.

Figure 3: Original images (a) Lena (b) peppers (c) Goldhill (d) couple

5  Experimental Results and Analyses

The section provides some analyses and experiments to validate the security and effectiveness of the proposed PPRILBP outsourcing algorithm. The algorithm is conducted on the USC-SIPI Image Database. Fig. 3 shows some test images from the image dataset. In the experiments, we set P = 8 and R = 1. The generated encrypted images by our PPRILBP algorithm are illustrated in Fig. 4. According to Fig. 4, one cannot observe useful information from the encrypted image by human eyes.

Figure 4: Encrypted images (a) Lena (b) peppers (c) Goldhill (d) couple

5.1 Security Analysis

In this section, the key space size is first investigated, which is the total number of different keys used in the encryption process. In the proposed PPRILBP algorithm, the secret key consists of three secret keys (key1, key2, and key3). If each secret key has a precision of 10−15 then there will be 15 + 15 + 15 = 45 uncertain digits of the secret key combination. This means that the complete key space for the proposed secure feature extraction reaches up to 1045, i.e., our PPRILBP algorithm possesses an effective key length of log2{1045}≈150 bits. The key space of our algorithm is larger than that of the 128-bit encryption. Therefore, we can say that the proposed PPRILBP algorithm has a large enough key space and can resist all kinds of brute-force attacks.

Besides, a good image encryption scheme should be sensitive to the secret keys. In our scheme, the sensitivity to key1, key2, and key3 is considered as 10−15. To test the key sensitivity, the original image (taking the Lena image as an example) is first encrypted using secret keys (key1 = 0.74, key2 = 0.79, key3 = 0.13), and the resultant encrypted mage is shown in Fig. 5a. Fig. 5b is the decrypted Lena image using the correct key, and Figs. 5c–5e are the decrypted images using the wrong key, respectively. From Fig. 5, we can find that even a secret key set with a tiny change (10−15) does not reveal any information on the plain-image. Therefore, the proposed scheme has a high key sensitivity.

Figure 5: Key sensitivity test. (a) Encrypted image using key (key1 = 0.74, key2 = 0.79, key3 = 0.13). (b) Decrypted image using key (key1 = 0.74, key2 = 0.79, key3 = 0.13). (c) Decrypted image using key (key1 = 0.74+10−15, key2 = 0.79, key3 = 0.13). (d) Decrypted image using key (key1 = 0.74, key2 = 0.79+10−15, key3 = 0.13). (e) Decrypted image using key (key1 = 0.74, key2 = 0.79, key3 = 0.13+10−15)

5.2 Adjacent Pixels Correlation Analysis

An efficient image encryption system should generate encrypted images with low correlation in the adjacent pixels. The distribution of the adjacent pixels in the original image and its corresponding encrypted image provide an effective visual measure way of the correlation of adjacent pixels. Fig. 6 shows the correlation distribution of two horizontally adjacent pixels of the original image and encrypted image generated by our proposed scheme. The left column and the right column are the correlation distribution of the original image and its corresponding encrypted image, respectively. We can see that the correlation between adjacent pixels in the encrypted image is diffused effectively. The encrypted images produced by our proposed scheme have a weaker correlation than their original images. Thus, the new image encryption algorithm can almost eliminate the correlation of pixels.

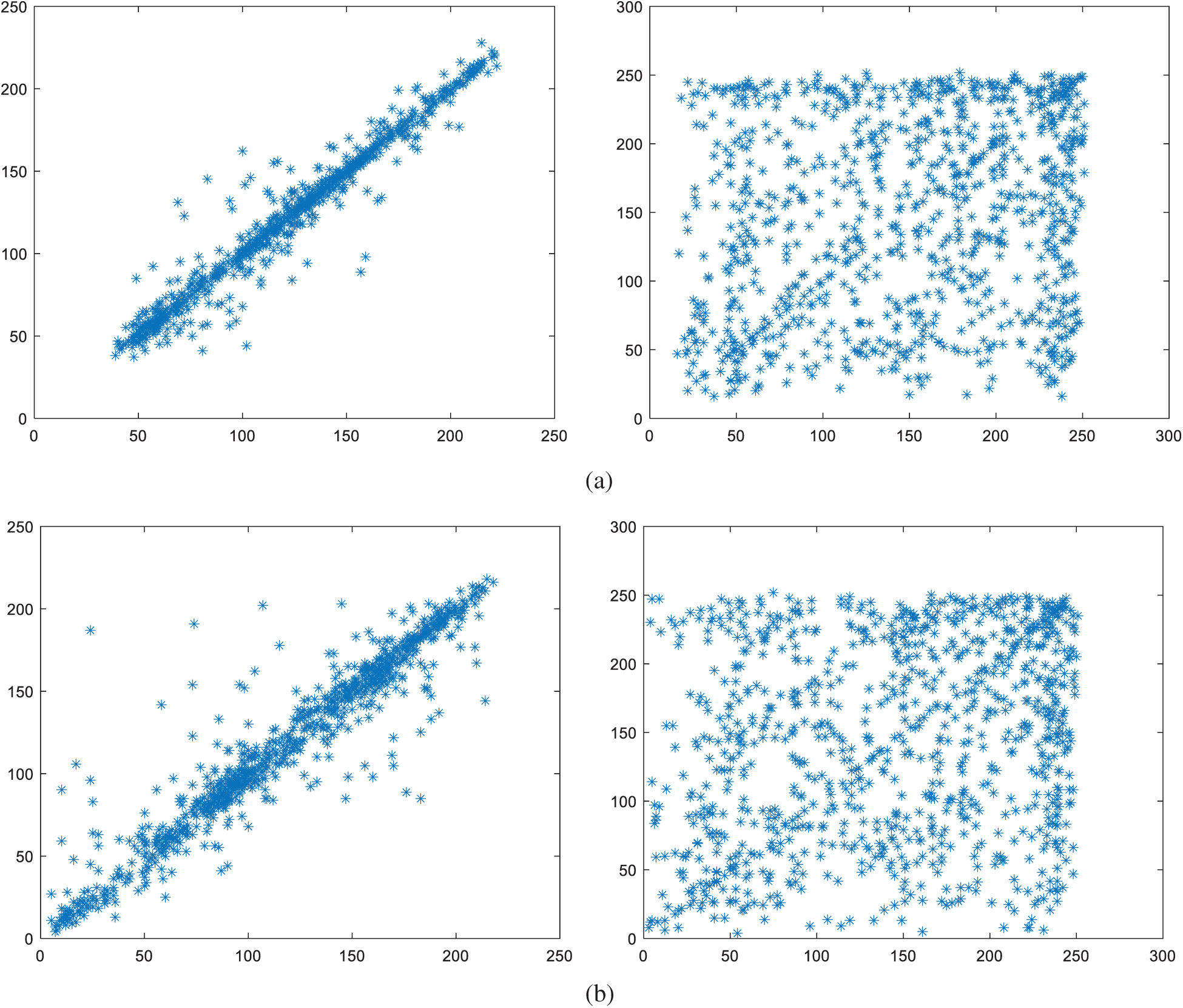
Figure 6: Correlation of two horizontally adjacent pixels. Left column: original images, right column: encrypted images (a) Lena (b) peppers

5.3 Direct PPRILBP Feature Extraction on Encrypted Data

We extract the features from original images and encrypted images for evaluating the accessibility of feature computation. The extracted RILBP features are shown in Fig. 7. The features from the original image and encrypted image are illustrated in the left column and the right column, respectively. It is not hard to notice that the image encryption scheme extracts the same PPRILBP features from the original image and encrypted images. So, the proposed PPRILBP scheme can achieve a high successful retrieval rate when used to image retrieval in cloud computing.

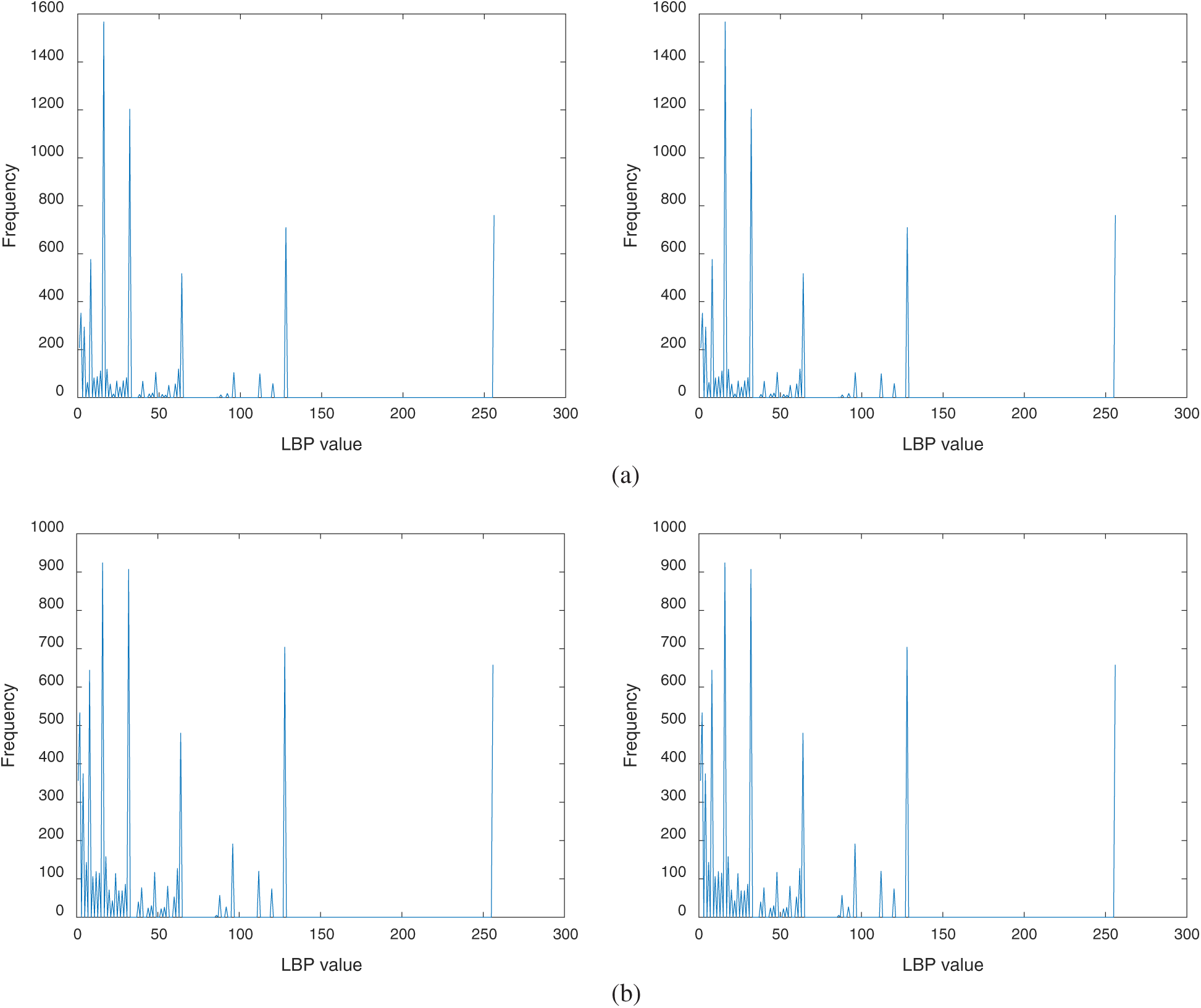
Figure 7: RILBP feature extraction before and after image encryption. Left column: features extracted from original images, right column: features extracted from encrypted images. (a) Lena (b) peppers

Moreover, we further calculate the similarities between different images for homomorphic evaluation. Pearson’s correlation coefficient is employed to evaluate feature similarity, where E(X) denotes the mathematical expectation.

sim=E(H1H2)-E(H1)E(H2)E(H12)-E2(H1)E(H22)-E2(H2)(10)

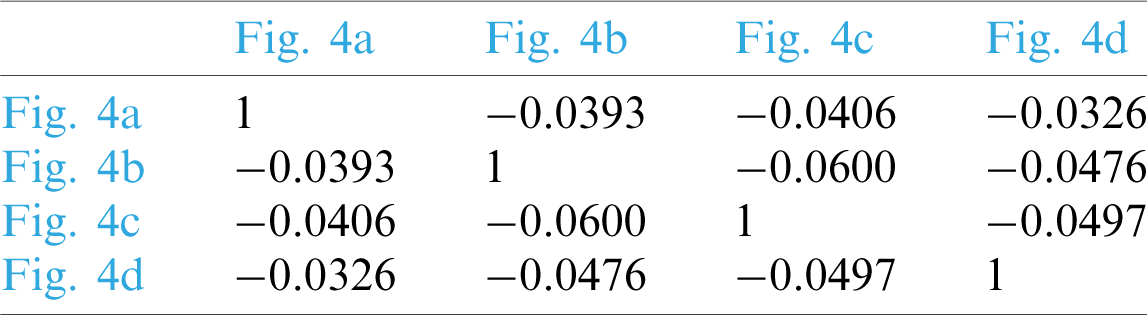
The corresponding test results are listed in Tabs. 1 and 2, respectively. It can be found that feature similarity remains unchanged before and after encryption by observing Tabs. 1 and 2. This indicates that the feature vector extracted by our PPRILBP scheme is homomorphic.

Table 1: Similarities of different original images in Fig. 3

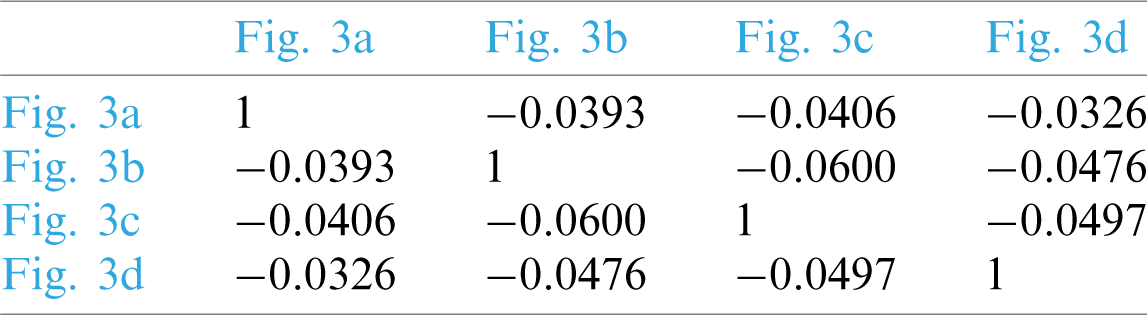
Table 2: Similarities of different encrypted images in Fig. 4

5.4 Case Study on Privacy-Preserving Image Retrieval

As an excellent texture descriptor, LBP has been successfully employed for feature extraction in image retrieval due to its high discriminating ability. In experiments. We apply the proposed PPRIBP algorithm and Xia et al. [24] scheme to search images under the USC-SIPI Image Database. General evaluation metrics recall and precision is employed to evaluate image matching. Fig. 8 shows the performance of the proposed method and Xia et al. [24] scheme. From Fig. 8, we can notice that the performance of the proposed PPRILBP method is better than that by existing work when recall is not more than 0.5. Since that the higher precision with low recall is of more practical significance for image retrieval application, it can be concluded that our PPRILBP outperforms the existing secure LBP feature extraction scheme [24].

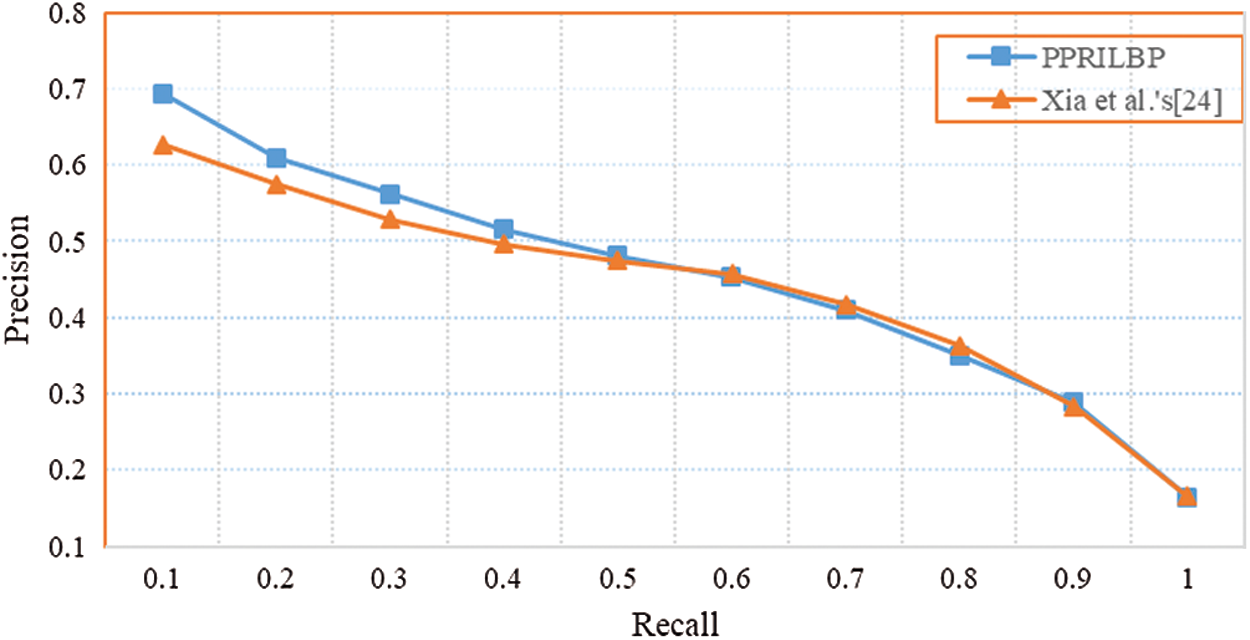
Figure 8: Precision-recall curves of different retrieval methods

6  Conclusion

Rotation Invariant Local Binary Pattern is a popular texture descriptor in computer vision applications. We propose a secure outsourcing scheme of RILBP feature computation. The image encryption using block scrambling, pixel circular shift, and pixel diffusion does not change the RILBP feature of each block. So, the same features can be computed from both the original images and encrypted images. Its security and performance are analyzed and evaluated. Experiments and analysis show that our scheme can directly extract features from encrypted data while preserving privacy and has better retrieval performance than the existing privacy-preserving LBP feature extraction method.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant No. 61872408, the Natural Science Foundation of Hunan Province (2020JJ4238), the Social Science Fund of Hunan Province under Grant No. 16YBA102, and the Research Fund of Hunan Provincial Key Laboratory of informationization technology for basic education under Grant No. 2015TP1017.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Y. Xiang, S. H. Yang, Y. H. Liu, Q. Li and C. Z. Zhu, “Novel linguistic steganography based on character-level text generation,” Mathematics, vol. 8, no. 9, pp. 1558–1558-18, 2020. [Google Scholar]

 2.  Z. Yang, S. Zhang, Y. Hu, Z. Hu and Y. Huang, “VAE-Stega: Linguistic steganography based on variational auto-encoder,” IEEE Transactions on Information Forensics, vol. 16, pp. 880–895, 2021. [Google Scholar]

 3.  H. Pham, J. Woodworth and M. A. Salehi, “Survey on secure search over encrypted data on the cloud,” Concurrency and Computation: Practice and Experience, vol. 31, no. 17, pp. 1–15, 2019. [Google Scholar]

 4.  D. X. Song, D. Wagner and A. Perrig, “Practical techniques for searches on encrypted data,” in 21st IEEE Symp. on Security and Privacy, Berkeley, CA, pp. 44–55, 2000. [Google Scholar]

 5.  R. Brinkman, J. Doumen and W. Jonker, “Using secret sharing for searching in encrypted data,” Int. Workshop on Secure Data Management in a Connected World in Conjunction with VLDB, vol. 3178, pp. 18–27, 2004. [Google Scholar]

 6.  D. Boneh, G. D. Crescenzo, R. Ostrovsky and G. Persiano, “Public key encryption with keyword search,” Advances in Cryptology-EUROCRYPT 2004, Int. Conf. on the Theory and Applications of Cryptographic Techniques, vol. 3027, pp. 506–522, 2004. [Google Scholar]

 7.  A. Swaminathan, Y. Mao, G.-M. Su, H. Gou, A. L. Varna et al., “Confidentiality preserving rank-ordered search,” in ACM Workshop on Storage, Security, and Survivability, Alexandria, VA, USA, pp. 7–12, 2007. [Google Scholar]

 8.  Y. Elmehdwi, B. K. Samanthula and W. Jiang, “Secure k-nearest neighbor query over encrypted data in outsourced environments,” in 2014 IEEE 30th Int. Conf. on Data Engineering, Chicago, IL, USA, pp. 664–675, 2014. [Google Scholar]

 9.  W. Zhang, Y. Lin, S. Xiao, J. Wu and S. Zhou, “Privacy preserving ranked multi-keyword search for multiple data owners in cloud computing,” IEEE Transactions on Computers, vol. 65, no. 5, pp. 1566–1577, 2016. [Google Scholar]

10. W. Lu, A. Swaminathan, A. L. Varna and W. Min, “Enabling search over encrypted multimedia databases,” SPIE-IS&T Electronic Imaging, vol. 7254, pp. 725418–725418-14, 2009. [Google Scholar]

11. C. Y. Hsu, C. S. Lu and S. C. Pei, “Image feature extraction in encrypted domain with privacy–preserving SIFT,” IEEE Transactions on Image Processing, vol. 21, no. 11, pp. 4593–4607, 2012. [Google Scholar]

12. Y. Liu, H. Peng and J. Wang, “Verifiable diversity ranking search over encrypted outsourced data,” Computers, Materials & Continua, vol. 55, no. 1, pp. 37–57, 2018. [Google Scholar]

13. J. Qin, Y. Cao, X. Xiang, Y. Tan, L. Xiang et al., “An encrypted image retrieval method based on simhash in cloud computing,” Computers, Materials & Continua, vol. 63, no. 1, pp. 389–399, 2020. [Google Scholar]

14. L. Qu, H. He, S. Zhang and F. Chen, “Reversible data hiding in encrypted images based on prediction and adaptive classification scrambling,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2623–2638, 2020. [Google Scholar]

15. C. Y. Hsu, C. S. Lu and S. C. Pei, “Homomorphic encryption-based secure SIFT for privacy–preserving feature extraction,” SPIE-IS&T Electronic Imaging, vol. 7880, no. 2, pp. 788005–788005-17, 2010. [Google Scholar]

16. S. Hu, Q. Wang, J. Wang, Z. Qin and K. Ren, “Securing SIFT: Privacy-preserving outsourcing computation of feature extractions over encrypted image data,” IEEE Transactions on Image Processing, vol. 25, no. 7, pp. 3411–3425, 2016. [Google Scholar]

17. L. Jiang, C. Xu, X. Wang, L. Bo and H. Wang, “Secure outsourcing SIFT: Efficient and privacy–preserving image feature extraction in the encrypted domain,” IEEE Transactions on Dependable Secure Computing, vol. 17, no. 1, pp. 179–193, 2020. [Google Scholar]

18. Q. Wang, S. Hu, J. Wang and K. Ren, “Secure surfing: Privacy-preserving speeded-up robust feature extractor,” in 2016 IEEE 36th Int. Conf. on Distributed Computing Systems, Nara, Japan, pp. 700–710, 2016. [Google Scholar]

19. M. Jiang and G. Sun, “A chaotic searchable image encryption scheme integrating with block truncation coding,” Int. Conf. on Cloud Computing and Security, Haikou, China, vol. 11065, pp. 349–358, 2018. [Google Scholar]

20. J. Qin, H. Li, X. Xiang, Y. Tan, W. Pan et al., “An encrypted image retrieval method based on harris corner optimization and LSH in cloud computing,” IEEE Access, vol. 7, pp. 24626–24633, 2019. [Google Scholar]

21. M. Jiang and H. Yang, “Secure outsourcing algorithm of BTC feature extraction in cloud computing,” IEEE Access, vol. 8, pp. 106958–106967, 2020. [Google Scholar]

22. H. Yang, J. Yin and Y. Yang, “Robust image hashing scheme based on low-rank decomposition and path integral LBP,” IEEE Access, vol. 7, pp. 51656–51664, 2019. [Google Scholar]

23. S. F. Sultana and D. C. Shubhangi, “Privacy preserving LBP based feature extraction on encrypted images,” in 2017 Int. Conf. on Computer Communication and Informatics, Coimbatore, pp. 1–4, 2017. [Google Scholar]

24. Z. Xia, L. Jiang, X. Ma, W. Yang, P. Ji et al., “A privacy–preserving outsourcing scheme for image local binary pattern in secure industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 16, no. 1, pp. 629–638, 2020. [Google Scholar]

25. T. Ojala, M. Pietikainen and T. Maenpaa, “Multiresolution gray-scale and rotation invariant texture classification with local binary patterns,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 7, pp. 971–987, 2002. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.