Computers, Materials & Continua DOI:10.32604/cmc.2021.017208
Article

Describe the Mathematical Model for Exchanging Waves Between Bacterial and Cellular DNA

Mohamed S. Mohamed1,*, Sayed K. Elagan1, Saad J. Almalki1, Muteb R. Alharthi1, Mohamed F. El-Badawy2 and Amr M. S. Mahdy1

1Department of Mathematics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Microbiology and immunology Department, Faculty of Pharmacy, University of Sadat City, Menoufiya Governorate, Egypt
*Corresponding Author: Mohamed S. Mohamed. Email: m.saaad@tu.edu.sa
Received: 23 January 2021; Accepted: 26 February 2021

Abstract: In this article, we have shown that bacterial DNA could act like some coils which interact with coil-like DNA of host cells. By decreasing the separating distance between two bacterial cellular DNA, the interaction potential, entropy, and the number of microstates of the system grow. Moreover, the system gives its energy to the medium and the temperature of the host body grows. This could be seen as fever in diseases. By emitting some special waves and changing the temperature of the medium, the effects of bacterial waves could be reduced and bacterial diseases could be controlled. Many investigators have shown that bacterial DNA could emit or absorb electromagnetic waves. One of the main experiments about bacterial waves has been done by Montagnier and his group. They have shown that the genomic DNA of most pathogenic bacteria includes sequences that are able to emit electromagnetic waves. The results have shown that wave affects the crucial physicochemical processes in both Gram-positive and Gram-negative bacteria. The emphasis in this survey is on the development of controlling model equations and computer emulation of the model equations rather than on mathematical methods for solving the model equations and differential equations of epidemics.

Keywords: DNA; bacteria; diseases; inductor; magnetic field

1  Introduction

Up to date, many investigators have shown that bacterial DNA could emit or absorb electromagnetic waves. One of the main experiments about bacterial waves has been done by Montagnier and his group. They have shown that the genomic DNA of most pathogenic bacteria includes sequences that are able to emit electromagnetic waves [1]. They have described the experimental conditions by which diluted aqueous solutions of some bacterial DNA emit electromagnetic waves [2]. Other groups have considered the effect of millimeter waves on the survival of UVC-exposed Escherichia coli [3]. Moreover, other scientists have argued that extremely high-frequency electromagnetic radiation enforces the bacterial effects of inhibitors and antibiotics. They have shown that the radiation of bacteria might lead to changed metabolic pathways and to antibiotic resistance [4]. Other investigators have studied the effect of extremely low-frequency electromagnetic fields on bacterial membranes, namely, membrane potential, surface potential, hydrophobicity, respiratory activity, and growth. The results have shown that wave affects crucial physicochemical processes in both Gram-positive and Gram-negative bacteria [5]. In another paper, the authors have described that by using extremely low-frequency electromagnetic waves at the resonance frequency, one can control the growth of Agrobacterium tumefaciens [6]. Another paper has considered the bactericidal effects of low-intensity extremely high-frequency electromagnetic fields. It has been shown that waves affect the cell-to-cell interactions in bacterial populations since bacteria might interact with each other through electromagnetic fields of sub-extremely high-frequency range [7]. In another research, novel data on millimeter wave’s effects on bacteria and their sensitivity to different antibiotics were presented and discussed that the combined action of millimeter wave and antibiotics resulted in more powerful effects [8].

Fractional order differential equations (FDEs) are usually used to model systems that have a memory that occurs in sundry physical phenomenas, models in the thermoelasticity field, and biological ideals see ([9–11], [12–14], [15–17], [18–20], [21–23], [24–26], [27–29], [30–32]).

This study allows the notion of mathematical biology and a preamble to mathematical modeling and fact for biological and biomedical systems ([33–35], [36–38], [39–41]). Models include the formation of animal coat patterns, the spread of diseases through the community, the interaction between pathogens and the immune system of the body, the growth of tumors, nerve cell signaling, population dynamics, pharmacokinetics, and bacterial growth ([42–44], [44–46]).

The emphasis in this study is on the development of the governing model equations and computer simulations of the model equations rather than on mathematical methods for solving the model equations. Differential equations of epidemics.

The outline of this paper is as follows: In Section 2, we propose a mathematical model for exchanging waves between bacterial and cellular DNA. In Section 3, we explain how this model can help us in curing diseases. The last section is devoted to a summary and conclusions.

2  A Quantum Model for Exchanging Waves Between Bacterial and Cellular DNA

Bacterial DNA divide into two groups: 1. Chromosomal DNA, and 2. Non-chromosomal DNA (plasmid). Both of these genetic matters are formed from charged particles and according to the laws of physics, by any motion, some waves are emitted. Especially, plasmids have a structure like round coils and emit some magnetic fields. On the other hand, a DNA within the cell acts like an inductor and emits some magnetic field.

By exchanging these magnetic fields, the bacterial coil and DNA inductors interact with each other (See Fig. 1).

This interaction causes the absorption of bacterial genetic matter by host cells and the emergence of infectious. For a coil, the magnetic field can be obtained from the below equation:

B≃μ0IN2a2[a2+z2]3/2, (1)

where I is the current, a is the radius of the loop, N is the number of loops, and z is the separation distance from the center of the coil or inductor to the desired point. For hexagonal and pentagonal bases within a DNA, the current along the plane of the molecule could be obtained as:

I5≃∑i=15qivisin⁡(2π5), (2)

I6≃∑i=16qivisin⁡(2π6), (3)

where I5/6 are the currents of hexagonal/pentagonal molecules, qi is the electric charge of atom i and vi is its velocity. Putting Eqs. (2) and (3) in Eq. (1), we obtain:

B≃∑j=1Nμ0[I5,j+I6,j]2aj2[aj2+zj2]3/2≃∑j=1Nμ0[∑i=15qijvijsin⁡(2π5)+∑i=16qijvijsin⁡(2π6)]2aj2[aj2+zj2]3/2. (4)

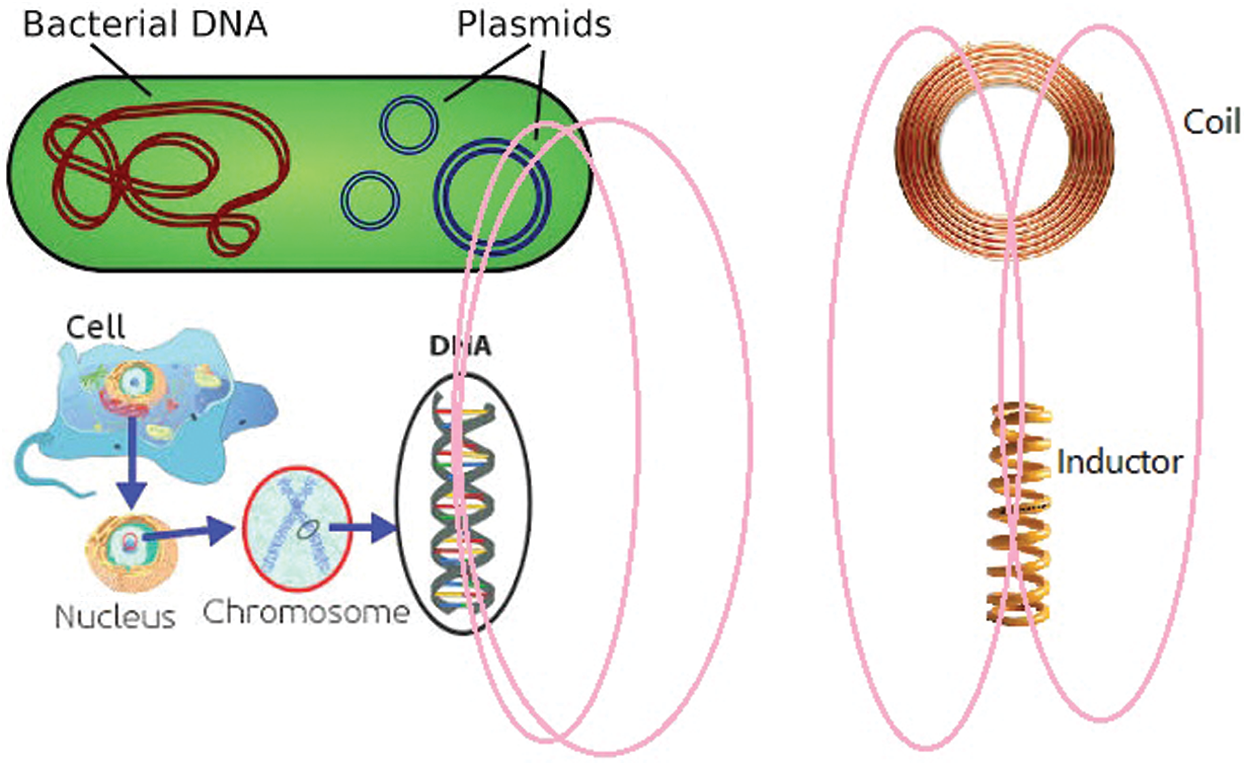
Figure 1: The interaction between bacterial and cellular DNA

Using the above equation, we can calculate the interaction potential between two cellular and bacterial DNA:

VCellular−bacteria≃Bbacteria.Bcellular2μ0≃[∑j=1Nμ0[∑i=15qijbacteriavijbacteriasin⁡(2π5)+∑i=16qijbacteriavijbacteriasin⁡(2π6)]2[ajbacteria]2[[ajbacteria]2+zj2]3/2×∑j=1M[∑i=15qijcellularvijcellularsin⁡(2π5)+∑i=16qijcellularvijcellularsin⁡(2π6)]2[ajcellular]2[[ajcellular]2+zj2]3/2]. (5)

The above potential shows that bacterial and cellular DNA could absorb or repel each other. The negative or positive signs of potential depend on the number of positive and negative charges on bacterial and cellular DNA. For large distances, we can rewrite the above equation as:

VCellular−bacteria≃YbacteriaYCellularzCellular−bacteria6, (6)

where

Ybacteria≃∑j=1N[ajbacteria]2μ0[∑i=15qijbacteriavijbacteriasin⁡(2π5)+∑i=16qijbacteriavijbacteriasin⁡(2π6)]2, (7)

and

YCellular≃∑j=1M[ajCellular]2μ0[∑i=15qijCellularvijCellularsin⁡(2π5)+∑i=16qijCellularvijCellularsin⁡(2π6)]2. (8)

Above potential causes that bacterial DNA are absorbed by cellular DNA. The wave equation for the motion of bacterial DNA in flat space-time can be written as:

−∂2DNABacteria∂τ2+∂2DNABacteria∂σ2=0. (9)

To regard to the interacting potential, we should use of replacements:

ρ=ρ0σ˙2=ρ0σ2w2,w=3τ3+[3−3τ3]VCellular−bacteriaV˙Cellular−bacteria=3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7,τ¯=γ∫0tdτ′ww˙−γσ22. (10)

Substituting the above equation in Eq. (9) gives:

{[(∂τ¯∂τ)2−(∂τ¯∂σ)2]∂2∂τ2+[(∂ρ∂σ)2−(∂ρ∂τ)2]∂2∂ρ2}DNABacteria=0. (11)

We compare the above equation with the general equation for scalar fields and write:

(−g)−1/2∂∂xμ[(−g)1/2gμν]∂∂xυDNABacteria=0, (12)

where

gτ¯τ¯∼−1β2(w′w)2(1−(ww′)21σ4)(1+(ww′)2(1+γ−2)σ4)1/2=−1β2([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)2×(1−(3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7[1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria8)21σ4)(1+(3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7[1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria8)2(1+γ−2)σ4)1/2gρρ∼−(gτ¯τ¯)−1 (13)

The above equation is very similar to the wave equation of a particle in curved space-time. This is because that DNA is a long object 7 meters long which is compacted in less than micrometers. Thus, this system could be similar to a black string with the below metric [9–22]:

ds2=D−1/2H¯−1/2(−fdt2+dx12)+D1/2H¯−1/2(dx22+dx32)+D−1/2H¯1/2(f−1dr2+r2dΩ5)2, (14)

where

f=1−r04r4,H¯=1+r04r4sinh2⁡α,D−1=cos2⁡ε+H−1sin2⁡ε,cos⁡ε=11+β2σ4. (15)

Now, we can arrange the parameters of this black string in terms of the parameters of the bacterial cellular system:

f=1−r04r4∼1−(ww′)21σ4=1−([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)−21σ4,H¯=1+r04r4sinh2⁡α∼1+(ww′)2(1+γ−2)σ4=1+([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)−2(1+γ−2)σ4D−1=cos2⁡ε+H¯−1sin2⁡ε≃1⇒r∼σ,r0∼([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)1/2,(1+γ−2)∼sinh2⁡α (16)

For a bacterial cellular system, the temperature could be obtained from the below equation:

Tbacterial−cellular−system=1πr0cosh⁡α=γπ(w′w)1/2∼γπ([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)1/2. (17)

The above equation shows that the temperature of the cellular bacteria system depends on the separation distance between bacteria and cells and by decreasing it, more interactions between DNA occur and consequently, the system gives its energy to the medium and becomes cooler, however, the medium around it becomes hotter. This may be a reason for the emergence of fever in diseases.

Tmedium/fever∼Tbacterial−cellular−system−1. (18)

Now, we calculate the total potential of the system:

Ebacterial−cellular−system=∫dσT00=∫dσπ22r04(5+4sinh2⁡α)∼π22(ww′)1/2(9+γ−2)∼π22([1+z˙Cellular−bacteriazCellular−bacteria][3τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6]z˙Cellular−bacteria2YbacteriaYCellularzCellular−bacteria83τ3+[3−3τ3]YbacteriaYCellularzCellular−bacteria6z˙Cellular−bacteriaYbacteriaYCellularzCellular−bacteria7)−1/2(9+γ−2) (19)

The above equation shows that by decreasing the separation distance between bacterial and cellular DNA, the interaction between charges increases, and the energy of the system grows. Using Eq. (19), we can obtain the entropy of the system.

Sbacterial−cellular−system∼Ebacterial−cellular−systemTbacterial−cellular−system. (20)

This entropy depends on the separation distance between bacterial and cellular DNA and by its decreasing growth. This means that the number of microstates of this system depends on the interaction between DNA. By closing bacterial DNA, they could exchange more waves with DNA of host cells and the energy of the system and its entropy increase.

3  Controlling Diseases by Exchanging Waves Between Bacterial and Cellular DNA

To control bacterial diseases, we need to obtain the number of micro states. We can write:

Sbacterial−cellular−system∼Kln⁡(Ωbacterial−cellular−system)⇒Ωbacterial−cellular−system∝eEbacterial−cellular−systemTbacterial−cellular−system. (21)

These micro states could be removed by emitting some waves which their energy and temperature can be obtained from the below equation:

1=Ωbacterial−cellular−system×Ωwave∝eEbacterial−cellular−systemTbacterial−cellular−systeme−EwaveTmedium. (22)

Consequently, the energy of the wave and the temperature of the medium should have a reverse relation with the energy and temperature of the bacterial cellular systems:

Ebacterial−cellular−systemTbacterial−cellular−system=[EwaveTmedium]−1. (23)

The above equation is in agreement with experiments. For example, in a bacterial disease, the temperature of its host body should be reduced. If we could measure the energy and temperature of the bacterial cellular system, we can obtain the energy and temperature of waves, which could help us to remove the effects of bacteria waves. To examine the model, we can measure the radiated waves from bacterial DNA within the milk. We can put a vessel of milk at a temperature around 380C for some hours. We put this vessel in a coil and connect it to a generator.

Fig. 2: Measured current in terms of time from one end. Then, we can connect it to a scope like an oscilloscope or radio sky pipe and an amperemeter from another end. We can measure the differences between input and output currents (See Fig. 2).

In Fig. 3, we bring some results. It is clear that bypassing time, the more bacteria in a vessel of milk grow, the more waves are emitted, and consequently the observed current increases. The emitted waves interact with free electrons along metal wires and cause their motion and the emergence of some extra currents.

Figure 2: A circuit to measure bacterial currents

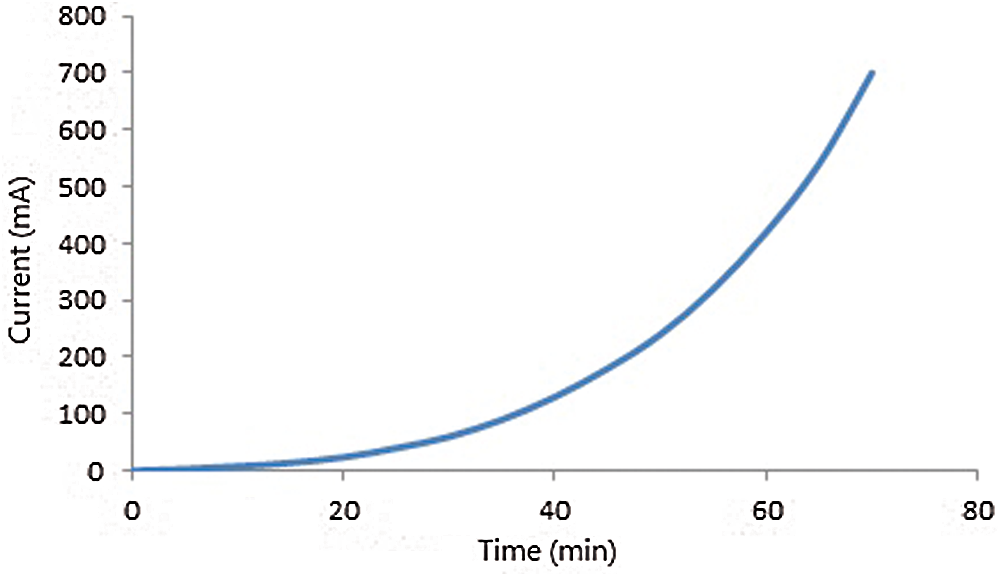
Figure 3: Measured current in terms of time

4  Results and Discussion

A DNA is formed from hexagonal pentagonal molecules and each molecule is formed from charged particles. By any motion of charge, some waves have emerged. The shape of these waves depends on the shape of their DNA sources. For example, some of the bacterial DNA like those in plasmid have a round shape like round coils. These DNA coils send some waves which are absorbed by DNA inductors within host cells. These exchanging of waves lead to the absorption of bacteria by host cells. By emitting some waves, we can cancel bacterial waves and prevent some bacterial diseases.

5  Conclusions

In this paper, some of the DNA within bacteria have the shape of coils. These DNA are formed from charged particles and by their motion, some currents have emerged. These currents emit some electromagnetic waves. These waves could be taken by cellular DNA and consequently, a cellular-bacterial system is formed. By closing bacterial DNA towards cellular DNA, the interacting potential grows, and the number of microstates increases. However, this system gives its energy to the medium and causes the growth of temperature and the emergence of loss. To control bacterial diseases, we should reduce temperature or emit some waves to cancel the bacterial waves. We design a circuit and measure the radiated currents by bacteria within the milk. This investigation permits a thought of numerical science and a prelude to numerical displaying and reality for organic and biomedical frameworks. Models incorporate the development of creature coat designs, the spread of sicknesses through the local area, the association between microbes and the safe arrangement of the body, the development of tumors, nerve cell flagging, populace elements, pharmacokinetics, and bacterial development.

Acknowledgement: This study was funded by the Deanship of Scientific Research, Taif University, KSA [research project number 1-441-104].

Funding Statement: This paper was funded by “Taif University Deanship of Scientific Research Project number (1-441-104), Taif University, Taif, Saudi Arabia”.

Conflicts of interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Montagnier, J. Aissa, S. Ferris, J. Montagnier and C. Lavalléee, “Electromagnetic signals are produced by aqueous nanostructures derived from bacterial DNA sequences,” Interdisciplinary Sciences Computational Life Sciences, vol. 1, pp. 81–90, 2009. [Google Scholar]

 2.  L. Montagnier, D. G. Emilio, J. Aissa, L. Claude, M. Steven et al., “Transduction of DNA information through water and electromagnetic waves,” Electromagnetic Biology & Medicine, vol. 34, no. 2, pp. 106–112, 2015. [Google Scholar]

 3.  M. A. R. Marvin and C. Ziskin, “Effect of millimeter waves on survival of uvc-exposed escherichia coli,” Bioelectromagnetics, vol. 16, no. 3, pp. 188–196, 1995. [Google Scholar]

 4.  H. Tadevosyan, V. Kalantaryan, V. Trchounian and A. Extremely, “High frequency electromagnetic radiation enforces bacterial effects of inhibitors and antibiotics,” Cell Biochemistry & Biophysics, vol. 51, no. 2-3, pp. 97–103, 2008. [Google Scholar]

 5.  S. Oncul, E. M. Cuce, B. Aksu and A. I. Garip, “Effect of extremely low frequency electromagnetic fields on bacterial membrane,” International Journal of Radiation Biology, vol. 92, no. 1, pp. 42–49, 2016. [Google Scholar]

 6.  M. A. Fadel, R. H. El Gebalya, S. A. Mohamed and A. M. M. Abdelbacki, “Biophysical control of the growth of agrobacterium tumefaciens using extremely low frequency electromagnetic waves at resonance frequency,” Biochemical & Biophysical Research Communications, vol. 494, no. 1–2, pp. 365–371, 2017. [Google Scholar]

 7.  H. Torgomyan and A. Trchounian, “Bactericidal effects of low-intensity extremely high frequency electromagnetic field: An overview with phenomenon, mechanisms, targets and consequences,” Critical Reviews in Microbiology, vol. 39, no. 1, pp. 102–111, 2013. [Google Scholar]

 8.  D. Soghomonyan, K. Trchounian and A. Trchounian, “Millimeter waves or extremely high frequency electromagnetic fields in the environment: What are their effects on bacteria,” Applied Microbiology & Biotechnology, vol. 100, no. 11, pp. 4761–4771, 2016. [Google Scholar]

 9.  A. Sepehri, “A mathematical model for DNA,” International Journal of Modern Physics D, vol. 14, pp. 1750152, 2017. [Google Scholar]

10. G. Grignani, T. Harmark, A. M. Obers and M. Orselli, “Open closed string duality and relativistic fluids,” Journal of High Energy Physics, vol. 1106, pp. 44, 2011. [Google Scholar]

11. A. H. Abdel-Aty, M. M. Khater, H. Dutta, J. Bouslimi and M. Omri, “Computational solutions of the HIV-1 infection of CD4+ T-cells fractional mathematical model that causes acquired immunodeficiency syndrome (AIDS) with the effect of antiviral drug therapy,” Chaos, Solitons & Fractals, vol. 139, pp.110092, 2020. [Google Scholar]

12. K. A. Gepreel, A. M. S. Mahdy, M. S. Mohamed and A. Al-Amiri, “Reduced differential transform method for solving nonlinear Biomathematics models,” Computers, Materials & Continua, vol. 61, no. 3, pp. 979–994, 2019. [Google Scholar]

13. A. M. S. Mahdy, M. S. Mohamed, K. A. Gepreel, A. AL-Amiri and M. Higazy, “Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model,” Chaos, Solitons & Fractals, vol. 141, no. 2, pp. 1–16, 2020. [Google Scholar]

14. K. A. Gepreel, M. S. Mohamed, H. Alotaibi and A. M. S. Mahdy, “Dynamical behaviors of nonlinear coronavirus (COVID-19) model with numerical studies,” Computers Materials & Continua, vol. 67, no. 1, pp. 675–686, 2021. [Google Scholar]

15. A. K. Khamis, K. H. Lotfy, A. A. El-Bary, A. M. S. Mahdy and M. H. Ahmed, “Thermal-piezoelectric problem of a semiconductor medium during photo-thermal excitation,” Waves in Random and Complex Media, vol. 71, pp. 1–15, 2020. [Google Scholar]

16. M. M. Khader, N. H. Sweilam and A. M. S. Mahdy, “Two computational algorithms for the numerical solution for system of fractional,” Arab Journal of Mathematical Sciences, vol. 21, no. 1, pp. 39–52, 2015. [Google Scholar]

17. A. M. S. Mahdy, “Numerical studies for solving fractional integro-differential equations,” Journal of Ocean Engineering & Science, vol. 3, no. 2, pp. 127–132, 2018. [Google Scholar]

18. Y. A. Amer, A. M. S. Mahdy and E. S. M. Youssef, “Solving fractional integro-differential equations by using sumudu transform method and Hermite spectral collocation method,” Computers Materials & Continua, vol. 54, no. 2, pp. 161–180, 2018. [Google Scholar]

19. A. M. S. Mahdy, N. H. Sweilam and M. Higazy, “Approximate solutions for solving nonlinear fractional order smoking model,” Alexandria Engineering Journal, vol. 59, no. 2, pp. 739–752, 2020. [Google Scholar]

20. A. A. M. Arafa, S. Z. Rida and M. Khalil, “Fractional modeling dynamics of HIV and CD4+ T-cells during primary infection,” Nonlinear Biomedical Physics, vol. 6, no. 1, pp. 1–7, 2012. [Google Scholar]

21. M. M. Khader, N. H. Sweilam, A. M. S. Mahdy and N. K. Abdel Moniem, “Numerical simulation for the fractional SIRC model and influenza a,” Applied Mathematics & Information Sciences, vol. 8, no. 3, pp. 1–8, 2014. [Google Scholar]

22. D. Kirschner and J. C. Panetta, “Modeling immunotherapy of the tumor-immune interaction,” Journal of Mathematical Biology, vol. 37, no. 3, pp. 235–252, 1998. [Google Scholar]

23. F. A. Rihan, M. Safan, M. A. Abdeen and D. Abdel Rahman, “Qualitative and computational analysis of a mathematical model for tumor-immune interactions,” Journal of Applied Mathematics, vol. 2012, no. 4, pp. 1–19, 2012. [Google Scholar]

24. R. Yafia, “Hopf bifurcation in differential equations with delay for tumor-immune system competition model,” SIAM Journal on Applied Mathematics, vol. 67, no. 6, pp. 1693–1703, 2007. [Google Scholar]

25. F. A. Rihan, “Numerical modeling of fractional-order biological systems,” Abstract & Applied Analysis, vol. 2013, no. 2, pp. 1–13, 2013. [Google Scholar]

26. E. Ahmed, A. Hashish and F. A. Rihan, “On fractional order cancer model,” Journal of Fractional Calculus & Applied Analysis, vol. 3, no. 2, pp. 1–6, 2012. [Google Scholar]

27. A. M. S. Mahdy, Kh. Lotfy, M. H. Ahmed, A. El-Bary and E. A. Ismail, “Electromagnetic hall current effect and fractional heat order for micro temperature photo-excited semiconductor medium with Laser Pulses,” Results in Physics, vol. 17, no. 1–9, pp. 103161, 2020. [Google Scholar]

28. A. M. S. Mahdy, Kh. Lotfy, E. A. Ismail, A. El-Bary, M. Ahmed et al., “Analytical solutions of time-fractional heat order for a magneto-photothermal semiconductor medium with thomson effects and initial stress,” Results in Physics, vol. 18, no. 8, pp. 1–11, 2020. [Google Scholar]

29. A. M. S. Mahdy, Kh. Lotfy, W. Hassan and A. A. El-Bary, “Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source,” Waves in Random and Complex Media, vol. 11, no. 3, pp. 1–18, 2020. [Google Scholar]

30. A. M. S. Mahdy, Kh. Lotfy, A. El-Bary, H. M. Atef and M. Allan, “Influence of variable thermal conductivity on wave propagation for a ramp-type heating semiconductor magneto-rotator hydrostatic stresses medium during photo-excited,” Waves in Random and Complex Media, vol. 31, pp. 1–23, 2021. [Google Scholar]

31. A. M. S. Mahdy, Y. A. Amer, M. S. Mohamed and E. S. M. Youssef, “General fractional financial models of awareness with Caputo Fabrizio derivative,” Advances in Mechanical Engineering, vol. 12, no. 11, pp. 1–9, 2020. [Google Scholar]

32. N. Bellomo, A. Bellouquid, J. Nieto and J. Soler, “Multiscale biological tissue models and flux-limited chemotaxis for multicellular growing systems,” Mathematical Models & Methods in Applied Sciences, vol. 20, no. 7, pp. 1179–1207, 2010. [Google Scholar]

33. A. Gokdogan, A. Yildirim and M. Merdan, “Solving a fractional ordermodel of HIVinfection of CD+ Tcells,” Mathematical and Computer Modelling, vol. 54, no. 9–10, pp. 2132–2138, 2011. [Google Scholar]

34. D. Kirschner and J. C. Panetta, “Modeling immunotherapy of the tumor-immune interaction,” Journal of Mathematical Biology, vol. 37, no. 3, pp. 235–252, 1998. [Google Scholar]

35. A. M. S. Mahdy and M. Higazy, “Numerical different methods for solving the nonlinear biochemical reaction model,” International Journal of Applied and Computational Mathematics, vol. 5, no. 6, pp. 1–17, 2019. [Google Scholar]

36. A. M. S. Mahdy, “Numerical solutions for solving model time-fractional Fokker–planck equation,” Numerical Methods for Partial Differential Equations, vol. 37, no. 2, pp. 1120–1135, 2021. [Google Scholar]

37. K. A. Gepreel, M. Higazy and A. M. S. Mahdy, “Optimal control, signal flow graph, and system electronic circuit realization for nonlinear anopheles mosquito model,” International Journal of Modern Physics C, vol. 31, no. 9, pp. 1–18, 2020. [Google Scholar]

38. A. M. S. Mahdy, H. Higazy, K. A. Gepreel and A. A. A. El-dahdouh, “Optimal control and bifurcation diagram for a model nonlinear fractional SIRC,” Alexandria Engineering Journal, vol. 59, no. 5, pp. 1–21, 2020. [Google Scholar]

39. A. A. Elsadany and A. E. Matouk, “Dynamical behaviors of fractional-order lotka-voltera predator-prey model and its discretization,” Applied Mathematics and Computation, vol. 49, pp. 269–283, 2015. [Google Scholar]

40. M. El-Shahed, J. J. Nieto, A. M. Ahmed and I. M. E. Abdelstar, “Fractional-order model for biocontrol of the lesser date moth in palm trees and its discretization,” Advances in Difference Equations, vol. 2013, pp. 1–16, 2013. [Google Scholar]

41. S. K. Elagan, S. J. Almalki, M. R. Alharthi, M. S. Mohamed and M. F. El-Badawy, “A mathematical quantum model for the replication of DNA waves within skin cell and for growth of melanoma,” Alexandria Engineering Journal, vol. 60, no. 1, pp. 1939–1943, 2021. [Google Scholar]

42. I. H. A. Hassan, M. I. A. Othman and A. M. S. Mahdy, “Variational iteration method for solving: Twelve order boundary value problems,” International Journal of Mathematical Analysis, vol. 3, no. 13–16, pp. 719–730, 2009. [Google Scholar]

43. A. M. A. El-Sayed and S. M. Salman, “On a discretization process of fractional order Riccati’s differential equation,” Journal of Fractional Calculus and Application, vol. 4, pp. 251–259, 2013. [Google Scholar]

44. R. P. Agarwal, A. M. A. El-Sayed and S. M. Salman, “Fractional-order chua’s system discretization, bifurcation and chaos,” Advances in Difference Equations, vol. 2013, pp. 1–13, 2013. [Google Scholar]

45. J. H. He, S. K. Elagan and Z. B. Li, “Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus,” Physics Letters A, vol. 376, no. 4, pp. 257–259, 2012. [Google Scholar]

46. S. K. Elagan, S. J. Almalki, M. R. Alharthi, M. S. Mohamed and M. F. El-Badawy, “A mathematical model for exchanging waves between cellular DNA and drug molecules and their roles in curing cancer,” Results in Physics, vol. 22, no. 16, pp. 103868–103872, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.