DOI:10.32604/cmc.2021.015168
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015168 | |
| Article |
A New Action-Based Reasoning Approach for Playing Chess
Faculty of Computers and Information, Department of Computer Science, Mansoura University, 35516, Egypt
*Corresponding Author: Osama Abu-Elnasr. Email: mr_abuelnasr@mans.edu.eg
Received: 09 November 2020; Accepted: 22 March 2021
Abstract: Many previous research studies have demonstrated game strategies enabling virtual players to play and take actions mimicking humans. The Case-Based Reasoning (CBR) strategy tries to simulate human thinking regarding solving problems based on constructed knowledge. This paper suggests a new Action-Based Reasoning (ABR) strategy for a chess engine. This strategy mimics human experts’ approaches when playing chess, with the help of the CBR phases. This proposed engine consists of the following processes. Firstly, an action library compiled by parsing many grandmasters’ cases with their actions from different games is built. Secondly, this library reduces the search space by using two filtration steps based on the defined action-based and encoding-based similarity schemes. Thirdly, the minimax search tree is fed with a list extracted from the filtering stage using the alpha-beta algorithm to prune the search. The proposed evaluation function estimates the retrievably reactive moves. Finally, the best move will be selected, played on the board, and stored in the action library for future use. Many experiments were conducted to evaluate the performance of the proposed engine. Moreover, the engine played 200 games against Rybka 2.3.2a scoring 2500, 2300, 2100, and 1900 rating points. Moreover, they used the Bayeselo tool to estimate these rating points of the engine. The results illustrated that the proposed approach achieved high rating points, reaching as high as 2483 points.
Keywords: Action based reasoning; case-based reasoning; chess engine; computer games; search algorithm
Generally, various gamers are playing games on personal computers. There are many different game categories, such as simulations, adventures, Real-Time Strategy (RTS), puzzles, and board games. A player can play against others or against a computer-virtual player, where artificial intelligence can be used to generate responsive, adaptive intelligent behaviors similar to human intelligence. While games are mostly played for fun, the majority are designed for learning purposes [1,2].
A chess game is a board game between two players, while an RTS game is a game among multiple ones. Chess is a perfect information game where both players, at any position, know all the actions that can be taken at this position. On the other hand, in RTS games, the information is hidden from the participants. In chess, each player has an army consisting of 16 pieces of six types (pawn, rook, knight, bishop, queen, and king). The players are asked to use a plan or a strategy to mate the opponent king while defending his pieces. On the contrary, in RTS games, each player is supposed to uplift his resources not only to defend the castle but to wage attacks as well.
CBR is mainly applicable to RTS games. Also, its phases mostly used when designing a chess engine [3–6]. CBR simulates human thinking concerning solving problems. Humans try to recall similar past situations from their experiences and adjust their solutions. CBR consists of four phases; retrieval, reuse, revision, and retention [7–9]. In CBR, the human experience is similar to the cases stored in a library called the Case Library (CL) [10]. Throughout the retrieval phase, the engine searches for similar CL cases and returns the most similar ones. The reuse phase checks if both retrieved and current states are identical, and then the solution is reused. Otherwise, it is adapted. Next, we can test solutions in the revision phase and we are able to evaluate the whole situation to measure the credibility of this solution to the current case. Finally, in the retention phase, the current state and the reused solution are collected in the CL as a new experience that could be retrieved and reused for future situations.
In chess, the goal of each player is to mate the opponent king through attacking the opponent’s pieces and defending his pawns. In addition to that the player attempt to pick the best move from a set of legal ones. Shannon [11] estimated that the total number of moves in a chess game is 10
In chess engine, the evaluation process requires estimating many features such as pawn structure, king safety, and available material for each side. Many researchers focused on tuning the weights of the evaluation function using different optimization algorithms. The algorithms included Genetic Algorithm (GA) [12,13], Genetic Programming (GP) [14,15], Evolutionary Programming (EP) [16–18] and Neural Network (NN) [19]. On the other hand, this paper tends to empower the evaluation function by extending its basic control parameters. It gives a high priority to the safety of pieces on the board.
This paper is organized as follows: Section 2 presents some related works. Section 3 discusses the proposed work. Section 4 presents the experimental results and compares them against some existing methods. Section 5 provides the conclusion.
In 1950, Shannon [11] was the first one who started teaching programming a computer to play chess. In 1951, Alan Turing made the first computer program playing chess and tested it through paper, not an actual machine. However, the first computer program that was able to play a complete chess game was developed in 1958. In the last decades, researchers’ aim was to build a chess engine capable of simulating human beings, evaluating positions, and choosing moves like humans.
Sinclair [10] proposed a selective move generation mechanism based on example-based reasoning. The games played by chess grandmasters were analyzed and, accordingly, the positions characterized. These characterizations mapped using Principle Component Analysis (PCA) and compared to those in the example base. Besides, a list of candidate moves returned and ranked according to the similarity to the mapping.
Hauptman et al. [15] used GP to build up the evaluation function of the chessboard endgames. They developed evaluation strategies similar to human experts’ analysis based on IF conditional functions that return TRUE or FALSE values. During the testing, the GP paradigm achieved a draw or won against the expert human-based strategy. It also got a draw against CRAFTY, which is a world-class chess engine.
Flinter et al. [20] seek to improve the process of creating the case library. They demonstrated a method for automatically generating a case library from a large set of grandmaster games using the chunking technique.
Kerner [21] proposed an intelligent system for educational purposes, which empowered the performance of the weak and intermediate players. This system developed a new case-based model for analyzing any given chess position by studying the most significant features in that position. This model provided explanatory comments better than those of the other existing game-playing programs. However, to strengthen this model, some searching capabilities are needed urgently to strengthen this model.
Ganguly et al. [22] proposed an IR-based approach for retrieving chess positions that resemble those stored in the chess games database. They presented and interpret each position in terms of mobility, reachability, and connectivity between pieces with a textual representation. The experiments proved that this approach could retrieve similar game positions to analyze the current piece’s position and predict each piece’s next best move.
Kubat et al. [23] tended to reduce the number of positions calculated for each move. They designed an agent that searches for the learned patterns, which reduced the search tree. The agent collected positive and negative models of scarification from the middle game patterns for the learning process and used Quinlan’s C5 for creating the decision tree. Instead of calculating billions of positions, the agent could recognize patterns with achieving acceptable classification performance.
Kendall et al. [24] proposed a methodology that used GA to select optimal weights for the evaluation function. Also, the minimax tree with the alpha-beta pruning algorithm was used for locating the best moves. Shannon’s simple evaluation function used includes player material and mobility parameters. Furthermore, a population of players was collected where two players were selected to play a chess game against each other. During the testing, the player could beat the chess master after 69 moves as the white player and lose after 97 ones as the black player. However, this methodology needed more additional games to get acceptable results. It also needed more depth for the search tree. Consequently this increased the learning time.
Boskovic et al. [25] proposed an approach that uses Differential Evolution Algorithm (DEA) to find the optimal weights for the evaluation function. To run the same chess engine many times, was the main purpose. Each time the engine is embedded with different parameters of the evaluation function. Preliminary results demonstrated a smaller number of generations generated acceptable parameters and improved the evaluation function.
Nasreddine et al. [26] proposed the dynamic boundary strategy, which uses an Evolutionary Algorithm (EA). It tried to find an optimal evaluation function by dynamically updating the weights associated with each chess piece except the king and the pawn. The engine’s performance is tested against another one that is using the same Shannon’s evaluation function. After 520 learning generations, it achieved a draw in the first game via a 50-moves limit, and however, it won in the second game after 21 moves. Furthermore, the chess engine is tested against the chess master 8000 in two games. It lost in the first game after 81 moves and achieved a draw in the second game because of the 50-moves limit.
Vázquez-Fernández et al. conducted a series of studies concerning the performance of the evaluation function. In [27], they build a search engine for a chess program based on EA. It automatically adjusted the weights of the evaluation function. Additionally, in [28], the research empowered the evaluation process using a selection mechanism that decides which virtual player will pass to the next generation. The virtual player passed according to the matching degree of his moves to the grandmasters’ moves. In [29], the study enhanced the engine’s rating using EA and the Hooke-Jeeves algorithm. In [30], work refined the performance using Neural Network (NN) based on unsupervised learning.
Fig. 1 shows our proposed framework. It is composed of four consecutive continuous phases as follows:
1. Building the action library. This library was built by parsing a large set of chess grandmasters games and stored as a set of descriptive cases, as described in Subsection 3.1.
2. Minimizing the search space. When the opponent makes a move, the proposed engine retrieves a list of reactions from the action library filtered twice as described in Subsection 3.3. Firstly, it returns only the reactions of the grandmasters to the same opponent’s move. Secondly, a similarity function is applied to select the most similar board.
3. Feeding the minimax search tree with the list resulted from the filtering stage and pruning the search using the alpha-beta algorithm. The minimax search tree expands the moves, and the retrieved positions are estimated using the proposed evaluation function. Besides, the best action that increases the case’s power is selected, as described in Subsection 3.4.
4. Retaining the updated representation of the case. After locating the best move, the board is updated and stored in the action library as a new case for future use, as described in Subsection 3.5.
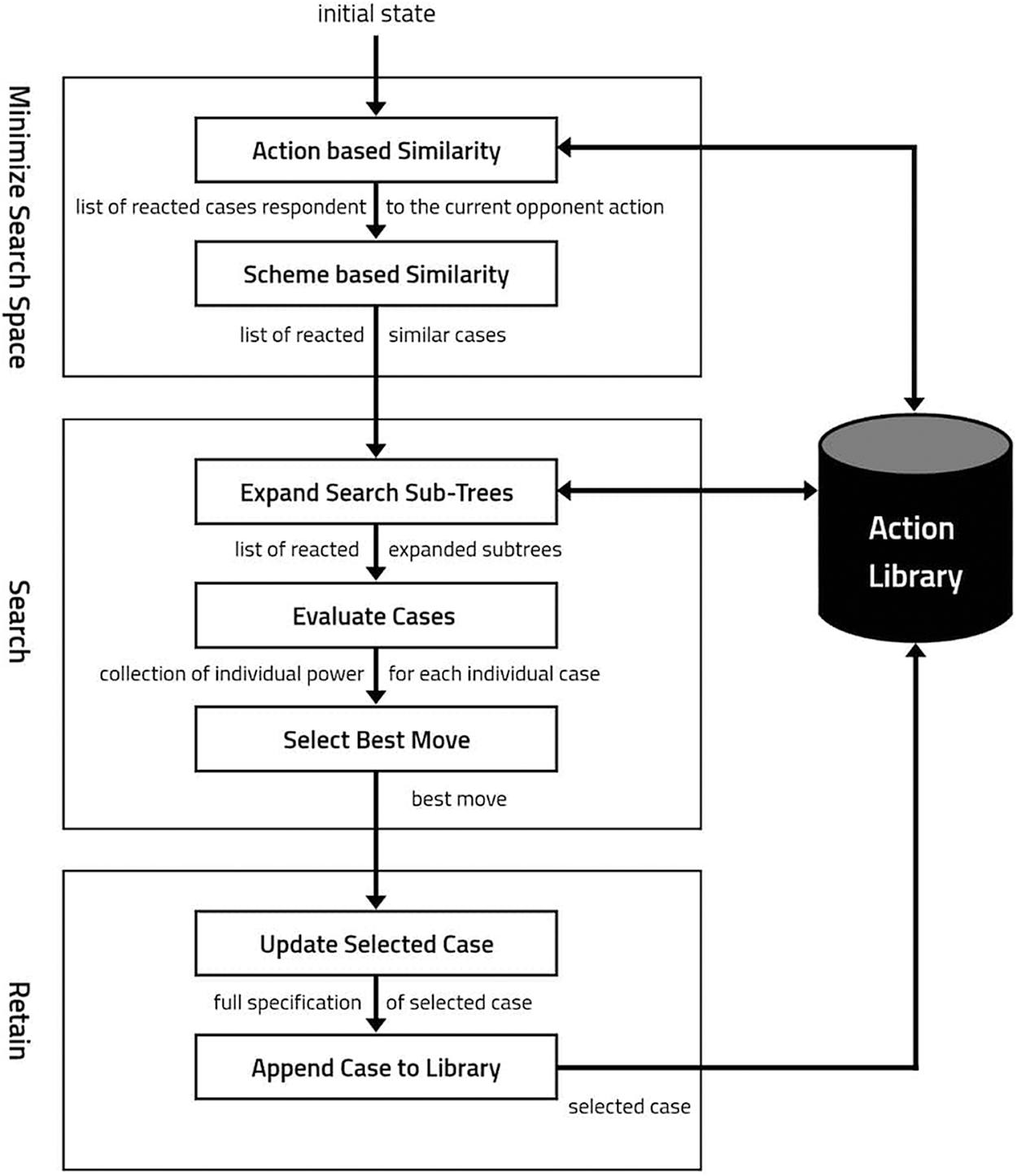
Figure 1: The proposed framework
The proposed action library was formed by mining 6,000 games. It consists of 300000 mapping action moves of the white opponent and the reactive actions of the black opponent. Moreover, the scheme of the case within the action library takes the form: C = {W
The researchers have to clarify the initial state, terminal state, set of operators, and the utility function to specify the chess engine.
Initially, all pawns are locating on the board in their legal positions. Once the game is starting, the white opponent starts to move one pawn to an allowed position. This case referred to the board’s physical representation as to the search space’s initial state.
A chess game can be terminated in one of the following cases; 1) Win/Loss: It happens when the king piece of one any player is threatened by the opponent and cannot move to a safe square while the player cannot capture the attacked piece. 2) Insufficient material: A game ends in a draw when both players do not have sufficient material, where capturing a checkmate through using the remaining pieces is impossible. 3) Threefold repetition: It happens when a specific position occurs three times in a game. In such a case, one of the players can ask for a draw and ends the game. The researchers refer to the terminal state as T, in which each case takes the value of 0 or 1. The starting position is referred to as T = {0, 0, 0}. Moreover, the terminal state in case of Win/Loss is T = {1, 0, 0}.
A set of operators make reference to all the possible actions that a player can make in his game turn. The possible action is a legal move in the game. for instance, a pawn can move either one square or two squares forward if it is its first move. A knight can move in an ‘L’ shape, which is one square along with any rank or file and then at an angle. A bishop can move in a diagonal direction any number of empty squares. A rook can move whether horizontally or vertically, any number of empty squares, in addition to its move in castling. A queen can proceed with any number of empty squares in a diagonal, horizontal, or vertical direction. Finally, a king can move only one square diagonally, horizontally, or vertically, in addition to a special castling move. The current research refers to the set of operators ‘O’ as the following:
O = {P: {F1, F2}, K
Utility function measures the performances over a set of game positions. The utility is calculated using an evaluation function, which evaluates the current chess position. Moreover, the selection of the best next move is made according to this evaluation. The proposed evaluation function is computed as given in Eq. (1).
3.3 Minimizing the Search Space
After each opponent’s move, the proposed engine performs two filtration steps to minimize the search space based on the similarity scheme. Two levels of similarity are considered; the action-based similarity and the encoding scheme-based similarity, respectively.
It retrieves all the grandmaster cases containing reactions to the current opponent’s move from the action library. Moreover, Fig. 2 shows the physical representation of the considered root of the search space from the Adams vs. the Pasman grandmaster game after the 20th move. Figs. 3–5 show the physical representation of the retrieved black reaction cases in response to the move hxg6 of the white opponent as in Fig. 2.
Figure 2: Board grand master games, Adams vs. Pasman after move 21
Figure 3: hxg6; black pawn at square h6 captures white pawn at square g6
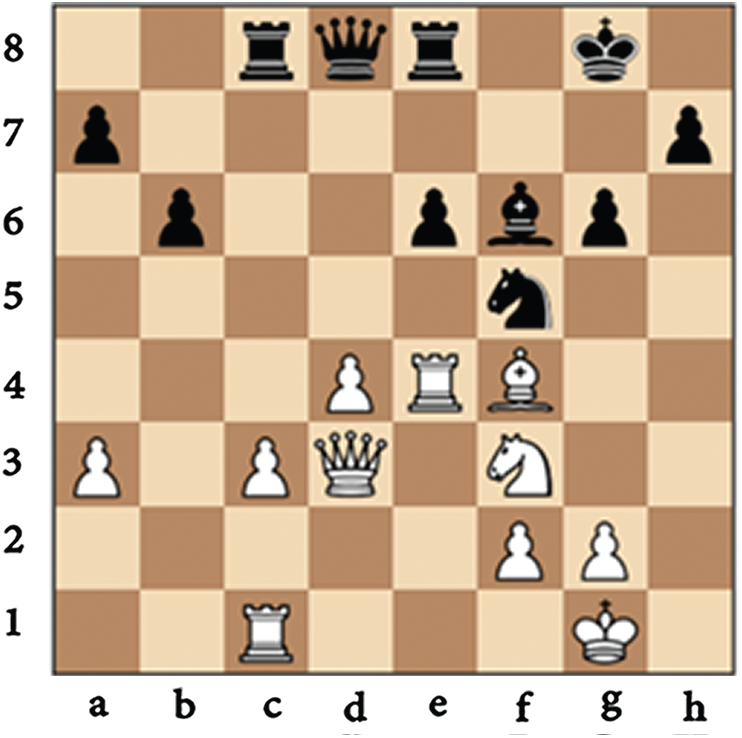
Figure 4: fxg6; black pawn at square f7 captures white pawn at square g6
Figure 5: Qd7; black queen at squarre d8 moves to square d7
3.3.2 The Encoding Scheme Based Similarity
It retrieves a list of the most similar retrieved cases based on two subsequence steps. The first step measures the similarity between the encoding string of the current and retrieved cases. Then afterward, it assigns the similarity degrees to them. Moreover, each similarity degree has a range (0 to 1). The second step discards the cases with a similarity degree, which is less than the value of the proposed similarity degree (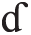
). Algorithm 1 illustrates the similarity scheme along with the sequence of the steps.
This stage includes three subsequence steps: expanding, evaluating, and selecting the best case responding to the active movement of the other opponent. The engine used the minimax algorithm with the alpha-beta algorithm to control the proposed search strategy.
3.4.1 Expanding the Search Tree
The retrieved list now contains the best reactions with their cases, which could be played as responses to the current opponent’s move. These reactions feed the search tree and expand to select the best of them.
Once the engine constructs the search tree and specifies the depth limit, it starts recursively from the leaf nodes to measure the power of its expanded nodes within the search space. It guides the search procedure to locate the best reactive move. The proposed engine alters the evaluation function form by maximizing the surrounding defenders’ and attackers’ roles. Moreover, the proposed evaluation function takes the form given below in Eq. (1).
• Pow(S) is the power of the side S under the evaluation.
• P is the pieces’ count of the side S under the evaluation, starting from n = 1 to n = p.
• Pow(P) is the power of the piece P.
Pow(P) is calculated using the formula given below in Eq. (2).
• Pow(P) is the power of the piece P of the side under evaluation.
• Pos(P) is the positional value of the piece P.
• Mat(P) is the material value of the piece P.
• D is the number of the defenders for the piece P starting from n = 1 to n = d.
• Pos(D) is the positional value of a defending piece D.
• Mat(D) is the material value of a defending piece D.
• A is the number of attackers for piece P, starting from n = 1 to n = a.
• Pos(A) is the positional value of an attacking piece A.
• Mat(A) is the material value of an attacking piece A.
Algorithm 2 illustrates that the implementation of the evaluation process is decomposed into three main steps as follows:
1. Creating both defenders’ net chain list and attackers’ net chain list of each piece.
2. Tracking the frequency of pushing each defender and attacker inside the lists.
3. Getting the power of each piece, as well as taking into account their associated net chain lists.
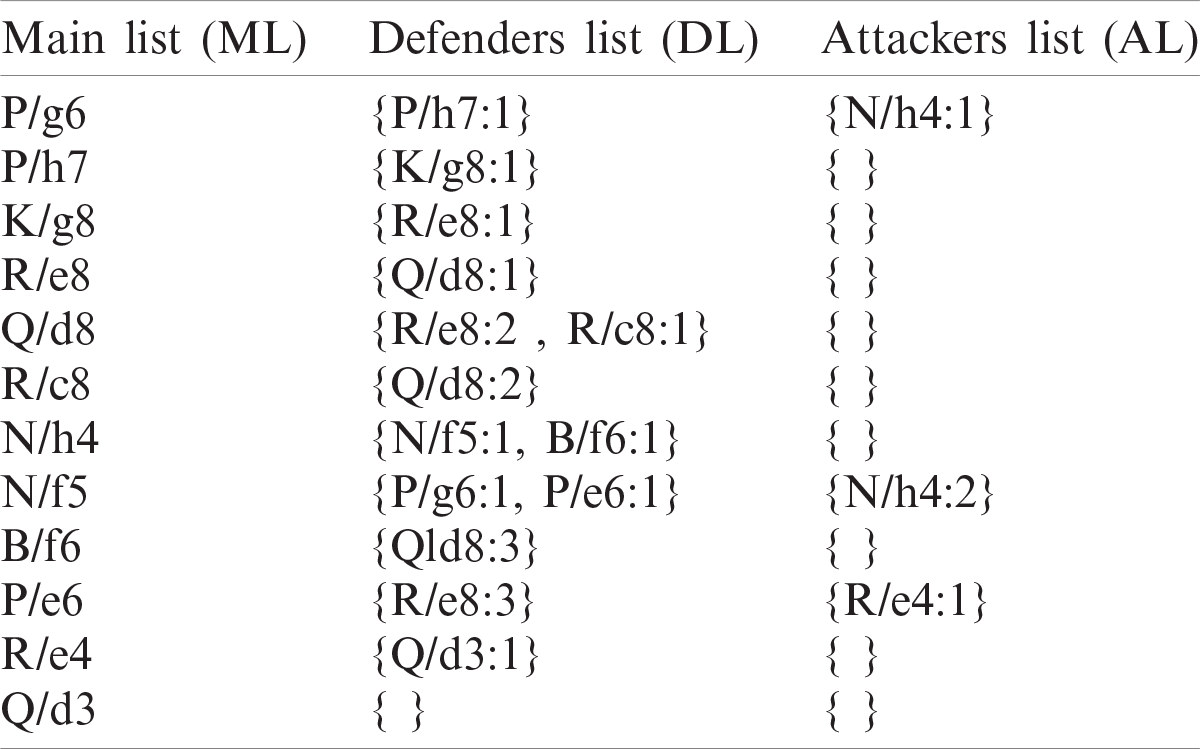
Moreover, to clarify the proposed evaluation function introduced in the research’s procedure, we traced the mechanism of getting the black pawn’s power resides at g6. In this case, we referred to it as P/g6, as shown in Fig. 6.
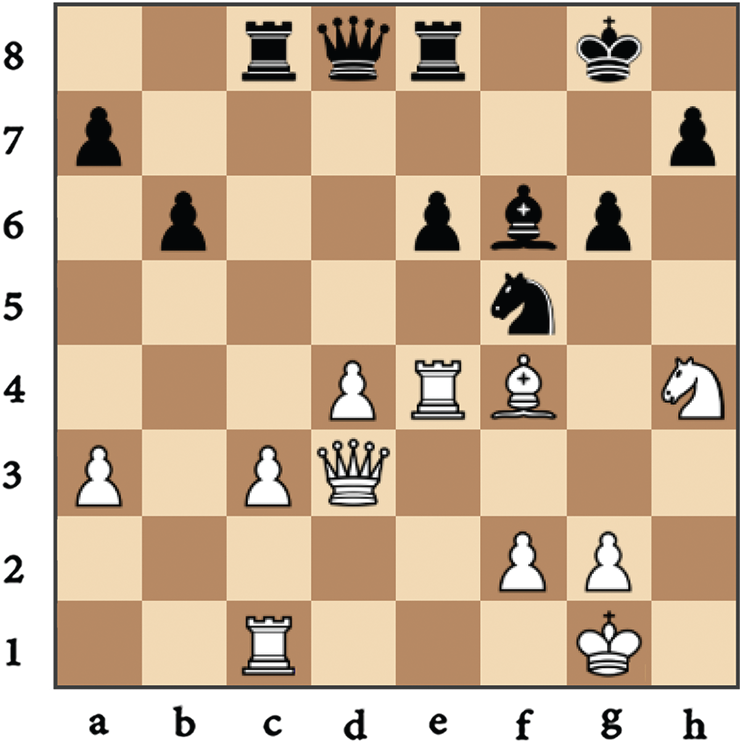
Figure 6: The physical representation of p/g6 position and its surrounding pieces
Once presenting the pawn P/g6 to calculate its power, the algorithm pushes the piece P to the Main list (ML) and locates it at position g6. Furthermore, the textual representation that configures the memory takes the form {piece/position: frequency}. In this case, the defenders’ net chain list (DL) for P/g6 and its appearance frequencies as a defender is represented by {P/h7:1}. On the other hand, the attackers’ net chain list (AL) for P/g6 and its appearance count as an attacker is represented by {N/h4:1}.
Besides, the algorithm iteratively passes through each piece within the associated DL and AL. It checks whether one of them with the specified position is visited or not, as follows:
1. If it is visited before, then its defenders and attackers will exist; there is no need to expand them again. Here the frequency of its repeated appearance is increased by 1.
2. If it has not been visited yet, the algorithm will push the piece as an item in the main list and expand its defenders and attackers.
In general, the above condition prevents the search procedure from getting stuck in an infinite loop. The relation between Rc8 and Qd8 is a clear example of such a case. Every time the engine investigates the defenders of the piece Rc8, the piece Qd8 appears as an item in its DL and vice versa. Tab. 1 illustrates the expansion lists (ML, DL, and AL) for the piece P/g6, as shown in Fig. 6. Algorithm 3 presents the procedure of estimating the power of every single piece within the board.
Table 1: Tracing expansion lists of a piece p/g6
Once evaluating each expanded case, the engine strives to select an optimal move for an opponent by assuming that the other opponent is also playing optimally. It motivates the max player to identify the maximum value of the power and the min player to select the minimum value [31].
Once selecting the best action is selected, the engine alters the given case’s incomplete textual representation. It adds the best black move Bm, FEN after the black move Bf and the complete specification of the encoding string S. Additionally, the engine extends its experience by pushing the new case to the action library as a revised gained experience, to which enhance its performance for further actions. Algorithm 4 illustrates the steps of updating the action library.
The course experiments used our action library, built by parsing the grandmaster games taken from: (https://ccrl.chessdom.com/ccrl/4040/games.html). Moreover, as mentioned in Section 3.5, its size grows while playing; therefore, the engine gains experience.
The proposed engine played 200 games for each experiment against Rybka 2.3.2a, which are available at: (http://www.rybkachess.com/index.php?auswahl=Demo+version). We conducted the experiments at 2500, 2300, 2100, and 1900 rating points. The Bayeselo tool responsible for estimating the engine’s rating is available at: (https://www.remi-coulom.fr/Bayesian-Elo/). We counted the number of the games where the engine achieved a draw, win-win, or defeat lost the game.
This experiment estimated the effect of implementing the evaluation function on empowering the pieces’ safety ratio. The proposed engine played 200 games twice. It used the standard evaluation function for the first round and the proposed evaluation function for the second.
Throughout this experiment, the proposed engine fed its search trees using all the legal moves at any position. Tab. 2 illustrates the results of both trials. At all rating points, the implementation of the proposed evaluation function produces better results due to considering both the defenders’ and the attackers’ net chain list of each piece.
Table 2: Results of experiment A
Throughout this experiment, the engine implemented the proposed evaluation function. Also, it fed its search tree with the legal moves retrieved from the action library.
Tab. 3 illustrates the results of extending the action library at different rating points. At the rating point of 1900, the number of games the engine achieved won case increased from 113 to 167 compared to the results mentioned in experiment A. The won cases also increased from 98 to 117 and 69 to 78, at the rating points of 2100 and 2300, respectively. It means that utilizing the moves played by grandmasters to feed the engine as a response to the current opponent’s move enhanced the results.
Table 3: Results of experiment B
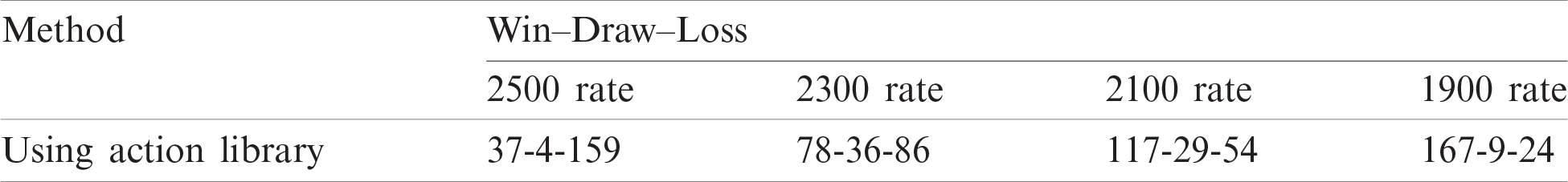
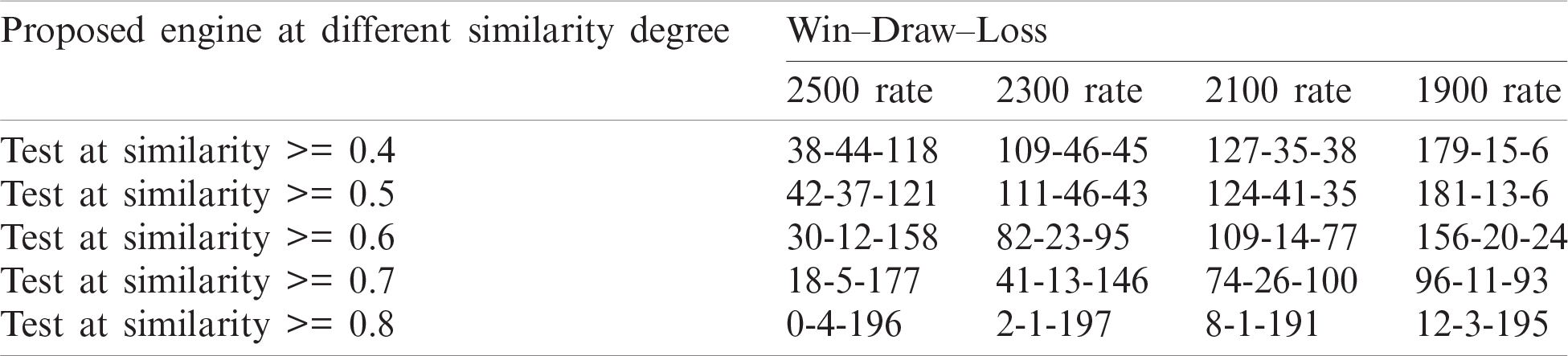
Throughout this experiment, the engine implemented the proposed evaluation function. Also, it fed its search tree with the legal moves retrieved from the action library after applying the two levels of the similarity schemes. Also, a series of similarity degrees tried to find the best value used to retrieve the most similar cases.
Tab. 4 illustrates the results of conducting a series of similarity degrees including 0.4, 0.5, 0.6, 0.7, and 0.8, respectively, with 200 games played for each. The results showed that the performance at the similarity degrees 0.4 and 0.5 are too close. Moreover, their values are better than the results of playing the games at other similar degrees. Furthermore, the performance of the engine has enhanced after adding the effects of these similarity schemes.
Table 4: Results of experiment C using different similarity degrees
4.4 The Proposed Engine vs. Another Engine
The proposed engine’s performance is compared with another engine developed by Vázquez-Fernández et al. [18]. The rating of the proposed engine in experiment A was 2167 points. It reached 2217 points and 2483 points in experiments B and C, respectively. Tab. 5 illustrates that the proposed engine achieved rating points higher than those presented in [18]. It achieved 166 rating points higher than those accomplished by the evolved virtual player. It also achieved 982 rating points higher than those managed by the non-evolved virtual player.
Table 5: The proposed engine results compared to Vázquez-Fernández et al. [18] results
In this research, we developed a new chess game engine that thinks and plays as human experts. It retrieved the best move by searching the constructed action library, acting as a repository of the grandmasters’ actions. This work introduced a proposed form of the evaluation function that implemented a minimax search tree with an alpha-beta pruning algorithm. Besides, it included two levels of similarity schemes.
Throughout the experiments, 200 games were played for each test against Rybka 2.3.2a, as the opponent chess engine, at different rating points. The number of games wherein the engine achieved a draw, win-win, or defeat lost was counted. The results showed that the similarity schemes enhanced the list of the moves retrieved from the action library and the two similarity levels. Overall, this work keeps the pieces safe as long the associated defenders and attackers could be tracked throughout the game. Moreover, the experience of the engine is increased with each game played. Additionally, the results demonstrated that the proposed engine achieved rating points higher than those of the other engine.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. M. Avouris and N. Yiannoutsou, “A review of mobile location-based games for learning across physical and virtual spaces,” Journal of Universal Computer Science, vol. 18, no. 15, pp. 2120–2142, 2012. [Google Scholar]
2. C. A. Collazos, L. A. Guerrero, J. A. Pino, S. F. Ochoa and G. Stahl, “Designing collaborative learning environments using digital games,” Journal of Universal Computer Science, vol. 13, no. 7, pp. 1022–1032, 2007. [Google Scholar]
3. D. W. Aha, M. Molineaux and M. Ponsen, “Learning to win: Case-based plan selection in a real-time strategy game,” in Int. Conf. on Case-Based Reasoning, Springer, pp. 5–20, 2005. [Google Scholar]
4. M. Aref, M. Zakaria and S. Sarhan, “Real-time strategy experience exchanger model [real-see],” International Journal of Computer Science Issues, vol. 8, no. 3, pp. 360, 2011. [Google Scholar]
5. Y.-B. Kang, S. Krishnaswamy and A. Zaslavsky, “A retrieval strategy for case-based reasoning using similarity and association knowledge,” IEEE Transactions on Cybernetics, vol. 44, no. 4, pp. 473–487, 2013. [Google Scholar]
6. J. Y. Kuo and H. Z. Lin, “Cooperative RoboCup agents using genetic case-based reasoning,” in IEEE Int. Conf. on Systems, Man and Cybernetics, Singapore, IEEE, pp. 613–618, 2008. [Google Scholar]
7. M. W. Floyd and B. Esfandiari, “A case-based reasoning framework for developing agents using learning by observation,” in 23rd Int. Conf. on Tools with Artificial Intelligence, Boca Raton, FL, USA, IEEE, pp. 531–538, 2011. [Google Scholar]
8. M. Molineaux, D. W. Aha and P. Moore, “Learning continuous action models in a real-time strategy environment,” in FLAIRS Conf., Coconut Grove, Florida, USA, vol. 8, pp. 257–262, 2008. [Google Scholar]
9. M. Sharma, M. P. Holmes, J. C. Santamaría, A. Irani, C. L. Isbell Jr et al., “Transfer learning in real-time strategy games using hybrid CBR/RL,” in Int. Joint Conf. on Artificial Intelligence, Hyderabad, India, vol. 7, pp. 1041–1046, 2007. [Google Scholar]
10. D. Sinclair, “Using example-based reasoning for selective move generation in two player adversarial games,” in European Workshop on Advances in Case-Based Reasoning, Berlin, Heidelberg, Springer, pp. 126–135, 1998. [Google Scholar]
11. C. Shannon, “Programming a computer for playing chess,” in D. Levy (Eds.Computer Chess Compendium, New York, NY: Springer, pp. 2–13, 1988. [Google Scholar]
12. O. David-Tabibi, M. Koppel and N. S. Netanyahu, “Expert-driven genetic algorithms for simulating evaluation functions,” Genetic Programming and Evolvable Machines, vol. 12, no. 1, pp. 5–22, 2011. [Google Scholar]
13. O. David-Tabibi, H. J. Van Den Herik, M. Koppel and N. S. Netanyahu, “Simulating human grandmasters: Evolution and coevolution of evaluation functions,” in Proc. of the 11th Annual Conf. on Genetic and Evolutionary Computation, Montreal, Qubec, Canada, pp. 1483–1490, 2009. [Google Scholar]
14. A. Hauptman and M. Sipper, “GP-endchess: Using genetic programming to evolve chess endgame players,” in European Conf. on Genetic Programming, Lausanne, Switzerland, Springer, pp. 120–131, 2005. [Google Scholar]
15. A. Hauptman and M. Sipper, “Evolution of an efficient search algorithm for the mate-in-N problem in chess,” in European Conf. on Genetic Programming, Berlin, Heidelberg, Springer, pp. 78–89, 2007. [Google Scholar]
16. D. Fogel, T. Hays, S. Hahn and J. Quon, “An evolutionary self-learning chess program,” Proceedings of the IEEE, vol. 92, no. 12, pp. 1947–1954, 2004. [Google Scholar]
17. D. B. Fogel, T. J. Hays, S. L. Hahn, J. Quon and G. Kendall, “Further evolution of a self-learning chess program,” in IEEE Symp. on Computational Intelligence and Games, Essex University, Colchester, Essex, UK, pp. 73–77, 2005. [Google Scholar]
18. E. Vázquez-Fernández and C. A. C. Coello, “An adaptive evolutionary algorithm based on tactical and positional chess problems to adjust the weights of a chess engine,” in IEEE Congress on Evolutionary Computation, Cancun, Mexico, IEEE, pp. 1395–1402, 2013. [Google Scholar]
19. B. Jianbo, D. Meng, Q. Yizhong and F. Yao, “Design of amazon chess evaluation function based on reinforcement learning,” in Chinese Control and Decision Conf., Nanchang, China, IEEE, pp. 6330–6333, 2019. [Google Scholar]
20. S. Flinter and M. T. Keane, “On the automatic generation of case libraries by chunking chess games,” in Int. Conf. on Case-Based Reasoning, Berlin, Heidelberg, Springer, pp. 421–430, 1995. [Google Scholar]
21. Y. Kerner, “Case-based evaluation in computer chess,” in European Workshop on Advances in Case-Based Reasoning, Chantilly, France, Springer, pp. 240–254, 1994. [Google Scholar]
22. D. Ganguly, J. Leveling and G. J. Jones, “Retrieval of similar chess positions,” in Proc. of the 37th Int. ACM SIGIR Conf. on Research & Development in Information Retrieval, Gold Coast, Queensland, Australia, pp. 687–696, 2014. [Google Scholar]
23. M. Kubat and J. Žižka, “Learning middle-game patterns in chess: A case study,” in Int. Conf. on Industrial, Engineering and Other Applications of Applied Intelligent Systems, New Orleans, Louisiana, USA, Springer, pp. 426–433, 2000. [Google Scholar]
24. G. Kendall and G. Whitwell, “An evolutionary approach for the tuning of a chess evaluation function using population dynamics,” Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), vol. 2, pp. 995–1002, 2001. [Google Scholar]
25. B. Boskovic, S. Greiner, J. Brest and V. Zumer, “A differential evolution for the tuning of a chess evaluation function,” in IEEE Int. Conf. on Evolutionary Computation, Vancouver, BC, Canada, IEEE, pp. 1851–1856, 2006. [Google Scholar]
26. H. Nasreddine, H. S. Poh and G. Kendall, “Using an evolutionary algorithm for the tuning of a chess evaluation function based on a dynamic boundary strategy,” in IEEE Conf. on Cybernetics and Intelligent Systems, Bangkok, Thailand, IEEE, pp. 1–6, 2006. [Google Scholar]
27. E. Vázquez-Fernández, C. A. Coello and F. D. S. Troncoso, “An adaptive evolutionary algorithm based on typical chess problems for tuning a chess evaluation function,” in Proc. of the 13th Annual Conf. Companion on Genetic and Evolutionary Computation, Dublin, Ireland, pp. 39–40, 2011. [Google Scholar]
28. E. Vázquez-Fernández, C. A. C. Coello and F. D. S. Troncoso, “An evolutionary algorithm for tuning a chess evaluation function,” in IEEE Congress of Evolutionary Computation, New Orleans, LA, USA, IEEE, pp. 842–848, 2011. [Google Scholar]
29. E. Vázquez-Fernández, C. A. C. Coello and F. D. S. Troncoso, “An evolutionary algorithm coupled with the Hooke-Jeeves algorithm for tuning a chess evaluation function,” in IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, IEEE, pp. 1–8, 2012. [Google Scholar]
30. E. Vázquez-Fernández, C. A. C. Coello and F. D. S. Troncoso, “Assessing the positional values of chess pieces by tuning neural networks’ weights with an evolutionary algorithm,” in World Automation Congress, Puerto Vallarta, Mexico, IEEE, pp. 1–6, 2012. [Google Scholar]
31. X. Kang, Y. Wang and Y. Hu, “Research on different heuristics for minimax algorithm insight from connect-4 game,” Journal of Intelligent Learning Systems and Applications, vol. 11, no. 2, pp. 15–31, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |