[BACK]
Computers, Materials & Continua
DOI:10.32604/cmc.2021.018182		 images
Article

A Soft Tissue Acupuncture Model Based on Mass-Spring Force Net

Xiaorui Zhang1,2,*, Tong Xu1, Wei Sun2, Jiali Duan1 and Sunil Kumar Jha3

1Jiangsu Engineering Center of Network Monitoring, Engineering Research Center of Digital Forensics, Ministry of Education, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET), Nanjing University of Information Science & Technology, Nanjing, 210044, China
3Faculty of Information Technology, University of Information Technology and Management, Rzeszow, 35-225, Poland
*Corresponding Author: Xiaorui Zhang. Email: zxr365@126.com
Received: 28 February 2021; Accepted: 02 April 2021

Abstract: In the simulation of acupuncture manipulation, it is necessary to accurately capture the information of acupuncture points and particles around them. Therefore, a soft tissue modeling method that can accurately track model particles is needed. In this paper, a soft tissue acupuncture model based on the mass-spring force net is designed. MSM is used as the auxiliary model and the SHF model is combined. SHF is used to establish a three-layer soft tissue model of skin, fat, and muscle, and a layer of the MSM based force network is covered on the surface of soft tissue to realize the complementary advantages and disadvantages of spherical harmonic function and MSM. In addition, a springback algorithm is designed to simulate the springback phenomenon of soft tissue skin during acupuncture. The evaluation results show that the soft tissue acupuncture modeling method based on mass-spring force net can effectively simulate the springback phenomenon of soft tissue surface during acupuncture surgery, and has good comprehensive performance in the application of virtual acupuncture surgery simulation.

Keywords: Mass-spring model; puncture simulation; virtual surgery; soft tissue simulation

1  Introduction

With the development of society, the demand for the quantity and quality of medical staff is higher than before. Surgeons need years of practice to become experts, and their growth needs long-term continuous practice. Also, the traditional training methods need a long cycle, lack of resources, and have high training costs. Therefore, it is urgent to shorten the training cycle of surgeons through advanced technical equipment and training methods. In recent years, the research and application of virtual reality technology have opened up a new way for surgical training. As a new cross research field, virtual surgery [1–3] combines virtual reality and computer graphics technology to use digital medical imaging technology and forces sensing equipment to simulate a virtual operation environment to carry out human-computer interactive training. Compared with the traditional surgical training methods, the advantage of virtual surgery is that the virtual surgery system can quickly restore the operation site. And the operation training can be repeated, so as to save the cost and improve the training efficiency.

Soft tissue model construction is the key technology of virtual surgery simulation. The quality of the model directly determines the quality of the virtual surgery simulation. Several commonly used soft tissue models are introduced below.

The mass-spring model (MSM) is a common soft-tissue model in virtual surgery [4]. It is composed of mass and spring. The mass-spring model is connected by a spring and receives elastic force and damping force, which meets Hooke’s law. The spring represents the internal force acting on the soft tissue particles and can well represent the soft tissue elasticity. This structure gives MSM advantages of simple modeling and low computational complexity. However, its stability, tactile, and visual accuracy is limited [5]. This is because the spring in the model is more suitable for acting as a force carrier rather than a medium for controlling particles. It is difficult to ensure the stability of the model only by relying on the spring.

The finite element model (FEM) [6–8] is composed of continuous volume elements, which has high precision but consumes a lot of computing resources. FEM is suitable for simulating organs with volume characteristics, especially for simulating the internal structure of organs. However, in surgical simulation, its interactive performance is relatively poor due to a large amount of computational cost. Yeung et al. [9] simulated cutting and deformation on a linear elastic model based on FEM, using an augmented matrix to provide rapid updating. However, this study mainly studies linear materials, and nonlinear material updating still needs to be accelerated. Townsend et al. [10] used the updated Lagrangian finite element formula to simulate the nonlinear material model. This method can be applied to simulate various biological soft tissue materials, providing a theoretical model, but its practicability has not been verified.

The boundary element model (BEM) [11–13] is similar to FEM, but different from the basic idea of FEM. BEM only divides the elements on the boundary of the defined domain, and then approximates the boundary conditions with functions satisfying specific equations. After modeling with BEM, the motion equation of soft tissue can be transformed into a boundary integral equation, and the force and deformation information can be obtained by solving the equation. BEM is suitable for simulating tissues with simple, linear, and homogeneous characteristics, such as the force on the tip of the surgical instrument when the instrument is in contact with soft tissue. However, compared with FEM, BEM cannot accurately simulate complex organizations with rich details, especially difficult to deal with the changes of organizational topology.

Spherical harmonic function (SHF) is a three-dimensional expansion of the Fourier series [14], which can well reconstruct medical image signals. The application of SHF to soft tissue modeling can improve the computational efficiency of soft tissue model deformation. Because of the multi-scale of SHF, the collision detection between surgical tools and soft tissues can be completed quickly, and the radius change of any point on the soft tissue surface before and after the collision can be quickly obtained, so as to accurately simulate the deformation of soft tissue. However, it is complicated to calculate the force by SHF, and it is necessary to obtain all-round parameters of soft-tissue materials [15,16], such as density, Young’s modulus, Poisson’s ratio, etc. Therefore, this modeling method is more suitable for the simulation of homogeneous materials. If it is used to simulate a variety of soft tissue materials with different characteristics, the force calculation process is relatively complex and may take up a lot of computing resources.

The present study focuses on improving the existing MSM method and the stability and accuracy without affecting the computational efficiency to expand the ability and application scope of MSM. Thus, it can better simulate the soft tissue and improve the overall quality of soft tissue model and virtual surgery simulation. The study is based on soft tissue acupuncture modeling based on the mass-spring force net and its application in acupuncture simulation. The main contributions of this work are summarized as follows:

1) In the simulation of acupuncture manipulation, it is necessary to accurately capture the information of the punctured point and its surrounding particles. Therefore, a soft tissue modeling method that can accurately track the model particle is needed. The spherical harmonic function (SHF) model can accurately track the acupuncture point. However, the calculation of the force is more complex, and MSM can make up for this deficiency. Therefore, a soft tissue acupuncture modeling method based on the mass-spring force net is designed. MSM is used as an auxiliary model and the SHF model is combined. SHF is used to build a three-layer soft tissue model of skin, fat, and muscle, and a layer of the MSM based force network is covered on the surface of soft tissue to realize the complementary advantages and disadvantages of spherical harmonic function and MSM.

2) In addition, a rebound algorithm [17,18] is designed, which defines that the acupuncture point and its surrounding particles will move to the original position to a certain extent after the soft tissue is punctured, so as to simulate the springback phenomenon when the skin of soft tissue is punctured in the process of acupuncture.

3) Through the construction of the virtual acupuncture system, the soft tissue acupuncture modeling method based on the mass-spring force network is applied to the virtual acupuncture simulation, and the evaluation experiment is designed to study its application effect.

The remainder of this paper is organized as follows. Section 2 illustrates the related works about the mass-spring model. Section 3 introduces the soft tissue acupuncture modeling method based on the mass-spring force net. Section 4 validates the performance of the proposed model. In the last section, a summary of present research is concluded and future research scopes are discussed.

2  Related Works

In virtual surgery simulation, different surgical simulation scenes are often involved, such as simulating specific surgical operations: suture, cutting, acupuncture, etc. or simulating specific tissue structure: tumor, organ, membrane, etc. In order to achieve the simulation requirements, many related types of research have improved the basic performance of the MSM, such as improving the accuracy of the model, improving the stability of the model, and improving the interaction of the model. In addition to improving the basic performance of MSM, we can also expand the application of MSM according to specific requirements, or combine MSM as an auxiliary means with other models to seek new breakthroughs. The improvement of MSM is as follows.

In order to improve the accuracy of MSM, Wang et al. [19] proposed a kind of MSM with elastic instability. Due to the high accuracy of FEM, they used FEM parameters to derive MSM parameters. In this kind of MSM, the parameters of each spring are different, and will change gradually with the deformation process, so the accuracy of MSM is improved. In order to improve the accuracy and reality of MSM in soft tissue puncture simulation, Lan et al. [20] proposed a real-time simulation method of soft tissue puncture based on a fast mass-spring method. In this method, MSM was used to establish a physical model of soft tissue, and the soft tissue puncture deformation was quickly solved by analyzing the dynamic model, and damping and soft tissue wrinkle algorithm were added in the process of soft tissue deformation Improve the simulation realism. Wang et al. [21] used MSM to represent vascular deformation. In order to improve the accuracy of MSM, they determined the spring coefficient according to the elastic distribution of the vessel wall, and derived the stiffness matrix of MSM, instead of setting the spring coefficient manually.

In order to improve the stability of MSM, Wang et al. [22] put forward an improved MSM modeling method, which simplifies the MSM with traditional quadrilateral topology, makes the MSM with a quadrilateral structure to obtain the stability advantages of triangle topology and improves the computational efficiency and stability of the model. Zhi et al. [23] proposed a method for modeling vascular pulsation based on MSM. They selected a central point in a small space and built an MSM between the central point and the particle of the vascular model. By applying force on the central point to pull other points, and setting a time-callback function to give a beating frequency, thus simulating the blood vessel pulsation. The MSM has good stability in small deformation, Therefore, the method of selecting the center point to establish the mass spring constraint modeling method in a small space can avoid the shortage of MSM stability and improve the overall stability of the soft tissue model.

In addition to improving the basic performance of MSM, it is often necessary to improve its structure in practical application, so as to expand its application in virtual surgery. Farhang et al. [24] used MSM to simulate a kind of volume of the soft tissue liver. The MSM is composed of two layers of multi-scale particle spring grids. The external force is transferred from the surface mesh to the internal mesh so that the simulated soft tissue model is no longer a layer of an empty shell. This improvement enables MSM to be used to simulate the compression of the volume of soft tissue. Duan et al. [25] added constraints in MSM so that it can be used to simulate the deformation of volumetric soft tissue. The model simulates the incompressibility of soft tissue by implementing volume preservation on a particle instead of a single tetrahedron. Experiments show that the model can simulate large deformation and maintain the volume characteristics of organs in the real-time calculation. In order to simulate the cutting operation, Kibsgaard et al. [26] proposed a MSM combined with tetrahedral volume mesh to enable MSM to simulate volume soft tissue. The algorithm allows cutting soft tissue at any angle. It is divided into three steps: detecting the interactive surface, subdividing the mesh, and aligning the vertices. The system is graded by experienced doctors. The results show that the model can restore the surgical cutting operation well. Pan et al. [27] expanded the basic structure of MSM to multi-layer tubular MSM in order to simulate rectal tumor resection. This improvement makes MSM suitable for simulating tissues with tubular structures, such as the small intestine and blood vessels. They proposed a real-time cutting technique to simulate the process of separating the rectum from its surrounding tissue. The technique uses residual stress to replace the removed spring to simulate the contractile effect of the surrounding tissue when it detaches from the rectum.

With the development of virtual reality soft-tissue modeling technology, more and more soft-tissue models are emerging. In recent years, many researchers combine MSM as an auxiliary model with other models or algorithms to establish a virtual surgery system, so as to seek a new breakthrough in soft tissue modeling technology. Tang et al. [28] demonstrated a virtual laparoscopic surgery system in which real-time soft tissue deformation was simulated by a special MSM and dynamic target animation. Users can interact with the virtual system using a force interaction device that combines two five-degree freedom manipulators. The laparoscopic training system can help users quickly establish surgical training programs, and provides two training modes: technical training and surgical training. Tai et al. [29] proposed an immersive needle puncture simulation, using a force model and algorithm based on mass-spring to simulate multi-layer soft tissue puncture operation, rendering a multi-layer deformed tissue model based on human anatomical structure, applying an immersion virtual training scheme, and inviting experts and interns to try out the system and provide suggestions. Guo et al. [30] proposed a robot catheter insertion training system based on VR to train surgical interns. The collision detection and physical modeling are realized by MSM and tetrahedron based topology. In addition, they also established the dynamic equation of moving particles in the physical model, and the relationship between collision force and soft tissue deformation. Then, they analyzed the elastic distribution of the vessel wall, and determined the spring coefficient according to the analysis results, realizing the calculation of force feedback and visual feedback.

3  Model Development

Acupuncture is a common operation in surgery, involving a variety of soft tissues, such as skin, fat, and muscle. During acupuncture operation, when the needle tip pierces the surface of soft tissue, the deformation of the surface of soft tissue will more or less rebound to the original position. This phenomenon is called the springback phenomenon of soft tissue surface in acupuncture operation. To simulate this phenomenon, we need to accurately capture the puncturing time point and the position information of the puncture point and its surrounding particles before and after being punctured Soft tissue modeling method.

Among the current mainstream soft tissue models, the SHF modeling method can meet this requirement. Because of the multi-scale of SHF, the collision detection between surgical tools and soft tissue can be completed quickly, and the deformation of any point on the soft tissue surface before and after the collision can be quickly obtained by the surface radius of SHF. Therefore, SHF is a modeling method that can accurately track the acupuncture points and surrounding particles before and after the soft tissue surface puncture.

However, the calculation process of forces in SHF model [31,32] is relatively complicated. Therefore, MSM is used to solve the problem of force calculation when SHF simulates soft tissue. Because MSM is composed of a mass and a spring, the particles are connected with each other through spring. The spring represents the internal elastic force acting between the particles of soft tissue. This structure enables the spring-mass model to have the ability of fast force feedback calculation. It is of great significance to improve MSM and combine it with SHF in the form of an auxiliary model and apply it to acupuncture simulation. In this chapter, a soft tissue acupuncture modeling method based on a mass-spring force network is proposed, and its application in acupuncture simulation is discussed.

3.1 Soft Tissue Surface Construction Based on SHF

The soft tissue model was constructed by SHF and consisted of three layers: skin, fat, and muscle. The three layers of tissue are combined in the following order: the top layer of skin, the middle layer of fat, and the bottom layer of muscle. SHF can be defined by (1).

Ylm(θ,φ)=(2l+1)(l−|m|)!4π(l+|m|)!Plm(cos⁡θ)eimφ(1)

where l is the scale of SHF. l and m are integers. |m|<l, θ and φ denote polar coordinates and coordinate azimuth. 0<θ<π, 0<φ<2π and i is an imaginary number. Also, Plm(x) is a joint Legendre polynomial of order m and l, which can be calculated by (2).

Plm(x)=(−1)m2ll!(1−x2)m2dl+mdxl+m(x2−1)l(2)

SHF is used to construct a soft tissue model, that is, the surface r(θ,φ) of soft tissue is represented by SHF. Soft tissue surface can be defined by r(θ,φ)=(x,y,z)T=(x(θ,φ),y(θ,φ),z(θ,φ))Tdy/dx. In SHF, r(θ,φ) also represents the radius of curvature of SHF at point r(θ,φ). When r(θ,φ) changes, it means that soft tissue collides with surgical tools, so SHF can accurately track the acupuncture point by monitoring r(θ,φ). In order to facilitate the calculation, the surface r(θ,φ) is mapped to the three-dimensional coordinates and parameterized, as shown in (3).

{r(θ,φ)=∑l=0∞∑m=−llclmYlm(θ,φ)x(θ,φ)=∑l=0∞∑m=−llcl,mxylm(θ,φ)y(θ,φ)=∑l=0∞∑m=−llcl,myylm(θ,φ)z(θ,φ)=∑l=0∞∑m=−llcl,mzylm(θ,φ)(3)

where clm=(clmx,clmy,clmz)T is the reconstruction coefficient, which contains the shape information of soft tissues. The larger the scale l, the finer the soft tissue construction, but at the same time it will increase the algorithm complexity. clm can be obtained by least square estimation [33]: To solve clm, we need to solve the mapping clmx, clmy and clmz on the three coordinate axes respectively. Taking the solution of clmx as an example, a linear system as shown in (4) is constructed. There are n sampling points and 1≤i≤n.

(y11y12y13⋯y1ky21⋯y22⋯y23⋯⋯⋯y2k⋯yn1yn2yn3⋯ynk)(a1a2a3⋯ak)=(x1x2x3⋯xn)(4)

where yij=Ylm(θi,φi), xi=x(θi,φi) is the mapping of the radius r(θi,φi) of the surface defined at the sampling points (θi,φi) on the x-axis, j=l2+l+m+1 and k=(Lmax+1)2. c^lmx=(a1,a2,a3,…,ak) can be obtained by least square fitting and c^lmx is an estimate of the original coefficient c^lmx. Similarly, the least square estimation is used to solve the estimates c^lmy and c^lmz of clmy and clmz. And we can also get the estimate c^lm of clm. According to c^lm, the original surface is reconstructed as (5).

r(θ,φ)≈r^(θ,φ)=∑l=0Lmax∑m=−llc^lmYlm(θ,φ)(5)

3.2 Construction of Mass-Spring Force Net

After the establishment of a soft tissue model based on SHF, the force net constructed by MSM is attached to the surface of the soft tissue layer to make up for the shortcomings of SHF in force calculation. There are two kinds of forces in acupuncture simulation. The first force acts before acupuncture breaks the surface of soft tissue. Through force network simulation based on MSM, it is defined as “surface spring force”. When the surface of the tissue is punctured, the surface force disappears, and the second force begins to act, the damping force. The damping force is related to soft tissue characteristics, acupuncture speed, and acupuncture depth. The force tactile models of the three soft tissue materials are shown in Tab. 1.

Table 1: Three kinds of force tactile models about soft tissue

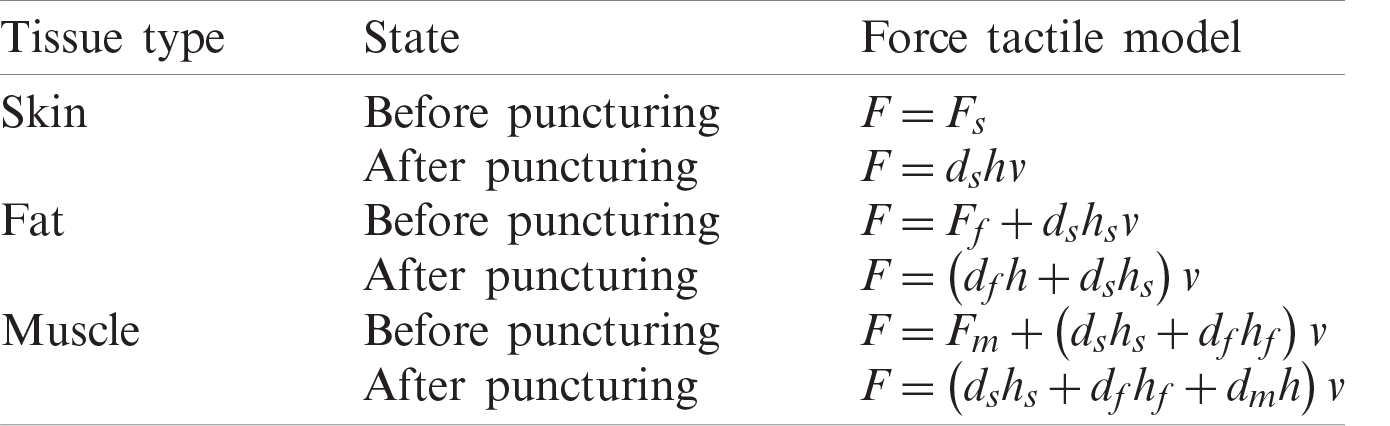
images

In Tab. 1, Fs, Ff, and Fm represent the surface force of skin, fat and muscle. h is the depth of acupuncture. hs and hf denote the thickness of skin and fat. v stands for acupuncture speed. ds, df and dm represent the damping coefficient of skin, fat and muscle. When the needle passes through these soft tissue layers, the force is transferred from layer to layer, and the operator will perceive the accumulated damping force produced by each layer of soft tissue.

The surface spring force Fs, Ff, and Fm are calculated by force net based on MSM. When the collision occurs, the force net is generated on the surface of the soft tissue model in real-time, and it will synchronously follow the deformation of soft tissue, so as to generate real-time surface force. First of all, build a force network. The mass-spring force network is composed of discrete particles connected by springs. The force network is designed with a triangle as a topology structure. The contact point N1 is taken as the center, and the radial surface concentric circles are used to layer. The adjacent mass points are equidistant. The spring connecting the adjacent particles is defined as the surface spring. The structure of the spring force network is shown in Force net structure (see Fig. 1).

As shown in Force net structure (see Fig. 1), the distribution of particles is regarded as a concentric circle. The center particle is white, which is the contact point N1, and is defined as the first layer particle. Six black particles connected to the contact point are defined as the second layer nodes. Similarly, the twelve red particles connected with the second layer are defined as the third layer particles, and so forth. w is defined as the maximum number of concentric circles of the force net, L is the length of the surface spring, and L and w can be adjusted according to the application needs and soft tissue material properties. Then, add a virtual spring to assist the calculation. The virtual spring is added to the mass point in the vertical direction. When the soft tissue is punctured, the virtual spring is removed. Cross section of virtual spring and force net (see Fig. 2) shows the cross-section of the force net with virtual spring.

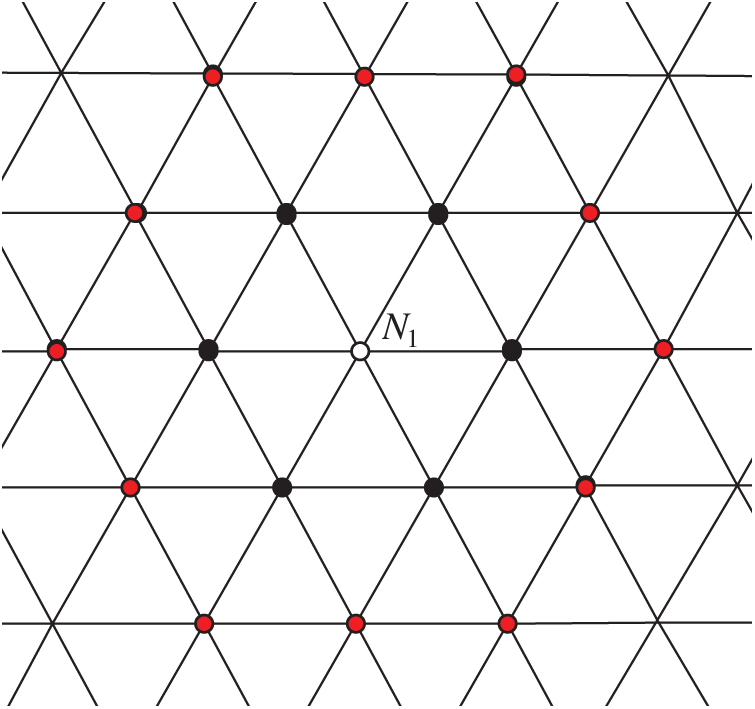
images

Figure 1: Force net structure

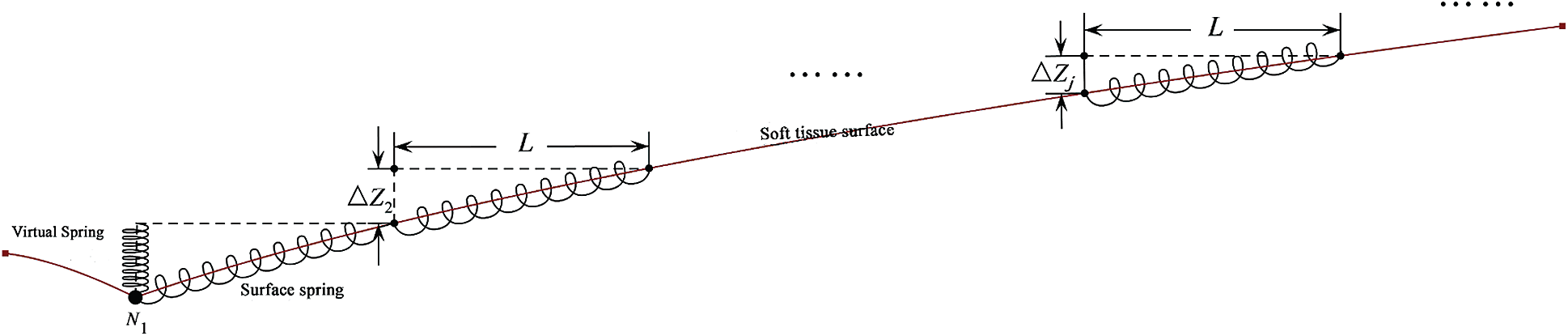
images

Figure 2: Cross section of virtual spring and force net

As shown in Cross section of virtual spring and force net (see Fig. 2), the external force is applied to the contact point N1. assuming that the concentric circle of the existing j layer is deformed, when j=w, the acupuncture reaches the critical point, and the soft tissue surface is about to be punctured. The spring force of the critical point is calculated by (6).

F=K⋅ΔZ1+K⋅∑j=2w6⋅(j−1)⋅ΔZj(6)

where K is elastic coefficient of virtual spring, and ΔZj is the deformation of particle Nj. ΔZj is the key to combine MSM and SHF, which can be obtained from the change of radius r(θ,ϕ) of the corresponding point surface.

3.3 Spring-Back Algorithm

In order to show the springback phenomenon when the soft tissue surface is punctured, a springback algorithm based on the improved shape matching algorithm [34] is adopted. The core idea of the algorithm is to define a target position, and then let the deformed particles move to its original position at a specific rate after being punctured on the surface of soft tissue. The curvature radius of SHF at the corresponding point will change synchronously with the mass of the mass spring force network. The principle of springback algorithm is shown in Schematic diagram of rebound algorithm (see Fig. 3).

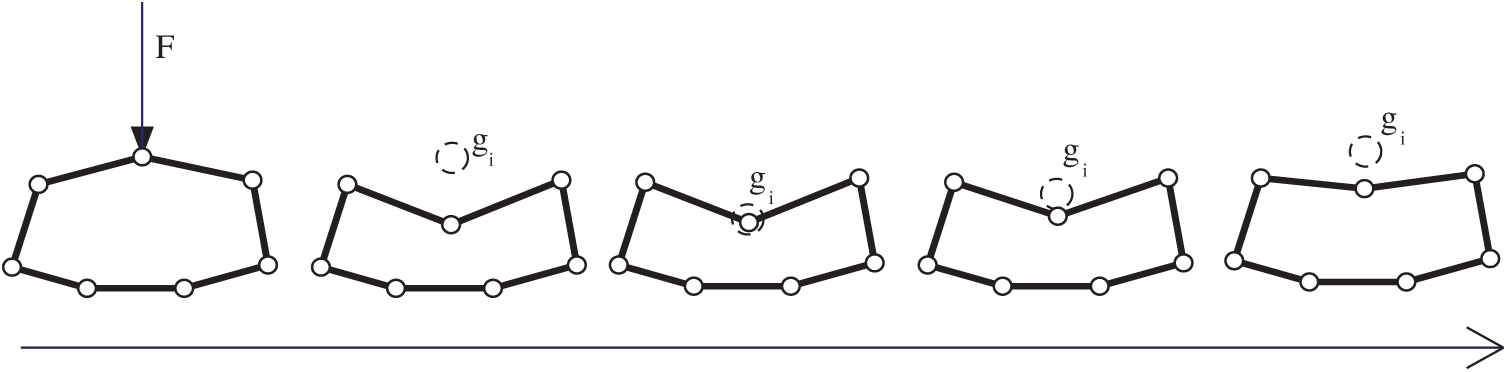
images

Figure 3: Schematic diagram of rebound algorithm

As shown in Schematic diagram of rebound algorithm (see Fig. 3), target position gi is the core of rebound algorithm. In order to obtain gi, a global deformation matrix A is defined, in which the centroid of soft tissue and the current and original positions of all deformed particles are recorded. The data in matrix A will be updated with the whole acupuncture simulation. Matrix A is defined as (7).

A=∑inMi(pi−pcm)(pi0−pcm0)(7)

where n is the number of mesh particle of soft tissue model and Mi is the particle mass. pi and pi0 are the current and original positions of each particle. pcm and pcm0 are the current and original positions of soft tissue centroid. The target position gi of each particle can be calculated by (8) according to the global deformation matrix A.

{gi=R(pi0−pcm0)+pcmR=α/Aα=ATA(8)

where R is the Rotation matrix [35], α is the symmetry coefficient and matrix AT is the transposition of matrix A. In the actual simulation, if the springback speed and springback degree are not controlled, the deformed particles will quickly return to the corresponding target position, and the springback algorithm cannot well represent the characteristics of soft tissue. In order to avoid too fast springback of soft tissue surface, it is necessary to add springback factor ηi when calculating the target position gi, as shown in (9).

{gi=gi+ηi(pi−gi)ηi=ηi−ηr(9)

According to (9), when ηi=0, particle i will directly move to the corresponding target position gi; when ηi=1, gi=pi, particle i will stay in its current position. ηr is a user-defined springback factor, which can control the springback speed of deformed particles.

4  Experiment Evaluations

4.1 System Construction

Through the construction of the virtual acupuncture system, the proposed modeling method is applied to the virtual acupuncture simulation, and the evaluation experiment is designed to study its application effect. After designing the soft tissue model, collision detection, and cutting algorithm in the virtual cutting system, the function of cutting simulation can be realized. Our system consists primarily of a mainframe computer and a haptic interaction facility called PHANTOM OMNI. The computer is based on Windows 10 and comes with an Intel(R) Xeon(R) CPU, E5-1650 v3 @ 3.5 GHz processor and NVIDIA GeForce GT 720 M graphics. The simulation is carried out on VC++ 2019 and 3DS MAX 2019 with OpenGL graphics libraries. The PHANTOM OMNI is a force feedback device that allows the operators to touch and operate on the virtual object simulated by our method. The experimental environment is shown in Experiment environment (see Fig. 4).

images

Figure 4: Experiment environment

The construction process of the system is also divided into three parts: virtual scene initialization, real-time calculation, and human-computer interaction, as shown in Fig. 5.

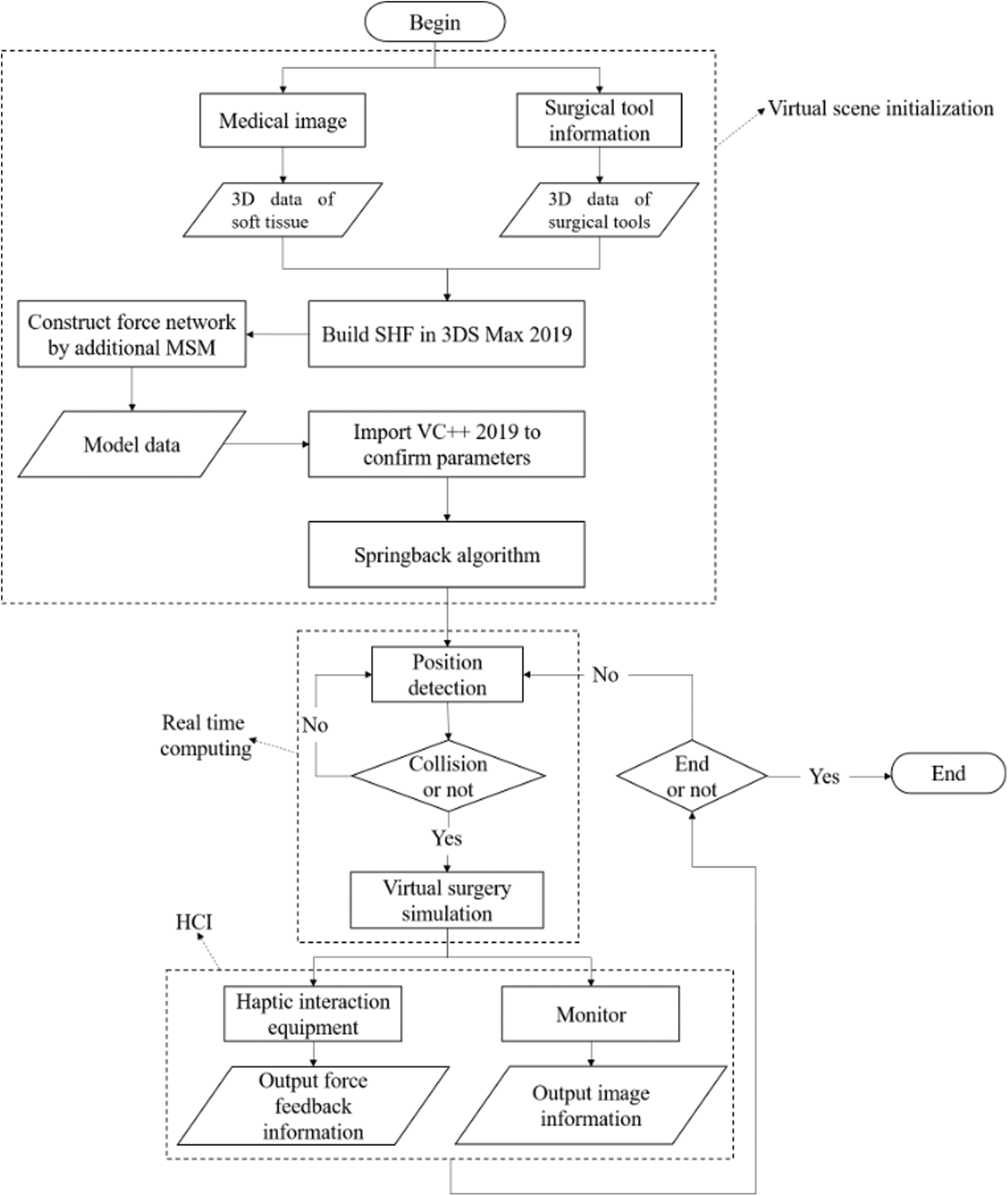
images

Figure 5: Flow chart of acupuncture system construction

First, the virtual scene is initialized. In 3DS MAX 2019, the surface of soft tissue was constructed according to SHF and 3D data, and then the force network was established by MSM, and the model data was exported as a file in obj format. Then, the model data file is imported into VC ++ 2019 and the model parameters are determined. According to the relevant research [29], the basic parameters of skin, fat, and muscle are set as shown in Tab. 2.

As shown in Tab. 2, K is the elastic coefficient of the virtual spring, d is the damping coefficient, w is the maximum number of concentric circles of the surface spring, and L is the length of the surface spring. After the parameters are determined, the rebound algorithm is written to simulate the springback phenomenon of soft tissue, and then real-time calculation and human-computer interaction are carried out, which is similar to the tumor sensing system.

According to the above process, the virtual acupuncture system is constructed, and the soft tissue acupuncture modeling method based on the mass-spring force network is applied to the acupuncture simulation. Acupuncture effect of three kinds of soft tissue (see Fig. 6) shows the rendering effect of skin, fat, and muscle before and after the puncture moment.

Table 2: Basic parameters of three types of soft tissue

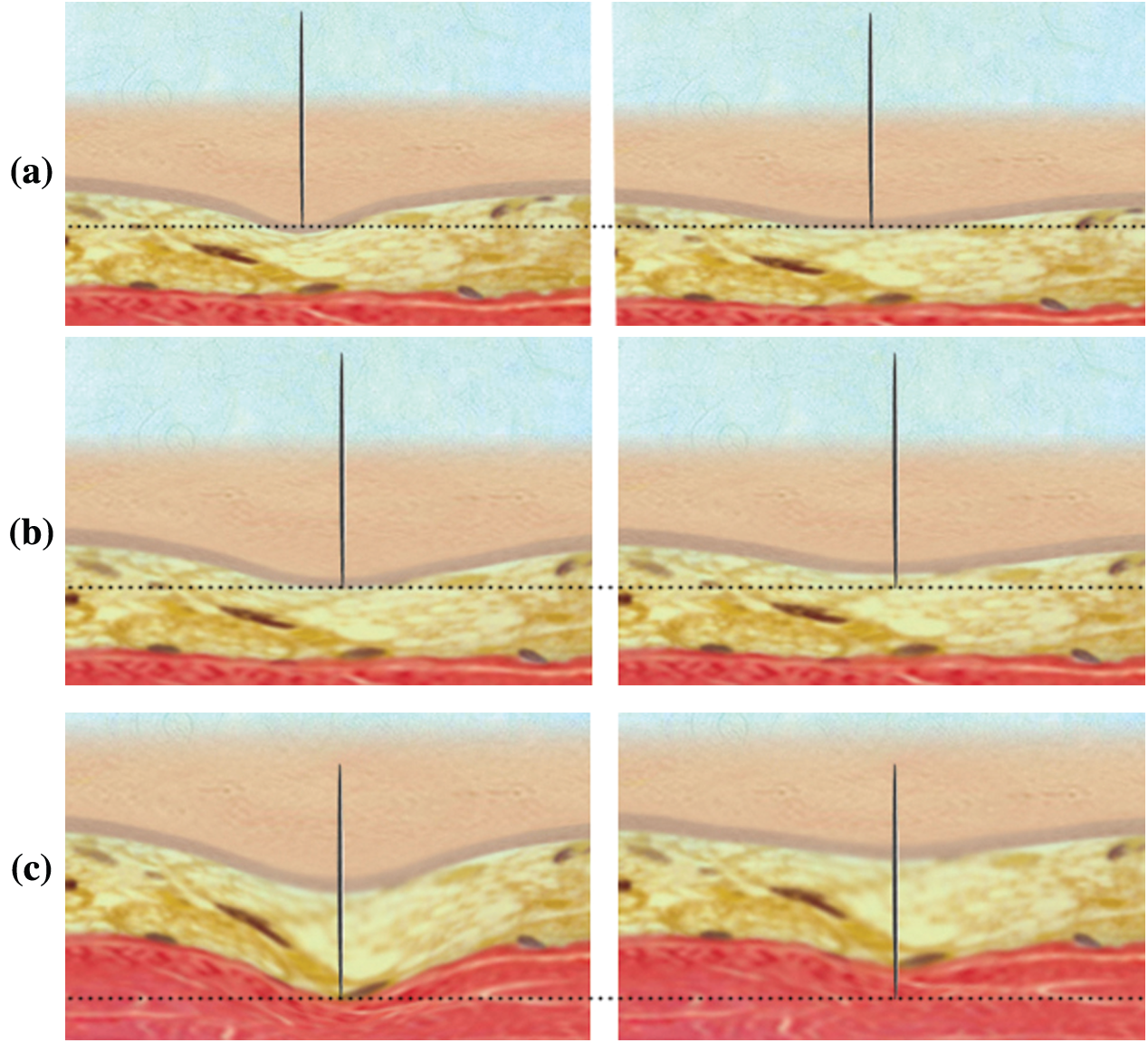
images

images

Figure 6: Acupuncture effect of three kinds of soft tissue. (a) Before and after skin puncture (b) Before and after fat puncture (c) Before and after muscle puncture

As shown in acupuncture effect of three kinds of soft tissue (see Fig. 5), the thinnest tissue layer at the top is the skin, the middle tissue layer is fat, the bottom tissue layer is a muscle, and the black dotted line is the reference line. The left image of each group of images is the rendering image intercepted before the needle punctures the soft tissue surface, while the right image is the rendered image after the needle punctures the soft tissue surface. The reference line was established based on the needle tip position before and after a puncture, and the needle tip position was not changed at the moment of puncture. In the right figure, all the soft tissue surfaces move above the reference line in varying degrees. Therefore, the model in this paper can well show the springback phenomenon [36,37] of soft tissue surface after being punctured, at the same time, the texture and elasticity of skin, fat, and muscle can be well presented.

Design and evaluate the application effect of the model in virtual acupuncture simulation. In the soft tissue acupuncture modeling method based on mass-spring force net, MSM belongs to the auxiliary model, and the accuracy of soft tissue model is mainly controlled by SHF, and the accuracy of SHF itself is better, and the research focus of this paper is not on the improvement and improvement of deformation accuracy of SHF. The key point of soft tissue acupuncture modeling method based on the mass-spring force net is to use MSM to make up for the deficiency of SHF force calculation and to simulate the rebound phenomenon in virtual acupuncture operation. The above-mentioned improvement effect is more intuitive through user experience feedback. Therefore, experts are invited to try out the virtual acupuncture system and comprehensively evaluate the system from seven indicators. In order to improve the objectivity of the scoring system, a comprehensive weighted scoring method was used to deal with the scores of the acupuncture system.

4.2 Multi-Index Comprehensive Evaluation

In order to evaluate the comprehensive performance of the soft tissue acupuncture model based on the mass-spring force net, a multi-index comprehensive evaluation experiment method was adopted, and 20 doctors from the First Affiliated Hospital of Nanjing Medical University were invited. Doctors were required to perform acupuncture operation experience and score on the virtual acupuncture system constructed from this model and other models. The acupuncture system constructed by other models, includes MSM [38], FEM [39], BEM [40], and SHF [41]. The selected models are based on four independent mainstream soft tissue models, and the modeling method is relatively pure and representative. It is suitable for comparison with the model in this paper which combines SHF and MSM, so as to measure the improvement of the simulation effect of the proposed combination method in acupuncture simulation. The virtual acupuncture system is represented by numbers, and the original construction model is hidden. Doctors can't know what kind of model the system is built. After completing the acupuncture operation experience, doctors were invited to score the five systems, with a full score of 10 points. The scoring data of the five models are shown in Appendix 3. The scoring indicators include the following seven: soft tissue material, force feedback performance, acupuncture effect, training environment, real-time, training effect, and system stability.

The comprehensive weighted scoring method was used to deal with the scores of different acupuncture systems. This comprehensive weighted scoring method has been widely used in multi-index evaluation problems [42]. This method determines the weight of each index according to the importance of the index in the whole test, and transforms the multi-index problem into a single index problem, making the evaluation results more convincing and objective. The core of the method is to determine the comprehensive weight of indicators, which is divided into two main parts: subjective weight and objective weight. In this evaluation, due to the invitation of experienced doctors, the subjective weighting method is the Delphi method [43]. In addition, since the score belongs to the unit consistent data, the mean square deviation method [44] is selected as the objective weighting method. The basic steps of the comprehensive weighted scoring method for multi-index test problems are as follows.

(1) Suppose that there are i={1,2,⋯,n} experimental schemes in the multi-index problem, including j={1,2,⋯,m} experimental indexes, the score of each experimental scheme i in each index j is recorded as xij. Each experimental protocol refers to an acupuncture operation by a physician, so n=20,m=7.

(2) Delphi method is a method based on expert knowledge and experience to determine the subjective weight. The standard steps are as follows:

Step 1: Select 10 to 30 experts with profound theoretical knowledge and rich working experience in the field. (We invited 20 experts.)

Step 2: Provide the experts with a list of indicators to be determined, and attach the relevant information on the indicators and the first round of weighting rules. Experts are required to give the weight α=(α1,α2,⋯,αm) of each index in the first round independently, where ∑j=1mαj=1.

Step 3: Retrieve the results, calculate the average value and standard deviation of each index weight in the round.

Step 4: If the standard deviation of the indicator exceeds the preset value, the average value and standard deviation of the indicators exceeding the preset value of the standard deviation are provided to the experts as reference materials. Therefore, all experts will modify the weight according to the new reference material, and give the weight of each index again.

Step 5: Repeat steps 3 and 4 until the standard deviation of each index weight given by the expert does not exceed the predetermined value. At this time, the expert opinion basically reached an agreement.

After completing step 5, the average value of each index weight is taken as the subjective weight of the index. The standard deviation of the index is 0.1. Each model has the same subjective weight. According to the Delphi method, the subjective weight of indicators is shown in Tab. 3.

Table 3: Subjective weight

images

(3) The objective weight is determined according to the mean square deviation method, which is an objective weighting method based on data determination, and the evaluation data need to have the same unit. The steps are as follows:

Step 1: Calculate the average value of the score xij of each index j in each experimental scheme i, as shown in (10).

E(j)=1n∑i=1nxij(10)

Step 2: Calculate the mean square error of xij as shown in (11).

σ(j)=1n∑i=1n(xij−E(j))2(11)

Step 3: Calculate the objective weight βj of each index, as shown in (12).

βj=σ(j)/∑j=1mσ(j)(12)

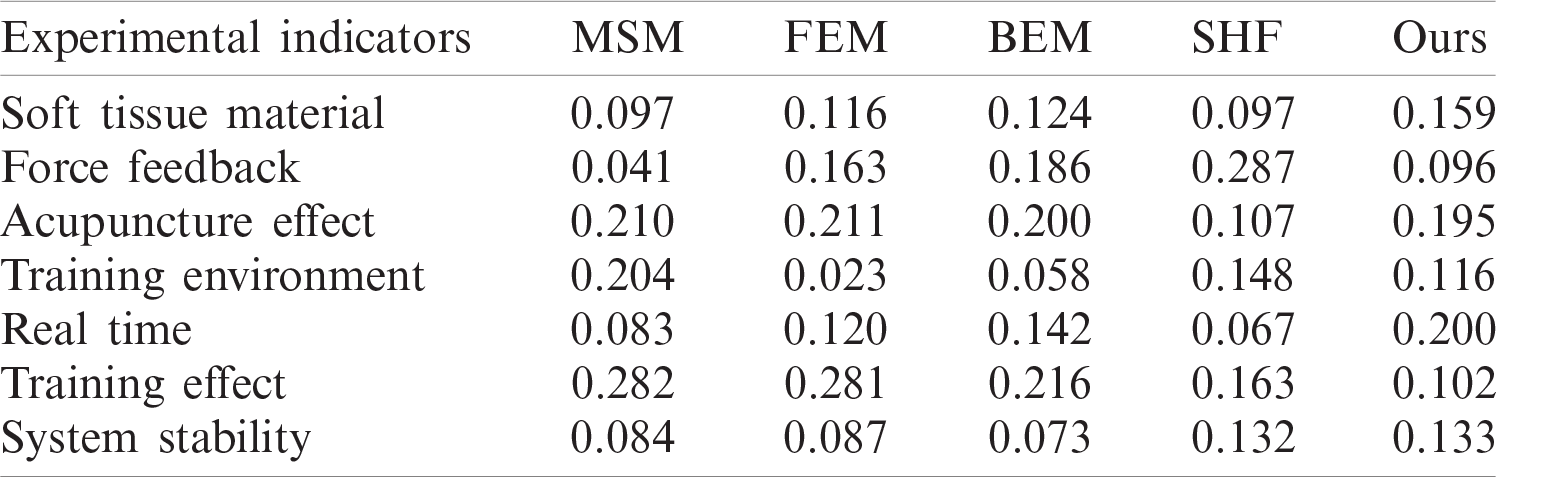
Different doctors have different scores of the systems constructed by different models. Because the mean square deviation method is an objective weight assignment method based on the scores, the systems constructed by different models have different objective weights, which can balance the subjective preferences of raters. According to the mean square deviation method, the objective weight of each index is shown in Tab. 4.

Table 4: Objective weight

images

(4) According to the subjective weight and objective weight, the comprehensive weight ωj is calculated, and the final score of all models is calculated. In order to take into account the subjective and objective weights and achieve the unity of subjective and objective, the calculation of comprehensive weight is shown in (13).

ωj=μαj+(1−μ)βj(13)

where μ is preference coefficient and 0<μ<1. The larger μ is, the greater the influence of subjective weight is; otherwise, the greater the influence of objective weight is. In this assessment, The value of μ is set to 0.4. Therefore, the final score fi of all experimental schemes can be calculated according to (14).

fi=∑j=1mωjxij(14)

The comprehensive score fi of all experimental schemes of the five models was calculated as column chart 7 The columns with different color blocks represent the scores of different doctors.

The average scores of MSM, FEM, BEM, SHF, and our model are 7.83, 7.90, 7.93, 7.88, and 8.94 respectively. As shown in Fig. 7, doctors generally believe that the acupuncture system proposed in the present research has a better performance than the acupuncture system simulated by other models, and the doctors’ opinions are more unified.

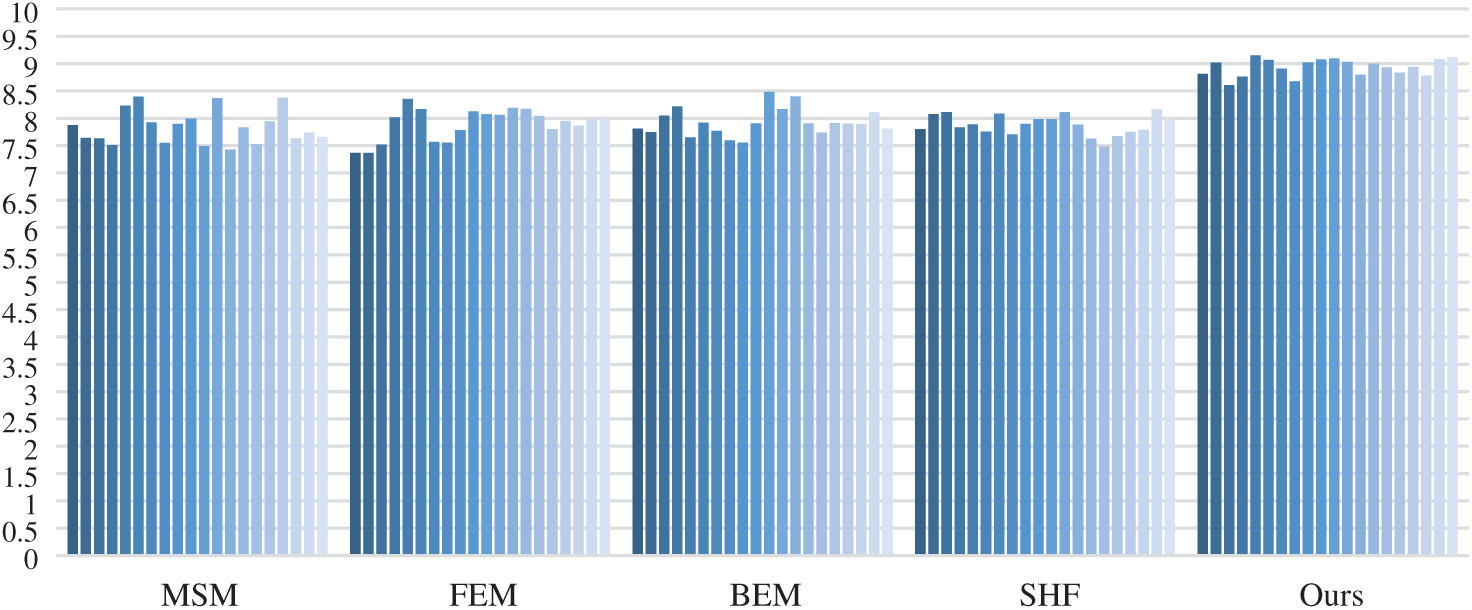
images

Figure 7: Comprehensive scores of all experimental schemes

5  Conclusions

In this paper, a soft tissue acupuncture modeling method [45,46] based on a mass-spring force network is proposed, and its application in acupuncture simulation is discussed. Because SHF can accurately track the needling point, SHF is used to simulate the tissue surface. However, SHF is more complex in force calculation. MSM is used to simulate the force net generated on the soft tissue surface in real-time, which makes up for the deficiency of SHF in force calculation. The two models are combined with the parametric surface radius of SHF, which can provide deformation data needed in the MSM force network at the same time, thus combining the advantages of SHF’s fast collision detection and MSM’s accurate force calculation. In addition, a springback algorithm is proposed to simulate the springback phenomenon when the soft tissue surface is punctured. Through the construction of the virtual acupuncture system, the soft-tissue acupuncture modeling method based on mass-spring force network was applied to virtual acupuncture simulation, and the evaluation experiment was designed to study its application effect. The multi-index comprehensive evaluation experiment was adopted, and doctors were invited to try out the acupuncture system in to score, and compared with other mainstream soft tissue model construction acupuncture system. In order to obtain more convincing scoring data, a comprehensive weighted scoring method was used to process physician's score data. The experimental results show that the model has higher scores and better performance than other models in soft tissue material, force feedback performance, puncture effect, training environment, real-time, training effect, and system stability.

Funding Statement: This work was supported, in part, by the National Nature Science Foundation of China under Grant Numbers 61773219; in part, by the Natural Science Foundation of Jiangsu Province under Grant Number BK20201136, BK20191401; in part, by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund; in part, by the Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET) fund; NUIST Students’ Platform for Innovation and Entrepreneurship Training Program.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. L. Guerriero, G. Quero, M. Diana, L. Soler, V. Agnus et al., “Virtual reality exploration and planning for precision colorectal surgery,” Diseases of the Colon & Rectum, vol. 61, no. 6, pp. 719–723, 2018.
  2. R. Joy, W. Santee and R. Aronovich, “Genioglossus advancement surgery—A modified technique using virtual surgical planning and a custom cutting guide,” International Journal of Oral and Maxillofacial Surgery, vol. 46, pp. 262, 2017.
  3. T. Steinhuber, S. Brunold, C. Gartner, V. Offermanns, H. Ulmer et al., “Is virtual surgical planning in orthognathic surgery faster than conventional planning? A time and workflow analysis of an office-based workflow for single-and double-jaw surgery,” Journal of Oral and Maxillofacial Surgery, vol. 76, no. 2, pp. 397–407, 2018.
  4. R. S. Campos, L. Marcelo and W. Rodrigo, “A GPU-based heart simulator with mass-spring systems and cellular automaton,” The Journal of Supercomputing, vol. 69, no. 1, pp. 1–8, 201
  5. Y. Cicek and D. Alpaslan, “The modelling of interactions between organs and medical tools: A volumetric mass-spring chain algorithm,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 17, no. 5, pp. 488–496, 2014.
  6. D. Thanoon, G. Marc and L. Barbara, “Deriving indicators for breast conserving surgery using finite element analysis,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 18, no. 5, pp. 533–544, 2015.
  7. C. J. Paulus, L. Untereiner, H. Courtecuisse, S. Cotin and D. Cazier, “Virtual cutting of deformable objects based on efficient topological operations,” The Visual Computer, vol. 31, no. 6–8, pp. 831–841, 2015.
  8. N. Haouchine, S. Cotin, I. Peterlik, J. Dequidt, M. S. Lopez et al., “Impact of soft tissue heterogeneity on augmented reality for liver surgery,” IEEE Transactions on Visualization and Computer Graphics, vol. 21, no. 5, pp. 584–597, 2014.
  9. Y. Yeung, C. Jessica and P. Alex, “Interactively cutting and constraining vertices in meshes using augmented matrices,” ACM Transactions on Graphics, vol. 35, no. 2, pp. 1–17, 2016.
  10. M. Townsend and S. Nesrin, “Updated Lagrangian finite element formulations of various biological soft tissue non-linear material models: A comprehensive procedure and review,” Computer Methods in Biomechanics and BiomediCal engineering, vol. 19, no. 11, pp. 1137–1142, 2016.
  11. C. N. Le, F. Rigollet and D. Petit, “An experimental identification of line heat sources in a diffusive system using the boundary element method,” International Journal of Heat and Mass Transfer, vol. 43, no. 12, pp. 2205–2220, 2000.
  12. D. Chen, W. Chen, L. Huang, X. Feng, T. Peters et al., “BEM-based simulation of lung respiratory deformation for CT-guided biopsy,” International Journal of Computer Assisted Radiology and Surgery, vol. 12, no. 9, pp. 1585–1597, 2017.
  13. P. Wang, A. A. Becker, I. A. Jones, A. T. Glover, S. D. Benford et al., “Virtual reality simulation of surgery with haptic feedback based on the boundary element method,” Computers & Structures, vol. 85, no. 7–8, pp. 331–339, 2007.
  14. H. B. Cheong, J. R. Park and H. G. Kang, “Fourier-series representation and projection of spherical harmonic functions,” Journal of Geodesy, vol. 86, no. 11, pp. 975–990, 2012.
  15. Y. H. Fang, W. U. Bin and Z. Y. Yang, “Research of soft tissue material haptic rendering based on spherical harmonic representation,” Computer Engineering and Design, vol. 32, no. 9, pp. 3091–3094, 2011.
  16. X. R. Zhang, W. F. Zhang, W. Sun, T. Xu and K. J. Sunil, “A robust watermarking scheme based on ROI and IWT for remote consultation of COVID-19,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1435–1452, 2020.
  17. X. R. Zhang, X. F. Yu, W. Sun and A. G. Song, “Soft tissue deformation model based on marquardt algorithm and enrichment function,” Computer Modeling in Engineering & Sciences, vol. 124, no. 3, pp. 1131–1147, 2020.
  18. X. R. Zhang, X. F. Yu, W. Sun and A. G. Song, “An optimized model for the local compression deformation of soft tissue,” KSII Transactions on Internet and Information Systems, vol. 14, no. 2, pp. 671–686, 2020.
  19. S. Wang, L. Chu, Y. Fu and W. Gao, “An unfixed-elasticity mass spring model based simulation for soft tissue deformation,” in Proc. of the IEEE Int. Conf. on Mechatronics and Automation, pp. 309–314, 2014.
  20. M. Lan, G. Chen and N. Wang, “Study on real-time simulation method of soft tissue puncture based on fast mass spring,” Journal of Guizhou University, vol. 34, no. 5, pp. 76–82, 2017.
  21. Y. Wang and S. Guo, “Elasticity analysis of Mass-spring model-based virtual reality vascular simulator,” in Proc. of the IEEE Int. Conf. on Mechatronics & Automation, pp. 292–297, 2014.
  22. L. Yan, “Simulation of soft tissue deformation based on improved mass-spring model,” Computer Simulation, vol. 29, no. 7, pp. 330–333, 2012.
  23. X. Zhi, Z. Zhang, Y. Gao and Z. Zhang, “Real-time vascular beating analog based on the mass-spring model,” in Proc. of the Ninth Int. Conf. on Intelligent Information Hiding & Multimedia Signal Processing, 2014.
  24. S. Farhang, A. H. Foruzan and Y. W. Chen, “A real-time stable volumetric mass-spring model based on a multi-scale mesh representation,” in Proc. of the 23rd Iranian Conf. on Biomedical Engineering and 1st Int. Iranian Conf. on Biomedical Engineering, pp. 165–169, 2016.
  25. Y. Duan, W. Huang, H. Chang, W. Chen, J. Zhou et al., “Volume preserved mass-spring model with novel constraints for soft tissue deformation,” IEEE Journal of Biomedical and Health Informatics, vol. 20, no. 1, pp. 268–280, 2014.
  26. M. Kibsgaard, K. K. Thomsen and M. Kraus, “Simulation of surgical cutting in deformable bodies using a game engine,” in Proc. of the Int. Conf. on Computer Graphics Theory and Applications, pp. 1–6, 2014.
  27. J. J. Pan, J. Chang, X. Yang, H. Liang, J. J. Zhang et al., “Virtual reality training and assessment in laparoscopic rectum surgery,” International Journal of Medical Robotics & Computer Assisted Surgery, vol. 11, no. 2, pp. 194–209, 2015.
  28. J. Tang, X. Lang, L. He, S. Guan, X. Ming et al., “Virtual laparoscopic training system based on VCH model,” Journal of Medical Systems, vol. 41, no. 4, pp. 58, 2017.
  29. Y. Tai, L. Wei, H. Zhou, S. Nahavandi and J. Shi, “Tissue and force modelling on multi-layered needle puncture for percutaneous surgery training,” in Proc. of the IEEE Int. Conf. on Systems, Man, and Cybernetics, pp. 2923–2927, 2017.
  30. J. Guo and S. Guo, “Design and characteristics evaluation of a novel VR-based robot-assisted catheterization training system with force feedback for vascular interventional surgery,” Microsystem Technologies, vol. 23, pp. 1–10, 2016.
  31. W. Sun, X. Zhang and X. He, “Lightweight image classifier using dilated and depthwise separable convolutions,” Journal of Cloud Computing, vol. 9, no. 1, pp. 1–12, 2020.
  32. W. Sun, X. Zhang, X. Zhang, G. Zhang and N. Ge, “Triplet erasing-based data augmentation for person re-identification,” International Journal of Sensor Networks, vol. 34, no. 4, pp. 226–235, 2020.
  33. S. Spadaro, S. Grasso, V. Cricca, F. C. Dalla, R. M. Di et al., “Comparing two different modes of mechanical ventilation by the least square fitting method: nava versus PSV,” Intensive Care Medicine Experimental, vol. 3, no. S1, pp. 1–3, 2015.
  34. K. Qian, J. Bai, X. Yang, J. Pan and J. Zhang, “Virtual reality based laparoscopic surgery simulation,” in Proc. of the 21st ACM Symp. on Virtual Reality Software and Technology, pp. 69–78, 2015.
  35. S. I. Kruglov and V. Barzda, “Modified gibbs’s representation of rotation matrix,” arXiv preprint arXiv, vol. 42, no. 2, pp. 1–17, 2017.
  36. Y. Mehmood and W. Shahzad, “An accelerated convergent particle swarm optimizer (ACPSO) of multimodal functions,” Intelligent Automation & Soft Computing, vol. 25, no. 1, pp. 91–103, 2019.
  37. Y. Li, Y. Wang and Y. Zhu, “Visual relationship detection with contextual information,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1575–1589, 2020.
  38. J. Q. Hu, Y. J. Feng, S. Q. Zhou, L. P. Huang, Q. R. Zeng et al., “An improved mass spring model based on internal point set domain constraint,” in Proc. of the 29th Chinese Control and Decision Conf., pp. 6826–6831, 2017.
  39. W. Tang and T. R. Wan, “Constraint-based soft tissue simulation for virtual surgical training,” IEEE Transactions on Bio-Medical Engineering, vol. 61, no. 11, pp. 2698–2706, 2014.
  40. B. Zhu and L. Gu, “A hybrid deformable model for real-time surgical simulation,” Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society, vol. 36, no. 5, pp. 356–365, 2012.
  41. Y. Fang and B. Wu, “An novel method of soft tissue haptic rendering based on the spherical harmonic representation,” in Proc. of the 2nd Int. Conf. on Information Science and Engineering, pp. 1847–1850, 2011.
  42. X. Han, L. Zhu and C. F. Yan, “Optimization of ethanol reflux extraction technique for panax ginseng by multi-index comprehensive weighted score evaluation,” Modern Chinese Medicine, vol. 20, no. 4, pp. 68–72, 2016.
  43. H. Guo, X. Wang, L. Wang and D. Chen, “Delphi method for estimating membership function of uncertain set,” Journal of Uncertainty Analysis & Applications, vol. 4, no. 1, pp. 3–13, 2016.
  44. S. Beheshti, M. Hashemi, E. Sejdic and T. Chau, “Mean square error estimation in thresholding,” IEEE Signal Processing Letters, vol. 18, no. 2, pp. 103–106, 2011.
  45. A. Bachir, I. M. Almanjahie and M. K. Attouch, “The k nearest neighbors estimator of the m-regression in functional statistics,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2049–2064, 2020.
  46. L. Wang, D. Gao, J. Fu, Y. Luo and S. Zhao, “Simulation of coupling process of flexible needle insertion into soft tissue based on abaqus,” Computers, Materials & Continua, vol. 64, no. 2, pp. 1153–1169, 2020.
images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.