Computers, Materials & Continua DOI:10.32604/cmc.2021.018191
Article

A New BEM Modeling Algorithm for Size-Dependent Thermopiezoelectric Problems in Smart Nanostructures

Mohamed Abdelsabour Fahmy1,2,*

1Department of Mathematics, Jamoum University College, Umm Al-Qura University, Alshohdaa, 25371, Jamoum, Makkah, Saudi Arabia
2Department of Basic Sciences, Faculty of Computers and Informatics, Suez Canal University, New Campus, Ismailia, 41522, Egypt
*Corresponding Author: Mohamed Abdelsabour Fahmy. Email: maselim@uqu.edu.sa
Received: 28 February 2021; Accepted: 09 April 2021

Abstract: The main objective of this paper is to introduce a new theory called size-dependent thermopiezoelectricity for smart nanostructures. The proposed theory includes the combination of thermoelastic and piezoelectric influences which enable us to describe the deformation and mechanical behaviors of smart nanostructures subjected to thermal, and piezoelectric loadings. Because of difficulty of experimental research problems associated with the proposed theory. Therefore, we propose a new boundary element method (BEM) formulation and algorithm for the solution of such problems, which involve temperatures, normal heat fluxes, displacements, couple-tractions, rotations, force-tractions, electric displacement, and normal electric displacement as primary variables within the BEM formulation. The computational performance of the proposed methodology has been demonstrated by using the generalized modified shift-splitting (GMSS) iteration method to solve the linear systems resulting from the BEM discretization. GMSS advantages are investigated and compared with other iterative methods. The numerical results are depicted graphically to show the size-dependent effects of thermopiezoelectricity, thermoelasticity, piezoelectricity, and elasticity theories of nanostructures. The numerical results also show the effects of the size-dependent and piezoelectric on the displacement components. The validity, efficiency and accuracy of the proposed BEM formulation and algorithm have been demonstrated. The findings of the current study contribute to the further development of technological and industrial applications of smart nanostructures.

Keywords: Boundary element method; size-dependent thermopiezoelectricity; smart nanostructures

1  Introduction

Nanoscience is that science through which atoms can be moved and manipulated in order to obtain the properties we need in a specific field of life, as for nanotechnology, it is concerned with manufacturing devices that can be used to study the properties of nanomaterials [1,2]. Nanostructures are one of the main products of nanotechnology. A nanostructure is a structure that has at least one dimension equal or less than 100 nanometers. Understanding the mechanical behaviour of deformed nanostructures is of great importance due to their applications in all fields such as industry, medicine, renewable energy, military and civil and architecture Engineering. In the field of industry, certain nanoparticles can be used in the manufacture of filters to purify and desalinate water more efficiently than other types of filters, and they are also used as a heat insulator with high efficiency. Some nanomaterials such as tungsten carbide and silicon carbide are distinguished by their high strength compared to ordinary materials, so they are used in the manufacture of some tools Cutting and drilling. Dust and water-repellent paints, clothing, and glass can also be made [3]. Recent developments in nanoscale electronics and photonics might lead to new applications such as high-density memory, high-speed transistors and high-resolution lithography [4–6]. In the medical field, certain nanoparticles can be used as drug-carrying materials, as these materials have a special sensitivity to the place to which the drug is intended to be sent, so when they reach it inside the human body, they release the drug accurately, in addition to promising research confirming the possibility of using nanomaterials as a treatment for cancer. Gold nanoparticles are also used in home testing devices to detect pregnancy. Nanowires are used as nanoscale biosensors to detect a large number of diseases in their early stages [7,8]. In the field of renewable energy, nanomaterials are involved in the manufacture of solar cells that are used in the production of electrical energy, where materials such as cobalt oxide or semi-conductive materials in general such as silicon and germanium are deposited on glass sheets or silica plates and because these materials have a nanoscale size, the surface area that is exposed to sunlight is greater, and thus we ensure that we absorb the largest amount of sunlight in a single cell. The panel usually consists of hundreds of solar cells that are connected through an electrical circuit that converts solar energy into electrical energy. In the military field, nanomaterials enter into the manufacture of nanoscale cylinders that are characterized by strength and rigidity, in addition to a storage capacity a million times greater than regular computers, the manufacture of military clothing that has the ability to absorb radar waves in order to stealth and infiltrate, and the manufacture of nanosatellites [9–11]. In the field of building and construction, some nanomaterials such as titanium dioxide TiO2, carbon nanotubes CNTs and silica nanoparticles are added to concrete to increase the durability and hardness of the concrete in addition to increasing its resistance to water penetration. Size-dependent porothermoelastic [12–15] interactions play a significant role in many areas of nanotechnology applications. Because of computational complexity in solving size-dependent thermopiezoelectric problems not having any general analytical solution [16], therefore, numerical methods should be developed to solve such problems. Among these numerical methods is the boundary element method (BEM) that has been used for engineering models [17], bioheat transfer models [18], and nanostructures [19]. The main feature of BEM [20] over the domain type methods [21] is that only boundary of the considered domain needs to be discretized. This feature is of great importance for solving complex nanoscience and nanotechnology problems with fewer elements, and requires less computational cost, less preparation of input data, and therefore easier to use.

In the present paper, we introduce a new theory called size-dependent thermopiezoelectricity for smart nanostructures to describe the mechanical behaviors of deformed nanostructures subjected to various types of mechanical, thermal, and piezoelectric loadings. Also, we develop a new boundary element formulation for solving the deformation problems associated with the proposed theory. The numerical results illustrate the size-dependent effects on the thermo-piezoelectric, thermoelastic, piezoelectric, and elastic smart nanostructures. The numerical results also show the effects of the length scale parameter and piezoelectric coefficient on the displacement components, and confirm the validity, efficiency and accuracy of the proposed BEM formulation and algorithm.

2  Formulation of the Problem

Consider a size-dependent thermopiezoelectric nanostructure occupies the cylindrical region V (cross section of the nanostructure in the x1x2-plane) that bounded by S, such that x3-axis parallel to the cylinder axis, as shown in Fig. 1. We take nα to be the outward unit vector that is perpendicular to the boundary surface S as follows

nα=εαβdxβds(1)

where εαβ(ε12=−ε21=1,ε11=ε22=0) is the two-dimensional permutation symbol.

Figure 1: Size-dependent thermopiezoelectric nanostructure definition

In the two-dimensional plane, all quantities are independent of x3. The deformation is described by the displacement vector u=(u1,u2), and the electric effect is specified by the electric potential ϕ

The rotation component is

ω=ω3=12(u2,1−u1,2)=12εαβuβ,α(2)

where

The electric field components are

Eα=−ϕ,α(3)

The strain tensor and the mean curvature vector

eαβ=12(uα,β+uβ,α)(4)

kα=εαβk3β=12εαβω,β(5)

where kα(k1=k32=12ω,2,k2=−k31=−12ω,1) is the mean curvature vector, kαβ(k3α=−kα3=12ω,α) is the pseudo mean curvature tensor.

The true couple-stress vector Mi can be expressed in terms of pseudo couple-stress tensor Mkj as

Mi=12εijkMkj(6)

where the true couple-stress vector Mi satisfies Mα=εαβM3β,M1=−M23,M2=M13,M3=M21=0, and Mij=−Mji, and εijk is the three-dimensional Levi–Civita permutation symbol.

The force-stress tensor can be decomposed into the following two parts

σαβ=σ(αβ)+σ[αβ](7)

where σαβ(σ3α=σα3=0) is the force-stress tensor, σ(αβ) is the symmetric force-stress tensor and σ[αβ] is the skew-symmetric force-stress tensor.

The electric field and mechanical deformation can induce polarization Pα in the piezoelectric material. The electric displacement Dα is given as

Dα=ε0Eα+Pα(8)

where ε0 is the vacuum permittivity, Eα is the electric field, Pα is the polarization of piezoelectric material.

The governing equations of size-dependent thermopiezoelectric problems in smart nanostructures subjected to various types of mechanical, thermal and piezoelectric loadings can be expressed as

The entropy balance equation

−qα,α+Q=0(9)

where qα is the heat flux vector.

The force equilibrium equation

σβα,β+Fα=0(10)

where Fα is the body force vector.

The moment equilibrium equation

σ[βα]=−M[α,β],σ[21]=−σ[12]=−M[1,2](11)

The Gauss’s law for electric field can be expressed as

Dα,α=ρE(12)

where ρE is the volume electric charge density.

Substitution of Eqs. (12) and (17) into force equilibrium Eq. (16) leads to

[σ(βα)−M[α,β]],β+Fα=0(13)

The constitutive relations of size-dependent thermopiezoelectric nanostructures can be written as:

The heat flux vector equation

qα=−kT,α(14)

The symmetric force-stress equation

σ(αβ)=λeγγδαβ+2μeαβ−(3λ+2μ)α¯Tδαβ(15)

where α¯ is the coefficient of thermal expansion, δαβ is the Kronecker delta function

the couple-stress equation

Mα=−8μl2kα+2fEα(16)

the electric displacement equation

Dα=εEα+4fkα(17)

Also, the force-traction vector tα, couple-traction m, and normal electric displacement d can be written as follows

tα=σβαnβ(18)

m=εβαMαnβ=M2n1−M1n2(19)

d=Dαnα(20)

where f is the piezoelectric coefficient.

The Lamé elastic constants λ ad μ for an isotropic material, can be related to the Poisson ratio v and Young's modulus E as

E=2μ(1+v),λ=2μv1−2v(21)

where v is the Poisson ratio, E is the Young’s modulus,

The electric permittivity of the material can be defined as

ε=εrε0(22)

where εr is relative permittivity.

The material length scale parameter used in couple stress theories can be written as

l2=ημ(23)

where η is the couple-stress parameter.

Now, the total force-stress tensor σβα can be expressed as

σβα=λeγγδαβ+2μeαβ+2μl2εαβ∇2ω−E1−2να¯Tδαβ(24)

Hence, the governing Eqs. (9), (10) and (12) can be written as

k∇2T+Q=0(25)

where k is the thermal conductivity, T is the temperature and Q is an external heat source.

[λ+μ(1+l2∇2)]uβ,βα+μ(1−l2∇2)∇2uα−E1−2να¯T,α+Fα=0(26)

ε∇2ϕ+ρE=0(27)

Now, the normal heat flux q, force-traction vector tα, couple-traction m, and normal electric displacement d can be written as follows

q=qαnα=−k∂T∂n(28)

tα=σβαnβ=(λeγγδαβ+2μeαβ+2μl2εαβ∇2ω−E1−2να¯Tδαβ)nβ(29)

m=εβαμαnβ=4μl2∂ω∂n−2f∂ϕ∂s(30)

d=Dαnα=−ε∂ϕ∂n+2f∂ω∂s(31)

3  Boundary Conditions

The considered boundary conditions may specify either temperature change T or normal heat flux q

T=T¯on ST(32)

q=q¯on Sq,ST∪Sq=S,ST∩Sq=∅(33)

Displacements uα or force-tractions tα

uα=u¯αon Su(34)

tα=t¯αon St,Su∪St=S,Su∩St=∅(35)

Rotation ω or couple-traction m

ω=ω¯on Sω(36)

m=m¯on Sm,Sω∪Sm=S,Sω∩Sm=∅(37)

and electric potential ϕ or normal electric displacement d

ϕ=ϕ¯on Sϕ(38)

d=d¯ on Sd,Sϕ∪Sd=S,Sϕ∩Sd=∅(39)

where ST, Sq, Su, St, Sω, Sm, Sϕ and Sd are the boundary parts at which the boundary values for the temperature change T, the normal heat flux q, the displacement vector uα, the force-traction vector tα, the rotation ω, the couple-traction m, the electric potential ϕ and the normal electric displacement d are specified.

4  Boundary Element Implementation

Now, we can write the boundary integral equations for temperature, displacements, rotation, and potential as follows

cQ∗(ξ)T(ξ)−∫SqQ∗(x,ξ)T(x)dS(x)=−∫STQ∗(x,ξ)q(x)dS(x)+∫VTQ∗(x,ξ)Q(x)dV(x)(40)

cαβ(ξ)uα(ξ)+∮StαβF*(x,ξ)uα(x)dS(x)+∫SmβF*(x,ξ)ω(x)dS(x)+∫ShβF*(x,ξ)T(x)dS(x)+∫SdβF*(x,ξ)ϕ(x)dS(x)=∫SuαβF*(x,ξ)tα(x)dS(x)+∫SωβF*(x,ξ)m(x)dS(x)+∫VuαβF*(x,ξ)Fα(x)dV+∫SfβF*(x,ξ)q(x)dS(x)−∫VfβF*(x,ξ)Q(x)dV(41)

cω(ξ)ω(ξ)+∫StαC*(x,ξ)uα(x)dS(x)+∮SmC*(x,ξ)ω(x)dS(x)+∮SdC*(x,ξ)ϕ(x)dS(x)=∫SuαC*(x,ξ)tα(x)dS(x)+∫SωC*(x,ξ)m(x)dS(x)+∫VuαC*(x,ξ)Fα(x)dV(42)

cϕ(ξ)ϕ(ξ)+∮SmR*(x,ξ)ω(x)dS(x)+∮SdR*(x,ξ)ϕ(x)dS(x)=∫SϕR*(x,ξ)d(x)dS(x)−∫VϕR*(x,ξ)ρE(x)dV(43)

where the superscripts Q∗, F∗, C∗ and R∗ are chosen to be kernel functions associated with point heat source, point force, point couple and point electrical source infinite space fundamental solutions, respectively, and ∮denotes the Cauchy principal value symbol. denotes the Cauchy principal value symbol. The full details for the derivations of the fundamental solutions used in the current formulation are given in [22–24].

The integral Eqs. (40)–(43) in absence of body forces and volume charge density can be written in matrix form as follows

=∫s[−ϑQ∗000fβF∗(x,ξ)uαβF∗(x,ξ)ωβF∗(x,ξ)00uαC∗(x,ξ)ωC∗(x,ξ)0000ϕR∗(x,ξ)][q(x)tα(x)m(x)d(x)]dS(x)(44)

Now, it is convenient to rewrite Eq. (44) in compact index-notation form as

cIJ(ξ)uI(ξ)+∮StIJ∗(x,ξ)uI(x)dS(x)=∫suIJ∗(x,ξ)tI(x)dS(x)(45)

where the generalized displacements uI in (45) include temperature T, displacement uα, rotation ω and electric potential ϕ, respectively. Similarly, the generalized tractions tI include normal flux q, force-tractions tα, couple-traction m and normal electric displacement d, respectively.

This leads to the following linear algebraic equations system

Tu=Ut(46)

where T and U are dense matrices related with the left and right hand sides of Eq. (44), respectively, and u represents the nodal boundary temperature, displacement, rotation and electric potential, respectively, while, t represents the nodal boundary normal flux, force-tractions, couple-tractions and normal electric displacement, respectively.

which can be written as

AX=B(47)

where A is the non-symmetric dense matrix, B is the known boundary values vector and X is the unknown boundary vector of unknown boundary values vector.

5  Numerical Results and Discussion

To illustrate the numerical calculations computed by the proposed methodology, we consider the thermopiezoelectric nanoplate with free boundary conditions on the sides, as shown in Fig. 2. A variable temperature field in the x2-direction is generated by applying Tb and Tt to the bottom and top surfaces, respectively. Also, a uniform electric field in the x2-direction is generated by applying constant electric potentials ϕb and ϕt to the bottom and top surfaces, respectively. Under thermal and piezoelectric loadings, the plate deforms and becomes electrically polarized. As a result, the thermal effect is specified by the thermal expansion coefficient α¯, the size dependent effect is specified by one characteristic length scale parameter l, and the piezoelectric effect is specified by one piezoelectric coefficient f.

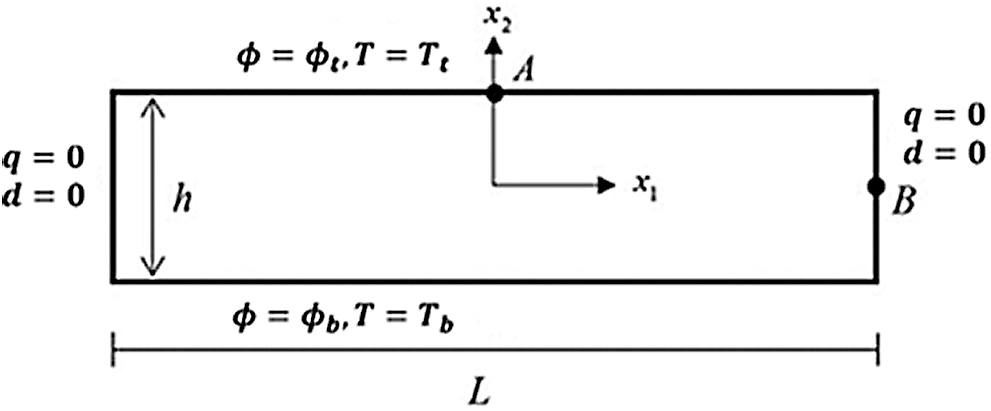
Figure 2: Geometry of the free piezo-thermo-elastic nanoplate

The solid line represents the Case A that corresponds to the size-dependent thermo-piezoelectric plates (α¯=1,f=−1). The dashed line represents the Case B which corresponds to size-dependent thermoelastic plates (α¯=1,f=0). The dash-dot line represents the Case C that corresponds to size-dependent piezoelectric plates (α¯=0,f=−1). The dash-two dot line represents the Case D which corresponds to size-dependent elastic plates (α¯=0,f=0).

Figs. 3 and 4 show the variation of the displacements u1 and u2 along x-axis for different size-dependent theories. It can be seen from these figures that the differences between size-dependent thermopiezoelectricity, size-dependent thermoelasticity, size-dependent piezoelectricity, and size-dependent elasticity theories are very pronounced.

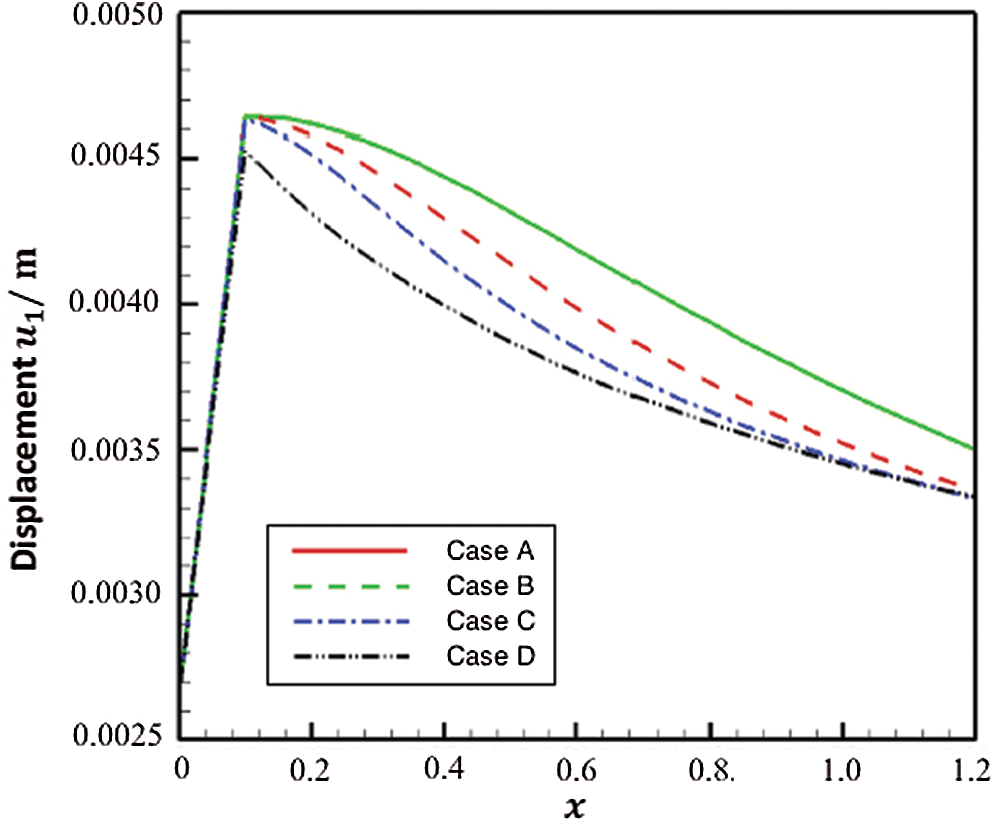
Figure 3: Variation of the displacement u1 along x-axis for different size-dependent theories

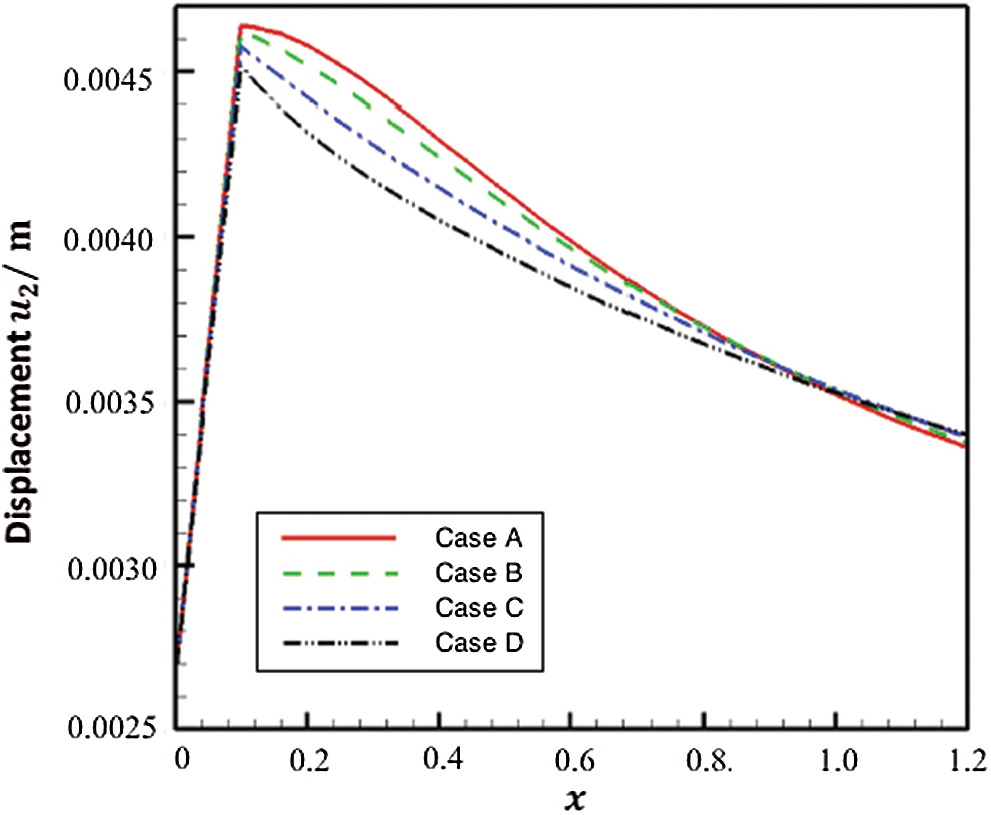
Figure 4: Variation of the displacement u2 along x-axis for different size-dependent theories

Figs. 5 and 6 show the variation of the displacements u1 and u2 along x-axis for different values of length scale parameter l. It can be seen from these figures that the displacement u1 decreases with the increase of the length scale parameter l, while, the displacement u2 increases with the increase of the length scale parameter l.

Figs. 7 and 8 show the variation of the displacements u1 and u2 along x-axis for different values of piezoelectric coefficient f. It can be seen from these figures that the displacements u1 and u2 increase with the increase of piezoelectric coefficient f.

The efficiency of our proposed methodology has been demonstrated through the use of the GMSS iteration method [25], which reduces the memory requirements and Processing time [26,27]. During our treatment of the considered problem, we implemented symmetric successive over relaxation (SSOR) [28], and preconditioned generalized shift-splitting (PGSS) iteration methods [29] to solve the linear systems resulting from the BEM discretization. Tab. 1 illustrates the iterations number (Iter.), processor time (CPU time), relative residual (Rr), and error (Err.) of the considered methods computed for various length scale parameter values (l=0.01,0.1 and 1.0). It is shown from Tab. 1 that the GMSS needs the lowest IT and CPU times, which implies that GMSS method has better performance than SSOR and PGSS.

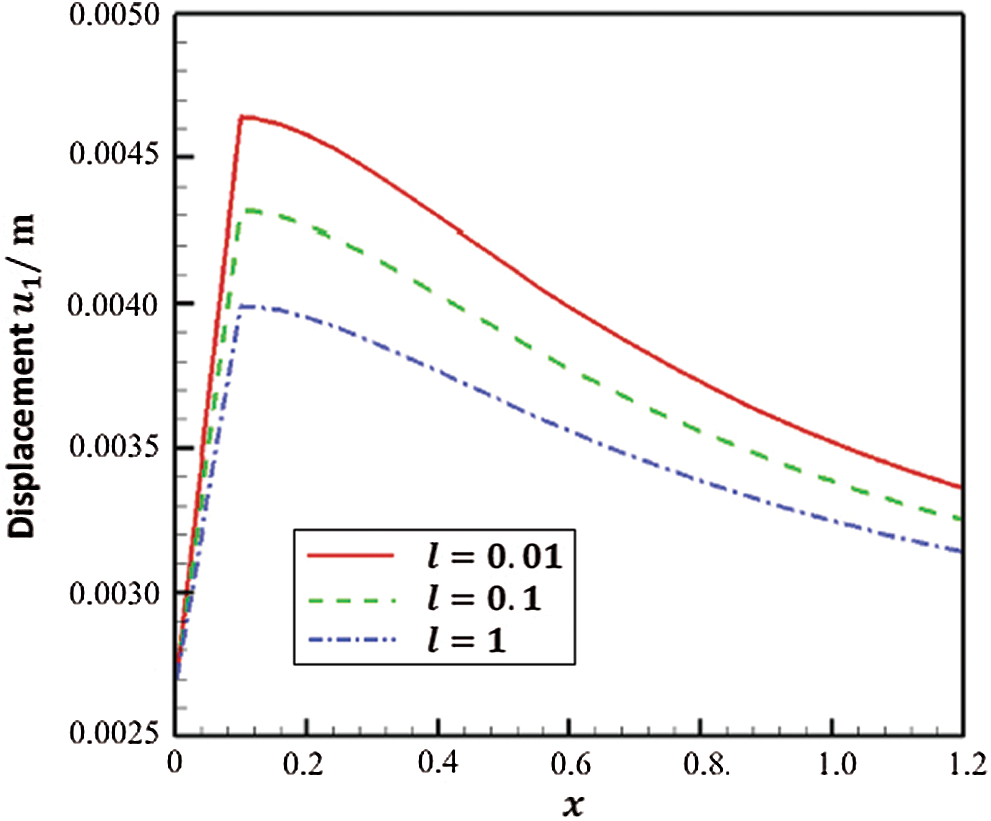
Figure 5: Variation of the displacement u1 along x-axis for different values of length scale parameter l

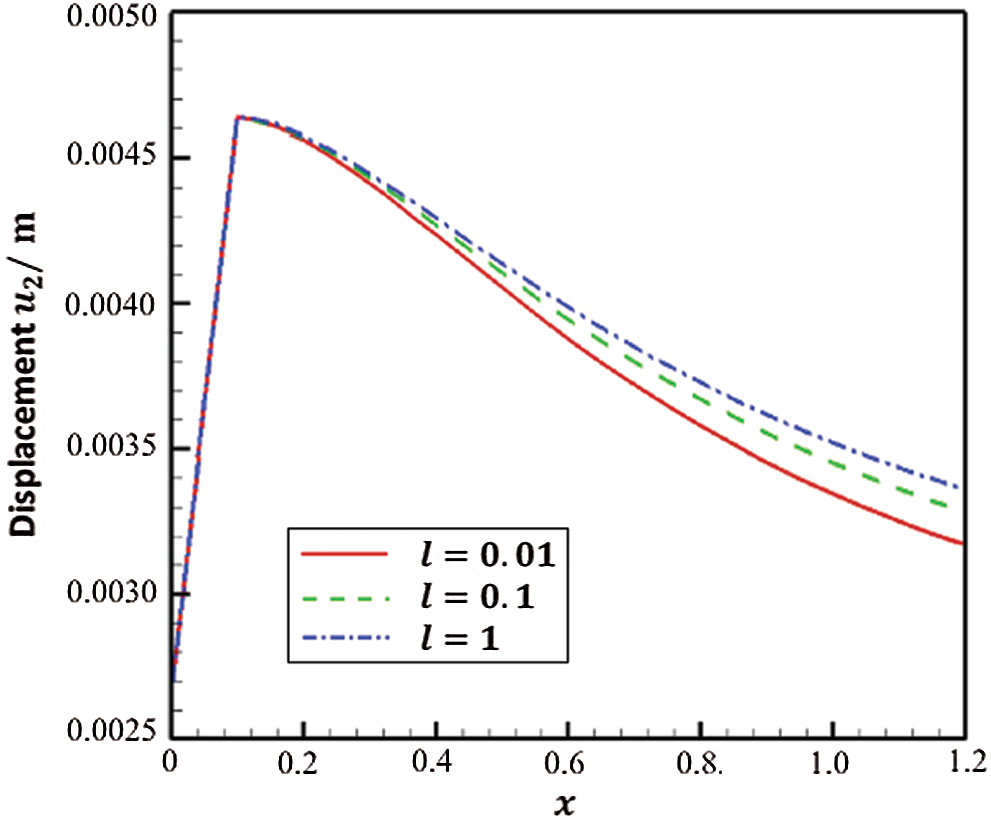
Figure 6: Variation of the displacement u2 along x-axis for different values of length scale parameter l

Tab. 2 summarizes the resulting numerical solutions for horizontal displacements u1 at points A and B for different values of length scale parameter l(l=0.01,0.1 and 1.0). This table also includes the finite element method (FEM) results of Sladek et al. [30], as well as the analytical solution of Yu et al. [31], it can be shown from Tab. 2 that the BEM results are in very good agreement with the FDM and analytical results. Thus, the validity and accuracy of the proposed BEM have been demonstrated.

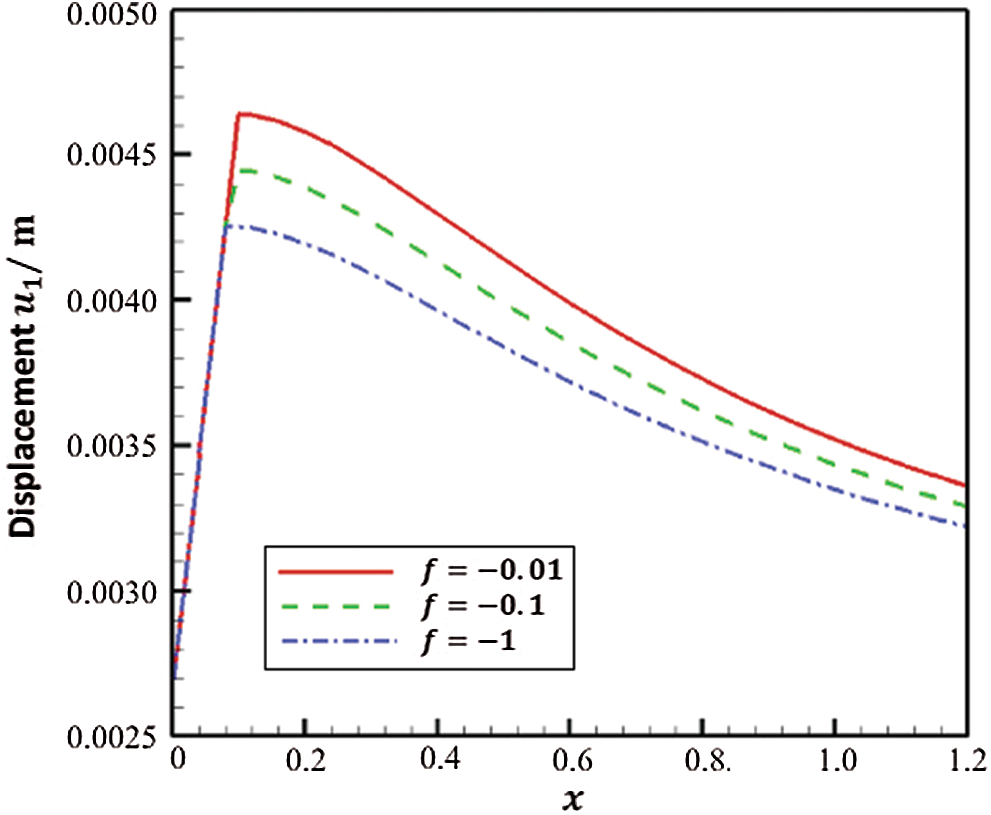
Figure 7: Variation of the displacement u1 along x-axis for different values of piezoelectric coefficient f

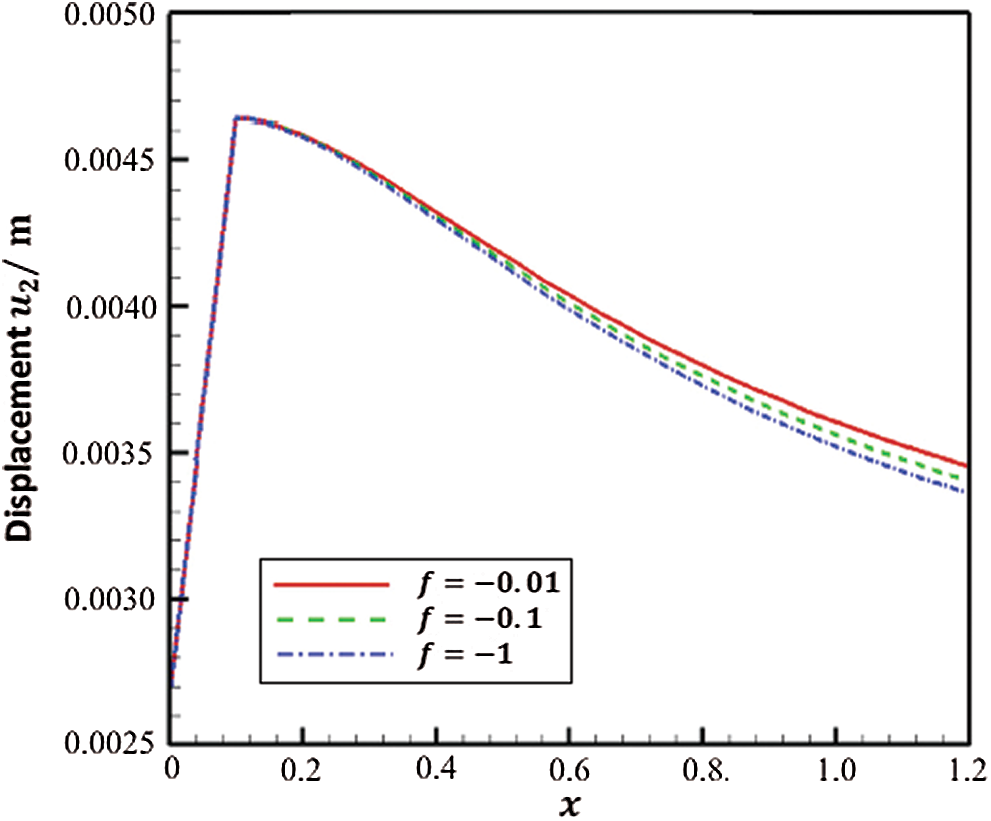
Figure 8: Variation of the displacement u2 along x-axis for different values of piezoelectric coefficient f

Table 1: Numerical results for the tested iteration methods

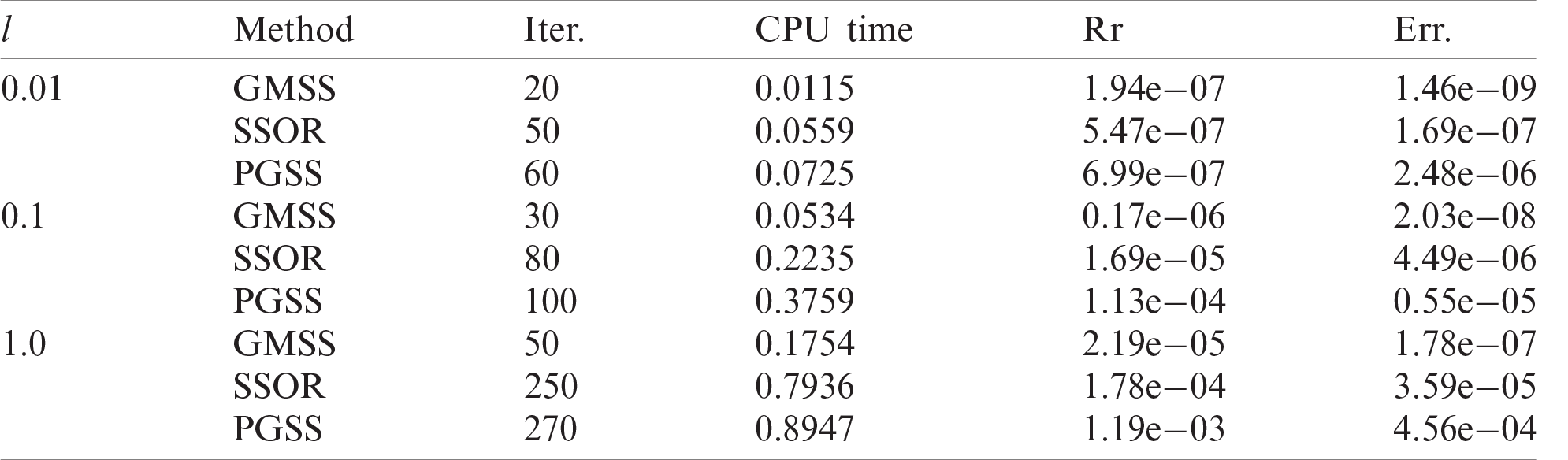
Table 2: Numerical values for horizontal displacement at points A and B

6  Conclusion

—A new theory called size-dependent thermopiezoelectricity for smart nanostructures is introduced.

—Because of the benefits of the BEM such as dealing with more complicated shapes of nanostructures and not requiring the discretization of the internal domain, also, it has low CPU time and memory. Therefore, it is versatile and efficient method for modeling of size-dependent thermopiezoelectric problems in smart nanostructures.

—A new BEM formulation is developed for solving the problems associated with the proposed theory, which involves temperatures, normal heat fluxes, displacements, couple-tractions, rotations, force-tractions, electric displacement, and normal electric displacement as primary variables within the BEM formulation.

—The BEM is accelerated by using the GMSS, which reduces the total CPU time and number of iterations.

—The proposed theory includes the combination of thermoelastic and piezoelectric influences which enable us to explain the differences between size-dependent thermopiezoelectricity, size-dependent thermoelasticity, size-dependent piezoelectricity and size-dependent elasticity theories of nanostructures.

—Numerical findings are presented graphically to show the effects of the size-dependent and piezoelectric on the displacement components.

—The computational performance of the proposed methodology has been demonstrated.

—The validity and accuracy of the proposed BEM technique have been demonstrated.

—From the proposed model that has been carried out using BEM formulation, it is possible to conclude that our proposed technique is more convenient, cost-effective, highly accurate, and has superiority over FDM or FEM.

—The proposed technique can be applied to study a wide variety of size-dependent problems in smart nanostructures subjected to mechanical, thermal and piezoelectric loadings.

—It can be concluded that our study has a wide variety of applications in numerous fields, such as electronics, chemistry, physics, biology, material science, optics, photonics, industry, military, and even medicine.

—Current numerical results for the proposed theory and its related problems, may provide interesting information for nanophysicists, nanochemists, nanobiologists, nanotechnology engineers, and nanoscience mathematicians as well as for computer scientists specializing in nanotechnology.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

 1.  J. Ghanbari and R. Naghdabadi, “Multiscale nonlinear constitutive modeling of carbon nanostructures based on interatomic potentials,” Computers, Materials & Continua, vol. 10, no. 1, pp. 41–64, 2009. [Google Scholar]

 2.  A. Chakrabarty and T. Çağin, “Computational studies on mechanical and thermal properties of carbon nanotube based nanostructures,” Computers, Materials & Continua, vol. 7, no. 3, pp. 167–190, 2008. [Google Scholar]

 3.  S. N. Cha, J. S. Seo, S. M. Kim, H. J. Kim, Y. J. Park et al., “Sound-driven piezoelectric nanowire-based nanogenerators,” Advanced Materials, vol. 22, no. 42, pp. 4726–4730, 2010. [Google Scholar]

 4.  I. Voiculescu and A. N. Nordin, “Acoustic wave based MEMS devices for biosensing applications,” Biosensors and Bioelectronics, vol. 33, no. 1, pp. 1–9, 2012. [Google Scholar]

 5.  D. Shin, Y. Urzhumov, Y. Jung, G. Kang, S. Baek et al., “Broadband electromagnetic cloaking with smart metamaterials,” Nature Communications, vol. 3, no. 11, pp. 1213, 2012. [Google Scholar]

 6.  S. Zhang, B. Gu, H. Zhang, X. Q. Feng, R. Pan et al., “Propagation of love waves with surface effects in an electrically-shorted piezoelectric nano film on a half-space elastic substrate,” Ultrasonics, vol. 66, no. 3, pp. 65–71, 2016. [Google Scholar]

 7.  I. F. Akyildiz and J. M. Jornet, “Electromagnetic wireless nanosensor networks,” Nano Communication Networks, vol. 1, no. 1, pp. 3–19, 2010. [Google Scholar]

 8.  J. He, X. Qi, Y. Miao, H. L. Wu, N. He et al., “Application of smart nanostructures in medicine,” Nanomedicine, vol. 5, no. 7, pp. 1129–1138, 2010. [Google Scholar]

 9.  A. Y. Al-Hossain, F. A. Farhoud and M. Ibrahim, “The mathematical model of reflection and refraction of plane quasi-vertical transverse waves at interface nanocomposite smart material,” Journal of Computational and Theoretical Nanoscience, vol. 8, no. 7, pp. 1193–1202, 2011. [Google Scholar]

10. L. L. Zhu and X. J. Zheng, “Stress field effects on phonon properties in spatially confined semiconductor nanostructures,” Computers, Materials & Continua, vol. 18, no. 3, pp. 301–320, 2010. [Google Scholar]

11. Y. Danlee, I. Huynen and C. Bailly, “Thin smart multilayer microwave absorber based on hybrid structure of polymer and carbon nanotubes,” Applied Physics Letters, vol. 100, no. 21, pp. 213105, 2012. [Google Scholar]

12. M. A. Ezzat, “State space approach to unsteady two-dimensional free convection flow through a porous medium,” Canadian Journal of Physics, vol. 72, no. 5–6, pp. 311–317, 1994. [Google Scholar]

13. M. Ezzat, M. Zakaria, O. Shaker and F. Barakat, “State space formulation to viscoelastic fluid flow of magnetohydrodynamic free convection through a porous medium,” Acta Mechanica, vol. 119, no. 1–4, pp. 147–164, 1996. [Google Scholar]

14. M. A. Ezzat, “Free convection effects on perfectly conducting fluid,” International Journal of Engineering Science, vol. 39, no. 7, pp. 799–819, 2001. [Google Scholar]

15. M. A. Ezzat, “State space approach to solids and fluids,” Canadian Journal of Physics, vol. 86, no. 11, pp. 1241–1250, 2008. [Google Scholar]

16. A. R. Hadjesfandiari, “Size-dependent piezoelectricity,” International Journal of Solids and Structures, vol. 50, no. 18, pp. 2781–2791, 2013. [Google Scholar]

17. M. A. Fahmy, “Boundary element algorithm for nonlinear modeling and simulation of three temperature anisotropic generalized micropolar piezothermoelasticity with memory-dependent derivative,” International Journal of Applied Mechanics, vol. 12, no. 3, pp. 2050027, 2020. [Google Scholar]

18. M. A. Fahmy, “A new boundary element algorithm for modeling and simulation of nonlinear thermal stresses in micropolar FGA composites with temperature-dependent properties,” Advanced Modeling and Simulation in Engineering Sciences, vol. 8, no. 6, pp. 1–23, 2021. [Google Scholar]

19. M. A. Fahmy, “A new boundary element formulation for modeling and simulation of three-temperature distributions in carbon nanotube fiber-reinforced composites with inclusions,” Mathematical Methods in the Applied Science, (In Press2021. [Google Scholar]

20. M. A. Fahmy, “A new boundary element algorithm for a general solution of nonlinear space-time fractional dual-phase-lag bio-heat transfer problems during electromagnetic radiation,” Case Studies in Thermal Engineering, vol. 25, no. 100918, pp. 1–11, 2021. [Google Scholar]

21. B. T. Darrall, A. R. Hadjesfandiari and G. F. Dargush, “Size-dependent piezoelectricity: A 2D finite element formulation for electric field-mean curvature coupling in dielectrics,” European Journal of Mechanics-A/Solids, vol. 49, no. 1–2, pp. 308–320, 2015. [Google Scholar]

22. A. R. Hadjesfandiari and G. F. Dargush, “Fundamental solutions for isotropic size-dependent couple stress elasticity,” International Journal of Solids and Structures, vol. 50, no. 9, pp. 1253–1265, 2013. [Google Scholar]

23. A. Hajesfandiari, A. R. Hadjesfandiari and G. F. Dargush, “Boundary element formulation for plane problems in size-dependent piezoelectricity,” International Journal for Numerical Methods in Engineering, vol. 108, no. 7, pp. 667–694, 2016. [Google Scholar]

24. A. Hajesfandiari, A. R. Hadjesfandiari and G. F. Dargush, “Boundary element formulation for steady state plane problems in size-dependent thermoelasticity,” Engineering Analysis with Boundary Elements, vol. 82, no. 9, pp. 210–226, 2017. [Google Scholar]

25. Z. G. Huang, L. G. Wang, Z. Xu and J. J. Cui, “The generalized modified shift-splitting preconditioners for nonsymmetric saddle point problems,” Applied Mathematics and Computation, vol. 299, no. 4, pp. 95–118, 2017. [Google Scholar]

26. M. A. Fahmy, “A new BEM for fractional nonlinear generalized porothermoelastic wave propagation problems,” Computers, Materials & Continua, vol. 68, no. 1, pp. 59–76, 2021. [Google Scholar]

27. M. A. Fahmy, “A novel BEM for modeling and simulation of 3T nonlinear generalized anisotropic micropolar-thermoelasticity theory with memory dependent derivative,” Computer Modeling in Engineering & Sciences, vol. 126, no. 1, pp. 175–199, 2021. [Google Scholar]

28. T. S. Siahkolaei and D. K. Salkuyeh, “A preconditioned SSOR iteration method for solving complex symmetric system of linear equations,” American Institute of Mathematical Sciences, vol. 9, no. 4, pp. 483–492, 2019. [Google Scholar]

29. Y. Xiao, Q. Wu and Y. Zhang, “Newton-PGSS and its improvement method for solving nonlinear systems with saddle point Jacobian matrices,” Journal of Mathematics, vol. 2021, no. 636943, pp. 1–18, 2021. [Google Scholar]

30. J. Sladek, V. Sladek, M. Repka and C. L. Tan, “Size dependent thermo-piezoelectricity for in-plane cracks,” Key Engineering Materials, vol. 827, no. 1, pp. 147–152, 2019. [Google Scholar]

31. Y. J. Yu, X. G. Tian and X. R. Liu, “Size-dependent generalized thermoelasticity using Eringen’s nonlocal model,” European Journal of Mechanics A/Solids, vol. 51, no. 5–6, pp. 96–106, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.