Computers, Materials & Continua DOI:10.32604/cmc.2021.016980
Article

An Efficient GCD-Based Cancelable Biometric Algorithm for Single and Multiple Biometrics

Naglaa F. Soliman1,2, Abeer D. Algarni1,*, Walid El-Shafai3, Fathi E. Abd El-Samie1,3 and Ghada M. El Banby4

1Department of Information Technology, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 84428, Saudi Arabia
2Department of Electronics and Communications, Faculty of Engineering, Zagazig University, Zagazig, 44519, Egypt
3Department of Electronics and Electrical Communications, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
4Department of Industrial Electronics and Control Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
*Corresponding Author: Abeer D. Algarni. Email: adalqarni@pnu.edu.sa
Received: 17 January 2021; Accepted: 10 April 2021

Abstract: Cancelable biometrics are required in most remote access applications that need an authentication stage such as the cloud and Internet of Things (IoT) networks. The objective of using cancelable biometrics is to save the original ones from hacking attempts. A generalized algorithm to generate cancelable templates that is applicable on both single and multiple biometrics is proposed in this paper to be considered for cloud and IoT applications. The original biometric is blurred with two co-prime operators. Hence, it can be recovered as the Greatest Common Divisor (GCD) between its two blurred versions. Minimal changes if induced in the biometric image prior to processing with co-prime operators prevents the recovery of the original biometric image through a GCD operation. Hence, the ability to change cancelable templates is guaranteed, since the owner of the biometric can pre-determine and manage the minimal change induced in the biometric image. Furthermore, we test the utility of the proposed algorithm in the single- and multi-biometric scenarios. The multi-biometric scenario depends on compressing face, fingerprint, iris, and palm print images, simultaneously, to generate the cancelable templates. Evaluation metrics such as Equal Error Rate (EER) and Area and Receiver Operator Characteristic curve (AROC) are considered. Simulation results on single- and multi-biometric scenarios show high AROC values up to 99.59%, and low EER values down to 0.04%.

Keywords: Cloud; IoT; cancelable biometrics; GCD; single- and multi-biometrics; security applications

1  Introduction

Compared to authentication systems based on passwords, tokens, IDs, and biometrics, cancelable biometric recognition systems provide better security for human identification purposes. They are more suitable for remote access networks such as cloud and IoT networks. Cancelable biometric systems can be built with a single or uni-biometric, hence the name uCBS, or with multiple biometrics, hence the name mCBS. The uCBS are considered less secure compared to the mCBS [1]. The general framework of uCBAS is presented in Fig. 1, where the recognition process involves a sensor module for image capturing, a pre-processing module for data alignment and noise removal, and a segmentation module to extract the region of interest from the input image followed by the feature extraction process, which heralds the user identification.

Figure 1: Framework of typical uCBS

User validation schemes are impeded by overlapping facial biometrics as in twins, poor data acquisition in the case of dry fingerprints, or even missing data, in typical cases of occluded biometric images. Therefore, mCBS are required to enhance the outcomes of the recognition process. Human facial, iris, fingerprint, ear, signature, voice, and other biometric modalities are now widely exploited to build robust mCBS. At the same time, such behavioral biometrics suffer from unavailability or poor coverage over large databases, and they also exhibit poor recognition accuracy [2]. Meanwhile, several studies focusing on numerical approaches to secure biometric templates have been published [3–5]. Notwithstanding these efforts, safeguarding biometric templates from illicit tampering remains a top priority deserving improvement in the face of sophisticated techniques to violate their intensity.

For increasing the security, accuracy, and genuine acceptance rate, mCBS have been implemented [6]. Different studies on improving the accuracy of mCBS have been published [6–17]. Multimodal biometric systems take more than one biometric template to fuse them for the identification and validation purposes. An effective fusion scheme is an important step for effective mCBS. In this regard, Rathgeb et al. [7] presented a privacy preserving technique based on feature level fusion with bloom filter applied on face and iris biometrics. They reported an EER of 0.4%. Similarly, Paul et al. [8] presented a facial and ear cancelable biometric mechanism based on fusion. Both face and ear templates are partitioned into 25 blocks, and a random projection process is applied on each block. Subsequently, the average fused projected blocks are used to generate the cancelable templates. The results reported improvements of 12% and 14% in the recognition accuracy compared to those of the face and ear recognition systems, respectively. In their contribution, Dwivedi et al. [9] presented a two-level cancelable multi-biometric recognition system based on a score fusion technique. This system depends on a rectangular area weighting technique that is applied on scores from different modalities. It achieved a high authentication performance compared to those of the single-biometric recognition systems. Moreover, Kaur et al. [10] proposed a framework for multi-server biometrics that integrates a pseudo-biometric identity with a revoked version from a pseudo-template. The authors claimed enhanced security using pseudo-identities generated using a Random Distance Method (RDM).

Furthermore, Yang et al. [11] proposed an mCBS based on both fingerprint and finger-vein. Their method generates cancelable templates by combining feature sets extracted from both biometrics. They accomplished feature-level fusion using Partial Discrete Fourier Transform (PDFT). They reported a higher security level for the Enhanced Partial Discrete Fourier Transform (EPDFT) compared to that of the PDFT. Goswami et al. [12] proposed feature-level fusion and classification for multi-modality biometric recognition. They applied a Group Sparse Representation Classifier (GSRC) on feature vectors extracted from multi-biometrics, which yields biometric authentication with an accuracy of 99.1%. Likewise, Canuto et al. [13] investigated four fusion approaches for mCBS using voice and iris biometrics. Their work proves that cancelable biometric schemes based on more than one transformation could offer more security, since these transformations complicate the verification task. In their effort, a fusion structure in the feature level for fingerprint templates was proposed by Sandhy et al. [14]. Therein, two transformed features are computed from the fingerprint minutiae to produce a bit string to be used in the fusion process. They achieved an EER of 1.6% on the Fingerprint Verification Competition (FVC 2002) database. Meanwhile, Barrero et al. [15] introduced a multi-modality biometric recognition system based on homomorphic encryption. They applied three fusion levels: feature, score, and decision to safeguard their templates, and they reported a minimum EER of 0.12%.

Similarly, Lai et al. [16] proposed a cancelable iris recognition scheme based on hashing. It depends on a Hadamard product operation and a modulo threshold function. The authors claimed improved accuracy in addition to enhanced security. Finally, Umer et al. [17] introduced a bio-hashing approach with a spatial pyramidal feature extraction process. It depends on a user-specific independent token that can be generated by each user with his selected generation method.

This paper presents a new algorithm that can be applied for both uCBS and mCBS. The main idea of the proposed algorithm depends on the Greatest Common Divisor (GCD) to generate the cancelable templates. It is known that if two co-prime operators are used on the same biometric image to obtain two blurred versions of that image, the original biometric itself can be obtained again through the 2D GCD between the two blurred versions. If some intended change is induced in the biometric image prior to or after the application of one of the blurring operators, this will lead to a distorted output from the 2D GCD operation. This output can be used instead of the original biometric template as a cancelable template. This idea is adopted in this paper to build uCBS and mCBS. The remainder of this study is outlined as follows. The basics of the related 1-D and 2-D Sylvester GCD algorithms are discussed in Section 2. The proposed cancelable template generation algorithm for uCBS and mCBS is presented in Section 3. Extensive simulation experiments are presented in Section 4 to validate the proposed algorithm. Finally, the concluding remarks are summarized in Section 5.

2  Basics of the Sylvester GCD Algorithms

This section introduces the major fundamental theories of the 1-D and 2-D Sylvester GCD algorithms that will be exploited in the proposed cancelable biometric algorithm to create the distorted versions of the original biometrics.

2.1 One-Dimensional (1-D) Sylvester GCD Algorithm

Let A(z) and B(z) be two polynomials defined as:

A(z)=a0+a1z+a2z2+...+an2zn2 (1)

and

B(z)=b0+b1z+b2z2+...+bn1zn1 (2)

Similarly, if the GCD between the two polynomials is equal to P(z), which is of degree r, then it can be computed in the form:

A(z)C(z)=B(z)D(z)=P(z) (3)

where

C(z)=c0+c1z+c2z2+...+cn2−rzn2−r (4)

and

D(z)=d0+d1z+d2z2+...+dn1−rzn1−r (5)

are two relatively co-prime polynomials. Consequently, it follows from [18] that

A(z)D(z)−B(z)C(z)=0 (6)

By equating the coefficients of like powers of z on both sides of Eq. (6), a matrix equivalence in the form in (7) is obtained [18]:

Sx=0 (7)

where

x=[dn1−r,...,d2,d1,d0,−c0,c1,−c2,...,−cn2−r] (8)

Hence, S is defined as presented in Eq. (9) [18].

S=[an2an2−1⋯⋯a1a00⋯00an2an2−1⋯⋯a1a0⋯0⋮⋮⋮⋮⋮⋮⋮⋮⋮0⋯0an2an2−1⋯⋯a1a000⋯0bn1bn1−1⋯b1b00⋯0bn1bn1−1⋯b1b00⋮⋮⋮⋮⋮⋮⋮⋮⋮bn1bn1−1⋯b1b000⋯0] (9)

By analyzing the matrix S in Eq. (9), it can be deduced that it has n2+n1−2r+2 rows and n2+n1−r+1 columns. Therefore, given r, x can be obtained via the application of Singular Value Decomposition (SVD) on S. Furthermore, since C(z) and D(z) are two unique polynomials of degrees n2−r and n1−r, it is deducible that x has a unique solution, and consequently, S must possess n2+n1−2r+1 linearly independent rows. As a result, the singular vector that corresponds to the zero singular value of S is the least-squares solution of Eq. (7) for x, and it contains the coefficient values of C(z) and D(z) as explained in [18].

In some cases, the degree r of the GCD is unknown, and hence, S cannot be formed. In that case, we have [18]:

S0x0=0 (10)

where

x0=[dn1−1,...,d2,d1,d0,−c0,c1,−c2,...,−cn2−1] (11)

with

dn1−1=...=dn1−r+1=cn2−r+1=...=cn2−1=0 (12)

Therefore, S0 can be computed using the standard Sylvester matrix presented in Eq. (13).

S0=[an2an2−1⋯⋯a1a00⋯00an2an2−1⋯⋯a1a0⋯0⋮⋮⋮⋮⋮⋮⋮⋮⋮0⋯0an2an2−1⋯⋯a1a000⋯0bn1bn1−1⋯b1b00⋯0bn1bn1−1⋯b1b00⋮⋮⋮⋮⋮⋮⋮⋮⋮bn1bn1−1⋯b1b000⋯0] (13)

Using arguments in (9), it can be deduced that S0 has dimensions of (n2+n1)×(n2+n1). Meanwhile, the necessary and sufficient condition for A(z) and B(z) to have a non-constant GCD is that the resultant Sylvester matrix S0 is singular. The structural relation between S0 and S is illustrated in Fig. 2. Furthermore, if we denote the sub-matrix of size (n2+n1−2k)×(n2+n1−k) as Sk, which is obtained by striking out the first k and last k rows of S0 and the first k columns of S0, then for GCD{A(z),B(z)}=P(z) with degree r, S0, S1,…, Sr−1 must be singular and Sr−1 must be of rank n2+n1−2r+1.

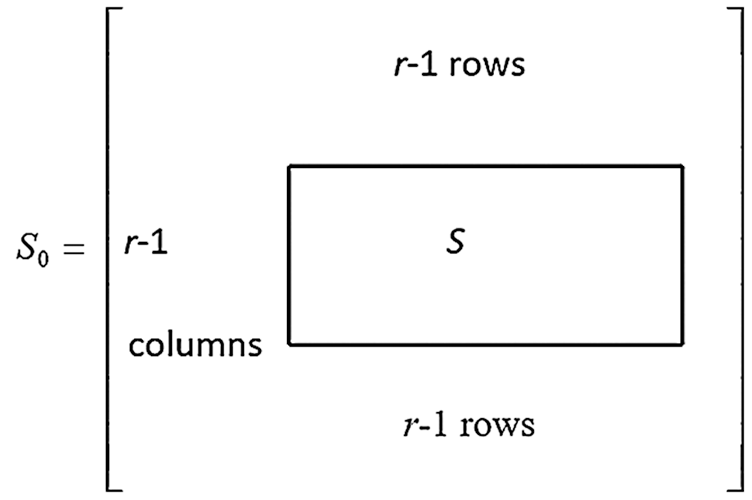
Figure 2: Structure of the Sylvester matrix used to estimate the GCD

2.2 Two-Dimensional (2-D) Sylvester GCD Algorithm

The direct extension of the 1-D Sylvester algorithm to the 2-D case in terms of constant matrices generated from the given 2-D polynomial coefficients leads to very large-size matrices. For N×N images, the matrix S will be of size 2N2×2N2. Since the SVD computation produces matrices with a size proportional to the cube of the original matrix size, operations of O(N6) are required to execute the SVD, directly. Hence, a more efficient strategy is needed to extend the 1-D Sylvester algorithm to a 2-D algorithm.

In doing so, we assume that the two blurred versions g1(n1,n2) and g2(n1,n2) of the original image f(n1,n2) are both N1×N2 matrices. The coefficients of these matrices are the coefficients of the z-transforms of their respective images. Using the Conventional Discrete Fourier Transform Least Squares (CDFT-LS) approach, we substitute z1=e−j2πn1/N1, n1=0,1,...,N1−1, into both G1(z1,z2) and G2(z1,z2). This results in two 1-D polynomials [17]:

Gk(e−j(2πn1/N1),z2)=F(e−j(2πn1/N1),z2)Hk(e−j(2πn1/N1),z2) (14)

where k=1,2.

It is trivial that F(e−j(2πn1/N1),z2) is still a common factor of G1(e−j(2πn1/N1),z2) and G2(e−j(2πn1/N1),z2) in a single variable, z2. Consequently, the 1-D GCD produces the scaled quantity c0(e−j(2πn1/N1))F(e−j(2πn1/N1),z2). Furthermore, for each value of n1 in Eq. (14), we substitute z2=e−j2πn2/N2 in this GCD and form a matrix of discrete Fourier transform elements [18]:

A(n1,n2)=c(n1)F(e−j(2πn1/N1),e−j(2πn2/N2)) (15)

We scale each row by a constant c(n1)=c0(e−j(2πn1/N1)). So, we obtain:

A(n1,n2)a(n1)=F(e−j(2πn1/N1),e−j(2πn2/N2)) (16)

Undertaking similar operations and substituting z2=e−j2πn2N2 in G1(z1,z2) and G2(z1,z2), whose 1-D GCD was obtained by substitution of z1=e−j2πn1N1, we obtain another matrix, B(n1,n2) in Eq. (17), which is related to the discrete Fourier transform of the original image by column-wise scaling [18]:

B(n1,n2)b(n2)=F(e−j(2πn1/N1),e−j(2πn2/N2)) (17)

From Eqs. (16) and (17), we have:

A(n1,n2)a(n1)−B(n1,n2)b(n2)=0 (18)

Eq. (18) can be written in matrix form as [18]:

Γy=0 (19)

where

y=[a(1),a(2),...,a(N1),b(1),b(2),...,b(N2)]T (20)

and

Γ=[A(1,1)00−B(1,1)0000A(1,2)000−B(1,2)000⋯⋯⋯⋯⋯⋯⋯⋯A(1,N2)000000−B(1,N2)0A(2,1)0−B(2,1)00000A(2,2)00−B(2,2)000⋯⋯⋯⋯⋯⋯⋯⋯0A(2,N2)00000−B(2,N2)⋮⋮⋮⋮⋮⋮⋮⋮00A(N1,1)−B(N1,1)000000A(N1,2)0−B(N1,2)000⋯⋯⋯⋯⋯⋯⋯⋯00A(N1,N2)0000−B(N1,N2)] (21)

Multiplying Eq. (21) by ΓT yields [18]:

ΓTΓy=0 (22)

Eq. (22) can be solved using the least-squares solution to produce Eq. (23):

ΓTΓy=λy (23)

For an eigenvector y corresponding to the smallest eigenvalue of ΓTΓ in Eq. (23), the estimated Fourier transform of the original image can be realized in the form [17]:

F(e−j(2πn1/N1),e−j(2πn2/N2))=12[A(n1,n2)a(n1)+B(n1,n2)b(n2)] (24)

Finally, the inverse Fourier transform can be used to estimate the GCD. If we use two blurred images of the same biometric and estimate their 2D GCD, we can get the original biometric template. On the other hand, if we make a slight change induced by the user prior to or after blurring, we severely distort the 2D GCD result. The result of the GCD in this case can be used as a cancelable template. The minor changes can be induced in each biometric template in a user-specific manner.

3  Proposed GCD-Based Cancelable Biometric Algorithm

Fig. 3 presents the outlines of the proposed algorithm. As seen in the figure, the original biometric images are firstly compressed using the Discrete Cosine Transform (DCT) compression algorithm. After that, they are merged together to form a unified biometric template. This template is blurred with an operator h1(n1,n2). Simultaneously, another blurred version of the biometric template is generated with another operator h2(n1,n2).

We have:

g1(n1,n2)=f(n1,n2)∗h1(n1,n2) (25)

g2(n1,n2)=f(n1,n2)∗h2(n1,n2) (26)

Applying z-transform on (25) and (26), we get:

Gk(z1,z2)=F(z1,z2)Hk(z1,z2)k=1,2 (27)

where

G1(z1,z2)=F(z1,z2)∗H1(z1,z2) (28)

and

G2(z1,z2)=F(z1,z2)∗H2(z1,z2) (29)

If H1(z1,z2) and H2(z1,z2) are co-prime, then

GCD{H1(z1,z2),H2(z1,z2)}=1 (30)

and

GCD{G1(z1,z2),G2(z1,z2)}=F(z1,z2) (31)

As shown in Fig. 3, if we induce some minimal change in the compressed template prior to blurring with h2(n1,n2), Eq. (31) does not hold. This leads to a distorted version of the fused templates that can be used as a cancelable template.

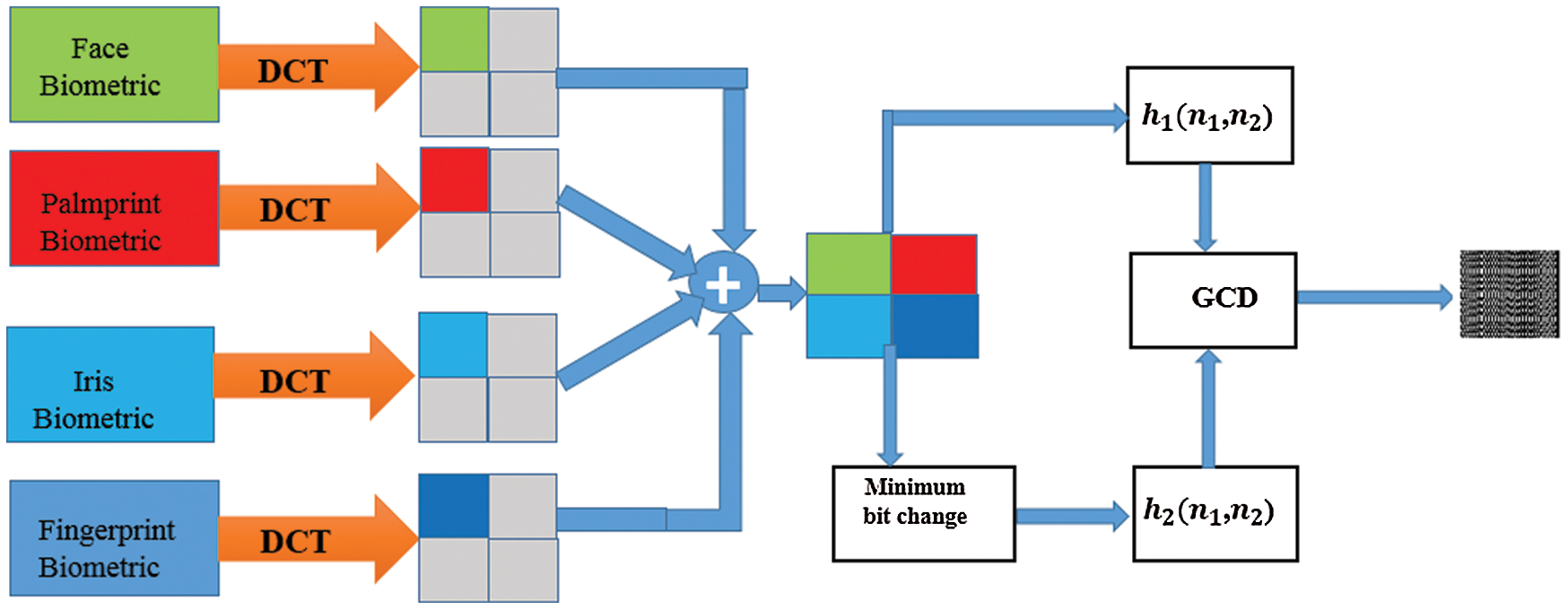
Figure 3: The proposed unified mCBS framework

4  Results and Discussion

In this section, the assessment of the suggested algorithm is introduced. Firstly, the security analysis of the suggested GCD-based algorithm as an encryption-like algorithm is presented in terms of visual analysis, correlation analysis, differential attack analysis, and entropy analysis [19] as provided in Tab. 1. It is well-known that the algorithm must break the correlation amongst the adjacent pixels. It is observed from the obtained outcomes that the suggested GCD-based algorithm succeeds in demolishing the very high correlation of pixels in the original biometric templates. Moreover, Tab. 1 demonstrates correlation, Unified Average Change Intensity (UACI), and Number of Changing Pixel Rate (NPCR) values [20] between two ciphered biometric templates. The outcomes reveal that the suggested GCD-based algorithm is robust and vulnerable to control parameters and secret keys. So, all results confirm that the suggested GCD-based algorithm can be executed, cost-effectively, for constructing an efficient and secure cancelable biometric recognition system. As a result, this encouraged us to develop it in our suggested work.

Figure 4: Dataset 1 consisting of nine facial images [21]

Figure 5: Cancelable facial images for those in Fig. 4 with GCD algorithm

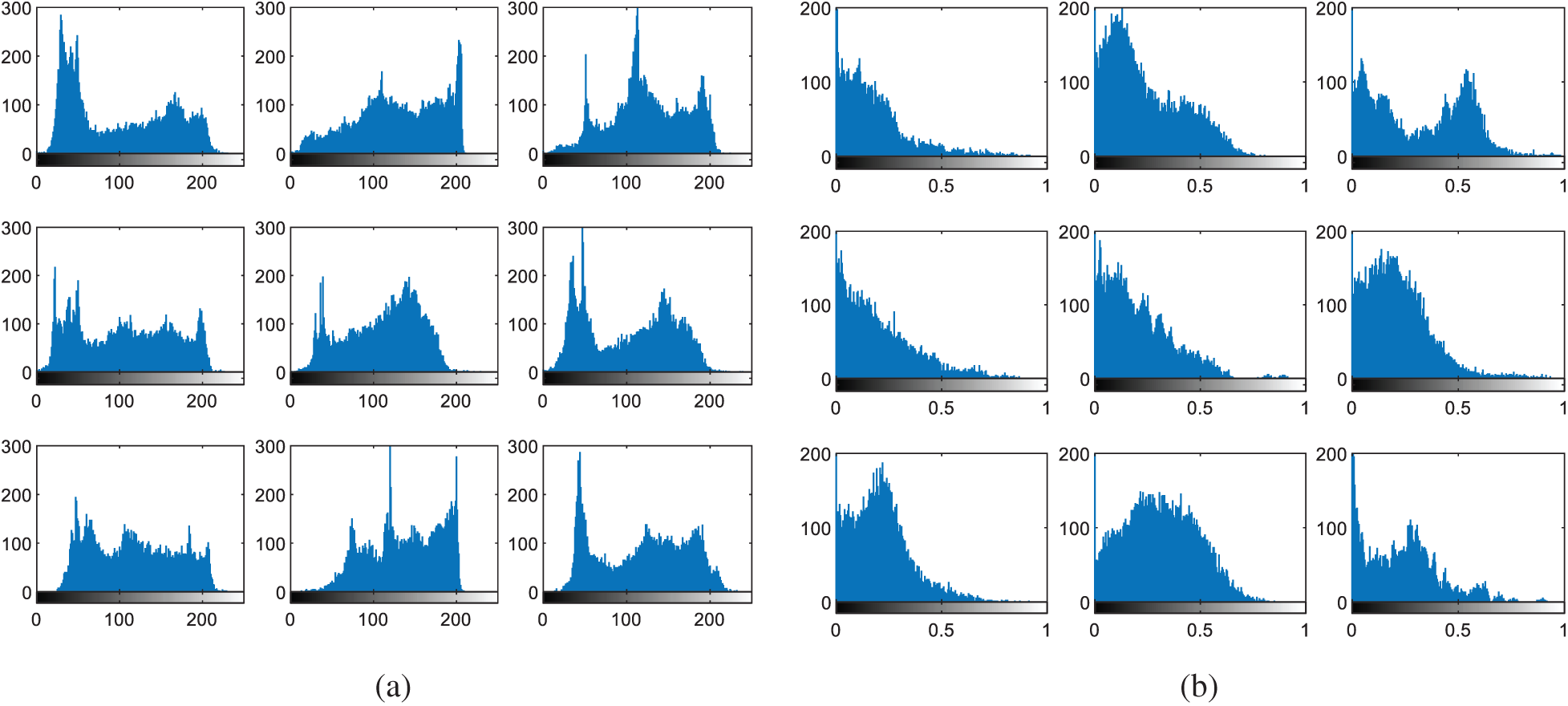
Figure 6: Histograms of facial images (a) original images (b) cancelable templates

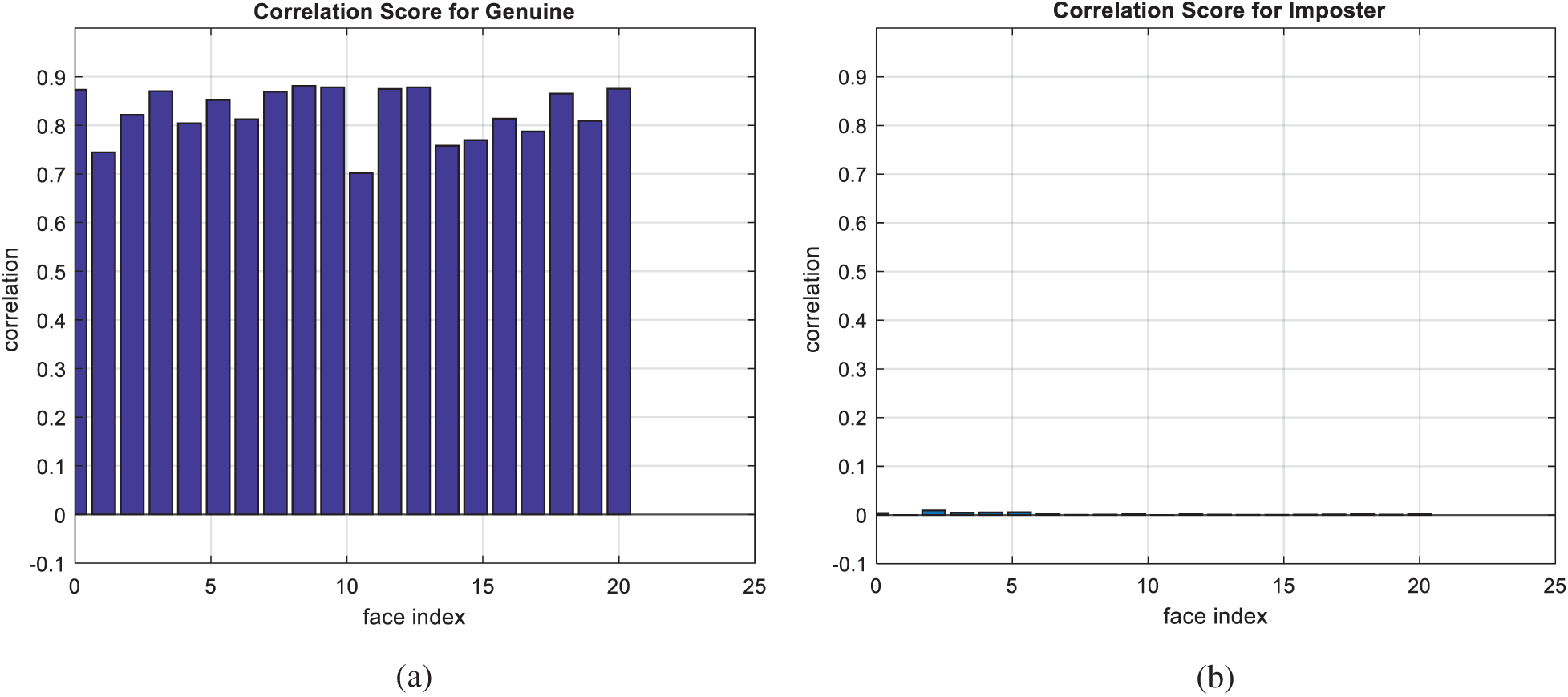
Figure 7: Correlation scores for original facial images (a) genuine (b) imposter

Furthermore, in this section, several experiments are introduced to verify the validity of the proposed uCBS and mCBS that depend on 2D GCD. They have been implemented using a workstation equipped with MATLAB Intel ® Core ™ i7-4210U on a CPU with a 1.7 GHz processor. Four datasets have been used in the uCBS experiments, namely ORL [21], FVC2000 DB1 [22], CASIA-IrisV3-Interval [23], and CASIA Palm print [24] for face, fingerprint, iris, and palm print images, respectively.

For the uCBS, the experiments are based on generating two blurred versions of each template and inducing a minor change in one of them prior to blurring. Hence, the 2D-GCD is implemented to generate the cancelable template of that biometric. The database of cancelable templates is composed, and hence the distance between new templates and those in the database is estimated based on the correlation score. Both EER and AROC values are estimated for the verification process. On the other hand, the proposed mCBS depends on estimating the DCTs of four biometric templates and generating a combined version based on the first quadrant of each DCT. This combined version is used as an initial template that is blurred twice. A minor change in one of these versions and the application of the 2D-GCD lead to the cancelable template.

The Receiver Operating Characteristic (ROC) curve, which represents the relationship between the true-positive correlation and false-positive correlation [25,26], is used to assess the performance of the suggested CBS. The scores of all patterns are distributed around a mean score, which is higher for authorized patterns compared to unauthorized ones.

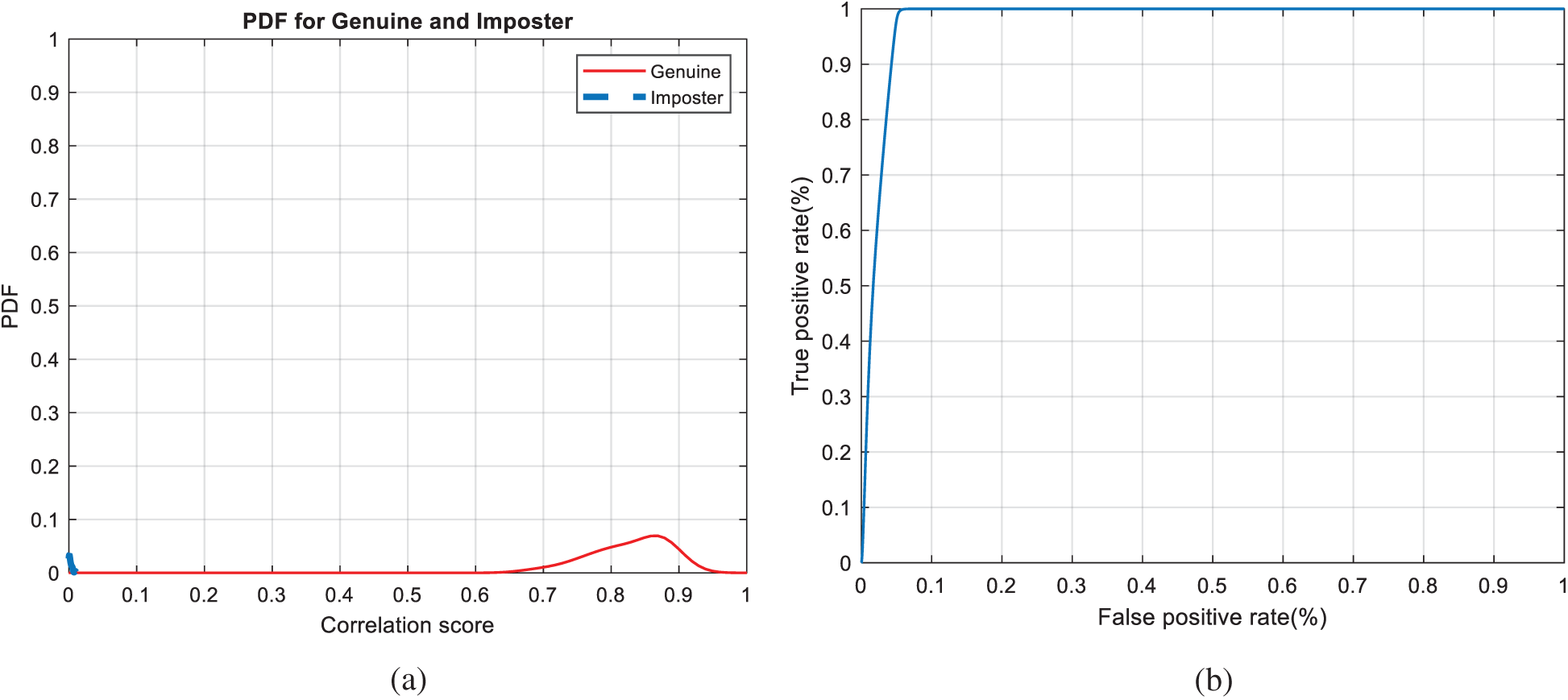
Figure 8: Authentication curves for facial biometrics (a) PFD curves (b) ROC curve

Figure 9: Dataset 2 consisting of nine fingerprint images [22]

Figure 10: Cancelable fingerprint images for those in Fig. 9 with GCD algorithm

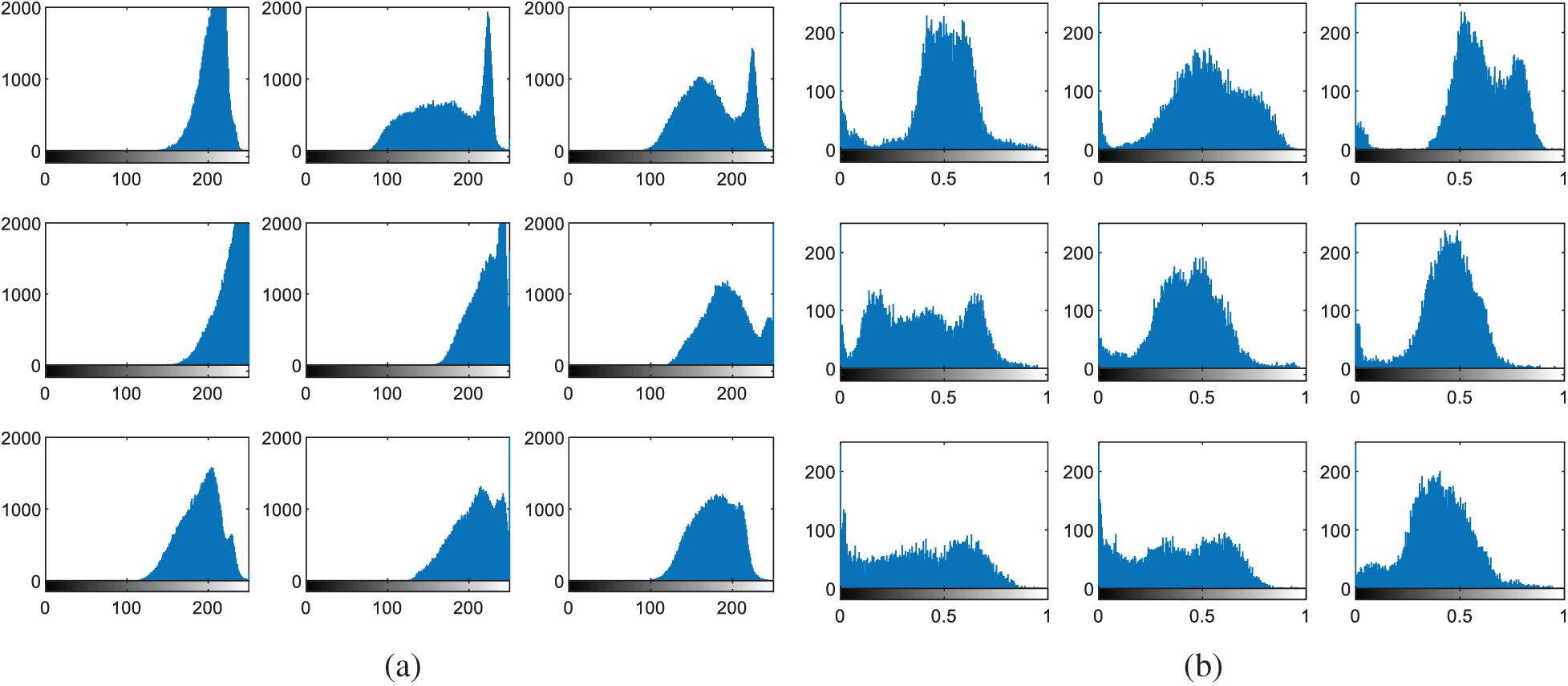
Figure 11: Histograms of fingerprint images (a) original images (b) cancelable templates

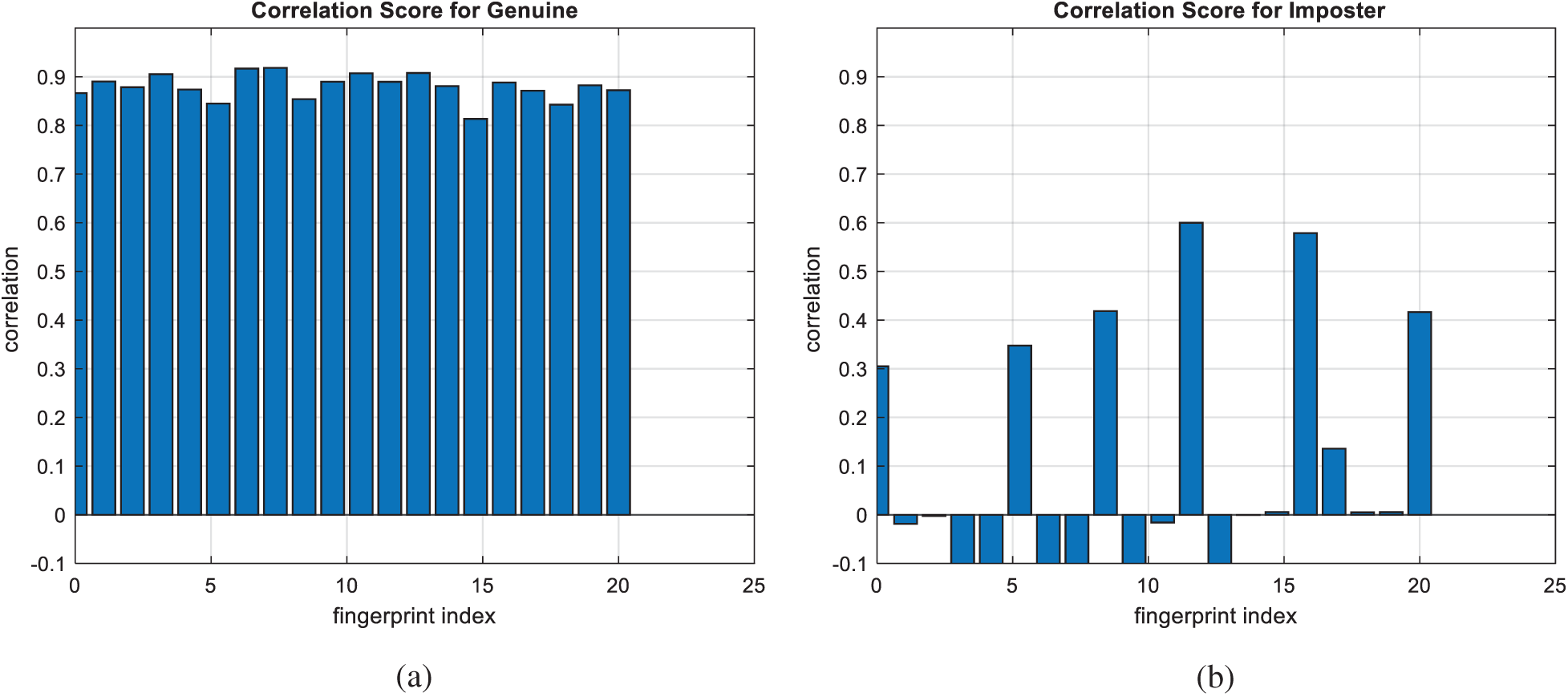
Figure 12: Correlation scores for original fingerprint images (a) genuine (b) imposter

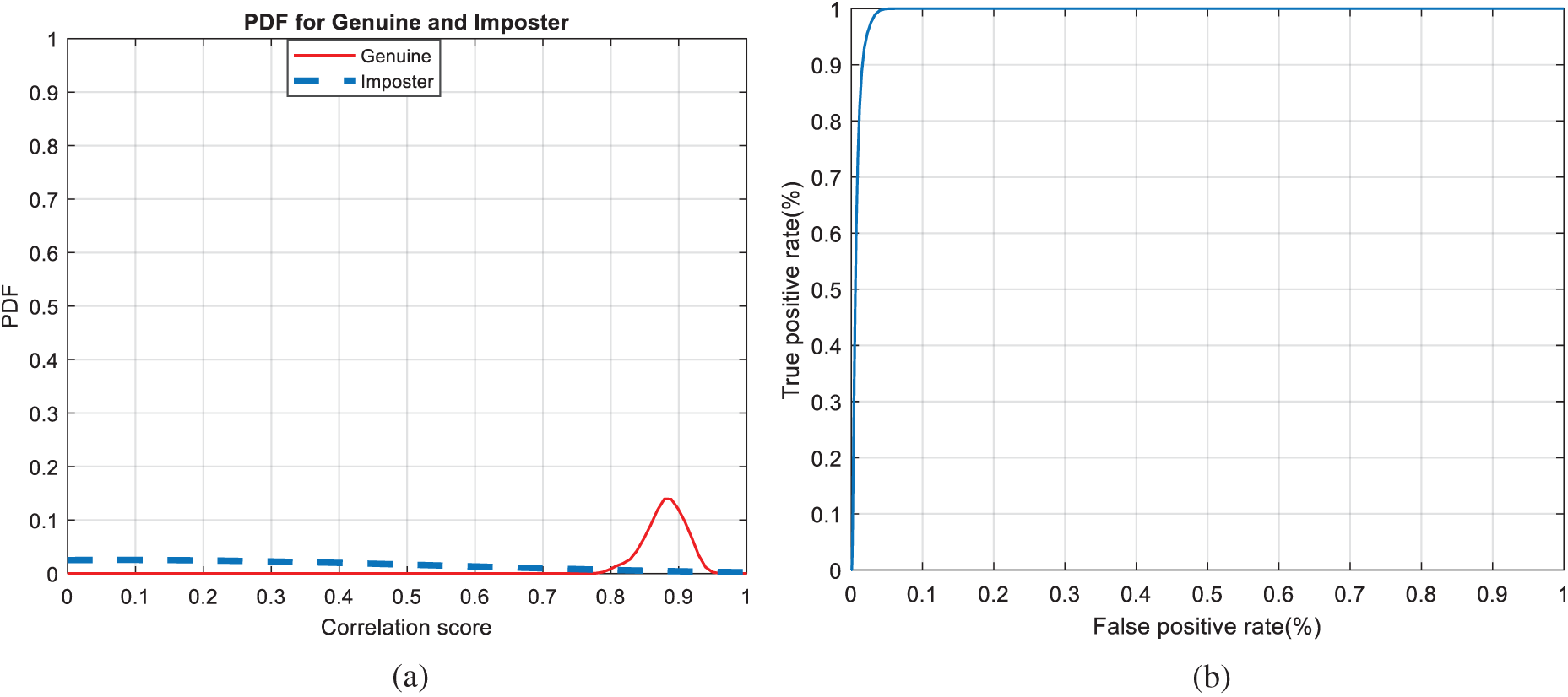
Figure 13: Authentication curves for cancelable fingerprint recognition (a) PFD curves (b) ROC curve

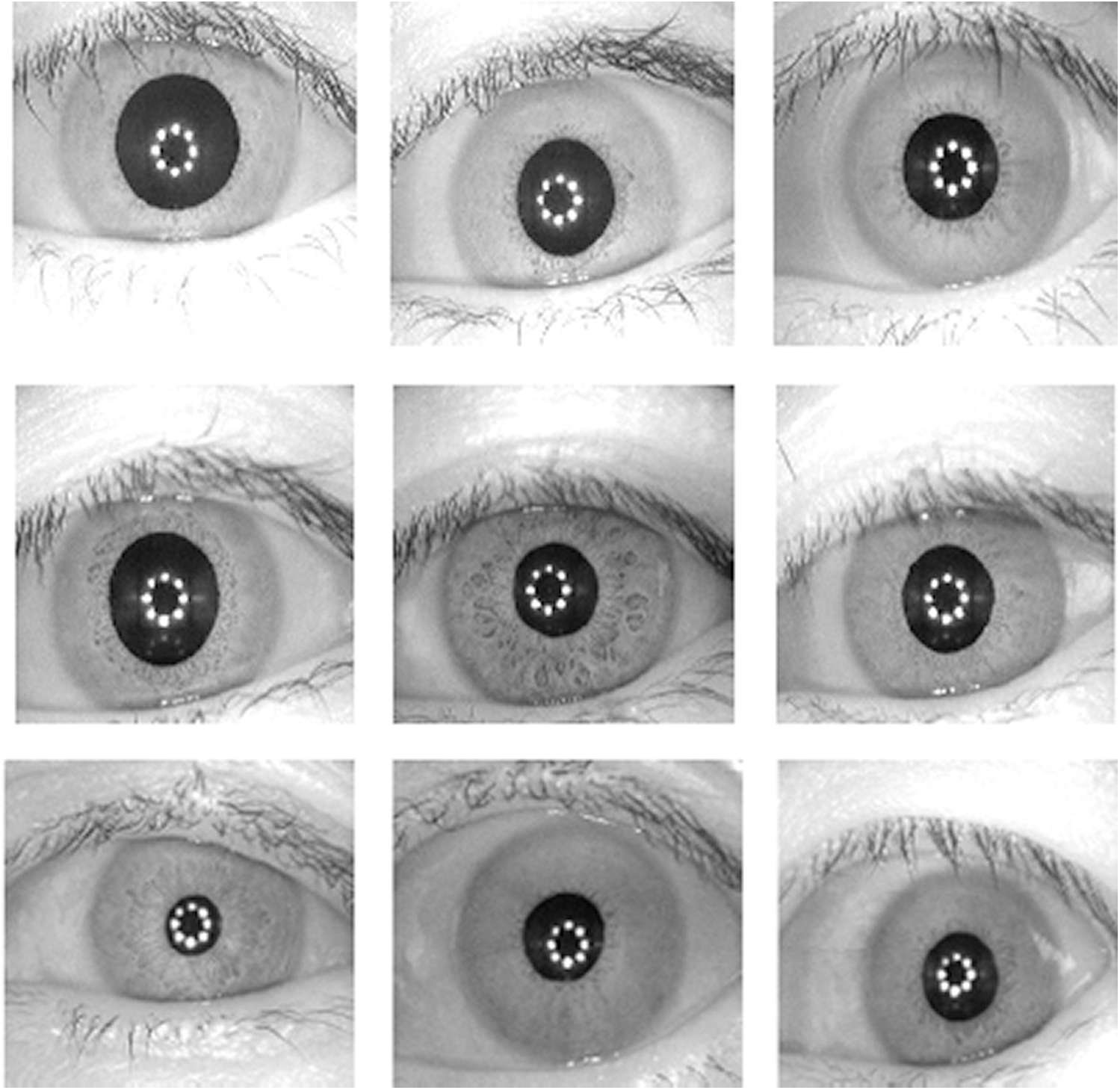
Figure 14: Dataset 3 consisting of nine biometric iris images [23]

Figure 15: Cancelable iris images for those in Fig. 14 with GCD algorithm

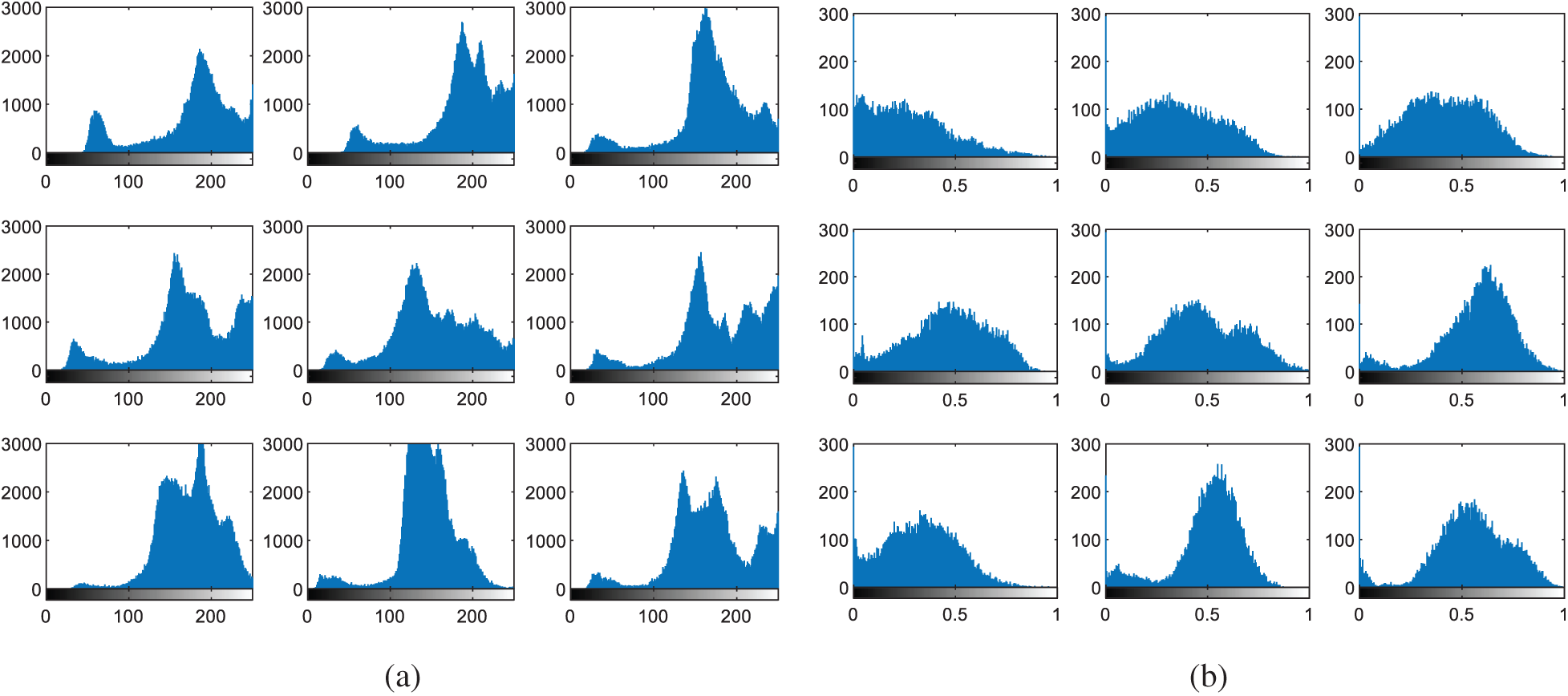
Figure 16: Histograms of iris images (a) original images (b) cancelable templates

The multi-modal biometrics used to validate the proposed CBS consist of facial, fingerprint, iris, and palm print images as presented in Fig. 4 (Faces), Fig. 9 (Fingerprints), Fig. 14 (Iris), and Fig. 19 (Palm prints). Figs. 5, 10, 15, and 20 present the unimodal cancelable templates with 2D GCD. The histograms of the pristine unimodal biometrics are presented in Figs. 6, 11, 16, and 21 for facial, fingerprint, iris, and palm print biometrics, respectively.

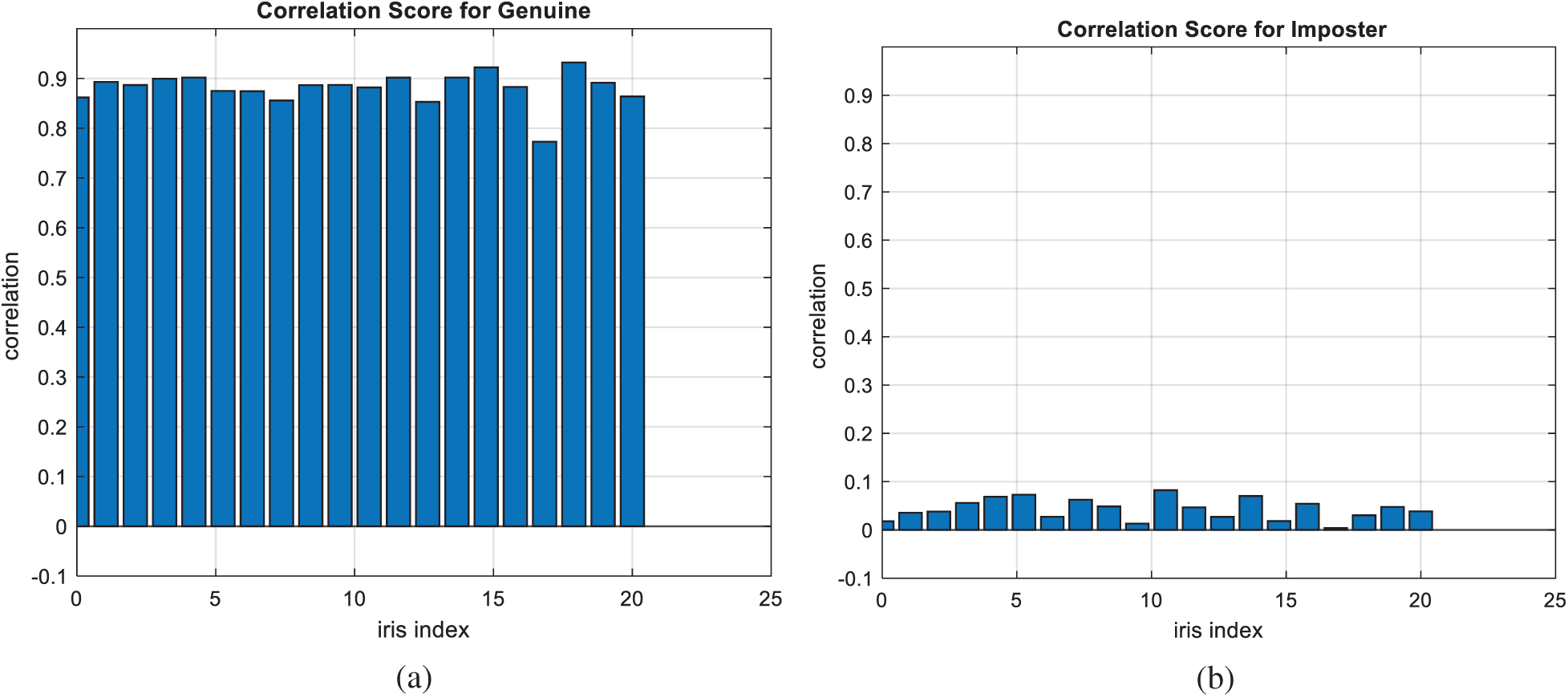
Figure 17: Correlation scores for original iris images (a) genuine (b) imposter

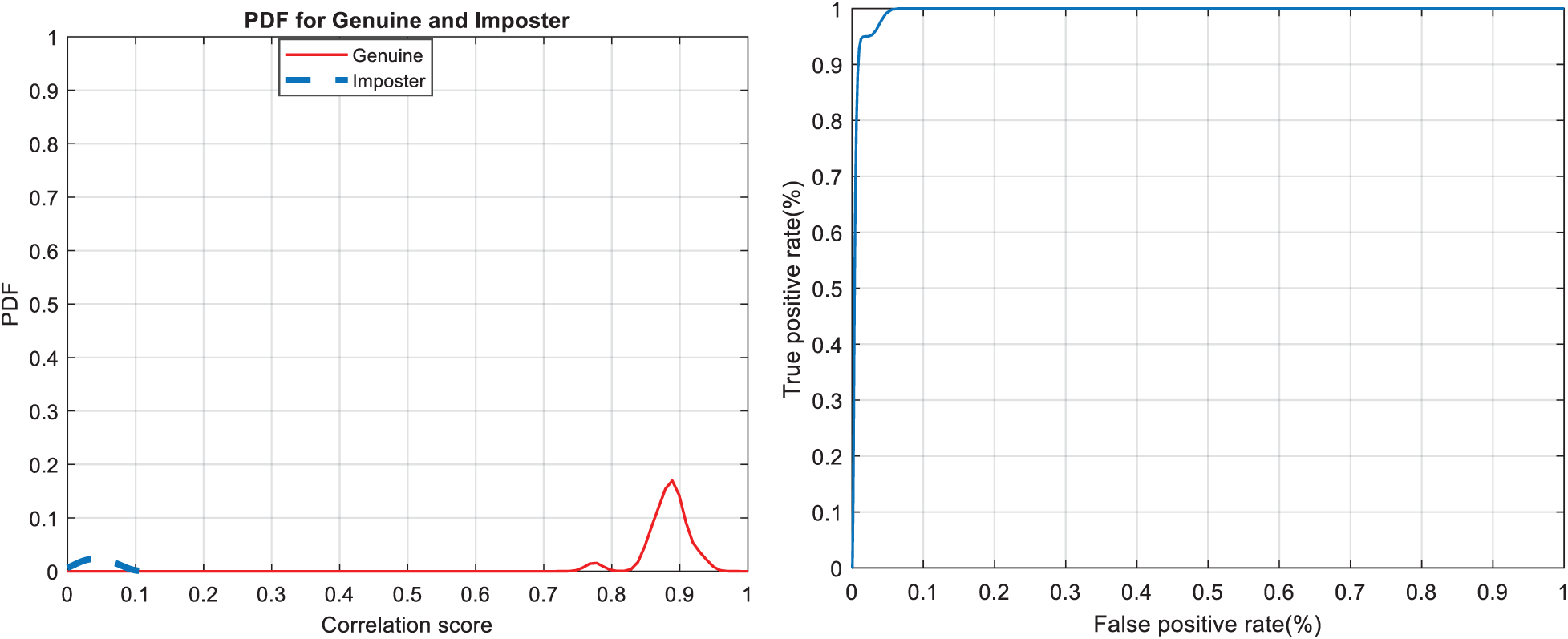
Figure 18: Authentication curves for cancelable iris recognition (a) PFD curves (b) ROC curve

Figs. 7, 12, 17, and 22 present the correlation scores for all nine unimodal biometric images used in the uCBS experiments. The PTD, PFD, and ROC curves for these biometrics are presented in Figs. 8, 13, 18, and 23. These curves display the threshold values used to distinguish authorized users from unauthorized ones. Fig. 24 presents the composite multi-biometric templates. Samples of the GCD cancelable multi-biometric templates and their respective histograms are presented in Fig. 25. Correlation scores for both authorized and unauthorized patterns are introduced in Fig. 26. Authentication curves for the proposed mCBS are presented in Fig. 27.

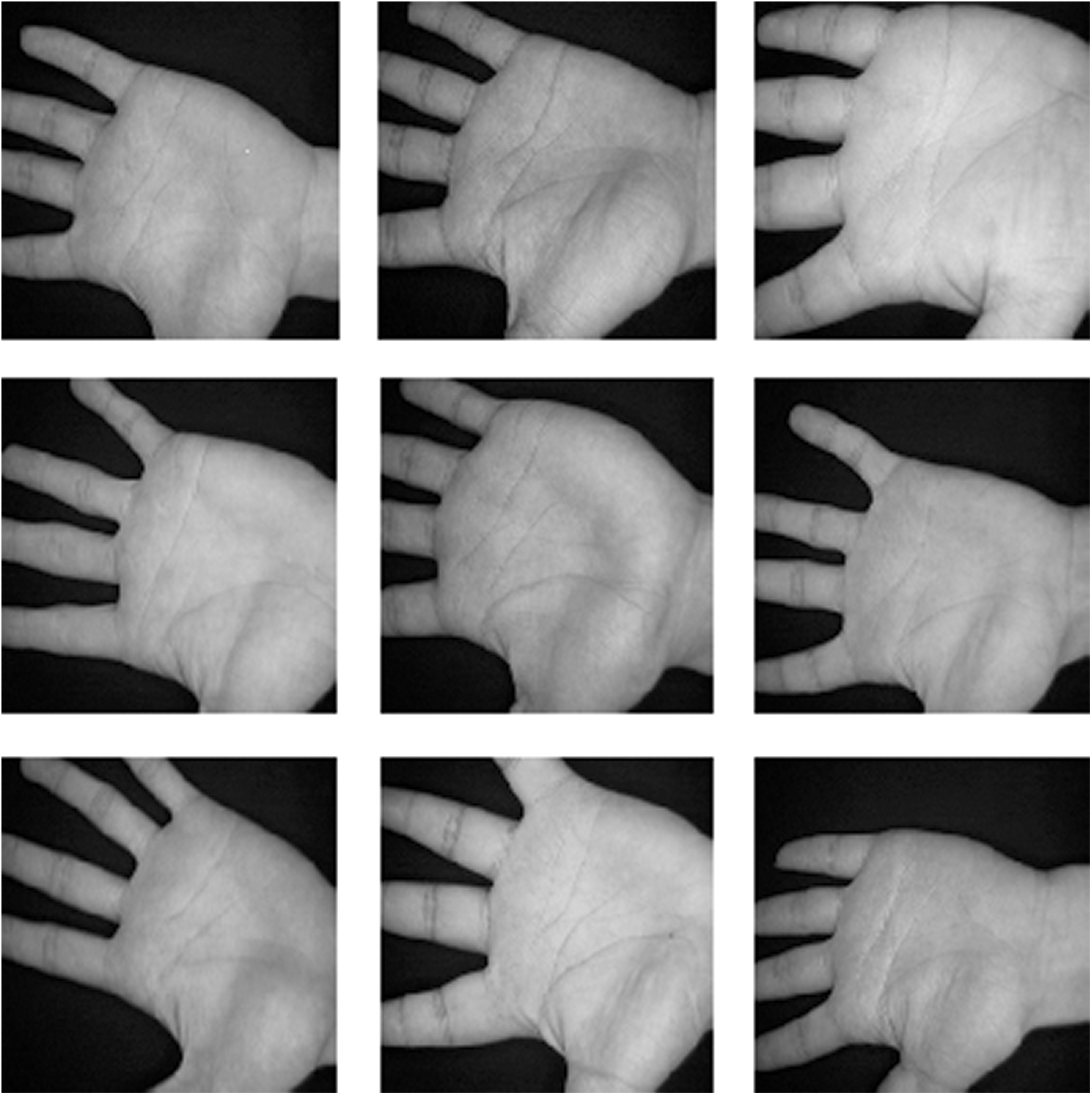
Figure 19: Dataset 4 consisting of nine palm print images [24]

Figure 20: Cancelable palm print images for those in Fig. 19 with GCD algorithm

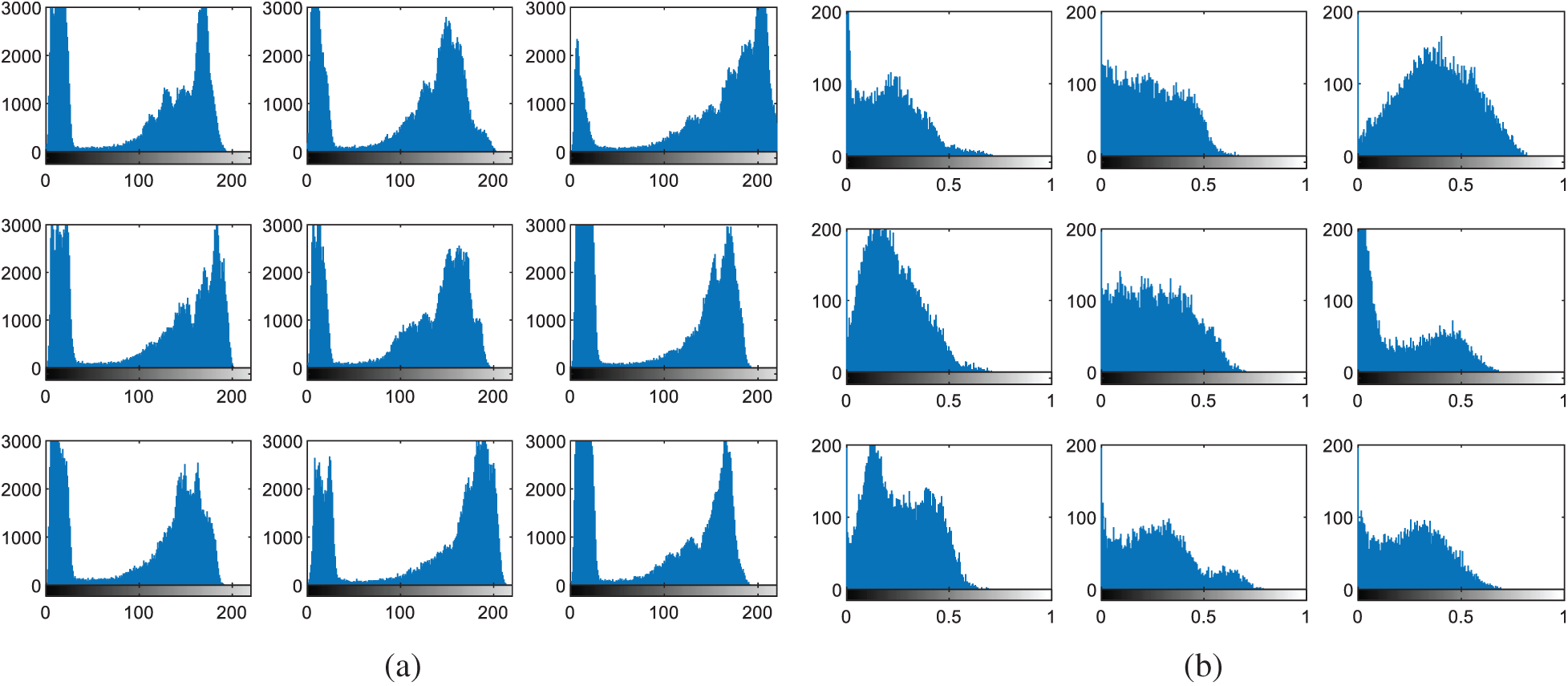
Figure 21: Histograms of palm print images (a) original images (b) cancelable templates

Finally, the average A ROC, mean correlation scores, False Acceptance Rate (FAR), False Rejection Rate (FRR), and ERR for the GCD-based mCBS are presented in Tab. 2.

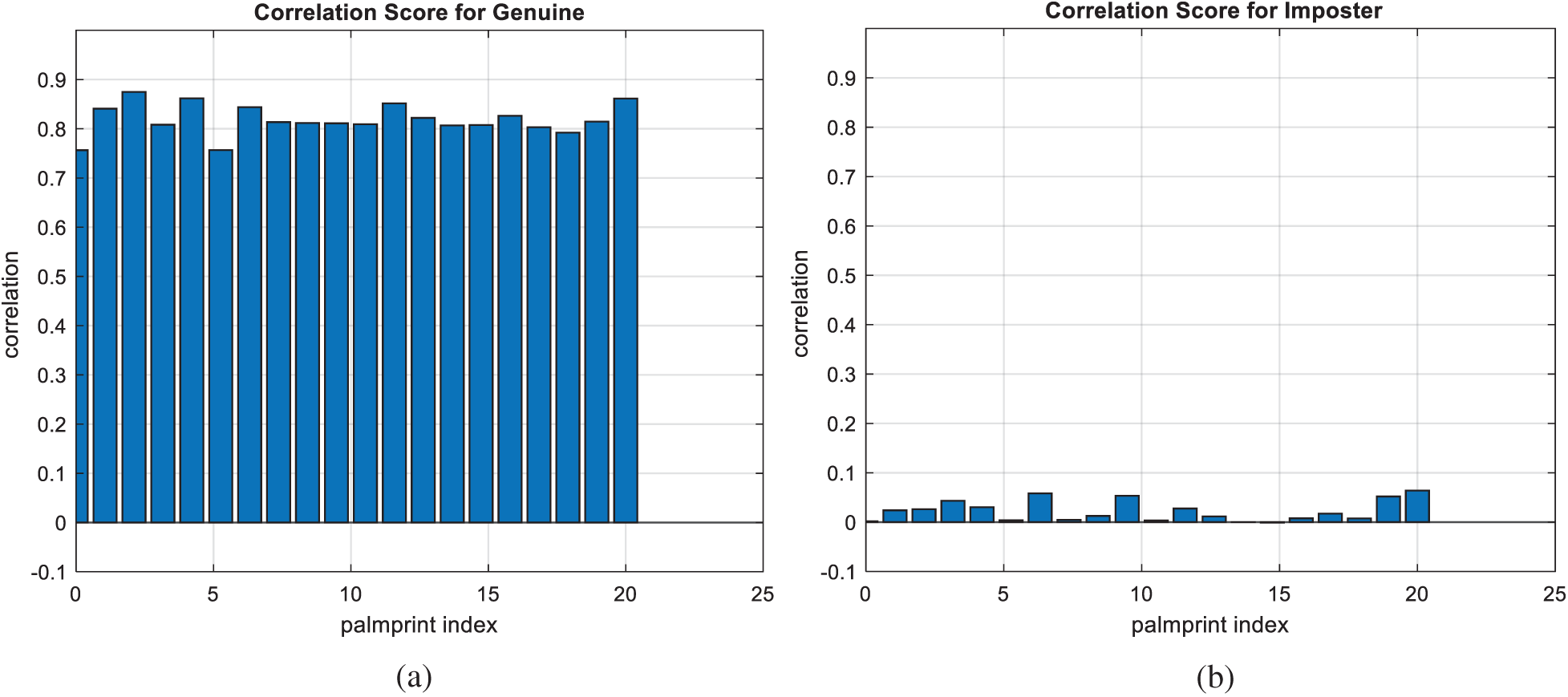
Figure 22: Correlation scores for original palm print images (a) genuine (b) imposter

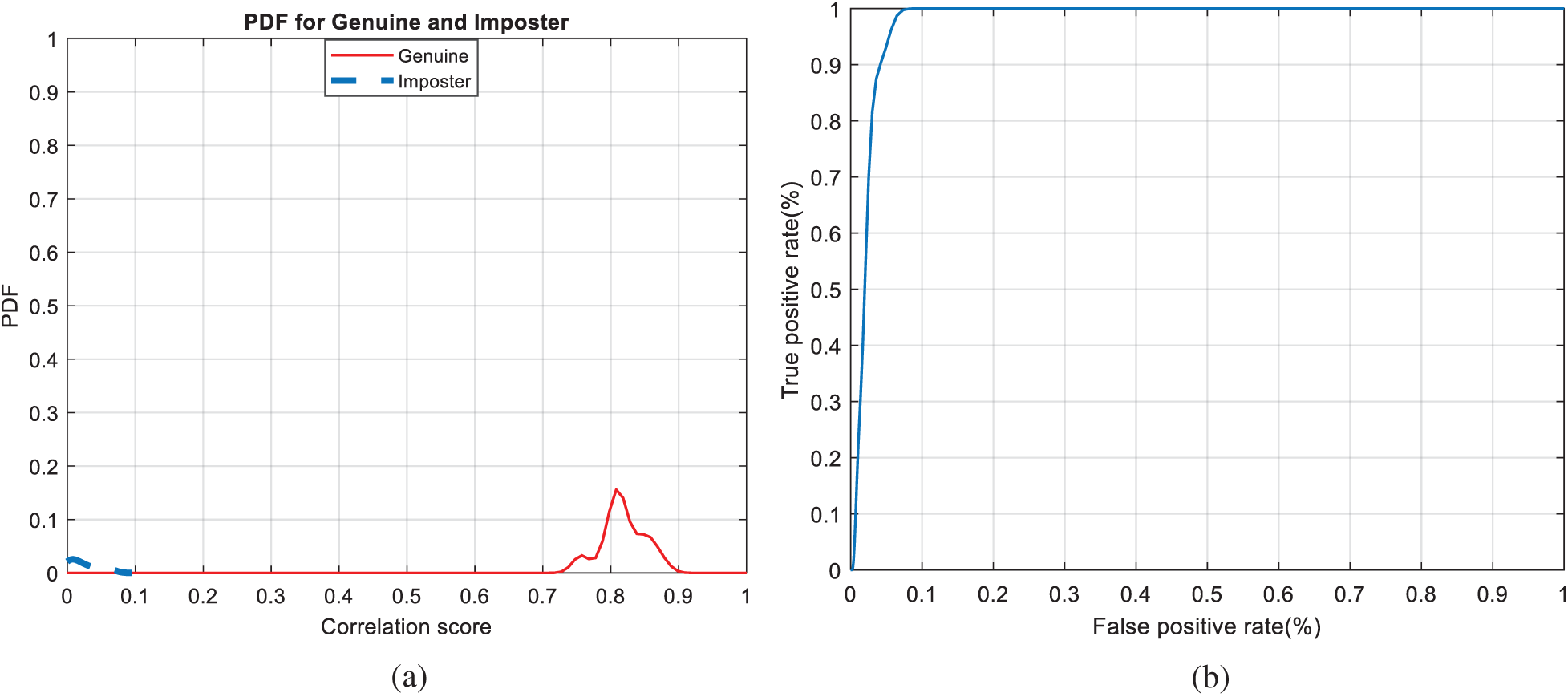
Figure 23: Authentication curves for cancelable palm print recognition (a) PFD curves (b) ROC curve

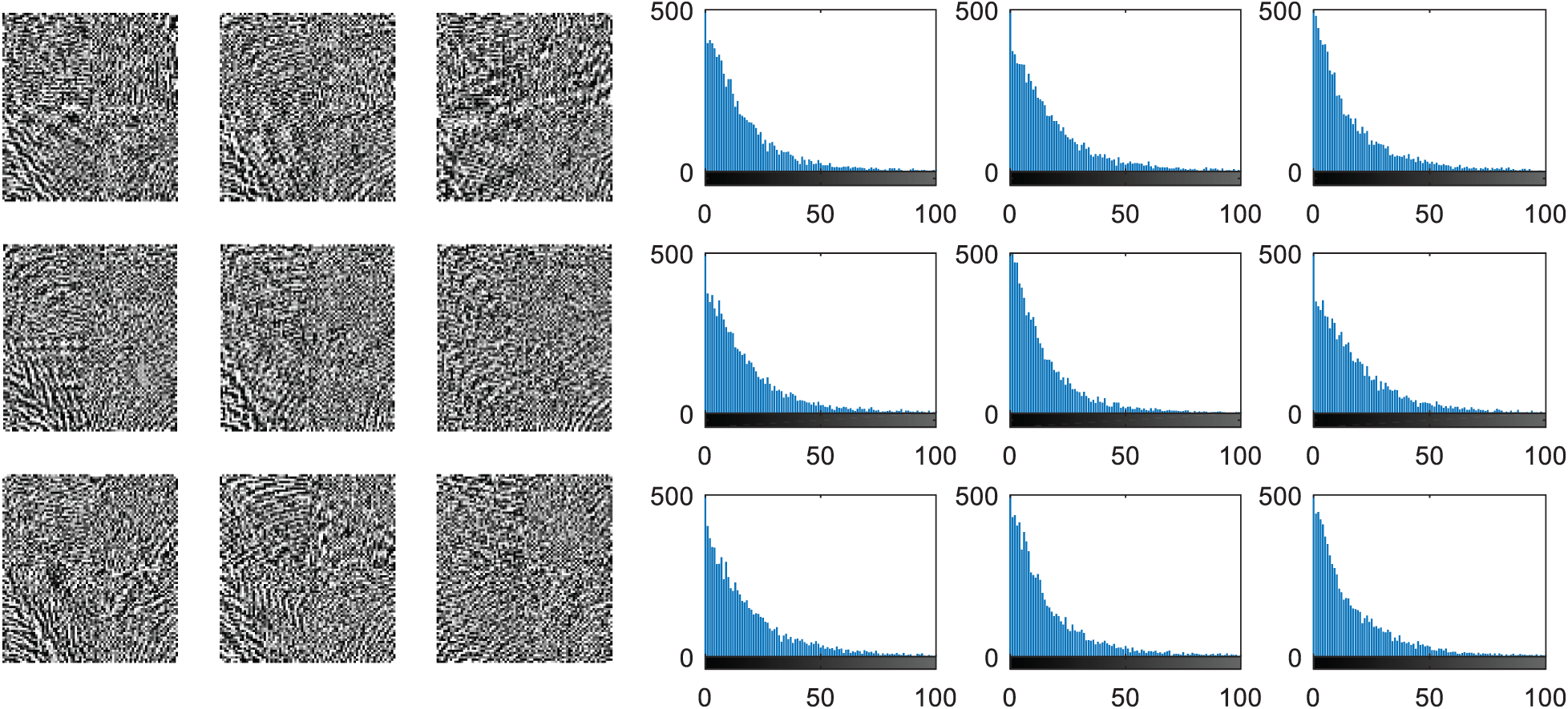
Figure 24: Composite DCT outputs of multi-biometric inputs and their histograms

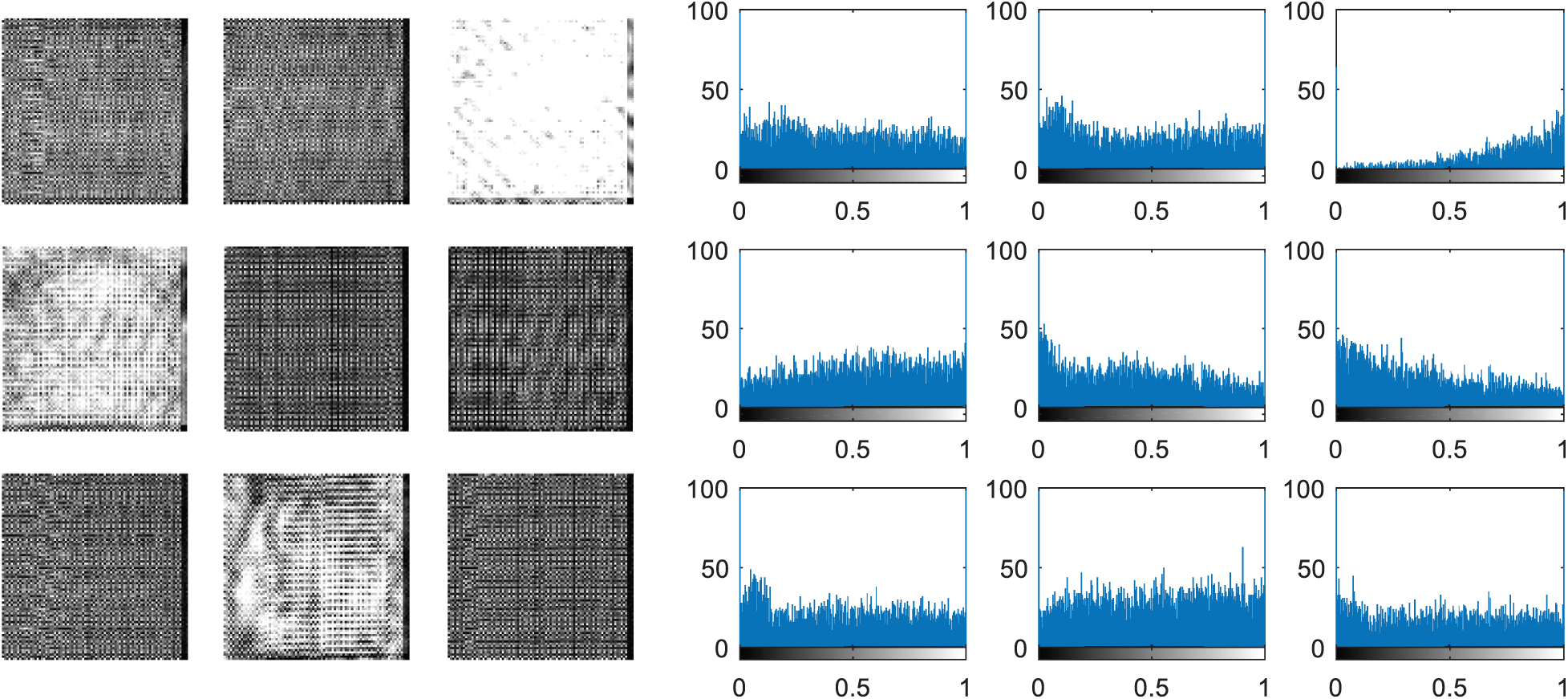
Figure 25: Cancelable templates for the proposed mCBS and their histograms

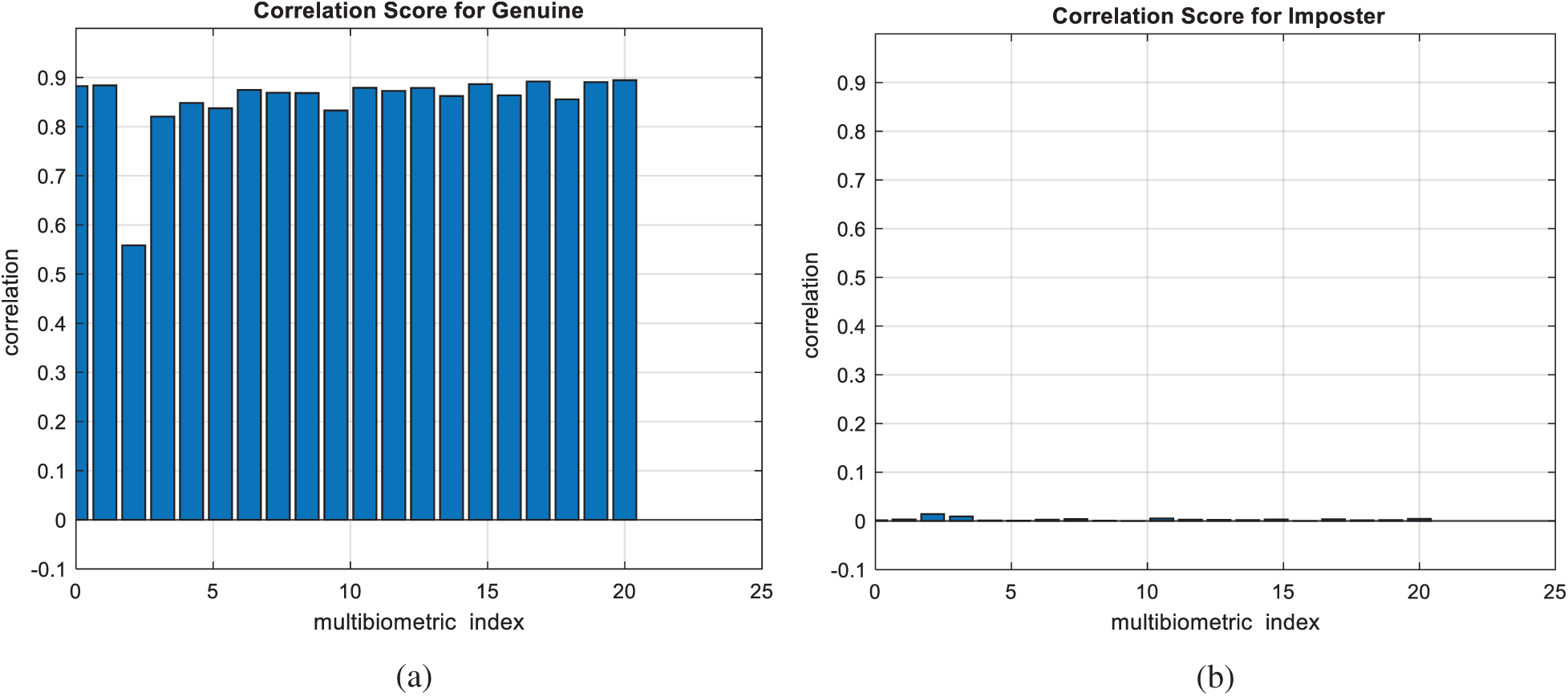
Figure 26: Correlation scores for the proposed mCBS (a) genuine (b) imposter

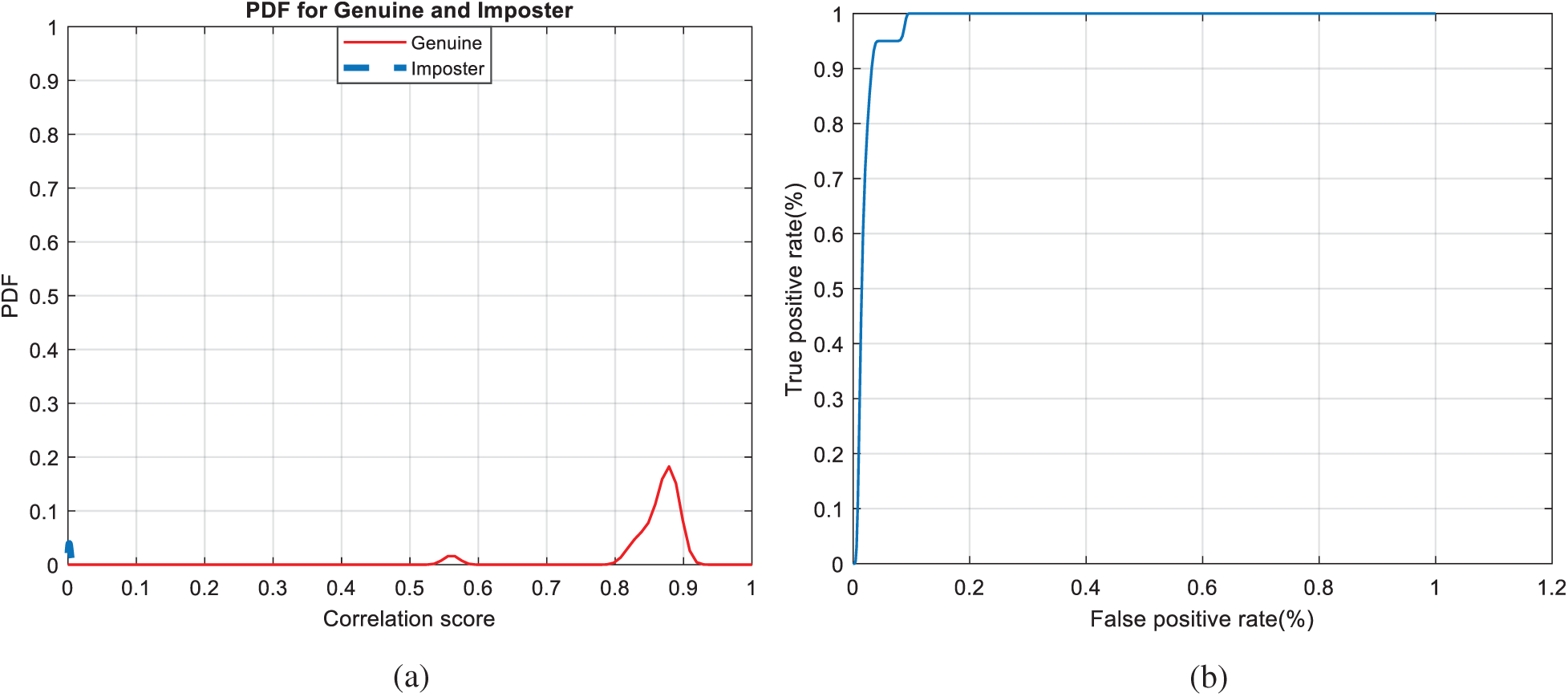
Figure 27: Authentication curves for the proposed mCBS (a) PFD curves (b) ROC curve

•   Comparison with Other Related Works

To validate the suggested CBS, more test investigations have been carried out for comparison of the suggested CBS with the latest algorithms [25–32]. We compared the average FAR, EER, AROC, and FRR of the suggested CBS with those of the CBS in [25–32] as presented in Tab. 3. From the introduced comparative study in Tab. 3, we ensure that the FAR, EER, AROC, and FRR of the suggested CBS are better than those of the other traditional CBS.

5  Conclusions and Future Work

This paper presented a new approach to build efficient CBS using single- and multi-biometric inputs for cloud and IoT biometric applications. Pre-determined distortions are induced in the biometric images for single- and multi-biometric inputs with the GCD algorithm. As a self-dependent approach, the need for auxiliary data or images is eliminated. The GCD with some minimal changes can be used efficiently in the generation of cancelable biometric templates. We validated the proposed uCBS and mCBS on inputs consisting of facial, fingerprint, iris, and palm print images. AROC values above 99% were recorded for all the examined biometrics. This work can be easily implemented for cloud, IoT, and wireless access applications. In addition, it can be enhanced with the utilization of encryption algorithms with the GCD algorithm. In the future, we can incorporate deep learning algorithms for compressing and encrypting the biometric images for enhancing the cancelable biometric system performance.

Acknowledgement: The authors would like to thank the support of the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University.

Funding Statement: This research was funded by the Deanship of Scientific Research at Princess Nourah Bint Abdulrahman University through the Fast-track Research Funding Program to support publication in the top journal (Grant No. 42-FTTJ-13).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Choudhury, P. Then, B. Issac, V. Raman and M. Haldar, “A survey on biometrics and cancelable biometrics systems,” International Journal of Image and Graphics, vol. 18, no. 1, pp. 1850006, 2018. [Google Scholar]

 2.  A. Algarni, G. El Banby, S. Ismail, W. El-Shafai, F. El-Samie et al., “Discrete transforms and matrix rotation based cancelable face and fingerprint recognition for biometric security application,” Entropy, vol. 22, no. 12, pp. 1–40, 2020. [Google Scholar]

 3.  A. Alarifi, M. Amoon, M. Aly and W. El-Shafai, “Optical PTFT asymmetric cryptosystem based secure and efficient cancelable biometric recognition system,” IEEE Access, vol. 8, pp. 221246–221268, 2020. [Google Scholar]

 4.  A. Jegede, N. Udzir, A. Abdullah and R. Mahmod, “Cancelable and hybrid biometric cryptosystems: Current directions and open research issues,” International Journal of Advanced and Applied Sciences, vol. 4, no. 11, pp. 65–77, 2017. [Google Scholar]

 5.  S. Ibrahim, M. Egila, H. Shawky, M. Elsaid, W. El-Shafa et al., “Cancelable face and fingerprint recognition based on the 3D jigsaw transform and optical encryption,” Multimedia Tools and Applications, pp. 1–26, 2020. [Google Scholar]

 6.  N. Soliman, M. Khalil, A. Algarni, S. Ismail, R. Marzouk et al., “Efficient HEVC steganography approach based on audio compression and encryption in QFFT domain for secure multimedia communication,” Multimedia Tools and Applications, vol. 80, no. 3, pp. 1–35, 2020. [Google Scholar]

 7.  C. Rathgeb, M. Gomez-Barrero, C. Busch, J. Galbally and J. Fierrez, “Towards cancelable multi-biometrics based on bloom filters: A case study on feature level fusion of face and iris,” in Proc. 3rd IEEE Int. Workshop on Biometrics and Forensics, Gjovik, Norway, pp. 1–6, 2015. [Google Scholar]

 8.  P. Paul and M. Gavrilova, “Multimodal biometrics using cancelable feature fusion,” in Proc. IEEE Int. Conf. on Cyberworlds, Santander, Spain, pp. 279–284, 2014. [Google Scholar]

 9.  R. Dwivedi and S. Dey, “Score-level fusion for cancelable multi-biometric verification,” Pattern Recognition Letters, vol. 126, no. 3, pp. 58–67, 2019. [Google Scholar]

10. H. Kaur and P. Khanna, “Privacy preserving remote multi-server biometric authentication using cancelable biometrics and secret sharing,” Future Generation Computer Systems, vol. 102, no. 11, pp. 30–41, 2020. [Google Scholar]

11. W. Yang, S. Wang, J. Hu, G. Zheng and C. Valli, “A fingerprint and finger-vein based cancelable multi-biometric system,” Pattern Recognition, vol. 78, pp. 242–251, 2018. [Google Scholar]

12. G. Goswami, P. Mittal, A. Majumdar, M. Vatsa and R. Singh, “Group sparse representation based classification for multi-feature multimodal biometrics,” Information Fusion, vol. 32, no. 2, pp. 3–12, 2015. [Google Scholar]

13. A. Canuto, F. Pintro and J. Xavier-Junior, “Investigating fusion approaches in multi-biometric cancelable recognition,” Expert Systems with Applications, vol. 40, no. 6, pp. 1971–1980, 2013. [Google Scholar]

14. M. Sandhya and M. Prasad, “Securing fingerprint templates using fused structures,” IET Biometrics, vol. 6, no. 3, pp. 173–182, 2017. [Google Scholar]

15. M. Barrero, E. Maiorana, J. Galbally, P. Campisi and J. Fierrez, “Multi-biometric template protection based on Homomorphic encryption,” Pattern Recognition, vol. 67, no. 10, pp. 149–163, 2017. [Google Scholar]

16. Y. Lai, Z. Jin, A. Teoh, B. Goi, W. Yap et al., “Cancelable iris template generation based on indexing-first-one hashing,” Pattern Recognition, vol. 64, no. 1, pp. 105–117, 2017. [Google Scholar]

17. S. Umer, B. Dhara and B. Chanda, “A novel cancelable iris recognition system based on feature learning techniques,” Information Sciences, vol. 406, no. 407, pp. 102–118, 2017. [Google Scholar]

18. S. El-Khamy, M. Hadhoud, M. Dessouky, B. Salam and F. Abd El-Samie, “Blind multichannel reconstruction of high-resolution images using wavelet fusion,” Journal of Applied Optics, vol. 44, no. 34, pp. 7349–7356, 2005. [Google Scholar]

19. A. Alarifi, S. Sankar, T. Altameem, K. Jithin, M. Amoon et al., “Novel hybrid cryptosystem for secure streaming of high efficiency H.265 compressed videos in IoT multimedia applications,” IEEE Access, vol. 8, pp. 128548–128573, 2020. [Google Scholar]

20. O. Faragallah, A. Afifi, W. El-Shafai, H. El-Sayed, E. Naeem et al., “Investigation of chaotic image encryption in spatial and FrFT domains for cybersecurity applications,” IEEE Access, vol. 8, pp. 42491–42503, 2020. [Google Scholar]

21. ORL database, [Online]. Available: https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html (Accessed on 1 November 2020). [Google Scholar]

22. Fingerprint verification competition, (FVC2000 DB1:Secure desktop scanner by keytronic[Online]. Available: http://bias.csr.unibo.it/fvc2000/databases.asp (Accessed on 1 November 2020). [Google Scholar]

23. CASIA-IrisV3 database, [Online]. Available: http://www.cbsr.ia.ac.cn/english/IrisDatabase.asp (Accessed on 1 November 2020). [Google Scholar]

24. CASIA palm print image database, [Online]. Available: http://biometrics.idealtest.org/dbDetailForUser.do?id=5 (Accessed on 1 November 2020). [Google Scholar]

25. P. Refregier and B. Javidi, “Optical image encryption based on input plane and Fourier plane random encoding,” Optics Letters, vol. 20, no. 7, pp. 767–769, 1995. [Google Scholar]

26. P. Kumar, J. Joseph and K. Singh, “Optical image encryption using a jigsaw transform for silhouette removal in interference-based methods and decryption with a single spatial light modulator,” Applied Optics, vol. 50, no. 13, pp. 1805–1811, 2011. [Google Scholar]

27. T. Dang, Q. Truong, T. Le and H. Truong, “Cancellable fuzzy vault with periodic transformation for biometric template protection,” IET Biometrics, vol. 5, no. 3, pp. 229–235, 2016. [Google Scholar]

28. S. Sree and N. Radha, “Cancellable multimodal biometric user authentication system with fuzzy vault,” in Proc. IEEE Int. Conf. on Computer Communication and Informatics, Coimbatore, India, pp. 1–6, 2016. [Google Scholar]

29. E. B. Tarif, S. Wibowo, S. Wasimi and A. Tareef, “A hybrid encryption/hiding method for secure transmission of biometric data in multimodal authentication system,” Multimedia Tools and Applications, vol. 77, no. 2, pp. 2485–2503, 2019. [Google Scholar]

30. R. F. Soliman, G. M. El Banby, A. D. Algarni, M. Elsheikh, N. F. Soliman et al., “Double random phase encoding for cancelable face and iris recognition,” Applied Optics, vol. 57, no. 35, pp. 10305–10316, 2018. [Google Scholar]

31. R. F. Soliman, M. Amin and F. E. Abd El-Samie, “A modified cancelable biometrics scheme using random projection,” Annals of Data Science, vol. 6, no. 2, pp. 223–236, 2019. [Google Scholar]

32. A. D. Algarni, G. M. El Banby, N. F. Soliman, F. E. A. El-Samie and A. M. Iliyasu, “Efficient implementation of homomorphic and fuzzy transforms in random-projection encryption frameworks for cancellable face recognition,” Electronics, vol. 9, no. 6, pp. 1046, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.