Computers, Materials & Continua DOI:10.32604/cmc.2021.018636
Article

An Optimal Lempel Ziv Markov Based Microarray Image Compression Algorithm

R. Sowmyalakshmi1,*, Mohamed Ibrahim Waly2, Mohamed Yacin Sikkandar2, T. Jayasankar1, Sayed Sayeed Ahmad3, Rashmi Rani3 and Suresh Chavhan4,5

1Department of Electronics and Communication Engineering, University College of Engineering, BIT Campus, Anna University, Tiruchirappalli, 620024, India
2Department of Medical Equipment Technology, College of Applied Medical Sciences, Majmaah University, Al Majmaah, 11952, Saudi Arabia
3Department of Computer Engineering, College of Engineering and Computing, Al Ghurair University, Dubai, 37374, United Arab Emirates
4Automotive Research Center, Vellore Institute of Technology, Vellore, 632014, India
5Federal University of Piauí, Teresina, 64049-550, PI, Brazil
*Corresponding Author: R. Sowmyalakshmi. Email: sowmya.anand2007@gmail.com
Received: 15 March 2021; Accepted: 20 April 2021

Abstract: In the recent years, microarray technology gained attention for concurrent monitoring of numerous microarray images. It remains a major challenge to process, store and transmit such huge volumes of microarray images. So, image compression techniques are used in the reduction of number of bits so that it can be stored and the images can be shared easily. Various techniques have been proposed in the past with applications in different domains. The current research paper presents a novel image compression technique i.e., optimized Linde–Buzo–Gray (OLBG) with Lempel Ziv Markov Algorithm (LZMA) coding technique called OLBG-LZMA for compressing microarray images without any loss of quality. LBG model is generally used in designing a local optimal codebook for image compression. Codebook construction is treated as an optimization issue and can be resolved with the help of Grey Wolf Optimization (GWO) algorithm. Once the codebook is constructed by LBG-GWO algorithm, LZMA is employed for the compression of index table and raise its compression efficiency additionally. Experiments were performed on high resolution Tissue Microarray (TMA) image dataset of 50 prostate tissue samples collected from prostate cancer patients. The compression performance of the proposed coding esd compared with recently proposed techniques. The simulation results infer that OLBG-LZMA coding achieved a significant compression performance compared to other techniques.

Keywords: Arithmetic coding; dictionary based coding; Lempel-Ziv Markov chain algorithm; Lempel-Ziv-Welch coding; tissue microarray

1  Introduction

Microarray analysis is a technology which enables the analysis and classification of genes in a rapid manner. At present, microarray is the main tool for gene-based investigations [1]. Microarray technique is used to monitor large number of tissue array images in a concurrent manner. Every microarray experiment produces numerous large-sized images which are hard to store or share [2]. Such massive number of microarray images imposes a new challenge for storage space and bandwidth resources. In the absence of high speed internet, it is difficult or sometimes impossible to share microarray images from some parts of the world. Several studies have been conducted to handle the storage of massive number of microarray image datasets in an efficient manner. Image compression is one of the ways to handle such huge volume of images.

In general, the intention of image compression is to transfer an image with fewer bits. Image compression has three major components such as recognition of redundant data in image, appropriate coding method and transformation method. The most important image compression standard is JPEG and its quantization can be divided into two kinds namely, scalar and vector (SQ and VQ). It is a non-convertible compression method and is commonly used in the compression of image with some loss of information. The foremost intention of VQ is to generate an optimal codeword that has a collection of codewords, where an input image vector is allocated based on minimum Euclidean distance. The popular VQ method is Linde–Buzo–Gray (LBG) model. LBG method offers simplicity, adaptability and flexibility. Further, the method depends on lower Euclidean distance between image vectors and respective codewords. It can generate local optimal solutions and in other terms, it fails in providing the best global solutions. The concluding solution of LBG algorithm is based on arbitrarily-produced codebook at the initial stage.

An enhanced form of LBG algorithm termed ‘ELBG’ algorithm was introduced in the literature which enhances its local optimal solution [3]. ELBG is mainly applied in the optimal exploitation of codewords, an efficient tool to resolve the difficulties of clustering techniques. The outcomes pointed out that ELBG outperformed LBG and is independent from initial codebook. Projection VQ (PVQ) was presented based on the adoption of quadtree decomposition to segment the images into different block sizes. This technique was defined by Single Orientation Reconstruction (SOR) and enhanced results were produced in terms of objective as well subjective ways in comparison with usage of predefined block sizes [4]. Object-relied VQ is carried out in three levels namely, initialization, iteration and finalization. Initially, it applies Max–Min algorithm while at the second level, it makes use of adaptive LBG algorithm. The third level removes the redundant data from codebook [5].

To overcome the limitations of existing algorithms found in the literature, the authors propose a GWO model in current research paper to construct a novel codebook that results in better VQ in terms of high PSNR and good quality reconstructed image. This paper presents a novel image compression technique i.e., Optimized Linde–Buzo–Gray (OLBG) with Lempel Ziv Markov Algorithm (LZMA) coding technique called OLBG-LZMA for microarray images without any loss of quality. The proposed OLBG-LZMA model is used to compress high resolution Tissue Microarray (TMA) images. LBG model is generally used in designing a local optimal codebook for image compression. Codebook construction is treated as an optimization issue and is solved with the help of Grey Wolf Optimization (GWO) algorithm. After the codebook is constructed by LBG-GWO algorithm, LZMA is employed in the compression of index table and to increase the compression efficiency. Experiments were performed on high resolution Tissue Microarray (TMA) image dataset containing 50 prostate tissue samples acquired from prostate cancer patients. The compression performance of the proposed method was compared with recently proposed techniques.

2  Literature Review

Quad Tree (QT) degradation is composed of VQ with different sized blocks under the examination of local sites [6]. At the same time, the researchers in the literature [7] noticed that the complexity level of local regions is highly important, when compared with homogeneity. In Vector Quantization (VQ) of images with different block sizes, tedious regions of an image are quantified using Local Fractal Dimension (LFD). A fuzzy-based VQ, which makes use of competing accumulation and new codeword migration approach, was introduced to perform image compression [8]. Likewise, the authors in the literature [9] employed a learning process which methodologically develops fast fuzzy clustering-based VQ techniques by integrating three learning modules [9]. On the other hand, a Multivariate VQ (MVQ) method was developed using Fuzzy C-Mean (FCM) to compress Hyperspectral Imagery (HSI). The experimentation inferred that the MVQ is superior to traditional VQ in terms of Mean Square Error (MSE) and the quality of recreated image [10]. In the literature [11], it is noted that the images can be compressed using the transformed VQ, in which the quantized image can be transformed using Discrete Wavelet Transform (DWT) [11].

Recently, evolutionary algorithms have been introduced to solve many engineering and technological problems. The study conducted earlier [12] employed Ant Colony Optimization (ACO) algorithm for codebook construction. A codebook was developed using ACO which mimics the wavelet coefficients in a bidirectional graph and defines an appropriate method to place the edges on graph. The method was found to be efficient than LBG though it requires more CT. A fast ACO algorithm was introduced in the literature [13] which generates the codebook based on the observation of repetitive computations present in ACO algorithm. Since the repetitive computations are identified in codebook design, the convergence time got reduced than the classical ACO algorithm. Furthermore, a PSO-based VQ was presented, which updates the particle global best (gbest) and local best (pbest) solutions which surpassed the LBG method [14].

A fuzzy-based PSO algorithm, proposed in the study [15], was able to provide efficient codebook globally. The enhanced results were attained in comparison with PSO and LBG methods. QPSO was introduced in the literature [16] to resolve the knapsack problem and maximize the PSO results. The attained simulation outcome of QPSO method was optimal than the traditional PSO. A tree-based VQ was presented for fast codebook design by applying the triangle inequality which in-turn offered better codewords. However, the method required high Computation Time (CT) [17]. Hence, in the study [18], the researchers presented a fast codebook search method which applies two test criteria to enhance the image encoding process with no additional image distortion. From the results, it is noted that the CT got reduced to an average of 95.23% for a codebook of 256 codewords [18]. A near optimal codebook was developed using Bacterial Foraging Optimization Algorithm (BFOA) to attain better reconstructed image quality with high PSNR [19].

Fuzzy Membership Functions (FMF) were selected as objective functions and were optimized using the modified BFOA. A HBMO algorithm-based VQ technique was presented in one of the investigations conducted earlier [20]. It achieved better image superiority and codebook with minimal distortion than PSO, QPSO and LBG algorithms altogether. The researchers [21] used FA to design the codebook for VQ. FF algorithm was stimulated by the nature of flashing patterns for communication and mating purposes. FFs, with high brightness, are attracted by low bright FFs or else random search takes place, which reduces the exploration part. Hence, FA was altered in the literature [22] which provided a particular mechanism to follow in case of unavailability of brighter FFs in the search space. A bat algorithm [23]-based codebook design was devised with a proper choice of tuning variables and the study ensured better performance with higher PSNR value and convergence time in comparison with traditional FF algorithm. An efficient VQ method was proposed by the researchers in [24] to encode the wavelet decomposed color image using Modified Artificial Bee Colony (ABC) optimization technology. The proposed model was compared with Genetic Algorithm (GA) and classical ABC. The model attained better PSNR and good reformed image supremacy [24]. In spite of the established models in literature, there is a gap still exists to be fulfilled.

3  The Proposed Methodology

The proposed model involves two stages such as OLBG-based codebook construction and LZMA-based codebook compression. The working processes are detailed in the succeeding sections.

3.1 Vector Quantization (VQ)

VQ is defined as a block coding model which is used to compress images at some loss of information. In VQ, codebook construction is an essential process. Let Y={yij} be the size of raw image with M×M pixels which are partitioned into different block sizes of nxn pixels. In other words, an input vector X=(xi, i=1,2,…,Nb) contains a set of Nb=[Nn]×[Nn] and L indicates n×n. The input vector xi, xi∈RL, is L-dimensional Euclidean space. A codebook C contains L-dimensional code words where C={c1,c2,…,cNc}, cj∈RL, ∀j=1,2,…,Nc. Every input vector is indicated by row vector xi=(xi1, xi2,…,xiL) and the jth codeword of codebook is denoted as cj=(cj1, cj2,...,cjL). The optimization of C, by means of MSE could be devised as the minimization of distortion function, D. Generally, the minimum value of D implies better C.

D(C)=1Nb∑j=1Nc∑i=1Nbμij⋅‖xi−cj‖2 (1)

The above equation is subjected to constraints given in Eqs. (2) and (3)

∑j=1Ncμij=1,∀i∈{1,2,…,Nb} (2)

μij={1if xi is in the jth cluster0 (3)

And Lk≤Cjk≤Uk, k=1,2,…,L, where Lk denotes the lower kth element in training vector whereas Uk defines a higher kth element in input vector. The ‖xi−ci‖ shows the Euclidean distance between the vector x and codeword, c.

3.2 LBG Algorithm

LBG is defined as a Scalar Quantization (SQ) algorithm and was devised in the year 1957 by Lloyd. By 1980, it was generalized as VQ. It employs two predefined conditions for input vectors to determine the codebook. Let xi, i=1,2,…,Nb be an input vector, distance function d and primary codewords cj(0), j=1,2,…,Nc. The LBG algorithm repeatedly employs two conditions to obtain optimal codebook according to the given procedures:

•   Divide the input vector into different groups using minimum distance rules. The resultant block is saved in a Nb×Nc binary indicator matrix U, where the components are expressed as follows,

μij={1 if d(xi,cj(k))=minpd(xi,cp(k))0 otherwise (4)

•   Identify the centroid of every portion. The previous codewords can be replaced with any available centroids:

cj(k+1)=∑i=1Nbμij⋅xi∑i=1Nbμij (5)

•   Go to step 1 till no modifications occur in cj.

3.3 The Proposed OLBG-LZMA Algorithm

The overall operation of the proposed OLBG-LZMA algorithm is illustrated in Fig. 1. The input image should be divided into non-overlapping blocks which then undergo quantization by LBG model. The codebook, which has been deployed using LBG approach, is trained first using GWO method in order to satisfy the needs of global convergence and assures the phenomenon. The index numbers are sent over transmission medium and reconstructed at the destination using decoder. Both reformed index and the corresponding codewords are arranged properly in order to generate the decompressed image size which is almost equal to the given input image. GWO algorithm was developed by Mirjalili et al. [25] in 2016 as a simulation from the hunting behavior of grey wolves. Grey wolves are assumed to be superior predators which often reside in group. Based on its hunting nature, the wolves are divided into alpha (α), beta (β), delta (δ), and omega (ω). The leader wolves are known to be α wolves which decide the place of sleep, hunting destination etc. The decisions taken by α are followed by the remaining members in the group. β is the second level of grey wolves which is referred to be subordinate wolves that guide the α wolves in decision making process. The subordinates can make decision in the absence of dominant wolves. Third level grey wolves are grouped under ω wolves which act as a scapegoat. When the wolves do not come under α, β, or ω, they are known to be subordinate or δ wolves.

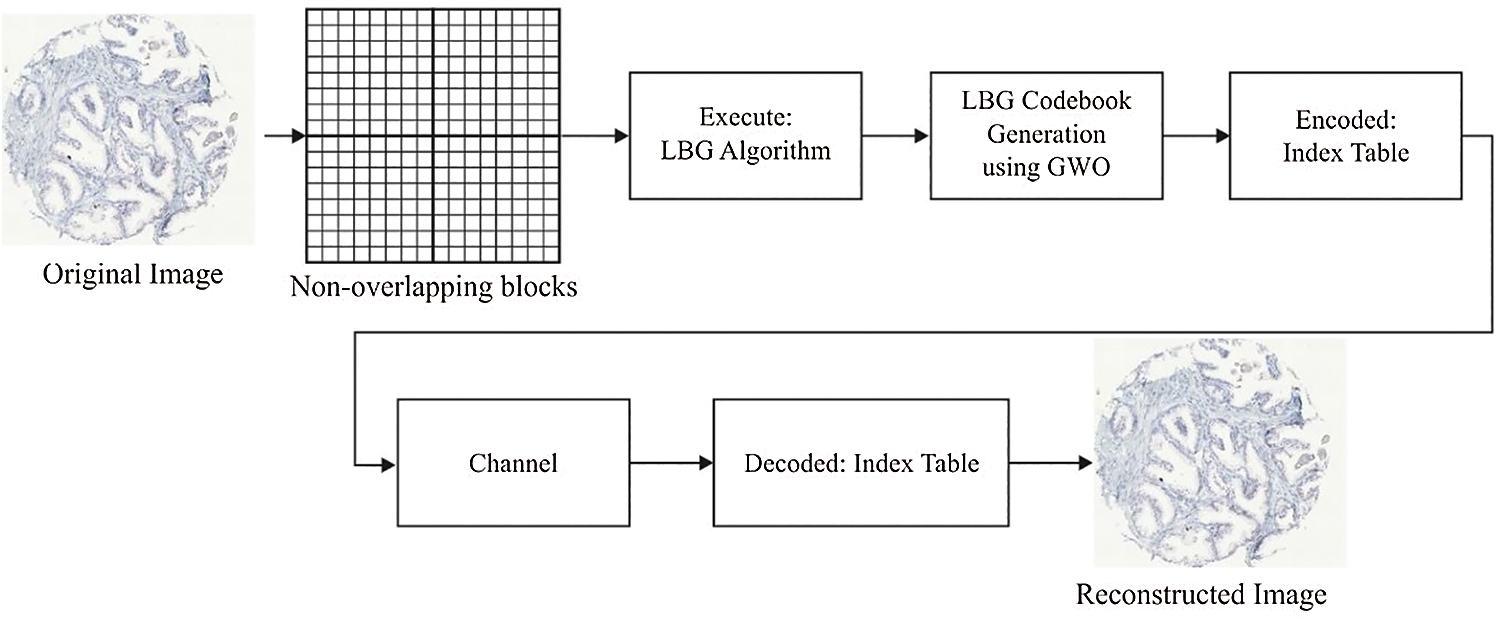
Figure 1: Working model of OLBG-LZMA algorithm

These wolves do not dominate α and β wolves, but dominate over ω. Different levels of grey wolf hunting are listed below.

•   Approaching prey

•   Encircling prey

•   Attacking the prey.

GWO algorithm is composed of two phases namely, exploration and exploitation. Initially, it is applied to explore the best solutions in local search area. The grey wolf surrounds and attacks the prey when searching for reliable solutions. Secondly, prey is identified by exploring the local space area. While encircling prey, the wolves finds the location of a victim and surrounds it. Hence, encircling prey is expressed as given herewith.

D→=|C→.Xp→(t)−X→(t)| (6)

X→(t+1)=Xp→(k)−A→.D→ (7)

where t depicts the present iteration and A→ and C→ are said to be coefficient vectors and position vector of the prey which are represented as Xp→(k). Here, X→ implies the position vector, A→.D→ exhibits the accurate value and X→(t+1) implies element multiplication. The vectors A→ and C→ can be denoted as follows.

A→=2a→.r→−a→ (8)

C→=2.r→ (9)

where the elements of ~a have been reduced in a linear manner from 2 to 0 during various iterations whereas r1 and r2 define the random vectors in [0, 1].

The default nature of grey wolves is to identify the locations of prey and encircle it. Hunting operation is carried out by α wolf, while β and δ involves in a few scenarios. Also, the numerical simulation of grey wolves is assumed to be α, β and δ which embeds massive aspects in terms of prey location. Thus, the top three solutions are saved which result in improving the position of search agents and is described as depicted in Eq. (10).

D→β=|C→b∗X→β−X→| (10)

where D→α, D→β and D→δ are the modified distance vectors among α, β and γ locations to alternate wolves and C→a, C→b, and C→c illustrate three coefficient vectors which are applied in distance vector.

X→b=X→β−A→b∗D→β (11)

where X→a represents the newly-attained position vector of α position X→α and the distance vector D→α. X→b implies a novel position vector accomplished using β position X→β and the distance vector D→β. X→v demonstrates the best position vector estimated with the application of δ position X→δ and distance vector D→δ, while A→a, A→b, and A→c are referred to as three coefficient vectors.

X→(k+1)=∑i=1nX→in (12)

where X→(k+1) is defined as a novel position vector that is calculated as an average of total number of positions attained by applying α, β and δ (n = 3). As mentioned earlier, the grey wolves wait to attack the prey till it becomes idle. To model the approach in a mathematical way, the value of ~a is to be reduced. The random measures of ~A lies in the range of [−1, 1]. There are few steps followed in GWO model as demonstrated in Fig. 2.

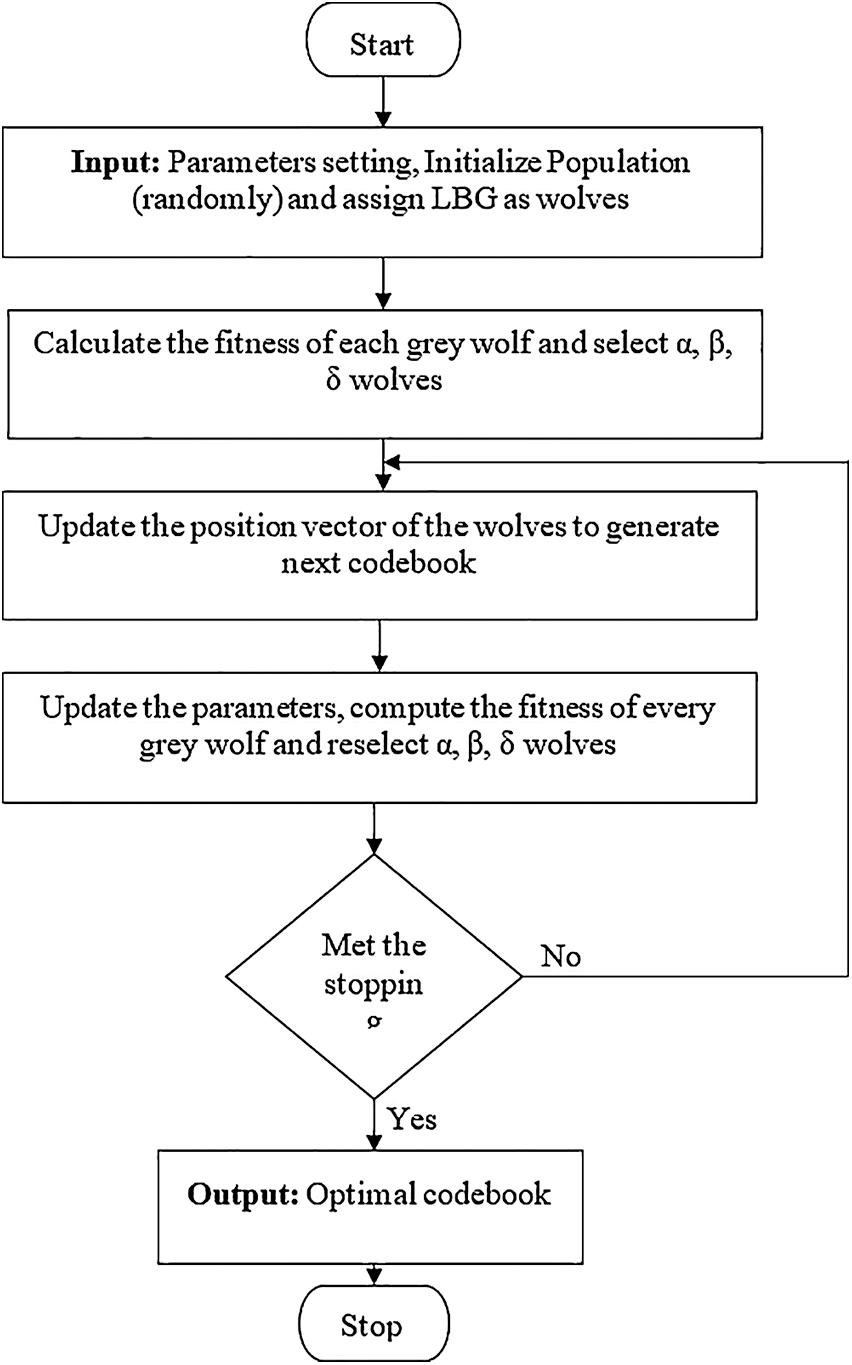
Figure 2: Overall operation of OLBG-LZMA algorithm

Step 1: Initializing parameters: Here, the codebook constructed using LBG approach is declared to be the initial solution whereas the remaining solutions are developed in a random manner. The attained solution refers to a codebook of NC codewords.

Step 2: (Selecting the present best solution): The fitness of each solution is processed using Eq. (1) and the higher fitness location is selected as an optimal result.

Step 3: (Generating novel solution): The position of grey wolves is updated using the location of prey. When an arbitrarily-created number (K) is higher than ~a, then the bad locations are replaced with newly-identified positions and the best location is kept unaltered.

Step 4: Rank the solutions under the application of fitness function and select the better solution.

Step 5: (Termination criteria): Follow the Steps 2 and 3 until the stopping condition is reached.

3.4 LZMA-Based Compression Process

LZMA coding is used in the compression of generated codebooks. It is used to compress real time data which is generated rapidly. Initially, the sensor nodes observe the physical environment. The sensed value is then tested for anomalies and the label value is appended. Label value is appended by the sensors to every individual sensed data. The labelled value ‘1’ is appended to the sensed data, when the latter differs from actual data i.e., an abnormal value is found. Likewise, the labelled value ‘0’ is appended to the sensed data, when the latter has no deviation from the actual data, i.e., normal value is found. The sensor node appends the label value to sensed data after which the compression is performed. Sensor node runs the LZMA algorithm whereas the compression algorithm compress the labelled data efficiently, irrespective of the label value. LZMA algorithm uses the dictionary, sliding window concept and range encoder to efficiently compress the labelled data. The compressed data is then transmitted to BS. BS receives the compressed data and performs decompression process. As LZMA is a lossless compression technique, the reconstructed data remains the exact replica of original data with no loss of information.

4  Performance Validation

In order to understand the effectiveness of the proposed model, TMA image dataset was used. The dataset contains 50 prostate tissue samples collected from prostate cancer patients. In addition, the results were compared with existing methods under different measures.

4.1 Dataset Details

For experimentation, a publicly-available microarray image dataset was employed from Zhong 2017. Besides, the particulars of the dataset is given in Fig. 3 and the sample TMA images are shown in Fig. 4. The dataset contains high resolution Tissue Microarray (TMA) image dataset containing 71 prostate tissue samples of cancer patients digitized by Carl Zeiss Axio Scan.Z1 scanner. The resolution of the image is 7000 × 7000 pixels for a core tissue and is named as *_PTEN_Zesis_7000.jpg. In some cases, 4096 × 4096 resolution is also used and is named as *_PTEN_Zesis_4096.jpg (where * indicates sample id).

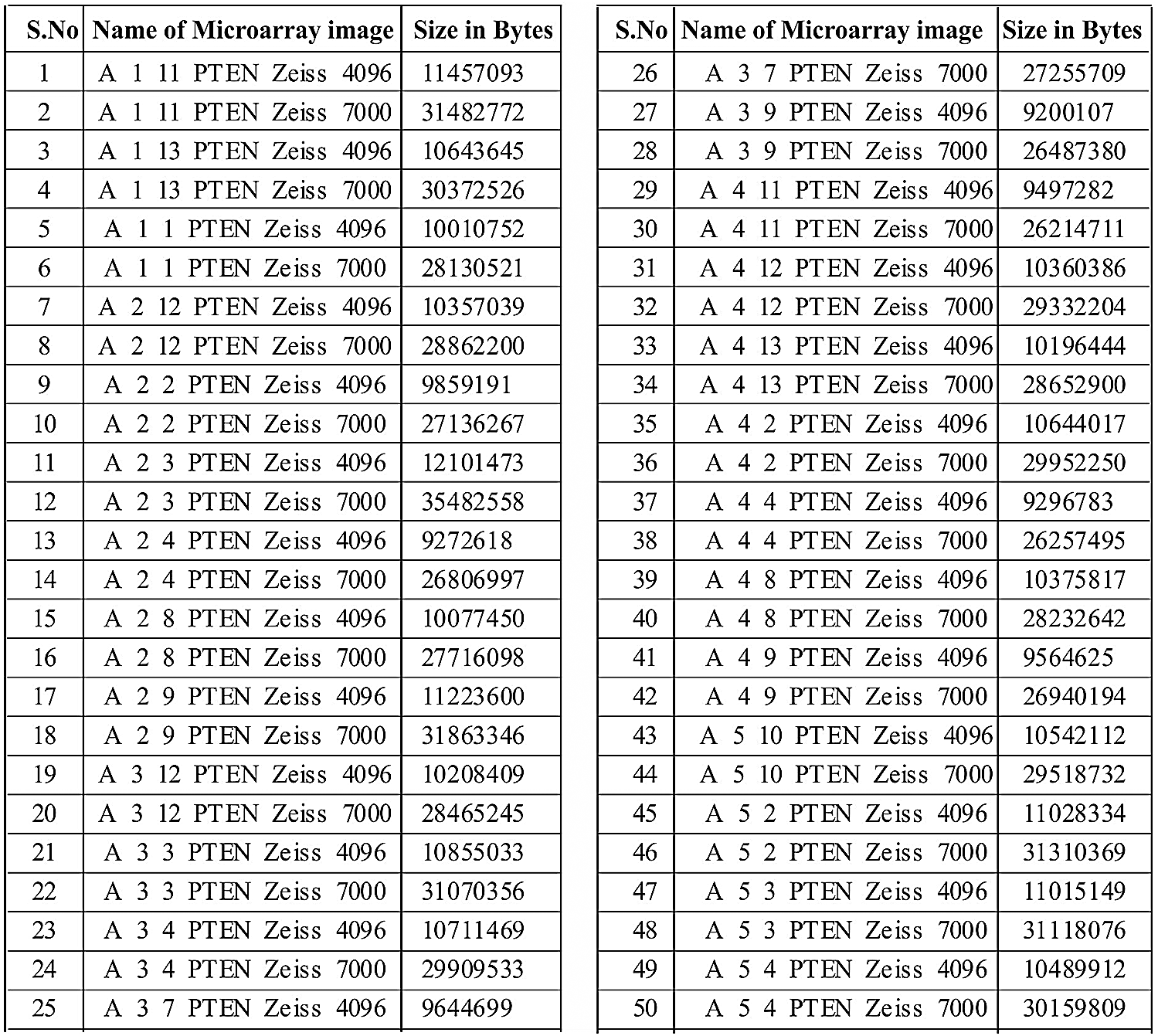
Figure 3: Particulars of microarray image dataset

Figure 4: Sample TMA images

4.2 Results

Tab. 1 and Figs. 5–8 show the results of PSNR analysis for the proposed algorithm against existing models on the applied images 1–4.

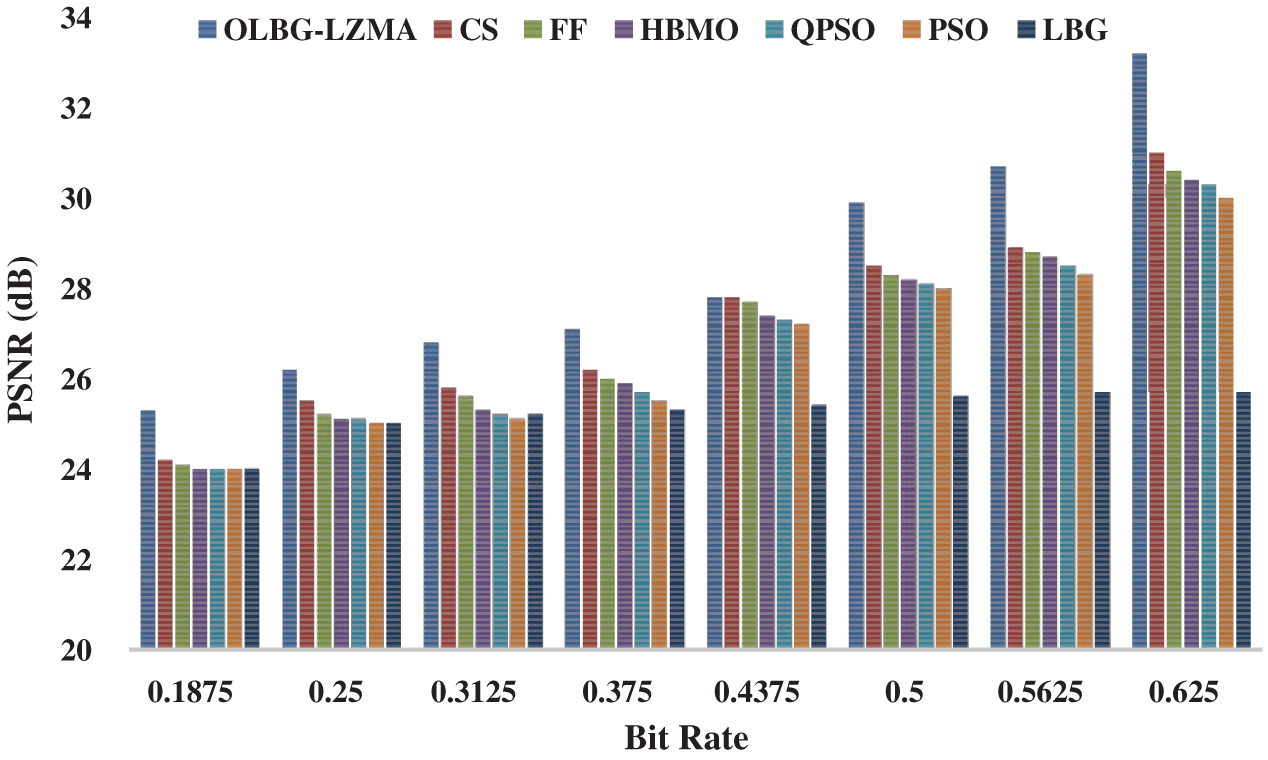
Figure 5: Comparative PSNR analysis of OLBG-LZMA model on image 1

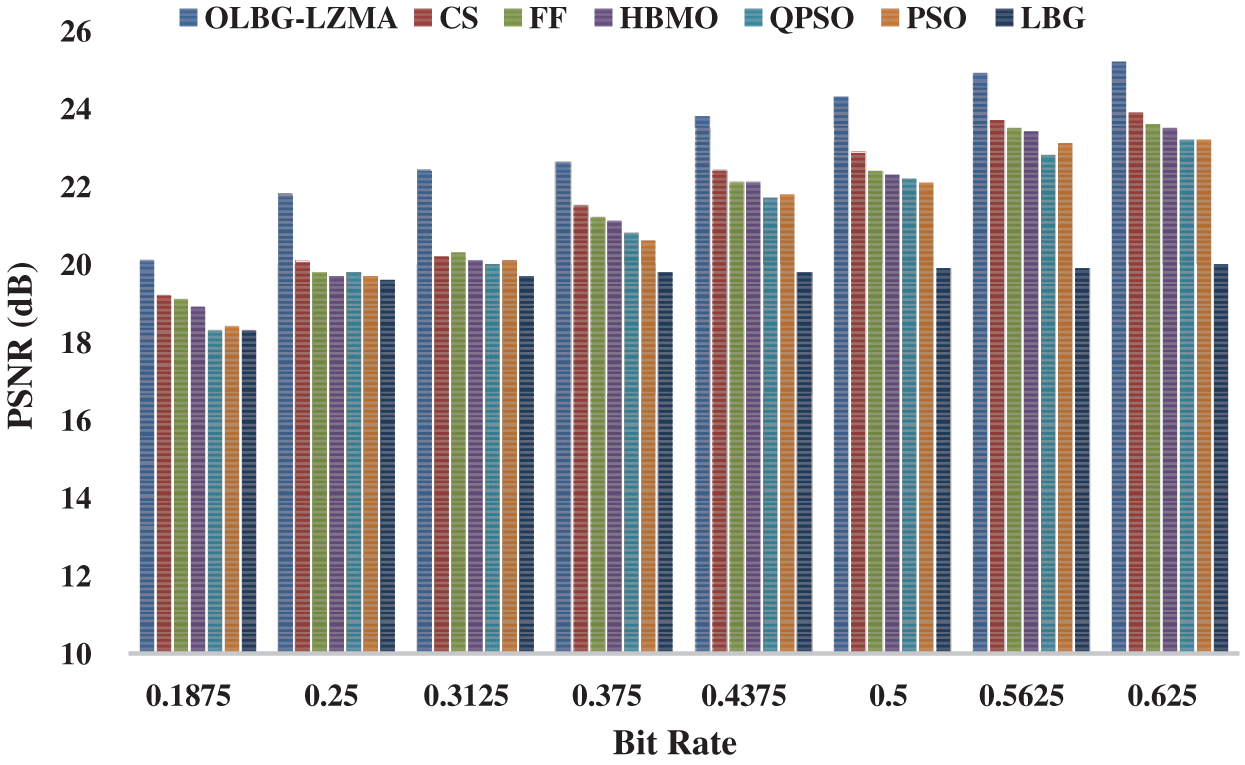
Figure 6: Comparative PSNR analysis of OLBG-LZMA model on image 2

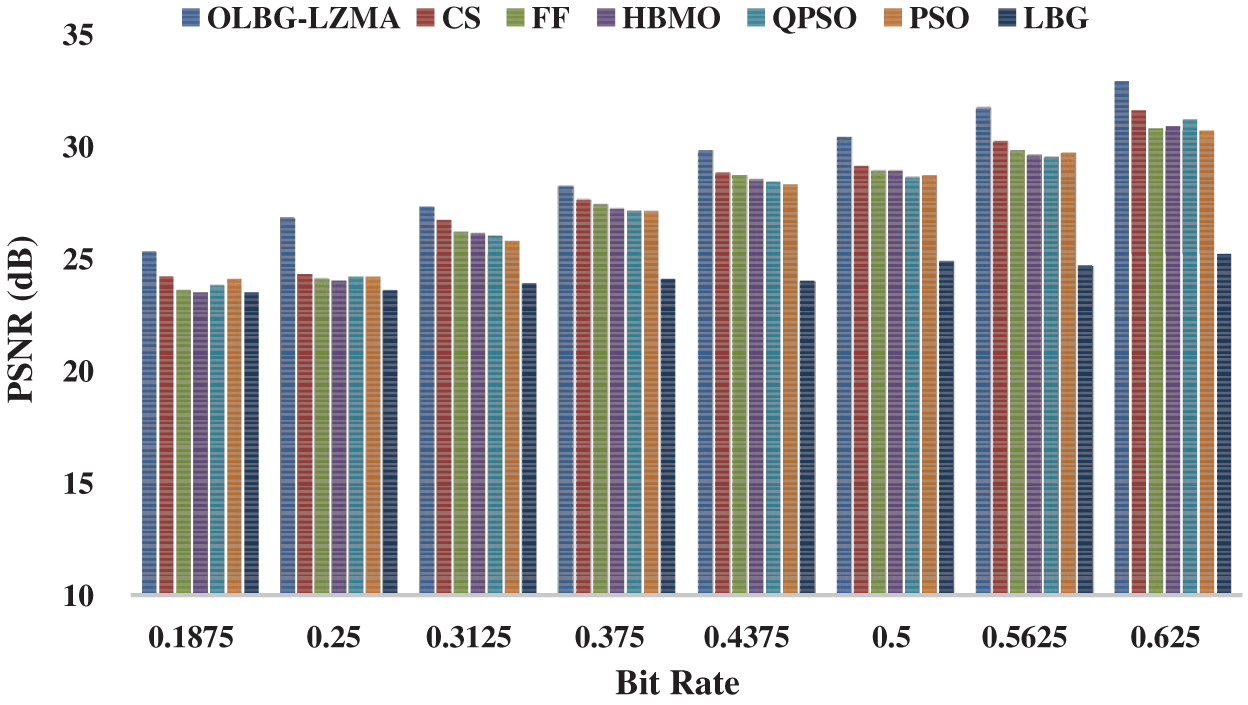
Figure 7: Comparative PSNR analysis of OLBG-LZMA model on image 3

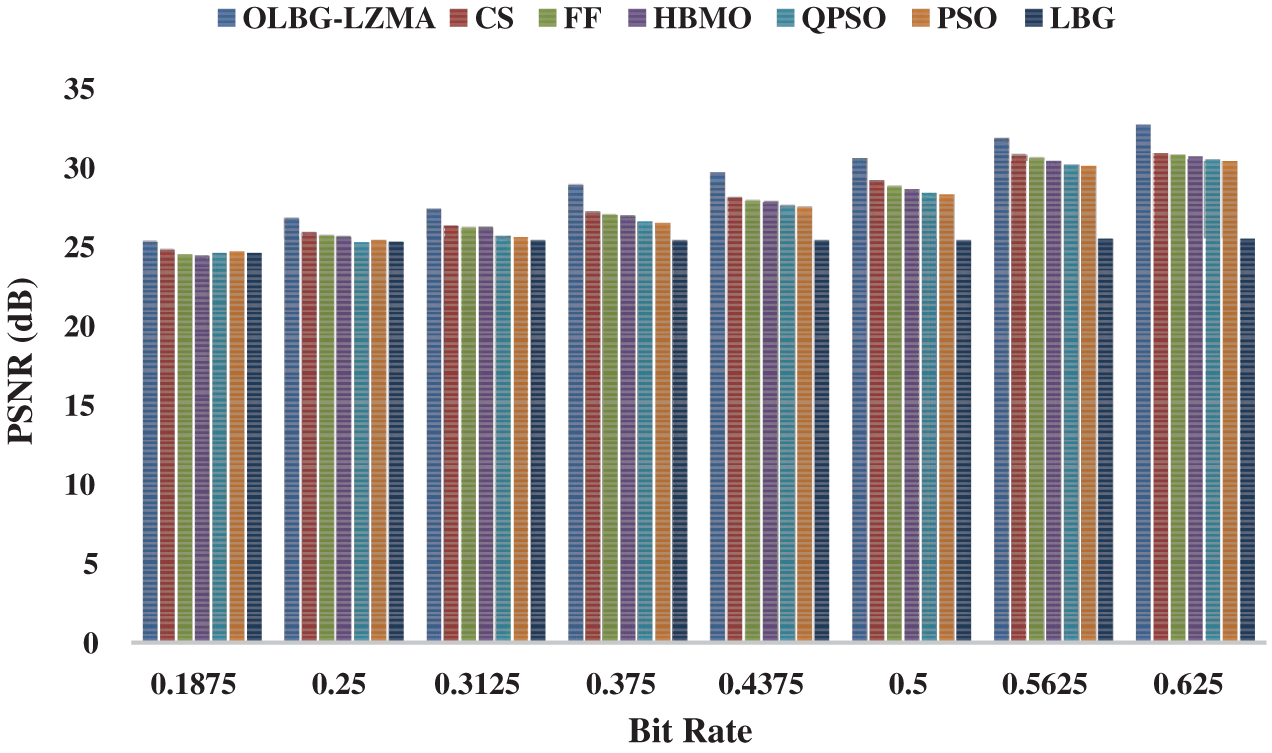
Figure 8: Comparative PSNR analysis of OLBG-LZMA model on image 4

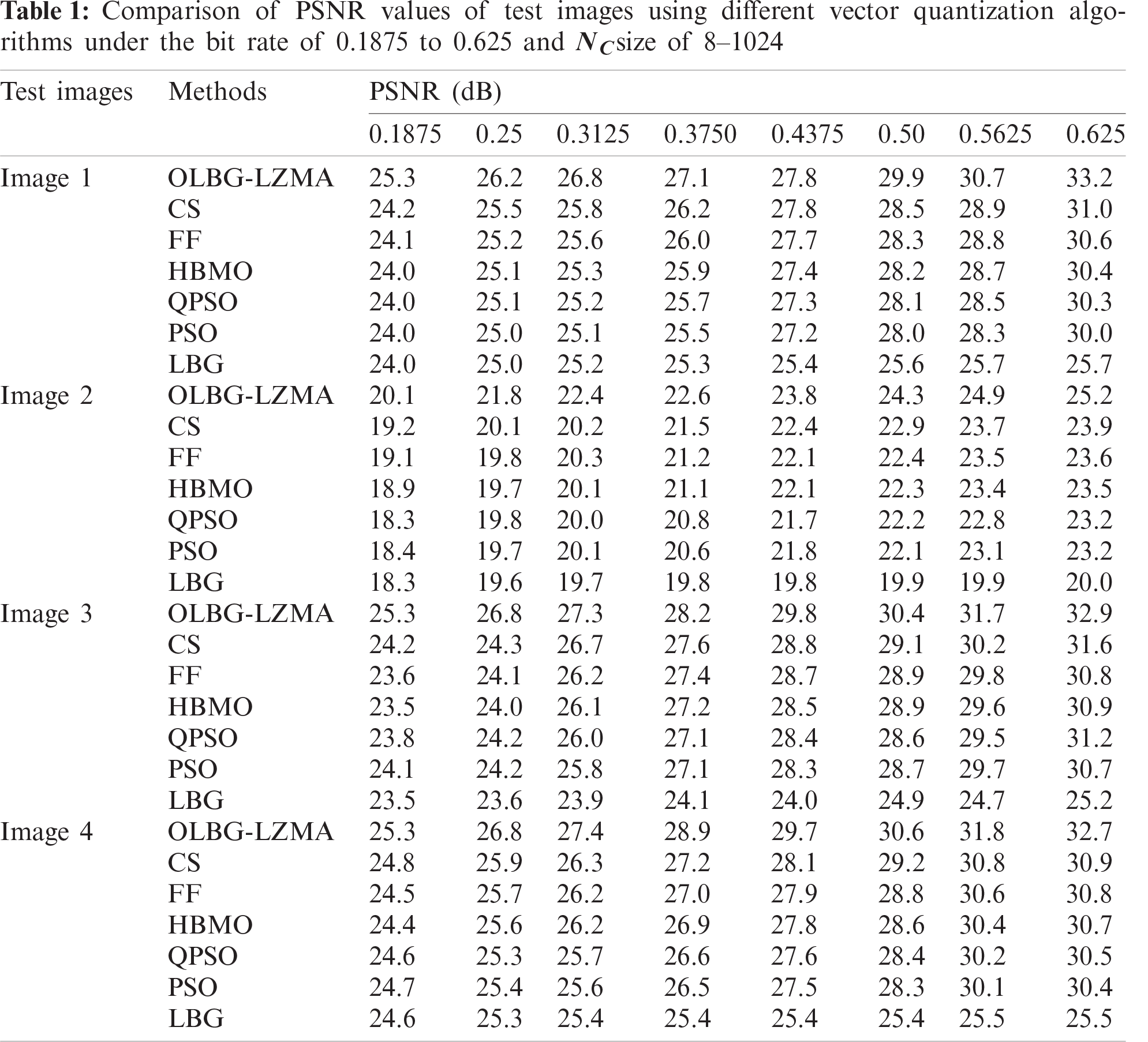
Fig. 9 shows the average PSNR values obtained by different methods under different bit rates. In addition, an average of all the PSNR values attained for the applied test images is tabulated in Tab. 2. For the applied test_image 1, under the least bit rate of 0.1875, the methods used for comparison such as LBG, PSO, QPSO and HBMO attained a PSNR value of 24.0 which was lower than other methods. At the same time, both FF and CS algorithms obtained a PSNR value of 24.1 and 24.3 respectively. However, the newly developed OLBG-LZMA model reached a maximum PSNR value of 25.3. Under a moderate bit rate of 0.3750, the presented algorithm attained the highest PSNR value of 27.1 whereas the CS, FF, HBMO, QPSO, PSO and LBG models achieved the least PSNR values of 26.2, 26.0, 25.9, 25.7, 25.5 and 25.3 respectively. Under the highest bit rate of 0.625, the OLBG-LZMA method yielded significant results with a PSNR value of 33.2 which was much higher than the compared algorithms.

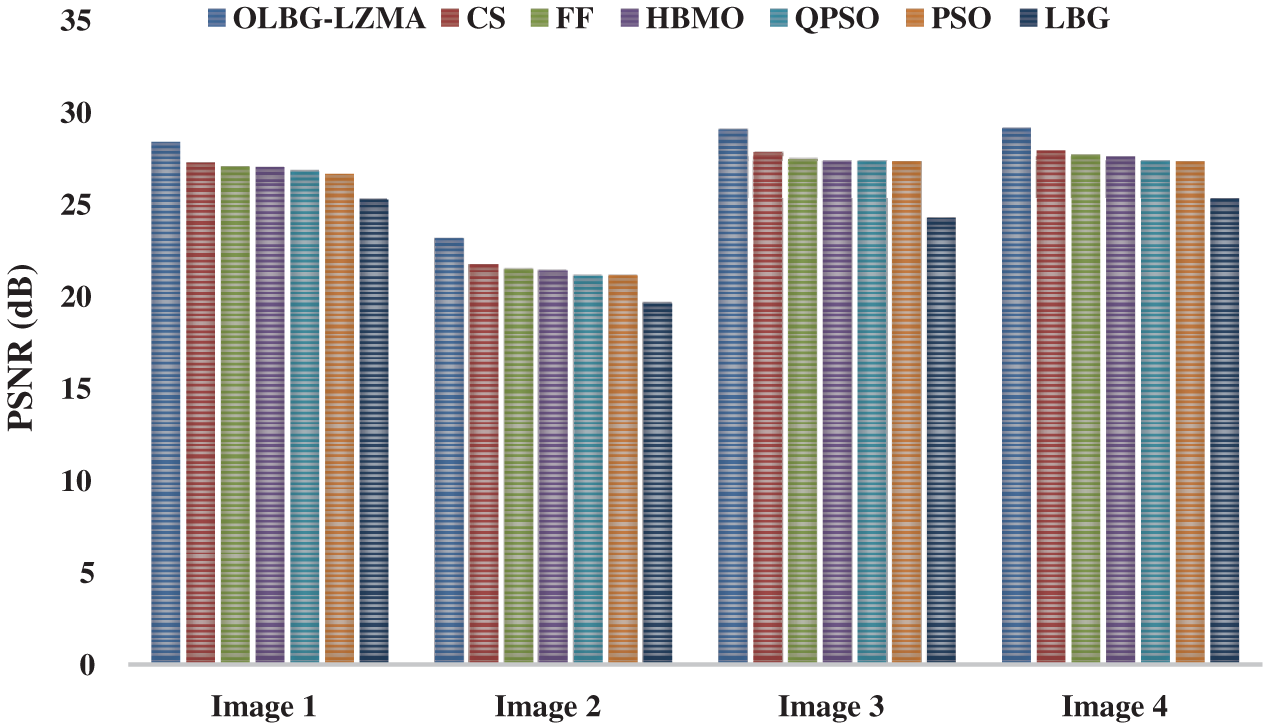
Figure 9: Comparative results of various algorithms in terms of average PSNR

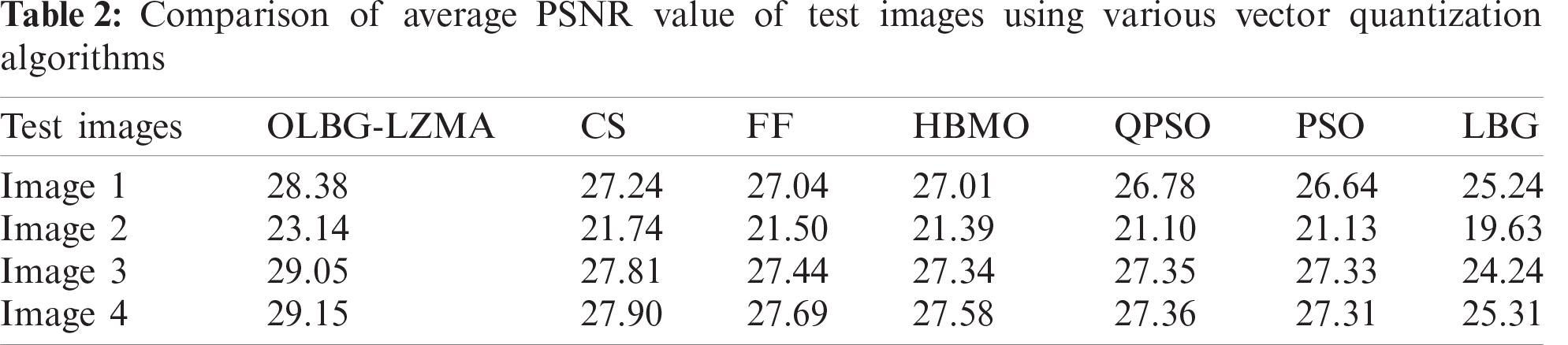
Similarly, for all the applied test images, the proposed OLBG-LZMA algorithm outperformed the existing algorithms in an efficient way. In table values, it is noted that the PSNR values start to rise with an increase in bit rate. This phenomenon can be observed from the PSNR values obtained for the least bit rate of 0.1875 and highest bit rate of 0.625 bit rate. The simulation results portray that the proposed OLBG-LZMA model is an efficient one compared to other algorithms under different codebook sizes.

Experimental validation was performed in Windows 10 operating system while its specifications were Intel(R) Core(TM) i7-7500U and 2.70 GHz CPU with 8 GB RAM. In addition, the execution code was developed and simulated in MATLAB. Tab. 3 and Fig. 10 shows the obtained average CT of various algorithms under different bit rates. The authors used 30 codebooks with 20 iterations. For a codebook of size 8 and a bit rate of 0.1875, the average CT required is shown in the table. From the table, for applied image 1, the highest CT of 977.200 was demanded by CS algorithm. In line with this, both HBMO and FF algorithms showed slightly lower CT values such as 890.254 and 877.123 respectively. The proposed OLBG-LZMA managed well with a moderate CT of 685.246.

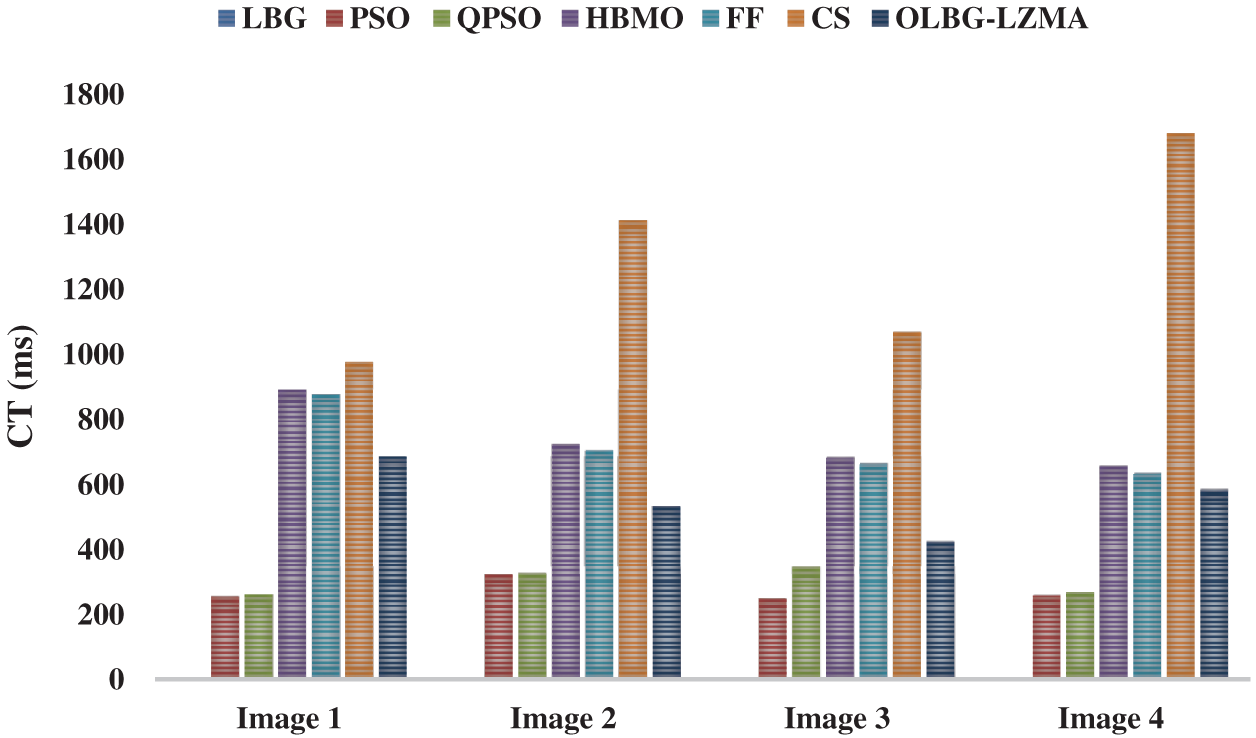
Figure 10: CT analysis of OLBG-LZMA model with other existing methods

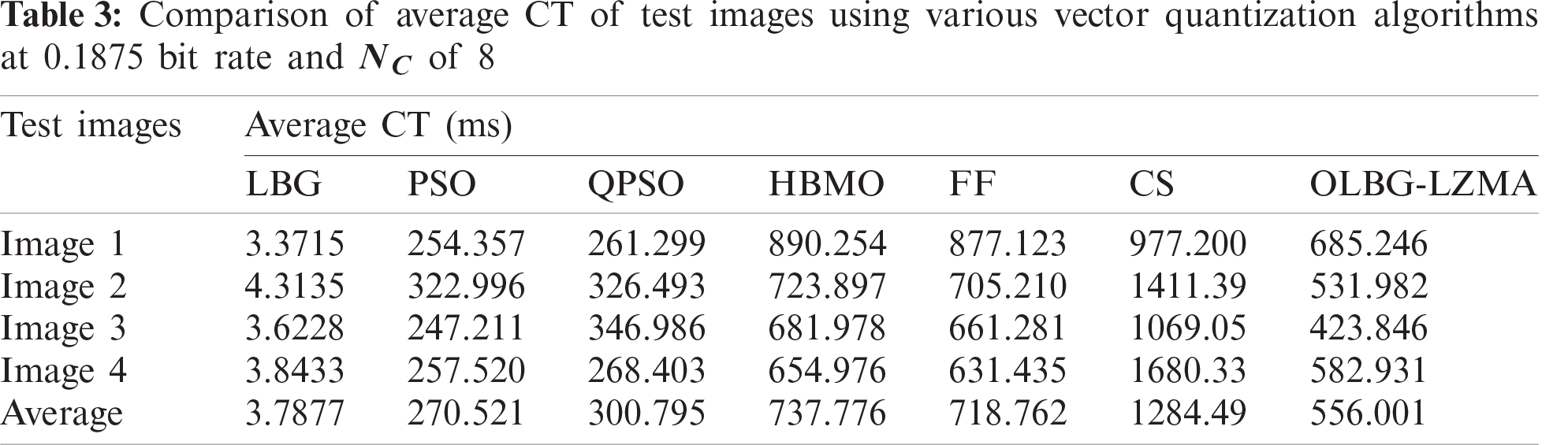
But, the existing LBG, PSO and QPSO algorithms achieved effective CT performance with least values of 3.3715, 254.357 and 261.299 respectively. It is clear that the LBG model needs a least CT of 3.3715 s which is highly appreciable. But, its poor performance in PSNR value limits its applications. However, the proposed OLBG-LZMA model has moderate CT and it yielded significant PSNR value which makes it preferable than the CT.

5  Conclusion

Image compression techniques are generally used to minimize the number of bits needed to store and share microarray images. The current research paper proposed an effective OGWO-LZMA model to compress microarray images. The proposed model involves two stages such as OLBG-based codebook construction and LZMA-based codebook compression. After the construction of codebook using LBG-GWO algorithm, LZMA is employed to compress the index table and increase the compression efficiency in addition. Experiments were performed on high resolution microarray dataset and the compression performance of OGWO-LZMA was compared with other methods. The simulation results inferred that the OGWO-LZMA algorithm achieves significant compression performance. At the same time, the OLBG-LZMA achieved a moderate CT and provided significant PSNR value which makes the CT, unnoticeable. In future, the performance of the OGWO-LZMA model can be improved by incorporating hybrid metaheuristic algorithms.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Mohandas, S. M. Joseph and P. S. Sathidevi, “An autoencoder based technique for DNA microarray image denoising,” in Int. Conf. on Communication and Signal Processing, Chennai, India, IEEE, pp. 1366–1371, 2020. [Google Scholar]

 2.  L. Herbsthofer, B. Prietl, M. Tomberger, T. Pieber and P. L. García, “C2G-Net: Exploiting morphological properties for image classification,” Computer Vision and Pattern Recognition, pp. 1–10, 2020. [Google Scholar]

 3.  G. Patane and M. Russo, “The enhanced LBG algorithm,” Neural Networks, vol. 14, no. 9, pp. 1219–1237, 2002. [Google Scholar]

 4.  K. H. Jung and C. W. Lee, “Image compression using projection vector quantization with quadtree decomposition,” Signal Processing: Image Communication, vol. 8, no. 5, pp. 379–386, 1996. [Google Scholar]

 5.  A. H. Abouali, “Object-based VQ for image compression,” Ain Shams Engineering Journal, vol. 6, no. 1, pp. 211–216, 2015. [Google Scholar]

 6.  K. Geetha, V. Anitha, M. Elhoseny, S. Kathiresan, P. Shamsolmoali et al., “An evolutionary lion optimization algorithm-based image compression technique for biomedical applications,” Expert Systems, vol. 38, no. 1, pp. e12508, 2021. [Google Scholar]

 7.  S. Kazuya, S. Sato, M. Junji and S. Yukinori, “Vector quantization of images with variable block size,” Applied Soft Computing, vol. 8, no. 1, pp. 634–664, 2008. [Google Scholar]

 8.  T. Dimitrios, E. T. George and T. John, “Fuzzy vector quantization for image compression based on competitive agglomeration and a novel codeword migration strategy,” Engineering Applications of Artificial Intelligence, vol. 25, pp. 1212–1225, 2012. [Google Scholar]

 9.  T. Dimitrios, E. T. George, D. N. Antonios and R. Anastasios, “On the systematic development of fast fuzzy vector quantization for grayscale image compression,” Neural Networks, vol. 36, no. 11, pp. 83–96, 2012. [Google Scholar]

10. L. Xiaohui, R. Jinchang, Z. Chunhui, Q. Tong and M. Stephen, “Novel multivariate vector quantization for effective compression of hyperspectral imagery,” Optics Communications, vol. 332, no. 20, pp. 192–200, 2014. [Google Scholar]

11. X. Wang and J. Meng, “A 2-D ECG compression algorithm based on wavelet transform and vector quantization,” Digital Signal Processing, vol. 18, no. 2, pp. 179–188, 2008. [Google Scholar]

12. A. Rajpoot, A. Hussain, K. Saleem and Q. Qureshi, “A novel image coding algorithm using ant colony system vector quantization,” in Int. Workshop on Systems, Signals and Image Processing, Poznan, Poland, pp. 1–4, 2004. [Google Scholar]

13. C. W. Tsai, S. P. Tseng, C. S. Yang and M. C. Chiang, “PREACO: A fast ant colony optimization for codebook generation,” Applied Soft Computing, vol. 13, no. 6, pp. 3008–3020, 2013. [Google Scholar]

14. Q. Chen, J. Yang and J. Gou, “Gou Image compression method using improved PSO vector quantization,” in First Int. Conf. on Neural Computation. Proc.: Lecture Notes in Computer Science Book Series, Berlin, Heidelberg, Springer, vol. 3612, pp. 490–495, 2005. [Google Scholar]

15. H. Feng, C. Chen and Y. Fun, “Evolutionary fuzzy particle swarm optimization vector quantization learning scheme in image compression,” Expert Systems with Applications, vol. 32, no. 1, pp. 213–222, 2007. [Google Scholar]

16. Y. Wang, X. Y. Feng, Y. X. Huang, W. G. Zhou, Y. C. Liang et al., “A novel quantum swarm evolutionary algorithm and its applications,” Neurocomputing, vol. 70, no. 4–6, pp. 633–640, 2007. [Google Scholar]

17. C. Chang, Y. C. Li and J. Yeh, “Fast codebook search algorithms based on tree-structured vector quantization,” Pattern Recognition Letters, vol. 27, no. 10, pp. 1077–1086, 2006. [Google Scholar]

18. H. Y. Chen, H. Bing and C. T. Chih, “Fast VQ codebook search for gray scale image coding,” Image and Vision Computing, vol. 26, no. 5, pp. 657–666, 2008. [Google Scholar]

19. N. Sanyal, A. Chatterjee and S. Munshi, “Modified bacterial foraging optimization technique for vector quantization-based image compression,” in Computational Intelligence in Image Processing. Berlin, Heidelberg: Springer, pp. 131–1522012. [Google Scholar]

20. M. Horng and T. Jiang, “Image vector quantization algorithm via honey bee mating optimization,” Expert Systems with Applications, vol. 38, no. 3, pp. 1382–1392, 2011. [Google Scholar]

21. M. Horng, “Vector quantization using the firefly algorithm for image compression,” Expert Systems with Applications, vol. 39, no. 1, pp. 1078–1091, 2012. [Google Scholar]

22. K. Chiranjeevi, U. R. Jena, B. M. Krishna and J. Kumar, “Modified firefly algorithm (MFA) based vector quantization for image compression,” in Computational Intelligence in Data Mining—Volume 2. Advances in Intelligent Systems and Computing. vol. 411. New Delhi: Springer, pp. 373–382, 2015. [Google Scholar]

23. K. Chiranjeevi and U. R. Jena, “Fast vector quantization using bat algorithm for image compression,” Engineering Science and Technology, an International Journal, vol. 19, no. 2, pp. 769–781, 2016. [Google Scholar]

24. M. Lakshmia, J. Senthilkumar and Y. Suresh, “Visually lossless compression for bayer color filter array using optimized vector quantization,” Applied Soft Computing, vol. 46, no. 2, pp. 1030–1042, 2016. [Google Scholar]

25. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.