DOI:10.32604/cmc.2021.018644

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018644 |  |
| Article |
Analysis and Assessment of Wind Energy Potential of Al-Hodeidah in Yemen
1Department of Computer Science, King Khalid University, Muhayel Aseer, Kingdom of Saudi Arabia
2Faculty of Computer and IT, Sana’a University, Sana’a, Yemen
3Department of Electrical Engineering – Communication Engineering, Sana’a University, Yemen
4Department of Computer Science, College of Computer, Qassim University, Saudi Arabia
5Department of Information Systems, King Khalid University, Mayahel Aseer, KSA
6Department of Computer Science, College of Computers and Information Technology, University of Bisha, KSA
7Department of Electronic, Faculty of Engineering, UST, Sana’a, Yemen
*Corresponding Author: Fahd N. Al-Wesabi. Email: falwesabi@kku.edu.sa
Received: 15 March 2021; Accepted: 17 April 2021
Abstract: Renewable energy is one of the essential elements of the social and economic development in any civilized country. The use of fossil fuels and the non-renewable form of energy has many adverse effects on the most of ecosystems. Given the high potential of renewable energy sources in Yemen and the absence of similar studies in the region, this study aimed to examine the wind energy potential of Hodeidah-Yemen Republic by analyzing wind characteristics and assessment, determining the available power density, and calculate the wind energy extracted at different heights. The average wind speed of Hodeidah was obtained only for the data currently available for the five years 2005–2009 (due to the current economic and the political situation in Yemen). The results show that the average wind speed in the five years is (25.2 W/m2 at 10 m, 93.9 W/m2 at 30 m, and 173.5 W/m2 at 50 m). The average yearly wind power density (25.2 W/m2 at 10 m, 93.9 W/m2 at 30 m and 173.5 W/m2 at 50m), and the average yearly energy density (220.8 KWh/m2/year at 10 m, 822.6 KWh/m2/year at 30 m and 1519.9 KWh/m2/year at 50 m). This research is a preliminary assessment of the potential of wind energy in Hodeidah, which provides useful information for developing wind energy and an efficient wind approach. According to the International Wind Energy Rating criteria, the region of Hodeidah falls under ‘Class 2’ and is classified as ‘Marginal’ for most of the year.
Keywords: Energy potential; wind speed; weibull distribution; wind power density
The increase in population and rate of industrialization has led to a rise in energy demand. Fossil fuels cannot meet this demand because they negatively affect the environment and ecosystem, causing a significant increase in pollution. In other words, the energy industry and the environment are in significant crises today. Today in modern societies, energy is the most important indicator of economic growth and many countries worldwide are taking steps toward achieving a renewable energy model to solve this crisis [1,2]. Renewable energy sources such as solar, thermal, geothermal, bioenergy, hydropower, and ocean have gained popularity all over the world due to their distinct characteristics. Simultaneously, the increasing use of fossil fuels and the resulting environmental pollution has motivated researchers to find other sustainable, clean, efficient, and economical energy sources. Wind power systems are known to operate on a wind speed system. In 2800 BC, wind energy was used to pump water and generate power in rural areas. Wind energy is used today as an alternative source of energy [3,4].
As seen in literature [5–9] and in various places around the world, great emphasis has been placed on the Weibull function because it is suitable for wind speed data analysis. It is also useful for distributing large statistical data and is presented as a continuous distribution for further analysis. Some literature [10–18] are related to renewable energy in the Republic of Yemen, despite the scarcity of that literature due to a similar study for this region. Geographically, Yemen is located between latitude 13 north and 16 norths and longitude 43.2–53.2 in southwestern Asia. The Red Sea surrounds it from the west and the Indian Ocean (Arabian Sea) from the south. The total area of Yemen is 527.970 km2, and as of 2016, the population was about 26,687,000 people. Yemen has a high potential for renewable energy sources such as solar, wind, and geothermal energy [19].
In 2009, the Yemeni government approved the National Renewable Energy and Efficiency Strategy, which aims to increase 15% of energy efficiency (EE) in the energy sector by 2025, and target renewable energy (RE) capacity (Geothermal energy 160 megawatts, concentrated solar power 100 megawatts, solid biomass 6 megawatts, solar photovoltaic system 8.25, and wind power 400 megawatts) of total electricity by 2025. The Yemeni energy sector consists of oil, natural gas, and biofuel production. Energy production in 2012 was “15.109 kilotons of oil equivalent (ktoe), while consumption was 6,923 kilotons” [20].
Solar irradiance ranges between 5.2–6.8 kWh/m2/day, and the average annual sunshine is between 7.3 and 9.1 h/day, even in winter. The average daily solar hours are between 8 and 16 h per day [21]. Yemen is considered one of the countries that possess large coastal areas, with a coastal area of 2,500 km and a width of 30 to 60 km. It also owns several islands, most notably Socotra Island and other marine areas. The report of the Ministry of Planning and International Cooperation, Economic Studies, and Forecasts for the Oil Sector on May 14, 2016 stated that oil and gas revenues were the primary resources for the state budget and it contributed about 53.6% of the total public revenues between 2010 and 2014. Also, oil and gas revenues declined by about 77.1% in 2015 due to the repercussions of war, conflict, and low global oil prices [22].
This study investigates the potential of wind energy in Socotra Island by analyzing and evaluating the wind characteristics, determining the available energy density, and calculating the wind energy extracted at different altitudes (10, 30, 50 m). This study also discussed one of the methods of selecting the suitable wind turbine for the studied site, which is the calculation of the capacity factor. The current study provides useful information for government departments concerned with developing wind energy in Yemen.
The rest of the paper has five more sections. Section 2 provides the background. Section 3 provides the proposed system model. Section 4 provides the calculation methodology of the proposed system model. Section 5 presents the simulation, results and discussion, and Section 6 offers conclusions.
This section provides a brief concise background on renewable energy, the reality, and the statement of the energy and power system problem in the Republic of Yemen.
Yemen has a very good potential for using renewable energy. Still, the problem is the state of the energy sector in Yemen because it relies heavily on conventional energy (fossil fuels, petroleum, and its derivatives). We will note that one of the practical solutions and alternative sources of electricity and the economy in the country is the use of renewable energy [23].
Weaknesses and Strengths of Renewable energy in Yemen in Tab. 1 [24] and the renewable energy capabilities in Yemen in Tab. 2 [20].


In 2009, the Government of Yemen approved the national strategy for RE and energy efficiency, aiming to increase 15% of energy efficiency (EE) in the power sector by 2025 [20]. The targeted capacity of RE in total electricity (in MW) by 2025 is shown in Fig. 1.
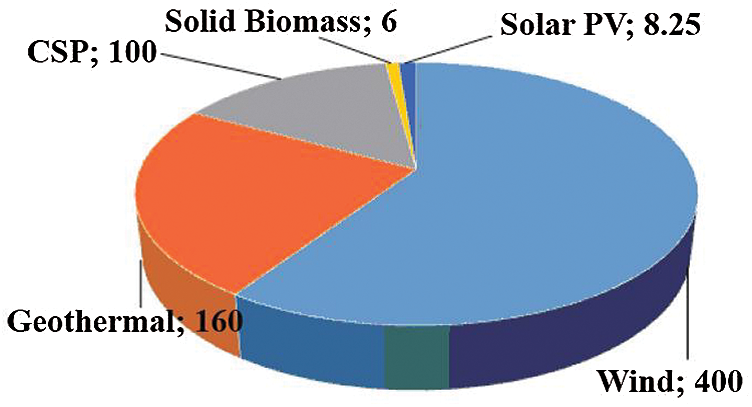
Figure 1: Targeted capacity of RE in total electricity (in MW) by 2025. (Geothermal 160 MW, Concentrated Solar Power (CSP) 100 MW, Solid Biomass 6 MW, Solar PV 8.25, Wind 400 MW)
2.2 Energy and Power System in Yemen
The Yemeni energy sector consists of oil, natural gas, and biofuels. Energy production in 2012 was «15,109 kiloton of oil equivalent (ktoe) while the consumption was 6,923 ktoe» [20].
The main components of the proposed system model are shown in Fig. 2, assuming that the assessment analysis of the wind speed data, average wind parameters and standard deviation for five years (2005–2009) by determining the parameters of the distribution functions.

Figure 2: Flowchart of the proposed system model
Statistical analysis of wind velocity data and average wind parameters of the two commonly used functions are also provided to fit the probability distribution of wind velocity measured at a given location over a given period in this section. The functions are the Weibull and Rayleigh distributions. In this section, the capacity factors of a few famous wind turbines are also calculated based on Weibull parameters and the speed characteristics of each of these turbines. The second section analyzes wind energy evaluation and finds the wind speed extrapolation, wind power density, and energy density for three heights (10, 30, and 50 m).
4 Basic Calculations of the Proposed System Model
4.1 Frequency Distribution of Wind Speed
The main aspects of literature regarding wind are on wind speed density and functional variations, and they have a wide range of known applications. Some of the functions commonly used to distribute the probability of measured wind velocity at a given location over a given time are the Weibull and Rayleigh distributions. The probability density function for the Weibull distribution is given by Eq. (1) below [23].
where f(v) is the probability of observing wind speed; v and k are the dimensionless Weibull shape parameter (k helps in finding how frequently wind speeds are close to some measured speed); c is the Weibull scale parameter with a unit equal to the wind speed unit (k and c characterize the wind potential of the sites under study). The corresponding cumulative probability function of the Weibull distribution is given by Eq. (2).
The Rayleigh distribution is a special case of the Weibull distribution in which the shape parameter k takes the value 2.0. From Eq. (1) the probability density function for the Rayleigh distribution can be simplified as shown in Eq. (3).
The two parameters of the Weibull distribution are probability functions, k and c, which can be related to the mean wind speed Vm and standard deviation σ as shown in Eqs. (4) and (5) below [23].
The Rayleigh distribution shape parameter k takes the value 2.0. From Eq. (1) the probability density function of the Rayleigh distribution can be simplified as shown in Eq. (6).
The mean value Vm and standard deviation σ of the Weibull distribution can then be computed as shown in Eqs. (7) and (8) [24].
where Γ is the gamma function (standard formula) and using the stirling approximation the gamma function of (x) can be given by Eq. (9) below.
4.2 Statistical Analysis of the Distributions
The square of the correlation coefficient (R2), chi-square (x2), and root mean square error analysis (RMSE) were used to evaluate the performance of the Weibull and Rayleigh distributions [20]. These parameters can be calculated by Eqs. (10)–(12).
where yi is the first measured data, zi is the mean value, xi is the first predicted data with the Weibull or Rayleigh distribution, N is the number of observations, and n is the number of constants.
4.3 Wind Speed Variation with Height
The most common equation used for the variation of wind speed with height is the power law expressed as shown in Eq. (13) [9].
where v1 is the actual wind speed recorded at height h1 (m), (m/s) and v2 is the wind speed at the required or extrapolated height h2 (m), (m/s).
The exponent α depends on the surface roughness and atmospheric stability. Numerically, it lies in the range from 0.05–0.5, with the most frequently adopted value being 0.14, which is widely applicable to low surfaces and well-exposed sites.
4.4 Wind Power Density Function
It is well known that the power of the wind at speed v (m/s) through a blade sweep area A (m2) increases as the cube of its velocity and is given by Eq. (14) below [16–18].
where ρ (kg/m3) is the mean air density with value of 1.220 kg/m3.
This depends on the altitude, air pressure, and temperature. The expected monthly or annual wind power density per unit area of a site based on the Weibull probability density function can be expressed as shown in Eq. (15).
The total wind power density P/A is the total available power per unit area given by Eq. (16).
where n is the number of days in a month.
Before calculating the average wind power density, vi3 of each day for the extrapolated height at 50 m was calculated
The electrical energy produced by a turbine over the year is given by the following relationship as shown in Eq. (17) [8].
where Cp is the power coefficient. For practical wind turbines, its value is usually in the range of 0 ≤ Cp ≤ 0.4 and T is the time (For the annual wind energy estimation, T = 8,760 h was used).
The available mean wind power density Pd, and the overall wind energy density Ed, of a wind turbine for a period of time T will be calculated as shown in Eqs. (18) and (19) [9].
Most wind turbines have power curves in their technical notes. This makes it easier to estimate the energy production of any wind turbine when a series of measurements are made at the studied site.
However, sometimes only a probability distribution function may be available. In this case, the wind turbine power output can be expressed as given by Eq. (20) [16].
where f(v) is the Weibull distribution given by Eq. (1) above, Pw is the electrical power output of the turbine. Fig. 3 expresses the wind turbine electric power/wind speed relationship curve.
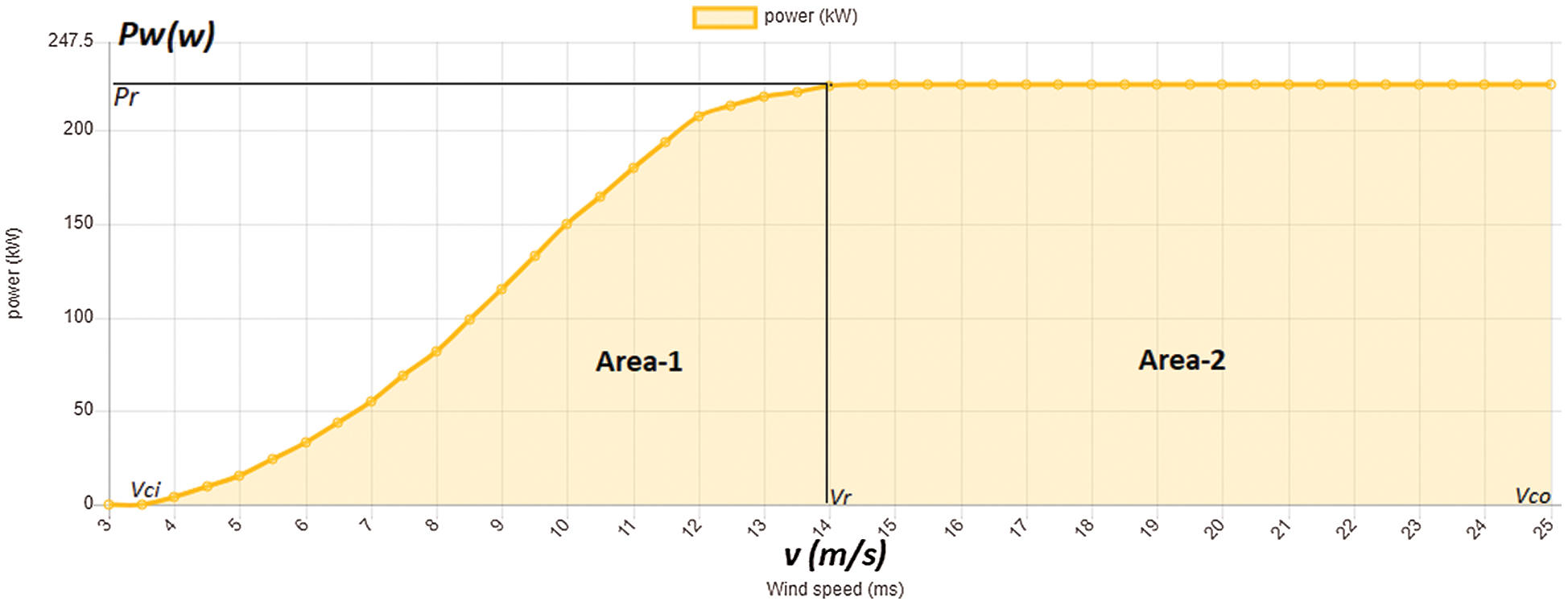
Figure 3: Wind turbine electric power/wind speed relationship curve
Where the curve increases semi-linearly, starting from the cut-in speed
Substituting Eqs. (1) and (21) into Eq. (20) yields Eq. (22) [16,17].
4.7 Capacity Factor of Turbine (CF)
Capacity Factor that was used to choose a suitable wind turbine, is defined as the ratio of average power output Pw,avg to the rated power output Pr as shown in Eq. (23).
From Eq. (22) above, we can calculate the capacity factor as given by Eq. (24).
The capacity factor is proportional to C and inversely to k and when fixing the values of C and k, we notice that CF is affected inversely by the difference between the (vr − vci), as it increases as this difference decreases. Since it is normal to choose the turbine with the smallest cut-in speed, on the other hand, one should choose the one with the smallest difference between the two speeds (vr − vci), (in other words, the lowest value of rated speed vr should be chosen if the cut-in speed
The average wind speed of Socotra Island was obtained from the recorded data of the Civil Aviation and Meteorological Authority (CAMA), only for the data available within five years from 2005–2009 (due to the current economical and the political situation of Yemen). The wind rose is a primary source for assessing wind energy due to its brief view of how wind velocity is distributed and how it remains distributed in the desired location according to the area’s topographical influences. Fig. 4 shows the mean wind speed for different month’s indifferent sets of years, and wind rose diagrams are shown in Fig. 5.
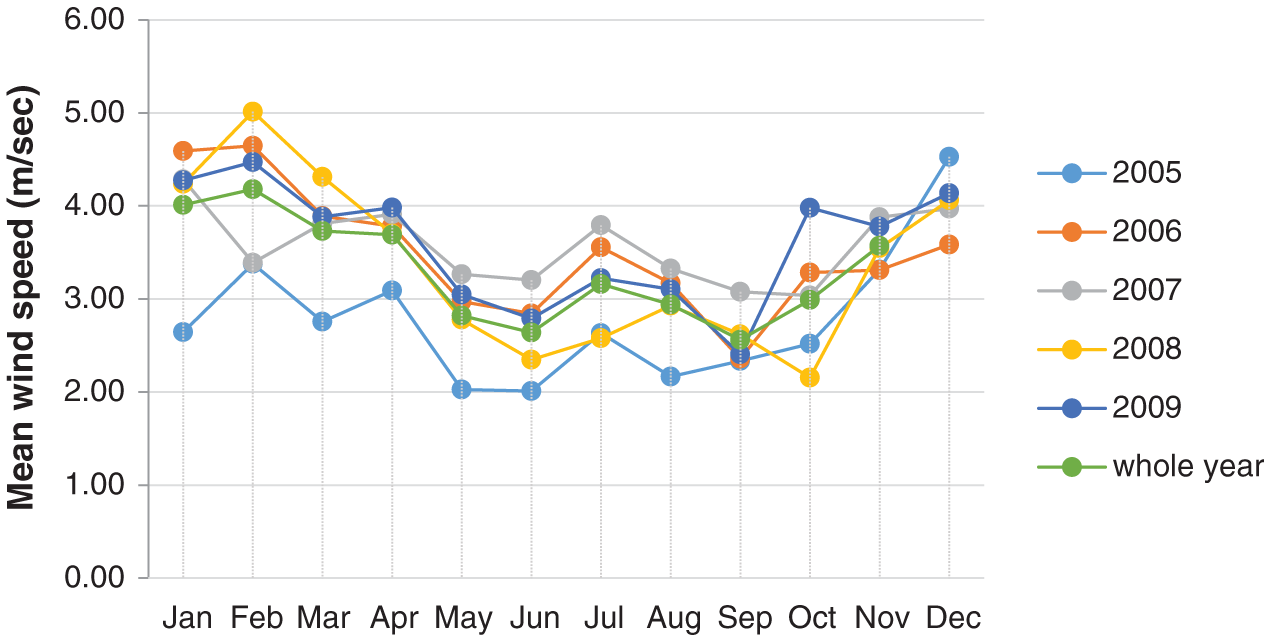
Figure 4: Monthly average wind speed in Hodeidah (2005–2009)
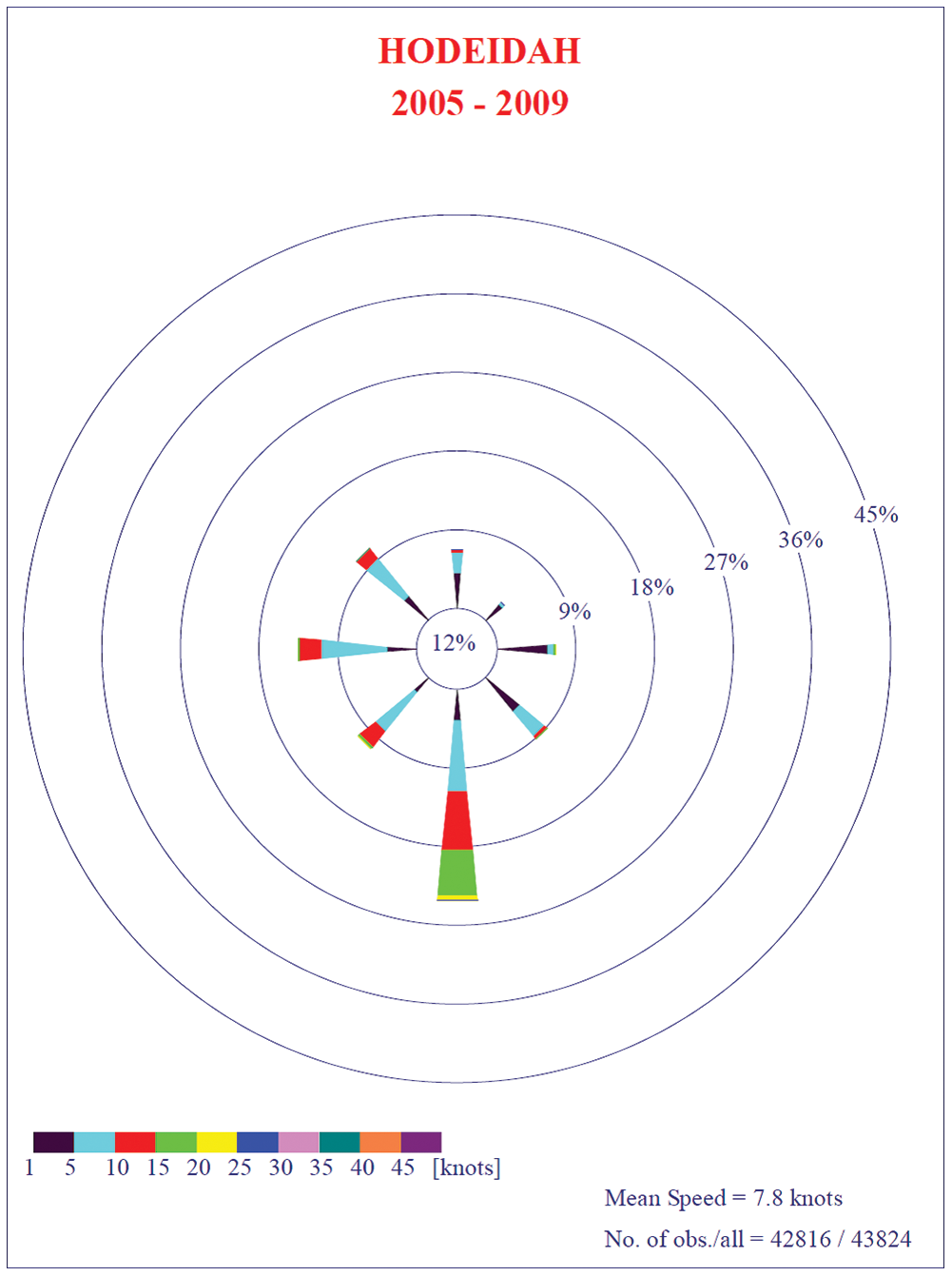
Figure 5: Wind rose of the Hodeidah
Where wind speed increases from February and reaches its peak value in May/June, then, wind speed decreases in July/August, and again rises wind speed in October & decreases gradually till December. Tab. 3 shows the monthly wind speeds in Hodeidah, and the standard deviations calculated from data are available for five years.

As shown in the five years, the average wind speed is 3.36 m/s. The wind speed for the entire year is the maximum monthly value of 4.18 m/s, which arises in February, while the minimum amount is 2.56 m/s that occurs in Sep. The smaller the value standard deviation, the smaller the speed samples are regular.
The wind speed changes with altitude, and actual wind turbines are placed at different lengths, more than 10 meters from the earth’s surface. And to choose the appropriate height for the wind turbines, the average monthly and annual wind speeds are calculated at different heights (10, 30, and 50 m) using Eq. (9). This is the first step to using this data to calculate and evaluate wind power within the specified location. At these heights, the annual average of wind speed became 8 m/s at 10 m, 12.3 m/s at 30 m, and 15.2 m/s at 50 m, respectively, as shown in Figs. 6 and 7.
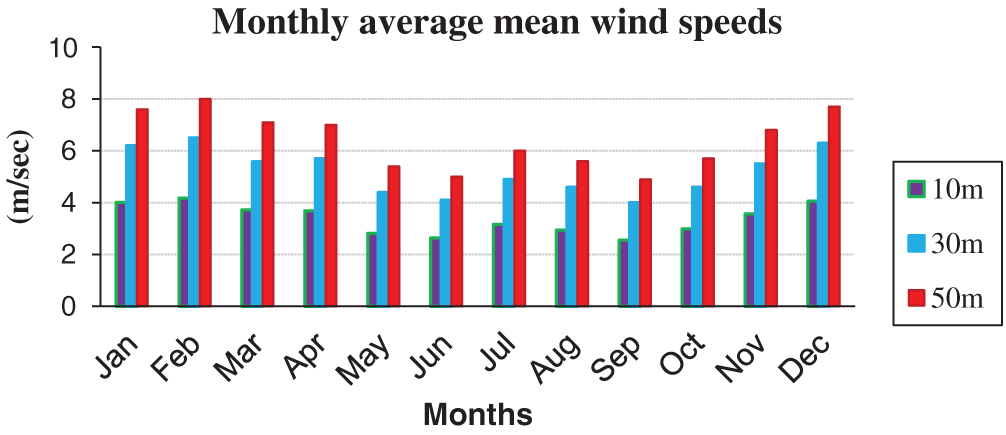
Figure 6: Monthly average wind speed profile at 10 m and extrapolation to 30 m and 50 m
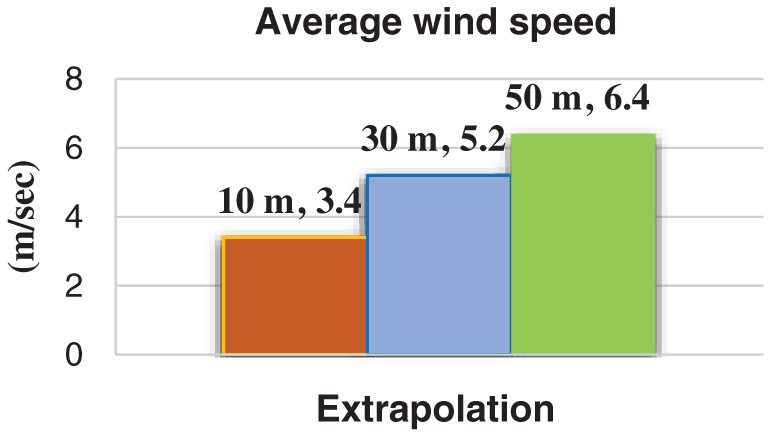
Figure 7: Average wind speed profile at 10 m and extrapolation to 30 m and 50 m
5.3 Probability Density and Cumulative Distributions
The variation of wind speeds is often described using the Weibull density function. It is a widely accepted statistical tool for evaluation of local wind probabilities and is considered as a standard approach. Eqs. (4) and (5) above were used to calculate the Weibull parameters for the available data, and the results are presented in Tab. 4.

As shows, yearly Weibull parameters and average Weibull parameters for the whole five years, from the table, while scale parameters vary between 3.14 (2005) and 4.05 (2009), the shape parameters range from 3.46 (2005) to 4.35 (2007). The five years’ average value of scale and shape parameters are 2.78 and 2.97, respectively.
There are many distribution functions to describe the wind speed frequency curve. In this study, Weibull functions were the most widely used and accepted in the specialized research journal. Yearly wind speed probability density and cumulative probability distributions derived from the measured data of Hodeidah for whole years are shown in Fig. 8.

Figure 8: Yearly wind speed probability density and cumulative probability distributions of Hodeidah for whole years
The Weibull approximation of the probability density distribution of wind speeds for the whole years is shown in Fig. 9.
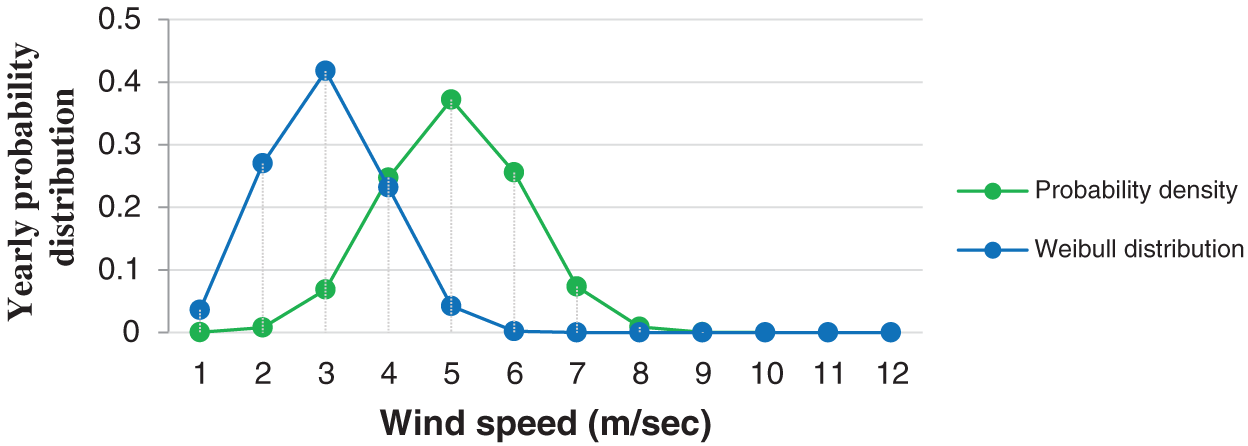
Figure 9: Yearly Weibull approximations of the probability density distribution of wind speeds
The monthly wind speed probability density distribution derived from the measured data of Hodeidah for whole years are shown in Fig. 10.
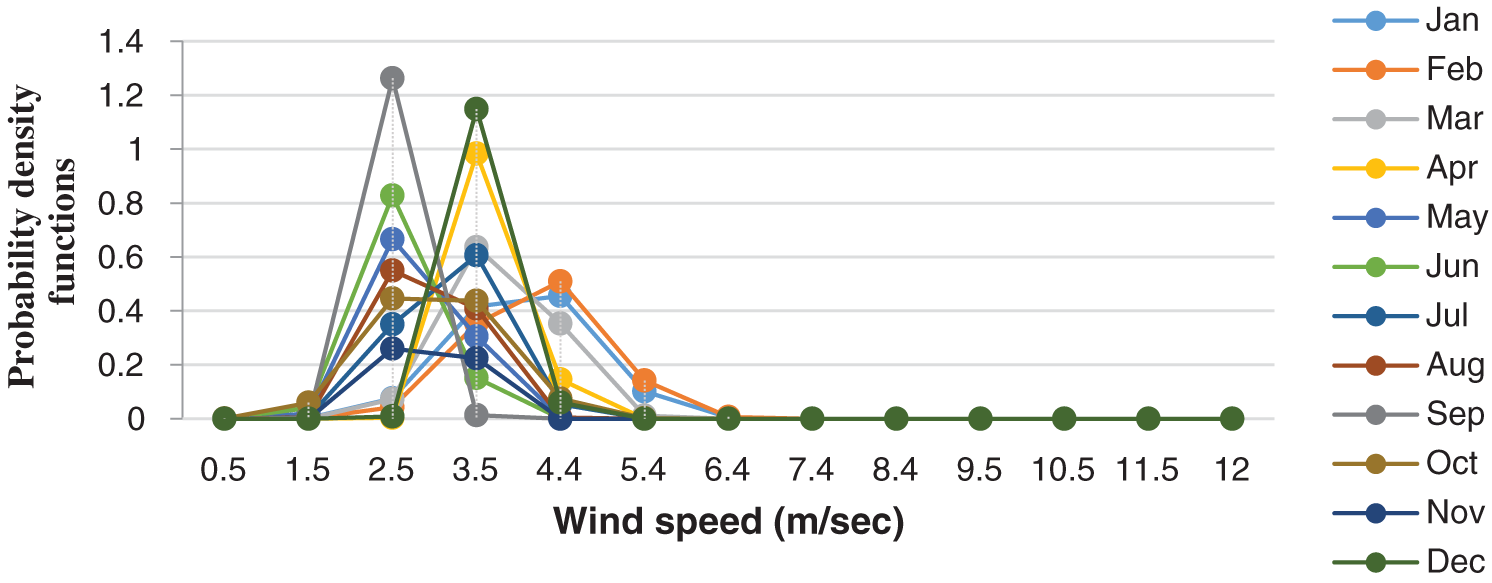
Figure 10: Monthly wind speed probability density distributions of Hodeidah for whole years
The monthly wind speed cumulative probability distribution derived from the measured data of Hodeidah for whole years are shown in Fig. 11.
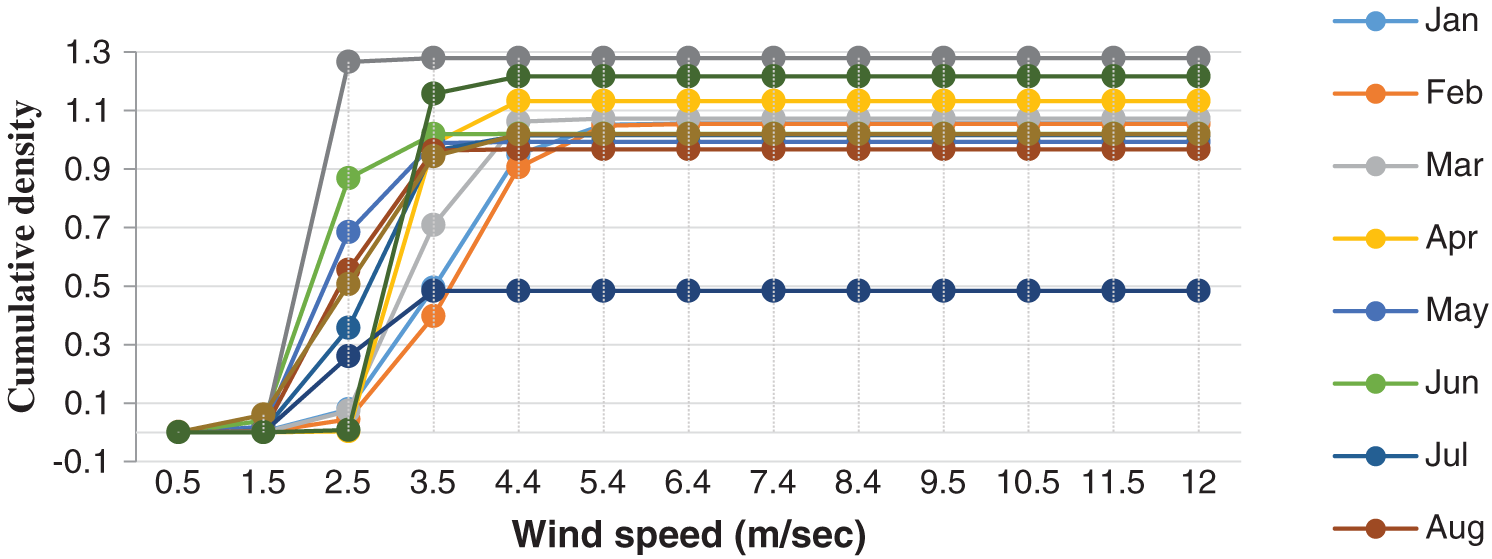
Figure 11: Monthly wind speed cumulative density functions of Hodeidah for whole years
The Weibull probability density distributions for each of the five years were analyzed. The distributions obtained are illustrated in Fig.12.
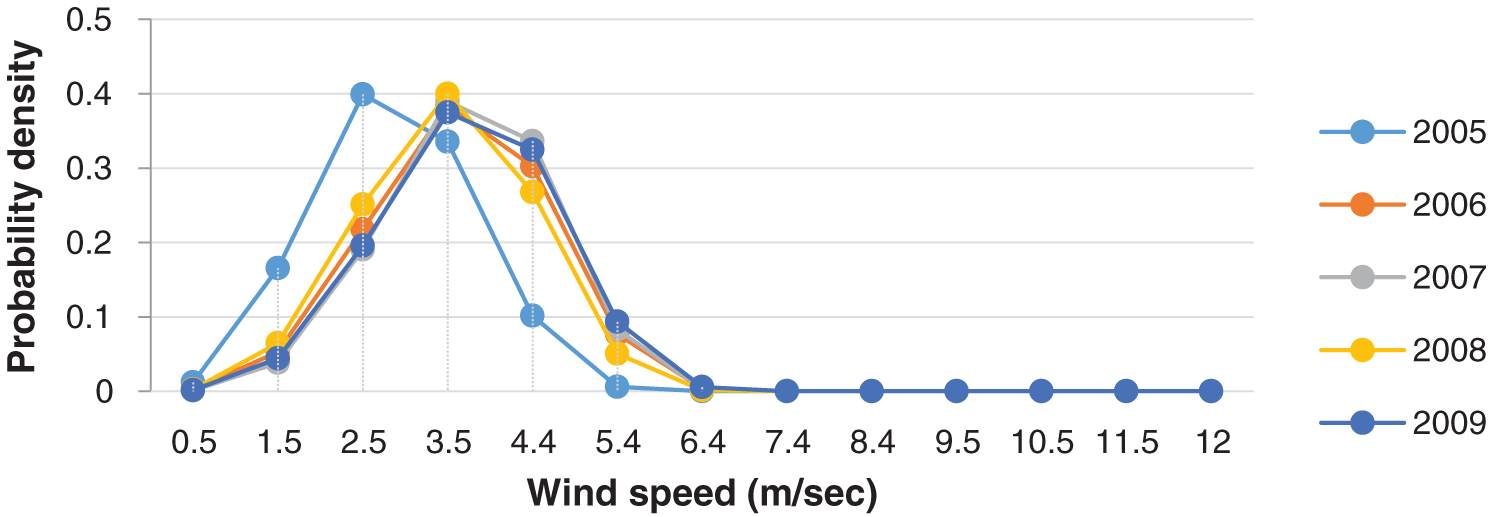
Figure 12: Yearly Weibull probability density distributions for the period 2005–2009 in Hodeidah
The results shown in Figs. 10–12 show that all curves have a similar tendency to wind speed for cumulative density and probability density. The annual probability density distribution obtained from the Weibull model were compared with measured data distributions to study their suitability. The yearly comparison of Study Location shows that the Weibull model corresponds to the distribution of the probability density of metric data as illustrated in Fig. 9 above.
To calculate the average monthly wind power per unit of the cross-section of the turbine, where the air density of 1.225 kg/m3 energy density is calculated at different heights: 10 m, 30 m and 50 m as shown in Tab. 5 and Fig. 13.

Figure 13: Average wind power density profile at 10 m and extrapolation to 30 m and 50 m

A slight difference in wind speed will result in a massive difference in the density of wind energy because the wind power density is proportional to the wind speed cube. This calculated wind energy was estimated, based on these calculated wind power estimates, for different wind categories based on the international wind energy classification, as shown in Tab. 6.

According to the standard of international wind power classification, the Hodeidah area falls under class 2 and is classified as ‘Marginal’ for most of the year. It has an average wind power density of 173.5 W/m2 at 50 m height and an average wind speed of 6.4 m/s at 50 m height, which means that the site is not considered suitable for electric wind on a large scale. It is sufficient for electrical and mechanical applications not connected to networks, such as wind generators, battery charging, water pumping, and agricultural applications.
Using Eqs. (17) and (18) above, we can calculate the average of monthly and annually wind energy per unit of the cross-section of the turbine. Thus, the wind energy of Hodeidah was estimated at different heights: 10, 30, and 50 m, as shown in Fig. 14.
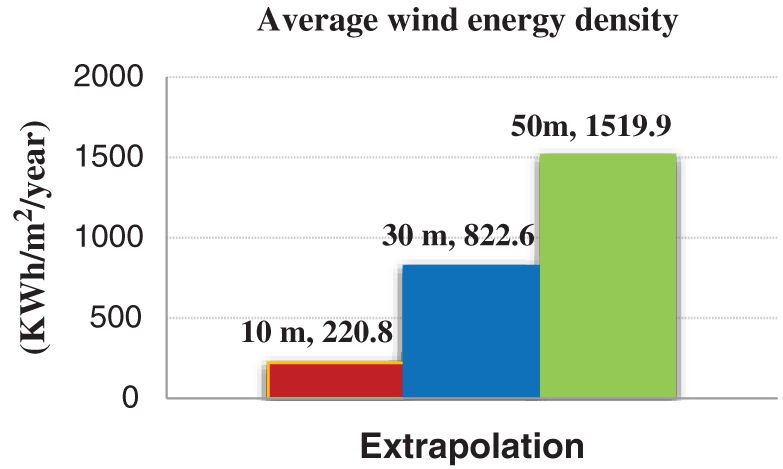
Figure 14: Average annual energy density profile at 10 m and extrapolation to 30 m and 50 m
Since wind energy is proportional to the height of the axis, the average annual wind energy density is 220.8 KWh/m2/year at 10 m, 822.6 KWh/m2/year at 30 m 1519.9 KWh/m2/year at 50 m, respectively.
In this study, the wind speed data in the period from 2005 to 2009 for Hodeidah-Yemen. The wind energy potential of the location has been studied based on the Weibull model. The monthly and yearly wind data analysis has been carried out to investigate the wind characteristics of Hodeidah, such as the monthly and annual wind speed, probability density distributions, and cumulative distributions.
Hodeidah area falls under ‘Class 2’ and is classified as ‘Marginal’ for most of the year. It is sufficient for electrical and mechanical applications not connected to networks, such as wind generators, battery charging, water pumping, and agricultural applications. The current work is a preliminary study only to assess the potential of the wind energy of Hodeidah, which can give useful insights to engineers and experts dealing with wind energy. In the end, we must go back to the famous parable, «the wind is a God gift, so let’s use it.».
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (R.G.P.2/25/42), Received by Fahd N. Al-Wesabi. https://www.kku.edu.sa.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
1. S. Kutty, M. Khan and M. Ahmed, “Wind energy resource assessment for Suva, Fiji, with accurate weibull parameters,” Energy Exploration & Exploitation, vol. 37, pp. 1009–1038, 2019. [Google Scholar]
2 L. Paraschiv, S. Paraschiv and I. Ion, “Investigation of wind power density distribution using Rayleigh probability density function,” Energy Procedia, vol. 157, pp. 1546-1552, 2019. [Google Scholar]
3. A. Liu, Y. Ma, J. Gunawardena, P. Egodawatta, G. Ayoko et al. “Heavy metals transport pathways: The importance of atmospheric pollution contributing to stormwater pollution,” Ecotoxicology and Environmental Safety, vol. 164, pp. 696–703, 2018. [Google Scholar]
4. A. Alkholidi, “Renewable energy solution for electrical power sector in Yemen,” International Journal of Renewable Energy Research, vol. 3, pp. 803–811, 2013. [Google Scholar]
5. Y. Li, W. Xiao-Peng, L. Qiu-Sheng and K. Fah, “Assessment of onshore wind energy potential under different geographical climate conditions in China,” Energy, vol. 152, pp. 498–511, 2018. [Google Scholar]
6. M. Salah, I. Supérieur and S. Ben, “Assessment of wind energy potential and optimal electricity generation in borj-cedria,” Renewable and Sustainable Energy Reviews, vol. 15, pp. 815–820, 2017. [Google Scholar]
7. I. Fyrippis, P. Axaopoulos and G. Panayiotou, “Wind energy potential assessment in naxos island, Greece,” Applied Energy, vol. 87, pp. 577–586, 2017. [Google Scholar]
8. S. Haralambos, G. Mihalakakou and L. Al-Hadhrami, “Wind power potential assessment for seven buoys data collection stations in aegean Sea using weibull distribution function,” Journal of Renewable and Sustainable Energy, vol. 4, pp. 1–17, 2012. [Google Scholar]
9. M. Baseer, J. Meyer, S. Rehman and M. Alam, “Wind power characteristics of seven data collection sites in jubail, Saudi Arabia using weibull parameters,” Renewable. Energy, vol. 102, pp. 35–49, 2017. [Google Scholar]
10. M. Almekhlafi, “Justification of the advisability of using solar energy for the example of the Yemen republic,” Scientific and Technical Journal, vol. 4, pp. 51–50, 2018. [Google Scholar]
11. A. Rawea and S. Urooj, “Strategies, current status, problems of energy and perspectives of Yemen’s renewable energy solutions,” Renewable and Sustainable Energy Reviews, vol. 82, pp. 1655–1663, 2018. [Google Scholar]
12. M. Al-Buhairi and A. Al-Haydari, “Monthly and seasonal investigation of wind characteristics and assessment of wind energy potential in Al-mokha, Yemen,” Energy and Power Engineering, vol. 4, pp. 125–131, 2012. [Google Scholar]
13. M. Al-Buhairi, “Analysis of monthly, seasonal and annual air temperature variability and trends in taiz city-republic of Yemen,” Journal of Environmental Protection, vol. 1, pp. 401–409, 2010. [Google Scholar]
14. M. Al-Buhairi, “A statistical analysis of wind speed data and an assessment of wind energy potential in taiz-Yemen,” Assiut University Bulletin for Environmental Researches, vol. 9, pp. 21–33, 2006. [Google Scholar]
15. A. AL-Ashwal, “All renewable energy applications in Yemen are best practice,” ISECO Science and Technology Vision, vol. 1, pp. 45–50, 2005. [Google Scholar]
16. L. Gabriela, C. Balaceanu and S. Stefan, “Annual air pollution level of major primary pollutants in greater area of zucharest,” Atmospheric Pollution Research, vol. 6, pp. 824–834, 2015. [Google Scholar]
17. T. Arslan, Y. Murat Bulut and A. Yavuz, “Comparative study of numerical methods for determining weibull parameters for wind energy potential,” Renewable and Sustainable Energy Reviews, vol. 40, pp. 820–825, 2014. [Google Scholar]
18. A. Al Shamma’a, K. Addoweesh and A. Eltamaly, “Optimum wind turbine site matching for three locations in Saudi Arabia,” Advanced Materials Research, vol. 347, pp. 2130–2139, 2011. [Google Scholar]
19. T. Chang, “Estimation of wind energy potential using different probability density functions,” Applied Energy, vol. 88, pp. 1848-1856, 2011. [Google Scholar]
20. UNDP, Policy Note 2014. Prospects of solar energy in Yemen, UNDP-Yemen, Sana’s, 2014. [Google Scholar]
21. M. Hadwan and A. Alkholidi, “Solar power energy solutions for Yemeni rural villages and desert communities,” Renewable and Sustainable Energy Reviews, vol. 57, pp. 838–849, 2016. [Google Scholar]
22. M. Almekhlafi, “Justification of the advisability of using solar energy for the example of the Yemen republic.” Scientific and Technical Journal—Technogenic and Ecological Safety, vol. 4, no. 8, 2018. http://jteb.nuczu.edu.ua/uk/potochnyi-nomer. [Google Scholar]
23. Guide to renewable energy and energy efficiency in the Arab states, League of Arab states, 2013. [Google Scholar]
24. N. Arreyndip, E. Joseph and A. David, “Wind energy potential assessment of Cameroon’s coastal regions for the installation of an onshore wind farm,” Heliyon, vol. 2, no. 11, pp. 1–20, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |