Computers, Materials & Continua DOI:10.32604/cmc.2021.018752
Article

Path Planning of Quadrotors in a Dynamic Environment Using a Multicriteria Multi-Verse Optimizer

Raja Jarray1, Mujahed Al-Dhaifallah2,*, Hegazy Rezk3,4 and Soufiene Bouallègue1,5

1Research Laboratory in Automatic Control (LARA), National Engineering School of Tunis (ENIT), University of Tunis El Manar, Tunis, 1002, Tunisia
2Department of Systems Engineering, King Fahd University of Petroleum & Minerals, Dhahran, 31261, Saudi Arabia
3College of Engineering at Wadi Addawaser, Prince Sattam Bin Abdulaziz University, Al-Kharj, 11911, Saudi Arabia
4Department of Electrical Engineering, Faculty of Engineering, Minia University, Minia, 61517, Egypt
5High Institute of Industrial Systems of Gabès (ISSIG), University of Gabès, Gabès, 6011, Tunisia
*Corresponding Author: Mujahed Al-Dhaifallah. Email: mujahed@kfupm.edu.sa
Received: 20 March 2021; Accepted: 23 April 2021

Abstract: Paths planning of Unmanned Aerial Vehicles (UAVs) in a dynamic environment is considered a challenging task in autonomous flight control design. In this work, an efficient method based on a Multi-Objective Multi-Verse Optimization (MOMVO) algorithm is proposed and successfully applied to solve the path planning problem of quadrotors with moving obstacles. Such a path planning task is formulated as a multicriteria optimization problem under operational constraints. The proposed MOMVO-based planning approach aims to lead the drone to traverse the shortest path from the starting point and the target without collision with moving obstacles. The vehicle moves to the next position from its current one such that the line joining minimizes the total path length and allows aligning its direction towards the goal. To choose the best compromise solution among all the non-dominated Pareto ones obtained for compromise objectives, the modified Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is investigated. A set of homologous metaheuristics such as Multiobjective Salp Swarm Algorithm (MSSA), Multi-Objective Grey Wolf Optimizer (MOGWO), Multi-Objective Particle Swarm Optimization (MOPSO), and Non-Dominated Genetic Algorithm II (NSGAII) is used as a basis for the performance comparison. Demonstrative results and statistical analyses show the superiority and effectiveness of the proposed MOMVO-based planning method. The obtained results are satisfactory and encouraging for future practical implementation of the path planning strategy.

Keywords: Quadrotors; path planning; dynamic obstacles; multi-objective optimization; global metaheuristics; TOPSIS decision-making; Friedman statistical tests

1  Introduction

In the last decades, unmanned aerial vehicles have acquired a great potential to complete an autonomous or semi-autonomous mission. A growing number of applications have appeared in real-world environments [1,2]. To achieve this autonomy, several challenges must be met. The trajectory planner is an essential part of the UAV autonomous control process [3]. Vehicles’ trajectory planning is used to find a sequence of valid moves that allow a robot to move from an initial state to the desired end state. In general, a valid movement is a displacement that does not produce a collision and that respects the kinematic constraints of the robot [4]. In some planning problems, the location of obstacles can change over time. Thus, trajectory planning must respect the dynamic constraints that arise from the environment, i.e., mobile obstacles, and the considered specifications of the vehicles. Besides, most real path planning problems need to be solved by considering different conflicting goals such as price and quality. The trajectory planning problem is then considered as a Multi-Objective Optimization Problem (MOOP).

Many researchers have carried out various works to solve the Multi-Objective Path Planning (MOPP) problem for UAVs in a dynamic environment. The authors in [5] proposed a new methodology based on an Improved Gravitational Search Algorithm (IGSA) to solve the path planning for multi-robots in a dynamic environment. In [6], the authors investigated a new algorithm for UAV path planning problems based on Ant Colony Optimization (ACO) and artificial potential field. In [7], a Pigeon-Inspired Optimization (PIO) algorithm is used to optimize the initial path and another Fruit Fly Optimization Algorithm (FFOA) is used to solve the global path planning problem in a three-dimensional dynamic environment of oilfields. The authors in [8] proposed a novel Predator-Prey Pigeon-Inspired Optimization (PPPIO) to solve the Uninhabited Combat Aerial Vehicle (UCAV) 3D path planning problem in a dynamic environment. In [9], a novel integrated path planning approach based on an A* algorithm and local trace-back model has been proposed to solve such kind of hard problems. The authors in [10] developed an Improved Artificial Bee Colony (IABC) algorithm to solve the path planning problem in an environment of dynamic threats thanks to its fewer control parameters and faster convergence.

Although these works have been developed to solve the MOPP problem for a UAV flying in a dynamic environment, most of them converted the multi-objective problem into a single objective problem by using a weighted sum function [11]. This technique is easy to implement, but it is difficult to determine the best weights for the various contradictory objectives. The bias will be enjoined throughout the optimization process. Other methods have been developed to deal with the MOPP problem and obtain a set of optimal Pareto solutions. These methods can be classified into two types: exact methods and approximate methods [12]. An exact method such as Multi-Objective Branch & Bound (MOBB) is used to get the best solutions in the Pareto Optimal Frontier (POF) for the given path planning problem [13]. However, the computational complexity is highly elevated. The approximate multi-objective optimization methods are thus developed and used extensively in recent years to solve the MOOP. The path planning problem for UAVs in a dynamic environment is no exception. In [14], the path planning problem in an uncertain and dynamic environment is considered as a constrained multi-objective optimization problem with uncertain coefficients which is solved using a constrained Multi-Objective Particle Swarm Optimization (MOPSO) technique. In [15], a Modified Central Force Optimization (MCFO) based technique is introduced to solve the path-planning problem for a 6 DOF rotary-wing quadrotor helicopter. In such work, the theory of the Particle Swarm Optimization (PSO) and the mutation operator of the Genetic Algorithm (GA) are combined to improve the original CFO method.

In the above-mentioned studies, the idea of using multi-objective metaheuristics for path planning problem’s formulation and the resolution seems a promising solution. To overcome the limits and inconveniences of the cited methods, particularly in terms of complexity and prohibitive time consuming, a systematic and efficient path planning method is proposed based on an advanced Multi-Objective Multi-Verse Optimization (MOMVO) algorithm. The main contributions of this paper are summarized as follows: 1) a novel strategy of reformulation and solving of a MOPP problem under operational constraints in a dynamic environment is proposed based on the concepts of the multi-criteria multi-verse optimization. Such a planning strategy allows guiding the quadrotor UAV to ensure destination position by calculate the next position in each step time while avoiding all moving obstacles. 2) A modified TOPSIS is employed as a higher-level decision-making approach to choose the best compromise solution among all the non-dominated solutions in the sense of Pareto. 3) A nonparametric statistical analysis method is proposed to compare all reported solvers for the hard path planning problem.

The remainder of this paper is organized as follows. In Section 2, the path planning problem for a quadrotor UAV is formulated as a multi-objective optimization problem under operational constraints. Section 3 presents the proposed multi-objective multi-verse optimizer to solve the formulated path planning problem. Section 4 describes the dynamical model of the studied quadrotor and the PID control design for the position and attitude dynamics stabilization and tracking. In Section 5, demonstrative results and comparisons are carried out and discussed. Section 6 concludes this paper.

2  Path Planning Problem Formulation

The quadrotor passed from the starting point A (x1,y1,z1) to the target one B (xn,yn,zn). The x-axis range (x1,xn) is divided into n−1 equal segments and defined as x1,x2,x3,…,xn. The time is incremented, the quadrotor has moved from position wi=(xi,yi,zi) to the next position wi+1=(xi+1,yi+1,zi+1) where the positions {xi}1≤i≤n are selected and the decision variables for optimization are defined as θ={yi+1,zi+1},∀i=1,2,…,n−2.

In the UAVs’ path planning formalism, the length of the flight path is very important. In this work, the robot determines its next position from its current one and tries to align its direction towards the goal. Consider initially, the UAV placed in the location at a time t in the space coordinate (xi,yi,zi). At the time (t+Δt), it wants to move to the next position (xi+1,yi+1,zi+1) such that the line joining between {(xi,yi,zi), (xi+1,yi+1,zi+1)} and {(xi+1,yi+1,zi+1), (xn,yn,zn)} minimizes the total path length and allows the UAV to align its direction towards the goal. So, the first proposed objective function of the multi-objective optimization problem, denoted as f1 , is defined as follows:

f1(θ)=(xi+1−xi)2+(yi+1−yi)2+(zi+1−zi)2+(xi+1−xn)2+(yi+1−yn)2+(zi+1−zn)2 (1)

Besides, the path planning process cannot totally ignore the dynamic characteristics of the UAV. When the UAV moves in the straighter path, the burden of the control system is reducing and the fuel cost of the flight process is decreasing [16]. The second objective function f2 is thus defined as follows:

f2(θ)=arccos⁡(φ→ψ→|φ→||ψ→|) (2)

where φ→ is (xi−1−xi,yi−1−yi,zi−1−zi) and ψ→ denotes (xi+1−xi,yi+1−yi,zi+1−zi).

On the other hand, avoidance of obstacles in a dynamic flight environment is more complex than in a static one. To simplify the characterization of moving obstacles, they can be modeled by spheres of radius R and center c. Thus, at the beginning of the program, the center, radius, and velocity vector of such spheres are initialized. At each time step Δt, the positions of a given moving obstacle are updated as:

vobs(t+Δt)=vobs(t)+aΔt (3)

xobs(t+Δt)=xobs(t)+vobs(t+Δt)Δt+1/2aΔt2 (4)

yobs(t+Δt)=yobs(t)+vobs(t+Δt)Δt+1/2aΔt2 (5)

zobs(t+Δt)=zobs(t)+vobs(t+Δt)Δt+1/2aΔt2 (6)

where vobs is the velocity of a dynamic obstacle, and a is its acceleration.

When the UAV moved from the actual position (xi,yi,zi) to the next position (xi+1,yi+1,zi+1), it does not intersect any obstacle. So, it should be tested if any obstacle intersects the line segment connecting the two positions. The line through (xi,yi,zi) and (xi+1,yi+1,zi+1) can be written as:

x=xi−1+tΔx;y=yi−1+tΔy;z=zi−1+tΔz (7)

where Δx=xi−xi−1, Δy=yi−yi−1, and Δz=zi−zi−1 denote the increments on the drone’s positions.

The equation of a given sphere with the center’s coordinates (xc,yc,zc) is written as follows:

(x−xc)2+(y−yc)2+(z−zc)2−R2=0 (8)

Then, substituting Eq. (7) into Eq. (8) leads to the following equation:

At2+Bt+C=0 (9)

where A, B, and C terms are defined as follows:

A=Δx2+Δy2+Δz2 (10)

B=2(Δx(xi−1−xc)+Δy(yi−1−yc)+Δz(zi−1−zc)) (11)

C=(xi−1−xc)2+(yi−1−yc)2+(zi−1−zc)2−R2 (12)

As explained in [17], the solving of Eq. (9) can give an idea of the intersection or not of the drone path with the considered moving obstacles. Indeed, when the discriminate Dj of Eq. (13) is negative there are no intersections with the obstacles:

Dj=B2−4AC (13)

where j=1,2,…,m, and m∈N is the number of moving obstacles.

Finally, the formulated multi-objective optimization problem for the path planning of the quadrotor UAV according to a given ith waypoint is defined as follows:

{Minimizeθ∈F⊆R2 φ(θ)={f1(θ), f2(θ)}s.t:gj(θ)≤0 (14)

where f1(.), f2(.), and gj(.)=Dj(.) are the cost and constraint functions given by Eqs. (1), (2), and (13), respectively, θ={yi+1,zi+1} is the decision variables and F={θ∈R2∣θmin≤θ≤θmax} is the bounded research space.

To handle the inequality constraints of the problem (14), the following external static type of penalty function is used as follows [18]:

ϕk(θ)=fk(θ)+∑j=1nconμjmax{0,gj(θ)}2 (15)

where μj∈R+ is the jth penalty parameter associated with the jth constraint, ncon is the total number of the inequality constraints, and k∈{1,2}.

3  Proposed Path Planning Algorithm

3.1 Multi-Objective Multi-Verse Optimizer

Originally proposed by Mirjalili et al. [19], the Multi-Verse Optimizer (MVO) is a population-based metaheuristic inspired by the physics theory of the existence of multi-verse. In this formalism, the interaction among different universes is ensured based on the concepts of white/black holes and wormholes. The main motion equations of the MVO metaheuristic are given as follows [19]:

xij={{xj+TDR+(ubj−lbj×r4+lbj)r3<0.5xj+TDR−(ubj−lbj×r4+lbj)r3<0.5r2<WEPxijr2≥WEP (16)

where xij denotes the jth component in the ith solution, xj is the jth variable of the best universe, lbj and ubj are the lower and upper bounds, respectively, r2, r3, and r4 are random numbers in the interval [0, 1].

In Eq. (16), the terms TDR and WEP present the traveling distance rate and the wormholes’ existence probability, respectively, and are defined as follows:

WEP=ρmin+iter(ρmax−ρmin)/Max_iter (17)

TDR=1−iter1/γ/Max_iter (18)

where ρmin and ρmax are the wormhole existence probabilities, iter is the current iteration, and γ defines the exploitation accuracy.

To develop a multi-objective version of the MVO metaheuristic for the problem (14), a concept of the archive is investigated. The leader selection and roulette wheel approaches are used to select the fittest solutions according to the following probabilistic mechanism [20]:

σi=ϑi/α (19)

where ϑi denotes the number of the vicinity solutions and α>1 is a constant.

Based on the above motion equations and the archive updating mechanism (19), a pseudo-code of MOMVO is given by Algorithm 1.

3.2 Decision-Making Model

The selection of an optimal solution requires in particular a higher-level decision-making approach. The modified TOPSIS method is used to choose with more safety the best compromise solution among all the non-dominated ones in the sense of Pareto. Such a multiple-criteria decision-making approach is implemented as follows [21]:

Step 1: Obtain the decision matrix

D=[x11x12…x1wx21x22…x2w⋮⋮⋱⋮xv1xv2…xvw];xij (i=1,2,…,v, j=1,2,…,w) (20)

Step 2: Normalize the decision matrix

sij=xij∑i=1vxij (21)

Step 3: Find the positive-and negative-ideal solutions

A+=(a1+,a2+,…,aw+);A−=(a1−,a2−,…,aw−) (22)

Step 4: Calculate the w-dimensional weighted Euclidean distances

δi+=[∑j=1wχj(aj+−aij)2]1/2;δi−=[∑j=1wχj(aj−−aij)2]1/2i=1,2,…,v;∑j=1wχj=1 (23)

Step 5: Calculate the relative closeness to the ideal solution

Ci=δi−/(δi++δi−)i=1,2,…,v (24)

Step 6: Choose an alternative with maximum Ci

4  Tracking of the Planned Paths

4.1 Dynamic Model

The basic movements of the quadrotor are realized by varying the speed of each rotor as shown in Fig. 1. To evaluate the mathematical model of the quadrotor, two coordinate systems have been used, i.e., earth reference frame Fe(Oe,xe,ye,ze) and body-fixed frame Fb(Ob,xb,yb,zb).

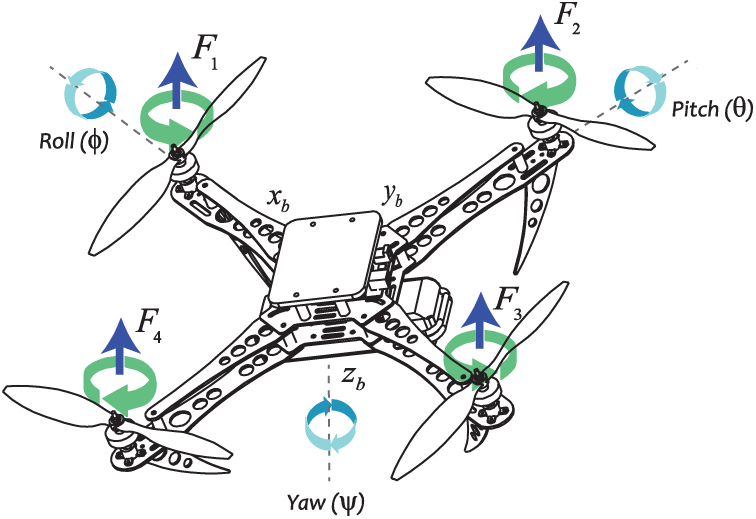
Figure 1: Quadrotor prototype and its related frames

The studied quadrotor is presented with its translational ξ=(x,y,z)T and rotational η=(ϕ,θ,ψ)T coordinates. Let a vector ϑ=(p,q,r)T denotes the angular velocity of the drone in the body-frame. Using the Newton-Euler formalism, a dynamic nonlinear model is given as follows [22–24]:

{x¨=1/mQ(cosϕcos⁡ψsin⁡θ+sin⁡ϕsin⁡ψ)u1−κ1/mQx˙y¨=1/mQ(cosϕsin⁡ψsin⁡θ−sin⁡ϕcos⁡ψ)u1−κ2/mQy˙z¨=1/mQcos⁡ϕcos⁡θu1−g−κ3/mQz˙p˙=(Iy−Iz)/Ixqr−Jr/Ixωrq−κ4/Ixp+1/Ixu2q˙=(Iz−Ix)/Iypr+Jr/Iyωrp−κ5/Iyq+1/Iyu3r˙=(Ix−Iy)/Izpq−κ6/Izr+1/Izu4 (25)

where −π/2≤ϕ≤π/2, −π/2≤θ≤π/2, and −π≤ψ≤π are the roll, pitch, and yaw Euler angles, respectively, mQ denotes the mass of the quadrotor, g is the gravitational acceleration, Jr is the z-axis inertia of the propellers, Ix, Iy and Iz denote the inertias of the quadrotor, κ1,2,…,6 are the aerodynamic friction and drag coefficients, and ωr=ω1−ω2+ω3−ω4 is the overall residual rotor angular velocity.

The control inputs u1, u2, u3 and u4 are defined as follows:

(u1u2u3u4)=(bbbb0−lb0lb−lb0lb0d−dd−d)(ω12ω22ω32ω42) (26)

where b and d denote the lift body and drag propellers coefficients, respectively, l denote the distance from the center of mass to each motor.

4.2 Tracking PID Controllers’ Design

The proposed control system of the quadrotor UAV is shown in Fig. 2. Such a control scheme is composed of an inner-loop attitude controller and an outer-loop position controller. The two controllers are designed with the classical PID structure as follows:

ufollow(t)=KPe(t)+KI∫0te(τ)dτ+KDde(t)dt (27)

where e is the tracking error between the desired reference and the accessible system output, KP, KI, and KD are the proportional, integral, and derivative gains of the PID controller, respectively.

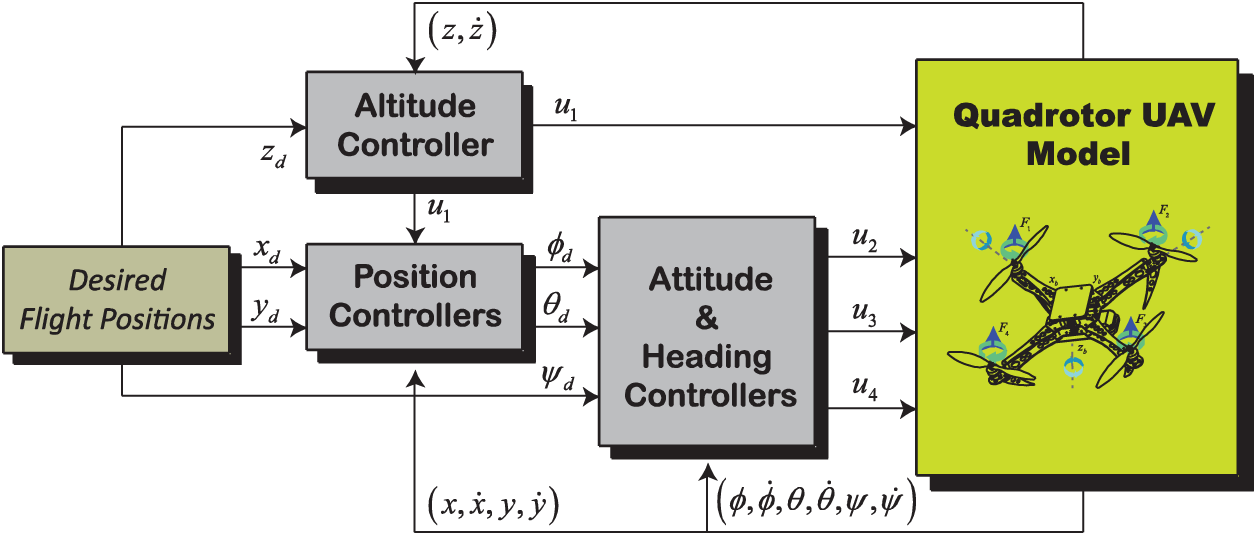
Figure 2: Full control scheme of the quadrotor

Two cascade loops for decoupling control of all flight dynamics are investigated. An inner loop is set to ensure the attitude and heading’s tracking. And the outer loop is designed for the positions (x,y) and altitude z dynamics [25]. The desired trajectories for the attitude variables ϕd and θd are generated from Eqs. (28) and (29) shown as virtual control laws for the translational dynamics [26–28]:

ux=(cosϕcos⁡ψsin⁡θ+sin⁡ϕsin⁡ψ) (28)

uy=(cosϕsin⁡ψsin⁡θ−sin⁡ϕcos⁡ψ) (29)

Solving Eqs. (28) and (29) for a given yaw angle ψ leads to the desired roll and pitch angles’ formula respectively given as follows:

ϕd=arctan⁡(uxsin⁡ψ−uycos⁡ψ(1−ux2sin2⁡ψ+2uxuycos⁡ψsin⁡ψ+uy2sin2⁡ψ−uy2)) (30)

θd=arcsin⁡(uxcos⁡ψ+uysin⁡ψ(1−ux2sin2⁡ψ+2uxuycos⁡ψsin⁡ψ+uy2sin2⁡ψ−uy2)) (31)

5  Simulation Results and Discussion

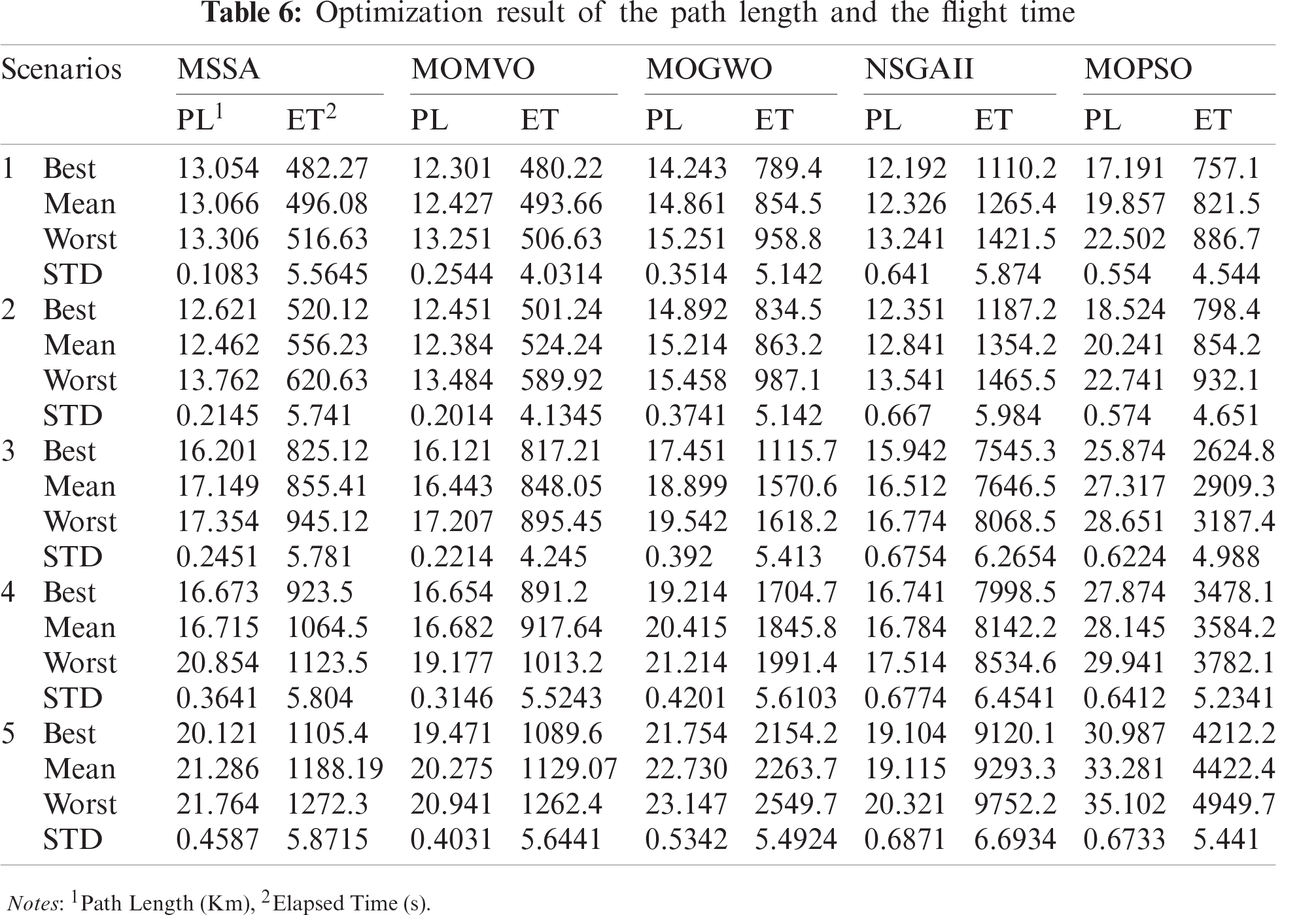
To illustrate the performance of the proposed MOMVO-based method, a 3D dynamic environment with moving obstacles is developed under the MATLAB/Simulink software. An interactive Graphical User Interface (GUI) has been implemented for the different simulations. The quadrotor’s 3D trajectory can be viewed by designing an animated quadrotor that receives the simulation data and performs the dynamical responses. Some performance index values, such as path length, flight time, and response plots of the quadrotor along the X, Y, and Z-axis, are presented and discussed. In this study, the quadrotor’s physical parameters are given in Appendix A. Tab. 1 gives the different flight scenarios considered in the dynamic environment.

To compare the performance of the proposed MOMVO-based planning method, others algorithms such as MSSA, MOGWO, MOPSO, and NSGAII are retained. The control parameters of such optimizers are summarized in Tab. 2.

To have a fair and reliable comparison, the common parameters such as the maximum number of iterations and the population size are set as 100 and 50, respectively. For statistical comparison purposes, all algorithms are independently executed 10 times and compared in the sense of the solutions’ quality. In each step time, the quadrotor calculates the next position by solving the formulated multi-objective optimization problem (14) based on a multi-objective optimization algorithm. The execution of the reported algorithms leads to obtain a set of non-dominated solutions as shown in Fig. 3. These Pareto fronts are considered at the first time-step to have a fair comparison.

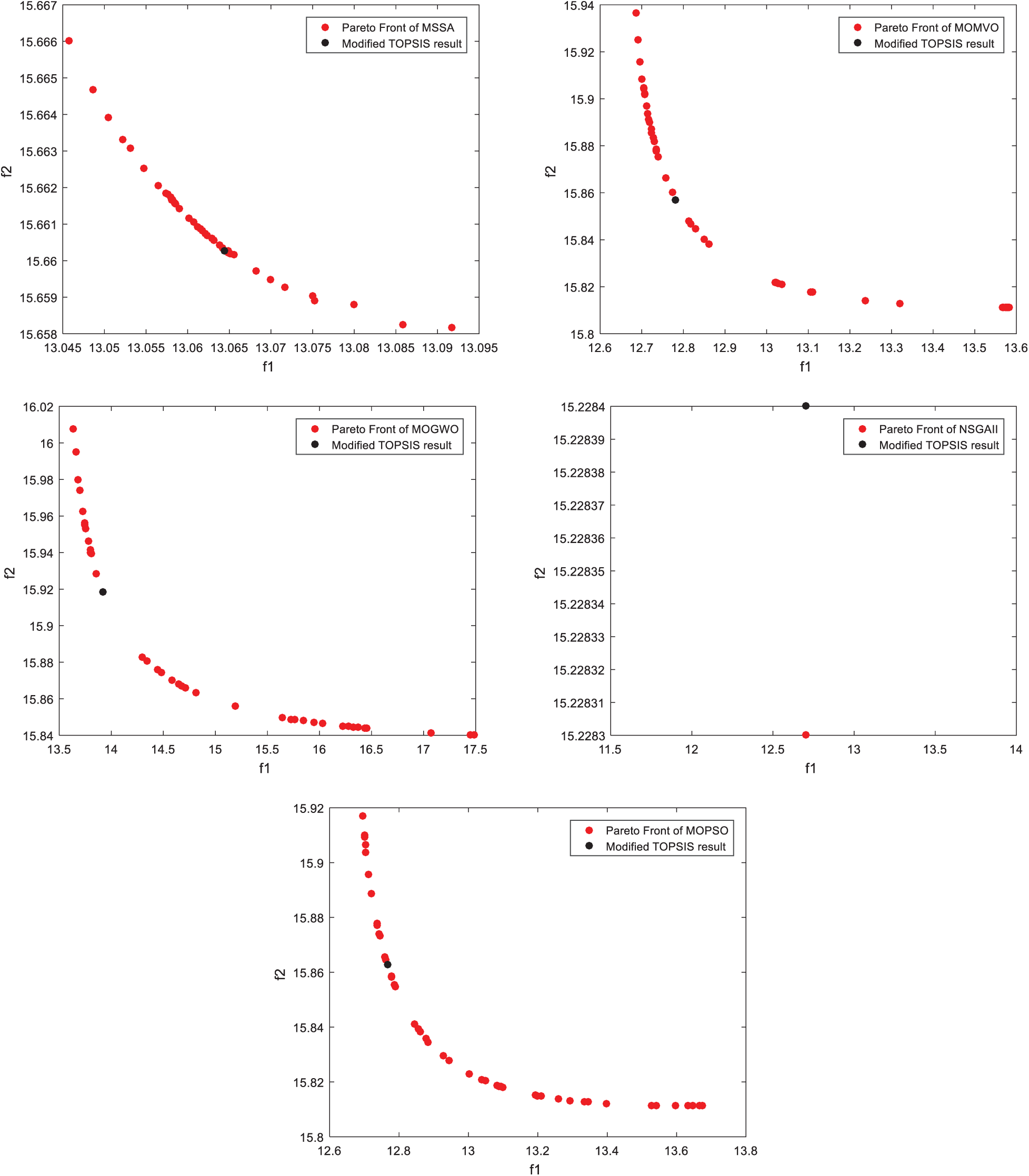
Figure 3: Pareto Fronts for the generation of the first position

These results show the repartition topology of the set of optimal non-dominated Pareto solutions on the compromised surface. A higher-level decision-making approach, i.e., the modified TOPSIS, selects the best compromise solution. These illustrative results show the high optimization performance of the proposed MOMVO algorithm in terms of convergence dynamics and solution distribution. The optimal Pareto solutions are strongly distributed for the two considered objectives of Eqs. (1) and (2) and under operational constraints of Eq. (13), which means a good coverage of the non-dominated set of solutions of the optimization problem (14) for proposed algorithms, except the NSGAII one which it could only find some feasible solutions.

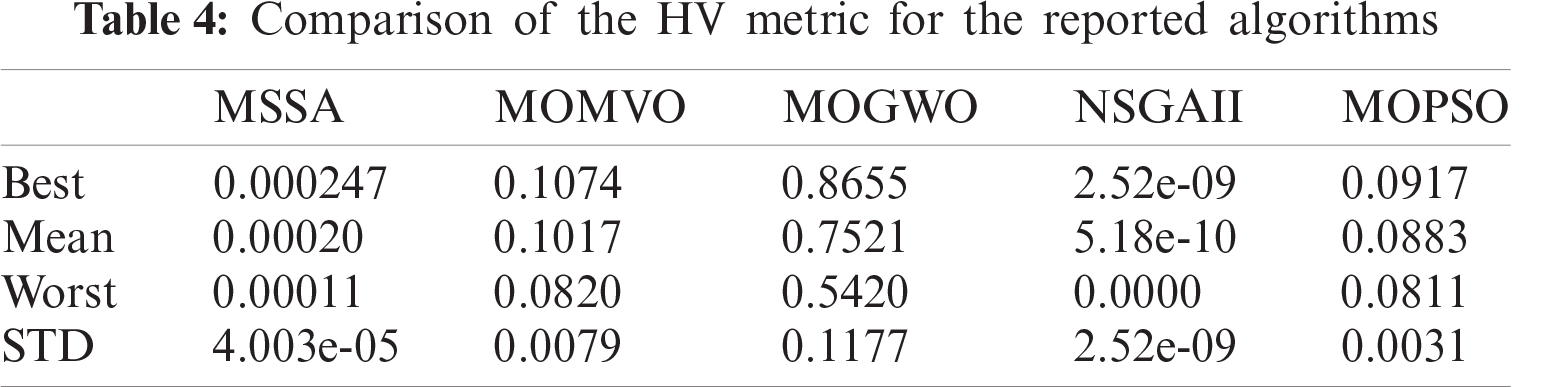
To highlight the diversity and coverage of the obtained non-dominated solutions, various metrics such as Maximum Spread (MS) [33,34], Hyper Volume (HV) [35], and C metric [36] have been employed in this study. The statistical results for the MS metric are presented in Tab. 3. The proposed MOMVO algorithm is superior to the other reported optimizers in terms of the largest value of MS metric. It becomes the best in terms of having high coverage properties. Tab. 4 shows the optimization results of the HV index for the reported algorithms. The statistical results show that the MOGWO algorithm followed by the MOMVO presents the two best solvers compared with other proposed algorithms in terms of diversity and convergence performance. Tab. 5 shows the comparative results for the reported algorithms in terms of the C metric. The proposed MOMVO solver surpassed all the other competitive ones and it dominates more than 2% of the MSSA solutions, 99% of the MOGWO solutions, 15% of the NSGA-II solutions, and 4 % of the MOPSO solutions on average.

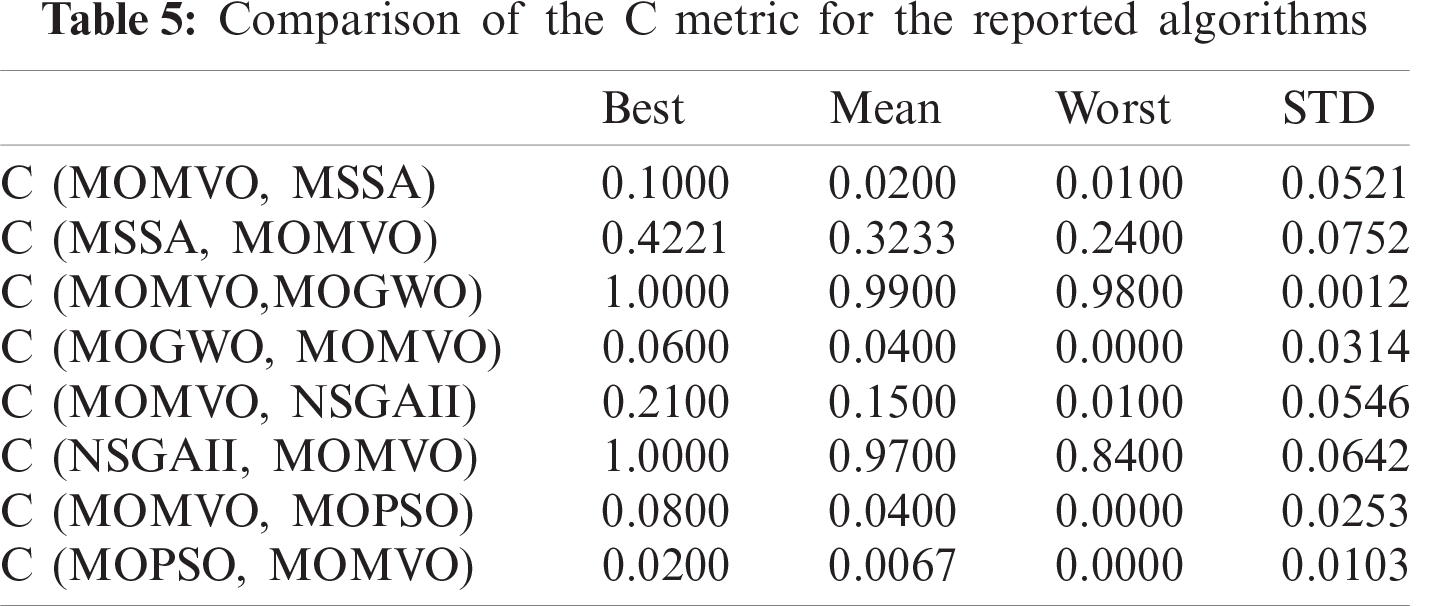
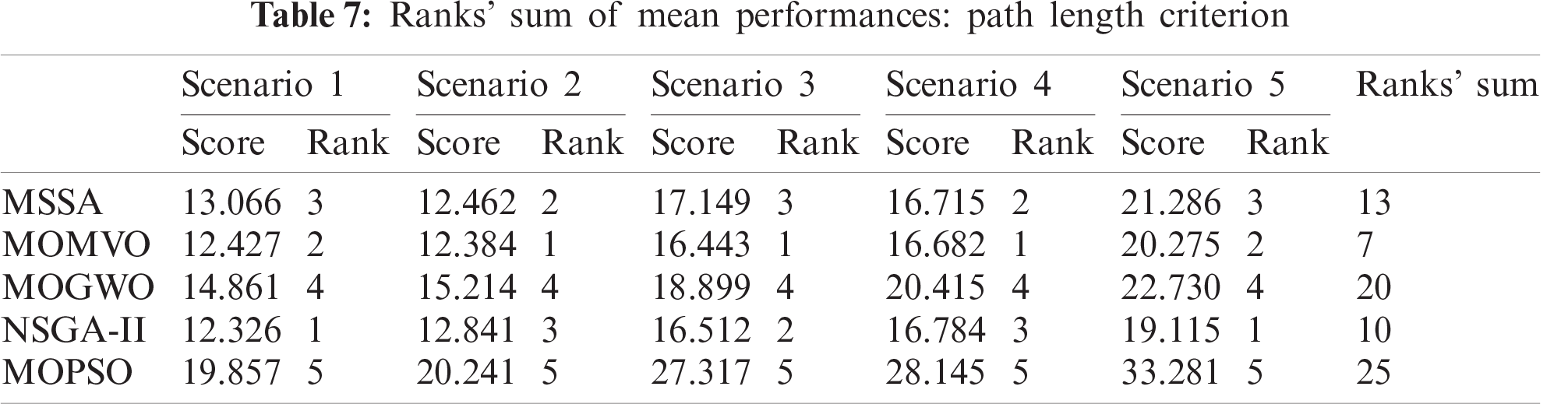
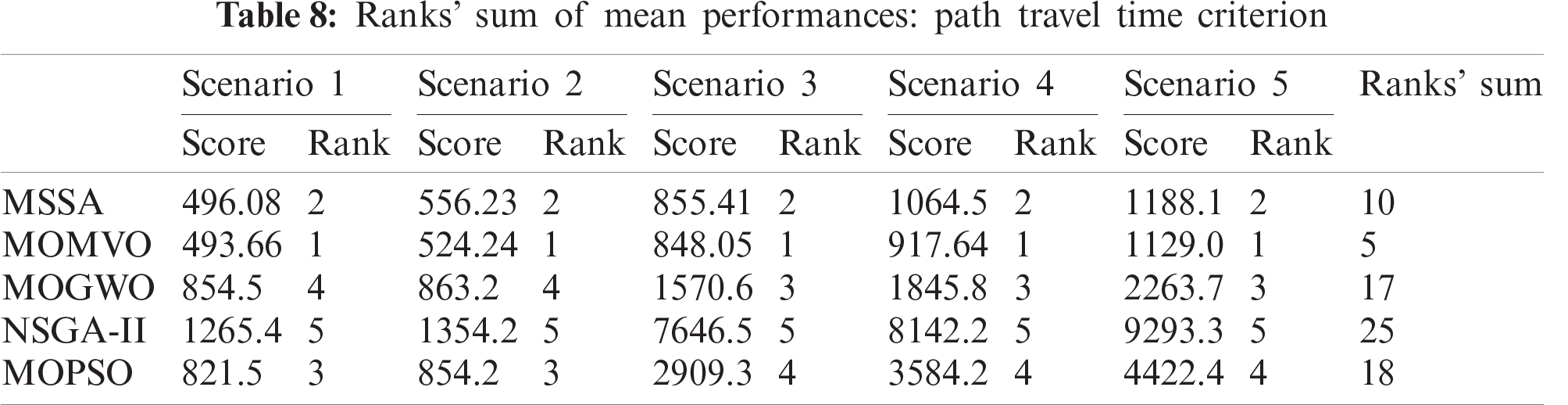
To analyze the statistical performance of the MOMVO-based planning method, a comparative study with MSSA, MOGWO, NSGAII, and MOPSO algorithms is performed on three performance criteria, such as path length, elapsed time, and capacity to avoid the moving obstacles as shown in Tab. 6. While considering two performance criteria, i.e., path length and path travel times, a statistical comparison according to its mean value based on the nonparametric Friedman test is implemented and discussed to indicate the significant differences among the performances of the reported algorithms. The Iman-Davenport extension of the classical Friedman test [37] provides the computed value FF1=27.25 for the elapsed time criterion and FF2=79.33 for the flight time criterion. For the five reported algorithms (ζ=5) and five scenarios (λ=5) at a 95% level of significance, the critical value of the F distribution with ζ−1 and (ζ−1)(λ−1) degrees of freedom is equal to F4,16,0.05=3.01<FF1<FF2. So the null hypothesis is declined and there are significant differences among the performance.

To find out which algorithms differ from the others, Fisher’s LSD post-hoc test is applied [37]. The ranks’ sums for all the proposed methods in the different scenarios for the two performance indices are summarized in Tabs. 7 and 8. The paired comparisons are given in Tabs. 9 and 10. The bold and underlined values indicate that the absolute difference of the rank’s sum |Ri−Rj| is greater than the critical values 4.2398 and 2.5963 for the path length and flight time criteria, respectively [37]. From the statistical results based on the two performance criteria, i.e., path length and path travel time, it is obvious that the MOMVO algorithm outperforms the other reported algorithms for the path planning problem of the quadrotor in the considered dynamic environment.

By visualizing the simulations of the 3D trajectory of the quadrotor, all proposed algorithms succeed in completing the flight mission still avoiding all the moving obstacles. The simulation results of the proposed MOMVO-based method are shown in Fig. 4. Several periods of time are given where T is the total time of the UAV path planning. These results show that the quadrotor avoids all dynamic obstacles in all four periods of time and guarantee the planning performance of the proposed MOMVO-based method. The time-domain responses of the controlled position dynamics are shown in Figs. 5–9 corresponding to the mean case of the multicriteria optimization. The proposed flight PID controllers allow the quadrotor to reach the desired trajectories. The PID controller gains’ selection is achieved by an iterative trials-errors-based method. Even though there were minor tracking errors in the time-domain responses of the closed-loop, these results remain encouraging. The tracking errors can be due to using PID gains that were not defined from the control design approach but by trials-errors based tuning.

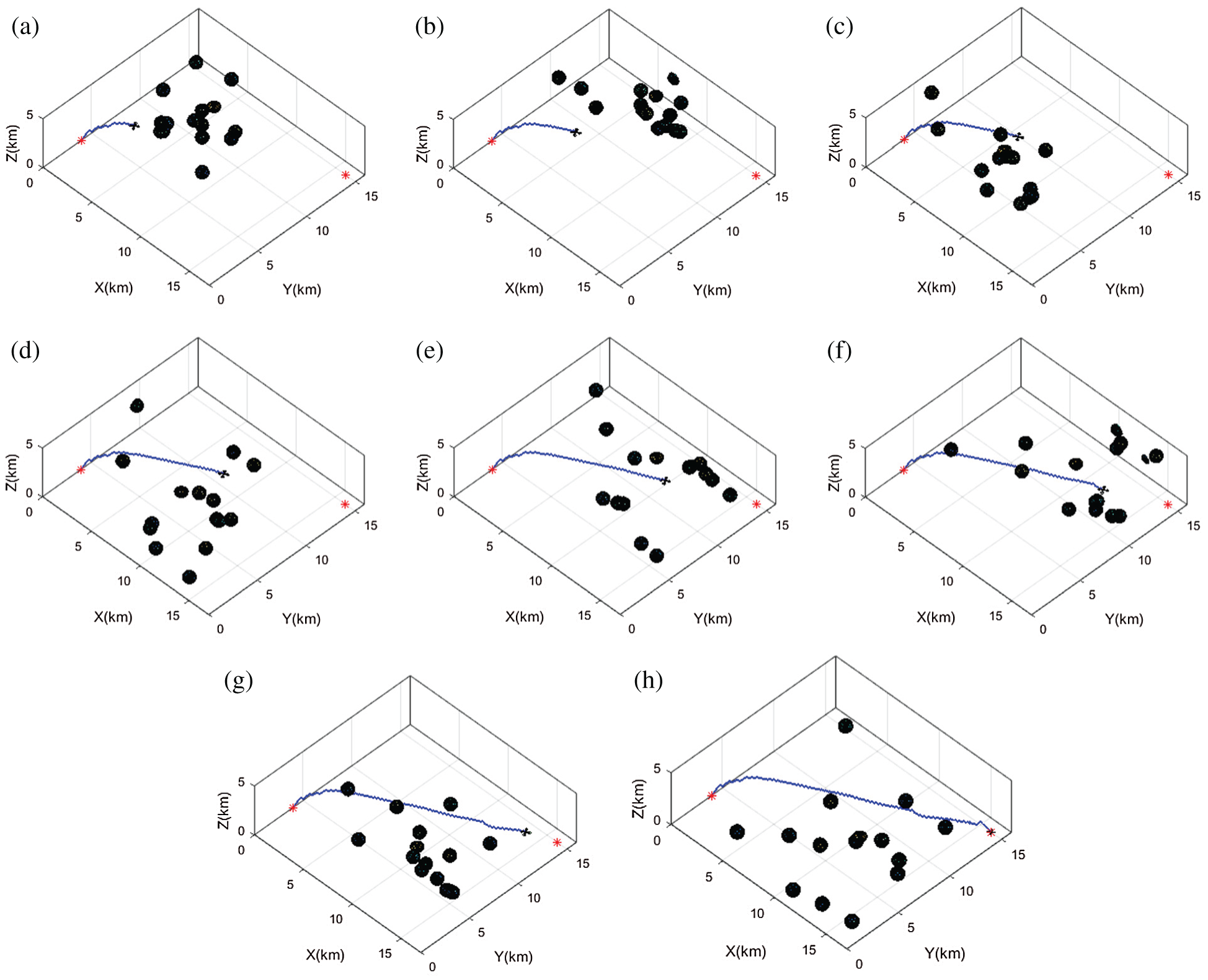
Figure 4: Planned path tracking in scenario 5 for the proposed MOMVO-based approach: (a) T/8; (b) 2T/8; (c) 3T/8; (d) 4T/8; (e) 5T/8; (f) 6T/8; (g) 7T/8; (h) total mission time (T)

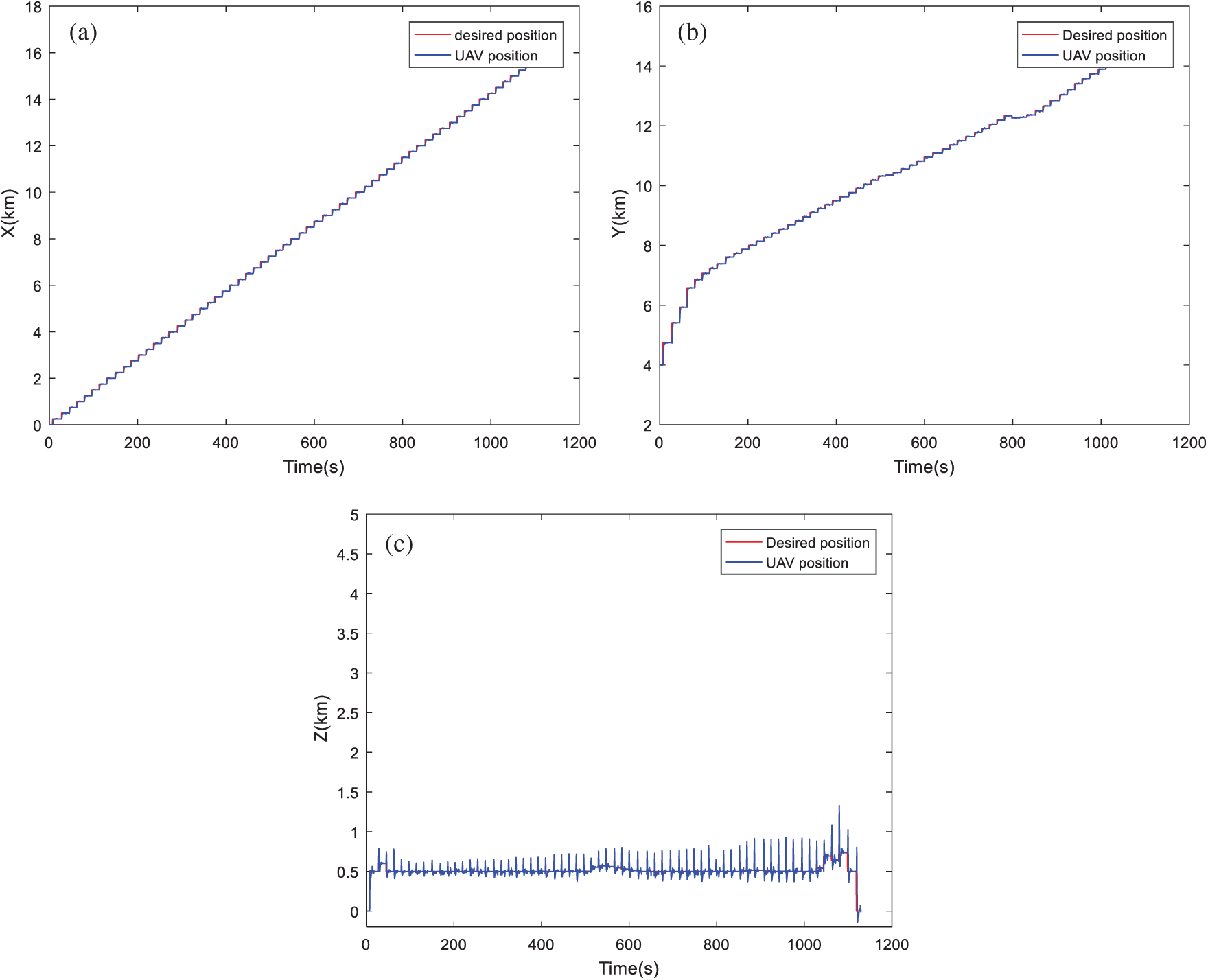
Figure 5: Position tracking based on MOMVO algorithm: (a) Tracking dynamics on X-axis; (b) Tracking dynamics on Y-axis; (c) Tracking dynamics on Z-axis

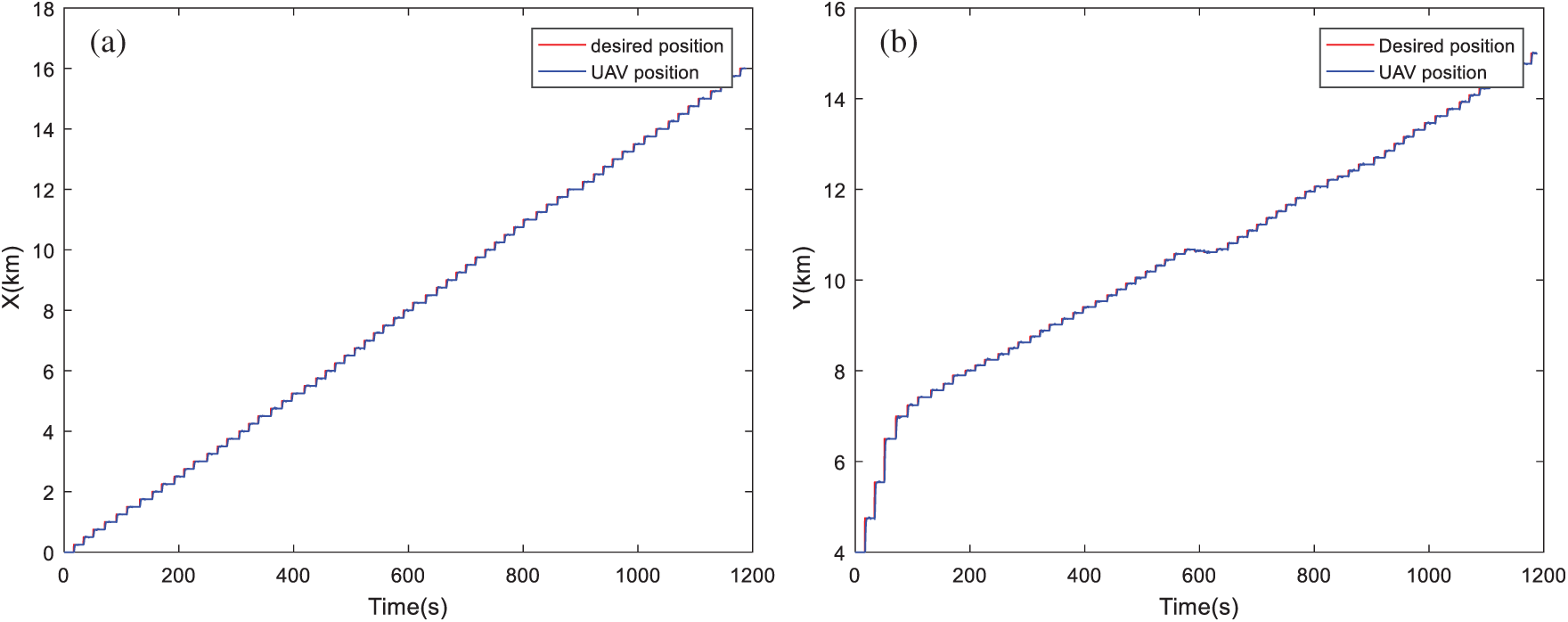
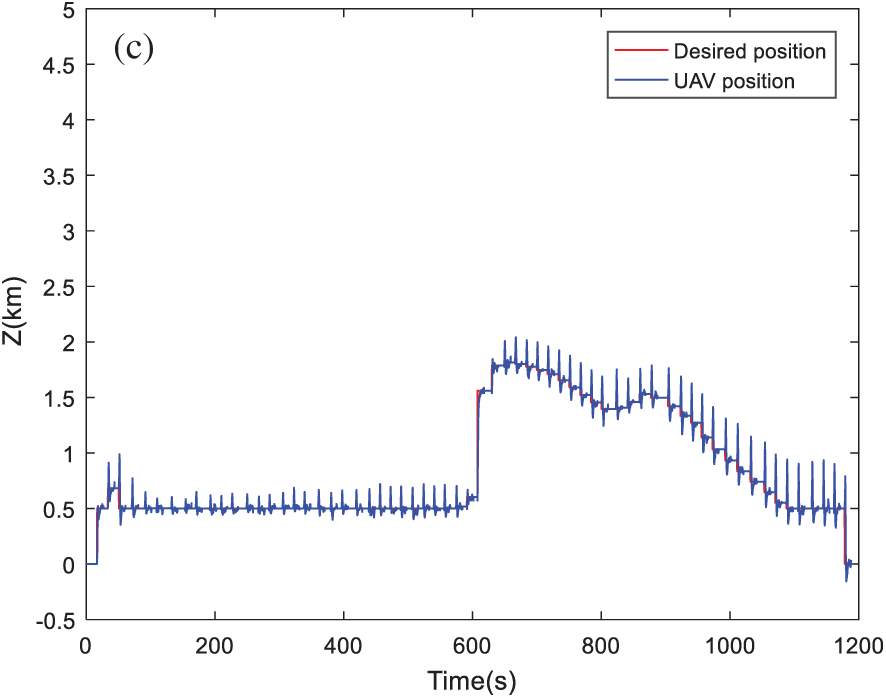
Figure 6: Position tracking based on MSSA algorithm: (a) Tracking dynamics on X-axis; (b) Tracking dynamics on Y-axis; (c) Tracking dynamics on Z-axis

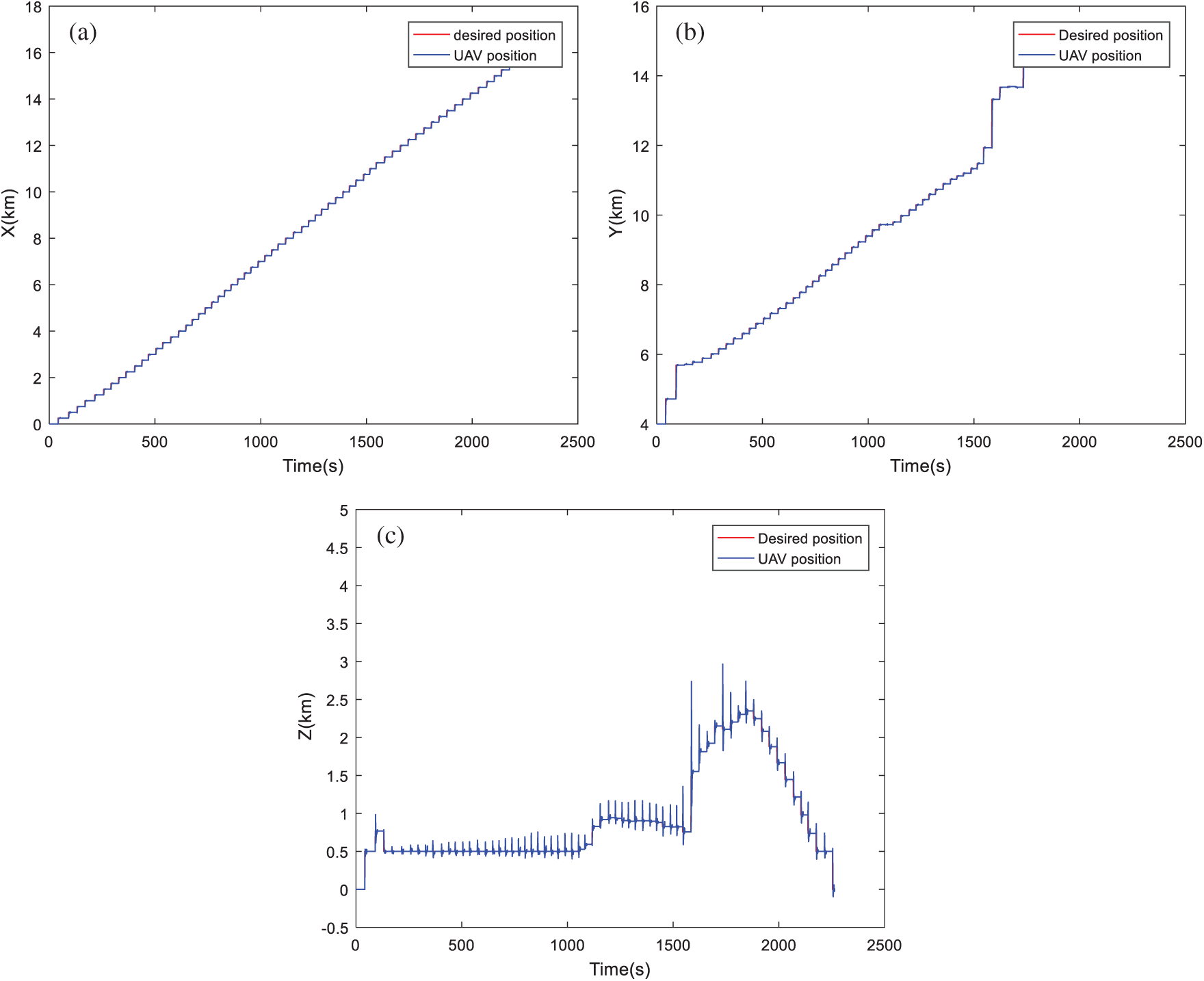
Figure 7: Position tracking based on MOGWO algorithm: (a) Tracking dynamics on X-axis; (b) Tracking dynamics on Y-axis; (c) Tracking dynamics on Z-axis

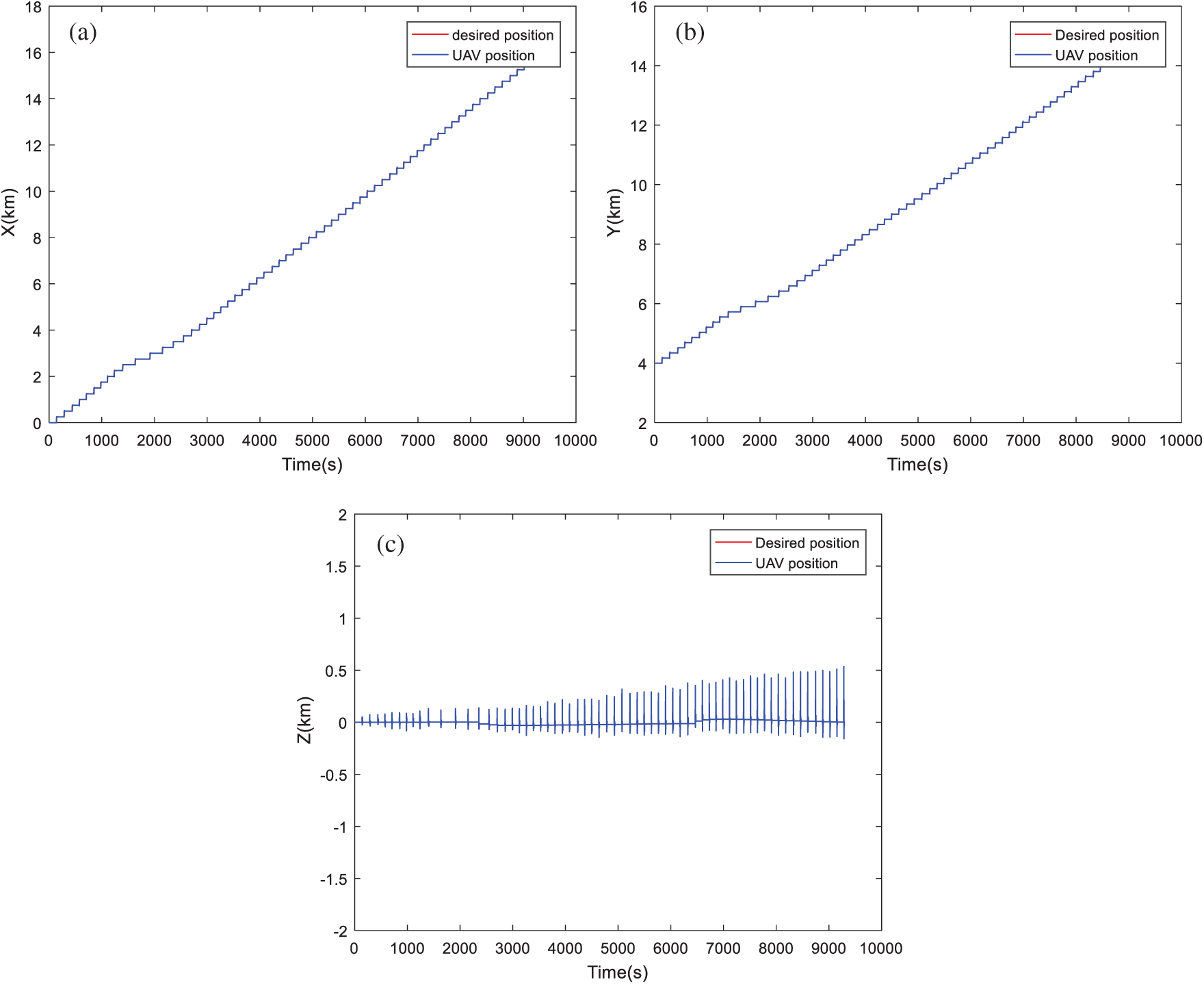
Figure 8: Position tracking based on NSGA-II algorithm: (a) Tracking dynamics on X-axis; (b) Tracking dynamics on Y-axis; (c) Tracking dynamics on Z-axis

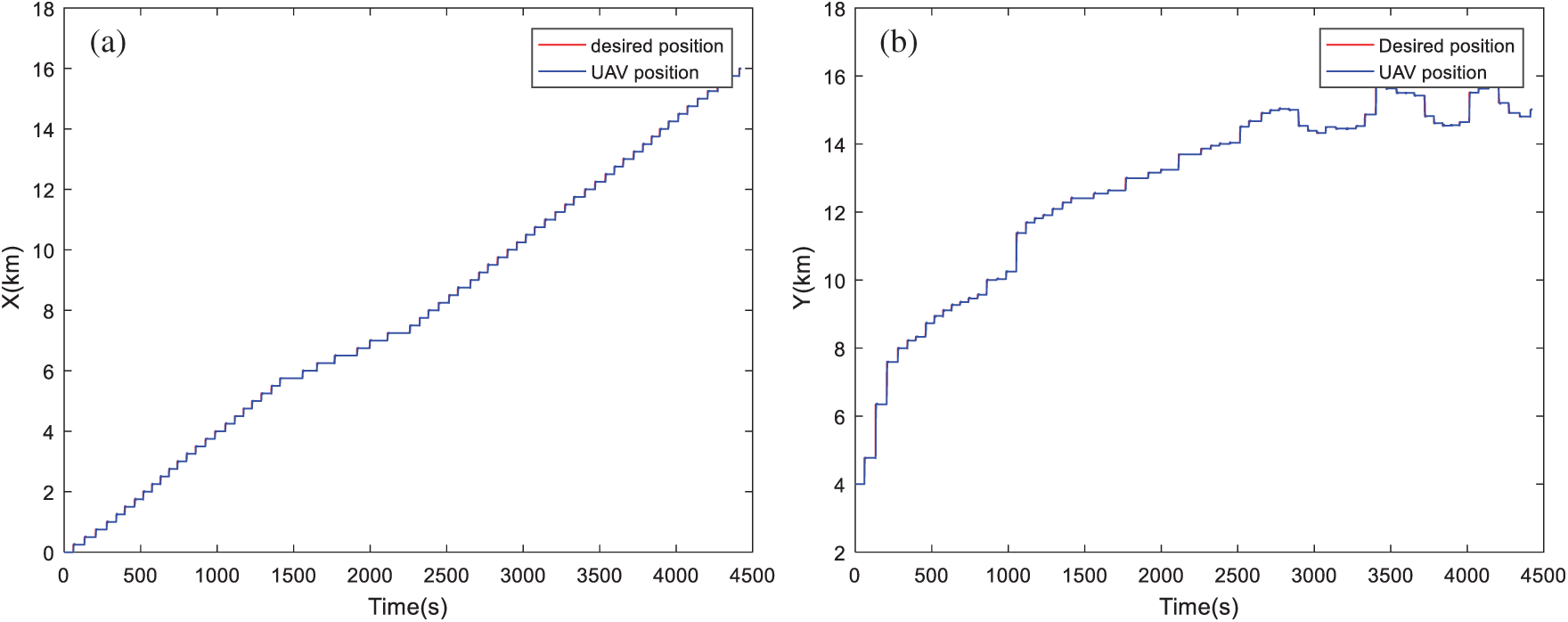
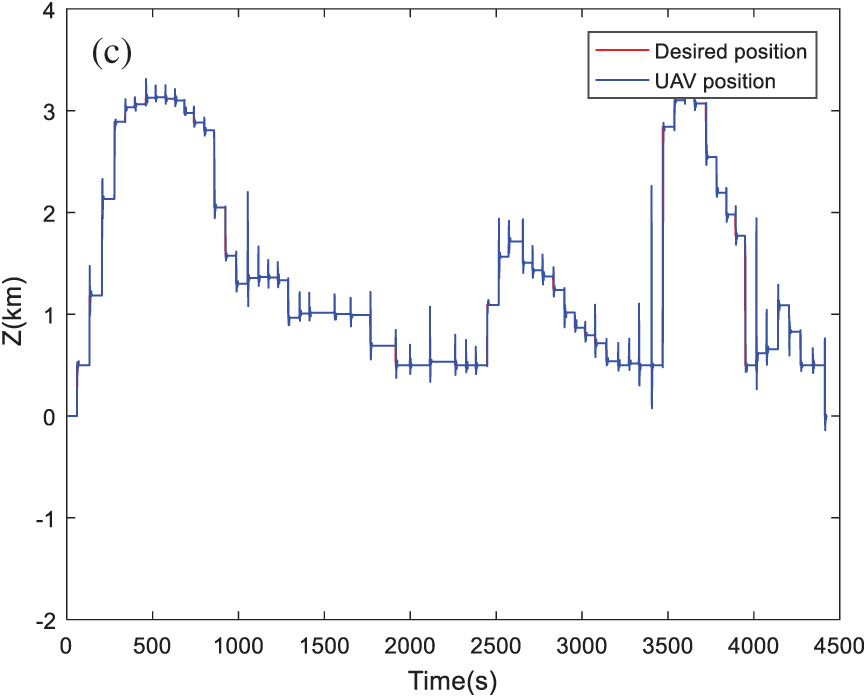
Figure 9: Position tracking based on MOPSO algorithm: (a) Tracking dynamics on X-axis; (b) Tracking dynamics on Y-axis; (c) Tracking dynamics on Z-axis

By visualizing these figures, we can notice that the proposed algorithm MOMVO gives the most direct path, which guarantees high efficiency in flight missions. The MOPSO algorithm generates a trajectory with many fluctuations along the Z-axis. From these results, the quadrotor has started the mission after a time delay which is due to the calculation time of the next point. A minimum execution time for an algorithm ensures the high efficiency of collision avoidance with the dynamic obstacles and causes a minimum flight time.

6  Conclusions

In this paper, a multi-objective multi-verse optimizer-based method has been proposed and successfully applied to solve the path planning problem of quadrotors UAV in a 3D dynamic environment. The path planning problem was formulated as a multi-objective optimization problem under operational constraints. The proposed planning approach aims to lead the drone to traverse a short and fast path in a dynamic environment without collision with the moving obstacles. An interactive graphical interface was developed under MATLAB/Simulink software environment to implement the proposed MOMVO-based path planning strategy. The demonstrative results and nonparametric statistical analyses in the sense of Friedman and the post-hoc tests show that the proposed MOMVO-based method is efficient and powerful compared to other reported algorithms. In comparison with MSSA, MOGWO, MOPSO, and NSGA-II optimizers, the main advantages of the proposed multi-verse algorithm are the remarkable simplicity of software implementation as well as the reduced number of its control parameters. The exploration/exploitation capabilities are superior to those of the other reported algorithms. Besides, the paired comparisons for two different optimization criteria showed that the MOMVO algorithm outperforms all the reported optimizers.

Future works deal with the real-world prototyping and experimentation of the proposed MOMVO-based planning approach using a real model of quadrotor available in our laboratory. The Parrot AR. Drone 2.0 kit associated with MATLAB/Simulink software will be used for the experimentations.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Fu, M. Ding, C. Zhou and H. Hu, “Route planning for unmanned aerial vehicle (UAV) on the sea using hybrid differential evolution and quantum-behaved particle swarm optimization,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 43, no. 6, pp. 1451–1465, 2013. [Google Scholar]

 2.  R. R. Pitre, X. R. Li and R. Delbalzo, “UAV route planning for joint search and track missions: An information-value approach,” IEEE Transactions on Aerospace and Electronic Systems, vol. 48, no. 3, pp. 2551–2565, 2012. [Google Scholar]

 3.  H. Chen, X. M. Wang and Y. Li, “A survey of autonomous control for UAV,” in Proc. of the 2009 Int. Conf. on Artificial Intelligence and Computational Intelligence, Shanghai, China, pp. 267–271, 2009. [Google Scholar]

 4.  M. Radmanesh, M. Kumar and A. Nemati, “Dynamic optimal UAV trajectory planning in the national airspace system via mixed integer linear programming, Proceedings of the Institution of Mechanical Engineers,” Part G: Journal of Aerospace Engineering, vol. 230, no. 9, pp. 1668–1682, 2016. [Google Scholar]

 5.  P. K. Das, H. S. Behera, P. K. Jena and B. K. Panigrahi, “Multi-robot path planning in a dynamic environment using improved gravitational search algorithm,” Journal of Electrical Systems and Information Technology, vol. 3, no. 2, pp. 295–313, 2016. [Google Scholar]

 6.  C. Huang, Y. Lan, Y. Liu, W. Zhou, H. Pei et al., “A new dynamic path planning approach for unmanned aerial vehicles,” Complexity, vol. 2018, no. 8420294, pp. 1–17, 2018. [Google Scholar]

 7.  F. Ge, K. Li, Y. Han, W. Xu and Y. Wang, “Path planning of UAV for oilfield inspections in a three-dimensional dynamic environment with moving obstacles based on an improved pigeon-inspired optimization algorithm,” Applied Intelligence, vol. 50, no. 1, pp. 2800–2817, 2020. [Google Scholar]

 8.  B. Zhang and H. Duan, “Three-dimensional path planning for uninhabited combat aerial vehicle based on predator-prey pigeon-inspired optimization in dynamic environment,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 14, no. 1, pp. 97–107, 2017. [Google Scholar]

 9.  X. Zhao, Y. Zhang and B. Zhao, “Robust path planning for avoiding obstacles using time-environment dynamic map,” Measurement and Control, vol. 53, no. 1–2, pp. 214–221, 2020. [Google Scholar]

10. G. Tian, L. Zhang, X. Bai and B. Wang, “Real-time dynamic track planning of multi-UAV formation based on improved artificial bee colony algorithm,” in Proc. of the 37th Chinese Control Conf., Wuhan, China, pp. 10055–10060, 2018. [Google Scholar]

11. S. Zajac and S. Huber, “Objectives and methods in multi-objective routing problems: A survey and classification scheme,” European Journal of Operational Research, vol. 290, no. 1, pp. 1–25, 2020. [Google Scholar]

12. R. Olaechea, D. Rayside, J. Guo and K. Czarnecki, “Comparison of exact and approximate multi-objective optimization for software product lines,” in Proc. of the 18th Int. Software Product Line Conf., Firenze, Italy, pp. 92–101, 2014. [Google Scholar]

13. V. Rodriguez-Fernandez, C. Ramirez-Atencia and D. Camacho, “A multi-UAV mission planning videogame-based framework for player analysis,” in Proc. of the IEEE Congress on Evolutionary Computation, Sendai, Japan, pp. 1490–1497, 2015. [Google Scholar]

14. Y. Zhang, D.-W. Gong and J.-H. Zhang, “Robot path planning in uncertain environment using multi-objective particle swarm optimization,” Neurocomputing, vol. 103, no. 1, pp. 172–185, 2013. [Google Scholar]

15. Y. Chen, J. Yu, Y. Mei, Y. Wang and X. Su, “Modified central force optimization (MCFO) algorithm for 3D UAV path planning,” Neurocomputing, vol. 171, no. 1, pp. 878–888, 2016. [Google Scholar]

16. V. Skala, “A new approach to line-sphere and line-quadrics intersection detection and computation,” in Proc. of the 12th Int. Conf. on Numerical Analysis and Applied Mathematics, Rhodes, Greece, pp. 1–4, 2014. [Google Scholar]

17. D. A. G. Vieira, R. Adriano and J. A. de Vasconcelos, “Handling constraints as objectives in a multiobjective genetic based algorithm,” Journal of Microwaves and Optoelectronics, vol. 2, no. 6, pp. 50–58, 2002. [Google Scholar]

18. S. Mirjalili, S. M. Mirjalili and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Computing and Applications, vol. 27, no. 1, pp. 495–513, 2016. [Google Scholar]

19. S. Mirjalili, P. Jangir, S. Z. Mirjalili, S. Saremi and I. N. Trivedi, “Optimization of problems with multiple objectives using the multi-verse optimization algorithm,” Knowledge-Based Systems, vol. 134, no. 1, pp. 50–71, 2017. [Google Scholar]

20. H. Deng, C.-H. Yeh and R. J. Willis, “Inter-company comparison using modified TOPSIS with objective weights,” Computers & Operations Research, vol. 27, no. 10, pp. 963–973, 2000. [Google Scholar]

21. A. Nagaty, S. Saeedi, C. Thibault, M. Seto and H. Li, “Control and navigation framework for quadrotor helicopters,” Journal of Intelligent & Robotic Systems, vol. 70, no. 1–4, pp. 1–12, 2013. [Google Scholar]

22. H. Elkholy and M. K. Habib, “Dynamic modeling and control techniques for a quadrotor,” in Unmanned Aerial Vehicles: Breakthroughs in Research and Practice, Information Resources Management Association (Eds.1st ed., USA: IGI Global, pp. 20–66, 2019. [Google Scholar]

23. S. Badr, O. Mehrez and A. E. Kabeel, “A design modification for a quadrotor UAV: Modeling, control and implementation,” Advanced Robotics, vol. 33, no. 1, pp. 13–32, 2019. [Google Scholar]

24. S. Abdelhay and A. Zakriti, “Modeling of a quadcopter trajectory tracking system using PID controller,” Procedia Manufacturing, vol. 32, no. 1, pp. 564–571, 2019. [Google Scholar]

25. A. Nagaty, S. Saeedi, C. Thibault, M. Seto and H. Li, “Control and navigation framework for quadrotor helicopters,” Journal of Intelligent & Robotic Systems, vol. 70, no. 1, pp. 1–12, 2013. [Google Scholar]

26. S. Bouallègue and K. BenKhoud, “Integral backstepping control prototyping for a quad tilt wing unmanned aerial vehicle,” International Review of Aerospace Engineering, vol. 9, no. 5, pp. 152–161, 2016. [Google Scholar]

27. N. BenAmmar, H. Rezk and S. Bouallègue, “Control strategy for a quadrotor based on a memetic shuffled frog leaping algorithm,” Computers, Materials & Continua, vol. 67, no. 3, pp. 4081–4100, 2021. [Google Scholar]

28. R. Fessi and S. Bouallègue, “LQG controller design for a quadrotor UAV based on particle swarm optimization,” International Journal of Automation and Control, vol. 13, no. 5, pp. 569–594, 2019. [Google Scholar]

29. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, no. 1, pp. 163–191, 2017. [Google Scholar]

30. S. Mirjalili, S. Saremi, S. M. Mirjalili and L. S. Coelho, “Multiobjective grey wolf optimizer: A novel algorithm for multi-criterion optimization,” Expert Systems With Applications, vol. 47, no. 1, pp. 106–119, 2016. [Google Scholar]

31. C. A. C. Coello, G. T. Pulido and M. S. Lechuga, “Handling multiple objectives with particle swarm optimization,” IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 256–279, 2004. [Google Scholar]

32. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

33. E. Zitzler, K. Deb and L. Thiele, “Comparison of multiobjective evolutionary algorithms: Empirical results,” Evolutionary Computation, vol. 8, no. 2, pp. 173–195, 2000. [Google Scholar]

34. S. Khalilpourazari, B. Naderi and S. Khalilpourazary, “Multi-objective stochastic fractal search: A powerful algorithm for solving complex multi-objective optimization problems,” Soft Computing, vol. 24, no. 4, pp. 3037–3066, 2020. [Google Scholar]

35. E. Zitzler, L. Thiele, M. Laumanns, C. M. Fonseca and V. G. Fonseca, “Performance assessment of multiobjective optimizers: An analysis and review,” IEEE Transactions on Evolutionary Computation, vol. 7, no. 2, pp. 117–132, 2003. [Google Scholar]

36. E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 4, pp. 257–271, 1999. [Google Scholar]

37. D. G. Pereira, A. Afonso and F. M. Medeiros, “Overview of Friedman’s test and post-hoc analysis,” Communications in Statistics-Simulation and Computation, vol. 44, no. 10, pp. 2636–2653, 2014. [Google Scholar]

Appendix A: Quadrotor’s model parameters

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.