Computers, Materials & Continua DOI:10.32604/cmc.2021.015984
Article

An Improved Machine Learning Technique with Effective Heart Disease Prediction System

Mohammad Tabrez Quasim1, Saad Alhuwaimel2,*, Asadullah Shaikh3, Yousef Asiri3, Khairan Rajab3, Rihem Farkh4,5 and Khaled Al Jaloud4

1College of Computing and Information Technology, University of Bisha, Bisha, 67714, Saudi Arabia
2King Abdulaziz City for Science and Technology, P.O. Box 6086, Riyadh, 11442, Saudi Arabia
3College of Computer Science and Information Systems, Najran University, Najran, 61441, Saudi Arabia
4College of Engineering, Muzahimiyah Branch, King Saud University, Riyadh, 11451, Saudi Arabia
5Department of Electrical Engineering, Laboratory for Analysis, Conception and Control of Systems, LR-11-ES20, National Engineering School of Tunis, Tunis El Manar University, 1002, Tunisia
*Corresponding Author: Saad Alhuwaimel. Email: huwaimel@kacst.edu.sa
Received: 17 December 2020; Accepted: 24 April 2021

Abstract: Heart disease is the leading cause of death worldwide. Predicting heart disease is challenging because it requires substantial experience and knowledge. Several research studies have found that the diagnostic accuracy of heart disease is low. The coronary heart disorder determines the state that influences the heart valves, causing heart disease. Two indications of coronary heart disorder are strep throat with a red persistent skin rash, and a sore throat covered by tonsils or strep throat. This work focuses on a hybrid machine learning algorithm that helps predict heart attacks and arterial stiffness. At first, we achieved the component perception measured by using a hybrid cuckoo search particle swarm optimization (CSPSO) algorithm. With this perception measure, characterization and accuracy were improved, while the execution time of the proposed model was decreased. The CSPSO-deep recurrent neural network algorithm resolved issues that state-of-the-art methods face. Our proposed method offers an illustrative framework that helps predict heart attacks with high accuracy. The proposed technique demonstrates the model accuracy, which reached 0.97 with the applied dataset.

Keywords: Machine learning; deep recurrent neural network; effective heart disease prediction framework

1  Introduction

Heart disease is the leading cause of death worldwide. Shortness of breath, physical shortcomings, and swollen feet are typically the indicators of heart disease (HD). In some cases clinical authorities are not available to treat the coronary illness and examinations are time-consuming. HD diagnosis is generally made by a specialist who examines the patient’s clinical history and creates a physical evaluation report. However, the outcomes are often inaccurate. Therefore, it is critical to build up a non-invasive structure that depends on classifiers of artificial intelligence (AI) (machine learning) for diagnosis. Using expert decision structures that depend on AI classifiers and the utilization of artificial fleecy reasoning can reduce the death rate from HD. A vital indicator of cardiovascular disease is arterial stiffness. In any case, the advancement of heart failure (HF) is limited to two assessments that sometimes offer conflicting information on confirming arterial stiffness. Additionally, there are two separations between HF aggregates, but no assessments. They are unmistakably identified by arterial stiffness [1,2]. This is dictated by measuring the time taken for the constrain wave to travel between the femoral artery and the carotid, which typically can only be measured via an external examination [3]. By assessing the range over the carotid arch and femoral waveform, taped with a tonometer, the time worth can be determined. Blood vessel reflection can be assessed to a certain degree by putting a tonometer of a fringe vessel and following certain procedures [4]. In data mining, the extraction of covered perceptive and imperative data from a large amount of data can be used to build new information [5,6]. Using data mining strategies to uncover critical information has been considered an approach to enhancing the evaluation and precision of social protection organizations while striking down the human administrations’ charge and analysis length [7]. HD patients utilize a data-based strategy to predict 1-(present moment), 5-(medium-term), and 9-year (long-term) results and how to reproduce the markers [8]. For more accurate recognition of the disorder symptoms, the density peak clustering (DPC) algorithm, which groups disease symptoms by a disease diagnosis and treatment recommendation system, is utilized [9]. It is capable of diagnosing a patient with HD. The momentum strategies use the best assortment [10,11]. Component extraction is a feature that can improve accuracy. To increase the accuracy, the suggested procedure uses a method for predicting HD: the effective HD prediction system (EHDP). EHDP is based on a hybrid machine learning algorithm. Receptive information on arterial stiffness, aortic, and mitral was more deplorable than models with rehashed inside and out neural organizations relying upon more than 50 prescient properties. The qualities were commonly full scale; be that as it may, the dataset had comparative numeric credits. The device finishes the execution of the proposed EHDP technique. The proposed method is investigated in terms of explicitness and accuracy.

The remainder of the article is organized as follows: Section 2 presents a summary of recent research studies. Section 3 elaborates on the structure of the EHDP system. Section 4 demonstrates the specific working limits of the proposed EHDP technique by utilizing a proper mathematical model. Section 5 discusses simulation results. Section 6 presents a discussion and the authors’ conclusions.

2  Literature Review

Alty et al. [12] present the possibility of diagnosing cardiovascular disease without having a blood test for fatigue. Ordonez et al. [13] proposed utilizing search constraints to decrease the number of limitations. This is done by looking for association rules in a preliminary set, then affirming them in the self-governing confirmation set. The clinical essentialness of the determined condition is estimated by help, affirmation, and lift. The standards of association apply to a file containing the clinical details of coronary HD patients. In the medical system, attachment laws include cardiac perforation assessments and risk factors associated with disease in four clear behaviors. Checking prerequisites and a test set assessment basically reduce the number of alliance rules and lead to better effectiveness.

Pilt et al. [14] examined the down-study at an emergency clinic. The Estimate Complex incorporates 10 physiological image chronicle channels and reference devices: Spigmocore, arteriography, etc. Dhote et al. [15] The conduct of swarm intelligence is the social frameworks, for example, peculiar creeps, ants (state movement of pterosaur creepy crawlies, ACO), and winged creatures. In this paper, particle swarm optimization (PSO) and the cuckoo search (CS) algorithms are swarm intelligence-based methods used for data collection.

Shaikh et al. [16] proposed a novel framework using a data mining procedure, specifically naïve Bayes, and a Java application where the client reacts to predetermined inquiries. This recovers the secure information from a fixed dataset and arranges an informational index. It can also answer complex questions in order to diagnose coronary HD and empower social protection experts to make clinical decisions that cannot be taken by truly solid frameworks.

Jabbar et al. [17] proposed an organization of passionate help for disease prediction. Data mining strategies were used to determine whether a patient suffers from HD or not. Hidden Naïve Bayes (HNB) is a data mining model that removes the restrictions of the traditional naïve Bayes approach. Our particular model cases can be applied in HNB HD grouping (prediction).

Anderson et al. [18] proposed for myocardial dead tissue, coronary HD (CHD), demise from CHD, heart attack, HD, and change from cardiovascular infections.

Gadekallu et al. [19] proposed a smart diagnosis system using CS with a rough set theory for feature reduction and disease prediction with a fuzzy logic system. All discussed methods [12–19] were based on single-machine algorithms. We identified this gap and proposed a hybrid approach to improve prediction accuracy.

3  System Model and Technique

The issue reasoning of the data mining technique and the five estimations are delineated in Section 3.1 as a comparable issue course of action. The particular structure can be derived from the model presented in Section 3.2.

3.1 Problem Methodology

Solanki et al. [20] have proposed a data mining technique for acute rheumatic fever (ARF). In Turkey, this is a disease with a high rate of incidence. To create a diagnosis for this kind of disease, we utilized the data request model specific to this ailment. The exploratory assessment prompted five unique evaluations of the frequency of ARF. New data appraisal frameworks might be related with this disease. It was necessary to find models that have not been successfully approved. Data processing of existing records and data stores may eventually improve the data related to the cause of ARF. The naive Bayes model is a systematic control system that initiates late-accumulated information. These systems learn a variety of tasks, as they can be drilled by extracting information when the process reaches a specified level of accuracy [20]. A fundamental test in the utilization of the Decision Treecomprehends the credits and all the evaluations that ought to be considered as root network focuses. It controls and knows the selection of highlights. We have diverse credit confirmation strategies to see the property that can be considered as a root note in each gage [21].

3.2 System Model

The proposed structure of the particular task is shown in Fig. 1. It is used to order information from a given guidance document, alongside the consolidated algorithm. To obtain an accurate estimation, we recommended the EHDP for determining why artery stiffness is subject to a combination of AI figuring’s. The goal is to build the necessary level of precision and reduce the false recognition rate utilizing confirmation technique arranging with progression strategies. This paper proposes to join CS and PSO smoothing out and a critical monotonous neural system to a coordinated methodology which will increase accuracy for better outcomes. The show is evaluated liable to organized contemplations of these frameworks in the dataset.

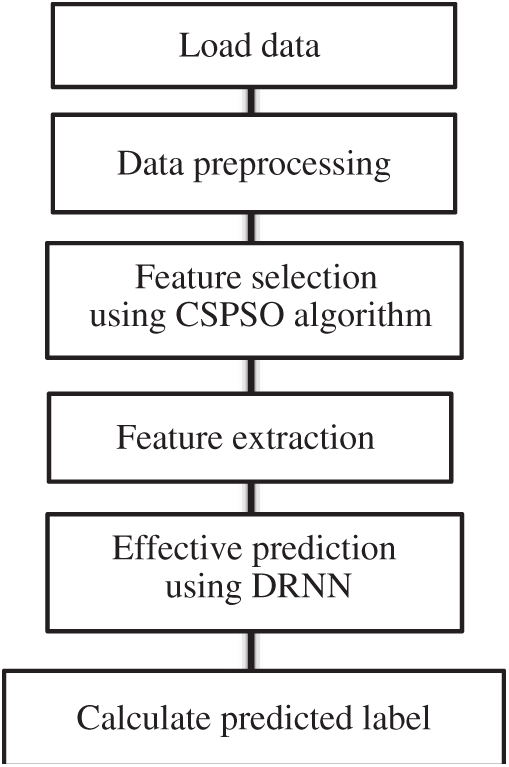
Figure 1: Framework model of a proposed CSPSO-DRNN calculation

4  Overview of CSPSO

4.1 Particle Swarm Optimization

The swarm {Ai,i=1,…,N}, N is approved in standard PSO with Ps particles. In the D-dimensional range, the ith particle Ai={ai1,…,aiD} is an inherent solution to the problem being investigated. ith particle velocity is Bi={bi1,…,biD} In the ith particle, the most desirable location of the tth level is shown as  Pbesti(t)={Pbesti1(t),…,PbestiD(t)}, whereas the most suitable position of the entire swarm is described as Gbest(t)={Gbest1(t),…,GbestiD(t)}. According to the (t+1)th step, the new state of the ith particle is determined as follows:

aij(t+1)=aij(t)+bij(t+1)bij(t+1)=ω×bij(t)+c1×rand1×[Pbestij(t)-aij(t)]+c2×rand2×, (1)

[Gbestij(t)-aij(t)], (2)

where aij(t) is the particle dimensional particle position; bij(t) is velocity with respect to dimension; w is a factor of inertia weight; c1 and c2 are acceleration coefficients; and rand1 and rand2 are uniformly dispersed arbitrary values in the domain [0, 1].

4.2 Cuckoo Search

4.2.1 Cuckoo Search Steps

A cuckoo search is a popular variant of a natural metaheuristic mechanism and an aggressive selection strategy for solving problems. There are three ideal rules. The last of these is the introduction of an innovative random decision algorithm. pa and n are the host nests to create new nests. The optimization problem to be resolved is defined as a goal function f(A),A={a1,…aD} on a D-dimensional interval. To refine the PSO-CS algorithm’s structural features, we determined CS and PSO variables. The essential function of CS is to search for a new group of Ai(t+1) nests. Current nests are accomplished by employing the Lévy flights that are given as follows:

xij(t+1)=xij(t)+∝⊕ Lévy(λ),(3)

where α is the step size, ⊕ denotes entry-wise multiplication operation, and λ is a parameter of the Lévy flight.

4.2.2 Lévy Flights

A Lévy flight is an arbitrary step length type that includes a Lévy circulation. It is embedded into the CS calculation to obtain a constant inquiry design without a Lévy size. It has been demonstrated that Lévy flights can boost the productivity of discovering assets in a dangerous condition, as shown in the following equation:

L(s,γ,μ)={γ2πexp[-γ2(s-μ)]1(s-μ)3/20<μ<s<00otherwise}(4)

If μ>0, the system step response is low. γ is a parameter scale.

In Mantegna’s calculation, the progression length s can be determined by

S=u|v|1β.(5)

u and v indicate normal distribution and are calculated respectively by the following equations:

where

σu={Γ(1+β)sin(πβ/2)Γ[(1+β)/2]β2(1+β)/2},1/β (6)

σv=1. (7)

Here, the Gamma function Γ(Z) is obtained as follows:

If z = n, the Gamma function is calculated using the following formula:

5  Cuckoo Search-Particle Swarm Optimization Algorithm

In PSO, ⊕ is said to be a work-related entry product but the random walking in Lévy crash is best tested in the research area. Since the distribution of the law of power is often tied to certain dimensionless quantities, a Lévy flight in combat models may show self-similarity and fractal performance. Typically, to develop the PSO, Lévy flight performance is assumed to replace the random search conventional PSO algorithm. Consequently, the modified PSO algorithm is characterized as CSPSO.

5.1 CS-PSO Algorithm

PSO lookup is influenced by the random variables rand1 and rand2 if we define the parameters c1 and c2 as standard values. A Lévy flight for random step length change was generated. The generated CS-PSO algorithm is as follows.

Step 1. Initialization of parameter priority values, for example, minimum and maximum weights (Wmin and Wmax, respectively), swarm population size (N), coefficients (C1 and C2), and acceleration.

Step 2. Mention of each particle’s lower and upper limits and velocities in various regions.

Step 3. Random initialization of the first generation in the defined space:

while t<Max Generation.

Step 4. Computation of every particle’s fitness function f(Ai)=fi. The best position Pbesti(t) and the best position of the entire swarm Gbest(t) are found (similarly to finding those in PSO).

Gbest(t)= min{Pbes1(t),Pbes2(t),…PbesN(t)}.(8)

Step 5. Gathering of A friction Pa of the most un-performing particles as a component of the fitness function. These must be dropped, and afterwards, the substitution of the haphazardly delivered particles is occupied with the predetermined investigation space (as with CS).

Step 6. Upgrading of the weight w of the inertia by utilizing the following formula:

w=Wmax-Wmax-WminT×t.(9)

Based on Eqs. (1) and (2), the velocity Bi and position Ai of each particle can be updated. In Eqs. (4)–(7), Lévy flight pattern parameters rand1 and rand2 vary and are different from those of the former PSO (hybrid of PSO and CS).

bij(t+1)=ω×bij(t)+(c1⊕Lévy(λ))×[Pbestij(t)-aij(t)]+(c2⊕Lévy(λ))×[Gbestij(t)-aij(t)],aij(t+1)=aij(t)+bij(t+1)(10)

Step 7. Increasing of iteration step (t=t+1). A stopping criterion is the final value of the fitness function, such as a different heuristic algorithm. If the termination standards are not met, go back to step 4. If they are met, proceed to the final step to solve the optimization problem.

Step 8. Enumeration of the optimization results. The proportion of the swarm population N depends on the size of the problem. Parameters depend on the hybrid algorithm problem, such as PSO algorithms and conventional CS. By utilizing the conventional PSO with a Monte Carlo method, a combination of fixed parameters is achieved; therefore, the proposed technique demonstrates better performance and provides an effective mechanism for selecting the parameters. Furthermore, Γ(z)=∫0∞tz-1e-tdt is performed by the Gamma function Γ=gamma(z) in MATLAB. The weight of the inertia changes from Wmin to Wmax. Pa inertia weight friction controls the use of an arbitrary significant distance investigation technique, mirroring the probability of whether the nest is deserted or refreshed. The higher the estimation accuracy of this parameter, the closer the search cycle is to the irregular inquiry.

5.2 Deep Recurrent Neural Network

A deep recurrent neural network (DRNN) is a type of artificial neural network in which connections between nodes form a directed graph along a temporal sequence with deep learning approaches. It includes a discontinuous s nerve system of a single monodirectional disguised surface, express valuable sort, how the latent elements, recognitions interface was genuinely optional. It is not a significant issue as long as we can show different kinds of associations. They included the sheet to fix the issues of the perceptron. The extra nonlinearity has the incorporate pick with the trickier degree of inner RNNs. Well, the models of progression have the other applied LSTM and it was essentially based on the underneath discussion. They use different surfaces instead of a single perceptron. The unaltered LSTM has the instrument to leave or further refine it. The autoregressive model work has the variable tropid. It has the many parts which portray a system of LSTM. Each head of LSTMs has the different stacks. Solution is a high versatile instrument, on account of the mix of a couple of essential surfaces.

5.2.1 Function of Dependencies

They have the small batch assumed by the step-up time Xt∈Rnxd (examples number: n, input number: d). The l (l=1, T) hidden layer from the hidden state was (concealed units’ number: h) the variable of yield layer (quantity of yields: q).

H t ( 1 ) = f 1 ( X t , H t−1 ( 1 ) (11)

H t ( 1 ) = f 1 ( H t ( l−1 ) , H t−1 ( 1 ) (12)

Finally, the yield surface is just found in the concealed condition of the shrouded surface. We utilize the yield work g to denote this:

Ot=g(Ht(L))(13)

Similar to the perceptron’s multilayer, the quantity of concealed surface and the unit of number was h shrouded as hyperparameters.

5.2.2 Recurrent Neural Network

The technique RNN [21–23] has the phony nerve framework which expands the common feedforward neural framework. Unlike a feedforward neural framework, an RNN can continue with the sequential commitments by having an irregular covered express whose inception at every movement is an endless supply of the past development. Hence, the framework can show a dynamic common lead. An RNN revives its irregular covered position ht as

mt={0,ift=0φ(mt-1,at),otherwise(14)

ϕ is a nonlinear capacity. In the customary, the intermittent shrouded state’s update rule in the RNN method is generally actualized as

mt=φ(Wxt+Umt-1).(15)

W and U are the coefficient lattices. Let p(a1, a2,…,aT) be the succession probability that can be decayed as

p(a1,a2,…,aT)=p(a1)…p(aT|a1,…aT-1).(16)

At that point, every contingent likelihood dissemination may be demonstrated by a repetitive system:

p(at|a1,…,at-1)=ϕ(mt).(17)

From Eqs. (11) and (12), we obtain ht. The motivation of this work was clear: a pixel of hyperspectral goes about data of progressive as opposed to vector component; along these lines, a discontinuous framework can be grasped to show the supernatural plan. As a huge aspect of the significant adjusting family, RNNs have started to exhibit promising results in numerous AI and PC vision research efforts. Regardless, this is seen as difficult to prepare the RNNs to oversee long take back to back data, as the points will all in all dissipate. One way of addressing this issue is to structure a more complex intermittent unit. An irregular layer with standard redundant disguised units is shown in Eq. (2), which basically determines a weighted direct all out of wellsprings of data and subsequently applies a nonlinear limit. The commencement of the LSTM units can be prepared as

mt=ot tanh(ct).(18)

tanh (⋅) is the hyperbolic tangent function. The yield entryway is refreshed as

ot=σ(Woixt+Wohmt-1+Wocct).(19)

σ (⋅) is a calculated sigmoid capacity, and W terms signify weight grids.

The conditions, figures both entryways are given by

it=σ(Wiixt+Wihmt-1+Wicct-1)ft=σ(Wfixt+Wfhmt-1+Wfcct-1).(20)

6  Results and Discussions

This section discusses the number of patients suffering from coronary diseases, basic patient details, and the impression a huge scope extent using proposed cuckoo search and particle swarm optimization (CSPSO). The total number of all outpatients was 200, of whom 97 (48%) were male and 103 (52%) were female. 10.4 was the extent of the adolescent’s first attack, from the period of 4 to 16. The conventional data of a solitary one was not added to the outline and left clear in light of the fact that the date of their first attack was not chosen. The information of 41 patients was not open, and as a result, they were unable to join into the pieces of information. The ordinariness of the essential assault subject to the dates in the first dataset appears. As necessities might be, for the most part, 66 patients in winter and 53 patients in spring are the fundamental attacks that occurred. In the fall, 37 patients had their first attack, and in summer, 44 patients had theirs. The normal age at when the patients guided a clinical community for enlistment was 15.1 years, with the age degree of 4–25. 14.3 days was of hospitalization break; nonetheless, the days were moved from 2 to 51. Of the 13.42% of patients on the dataset (27), 66.16% unexpectedly suffered from other various diseases.

The majority of the 104 patients were put into the “withdrew” class, which declared the progression of their use of medications. Of the total number of patients, 98.4% used benzathine penicillin; 77.60%, cerebral torment medicine, 65.66%, procaine penicillin; and 62.67%, cortisone. Furthermore, the speed utilization of different drugs, for instance, antagonism with analgesics, antifebrile, and hypersensitivity pills, was 52.22%. Highlights demonstrating the significant assault, movement, and speed of responsibility in mitral and aortic valves were utilized to examine the patient’s condition. Patients were classified as “recuperated” (46), “unaltered” (30), and “advanced” (21). The dataset of “straight out” was offered from the assessment of diagnostic features with the outcome information, unmitigated qualities, numerical are the dependent with a vast, most observable pace of recognizable proof of patients’ actual models of carditis, generally not quite the same as those underneath Korea. There were no records of a patient with erythema marginatum and subcutaneous nodules. Patients’ diligent adaptability of little standards, proof of expansion in raised aggravation markers, and deferred PR stretch is seen through and through.

The usage coordinates derived from the strategies can be found in Tabs. 1–3. As indicated by the outcomes derived from all the techniques, the strategy with the most significant exactness rate is the organization procedure (80% arrangement, 20% testing) utilizing the hold-strategy. The disarray of the best performing CSPSO calculation is in the given structure.

Considering the results shown in Fig. 2, the precision is pronounced as the model test set; where the model is arranged effectively, and in the light of the given result, the higher reach exactness is resolved. Here, the measure of records expected to be compelling is isolated from the models by the number of random grids. By consolidating the two computations, we improved the proposed precision. This is the most elevated reach model exactness in the numeric dataset as per the predetermined estimation. The advancement of CSPSO was coordinated to get a more exact improvement than that of the past method.

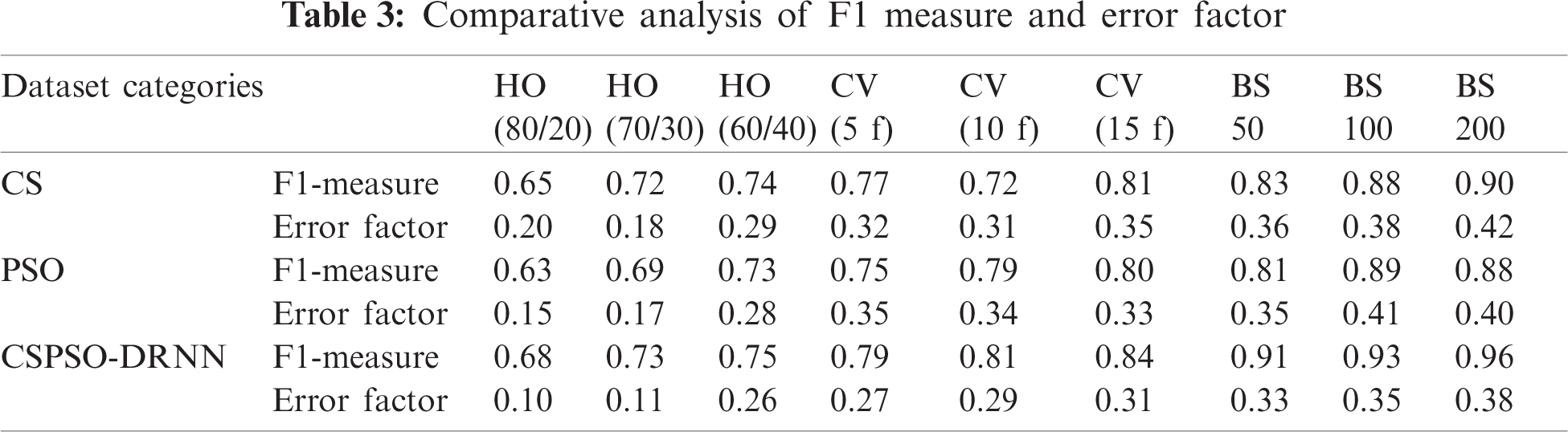
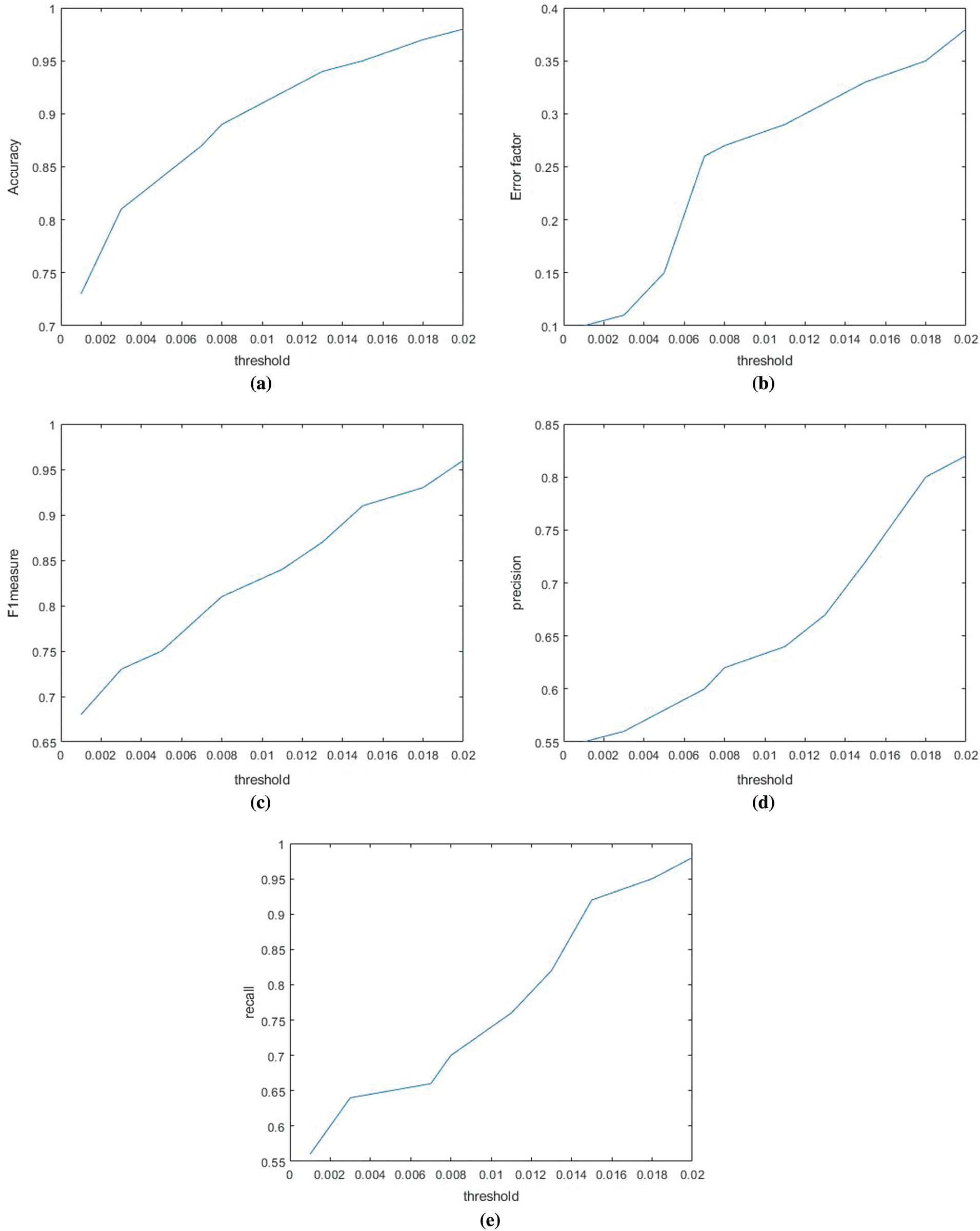
Figure 2: Analysis of (a) accuracy, (b) error factor, (c) F1 measure, (d) precision, (e) recall

6.1 Performance Evaluation Matrix

The accompanying measurements were determined for assessing the performance of the developed framework. Based on these measurements, one can choose which method is most appropriate for this work.

6.1.1 Accuracy

Accuracy refers to the precision of the model’s exhibition. Exactness is the measurement for assessing grouping types. Eq. (21) estimates solitary class exactness.

 Accuracy =TP+TNTP + TN + FP + FN (21)

6.1.2 Precision

Precision refers to the percentage of the number of true positives by which the model opposes the number of positives. The precision estimate for a class is given by the following:

 Precision =TPTP +FP.(22)

6.1.3 Recall

Recall indicates an actual fixed rate, which implies the number of incentive points in the model cases rather than the actual number of positive points in all information. A privacy recall is provided in the companion status:

Recall =TPTP+FN.(23)

6.1.4 F1 Measure

Eq. (24) gives the outcome of F1 could check a pattern similar to the F1 result. It is a powerful measure of model accuracy and revision. The idea of creating a uniform class.

F1measure=2*TP2*TP + FP + FN.(24)

7  Conclusion

The proposed work leverages the CSPSO hybrid algorithm for decision systems through the deep recurrent neural network (DRNN). The DRNN was utilized for aortic and mitral change models which did not meet quality requirements. Subsequent to testing, we proposed the use of CSPSO-DRNN to make the structure more accurate in predicting coronary disease. Compared to conventional PSO and CS techniques, our method demonstrated higher accuracy, precision, recall and F1 measure in effective heart disease prediction (EHDP) based on the proposed CSPSO-DRNN system. In future work the proposed technology will be considered for further enhancing the performance and efficiency on EHDP, will also involve testing the algorithm based on real-time data received from sensors.

Acknowledgement: The authors sincerely thank the University of Bisha, Bisha, Kingdom of Saudi Arabia, for the facilities and support provided during the research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. K. Sahani, M. I. Shah, R. Radhakrishnan, J. Joseph and M. Sivaprakasam, “An imageless ultrasound device to measure local and regional arterial stiffness,” IEEE Transactions on Biomedical Circuits and Systems, vol. 10, no. 1, pp. 200–208, 2016. [Google Scholar]

 2.  H. T. Wu, C. H. Lee, A. B. Liu, W. S. Chung, C. J. Tang et al., “Arterial stiffness using radial arterial waveforms measured at the wrist as an indicator of diabetic control in the elderly,” IEEE Transactions on Bio-Medical Engineering, vol. 58, no. 2, pp. 243–252, 2011. [Google Scholar]

 3.  C. J. Su, T. Y. Huang and C. H. Luo, “Arterial pulse analysis of multiple dimension pulse mapping by local cold stimulation for arterial stiffness,” IEEE Sensors Journal, vol. 16, no. 23, pp. 8288–8294, 2016. [Google Scholar]

 4.  D. G. Jang, U. Farooq, S. H. Park, C. W. Goh and M. Hahn, “A knowledge-based approach to arterial stiffness estimation using the digital volume pulse,” IEEE Transactions on Biomedical Circuits and Systems, vol. 6, no. 4, pp. 366–374, 2012. [Google Scholar]

 5.  F. Miao, X. Wang, L. Yin and Y. Li, “A wearable sensor for arterial stiffness monitoring based on machine learning algorithms,” IEEE Sensors Journal, vol. 19, no. 4, pp. 1426–1434, 2018. [Google Scholar]

 6.  K. Uyar and A. Ilhan, “Diagnosis of heart disease using genetic algorithm based trained recurrent fuzzy neural networks,” Procedia Computer Science, vol. 120, no. 3, pp. 588–593, 2017. [Google Scholar]

 7.  Z. Arabasadi, R. Alizadehsani, M. Roshanzamir, H. Moosaei and A. A. Yarifard, “Computer aided decision making for heart disease detection using hybrid neural network-genetic algorithm,” Computer Methods and Programs in Biomedicine, vol. 141, pp. 19–26, 2017. [Google Scholar]

 8.  M. A. Khan, “An IoT framework for heart disease prediction based on MDCNN classifier,” IEEE Access, vol. 8, pp. 34717–34727, 2020. [Google Scholar]

 9.  A. K. Gupta, C. Chakraborty and B. Gupta, “Monitoring of epileptical patients using cloud-enabled health-IoT system,” Traitement du Signal, vol. 36, no. 5, pp. 425–431, 2019. [Google Scholar]

10. M. A. Khan and F. Algarni, “A healthcare monitoring system for the diagnosis of heart disease in the IoMT cloud environment using MSSO-ANFIS,” IEEE Access, vol. 8, pp. 122259–122269, 2020. [Google Scholar]

11. I. E. Emre, N. Erol, Y. I. Ayhan, Y. Özkan and Ç. Erol, “The analysis of the effects of acute rheumatic fever in childhood on cardiac disease with data mining,” International Journal of Medical Informatics, vol. 123, no. 1, pp. 68–75, 2019. [Google Scholar]

12. S. R. Alty, S. C. Millasseaut, P. J. Chowienczykt and A. Jakobssont, “Cardiovascular disease prediction using support vector machines,” Midwest Symposium on Circuits and Systems, vol. 1, pp. 376–379, 2004. [Google Scholar]

13. C. Ordonez, “Association rule discovery with the train and test approach for heart disease prediction,” IEEE Transactions on Information Technology in Biomedicine, vol. 10, no. 2, pp. 334–343, 2006. [Google Scholar]

14. K. Pilt, K. Meigas, M. Viigimaa, K. Temitski, J. Kaik et al., “An experimental measurement complex for probable estimation of arterial stiffness,” in Annual Int. Conf. of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, pp. 194–197, 2010. [Google Scholar]

15. C. A. Dhote, A. D. Thakare and S. M. Chaudhari, “Data clustering using particle swarm optimization and bee algorithm,” in Fourth Int. Conf. on Computing, Communications and Networking Technologies, Tiruchengode, Tamil Nadu, India, pp. 1–5, 2013. [Google Scholar]

16. S. Shaikh, A. Sawant, S. Paradkar and K. Patil, “Electronic recording system-heart disease prediction system,” in Int. Conf. on Technologies for Sustainable Development, Mumbai, Maharashtra, India, pp. 1–5, 2015. [Google Scholar]

17. M. A. Jabbar and S. Samreen, “Heart disease prediction system based on hidden naïve bayes classifier,” in Int. Conf. on Circuits, Controls, Communications and Computing, Bangalore, Karnataka, India, pp. 1–5, 2016. [Google Scholar]

18. K. M. Anderson, P. M. Odell, P. W. Wilson and W. B. Kannel, “Cardiovascular disease risk profiles,” American Heart Journal, vol. 121, no. 1 Pt 2, pp. 293–298, 1991. [Google Scholar]

19. T. R. Gadekallu and N. Khare, “Cuckoo search optimized reduction and fuzzy logic classifier for heart disease and diabetes prediction,” International Journal of Fuzzy System Applications, vol. 6, no. 2, pp. 25–42, 2017. [Google Scholar]

20. R. K. Solanki, K. Verma and R. Kumar, “Spam filtering using hybrid local-global Naive Bayes classifier,” in Int. Conf. on Advances in Computing, Communications and Informatics, Kochi, India, IEEE, pp. 829–833, 2015. [Google Scholar]

21. P. Sutheebanjard and W. Premchaiswadi, “Fast convert OR-decision table to decision tree,” in Eighth Int. Conf. on ICT and Knowledge Engineering, Bangkok, Thailand, IEEE, pp. 37–40, 2010. [Google Scholar]

22. X. Ma, J. Guo, K. Xiao and X. Sun, “PRBP: Prediction of RNA-binding proteins using a random forest algorithm combined with an RNA-binding residue predictor,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 12, no. 6, pp. 1385–1393, 2015. [Google Scholar]

23. M. A. Khan, M. T. Quasim, N. S. Alghamdi and M. Y. Khan, “A secure framework for authentication and encryption using improved ECC for IoT-based medical sensor data,” IEEE Access, vol. 8, pp. 52018–52027, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.