DOI:10.32604/cmc.2021.016002

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016002 |  |
| Article |
Addressing Economic Dispatch Problem with Multiple Fuels Using Oscillatory Particle Swarm Optimization
1KIIT University, Bhubaneswar, Odisha, India
2Department of Electrical Engineering, CET, Bhubaneswar, Odisha, India
3Department of Computer Science, Government Bikram College of Commerce, Patiala, India
4Department of Computer Science & Engineering, Pandit Deendayal Petroleum University, Gandhinagar, India
5Raytheon Chair for Systems Engineering, Advanced Manufacturing Institute, King Saud University, Riyadh, 11421, Saudi Arabia
6Industrial Engineering Department, College of Engineering, King Saud University, Riyadh, 11421, Saudi Arabia
*Corresponding Author: Mustufa Haider Abidi. Email: mabidi@ksu.edu.sa
Received: 17 December 2020; Accepted: 20 February 2021
Abstract: Economic dispatch has a significant effect on optimal economical operation in the power systems in industrial revolution 4.0 in terms of considerable savings in revenue. Various non-linearity are added to make the fossil fuel-based power systems more practical. In order to achieve an accurate economical schedule, valve point loading effect, ramp rate constraints, and prohibited operating zones are being considered for realistic scenarios. In this paper, an improved, and modified version of conventional particle swarm optimization (PSO), called Oscillatory PSO (OPSO), is devised to provide a cheaper schedule with optimum cost. The conventional PSO is improved by deriving a mechanism enabling the particle towards the trajectories of oscillatory motion to acquire the entire search space. A set of differential equations is implemented to expose the condition for trajectory motion in oscillation. Using adaptive inertia weights, this OPSO method provides an optimized cost of generation as compared to the conventional particle swarm optimization and other new meta-heuristic approaches.
Keywords: Economic load dispatch; valve point loading; industry 4.0; prohibited operating zones; ramp rate limit; oscillatory particle swarm optimization
Management of energy would-be highly effective and efficient by optimizing the generating cost of fossil fuel-based systems. Economic operation of the power system with effective and reliable generation is highly essential for Industry 4.0, as the electricity market is moving towards the deregulated market. The generation cost of thermal power plants mostly relies on fuel cost. Economic load dispatch is a process of economic scheduling of generating power from each generator to meet the demand and attain the optimum fuel cost by considering various constraints [1]. Economic Dispatch is an optimization problem-solving method where the entire requisite generation is being dispersed amongst the operated generating units, by reducing the consumed fuel cost, considering equality, inequality and operational constraints. ELD governs the output power of every generating division for the specific system under a specified load condition by minimizing the fuel cost to meet the load demand. ELD processes such a real-time management of energy in the current power system to control, assign, and distribute the total generation among the accessible units [2]. Generating units used different types of fuel for power generation. During the practical operation, the spinning reserve constraints make a significant impact on financial planning. Considering all the constraints, the economic dispatch problem behaves as a non-convex, complex, and non-smooth optimization problem.
In recent years, the generator processed for the generation of electricity is non-linear as compared to the customary generator. The non-linearity are by the concern of valve point loading, prohibited operating zones, and ramp rate limit. The practical economic dispatch (ED) also satisfies the problems due to non-linearity, non-convexity, and non-smooth operation of the generator. Previously for solving ELD problem, some classical and conventional methods such as lambda iteration [3], quadratic programming [4], gradient programming [5], and non-linear programming [6] others were applied. These classical methods face many challenges during the problem solving of ELD with non-linearity. To overcome the challenges, many meta-heuristic approaches, swarm evolutionary methods, and evolutionary computing methods were applied to the problem. These methods are Particle swarm optimization [7], Genetic Algorithm [8], Differential Evolution [9], Exchange Market Algorithm [10], Social Spider Algorithm [11], Biogeography based optimization [12], Tabu Search Method [13], Particle Diffusion [14], Artificial Bee Colony [15], Grey wolf optimization [16,17] and Spotted Hyena Optimization [18]. Some of the original methods get stock in the local optima and take more time for the searching process; therefore, to improve the quality of the solution, many hybrid techniques were proposed to overcome the difficulties. Recently some hybridized and modified version of existing techniques are applied to ELD problem such as Differential evolution-biogeography based optimization (DE-BBO) [19], Differential Evolution and harmony search (DHS) [20], Hybridization of Genetic Algorithm with Differential evolution (HDEGA) [21], Combination of Simulated Annealing and PSO (SAPSO) [22], Particle Swarm Optimization and Sequential Programming technique (PSO-SQP) [23], Hybrid Chemical Reaction optimization and Differential Evolution Algorithm (CRO-DE) [24], Multi-objective Spotted Hyena Optimizer and Emperor Penguin Optimizer (MOSHEPO) [25], Hybrid Firefly and Genetic algorithm [26], Adaptive real coded genetic algorithm (ARCGA) [27], Improved harmony search (IHS) [28], Modified differential evolution (MDE) [29], Species-based Quantum Particle Swarm Optimization (SQPSO) [30], Modified particle swarm optimization [31], Improved Differential Evolution [32], Modified Artificial Bee Colony algorithm [33], Modified Bacterial Foraging Algorithm (MBFA) [34], Improved Harmony Search with Wavelet Mutation (IHSWM) [35], DHIMAN Algorithm [36] . In addition, authors in [37] propose a Clustering-based Travel Planning System while a network route optimizations scheme is proposed in [38]. According to No Free Lunch theorem (NFL) [39], no optimization technique will be able to claim as the superior optimized solution for the concerned problem. The existence for improvement of cost for economic dispatch problem encourages to further improving the quality of solution regarding optimum cost and convergence property. Each applied technique to get the solution of the economic dispatch problem is having some advantages and disadvantages.
In this paper, an improved version of conventional Particle Swarm Optimization (PSO) is applied to overwhelm certain difficulties. Oscillatory PSO instincts the particle to acquire the total search space for finding optimum cost in ELD problem by balancing exploration and exploitation perfectly. An actual setting of parameter attains the optimum cost. The selections of cognitive and social learning factors are taken by confirming that the divergence does not occur before the optimum cost.
The formulated problem of ELD is the economic scheduling of electric power among the committed generating units to satisfy the load demand and satisfying various constraints. The major objective is to optimize the cost of fuel by generator scheduling [15].
2.1 Objectives for Economic Load Dispatch Problem
The characteristics of every generator are unique with respect to cost. The steam valve controls the operation of the turbine for the generation of power and is known as the valve point loading effect. This practical approach due to valve point loading characteristics curve of the generator becomes non-convex curve. The cost curve behaves as a piecewise linear increasing quadratic function as shown in Fig. 1. The fuel cost function is dependent on the real power generation from each unit and is shown in Eq. (1) [15].

Figure 1: Cost characteristics of fossil fuel-based generator
Here FCC is the fuel cost of all committed generator. F(Pgenc) is the cost function of the generator. Agenc, Bgenc and Cgencare the cost co-efficients and, Egenc and Fgenc are the co-efficients due to the valve point loading effect. Pgenc is the scheduled output power. The cost function for multiple fuel options is represented in Eq. (2) [40].
Agencj, Bgencj, Cgencj, Egencj and Fgencj are the cost co-efficients for genc number of generating units and ‘j’ type of fuel.
The economic scheduling of the generator should have to satisfy the practical operational constraints.
2.2.1 Power Balance Constraint
This is an equality constraint. In a given period, the total scheduled output power of committed generators should satisfy the load estimated following electricity demand and the transmission line losses in the power system [16].
Here Pgenc total scheduled power generation. Pde is forecasted load demand by the consumer. PLoss is Transmission line loss. PLoss is expressed in terms of B co-efficient by using Eq. (4) [16].
2.2.2 Generating Capacity Constraint
Real power generates at the output of the generator should be within a prescribed limit higher and basic limit as shown in Eq. (5) [16].
Pgencmain and Pgencmax are the minimum and higher bound for the generation of power.
2.2.3 Generator Ramp Rate Limit
The operational performance for generating units is reserved by ramp rate limits. These limits influencefunctional decisions. The present scheduling may interrupt the upcoming scheduling as a generation grows due to ramp rate bounds [19].
2.2.4 Prohibited Operating Zones
The generator performance is having some discontinuous portions due to some unsought and uncontrollable physical restrictions such asmechanical lossesorfailures. The generator discontinuities are shown in Fig. 2 and Eq. (7) [19].

Figure 2: Generator characteristics with existing prohibited zones
The approached method is a swarm intelligence method based upon the process of collection of food by bird and fish. PSO works in the mechanism of birds to search for food randomly in a specified region. The key approach is to detect food with a reduced time [41]. This approach is based on the procedure to get the food and to observe the bird nearer to the food. The orthodox PSO learned from the condition and handled it to resolve the course to achieve an optimum value. Each bird is an alone solution in the total search space is known as a particle. All the particles are assessed by their corresponding fitness function, which is to be optimized. All the particles in the search space are having their velocities to search for the direction of food.
The initialization of PSO was done by using an arbitrary particle, which is the solution to find the optimal position by the process of updating during generations. During each reiteration course, the entire solutions particles are updated with two optimum values: (1) The finest value among the whole particles obtained by searching the food known as global best and, (2) the finest value monitored by the swarm itself during exploration in repetition process known as personal best. During the process of searching food, the velocity of the bird is to be maintained, by using the following formula by Eq. (8) [42].
In the above equation, Vk(i + 1) and Vk(i) is the velocity component and
Vmax and Vmin are the velocity indicesfor upper and lower boundaries of the particle to move in the search space to locate the food. If Vmax is extremely high, the particles have a chance to past better solutions. If Vmin is much small, then particles have a chance not to discover further than local optima. Ce1 and Ce2 are two constants to attract each solution towards the best among individual and whole particle locations.
The weight of inertia (w) follows the equation,
where we, wemax, wemin are the weight of inertia and (iter) is the iteration number.
4 Oscillatory Particle Swarm Optimizer
In this algorithm, the update equation of the conventional PSO isspecified as a differential equation of second order. The characteristics of convergence are resultant of social and cognitive learning rates. The particle transitional activities dependency on the inertia weight is discovered. Further, the induced oscillation feature and adaption of weight are derived.
4.1 Updating PSO as a Differential Equation of Second Order
In the conventional PSO, the velocity and position as per the above Eqs. (8) and (9) is processed. By reducing the iteration count, i + 1 to i the velocity particle is like
The updated position is represented in the expansion form as in Eq. (12):
Rearranging the above Eq. (13) can be rewritten as:
Here the coefficients are
4.2 Factors of Cognitive and Social Learning
From Eq. (14), the coefficients Po1 and Po2 determine the particle behavior. Assume the best position of a particle and global as Pebestk and gebestk respectively remain constant, and both are equal for two successive iterations as shown in Eq. (15). One particle is having the personal best as the global best and the Eq. (15) can be rewritten as Eq. (16) as,
Letting
Here the right-hand side shows the weighted sum of particle best and global best. Consider the complementary equation.
In the last iteration, the best particle value (
When the cognitive and social learning factor is
For oscillating condition, considering the characteristics Eq. (21) with roots are shown in Eqs. (22) and (23) respectively.
Applying De Moivre's formula for the condition
Another phase angle φ is presented in Eq. (25).
The homogeneous equation solution will be shown in Eq. (26).
where
From Eq. (26), Pk(i) will converge for r < 1 and ‘r’ will be
The oscillatory behavior of particle is governed by the amplitude an phase angle. The frequency of oscillation is determined by angles of the complex roots of the characteristics equation. And by substituting Po1 = −we and Po2 = we, the angle of the root is given byte Eq. (28).
Determination of inertia weight can be done by applying normal distribution to the random inertia weights according to Eq. (29).
In this method the inertia weight is calculated by using the Eq. (30).
The detail pseudo of the applied algorithm for economic load dispatch is given in Algorithm~1.

The proposed technique is applied to optimize the overall cost of four different test systems within the framework of different linear and non-linear technical constraints and multiple fuel systems. The four test systems considered in this study are: (1) A 6-unit system considering the transmission losses, (2) A 15-unit system considering the transmission losses (3) A large power system with 40 generating units considering valve-point loading and, (4) A ten-unit test system for different types of fuel. The simulation is performed on the MATLAB (version R2016b) platform. A total of 100 runs have been executed for generating an optimum solution to the discussed dispatch problem.
Case 1: Six generating Units test system
This case consists of six generating units to fulfill the load demand of 1263 MW. As transmission losses make a huge impact on the power system, transmission losses, prohibited operating zones, ramp rate limits, and valve point loading effect are considered. The system input data for all the constraints, cost co-efficient, and loss co-efficient are considered from [7]. The scheduled generation among all the six generating units within the capacity constraint with the optimum cost is presented in Tab. 1. The comparison of cost and scheduled generation with other techniques is also presented in Tab. 1. Fig. 4 shows the comparison graph of optimum cost with other techniques to validate the superiority of the applied technique. The optimum cost for this test system is found as 15,440.0982 $/h with a lesser transmission loss of 12.178 MW. The convergence graph is shown in Fig. 3. Prohibited operating zones, valve point loading, and ramp rate constraints are also considered for the complex problem. All the input data and co-efficient are referred to from [7] for this test system.


Figure 3: Convergence characteristics for case 1 with 1263 MW load demand

Figure 4: Comparison graph for six generating units with other applied techniques

Case 2: Fifteen generating units test system with transmission losses
Fifteen generating units are used for the generation of demand of 2630 with consideration of transmission losses, in the test generation for optimum cost from the applied technique with comparison to other techniques. Tab. 2 shows the evidence of the superiority of the applied technique for optimum cost with lesser variation during the iteration process as compared to MPSO-GA [50], NRTO [53], MsBBO [55], DEPSO [57], λ-Con [58], ICS [51] techniques. Fig. 5 represents the optimum cost comparison of the applied technique to the other techniques and Fig. 6 represents the convergence characteristics of the applied technique with the conventional PSO. Tab. 3 compares scheduled generation and optimum cost for case 2 with losses.

Figure 5: Comparison graph for fifteen generating units with other techniques
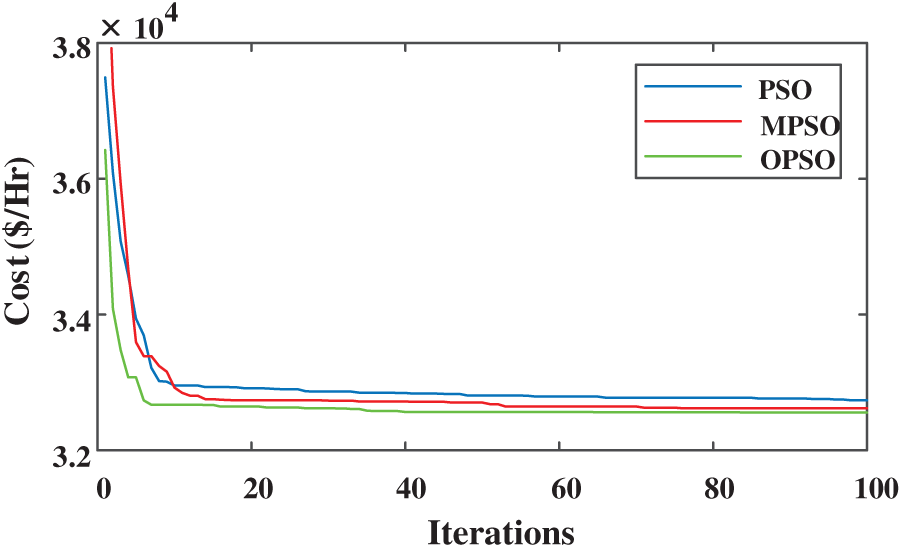
Figure 6: Convergence characteristics of case 2 for fifteen generating units

Case 3: Test system 3 for forty generating units
This test system is considered for a large power system consisting of 40 generators. In this case, the effect of valve-point loading is considered as the non-linear constraint. The input data is referred from [61] for the co-efficient and various load demands. The scheduled generation among 40 units to meet the total demand of 10500 MW is illustrated in Tab. 4. Tab. 5 shows a comparison with other recent techniques for minimum cost. The deviation of the costs among different optimization techniques along with the proposed technique is presented in Tab. 5. The convergence graphs and cost comparison are shown in Figs.7 and 8 respectively. It is analyzed from this case study that the applied OPSO algorithm provides better performance for minimizing the cost of the power supply, losses, and the convergence time as compared to the existing optimization techniques under the considered operating condition.



Figure 7: Convergence characteristics for test system 3 with 40 generators
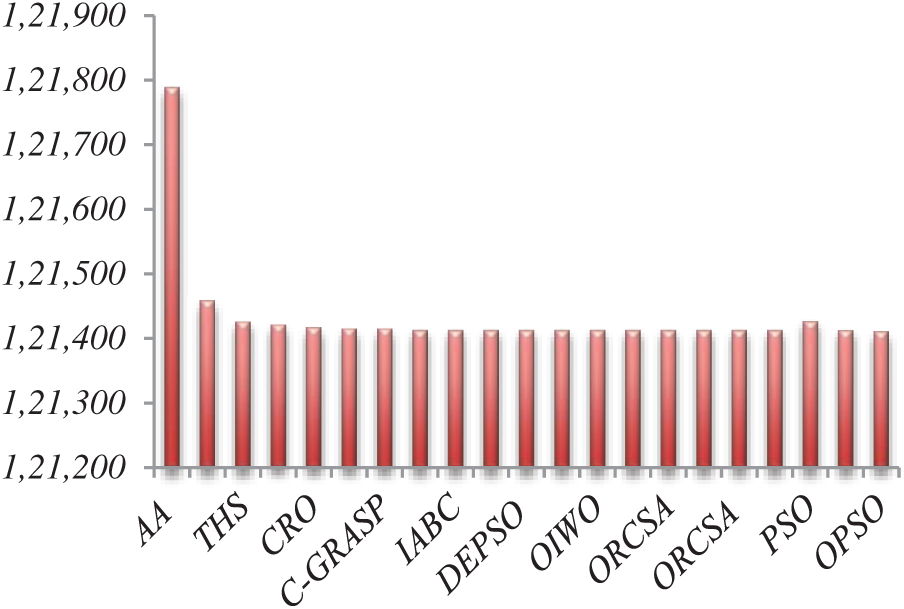
Figure 8: Comparison graph for forty generating units with other techniques

Case 4: Test system 4 for ten generating units with multiple fuels as input
In this case, the performance is evaluated on a system with 10 generating units with multiple fuel options and valve point loading effects. The input data have been referred to from [71]. From the input data, it has been observed that the first generator is having options of two types of fuel and the other generating units have an option of three types of fuel. The total load demand is 2700 MW with no transmission losses. The optimum cost produced during the experiment is 623.542 $/h for OPSO. The comparison of cost with different techniques is represented in Tab. 7 and, it is found that the OPSO is optimizing the system cost for multiple fuel systems. Fig. 9 shows the convergence graph of OPSO and PSO with a faster convergence rate. The scheduled output with different fuels is depicted in Tab. 6.

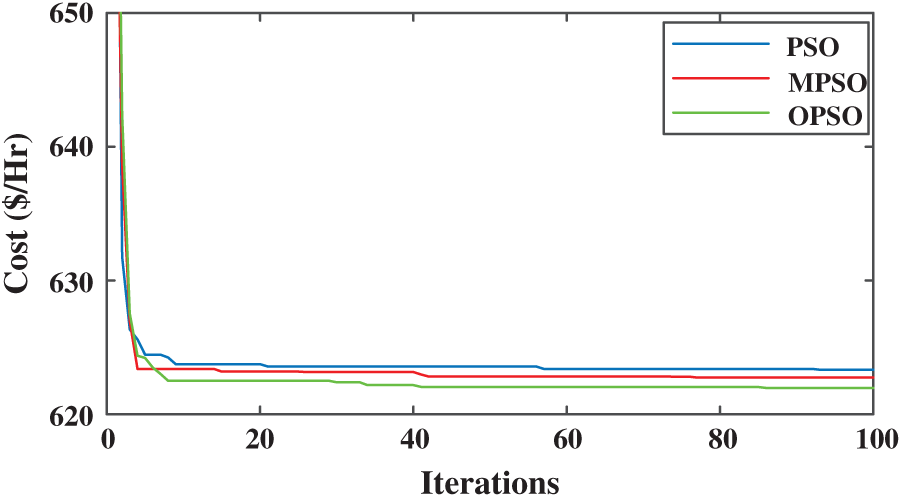
Figure 9: Comparison graph for ten generating units for case 4
Recent works presented in [75–78] depict interesting optimization works in different domains.
The increasing complexity of today’s electrical networks in Industry 4.0 further adds to the severity of the issue which can be mitigated through robust economic load dispatch strategies. Application of Oscillatory Particle Swarm Optimization algorithm-a meta-heuristic algorithm, to solve complex ELD problems is presented in this paper. The performance of OPSO is evaluated for four different test systems with increasing complications considering various practical technical constraints such as valve-point loading effect, prohibited operating zones, ramp rates, and multiple fuel system. The effectiveness of different techniques for optimizing the cost and their convergence profiles and times have been studied for all these cases. A comparison is performed between the proposed and existing techniques based on the above-discussed problem. It is concluded from the work that the proposed OPSO algorithm provides better performance for minimizing the cost of the power supply, losses, and the convergence time as compared to the existing optimization techniques.
The applied technique can be further applied to an enhanced version of economic dispatch problems such as economic emission dispatch problem, dynamic dispatch problem, and economic dispatch incorporating renewable energy system.
Acknowledgement: The authors are grateful to the Raytheon Chair for Systems Engineering for funding. The authors are also grateful to the management of authors’ institutions.
Funding Statement: The authors are grateful to the Raytheon Chair for Systems Engineering for funding.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. J. Wood, B. F. Wollenberg and G. B. Sheblé, Power Generation, Operation, and Control. NJ, USA: John Wiley & Sons, 2013. [Google Scholar]
2. J. S. Dhillon and D. P. Kothari, Power System Optimization. New Delhi, India: Preintce Hall of India Private Limited, 2010. [Google Scholar]
3. B. H. Chowdhury and S. Rahman, “A review of recent advances in economic dispatch,” IEEE Transactions on Power Systems, vol. 5, no. 4, pp. 1248–1259, 1990. [Google Scholar]
4. G. F. Reid and L. Hasdorff, “Economic dispatch using quadratic programming,” IEEE Transactions on Power Apparatus and Systems, vol. 6, pp. 2015–2023, 1973. [Google Scholar]
5. G. B. Sheble, “Real-time economic dispatch and reserve allocate,ion using merit order loading and linear programming rules,” IEEE Transactions on Power Systems, vol. 4, no. 4, pp. 1414–1420, 1989. [Google Scholar]
6. D. Streiffert, “Multi-area economic dispatch with tie line constraints,” IEEE Transactions on Power Systems, vol. 10, no. 4, pp. 1946–1951, 1995. [Google Scholar]
7. Z. Gaing, “Particle swarm optimization to solving the economic dispatch considering the generator constraints,” IEEE Transactions on Power Systems, vol. 18, no. 3, pp. 1187–1195, 2003. [Google Scholar]
8. D. C. Walters and G. B. Sheble, “Genetic algorithm solution of economic dispatch with valve point loading,” IEEE Transactions on Power Systems, vol. 8, no. 3, pp. 1325–1332, 1993. [Google Scholar]
9. N. Noman and H. Iba, “Differential evolution for economic load dispatch problems,” Electric Power Systems Research, vol. 78, no. 8, pp. 1322–1331, 2008. [Google Scholar]
10. N. Ghorbani and E. Babaei, “Exchange market algorithm for economic load dispatch,” International Journal of Electrical Power & Energy Systems, vol. 75, pp. 19–27, 2016. [Google Scholar]
11. J. Q. James and V. Li, “A social spider algorithm for solving the non-convex economic load dispatch problem,” Neurocomputing, vol. 171, no. 2, pp. 955–965, 2016. [Google Scholar]
12. A. Bhattacharya and P. Chattopadhyay, “Biogeography-based optimization for different economic load dispatch problems,” IEEE Transactions on Power Systems, vol. 25, no. 2, pp. 1064–1077, 2009. [Google Scholar]
13. W. Lin, F. Cheng and M. Tsay, “An improved tabu search for economic dispatch with multiple minima,” IEEE Transactions on Power Systems, vol. 17, no. 1, pp. 108–112, 2002. [Google Scholar]
14. L. Han, C. E. Romero and Z. Yao, “Economic dispatch optimization algorithm based on particle diffusion,” Energy Conversion and Management, vol. 105, no. 6, pp. 1251–1260, 2015. [Google Scholar]
15. S. Hemamalini and S. P. Simon, “Artificial bee colony algorithm for economic load dispatch problem with non-smooth cost functions,” Electric Power Components and Systems, vol. 38, no. 7, pp. 786–803, 2010. [Google Scholar]
16. M. Pradhan, P. Roy and T. Pal, “Grey wolf optimization applied to economic load dispatch problems,” International Journal of Electrical Power & Energy Systems, vol. 83, pp. 325–334, 2016. [Google Scholar]
17. V. Kamboj, S. K. Bath and J. S. Dhillon, “Solution of non-convex economic load dispatch problem using grey wolf optimizer,” Neural Computing and Applications, vol. 27, no. 5, pp. 1301–1316, 2016. [Google Scholar]
18. G. Dhiman, S. Guo and S. Kaur, “ED-SHO: A framework for solving nonlinear economic load power dispatch problem using spotted hyena optimizer,” Modern Physics Letters A, vol. 33, no. 40, pp. 850239, 2018. [Google Scholar]
19. A. Bhattacharya and P. Chattopadhyay, “Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch,” IEEE Transactions on Power Systems, vol. 25, no. 4, pp. 1955–1964, 2010. [Google Scholar]
20. L. Wang and L. Li, “An effective differential harmony search algorithm for the solving non-convex economic load dispatch problems,” International Journal of Electrical Power & Energy Systems, vol. 44, no. 1, pp. 832–843, 2013. [Google Scholar]
21. A. Trivedi, D. Srinivasan, S. Biswas and T. Reindl, “Hybridizing genetic algorithm with differential evolution for solving the unit commitment scheduling problem,” Swarm and Evolutionary Computation, vol. 23, pp. 50–64, 2015. [Google Scholar]
22. V. Karthikeyan, S. Senthilkumar and V. J. Vijayalakshmi, “A new approach to the solution of economic dispatch using particle swarm optimization with simulated annealing,” arXiv preprint arXiv: 1307.3014, 2013. [Google Scholar]
23. T. Victoire and A. E. Jeyakumar, “Hybrid PSO-SQP for economic dispatch with valve-point effect,” Electric Power Systems Research, vol. 71, no. 1, pp. 51–59, 2004. [Google Scholar]
24. P. Roy, S. Bhui and C. Paul, “Solution of economic load dispatch using hybrid chemical reaction optimization approach,” Applied Soft Computing, vol. 24, pp. 109–125, 2014. [Google Scholar]
25. G. Dhiman, “MOSHEPO: A hybrid multi-objective approach to solve economic load dispatch and micro grid problems,” Applied Intelligence, vol. 50, no. 1, pp. 119–137, 2020. [Google Scholar]
26. M. P. Varghese and A. Amudha, “Enhancing the efficiency of wind power using hybrid fire fly and genetic algorithm-economic load dispatch model,” Current Signal Transduction Therapy, vol. 13, no. 1, pp. 3–10, 2018. [Google Scholar]
27. P. Subbaraj, R. Rengaraj and S. Salivahanan, “Enhancement of self-adaptive real-coded genetic algorithm using Taguchi method for economic dispatch problem,” Applied Soft Computing, vol. 11, no. 1, pp. 83–92, 2011. [Google Scholar]
28. S. C. Dos, Leandro and V. C. Mariani, “An improved harmony search algorithm for power economic load dispatch,” Energy Conversion and Management, vol. 50, no. 10, pp. 2522–2526, 2009. [Google Scholar]
29. S. Sayah and K. Zehar, “Modified differential evolution algorithm for optimal power flow with non-smooth cost functions,” Energy Conversion and Management, vol. 49, no. 11, pp. 3036–3042, 2008. [Google Scholar]
30. V. Hosseinnezhad, M. Rafiee, M. Ahmadian and M. T. Ameli, “Species-based quantum particle swarm optimization for economic load dispatch,” International Journal of Electrical Power & Energy Systems, vol. 63, pp. 311–322, 2014. [Google Scholar]
31. S. S. Subramani and P. R. Rajeswari, “A modified particle swarm optimization for economic dispatch problems with non-smooth cost functions,” International Journal of Soft Computing, vol. 3, no. 4, pp. 326–332, 2008. [Google Scholar]
32. H. Liu, J. Qu and Y. Li, “The economic dispatch of wind integrated power system based on an improved differential evolution algorithm,” Recent Advances in Electrical & Electronic Engineering, vol. 13, no. 3, pp. 384–395, 2020. [Google Scholar]
33. D. C. Secui, “A new modified artificial bee colony algorithm for the economic dispatch problem,” Energy Conversion and Management, vol. 89, no. 1, pp. 43–62, 2015. [Google Scholar]
34. I. A. Farhat and M. E. El-Hawary, “Modified bacterial foraging algorithm for optimum economic dispatch,” in Proc. 2009 IEEE Electrical Power & Energy Conf., Montreal, QC, Canada, IEEE, pp. 1–6, 2009. [Google Scholar]
35. V. R. Pandi, B. K. Panigrahi, A. Mohapatra and M. Mallick, “Economic load dispatch solution by improved harmony search with wavelet mutation,” International Journal of Computational Science and Engineering, vol. 6, no. 1–2, pp. 122–131, 2011. [Google Scholar]
36. G. Dhiman, P. Singh, H. Kaur and R. Maini, “DHIMAN: A novel algorithm for economic dispatch problem based on optimization met Hodus Ing Monte Carlo simulation and astrophysics concepts,” Modern Physics Letters A, vol. 34, no. 4, pp. 1950032, 2019. [Google Scholar]
37. L. Ravi, V. Subramaniyaswamy, V. Vijayakumar, R. H. Jhaveri and J. Shah, “Hybrid user clustering-based travel planning system for personalized point-of-interest recommendation,” in Proc. Int. Conf. on Mathematical Modeling, Computational Intelligence Techniques and Renewable Energy, Ahmedabad, India, 2020. [Google Scholar]
38. R. H. Jhaveri, R. Tan and S. V. Ramani, “Real-time QoS routing scheme in SDN-based robotic cyber-physical systems,” in Proc. 5th Int. Conf. on Mechatronics System and Robots, Singapore, pp. 18–23, 2019. [Google Scholar]
39. S. Kaboli and A. Alqallaf, “Solving non-convex economic load dispatch problem via artificial cooperative search algorithm,” Expert Systems with Applications, vol. 128, pp. 14–27, 2019. [Google Scholar]
40. D. N. Vo and W. Ongsakul, “Economic dispatch with multiple fuel types by enhanced augmented Lagrange Hopfield network,” Applied Energy, vol. 91, no. 1, pp. 281–289, 2012. [Google Scholar]
41. J. Kennedy and R. Eberhart, “PSO optimization,” in Proc. IEEE Int. Conf. Neural Networks, Piscataway, NJ, IEEE Service Center, vol. 4, pp. 1941–1948, 1995. [Google Scholar]
42. A. Mahor, V. Prasad and S. Rangnekar, “Economic dispatch using particle swarm optimization: A review,” Renewable and Sustainable Energy Reviews, vol. 13, no. 8, pp. 2134–2141, 2009. [Google Scholar]
43. M. Mostafa, S. Kaboli, E. Taslimi-Renani and N. Rahim, “Backtracking search algorithm for solving economic dispatch problems with valve-point effects and multiple fuel options,” Energy, vol. 116, no. 1, pp. 637–649, 2016. [Google Scholar]
44. A. Rathinam and R. Phukan, “Solution to economic load dispatch problem based on firefly algorithm and its comparison with BFO, CBFO-S and CBFO-Hybrid,” in Proc. Int. Conf. on Swarm, Evolutionary, and Memetic Computing, Berlin, Heidelberg, Springer, pp. 57–65, 2012. [Google Scholar]
45. K. Bhattacharjee, A. Bhattacharya and S. Dey, “Chemical reaction optimisation for different economic dispatch problems,” IET Generation, Transmission & Distribution, vol. 8, no. 3, pp. 530–541, 2013. [Google Scholar]
46. T. Ding, R. Bo, F. Li and H. Sun, “A bi-level branch and bound method for economic dispatch with disjoint prohibited zones considering network losses,” IEEE Transactions on Power Systems, vol. 30, no. 6, pp. 2841–2855, 2014. [Google Scholar]
47. S. Özyön and D. Aydin, “Incremental artificial bee colony with local search to economic dispatch problem with ramp rate limits and prohibited operating zones,” Energy Conversion and Management, vol. 65, pp. 397–407, 2013. [Google Scholar]
48. A. Selvakumar and K. Thanushkodi, “A new particle swarm optimization solution to nonconvex economic dispatch problems,” IEEE Transactions on Power Systems, vol. 22, no. 1, pp. 42–51, 2007. [Google Scholar]
49. V. Hosseinnezhad and E. Babaei, “Economic load dispatch using θ-PSO,” International Journal of Electrical Power & Energy Systems, vol. 49, pp. 160–169, 2013. [Google Scholar]
50. H. Barati and M. Sadeghi, “An efficient hybrid MPSO-GA algorithm for solving non-smooth/non-convex economic dispatch problem with practical constraints,” Ain Shams Engineering Journal, vol. 9, no. 4, pp. 1279–1287, 2018. [Google Scholar]
51. E. Afzalan and M. Joorabian, “An improved cuckoo search algorithm for power economic load dispatch,” International Transactions on Electrical Energy Systems, vol. 25, no. 6, pp. 958–975, 2015. [Google Scholar]
52. B. K. Panigrahi, V. R. Pandi and S. Das, “Adaptive particle swarm optimization approach for static and dynamic economic load dispatch,” Energy Conversion and Management, vol. 49, no. 6, pp. 1407–1415, 2008. [Google Scholar]
53. Y. Labbi, D. Attous, H. Gabbar, B. Mahdad and A. Zidan, “A new rooted tree optimization algorithm for economic dispatch with valve-point effect,” International Journal of Electrical Power & Energy Systems, vol. 79, pp. 298–311, 2016. [Google Scholar]
54. K. Bhattacharjee, A. Bhattacharya and S. Dey, “Oppositional real coded chemical reaction optimization for different economic dispatch problems,” International Journal of Electrical Power & Energy Systems, vol. 55, pp. 378–391, 2014. [Google Scholar]
55. G. Xiong, D. Shi and X. Duan, “Multi-strategy ensemble biogeography-based optimization for economic dispatch problems,” Applied Energy, vol. 111, no. 2, pp. 801–811, 2013. [Google Scholar]
56. G. Xiong and D. Shi, “Orthogonal learning competitive swarm optimizer for economic dispatch problems,” Applied Soft Computing, vol. 66, pp. 134–148, 2018. [Google Scholar]
57. S. Sayah and A. Hamouda, “A hybrid differential evolution algorithm based on particle swarm optimization for nonconvex economic dispatch problems,” Applied Soft Computing, vol. 13, no. 4, pp. 1608–1619, 2013. [Google Scholar]
58. G. Binetti, A. Davoudi, F. L. Lewis, D. Naso and B. Turchiano, “Distributed consensus-based economic dispatch with transmission losses,” IEEE Transactions on Power Systems, vol. 29, no. 4, pp. 1711–1720, 2014. [Google Scholar]
59. M. Basu, “Kinetic gas molecule optimization for nonconvex economic dispatch problem,” International Journal of Electrical Power & Energy Systems, vol. 80, no. 3, pp. 325–332, 2016. [Google Scholar]
60. M. A. Elhameed and A. A. El-Fergany, “Water cycle algorithm-based economic dispatcher for sequential and simultaneous objectives including practical constraints,” Applied Soft Computing, vol. 58, pp. 145–154, 2017. [Google Scholar]
61. J. Cai, Q. Li, L. Li, H. Peng and Y. Yang, “A hybrid CPSO-SQP method for economic dispatch considering the valve-point effects,” Energy Conversion and Management, vol. 53, no. 1, pp. 175–181, 2012. [Google Scholar]
62. G. Binetti, A. Davoudi, D. Naso, B. Turchiano and F. L. Lewis, “A distributed auction-based algorithm for the nonconvex economic dispatch problem,” IEEE Transactions on Industrial Informatics, vol. 10, no. 2, pp. 1124–1132, 2013. [Google Scholar]
63. M. A. Al-Betar, M. A. Awadallah, A. T. Khader and A. L. Bolaji, “Tournament-based harmony search algorithm for non-convex economic load dispatch problem,” Applied Soft Computing, vol. 47, no. 1, pp. 449–459, 2016. [Google Scholar]
64. G. Chen and X. Ding, “Optimal economic dispatch with valve loading effect using self-adaptive firefly algorithm,” Applied Intelligence, vol. 42, no. 2, pp. 276–288, 2015. [Google Scholar]
65. J. Neto, G. Reynoso-Meza, T. H. Ruppel, V. C. Mariani and L. S. Coelho, “Solving non-smooth economic dispatch by a new combination of continuous GRASP algorithm and differential evolution,” International Journal of Electrical Power & Energy Systems, vol. 84, pp. 13–24, 2017. [Google Scholar]
66. M. Azmi, M. A. Awadallah, A. T. Khader, A. L. Bolaji and A. Almomani, “Economic load dispatch problems with valve-point loading using natural updated harmony search,” Neural Computing and Applications, vol. 29, no. 10, pp. 767–781, 2018. [Google Scholar]
67. W. Elsayed and E. F. El-Saadany, “A fully decentralized approach for solving the economic dispatch problem,” IEEE Transactions on Power Systems, vol. 30, no. 4, pp. 2179–2189, 2014. [Google Scholar]
68. A. K. Barisal and R. C. Prusty, “Large scale economic dispatch of power systems using oppositional invasive weed optimization,” Applied Soft Computing, vol. 29, pp. 122–137, 2015. [Google Scholar]
69. T. T. Nguyen and D. N. Vo, “The application of one rank cuckoo search algorithm for solving economic load dispatch problems,” Applied Soft Computing, vol. 37, pp. 763–773, 2015. [Google Scholar]
70. A. Rabiee, B. Mohammadi-Ivatloo and M. Moradi-Dalvand, “Fast dynamic economic power dispatch problems solution via optimality condition decomposition,” IEEE Transactions on Power Systems, vol. 29, no. 2, pp. 982–983, 2013. [Google Scholar]
71. C. Chiang, “Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels,” IEEE Transactions on Power Systems, vol. 20, no. 4, pp. 1690–1699, 2005. [Google Scholar]
72. N. Amjady and H. Nasiri-Rad, “Economic dispatch using an efficient real-coded genetic algorithm,” IET Generation, Transmission & Distribution, vol. 3, no. 3, pp. 266–278, 2009. [Google Scholar]
73. H. Lu, P. Sriyanyong, Y. H. Song and T. Dillon, “Experimental study of a new hybrid PSO with mutation for economic dispatch with non-smooth cost function,” International Journal of Electrical Power & Energy Systems, vol. 32, no. 9, pp. 921–935, 2010. [Google Scholar]
74. N. Amjady and H. Nasiri-Rad, “Solution of nonconvex and nonsmooth economic dispatch by a new adaptive real coded genetic algorithm,” Expert Systems with Applications, vol. 37, no. 7, pp. 5239–5245, 2010. [Google Scholar]
75. S. P. RM, P. K. Maddikunta, M. Parimala, S. Koppu S, T. R. Gadekallu et al., “An effective feature engineering for DNN using hybrid PCA-GWO for intrusion detection in IoMT architecture,” Computer Communications, vol. 160, pp. 139–149, 2020. [Google Scholar]
76. T. R.Gadekallu, D. S. Rajput, P. K. Reddy, K. Lakshmanna, S. Bhattacharya et al., “A novel PCA-whale optimization-based deep neural network model for classification of tomato plant diseases using GPU,” Journal of Real-Time Image Processing, 2020. https://doi.org/10.1007/s11554-020-00987-8. [Google Scholar]
M. Alazab, S. Khan, S. S. R. Krishnan, Q. V. Pham, P. K. Reddy et al., “A multidirectional LSTM model for predicting the stability of a smart grid,” IEEE Access, vol. 8, pp. 85454–85463, 2020. [Google Scholar]
78. T. Reddy, S. Bhattacharya, P. K. R. Maddikunta, S. Hakak, W. Z. Khanet et al., “Antlion re-sampling based deep neural network model for classification of imbalanced multimodal stroke dataset,” Multimedia Tools and Applications, 2020. https://doi.org/10.1007/s11042-020-09988-y. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |