DOI:10.32604/cmc.2021.016973

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016973 |  |
| Article |
Emergency Decision-Making Based on q-Rung Orthopair Fuzzy Rough Aggregation Information
1Department of Mechanical Engineering, King Abdulaziz University, Jeddah, Saudi Arabia
2Department of Mathematics, Abdul Wali Khan University Mardan, Mardan, 23200, Pakistan
3Department of Mathematics and Statistics, Bacha Khan University, Charsadda, 24420, Pakistan
4Deanship of Combined First Year, Umm Al-Qura University, Makkah, Saudi Arabia
*Corresponding Author: Shahzaib Ashraf. Email: shahzaibashraf@bkuc.edu.pk
Received: 17 January 2021; Accepted: 07 May 2021
Abstract: With the frequent occurrences of emergency events, emergency decision making (EDM) plays an increasingly significant role in coping with such situations and has become an important and challenging research area in recent times. It is essential for decision makers to make reliable and reasonable emergency decisions within a short span of time, since inappropriate decisions may result in enormous economic losses and social disorder. To handle emergency effectively and quickly, this paper proposes a new EDM method based on the novel concept of q-rung orthopair fuzzy rough (q-ROPR) set. A novel list of q-ROFR aggregation information, detailed description of the fundamental characteristics of the developed aggregation operators and the q-ROFR entropy measure that determine the unknown weight information of decision makers as well as the criteria weights are specified. Further an algorithm is given to tackle the uncertain scenario in emergency to give reliable and reasonable emergency decisions. By using proposed list of q-ROFR aggregation information all emergency alternatives are ranked to get the optimal one. Besides this, the q-ROFR entropy measure method is used to determine criteria and experts’ weights objectively in the EDM process. Finally, through an illustrative example of COVID-19 analysis is compared with existing EDM methods. The results verify the effectiveness and practicability of the proposed methodology.
Keywords: q-rung orthopair fuzzy rough set; q-ROFR entropy measure; aggregation information; emergency decision making
Catastrophic events such as earthquakes, hurricanes, flooding, and droughts, among others lead to mass destruction such as a large number of deaths, infrastructure damage, and adverse social instability and public security consequences [1]. For example, the 2005 Kashmir earthquake in Pakistan destroyed more than 780,000 buildings and killed 87,350 humans and over a billion animals. In 2019, the Super Typhoon Lekima brought catastrophic damages to mainland China and the direct economic losses amounted to approximately 52 billion yuan. The corona virus disease 2019 (COVID-19) spread to over 200 countries and about 370,000 people have died so far. While emergency response and immediate measures play a key role in addressing such situations, the implementation of emergency decision-making (EDM) with outdated procedures will ultimately lead to possible failures in emergency decisions. Therefore, the EDM process is a vital and essential part of the whole emergency response [2–4]. In fact, inappropriate information on decision-making and tight time pressures in the context of the unforeseen environment of decision-making make it hard for decision-makers to make an effective and reasonable choice [5]. Therefore, to detect the optimum solution for the EDM procedure in order to reduce the economic losses and casualties, it is very important to develop systematic and scientific EDM techniques [6]. Therefore, tackling EDM quickly and effectively has become an important research topic in recent years [7].
Nowadays, the information management and decision-making have become much more important because of increasing emergency situations. With the increasing complexity of the data, new and more accurate tools are necessary because they handle human inaccuracy or ambiguous knowledge more effectively when compared to the classical tools. Zadeh [8] introduced the concept of fuzzy sets (FSs) to deal with uncertain information in real-life situations. Atanassov [9] proposed in 1986 the notion of intuitionistic FSs (IFSs) by generalizing the well-known theory of FSs. Although IFSs are successful in a wide range of applications, they still have some limitations because of the restriction that the sum of membership grade and that of non-membership grade must not exceed 1. To handle this issue, Yager [10] further extended the theory of IFSs and proposed the notion of Pythagorean FSs (PFSs) for modeling the higher-level imprecise and vague information. After Yager’s pioneering work, several researchers initiated the study in the field of PFS theory to show its applications in various disciplines. Khan et al. [11] introduced the Dombi norm based on PFSs and discussed their applications in decision-making problems (DMPs). Yager et al. [12] presented a link between Pythagorean fuzzy membership grades and complex numbers. Batool et al. [13] extended the PFSs to Pythagorean probabilistic hesitant FSs and elaborated their applications in DMPs. Peng et al. [14] established the division and subtraction operations under the Pythagorean fuzzy environment and studied their properties in detail. Ashraf et al. [15] proposed the novel approach using the sine function under Pythagorean fuzzy settings. Zhang [16] defined a similarity measure for DMPs under the Pythagorean fuzzy environment.
Let us assume that the value of membership grade (MG) is set to 0.8 and that of non-membership grade (NMG) is set to 0.9. From the available information, it is clear that
Pawlak [25] initiated the important notion of rough set theory in 1982, which handles imprecise and ambiguous data more effectively. Investigation into the rough set, both theoretically and practically, in the recent era has made tremendous progress. The notion of rough sets has been enhanced in various ways by several scholars. Dubois et al. [26] established the structure of fuzzy rough sets (FRSs). Zhang et al. [27] established the decision-making methodology using FRSs to tackle the uncertain information in DMPs. Khan et al. [28] established the novel notion of probabilistic hesitant FRSs and discussed their applications in DMPs. Chinram et al. [29] proposed the evaluation based on distance from average solution methodology under intuitionistic FRSs to tackle the multi-attribute group decision-making. Zhou et al. [30] established the generalized approximation operators under intuitionistic FRSs.
In some real-life circumstances, decision-makers (DMs) have a strong point of view about the ranking or rating of plans, projects, or political statements of a government. For example, the construction of a cricket ground by a university to render its accomplishment and performance. The members of the university administration may rate their project highly by assigning a DM (
This paper is organized as follows: In Section 2, we review some concepts related to q-ROFSs and rough sets. In Section 3, we proposed the novel notion of q-ROFRS and discussed its basic operations. In Section 4, we proposed the list of averaging/geometric aggregation operators for q-ROPFR information. In Section 5, we present the entropy measure and decision-making methodology. In Section 6, we demonstrate the numerical example of the public health emergency problem to show the applicability and effectiveness of the proposed methodology. Finally, Section 8 concludes the paper, illustrating achievements and setting future directions.
In this section, we resolve the essential knowledge about q-ROFS and rough sets.
Definition 1 ( [17]). Let M be a non-empty set. A q-ROFS Z of a set M is a set having the form
where the values
For simplicity,
Definition 2 ( [25]). Let M be a non-empty set and
3 q-Rung Orthopair Fuzzy Rough Aggregation Information
The aggregation information plays an important role in combining data into one format and addressing the DMP. In this section, we propose a list of novel aggregation information.
3.1 q-Rung Orthopair Fuzzy Rough Averaging Aggregation operators
Definition 3. Let us consider
where
Theorem 1. Suppose
In algebraic-strict Archimedean t-norm and t-conorm, if we assign values to generators t and s, then we obtain two algebraic operations for q-ROFRVs:
Proof: The proof is straightforward by using mathematical induction.
Definition 4. Suppose
where
Theorem 2. Suppose
In algebraic-strict Archimedean t-norm and t-conorm, if we assign values to generators t and s, then we have algebraic operations for q-ROFRVs:
Proof: The proof is straightforward by using mathematical induction.
Definition 5. Suppose
where
Theorem 3. Suppose
In algebraic-strict Archimedean t-norm and t-conorm, if we assign values to generators t and s, then we have two algebraic operations for q-ROFRVs:
Proof: The proof is straightforward by using mathematical induction.
4 Development of q-ROFR Entropy Measure
To calculate the differences between two q-ROFRVs, this segment developed the generalized and weighted generalized distance measures of q-ROFR information. To measure the fuzziness of q-ROFRVs, we propose entropy measures for q-ROFRS based on the developed distance operators.
Definition 6. Suppose
Definition 7. Suppose
where
Definition 8. Suppose
Novel entropy measure for q-ROFRVs is developed in this segment.
Definition 9. Suppose
where
For q-ROF approximation space
(1)
(2)
(3)
Here, we have developed a framework for addressing uncertainty in DM under q-rung orthopair fuzzy rough information. Consider a DM problem with
Step 1. The expert’s evaluation matrices are constructed.
Step 2(a). The expert ideal matrix (EIM) is calculated using a q-ROFRWA aggregation operator, which is closer to each expert information.
Step 2(b). Compute the expert right ideal matrix (ERIM) and expert left ideal matrix (ELIM) as follows:
Step 2(c). The distance of
for
Step 2(d). Evaluate closeness indices (CIs) as follows:
Step 2(e). Expert weight information is evaluated as
Step 3(a). Evaluate revised expert ideal matrix (RvEIM) based on the developed entropy measure as
Step 3(b). The entropy measure corresponding to each attribute is computed as
Step 3(c). The attribute weight information is calculated as follows:
Step 4. Aggregate the revised expert ideal matrix based on the proposed aggregation operators to construct the aggregated matrix using attribute weights
Step 5. Compute the score (according to Definition 7) of overall values
Step 6. According to Definition 8, the alternatives
6 Numerical Application of the Proposed Algorithm
In this section, a practical EDM problem concerning a public health emergency is considered to validate the applicability and practicality of the developed methodology.
Wuhan Province of China has reported many unexplained cases in December 2019. The cause of pneumonia was identified as the new coronavirus, later labeled corona virus disease 2019 (COVID-19). Since 1–14 days of the incubation period is required, infected persons without symptoms can quickly pass on the virus through drops and intimate contact with others. A total of 81,000 people had been diagnosed in China by 22 March 2020, of whom more than 3000 died. Wuhan was the center of the epidemic with approximately 50,000 people, representing 81.31% of all patients, and the mortality rate stood at approximately 5.02%. This acute, rapidly spreading disease has led to enormous economic disorders for the catering, entertainment, retail, and tourism industries. Controlling virus sources and virus transmission are generally the essential solutions for the prevention and control of such infectious diseases. Quarantine measures must, therefore, be taken on time and the movements of the population must be monitored. Four alternative emergency responses are recommended to Wuhan citizens on the basis of the above-mentioned analysis:
(1) The infected individuals are quarantined and closely monitored
(2) Suspected individuals with infections and those who have recently been in close contact with infected individuals are also quarantined. Moreover, uninfected people are advised to work for themselves, for example, wearing masks
(3) Participation in public meetings is strictly prohibited. If people go out, they must take protective measures such as wearing masks, measuring temperature if they enter public places, and so on
(4) All classes and work are suspended, all people must stay at home, and their travel freedom is restricted
In addition, four emergency response alternatives are assessed using four criteria: (1) life satisfaction
The invited DMs are divided into three expert panels:
Step 1(a). Tabs. 1a–1c presents the expert evaluation information in the form of q-rung orthopair fuzzy rough.

Step 2(a). The EIM is calculated in Tab. 2.
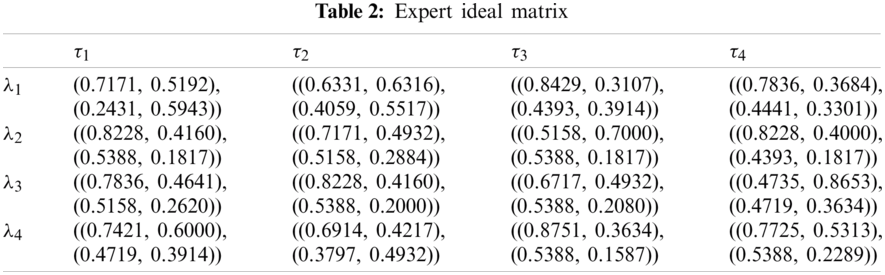
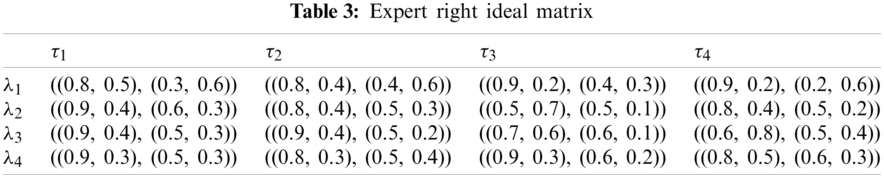
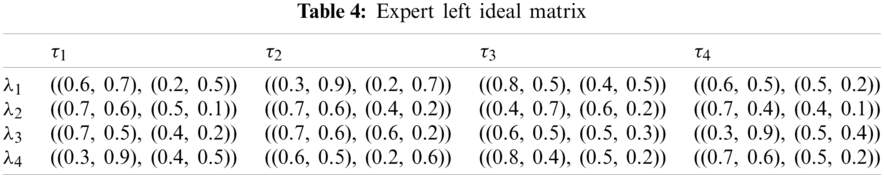
Step 2(b). The ERIM and ELIM are calculated in Tabs. 3 and 4.
Step 2(c). The distance of
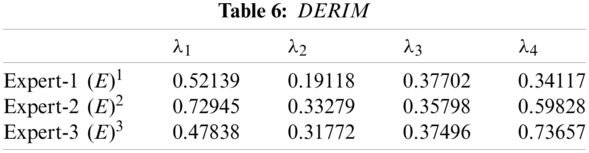
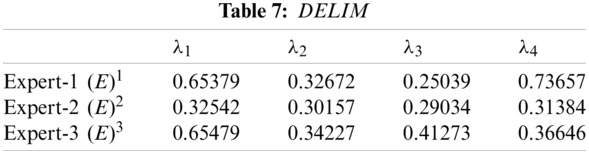
Step 2(d). The CIs are calculated as follows:
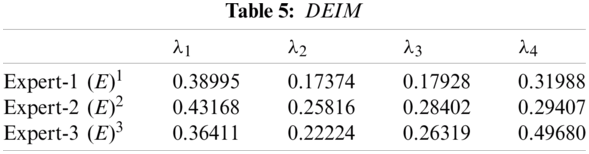
Step 2(e). Expert weight information is calculated as follows:
Step 3(a). The revised expert ideal matrix is given in Tab. 8.
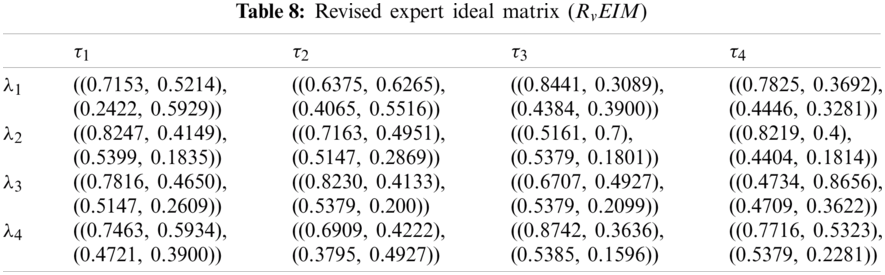
Step 3(b). The entropy measure corresponding to each attribute is computed as follows:
Step 3(c). The attribute weight information is given as
Step 4. The collective preference values of each alternative in the revised expert ideal matrix are calculated using the proposed list of aggregation operators as follows:
Case 1. Using
Case 2. Using


Case 3. Using
Case 4. Using


Case 5. Using
Case 6. Using


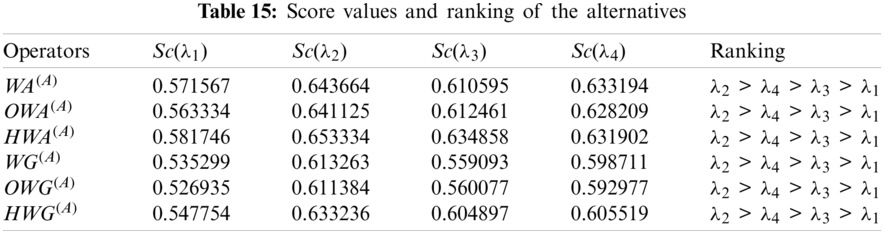
Step 5. The score of collective overall preference values of each alternative is given in Tab. 15.
Step 6. The ranking of the alternatives
From the above computational process, we concluded that alternative
In this study, we proposed a novel method to deal with EDM problems based on the novel notion of q-ROFRS and the list of aggregation operators. First, the q-ROFRSs provide a flexible and natural way for DMs with different backgrounds to express uncertain assessment information on emergency alternatives. Then, the novel methodology based on the aggregation operators is modified to rank emergency alternatives to help DMs to determine the best one. The expert and the criteria weights are calculated by the entropy measure method, which are derived from initial evaluation information directly avoiding human intervention and secondary information collection. Eventually, to demonstrate the effectiveness and practicability of our proposed method, it is applied to a real EDM example of COVID-19 and compared against those of the existing EDM method.
Our established methodology can be extended to cover heterogeneous information because different types of information are closer to the actual situation and suitable for various criteria. We can use Hamacher, Yager, and Dombi norms to develop generalized aggregation operators to address the uncertain information more accurately in EDM problems. These will be used in future research directions.
Funding Statement: This Project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under the Grant No. (G: 578-135-1441). The authors, therefore, acknowledge with thanks DSR for technical and financial support.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Qi, Q. Wang, Q. Duan, L. Gong, J. Sun et al., “A multi criteria comprehensive evaluation approach for emergency response capacity with interval 2-tuple linguistic information,” Applied Soft Computing, vol. 72, no. 1, pp. 419–441, 2018. [Google Scholar]
2. S. Ashraf and S. Abdullah, “Emergency decision support modeling for COVID-19 based on spherical fuzzy information,” International Journal of Intelligent Systems, vol. 35, no. 11, pp. 1601–1645, 2020. [Google Scholar]
3. Z. Hao, Z. Xu, H. Zhao and H. Fujita, “A dynamic weight determination approach based on the intuitionistic fuzzy Bayesian network and its application to emergency decision making,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 4, pp. 1893–1907, 2017. [Google Scholar]
4. S. Ashraf, S. Abdullah and A. O. Almagrabi, “A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19,” Soft Computing, vol. 54, no. 1–4, pp. 1–17, 2020. [Google Scholar]
5. X. Xu, X. Yin and X. Chen, “A large-group emergency risk decision method based on data mining of public attribute preferences,” Knowledge-Based Systems, vol. 163, no. 10, pp. 495–509, 2019. [Google Scholar]
6. X. Peng and H. Garg, “Algorithms for interval-valued fuzzy soft sets in emergency decision making based on WDBA and CODAS with new information measure,” Computers & Industrial Engineering, vol. 119, pp. 439–452, 2018. [Google Scholar]
7. X. F. Ding and H. C. Liu, “A new approach for emergency decision-making based on zero-sum game with Pythagorean fuzzy uncertain linguistic variables,” International Journal of Intelligent Systems, vol. 34, no. 7, pp. 1667–1684, 2019. [Google Scholar]
8. L. A. Zadeh, “Fuzzy sets,” Information and control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
9. K. Atanassov, “Intuitionistic fuzzy sets,” Fuzzy Sets Systems, vol. 20, pp. 87–96, 1986. [Google Scholar]
10. R. R. Yager, “Pythagorean membership grades in multicriteria decision making,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 4, pp. 958–965, 2013. [Google Scholar]
11. A. A. Khan, S. Ashraf, S. Abdullah, M. Qiyas, J. Luo et al., “Pythagorean fuzzy Dombi aggregation operators and their application in decision support system,” Symmetry, vol. 11, no. 3, pp. 383, 2019. [Google Scholar]
12. R. R. Yager and A. M. Abbasov, “Pythagorean membership grades, complex numbers, and decision making,” International Journal of Intelligent Systems, vol. 28, no. 5, pp. 436–452, 2013. [Google Scholar]
13. B. Batool, M. Ahmad, S. Abdullah, S. Ashraf and R. Chinram, “Entropy based Pythagorean probabilistic hesitant fuzzy decision-making technique and its application for fog-haze factor assessment problem,” Entropy, vol. 22, no. 3, pp. 318, 2020. [Google Scholar]
14. X. Peng and Y. Yang, “Some results for Pythagorean fuzzy sets,” International Journal of Intelligent Systems, vol. 30, no. 11, pp. 1133–1160, 2015. [Google Scholar]
15. S. Ashraf, S. Abdullah and S. Khan, “Fuzzy decision support modeling for internet finance soft power evaluation based on sine trigonometric Pythagorean fuzzy information,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 2, pp. 3101–3119, 2021. [Google Scholar]
16. X. Zhang, “A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making,” International Journal of Intelligent Systems, vol. 31, no. 6, pp. 593–611, 2016. [Google Scholar]
17. R. R. Yager, “Generalized orthopair fuzzy sets,” IEEE Transactions on Fuzzy Systems, vol. 25, no. 5, pp. 1222–1230, 2016. [Google Scholar]
18. R. R. Yager, N. Alajlan and Y. Bazi, “Aspects of generalized orthopair fuzzy sets,” International Journal of Intelligent Systems, vol. 33, no. 11, pp. 2154–2174, 2018. [Google Scholar]
19. M. J. Khan, P. Kumam and M. Shutaywi, “Knowledge measure for the q-rung orthopair fuzzy sets,” International Journal of Intelligent Systems, vol. 36, no. 2, pp. 628–655, 2020. [Google Scholar]
20. A. Hussain, M. I. Ali, T. Mahmood and M. Munir, “q-Rung orthopair fuzzy soft average aggregation operators and their application in multicriteria decision-making,” International Journal of Intelligent Systems, vol. 35, no. 4, pp. 571–599, 2020. [Google Scholar]
21. P. Liu and P. Wang, “Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making,” International Journal of Intelligent Systems, vol. 33, no. 2, pp. 259–280, 2018. [Google Scholar]
22. M. J. Khan, M. I. Ali and P. Kumam, “A new ranking technique for q-rung orthopair fuzzy values,” International Journal of Intelligent Systems, vol. 36, no. 1, pp. 558–592, 2021. [Google Scholar]
23. B. P. Joshi and A. Gegov, “Confidence levels q-rung orthopair fuzzy aggregation operators and its applications to MCDM problems,” International Journal of Intelligent Systems, vol. 35, no. 1, pp. 125–149, 2020. [Google Scholar]
24. R. Verma, “Multiple attribute group decision-making based on order-
25. Z. Pawlak, “Rough sets,” International Journal of Computer & Information Sciences, vol. 11, no. 5, pp. 341–356, 1982. [Google Scholar]
26. D. Dubois and H. Prade, “Rough fuzzy sets and fuzzy rough sets,” International Journal of General System, vol. 17, no. 2–3, pp. 191–209, 1990. [Google Scholar]
27. L. Zhang and J. Zhan, “Fuzzy soft Beta-covering based fuzzy rough sets and corresponding decision-making applications,” International Journal of Machine Learning and Cybernetics, vol. 10, no. 6, pp. 1487–1502, 2019. [Google Scholar]
28. M. A. Khan, S. Ashraf, S. Abdullah and F. Ghani, “Applications of probabilistic hesitant fuzzy rough set in decision support system,” Soft Computing, vol. 24, pp. 16759–16774, 2019. [Google Scholar]
29. R. Chinram, A. Hussian, T. Mahmood and M. I. Ali, “EDAS method for multi-criteria group decision making based on intuitionistic fuzzy rough aggregation operators,” IEEE Access, vol. 9, pp. 10199–10216, 2021. [Google Scholar]
30. L. Zhou and W. Z. Wu, “On generalized intuitionistic fuzzy rough approximation operators,” Information Sciences, vol. 178, no. 11, pp. 2448–2465, 2008. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |