Computers, Materials & Continua DOI:10.32604/cmc.2021.017087
Article

Controlled Quantum Network Coding Without Loss of Information

Xing-Bo Pan1, Xiu-Bo Chen1,*, Gang Xu2, Haseeb Ahmad3, Tao Shang4, Zong-Peng Li5,6 and Yi-Xian Yang1

1Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
2School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
3Department of Computer Science National Textile University, Faisalabad, 37610, Pakistan
4School of Cyber Science and Technology, Beihang University, Beijing, 100083, China
5Huawei Technologies Co. Ltd., Shenzhen, 518129, China
6School of Computer Science, Wuhan University, Wuhan, 430072, China
*Corresponding Author: Xiu-Bo Chen. Email: cflyover100@163.com
Received: 20 January 2021; Accepted: 12 March 2021

Abstract: Quantum network coding is used to solve the congestion problem in quantum communication, which will promote the transmission efficiency of quantum information and the total throughput of quantum network. We propose a novel controlled quantum network coding without information loss. The effective transmission of quantum states on the butterfly network requires the consent form a third-party controller Charlie. Firstly, two pairs of three-particle non-maximum entangled states are pre-shared between senders and controller. By adding auxiliary particles and local operations, the senders can predict whether a certain quantum state can be successfully transmitted within the butterfly network based on the Z-{|0⟩,|1⟩} basis. Secondly, when transmission fails upon prediction, the quantum state will not be lost, and it will still be held by the sender. Subsequently, the controller Charlie re-prepares another three-particle non-maximum entangled state to start a new round. When the predicted transmission is successful, the quantum state can be transmitted successfully within the butterfly network. If the receiver wants to receive the effective quantum state, the quantum measurements from Charlie are needed. Thirdly, when the transmission fails, Charlie does not need to integrate the X-{|+⟩,|−⟩} basis to measure its own particles, by which quantum resources are saved. Charlie not only controls the effective transmission of quantum states, but also the usage of classical and quantum channels. Finally, the implementation of the quantum circuits, as well as a flow chart and safety analysis of our scheme, is proposed.

Keywords: Controlled quantum network coding; without information loss; quantum teleportation; perfect transmission

1  Introduction

In 2000, classic network coding was first proposed by Ahlswede et al. [1], which improved the transmission efficiency of classic information by coding at bottleneck nodes in the network. In 2007, Hayashi et al. [2] considered the features and advantages of classical network coding, and proposed the idea of quantum network coding for the first time. However, because the exact replication of an unknown quantum state is impossible in quantum mechanics [3,4], only approximate transmissions between quantum states can be realized on the butterfly network without auxiliary entanglements. The scheme has been applied to solve congestion problems in quantum information transmissions by unitary operations on the bottleneck nodes, and has been proved to improve the transmission efficiency of quantum information. Since quantum approximation clone machines were used [4], the fidelity of the quantum states received by the receiver could not reach 1. Based on Hayashi’s scheme, a controllable quantum network coding based on a single controller was proposed by Shang et al. [5], which realized decoding control in the receiver in a conventional quantum network coding. However, because Shang’s scheme employed quantum approximation cloning, the fidelity of the received quantum states still could not reach 1. Later, Kobayashi et al. proved that quantum network coding with a fidelity of 1 can be achieved with assistance from auxiliary resources [6–8]. Since then, perfect and cross transmission of quantum states on quantum networks has become a research interest for many researchers. By definition, perfect transmission means that the fidelity of the quantum states received by the receiver is 1.

In 2007, Hayashi [9] realized perfect and cross transmission of quantum states by pre-sharing two pairs of entangled states among senders on the butterfly network. By adding auxiliary resources and combining with classical network coding, quantum states were transmitted in the scheme with a fidelity of 1. In 2012, another quantum network coding scheme based on quantum repeaters [10–12] was proposed by Satoh et al. [13]. In this scheme, each node in the butterfly network was regarded as a quantum repeater, and every two adjacent quantum repeaters shared an EPR pair. With local operations and classical communications, entanglement between the receiver and the sender was created. After that, quantum teleportation [14,15] was applied to realize perfect and cross transmission of quantum states within the butterfly network. Schemes [9,13] used the maximally-entangled states as the auxiliary resources to realize perfect and cross transmission of quantum states on the butterfly network. However, it is difficult to prepare such states in practice, and non-maximum entangled states are more feasible, which was employed by Ma et al. [16] to develop a probabilistic quantum network coding. Moreover, they have been applied by Shang et al. [17] to propose another quantum network coding based on universal quantum repeater networks.

In addition, Satoh et al. [18] continued to use entanglement swap and graph states [19] to achieve perfect and cross transmission of quantum states. Subsequently, Li et al. [20] extended the conclusion from [13] to quantum multi-unicast networks, which solved the quantum 3-pair communications problem. Besides, Li et al. also proposed a solution to the problem of quantum k-pair communications in 2018. At present, research on quantum network coding has become a hot spot with more and more schemes being proposed [21–27].

When non-maximum entangled states are used as a quantum channel, the quantum states will be transmitted with a certain probability. If transmission fails, the quantum states will be lost. Therefore, the preservation of quantum states during transmission has become an urgent problem. In 2015, Roa et al. [28] proposed probabilistic quantum teleportation without information loss, in which the non-maximum entangled states are pre-shared between the sender and the receiver. By adding auxiliary particles and local operations [29], the transmission of quantum states can be realized without information loss, and the quantum states will remain at the sender if transmission fails. As long as the entangled resources are sufficient, the transmission of quantum states can be tried repeatedly until success. Such idea is adopted into this work, in which the advantages of classical network coding are combined to create a controlled quantum network coding scheme that could achieve perfect and cross transmission of quantum states without information loss.

Since coupling between the quantum states and the surrounding environment is inevitable in practice [30], it is of more practical significance to use non-maximum entangled states as the auxiliary resources to achieve perfect transmission of quantum states [31]. However, under such circumstances, the successful transmission of quantum states on the butterfly network is not guaranteed [16,17]. If the transmission fails, the quantum states will be lost, resulting in invalid communication and waste of channel resources. Here in this paper, we consider pre-sharing two pairs of three-particle non-maximum entangled states between the senders and the controller Charlie on the butterfly network. Our scheme combines quantum teleportation with classical network coding to solve the bottleneck problem of quantum state transmission. Under Charlie’s control, perfect and cross transmission of the quantum states can be achieved. Particularly, the senders can predict whether the quantum states can be successfully transmitted over the butterfly network with the help of auxiliary particles. When transmission fails, the quantum states will not be lost, and they will remain at the sender to be used for the next transmission. Moreover, both classical and quantum channels are not occupied if transmission fails. In this scheme, Charlie controls not only whether the receiver can receive the quantum states, but also the usage of classical and quantum channels over the butterfly network. Therefore, our scheme improves the utilization efficiency of both channels.

In the following sections, the paper content is organized as below. Some preliminary definitions and equations involved in our scheme will be given in Section 2. In Section 3, the implementation procedure of our controlled quantum network coding without information loss will be discussed in detail. In addition, the implementation of the quantum circuit implementation, as well as the flow chart and safety analysis for our scheme will be demonstrated in this section as well, which could be of great reference value for future researches. Finally, our conclusions will be stated in Section 4.

2  Preliminaries

2.1 Three-Particle Non-Maximum Entangled State

In our scheme, we will use a three-particle non-maximum entangled state as quantum channel.

|Φ⟩ABC=α|000⟩ABC+β|111⟩ABC (1)

where α, β are positive real numbers and α≤β. It satisfies the normalization condition α2+β2=1, and particles A, B and C belong to different parties.

2.2 Local Operations

Some single-particle gate operations and two-particle local operations [29] are applied. The single-particle gate operations are:

σx=[0110],σz=[100−1],H=[121212−12] (2)

The influences from the single-particle gates on the quantum states are:

σx|0⟩=|1⟩,σx|1⟩=|0⟩,σz|0⟩=|0⟩,σz|1⟩=−|1⟩,H|0⟩=|0⟩+|1⟩2,H|1⟩=|0⟩−|1⟩2. (3)

The two-particle local operations are:

Cij=|0⟩i⟨0|i⊗Ij+|1⟩i⟨1|i⊗σx(j) (4)

This operation is called a controlled NOT gate, in which particle i is a control qubit and particle j is a target qubit.

In our scheme, a controlled unitary operation is applied to ensure that quantum states are not lost.

CijUj=|0⟩i⟨0|i⊗Ij+|1⟩⟨1|⊗Uj (5)

Here,

Uj=[αβ1−α2β21−α2β2−αβ] (6)

2.3 Controlled Quantum Teleportation

In our scheme, controlled quantum teleportation [32–34] is introduced into quantum network coding. Its realization can be described as follows.

Alice, Bob and the controller Charlie share a three-particle non-maximum entangled state |Φ⟩ABC. Particle A belongs to the sender Alice, particle B belongs to the receiver Bob, and particle C belongs to the controller Charlie. Now Alice wants to transmit an unknown quantum state |ψ⟩a to Bob. The combined state of |Φ⟩ABC and |ψ⟩a is:

|ψ⟩a|Φ⟩ABC=12[|Ψ+⟩aA(a|00⟩+b|11⟩)BC+|Ψ−⟩aA(a|00⟩−b|11⟩)BC+|Φ+⟩aA(b|00⟩+a|11⟩)BC+|Φ−⟩aA(b|00⟩−a|11⟩)BC] (7)

where |Ψ±⟩=α|00⟩±β|11⟩, |Φ±⟩=α|10⟩±β|01⟩. We use a two-particle basis {|Ψ±⟩,|Φ±⟩} to measure particles aA. The following equations illustrate the four states measured by {|Ψ±⟩,|Φ±⟩} with an equal probability.

|ϒ1⟩BC=a|00⟩BC+b|11⟩BC|ϒ2⟩BC=a|00⟩BC−b|11⟩BC|ϒ3⟩BC=b|00⟩BC+a|11⟩BC|ϒ4⟩BC=b|00⟩BC−a|11⟩BC (8)

After that, Charlie integrates the X-{|+⟩,|−⟩} basis to measure particle C. The Charlie needs to tell Bob the measurement results, so that Bob can recover the unknown quantum state transmitted by Alice. For example, if the measurement result from Alice is |Ψ+⟩aA, the quantum state |Υ1⟩BC is subsequently obtained, and Charlie measures particle C. When the measurement result from Charlie is |+⟩C, Bob executes an identity operator I to particle B based on |Ψ+⟩aA and |+⟩C to obtain the quantum state |ψ⟩B. When the measurement result from Charlie is |−⟩C, Bob executes an Pauli operator σz to particle B based on |Ψ+⟩aA and |−⟩C to obtain the quantum state |ψ⟩B.

Therefore, in order to receive the unknown quantum state transmitted by Alice, measurement results from Alice and Charlie are both needed for Bob to realize satisfactory quantum state recovery.

3  Our Work

In this section, we propose a controlled quantum network coding scheme without information loss. Our scheme will be discussed based on the measurement results from auxiliary particles. In addition, the flow chart and safety analysis of our scheme will also be given.

3.1 Controlled Quantum Network Coding without Loss of Information

In our scheme, a third-party controller Charlie is added. As is shown in Fig. 1, the capacity of the bidirectional classical channel is 1 bit, and the dotted line represents a quantum channel with a capacity of 1 qubit, while the solid line stands for a classical channel with a capacity of 2 bit. Effective transmission of quantum states between the sender and the receiver require consent from Charlie C, so that the receivers can receive quantum states as they originally are. In our scheme, Charlie not only controls the transmission of quantum states, but also inhibits the unnecessary transmission of classical and quantum information on the butterfly network. When transmission fails, the transmitted quantum states will not be lost and still at the sender. The specific protocol is demonstrated as follows:

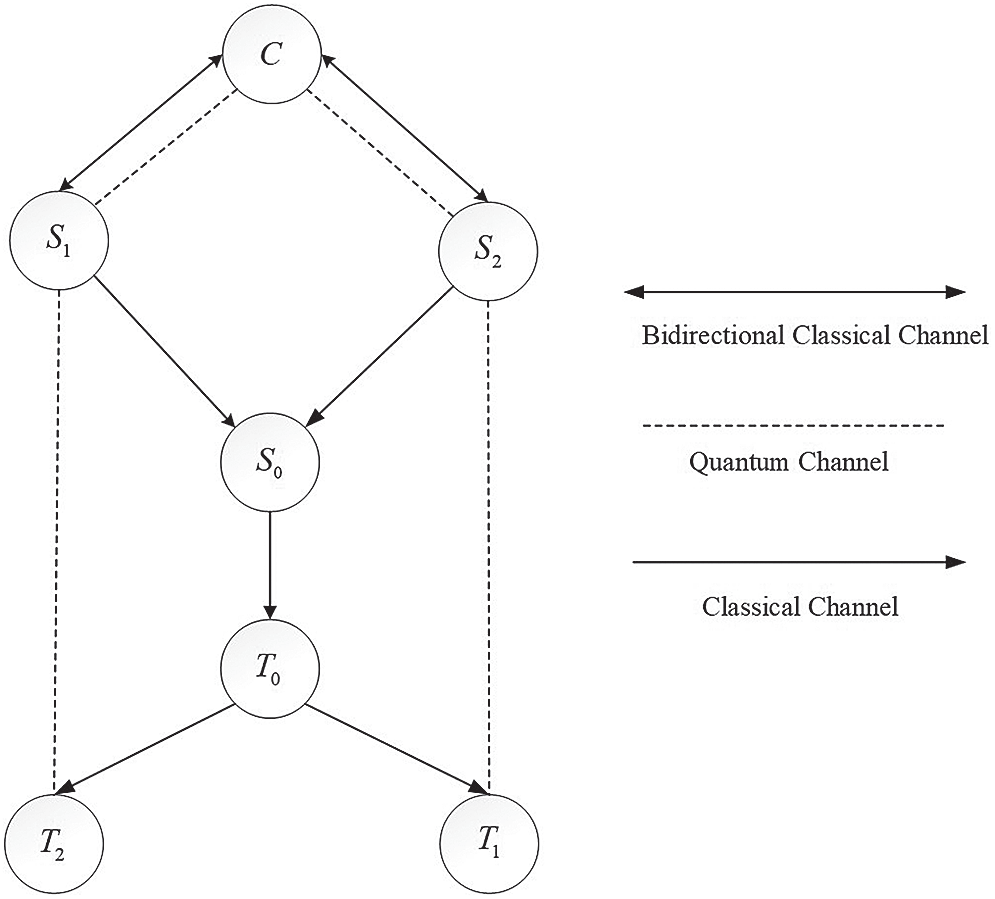
Figure 1: Quantum butterfly network based on controller Charlie

In our scheme, the three-particle non-maximum entangled states, which are prepared by Charlie, are pre-shared between the senders and Charlie on the butterfly network. Two pairs of three-particle non-maximum entangled states, namely |Φ1⟩=(α|000⟩+β|111⟩)s1,1s2,1c1 and |Φ2⟩=(γ|000⟩+δ|111⟩)s1,2s2,2c2, are necessary for transmission of quantum states. After preparation of the entangled states, Charlie sends them to the senders of S1 and S2 through the quantum channels of Q(C,S1) and Q(C,S2), respectively. The particles of s1,1, s1,2 are owned by S1, the particles of s2,1, s2,2 are owned by S2, and the particles of c1,c2 are owned by Charlie. Both S1 and S2 prepare arbitrary quantum states to be transmitted, which are |ψ1⟩s1=(a1|0⟩+b1|1⟩)s1 and |ψ2⟩s2=(a2|0⟩+b2|1⟩)s2, respectively. Specifically, a1, a2, b1 and b2 are complex numbers and satisfy the normalization condition |a1|2+|b1|2=1, |a2|2+|b2|2=1. Our scheme contains four stages, namely local operations, encoding, transmission and decoding.

Firstly, in local operations, the combined state of the unknown state |ψi⟩si and the three-particle non-maximum entangled state |Φi⟩ is expressed as

|Π⟩=|ψi⟩si|Φi⟩=(ai|0⟩+bi|1⟩)si(αi|000⟩+βi|111⟩)si,isi⊕1,ici (9)

i∈{1,2} in our entire protocol.

Sender Si applies Csi,isi to its own bipartite system si,isi, and the initial state |Π⟩ becomes

|Π1⟩=Csi,isi|ψi⟩si|Φi⟩=(αiai|0000⟩+αibi|1000⟩+βiai|1111⟩+βibi|0111⟩)sisi,isi⊕1,ici (10)

Sender Si adds an auxiliary particle ei, which is initialized to |0⟩ei. Subsequently, Si applies Csiei on the bipartite system siei, and the quantum state |Π1⟩ becomes

|Π2⟩=CsieiCsi,isi|ψi⟩si|Φi⟩|0⟩ei=(αiai|00000⟩+αibi|10001⟩+βiai|11111⟩+βibi|01110⟩)sisi,isi⊕1,iciei (11)

After obtaining |Π2⟩, Si applies Csi,isiUsi on the bipartite system si,isi, and the quantum state |Π2⟩ becomes

|Π3⟩=Csi,isiUsiCsieiCsi,isi|ψi⟩si|Φi⟩|0⟩ei=(αiai|00000⟩+αibi|10001⟩−βiai|11111⟩+βibi|01110⟩)sisi,isi⊕1,iciei+βi2−αi2(ai|01111⟩+bi|11110⟩)sisi,isi⊕1,iciei (12)

After that, Si applies Csiei on the bipartite system siei, and the quantum state |Π3⟩ becomes

|Π4⟩=CsieiCsi,isiUsiCsieiCsi,isi|ψi⟩si|Φi⟩|0⟩ei=(αiai|0000⟩+αibi|1000⟩−βiai|1111⟩+βibi|0111⟩)sisi,isi⊕1,ici|0⟩ei+βi2−αi2(ai|0⟩+bi|1⟩)si|111⟩si,isi⊕1,ici|1⟩ei (13)

Secondly, in the stage of encoding, Si uses the Z-{|0⟩,|1⟩} basis to measure the auxiliary particle ei. When the measurement result is |0⟩, it suggest that perfect and cross transmission of quantum states on the butterfly network is possible, and the following quantum state can be obtained.

|T00⟩=(αiai|0000⟩+αibi|1000⟩−βiai|1111⟩+βibi|0111⟩)sisi,isi⊕1,ici (14)

Subsequently, Si transmits the measurement result to Charlie through the classical channel C(Si,C). When Charlie receives a transmission request from the senders, it will employ the X-{|+⟩,|−⟩} basis to measure particle ci, and the measurement results are encoded according to Tab. 1.

When the measurement result is |+⟩ci, the quantum state collapses to |K1⟩.

|K1⟩=(αiai|000⟩+αibi|100⟩−βiai|111⟩+βibi|011⟩)sisi,isi⊕1,i (15)

When the measurement result is |+⟩ci, the quantum state collapses to |K2⟩.

|K2⟩=(αiai|000⟩+αibi|100⟩+βiai|111⟩−βibi|011⟩)sisi,isi⊕1,i (16)

Particularly, Tab. 1 only needs to be held by Charlie and Si, and the receiver Ti does not need to know. After encoding the measurement results, Charlie sends the classic bit Yi to its corresponding sender Si⊕1 through the classical channel C(C,Si⊕1). When Si⊕1 receives Yi, a unitary operation U(Yi) is applied to the particle si⊕1,i according to Tab. 1. Next, Si employs the Z-{|0⟩,|1⟩} basis and the X-{|+⟩,|−⟩} basis to measure particles si and si,i, respectively, and the measurement results are encoded according to Tab. 2.

With the help of Tab. 2, Si encodes its measurement results into a classic bit Xi. After measurements with the single-particle bases, Si obtains the measured quantum state U(Xi⊕1)|ψ⟩si,i⊕1, to which Si applies the unitary operation U(Xi) to find U(X1⊕X2)|ψi⊕1⟩si,i⊕1. Specifically, since in a quantum system, U(Xi)U(Xi⊕1)|ψi⊕1⟩si,i⊕1=|±1|U(X1⊕X2)|ψi⊕1⟩si,i⊕1, the global phase can be ignored.

Thirdly, in the transmission stage, Si sends the quantum state U(X1⊕X2)|ψi⊕1⟩si,i⊕1 to the receiver Ti⊕1 via the quantum channel Q(Si,Ti⊕1), and the classic bit Xi to the intermediate node S0 via the classical channel C(Si,S0). After successful transmission of Xi to S0, an EX-OR (Exclusive-OR) operation is performed to obtain X1⊕X2, which is then transmitted to another node T0 via the classic channel C(S0,T0). At T0, X1⊕X2 is copied and transmitted to Ti via the classic channel C(T0,Ti).

Finally, in the decoding stage, Ti applies the unitary operation U(X1⊕X2)−1 to U(X1⊕X2)|ψi⟩si⊕1,ibased on X1⊕X2; that is, U(X1⊕X2)−1 U(X1⊕X2)|ψi⟩si⊕1,i=|ψi⟩si⊕1,i. By the end of the unitary operation, perfect and cross transmission of the quantum states can be realized with the help of the controller Charlie on the butterfly network.

Next, we present an implementation of our scheme on a quantum circuit. As is shown in Fig. 2, Charlie prepares and distributes entangled particles to the senders of S1 and S2. In Fig. 2, single lines represent quantum channels, and double lines stand for classical channels. In this implementation, controlled quantum network coding without information loss is realized with the help of both classical and quantum channels.

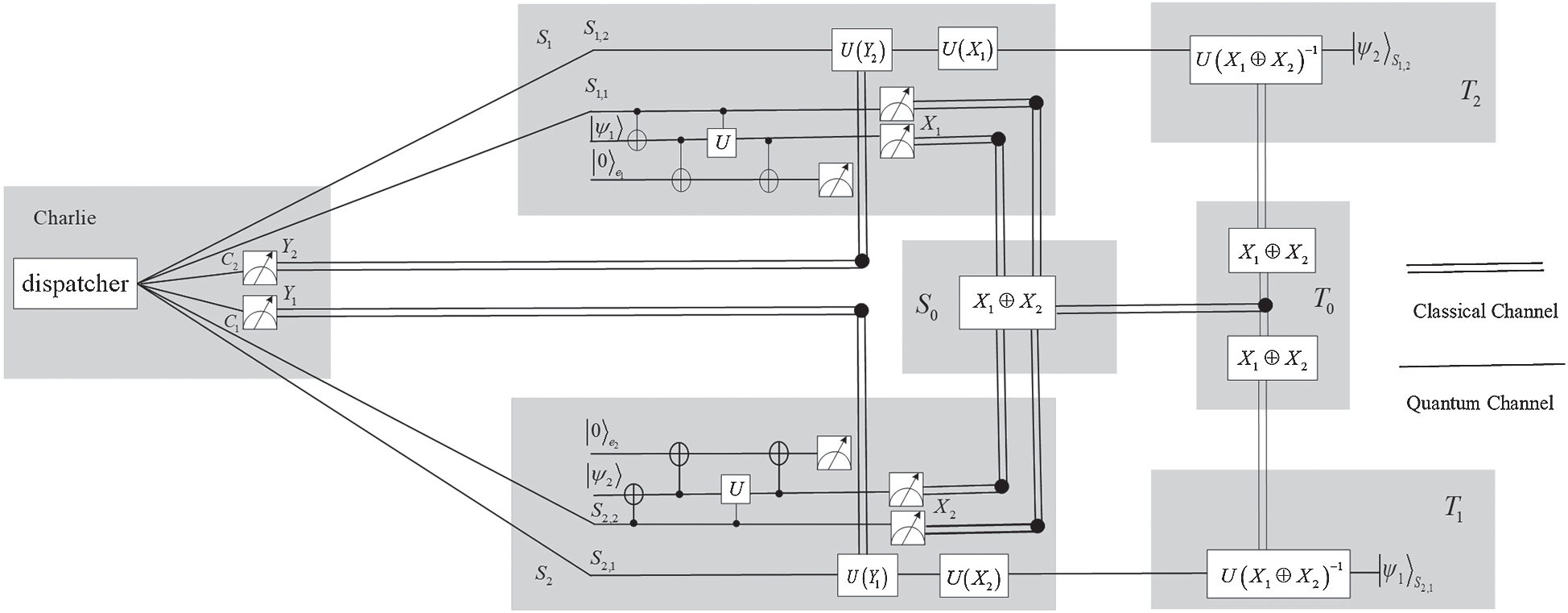
Figure 2: Quantum circuit implementation

Specifically, only senders are controlled by the controller Charlie, which is a feature of this scheme. The receiver only needs to perform unitary operations on the quantum states it received according to Tab. 2, and storage of Tab. 1 becomes unnecessary for the receiver. If Si sends the quantum states to Ti without the consent from Charlie, then Ti will not be able to effectively recover the original quantum states.

3.2 Discussions

In our scheme, the measurement results of the auxiliary particle ei given by Si are sent to Charlie via the classical channel C(Si,C). When the measurement results of both auxiliary particles are |0⟩, Charlie would control the transmission of quantum states on the butterfly network to be successful. On the other hand, if both measurement results are |1⟩, the quantum states will not be successfully transmitted, as described in the following:

|T11⟩=(ai|0⟩+bi|1⟩)si|111⟩si,isi⊕1,ici (17)

However, the quantum states will not be lost. Si will get a quantum state (ai|0⟩+bi|1⟩)si with a probability of βi2−αi2. Besides, Charlie does not need to employ the X-{|+⟩,|−⟩} basis to measure its own particles. In this way, Charlie only needs to re-prepare two pairs of three-particle non-maximum entangled states for a new cycle until the measurements given by the senders for both auxiliary particles are |0⟩.

When the measurement given by one party on its own auxiliary particle is |0⟩, and that from the other party is |1⟩, only one quantum state can be transmitted successfully on the butterfly network. We assume that the measurement given by S1 on e1 is |0⟩e1 and that given by S2 is |1⟩e1. At such circumstances, the quantum state will collapse to |T01⟩.

|T01⟩=(αiai|0000⟩+αibi|1000⟩−βiai|1111⟩+βibi|0111⟩)s1s1,1s2,1c1⊗(ai|0⟩+bi|1⟩)s2|111⟩s2,2s1,2c2 (18)

Here, Charlie re-prepares one three-particle non-maximum entangled state, and distributes the particles to the senders for retransmission of the quantum state. The party who failed in the beginning joins a new round of our scheme until Charlie receives the measurements of its auxiliary particles given by both senders are |0⟩. Subsequently, the Z-{|0⟩,|1⟩} basis is employed to measure the remaining particles. In this way, when transmission fails, the quantum and classical channels will not be occupied. Additionally, a buffer time T is set in our scheme. If the measurements of the auxiliary particles remain |1⟩ within T for one party, a new round will start.

3.3 Scheme Flow Chart

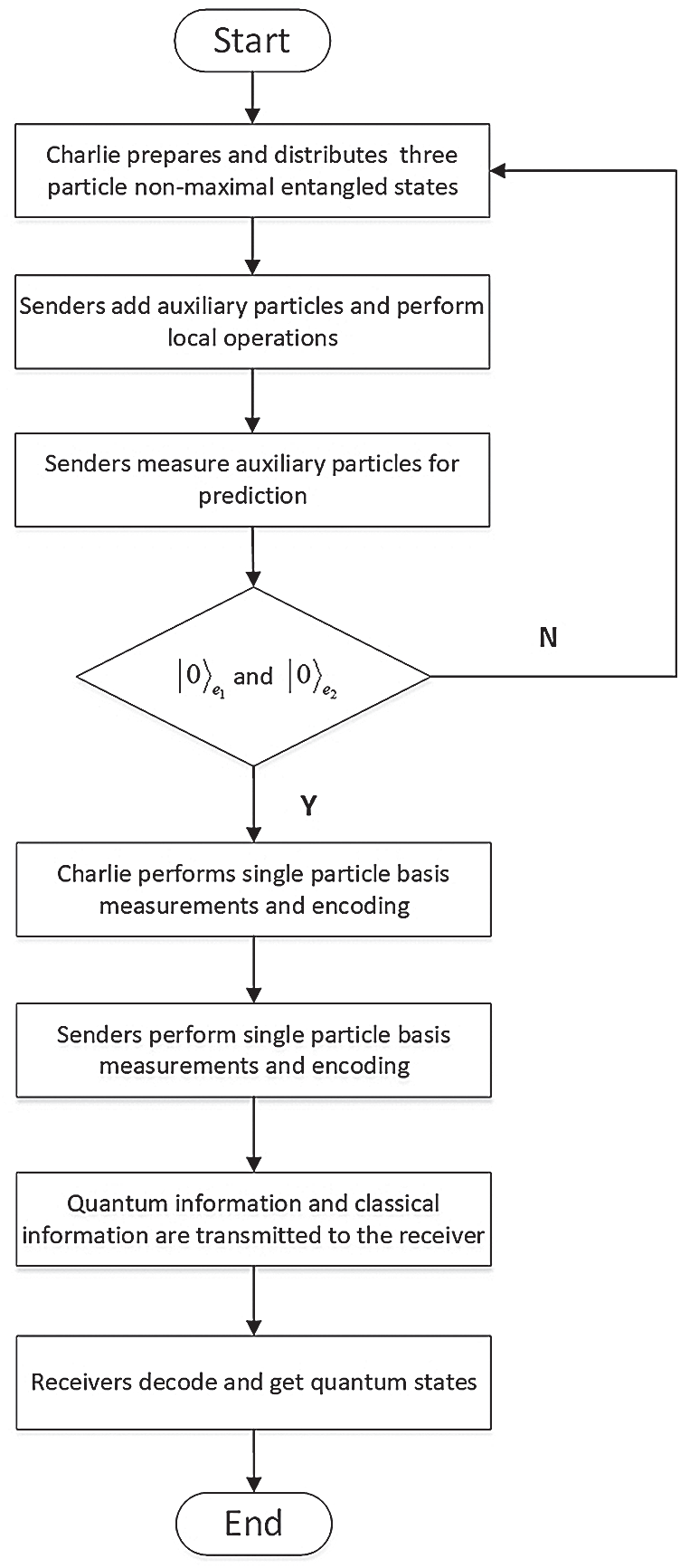
Figure 3: The flow chart of our scheme

In order to demonstrate our scheme more clearly, we hereby give a flow chart in Fig. 3. By measuring the auxiliary particles, senders can predict whether the quantum states can be transmitted on the butterfly network in a controlled way. Only the parties with a measurement result of |1⟩, instead of the quantum states, can inform the controller Charlie to re-prepare three-particle non-maximum entangled states.

3.4 Safety Analysis

Quantum network coding is used to solve the congestion problem in the transmission of quantum information, as well as to improve the transmission efficiency, increase network throughput and promote network security. In our scheme, if the sender wants to send a quantum state to the receiver, it needs the consent from a third party Charlie for effective transmission. Therefore, with our scheme, an eavesdropper Eve shall not obtain the original quantum information. In addition, we have not considered inevitable information destruction.

In our scheme, it is Charlie’s responsibility to prepare the three-particle non-maximum entangled states and distribute the auxiliary particles to the senders. Information security in this procedure is guaranteed by the BB84 protocol [35]. When the measurement results given by both senders on the auxiliary particles are |0⟩, it shows that the quantum states can be transmitted over the butterfly network under the control of Charlie. In our scheme, Charlie performs measurement according to the X-{|+⟩,|−⟩} basis, and the senders acts upon both the Z-{|0⟩,|1⟩} basis and the X-{|+⟩,|−⟩} basis. After encoding, a quantum state U(X1⊕X2)|ψ⟩ and its corresponding classical information are obtained at the sender. If Eve gets U(X1⊕X2)|ψ⟩ via the quantum channel but fails to acquire the classical information X1⊕X2, the quantum state |ψ⟩ will not be obtained. On the other hand, if Eve obtains the classical information X1, X2 and X1⊕X2 from the classical channel without U(X1⊕X2)|ψ⟩, information in |ψ⟩will still be secure. Moreover, even if Eve gets U(X1⊕X2)|ψ⟩ and X1⊕X2 simultaneously, |ψ⟩ will still not be decoded without the coding table, which has been well communicated between the sender and the receiver before transmission.

To summarize the analysis above, as long as the coding table, which is not seen during the transmission, is not leaked, our scheme is secure. Therefore, our scheme ensures sufficient information security against external eavesdroppers.

4  Conclusions

In the paper, we propose a controlled quantum network coding without information loss by the employment of three-particle non-maximum entangled states on the butterfly network. In our scheme, a third party Charlie is necessary as the controller for perfect and cross transmission of quantum states.

Compared with previous schemes, our scheme is advantageous in several aspects. First of all, compared with the scheme in [5], our scheme realizes perfect and cross transmission of quantum states. Secondly, compared with the scheme in [9], non-maximum entangled states are employed to realize controlled quantum network coding without information loss instead of maximum ones. Specifically, our scheme avoids preparation of the Bell basis and employs single particle bases to measure particles, which is easier for practical applications. Thirdly, compared with the scheme in [16], we consider the probability of failed transmission with the non-maximum entangled states employed as the quantum channel. When the auxiliary particles are measured to be |1⟩, we avoid the re-preparation of quantum states and invalid information transmission on the butterfly network, which improve the utilization efficiency of the channels. Finally, we give an implementation of our scheme on the quantum circuit, which is of great reference value for future studies.

As for the future prospects, we hope that our scheme can be applied in practice. Moreover, this scheme could be extended to a quantum k-pair butterfly network to achieve perfect, cross and controlled transmission of k quantum states with further researches. We also hope that our work can contribute to the development of quantum communication [36–41].

Funding Statement: This work is supported by NSFC (Grant Nos. 92046001, 61571024, 61671087, 61962009, 61971021), the Aeronautical Science Foundation of China (2018ZC51016), the Fundamental Research Funds for the Central Universities (Grant No. 2019XD-A02), the Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant Nos. 2018BDKFJJ018, 2019BDKFJJ010, 2019BDKFJJ014), the Open Research Project of the State Key Laboratory of Media Convergence and Communication, Communication University of China, China (Grant No. SKLMCC2020KF006). Huawei Technologies Co. Ltd (Grant No. YBN2020085019), the Scientific Research Foundation of North China University of Technology.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Ahlswede, N. Cai, S. R. Li and R. W. Yeung, “Network information flow,” IEEE Transactions on Information Theory, vol. 46, no. 4, pp. 1204–1216, 2000. [Google Scholar]

 2.  M. Hayashi, K. Iwama and H. Nishimura, “Quantum network coding,” in Proc. STACS, Berlin, Heidelberg, Springer, pp. 610–621, 2007. [Google Scholar]

 3.  W. K. Wootters and W. H. Zurek, “A single quantum cannot be cloned,” Nature, vol. 299, no. 5886, pp. 802–803, 1982. [Google Scholar]

 4.  V. Buzek and M. Hillery, “Quantum copying: Beyond the no-cloning theorem,” Physical Review A, vol. 54, no. 3, pp. 1844–1852, 1996. [Google Scholar]

 5.  T. Shang, X. J. Zhao, C. Wang and J. W. Liu, “Controlled quantum network coding scheme based on single controller,” Acta Electronica Sinica, vol. 42, no. 10, pp. 1913–1917, 2014. [Google Scholar]

 6.  H. Kobayashi, F. L. Gall, H. Nishimura and M. Rotteler, “General scheme for perfect quantum network coding with free classical communication,” in Proc. ICALP, Lecture Note in Computer Science, Rhodes, Greece, Berlin, Heidelberg: Springer, vol. 5555, pp. 622–633, 2009. [Google Scholar]

 7.  H. Kobayashi, F. Le Gall, H. Nishimura and M. Rotteler, “Perfect quantum network communication protocol based on classical network coding,” in IEEE Int. Symp. on Information Theory, Austin, TX, USA, IEEE, pp. 2686–2690, 2010. [Google Scholar]

 8.  H. Kobayashi, F. Le Gall, H. Nishimura and M. Rotteler, “Constructing quantum network coding schemes from classical nonlinear protocols,” in IEEE Int. Symp. on Information Theory Proceedings, St. Petersburg, Russia, IEEE, pp. 109–113, 2011. [Google Scholar]

 9.  M. Hayashi, “Prior entanglement between senders enables perfect quantum network coding with modification,” Physical Review A, vol. 76, no. 4, pp. 40301, 2007. [Google Scholar]

10. L. Jiang, J. M. Taylor, K. Nemoto, W. J. Munro, R. V. Meter et al., “Quantum repeater with encoding,” Physical Review A, vol. 79, no. 3, pp. 32325, 2009. [Google Scholar]

11. T. J. Wang, S. Y. Song and G. L. Long, “Quantum repeater based on spatial entanglement of photons and quantum-dot spins in optical microcavities,” Physical Review A, vol. 85, no. 6, pp. 62311, 2012. [Google Scholar]

12. Z. D. Li, R. Zhang, X. F. Yin, Y. Hu and Y. Q. Fang, “Experimental quantum repeater without quantum memory,” Nature Photonics, vol. 13, no. 9, pp. 644–648, 2019. [Google Scholar]

13. T. Satoh, F. Le Gall and H. Imai, “Quantum network coding for quantum repeaters,” Physical Review A, vol. 86, no. 3, pp. 32331, 2012. [Google Scholar]

14. C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres et al., “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Physical Review Letters, vol. 70, no. 13, pp. 1895, 1993. [Google Scholar]

15. D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H. Weinfurter et al., “Experimental quantum teleportation,” Nature, vol. 390, no. 6660, pp. 575–579, 1997. [Google Scholar]

16. S. Y. Ma, X. B. Chen, M. X. Luo, X. X. Niu and Y. X. Yang, “Probabilistic quantum network coding of M-qudit states over the butterfly network,” Optics Communications, vol. 283, no. 3, pp. 497–501, 2010. [Google Scholar]

17. T. Shang, J. Li, Z. Pei and J. W. Liu, “Quantum network coding for general repeater networks,” Quantum Information Processing, vol. 14, no. 9, pp. 3533–3552, 2015. [Google Scholar]

18. T. Satoh, K. Ishizaki, S. Nagayama and R. V. Meter, “Analysis of quantum network coding for realistic repeater networks,” Physical Review A, vol. 93, no. 3, pp. 32302, 2016. [Google Scholar]

19. T. Matsuo, T. Satoh, S. Nagayama and R. V. Meter, “Analysis of measurement-based quantum network coding over repeater networks under noisy conditions,” Physical Review A, vol. 97, no. 6, pp. 62328, 2018. [Google Scholar]

20. D. D. Li, F. Gao, S. J. Qin and Q. Y. Wen, “Perfect quantum multiple-unicast network coding protocol,” Quantum Information Processing, vol. 17, no. 1, pp. 13, 2018. [Google Scholar]

21. G. Xu, X. B. Chen, J. Li, C. Wang and Y. X. Yang, “Network coding for quantum cooperative multicast,” Quantum Information Processing, vol. 14, no. 11, pp. 4297–4322, 2015. [Google Scholar]

22. J. Li, X. B. Chen, G. Xu and Y. X. Yang, “Perfect quantum network coding independent of classical network solutions,” IEEE Communication Letters, vol. 19, no. 2, pp. 115–118, 2014. [Google Scholar]

23. Z. Li, G. Xu, X. B. Chen and Y. X. Yang, “Secure quantum network coding based on quantum homomorphic message authentication,” Quantum Information Processing, vol. 18, no. 1, pp. 14, 2019. [Google Scholar]

24. X. B. Chen, Y. L. Wang, G. Xu and Y. X. Yang, “Quantum network communication with a novel discrete-time quantum walk,” IEEE Access, vol. 7, pp. 13634–13642, 2019. [Google Scholar]

25. P. Pathumsoot, T. Matsuo, T. Satoh, M. Hajdušek, S. Suwanna et al., “Modeling of measurement-based quantum network coding on a superconducting quantum processor,” Physical Review A, vol. 101, no. 5, pp. 52301, 2020. [Google Scholar]

26. H. Lu, Z. D. Li, X. F. Yin, R. Zhang, X. X. Fang et al., “Experimental quantum network coding,” npj Quantum Information, vol. 5, no. 1, pp. 89, 2019. [Google Scholar]

27. T. Shang, R. Liu, J. Liu and Y. Hou, “Continuous-variable quantum network coding based on quantum discord,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1629–1645, 2020. [Google Scholar]

28. L. Roa and C. Groiseau, “Probabilistic teleportation without loss of information,” Physical Review A, vol. 91, no. 1, pp. 12344, 2015. [Google Scholar]

29. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information. Cambridge: Cambridge University Press, pp. 171–200, 2000. [Google Scholar]

30. Z. G. Qu, S. Y. Wu, W. J. Liu and X. J. Wang, “Analysis and improvement of steganography protocol based on bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624, 2019. [Google Scholar]

31. W. L. Li, C. F. Li and G. C. Guo, “Probabilistic teleportation and entanglement matching,” Physical Review A, vol. 61, no. 3, pp. 34301, 2000. [Google Scholar]

32. T. Gao, F. L. Yan and Z. X. Wang, “Controlled quantum teleportation and secure direct communication,” Chinese Physics, vol. 14, no. 5, pp. 893–897, 2005. [Google Scholar]

33. C. P. Yang, S. H. Chu and S. Y. Han, “Efficient many-party controlled teleportation of multiqubit quantum information via entanglement,” Physical Review A, vol. 70, no. 2, pp. 22329, 2004. [Google Scholar]

34. Z. G. Qu, S. Y. Chen and X. J. Wang, “A secure controlled quantum image steganography algorithm,” Quantum Information Processing, vol. 19, no. 380, pp. 1–25, 2020. [Google Scholar]

35. C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” in Proc. of IEEE Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India, pp. 175–179, 1984. [Google Scholar]

36. N. Gisin and R. Thew, “Quantum communication,” Nature Photon, vol. 1, no. 3, pp. 165–171, 2007. [Google Scholar]

37. S. Wengerowsky, S. K. Joshi, F. Steinlechner, H. Hübel and R. Ursin, “An entanglement-based wavelength-multiplexed quantum communication network,” Nature, vol. 564, no. 7735, pp. 225–228, 2018. [Google Scholar]

38. Z. Dou, G. Xu, X. B. Chen and K. Yuan, “Rational non-hierarchical quantum state sharing protocol,” Computers, Materials & Continua, vol. 58, no. 2, pp. 335–347, 2019. [Google Scholar]

39. X. B. Chen, Y. R. Sun, G. Xu and Y. X. Yang, “Quantum homomorphic encryption scheme with flexible number of evaluator based on (k, n)-threshold quantum state sharing,” Information Sciences, vol. 501, no. 1, pp. 172–181, 2019. [Google Scholar]

40. G. Xu, K. Xiao, Z. P. Li, X. X. Niu and M. Ryan, “Controlled secure direct communication protocol via the three-qubit partially entangled set of states,” Computers, Materials & Continua, vol. 58, no. 3, pp. 809–827, 2019. [Google Scholar]

41. S. Pirandola, “End-to-end capacities of a quantum communication network,” Communications Physics, vol. 2, no. 51, pp. 1023, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.