Computers, Materials & Continua DOI:10.32604/cmc.2021.017854
Article

Medical Feature Selection Approach Based on Generalized Normal Distribution Algorithm

Mohamed Abdel-Basset1, Reda Mohamed1, Ripon K. Chakrabortty2, Michael J. Ryan2, Yunyoung Nam3,* and Mohamed Abouhawwash4,5

1Faculty of Computers and Informatics, Zagazig University, Zagazig, 44519, Egypt
2Capability Systems Centre, School of Engineering and IT, UNSW, Canberra, Australia
3Department of Computer Science and Engineering, Soonchunhyang University, Asan, 31538, Korea
4Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt
5Department of Computational Mathematics, Science, and Engineering (CMSE), Michigan State University, East Lansing, 48824, MI, USA
*Corresponding Author: Yunyoung Nam. Email: ynam@sch.ac.kr
Received: 12 February 2021; Accepted: 16 March 2021

Abstract: This paper proposes a new pre-processing technique to separate the most effective features from those that might deteriorate the performance of the machine learning classifiers in terms of computational costs and classification accuracy because of their irrelevance, redundancy, or less information; this pre-processing process is often known as feature selection. This technique is based on adopting a new optimization algorithm known as generalized normal distribution optimization (GNDO) supported by the conversion of the normal distribution to a binary one using the arctangent transfer function to convert the continuous values into binary values. Further, a novel restarting strategy (RS) is proposed to preserve the diversity among the solutions within the population by identifying the solutions that exceed a specific distance from the best-so-far and replace them with the others created using an effective updating scheme. This strategy is integrated with GNDO to propose another binary variant having a high ability to preserve the diversity of the solutions for avoiding becoming stuck in local minima and accelerating convergence, namely improved GNDO (IGNDO). The proposed GNDO and IGNDO algorithms are extensively compared with seven state-of-the-art algorithms to verify their performance on thirteen medical instances taken from the UCI repository. IGNDO is shown to be superior in terms of fitness value and classification accuracy and competitive with the others in terms of the selected features. Since the principal goal in solving the FS problem is to find the appropriate subset of features that maximize classification accuracy, IGNDO is considered the best.

Keywords: Generalized normal distribution optimization; feature selection; transfer function; novel restarting strategy; UCI repository

1  Introduction

In the last few years, the dimensionality of problem features has significantly grown which has negatively affected several fields such as data mining, data science, big data, and several others. High-dimensional features cause a number of problems during analysis complexity, dimensionality, and sparsity [1], in addition to reducing classification accuracy and increasing the cost of the machine learning techniques. Researchers therefore seek a feature-selection technique that is able to select the most effective subset of features which maximize classification accuracy and minimize expensive computation [2]. Of the feature extraction approaches available, filter-based approaches evaluate the features independently but suffer from the issues of local minima and computation time. On the other hand, a wrapper-based approach has received significant interest from researchers due to better classification quality as a result of using a machine learning technique to evaluate the quality of the extracted features.

In a wrapper-based approach, evolutionary algorithms and meta-heuristic algorithms are used as optimizers to select the best subset of features. It is also worth mentioning that there are several traditional techniques for tackling this problem, including greedy search, and random search, but those techniques suffer from becoming stuck in local minima and have expensive computational costs, so researchers have moved toward the evolutionary and meta-heuristic algorithms. In particular, meta-heuristic algorithms have received significant attraction due to their strengths in achieving better outcomes in a reasonable time for several optimization problems [3–8]. The remainder of this section reviws of the major published meta-heuristic and evolutionary feature selection techniques.

In [9], a new feature selection technique based on the improved Harris hawks optimization algorithm (IHHO) using the opposition-based mechanism and a new search mechanism was proposed by Sihwail et al. [9]. IHHO can avoid local minima and subsequently improve the quality of the solutions by accelerating convergence providing superior performance to the standard HHO. IHHO was verified on 20 datasets and was shown to be better than (in terms of fitness values, accuracy, and extracted features) than a number of other optimizers: grasshopper optimization algorithm (GOA), whale optimization algorithm (WOA), generic algorithm (GA), particle swarm optimization (PSO), butterfly optimization algorithm (BOA), ant lion optimizer (ALO) and slime mould algorithm (SMA).

Bhattacharyya et al. [10] combined the mayfly algorithm with harmony search for FS, in an approach called mayfly-harmony search (MA-HS). MA-HS improves exploitation capability by avoiding local minima to achieve better outcomes. MA-HS was shown to have better performance than 12 optimization techniques verified on 18 UCI datasets. The sailfish (BSF) optimizer improved using β-hill climbing (AβHC) meta-heuristic algorithm was proposed by Ghosh et al. [11] who used 18 UCI datasets to verify the performance, showing that its performance was superior to 10 state-of-the-art algorithms.

In [12], the quantum whale optimization algorithm (QWOA) has been recently proposed for the FS problem. QWOA was compared with 8 well-known optimization algorithms to see its effectiveness in extracting the best subset of features for 14 datasets from diversified domains. Furthermore, Abdel-Basset et al. [13] proposed a binary version of the improved HHO (HHOSA) for FS which used the bitwise operator and simulated annealing with HHO to avoid local minima, improving the quality of the solutions. HHOSA was verified using 43 instances and was shown to be superior to some well-established algorithms.

A new variant of the grey-wolf optimizer (GWO) hybridized with a two-phase mutation (TMGWO) was proposed by Abdel-Basset et al. [14] to improve the exploitation capability of GWO. TMGWO was shown to be superior to a number of well-known optimization algorithms such as flower algorithm, particle swarm optimization algorithm, multi-verse optimizer algorithm, whale optimization algorithm, and bat algorithm.

Several other meta-heuristic algorithms have recently been adapted for the FS problem such as binary dragonfly algorithm [15], brainstorm optimization [16], whale optimization algorithm [17], genetic algorithm [18], enhanced Harris hawks optimization [19], harmony search and naked mole-rat algorithms [20], cosine similarity-based harmony search algorithm [21], modified harmony search algorithm [22], and several others [2].

Recently, a new optimization algorithm has been proposed for tackling the parameter estimations problem of the solar cell and photovoltaic module models [23]. This algorithm was called the generalized normal distribution optimization algorithm (GNDO) since it was inspired by the normal distribution theory. GNDO can estimate the parameter values that minimize the sum of squared error between the I-V measured and I-V estimated, showing its effectiveness in avoiding local minima. To the best of our knowledge, the effectiveness of this algorithm in tackling binary problems such as knapsack and FS is not yet known. Therefore, in this paper, two variants of GNDO are proposed for FS. The first variant applies the standard GNDO transformed using the arctangent transfer function; the second uses a novel strategy known as a novel restarting strategy (RS) to preserve the diversity among the members of the population. RS searches for the solutions that exceed a specific critical distance from the best-so-far solution; then, a novel updating scheme is used to update those solutions to preserve the diversity by improving the quality of the solutions. This RS is integrated with the standard GNDO to propose a new binary variant called IGNDO. The proposed GNDO and IGNDO algorithms are experimentally verified using 13 UCI instances and compared with seven well-known recently-published binary optimization algorithms, namely TMGWO [14], non-linear particle swarm optimization algorithm (NLPSO) [24], WOA [25], marine predators algorithm (MPA) [26], equilibrium optimizer (EO) [27], binary slime mould algorithm integrated with a novel attacking-feeding strategy (FMBSMA) [2], and HHOSA [13]. The experimental outcomes confirm the superiority of the proposed IGNDO and GNDO algorithms in terms of classification accuracy and fitness values, and show them to be competitive in terms of the number of selected features. Further, IGNDO outperforms GNDO in terms of the number of selected features, classification accuracy and average fitness value.

The remainder of this paper is arranged as follows. Section 2 describes the methods used and the proposed algorithm; Section 3 presents outcomes and discussions; and Section 4 draws conclusions and introduces intended future work.

2  Methods and Proposed Algorithm

2.1 Generalized Normal Distribution Optimization

A novel optimization algorithm [23] called generalized normal distribution optimization (GNDO) has been recently proposed for tackling the nonlinear optimization problems, specifically the solar cell parameters estimation problems. This algorithm was inspired by the normal distribution theory and is based on the two main stages of optimization methods: exploration and exploitation. In the exploration stage, the algorithm works on exploring the search space to find the most promising region, which might involve the optimal solution. The latter stage focuses on this region to reach the optimal solution. In the remainder of this section, those two stages in GNDO are explained in detail.

2.1.1 Local Exploitation

The local exploitation stageconsiders the mean μi of three selected solutions—the best-so-far solution X∗, the position vector of the ith solution Xit, and the mean M of the solutions calculated using Eq. (3)—as the promising region in the current generation t, which is mathematically calculated by Eq. (2). Then, it searches around this promising region based on a step size generated by Eq. (4) to generate a new trial solution Tit as described in Eq. (1), which might be better than the current one. This trial solution will be compared with the current one, and if it is better, it will be used in the next generation.

Tit=μi+δi×η,∀i=1:N (1)

μi=(Xit+X∗+M)/3.0 (2)

M=∑i=1NXitN (3)

δi=13[(Xit−μ)2+(X∗−μ)2+(M−μ)2)] (4)

N is the population size. η, which is mathematically modeled in Eq. (5), is the penalty factor.

η={−log⁡(ℷ1)×cos⁡(2πℷ2),r1≤r2−log⁡(ℷ1)×cos⁡(2πℷ2+π),r1>r2 (5)

r1,r2, ℷ1, and ℷ2 are four numbers randomly created between 0 and 1.

2.1.2 Global Exploration

In the global exploration phase, the search space of the optimization problem will be intensively explored to identify the most promising region that might involve the optimal solution. This phase is mathematically formulated as follows:

Tit=Xit+β×(|ℷ3|×v1)+(1−β)×(|ℷ4|×v2) (6)

ℷ3 and ℷ4 are numerical values generated randomly based on the standard normal distribution, β is a numerical value generated randomly between 0 and 1. v1 and v2 are two trial vectors generated by:

v1={Xit−Xp1t,if f(Xit)≤f(Xp1t)Xp1t−Xit,otherwise (7)

v2={Xp2t−Xp3t,if f(Xp2t)≤f(Xp3t)Xp3t−Xp2t,otherwise (8)

p1,p2, and p3 are indices picked randomly from the solutions, such that p1≠p2≠p3≠i. Exchanging between the exploration and exploitation in GNDO is undertaken randomly.

2.2 Proposed Algorithm: Improved GNDO (IGNDO)

This section describes a novel restarting strategy that is used to improve GNDO in its performance to estimate the number of features that might maximize the classification accuracy of the machine learning technique; this proposed algorithm is called improved GNDO (IGNDO).

2.2.1 Initialization

To start, N solutions with d dimensions indicate the feature length. Each solution is created and initialized randomly with a binary value: 0 to distinguish the unselected features and 1 for the selected ones. Those initialized solutions will then be evaluated as explained in the next section.

2.2.2 Evaluation

The solutions of the FS problem are evaluated using two objectives: the number of the selected features, and the classification accuracy based on those selected features. In [28], an objective function was proposed to relate between those two conflicting objectives based on a weighting variable α, which is a value between 0 and 1, that might pay attention toward one objective at the expense of the other according to the need of the decision makers. In this problem, the main objective is to maximize the classification accuracy, even if the number of features is still high. Therefore, the weighting variable will be moved toward maximizing the classification accuracy of the selected features. This function is mathematically formulated according to that:

f(Xit)=α ∗ γR(D)+(1−α)∗|S||L| (9)

γR(D) indicates the classification error rate obtained according to the extracted features used to train the k-nearest neighbor classifier (KNN), |S| is the selected features length, and |L| is the feature-length in the studied instance. In our work, each dataset is divided into two parts based on the holdout method [29]: the first part will be used as a training dataset and represents 80% of the original dataset, while the other is used as a test dataset.

2.2.3 Transfer Function

Unfortunately, the solutions created by GNDO are continuous, not binary, which means that they cannot be used as solutions to this problem. Consequently, a transfer function of the V-Shaped family, namely arcTan described in Eq. (10), has been used to normalize the continuous values between 0 and 1, and Eq. (11) is then used to convert those values to binary values.

F(a)=|2π arcTan(π2a)| (10)

Vj={1if Vj>0.50otherwise (11)

2.2.4 A Novel Restarting Strategy

In this section, a new strategy, known as restarting strategy (RS), is proposed to avoid local minima, which affect several optimization algorithms. This strategy calculates the distance between the fitness of the current solution and the best-so-far distance; if this distance exceeds a specific limit, the solution will be restarted within the search space of the problem using a novel updating scheme. At the start, this strategy calculates the distance between the fitness of the current solution Xit and the best-so-far one X∗ as follows:

dist=|f(X∗)−f(Xit)|×−1 (12)

ϵ=edist (13)

where ϵ is the normalized distance. Then, if ϵ is greater than a predefined threshold ρ, Xit will be updated using the following scheme estimated based on our experiments:

Xit=r1X∗+l1×(l2∗X∗−Xit) (14)

where r1 is a random number created based on the uniform distribution, l1 and l2 are two real values generated using the Lévy-flight strategy. Last but not least, this novel strategy is integrated with GNDO to propose a new variant, namely improved GNDO (IGNDO), to solve the FS problem. The steps of IGNDO are presented in Algorithm 1.

3  Experiments and Discussion

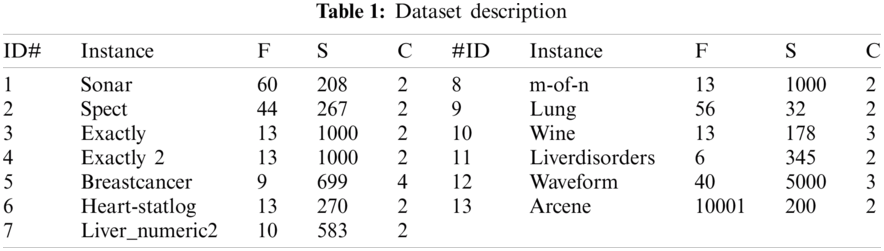
The performance of our proposed algorithm was verified by 13 instances with various feature lengths selected from the UCI machine learning repository [30]. The description of this dataset is briefly presented in Tab. 1, which has five columns: record id (ID), instance, feature lengths (F), number of classes (C), and number of samples (S).

In addition, under the same environment settings, the proposed algorithm is compared with eight robust optimizations algorithms—TMGWO [14], NLPSO [24], WOA [25], marine predators algorithm (MPA) [26], equilibrium optimizer (EO) [27], HHOSA [13], FMBSMA [2], and GNDO—implemented using the Java programming language under the same parameters values cited in the original paper. However, IGNDO has one parameter, ρ, that needs to be estimated accurately to maximize its performance. Therefore, extensive experiments were conducted with various values for this parameter, which show that the performance of this algorithm is maximized when ρ=0.9999. In our experiment, σ is set to a value of 0.99 to pay more attention to classification accuracy. All algorithms were evaluated under the same number of function evaluations, population size, and the number of runs, which were of 1000, 20, and 30, respectively.

The classification accuracy (ACC), fitness values (FV), and selected feature numbers (SFN) were used as performance metrics to evaluate the performance of the algorithms under various statistical analyses: average (Avg), standard deviation (SD), and boxplot.

4  Results and Discussion

In this section, the proposed algorithms: IGNDO and GNDO are compared with the others in terms of the average of FV, the average of ACC, the average of SFN, and the average of SD for values of each performance metric within 30 independent trials. After running each algorithm for 30 independent trials, the average of FV, ACC, and SFN are calculated and presented in Fig. 1, which show the superiority of the proposed IGNDO and GNDO algorithms over the others in terms of ACC and FV, whereby IGNDO occupies the first rank with values of 0.095 and 0.908, respectively. Unfortunately, IGNDO is in fourth rank after HHOSA, MPA, GNDO, and FMBSMA in terms of SFN. However, the main objective in solving the FS problem is to find the subset of features that maximizes the classification accuracy with as few features as possible. Since IGNDO and GNDO outperform the other techniques in terms of classification accuracy, they are deemed to be the best.

In terms of the stability of the algorithms, Fig. 2 shows the average of SD for FV, ACC and SFN values within 30 independent runs, from which it is clear that IGNDO is the best in terms of SD for FV and ACC. However, HHOSA is the best in terms of SD for SFN values within 30 independent runs.

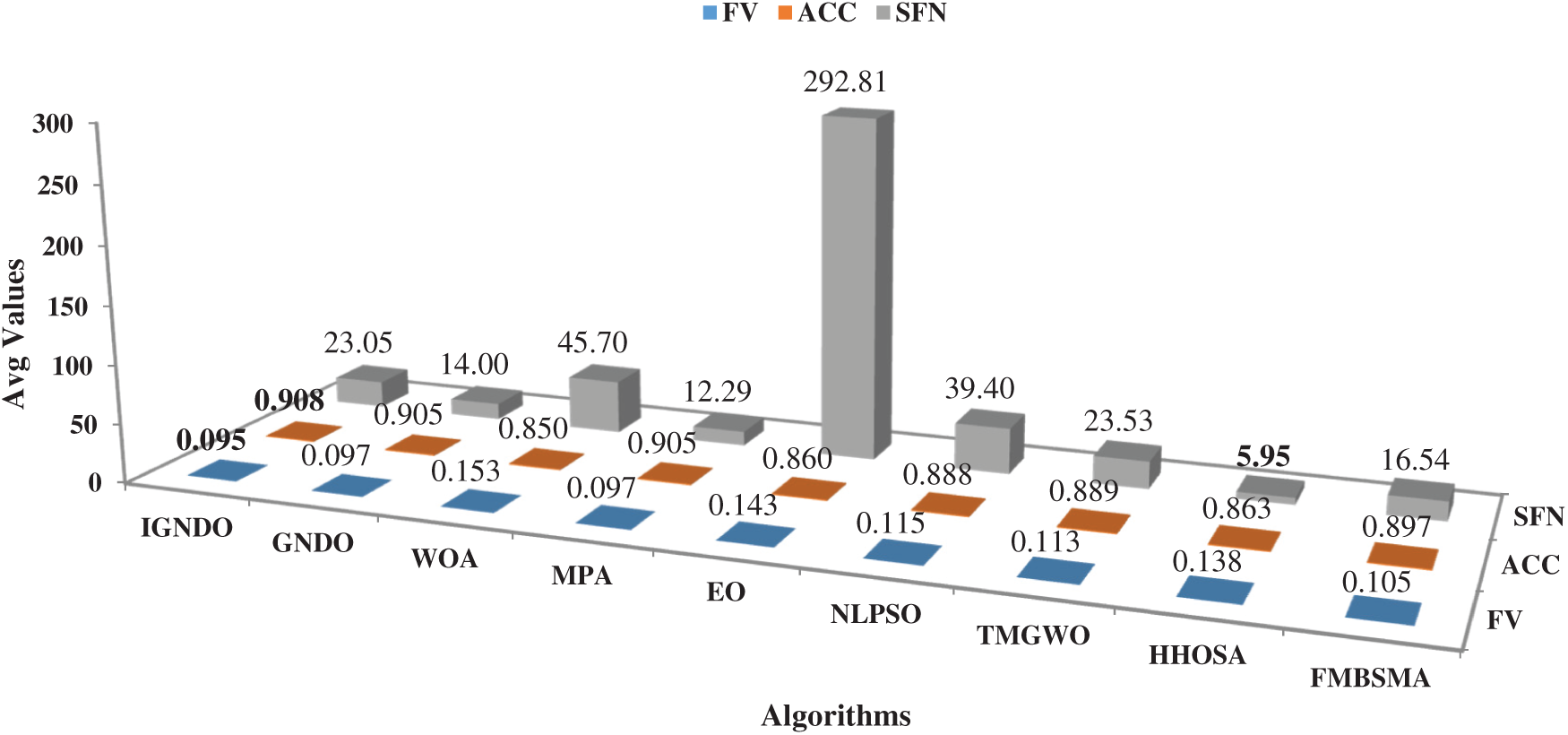
Figure 1: Comparison among algorithms in terms of average of FV, ACC, and SFN

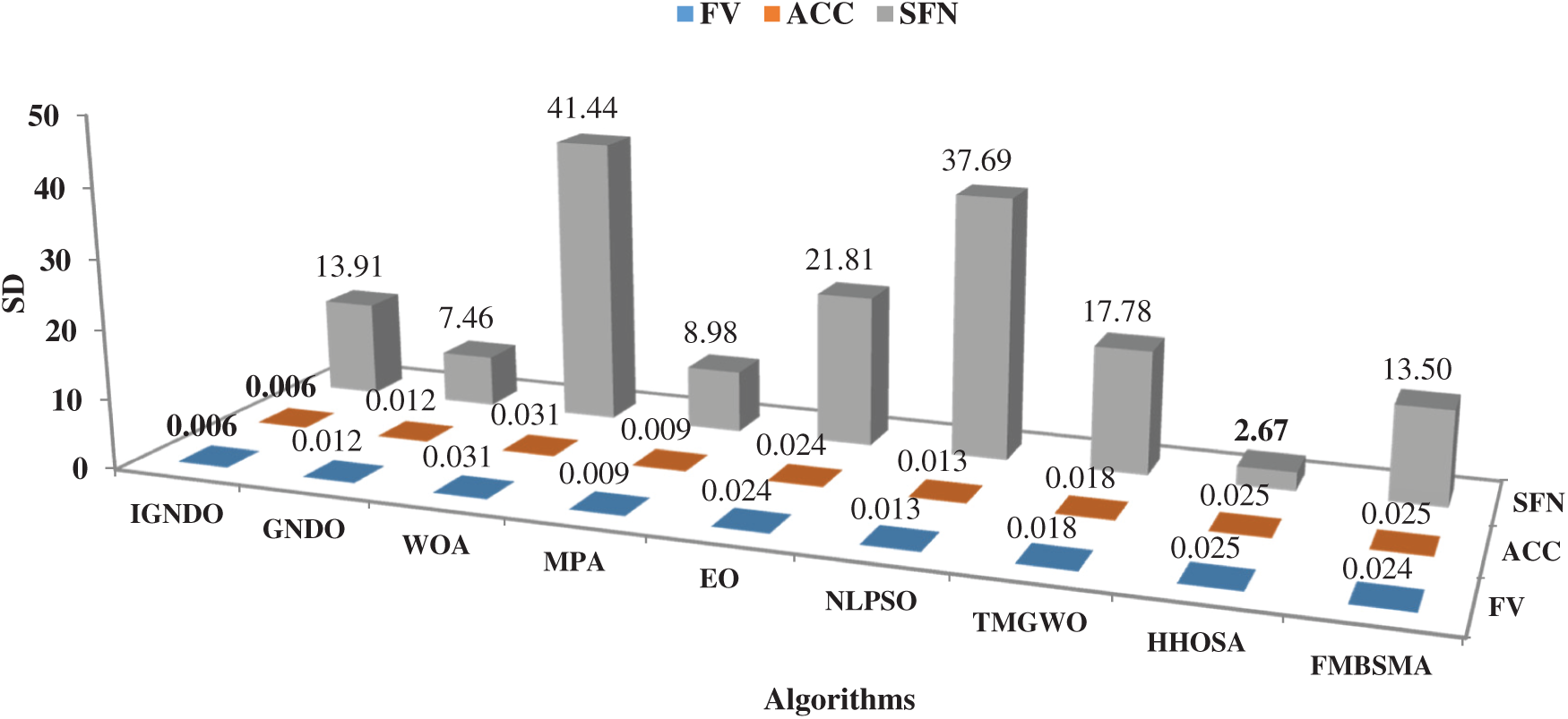
Figure 2: Comparison among algorithms in terms of average SD for FV, ACC, and SFN values

Figs. 3–8 shows the boxplot of the fitness values within 30 independent runs for six instances with the highest dimensions: ID#1, ID#2, ID#3, ID#9, ID#12 and ID#13. The figure shows that the proposed algorithms are better for the worst, mean and SD values in comparison with the other algorithms in most test cases. However, IGNDO does not outperform GNDO in terms of the best values for ID#1, and ID#2. Furthermore, in terms of the classification accuracy, {Figs. 9–14} presents the values of this performance metric obtained by the different compared algorithms within 30 independent runs. It is clear that IGNDO is more stable than the others, in addition to its significant ability in reaching better values for the mean and the minimum in most test cases depicted in Figs. 9–14. This stability and superiority in most test cases for IGNDO are due to the novel restarting strategy, that enables the proposed algorithm to avoid local minima.

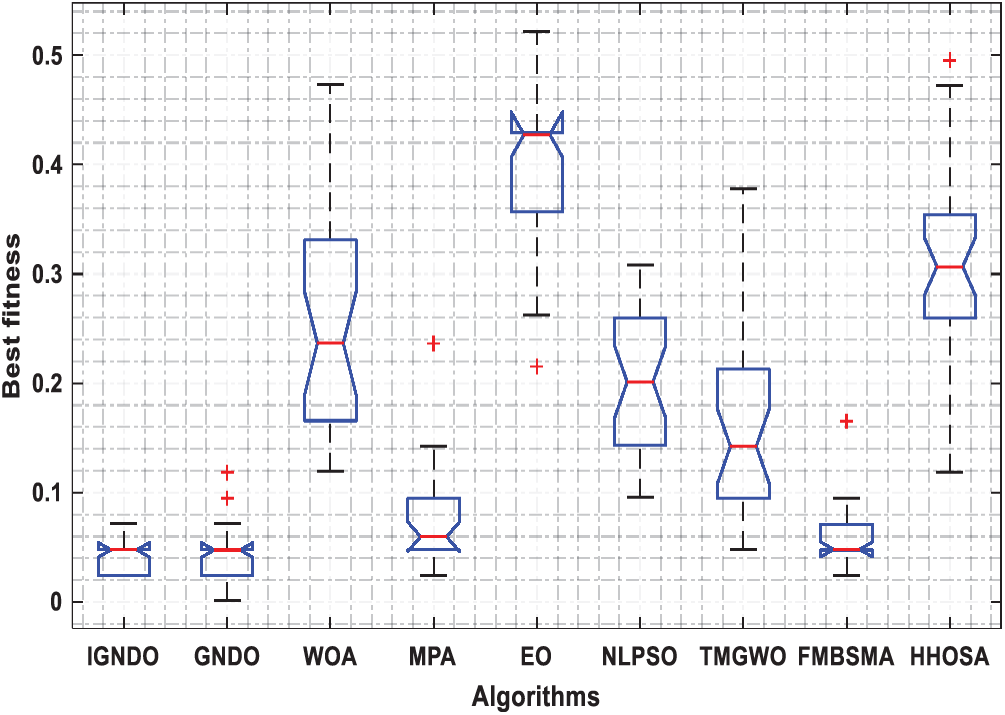
Figure 3: Boxplot for ID#1 in terms of fitness values

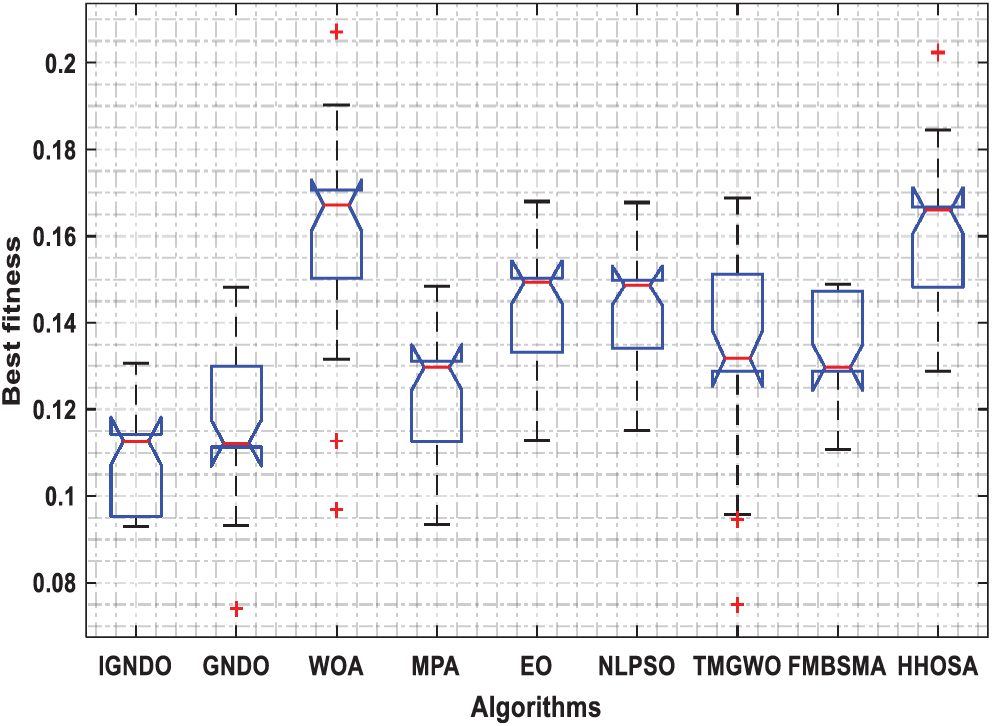
Figure 4: Boxplot for ID#2 in terms of fitness values

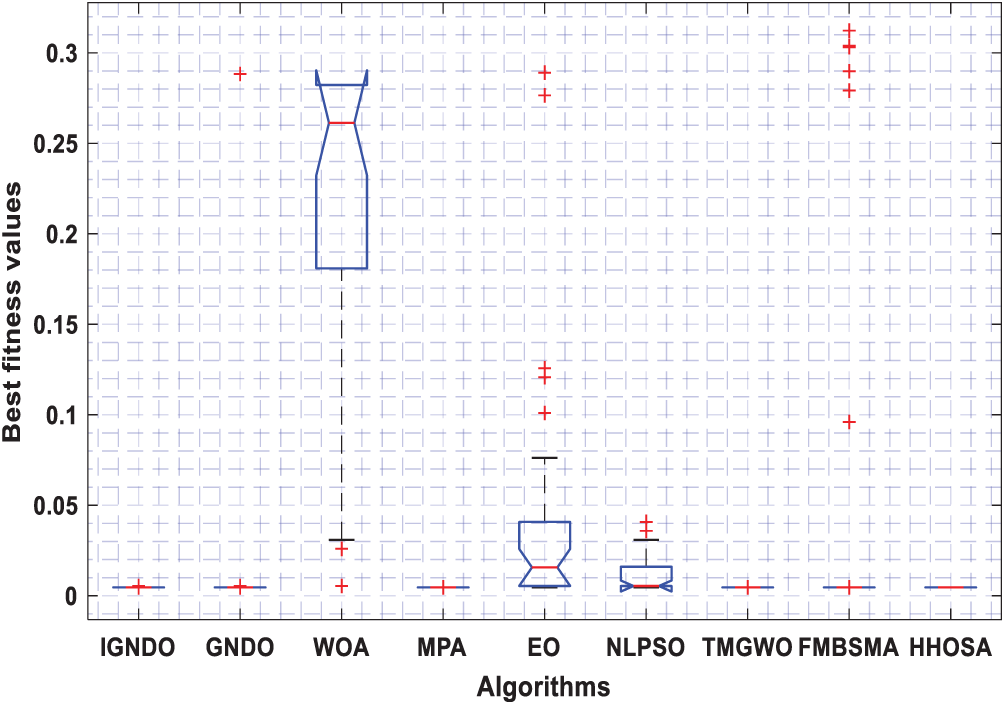
Figure 5: Boxplot for ID#3 in terms of fitness values

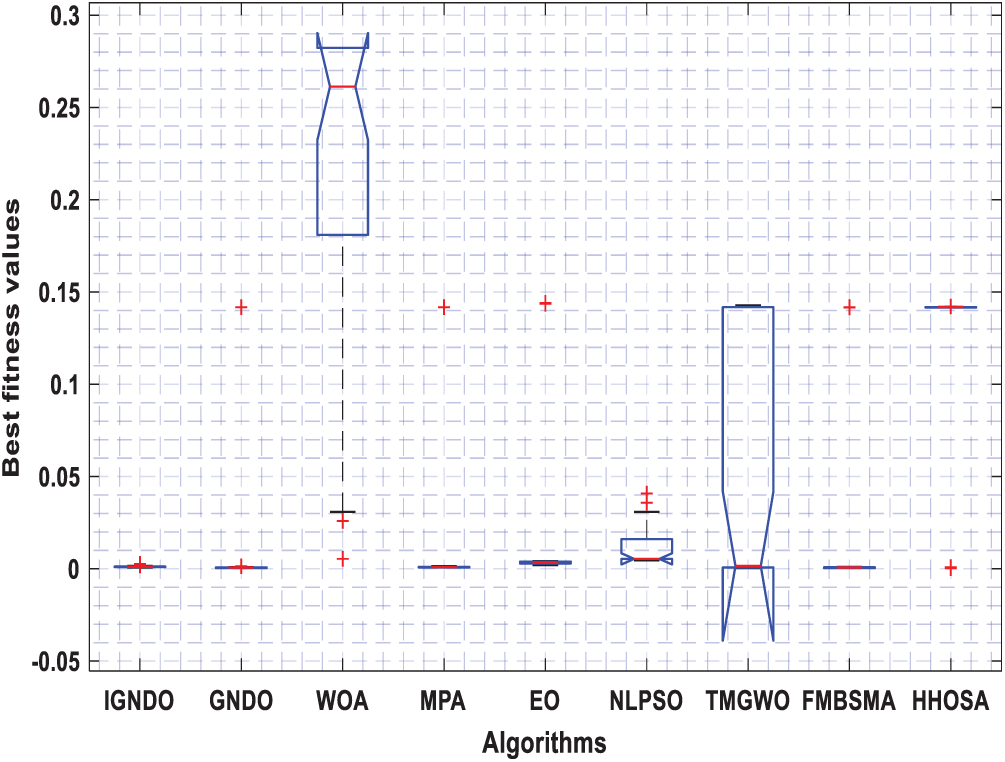
Figure 6: Boxplot for ID#9 in terms of fitness values

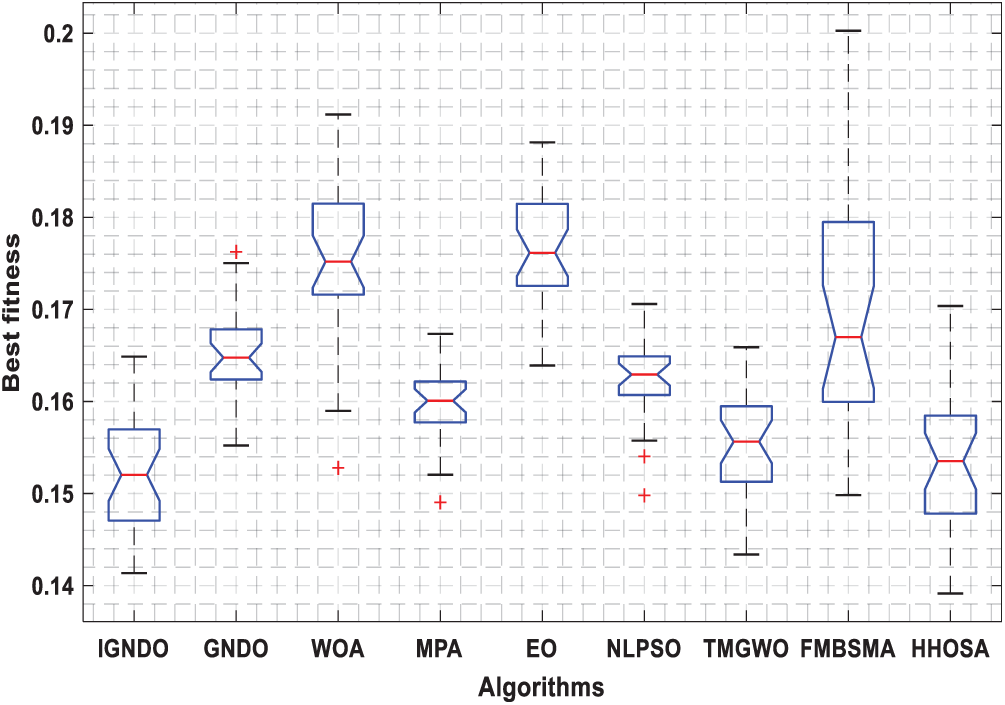
Figure 7: Boxplot for ID#12 in terms of fitness values

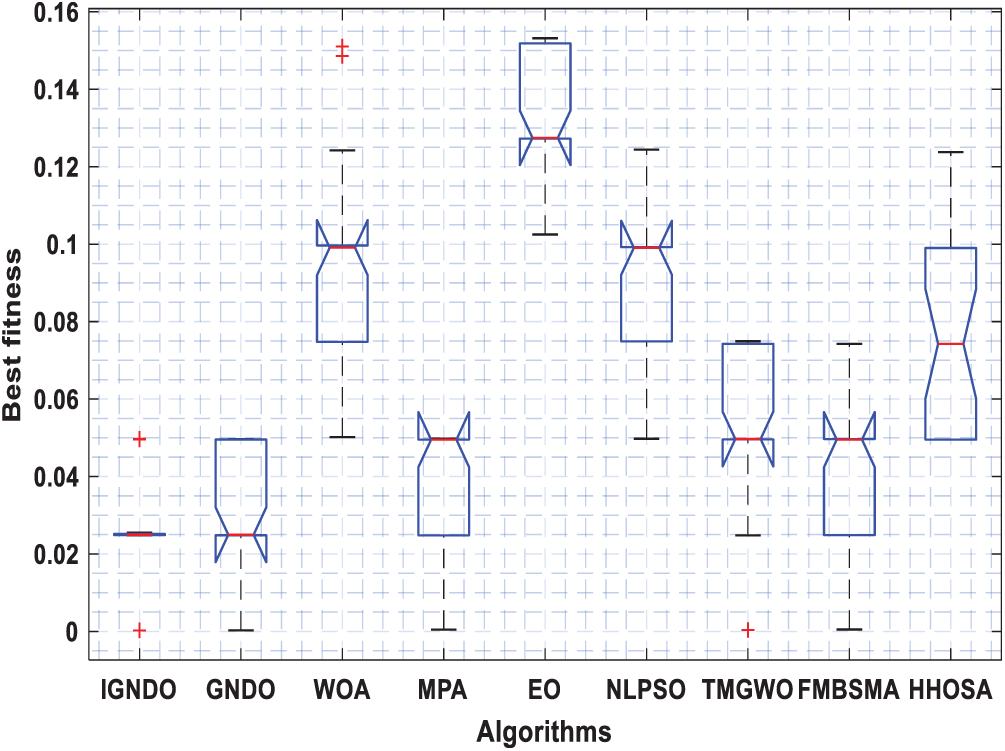
Figure 8: Boxplot for ID#13 in terms of fitness values

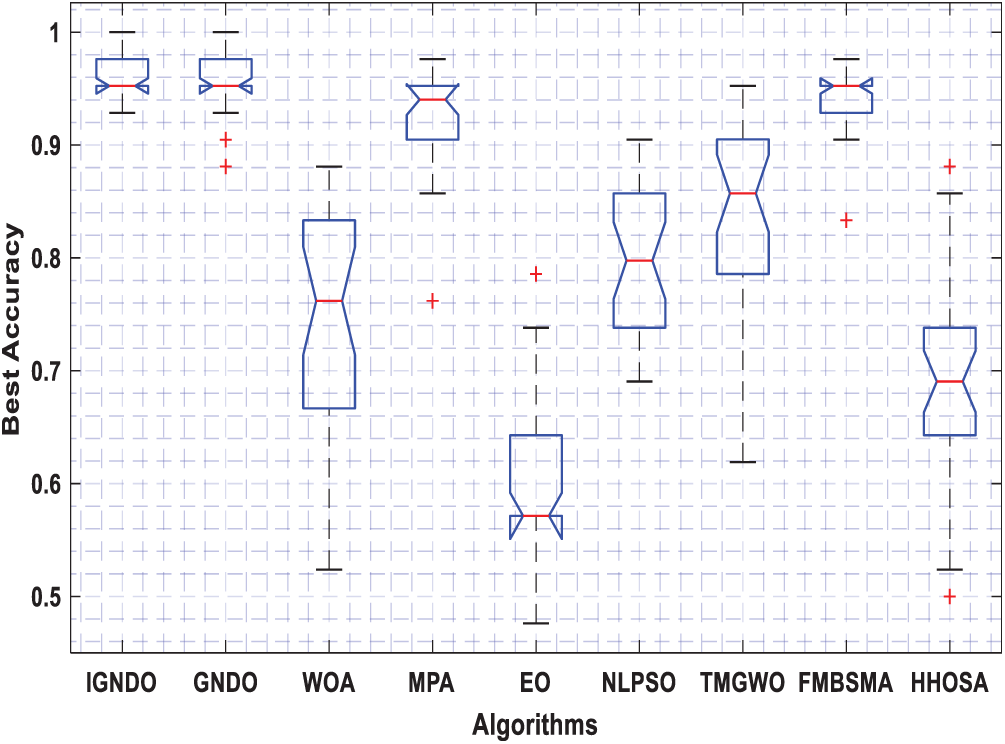
Figure 9: Boxplot for ID#1 in terms of accuracy values

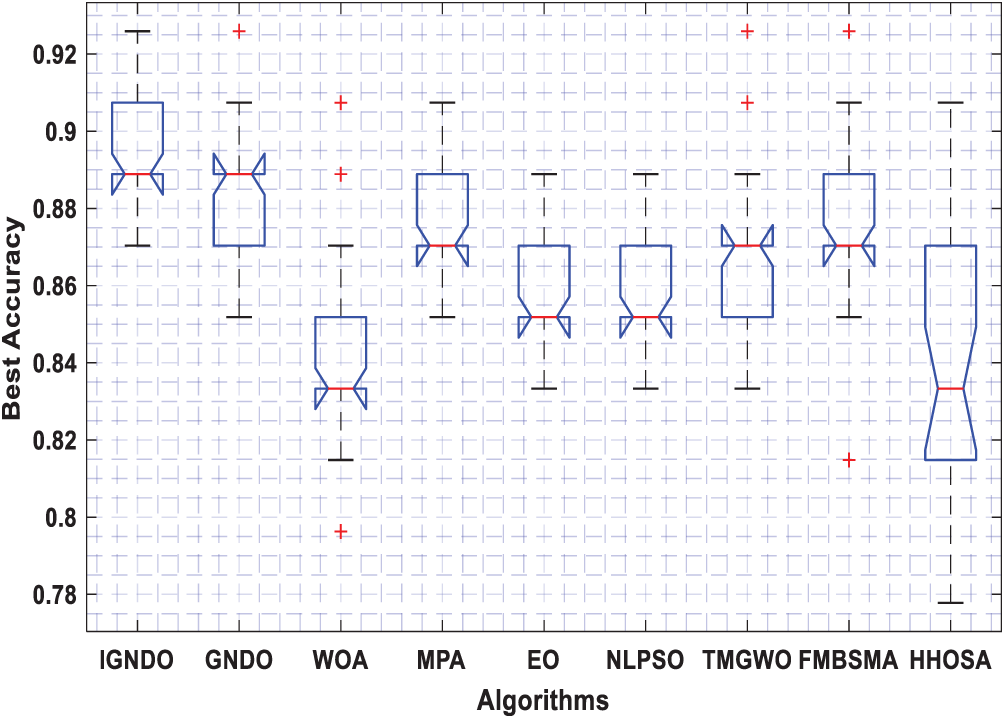
Figure 10: Boxplot for ID#2 in terms of accuracy values

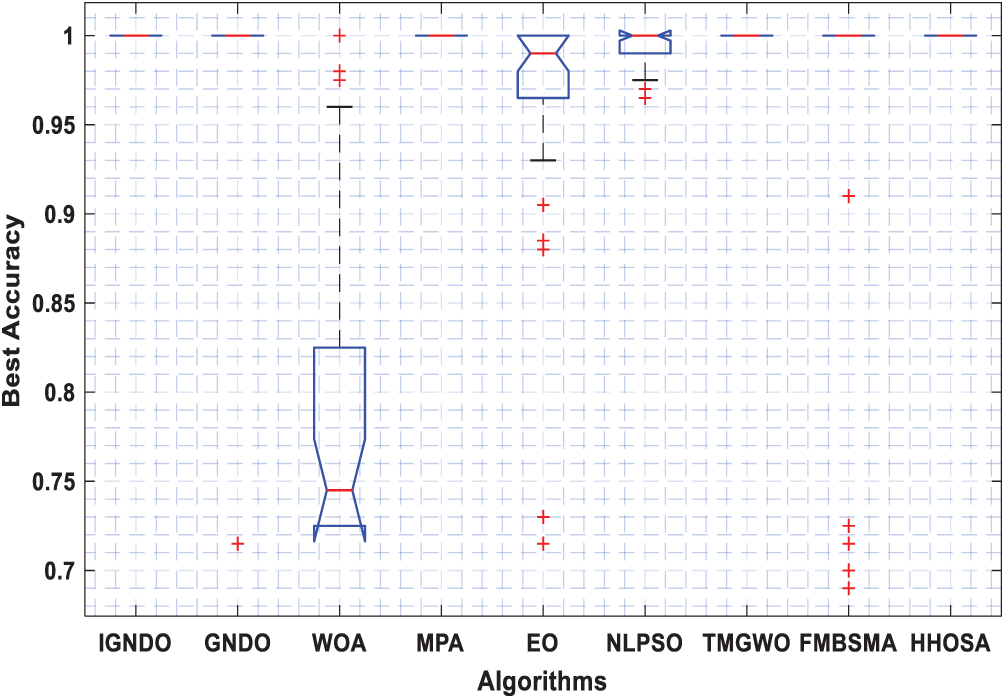
Figure 11: Boxplot for ID#3 in terms of accuracy values

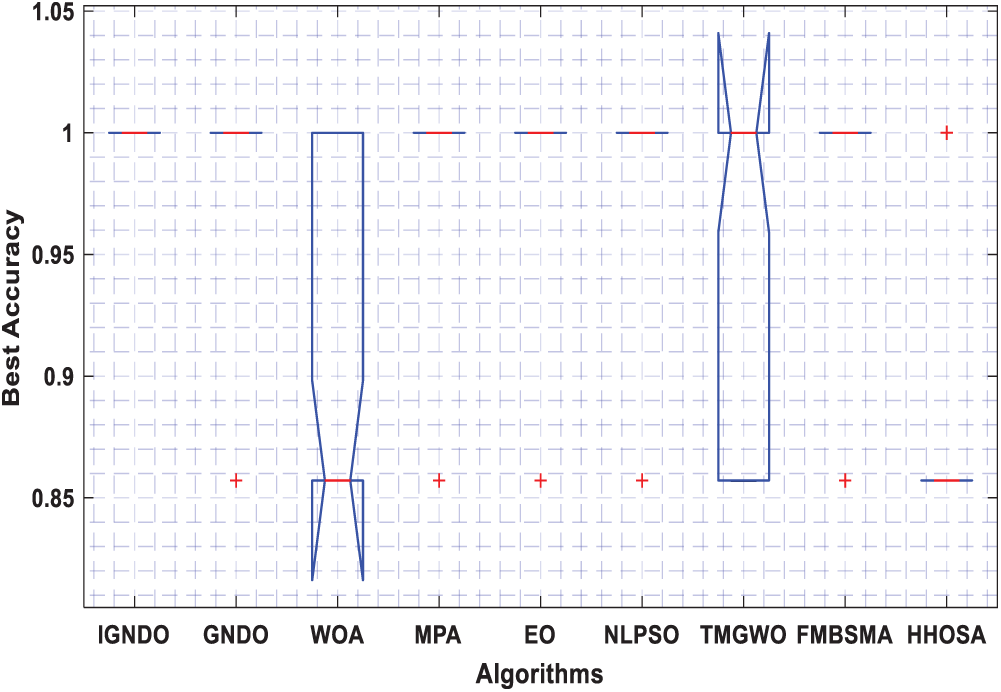
Figure 12: Boxplot for ID#9 in terms of accuracy values

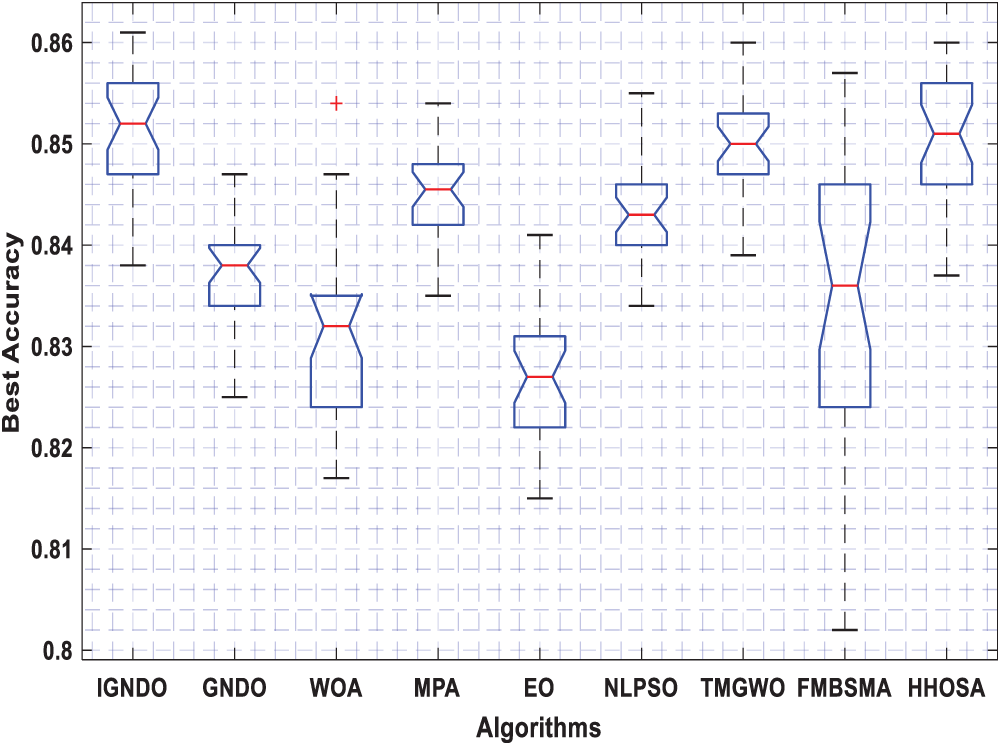
Figure 13: Boxplot for ID#12 in terms of accuracy values

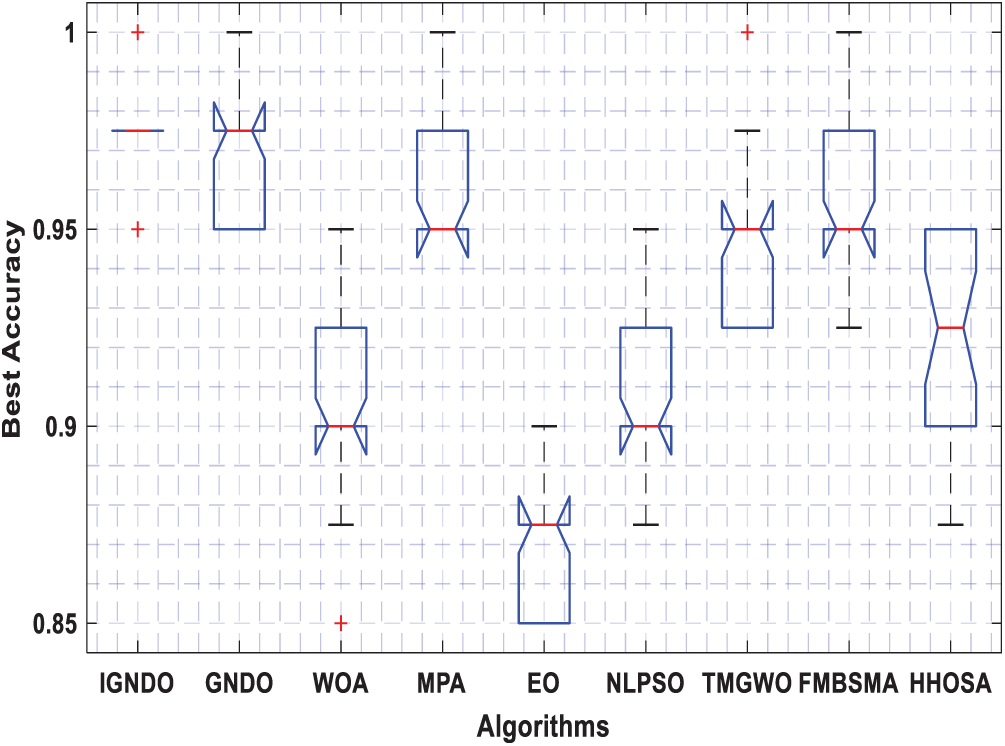
Figure 14: Boxplot for ID#13 in terms of accuracy values

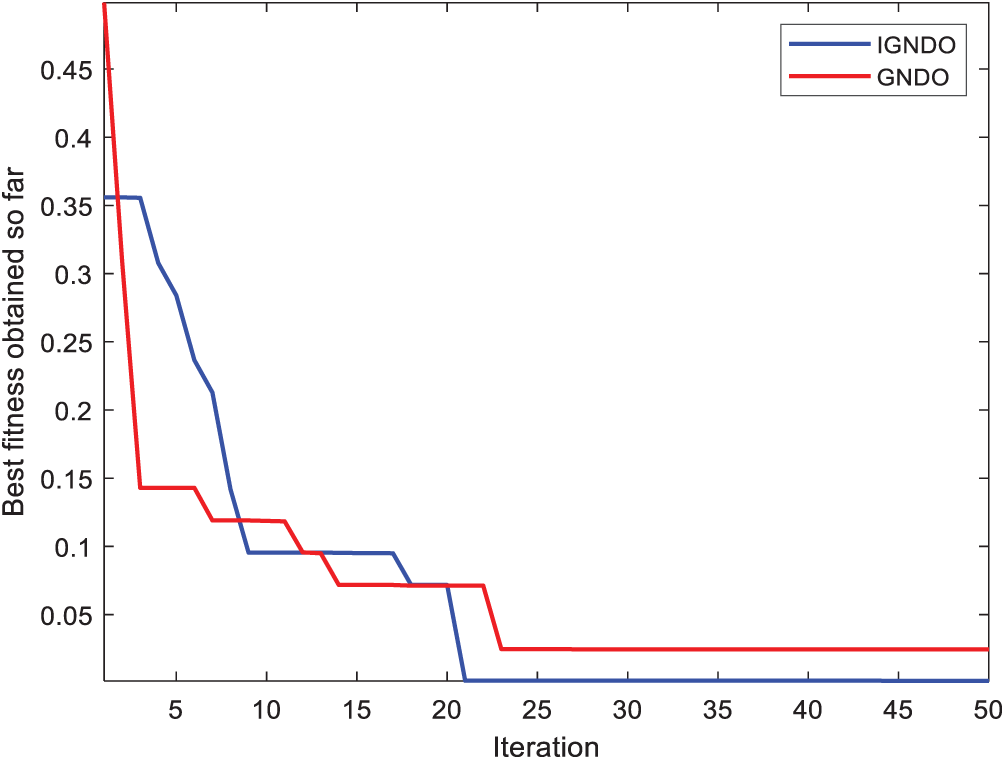
Figure 15: Convergence curve for IGNDO and GNDO on ID#1

In Figs. 15–24, IGNDO and GNDO are compared with each other regarding convergence speed in the direction of the near-optimal solution. Those figures show that IGNDO is faster than GNDO in reaching a lower fitness value in all observed test instances. This superiority is due to the ability of the proposed strategy to replace the unbeneficial solutions with others, exploring other regions within the search space of the problem that are unable to be reached by the standard GNDO.

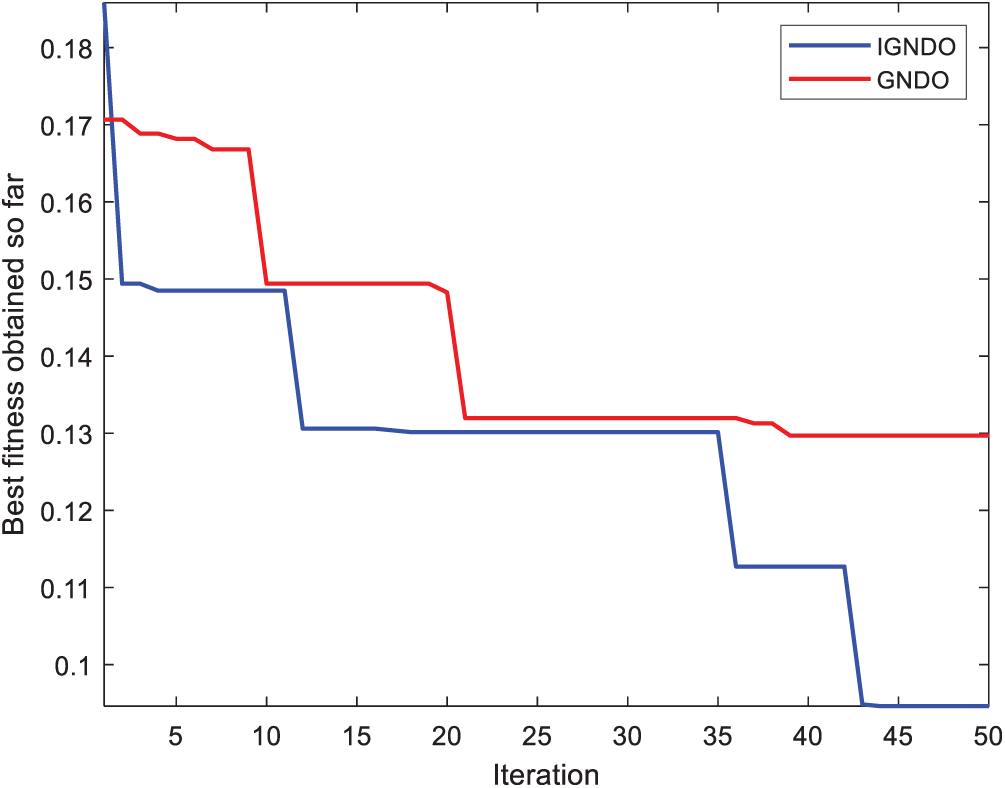
Figure 16: Convergence curve for IGNDO and GNDO on ID#2

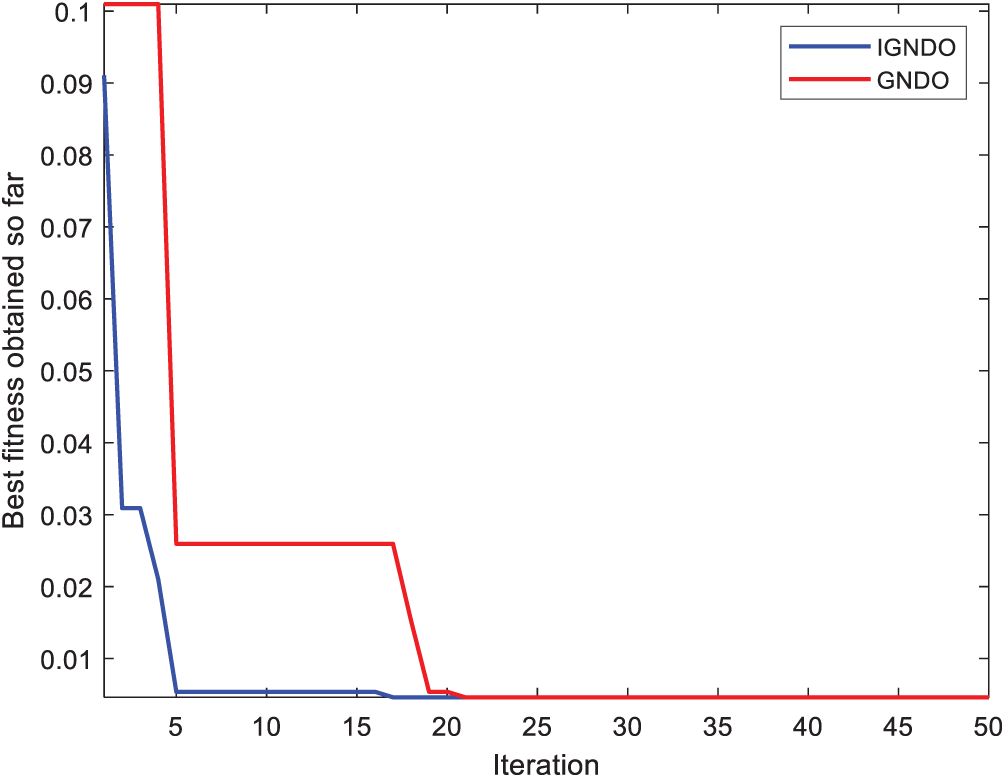
Figure 17: Convergence curve for IGNDO and GNDO on ID#3

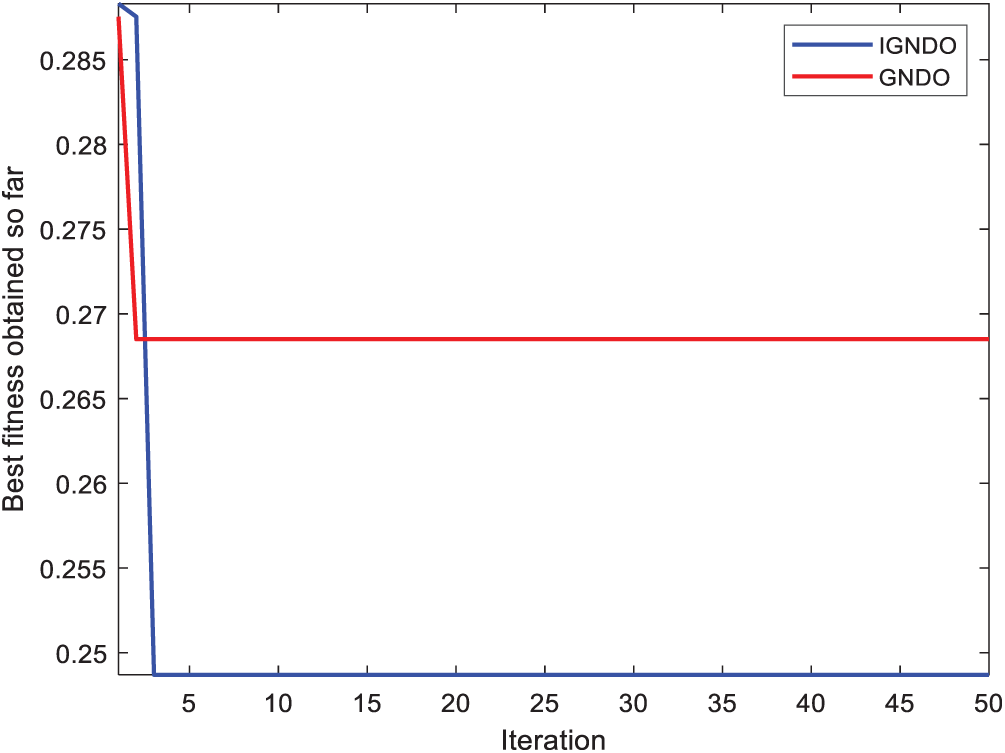
Figure 18: Convergence curve for IGNDO and GNDO on ID#4

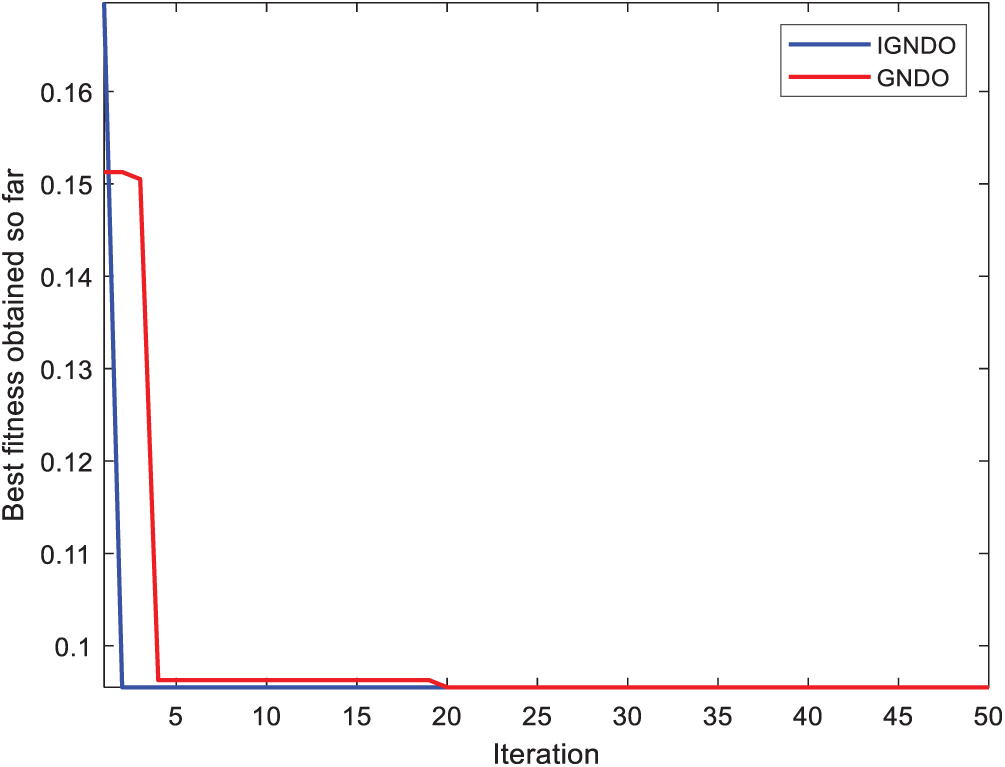
Figure 19: Convergence curve for IGNDO and GNDO on ID#6

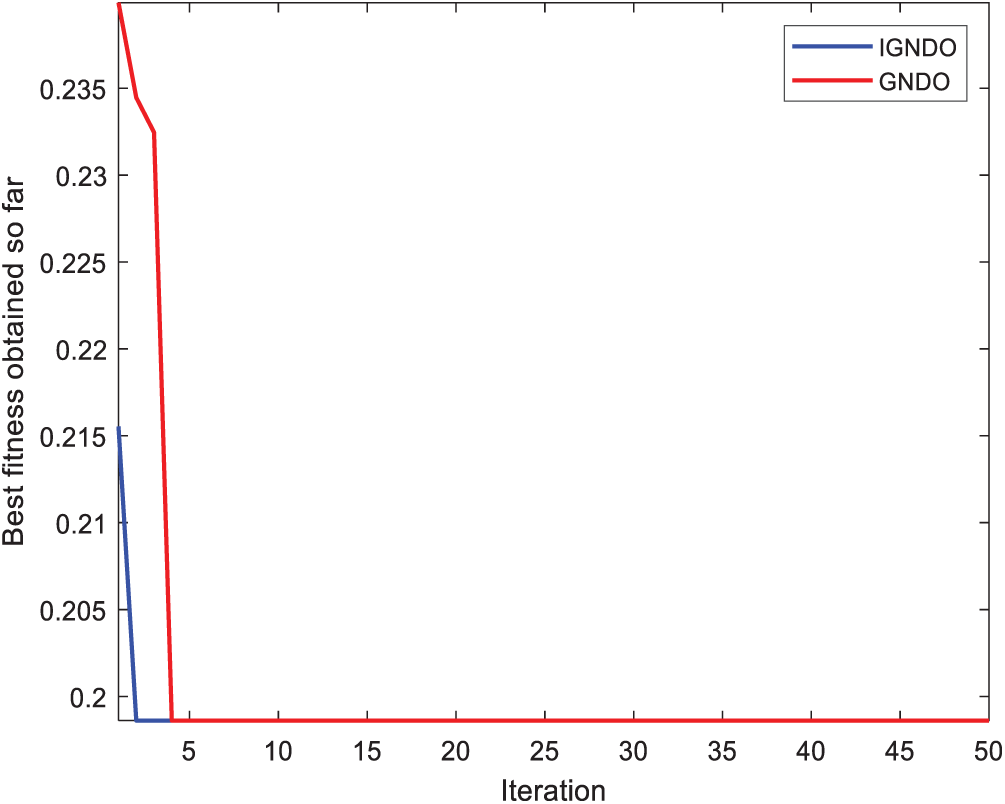
Figure 20: Convergence curve for IGNDO and GNDO on ID#7

Figure 21: Convergence curve for IGNDO and GNDO on ID#8

Figure 22: Convergence curve for IGNDO and GNDO on ID#10

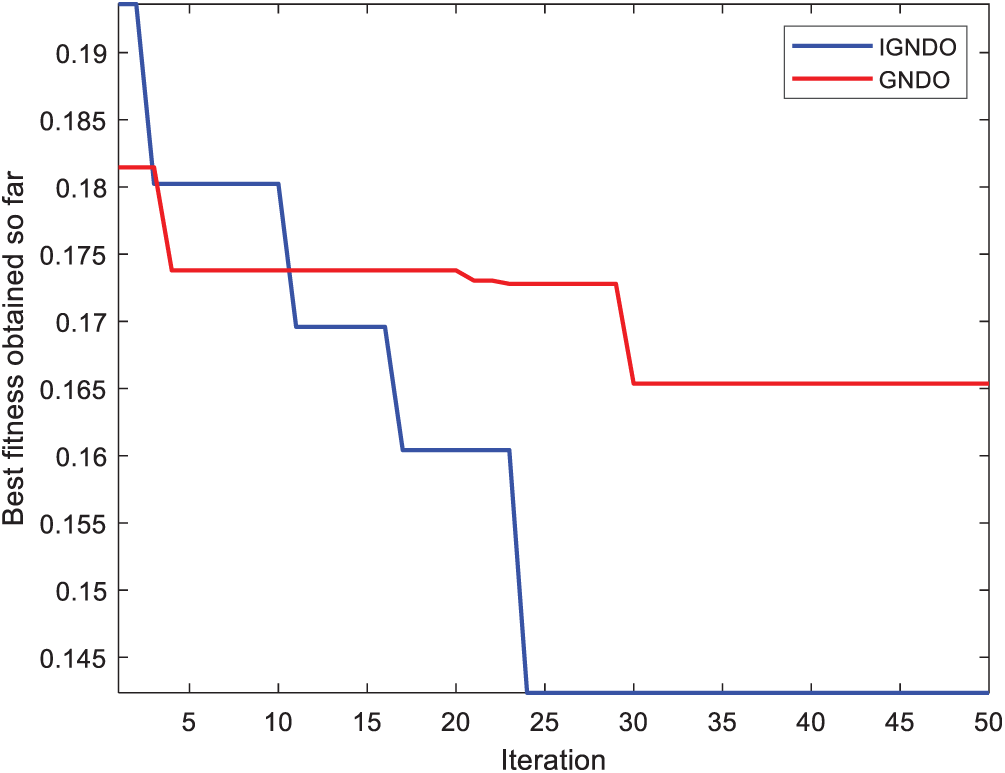
Figure 23: Convergence curve for IGNDO and GNDO on ID#12

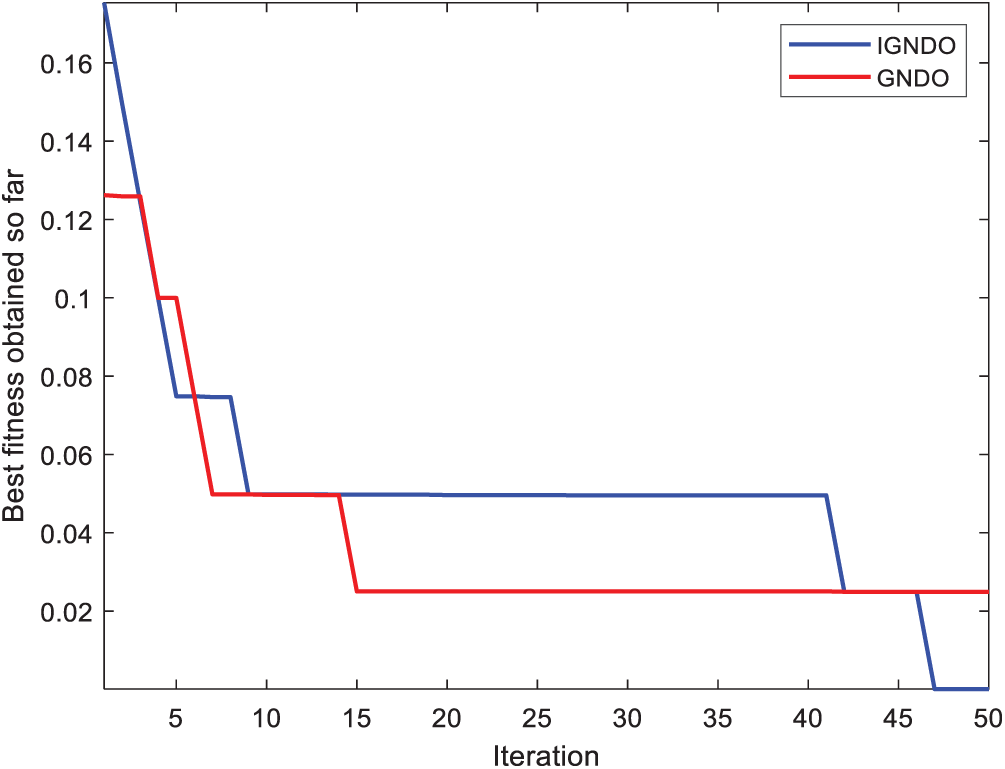
Figure 24: Convergence curve for IGNDO and GNDO on ID#13

Fig. 25 shows the computational cost (in milliseconds) of the various algorithms in for extracting the optimal features of ID#12. From this figure, it is obvious that the computational times of both IGNDO and GNDO are almost equal and are superior to all the other algorithms. Consequently, our proposed algorithms are best in terms of classification accuracy, computational cost, and fitness values. However, some of the other algorithms are better regarding the selected features number and worst for the classification accuracy. Since the main objective of machine learning techniques is better classification accuracy regardless of the training time, our proposed IGNDO and GNDO algorithms: are strong alternatives to existing techniques.

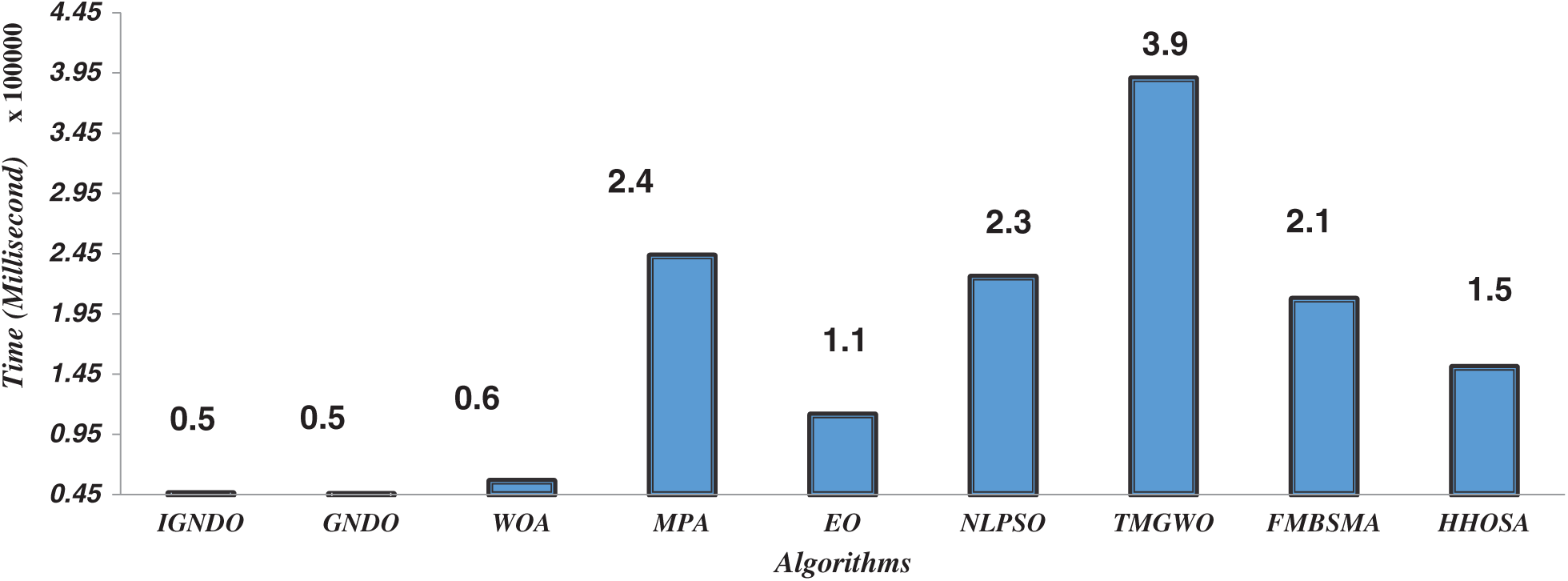
Figure 25: Computational cost of the algorithms on ID#12

5  Conclusion and Future Work

Generalized normal distribution optimization (GNDO) is a novel recent optimization algorithm that has high performance for accurate and efficient estimation of the unknown parameters of the single-diode model and double-diode model of the photovoltaic systems. This significantly better performance motivates us to propose a binary variant for tackling the FS problem to find the subset of features that maximize classification accuracy and minimize the computational cost of machine learning techniques. The arc tangent transfer function is used to transform the continuous values produced by GNDO into binary values to be relevant tosolving the FS problem. Furthermore, a novel restarting strategy is proposed in this paper to re-initialize the solutions that are close to the best-so-far solutions as an attempt to preserve the diversity of the solutions to avoid local minima while accelerating convergence. In addition, a new binary variant of GNDO improved using RS is proposed for FS. IGNDO and GNDO are validated on thirteen instances taken from the UCI repository and compared with seven state-of-the-art feature selection techniques. IGNDO is shown to be superior in terms of classification accuracy and fitness value, and is competitive for the number of the selected features.

Our future work includes testing the performance of this novel strategy with some of the state-of-the-art algorithms in an attempt to identify better solutions for the FS problem.

Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Funding Statement: This work has supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2021R1A2C1010362) and the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Khanan, S. Abdullah, A. H. H. Mohamed, A. Mehmood and K. A. Z. Ariffin, “Big data security and privacy concerns: A review,” Smart Technologies and Innovation for a Sustainable Future, vol. 1, no. 1, pp. 55–61, 2019. [Google Scholar]

 2.  M. Abdel-Basset, R. Mohamed, R. K. Chakrabortty, M. J. Ryan and S. Mirjalili, “An efficient binary slime mould algorithm integrated with a novel attacking-feeding strategy for feature selection,” Computers & Industrial Engineering, vol. 153, no. 1, pp. 107078, 2021. [Google Scholar]

 3.  M. Abdel-Basset, R. Mohamed, M. Elhoseny, A. K. Bashir, A. Jolfaei et al., “Energy-aware marine predators algorithm for task scheduling in IoT-based fog computing applications,” IEEE Transactions on Industrial Informatics, vol. 1, no. 1, pp. 1–13, 2020. [Google Scholar]

 4.  M. Abdel-Basset, R. Mohamed, M. Elhoseny, R. K. Chakrabortty and M. Ryan, “A Hybrid COVID-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy,” IEEE Access, vol. 8, no. 1, pp. 79521–79540, 2020. [Google Scholar]

 5.  M. Abdel-Basset, R. Mohamed, S. Mirjalili, R. K. Chakrabortty and M. J. Ryan, “Solar photovoltaic parameter estimation using an improved equilibrium optimizer,” Solar Energy, vol. 209, no. 1, pp. 694–708, 2020. [Google Scholar]

 6.  M. Abdel-Basset, R. Mohamed, S. Mirjalili, R. K. Chakrabortty and M. J. Ryan, “MOEO-EED: A multi-objective equilibrium optimizer with exploration-exploitation dominance strategy,” Knowledge-Based Systems, vol. 214, no. 1, pp. 106717, 2021. [Google Scholar]

 7.  M. Abdel-Basset, R. Mohamed, K. M. Sallam, R. K. Chakrabortty and M. J. Ryan, “An efficient-assembler whale optimization algorithm for dna fragment assembly problem: Analysis and Validations,” IEEE Access, vol. 8, no. 1, pp. 222144–222167, 2020. [Google Scholar]

 8.  M. Li, L. Wang, S. Deng and C. Zhou, “Color image segmentation using adaptive hierarchical-histogram thresholding,” PloS One, vol. 15, no. 1, pp. e0226345, 2020. [Google Scholar]

 9.  R. Sihwail, K. Omar, K. A. Z. Ariffin and M. Tubishat, “Improved harris hawks optimization using elite opposition-based learning and novel search mechanism for feature selection,” IEEE Access, vol. 8, no. 1, pp. 121127–121145, 2020. [Google Scholar]

10. T. Bhattacharyya, B. Chatterjee, P. K. Singh, J. H. Yoon, Z. W. Geem et al., “Mayfly in harmony: A new hybrid meta-heuristic feature selection algorithm,” IEEE Access, vol. 8, no. 1, pp. 195929–195945, 2020. [Google Scholar]

11. K. K. Ghosh, S. Ahmed, P. K. Singh, Z. W. Geem and R. Sarkar, “Improved binary sailfish optimizer based on adaptive β-hill climbing for feature selection,” IEEE Access, vol. 8, no. 1, pp. 83548–83560, 2020. [Google Scholar]

12. R. K. Agrawal, B. Kaur and S. Sharma, “Quantum based whale optimization algorithm for wrapper feature selection,” Applied Soft Computing, vol. 89, no. 1, pp. 106092, 2020. [Google Scholar]

13. M. Abdel-Basset, W. Ding and D. El-Shahat, “A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection,” Artificial Intelligence Review, vol. 1, no. 1, pp. 1–45, 2020. [Google Scholar]

14. M. Abdel-Basset, D. El-Shahat, I. El-henawy, V. H. C. Albuquerque and S. Mirjalili, “A new fusion of grey wolf optimizer algorithm with a two-phase mutation for feature selection,” Expert Systems with Applications, vol. 139, no. 1, pp. 112824, 2020. [Google Scholar]

15. M. M. Mafarja, D. Eleyan, I. Jaber, A. Hammouri and S. Mirjalili, “Binary dragonfly algorithm for feature selection,” in 2017 Int. Conf. on New Trends in Computing Sciences, Amman, Jordan, IEEE, pp. 12–17, 2017. [Google Scholar]

16. X. T. Zhang, Y. Zhang, H. R. Gao and C. L. He, “A wrapper feature selection algorithm based on brain storm optimization,” in Int. Conf. on Bio-Inspired Computing: Theories and Applications, Singapore: Springer, pp. 308–315, 2018. [Google Scholar]

17. M. Mafarja and S. Mirjalili, “Whale optimization approaches for wrapper feature selection,” Applied Soft Computing, vol. 62, no. 1, pp. 441–453, 2018. [Google Scholar]

18. M. Rostami, K. Berahmand and S. Forouzandeh, “A novel community detection based genetic algorithm for feature selection,” Journal of Big Data, vol. 8, no. 1, pp. 1–27, 2021. [Google Scholar]

19. H. Turabieh, S. Al Azwari, M. Rokaya, W. Alosaimi, A. Alharbi et al., “Enhanced Harris Hawks optimization as a feature selection for the prediction of student performance,” Computing, vol. 1, no. 1, pp. 1–22, 2021. [Google Scholar]

20. S. Guha, A. Das, P. K. Singh, A. Ahmadian, N. Senu et al., “Hybrid feature selection method based on harmony search and naked mole-rat algorithms for spoken language identification from audio signals,” IEEE Access, vol. 8, no. 1, pp. 182868–182887, 2020. [Google Scholar]

21. S. Saha, M. Ghosh, S. Ghosh, S. Sen, P. K. Singh et al., “Feature selection for facial emotion recognition using cosine similarity-based harmony search algorithm,” Applied Sciences, vol. 10, no. 8, pp. 2816, 2020. [Google Scholar]

22. A. D. Rahajoe, R. F. Zainal, B. M. Mulyo, B. Plangkang and R. F. Tias, “Feature selection based on modified harmony search algorithm,” in 2020 Int. Conf. on Smart Technology and Applications, Surabaya, East Java Province, Indonesia, IEEE, pp. 1–7, 2020. [Google Scholar]

23. Y. Zhang, Z. Jin and S. Mirjalili, “Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models,” Energy Conversion and Management, vol. 224, no. 1, pp. 113301, 2020. [Google Scholar]

24. M. Mafarja, R. Jarrar, S. Ahmad and A. A. Abusnaina, “Feature selection using binary particle swarm optimization with time varying inertia weight strategies,” in Proc. of the 2nd Int. Conf. on Future Networks and Distributed Systems, Amman, Jordan, pp. 1–9, 2018. [Google Scholar]

25. A. G. Hussien, A. E. Hassanien, E. H. Houssein, S. Bhattacharyya and M. Amin, “S-shaped binary whale optimization algorithm for feature selection,” in Recent Trends in Signal and Image Processing. Singapore: Springer, pp. 79–87, 2019. [Google Scholar]

26. M. Abdel-Basset, R. Mohamed, R. K. Chakrabortty, M. Ryan and S. Mirjalili, “New binary marine predators optimization algorithms for 0-1 knapsack problems,” Computers & Industrial Engineering, vol. 151, no. 1, pp. 106949, 2021. [Google Scholar]

27. M. Abdel-Basset, R. Mohamed and S. Mirjalili, “A binary equilibrium optimization algorithm for 0-1 knapsack problems,” Computers & Industrial Engineering, vol. 1, no. 1, pp. 106946, 2020. [Google Scholar]

28. E. Emary, H. M. Zawbaa and A. E. Hassanien, “Binary ant lion approaches for feature selection,” Neurocomputing, vol. 213, no. 1, pp. 54–65, 2016. [Google Scholar]

29. S. Yadav and S. Shukla, “Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification,” in 2016 IEEE 6th Int. Conf. on Advanced Computing, Bhimavaram, India, IEEE, pp. 78–83, 2016. [Google Scholar]

30. A. Frank, UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 2010. [Online]. Available: http://archive.ics.uci.edu/ml. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.