DOI:10.32604/cmc.2021.018658

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018658 |  |
| Article |
Task Scheduling Optimization in Cloud Computing Based on Genetic Algorithms
1Faculty of Computers and Information, Department of Computer Science, Sohag University, Sohag, 82524, Egypt
2Department of Computer Science and Artificial Intelligence, College of Computer Science and Engineering, University of Jeddah, Jeddah, 21959, Saudi Arabia
*Corresponding Author: Ahmed Y. Hamed. Email: a.yhamed@yahoo.com
Received: 16 March 2021; Accepted: 18 April 2021
Abstract: Task scheduling is the main problem in cloud computing that reduces system performance; it is an important way to arrange user needs and perform multiple goals. Cloud computing is the most popular technology nowadays and has many research potential in various areas like resource allocation, task scheduling, security, privacy, etc. To improve system performance, an efficient task-scheduling algorithm is required. Existing task-scheduling algorithms focus on task-resource requirements, CPU memory, execution time, and execution cost. In this paper, a task scheduling algorithm based on a Genetic Algorithm (GA) has been presented for assigning and executing different tasks. The proposed algorithm aims to minimize both the completion time and execution cost of tasks and maximize resource utilization. We evaluate our algorithm’s performance by applying it to two examples with a different number of tasks and processors. The first example contains ten tasks and four processors; the computation costs are generated randomly. The last example has eight processors, and the number of tasks ranges from twenty to seventy; the computation cost of each task on different processors is generated randomly. The achieved results show that the proposed approach significantly succeeded in finding the optimal solutions for the three objectives; completion time, execution cost, and resource utilization.
Keywords: Cloud computing; task scheduling; genetic algorithm; optimization algorithm
Recently, cloud computing is the most popular technology; resource allocation, task scheduling, security, and privacy have been widely used in various fields. Scheduling plays an important role in improving the efficiency of all cloud-based services. In cloud computing, task scheduling is used to assign the task to the optimal resource for execution. Task scheduling algorithms have different types of algorithms and different issues as completion time, execution cost, complexity, etc.
Cloud computing has emerged as a new computing platform according to the development of virtualization and Internet technologies [1]. It can be viewed as a distributed system containing interconnected and virtualized computers that are dynamically provisioned. It maintains the service-level agreements (SLA) between the users and the host applications [2].
Cloud computing is interested in resource management, security, performance, reliability, etc., [3]. Resource management is one of the important issues in task scheduling. The task scheduling problem in cloud computing is how to distribute the tasks of users on the available hardware to improve the overall performance of the cloud computing environment [4].
In [5], the authors presented an implementation to the task scheduling using .NET and a GA-based scheduling algorithm to achieve the task and its priority. They grouped the available jobs and executed them using different proposed algorithms. In addition, in [6], a GA was proposed to solve the task scheduling in cloud computing under considering total task completion time, average task completion time, and cost constraint.
The objective of task scheduling in the multiprocessor system is to assign a dependent task to the processors, and the processing time will be reduced. To minimize the processing time, the GA has applied to the processors to obtain various solutions and faster processing time. Task scheduling considers two aspects: the earliest start time (EST) and some task dependencies (NTD). This comparison made by using Java simulation and the result obtained that the proposed algorithm solves minimum EST attains faster processing time than the maximum EST [7].
The task scheduling algorithms using Efficient State Space Search GA (ESSSGA) use the benefits of heuristic-based algorithms to minimize space search and time to obtain effective solutions [8]. The task to processor mapping has been made using a heuristic-based earliest finish time approach that reduces the time regarding task execution time.
A new GA for task scheduling in the multiprocessor systems has indicated that task execution priority depends on the height of task graphs to perform scheduling. This method is simulated and used to compare with the basic genetic algorithm [9]. The GA efficiency could be attained by the optimization of different parameters like mutation, crossover, selection function, and crossover probability. These GA parameters on the reduction of bi-criteria fitness functions and parameter setting will be accomplished by a central composite design approach with design experiments. The experiments use these parameters and analysis of variance, which reduce the total completion time and makespan [10].
A new GA is used for solving the problems in scheduling task graphs. The algorithm is entirely dependent on the new approach to reduce the communication cost of processors and the length of critical time. In order to solve the scheduling of the task graph, effective GA has been applied. GA proposed for scheduling the task graph that can be acquired is effective in scheduling with low time. The results obtained from the study stated that the algorithm related to graphs without communication cost could act quickly when compared to other MCP algorithms [11].
The GA chromosomes like task list (TL), processor list (PL), and integration of both (TLPLC). The experiments on real-world application graphs like Gaussian elimination, Gauss Jordan and Laplace equation, and LU decompositions. TLPLCGA is related to GA and heuristic algorithms regarding the processor’s time and efficiency conducted. The result experienced was that the hybrid approach performs better than the other algorithms [12].
The effectiveness of Node Duplication GA (NGA) based approach against the existing deterministic scheduling techniques for reducing the interprocessor traffic communication. The results obtained from the simulations indicate that the GA can use the scheduled task to meet deadlines and acquire high processor utilization. Performance analysis of NGA is compared with GA, FCFS, and List Scheduler [13].
An effective method based on GA is created to solve the problem of multiprocessor scheduling. This paper used GA for scheduling precedence task graphs with inter-task communication onto multiprocessors without considering the communication channel. Experimental results show that hard problems have been taken from the internet, illustrates GA with optimization of parameters [14].
The task scheduling problem has been formulated as a multi-objective optimization problem [15,16]. In [15], the authors proposed a GA-DE algorithm based on GA and Differential Evolution (DE) to solve the problem under three constraints; total time, cost, and virtual machine load balancing. While [16] developed an EDA-GA hybrid scheduling algorithm based on EDA (estimation of distribution algorithm) and GA to solve the scheduling problem.
The optimal solution to the task scheduling problem cannot be obtained in a limited time and can be found by performing a comprehensive search. So, it is one of the NP-Complete problems [17–20]. Therefore, this paper develops a GA-based algorithm to solve the task scheduling problem in the cloud environment. The proposed algorithm’s objective is to allocate and execute dependent tasks in an optimal manner to minimize both the completion time and execution cost and maximize resource utilization.
The rest of this paper is presented as follows: Section 2 discusses problem definition. In Section 3, the operations of the proposed algorithm are illustrated. Our GA approach to finding the optimal task scheduling for a cloud computing system is described in Section 4. Section 5 discusses the results, and in Section 6, conclusions are given.


We denote the task scheduling in the cloud computing as a Graph G (M, E) with M nodes (n1, n2, n3,
The execution time of a node ni is denoted by (ni) weight. If the processor’s processing speed is Ps
The computation cost of node i on the processor j (W
Let C(n
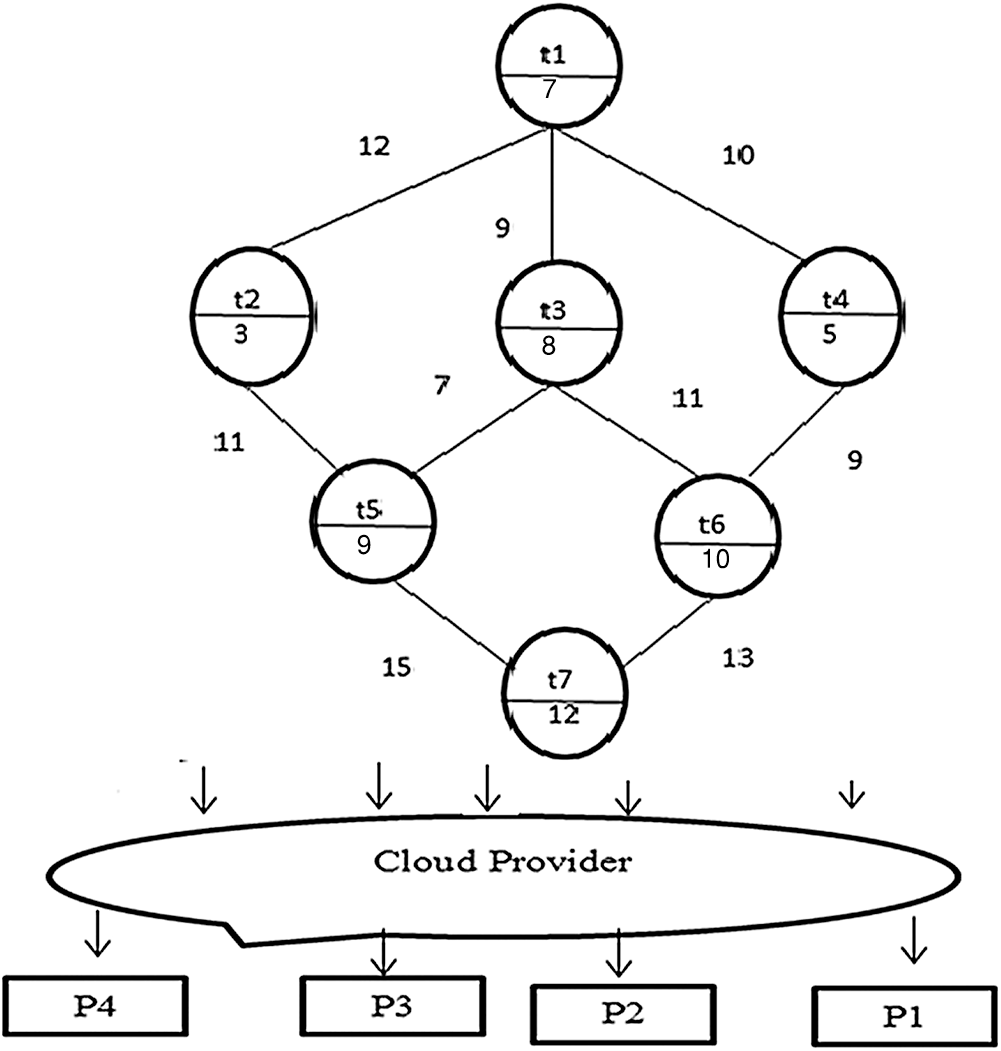
Figure 1: The computation and communication costs of DAG
In this paper, the processors in cloud computing are heterogeneous. Therefore, the task’s computation cost varies according to the processor. The start and finish time of ni is denoted by ST(ni; pj) and FT(ni; pj), respectively.
The Data Arrival Time (DAT) of t
where N_parent is the number of t
The task scheduling problem in cloud computing can be defined as; Find the best assignment of the start times of the given tasks on processors such that the schedule length (the completion time) and execution cost are minimized with the condition that precedence-constrained is preserved.
The completion time is defined as the schedule length or finish time and is computed by:
where,
The following pseudo-code shows how to find the schedule length (denoted by S_Length) using SGA, [21]:

The total cost (Executin Cost) of all tasks on the available processors is calculated by:
The utilization of resources is given by dividing the total value of Bj over the completion time of an application. As follows, [22]:
That is, the objective is to minimize Eqs. (3), (5) and (6).
The following subsections investigate the different components of the proposed GA, encoding, initialization, objective function, crossover, and mutation operations. The GA is terminated when the best solution found, or the number of generations exceeds the Maxgn.
In the proposed GA, if we have M tasks and N processors, the chromosome is divided into two parts; distributing and scheduling parts. The distributing part represents the processor’s indices, and the scheduling part shows the tasks to be processed, as shown in Fig. 2. According to Fig. 2, the processor P1 processes the tasks t1, t3, while t4 and t6 will be processed by P2,

Figure 2: Tasks representation on processors
The initial population is generated randomly and according to the following steps:
(1) A chromosome X is generated, as shown in Fig. 2.
(2) The first part of X is generated randomly from 1 to N.
(3) The second part is generated randomly from 1 to M taking into account the precedence-constrained.
(4) Repeat from 1 to 3 to generate the number of chromosomes (population size).
This paper’s main objective is to map all the tasks to all the processors, minimize the completion time, execution cost, and maximize resource utilization. Therefore, the fitness function (Fit) of the candidate solution is the minimum value of the completion time. i.e.,
In the crossover, we use a 1-point crossover to produce one child from two selected parents based on the Pc value. The distributing part of the child is taken from the distributing part of the first parent, and the scheduling part of it is taken from the second parent. Fig. 3 explains the crossover operation:
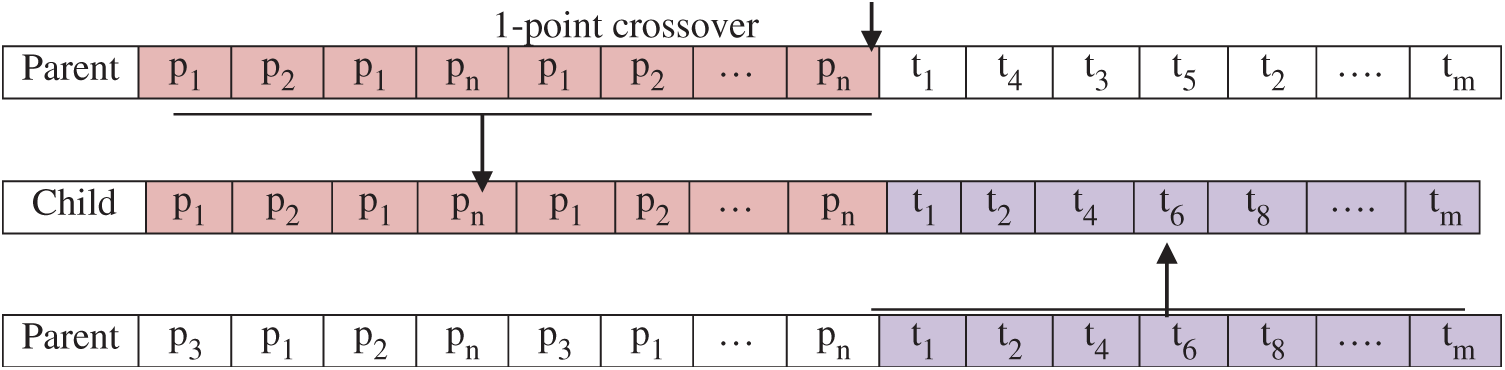
Figure 3: The crossover operation
The mutation operation is performed on the distributing part of the selected parent based on the Pm value. The position to be mutated is selected randomly to change its value as shown in Fig. 4.

Figure 4: The mutation operation
The following algorithm explains how to use the different components of the proposed GA as described in Section 3 to solve the task scheduling problem.

In this section, the proposed GA has been applied to two examples. The values of pop_size, P
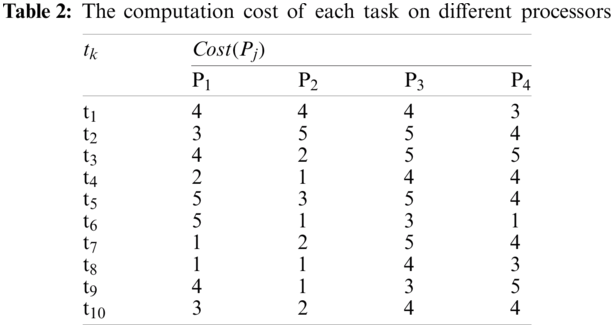
In this example, the number of M is 10 tasks, and N is 4 processors. The communication cost between the tasks and the computation cost of each task on different processors are generated randomly from 1 to 20, and 1 to 5, respectively. The communication cost and the computation cost are shown in Tabs. 1 and 2, respectively.

The cost of different processors per second is generated randomly from 1 to 10 and is shown in Tab. 3.
The best solution obtained by the proposed genetic algorithm is shown in Fig. 5.

Figure 5: The best solution
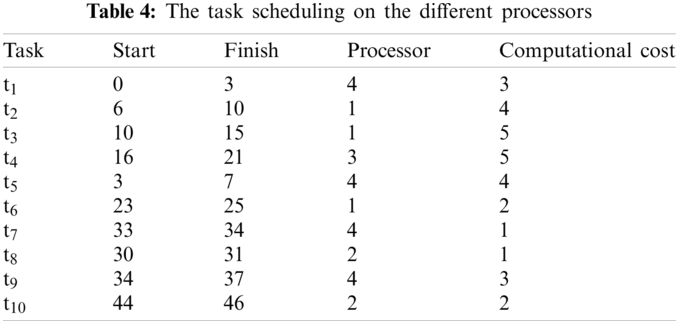
The task scheduling on the different processors is shown in Tab. 4 and Fig. 6.

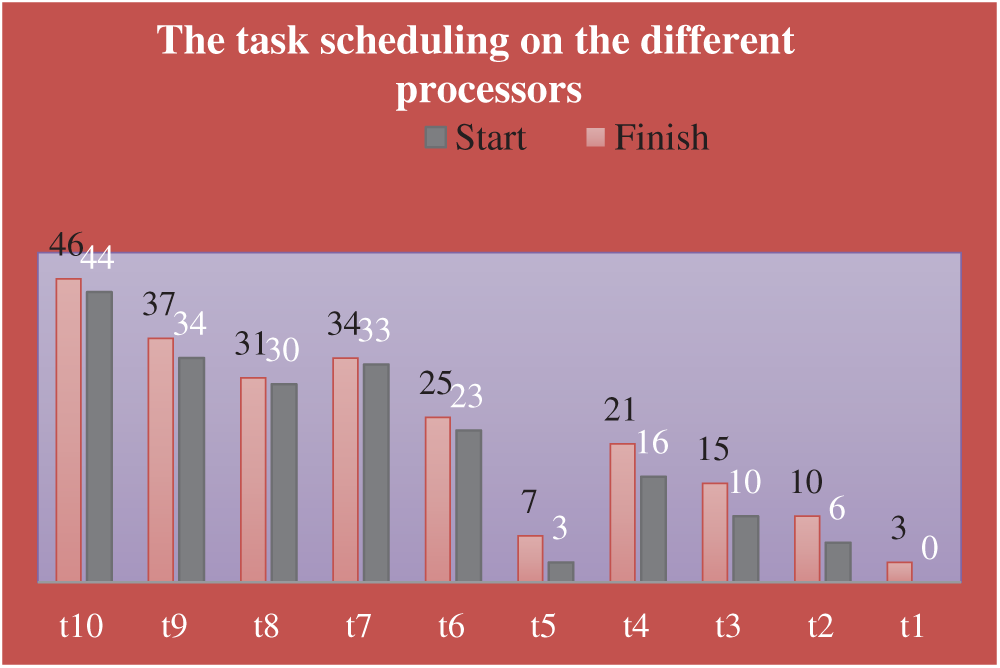
Figure 6: The task scheduling on the different processors
The busy time of the processors is shown in Tab. 5 and Fig. 7.

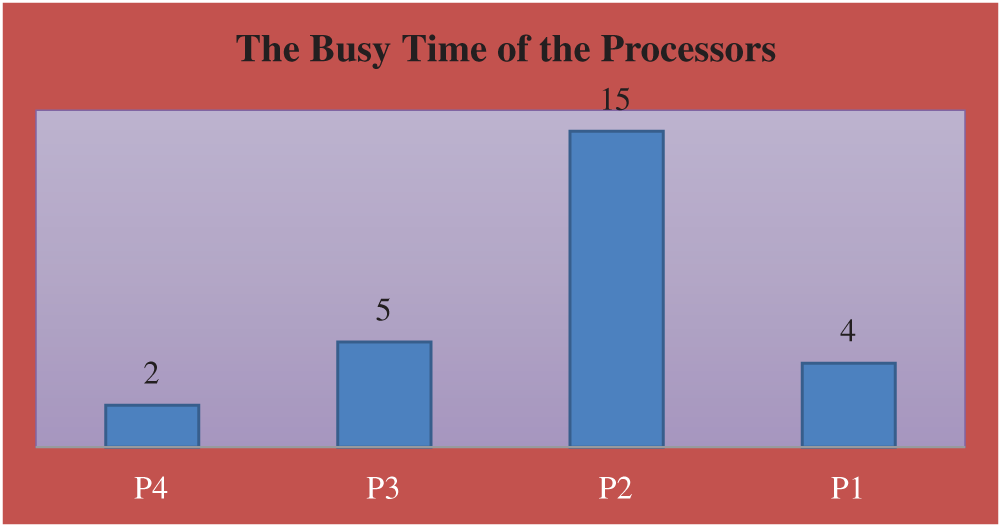
Figure 7: The busy time for each processor
The available time of the processors is shown in Tab. 6 and Fig. 8.

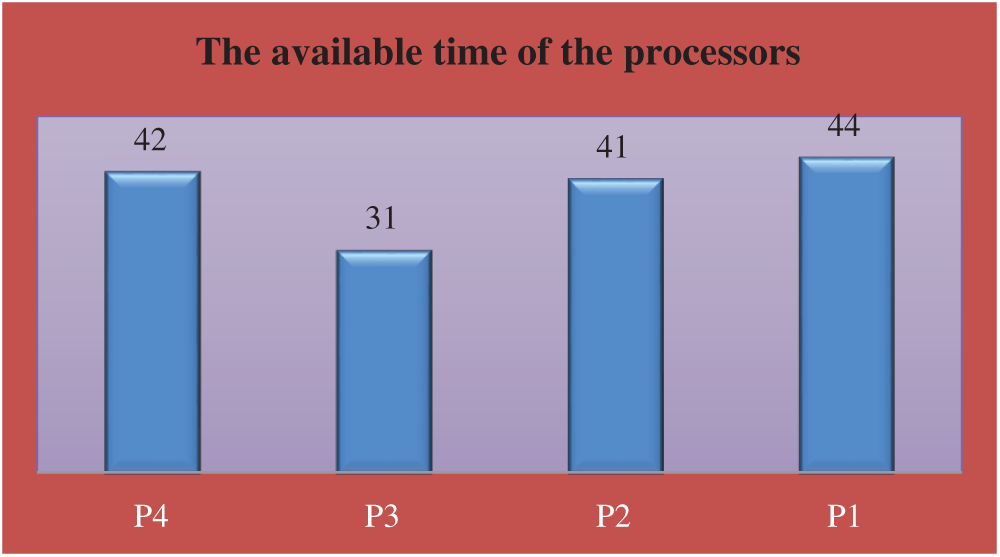
Figure 8: The available time of the processors
The completion time, execution cost, utilization, speedup, and efficiency are shown in the following table, Tab. 7.
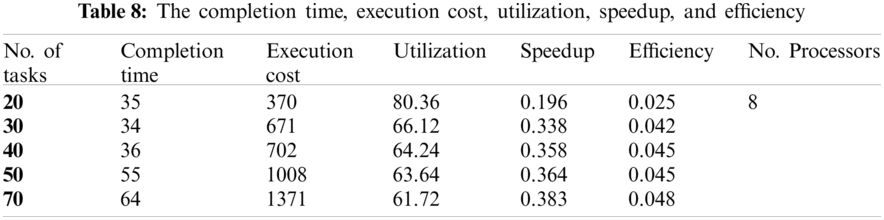
In this example, consider four cases with N = 8 processors. The number of tasks is: 20, 30, 40, 50, and 70 tasks in the first, second, third, and fourth case (M = 20, 30, 40, 50, and 50). The communication cost between the tasks and the computation cost of each task on different processors are generated randomly from 1 to 20, and 1 to 5, respectively.
The completion time, execution cost, utilization, speedup, and efficiency are shown in the following table, Tab. 8 and Figs. 9–11.
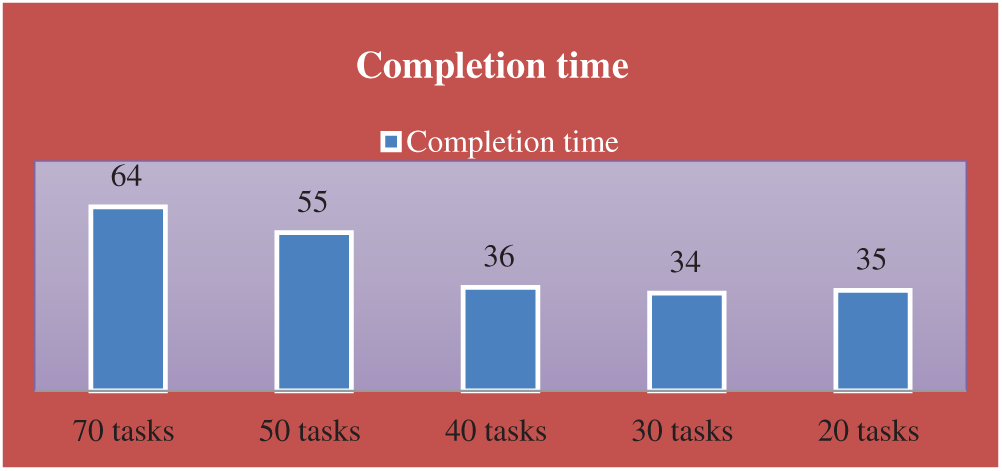
Figure 9: The completion time of the problems
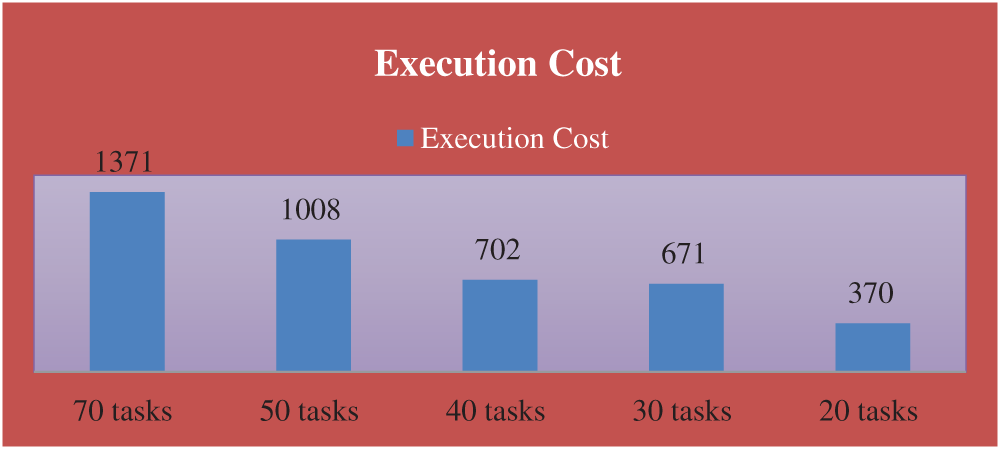
Figure 10: The execution cost of the problems
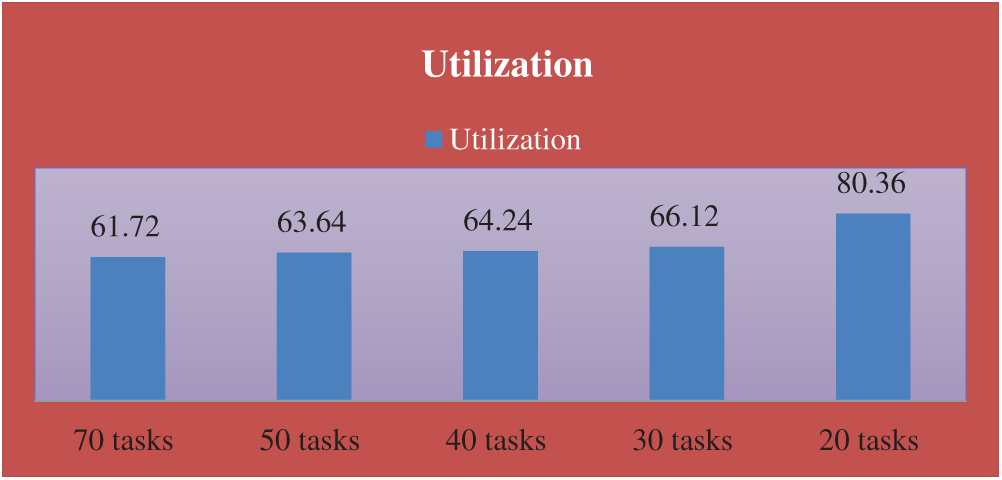
Figure 11: The resource utilization of the problems
The proposed GA has successfully solved task scheduling problem in Cloud computing in this paper. The proposed algorithm targets to minimize completion time, execution cost and maximize resource utilization. The completeness and correctness of the proposed algorithm have been tested. This has proven that our proposed technique enabled us to obtain results faster, leading to saving time and effort. In other words, the use of the proposed genetic algorithm has played a major role in reducing the search space generated by the problem.
In summary, our experimental results indicate that the algorithm is more efficient than other heuristics. To the best of our knowledge, our method’s structure and design are designed for the task scheduling problem in the cloud computing environment. This has made it very hard to find common features with other previous methods for comparison reasons.
Acknowledgement: The authors thank the anonymous referees for their careful readings and provisions of helpful suggestions to improve the presentation.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. H. Jang, T. Y. Kim, J. K. Kim and J. S. Lee, “The study of genetic algorithm-based task scheduling for cloud computing,” International Journal of Control and Automation, vol. 5, no. 4, pp. 157–162, 2012. [Google Scholar]
2. T. Goyal and A. Agrawal, “Host scheduling algorithm using genetic algorithm in cloud computing environment,” International Journal of Research in Engineering & Technology, vol. 1, no. 1, pp. 7–12, 2013. [Google Scholar]
3. B. Furht and A. Escalante, “Handbook of Cloud Computing,” Springer, Boston, MA, 2010. [Google Scholar]
4. F. Etro, “Introducing cloud computing,” London Conf. on Cloud Computing for the Public Sector, pp. 1–20, 2010. [Google Scholar]
5. R. Kaur and S. Kinger, “Enhanced genetic algorithm-based task scheduling in cloud computing,” International Journal of Computer Applications, vol. 101, no. 14, pp. 1–6, 2014. [Google Scholar]
6. J. W. Ge and Y. S. Yuan, “Research of cloud computing task scheduling algorithm based on improved genetic algorithm,” in Proc. of the 2nd Int. Conf. on Computer Science and Electronics Engineering, Hangzhou, China, pp. 2134–2137, 2013. [Google Scholar]
7. T. Kaiser, O. Jegede, K. Ferens and D. Buchanan, “A genetic algorithm for multiprocessor task scheduling,” Ph.D. dissertation, University of Manitoba, 2015. [Google Scholar]
8. M. Akbari and H. Rashidi, “An efficient algorithm for compile-time task scheduling problem on heterogeneous computing systems,” International Journal of Academic Research, vol. 7, no. 1, pp. 192–200, 2015. [Google Scholar]
9. A. Sharma and M. Kaur, “An efficient task scheduling of multiprocessor using genetic algorithm based on task height.” International Journal of Hybrid Information Technology, vol. 8, no. 8, pp. 83–90, 2015. [Google Scholar]
10. S. Dhingra, S. Gupta and R. Biswas, “Genetic algorithm parameters optimization for bi-criteria multiprocessor task scheduling using design of experiments,” International Journal of Computer, Electrical, Automation, Control and Information Engineering, vol. 8, no. 1, pp. 661–665, 2014. [Google Scholar]
11. M. Mahi and H. Kodaz, “Genetic algorithm with descendants idea for scheduling tasks graph in the multi-processor architecture,” Journal of Advances in Computer Networks, vol. 2, no. 1, pp. 10–13, 2014. [Google Scholar]
12. M. Rashid and M. Awadalla, “Hybrid algorithm for multiprocessor task scheduling,” International Journal of Computer Science Issues, vol. 3, no. 2, pp. 79–88, 2011. [Google Scholar]
13. H. Heidari and A. Chalechale, “Scheduling in multiprocessor system using a genetic algorithm,” International Journal of Advanced Science and Technology, vol. 43, pp. 81–92, 2012. [Google Scholar]
14. S. A. Hamad and F. A. Omaraa, “Genetic-based task scheduling algorithm in cloud computing environment,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 4, pp. 550–556, 2016. [Google Scholar]
15. Y. Li, S. Wang, X. Hong and Y. Li, “Multi-objective task scheduling optimization in cloud computing based on genetic algorithm and differential evolution algorithm,” in 37th Chinese Control Conf., Wuhan, China, pp. 4489–4494, 2018. [Google Scholar]
16. S. Pang, W. Li, H. He, Z. Shan and X. Wang, “An EDA-ga hybrid algorithm for multi-objective task scheduling in cloud computing,” IEEE Access, vol. 7, pp. 146379–146389, 2019. [Google Scholar]
17. Y. Yin, L. Chen, Y. Xu and J. Wan, “Location-aware service recommendation with enhanced probabilistic matrix factorization,” IEEE Access, vol. 6, no. 99, pp. 62815–62825, 2018. [Google Scholar]
18. H. Gao, S. Mao, W. Huang and X. Yang, “Applying probabilistic model checking to financial production risk evaluation and control: A case study of alibaba’s yu’e Bao,” IEEE Transactions on Computational Social Systems, vol. 5, no. 3, pp. 785–795, 2018. [Google Scholar]
19. H. Topcuouglu, S. Hariri and M. Y. Wu, “Performance-effective and low complexity task scheduling for heterogeneous computing,” IEEE Transaction Parallel Distributed Systems, vol. 13, no. 3, pp. 260–274, 2002. [Google Scholar]
20. E. Ilavarasan and P. Thambidurai, “Low complexity performance effective task scheduling algorithm for heterogeneous computing environments,” Journal of Computer Society, vol. 3, no. 2, pp. 94–103, 2007. [Google Scholar]
21. F. A. Omaraa and M. M. Arafa, “Genetic algorithms for task scheduling problem,” Journal of Parallel and Distributed Computing, vol. 70, no. 1, pp. 13–22, 2010. [Google Scholar]
22. D. M. Abdelkader and F. Omara, “Dynamic task scheduling algorithm with load balancing for heterogeneous computing system,” Egyptian Informatics Journal, vol. 13, no. 2, pp. 135–145, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |