DOI:10.32604/cmc.2021.019114

| Computers, Materials & Continua DOI:10.32604/cmc.2021.019114 |  |
| Article |
Advance Artificial Intelligence Technique for Designing Double T-Shaped Monopole Antenna
1Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
2Electrical Engineering Department, College of Engineering, Taibah University, Medina 42353, Saudi Arabia
3Operations Research Department, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza 12613, Egypt
4Wireless Intelligent Networks Center (WINC), School of Engineering and Applied Sciences, Nile University, Giza, Egypt
5Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, 35516, Egypt
*Corresponding Author: Abdelhameed Ibrahim. Email: afai79@mans.edu.eg
Received: 01 April 2021; Accepted: 02 May 2021
Abstract: Machine learning (ML) has taken the world by a tornado with its prevalent applications in automating ordinary tasks and using turbulent insights throughout scientific research and design strolls. ML is a massive area within artificial intelligence (AI) that focuses on obtaining valuable information out of data, explaining why ML has often been related to stats and data science. An advanced meta-heuristic optimization algorithm is proposed in this work for the optimization problem of antenna architecture design. The algorithm is designed, depending on the hybrid between the Sine Cosine Algorithm (SCA) and the Grey Wolf Optimizer (GWO), to train neural network-based Multilayer Perceptron (MLP). The proposed optimization algorithm is a practical, versatile, and trustworthy platform to recognize the design parameters in an optimal way for an endorsement double T-shaped monopole antenna. The proposed algorithm likewise shows a comparative and statistical analysis by different curves in addition to the ANOVA and T-Test. It offers the superiority and validation stability evaluation of the predicted results to verify the procedures’ accuracy.
Keywords: Antenna optimization; machine learning; artificial intelligence; multilayer perceptron; sine cosine algorithm; grey wolf optimizer
Over the past couple of decades, the art of machine learning (ML) has taken the world by a tornado with its prevalent applications in automating ordinary tasks and using turbulent insights throughout all strolls of scientific research and design. Though perhaps still in its early stage, ML has just about revolutionized the technology sector. ML professionals have handled to modify the foundations of many industries and fields, consisting of lately the style and optimization of antennas. In the light of the Big Information age the world is experiencing, ML has amassed a great deal of interest in this area. ML shows excellent assurance in the field of antenna layout and antenna behavior prediction, whereby the substantial acceleration of this process can be accomplished while preserving high precision [1].
ML has been thought about thoroughly as a complementary method to Computational Electromagnetics (CEM) in developing and enhancing different kinds of antennas for several benefits because of their integral nonlinearities. ML is a vast area within artificial intelligence (AI) that focuses on obtaining valuable information out of data, explaining why ML has been often related to stats and data science [2]. Undoubtedly, the data-driven technique of ML has enabled us to create systems like never previously, taking the world’s actions closer to constructing autonomous systems that can match, compete, and occasionally outperform human capacities as well as intuition. Nonetheless, ML techniques’ success counts heavily on the top quality, amount, and availability of data, which can be testing to obtain in specific instances. From an antenna style viewpoint, this information requires to be gotten, otherwise already available, because no standard dataset for antennas, such as the ones readily available for computer system vision, are yet available. This can be accomplished by replicating the wanted antenna on a wide variety of values using CEM simulation software [3].
The coming era of the worldwide network of factors has allowed an enormous growth in the need for virtually all electronic gadgets for application-specific antennas. The need for a wise and effective means of aerial architecture has thus become imminent. The new antenna architecture relies heavily on the builder’s pragmatic adventures and even electromagnetic (EM) simulations. Standard methods, like 3-D imprinted antennas, are fundamentally unproductive and computationally intensive. Rendering them unfeasible as several antenna concept parameters are improved [4]. Machine learning (ML) techniques can be helpful to solve the issue of constructing complex 3-D structures. ML is widely used as a simple data analysis and decision-making resource in a large set of applications from handwritten finger recognition [5] to individual genomics [6]. Analysts have analyzed antenna establishments’ marketing by applying heuristic optimization techniques, such as particle swarm optimization and genetic algorithm, to antenna concepts [7,8]. However, these protocols also look for the right solution by evaluating the findings on individual data points and producing totally different and perhaps even better search directions before determining global optimums or minimums.
On the other hand, ML extends to both procedures and marketing formulas to analyze the data and check for the covert algebraic relationship in data. The organization can quickly connect input actions to output actions and use this link to generate future predictions or even decisions [9]. The critical conveniences in using ML approaches are that the team can predict the outcome for any data point once they have the relational architecture instead of merely going for fine and minimal required points worldwide. This continuity is exceptionally beneficial because the experts wish to use the same information prepared for multiple purposes. As demonstrated in [10], to design an oblong spot antenna, the support vector machine (SVM) functionality is evaluated. There is an early operation using ML methods for antenna review and preparation [11–14]. Oblong set of patches when using SVMs in the process for linear and nonlinear beamforming and the type of parameters. Artificial Neural Network, an ML technique, has also been used in this field.
The clustering approach is also applied in [14]. Find the optimal microstrip function for shorting blog posts. To achieve adequate bandwidth, browse the Spot Range Layout, Slant, and polarization, some searches, as noted away. For making use of ML techniques for marketing antenna layout, a rigorous review was carried out and coordinated. Indeed, the assessment of several ML techniques for antennas does not. It was revealed that loading is a required payment for this unique task, the distance by offering brand-new ML-based methods courses. There were evaluating for automated aerial concept optimization—performance in predicting accuracy and robustness, EM simulations, and making contrasts. ML is an excellent alternative for automatic, viable, efficient computing, and effective strategies for the antenna concept. This study’s utmost goal is to broaden the built principles to different complicated style aerials, and scalable and functional algorithms [15]. Facing computer barriers by handling a range of design requirements [16].
An advanced meta-heuristic optimization algorithm based on the hybrid of the Sine Cosine Algorithm (SCA) and the Grey Wolf Optimizer (GWO) is proposed in this paper to train the Multilayer Perceptron (MLP) neural network. For antenna design optimization, the proposed algorithm is designed to illustrate these modern antenna design methods’ feasibilities via their application of a reference double T-shaped monopole antenna optimization problem.
A double T-shaped monopole antenna reference is employed in this paper. This antenna’s efficiency typically depends on five design parameters of l21, l22, w1, w2, and w, as shown in Fig. 1. The design allows these five parameters to differ in the definition of the process while retaining the various other three parameters: L; h1 and h2, in their values, as indicated in [17]. For each example score, antenna performance is calculated by removing the amount of value (
where
Several industry situations, monitoring, organizing, style, engineering, clinical solutions, and logistics are considered. Any question for a world-class (fastest, most affordable, most robust, very most beneficial, etc.) is a marketing problem; a metaheuristic is a way of dealing with these complications. A metaheuristic is an approach to fix challenging concerns. A concern is challenging if locating the most effective feasible option that may not always be achievable within a feasible time [18–22].
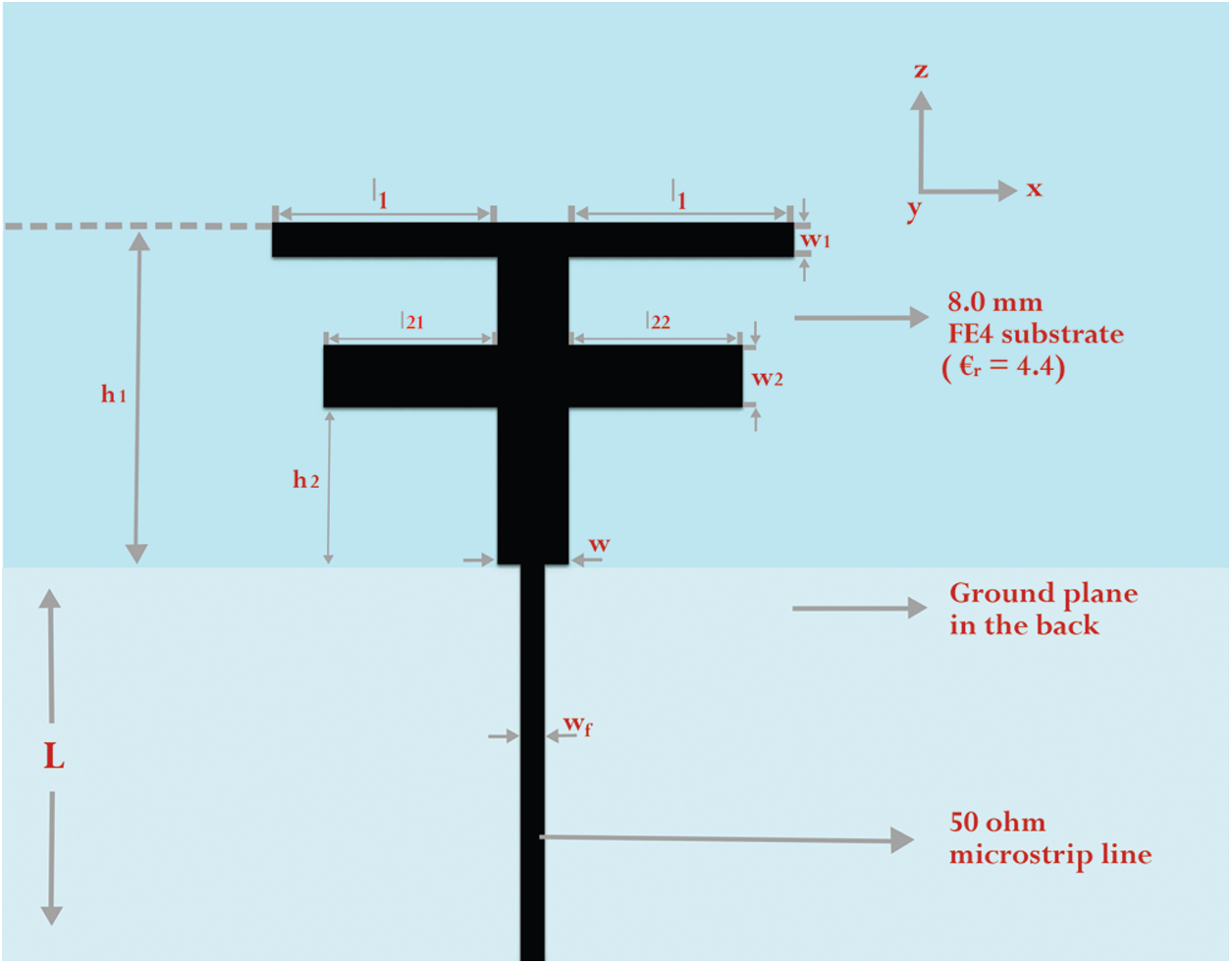
Figure 1: Industry double T-shaped monopole antenna
The GWO algorithm is mainly simulating the movements of the wolves during the hunting for prey process. Wolves live in packs; usually, there are four wolves in one pack, named alpha, beta, delta, and omega [23]. In one pack, the alpha wolves can make choices, and the beta wolves support them in making decisions. The GWO algorithm is introduced step by step in Algorithm 1. In equation form, the alpha (Xα) represents the best solution while the beta (Xβ) and the delta (Xδ) indicate second and third optimal solutions. The rest of the solutions are named omega (Xω). In the catching process of the prey, the first, second, and third best solution guide the rest of the wolves, as shown in the following Equations.

where t indicates current iteration,
where a is decreasing from 2 to 0, and the vectors of r1, r2 have values random in [0, 1]. a can control the processes exploitation and exploration. The a value is calculated as follows.
where
The Xα, Xβ, and Xδ, the best solutions, can guide the rest of solutions (Xω) for updating their positions to be near the prey’s position. The following equations indicate the updating process of the estimated positions.
where A1–A3, C1–C3 are computed as in Eq. (3). The population updated positions
Basic Sine Cosine Algorithm (SCA) was firstly proposed in [24] for optimization problems. Initially, the algorithm is based on sine and cosine oscillations’ functions for updating candidate solutions’ location. SCA uses a series of random variables to denote the direction of motion, how far the movement should be, emphasize/deemphasize the destination effect, and switch between the components of cosine and sine components [25,26]. For updating positions of various solutions, SCA uses the following mathematical method.
where
where
The initial population positions with n agents in the SCA algorithm are randomly set up as shown in Algorithm (1). The objective function is computed, Step (5), for all agents to find the best solution's position. P in Step (6) indicates the best solution. The parameter r1 is updated according to Eq. 2 in Step (7). The positions of different agents are updated by Eq. (1) in Steps (8–13). Steps from Steps 4–16 are repeated according to the number of iterations. The best solution P will be updated until the end of iterations.
Compared to a wide variety of other meta-heuristics, the original SCA algorithm demonstrates robust manipulation due to using a single, best approach to direct other candidate solutions. In terms of memory use and speed of convergence, this makes the helpful algorithm. However, on issues with many locally optimal solutions, this algorithm might show slightly degraded efficiency. The proposed Sine Cosine Grey Wolf Optimizer (SCGWO) algorithm inspired our attempt to mitigate this downside.

Artificial Neural Networks (ANN) follow the biological nervous system principles for information processing and communication among the distributed nodes. The Synapse (the connection between neurons) is used to transmit signals from one neuron to other neurons. Speech recognition, regression, and machine learning algorithms are the most common areas of application of ANN [27,28]. The learning process and optimization of parameters have a significant impact on the performance of ANN. One of the most commonly applied ANN is MLP. The MLP structure is shown in Fig. 2.
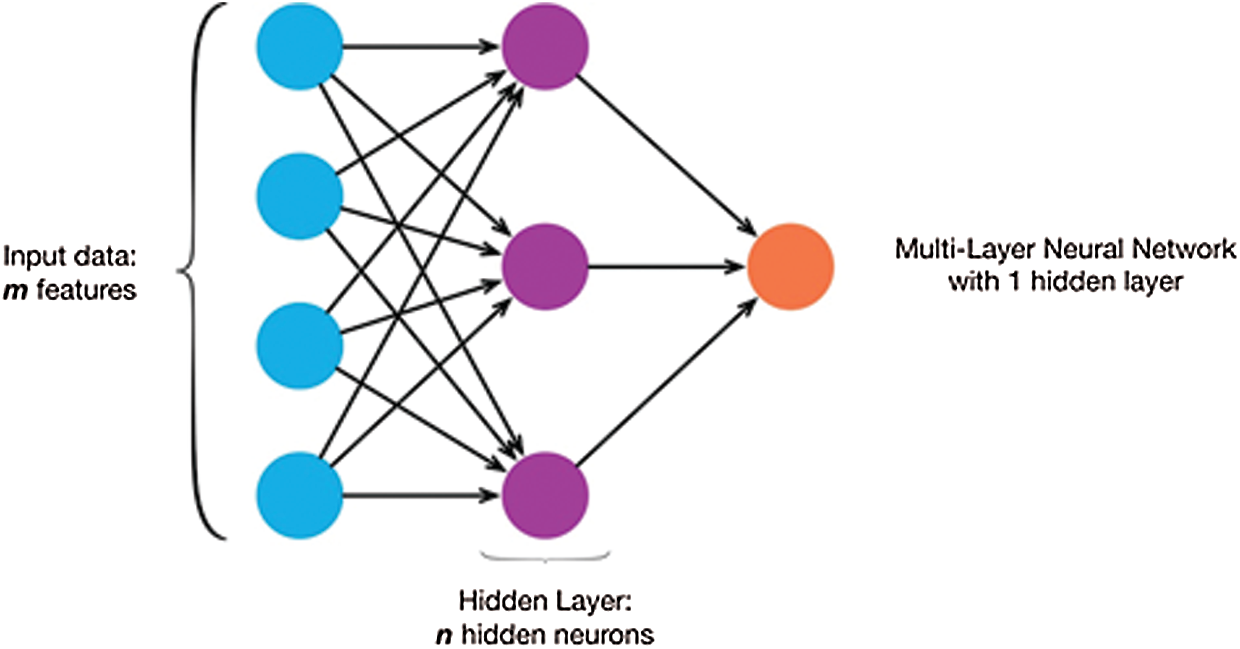
Figure 2: Multilayer perceptron (MLP)
where
The following equation can define the network output based on the value of
where
3 Proposed Sine Cosine Grey Wolf Optimizer
The proposed Sine Cosine Grey Wolf Optimizer (SCGWO) algorithm is shown in Algorithm 3. The SCGWO algorithm takes advantage of the Sine Cosine algorithm and the Grey Wolf Optimizer in exploitation and exploration processes. SCGWO starts with initializing the population X (i = 1, 2, …, n) with size n. Then the parameters of a, A, and C are initializing as in Eqs. (3) and (4). The objective function Fn is then calculated for each agent Xi in the population. During the iterations, the parameter pd is randomly initialized between 0 and 1. One of the two GWO or SCA algorithms will be employed to update the agents’ positions based on the selected value. From Algorithm 3, steps from 6–15 will get the best position Xbest based on the GWO algorithm. Steps from 17–26, the best position Xbest will be updated based on the SCA algorithm.
In this section, the SCGWO algorithm is evaluated for optimizing the double T-shaped monopole antenna problem’s parameters. The SCGWO algorithm is applied in the experiments to optimize the weights of the MLP network. The input layer consists of five nodes representing a single parameter of the design and a single node output layer representing the FOM as shown in Tab. 1. The results, Tab. 1, of the proposed algorithm show that it is more precise than using the KNN and MLP techniques with a minimum time of 272.13 s in optimizing the design parameters of l21, l22, w1, w2, and w.
Descriptive statistics, shown in Tab. 2, are short, summarizing, descriptive coefficients that can either represent the results. The descriptive data is broken down into measurements of central propensity and measures of uncertainty. Tests are for the mean, median, and mode, while the uncertainty is measured for the standard deviation, variance, minimum and maximum variables. Tab. 2 shows the superiority of the proposed SCGWO MLP algorithm.

A statistical methodology of ANOVA and t-test are applied to compare the populations to determine if there is a major difference between the proposed and compared techniques. Tab. 3 shows the two-way ANOVA test results. For this test, the statistical hypothesis can be formulated as follows.
• Null hypothesis (H0): mean the difference between groups are not significant.
• Alternative hypothesis (H1): significant difference between means of populations, which is the distinction.

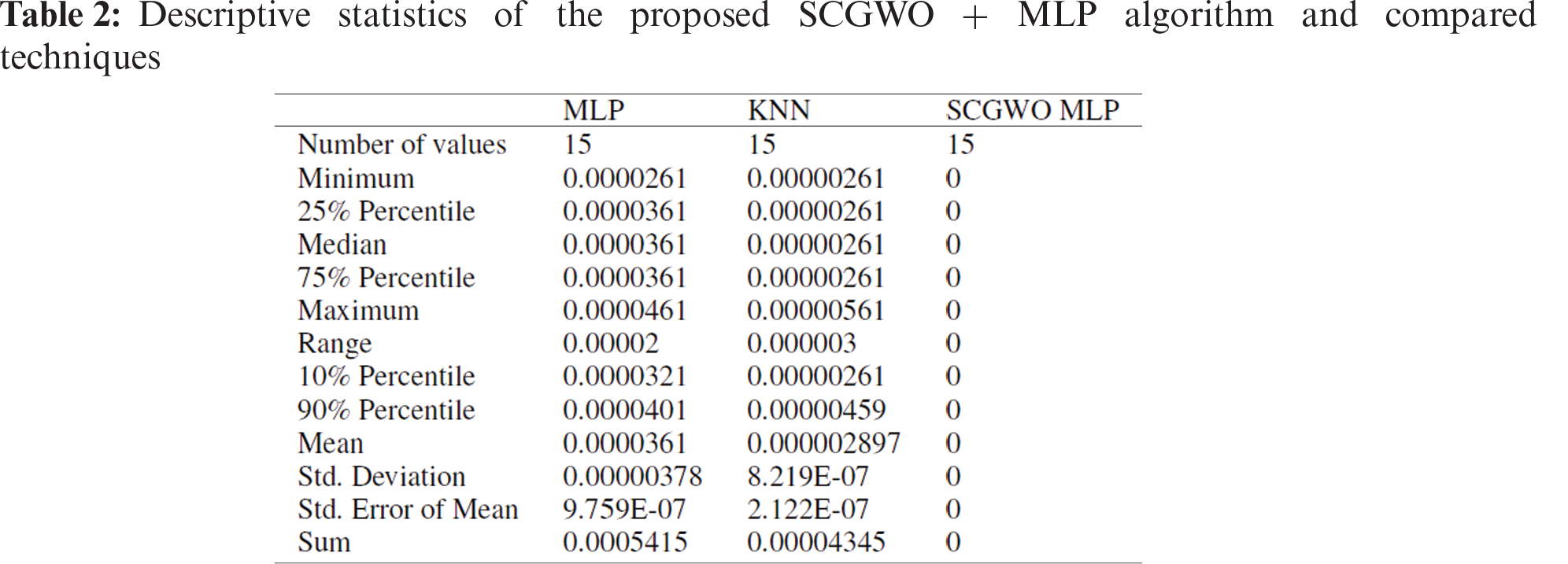
As also seen in Tab. 4, the statistical hypothesis for the one-sample t-test can be formulated as follows.
• Null hypothesis (H0): mean the difference between two groups is not significant.
• Alternative hypothesis (H1): the considerable difference between the two means of the population is the distinction.
Tab. 3 for the two-way ANOVA test and Tab. 4 for the one-sample t-test indicate the superiority of the proposed (SCGWO + MLP) algorithm.
The histogram of the compared techniques performance vs. the proposed algorithm is investigated in Fig. 3. The (SCGWO + MLP) algorithm shows better behavior in both curves of histogram smooth and normalize. The QQ plot shown in Fig. 3 indicates that the proposed algorithm’s actual and predicted values are almost fit.

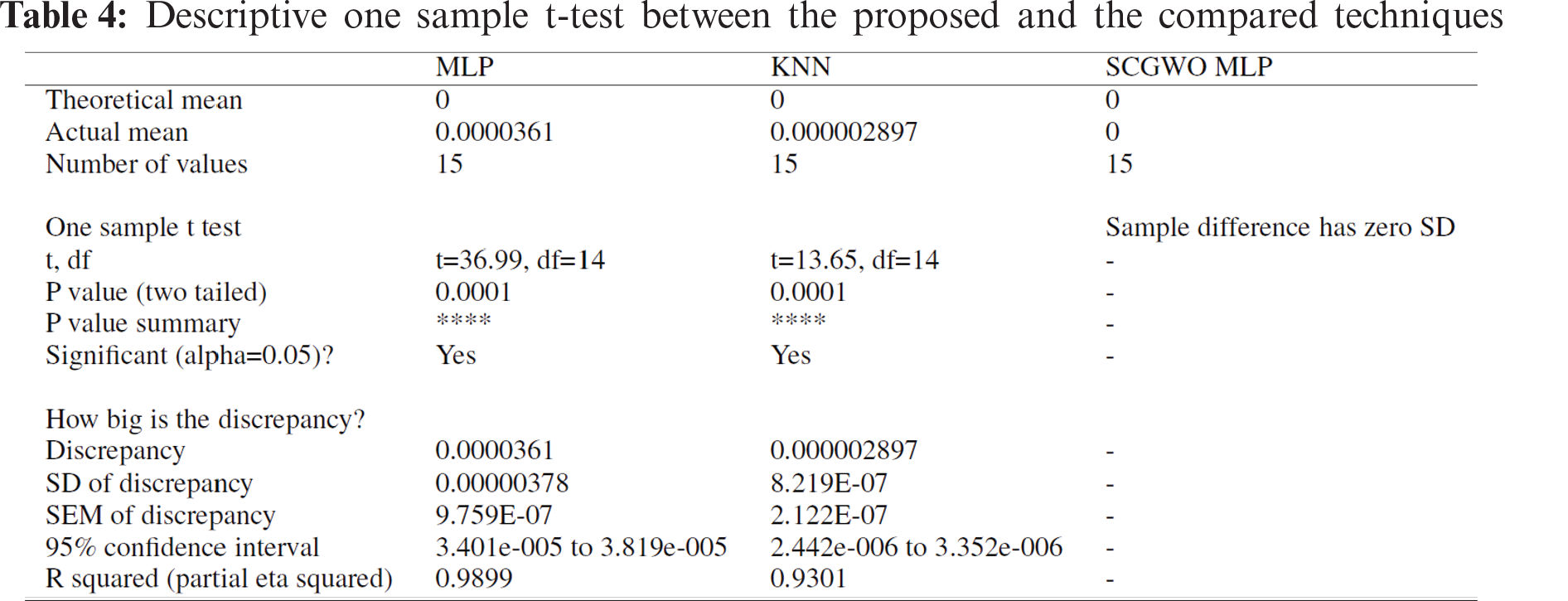
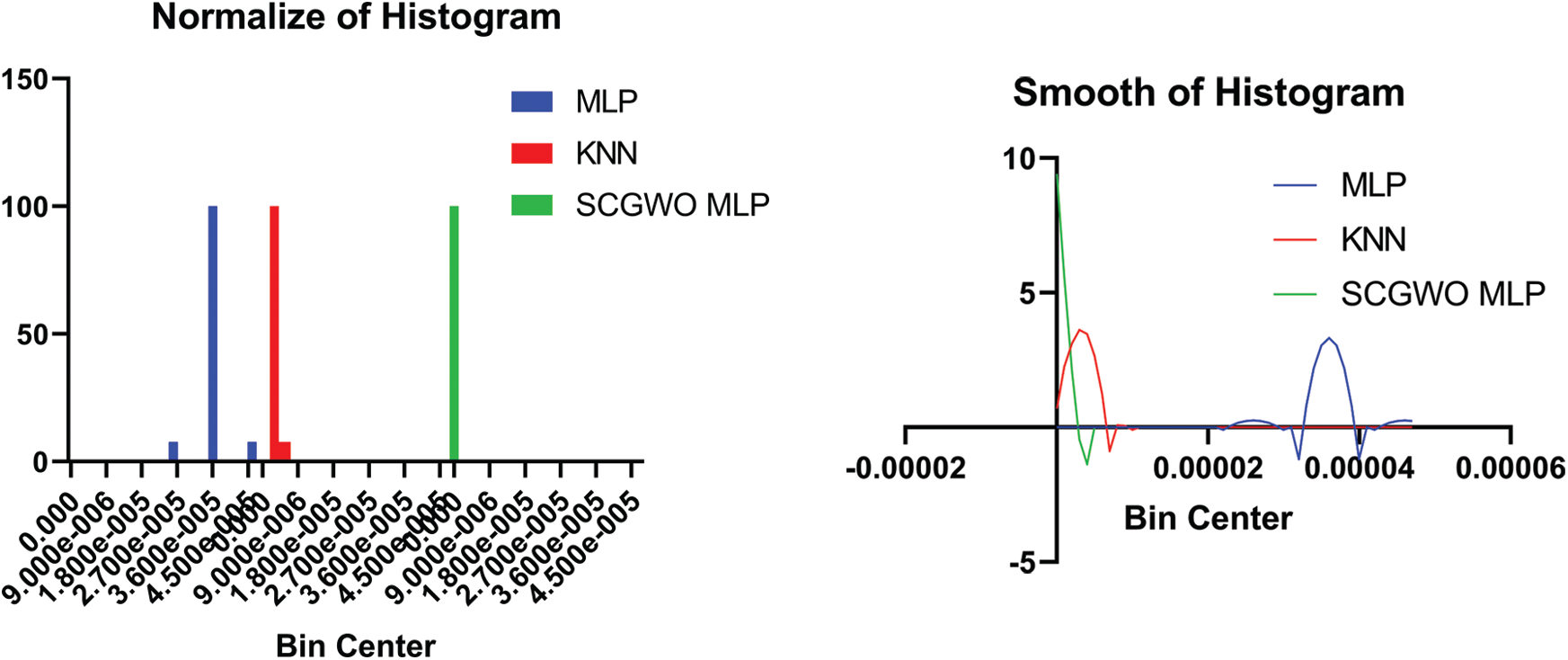
Figure 3: Smooth and normalize histogram curves of the proposed and compared techniques
The ROC analysis is also done to a standard of ranking and continuous diagnostic test results. Derived accuracy indexes, particularly the area under the curve (AUC), have a meaningful understanding of classification shown in Fig. 4. Tab. 5 shows that the AUC value of the proposed algorithm is much better than other techniques, close to 1.
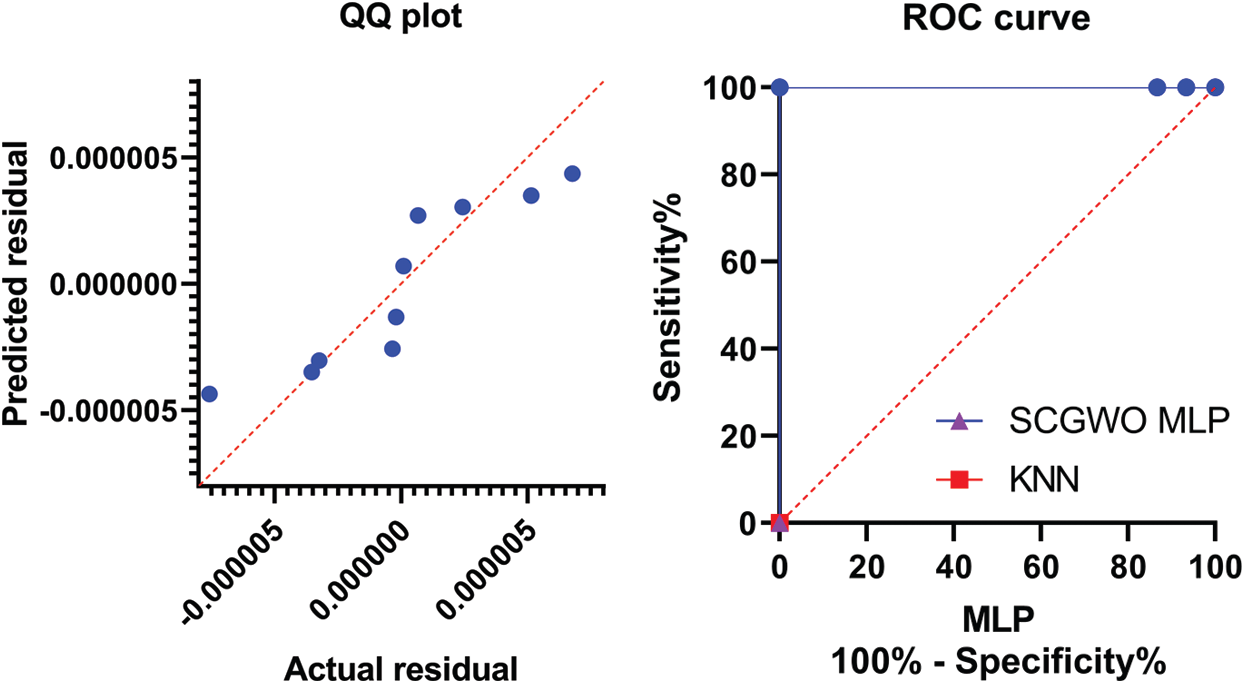
Figure 4: QQ and ROC curves of the proposed and compared techniques
In Fig. 5, different algorithms’ performance vs. the objective function is shown. It can be noted that the minimum, maximum, and average values based on the proposed algorithm are almost the same. This curve indicated the stability of the proposed (SCGWO + MLP) algorithm.
The proposed SCGWO algorithm is used for optimizing the double T-shaped monopole antenna problem’s parameters. Results show that the algorithm is precise than the KNN and MLP techniques with a minimum time of 272.13 s to optimise the design parameters of l21, l22, w1, w2, and w. Descriptive statistics show the superiority of the proposed SCGWO MLP algorithm. The two-way ANOVA test and the one-sample t-test indicate the worth of the proposed (SCGWO + MLP) algorithm. The (SCGWO + MLP) algorithm also shows better behavior in both curves of histogram smooth and normalize. The QQ plot indicates the proposed algorithm’s actual and predicted values. From the ROC curves analysis, the AUC value of the proposed algorithm is much better than other techniques, and it is close to 1. It is also noted that the minimum, maximum, and average values based on the proposed algorithm are almost the same vs. objective function, which indicated the stability of the proposed (SCGWO + MLP) algorithm.
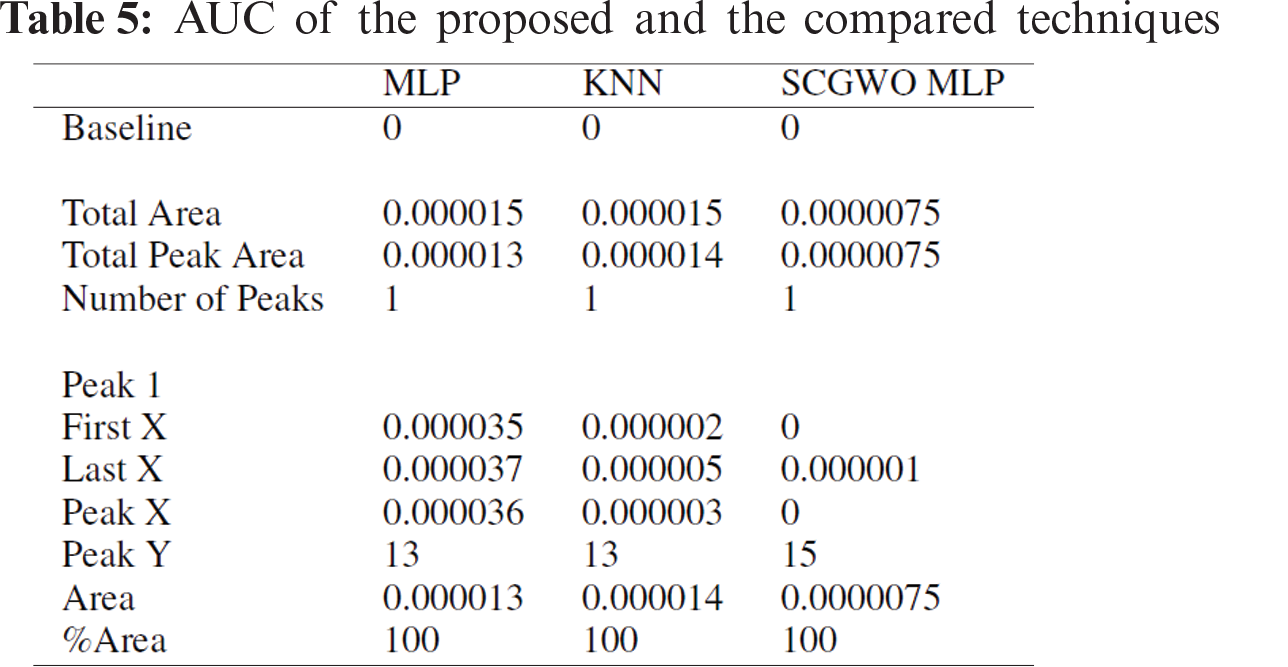
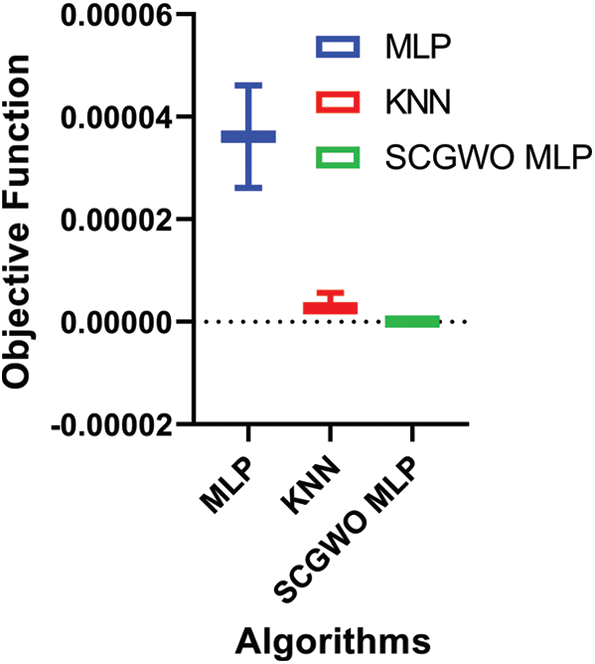
Figure 5: The proposed algorithm and compared techniques vs. objective function
Multilayer Perceptron (MLP) weights are optimized through the proposed advanced Meta-Heuristic Optimization, based on the Sine Cosine Algorithm (SCA) and the Grey Wolf Optimizer (GWO). The experimental results have shown that the machine learning techniques, based on the proposed SCGWO algorithm, can allow a double T-shaped monopole antenna to be scalable and theoretically autonomous architecture, which will be useful for many applications, including the Internet of Things. The proposed algorithm showed a comparative and statistical analysis of the ROC curve and the T-Test that indicated the superiority and validation stability evaluation of the predicted results to verify the procedures’ accuracy.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. M. E. Misilmani, T. Naous and S. K. A. Khatib, “A review on the design and optimization of antennas using machine learning algorithms and techniques,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 30, no. 10, pp. e22356, 2020. [Google Scholar]
2. P. Testolina, M. Lecci, M. Rebato, A. Testolin, J. Gambini et al., “Enabling simulation-based optimization through machine learning: A case study on antenna design,” in 2019 IEEE Global Communications Conf., Waikoloa, HI, USA, pp. 1–6, 2019. [Google Scholar]
3. H. M. E. Misilmani and T. Naous, “Machine learning in antenna design: An overview on machine learning concept and algorithms,” in 2019 Int. Conf. on High Performance Computing & Simulation, Dublin, Ireland, IEEE, pp. 600–607, 2019. [Google Scholar]
4. J. Dong, Q. Li and L. Deng, “Design of fragment-type antenna structure using an improved BPSO,” IEEE Transactions on Antennas and Propagation, vol. 66, no. 2, pp. 564–571, 2018. [Google Scholar]
5. W. Qin, J. Dong, M. Wang, Y. Li and S. Wang, “Fast antenna design using multi-objective evolutionary algorithms and artificial neural networks,” in 2018 12th Int. Symp. on Antennas, Propagation and EM Theory, Hangzhou, China, IEEE, pp. 1–3, 2018. [Google Scholar]
6. T. J. Santner, B. J. Williams and W. I. Notz, The Design and Analysis of Computer Experiments, 2nd ed., New York, NY: Springer, 2018. [Google Scholar]
7. S. Koziel and S. Ogurtsov, “Multi-objective design of antennas using variable-fidelity simulations and surrogate models,” IEEE Transactions on Antennas and Propagation, vol. 61, no. 12, pp. 5931–5939, 2013. [Google Scholar]
8. H. Xin and M. Liang, “3-D-printed microwave and THz devices using polymer jetting techniques,” Proceedings of the IEEE, vol. 105, no. 4, pp. 737–755, 2017. [Google Scholar]
9. D. Z. Zhu, P. L. Werner and D. H. Werner, “Design and optimization of 3-D frequency-selective surfaces based on a multiobjective lazy ant colony optimization algorithm,” IEEE Transactions on Antennas and Propagation, vol. 65, no. 12, pp. 7137–7149, 2017. [Google Scholar]
10. Y. Rahmat-Samii, J. M. Kovitz and H. Rajagopalan, “Nature-inspired optimization techniques in communication antenna designs,” Proceedings of the IEEE, vol. 100, no. 7, pp. 2132–2144, 2012. [Google Scholar]
11. A. Massa, G. Oliveri, M. Salucci, N. Anselmi and P. Rocca, “Learning-by-examples techniques as applied to electromagnetics,” Journal of Electromagnetic Waves and Applications, vol. 32, no. 4, pp. 516–541, 2017. [Google Scholar]
12. Z. Zheng, X. Chen and K. Huang, “Application of support vector machines to the antenna design,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 21, no. 1, pp. 85–90, 2010. [Google Scholar]
13. H. Moon, F. L. Teixeira, J. Kim and Y. A. Omelchenko, “Trade-offs for unconditional stability in the finite-element time-domain method,” IEEE Microwave and Wireless Components Letters, vol. 24, no. 6, pp. 361–363, 2014. [Google Scholar]
14. M. Martínez-Ramón and C. Christodoulou, “Support vector machines for antenna array processing and electromagnetics,” Synthesis Lectures on Computational Electromagnetics, vol. 1, no. 1, pp. 1–120, 2006. [Google Scholar]
15. T. Sallam, A. B. Abdel-Rahman, M. Alghoniemy, Z. Kawasaki and T. Ushio, “A neural-network-based beamformer for phased array weather radar,” IEEE Transactions on Geoscience and Remote Sensing, vol. 54, no. 9, pp. 5095–5104, 2016. [Google Scholar]
16. J.-M. Wu, “Multilayer potts perceptrons with Levenberg–Marquardt learning,” IEEE Transactions on Neural Networks, vol. 19, no. 12, pp. 2032–2043, 2008. [Google Scholar]
17. Y.-L. Kuo and K.-L. Wong, “Printed double-t monopole antenna for 2.4/5.2 GHz dual-band WLAN operations,” IEEE Transactions on Antennas and Propagation, vol. 51, no. 9, pp. 2187–2192, 2003. [Google Scholar]
18. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization,” IEEE Access, vol. 8, pp. 81747–81764, 2020. [Google Scholar]
19. E.-S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]
20. M. M. Fouad, A. I. El-Desouky, R. Al-Hajj and E.-S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, pp. 148378–148403, 2020. [Google Scholar]
21. E.-S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, no. 1, pp. 635–649, 2020. [Google Scholar]
22. E.-S. El-Kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]
23. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey Wolf Optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
24. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, no. 63, pp. 120–133, 2016. [Google Scholar]
25. M. M. Eid, E.-S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf., Taif, Saudi Arabia, IEEE, pp. 1–6, 2021. [Google Scholar]
26. E.-S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy and M. El-Said, “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 x-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]
27. E. M. Hassib, A. I. El-Desouky, L. M. Labib and E.-S. M. T. El-Kenawy, “Woa + BRNN: An imbalanced big data classification framework using whale optimization and deep neural network,” Soft Computing, vol. 24, no. 8, pp. 5573–5592, 2020. [Google Scholar]
28. E. M. Hassib, A. I. El-Desouky, E. M. El-Kenawy and S. M. El-Ghamrawy, “An imbalanced big data mining framework for improving optimization algorithms performance,” IEEE Access, vol. 7, pp. 170774–170795, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |