Computers, Materials & Continua DOI:10.32604/cmc.2021.019153
Article

Double Encryption Using Trigonometric Chaotic Map and XOR of an Image

Orawit Thinnukool1, Thammarat Panityakul2 and Mahwish Bano3,*

1College of Arts, Media and Technology, Chiang Mai University, Chiang Mai, 50200, Thailand
2Division of Computational Science, Prince of Songkla University, Hat Yai, Songkhla, 90110, Thailand
3Department of Mathematics, Air University, Islamabad, 44000, Pakistan
*Corresponding Author: Mahwish Bano. Email: mahwish@mail.au.edu.pk
Received: 03 April 2021; Accepted: 04 May 2021

Abstract: In the most recent decades, a major number of image encryption plans have been proposed. The vast majority of these plans reached a high-security level; however, their moderate speeds because of their complicated processes made them of no use in real-time applications. Inspired by this, we propose another efficient and rapid image encryption plan dependent on the Trigonometric chaotic guide. In contrast to the most of current plans, we utilize this basic map to create just a couple of arbitrary rows and columns. Moreover, to additionally speed up, we raise the processing unit from the pixel level to the row/column level. The security of the new plot is accomplished through a substitution permutation network, where we apply a circular shift of rows and columns to break the solid connection of neighboring pixels. At that point, we join the XOR operation with modulo function to cover the pixels values and forestall any leaking of data. High-security tests and simulation analyses are carried out to exhibit that the scheme is very secure and exceptionally quick for real-time image processing at 80 fps (frames per second).

Keywords: Double image encryption; target image; random image; trigonometric chaotic map

1  Introduction

With the quick development of multimedia and communication technologies, the amount of information stored and communicated has exponentially expanded. The security of this information became a significant issue examined by numerous specialists, researchers, and analysts. Tragically, traditional text encryption plans like data encryption standard (DES) [1], advanced encryption standard (AES) [2], or the RSA [3] algorithms cannot have secure image data, essentially due to the differences that exist among text and image data, such as the massive size of images, solid excess and solid relation among adjacent pixels. Besides, little distortions in the decipher image data are adequate as it generally relies upon human recognition. In this manner, considering the exceptional properties of digital pictures, a few image encryption schemes have been proposed utilizing different sort of technologies, for example, chaotic maps [4–6], DNA encoding [7–9], quantum theory [10–12], scalable encoding [13], flexible compression and image imprinting [14], and so forth [15]. Chaos theory has been broadly utilized in cryptography, it has remarkable features like ergodicity, sensitivity to the parameters and initial values, capriciousness, random-like conduct, and many more, which have coordinated the fundamental necessities of cryptography [16,17]. A large number of proposed image encryption frameworks have been dependent on famous chaotic maps like the logistic guide [18,19], sine map [20–22], tent guide [23,24], and Arnold cat map [25,26]. Some new chaotic maps [27–31] have not been yet utilized in cryptography; even they have a more extensive chaotic range, better ergodicity, flightiness, and an easier structure than a few well-known chaotic maps. Besides, the greater part of the current image encryption plans utilized the adopted chaotic guides where a few chaotic values have been created for every pixel in the plain-text image. The generation of such a major number of chaotic values devours a lot of computation time and extensively eases the entire encryption process speed. Consequently, these sorts of encryption plans are not reasonable for constant image processing. In the present paper, quick and efficient image encryption conspires because the Trigonometric chaotic map with XOR is proposed. The Trigonometric map has been founded by Orcan Alpar [31] has an extremely basic equation like the logistic map which makes it reasonable for the plan of a real-time image encryption plot. Unlike the logistic map, the Trigonometric map also shows high chaotic conduct in a bigger chaotic scope of the boundaries' qualities, which develops the keyspace and expands the security level. To build the encryption/decryption process speed, the proposed scheme raises the little treatment unit from the pixel level to the row/column level. Moreover, unlike the greater part of the current image encryption plots, the wise utilization of the straightforward chaotic map is adopted. Surely, the new scheme creates just 3 rows and 3 columns for each encryption round. The high security and speed of the proposed scheme are demonstrated through a few notable performances and security tests. The exhibitions of the new strategy can undoubtedly fulfill the prerequisites of real-time image processing at 80 fps (frames per second) for 512 × 512 size images and its security level is parallel to state-of-the-art encryption strategies. Consequently, the proposed strategy is an ideal contender for making sure about real-time image processing applications and communications, for example, ensuring the communicated satellite images, procuring the sent images from remote-controlled drones, real-time encryption/decryption of spared Iris biometric recognition images, and so forth. The primary commitments in this paper are continued as follows.

(i) We propose a novel chaos-based image encryption strategy with a high-security level for real-time image processing at 80 fps.

(ii) We make the first and efficient use of the Trigonometric chaotic map in the field of picture encryption.

(iii) We carefully upgrade the utilization of the chaotic map to create arbitrary-like numbers.

(iv) We raise the little processing unit from the pixels level to the rows/columns level.

2  Image Encryption Using Trigonometric Chaotic Map

Chaotic maps hold attractive properties, for example, high affectability to a little change in introductory value and control boundaries, pseudorandom, the precariousness of the framework circle, and simplicity of execution. For the most part, chaotic maps are utilized to produce chaotic key streams that can be utilized in image encryption to accomplish secure correspondence. Numerous chaotic maps have restricted range boundaries making them shaky for image transmission. This paper proposes a clamorous guide alluded to as the trigonometric chaotic map with XOR (TCMX). The qualities of the TCM are researched and used to build up an image encryption strategy. Exploratory outcomes on the TCM show a wide extend of chaotic disorganized conduct, s-unimodality property, and high affectability to a little change in the initial condition. Results likewise show that the arbitrarily produced key streams by the TCM finished the NIST measurable assessments. At long last, encryption results utilizing grey-scale images show that the TCM-based image encryption technique offers exceptionally secure encryption with a short encryption time.

3  Quick Survey of Literature

The brisk advancement of multimedia technology and computer networks with the expanded utilization of cloud-based capacity and enormous information expect strategies to ensure individuals' private and confidential information. Simultaneously, the pre-owned assurance technique ought to be exceptionally secure without trading off the usefulness and convenience of the framework to give accommodation to clients. Image encryption is one of the generally utilized and viable strategies to secure images during storage and transmission. Conventional encryption techniques are not appropriated to encrypt images due to image intrinsic qualities, for example, the connection between image pixels, low affectability to information change, and information excess. Chaotic maps hold appealing attributes, for example, insecurity of system orbit, basic execution, and high affectability to a little change in initial values, control boundaries, and pseudo-randomness. Distinctive chaotic maps have been accounted for in the literature, for example, convex sinusoidal map, parameter-varying baker map, cross chaotic map, generalized sine map, combined sine and tent map, generalized logistic map. Each proposed chaotic map has its points of interest and detriments regarding encryption time, security, and unpredictability. The logistic map, one of the most normally utilized chaotic maps, has a little keyspace making it not invulnerable against brute force attacks, doesn't give uniform dissemination of the iterative variable, and has a flimsy value of Lyapunov exponent [8,11]. It has been discovered that the vast majority of confusing cryptosystems have lacking strength and security [12]. Another work detailed that the logistic map, mandelbrot map, and symmetric tent map hold an enormous arrangement of weaknesses. The literature likewise announced distinctive chaotic-based image encryption techniques, for example [14–16]. A one-dimensional chaotic map is proposed in this paper; the trigonometric chaotic map (TCMX). At that point, the qualities of the TCM are examined. The investigated qualities are affectability to a little change in the initial condition, chaotic conduct, s-unimodality, and randomness. Based on the examined qualities, an image encryption strategy is created. At last, factual properties and the encryption performance of the created image encryption strategy are dissected.

4  Trigonometric Chaotic Map

Eq. (1) displays the proposed trigonometric chaotic map.

sn+1={λsn(sin⁡(π2sn)+cos⁡(π2sn)),0≤sn≤0.5λ(1−sn)(sin⁡(π2(1−sn))+cos(π2(1−sn))),0.5<sn≤1 (1)

where sn+1 ∈ [0, 1], s0 represents the initial condition, and λ represents the control parameter.

5  TCM Characteristics Investigation

Attributes of the trigonometric chaotic map are examined here. The assessed qualities are chaotic conduct, s-unimodality, affectability to a little change in starting condition, and haphazardness. Fig. 1 shows the iterations of the trigonometric chaotic map. The iteration begins from zero and continues expanding until it arrives at its most extreme worth and afterward diminishes back to zero. Likewise, the iteration function has a single maximum value. In this way, the TCM accomplishes the unimodality property at λ = 1.42. Then, the range of the control parameter λ within which the trigonometric chaotic map accomplishes the unimodality trademark is considered. The bifurcation outline is utilized for this reason [6], as appeared in Fig. 2 for control boundary range λ ∈ [1.3, 1.55]. The bifurcation outline shows that the TCM fulfills the unimodality characteristic for λ ∈ [1.3859, 1.4424].

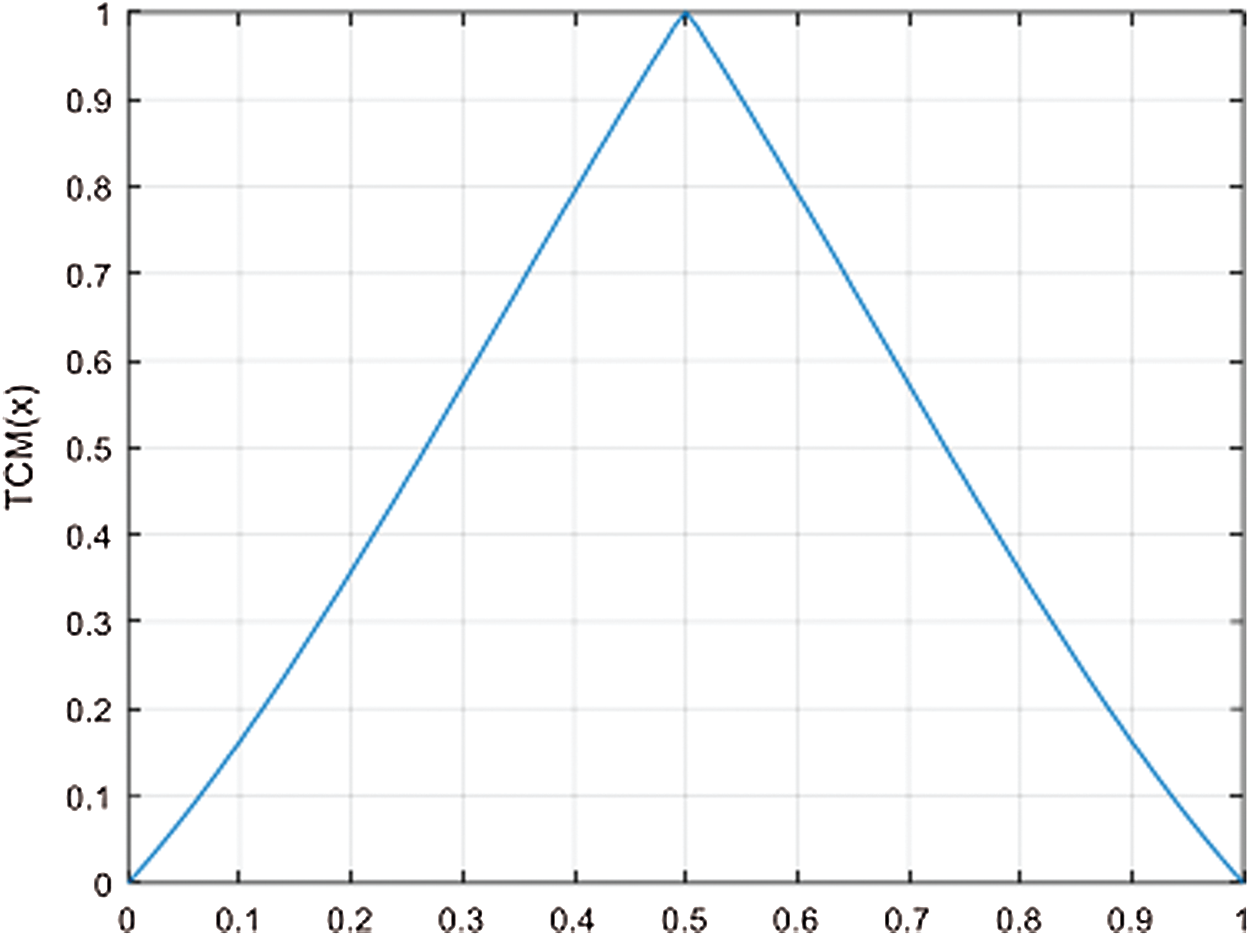
Figure 1: The iteration function of TCM for λ = 1.42

The chaotic conduct of the TCM is examined utilizing the Schwarzian derivative. Condition (2) shows the Schwarzian derivative of the TCM. Fig. 3 shows the charted Schwarzian derivative of the TCM for control boundary λ = 1.42 and introductory condition s0 = 0.26. Fig. 3 shows a negative Schwarzian derivative along with the entire interval which demonstrates that the TCM gives chaotic conduct at the chosen estimation of initial condition and control boundary.

Sf(s)=f′′′(s)f′(s)−1.5(f′′(s)f′(s))2 (2)

In summary, the obtained robust chaos and unimodality characteristics demonstrate that the trigonometric chaotic map satisfies the s-unimodality property at the chosen values of the control parameter and initial condition. Another thing to investigate is the sensibility to a little change in the initial condition. Fig. 4 displays two sequences; we get using (1). The two produced sequences have become complicated, after some iteration, shows the high sensitivity of the TCM to a smaller change in the initial condition.

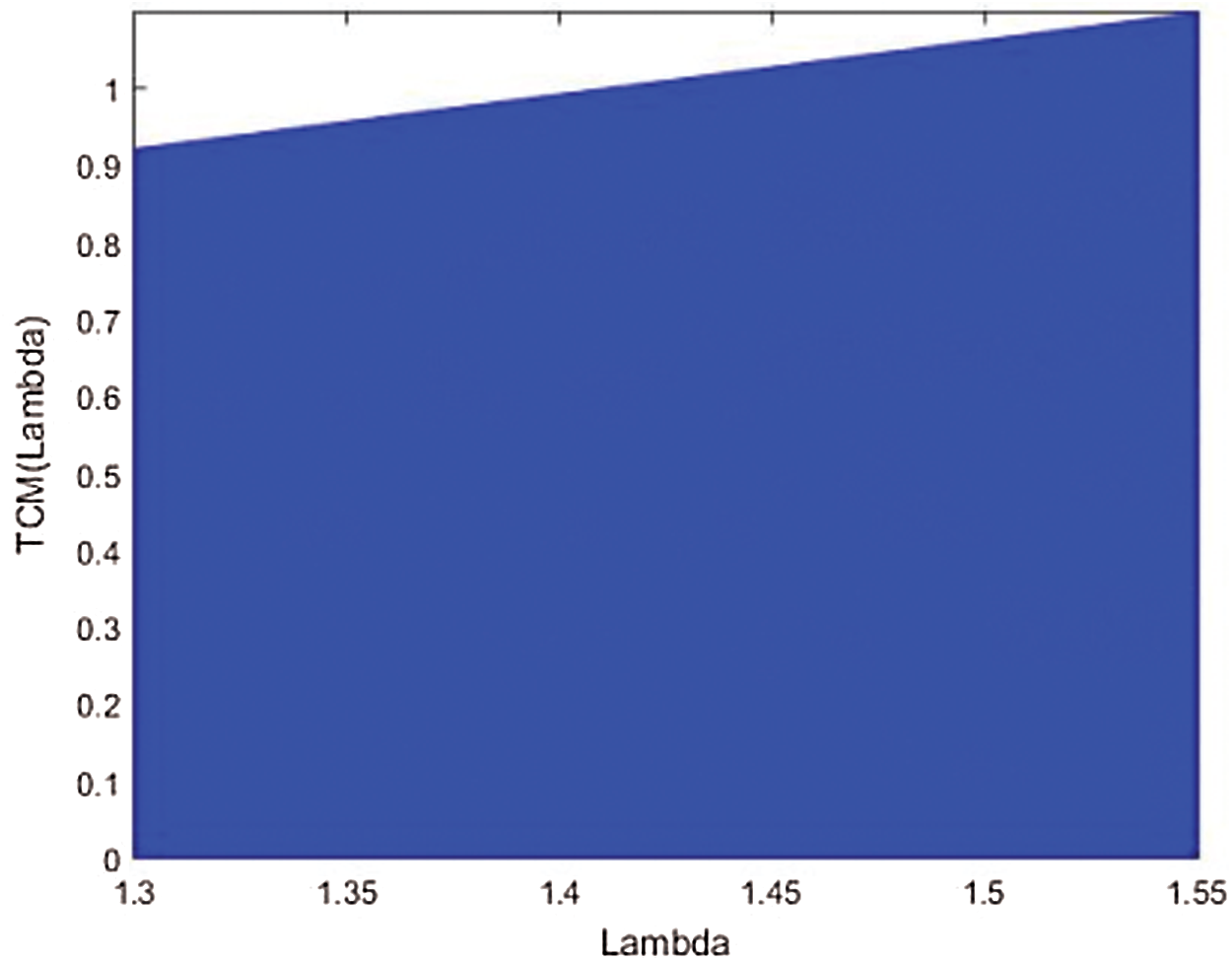
Figure 2: The bifurcation diagram of TCM for λ ∈ [1.3, 1.55]

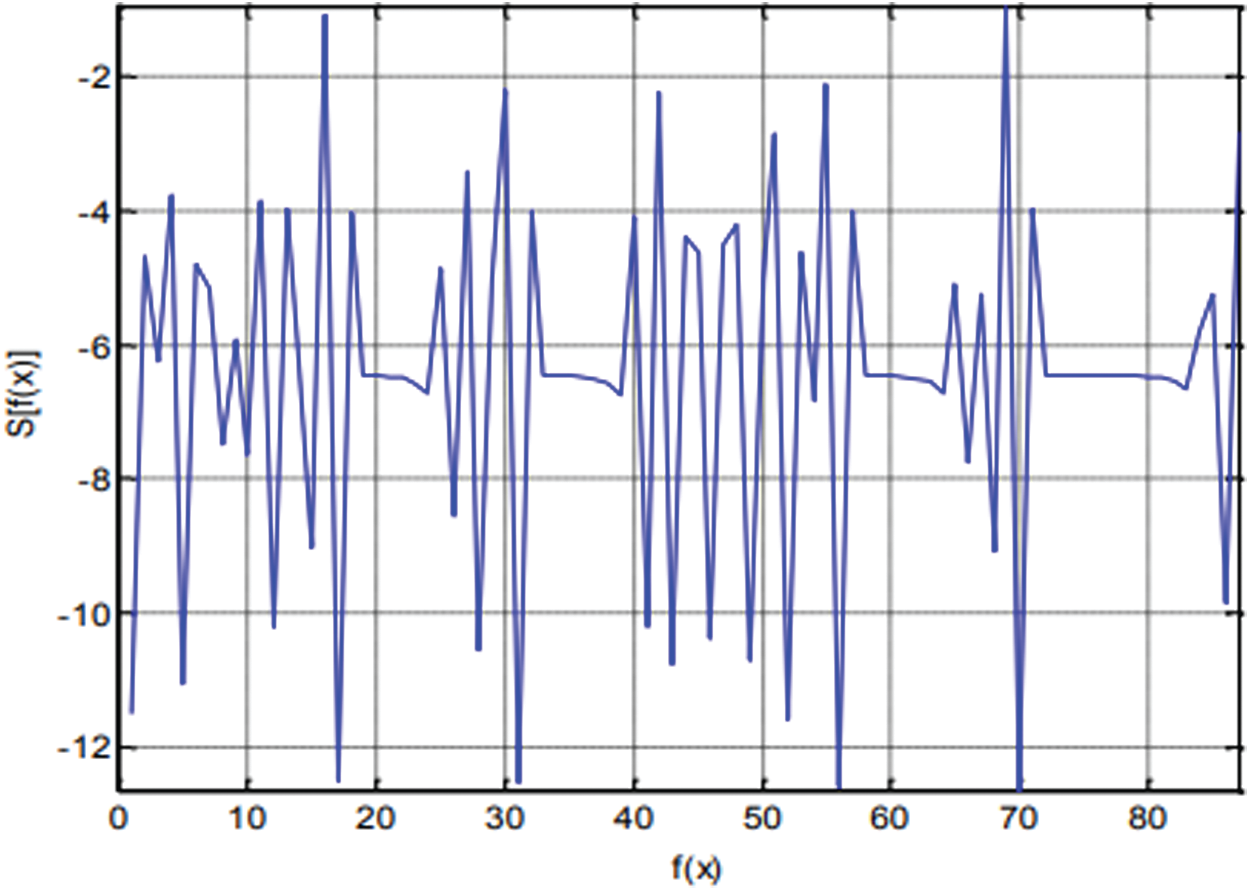
Figure 3: The schwarzian derivative of TCM for λ = 1.42

Then again, the Lyapunov exponent is utilized to explore the chaotic behavior of the TCM as appeared in (3). Condition (4) shows the derivative of (1). The produced Lyapunov type of the TCM appears in Fig. 5 for the control boundary range λ ∈ [1, 1.6]. As mentioned in the literature, any chaotic map should give chaotic conduct to the Lyapunov exponent inside the scope of [0, 0.69]. Fig. 5, the TCM gives chaotic conduct to λ ∈ [1, 1.466]. The acquired experimental after-effects of the bifurcation chart and Lyapunov exponent show that the TCM has chaotic conduct and fulfills the s-unimodality attribute for λ ∈ [1.3859, 1.4424]. In correlation, the logistic and tent maps give chaotic conduct and fulfill the s-unimodality trademark for λ ∈ [3.96, 4] and λ ∈ (1.999, 2), separately. This demonstrates the trigonometric chaotic map has a wide range of chaotic conduct.

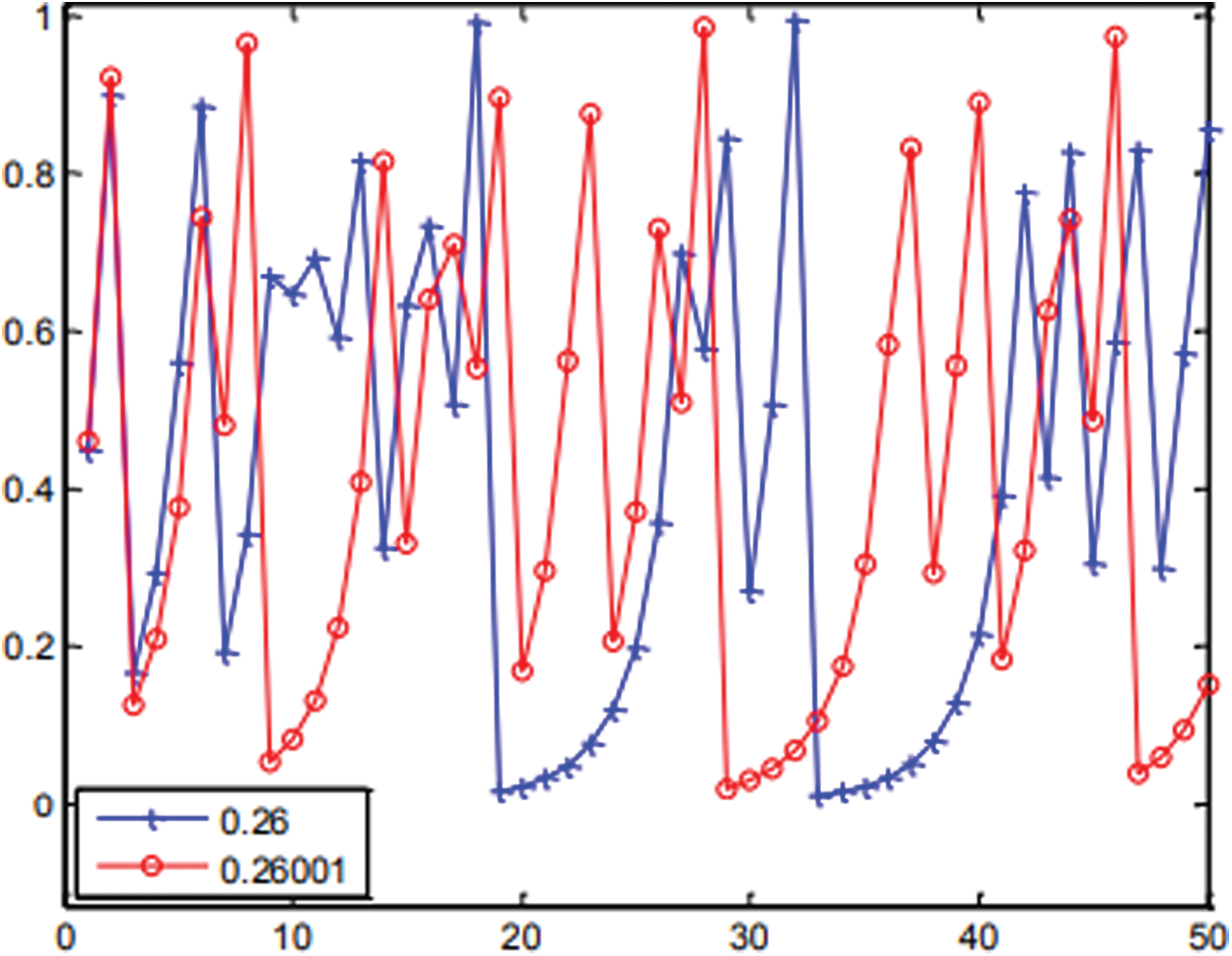
Figure 4: Two sequences obtained for (s0, λ) = (0.26, 1.42), marked with squares, and for (s0, λ) = (0.26001, 1.42), marked with circles

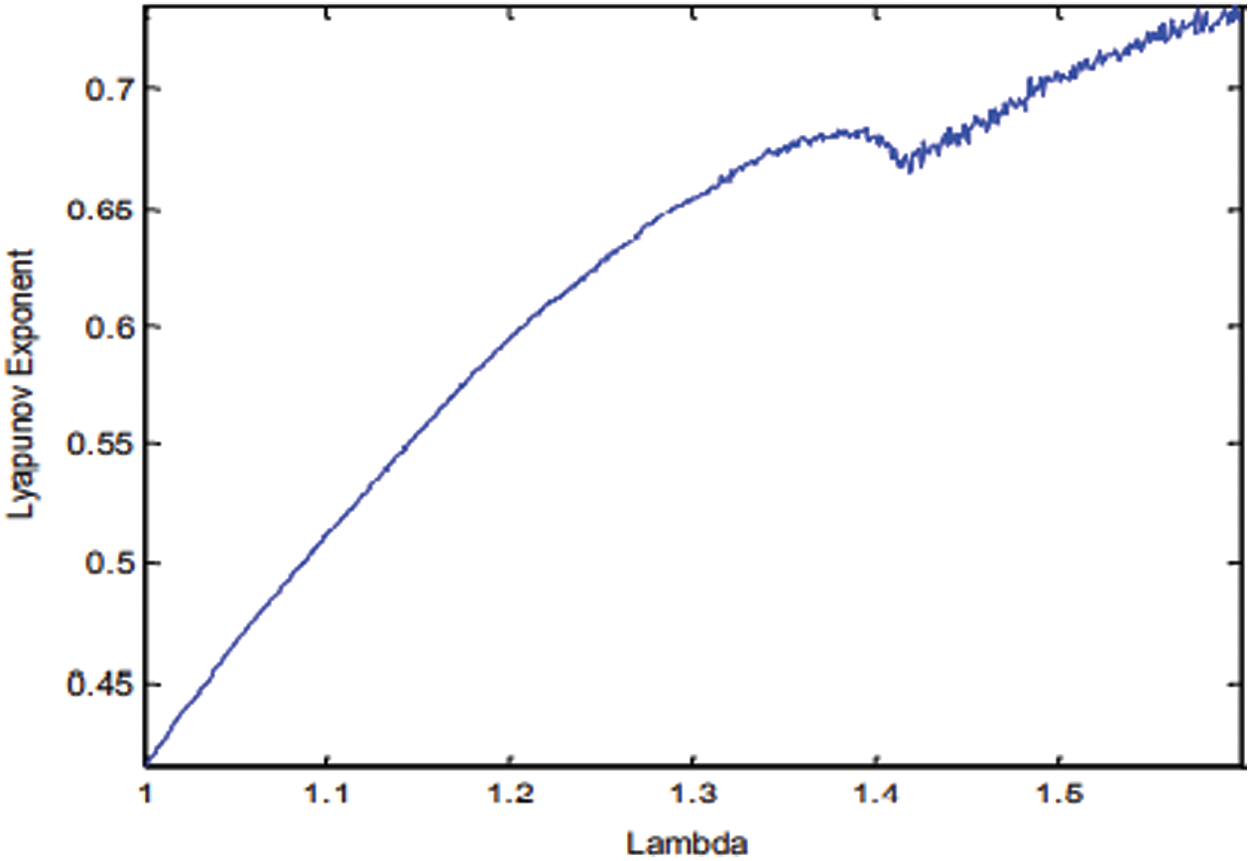
Figure 5: The Lyapunov exponent of the TCM for λ ∈ [1,1.6]

λLE(s0)=limn→∞1N∑n=0N−1ln⁡|f′(sn,λ)| (3)

The last characteristic to explore is arbitrariness which can be utilized to decide the appropriateness of utilizing the TCM in cryptographic applications. A protected keystream generator shouldn’t show deterministic attributes or essential statistical predispositions. The NIST statistical test suite is utilized to tentatively approve whether the created key streams by the TCM hold arbitrary conduct. The NIST suite is utilized to direct 15 statistical tests intended to test various sorts of non-arbitrariness in a binary sequence. As a pre-preparing step, iterates of the TCM are changed over into binary sequences as appeared in (4).

βi={0,0≤si<0.51,1≥si≥0.5 (4)

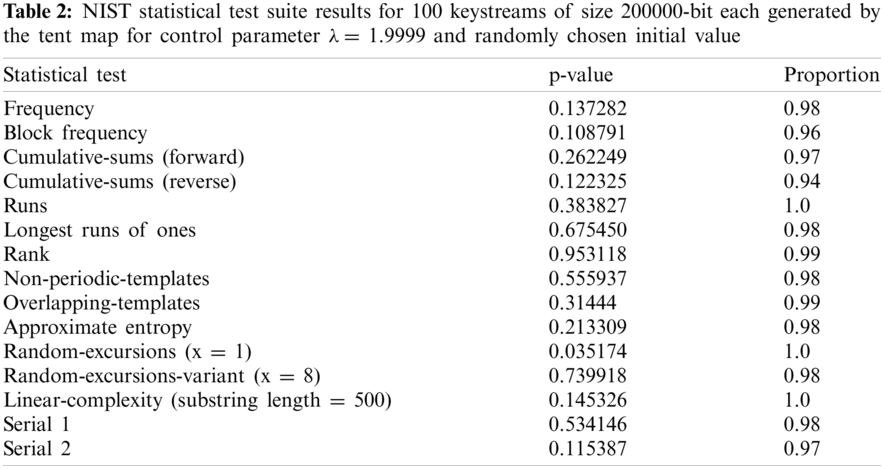
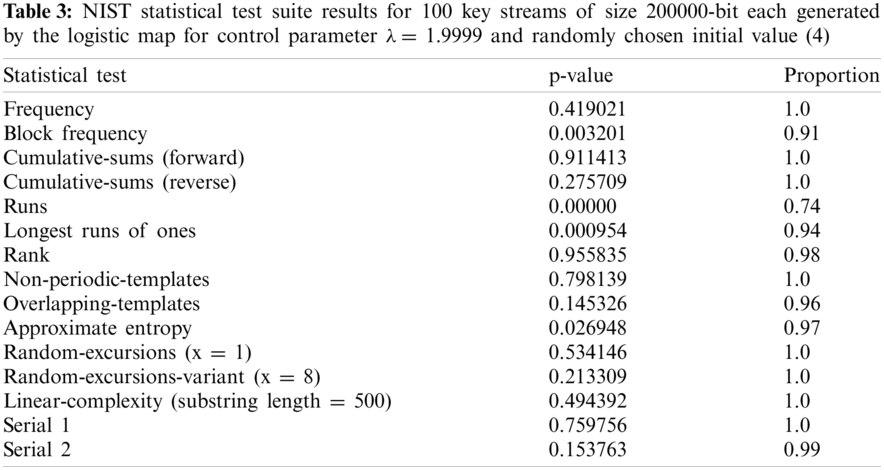
The degree of significance α for all NIST tests is set to 1% which shows that one arrangement in 100 successions is expected to be dismissed. The p-esteem is figured for each statistical test. In every statistical test, if the p-esteem is larger than the degree of significance then the succession is acknowledged as an arbitrary sequence with a 99% significance level. Or, the succession is dismissed.

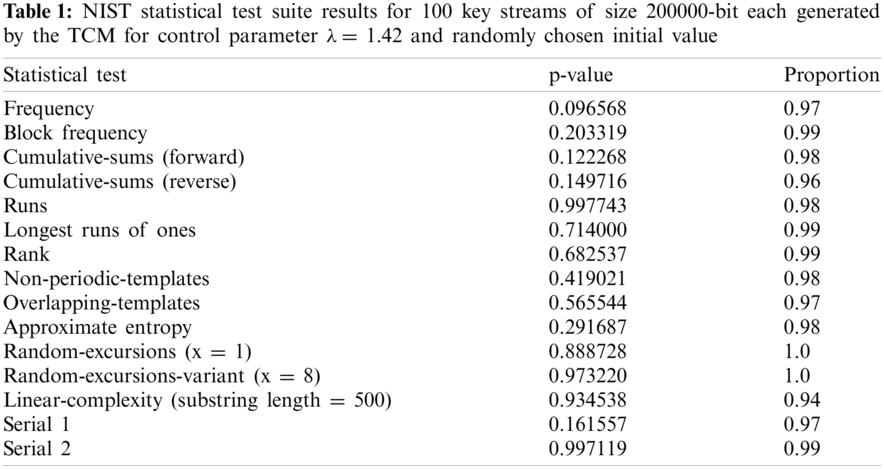
As Tabs. 1–3 show, the NIST statistical test suite is performed on a lot of 100 key streams of size 200000 pieces each created by the TCM, tent map, and logistic map, individually. For each test, the p-values are registered and the extent of key streams that pass the condition p-esteem ≥ α is figured. The TCM, as appeared in Tab. 1, has a better extent of key streams that pass the condition p-esteem ≥ 0.01 than a tent and logistic maps. Additionally, the P-values of p-values, found through the chi-square test, are for the most part higher than the level of significance α in the occurrence of the TCM and tent guide. In any case, the logistic map fizzled in three tests: block frequency, runs, and longest-runs of ones. In the three map results, the p-values are consistently distributed over the stretch (0, 1). For the TCM and tent map, since all p-values are larger than 0.01 then the produced key streams are analyzed arbitrarily with a certainty of 99%.

6  Proposed Image Encryption Method

The proposed image encryption strategy is summed up as follows. Without the loss of over-simplification, the dimension of the image encryption I is expected as M × N.

(i) The original image is scaled into a size of 256 × 256 pixels.

(ii) Consider a random image of the same size (M × N) as the original image for confusion and diffusion processes.

(iii) The original image and random image are separated into square blocks. Each square of size m × m pixels where (5) is proposed to find m.

m=M×Nr2 (5)

where r forms an aspect of the secret key; in addition to the control boundary and initial condition of TCM.

(iv) The accompanying advances are performed on each square of the original and random images.

a. The corresponding square of original and random images is changed over into a row vector. Perform XOR on the row vector of the original image and random image to obtain a row vector.

b. A row vector, of size [1, m × m], is obtained by using (1) to create pseudorandom numbers. The produced numbers are utilized as pixel location files to rearrange the pixel areas of the row vector.

c. Pixel intensity estimations of the scrambled row vector, obtained from the last step, are changed as per (6),

K=sin⁡(K+b)+K (6)

where K is a created keystream utilizing Eq. (1) and b is the acquired line vector having performed XOR of original and random row vectors from the past advance.

d. The resultant row vector is changed over into a square, of size m × m pixels, and secured to shape the encoded image.

(v) Pixel intensity estimations of the encoded image are changed utilizing (6). This progression is proposed to improve the security of the proposed encryption process.

7  Experimental Results

To test the execution of the proposed image encryption technique, the notable Lena and Cameraman images are utilized. The proposed encryption technique is executed utilizing MATLAB. In this paper, the Lena image is utilized as appeared in Figs. 6 and 7 shows a non-uniform histogram of Lena image which demonstrates that the dominant part of image pixel values of intensity is concentrated around the center. The boundary r of (6) is set to four resulting in a square size of 16 × 16 pixels. The proposed encryption technique is used to get the encoded Lena image as appeared in Fig. 8. This figure demonstrates a total blurring of image content. The histogram of the encoded image, as appeared in Fig. 9, shows the semi-uniform dissemination of encoded image pixels and the power of the encryption strategy against histogram assault strategies. Encryption resistance against Brute-Force Attacks is examined. Brute Force Attack strategies utilize a broad search of the set of all values of secret key parameters to decode an encoded image. Exploratory outcomes demonstrate that the parameters x0, λ, K ought to be changed by the accuracy of one part in 1018, 1017,1016 to recuperate the real image from the encoded image. As such, the proposed encryption technique has an intricacy of order O(2169). Any encryption algorithm ought to have an intricacy (complexity) bigger than (2128) to be adequately secure against brute power attacks [17].

Figure 6: The Lyapunov exponent of the TCM for λ ∈ [1, 1.6]

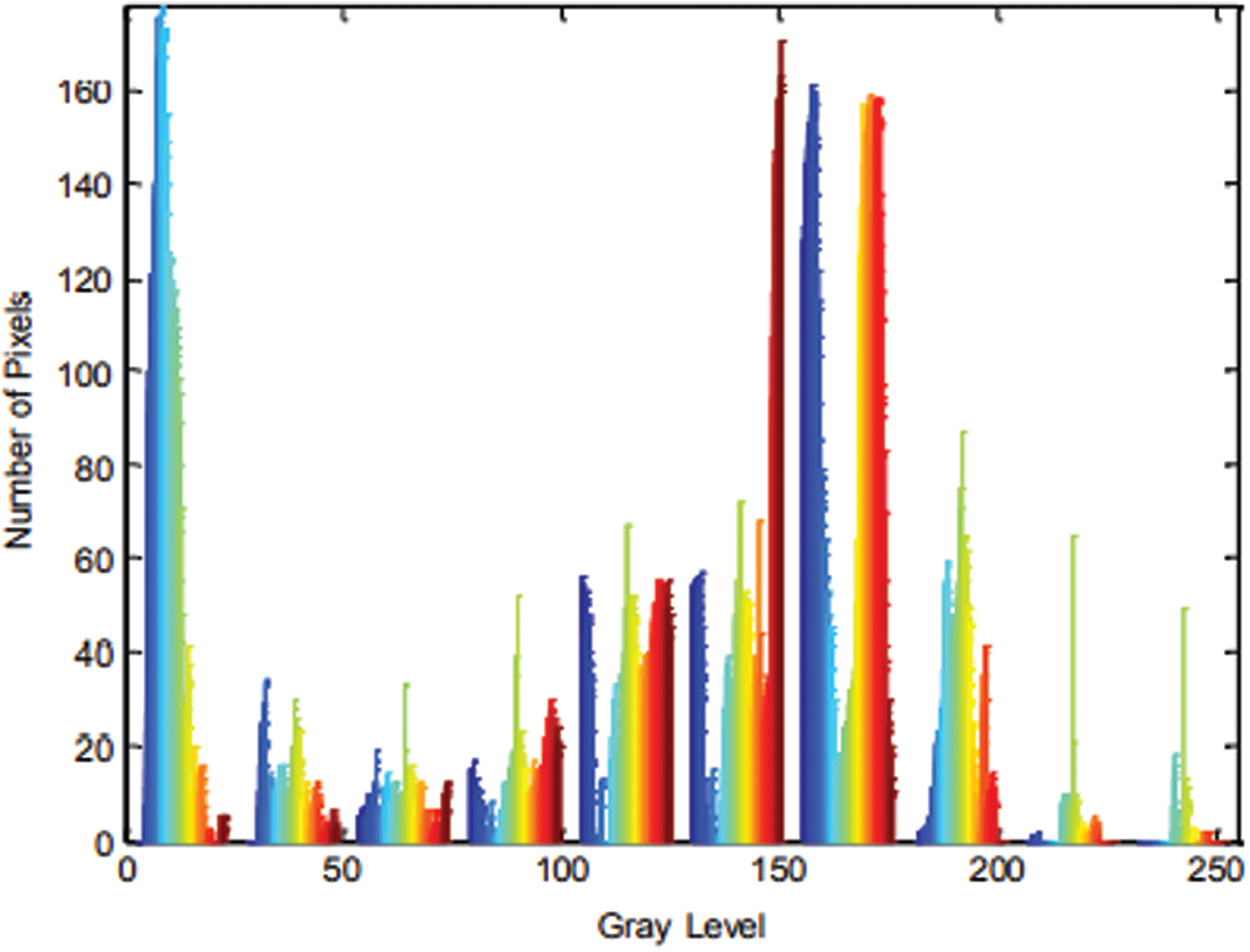
Figure 7: Histogram of Lena image of Fig. 6

Figure 8: Encrypted image using encryption method

Encryption insusceptibility against the high connection between contiguous image pixels is explored. Condition (7) is used to quantify the horizontal, vertical, and diagonal correlation between two contiguous pixels of an image,

r=2∑i=12(xi,yi)−∑i=12xi∑i=12yi(2∑i=12xi2−(∑i=12xi)2)(2∑i=12yi2−(∑i=12yi)2) (7)

where (x0,y0) demonstrates pixel intensity estimation of two haphazardly chosen neighboring pixels. 1,000 neighboring pixels are arbitrarily chosen to figure out their vertical, horizontal, and diagonal correlation. Encryption execution of the proposed Trigonometric Chaotic Map is analyzed against the execution of notable maps, for example, Logistic Map (LM), Tent Map (TM), and Nonlinear Chaotic Map (NCA), Eqs. (8)–(10), has appeared in Tab. 4. Tab. 4 shows a high connection between pixels of the original image and a poor connection between pixels of encoded images. The proposed TCM-based encryption strategy accomplished the best average correlation result. Then again, Entropy is utilized to discover a measure of arbitrariness in an image. The consequences of Tab. 4 demonstrate that the original image has low entropy esteem. Conversely, the encrypted images have high entropy esteem where the ideal worth ought to be 8. The Tent Map-based image encryption technique accomplished the best entropy result. In any case, the proposed TCM-based strategy accomplished close entropy results to that of the TCM-based encryption strategy. This demonstrates the strength of the proposed image encryption technique against entropy assault strategies. In outline, the acquired semi-uniform histogram, statistical correlation, and entropy results show the superior permutation and substitution properties of the proposed TCM-based encryption technique. The decoding stage is done by reversing the steps associated with segment IV.

sn+1=λsn(1−sn) (8)

sn+1=(1−λ−4)cot(α1+λ)(1+1λ)tan⁡(αsn)(1−sn)λ (9)

Sn+1={λsn,sn<0.5λ(1−sn),sn≥0.5 (10)

A one-dimensional trigonometric chaotic map (TCM) is proposed. Experimental results show that the TCM has high affectability to a little change in introductory condition, fulfills the s-unimodality trademark, and has wide chaotic conduct. The NIST factual test suite tentatively approves that the produced key streams by the TCM hold arbitrary conduct making the TCM reasonable for cryptographic applications. The proposed TCM is used to build up an image encryption strategy that for the most part comprises of two stages. The image substitution step rearranges image pixel locations. Trial results demonstrate immunity against Brute-Force and Entropy assaults. Results additionally demonstrate the unrivaled substitution and permutation properties of the proposed image encryption strategy. Future work ought to be examined the resistance of the proposed encryption technique against regular assaults, for example, man-in-the-middle and replay.

Figure 9: Histogram of an encrypted image of Fig. 8

8  Conclusions

In this paper, we have developed a more secure image cryptosystem dependent on a trigonometric chaotic map and XOR of an arbitrary image. To make the encryption more secure and unbreakable, we utilized a basic chaotic map; produced a row vector of original and a random image. The confusion and diffusion have been done in a row-wise approach like XOR. It has produced a row vector which further applied a TCM resulted in the form of an encrypted image. Usual tests have been performed for the security of the algorithm; results have been produced and presented using the proposed algorithm.

Funding Statement: This research work was partially funded by the Chiang Mai University.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  FIPS. PUB 46-3, “Data encryption standard (DES),” Journal of Research of the National Institute of Standards and Technology, vol. 25, no. 10, pp. 1–22, 1999. [Google Scholar]

 2.  NIST. Flips-Pub, “Advanced encryption standard (AES),” Federal Information Processing Standard Publication, vol. 197, no. 441, pp. 311, 2001. [Google Scholar]

 3.  R. L. Rivest, A. Shamir and L. Adleman, “A method for obtaining digital signatures and public-key cryptosystems,” Communications of the Association for Computing Machinery, vol. 21, no. 2, pp. 120–126, 1978. [Google Scholar]

 4.  M. S. Azza, C. Tanougast, S. Sadoudi and A. Dandache, “Robust chaotic keystream generator for real-time images encryption,” Journal of Real-time Image Processing, vol. 8, no. 3, pp. 297–306, 2013. [Google Scholar]

 5.  Ü. Çavuşoğlu, S. Kaçar, I. Pehlivan and A. Zengin, “Secure image encryption algorithm design using a novel chaos based S-Box,” Chaos, Solitons & Fractals, vol. 95, no. 11, pp. 92–101, 2017. [Google Scholar]

 6.  Y. Zhang, “The unified image encryption algorithm based on chaos and cubic S-Box,” Information Sciences, vol. 450, no. 3, pp. 361–377, 2018. [Google Scholar]

 7.  P. Zhen, G. Zhao, L. Min and X. Jin, “Chaos-based image encryption scheme combining DNA coding and entropy,” Multimedia Tools and Applications, vol. 75, no. 11, pp. 6303–6319, 2016. [Google Scholar]

 8.  Q. Zhang, X. Xue and X. Wei, “A novel image encryption algorithm based on DNA subsequence operation,” Science World Journal, vol. 2012, pp. 1–10, 2012. [Google Scholar]

 9.  Q. Zhang, S. Zhou and X. Wei, “An efficient approach for DNA fractal-based image encryption,” Applied Mathematics and Information Sciences, vol. 5, no. 3, pp. 445–459, 2011. [Google Scholar]

10. Y. Guang, J. Yang, H. L. Tian, Y. H. Zhou and W. M. Shi, “Novel quantum image encryption using one-dimensional quantum cellular automata,” Information Sciences, vol. 345, no. 13, pp. 257–270, 2016. [Google Scholar]

11. Y. G. Yang, J. Xia, X. Jia and H. Zhang, “Novel image encryption/decryption based on quantum Fourier transform and double phase encoding,” Quantum Information Processing, vol. 12, no. 11, pp. 3477–3493, 2013. [Google Scholar]

12. R. G. Zhou, W. Qian, M. Q. Zhang and C. Y. Shen, “Quantum image encryption and decryption algorithms based on quantum image geometric transformations,” International Journal of Theoretical Physics, vol. 52, no. 6, pp. 1802–1817, 2013. [Google Scholar]

13. X. Zhang, G. Feng, Y. Ren and Z. Qian, “Scalable coding of encrypted images,” IEEE Transactions on Image Processing, vol. 21, no. 6, pp. 3108–3114, 2012. [Google Scholar]

14. C. Qin, Q. Zhou, F. Cao, J. Dong and X. Zhang, “Flexible lossy compression for selective encrypted image with the image inpainting,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 11, pp. 3341–3355, 2018. [Google Scholar]

15. X. Duan, J. Liu and E. Zhang, “Efficient image encryption and compression based on a viegenerative model,” Journal of Real-Time Image Processing, vol. 16, no. 3, pp. 1–9, 2018. [Google Scholar]

16. X. Wang, J. Zhao and Z. Zhang, “A chaotic cryptosystem based on multi-one-dimensional maps,” Modern Physics Letters B, vol. 23, no. 2, pp. 183–189, 2009. [Google Scholar]

17. J. Meng and X. Wang, “Generalized projective synchronization of a class of delayed neural networks,” Modern Physics Letters B, vol. 22, no. 3, pp. 181–190, 2008. [Google Scholar]

18. F. Li, H. Wu, G. Zhou and W. Wei, “Robust real-time image encryption with aperiodic chaotic map and random-cycling bit shift,” Journal of Real-Time Image Processing, vol. 16, pp. 775–790, 2018. [Google Scholar]

19. L. Sui, K. Duan, J. Liang and X. Hei, “Asymmetric double-image encryption based on cascaded discrete fractional random transform and logistic maps,” Optics Express, vol. 22, no. 9, pp. 10605–10621, 2014. [Google Scholar]

20. Z. Hua, Y. Zhou, C. M. Pun and C. L. P. Chen, “2d Sine logistic modulation map for image encryption,” Information Sciences, vol. 297, pp. 80–94, 2015. [Google Scholar]

21. H. Natiq, N. M. G. Al-Saidi, M. R. M. Said and A. Kilicman, “A new hyperchaotic map and its application for image encryption,” The European Physical Journal Plus, vol. 133, no. 1, pp. 6, 2018. [Google Scholar]

22. J. Wu, X. Liao and B. Yang, “Image encryption using 2d Hénon-sine map and DNA approach,” Signal Processing, vol. 153, pp. 11–23, 2018. [Google Scholar]

23. C. Li, G. Luo, K. Qin and C. Li, “An image encryption scheme based on chaotic tent map,” Nonlinear Dynamics, vol. 87, no. 1, pp. 127–133, 2017. [Google Scholar]

24. Y. Luo, L. Cao, S. Qiu, H. Lin, J. Harkin et al., “A chaotic map-control-based and the plain image-related cryptosystem,” Nonlinear Dynamics, vol. 83, no. 4, pp. 1–18, 2015. [Google Scholar]

25. G. Chen, Y. Mao and C. K. Chui, “A symmetric image encryption scheme based on 3d chaotic cat maps,” Chaos, Solitons & Fractals, vol. 21, no. 3, pp. 749–761, 2004. [Google Scholar]

26. F. Musanna and S. Kumar, “A novel fractional-order chaos-based image encryption using Fisher-Yates algorithm and 3-D cat map,” Multimedia Tools and Applications, vol. 78, pp. 14867–14895, 2018. [Google Scholar]

27. S. Dadras, H. R. Momeni and G. Qi, “Analysis of a new 3d smooth autonomous system with different wing chaotic attractors and transient chaos,” Nonlinear Dynamics, vol. 62, no. 1–2, pp. 391–405, 2010. [Google Scholar]

28. D. Arroyo, J. Amigo, S. Li and G. Alvarez, “On the inadequacy of unimodal maps for cryptographic applications,” in Proceedings of 11th Spanish Meeting on Cryptology and Information Security, Beijing, China, pp. 37–42, 2010. [Google Scholar]

29. P. Glendinning, Stability, instability and chaos, 1sted., Cambridge, UK: Cambridge University Press, 1994. [Google Scholar]

30. C. Guanghui, H. Kai, Z. Yizhi, Z. Jun and Z. Xing, “Chaotic image encryption based on running-key related to plaintext,” The Scientific World Journal, vol. 490179, pp. 1–9, 2014. [Google Scholar]

31. L. Lingfeng and M. Suoxia, “An image encryption algorithm based on baker map with varying parameter,” Multimedia Tools and Applications, vol. 76, no. 15, pp. 16511–16527, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.