Computers, Materials & Continua DOI:10.32604/cmc.2021.019462
Article

Road Distance Computation Using Homomorphic Encryption in Road Networks

Haining Yu1, Lailai Yin1,*, Hongli Zhang1, Dongyang Zhan1,2, Jiaxing Qu3 and Guangyao Zhang4

1School of Cyberspace Science, Harbin Institute of Technology, Harbin, 150001, China
2The Ohio State University, Columbus, 43202, USA
3Heilongjiang Province Cyberspace Research Center, Harbin, 150001, China
4National Internet Emergency Response Center, Harbin, 150001, China
*Corresponding Author: Lailai Yin. Email: yinlailai163@163.com
Received: 14 April 2021; Accepted: 26 May 2021

Abstract: Road networks have been used in a wide range of applications to reduces the cost of transportation and improve the quality of related services. The shortest road distance computation has been considered as one of the most fundamental operations of road networks computation. To alleviate privacy concerns about location privacy leaks during road distance computation, it is desirable to have a secure and efficient road distance computation approach. In this paper, we propose two secure road distance computation approaches, which can compute road distance over encrypted data efficiently. An approximate road distance computation approach is designed by using Partially Homomorphic Encryption and road network set embedding. An exact road distance computation is built by using Somewhat Homomorphic Encryption and road network hypercube embedding. We implement our two road distance computation approaches, and evaluate them on the real city-scale road network. Evaluation results show that our approaches are accurate and efficient.

Keywords: Road network; road distance; homomorphic encryption

1  Introduction

Nowadays, road networks have been widely used in many application domains for sciences and engineering, such as closeness testing in spatial social networks, route planning, ride hailing or navigation in road networks, etc. For example, online ride hailing services such as Uber and DiDi employ large road networks with millions or even billions of vertices and edges in their operation. A well-maintained road network computation system plays a significant role. It not only reduces the cost of transportation, both in terms of money and time, but also improves the quality of upper services.

The shortest road distance computation has been considered as one of the most fundamental operations of road networks computation and has a wide range of applications. There are many efficient shortest distance (path) algorithms, such as Dijkstra's algorithm and Bellman Ford's Algorithm. In some application scenarios, the shortest road distance must be computed in encryption form to avoid privacy leaks. As an example, an online ride hailing service enables a rider to find the closest driver to offer ride service. To enjoy this service, both riders and drivers have to update their locations to the online ride hailing service provider, while the service provider computes the shortest road distances from the rider to all drivers, and select the closest driver. But the service providers are not always honest, they may track users or infer their profiles for economic advantage. To alleviate this privacy concerns, the riders and the driver submit their encrypted locations, and the service provider can compute the encrypted road distance over received ciphertexts. However, it is not a trivial problem to compute shortest road distance in ciphertext domain. Some schemes have been presented in the literature to compute shortest road distance in a secure manner, which make use of cryptographic primitives to encrypt the road network itself or the corresponding pre-generated index, e.g., Partially Homomorphic Encryption (PHE), Somewhat Homomorphic Encryption (SHE), Yao’s garbled circuits (GCs). Shen et al. [1] proposed a graph encryption scheme based on symmetric-key primitives and SHE, which enables approximate constrained shortest distance queries. Meng et al. [2] presented three schemes based on distance oracle and structured encryption for approximate shortest distance queries. Wang et al. [3] proposed a secure Graph DataBase (SecGDB) encryption scheme based on PHE and Yao's GCs, which supports exact shortest distance/path queries. Wu et al. [4] proposed an efficient cryptographic protocol for fully-private navigation based on compressing the next-hop routing matrices, symmetric Private Information Retrieval (PIR) and Yao's GCs. However, existing schemes are not efficient enough to compute large-scale shortest distances in real time.

To tackle the practical limitations of the state-of-the-art, we propose two secure road distance computation approaches, which can compute road distance over encrypted data efficiently. We summarize main contributions as:

•   We propose an efficient approximate road distance computation approach over encrypted data, by using PHE and road network set embedding. Our approach only needs several additive homomorphic operations to compute an encrypted approximate road distance.

•   We propose an efficient exact road distance computation approach over encrypted data, by using SHE and road network hypercube embedding. Our approach only needs several additive and multiplicative homomorphic operations over packed ciphertexts to compute an encrypted exact road distance.

•   We implement our approximate road distance computation approach using Paillier Cryptosystem and exact road distance computation approach using FV scheme. Their performance is evaluated on the real city-scale road network. Evaluation results show that they achieve high accuracy, and keep efficient.

The remainder of this paper is structured as follows. In Section 2, we briefly introduce necessary preliminaries. In Section 3, we propose two road distance computation approaches over encrypted data. In Section 4, we evaluate their performance. Finally, we review the related literature and summarize the paper.

2  Preliminaries

2.1 Paillier Cryptosystem

Partially homomorphic encryption (PHE) allows to carry out operations over ciphertexts. Paillier cryptosystem [5] is a popular PHE scheme, which relies on the decisional composite residuosity assumption. We briefly summarize it as follows for better understanding and description of our plan.

•   Key Generation: (pkPHE,skPHE)←KeyGenPHE(1λ). Select two primes p, q and calculate N=p×q and λ=lcm(p−1,q−1), where lcm means to take the least common multiple of p−1 and q−1. Then, choose a random g∈ZN2∗ so that gcd(L(gλmodN2),N)=1, where L(x)=(x−1)/N. The public key is pkPHE=(N,g) and the private key is skPHE=λ.

•   Encryption: c^←EncPHE(m,pkPHE). Given a plaintext m∈ZN and a random number r∈ZN, the ciphertext can be derived as c^=EncPHE(mmodN;rmodN)=gmrNmodN2.

•   Decryption: m←DecPHE(c^,skPHE). Let c^∈ZN2 be a ciphertext, the plaintext of it is given by

Paillier cryptosystem has properties of additive homomorphism and the mixed multiplication homomorphism: for any m1,m2,r1,r2∈ZN, we obtain EncPHE(m1,r1)⋅EncPHE(m2,r2)=EncPHE(m1+m2,r1r2)modN2, EncPHEm2(m1,r1)=EncPHE(m1m2,r1m2)modN2.

2.2 FV Scheme

FV scheme [6] is a widely used SHE scheme which can support a finite number of both multiplications and additions on data in the cipher domain. Mathematically, FV scheme depends on a hard computation problem named as Ring Learning with Errors (RLWE) problem. Set Rt=Zt[x]/(xn+1), and in the ring structure Rt, xn will be converted to –1. The plain text space in FV scheme is Rt, and the cipher text is the polynomial array in Rq. Given w being a base, ℓ+1=⌊log2⁡q⌋+1 represents the number of terms when the integer in the base q is decomposed into the base w. The ℓ+1 polynomials is obtained by decomposing the polynomials in Rq into base-w components coefficient-wise. With a←$S we uniformly sample a from the finite set S, and [⋅]q represent reduction modulo q into the interval (−q/2,q/2]. The FV scheme is briefly introduced as follows.

•   Key Generation: KeyGenSHE(n,q,t,χ,w). Sample a←$R2 and output skSHE=s. Sample a←$Rq, and e←χ. Output pkSHE=([−(as+e)]q,a). For i∈{0,…,ℓ}, sample ai←$Rq, ei←χ. Output evk=([−(ais+ei)+wis2]q,ai).

•   Encryption: c^←EncSHE(m,pkSHE). For p∈Rt, let pkSHE=(b,a). Sample u←$R2, e1,e2←χ and output c^=([⌊q/t⌋m+bu+e1]q,[au+e2]q)∈Rq2.

•   Decryption: m←DecSHE(c^,skSHE). Set s=skSHE,c0=c^[0],c1=c^[1]. Output m=[⌊t/q⋅[c0+c1s]q⌉]t∈Rt.

•   Homomorphic Addition: ([c^0[0]+c^1[0]]q,[c^0[1]+c^1[1]]q)←c^0⊞c^1. We have DecSHE(c^0⊞c^1,skSHE)≡DecSHE(c^0,skSHE)+DecSHE(c^1,skSHE).

•   Homomorphic Multiplication: (c0′,c1′)←c^0⊠c^1. Calculate c0=[⌊tqc^0[0]c^1[0]⌉]q, c1=[⌊tq(c^0[0]c^1[1]+c^0[1]c^1[0])⌉]q and c2=[⌊tqc^0[1]c^1[1]⌉]q.

Express c2 in base w as c2=∑i=0ℓc2(i)wi. Set c0′=c0+∑i=0ℓevk[i][0]c2(i), c1′=c1+∑i=0ℓevk[i][1]c2(i), and output (c0′,c1′). Note that we have DecSHE(c^0⊠c^1,skSHE)≡DecSHE(c^0,skSHE)⋅DecSHE(c^1,skSHE).

3  Secure Distance Computation

In this section, we propose two different methods to compute road distance in ciphertext domain.

3.1 Approximate Road Distance Computation with PHE

3.1.1 Road Network Set Embedding

By using Road Network Set Embedding (RNSE) technique [7], the planar road network can be converted into a high-dimensional space, in which we can convert the complex calculation of the shortest road distance into a simple calculation supported through existing encryption primitives.

We model the road network as a weighted planar graph G=(V,E,W). Define V as the set of vertices in G (i.e., road junctions) and E as the set of edges in G (i.e., road sections). Let R be a set of subsets of V and it describes a high-dimensional embedding space:

R={V1,1,…,V1,α,…,Vβ,1,…,Vα,β}, (1)

where α and β are equal to O(log⁡|V|). Subset Vi,j is composed of 2i nodes randomly selected from V. The shortest road distance between node v∈V and subset Vi,j can be calculated by

distR(v,Vi,j)=minv′∈Vi,jdistR(v,v′). (2)

Based on the above definition, the coordinate of a node v, which is a vector with O(log2⁡|V|) dimensions, is defined as the distance from the node v to each subset:

cv=⟨distR(v,V1,1),…,distR(v,V1,α),…,distR(v,Vβ,1),…,distR(v,Vα,β)⟩. (3)

Then we can use Ω={cv∣v∈V} to represent the embedded road network of G.

For the coordinate of a position l on the road section (vs,vd)∈E, it can be denoted by

cl=⟨distR(l,V1,1),…,distR(l,V1,α),…,distR(l,Vβ,1),…,distR(l,Vα,β)⟩, (4)

where distR(l,Vi,j)=min{distR(l,vs)+distR(vs,Vi,j),distR(l,vd)+distR(vd,Vi,j)}.

Without losing generality, let the embedded road network have ω dimensions, s.t. ω≤⌈log2⁡|V|⌉. By calculating the chessboard distance from cs to cd, the shortest distance from location ls to ld can be approximately represented as

distA(ls,ld)≈distC(cs,cd)=maxVi,j∈R|distR(ls,Vi,j)−distR(ld,Vi,j)|=max1≤i≤ω|cs[i]−cd[i]|, (5)

where distC(⋅,⋅) denotes the chessboard distance amid two coordinates.

3.1.2 Encrypted Approximate Road Distance Computation Using Paillier Cryptosystem

Suppose that the road network is represented by G=(V,E,W) and the dimension of the embedded road network is ω, we can use the RNE technique described in Section 3.1.1 to calculate the coordinates of each point in G, where the coordinate is a vector of ω dimension. Then, we will obtain the embedded road network denoted by ΩA={cv∣v∈V}. Given a pair of points on the road networks (ls,ld), let cs=(cs[1],…,cs[ω]) and cd=(cd[1],…,cd[ω]) denote the coordinates of ls and ld in the embedded road network ΩA.

The coordinates cls and cld can be encrypted element-by-element using the public key pkPHE generated by Paillier cryptosystem, respectively. The encrypted coordinates are represented as

[[cs]]=(EncPHE(cu[1],pkPHE),…,EncPHE(cu[ω],pkPHE)), (6)

[[cd]]=(EncPHE(cd[1],pkPHE),…,EncPHE(cd[ω],pkPHE)). (7)

The encrypted approximate road distance between ls and ld can be computed as follows:

1) Compute the ciphertext vector [[dist(ls,ld)]] over [[cs]] and [[cd]] based upon homomorphism operations of the Paillier cryptosystem:

[[dist(ls,ld)]]=(EncPHE(cs[1]−cd[1]+2ℓ),…,EncPHE(cs[ω]−cd[ω]+2ℓ))=(EncPHE(cs[1])EncPHE−1(cd[1])EncPHE(2ℓ),…,EncPHE(cs[ω])EncPHE−1(cd[ω])EncPHE(2ℓ)). (8)

Note that EncPHE(2ℓ) is used to make sure that every element in [[dist(ls,ld)]] is positive.

2) Because Paillier cryptosystem has a plaintext space much larger than the upper limit of the road distance, several ciphertexts can be packed into one ciphertext using ciphertext packing technology, which can improve the efficiency. In the Paillier cryptosystem, assuming that p=⌊N/(ℓ+1)⌋ is the number of slots in a single packed ciphertext, p ciphertexts can be packed into one ciphertext. The main idea of the ciphertexts packing technique is described as follows. Assuming a1,…,al are integers of ℓ bits (1≤l≤p), we use [[a1]],…,[[al]] to express their ciphertexts. The packed ciphertext is constructed by [[[a1]]|⋯|[[al]]]=∏i=1l[[ai]]2ℓ(l−i).

After performing a decryption operation, we can get the packed plaintext [a1|⋯|al]=∑i=0lai2ℓ(l−i), and then recover a1,…,al. Using the above ciphertext packing technique, every encrypted element in [[dist(ls,ld)]] can be packed into a same packed ciphertext:

[[dist(ls,ld)]]=[[[dist1(ls,ld)]]|⋯|[[distω(ls,ld)]]]=∏i=1ω[[disti(ls,ld)]]2ℓ(ω−i), s.t., p≥ω.

3) The approximate road distance between ls and ld , i.e. distA(ls,ld), is the maximum element in dist(ls,ld), which is hidden in [[dist(ls,ld)]]. Further post-process is required to extract the maximum from dist(ls,ld). In the simplest way, [[dist(ls,ld)]] can be decrypted with the secret key skPHE, and then unpacked to recover dist(ls,ld). There are, of course, other more complex scenes, where the maximum needs to be selected in an oblivious manner. For these scenes, some well-established cryptographic tools can be integrated, such as Yao’s garbled circuit and secret sharing scheme. More details about secure comparison over encrypted integers can be referred to [8–11].

3.2 Exact Road Distance Computation with SHE

3.2.1 Road Network Hypercube Embedding

The m-dimensional hypercube Hm, is a graph whose node set V consists of 2m m-dimensional boolean vectors, i.e., vectors with binary coordinates 0 or 1, where two nodes are adjacent whenever they are different in exactly one coordinate. Moreover, the size of Hm is m2m−1 and its older is 2m. Road Network Hypercube Embedding (RNHE) technique [7] is concerned with finding mappings between a road network and a higher-dimensional hypercube that preserve certain topological properties. Let the weighted graph G=(V,E,W) represent the road network. The vertices set is V and the edge set is E. Every edge (vi,vj) in E is related to a weight W(vi,vj), which denotes the road distance of the edge. For a vertex vi∈V, its coordinate can be expressed by a boolean vector vi with m dimensions, and we use ΩH={vi∣vi∈V} represents the embedded road network. We can obtain the shortest road distance between arbitrary two vertices by computing Hamming distance between their coordinates. Note that the location in the road network and its position in corresponding planar graph can typically be converted from one to the other, and hereafter they are used interchangeably.

Related definitions are as follows.

•   The interior face F indicates a cycle of G surrounding a connected domain, and the outer face of G indicates an unbounded face.

•   An even(odd ) face means a face with even(odd ) edges. Let diaF be the diameter of F, and if d(vi,vi′)=d(vj,vj′)=diaF holds, edges e=(vi,vj) and $e′=(vi′,vj′) in face F are opposite. For each edge e∈F, it will have a unique opposite edge when F is an even face and have two opposite edges when F is an odd face.

•   A cut L means a series of edges {e1,e2,e3,…,ek} satisfying the following three properties: 1) Either e1=ek or ek and e1 are all the edge of a outer face; 2) ∃F(ei,ei+1∈F); 3) in face F, edges ei and ei+1 are opposite. If graph G removes the edges of a cut L, then G is divided into two subgraphs {G/L}0 and {G/L}1.

•   An alternating cut refers to a cut which alternates on the odd faces. In other words, if the cut turns left (resp. right) on an odd face, then it turns right (resp. left) on the following odd face. We can view an alternating cut as a line which passes through the graph and intersects only the selected edges.

The embedded road network ΩH can be constructed by G as follows. Each alternating cut L corresponds to two connected components {G/L}0 and {G/L}1. The coordinate of every vertex in {G/L}0 will be appended with 0 and the coordinate of every vertex in {G/L}1 will be appended with 1. We can find all alternating cuts which contain e as below.

•   Starting with e, we move in both directions, take opposite edge on even face and end when we meet the first odd face in both directions.

•   Next, we turn right on one odd face and left on the other (we can obtain more alternating cuts by changing the selection of odd face).

•   Proceeding in both directions, we alternate at all odd faces and end up with reaching the outer face. Clearly, the coordinate is an m-dimensional boolean vector, where m is the total number of alternating cuts. At last, G can be embedded into an m-dimensional hypercube Hm.

The computational complexity of hypercube embedding is O(|V||V|). In Fig. 1, the road network corresponds to the hypercube H14, and its embedded road network is shown in Tab. 1. Note that above hypercube embedding is not affected by different road network topology.

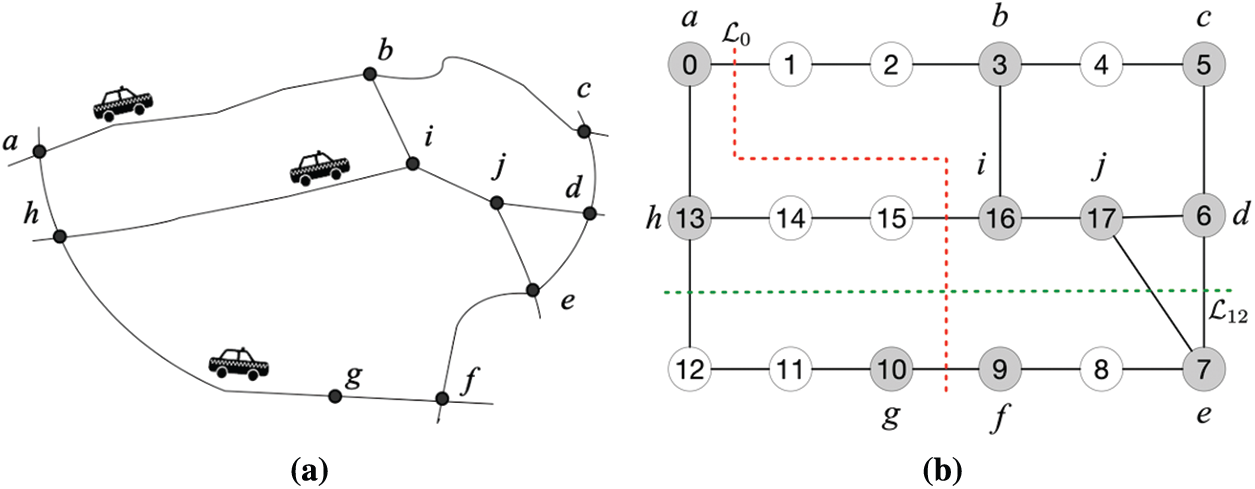
Figure 1: An example of alternating cuts of a road network (a) A simple road network. (b) Alternating cuts (e.g., L0 and L12 )

Let ΩH be the embedded road network of the road network G. The coordinates of two nodes vs,vd∈V in ΩH are expressed as vs=(vs[0],…,vs[m−1]) and vd=(vd[0],…,vd[m−1]). We can calculate the shortest road distance from vs to vd as below.

distE(vs,vd)=12distH(vs,vd)=12∑i=0m−1(vs[i]⊕vd[i])=12(∑i=0m−1vs[i]+∑i=0m−1vd[i]−2∑i=0m−1vs[i]vd[i]), (9)

where distE(vs,vd) means the exact shortest road distance, distH(⋅,⋅) means the Hamming distance. In Fig. 1, the shortest road distance from va to ve is calculated by distE(va,ve)=12dH(va,ve)=6.

Given l=(v,Δ) denoting a location in the road network G, v means the nearest node to l and Δ means the shortest road distance between v and l. Let two locations be ls=(vs,Δs) and ld=(vd,Δd) respectively, and the shortest road distance from ls to ld is computed by

distE(ls,ld)=distE(vs,vd)+Δs+Δd=12distH(vs,vd)+Δs+Δd. (10)

3.2.2 Encrypted Exact Road Distance Computation Using FV Scheme

For locations ls=(vs,Δs) and ld=(vd,Δd), the road distance between them can be computed in ciphertext domain by using FV Scheme. In a basic way, we can encrypt the respective coordinate vs=⟨vs[0],…,vs[m−1]⟩ and vd=⟨vd[0],…,vd[m−1]⟩ of vs and vd bit-by-bit with the public key pkSHE to obtain two ciphertext sequences, denoted as:

[[vs]]=⟨EncSHE(vs[0],pkSHE),…,EncSHE(vs[m−1],pkSHE)⟩, (11)

[[vd]]=⟨EncSHE(vd[0],pkSHE),…,EncSHE(vd[m−1],pkSHE)⟩. (12)

Using the homomorphic property of FV Scheme, the encrypted distE(vs,vd) can be calculated over [[vs]] and [[vd]] by:

[[distE(vs,vd)]]=12(∑i=0m−1EncSHE(vs[i],pkSHE)⊞∑i=0m−1EncSHE(vd[i],pkSHE)⊟2∑i=0m−1EncSHE(vs[i],pkSHE)⊠EncSHE(vd[i],pkSHE)). (13)

Then, the encrypted distE(ls,ld) can be computed by [[distE(ls,ld)]]=[[distE(vs,vd)]]⊞[[Δs]]⊞[[Δd]].

When the length of m is long, the computation overhead of above basic distance computation method is heavy, since it is inefficient to encrypt/decrypt coordinate bit-by-bit. To reduce computation overhead, we propose an optimized approach with ciphertext packing to compute the shortest road distance efficiently. We now describe the details of two packed ciphertext constructions for the coordinates vs and vd as follows.

For the coordinate vs=⟨vs[0],…,vs[m−1]⟩, let fs(vs) represent the packed plaintext:

fs(vs)=∑i=0m−1vs[i]xi∈Rt,(m≤n), (14)

where vs can be converted into the polynomial coefficients of fs(vs) by packing. The packed ciphertext of vs is calculated by encrypting fs(vs) as follows:

v^s=EncSHE(fs(vs),pkSHE). (15)

Given the coordinate vd=⟨vd[0],…,vd[m−1]⟩, let vd represent the packed plaintext:

fd(vd)=−∑j=0m−1vd[j]xn−j∈Rt,(m≤n), (16)

where vd is converted into the polynomial coefficients of fd(vd) by packing. The packed ciphertext of vd is calculated by encrypting fd(vd) as follows:

v^d=EncSHE(fd(vd),pkSHE). (17)

Encrypted distE(vs,vd) can be computed by two packed ciphertexts denoted by v^s and v^d. Using multiplicative homomorphism, the ciphertext of Hamming weight of vs is calculated by the plaintext polynomial and the packed ciphertext, denoted as:

v^s⊠(−∑j=0m−1xn−j), (18)

then we have

fs(vs)×(−∑j=0m−1xn−j)=−∑i=0m−1vs[i]xn+(the other terms)(mod t)=∑i=0m−1vs[i]+(non-constant terms)(mod t), (19)

where xn=−1(modxn+1). For plaintext modulus t that is large enough, the constant term in Eq. (19) equals the Hamming weight of vs. Likewise, the ciphertext of Hamming weight of vd is calculated by the plaintext polynomial and the packed ciphertext, denoted as:

v^d⊠∑i=0m−1xi, (20)

then we have

fd(vd)×∑i=0m−1xi=−∑i=0m−1vd[i]xn+(the other terms)(mod t)=∑i=0m−1vd[i]+(non-constant terms)(mod t). (21)

The constant term in Eq. (21) equals the Hamming weight of vd. Using multiplicative homomorphism, the ciphertext of the inner product of coordinates vs and vd is calculated by two packed ciphertexts as follows:

v^s⊠v^d, (22)

then we have

fs(vs)×fd(vd)=∑i=0m−1vs[i]xi×(−∑j=0m−1vd[j]xn−j)=−∑i=0m−1vs[i]vd[i]xn+(the other terms)(mod t)=∑i=0m−1vs[i]vd[i]+(non-constant terms)(mod t). (23)

The inner product of two coordinates vs and vd is equal to the constant term in Eq. (23).

Based on Eq. (9), we can use three packed ciphertexts (18), (20) and (22) to calculate the encrypted distE(ls,ld) as follows:

dist^E(vs,vd)=v^s⊠(−12∑j=0m−1xn−j)⊞v^d⊠12∑i=0m−1xi⊟v^s⊠v^d. (24)

Based on Eq. (10) and (24), the ciphertext of the distance between location ls=(vs,Δs) and ld=(vd,Δd) as follows:

d^R(ls,ld)=d^R(vs,vd)⊞Δ^s⊞Δ^d, (25)

where we have Δ^s=EncSHE(Δs,pkSHE) and Δ^d=EncSHE(Δd,pkSHE).

It needs only three multiplicative homomorphisms operations and four subtractive/additive homomorphisms operations for the calculation of the shortest road distance over two locations.

4  Experiment Evaluation

Our experiments are performed on the real road network of California, which consists of 21048 vertices and 21693 edges (https://www.cs.utah.edu/~lifeifei/SpatialDataset.htm). Following the assumptions made in [7], we need to delete some trivial edges and insert virtual vertices on edges with fixing the unit distance. For PHE, we use the Paillier cryptosystem library (https://acsc.cs.utexas.edu/libpaillier). For the modified Paillier cryptosystem, we set N and g to 1024 bits and 160 bits, respectively. For SHE, we use FV scheme built on FV-NFLlib (https://github.com/CryptoExperts/FV-NFLlib), and the degree of polynomials in FV scheme n is set to 2048. All our experiments are conducted and executed on a PC running Ubuntu 18.04 LTS, with an Intel i7 processor at 3.4GHZ and 16GB RAM.

We evaluate the accuracy and the efficiency of our proposed road distance approaches in a k-Nearest Neighbors (kNN) query application [12,13]. We first generate some locations on the edges of the road networks in a random fashion. Then, one location is randomly picked as the starting location, from which all road distances to other locations are computed by using our approaches. Finally, the closest location is selected as the nearest neighbor. Fig. 2 depicts the accuracy of kNN query by using Euclidean distance, approximate road distance (dimension ω=8,16,24,32) and exact road distance under different location scales. Euclidean distance is considered as the lower bound of accuracy, which always stays from 85% to 90%. We can see the accuracy of approximate road distance raises steadily as the dimension of the embedded road network increases. It is roughly 95% when the dimension is higher than 24. That is because higher dimension indicates higher accurate approximation. When we vary the location scale from 1000 to 4000, the accuracy of Euclidean distance gradually increases as the location scale increases, because larger location scale means there may exist closer destination locations located around the starting location. But the accuracy of Euclidean distance is still less than 90%. The accuracy of approximate road distance is always high under any driver scale, which is roughly 95% if the dimension is higher than 24. As expected, the accuracy of exact road distance keeps almost 100% under any location scale. Above experimental results demonstrate that both approximate road distance computation approach and exact road distance computation approach can reach a higher accuracy due to the choice of road distance. We use average online computation cost for per kNN query to evaluate the efficiency. As shown in Fig. 3, the computation cost of the approximate road distance computation approach raises with the dimension increases. The reason is that higher dimension requires more encryption operations over a location coordinate. Meanwhile, the computation cost of both the approximate road distance computation approach and the exact road distance computation approach increase almost linearly as the location scale increases. That is because more distance computation is required with larger location scale. From above evaluation, we can see that the two approaches achieve high accuracy and efficiency.

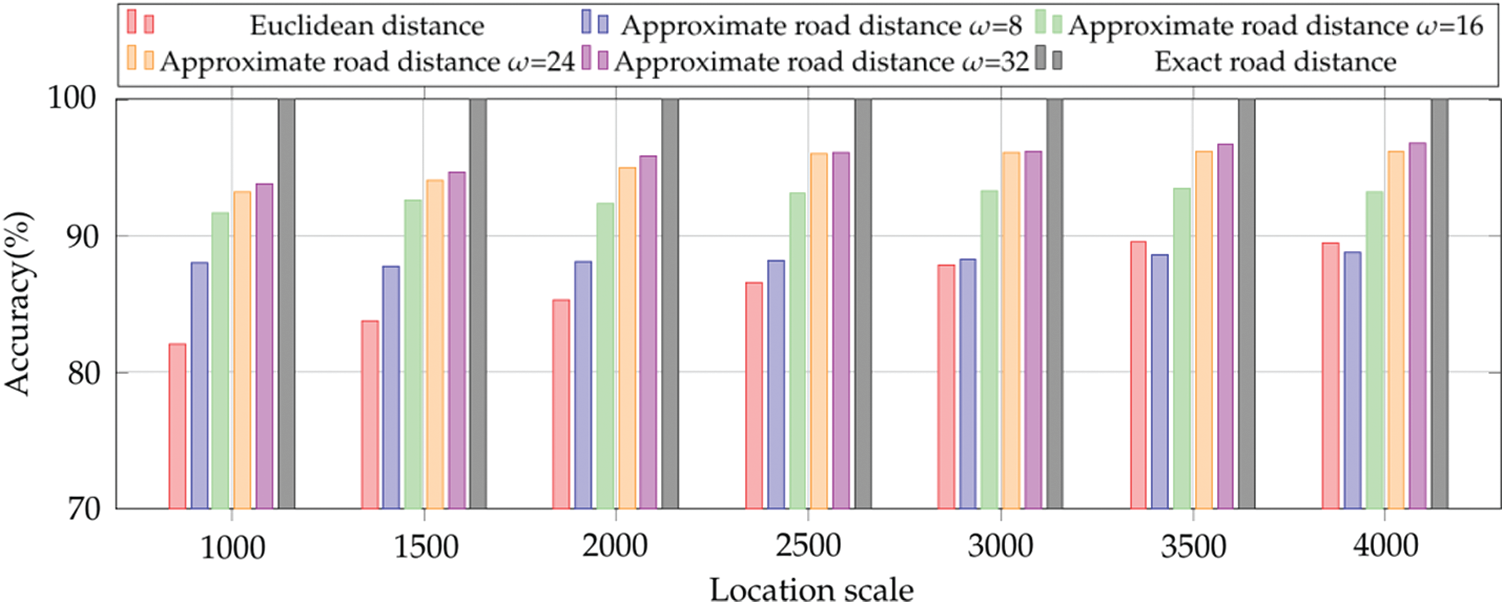
Figure 2: The accuracy of Euclidean distance, approximate road distance and exact road distance

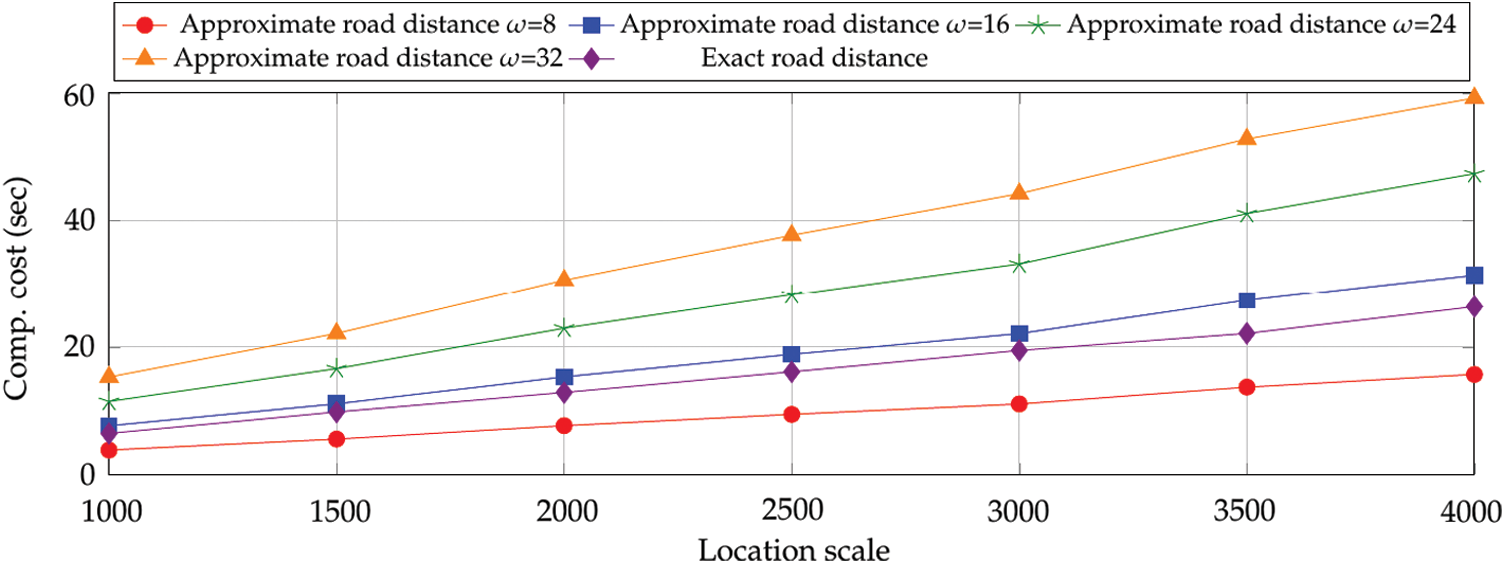
Figure 3: The accuracy of Euclidean distance, approximate road distance and exact road distance

5  Related Works

Numerous protocols have been proposed for private shortest road distance computation in different applications, such as kNN query and navigation. For (yet related) privacy issues of distance computation, some approaches utilize structural anonymization [14], differential privacy [15–17] or Private Information Retrieval (PIR) [18] to guarantee privacy for the client or the server. However, these approaches suffer from limited privacy, performance or scalability. There is also a vast literature on privacy-preserving shortest distance computation in structured encryption [19] or graph encryption, which focuses on protecting graph data when outsourced to third-party servers or on the cloud [20–22]. The most famous class of structured encryption schemes are searchable symmetric encryption (SSE) schemes [23]. Generally speaking, SSE schemes usually encrypt indexes or search trees for the purpose of efficiently searching on encrypted data. Another line of work executing graph algorithms over encrypted graphs is to develop data-oblivious algorithms [24] or data structures [25]. In these solutions, the graph data is stored in an Oblivious RAM (ORAM) [26] or an oblivious data structure on the server. The client can compute the shortest distances on the server without leaking its access patterns. Also relevant are the works based on SMC, such as Yao’s GCs and ORAM. The generic solution is to construct a GC that contains the entire graph structure for a shortest-path algorithm and apply Yao’s protocol. However, above approaches are often prohibitively expensive and impractical for city-scale road networks [27,28]. For instance, the GC-based approach by Carter et al. [29,30] requires several minutes to compute a single shortest path in a road network with just 100 vertices. Another generic approach combining GCs and ORAM requires communication overhead on the order of GB and run-times ranging from tens of minutes to several hours for a single computation on a network with 1024 vertices. Recently, some schemes are proposed to support computation over large-scale encrypted graphs. Shen et al. [1] proposed a graph encryption scheme based on symmetric-key primitives and SHE, which enables approximate constrained shortest distance queries. Meng et al. [2] presented three schemes based on distance oracle and structured encryption for approximate shortest distance queries. Above two schemes provide an estimate on the shortest distance, along with sacrificing accuracy. Wang et al. [3] proposed a secure Graph Data Base (SecGDB) encryption scheme based on PHE and Yao's GCs, which supports exact shortest distance/path queries. Wu et al. [4] proposed an efficient cryptographic protocol for fully-private navigation based on compressing the next-hop routing matrices, symmetric Private Information Retrieval (PIR) and Yao's GCs, which requires about 1.5 s and less than 100 KB of bandwidth for each hop in city-scale road network. Compared with existing schemes, our two road distance computation approaches are more efficient to compute large-scale shortest distances in real time.

6  Conclusions

In this paper, we proposed two secure road distance computation approaches, which can compute road distance over encrypted data efficiently. An approximate road distance computation approach is designed by using Partially Homomorphic Encryption and road network set embedding. An exact road distance computation is built by using Somewhat Homomorphic Encryption and road network hypercube embedding. According to the evaluation over a real city-scale road network, we have verified that our approaches are accurate and efficient.

Funding Statement: This work was partially supported by National Natural Science Foundation of China (Grant Nos. 61601146, 61732022), National Key R&D Program of China (Grant No. 2016QY05X1000).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Shen, B. Ma, L. Zhu, R. Mijumbi and X. Du, “Cloud-based approximate constrained shortest distance queries over encrypted graphs with privacy protection,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 4, pp. 940–953, 2018. [Google Scholar]

 2.  X. Meng, S. Kamara, K. Nissim and G. Kollios, “GRECS: Graph encryption for approximate shortest distance queries,” in 22nd ACM SIGSAC Conf. on Computer and Communications Security, Denver, Colorado, USA, pp. 504–517, 2015. [Google Scholar]

 3.  Q. Wang, K. Ren, M. Du, Q. Li and A. Mohaisen, “SecGDB: Graph encryption for exact shortest distance queries with efficient updates,” in 21st Int. Conf. on Financial Cryptography and Data Security, Sliema, Malta, pp. 79–97, 2017. [Google Scholar]

 4.  D. J. Wu, J. Zimmerman, J. Planul and J. C. Mitchell, “Privacy-preserving shortest path computation,” in 23rd Annual Network and Distributed System Security Sym., NDSS 2016, San Diego, California, USA, 2016. [Google Scholar]

 5.  P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, pp. 223–238, 1999. [Google Scholar]

 6.  J. Fan and F. Vercauteren, “Somewhat practical fully homomorphic encryption,” IACR Cryptology ePrint Archive, vol. 2012, pp. 144, 2012. [Google Scholar]

 7.  S. Gupta, S. Kopparty and C. Ravishankar, “Roads, codes, and spatiotemporal queries,” in 23rd ACM SIGMOD-SIGACT-SIGART Sym. on Principles of Database Systems, Paris, France, pp. 115–124, 2004. [Google Scholar]

 8.  H. Yu, X. Jia, H. Zhang, X. Yu and J. Shu, “PSRide: Privacy-preserving shared ride matching for online ride hailing systems,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1425–1440, 2019. [Google Scholar]

 9.  H. Yu, J. Shu, X. Jia, H. Zhang, X. Yu et al., “Lightweight and privacy-preserving ride matching over road networks in online ride hailing systems,” IEEE Transactions on Vehicular Technology, vol. 68, no. 11, pp. 10418–10428, 2019. [Google Scholar]

10. H. Yu, H. Zhang, X. Yu, X. Du and M. Guizani, “PGRide: Privacy-preserving group ridesharing matching in online ride hailing services,” IEEE Internet of Things Journal, vol. 8, no. 7, pp. 5722–5735, 2020. [Google Scholar]

11. H. Yu, X. Jia, H. Zhang and J. Shu, “Efficient and privacy-preserving ride matching using exact road distance in online ride hailing services,” IEEE Transactions on Services Computing, 2020. https://doi.org/10.1109/TSC.2020.3022875. [Google Scholar]

12. C. Shahabi, M. R. Kolahdouzan and M. Sharifzadeh, “A road network embedding technique for k-nearest neighbor search in moving object databases,” GeoInformatica, vol. 7, no. 3, pp. 255–273, 2003. [Google Scholar]

13. A. Bachir, I. M. Almanjahie and M. K. Attouch, “The k nearest neighbors estimator of the m-regression in functional statistics,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2049–2064, 2020. [Google Scholar]

14. J. Gao, J. X. Yu, R. Jin, J. Zhou, T. Wang et al., “Neighborhood privacy protected shortest distance computing in cloud,” in 2011 ACM SIGMOD Int. Conf. on Management of Data, Athens, Greece, pp. 409–420, 2011. [Google Scholar]

15. A. Sealfon, “Shortest paths and distances with differential privacy,” in 35th ACM SIGMOD-SIGACT-SIGAI Sym. on Principles of Database Systems, San Francisco, California, USA, pp. 29–41, 2016. [Google Scholar]

16. H. Chen, S. Li and Z. Zhang, “A differential privacy based (k-ψ)-anonymity method for trajectory data publishing,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2665–2685, 2020. [Google Scholar]

17. W. Han, M. Cheng, M. Lei, H. Xu, Y. Yang et al., “Privacy protection algorithm for the internet of vehicles based on local differential privacy and game model,” Computers, Materials & Continua, vol. 64, no. 2, pp. 1025–1038, 2020. [Google Scholar]

18. Y. Xi, L. Schwiebert and W. Shi, “Privacy preserving shortest path routing with an application to navigation,” Pervasive and Mobile Computing, vol. 13, pp. 142–149, 2014. [Google Scholar]

19. M. Chase and S. Kamara, “Structured encryption and controlled disclosure,” in Int. Conf. on the Theory and Application of Cryptology and Information Security, Singapore, pp. 577–594, 2010. [Google Scholar]

20. J. Qiu, Z. Tian, C. Du, Q. Zuo, S. Su et al., “A survey on access control in the age of internet of things,” IEEE Internet of Things Journal, vol. 7, no. 6, pp. 4682–4696, 2020. [Google Scholar]

21. L. Jiang and Z. Fu, “Privacy-preserving genetic algorithm outsourcing in cloud computing,” Journal of Cyber Security, vol. 2, no. 1, pp. 49–61, 2020. [Google Scholar]

22. X. Liu, J. Zhang, X. Li, S. Zhou, S. Zhou et al., “A block compressed sensing for images selective encryption in cloud,” Journal of Cyber Security, vol. 1, no. 1, pp. 29–41, 2019. [Google Scholar]

23. F. Hahn and F. Kerschbaum, “Searchable encryption with secure and efficient updates,” in 2014 ACM SIGSAC Conf. on Computer and Communications Security, Scottsdale, Arizona, USA, 310–320, 2014. [Google Scholar]

24. M. Blanton, A. Steele and M. Alisagari, “Data-oblivious graph algorithms for secure computation and outsourcing,” in 8th ACM SIGSAC Sym. on Information, Computer and Communications Security, Hangzhou, China, pp. 207–218, 2013. [Google Scholar]

25. M. Keller and P. Scholl, “Efficient, oblivious data structures for MPC,” in Proc. of Int. Conf. on the Theory and Application of Cryptology and Information Security, Berlin, Germany, pp. 506–525, 2014. [Google Scholar]

26. E. Stefanov, M. Van Dijk, E. Shi, C. Fletcher, L. Ren et al., “Path ORAM: An extremely simple oblivious ram protocol,” in 2013 ACM SIGSAC Conf. on Computer & Communications Security, Berlin, Germany, pp. 299–310, 2013. [Google Scholar]

27. S. Su, Z. Tian, S. Liang, S. Li, S. Du et al., “A reputation management scheme for efficient malicious vehicle identification over 5G networks,” IEEE Wireless Communications, vol. 27, no. 3, pp. 46–52, 2020. [Google Scholar]

28. Z. Tian, X. Gao, S. Su and J. Qiu, “Vcash: A novel reputation framework for identifying denial of traffic service in internet of connected vehicles,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 3901–3909, 2020. [Google Scholar]

29. H. Carter, B. Mood, P. Traynor and K. Butler, “Secure outsourced garbled circuit evaluation for mobile devices,” in 22nd USENIX Conf. on Security, Washington D.C., USA, pp. 289–304, 2013. [Google Scholar]

30. M. Shen, B. Ma, L. Zhu, R. Mijumbi, X. Du et al., “Cloud-based approximate constrained shortest distance queries over encrypted graphs with privacy protection,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 4, pp. 940–953, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.