DOI:10.32604/cmc.2021.020368

| Computers, Materials & Continua DOI:10.32604/cmc.2021.020368 |  |
| Article |
Image Splicing Detection Based on Texture Features with Fractal Entropy
1Department of Laser and Optoelectronics Engineering, University of Technology, Baghdad, 10066, Iraq
2Department of Applied Sciences, University of Technology, Baghdad, 10066, Iraq
3Department of Computer System and Technology, Faculty of Computer Science and Information Technology, Universiti Malaya, Kuala Lumpur, 50603, Malaysia
4IEEE: 94086547, Kuala Lumpur, 59200, Malaysia
5Department of Mathematics, Cankaya University, Balgat, 06530, Ankara, Turkey
6Institute of Space Sciences, R76900 Magurele-Bucharest, Romania
7Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
*Corresponding Author: Hamid A. Jalab. Email: hamidjalab@um.edu.my
Received: 20 May 2021; Accepted: 21 June 2021
Abstract: Over the past years, image manipulation tools have become widely accessible and easier to use, which made the issue of image tampering far more severe. As a direct result to the development of sophisticated image-editing applications, it has become near impossible to recognize tampered images with naked eyes. Thus, to overcome this issue, computer techniques and algorithms have been developed to help with the identification of tampered images. Research on detection of tampered images still carries great challenges. In the present study, we particularly focus on image splicing forgery, a type of manipulation where a region of an image is transposed onto another image. The proposed study consists of four features extraction stages used to extract the important features from suspicious images, namely, Fractal Entropy (FrEp), local binary patterns (LBP), Skewness, and Kurtosis. The main advantage of FrEp is the ability to extract the texture information contained in the input image. Finally, the “support vector machine” (SVM) classification is used to classify images into either spliced or authentic. Comparative analysis shows that the proposed algorithm performs better than recent state-of-the-art of splicing detection methods. Overall, the proposed algorithm achieves an ideal balance between performance, accuracy, and efficacy, which makes it suitable for real-world applications.
Keywords: Fractal entropy; image splicing; texture features; LBP; SVM
The advancements in digital image-editing software over the past decade have made image manipulation accessible to the masses. Consumers nowadays have unrestricted access to hundreds of advanced image editors, which also happen to be available for mobile devices, such that it has never been more convenient to morph and tamper images. The saturated market of application has forced developers to come up with novel ways to edit images, making the process of image forgery not only effortless and straightforward, but also accurate and imperceptible. As a result, human eyes can no longer differentiate forged from original images; and, although the consequences of image tampering are beyond the scope of this discussion, it is undeniable that this may exacerbate the spread of misinformation and fake news [1]. The act of image forgery can fall under either image manipulation such as the case of “copy-move”, or “splicing” [2,3]. In the former type (i.e., copy-move), a portion of an image is transposed into a different location within the same image in a way that cannot be (easily) recognized by the naked eye [4]. In contrast to copy-move forgery, image splicing represents the act of copying contents from an image into a different image [5] as shown in Fig. 1.

Figure 1: Example of image splicing
Since image forgery can be considered as a binary condition (i.e., either authentic (original) or tampered (forged)), it can be automatically classified using the classification techniques of machine learning. In image forensics, the image is processed through two main detection methods: active and passive (also known as blind) [1]. The active detection entails the use of additional information which is inserted into the image prior to distribution, such as in the case of digital watermarking [2]. In contrast, the passive detection employs statistical approaches to detect alterations in the features of an image [3]. Corresponding to the increase in image forgery, forgery detection methods have thrived over the years, with more sophisticated algorithms being proposed every year. The various works reported in the literature incorporate advanced detection methodologies and show superb performance under different conditions. There are still few limitations in the works reported in the literature, such as: the lacking of statistical information required for feature extraction, mainly on the forged image regions. Furthermore, the deficiency of statistical characteristics over flat forged image regions, which affects the detection performance. In the present study, we only focused on recent works that are associated with image splicing detection, whose algorithms involve the use of Texture Features from images. These criteria were implemented to facilitate relative comparison between our and past works.
Over the years, many passive algorithms have been proposed for image splicing detection. These algorithms employ different techniques for features extraction, including the “Local Binary Pattern” (LBP), Markov, Transform model (wavelet transform, Discrete Cosine Transform (DCT) and deep learning. In the first type, the LBP algorithm is applied as a feature extraction from the spliced images, by Zhang et al. [4]. This image splicing detection was based on the “Discrete Cosine Transform” (DCT) and LBP. The DCT is applied to each block of the input image, and then features were extracted by the LBP approach. The final feature vector classified by using the SVM classifier. Alahmadi et al. [5] proposed an algorithm for passive splicing detection which is based on DCT and “local binary pattern” (LBP). This algorithm relies on initial conversion of the input image from RGB into YCbCr, then the LBP output is generated by dividing the converted image’s chrominance channel into overlapping blocks. The LBP output is converted into the DCT frequency domain to enable the use of the DCT coefficients as a feature vector. The feature vectors are then used with the SVM classifier, which is responsible for deciding whether an image is forged or authentic. This method reportedly achieved accuracies of 97%, 97.5% and 96.6% when tested with the three dataset “CASIA v1.0 & v2.0” and “COLUMBIA” respectively. In the same approach, In Han et al. [6], proposed a feature extraction based on “Markov features” to detect the spliced images based on the maximum value of pixels in the DCT domain. The high numbers of extracted features were reduced by using the even-odd “Markov algorithm”. However, the limitation of Markov models is the high complexity and time consumption. Accordingly, Jaiprakash et al. [7] proposed a “passive” forgery detection technique where image features are extracted from the “discrete cosine transforms” (DCT) and “discrete wavelet transform” (DWT) domains. Their approach employed the ensemble classifier for both training and testing to discriminate between forged and authentic images. The algorithm operates under the Cb + Cr of the YCbCr color space, and the authors showed that the features obtained from these channels demonstrated better performance compared to features extracted by using individual Cb and Cr channels. The algorithm has reportedly achieved classification accuracies of 91% and 96% for “CASIA v1.0” and “CASIA v2.0” datasets, respectively. Subramaniam et al. [8] utilized a set of “conformable focus measures” (CFMs) and “focus measure operators” (FMOs) to acquire “redundant discrete wavelet transform” (RDWT) coefficients that were subsequently used to improve the detection of the proposed splicing detection algorithm. Since image splicing causes disfigurement in the contents and features of an image, blurring is usually employed to flush the boundaries of the spliced region inside the image. Even though this may reduce the artifacts generated by splicing, the blurring information can be exploited to detect forgeries. Both CFM and FMO were utilized to measure the amount of blurring that exists in the boundaries of the spliced region in the aforementioned algorithm. The 24-D feature vector algorithm was tested with two public datasets “IFS-TC” and “CASIA TIDE V2” and has reportedly achieved accuracy rates of 98.30% for the Cb channel from the former dataset and 98.60% for the Cb channel from the latter dataset. With such accurate classification performance, this method outperforms other image splicing detection methods. Moreover, the third type of feature extraction for detection the spliced images is suggested by El-Latif et al. [3]. This approach presented a deep learning algorithm and wavelet transform for detecting the spliced image. The final features are classified by SVM classifier. Two publicly image splicing datasets (CASIA v1.0 and CASIA v2.0) were used to evaluated the method. The large number of features with high complexity of calculations are the main limitations.
Wang et al. [9] proposed an approach that employs the “convolutional neural networks” (CNN) with a novel strategy to dynamically adjust the weights of features. They utilized three feature types, namely YCbCr, edge and “photo response non-uniformity” (PRNU) features, to discriminate original from spliced images. Those features were combined in accordance to a predefined weight combination strategy, where the weights are dynamically adjusted throughout the training process of the CNN until an ideal ratio is acquired. The authors claimed that their method outperforms similar methods that also utilize CNN, in addition to the fact that their CNN has significantly less depth than the compared methods, which overall counts as an advantage.
Zhang et al. [10] employed deep learning in their splicing forgery detection. In their proposed work, a stacked model of autoencoder is used in the first stage of the algorithm to extract features. The detection accuracy of the algorithm was further enhanced by integrating the contextual information obtained from each patch. They reported a maximum accuracy rate of 87.51% with “CASIA 1.0” and “CASIA 2.0” datasets. As seen from the above-mentioned works, some algorithms employ texture and color features, whereas others use frequency-based features. In order to make full use of the color information of the input images, a texture feature-based algorithm in which four features (i.e., FrEp, LBP, skewness and kurtosis) are extracted from a YCbCr-converted image.
In the present study, we propose a texture feature-based algorithm in which four features (i.e., FrEp, LBP, skewness and kurtosis) are extracted from a YCbCr-converted image. These features are then combined together to obtain a feature vector. The resulting 4D feature vector is subsequently used for the SVM classifier to determine whether an image is spliced or authentic. The algorithm comprises three main steps: first, in the pre-processing step, the RGB image is transformed into the YCbCr format; second, in the feature extraction step, image features (i.e., FrEp, LBP, skewness and kurtosis) are acquired from the YCbCr-converted image and are combined together to obtain a feature vector; lastly, in the classification step, SVM is used with the obtained feature vector to discriminate spliced from authentic images. The classification accuracy of the proposed method is further enhanced by employing a combination of texture features and reducing the total feature dimension. A diagrammatic representation of the proposed algorithm is shown in Fig. 2.
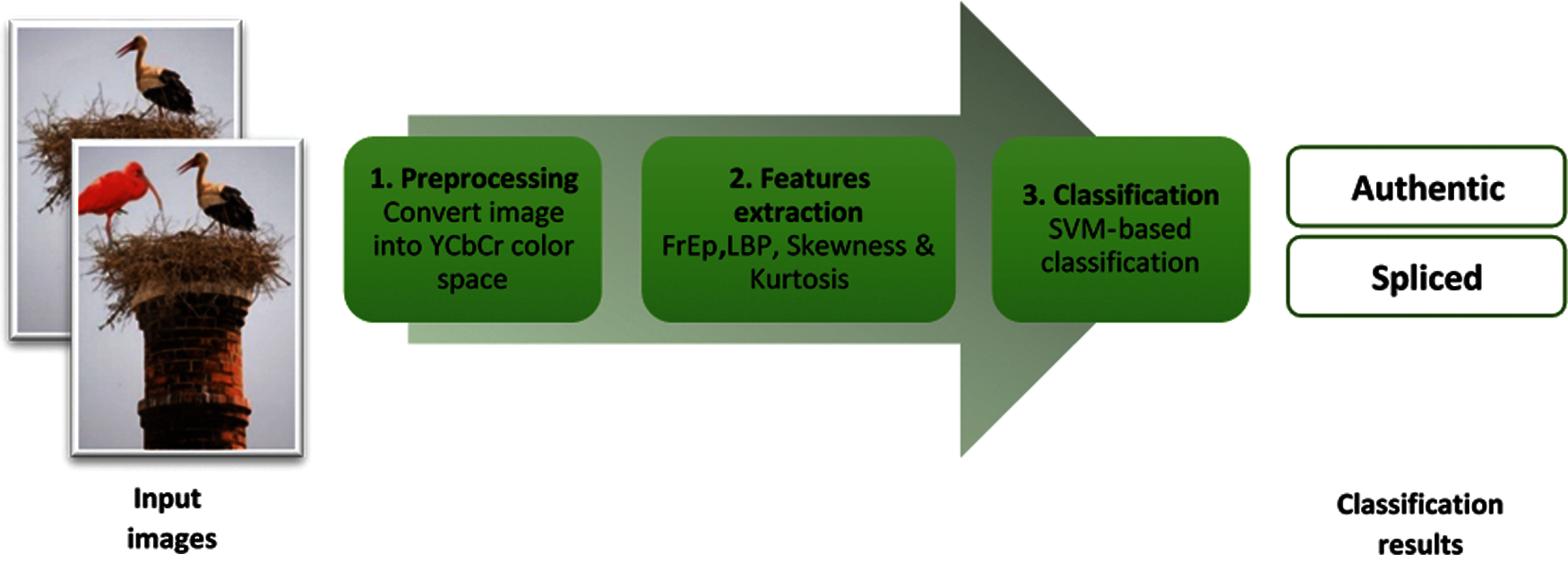
Figure 2: A diagram depicting the proposed method
In this step, the input image is converted from its original RGB color space into the YCbCr color space where Y symbolizes the luminance, and Cb and Cr characterize the chrominance color. Compared to the latter two channels, the Y channel holds the most information; thus, any changes to this channel will lead to prominent changes to the image, which can be recognized by the naked eye. In contrast, the information held by the Cb and Cr channels does not visibly affect the image, and therefore, any changes to these channels are more difficult to spot. In light of the above, the proposed method utilizes the chrominance channel for features extraction.
Since the process of image splicing involves transformations to the image which include: translation, rotation and scaling, the proposed method extracts the following features from the Cb and Cr channels: FrEp, LBP, skewness, and kurtosis. These features have been chosen in the present study because they are amongst the most used features reported in the literature, and they give good representation of the texture of an image. LBP is an effective image descriptor to define the patterns of the local texture in images by capturing the local spatial patterns and the gray scale contrast in an image. It is extensively applied in the different image processing applications [11–13]. The most important component of image splicing detection is to have sensitive features to any alterations due to tampering. The of textural features distributions offering a statistical basis for separation between authentic and spliced images. Moreover, three statistical features such as FrEp, skewness and kurtosis are used extracted image features from each Cb, and Cr image in order to identify the differences between the spliced or authentic images [14]. The state of the image texture is of great importance in splicing detection since all alterations done to the image are reflected by altered image texture [15,16].
Entropy is a statistical measure of randomness, which can be used to gauge the texture of an image. It calculates the brightness entropy of each pixel of the image, and therefore, it is defined as [17]
where G(G1, G2, …, Gn) represents normalized histogram counts returned from the histogram of the input image. The entropy as a texture descriptor mostly provides randomness of image pixel with its local neighborhood. Ubriaco [18] formalized the definition of Shannon fractional entropy as follows:
where p is the pixel probability of the image, and α is the fractional power of entropy (the order of entropy). Valério et al. [19] generalized (1) as follows:
The local fractional calculus is also used to define a modified fractal entropy [20] as follows
In this study, we introduce more modification on fractional entropy using Re’nyi entropy. Since Re’nyi entropy satisfies the following relation [21,22]
By substituting the fractal Re’nyi entropy of (3) into (4), we get the proposed FrEp as follows [17]:
The logic behind using Fractal Entropy as a texture feature extraction is that the entropy and the fractal dimension are both considered as spatial complexity measures. For this reason, the fractal entropy has the ability to extract the texture information contained in the input image efficiently. The proposed fractal entropy model estimates the probability of pixels that represent image textures based on the entropy of the neighboring pixels, which results in local fractal entropy. The main advantage of FrEp lies in their ability to accurately describe the information contained in the image features, which makes them an efficient feature extraction algorithm. In the proposed FrEp feature extraction model, the key parameter is α, where the performance of the FrEp basis function of the α power is utilized to enhance the intensity value of the pixels of the image, which might influence the accuracy of the detection process of image splicing. The optimal value of α has be chosen experimentally equal to 0.5.
LBP, like proposed FrEp, describes the texture state of an image. In LBP, pixel values are transformed into a binary number using thresholding. This is done by considering the binary value in a clockwise fashion, beginning with the top-left neighbor. LBP can be defined as follows:
where Jm represents the m neighborhood pixel intensity value, and Jct is the central pixel value, p is the sampling points, and q is the circle radius. The thresholding function F(m) is given by:
The image texture extracted by the LBP is characterized by the distribution of pixel values in a neighborhood, where each pixel is modified according to thresholding function F(m).
Skewness is a statistical quantity of asymmetry distribution of a variable, and can be defined as:
where σ represents the standard deviation, μ denotes the mean of an image, and n is the number of pixels.
Kurtosis is a measure used to describe the form (peakedness or flatness) of a probability distribution. The formula for kurtosis is as follows:
These features have been chosen due to its ability to show the significant detail of the image. These four features highlighted the texture detail of the internal statistics of forged parts. The proposed method is summarizing as follows:
(1) Convert the image color space into YCbCr color space.
(2) Extract the Cb and the Cr images.
(3) Split the input image into non-overlapping image blocks of size of 3
(4) Extract the four proposed texture features (FrEp, LBP based features, Skewness, and Kurtosis) each block from Cb and Cr images.
(5) Save the extracted features vector as the final texture features for all Cb, and Cr image.
(6) Apply the SVM to classify the input image into “authentic” or “spliced forged image”.
In this study, the proposed algorithm consists the following flow chart stages as shown in Fig. 3.
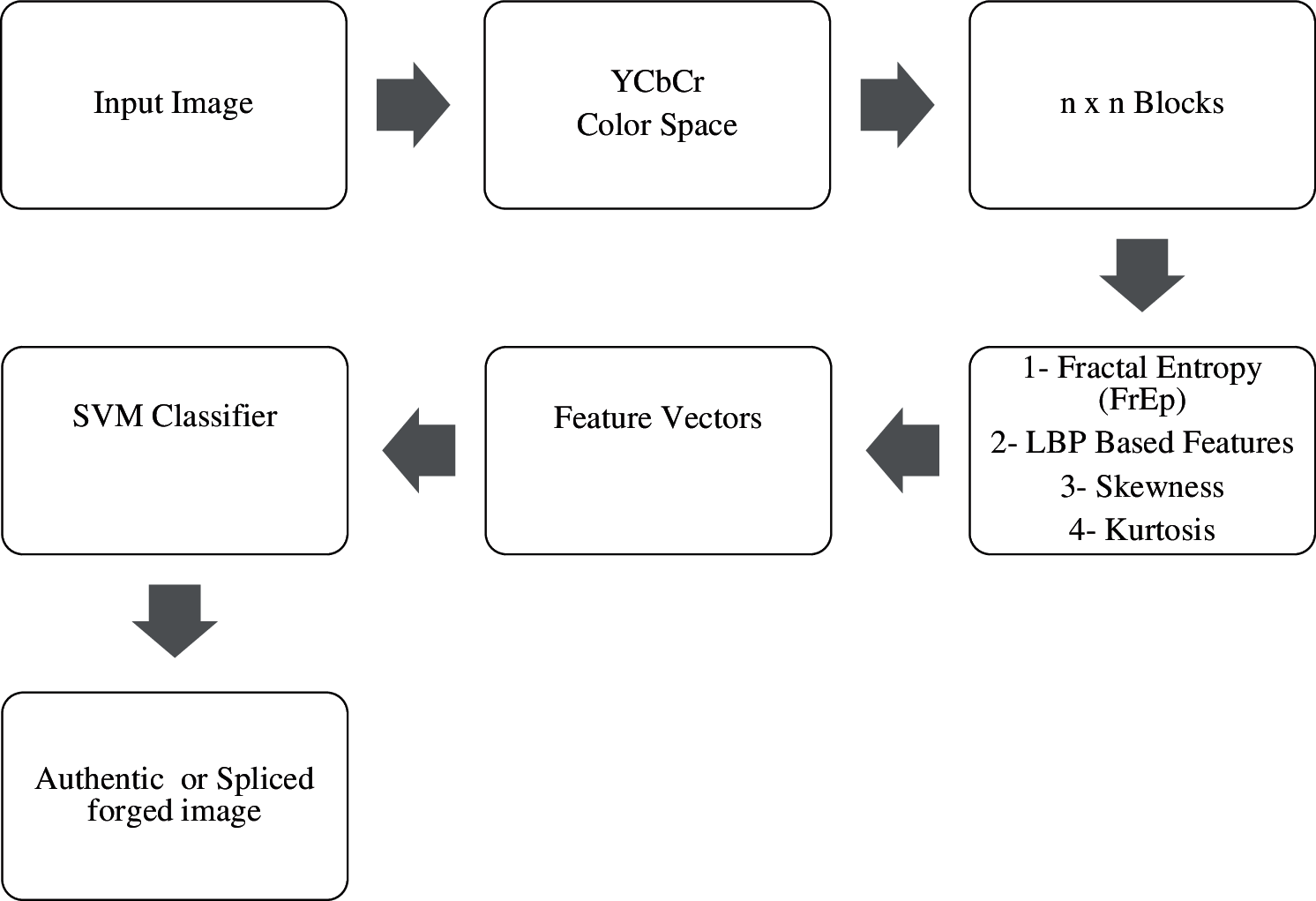
Figure 3: The proposed algorithm
The performance of the proposed method was assessed using the accuracy metric along with several experiments. The methods and tests were designed and conducted using Matlab R2020b.
The two datasets, which have been used for evaluation and comparative analysis purposes, [23,24] are described in Tab. 1. The “CASIA v1.0” dataset [23] consists of 1721 images classified under 8 different categories, with 921 of which being spliced. The spliced images were originally generated by splicing regions from one image into another using “Adobe Photoshop” software. Similarly, the second dataset “CASIA v2.0” [24] consists of 12,614 images classified under 9 categories, and it includes 5123 spliced images. These two datasets were chosen for the present study because their images have undergone several transformation operations and some post-processing, making the datasets thorough and comprehensive. Moreover, the two datasets have been extensively used in the literature, and thus, they could be considered as a benchmark in the field of image splicing detection.

Examples of CASIA v1, and CASIA v2 image dataset are shown in Figs. 4 and 5 respectively.
Accuracy was used as the primary performance metric. Here, it represents the ratio of the number of correctly classified images to that of the total number of all images, and it is calculated as follows:
where TP (“True Positive”) and TN (“True Negative”) denote the number of spliced and original images that are correctly classified as such, respectively; whereas FN (“False Negative”) and FP (“False Positive”) represent the number of spliced and original images that are incorrectly classified as such, respectively.
For the detection of color image splicing, we selected the two datasets CASIA v1.0 and CASIA v2.0. Both datasets contain images whose spliced regions have been scaled and/or rotated. The CASIA v1.0 dataset contains 800 authentic and 921 spliced color images, while CASIA v2.0 dataset consists of 7491 authentic and 5123 forged color images. The results of the proposed method achieve 96% of detection accuracy on four feature dimensions on all images of CASIA v1.0. The accuracy increased to 98% of detection accuracy for four feature dimensions on all images of CASIA v2.0 as well. The detection accuracy was measured using only Cb-Cr color spaces for both datasets. The proposed image splicing detection model shows better accuracy on CASIA v2.0 than on CASIA v1.0 when the features of Cb and Cr color spaces are combined. The extraction time was about 2 s, which shows that the proposed model is efficient.

Figure 4: Samples of CASIA v1 dataset. First row (authentic images). Second row (splicing images)

Figure 5: Samples of CASIA v2 image dataset. Authentic images in first row, and image splicing in the second row
4.4 Comparison with Other Methods
In order to demonstrate the robustness of the proposed algorithm, its performance has been compared with the performance of similar state-of-the-art splicing detection methods. Tab. 2 shows the results of an experiment conducted using the “CASIA v1.0” dataset on a given number of methods [3,10,25]. The results shown in the table confirm that the accuracy of the proposed method is higher than the referenced methods.
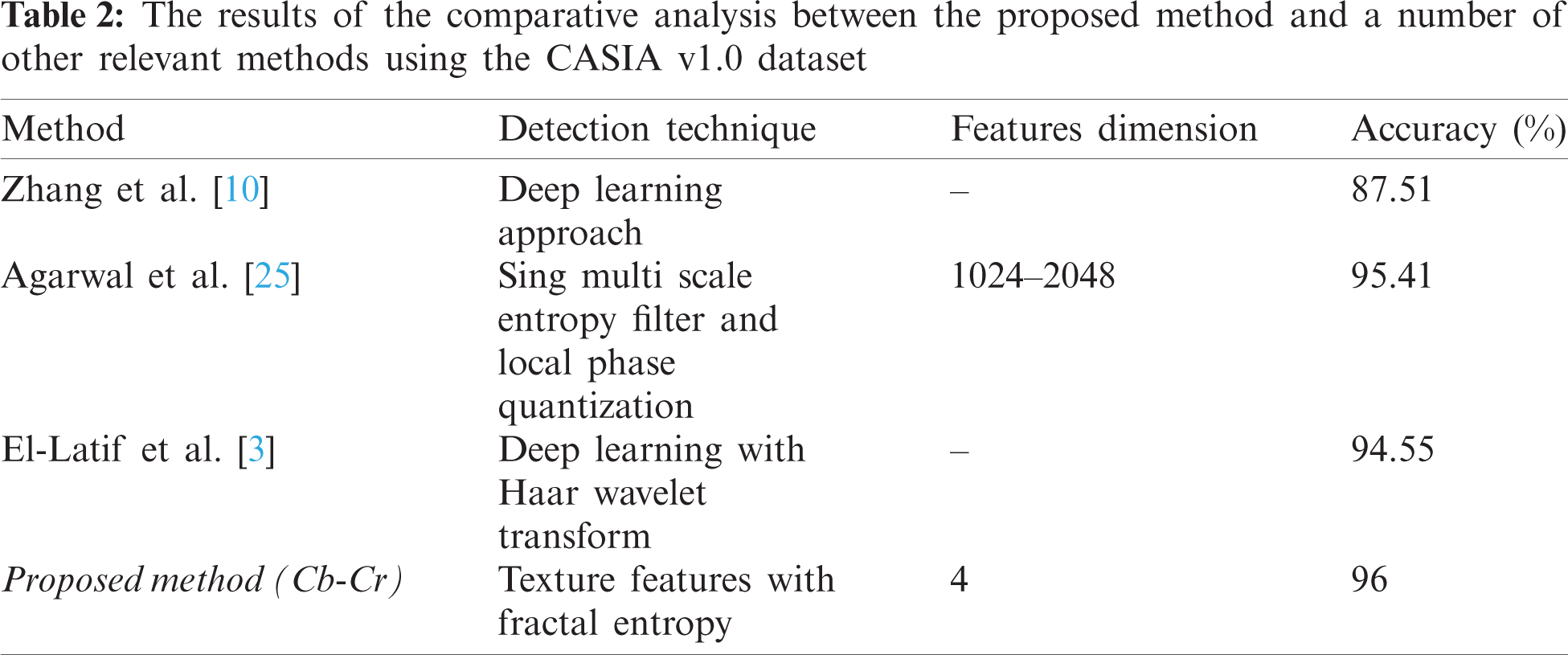
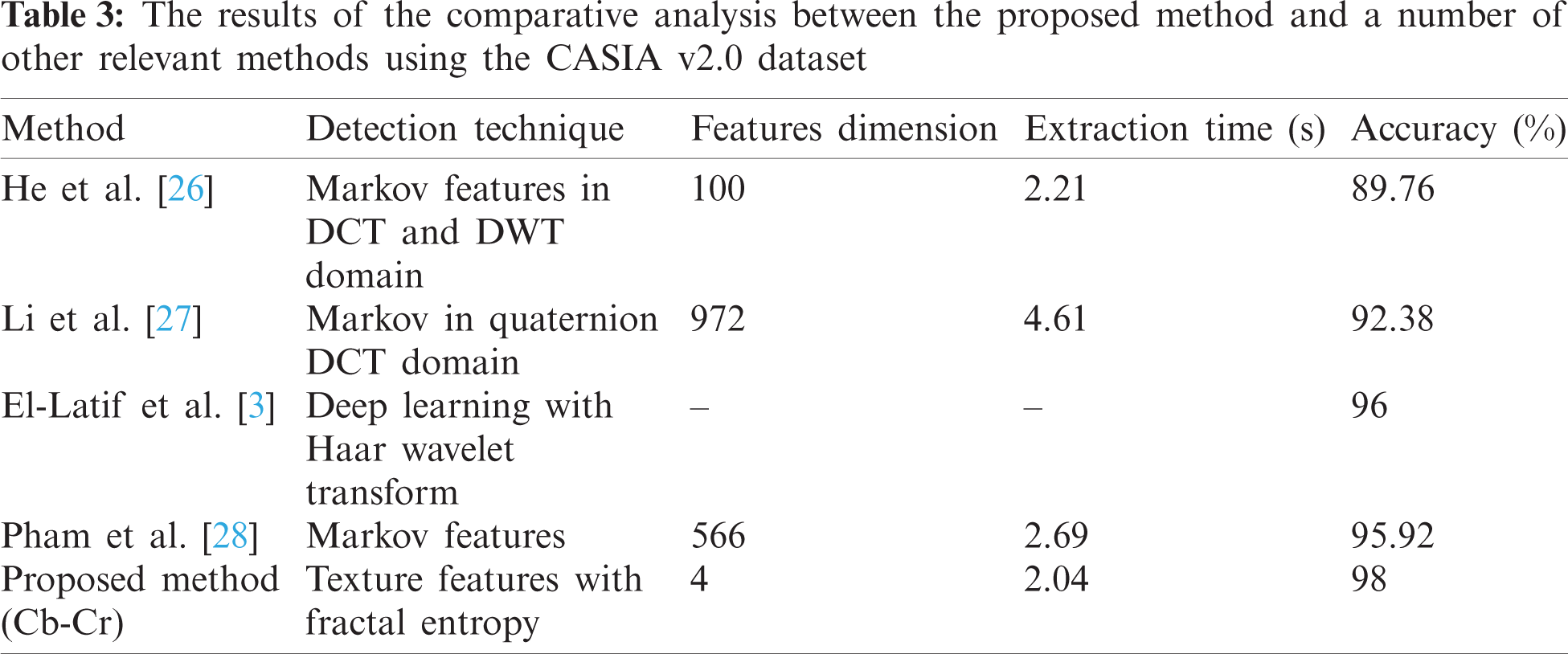
Similarly, Tab. 3 shows the results of the comparison between the proposed method and some other splicing detection methods [3,26–28] using the “CASIA v2.0” dataset. The proposed approach achieves better than mentioned state-of-the-art methods in terms of the extraction time and the detection accuracy. We compare the processing time per image for feature extraction time with previous works. The dimension of feature vector in He et al. [26] are high enough, therefore, they used feature dimension reduction to reduce the features dimension up to 100. While, Pham et al. [28], which applied Markov features for image splicing detection algorithm, they achieved 95.92% accuracy with 2.692 s of extraction time. It is evident that the proposed method performs better than some of the state-of-the-art methods, as judged by the obtained accuracy rates for the “CASIA v1.0” and “CASIA v2.0” datasets, which are 96% and 98%, respectively which is higher than that of those methods with shorter feature extraction time. As mentioned previously, these datasets offer a comprehensive range of images that are of various natures to test splicing detection methods with, and as such, they can be considered as a reliable benchmark to facilitate relative comparisons between different methods. All in all, the use of 4D feature vector along with the SVM has proved to be an effective approach to creating a highly-accurate yet simple splicing detection algorithm. The overall balance between efficiency and accuracy makes the proposed algorithm suitable for day-to-day uses.
In this work, we proposed an automatic tool to discriminate between spliced and authentic images using the SVM classifier. We have extracted the texture features using four features extraction stages namely, Fractal Entropy (FrEp), local binary patterns (LBP), Skewness, and Kurtosis to get cues of any type of manipulation on images in order to enhance the classification performance of the SVM classifier. Experimental validation on “CASIA v1.0 & v2.0” image datasets shows that the proposed approach gives good detection accuracy to identify the tampered images with reasonable feature extraction time. Proposed model gives higher detection accuracy than that of those methods with shorter feature extraction time. The proposed work has demonstrated striking accuracy rates of 96% and 98% when tested with the very versatile and comprehensive “CASIA v1.0 & v2.0” datasets respectively. These rates are superior to some of the recent state-of-the-art splicing detection methods. The experimental findings showed that the proposed image splicing detection method helps for the detection splicing attack in images using image texture features with proposed fractal entropy. In future splicing detection works, one could consider locating the spliced objects within a forged image.
Funding Statement: This research was funded by the Faculty Program Grant (GPF096C-2020), University of Malaya, Malaysia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Sadeghi, S. Dadkhah, H. A. Jalab, G. Mazzola and D. Uliyan, “State of the art in passive digital image forgery detection: Copy-move image forgery,” Pattern Analysis and Applications, vol. 21, no. 2, pp. 291–306, 2018. [Google Scholar]
2. A. S. Kapse, Y. Gorde, R. Rane and S. Yewtkar, “Digital image security using digital watermarking,” International Research Journal of Engineering and Technology, vol. 5, no. 3, pp. 163–166, 2018. [Google Scholar]
3. I. E. A. El-Latif, A. Taha and H. Zayed, “A passive approach for detecting iImage splicing using deep learning and Haar wavelet transform,” International Journal of Computer Network & Information Security, vol. 11, no. 5, pp. 1–9, 2019. [Google Scholar]
4. Y. Zhang, C. Zkao, Y. Pi, S. Li and S. Wang, “Image-splicing forgery detection based on local binary patterns of DCT coefficients,” Security and Communication Networks, vol. 8, no. 14, pp. 2386–2395, 2015. [Google Scholar]
5. A. Alahmadi, M. Hussain, H. Aboalsamh, G. Muhammad and G. Bebis, “Splicing image forgery detection based on DCT and LBP,” in 2013 IEEE Global Conf. on Signal and Information Processing, 2013, Austin, TX, USA, IEEE, pp. 253–256, 2013. [Google Scholar]
6. J. Han, T. H. Park, Y. Moon and K. Eom, “Efficient Markov feature extraction method for image splicing detection using maximization and threshold expansion,” Journal of Electronic Imaging, vol. 25, no. 2, pp. 1–8, 2016. [Google Scholar]
7. S. P. Jaiprakash, M. B. Desai, C. S. Prakash, V. H. Mistry and K. Radadiya, “Low dimensional DCT and DWT feature based model for detection of image splicing and copy-move forgery,” Multimedia Tools and Applications, vol. 79, no. 39, pp. 29977–30005, 2020. [Google Scholar]
8. H. A. Jalab, T. Subramaniam, R. W. Ibrahim and N. F. Mohd Noor, “Improved image splicing forgery detection by combination of conformable focus measures and focus measure operators applied on obtained redundant discrete wavelet transform coefficients,” Symmetry, vol. 11, no. 1392, pp. 1–16, 2019. [Google Scholar]
9. J. Wang, Q. Ni, G. Liu, X. Luo and S. Jha, “Image splicing detection based on convolutional neural network with weight combination strategy,” Journal of Information Security and Applications, vol. 54, no. 102523, pp. 1–8, 2020. [Google Scholar]
10. Y. Zhang, J. Goh, L. Win and V. Thing, “Image region forgery detection: A deep learning approach,” in Proc. of the Singapore Cyber-Security Conf. 2016, Singapore, vol. 14, pp. 1–11, 2016. [Google Scholar]
11. N. J. Sairamya, L. Susmitha, S. Thomas George and M. S. P. Subathra, “Hybrid approach for classification of electroencephalographic signals using time-frequency images with wavelets and texture features,” Intelligent Data Analysis for Biomedical Applications, vol. 27, no. 12, pp. 253–273, 2019. [Google Scholar]
12. H. A. Jalab, H. Omer, A. Hasan and N. Tawfiq, “Combination of LBP and face geometric features for gender classification from face images,” in 2019 9th IEEE Int. Conf. on Control System, Computing and Engineering, 2019, Penang, Malaysia, IEEE, pp. 158–161, 2019. [Google Scholar]
13. P. K. Bhagat, P. Choudhary and K. H. ManglemSingh, “A comparative study for brain tumor detection in MRI images using texture features,” in Sensors for Health Monitoring. vol. 2019. Amsterdam, Netherlands: Elsevier, pp. 259–287, 2019. [Google Scholar]
14. B. Attallah, A. Serir and C. Youssef, “Feature extraction in palmprint recognition using spiral of moment skewness and kurtosis algorithm,” Pattern Analysis and Applications, vol. 22, no. 3, pp. 1197–1205, 2019. [Google Scholar]
15. Y. Suhad, J. Arkan and M. Nadia Al-Saidi, “Texture images analysis using fractal extracted attributes,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 4, pp. 1297–1312, 2020. [Google Scholar]
16. Y. Suhad, Y. Hussam and M. Nadia Al-Saidi, “Extracting a new fractal and semi-variance attributes for texture images,” AIP Conference Proceedings, vol. 2183, no. 80006, pp. 1–4, 2019. [Google Scholar]
17. H. A. Jalab, R. W. Ibrahim, A. M. Hasan, F. K. Karim, A. R. Shamasneh et al., “A new medical image enhancement algorithm based on fractional calculus,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1467–1483, 2021. [Google Scholar]
18. M. R. Ubriaco, “Entropies based on fractional calculus,” Physics Letters A, vol. 373, no. 30, pp. 2516–2519, 2009. [Google Scholar]
19. D. Valério, J. J. Trujillo, M. Rivero, J. A. T. Machado and D. Baleanu, “Fractional calculus: A survey of useful formulas,” The European Physical Journal Special Topics, vol. 222, no. 8, pp. 1827–1846, 2013. [Google Scholar]
20. H. A. Jalab, T. Subramaniam, R. W. Ibrahim, H. Kahtan and M. N. Nurul, “New texture descriptor based on modified fractional entropy for digital image splicing forgery detection,” Entropy, vol. 21, no. 371, pp. 1–9, 2019. [Google Scholar]
21. C. Essexa, C. Schulzky, A. Franz and K. H. Hoffmann, “Tsallis and Rényi entropies in fractional diffusion and entropy production,” Physica A: Statistical Mechanics and Its Applications, vol. 284, no. 4, pp. 299–308, 2000. [Google Scholar]
22. H. A. Jalab, A. A. Shamasneh, H. Shaiba, R. W. Ibrahim and D. Baleanu, “Fractional Renyi entropy image enhancement for deep segmentation of kidney MRI,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2061–2075, 2021. [Google Scholar]
23. J. Dong, W. Wang and T. Tan, “CASIA tampered image detection evaluation database (CASIA TIDE v1.0),” 2013. [Online]. Available: http://forensics.idealtest.org:8080/index_v1.html (accessed on May 2021). [Google Scholar]
24. J. Dong, W. Wang and T. Tan, “CASIA tampered image detection evaluation database (CASIA TIDE v2.0),” 2013. [Online]. Available: http://forensics.idealtest.org:8080/index_v2.html (accessed on May 2021). [Google Scholar]
25. S. Agarwal and S. Chand, “Image forgery detection using multi scale entropy filter and local phase quantization,” International Journal of Image, Graphics and Signal Processing, vol. 2015, no. 10, pp. 78–85, 2015. [Google Scholar]
26. Z. He, W. Lu, W. Suna and J. Huang, “Digital image splicing detection based on Markov features in DCT and DWT domain,” Pattern Recognition, vol. 45, no. 12, pp. 4292–4299, 2012. [Google Scholar]
27. C. Li, Q. Ma, L. Xiao, M. Lib and A. Zhang, “Image splicing detection based on Markov features in QDCT domain,” Neurocomputing, vol. 228, no. 2017, pp. 29–36, 2017. [Google Scholar]
28. N. T. Pham, J. W. Lee, G. R. Kwon, G. R. Kwon and C. S. Park, “Efficient image splicing detection algorithm based on Markov features,” Multimedia Tools and Applications, vol. 78, no. 9, pp. 12405–12419, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |