DOI:10.32604/cmc.2022.019343

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019343 |  |
| Article |
High Throughput Scheduling Algorithms for Input Queued Packet Switches
1Department of IT, Dr. Sivanthi Aditanar College of Engineering, Tiruchendur, 628205, India
2Department of CSE, Dr. Sivanthi Aditanar College of Engineering, Tiruchendur, 628205, India
3School of CSE, Vellore Institute of Technology, Vellore, 632014, India
*Corresponding Author: R. Chithra Devi. Email: rcdnnp@gmail.com
Received: 10 April 2021; Accepted: 20 May 2021
Abstract: The high-performance computing paradigm needs high-speed switching fabrics to meet the heavy traffic generated by their applications. These switching fabrics are efficiently driven by the deployed scheduling algorithms. In this paper, we proposed two scheduling algorithms for input queued switches whose operations are based on ranking procedures. At first, we proposed a Simple 2-Bit (S2B) scheme which uses binary ranking procedure and queue size for scheduling the packets. Here, the Virtual Output Queue (VOQ) set with maximum number of empty queues receives higher rank than other VOQ’s. Through simulation, we showed S2B has better throughput performance than Highest Ranking First (HRF) arbitration under uniform, and non-uniform traffic patterns. To further improve the throughput-delay performance, an Enhanced 2-Bit (E2B) approach is proposed. This approach adopts an integer representation for rank, which is the number of empty queues in a VOQ set. The simulation result shows E2B outperforms S2B and HRF scheduling algorithms with maximum throughput-delay performance. Furthermore, the algorithms are simulated under hotspot traffic and E2B proves to be more efficient.
Keywords: Crossbar switch; input queued switch; virtual output queue; scheduling algorithm; high performance computing
In recent years, a lot of the commercial and scientific application requires high-performance computing (HPC). Modeling the environmental issues, product designing, materials, and biological research, managing Internet traffic are such example applications [1]. HPC is a paradigm that solves problems that demand a high degree of computations in a shorter time with maximum accuracy [2]. HPC aggregates resources from multiple machines or computes nodes to build a powerful infrastructure such as a high-end cluster, supercomputer, grid, or cloud to resolve complex problems [3]. An HPC cluster consist of a large number of worker nodes and servers interconnected through a high-speed network using a Gigabit Ethernet preferably InfiniBand or Myrinet. The performance of the cluster largely depends on how fast the data communication was established between their components. As data are mostly residing in data centers, which are accessed by various resources in the cluster might create huge IP traffic around them. In some centers, Storage Area Networks (SAN) are used for carrying data between these cluster resources despite its implementation complexity. However, a widely preferred option for these data centers is to use high-speed switches [4]. These switches can provide high-speed data transmission with maximum throughput and minimum latency on any kind of traffic [5]. As the number of compute node get increases, the traffic around the data center too increase. As a result, the number of ports in the switch fabric has been increased however it is not a viable solution because it might minimize the data throughput [6].
In order to design a fast as well as cheap switch, crossbar fabric is preferred. Here, between input and output ports all possible permutation of connections can be designed. A crossbar switch fabric can be classified as Input Queued (IQ), Output Queued (OQ), Combined Input and Output Queued (CIOQ) and Crosspoint Queued (CQ) switches [7]. Among all the types of crossbars, input queued switch remains simple to implement and more effective because the memory bandwidth required for packet transmission at each timeslot is very less. This makes it highly preferred and most suitable for high-speed communications in Internet routers or data centers [7,8,9]. The structure of the IQ switch is shown in Fig. 1 and is discussed detailed in Section 3. A switch is driven by its arbitration scheme, which makes it more powerful. The performance of a switch is purely based on its employed scheduling algorithm. In IQ switch, iterative scheduling is preferred by various scheduling schemes such as iSLIP, RRM, etc. where scheduling is done in three phases: request, grant and accept. A matching request is sent by each input to the output during the request phase. One of the received requests is selected by the output during the grant phase. Respective Input will accept one of the available grants received from the output in the last phase. The same set of handshake operations will be performed at each iteration to establish a maximum matching. The drawback of the scheme, it is not possible to achieve maximum matching at every timeslot and hence suffers from average throughput performance.
Some classes of algorithms such as DRRM, Grant Aware (GA) designed to work with two phases i.e., request and grant [10]. But still, a considerable amount of time is spent in finalizing the maximal matching, and hence the switching is not possible within a timeslot. In the case of HPC, switches are designed to handle huge traffic. Therefore the deployed arbitration scheme should be capable to find maximum matching at each timeslot in order to achieve maximum throughput-delay performance. For instance, on a 10 GPS line carrying 32-byte packets, 5 ns is about to be one timeslot. A timeslot is allotted to make scheduling decisions as well as for data transmission. Completing all the iterations and making scheduling decisions within the minimum duration of 5 ns is a highly challenging task. This time-critical task offer severe headache to scheduling schemes used in high-speed switches. In some instances, the severity of task might lead to additional timeslot or in need of speedup. This will further reduce the switch performance or increase the implementation complexity, for the latter case. Therefore a high-performance scheduling algorithm is required to attain maximum matching at every timeslot to meet the demand of compute-intensive applications.
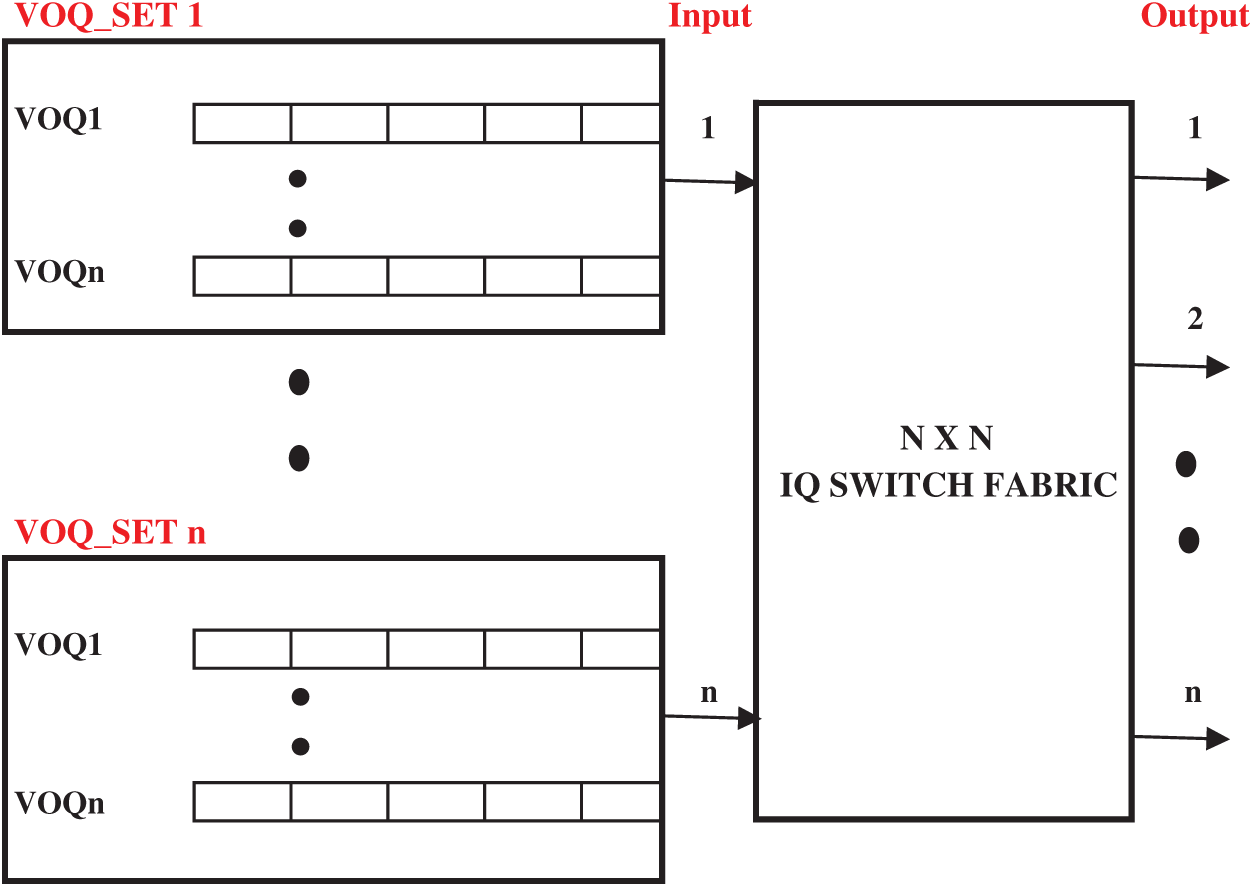
Figure 1: Input queued switch with virtual output queue
The rest of the paper is discussed as follows: Several iterative algorithms are discussed in the next section. In Section 3, we introduce the S2B and E2B algorithms with necessary examples. In Section 4, the performance of the proposed algorithms is evaluated and compared with existing schemes. In Section 5, we concluded the paper.
One of the remarkable scheduling scheme in the history of IQ is iSLIP proposed by Nick McKeown [11], achieves 100% through under uniform traffic but offers poor performance under non-uniform traffic [11,12]. It is an iterative scheduler which took three phases for every queue matching. A matching is computed in O (log n) iterations but largely suffers from longer queuing delay and matching overhead. Iterative Least Recently Used (iLRU) uses a similar procedure of iSLIP except for the choice of next scheduled cell. Here, the least recently used cell will be given maximum priority for the next schedule compared to RR fashion used in iSLIP. Parallel Iterative Matching (PIM) is an iterative maximal matching scheduler where the input-output matching is done in two phases i.e., accept and grant by using random selection arbiters. It provides less than 65% of throughput under heavy load which is the limiting factor along with its high implementation cost and unfairness among the queues during switch schedule [13]. Performance of iSLIP, iLRU and PIM are compared with 16
Modified Round Robin Algorithm (MRRA) proposed by (Shanmugam) made an attempt to reduce the number of iterations at each timeslot to achieve maximum matching. The throughput performance of MRRA is similar to iSLIP under Bernoulli traffic however under bursty and their self-similar traffic model, they offer high delay. Authors preferred to use speedup in the future to improve the throughput and delay performance. On real-time applications, Dynamic Round Robin Matching (DRRM) is a widely used scheduler among high-speed switches because of its high arbitration rate. It is an iterative scheduler which took only two phases for every queue matching. It is commonly preferred because it is simple to implement, offer high efficiency and fairness. However, its throughput under heavy load is less than 50% which limits the scheduler usage in compute-intensive applications [14].
To further reduce the scheduling overhead and complexity, few schemes are proposed with single iterations. Synchronous Round Robin (SRR) is the first of its kind, a distributed scheduler for Input Queued switches [15]. It is a single bit single request algorithm which means only one request will be sent by an input during the request phase. Either global RR or longest queue strategy will be used to generate the 1-request. SRR performance under non-uniform traffic is average, hence not suited for high-speed networks. In [16], the author proposed three algorithms to support multiple server architecture. They are designed in such a way they can switch more than one fixed-sized cell in a timeslot. However, the hardware implementation and complexity seems to be stumbling block for practical. π-RGA is another single iteration algorithm that uses multiple bits during the request phase. The multi-bit is used to convey the history of information about the VOQ and is used while making scheduling decisions. It provides better performance under bursty traffic, however for other traffic, the performance is poor and its implementation is very difficult for high-speed networks.
Another interesting single bit algorithm is the Round Robin with Longest Queue First (RR.LQF) [17]. It uses a global RR scheduler and LQF scheduler to switch the cell from the longest queue. At every slot, a single bit is sent to the output indicating whether the VOQ receives a new cell or not. A counter is required at the output port to record the bit information however it increases the implementation as well as maintenance complexity. Some class of algorithms made an approach to introduce bonus schemes in order to improve the priority of waiting packets [18,19], thereby they avoided starvation and achieves better throughput delay performance. However, the scheme is most suited to buffered crossbar switches rather than IQ switch.
As of now, most of the algorithm adopts a queue-based approach for scheduling the packets. But Highest Ranking First (HRF) uses a rank-based approach instead of using queue details for scheduling. It is one of the most successful single bit algorithm proposed by [20]. In the basic model, every VOQ of the respective input is ranked based on the length of the queue. The rank is sent to the output during the request phase. The queue holding the highest rank will be granted permission by the output. On the accept phase, input accepts the received grant. If input receives more than one grant, the length of the queue will be considered to select a grant. In the next model, the RR scheduler is used to avoid packet delay, especially when working with a heavy load. These classes of the algorithm can offer better performance however the implementation complexity is relatively high. So in the third model, a three rank approach is used to rank all the VOQ. They made an attempt to reduce the complexity however it still looks very complicated for practical implementation in high-speed networks. HRF throughput-delay-performance under non-uniform traffic or hotspot traffic is not good. Moreover, their ranking procedure still based on queue length, and in most cases (under non-uniform traffic), it hugely suffers from packet delay which may lead to starvation.
For example, consider a 4
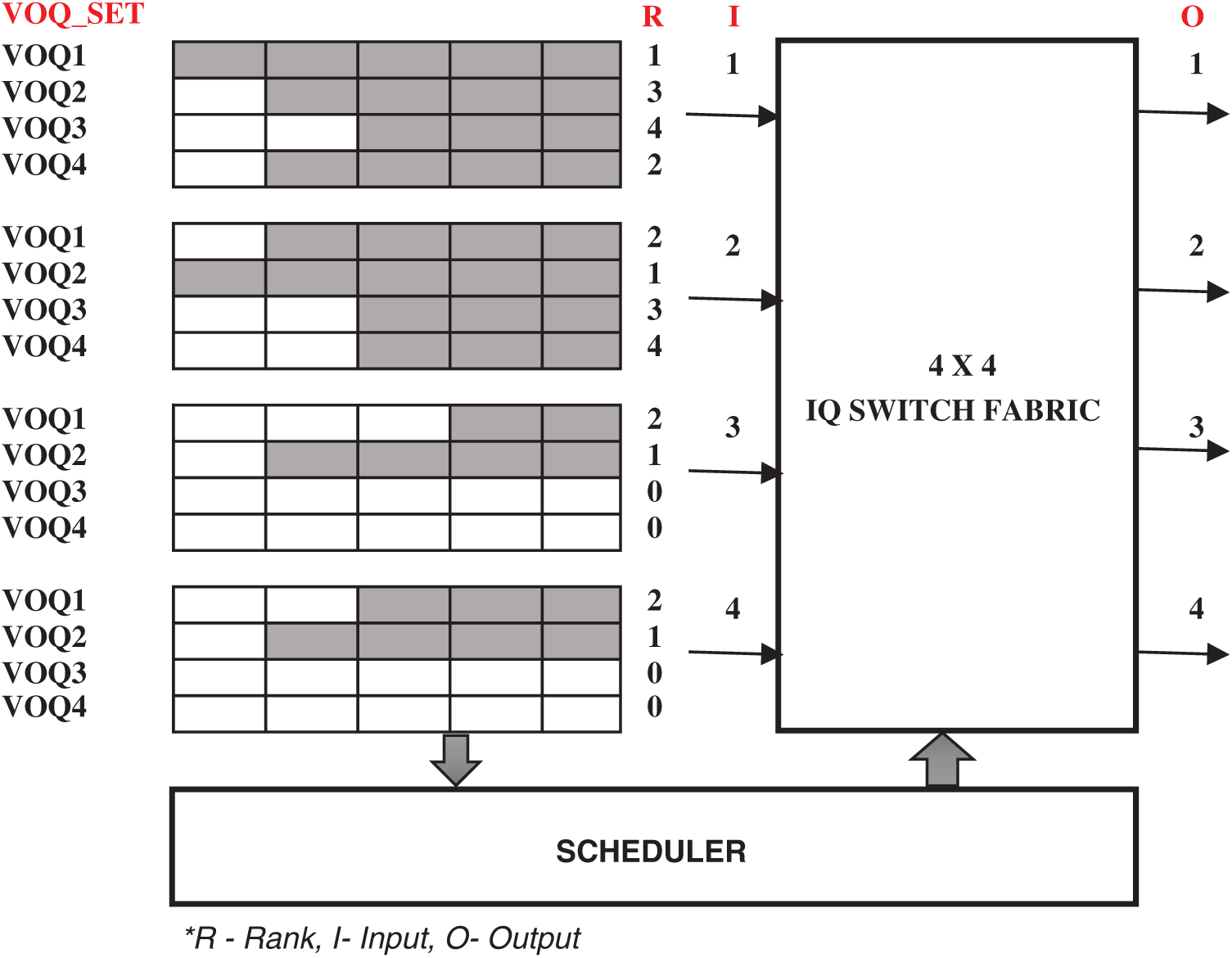
Figure 2: A VOQ based input queued switch with ranking procedure
We consider an N
3.1 A Simple 2-Bit (S2B) Approach
As HRF failed to consider the empty VOQ, switch suffers from latency issues. We proposed a Simple Two Bit scheduling approach for IQ switches. This simple scheme considers empty VOQ as a vital factor for the ranking process. Like other iterative algorithms, this scheme works in three phases. During the request phase, VOQ in each input sends two bits (R, P) to output. R is the rank of the VOQ_Set, which is a binary value, states whether the respective VOQ_Set has empty VOQ or not (say 0 or 1, 0-non-empty and 1-empty queue) and P is an integer which specifies the number of packets in the Queue. In the grant phase, R-bit is compared to ensure the input with empty queues got the preference. That is, input-R bit with value 1 will be given preference for the grant, in case, if R-bit is the same for more than one input, then P value will be considered i.e., input with maximum P value will be granted. If still not able to grant, the RR scheme will be used to grant an input. During the accept phase, input accepts the grant and gets ready for switching. If an input receives more than one grant from the output, it accepts the grant which has a larger P-bit value.
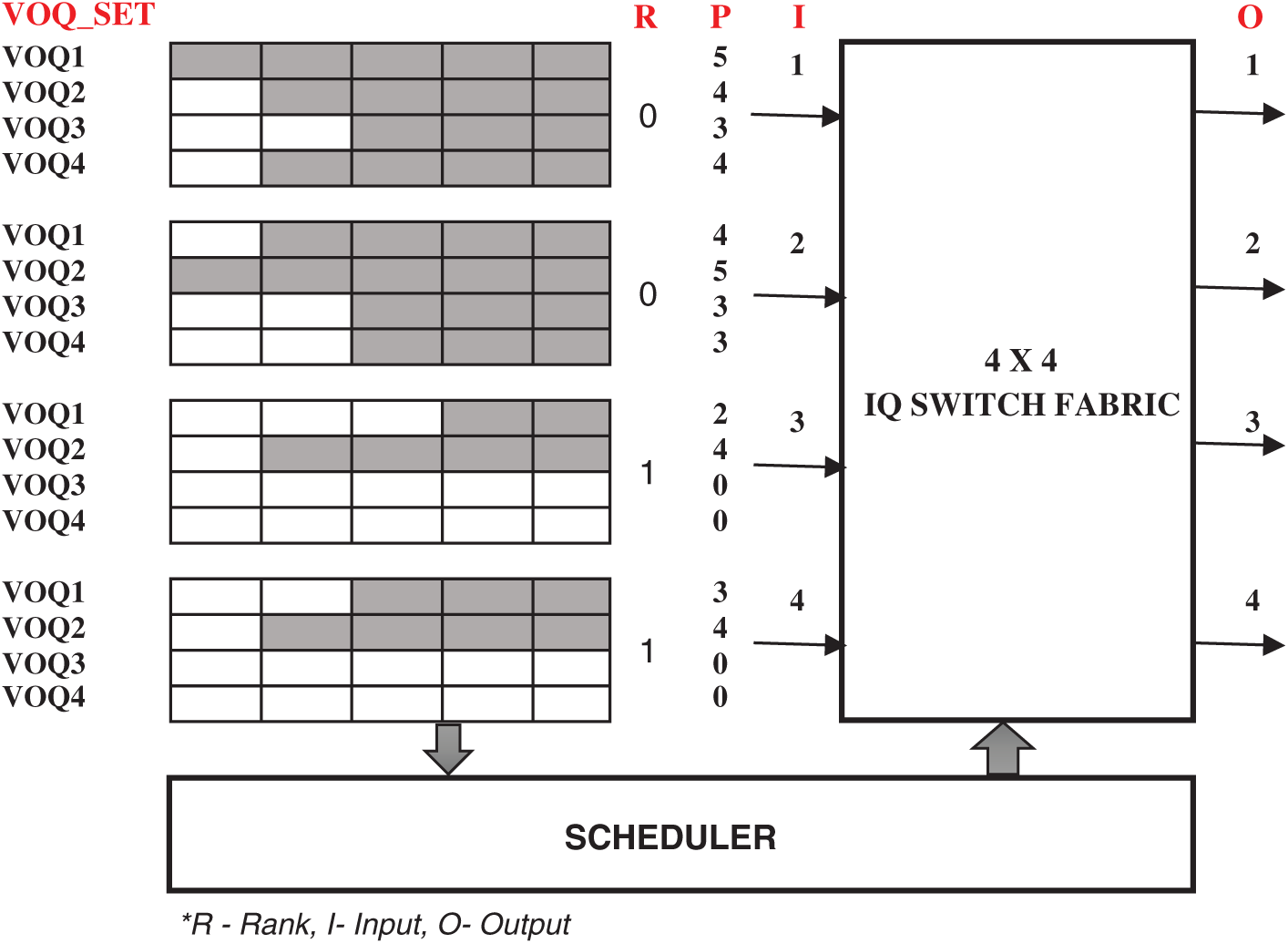
Figure 3: A simple 2-bit arbitration scheme
For example, consider the 4
Algorithm

3.2 Enhanced 2-Bit (E2B) Approach
A simple 2-bit approach can improve the latency performance compared to the HRF algorithm. S2B uses ranking procedures as well as queue lengths to make scheduling decisions. Ranks used are binary values which imply whether a VOQ_Set has empty queues or not. The ranking procedure can be further enhanced by considering the number of empty queues in the VOQ_SET by using an integer representation instead of binary. The rank defined by this integer indicates the number of empty queues in the VOQ_SET. Consider Fig. 4, VOQ1 of input 1 send value pairs (1, 5) to output in the request phase. Here, VOQ1 rank is 1 and length is 5. Similarly, VOQ1 of inputs 2–4 send the value pairs [(1,4), (2,4), (3,3)] respectively to output1. In the grant phase, the rank of the VOQ (R-bit) is compared, input having the highest rank will be preferred. If more than one VOQ holds a similar rank then P-bit is compared and the input having a larger P-bit value will be granted.
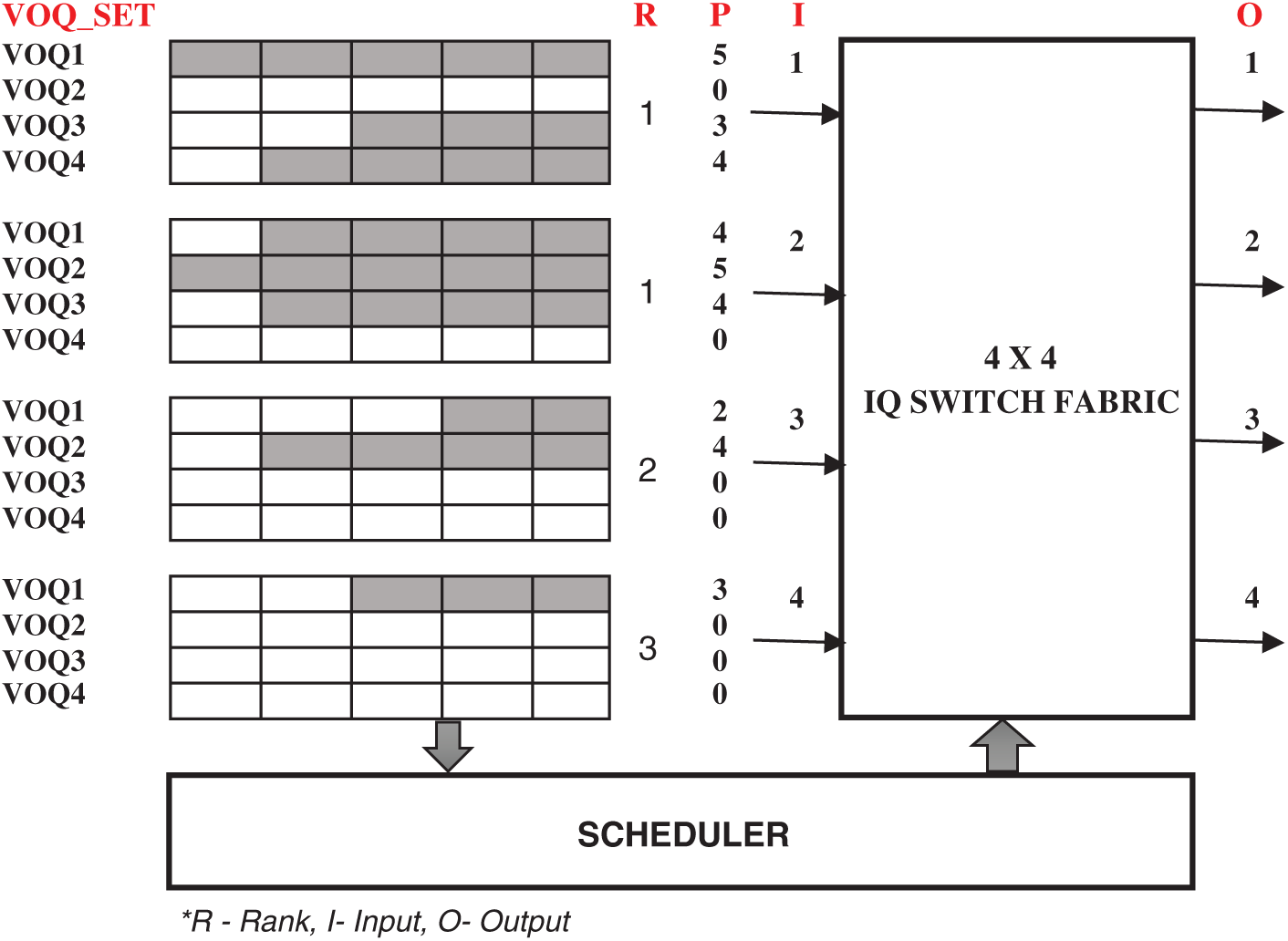
Figure 4: Enhanced 2-bit arbitration scheme
In our example, output1 grant input 4 (I4 −> O1) and is accepted in the last phase. However, if an input receives more than one grant, input checks for larger P-bit and accepts the respective output. In our example, already output 1 is granted for input 4, output 2 grants the input 3, output 3 grants Input 2 and output 4 grants input 1. For the given example, the maximum matching [(I1 −> O4), (I2 −> O3), (I3 −> O2), (I4 −> 01)] is achieved with a single iteration of a timeslot. However, in some cases maximum matching is possible with two iterations. The time complexity of E2B is O(N). The proposed arbitration schemes are better suited to IQ switches than the existing schemes because of the following:
• Probability to achieve maximum matching is very high because it prioritizes the VOQ_Set with maximum empty queues for scheduling
• Matching is possible in the first iteration itself (most of the cases) of a timeslot, hence reduces the overhead issue
• It is designed in such a way to achieve maximum throughput performance under non-uniform traffic where other algorithms failed.
• Most suited to real time high-performance applications.
Algorithm

A simulation environment is developed to measure the throughput and delay performance of S2B and E2B scheduling schemes. Both the algorithms executed with a load 10,000 fixed-sized packets under various traffic patterns and their performances are noted. The performance of S2B and E2B are compared with the HRF scheme with respect to throughput and delay metrics. Throughout our simulation, a 4
At first, we investigate the throughput performance of HRF, S2B, and E2B scheduling schemes under uniform traffic distribution. The throughput is analysed under various load strengths (ranging from 10% to 100%) and the result is depicted in Fig. 5. At 40% of the load, HRF managed to deliver 85% of throughput, however, it drops below 80% when maximum load is offered. The effect of prioritizing the empty VOQ during the scheduling process provides a considerable impact on S2B throughput performance, which manages a 5% improvement than HRF at all load levels.
Further enhancement in S2B leads to E2B which achieves a maximum throughput of 100% for all the load levels. E2B is also tested with various uniform workloads and it achieves 100% in all the cases. This is achieved because it provides 100% matching in most of the switching cases with one or more iterations in a slot. Fig. 6 shows the throughput performance of HRF, S2B, and E2B under non-uniform traffic. Until 40% of the load, HRF and S2B provide similar performance, however, when the load increases, the difference in throughput reaches at a maximum of 10%. This is the point where most of the schedulers struggle to deliver an acceptable throughput when the load get increases (>50%) under non-uniform traffic. However, it is understood that the decrease in throughput performance is due to minimal matching at each slot. If the amount of matching can be improved then the overall performance will increase. E2B is designed in such a way to increase the number of matchings at each slot. Fig. 6 also shows the throughput performance of E2B which is approximately 95% when maximum load is offered. E2B is simulated with various non-uniform load structures (up to 100,000 packets) and in all the cases its throughput performance is not less than 94% however for few load structures it achieves 100% throughput too. To our knowledge, this is the first IQ scheduler which can attain 100% throughput under certain non-uniform load patterns.
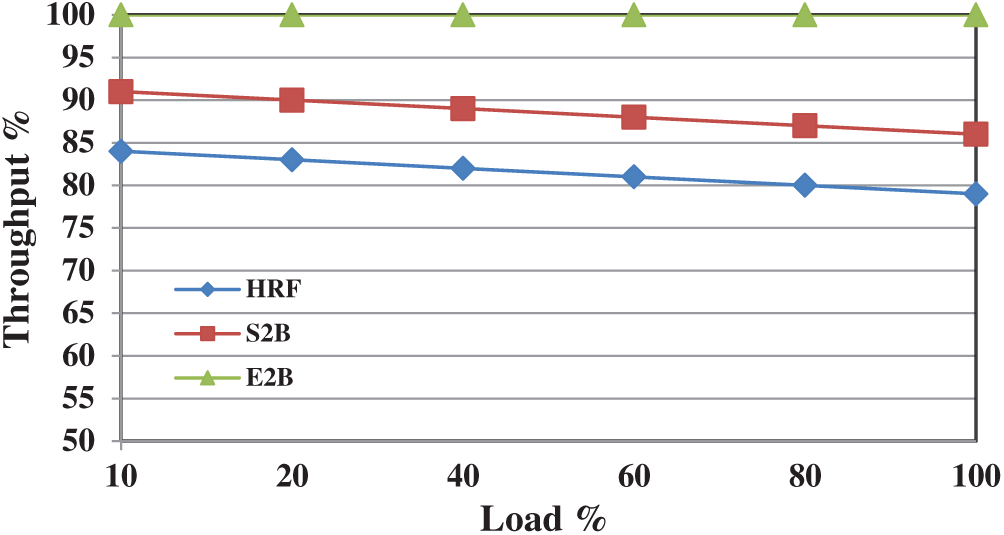
Figure 5: Throughput performance of HRF, S2B and E2B under uniform traffic
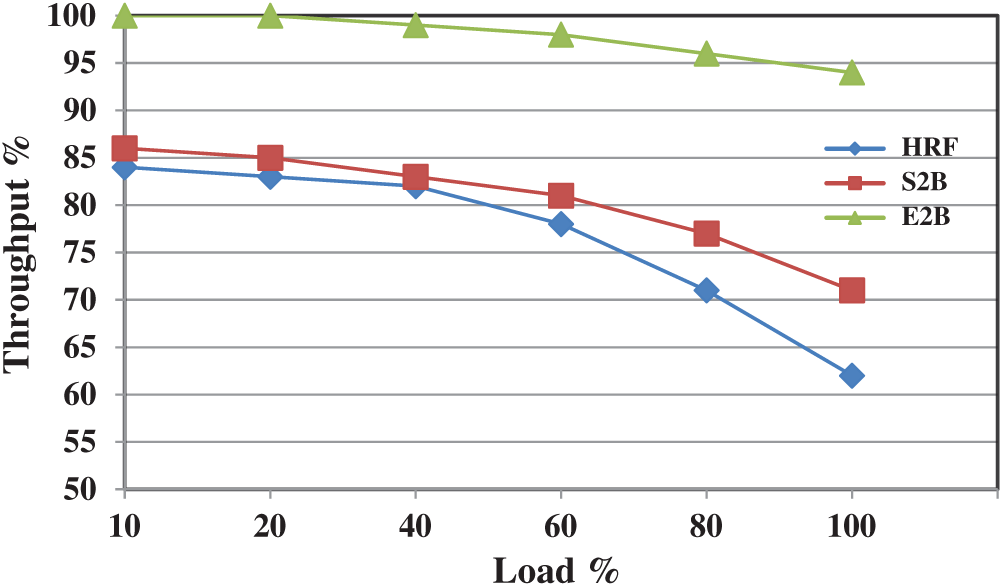
Figure 6: Throughput performance of HRF, S2B, and E2B under non-uniform traffic
In a switch fabric, a packet can arrive and depart within the same slot in the best possible case for delay analysis. However, it is not possible for all the packets in real-time scenarios. Delay measure is defined as the total number of timeslots spent by a packet in the switch or, it is the difference between the output port times to the input port time of a packet. Fig. 7 shows the delay performance of HRF, S2B, and E2B scheduling schemes under uniform traffic. All three schemes provide similar delay performance under any workload. This is because all these schemes adopted ranking based approaches and hence they attain similar performances. Moreover, there is no much difference to separate these schemes under non-uniform traffic too, and is depicted in Fig. 8. Therefore it is understood the change of approach in the ranking process by S2B and E2B has no delay improvement over HRF.
In the real world high-performance computing environment, the study shows there are numerous situations where traffic is targeted at a specific destination. In an interconnection network, numerous application faces hotspot traffic, for example, multiple clients access a server is one such scenario that will generate a lot of traffic in and around the ports. For summer vacation, a number of students from a particular lab is attempting to reserve an airline ticket at a discounted price at a specific period of time is a perfect scenario for hotspot traffic. When n number of inputs targeting a single output port at a given period of time, then the traffic occurred in the crossbar interconnection is said to be hotspot traffic. From the study, we understood that most of the scheduling schemes are not simulated with hotspot traffic however we analysed the throughput and delay performance of HRF, S2B, and E2B algorithms. For our simulation, uniform traffic is generated with a hotspot fraction f = 0.8 and their throughput performance is depicted in Fig. 9.
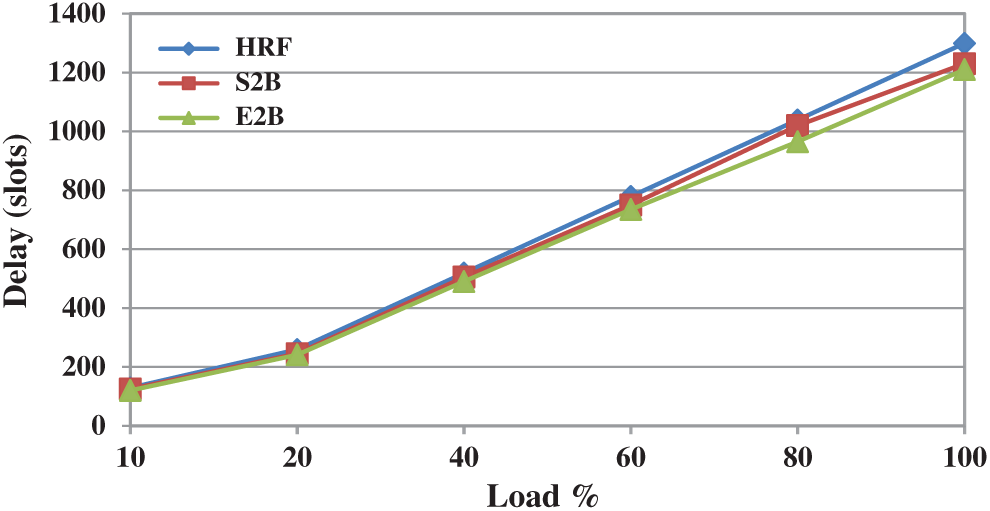
Figure 7: Delay performance of HRF, S2B and E2B under uniform traffic
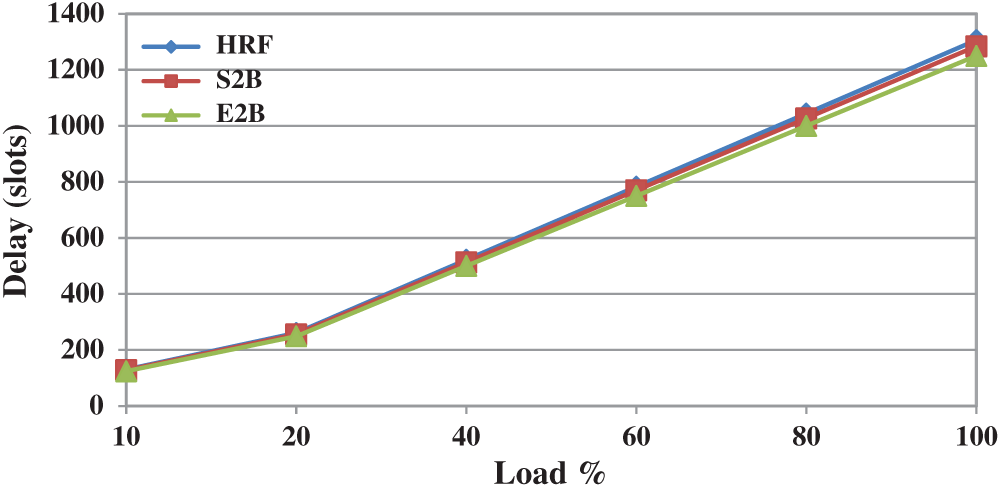
Figure 8: Delay performance of HRF, S2B and E2B under non-uniform traffic
The distribution of load has less impact on the overall throughput performance of S2B and HRF schemes. With maximum load, the throughput performance of HRF is 70% and S2Bc is 65% however the method of prioritizing the queue with empty slots for switching gives significant improvement. Therefore E2B achieves 95% throughput when maximum load is offered. We conducted numerous simulations by changing the load structures and hotspot fraction however the minimum achieved throughput at any scenario is 95%. To our knowledge, this is the maximum achieved throughput by any IQ scheduler under hotspot traffic. Fig. 10 shows the delay performance of HRF, S2B, and E2B under hotspot traffic. Up to 50% of the load, all three algorithms have similar delay however E2B performs better when the load exceeds. At maximum load, E2B is comparatively better than S2B and HRF by a minimum of 5%.
In summary, E2B outperforms HRF and S2B with maximum throughput under uniform, non-uniform and hotspot traffic. E2B delay performance under uniform and non-uniform is almost similar to S2B and HRF however under hotspot traffic it offers better delay.
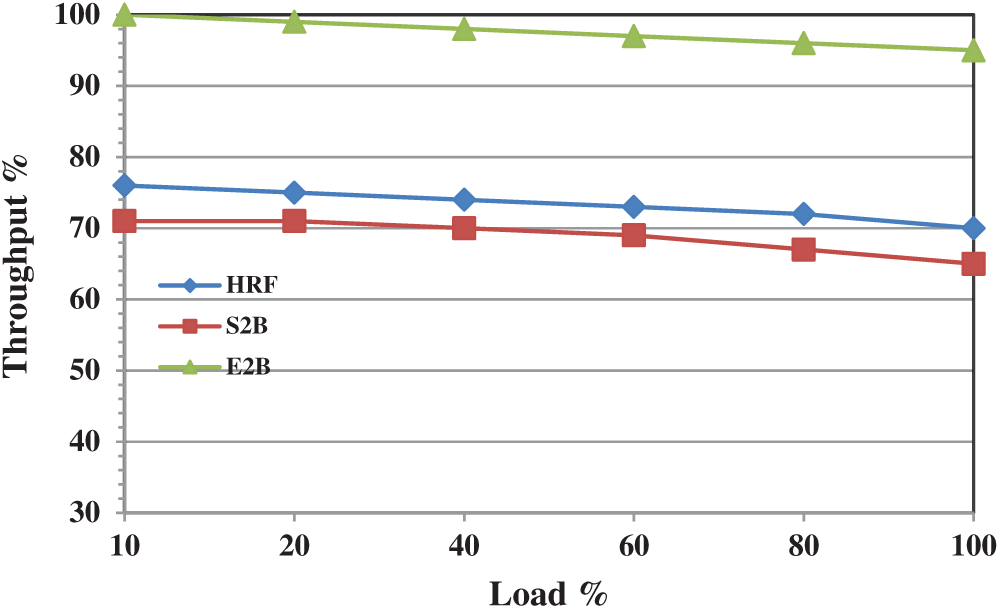
Figure 9: Throughput performance of HRF, S2B and E2B under hotspot traffic
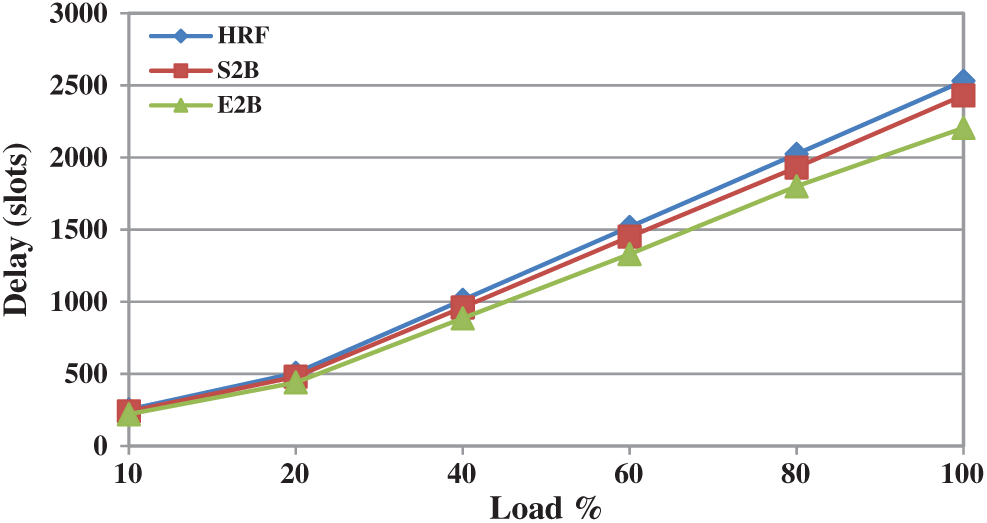
Figure 10: Delay performance of HRF, S2B and E2B under hotspot traffic
In this paper, we first proposed a simple 2-bit scheduling algorithm for input queued switches. It uses a simple ranking procedure and VOQ length for scheduling the packets. The simulation result shows S2B offers better throughput performance for all the tested traffic patterns. To further improve the performance, an extended 2-bit scheme is proposed and simulated under various traffic patterns. We showed that E2B throughput-delay performance is far better than S2B and HRF under heavy loads and hence it is most suited for high-performance computing environments. As a future work, scheduling schemes can be designed in a non-iterative fashion to reduce the overhead involved.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Xiao, K. L. Yeumg and S. Jamin, “CLF: An online coflow–aware packet scheduling algorithm,” in Proc. of the IEEE 43rd Conf. on Local Computer Networks, Chicago, USA, pp. 648–656, 2018. [Google Scholar]
2. F. Hassen and L. A. Mhamdi, “Scalable packet-switch based on output-queued NoCs for data centre networks,” in Proc. of the IEEE Int. Conf. on Communications, Kuala Lumpur, Malaysia, pp. 1–6, 2016. [Google Scholar]
3. D. Qian, “High performance computing: A brief review and prospects,” National Science Review, vol. 3, no. 16, pp. 16, 2016. [Google Scholar]
4. Cisco Nexus 5000 Series Architecture, The building blocks of the unified fabric. in: White Paper. San Jose, California: Cisco, 2009. [Online]. Available: https://www.dell.com/downloads/global/products/pwcnt/en/cisco_nexus_architecture.pdf. [Google Scholar]
5. N. Prasanth and K. Balasubramanian, “Performance analysis of buffered crossbar switch scheduling algorithms,” International Journal of Information and Computer Security, vol. 7, no. 1, pp. 49–63, 2015. [Google Scholar]
6. S. Chen and C. T. Lea, “Constraint-based scheduling algorithm with the non-adjacency requirement for multi-flow AWG switches,” Journal of Network and Computer Applications, vol. 124, no. 15, pp. 158–168, 2018. [Google Scholar]
7. N. McKeown and E. T. Anderson, “A quantitative comparison of iterative scheduling algorithm for input-queued switches,” Computer Networks and ISDN Systems, vol. 3, no. 4, pp. 2309–2326, 1998. [Google Scholar]
8. L. Gong, P. Tune, L. Liu, S. Yang and J. J. Xu, “Queue-proportional sampling: A better approach to crossbar scheduling for input-queued switches,” in Proc. of the ACM on Measurement and Analysis of Computing, Systems, IL, USA, pp. 4–36, 2017. [Google Scholar]
9. C. G. Emilio and J. R. Hoffman, “GENIUS---A genetic scheduling for high performance switches,” International Journal of Electronics and Communications, vol. 69, no. 3, pp. 629–635, 2014. [Google Scholar]
10. B. Hu, K. L. Yeung and Z. Zhang, “An efficient single-iteration single-bit request scheduling algorithm for input-queued switches,” Journal of Network and Computer Applications, vol. 36, no. 1, pp. 187–194, 2013. [Google Scholar]
11. N. McKeown, “The iSlip scheduling algorithm for input-queued switches,” IEEE/ACM Transaction on Networks, vol. 7, no. 2, pp. 188–200, 1999. [Google Scholar]
12. L. Gong, L. Liu, S. Yang, J. Xu, Y. Xie et al., “Serenade: A parallel randomized algorithm suite for crossbar scheduling in input-queued switches,” CoRR, pp. 1–16, 2017. [Online]. Available: https://arxiv.org/abs/1710.07234. [Google Scholar]
13. T. E. Anderson, S. S. Owicki, J. B. Saxe and C. P. Thacker, “High speed switch scheduling for local area networks,” ACM Transactions on Computer Systems, vol. 11, no. 4, pp. 319–352, 1993. [Google Scholar]
14. H. J. Chao and B. Liu, High Performance Switches and Routers. NJ, USA: John Wiley & Sons Inc, 2007. [Online]. Available: https://onlinelibrary.wiley.com/doi/book/10.1002/0470113952. [Google Scholar]
15. A. Scicchitano, A. Bianco, P. Giaccone, E. Leonardi and E. Schiattarella, “Distributed scheduling in input queued switches,” in Proc. of IEEE Int. Conf. on Communications, Glasgow, UK, pp. 6330–6335, 2007. [Google Scholar]
16. G. Damm, J. Blanton, D. Golla, D. Verchere and M. Yang, Fast Scheduler Solutions to the Problem of Priorities for Polarized Data Traffic. Texas, USA: Research and Innovation Department, Alcatel, 2001. [Google Scholar]
17. B. Hu, F. Fan, K. L. Yeung and S. Jamin, “Highest rank first: A new class of single iteration scheduling algorithms for input-queued switches,” IEEE Access, vol. 8, pp. 11046–11062, 2018. [Google Scholar]
18. N. Prasanth, K. Balasubramanian and R. Chithra, “Starvation free scheduler for buffered crossbar switches,” International Journal of Engineering, vol. 28, no. 4, pp. 523–528, 2015. [Google Scholar]
19. N. Prasanth, B. Kannan and C. Devi, “Prioritized queue with round-robin scheduler for buffered crossbar switches,” ICTACT Journal on Communication Technology, vol. 5, no. 1, pp. 890–893, 2014. [Google Scholar]
20. B. Hu, K. L. Yeung, Q. Zhou and C. He, “On iterative scheduling for input-queued switches with a speedup of 2–1/N,” IEEE/ACM Transactions on Networking, vol. 24, no. 6, pp. 3565–3577, 2016. [Google Scholar]
21. M. Jamali and A. Ghiasian, “Randomized scheduling algorithm for virtual output queuing switch at the presence of non-uniform traffic,” IET Networks, vol. 8, no. 2, pp. 138–142, 2019. [Google Scholar]
22. D. Banovic and I. Radusinovic, “Scheduling algorithm for VOQ Switches,” International Journal of Electronics and Communications (AEÜ), vol. 62, no. 6, pp. 455–458, 2008. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |