DOI:10.32604/cmc.2022.019455

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019455 |  |
| Article |
Amino Acid Encryption Method Using Genetic Algorithm for Key Generation
1Department of Information System, Faculty of Computers and Information, Menofia University, Egypt
2Department of Machine learning and Information Retrieval, Faculty of Artificial Intelligence, Kafrelsheikh University, Egypt
3Department of Computer Science, Faculty of Computers and Information, Kafrelshiekh University, Egypt
4Hurghada Faculty of Computers and Artificial Intelligence, South Valley University, Egypt
*Corresponding Author: Mohammed Zidan. Email: comsi2014@gmail.com
Received: 13 April 2021; Accepted: 14 May 2021
Abstract: In this new information era, the transfer of data and information has become a very important matter. Transferred data must be kept secured from unauthorized persons using cryptography. The science of cryptography depends not only on complex mathematical models but also on encryption keys. Amino acid encryption is a promising model for data security. In this paper, we propose an amino acid encryption model with two encryption keys. The first key is generated randomly using the genetic algorithm. The second key is called the protein key which is generated from converting DNA to a protein message. Then, the protein message and the first key are used in the modified Playfair matrix to generate the cypher message. The experimental results show that the proposed model survives against known attacks such as the Brute-force attack and the Ciphertext-only attack. In addition, the proposed model has been tested over different types of characters including white spaces and special characters, as all the data is encoded to 8-bit binary. The performance of the proposed model is compared with other models using encryption time and decryption time. The model also balances all three principles in the CIA triad.
Keywords: Cryptography; amino acid; genetic algorithm; playfair; deep learning; DNA computing
Internet and wireless networks offer ubiquitous channels to deliver and exchange data. Some models, such as cryptography, are used to improve the security of data transfer. Cryptography keeps data secure by ensuring that it is not understandable to unauthorized persons. There are two types of encryption: symmetric and asymmetric.
In cryptography, messages are scrambled and become gibberish to help ensure their secrecy. Once a message is encrypted, everyone can see that there is a message, but it cannot be understood or read by anyone who does not have the decryption key. As a result, decryption keys must be very difficult to access and use, so that only the intended recipients can read encrypted messages [1–3].
One potential model for key generation is the use of Genetic Algorithms (GA) [4]. Genetic Algorithms are based on Darwin’s theory of natural selection and “survival of the fittest.” Genetic Algorithms are used to search among many solutions and find the optimal one. This model depends on randomly selecting several solutions and calculating how good each solution is. Each solution is represented by a chromosome. To calculate each solution’s degree and rank, a fitness function is used. A generation consists of a number of chromosomes. After calculating the fitness function for each suggested solution (chromosome) a generation is finished. A portion of the chromosomes is selected to be part of the next generation. New chromosomes are generated by applying crossover and mutation functions. (The best chromosomes generate the best results.) After that, the old selected chromosomes and the newly generated ones are combined to construct the new generation. These iterations continue until a pre-defined threshold is reached. In the end, the best solution is selected for the minimization or maximization function. The solution consists of the best chromosome that achieves the best results for the objective function {[5–7]}. The encryption system then uses machine learning and DNA-based encryption to improve security. DNA-based encryption is an emerging approach for information security because of its capabilities.
In biology, DNA is the master molecule whose structure encodes all the information needed to create and direct the chemical machinery of life. In 1953, the structure of DNA was correctly predicted by Watson and Crick. They predicted that DNA molecules consist of two long polynucleotide chains. Each of these chains is known as a DNA chain, or a DNA strand, which is made up of simple subunits, called nucleotides. Each nucleotide consists of a sugar-phosphate molecule with a nitrogen-containing side group, or base. The bases are of four types—adenine, guanine, cytosine, and thymine—corresponding to four distinct nucleotides, labeled A, G, C, and T [8–14].
In the proposed model, Genetic Algorithms are used to generate a random key for encryption and decryption. The generated key is used to encrypt data using DNA encryption.
The rest of this paper is organized as follows: first we discuss a review of related work, next we explain the proposed model, then we report the simulation results and performance analysis, and finally we discuss the conclusions and future work.
In [15] the authors significantly modify the old Playfair cipher by introducing a DNA-based and amino acid structure. In their work a plain message is converted to a sequence of DNA. They propose assigning each letter of the alphabet a corresponding codon, so that the English alphabet’s form of amino acids can go through the traditional Playfair cipher process using the secret key.
In [16], the authors propose a novel algorithm that is composed of encryption and steganography using (DNA) sequences. Their model consists of two phases. In the first phase, the plain data is encrypted using a DNA-and amino acids-based Playfair cipher. In the second phase, the encrypted data is inserted into a DNA sequence. Their algorithm works on any binary data as it is transformed into DNA nucleotides. Then, these DNA nucleotides are converted to the amino acids structure so that they can go through the specially designed Playfair cipher and be encrypted into another DNA sequence. Then, this encrypted DNA data is randomly inserted into a reference DNA sequence to produce a faked DNA sequence whose encrypted data is hidden.
In [17] a model and implementation for key generation using the genetic algorithm with the Needleman–Wunsch (NW) algorithm is proposed. The authors introduce a model for implementing encryption and decryption based on DNA computing using the biological operations Transcription, Translation, DNA Sequencing, and Deep Learning. They evaluate the time taken for encryption and decryption based on the size of the message.
In [18] a Bio-Inspired Cryptosystem for encrypting data is proposed. The authors propose a system based on the Central Dogma of Molecular Biology (CDMB) for encryption and decryption. They used a Bidirectional Associative Memory Neural Network (BAMNN) for key generation. Their cryptosystem shows competent encryption and decryption times even on large data sizes when compared with other systems.
The proposed encryption model contains three phases: the first phase is key generation in which genetic algorithm is used to generate a random key for encryption and decryption. In the second phase the message data is converted to amino acid throw mutable operation. in the third phase the key generated from genetic algorithm is used to encrypt amino acid data using play faire cypher. the three is discussed in detail as follows.
3.1 First Phase: Key Generation
Genetic algorithms will be used to generate a random key in the encryption process as follows:
3.1.1 Initial Population (Generation 0)
The genes of the chromosomes of the initial population will be filled using a random number function that returns (1 or 0). Each chromosome will contain 64 genes and the initial population will contain 100 chromosomes.
The key in the encryption process must be random to ensure a low guessing factor, so the Run Test of Randomness will be used as the fitness function in our algorithm.
The Run Test of Randomness is a statistical test that is used to calculate the randomness of data. This test is based on the run. Run is basically a sequence of two types of symbols, such as 0 or 1. The test statistic can be calculated by using an approximation of the normal distribution via the following formula as shown in Eq. (1).
where r is the number of runs, μ is the expected number of runs, and σ is the standard deviation of the number of runs. The values of μ and σ are computed as in Eqs. (2) and (3).
where

Figure 1: An example of how to calculate the value of randomness
The selection policy determines which individuals are to be kicked out and which are to be kept in the next generation to be mated and combined to create offspring. A selection policy based on the fitness function is applied to choose which individuals to use.
Crossover is used to combine the genetic information of two parents’ offspring to generate new offspring. The K-Point is used to determine the crossover. K-Point crossover uses more than one crossover point to produce two offspring chromosomes. Two parent chromosomes are selected and a number is generated at random because the number of crossover points is randomly selected. This is shown in Fig. 2.

Figure 2: Crossover selection
A mutation is a small random tweak in the chromosome, to get a new solution. Bit string mutations are used as mutation operators. Bit string mutation works by selecting one or more random bits and flipping them, see Fig. 3 below.

Figure 3: Mutation process
After choosing the best key using the fitness function, this key’s similarity to other keys from the last generation is calculated using the Needleman-Wunsch (NW) Algorithm.
3.1.7 Needleman-Wunsch (NW) Algorithm
The Needleman-Wunsch (NW) Algorithm is a dynamic programming application. It is used for arranging two or more sequences of characters to identify regions of similarity [17]. It uses a scoring system to calculate the degree of similarity or dissimilarity between the two sequences. The greater the score, the more similar the sequences. NW is used to calculate the similarity between the chosen key and other keys from the last generation. The less similar key is selected to be the encryption key. The key generation process is summarized in Fig. 4.
3.2 Second Phase: Data Preparation
The plain data is converted to 8-bit binary format, and then converted to a DNA Nitrogen Base sequence as shown in Tab. 1. Then the DNA Nitrogen Base sequence is converted to an RNA Nitrogen Base as shown in Tab. 2. The RNA Nitrogen Base is then converted to an amino acid according to RNA to Amino Acid table in [15], and then the Ambiguity number as Protein Key (PK) is extracted. The same model will be applied to the generated key.
3.3 Third Phase: Data Encryption Using Amino Acid Based Playfair
Playfair is a polyalphabetic cipher, in which diagrams in plaintext are treated as single units and these units are translated into cipher text diagrams. Playfair encrypts pairs of letters, rather than encrypting single letters as a simple substitution cipher would do. The traditional Playfair algorithm is based on a
In our model, the key generated from the genetic algorithm is used as a Playfair cipher key, and the alphabet is the modified amino acid alphabet. The data preparation phase and the encryption phase are summarized in Fig. 5. Also, a simple example of our proposed algorithm is shown in Fig. 6. The algorithm steps of the encryption process are shown as follows.
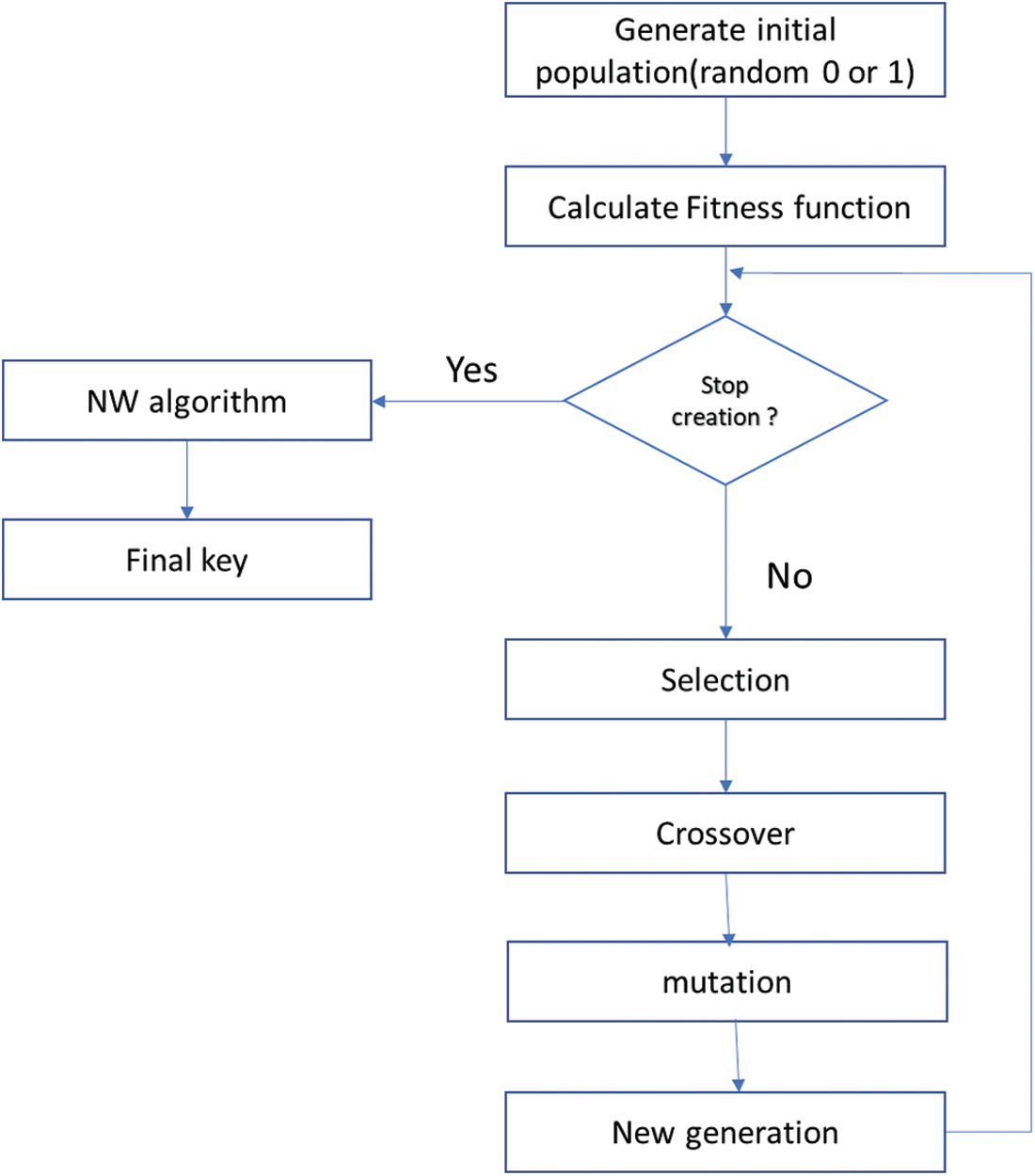
Figure 4: The key generation processes



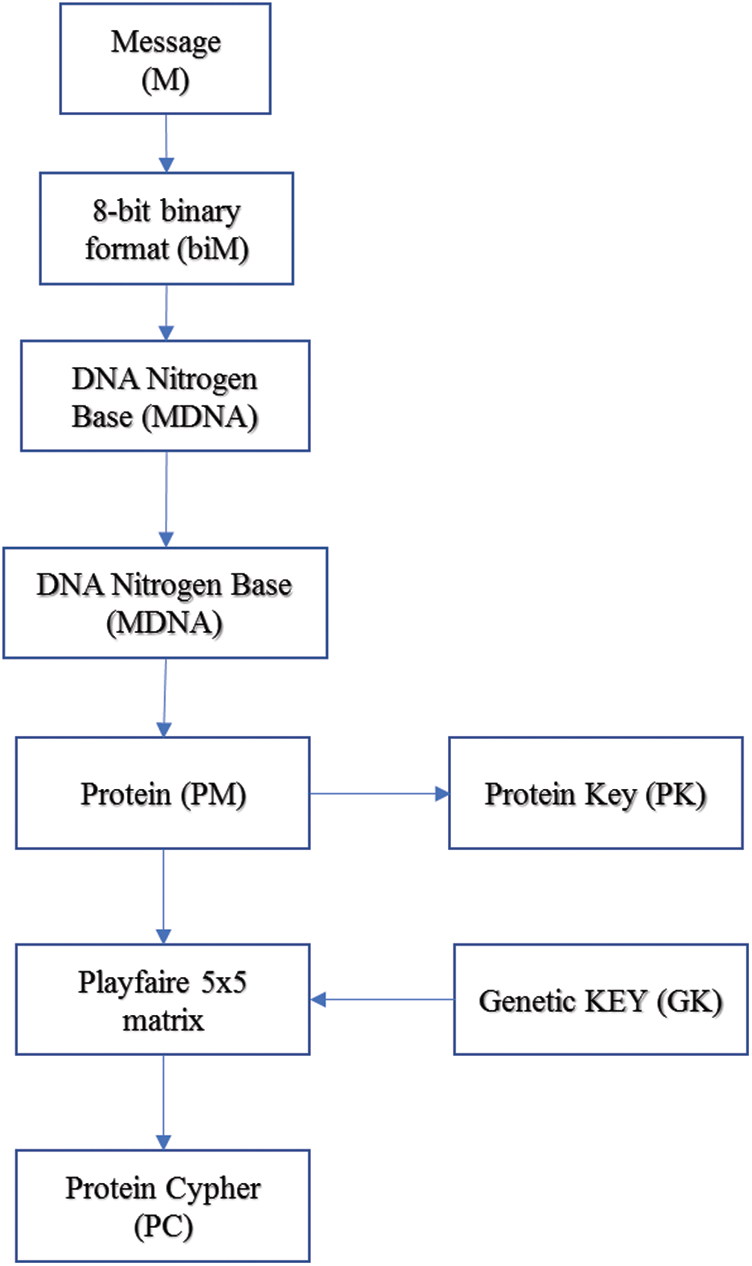
Figure 5: Encryption algorithm
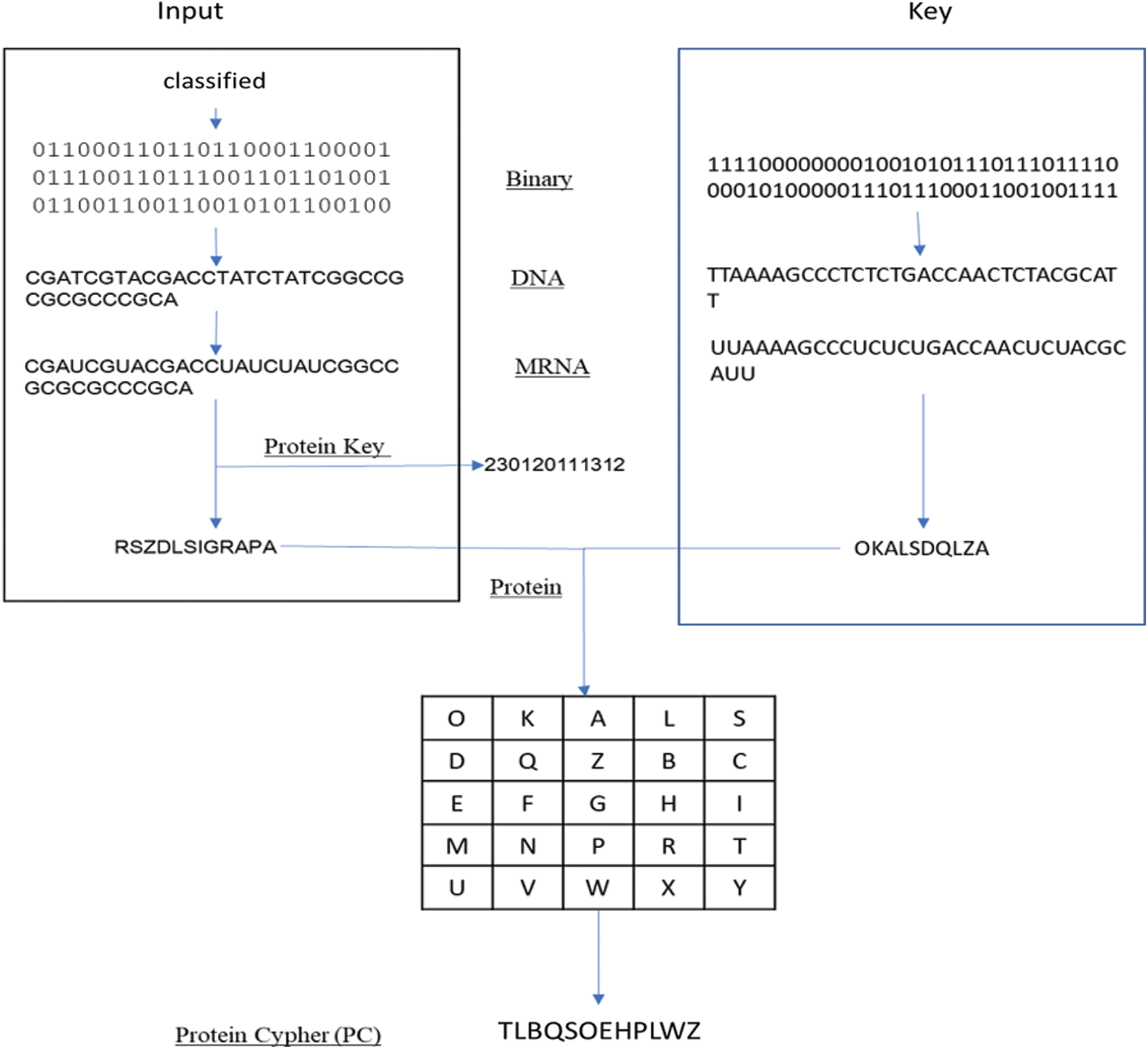
Figure 6: Simple example of proposed algorithm
4 Simulation and Performance Analysis
This section presents the experimental results of the proposed model. In addition, a comparison between the proposed model and Genetic Algorithm with NW model [17] is included in this section. All the models were implemented on a PC with a Pentium core i7 processor, 8 GB of RAM, and the Windows 10 operating system. Python was used to implement both the proposed models and the Kalsi et al. model.
The encryption time is the amount of time each model takes to generate cypher text after generating the key. Tab. 3 compares the encryption times (in milliseconds) of the proposed model and Genatic Algorithem with NW [17] model. The results show that our proposed model takes slightly more time than Genatic Algorithem with NW model, because in Genatic Algorithem (GA) with NW model the main operation is XOR but in our model the Playfair matrix takes more time to encrypt.

The decryption time is the amount of time each model takes to generate plain text from cypher text. Tab. 4 compares the decryption time (in milliseconds) of the proposed model and Genatic Algorithem with NW [17] model. The results show that our proposed model takes slightly more time than GA with NW model, because in GA with NW [17] model the main operation is XOR but in our model the Playfair matrix takes more time to encrypt.

Confusion means that each bit of ciphertext should depend on several bits of the key. In the proposed model, when a message is translated to protein, the process is one-to-many, because one protein can come from more than one RNA. Also, in the proposed model if we use the key and plaintext independently, the cipher text can’t be produced because it goes through several steps.
Diffusion means that if a change happens in one character of the plaintext, it changes several characters in the ciphertext. In the proposed model, when a character of the plaintext is changed it will affect the DNA value, which in turn will affect the protein value and the cipher text. Also, in the proposed model, the same plaintext will result in different cipher text each time because we use a different key each time.
In cryptography, the avalanche effect means that if a character in plaintext is changed slightly, the cipher text changes significantly. In the proposed model, when a character of the plaintext is changed slightly it will affect the DNA value, which in turn will give a different protein value and change the cipher text.
A brute force attack is an attempt to crack a password or username, find a hidden web page, or find the key used to encrypt a message, using a trial-and-error approach, and hoping, eventually, to guess correctly [19].
In a ciphertext-only attack, the attacker has access to some amount of ciphertext and has some information about the plaintext. This type of attack will succeed if the attacker can get either the plaintext or the key. In the proposed system this is impossible because of the randomness of the key generated by the genetic algorithm. Also, in this model, the plaintext goes through multiple steps to become ciphertext [20].
4.4.3 The Known-Plaintext Attack (KPA)
The known-plaintext attack is an attack model in which the attacker has access to both the plaintext and the ciphertext and attempts to get the key. In the proposed system the attacker can’t succeed because of the randomness of the key generated by the genetic algorithm. It gives a different key each time [21].
4.4.4 Differential cryptanalysis Attack
In a differential cryptanalysis attack, the attacker gets ciphertext from a set of chosen plaintext. In the proposed system this can’t happen because of the randomness of the key generated by the genetic algorithm. It gives a different key each time [22]. Tab. 5 outlines the implementation of the system proposed in relation to the multiple attacks with other systems.

Confidentiality
Confidentiality is keeping information away from unauthorized people. In the proposed system this is achieved as all transmitted entities and parameters are encrypted [25].
Integrity
Integrity is the ability to ensure that data is accurate and remains unchanged. In the proposed system this is achieved because if a change happens in the cipher text it will affect the protein value and the DNA value, and the plaintext won’t be able to be extracted [25].
Availability
It is important to ensure that the information concerned is always readily accessible to the authorized viewer. In the proposed system, this is achieved because it works with different plaintext size and types [25].
An amino acid cryptosystem has been proposed that uses genetic algorithms and amino acid cryptography for securing data. The goal of data encryption is to keep data away from unauthorized people. In our system, the input message is encoded to an 8-bit binary format and converted to an amino acid. A genetic algorithm is used to generate an encryption key and the Tun Test of Randomness is used as the fitness function. The MG algorithm is used to select the key that is the least similar to the others. The encoded message is used with Playfair using a generated key. The proposed model can survive over known attacks such as the Brute-force attack and the Ciphertext-only attack. The proposed model has been tested over different types of characters including white spaces and special characters as all the data is encoded to 8-bit binary. The performance of the proposed model is compared with other models on the basis of encryption time. The CIA principle is achieved by the proposed model. Also, using the amino acid ambiguity number gives us more security because even if the intruder knows the input of plaintext, he can’t know the real message without using the ambiguity number.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Broumandnia, “Image encryption algorithm based on the finite fields in chaotic maps,” Journal of Information Security and Applications, vol. 54, no. 4, pp. 1–22, 2020. [Google Scholar]
2. P. M. Lima, M. V. Alves, L. K. Caracvalhi and M. V. Moreira, “Security against network attacks in supervisory control systems,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 12333–12338, 2017. [Google Scholar]
3. B. Delman, “Genetic algorithms in cryptography,” Master thesis. Rochester Institute of Technology, New York, 2004. [Google Scholar]
4. K. Alla, Praneetha and V. Ramachandran, “A novel encryption using genetic algorithms and quantum computing with roulette wheel algorithm for secret key generation,” in ICT Analysis and Applications, Lecture Notes in Networks and Systems. vol. 93. Singapore: Springer, pp. 263–271, 2020. [Google Scholar]
5. S. Mirjalili, J. S. Dong, A. S. Sadiq and H. Faris, “Genetic algorithm: Theory, literature review, and application in image reconstruction,” in Nature-Inspired Optimizers, Studies in Computational Intelligence Springer. vol. 811. Switzerland: Springer Nature, pp. 69–85, 2020. [Google Scholar]
6. E. Rutkowski and H. Sheridan, “Cryptanalysis of RSA: Integer prime factorization using genetic algorithms,” in 2020 IEEE Congress on Evolutionary Computation, Glasgow, UK, 1–8, 2020. [Google Scholar]
7. A. Bajaj and O. P. Sangwan, “A systematic literature review of test case prioritization using genetic algorithms,” IEEE Access, vol. 7, pp. 126355–126375, 2019. [Google Scholar]
8. A. M. Sauber, M. M. Nasef, A. S. Sakr and K. Geba, “An efficient model to encrypt text and gray image based on amino acid chains,” The Egyptian Journal of Language Engineering, vol. 7, no. 2, pp. 20–31, 2020. [Google Scholar]
9. A. Reddy, M. Indrasena, A. P. Siva Kumar and K. Subba Reddy, “A secured cryptographic system based on DNA and a hybrid key generation approach,” Biosystems, vol. 197, pp. 1–10, 2020. [Google Scholar]
10. G. Z. Cui, Y. Liu and X. Zhang, “New direction of data storage: DNA molecular storage technology,” Computer Engineering and Applications, vol. 42, pp. 29–32, 2006. [Google Scholar]
11. J. Steinkoenig, R. Aksakal and F. D. Prez, “Molecular access to multi-dimensionally encoded information,” European Polymer Journal, vol. 120, pp. 1–7, 2019. [Google Scholar]
12. X. Chai, X. Fu, Z. Gan, Y. Lu and Y. Chen, “A color image cryptosystem based on dynamic DNA encryption and chaos,” Signal Processing, vol. 155, no. 9, pp. 44–62, 2019. [Google Scholar]
13. Y. Niu, K. Zhao, X. Zhang and G. Cui, “Review on DNA cryptography,” in Int. Conf. on Bio-Inspired Computing: Theories and Applications, Singapore, Springer, pp. 134–148, 2019. [Google Scholar]
14. Z. Wang, X. Ren, Z. Ji, W. Huang and T. Wu, “A novel bio-heuristic computing algorithm to solve the capacitated vehicle routing problem based on Adleman–Lipton model,” Biosystems, vol. 184, no. 1, pp. 1–9, 2019. [Google Scholar]
15. M. Sabry, M. Hashem, T. Nazmy and M. E. Khalifa, “A DNA and amino acids-based implementation of playfair cipher,” International Journal of Computer Science and Information Security, vol. 8, pp. 129–136, 2010. [Google Scholar]
16. A. Atito, A. Khalifa and S. Z. Rida, “DNA-based data encryption and hiding using playfair and insertion techniques,” Journal of Communications and Computer Engineering, vol. 2, no. 3, pp. 44–49, 2012. [Google Scholar]
17. S. Kalsi, H. Kaur and V. Chang, “DNA cryptography and deep learning using genetic algorithm with NW algorithm for key generation,” Journal of Medical Systems, vol. 42, no. 1, pp. 1–12, 2018. [Google Scholar]
18. S. Basu, M. Karuppiah, M. Nasipuri, A. K. Halder and N. Radhakrishnan, “Bio-inspired cryptosystem with DNA cryptography and neural networks,” Journal of Systems Architecture, vol. 94, no. 4–5, pp. 24–31, 2019. [Google Scholar]
19. F. Erlache and F. Dressler, “On high-speed flow-based intrusion detection using snort-compatible signatures,” IEEE Transactions on Dependable and Secure Computing, pp. 1–12, 2020. [Google Scholar]
20. K. Ramezanpour, P. Ampadu and W. Diehl, “A statistical fault analysis modelology for the ascon authenticated cipher,” in IEEE Int. Symp. on Hardware Oriented Security and Trust, McLean, VA, USA, pp. 41–50, 2019. [Google Scholar]
21. X. Chai, J. Bi, XLiu Z.Gan, Y. Zhang and Y. Chen, “Color image compression and encryption scheme based on compressive sensing and double random encryption strategy,” Signal Processing, vol. 176, pp. 107684, 2020. [Google Scholar]
22. A. Mansouri and X. Wang, “A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme,” Information Sciences, vol. 520, pp. 46–62, 2020. [Google Scholar]
23. R. Ramamurthy, C. Bauckhage, K. Buza and S. Wrobel, “Using echo state networks for cryptography,” in Int. Conf. on Artificial Neural Networks, Alghero, Sardinia, Italy, Springer, pp. 663–671, 2017. [Google Scholar]
24. U. N. Hussain, T. Chithralekha, A. N. Raj, G. Sathish and A. Dharani, “A hybrid DNA algorithm for DES using central dogma of molecular biology (CDMB),” International Journal of Computer Applications, vol. 42, no. 20, pp. 1–4, 2012. [Google Scholar]
25. J. Zheng, H. Okamura, T. Dohi and K. S. Trivedi, “Quantitative security evaluation of intrusion tolerant systems with markovian arrivals,” IEEE Transactions on Reliability, pp. 1–16, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |