Computers, Materials & Continua DOI:10.32604/cmc.2021.015434
Article

Multi-Attribute Selection Procedures Based on Regret and Rejoice for the Decision-Maker

Hanan Abdullah Mengash* and Manel Farouk Ayadi

Department of Information Systems, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
*Corresponding Author: Hanan Abdullah Mengash. Email: hamengash@pnu.edu.sa
Received: 20 November 2020; Accepted: 11 June 2021

Abstract: Feelings influence human beings’ decision-making; therefore, incorporation of feeling factors in decision-making is very important. Regret and rejoice are very important emotional feelings that can have a great impact on decision-making if they are considered together. While regret has received most of the attention in related research, rejoice has been less considered even though it can greatly influence people’s preferences in decision-making. Furthermore, systematically incorporating regret and rejoice in the multi-criteria decision-making (MCDM) modeling frameworks for decision-making has received little research attention. In this paper, we introduce a new multi-attribute selection procedure that incorporates both regret and rejoice to select the best choice. We utilize the positional advantage operator concept to develop regret and rejoice mathematical equations, and prove them. The proposed MCDM procedure that incorporates these two emotional factors offers a decision-maker the flexibility to trade off some benefits in order to gain a state of psychological satisfaction. More specifically, regret and rejoice are presented mathematically to enable the decision-maker to determine the values of regret and rejoice, and then make the decision in which the rejoice value is higher than the regret value. To test the performance of this new procedure, we apply it to three numerical examples proposed in previous works. The results are matched with those obtained by other methods such as the regret model, VIKOR, PROMETHEE I, and PROMETHEE II, thereby proving the efficacy of the new procedure.

Keywords: Multi-criteria decision-making; positional advantage operator; regret; rejoice

1  Introduction

For many years, decision-making methods and decision-support systems have been proposed to support decision-makers (DMs) in the use of effective decision-making processes. Multi-criteria decision-making (MCDM) methods are considered the most common decision-making methodologies in various fields, such as the science, business, and engineering. There are a vast number of MCDM methods, some of which are based on an underlying assumption that the mythical rational individual does not take into account the influence of aspects of behavior like feelings.

According to [1] the rational decision-making requires emotion and leads to the concept of emotional rationality. He mentioned that happiness and sadness are the feelings experienced most by human beings. In contrast, the author in [2] insisted that the feeling of happiness is the most frequently experienced feeling by people. Happiness has also received scie.pngic attention since the early days of psychology research.

With respect to post-choice feeling, a DM may feel regret when he makes the worst decision, and he may feel rejoicing when the chosen decision yields the more favorable alternative. The feelings of regret and rejoice are parts of the human feeling experience, their roles in complex decisions have been widely debated. Unfortunately, there are many unresolved issues such as the impact of these emotional factors have on the decision-making problems and how these factors can play an important role in evaluating decisions.

In literature, the incorporation of the feeling of regret in MCDM have been proposed in several research papers. However, the integration of regret and its counterpart, rejoice, tends to be an important consideration in decision-making [3]. Moreover, a decision that is solely derived from regret may be considered deficient and/or irrational.

Decisions can be changed because people’s rational preferences may change due to feelings of rejoice. In support of the importance of the DM’s rejoice in decision-making, the author in [4] proposed a hypothetical example that explains how rejoice could affect decisions. This example explains the decision process for buying a car, and how rejoice feeling can change the decision of customers based on two scenarios.

Scenario 1: The dealer offers two cars to the customer: car A, which is less expensive than car B and has acceptable quality, and car B, which is more expensive and has better quality than car A. In this case, the customer might choose to buy car A because it is less expensive than car B and has acceptable quality.

Scenario 2: The dealer offers three cars to the customer: car A, car B (both have the same values as in Scenario 1 for the cost and quality criteria), and car C (which has been publicized by the media, is the most expensive of the three cars, and has a little better quality than car B). Due to the introduction of this third car by the dealer, the customer may change his or her decision and choose to buy car B instead of car A, even though the criteria values for cars A and B remain the same as in Scenario 1. When the customer compares car B with car C, he or she feels very happy because he or she will get a great deal: a car with almost the same quality as and less cost than car C.

This example shows how the anticipated feeling of rejoice can unintentionally reverse the DM’s preference between cars A and B. The author in [4] called the third car a phantom alternative. In reality, the customer will never choose car C, but because of its existence, the customer changes his or her choice on the basis of his or her feeling of rejoice when he or she compares car A and car B with car C.

Although the feeling of rejoice is important in decision-making, it unfortunately does not receive the same attention from researchers as the feeling of regret. Therefore, models that incorporate the DM’s rejoice in MCDM need to be developed.

In this paper, we develop a new multi-attribute selection procedure based systematically on regret and rejoice by utilizing the positional advantage operator (PAO) [5]. This procedure will help the DM to choose the decision in which the rejoice value is higher than the regret value.

In Section 2, an overview of regret and rejoice is presented. In Section 3, regret and rejoice expressions are built with the PAO. The proposed methodology is discussed in Section 4. In Section 5, some illustrative examples are given to prove the efficacy of the proposed method. Finally, conclusions are presented in Section 6.

2  Overview of Regret and Rejoice in MCDM

The MCDM problem was introduced in 1951 by two research teams (Koopmans and Kuhn, and Tuker). This problem can be defined as the problem of finding the best alternative (or ranking all alternatives) while considering multiple conflicting criteria. Since the 1960s, MCDM research has experienced explosive growth and has been extensively studied in decision science [6].

In daily decision-making processes, very few decisions are made without a number of competing alternatives and criteria. A decision maker must choose an alternative by evaluating a number of criteria. As the number of alternatives and criteria increases, the task of selecting the best alternative becomes increasingly difficult. Many research papers have been published on this topic, using different methods to help a DM make the best possible decision. Such methods included the ELECTRE method, which aims to utilize “outranking relations” to rank a set of alternatives [6]. The analytic hierarchy process (AHP) method can help people set priorities and choose the best options by reducing complex decision problems to a system of hierarchies [7]. In the TOPSIS method, the best alternative is nearest to the positive-ideal solution and farthest from the negative-ideal solution [8]. Meanwhile, the VIKOR method was developed for multi-criteria optimization of complex systems [9].

According to [10], the incorporation of regret and rejoice feelings is crucial to decision-making, and it can be based on two key assumptions. The first assumption is that people may experience feelings of regret and rejoice that can influence the current decision-making. The second is that while making decisions people may try to anticipate the results of their decisions and take into account potential feelings of regret and rejoice.

Psychologists investigated the relationship between feelings and decision-making, and reached a consensus: the anticipation of regret can increase the attractiveness of certain alternatives [11]. The earliest regret model was introduced by [12] and is known as the mini-max (or Savage) model. This model is used for decision-making in situations of uncertainty, and its main goal is to ide.pngy the alternative that has the least-negative possible outcome in order to minimize regret. The Savage model defines regret as the difference between the best possible utility value among all alternatives for each state of nature and the actual utility value of each alternative. Thus, a DM who chooses an alternative Ai will express a level of regret Rik for the state of nature Sk equal to the difference between its best possible value and its actual value for Ai.

In the 1980s, there was a growing interest in the role of regret in decision-making. Indeed, in [13,14], the authors proposed two regret theories (together referred to as RT-B/LS) for rational decision-making in situations of uncertainty. They assumed that regret depends on the differences between the utilities of the chosen alternative and the considered–-but not chosen–-alternatives.

In 2005, the authors in [15] proposed the reference-dependent regret model (RDRM) for deterministic decision-making, which focuses on decision-making in situations of certainty. In this model, the level of an individual’s regret depends on the absolute values rather than the differences of the utilities of the chosen and forgone options. In [16], the authors revised the VIKOR method based on the concept of regret theory. In [10], the authors studied the feeling of regret to develop a new MCDM method for supplier selection problems. Lastly, in [17], the authors used two demonstrative examples to compare various VIKOR methods and assess the ranking performance of each variant.

None of the above models considered the feeling of rejoicing, which is considered as very important in the decision-making process; it can influenced DM’s decisions.

The first model that systematically incorporated the regret and rejoice feelings in MCDM was proposed in [4]. The author proposed a linguistic scale to measure regret and rejoice by building their matrices based on pairwise comparisons to determine the alternative value of regret and rejoice. He used the rule of (seven plus or minus two) to develop a set of nine linguistic choices that include four intermediate values in order to estimate the regret value for choosing an option and rejecting another under a specific criterion. This model was later used to develop pairwise regret matrices for each decision criterion. However, with the use of linguistic terms, the DM’s feelings cannot be perfectly accurate because the definitions of these feelings are limited by the scale specified to express them.

A model called a random regret minimization model (RRM) to analyze multi-attribute consumer choices from multi-nominal choice sets was used in marketing [18]. Meanwhile, the authors in [19] developed a grey stochastic MCDM approach based on regret theory and TOPSIS. They tried to construct perceived utility value functions of extended grey numbers (EGNs) based on both the utility value functions and the regret value functions.

The authors in [20] also used regret theory without considering rejoice. They proposed a model that considers various psychological behaviors and the ambiguity of linguistic variable assessment across multi-criteria risks. They improved the feedback adjustment mechanism using regret theory. In [21], the authors considered both regret and rejoice feelings and developed a new method to solve the risky multi-attribute decision-making (RMADM) problems. They assumed that the potential psychological behavior of a DM can influence decision-making, and they calculated regret and rejoice values with pairwise comparisons of options. An aggregating method has also been proposed to derive the ranking of products using the regret behavior of customers in the product-selection process [22]. This method calculated gain and loss degrees for each alternative product based on regret and rejoice values for each product. Moreover, researchers have used the concept of regret aversion to develop a new grey RMADM method based on the general grey numbers (GGNs) [23]. In this work, the authors first built a normalized grey decision-making matrix, and then integrated regret theory into the decision-making process by constructing a grey perceived utility function based on GGNs.

Recently, several researchers proposed regret theory-based methods to solve decision–making problems. For example, the authors in [24] proposed a regret theory-based decision-making method in order to solve problems of urban transportation systems stressed by rainstorms in Tianjin; this method could improve the reliability and risk-response capability of local public transportation service.

Overall, very little literature has systematically considered both regret and rejoice. The applications of regret and rejoice in MCDM need to be further developed, and this is the focus of the present paper.

3  Mathematical Modeling of Regret and Rejoice

In this section, we will develop regret and rejoice models using the PAO [5].

3.1 Regret Model

We derived appropriate definitions and properties from the definitions and properties of PAO [5]. We also provided our proofs for all these definitions, examples, and properties of regret in the appendices of this paper.

Definition 1:

Let I be an interval of real members; I = [L, U] with 0≤L≤U<1. R is defined as regret on the interval I.

Definition 2:

Using PAO, regret expression can be defined as follows,

For all x, y∈I and x > y,

R(y/x)=2(xⓅy)−1 (1)

The proof of this expression is presented in Appendix A.

Examples of Regret

By applying the regret expression (1) on the four PAO examples presented in [5], we can reformulate each example as a measure of the regret intensity of x over y:

     i)  R1(y/x){x−yU−L,if x>yo,otherwise

    ii)  R2(y/x){x−yx+y−2Lif x>yo,otherwise

   iii)  R3(y/x){x−yx−Lif x>yo,otherwise

    iv)  R4(y/x){x−y2U−x−yif x>yo,otherwise

The proof of these examples is presented in Appendix B.

Definition 3:

     i)  Translation independence

For x,y∈I, the regret of x over y remains unchanged if we add or subtract the same constraint Δ to x and y.

R((x+Δ)/(y+Δ))=R(y/x) (2)

    ii)  Scalar multiplication independence

For x,y,k∈I, the regret of x over y remains unchanged if we multiply x and y by the same positive constant k.

R((kx)/(ky))=R(y/x) (3)

Definition 4:

Based on Definition 3, three typologies can be applied to regret:

     i)  Regret can be of type I if it is translation independent.

    ii)  Regret can be of type II if it is scalar multiplication independent.

   iii)  Regret can be of type III if it cannot be type I or type II.

R1 is of type I, R2 is of type III, R3 is of type III for L≠0, and R4 is of type III for U≠0.

The proof of Definition 4 is presented in Appendix C.

3.1.1 Properties of Regret

For all values of x,y∈I and x > y:

     i)  R (x/x) = 0

    ii)  x>y→0≤R(y/x)≤1

   iii)  x′>x→R(y/x)<R(y/x′)

The proof of these properties is presented in Appendix D.

3.1.2 Regret Expression

We will take term [x−, x*] as the lower value and the upper value. According to the previous regret examples, we obtain four regret intensity expressions (RIE) as follows:

i.RIE1(x/y){x−yx∗−x−,if x>yo,otherwise (4)

ii.RIE2(y/x){x−yx+y−x−if x>yo,otherwise (5)

iii.RIE3(yx){x−yx−x−if x>yo,otherwise (6)

iv.RIE4(y/x){x−y2x∗−x−yif x>yo,otherwise (7)

Now, we will choose only RIE2 and RIE4 expressions and apply them in the next section because they have the same type (type III), in which the first expression uses the lower value (x−), and the second uses the upper value (x*).

3.2 Rejoice Model

Rejoice is considered as the opposite of regret and can be analyzed in an analogous manner [15].

J(y/x)=−R(y/x)) (8)

Therefore, we can have two rejoice intensity expressions, JIE1 and JIE2, in which the first is based on RIE1, and the second is based on RIE2:

J2(y/x){y−xx+y−2x−if x>yo,otherwise (9)

J4(y/x){y−x2x∗−x−yif x>yo,otherwise (10)

Finally, we end with two models of regret and rejoice intensity expressions, as summarized in Tab. 1.

4  Development of the Methodology

A typical MCDM method based on regret and rejoice helps a DM to make the best decisions that result in minimal regret. Therefore, in this section, we propose a set of procedures that applies the MCDM method with the regret and rejoice intensity expressions presented in Section 3.

In the decision matrix shown in Fig. 1, A={A1, A2, A3,…,Am} is a set of m alternatives that are evaluated with n criteria C={C1,C2,C3,…,Cn}, and wj is the weight of action j,j={1,2,3,…,n}, where all weights satisfy the following two conditions:

     i)  wj≥0

    ii)  ∑jnwj=1

Figure 1: Decision matrix

Let Xj∗=max xij

and Xj−=min xij

Using RIE2 in Tab. 1, the overall regret of action Ai can be written as

R1(Ai)=∑j=1nwj11−m∑j(Min/Max)|xkj−xijxkj+xij−2xj−|, (11)

where xkj is the forgone action value, xij is the chosen action value, m is the number of actions, and n is the number of criteria.

Using JIE2 in Tab. 1, the overall rejoice associated with alternative Ai is defined by

J1(Ai)=∑j=1nwj1m−1∑j(Min/Max)|xij−xkjxkj+xij−2xj−| (12)

By using RIE4 and JIE4 in Tab. 1, we derive two other regret and rejoice expressions, which can be defined as follows:

R2(Ai)=∑j=1nwj1m−1∑j(Min/Max)|xkj−xij2xj∗−xkj−xij| (13)

J2(Ai)=∑j=1nwj11−m∑j(Min/Max)|xkj−xij2xj∗−xkj−xij| (14)

Finally, we propose a set of selection procedures based on the regret and rejoice expressions (R1, J1 and R2, J2) to help DMs select the best action. These multi-attribute selection procedures contain two phases. Each phase uses one regret and one rejoice expression.

4.1 Phase I: Looking for Better Actions (BT)

Based on Eqs. (11) and (12) for R1 and J1, respectively, we can select actions (Ai) with higher rejoice values and reject actions with higher regret values according to rejection rule RU1, where

RU1: SELECTAi∖J1(Ai)>R1(Ai) (15)

The set of actions derived from this first phase is called better actions (BT).

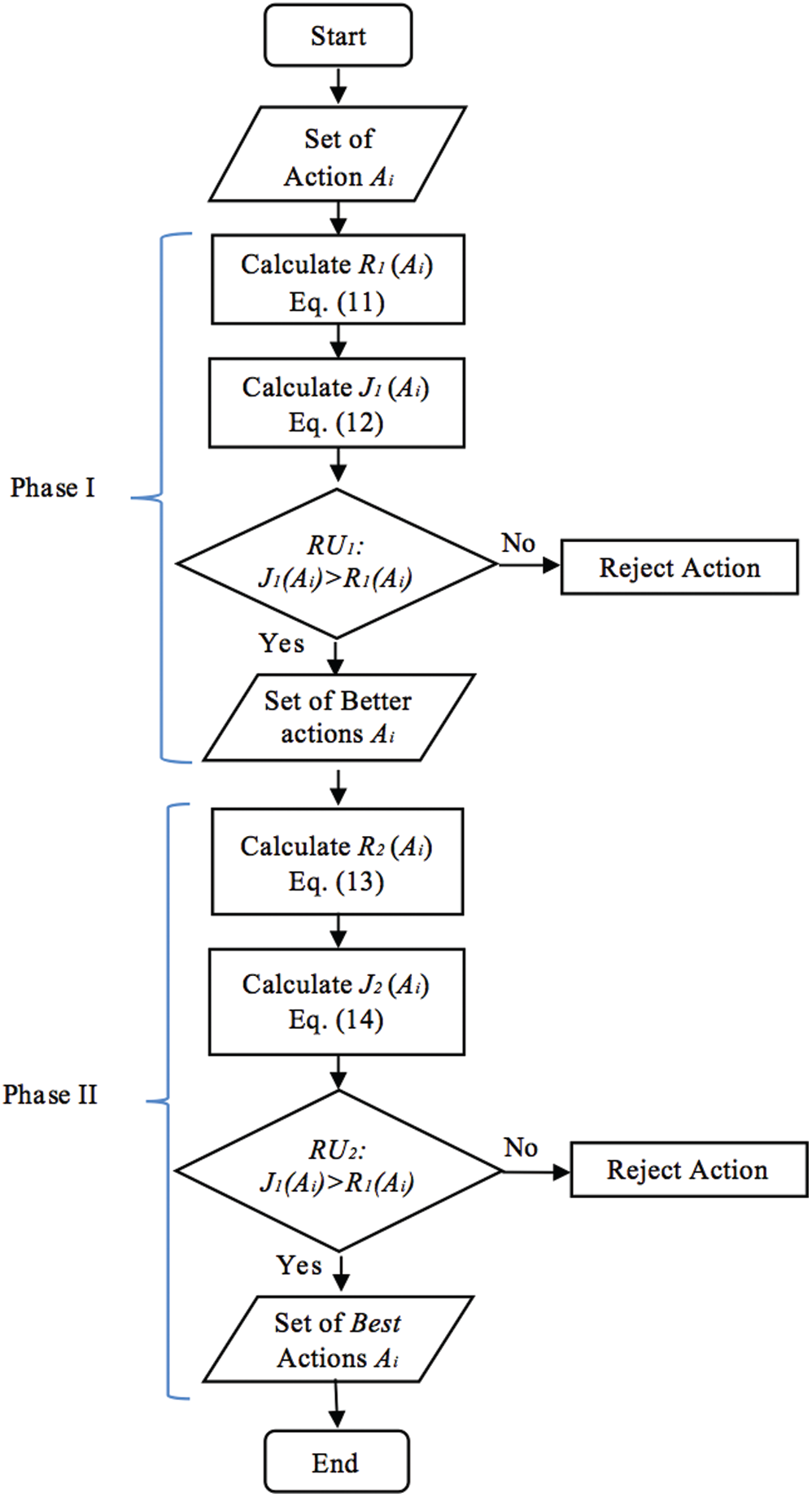
Figure 2: BTBSP algorithm

4.2 Phase II: Looking for Best Actions (B)

From the first set (BT) and by using Eqs. (13) and (14) for R2 and J2, respectively, we can select actions (Ai) with higher rejoice values and reject actions with higher regret values according to rejection rule RU2, where

RU2: SELECTAi∖J2(Ai)>R2(Ai) (16)

The set of actions derived from this second phase is called best actions (B).

4.3 The Better and Best Selection Procedures (BTBSP) Algorithm

To solve a decision-making problem, we propose a multi-attribute selection procedure based on regret and rejoice, which is explained by the BTBSP algorithm shown in Fig. 2.

5  Illustrative Examples

In this section, we use numerical examples to illustrate the BTBSP algorithm and prove the efficacy of our new method.

5.1 Example 1

We consider six alternatives, A1, A2,…,A6, that are associated with three criteria, C1, C2, C3, of respective weights w1, w2, w3. This decision matrix is shown in Tab. 2.

Phase I: Looking for better actions

We use Eqs. (11) and (12) to calculate regret (R1) and rejoice (J1). Based on the rejection rule RU1 in Eq. (15), we choose the better alternatives and reject the worse ones, as summarized in Tab. 3.

At the end of Phase I, we obtain a set of better alternatives, BT={A1,A3,A6}.

Phase II: Looking for best actions

We use Eqs. (13) and (14) to calculate regret (R2) and rejoice (J2). Based on the rejection rule RU2 in Eq. (16), we choose the best alternatives and reject the worst ones, as summarized in Tab. 4.

Finally, we obtain the set of the best alternatives, B={A1,A6}, from which the DM can choose.

5.2 Example 2

Here we use the same example given by [16] to prove the efficacy of our new method.

We consider three alternatives, A1, A2, and A3, for a house-selection problem. These alternatives are evaluated against two criteria: C1 and C2. The decision matrix for this problem is shown in Tab. 5.

We apply our proposed BTBSP to this example, and then compare the results with those obtained by the revised VIKOR and the regret model proposed by [16]. This comparison is shown in Tab. 6.

Tab. 6 demonstrates that the regret model, revised VIKOR, and proposed BTBSP could produce appropriate performance rankings of the alternatives. Phase II of the proposed method BTBSP gives the same results as that of the regret model and the revised VIKOR. They all rank A2 as the best alternative and A3 as the worst.

5.3 Example 3

We use another numerical example (a location preference-ranking problem) to further illustrate the performance of BTBSP. This example is borrowed from [25,26].

Let A1,A2,…,A6 be six alternatives associated with six criteria, g1,g2,…,g6, and for all decision criteria, the weight is wj = 1/6 (j=1,…,6) [25]. The decision matrix is shown in Tab. 7.

We apply our proposed BTBSP to this example to determine the best actions. The decisions obtained in Phases I and II are listed in Tabs. 8 and 9, respectively.

The list of the better actions obtained from Phase I of BTBSP is BT={A2,A4,A5}; meanwhile, the list of the best actions obtained from Phase II of BTBSP is B={A4,A5}.

We compare BTBSP’s results to obtained using the PROMETHEE I and PROMETHEE II methods [25]. This comparison is presented in Tab. 10.

In the PROMETHEE I method, some actions cannot be compared with each other; A4 is incomparable with A3 and A2, and A2 is incomparable with A3. Therefore, the resulting ranking of this method is presented in Tab. 10 by three different ranking lists. However, in the proposed BTBSP, all actions are comparable and only one ranking list is presented, where A5 is the best action and A1 is the worst, which matches PROMETHEE I results.

The result of the PROMETHEE II method is also presented by only one ranking in Tab. 10, in which A5 is the best action and A1 is the worst; this matches BTBSP’s results.

Finally, we compare our results to those obtained by the SIR.SAW and SIR.TOPSIS [26] on the same problem. This comparison is presented in Tab. 11.

Regarding the worst action (A1) and the best action (A5), the performance ranking given by BTBSP is almost the same as those given by SIR.SAW and SIR.TOPSIS. Although there is little difference in the ranking of other actions (A2, A3, A4, and A6), BTBSP rejects A3 and A6 in Phase I, which means that they are considered as the worse actions; moreover, BTBSP rejects A2 in Phase II since it is considered as a better action but not the best one.

All examples presented in this section clearly prove the efficiency of our new method.

6  Conclusions

In this paper, we proposed a new multi-attribute selection method based on feelings. Most MCDM methods consider only the rational side of decision-making while neglecting the feelings of the DM, which could greatly influence preferences in decision-making. Unlike most MCDM methods that consider only the feeling of regret, our multi-attribute selection procedure incorporates both regret and rejoice in the selection of the best alternatives. We utilized the PAO [5] to mathematically develop regret and rejoice equations. Based on these equations, we proposed a new multi-attribute selection procedure BTBSP that consists of two phases. Each phase uses regret and rejoice equations to measure the value of those feelings and select the best actions. We used illustrative examples from the extant literature to compare BTBSP to the regret model, the revised VIKOR, SIR.SAW, SIR.TOPSIS, PROMETHEE I, and PROMETHEE II. All examples clearly prove the strong performance and efficacy of our proposed method.

We believe that the application of our proposed method with the implementation of a decision-support system merits further scrutiny in future work. Therefore, we will try to develop more features for BTBSP and design software that is able to handle real-world multi-criteria decision problems. Furthermore, it will be interesting to apply our method to real case studies.

Funding Statement: This research was funded by the Deanship of Scie.pngic Research at Princess Nourah bint Abdulrahman University, through the Research Funding Program (Grant No. FRP-1440-31).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Wenstop, “Mindsets, rationality and emotion in multi-criteria decision analysis,” Journal of Multi-Criteria Decision Analysis, vol. 13, no. 4, pp. 161–172, 2005. [Google Scholar]

 2.  P. V. Cappellen, “The emotion of joy: Commentary on johnson,” The Journal of Positive Psychology, vol. 15, no. 1, pp. 40–43A, 2020. [Google Scholar]

 3.  G. A. Hazelrigg, Systems Engineering: An Approach to Information-Based Design, 1st ed., Upper Saddle River, NJ, USA: Prentice Hall, pp. 469, 1996. [Google Scholar]

 4.  X. Wang, “A study of regret and rejoicing and a new MCDM method based on them,” Ph.D. dissertation, Louisiana State University, Shreveport, Louisiana, US, 2008. [Google Scholar]

 5.  A. Rebai, B. Aouni and J. M. Martel, “A multi-attribute method for choosing among potential alternative with ordinal evaluation,” European Journal of Operational Research, vol. 174, no. 4, pp. 360–373, 2006. [Google Scholar]

 6.  B. Roy, Méthodologie Multicritère D’aide à la Decision, 1st ed., Paris, France: Economica, pp. 423, 1985. [Google Scholar]

 7.  T. L. Saaty, The Analytic Hierarchy Process, 1st ed., New York, NY, USA: Mc-Graw-Hill, 1980. [Google Scholar]

 8.  C. L. Hwang and K. Yoon, “Introduction,” in Multiple Attribute Decision Making: Methods and Applications, 1st ed., vol. 186. Berlin, Heidelberg: Springer-Verlag, pp. 1–15, 1981. [Google Scholar]

 9.  S. Opricovic, “Multi-criteria optimization of civil engineering systems,” Ph.D. dissertation, Faculty of Civil Engineering, Belgrade, pp. 302, 1998. [Google Scholar]

10. M. Azadfallah, “A supplier selection using an extension of MCDM models,” Journal of Supply Chain Management Systems, vol. 3, no. 2, pp. 41–46, 2014. [Google Scholar]

11. I. Simonson, “The influence of anticipating regret and responsibility on purchase decisions,” Journal of Consumer Research, vol. 19, pp. 105–118, 1992. [Google Scholar]

12. L. J. Savage, “The theory of statistical decision,” Journal of American Statistical Association, vol. 46, pp. 55–67, 1951. [Google Scholar]

13. G. Loomes and R. Sugden, “Regret theory: An alternative theory of rational choice under uncertainty,” the Economic Journal, vol. 92, no. 368, pp. 805–824, 1982. [Google Scholar]

14. D. E. Bell, “Regret in decision making under uncertainty,” Operations Research, vol. 30, pp. 961–981, 1982. [Google Scholar]

15. E. Kujawski, “A reference-dependent regret model for deterministic trade off studies,” Systems Engineering, vol. 8, pp. 119–137, 2005. [Google Scholar]

16. J. Huang, G. Tzeng and H. Liu, “A revised VIKOR model for multiple criteria decision making–-The perspective of regret theory,” in Int. Conf. on Multiple Criteria Decision Making, Chengdu, China, vol. 35, pp. 761–768, 2009. [Google Scholar]

17. P. Chatterjee and S. Chakraborty, “A comparative analysis of VIKOR method and its variants,” Decision Science Letter, vol. 5, no. 4, pp. 469–486, 2016. [Google Scholar]

18. C. Chorus, S. Cranenburgh and T. Dekker, “Random regret minimization for consumer choice modeling: Assessment of empirical evidence,” Journal of Business Research, vol. 67, pp. 2428–2436, 2014. [Google Scholar]

19. H. Zhou, J. Wang and H. Zhang, “Grey stochastic multi-criteria decision-making based on regret theory and TOPSIS,” International Journal of Machine Learning and Cybernetics, vol. 8, no. 2, pp. 651–664, 2017. [Google Scholar]

20. Y. Song, H. Yao, S. Yao, D. Yu and Y. Shen, “Risky multi-criteria group decision making based on cloud prospect theory and regret feedback,” Mathematical Problems in Engineering, vol. 2017, pp. 1–12, 2017. [Google Scholar]

21. X. Zhang, H. Lianga, F. Fangab and X. Chena, “A method for risky multiple attribute decision making considering regret and rejoicing of the decision maker,” Computers & Industrial Engineering, vol. 124, pp. 422–434, 2018. [Google Scholar]

22. X. Liang, P. Liu and Z. Liu, “Selecting products considering the regret behavior of consumer: A decision support model based on online ratings,” Symmetry, 2018, vol. 10, no. 178, pp. 2018. [Google Scholar]

23. L. Quian, S. Liu and Z. Fang, “Grey risky multi-attribute decision-making method based on regret theory and EDAS,” Grey Systems: Theory and Application, vol. 9, no. 1, pp. 101–113, 2019. [Google Scholar]

24. Y. Wang, Y. Liang and H. Sun, “A regret theory-based decision-making method for urban rail transit in emergency response of rainstorm disaster,” Journal of Advanced Transportation, vol. 2020, pp. 1–12, 2020. [Google Scholar]

25. J. P. Brans, Ph. Vincke and B. Marschal, “How to select and haw to rank projects: The PROMETHEE methods,” European Journal of Operational Research, vol. 24, no. 2, pp. 228–238, 1986. [Google Scholar]

26. X. Xu, “The sir method: A superiority and inferiority ranking method for multiple criteria decision making,” European Journal of Operational Research, vol. 131, no. 3, pp. 587–602, 2001. [Google Scholar]

Appendix A. The Proof of Definition 2

Appendix B. The Proof of Regret Examples

Using the examples given by [5] for the PAO

     i)  xⓅ1y=x−y+U−L2(U−L)

R(y/x)=2(xⓅy)−1

2(xⓅ1y)−1=2[x−y+u−l2(U−L)]−1=x−yU−L

⇒R1(y/x)=x−yU−L

    ii)  xⓅ2y={(x−L)/(x+y−2L)if (x,y)≠(L,L)12if x=y=L

R(y/x)=2(xⓅy)−1

if(x,y)≠(L,L) and x>y

2(xⓅ2y)−1=2[(x−L)x+y−2L]−1=x−yx+y−2L

R2(y/x)=x−yx+y−2L

if x = y = L

2(xⓅ2y)−1=2(1/2)−1=0

R2(y/x)=0

⇒R2(y/x){x−yx+y−2Lif x>yo,otherwise

   iii)  xⓅ3y={(2x−y−L)2(x−L)if L<y≤x≤U(x−L)2(y−L)if L<x≤y≤U12if x=y=L

R(y/x)=2(xⓅy)−1

if x>y

2(xⓅ3y)−1=2[(2x−y−L)2(x−L)]−1=x−yx−L

R3(y/x)=x−yx−L

if x = y = L

2(xⓅ3y)−1=1/2=0

R3(y/x)=0

⇒R3(y/x){x−yx−Lif x>yo,otherwise

    iv)  xⓅ4y={(U−y)/(2U−x−y)if(x,y)≠(L,L)12ifx=y=U

R(y/x)=2(xⓅy)−1

if (x,y)≠(L,L) and x > y

2(xⓅ4y)−1=2[U−y2U−x−y]−1=x−y2U−x−y

R4(y/x)=x−y2U−x−y

if x = y = L

2(xⓅ4y)−1=1/2=0

R4(y/x)=0

⇒R4(yx){x−y2U−x−yif x>yo,otherwise

Appendix C. The Proof of Definition 4

     i)  Regret can be of type I if it is translation independent

Regret is translation independent if for x,y∈I, the regret of x over y remains unchanged if we add or subtract the same constraint Δ to x and y.

Hence R1 is of type I

    ii)  Regret can be of type II if it is scalar multiplication independent

Regret is scalar multiplication independent if for x,y,k∈ I, the Regret of x over y remains unchanged if we multiply x and y by the same positive constant k.

⇒R2 is not scalar translation independent

⇒R2 is not scalar multiplication independent

⇒R3 is not scalar translation independent

⇒R3 is not scalar multiplication independent

⇒R4 is not scalar translation independent

⇒R4 is not scalar translation independent

   iii)  Regret can be type III if it cannot be type I or type II

Hence, R2 is of type III, R3 is of type III for L≠0 and R4 is of type III for U≠0

Appendix D. The Proof of Regret Properties

     i)  R(x/x)=0

xⓅx=1/2

R(x/x)=2(xⓅx)−1=2(1/2)−=0

⇒R(x/x)=0

    ii)  x>y→0≤R(y/x)≤1

x>y=>xⓅy

0≤2(xⓅx)−1≤1

0≤(xⓅx)≤1

⇒0≤R(y/x)≤1

   iii)  x′>x→R(y/x)<R(y/x′)

xⓅy<x′Ⓟy

2(xⓅy)<2(x′Ⓟy)

2(xⓅy)−1<2(x′Ⓟy)−1

⇒R(y/x)<R(y/x′)

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.