DOI:10.32604/cmc.2022.015987

| Computers, Materials & Continua DOI:10.32604/cmc.2022.015987 |  |
| Article |
Graphical Transformation of OWL Ontologies to Event-B Formal Models
Department of Computer Science, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
*Corresponding Author: Eman H. Alkhammash. Email: eman.kms@tu.edu.sa
Received: 17 December 2021; Accepted: 18 February 2021
Abstract: Formal methods use mathematical models to develop systems. Ontologies are formal specifications that provide reusable domain knowledge representations. Ontologies have been successfully used in several data-driven applications, including data analysis. However, the creation of formal models from informal requirements demands skill and effort. Ambiguity, inconsistency, imprecision, and incompleteness are major problems in informal requirements. To solve these problems, it is necessary to have methods and approaches for supporting the mapping of requirements to formal specifications. The purpose of this paper is to present an approach that addresses this challenge by using the Web Ontology Language (OWL) to construct Event-B formal models and support data analysis. Our approach reduces the burden of working with the formal notations of OWL ontologies and Event-B models and aims to analyze domain knowledge and construct Event-B models from OWL ontologies using visual diagrams. The idea is based on the transformation of OntoGraf diagrams of OWL ontologies to UML-B diagrams for the purpose of bridging the gap between OWL ontologies and Event-B models. Visual data exploration assists with both data analysis and the development of Event-B formal models. To manage complexity, Event-B supports stepwise refinement to allow each requirement to be introduced at the most appropriate stage in the development process. UML-B supports refinement, so we also introduce an approach that allows us to divide and layer OntoGraf diagrams.
Keywords: Data analysis; OWL ontologies; event-B formal method; refinement; requirements; OntoGraf
Event-B is a refinement-based formal method with tool support for developing various kinds of systems. Despite the several benefits of using Event-B to build large and critical systems, it is difficult to build Event-B formal models and organize their refinement levels from informal requirements. Efficient mechanisms are needed to bridge the gap between informal requirements and formal models and to support data analysis. Our approach aims to address this challenge by constructing Event-B models incrementally from OWL ontologies using graphical diagrams.
Ontologies provide conceptual representations of the domain of interest in a formal language. There are a wide range of ontologies in different domains. OWL ontologies are rich in knowledge, and a large number of OWL ontologies are available in several repositories. Moreover, OWL ontologies are supported by different tools, such as Protégé [1], and such tools are used by a large number of people from different disciplines. Many published studies describe the roles of ontologies in requirements engineering and data analysis [2,3]. Dermeval et al. [4] conducted a literature survey that summarized approximately sixty-seven studies that used ontologies in several phases of requirements engineering, and they concluded that ontologies show great advantages in requirements engineering phases in academic and industrial settings. These studies clearly indicate that ontologies can benefit requirements engineering.
Our approach aims to utilize and transform OWL ontologies into Event-B formal models, and it supports refinement to reduce complexity and ide.pngy abstraction levels. We transform OntoGraf diagrams into UML-B diagrams. OntoGraf is a tool that allows for a visual, interactive navigation of the relationships in OWL ontologies. OntoGraf captures large elements of OWL structures. UML-B provides graphical modeling based on UML, thereby supporting the development of an Event-B formal model. We transform the diagrammatic notation of OntoGraf into the corresponding diagrammatic notation in UML-B. Nodes are transformed into classes. The object properties displayed in arches are transformed into axioms and invariants in UML-B diagrams. Data properties are transformed into axioms and invariants. Class expressions are transformed into invariants. This paper is structured as follows: Section 2 presents an overview and a literature review of OWL ontologies, Event-B, and UML-B. Section 3 introduces the methodology employed in this paper. Section 4 describes the application of the proposed approach to case studies. Section 5 outlines the lessons learned from the application of the proposed approach to case studies. Finally, Section 6 presents conclusions and future work.
2 Preliminaries and Related Work
Most ontologies provide formal descriptions for representing domains to enable knowledge representation and sharing. Currently, OWL is a widely used ontology language. It [5] is a semantic web language based on description logic; it represents knowledge and shares it on the Worldwide Web. OWL is highly expressive and provides reasoning power to the semantic web. OWL defines a hierarchy of concepts, including classes (collections of individuals), properties (collections of the relationships between individuals or data), and individuals (objects belonging to classes). Several elements are used by OWL to represent ontology components, such as the following: owl:Class represents a concept or a group. Owl:ObjectProperty relates an individual to another individual. Owl:DatatypeProperty relates an individual to a data value. Rdf:Property represents the relationships between the domain and a range of instances or classes (e.g., “rdfs:domain” and “rdfs:range”). owl:Individual represents the domain of objects. In Fig. 1, Person and Organization are classes, and members are object properties that relate individuals from the domain Person to individuals from the range Organization.
OntoGraf (http://protegewiki.stanford.edu/wiki/OntoGraf) is a graph visualization plug-in in the Protégé editor. It allows us to view classes, individuals, domain/range object properties, and equivalences. Classes and individuals are represented as nodes of a graph, and the relationships between them are represented as edges. OntoGraf allows us to navigate the relationships between OWL ontologies. It provides several layouts to organize the structure of an ontology, and the user is also able to move every node. Moreover, OntoGraf allows us to focus the view on the desired part of an OWL ontology. OntoGraf enables quick visualizations of all important details present in OWL ontologies. In this paper, we make use of OntoGraf for demonstrating the details of OWL ontologies to transform them to the corresponding notations of UML-B and then to Event-B formal models. In this way, the user does not need to interact directly with the formal notations of OWL ontologies and Event-B. Fig. 2 graphically describes the object property member that relates the domain Person and range Organization in OntoGraf.

Figure 1: Representation of the object properties in an OWL ontology

Figure 2: Representation of the object property member and the relation between the person domain and the range organization
Event-B [6] is a formal method that provides a rich modeling language based on set theory and predicate logic for specifying, modeling, and reasoning with regard to systems. Constructing an Event-B model starts from an abstract model, and we continue to add details and model the system at several levels using the refinement technique. Event-B provides a mechanism for verifying the consistency of the constructed model using a mathematical proof. An Event-B model consists of a context and a machine. The context contains the static part of the model (i.e., sets, constants, and axioms). The machine contains the dynamic functional behavior of the model (i.e., variables, invariants, and events). Axioms specify the assumptions about the constants. Invariants specify the properties of model variables that should always remain true. An event consists of two parts. The first part contains guards, which define the necessary conditions for the event to occur. Each guard is a predicate over the state variables and constants. The second part contains the actions, which describe how the state variables are modified as a result of the event being executed.
A concrete machine refines the abstract machine. The refinement must preserve the abstract invariants. The states of the abstract machine are connected to the states of the concrete machine by gluing invariants. Each event of the abstract machine is refined by one or more concrete events. A refinement may also introduce new concrete events, variables, and invariants.
UML-B [7] is a formal graphical modeling notation based on UML. It provides a UML-like graphical notation that allows for the development of an Event-B formal model. UML-B provides four types of diagrams: package diagrams, context diagrams, class diagrams, and state machine diagrams. The package diagrams represent Event-B contexts and machines and the relationships between them. The sets and constants of an Event-B model are represented by context diagrams that describe the abstract view of the system architecture.
The class diagrams represent the entities of the system whose properties are specified as class attributes. The state machine diagrams define the behavior of classes. The class diagrams in UML-B may contain attributes, associations, events, and state machines (transitions between states) that correspond to variables, invariants, and events in Event-B models. The notion of refinement is realized in UML-B [7]. A class in a concrete machine refines a class of abstract machines. The refined class holds the attribute of its abstract machine. The refined class may contain other new attributes and events. It is also possible that a refined class deletes some of the attributes of the abstract class. Fig. 3 represents members that link the Person and Organization classes.

Figure 3: UML-B for two classes, person and organization, and the member relation
Several works have aimed to bridge the gap between informal requirements and Event-B formal models. A work by [8] presented an approach based on that of UML-B and atomicity decomposition (AD) to construct Event-B models. It classifies informal requirements into five types: data-oriented, constraint-oriented, event-oriented, flow-oriented, and others. It uses the AD approach, which provides a graphical notation to structure refinement levels and manage flows in an Event-B model. Although our approach uses UML-B, we use it in the proposed approach to generate Event-B models from OWL ontologies, whereas in [8], UML-B was used to map data-oriented requirements to an Event-B model. Another work by [9,10] aimed to build Event-B models from OWL ontologies. It used an OWL-verbalizer to generate controlled English requirements called Attempto Controlled English (ACE) from OWL ontologies, and these could then be used to construct Event-B models. Our approach uses OntoGraf and UML-B diagrams to generate Event-B models from OWL ontologies, thereby reducing the burden of constructing Event-B models manually.
Another work proposed by the authors of [11,12] transformed ontologies to Event-B contexts. It was supported by tool called OntoEvent-B. The approach consists of three stages: (1) it takes ontologies as input, (2) it translates the inputs into generic concepts using the Pivot model, and (3) it translates generic concepts into Event-B contexts. Input ontologies can be described in the OWL and OntoML/Plip languages.
Properties are not ide.pngied in this approach. Moreover, the authors of [13] extracted requirements of concurrent systems from documentation to verify the designs of the systems and ensure their correctness. They adopted ontologies to extract requirements and used ontology instances to represent system modules for supporting formal verification. In comparison with the abovementioned approaches, the approach proposed in this paper uses a diagrammatic view of an ontology using OntoGraf and transforms it into UML-B notation without the need for directly handling the mathematical notation. Moreover, our approach supports the organization of the refinement structure.
Ontologies have been successfully used in various phases of requirements engineering. Ontologies can be used to capture knowledge about a domain. This paper focuses on capturing the knowledge represented in OWL ontologies and transforming it into Event-B models. In this way, we ide.pngy the precise knowledge contained in an OWL ontology and use it for formal modeling. This enables precise requirements for Event-B formal modeling. There are various OWL ontologies that exist in several repositories, such as the Aber OWL repository [14] and OntoKhoj Portal [15]. These ontologies could contribute to introducing precise definitions of the system being modeled in Event-B. We introduce an approach that allows users to focus on the transformation of OntoGraf and UML-B graphical notations to reduce the burden of transforming formal notations from OWL ontologies into Event-B formal models. The transformation of ontologies into Event-B models is performed by the translation of OntoGraf diagrams that visualize OWL ontologies into UML-B diagrams that visualize Event-B models. UML-B diagrams can be automatically translated into Event-B models. The following steps show how to transform OntoGraf diagrams that capture ontologies into UML-B diagrams. We show the corresponding Event-B model (variables and invariants only) generated from UML-B. The initialization event sets the default values for the defined variables.

Figure 4: Representations of a class in UML-B (A) and OntoGraf (B)
The set Class_SET is defined in the context c.

Figure 5: Representations of properties in UML-B (A) and OntoGraf (B)
The Event-B model corresponding to UML-B in Fig. 5, which extends the previous Event-B model, is shown in Fig. 6.
OWL distinguishes between the two main categories of properties that an ontology contains: object properties that link individuals to individuals and datatype properties that link individuals to data values. OWL properties are converted as invariants or axioms in the UML-B class diagram. There are various types of object properties in OWL ontologies. Although OntoGraf does not distinguish the particular type of an object property, it ide.pngies the name of the property, the domain, and the range. The Protégé platform [1] can provide more details about the exact types of properties. Therefore, we make use of the properties tab in Protégé to determine the exact types of object properties in the UML-B class diagram for overcoming this weakness in OntoGraf. Here, we describe several types of object properties and offer some examples to show how to transform them into invariants or axioms in Event-B.

Figure 6: Event-B model corresponding to UML-B
If a property links class A to class B and class B to class C, then it can be inferred that it links class A to class C. Fig. 7 shows an example of a transitive property. The subRegionOf property between two regions is transitive. In the UML-B class diagram, Region is converted into the Region class, and the object property subRegionOf is converted as an invariant to indicate that subRegionOf is a transitive property (i.e., subRegionOf;
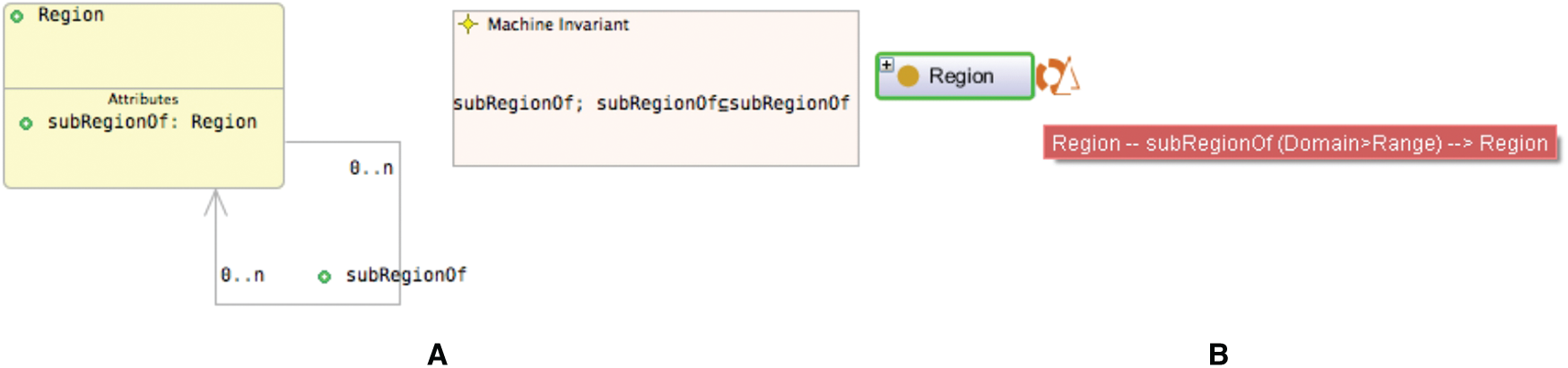
Figure 7: Representations of a transitive property in UML-B (A) and OntoGraf (B)
The Event-B model corresponding to the UML-B class diagram in Fig. 7 is shown in Fig. 8.

Figure 8: Event-B model corresponding to UML-B
The set Region_SET is defined in context c.
If a property links A to B, then it can be inferred that it links B to A. A popular example of a symmetric property is the friendOf relation. Fig. 9 describes the symmetric property friendOf. We add the invariant
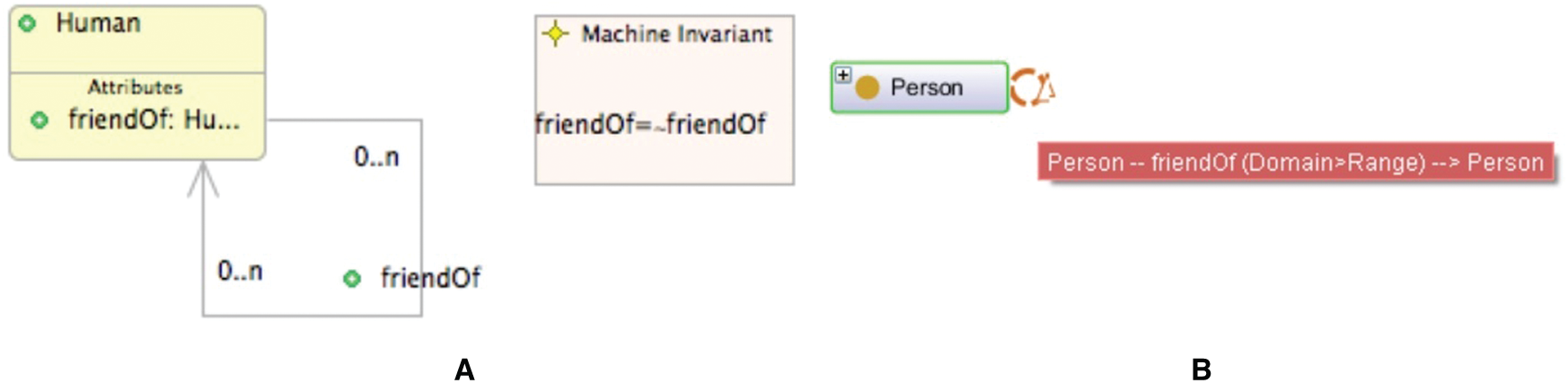
Figure 9: Representations of a symmetric property in UML-B (A) and OntoGraf (B)
The Event-B model corresponding to the UML-B class diagram in Fig. 9 is shown in Fig. 10.

Figure 10: Event-B model corresponding to UML-B
A property can be asymmetric. For example, if x is a parent of y, then y is not a parent of x. Fig. 11 describes the translation of the parent of property.
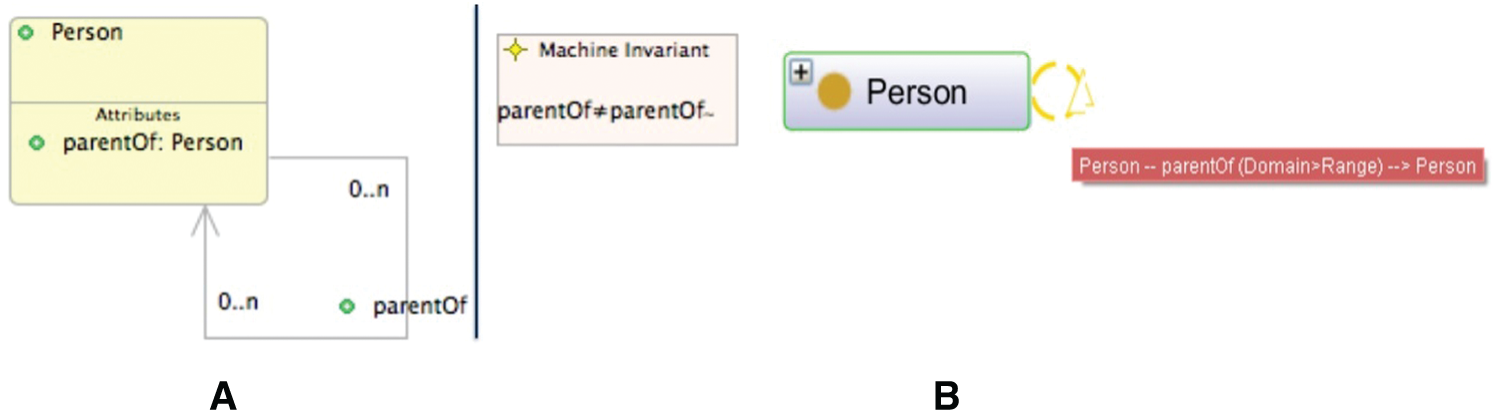
Figure 11: Representations of an asymmetric property in UML-B (A) and OntoGraf (B)
The Event-B model corresponding to the UML-B class diagram in Fig. 11 is shown in Fig. 12.

Figure 12: Event-B model corresponding to UML-B
In a functional property, a given individual takes only one value. Fig. 13 describes a functional property.
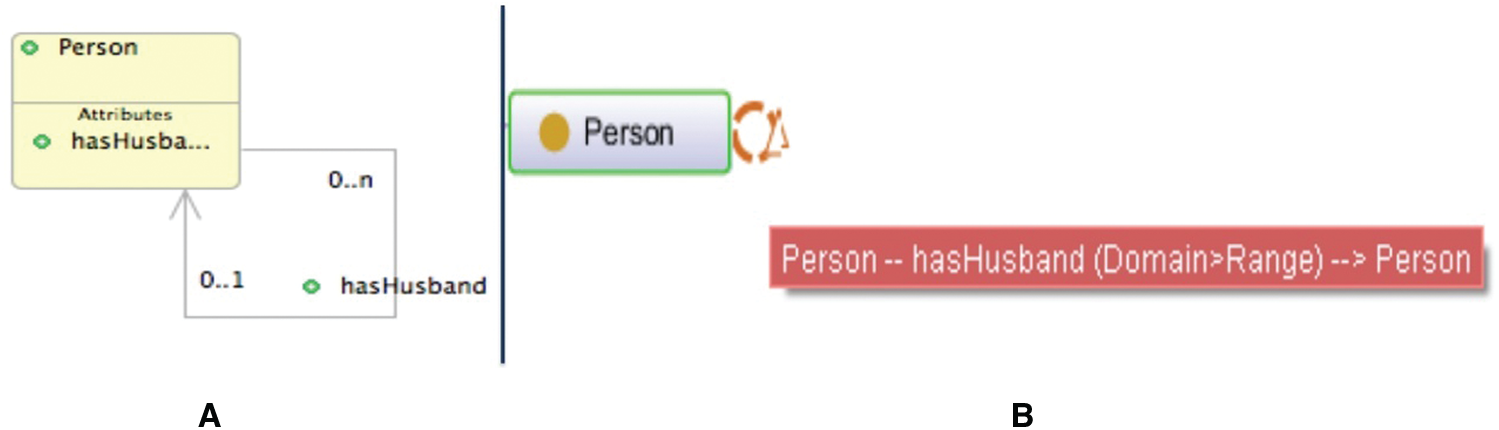
Figure 13: Representations of a functional property in UML-B (A) and OntoGraf (B)
A property can be of the inverse type. This means that if property p has an inverse property q and p links A to B, then it can be inferred that q links B to A. The inverse can be functional or not. An inverse property is represented as an invariant or an axiom in the UML-B class diagram.
The Event-B model corresponding to the UML-B class diagram in Fig. 13 is shown in Fig. 14.

Figure 14: Event-B model corresponding to UML-B
A reflexive property relates an individual to itself. For instance, every human knows him/herself. This is formalized in OntoGraf as a node Human, and the reflexive property Knows has a domain Human and a range Human. In the UML-B class diagram, the node Human is converted into a class and an association, and Knows is added to link the domain Human to the range Human, as shown in Fig. 15. Moreover, we add the invariant id(Human)
Unlike a reflexive property, the irreflexive property represented in Fig. 16 (yellow relationship) explicitly states that an individual is not related to itself. Example, nobody can be married to him/herself. The invariant that must be added to specify this type of property in the UML-B class diagram is the following:
The Event-B model that shows examples of reflexive/irreflexive properties is shown in Fig. 17.
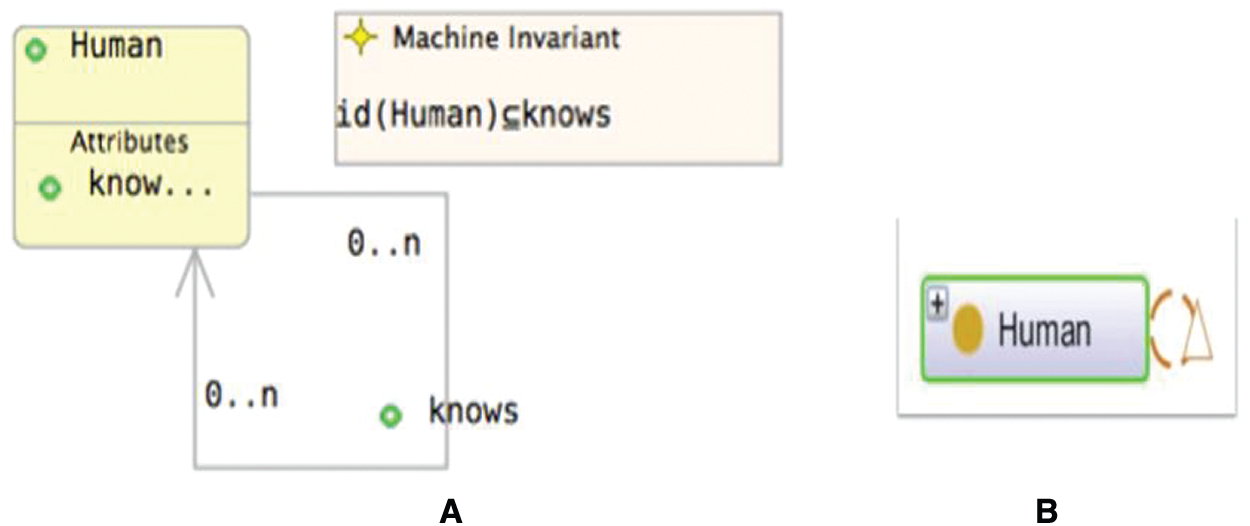
Figure 15: Representations of a reflexive property in UML-B (A) and OntoGraf (B)
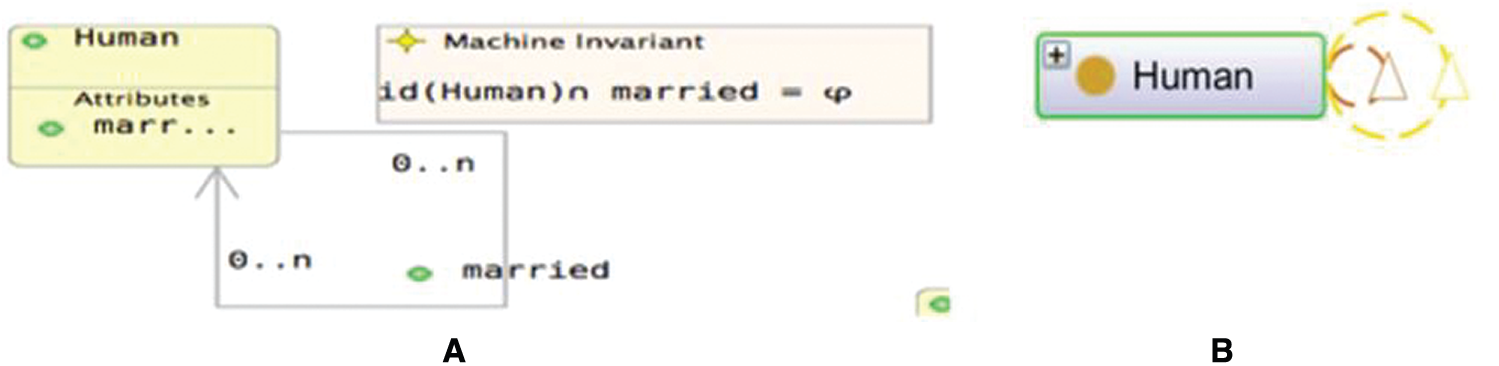
Figure 16: Representations of an irreflexive property in UML-B (A) and OntoGraf (B)

Figure 17: Representations of equivalent classes in UML-B (A) and OntoGraf (B)
There are three main types of axioms that allow relationships to be established between class expressions, and they are as follows:
1. Hierarchies Classes can be subclasses or superclasses, as illustrated in Fig. 5.
2. Equivalent classes.
Equivalent classes mean that class expressions are semantically equivalent to each other. Example: The class Spiciness is equivalent to the union of the classes Hot, Medium, and Mild. This can be converted to an invariant in the UML-B class diagram:

Figure 18: Representations of equivalent classes in UML-B (A) and OntoGraf (B)
The Event-B model corresponding to the UML-B class diagram in Fig. 18 is shown in Fig. 19.

Figure 19: Event-B model corresponding to UML-B
1. Disjoint classes mean that the class expressions are pairwise disjoint; that is, no individual can be instances of multiple classes at the same time. Example: Hot cannot be Medium or Mild, as shown in Fig. 20.
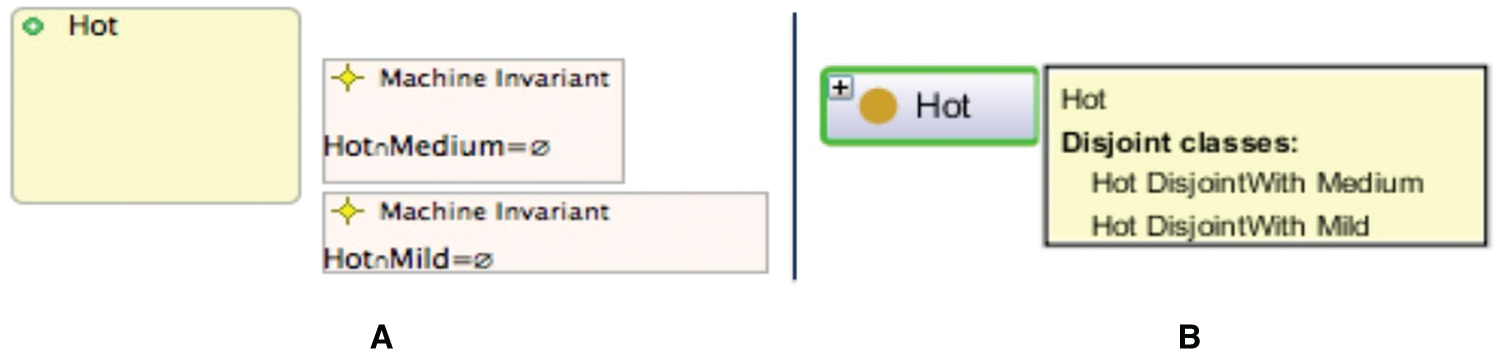
Figure 20: Representations of disjoint classes
The Event-B model corresponding to Fig. 20 is shown in Fig. 21.

Figure 21: Event-B model corresponding to UML-B
Axiomatic definitions that appear in the tooltips of OntoGraf can be translated into Event-B models manually or by using the approach mentioned in [9].
Both refinement and abstraction are used to structure the formal models and manage complexity [16,17]. Refinement means that models represent several abstraction levels of a system. Formal verification is used to ensure consistency between abstraction levels. UML-B already supports refinement. Therefore, we must find a way to introduce the notion of refinement while converting OntoGraf into UML-B diagrams. In fact, OntoGraf has numerous good features that could support refinement. It can provide several views of an OWL ontology and enables the OWL ontology to be captured fully or partially. It is easy to move nodes in OntoGraf and layer them. Therefore, we find it possible to layer the OntoGraf diagrams and then convert them into UML-B diagrams. After that, we translate OntoGraf to UML-B and then to Event-B models.
4 Application of the Proposed Approach to Case Studies
4.1 Case Study 1: Lehigh University Benchmark (LUBM) Ontology
In this section, we describe the application of the proposed approach to a case study that describes university concepts. The LUBM ontology [18] contains various relations between various concepts used in a university environment (people, organizations, and other classes). To apply the proposed approach, we capture the ontology using OntoGraf and organize the refinement levels, as shown in Fig. 22. We decide to organize the refinement steps of the OWL ontology into three levels: m0–m2. OntoGraf provides the modeler with a good view of how to organize the refinement levels.
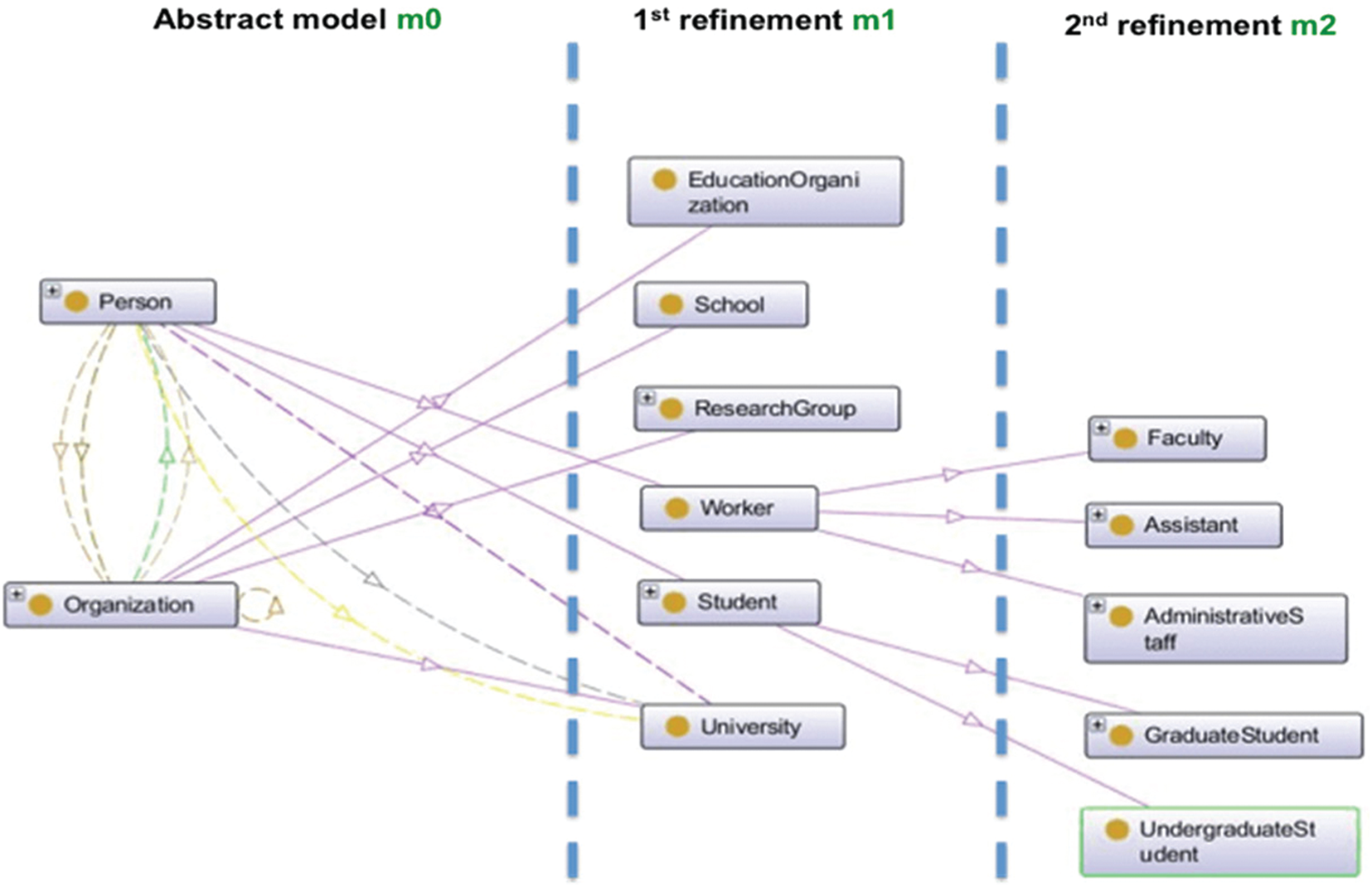
Figure 22: The overall representation of the LUBM OWL ontology in OntoGraf
The second step is to represent the UML-B class diagrams that correspond to abstract models m0–m2, as shown in Figs. 23–25, respectively, using the steps mentioned in Section 3.
The Event-B models that are generated automatically from the UML-B class diagrams in Figs. 23–25 are shown in Figs. 26–28, respectively. For m0, seven variables and seven invariants are generated from the class diagram shown in Fig. 23. The variables member and alumnus are represented as relations, whereas affiilatedOf, head, and affilatedOrganization are represented as partial functions.
In the first refinement (m1) nine variables and nine invariants are generated, as shown in Fig. 27. Three relations correspond to Fig. 24 : mastersDegreeFrom, undergraduateDegreeFrom, and doctoralDegreeFrom.
In the second refinement (m2) five variables and invariants are generated. Five sets are generated from the class diagram of Fig. 25. A total of 24 POs are generated from the m0–m2 Event-B models and automatically discharged. The proof statistics of the LUBM models are presented in Tab. 1.
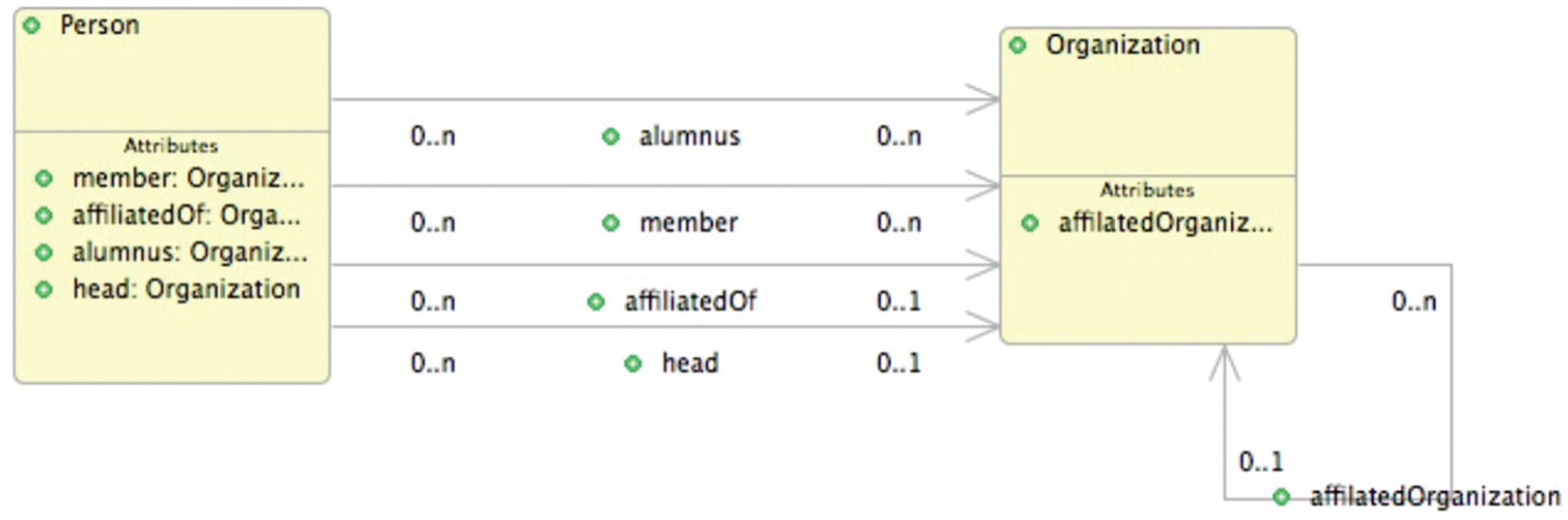
Figure 23: The UML-B class diagrams of m0
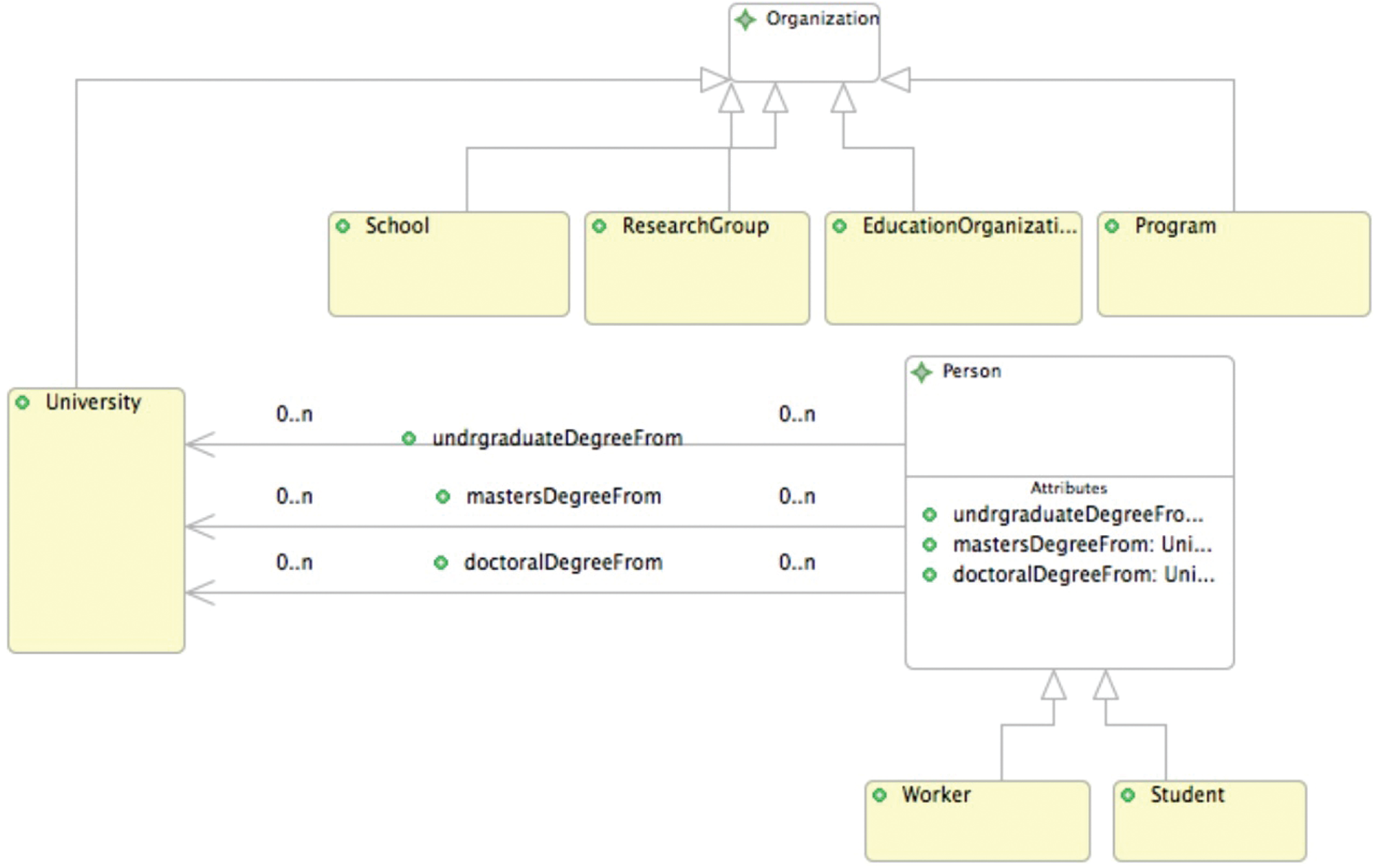
Figure 24: The UML-B class diagrams of m1
Figure 25: The UML-B class diagrams of m2
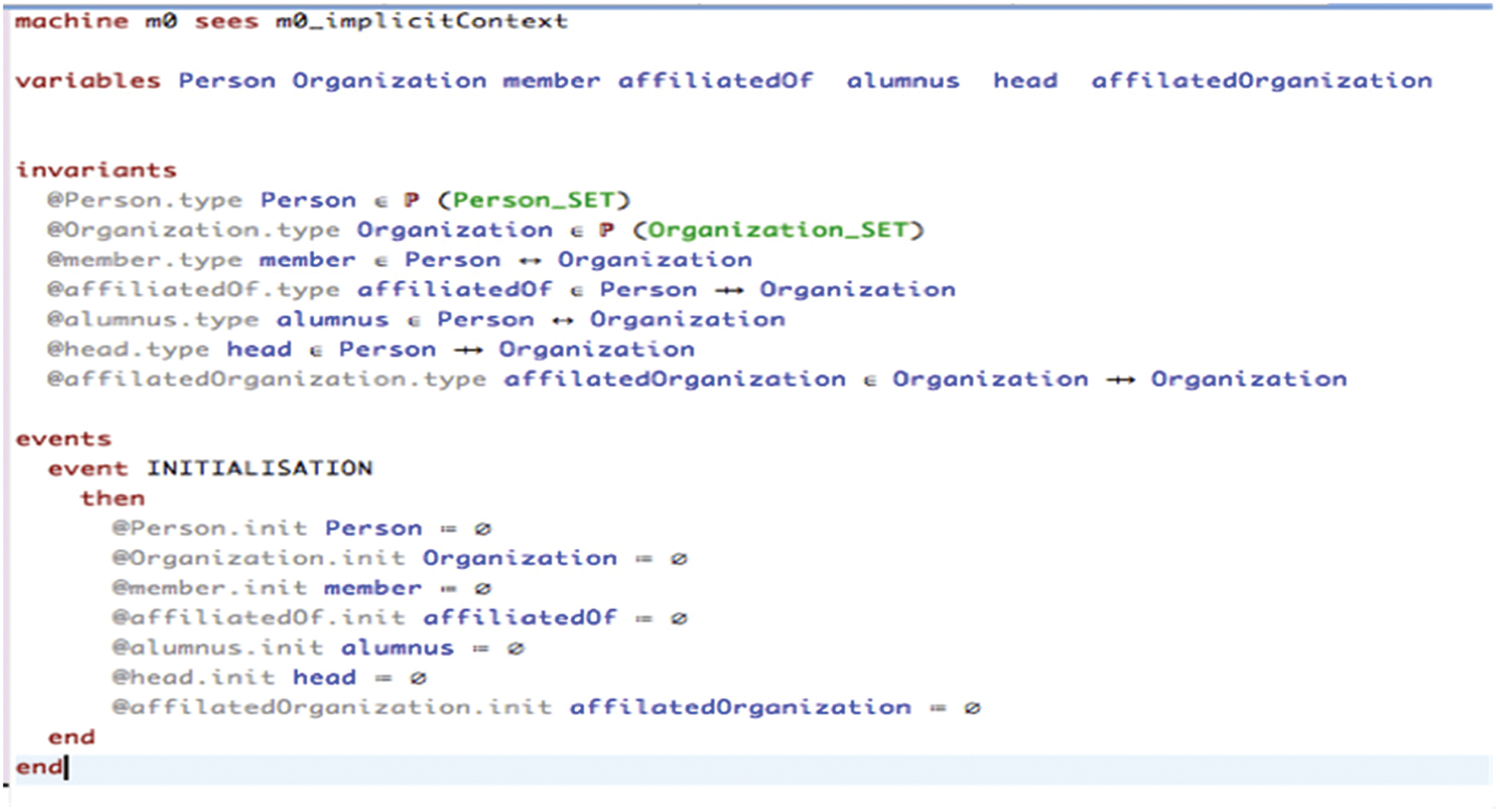
Figure 26: The event-B models generated from the class diagrams of m0
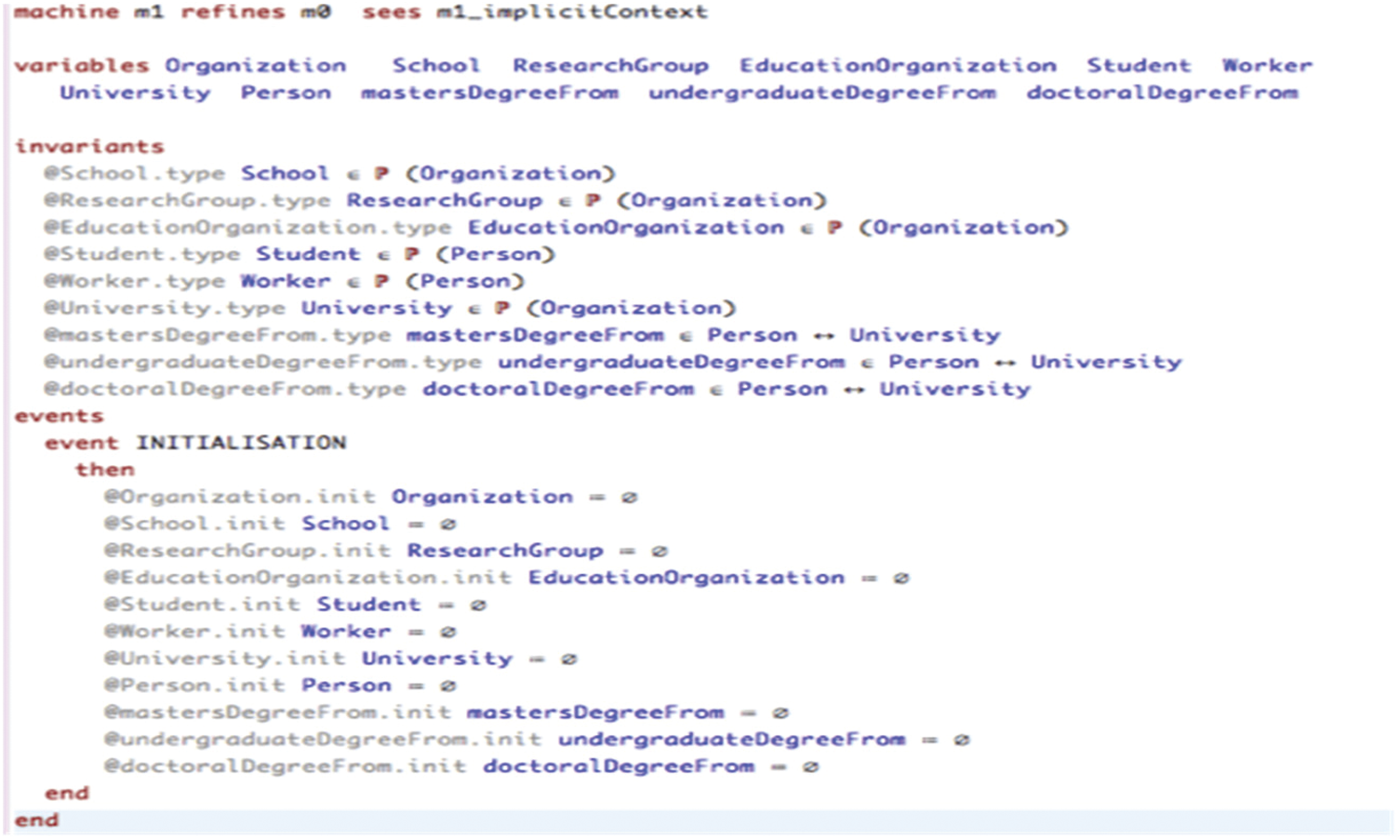
Figure 27: The event-B models generated from the class diagrams of m1
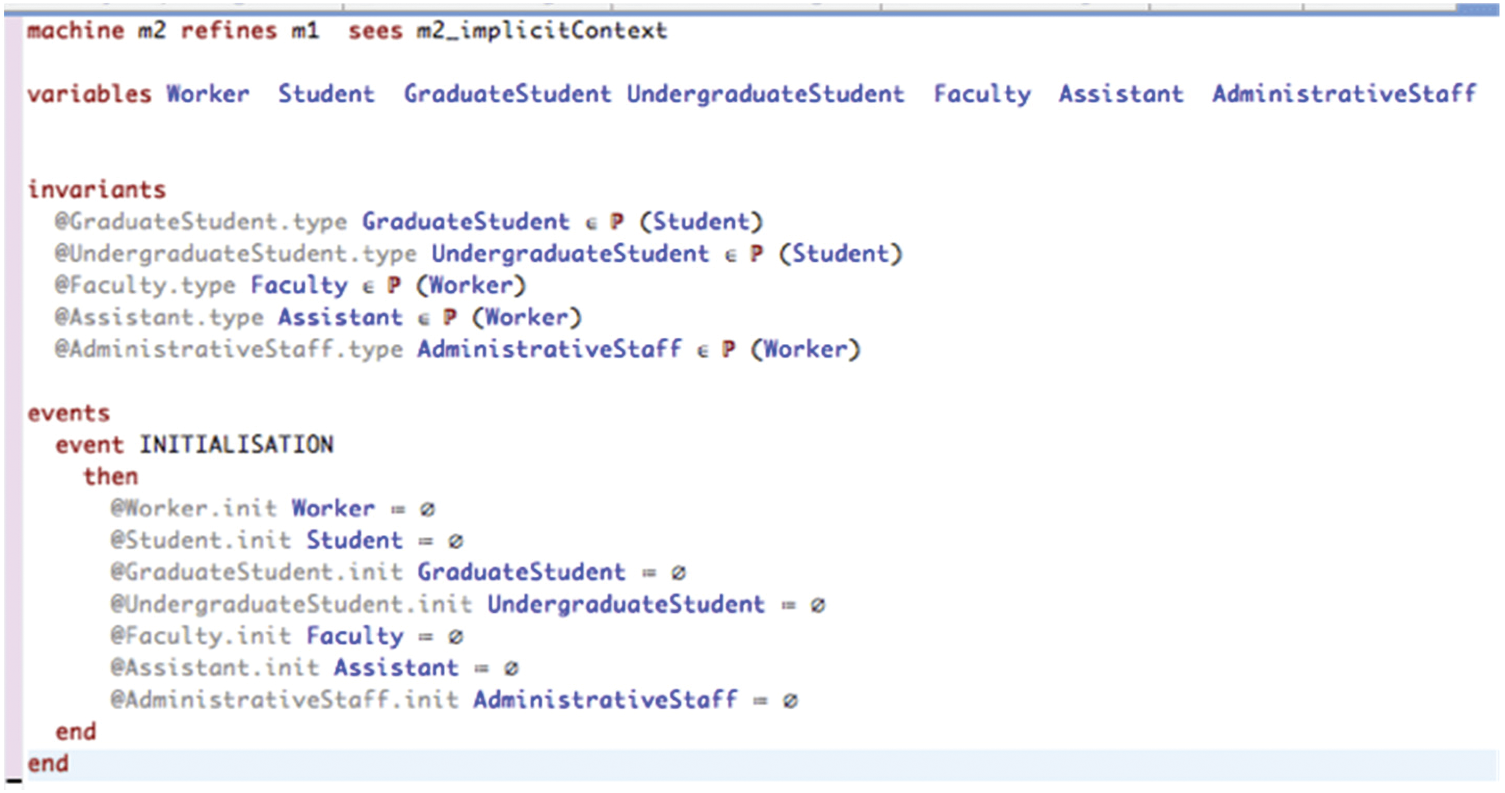
Figure 28: The event-B models generated from the class diagrams of m2

4.2 Case Study 2: Smart Home Weather Ontology
The Smart Home Weather ontology [19] handles data regarding weather phenomena that occur at a certain location on Earth between the present time and 24 h in the future. It enables a smart home system that uses SmartHomeWeather to make decisions based on current and future weather conditions for efficient energy use in buildings. The Smart Home Weather ontology covers a wide range of weather and climate data, such as atmospheric pressure, humidity, temperature, precipitation, and wind. The Smart Home Weather ontology covers a set of concepts, such as weather phenomena (i.e., temperature, humidity, speed, and so on) and weather conditions (fog, rain, snow, thunder, and so on). Weather is a state that summarizes all weather phenomena over a certain time frame. We decide to organize the refinement steps of the OWL ontology into four levels: m0–m3, as shown in Fig. 29. OntoGraf provides the modeler with a good view of how to organize the refinement levels.
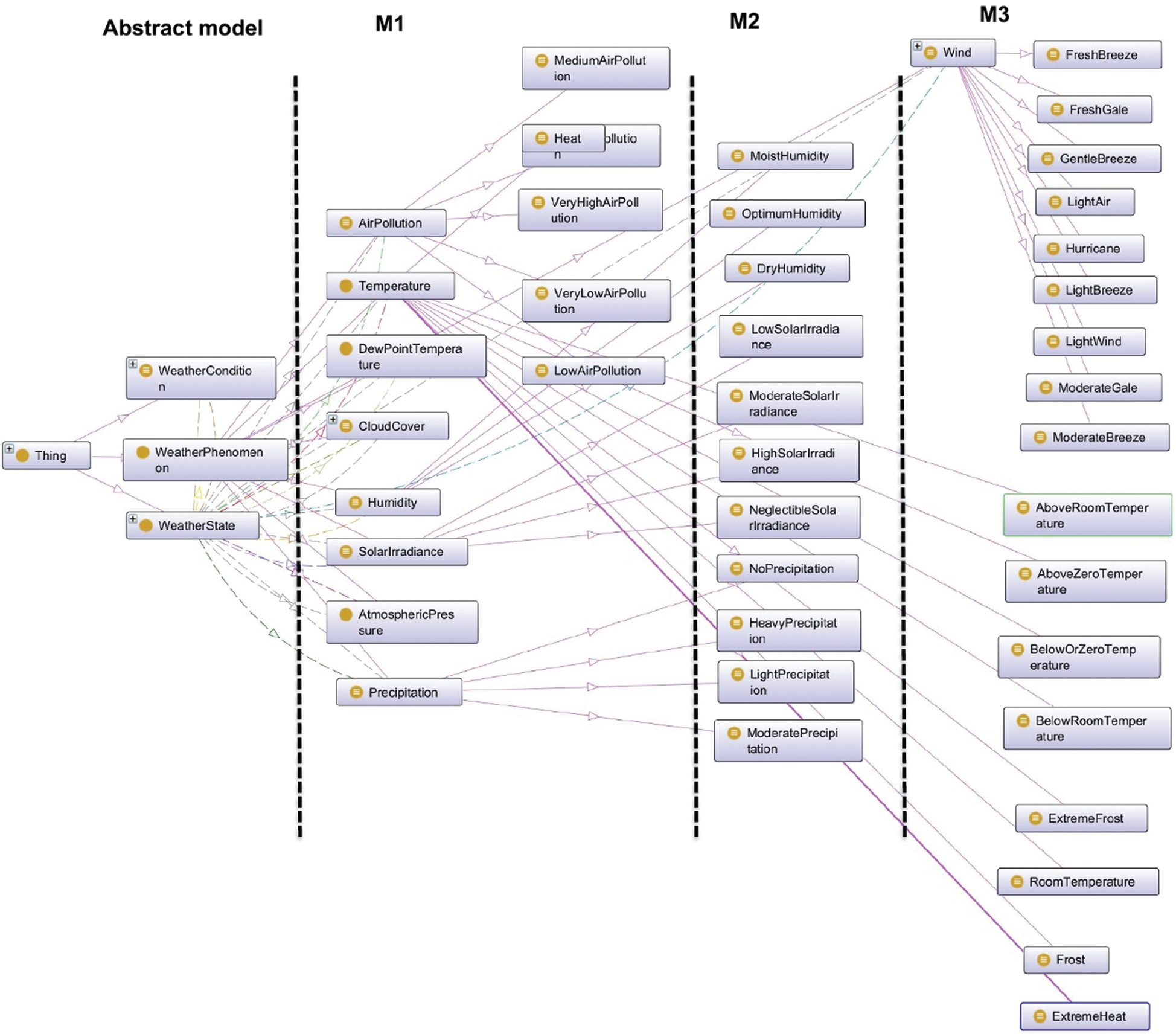
Figure 29: The overall representation of the smart home weather OWL ontology in OntoGraf
We transfer the diagram to UML-B diagrams using the steps mentioned in Section 3, and Event-B models with a total of 119 POs are generated from the m0–m3 Event-B models and automatically discharged. The proof statistics of the Smart Home Weather ontology models are given in Tab. 2.

In this section, we outline the lessons learned from the application of the proposed approach to case studies and discuss the improvements that could address the limitations of the proposed methodology. Regarding the strengths of the proposed approach, we outline three main benefits as follows:
1)The proposed approach allows us to capture knowledge in OWL ontologies and convert it to Event-B models. Moreover, large sets of OWL ontologies for different domains exist in several repositories. Thus, the Event-B modeler can use OWL ontologies to gather precise, complete, and consistent requirements for the system to be modeled.
2)OntoGraf is found to be useful in organizing refinement levels. It allows the modeler to focus on a specific level of the ontology and decide the levels of refinements. The organization of refinement levels is often considered a source of difficulty, especially for requirements written in English.
3)We find that most POs are run automatically, which reduces the burden on the modeler to work on POs. The axioms of OWL ontologies must be translated manually; therefore, the axioms may be written in an incorrect way, resulting in mistakes in POs. Model correctness is established by discharging POs.
These are the three important benefits of the proposed approach. However, it has two limitations, which are as follows:
a) Tooltips introduce details about particular classes, such as disjoint classes, superclasses, equivalent classes, and axiomatic definitions. Sometimes, the modeler cannot introduce all details of the tooltip in the current level to be modeled. For instance, the definitions of equivalent classes of AirPollution for model m1 must be postponed until the modeler defines all classes that are equivalent to AirPollution, and these are HighAirPollution, LowAirPollution, and MediumAirPollution, as illustrated in Fig. 30.
b) OntoGraf does not demonstrate object properties and data properties; therefore, we use the object properties and data properties tabs in Protégé to model these properties. We must ensure that the domain and range of the properties exist on that level to investigate the suitable refinement level for these properties. Otherwise, we must postpone the definition of these properties until we introduce the class of the domain and the range. For instance, in Fig. 24, the property UndergraduateDegreeFrom is defined in model m1, where we introduce the range University.
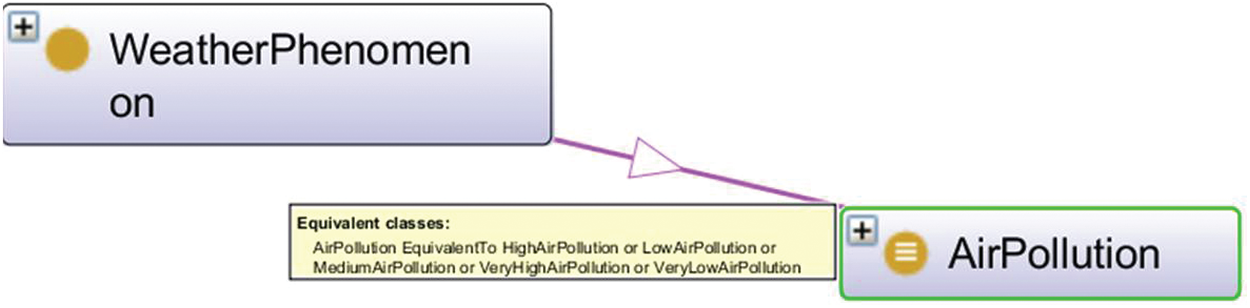
Figure 30: Equivalent classes of AirPollution
The proposed approach does not show how to create events. However, we can use the approach mentioned in [8] to address this issue. Reference [8] classifies requirements into several classes. One such class that defines events is the class of event-oriented requirements, which are defined as requirements that describe a function or activity of the system or its components, and they are normally ide.pngied by verbs. This definition leads us to think of modeling events based on the object properties and data properties of OWL ontologies. For instance, we can introduce the event getMastersDegreeFrom from the object property mastersDegreeFrom in Fig. 24 and define it in Fig. 31.
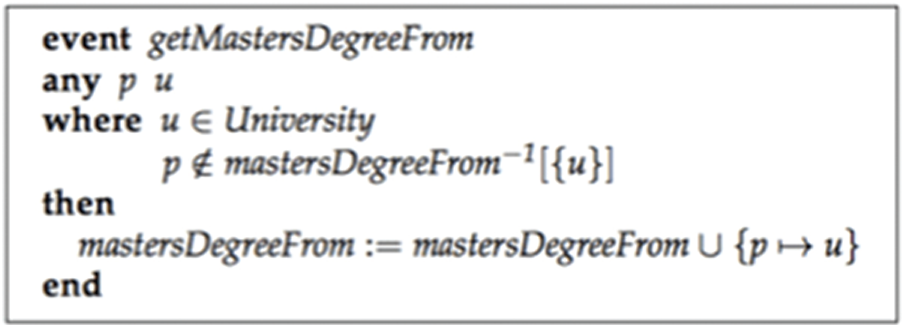
Figure 31: Event-B model corresponding to UML-B
Similarly, since we have constants, sets, variables, and invariants, we can ide.pngy several events, such as getUndergraduateDegreeFrom and getDoctoralDegreeFrom.
In this paper, we proposed an approach that uses OWL ontologies to construct Event-B formal models. The approach transforms OntoGraf diagrammatic notations into UML-B diagrammatic notations and supports data analysis. The proposed approach has many advantages. It (1) is a new approach for capturing requirements and transforming OWL ontologies into Event-B formal models, (2) bridges the gap between ontologies and Event-B formal models, and (3) reduces the effort required for verification because the transformation is performed from the formal representations (ontologies) to Event-B formal models. Furthermore, (4) the transformation is performed using graphical structures, including OntoGraf and UML-B, and (5) the refinements are supported by the proposed approach by layering OntoGraf diagrams first and then transforming them into UML-B diagrams. In the future, we will develop a tool to automatically transform OntoGraf into UML-B. Another direction of future work will be to evaluate the approach mentioned in Section 3 for developing events from OWL ontologies.
Acknowledgement: The author would like to acknowledge Taif University Researchers Supporting Project Number (TURSP-2020/292), Taif University, Saudi Arabia.
Funding Statement: This work was supported by Taif University Researchers Supporting Project Number (TURSP-2020/292), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Knublauch, R. W. Fergerson, N. F. Noy and M. A. Musen, “The protege OWL plugin: An open development environment for semantic web applications,” in Int. Semantic Web Conf., Berlin, Heidelberg, pp. 229–243, 2004. [Google Scholar]
2. T. Avdeenko and N. Pustovalova, “The ontology-based approach to support the completeness and consistency of the requirements specification,” in Int. Siberian Conf. on Control and Communications, Omsk, IEEE, pp. 1–4, 2015. [Google Scholar]
3. H. E. Elsherbeiny and A. A. El-Aziz, “Survey on attempts to enhance requirements engineering process,” CIIT International Journal of Software Engineering and Technology, vol. 8, no. 6, pp. 135–139, 2016. [Google Scholar]
4. D. Dermeval, J. Vilela, I. I. Bittencourt, J. Castro, S. Isotani et al., “Systematic review on the use of ontologies in requirements engineering,” in 2014 Brazilian Symp. on Software Engineering, Maceio, Brazil, IEEE, pp. 1–10, 2014. [Google Scholar]
5. D. Connolly, F. van Harmelen, I. Horrocks, D. L. McGuinness, P. F. Patel-Schneider et al., “Daml + oil (March 2001) reference description, December 2001,” Internetquelle, 2007. [Online]. Available: http://www.w3.org/TR/daml+oilreference,heruntergeladenam5. [Google Scholar]
6. J. S. Dong, J. Sun and H. Z. Wang, “Z approach to semantic web,” in Int. Conf. on Formal Engineering Methods, Berlin, Heidelberg, pp. 156–167, 2002. [Google Scholar]
7. S. J. T. Fotso, A. Mammar, R. Laleau and M. Frappier, “Event-B expression and verification of translation rules between SysML/KAOS domain models and B system specifications,” in Int. Conf. on Abstract State Machines, Alloy, B, TLA, VDM, and Z, Cham, pp. 55–70, 2018. [Google Scholar]
8. E. H. Alkhammash, M. Butler, A. S. Fathabadi and C. Cîrstea, “Building traceable event-B models from requirements,” Science of Computer Programming, vol. 111, no. 6, pp. 318–338, 2015. [Google Scholar]
9. E. H. Alkhammash, “Derivation of event-B models from owl ontologies,” MATEC Web of Conferences, vol. 76, no. 6, pp. 4008, 2016. [Google Scholar]
10. E. H. Alkhammash, “Formal modelling of OWL ontologies-based requirements for the development of safe and secure smart city systems,” Soft Computing, vol. 24, no. 15, pp. 1–14, 2020. [Google Scholar]
11. I. Ait-Sadoune and L. Mohand-Oussaid, “Building formal semantic domain model: An Event-B based approach,” in Int. Conf. on Model and Data Engineering, Cham: Springer, pp. 140–155, 2019. [Google Scholar]
12. L. Mohand-Oussaïd and I. Aït-Sadoune, “Formal modelling of domain constraints in event-B,” in Int. Conf. on Model and Data Engineering, Cham: Springer, pp. 153–166, 2017. [Google Scholar]
13. N. Garanina, I. Anureev, E. Sidorova, V. Zyubin and S. Gorlatch, “An ontology-based approach to support formal verification of concurrent systems,” in Int. Symp. on Formal Methods, Cham: Springer, pp. 114–130, 2019. [Google Scholar]
14. R. Hoehndorf, L. Slater, P. N. Schofield and G. V. Gkoutos, “Aber-OWL: A framework for ontology-based data access in biology,” BMC Bioinformatics, vol. 16, no. 1, pp. 26, 2015. [Google Scholar]
15. C. Patel, K. Supekar, Y. Lee and E. K. Park, “OntoKhoj: A semantic web portal for ontology searching, ranking and classification,” in Proc. of the 5th ACM Int. Workshop on Web Information and Data Management, New Orleans, Louisiana, USA, pp. 58–61, 2003. [Google Scholar]
16. M. Y. Said, M. Butler and C. Snook, “A method of refinement in UML-B,” Software & Systems Modeling, vol. 14, no. 4, pp. 1557–1580, 2015. [Google Scholar]
17. J. R. Abrial and S. Hallstead, “Refinement, decomposition, and instantiation of discrete models: Application to event-B,” Fundamenta Informaticae, vol. 77, no. 1–2, pp. 1–28, 2007. [Google Scholar]
18. Y. Guo, Z. Pan and J. Heflin, “LUBM: A benchmark for OWL knowledge base systems,” Journal of Web Semantics, vol. 3, no. 2–3, pp. 158–182, 2005. [Google Scholar]
19. P. Staroch, “A weather ontology for predictive control in smart homes,” Ph.D. dissertation, Vienna University of Technology, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |