DOI:10.32604/cmc.2022.018247

| Computers, Materials & Continua DOI:10.32604/cmc.2022.018247 |  |
| Article |
Process Modelling and Experimental Analysis of Optimal Specimen Selection in Organic CMCs
1Faculty of Mechanical Engineering, Saranathan College of Engineering, Trichy, 620012, India
2Department of Mechanical Engineering, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Chennai, 600062, India
3School of Computing, University of Eastern Finland, Kuopio, FI-70211, Finland
*Corresponding Author: Kanak Kalita. Email: drkanakkalita@veltech.edu.in
Received: 02 March 2021; Accepted: 06 June 2021
Abstract: Bone grafting is a surgical restructuring procedure of replacing broken bones and reconstructing missing bone pieces so that complex bone fractures can be repaired to avoid any serious health risk as well as permanent bone disfiguration. Normally, human bones tend to regenerate and heal completely from fracture. But it needs a small scaffold to provide the necessary space to grow. Bone implants allow a broken bone to grow seamlessly. Traditionally, non-corrosive metal alloys are used for fixing broken bones. A metal plate is fastened between two ends of broken bones to join them. However, issues like high weight, high cost, low wear resistance, etc. led to the emergence of ceramics and ceramic-based composites in surgical engineering. Recent trends indicate the usage of organic ceramics and their associated composites as biomimetic materials for prostheses and other biomedical applications. This research paper deals with the fabrication of one such type of ceramic matrix composite (CMC) specimen with sea sponge and cuttlebone using powder metallurgy process by varying composition of cuttlebone, the particle size of the ceramics and sintering temperature of green compacts. Evaluation of thermo-mechanical properties and optimization of process parameters is carried out using the preferential selection index (PSI) method. The results obtained from this technique are further validated using Multi-Level General Factorial Design (MLGFD).
Keywords: Grafting; implants; ceramics; composites; prostheses; powder metallurgy; optimization
Composites find numerous applications in a wide range of domains such as engineering, marine, medical, space sciences, domestic multi-purpose commodities, aircraft exterior and interior structures due to their attractive properties and characteristic superiority over conventional materials. A wide range of metal matrix, polymer matrix and ceramic matrix composites are extensively used in biomedical as well as surgical applications such as orthopaedic implants, teeth and bone prostheses and fixation, hip joint replacements, curing femoral and collar bone fractures, treating minor maxillofacial irregularities etc. due to their chemical inertness, speedy and uniform crack growth propagation, corrosion resistance and biodegradability. Ibrahim et al. [1] in their paper reviewed various literature regarding the usage of bio-metals, bio-ceramics and bio-polymers and described various fabrication techniques to enhance the tribological, mechanical and biomedical properties of orthopaedic implants. They also indicated that some commonly used metals like stainless steel, Ti-alloys and Co-alloys failed to prove long-term durability and did not provide sufficient bond with human bone. Agarwal et al. [2] conducted a literature survey based on the corrosion behaviour, biocompatibility and surface modifications of biodegradable magnesium alloys for orthopaedic applications.
Ceramic matrix composites (CMCs) find enormous use in fixing broken orthopaedic structures. This is because they mimic the structural and decomposition properties of original bones. Their non-reactance with blood as well as their absorbance in natural bones as bones grow spontaneously in the fractured area makes them robust and most sought after. Moreover, there is no need to remove these synthetic composites after the growth of natural bone in the concerned body part. These are often preferred over corrosion-resistant metals and their alloys like chromium, stainless steel, copper etc. The main disadvantages of using metals in orthopaedic joints are their uneasiness in a normal lifestyle and the necessity to remove metal plates after the growth and fixing of normal bones at the localized area inside the body part [3].
The use of natural, synthetic, and organic ceramics like alumina, zirconia, calcium phosphate, bioactive glass, bone skeletons of dead marine animals, etc. has increased in biomedical surgeries in the form of collagen and chitosan. Choi and Nissan, in their book, elaborated the preparation methods, synthesis and applications of marine-based bio-ceramics such as corals, sea sponges, sea urchins, crab shells and oyster shells in bone tissue engineering [4]. Pallela and Ehrlich, in their book, briefed the biological and chemical structure of sea sponge fossils. This book concentrated more on the DNA functionality and biological drug derivatives of sea sponges [5].
Cadman et al. [6] have dealt with the characterization, development and application of a lightweight coral-like structure called cuttlebone. It is extracted from a marine organism called cuttlefish. Their work gave immense details about the porous filled cellulose structure, biological nature and mechanical behaviour of cuttlebone. The use of a marine-derived biomaterial called cuttlebone and its associated composites as biomimetic materials for bone growth and bone tissue engineering is on the verge of increasing in the modern world, according to Palaveniene et al. [7]. In their research article, they determined the essential properties of cuttlefish-based bio composites such as porosity, modulus of elasticity, biocompatibility, strength and non-toxicity through various experiments by conducting various tests.
The use of any such natural source as reinforcement for CMC would require a good understanding of the various parameters involved. Determining the optimal combination of the various parameters can be carried out by using any global optimization approach. In this regard, an attempt has been made in this paper to use multi-criteria decision making (MCDM) methods to provide an efficient and inexpensive alternative. Preferential selection index (PSI), a popularly used MCDM technique developed by Maniya and Bhatt in 2010 is used in the current work. The main advantage of this method is that there is no necessity to assign any relative importance (weightage) between attributes [8]. Further, general factorial design (GFD), a type of factorial design of experiments, that initiates the optimization procedure by identifying the number of experimental runs based on the types and the levels of process parameters [9] is also used in form of MLGFD. Multi-level general factorial design (MLGFD) is a novel category in GFD, which is more flexible and user-friendly when compared to other design of experiments. Its adaptability and flexibility lie in selecting a varying number of levels for every factor. Different levels can be chosen for each factor in the same experimental design. The factors, as well as the levels, need not be uniform.
The selection of matrix and reinforcement materials for CMC is the preliminary step in this type of research [10]. In the current work, sea sponge is selected as the matrix and Cuttlebone is selected as the reinforcement.
Matrix is the major constituent, which is present at a larger proportion in the composite. It provides rigidity to the composite and protects it from dissociation. The matrix material selected for the present research work is sea sponge. Sea sponge is a deep-sea marine multi-cellular organism, belonging to the phylum Porifera, which has a porous body. It is a hard and brittle organic ceramic, whose body is full of fatty acids of hydrocarbons with significant metal concentration. Its properties like high refractoriness, high oxidation, high decomposition temperature and high-pressure withstanding ability make it a perfect choice for composites [11].
Reinforcement is the minor constituent, which is dispersed inside the matrix at a comparatively lesser proportion in the form of particles, fibres or flakes. It provides binding strength and integrity to the composite. The reinforcement material selected for the present research work is Cuttlebone [12]. Cuttlebone is the hard and brittle internal structure of Cuttlefish shell. It belongs to the phylum Sepia Officinalis of the family Sepiidae. It is primarily composed of Aragonite, one of the common natural carbonate materials. As it is rich in calcium carbonate, it can be widely used to replace broken bones and enhance bone density [13].
The CMCs are fabricated by powder metallurgy technique, which is very precise and produces a good surface finish in composites [3]. This technique consists of five steps namely, preparation of ceramic powders, pulverization, blending, compaction and sintering.
In the first step, sea sponges and cuttlebones are washed, cleaned, dried and weighed. In the second step, both sea sponges and cuttlebones are put together in a ball mill and broken into uniform-sized microparticles [14]. Fine particulate powder can be obtained by passing the mixture through a set of sieves that are arranged from top to bottom in decreasing mesh size. In the next step, sea sponge powder along with cuttlebone powder is mixed evenly and thoroughly with the application of a bio-inert binder PVC. Then, the blended powders (40 g in total) are charged inside the die. Pressure is exerted on the powders using a plunger, which is pressed against the die using the compression section of a universal testing machine (UTM). The resultant green compact has a length of 100 mm and a diameter of 15 mm. Finally, the green compact is removed from the punch and is kept inside a closed chamber muffle furnace for sintering. The sintering temperature is always below the melting point of ceramic powders [15]. After heating, the composite specimens are taken out and cooled in open air [16]. The process parameters for powder metallurgy and their associated values are given in Tab. 1 below.
A total of 18 specimens are required based on the following experimental runs [17] derived from GFD as shown in Tab. 2. Four samples are prepared for each of the 18 specimen combinations to account for experimental error and check the repeatability of experiments [18].
2.4 Mechanical and Thermal Tests
Various tests are conducted to experimentally investigate the mechanical and thermal properties as per ASTM standard testing procedures [19].
These tests are conducted to observe the mechanical characteristics of the specimens. In this work, compression test and hardness test are carried out to identify compressive strength and microhardness. A material used for bone implants should have a high load-bearing capacity [20]. Compression tests for all the 18 specimens are done at the compression section of UTM and the respective compressive strength is tabulated in Tab. 2 below. The diameter of the specimens is 15 mm.
Hardness is the ability of a material to withstand load in the form of scratch, abrasion or indentation without deformation. Normally, ceramics exhibit a high degree of hardness, as they are tough and brittle [21]. All the specimens are subjected to Vickers hardness, by applying a point load using an indenter tip. Point load exerted on the specimen by diamond indenter is 10 gf and the time taken for applying load is 10 s. The results for Vickers hardness are tabulated in Tab. 2.
These tests are conducted to observe the behaviour of the specimens when heat is applied to them. In this work, flammability test and thermal analysis are carried out to measure the heat retention and heat-resisting capacity of the specimens. A bone implant material necessarily should be heat resistant so that it can withstand high temperature without deformation [22]. Flammability test methods measure how easily materials ignite, how quickly they burn and how they react when burned. A flammability test is done to observe the flame retardance tendency of a material. During this test, a material is observed for the length of time it burns after the igniting flame is removed. How much of the specimen burns and whether it drips flaming particles are also studied. In this test, 2 samples each of equal mass are taken from all the 18 composite specimens and are made to burn continuously for 5 min in horizontal as well as vertical positions. Then, the mass loss resulted due to burning is noted. The test results are represented in Tab. 3.
Thermal analysis is a branch of material science where the properties of materials are studied as they change with respect to temperature. Here, the composite specimens are kept in an electrical oven and heated at a temperature of 50°C and the weight loss with respect to time is measured. When the specimens are heated, the gas and air bubbles, previously entrapped inside the micropores of the specimen will get evaporated and the resultant weight is reduced [23]. Tab. 4 represents the results obtained from the thermal analysis of composite samples.
2.5 Optimization of Process Parameters
Optimization is the process of selecting the best possible specimen from a set of given alternatives by evaluating various properties associated with those specimens and the effect of process parameters over the properties. In this study, an experimental investigation is done on thermo-mechanical properties namely flammability, heat retention capacity, compressive strength and microhardness. The process parameters and the corresponding properties are optimized by Preferential Selection Index (PSI). The results obtained from PSI are further validated using Multi-Level General Factorial Design (MLGFD).
2.5.1 Multi-Criteria Decision Making (MCDM) using Preferential Selection Index (PSI)
Multi-Criteria Decision Making is an optimization methodology in which the best alternative is chosen from a set of combinations [24]. In MCDM, the different thermo-mechanical properties are considered as criteria or attributes.
Preferential Selection Index (PSI) is a recently developed MCDM technique in which ranking of the best alternative is done without considering the weight factor of different criteria [25]. In this research work, the optimal composite specimen is identified by carrying out optimization using PSI. The procedural steps, as well as formulae for each step, are given below:
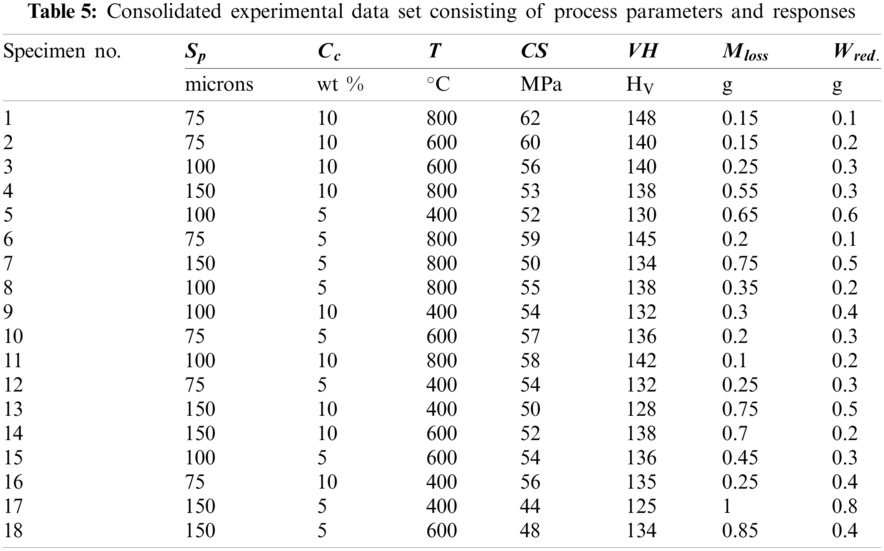
Step 1: Design of experiments table consisting of the parameters and properties of all the 18 specimens as presented in Tab. 5 is considered.
Step 2: Next the type of criteria is determined.
Step 3: Next, a decision matrix is constructed in which each row comprises one alternative (i.e., experimental run) and each column represents one attribute (i.e., criterion) [26]. Therefore, an element ‘xij’ of decision matrix D gives the value of the jth attribute for the ith experimental run. If the number of alternatives is m and the number of criteria is n, then the decision matrix can be represented as follows.
Step 4: Normalization of criteria elements is done to maintain uniformity by keeping the values between 0 and 1 [27].
If the criterion is of beneficial type, then the normalization can be done as per Eq. (2):
If the criterion is of non-beneficial type, then the normalization can be done as per Eq. (3):
where, xij is the individual element in each attribute (i = 1, 2, 3, … , n and j = 1, 2, … , m).
Step 5: Next, the mean value of the normalized data of every attribute is computed as per Eq. (4):
Step 6: In this step, a preference variation value between the values of every attribute is computed as per Eq. (5):
Step 7: The deviation in the preference value is then computed for every attribute using Eq. (6):
Step 8: The overall preference value for every attribute is then determined using Eq. (7):
Step 9: Finally, the preference selection index is calculated for each alternative as per Eq. (8):
2.5.2 Multi-Level General Factorial Design (MLGFD)
General Factorial Design (GFD) or Full Factorial Design is one of the widely used forms of optimizing methodologies, in which the experimental run values are formed with the help of factorial of several trials [28]. MLGFD is a novel sub-category in GFD. It is very flexible as the variation in levels of each factor doesn’t need equal intervals. Moreover, the number of levels need not be uniform and can vary between the factors, [29,30] which is evident from the following work. The various process parameters and their corresponding levels are shown below in Tab. 1. Design of Experiments (DoE) with 18 experimental runs showing 3 factors and 4 responses are represented as Tab. 2.
From Tab. 2, it is clear that the compressive strength of the composite specimens is inversely proportional to the particle size of the powders. Fine powders produce good binding strength and hence produce more strength. The compressive strength reduces with increased particle size. It is also noted that the other two parameters—composition and sintering temperature have very little effect on compressive strength.
The results in Tab. 2, indicate that the Vickers hardness increases with a decrease in particle size. They also show that the Vickers hardness values are directly proportional to the composition of cuttlebone and sintering temperature.
The results presented in Tab. 3, infer that the flammability of the composite specimens is more in vertical position than in horizontal position. The average mass loss is less in composite samples having small particle size and more in composite samples having larger particle size. The composition and sintering temperature have a direct effect on average mass loss resulting due to flammability.
From the results presented in Tab. 4, it is evident that the combined influence of process parameters is considerably high when compared to the individual effect. The weight reduction due to the application of heat is less in specimens having small particle size and vice versa. The weight loss due to thermal exposure reduces with an increase in % composition of cuttlebone as well as sintering temperature.
3.3 Optimal Process Parameter Selection with PSI
Based on the steps illustrated in Section 2.5.1, optimal process parameters are identified using PSI. The consolidated experimental dataset consisting of the process parameters and the four responses is presented in Tab. 5. Compressive strength, Vickers hardness, average mass loss and reduction in weight are considered as the four responses that act as the criteria in the MCDM process for the selection of the best alternative. The best alternative represents the optimal solution among the carried-out experiments. Compressive strength and Vickers hardness are considered as the beneficial type objectives i.e., a higher value is desired. On the other hand, average mass loss and weight reduction are the cost type criteria i.e., lower values are desired. The decision matrix in original form and the normalized form is presented in Tab. 6.
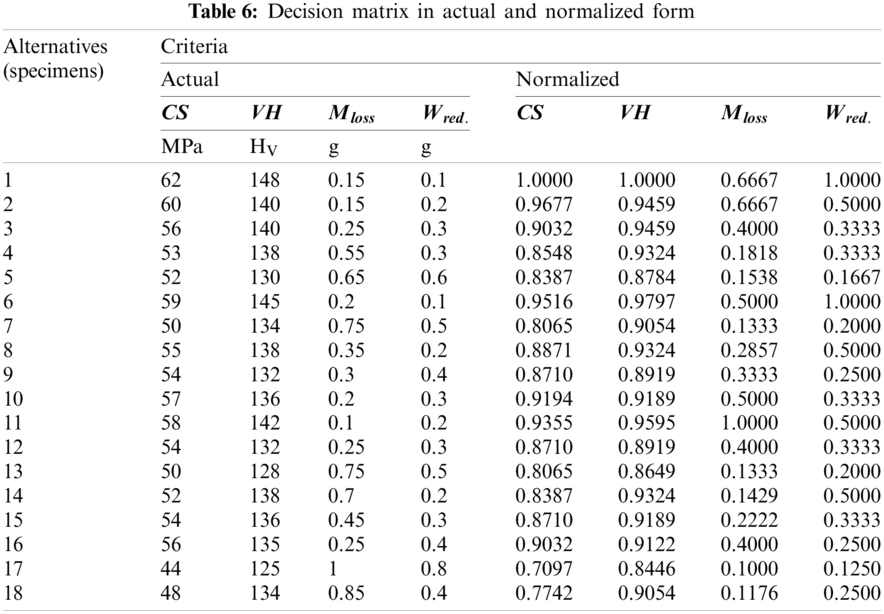
Tab. 7 represents the sum of squares of deviation (preference variation value) (Φj), negation (deviation in the preference value) (Ωj) and overall preference value (ωj). The PSI-based ranks of the alternatives are presented in Fig. 1. The best alternative as per the PSI methodology is highlighted in Tab. 8.
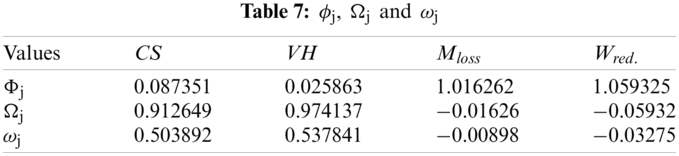
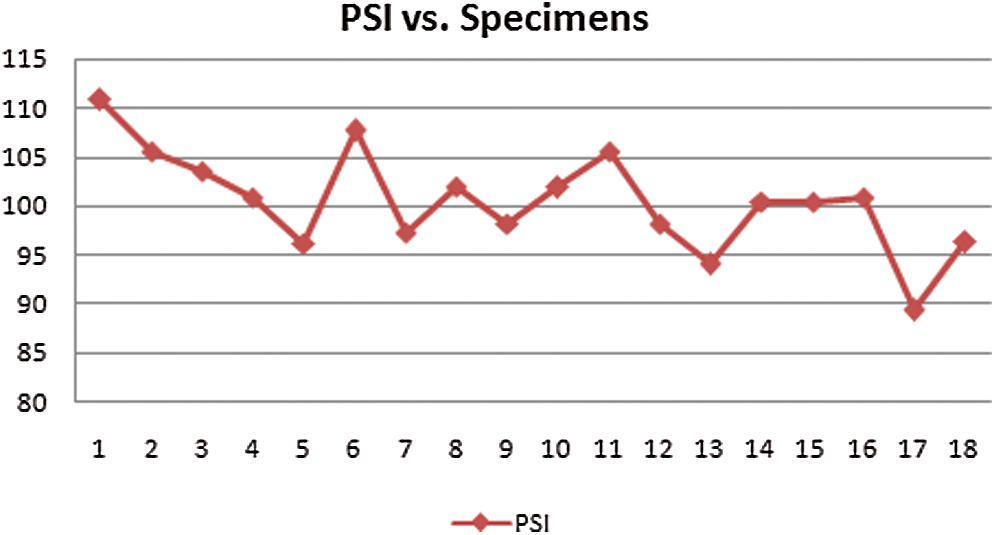
Figure 1: PSI based ranks of the specimens

3.4 Optimal Process Parameter Prediction with MLGFD and Polynomial Regression
Initially full quadratic models are developed for each response using a polynomial regression approach. ANOVA is then applied to the models and the insignificant terms are removed based on p-value > 0.1. The following regression model is developed for expressing compressive strength as a function of particle size of ceramic powders, the composition of Cuttlebone and sintering temperature.
The ANOVA table for compressive strength is shown in Tab. 9. It is seen that all the terms in the selected regression model have a p-value less than 0.1, indicating that they are statistically significant. The model is further probed using various statistical measurements. The externally standardized residuals for the model are plotted as a normal probability plot in Fig. 2a. It is seen that the data points do not cross the lower and upper percentile reference lines and thus, don't show the presence of an outlier or anomaly.
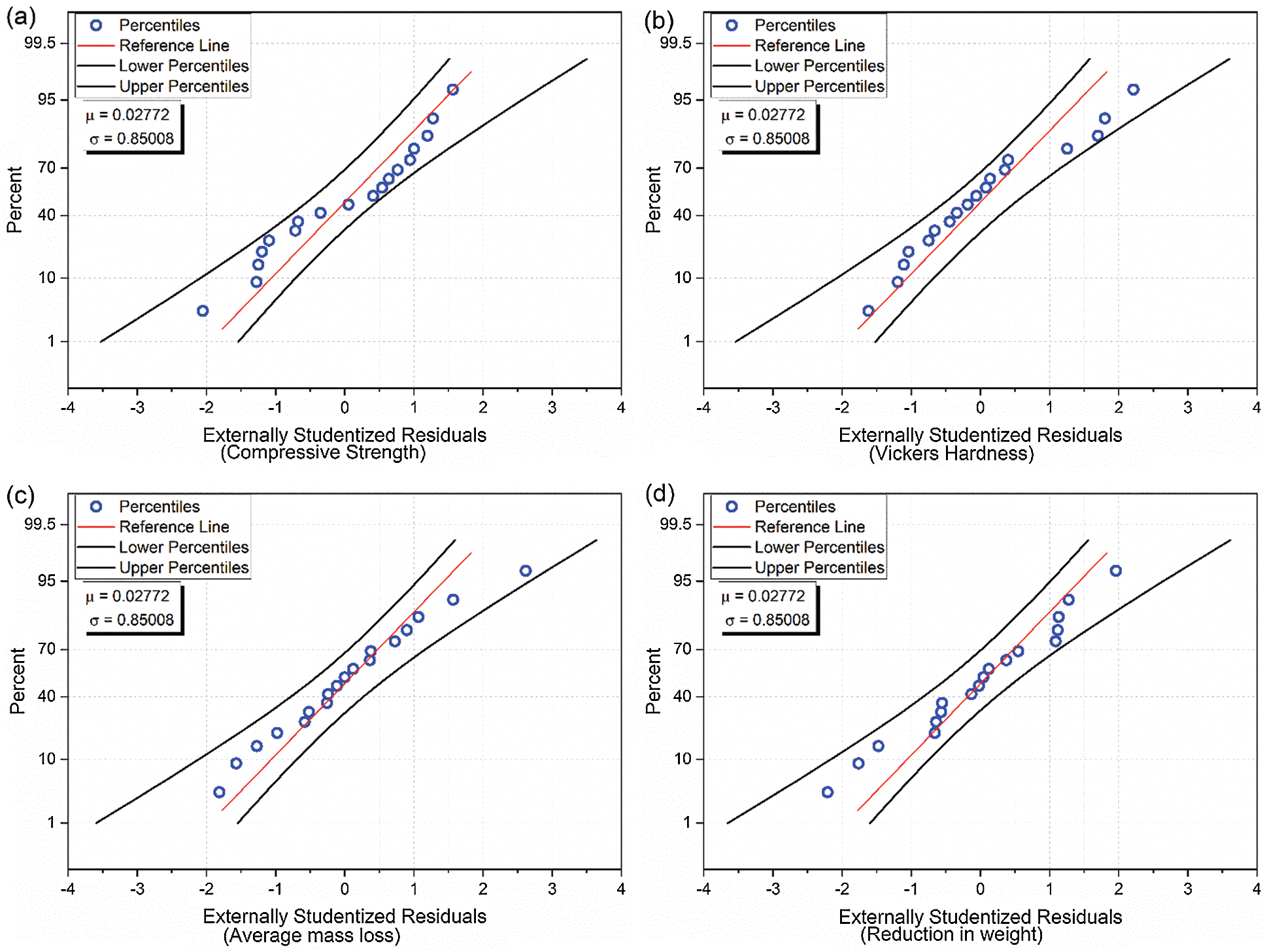
Figure 2: Normal probability plot of externally standardized residuals for (a) Compressive strength (b) Vickers hardness (c) Average mass loss (d) Reduction in weight
Similarly, the externally standardized residuals are plotted against the predicted values in Fig. 3a. Here the scatter is seen to be random and no clusters of datapoints are seen. This indicates the model is not biased. Finally, the predicted compressive strength is plotted vs. the actual compressive strength in Fig. 4a. Here, most of the data points are seen to be hugging the diagonal or the identity line indicating that the predictions are very accurate. The accuracy of the model is further assessed by using
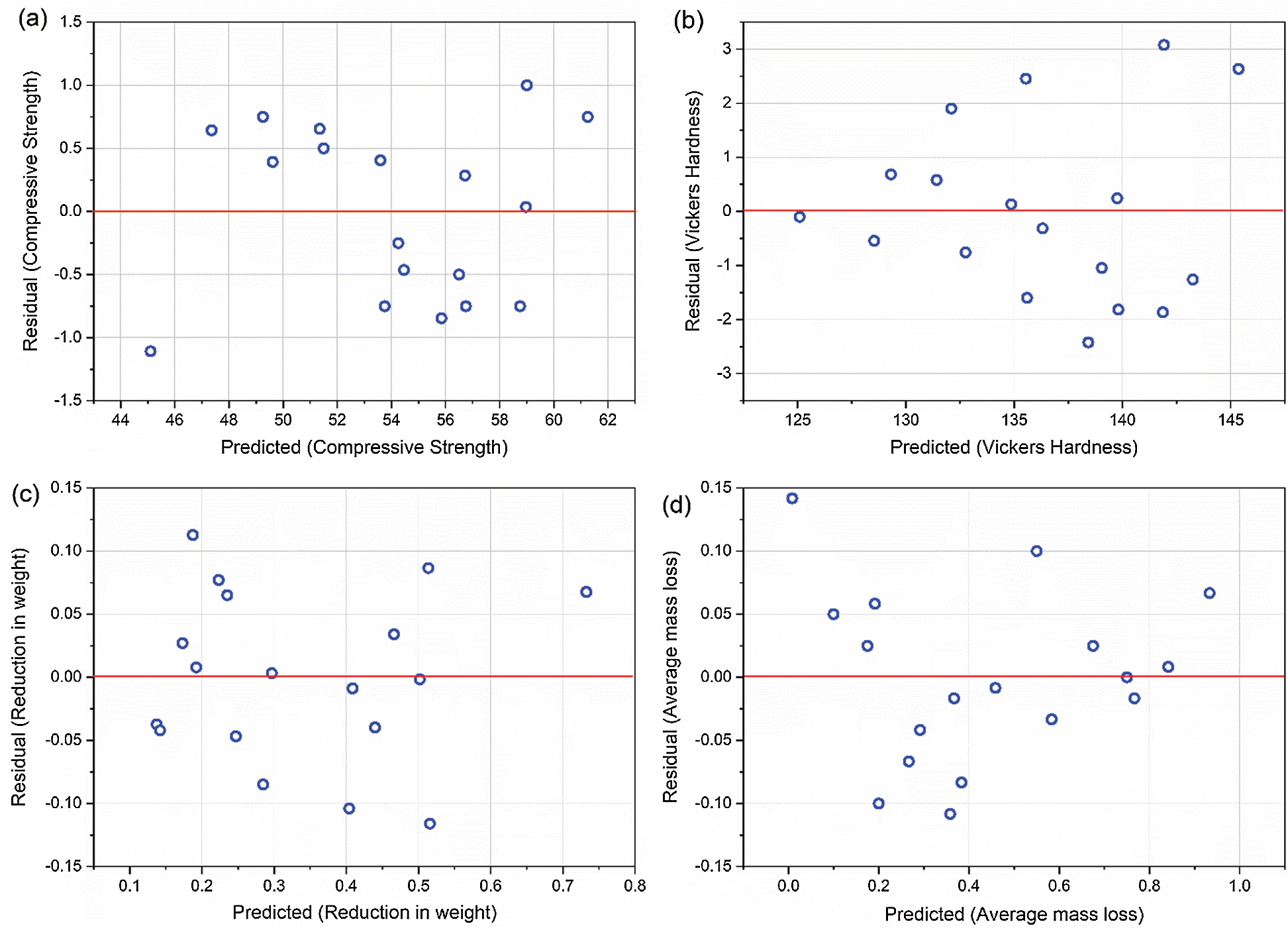
Figure 3: Predicted vs. externally standardized residuals for (a) Compressive strength (b) Vickers hardness (c) Average mass loss (d) Reduction in weight
The
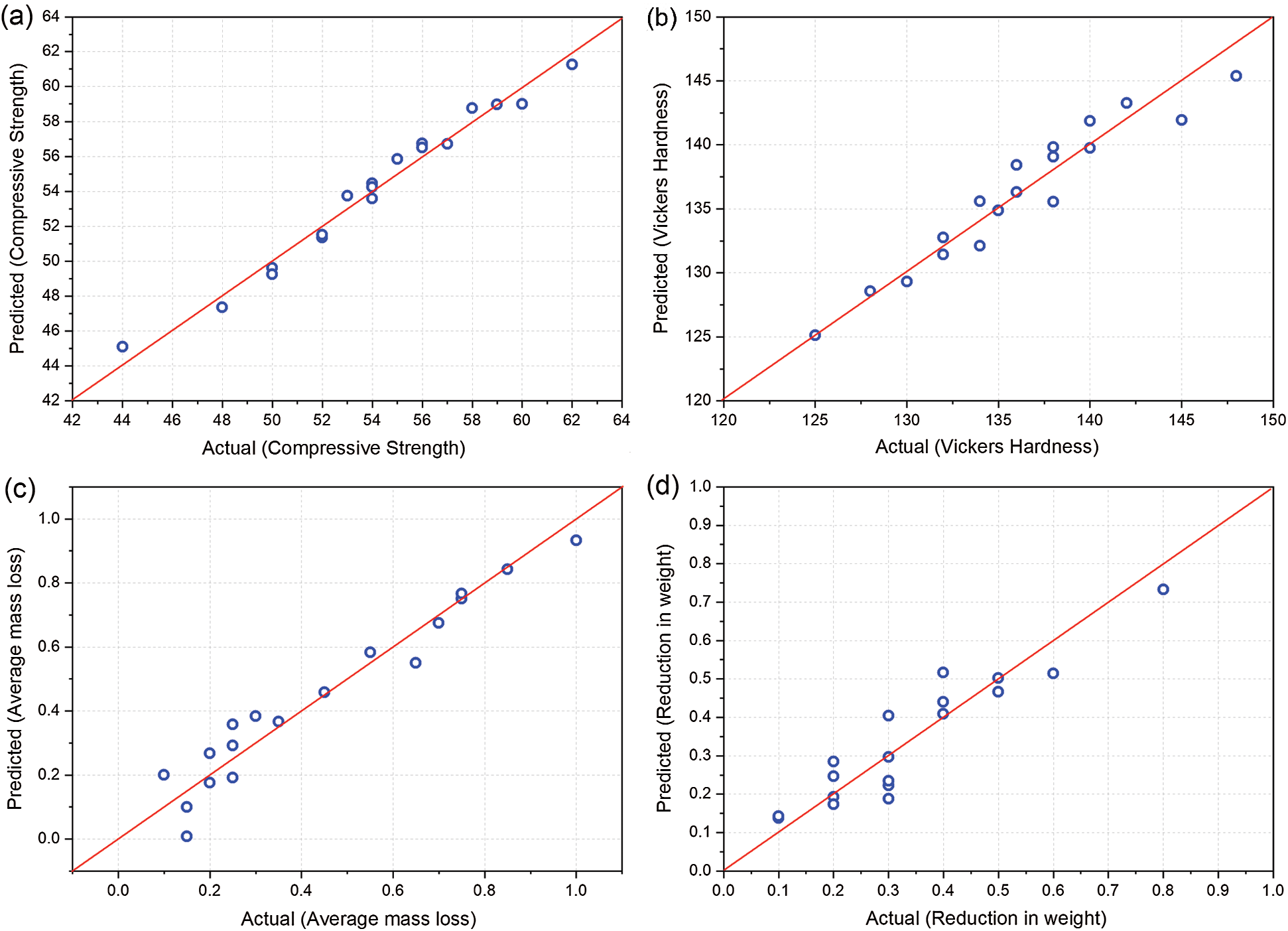
Figure 4: Actual vs. predicted responses for (a) Compressive strength (b) Vickers hardness (c) Average mass loss (d) Reduction in weight
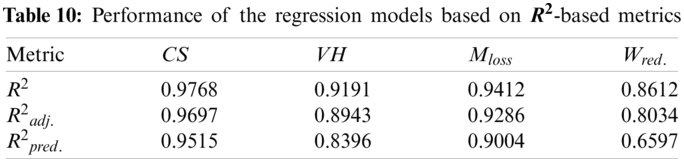
Similarly, a regression model for the Vickers hardness is fitted based on the experimental dataset.
The ANOVA table for Vickers hardness is shown in Tab. 9. The normal probability plot of externally standardized residuals for Vickers hardness is shown in Fig. 2b. The predicted Vickers hardness vs. externally standardized residuals and the predicted Vickers hardness vs. the actual Vickers hardness is shown in Figs. 3b and 4b respectively. The
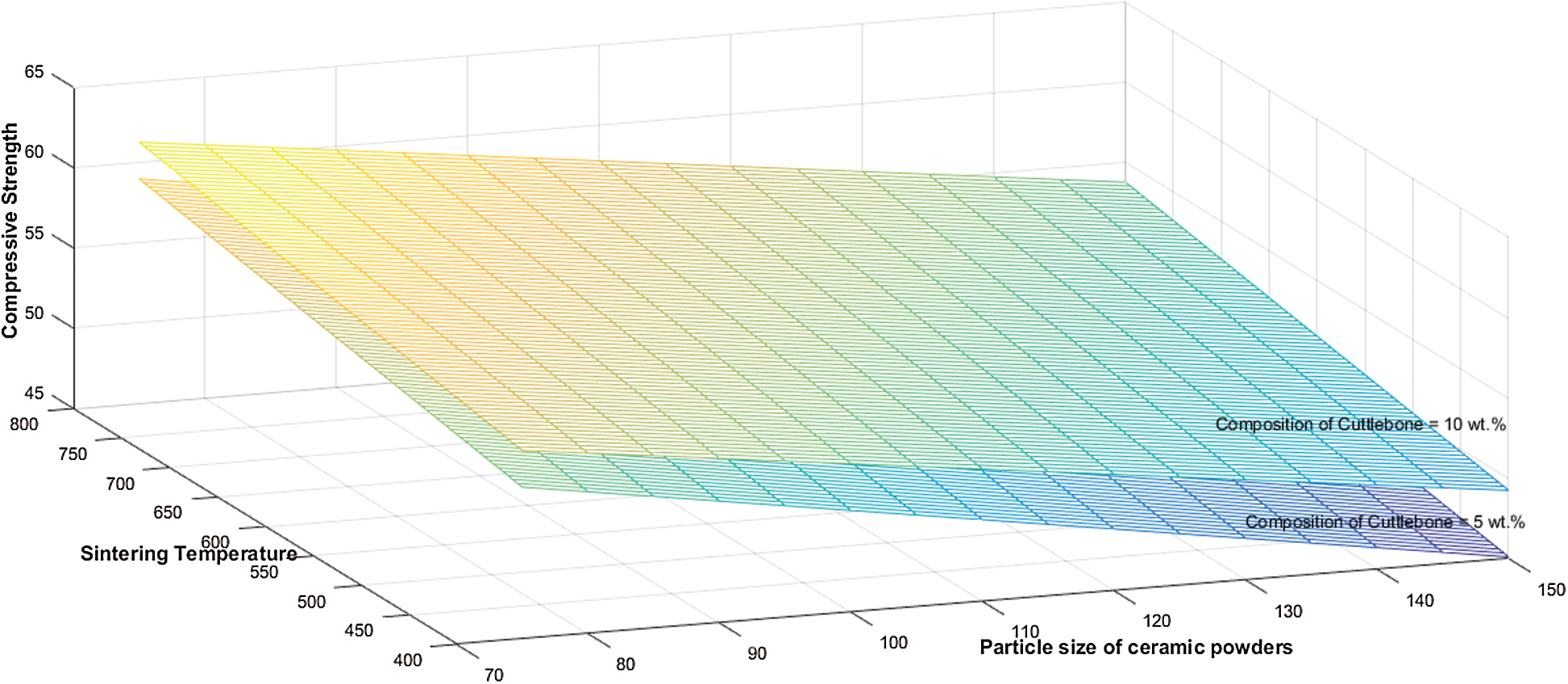
Figure 5: 3D surface interaction plot showing the effect of the particle size of ceramic powders and sintering temperature on compressive strength
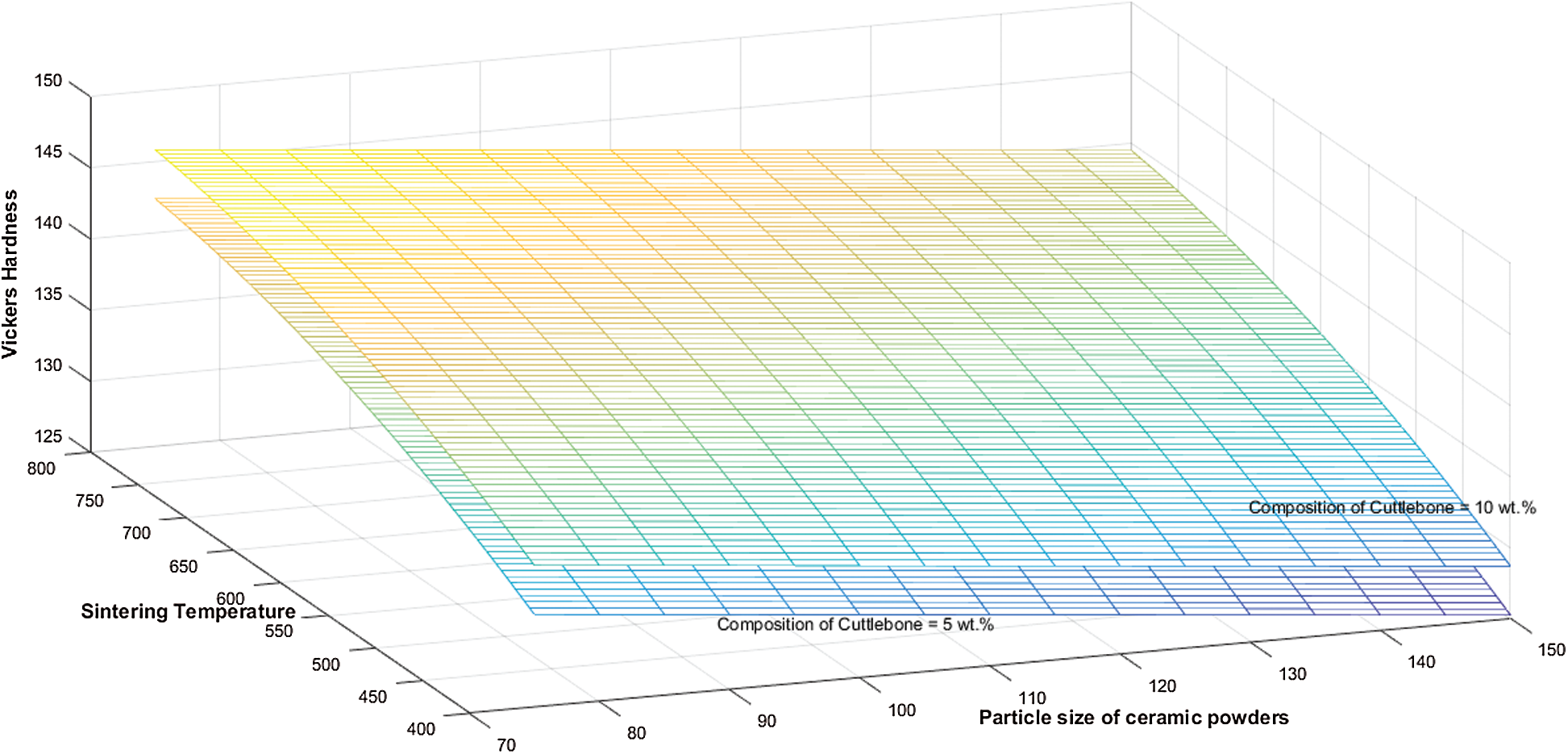
Figure 6: 3D surface interaction plot showing the effect of particle size of ceramic powders and sintering temperature on Vickers hardness
The regression model for average mass loss and reduction in weight is presented in Eqs. (11) and (12) respectively. The ANOVA for average mass loss and reduction in weight regression models are presented in Tab. 11.
The 3D surface interaction plot showing the effect of particle size of ceramic powders and sintering temperature on average mass loss and reduction in weight is presented in Figs. 7 and 8 respectively. Based on the developed regression models presented in Eqs. (9)–(12) and optimization study is carried out using desirability analysis concept. The constraints are tabulated in Tab. 12. Tab. 13 provides the overall optimized solution for 18 combinations of factor levels.
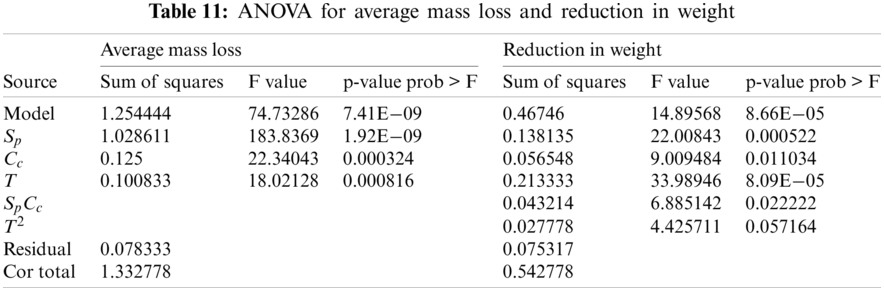
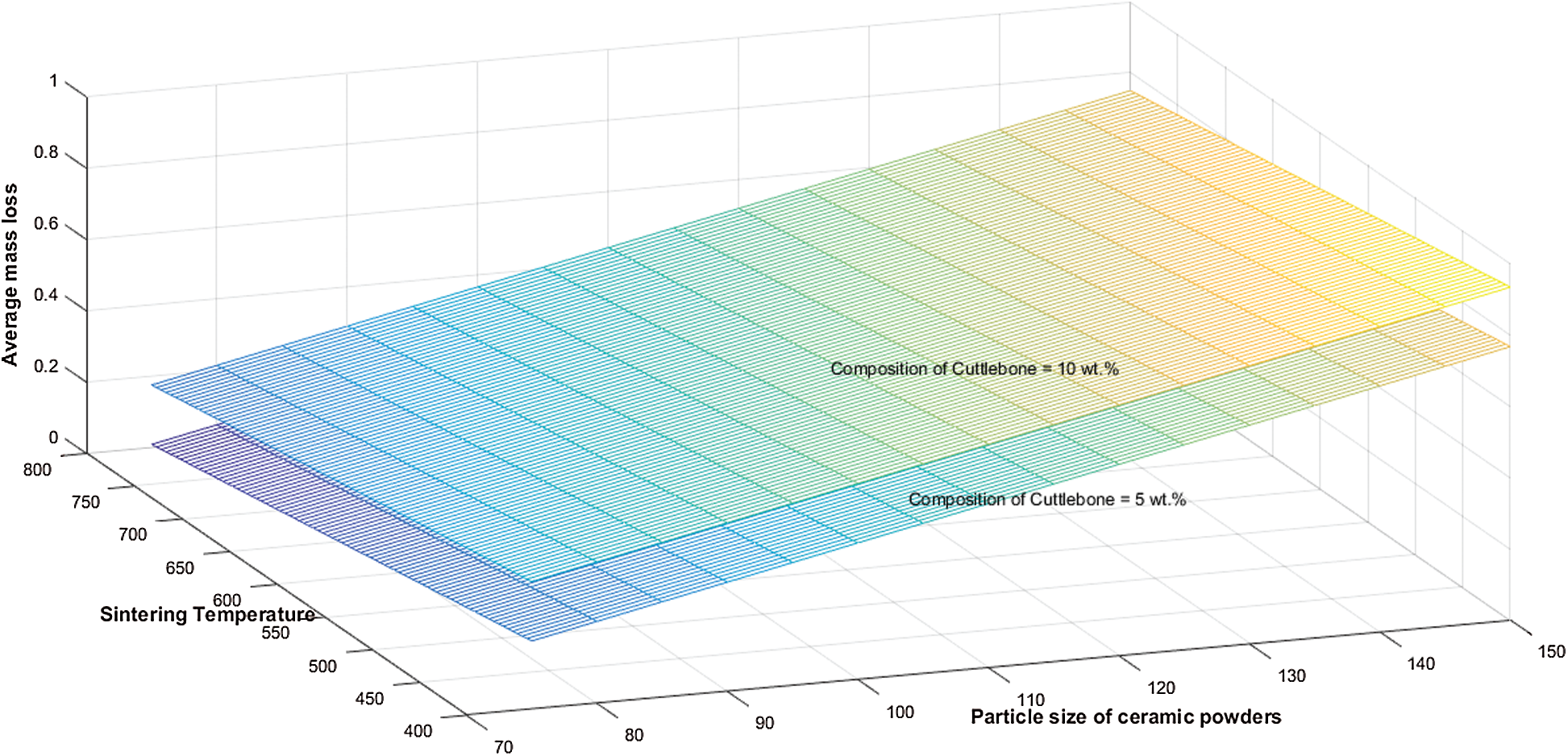
Figure 7: 3D surface interaction plot showing the effect of particle size of ceramic powders and sintering temperature on average mass loss

Figure 8: 3D surface interaction plot showing the effect of particle size of ceramic powders and sintering temperature on reduction in weight

• Bio-ceramics and their associated composites obtained from the body parts of dead marine organisms prove to promising materials to be used as implants in bone replacement.
• Ceramic Matrix Composite with sea sponge as matrix and cuttlebone reinforcement provides excellent thermo-mechanical properties.
• Powder metallurgy is a reliable technique for fabricating CMCs.
• For replacing broken natural bones in the skull, hip or femoral region with synthetic bones formed by CMCs, they should be mechanically as well as thermally stable and inert.
• The Preferential Selection Index is a reliable MCDM technique that can be used to determine the best process parameters.
• The results obtained from PSI are validated by Multi-Level General Factorial Design. The optimized specimen combination obtained from PSI and MLGFD is the same.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Z. Ibrahim, A. A. D. Sarhan, F. Yusuf and M. Hamdi, “Biomedical materials and techniques to improve the tribological, mechanical and biomedical properties of orthopedic implants—A review article,” Journal of Alloys and Compounds, vol. 714, no. 1, pp. 636–667, 2017. [Google Scholar]
2. S. Agarwal, J. Curtin, B. Duffy and S. Jaiswal, “Biodegradable magnesium alloys for orthopedic applications: A review on corrosion, biocompatibility and surface modifications,” Materials Science & Engineering. C, vol. 68, pp. 948–963, 2016. [Google Scholar]
3. R. Elsen, T. R. Babu and B. Aravinth, “Optimization of process parameters of zirconia reinforced alumina by powder forming process using response surface method,” Advanced Materials Research, vol. 984, pp. 385–415, 2014. [Google Scholar]
4. A. H. Choi and B. Ben-Nissan, Marine-Derived Biomaterials for Tissue Engineering Applications. vol. 14. Singapore: Springer, 2019. [Google Scholar]
5. R. Pallela and H. Ehrlich, “Introduction to the global scenario of marine sponge research,” in Marine Sponges: Chemicobiological and Biomedical Applications. New Delhi: Springer, pp. 1–23, 2016. [Google Scholar]
6. J. Cadman, S. Zhou, Y. Chen and Q. Li, “Cuttlebone: Characterization, application and development of biomimetic materials,” Journal of Bionic Engineering, vol. 9, no. 3, pp. 367–376, 2012. [Google Scholar]
7. A. Palaveniene, “Cuttlebone as a marine-derived material for preparing bone grafts,” Marine Biotechnology, vol. 20, no. 3, pp. 363–374, 2018. [Google Scholar]
8. K. Maniya and M. G. Bhatt, “A selection of material using a novel type decision-making method: Preference selection index method,” Materials & Design, vol. 31, no. 4, pp. 1785–1789, 2010. [Google Scholar]
9. S. Jayabal, U. Natarajan and U. Sekar, “Regression modeling and optimization of machinability behavior of glass-coir-polyester hybrid composite using factorial design methodology,” The International Journal of Advanced Manufacturing Technology, vol. 55, no. 1, pp. 263–273, 2011. [Google Scholar]
10. B. Noriega-Luna, L. A. Godínez, F. J. Rodríguez, A. Rodríguez, G. Zaldívar-Lelo de Larrea et al., “Applications of dendrimers in drug delivery agents, diagnosis, therapy, and detection,” Journal of Nanomaterials, vol. 2014, pp. 19, 2014. [Google Scholar]
11. J. N. Hooper and R. W. M. Van Soest, “Systema porifera: A guide to the classification of sponges,” in Systema Porifer. Boston, MA: Springer, pp. 1–7, 2002. [Google Scholar]
12. E. Dogan and Z. Okumus, “Cuttlebone used as a bone xenograft in bone healing,” Veterinarni Medicina, vol. 59, no. 5, pp. 1–25, 2014. [Google Scholar]
13. J. Venkatesan, “Hydroxyapatite from cuttlefish bone: Isolation, characterizations, and applications,” Biotechnology and Bioprocess Engineering, vol. 23, no. 4, pp. 383–393, 2018. [Google Scholar]
14. S. Saravanan, S. Vimalraj, G. Lakshmanan, A. Jindal, D. Sundaramoorthi et al., “Chitosan-based biocomposite scaffolds and hydrogels for bone tissue regeneration,” in Marine-Derived Biomaterials for Tissue Engineering Applications. Singapore: Springer, pp. 413–442, 2019. [Google Scholar]
15. Z. Cui, Y. Zhang, Y. Cheng, D. Gong and W. Wang, “Microstructure, mechanical, corrosion properties and cytotoxicity of beta-calcium polyphosphate reinforced ZK61 magnesium alloy composite by spark plasma sintering,” Materials Science and Engineering: C, vol. 99, pp. 1035–1047, 2019. [Google Scholar]
16. M. I. Ramli, A. B. Sulong, N. Muhamad, A. Muchtar and M. Y. Zakaria, “Effect of sintering on the microstructure and mechanical properties of alloy titanium-wollastonite composite fabricated by powder injection moulding process,” Ceramics International, vol. 45, no. 9, pp. 11648–11653, 2019. [Google Scholar]
17. G. Vincente, M. Martinez, A. Coteron and J. Aracil, “Application of the factorial design of experiments and response surface methodology to optimize biodiesel production,” Industrial Crops and Products, vol. 8, no. 1, pp. 29–35, 1998. [Google Scholar]
18. F. Baino, M. A. Montealegre, J. Minguella-Canela and C. Vitale-Brovarone, “Laser surface texturing of alumina/zirconia composite ceramics for potential use in hip joint prosthesis,” Coatings, vol. 9, no. 6, pp. 369, 2019. [Google Scholar]
19. V. K. Bommala, M. Gopi Krishna and T. Rao, “Magnesium matrix composites for biomedical applications: A review,” Journal of Magnesium and Alloys, vol. 7, no. 1, pp. 72–79, 2019. [Google Scholar]
20. A. Garimella, G. Awale, R. Parai, S. B. Ghosh and S. Bandyopadhyay-Ghosh, “An integrated approach to develop engineered metal composite bone scaffold with controlled degradation,” Materials Technology, vol. 34, no. 14, pp. 858–866, 2019. [Google Scholar]
21. Y. Guesmi, H. Agougui, M. Jabli and A. M. Alsharabasy, “Bioactive composites of hydroxyapatite/polyvinyl pyrrolidone for bone regeneration applications,” Chemical Engineering Communications, vol. 206, no. 3, pp. 279–288, 2019. [Google Scholar]
22. G. Willmann, “Ceramics for total hip replacement-what a surgeon should know,” Orthopedics, vol. 21, no. 2, pp. 173–177, 1998. [Google Scholar]
23. H. Essabir, M. O. Bensalah, D. Rodrigue, R. Bouhfid and A. Qaiss, “Structural, mechanical and thermal properties of bio-based hybrid composites from waste coir residues: Fibers and shell particles,” Mechanics of Materials, vol. 93, no. 1, pp. 134–144, 2016. [Google Scholar]
24. E. Triantaphyllou, Multi-Criteria Decision-Making Methods. Vol. 44. US: Springer, 2000. [Google Scholar]
25. M. Kumar and A. Kumar, “Application of preference selection index method in performance based ranking of ceramic particulate (SiO2/SiC) reinforced AA2024 composite materials,” Materials Today: Proceedings, vol. 27, pp. 2667–2672, 2020. [Google Scholar]
26. S. Diyaley, P. Shilal, I. Shivakoti, R. K. Ghadai and K. Kalita, “PSI and TOPSIS based selection of process parameters in WEDM,” Periodica Polytechnica Mechanical Engineering, vol. 61, no. 4, pp. 255–260, 2017. [Google Scholar]
27. R. Khorshidi and A. Hassani, “Comparative analysis between TOPSIS and PSI methods of materials selection to achieve a desirable combination of strength and workability in Al/SiC composite,” Materials & Design, vol. 52, pp. 999–1010, 2013. [Google Scholar]
28. R. K. Ghadai, K. Kalita, S. C. Mondal and B. P. Swain, “PECVD process parameter optimization: Towards increased hardness of diamond-like carbon thin films,” Materials and Manufacturing Processes, vol. 33, no. 16, pp. 1905–1913, 2018. [Google Scholar]
29. R. K. Ghadai and K. Kalita, “Accurate estimation of DLC thin film hardness using genetic programming,” International Journal of Materials Research, vol. 11, no. 6, pp. 453–462, 2020. [Google Scholar]
30. N. Ganesh, R. K. Ghadai, A. K. Bhoi, K. Kalita and X.-Z. Gao, “An intelligent predictive model-based multi-response optimization of EDM process,” Computer Modeling in Engineering & Sciences, vol. 124, no. 2, pp. 459–476, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |