Computers, Materials & Continua DOI:10.32604/cmc.2022.020206
Article

Sustainable Supplier Selection Model in Supply Chains During the COVID-19 Pandemic

Chia-Nan Wang1, Chao-Fen Pan1,*, Viet Tinh Nguyen2 and Syed Tam Husain2

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Chao-Fen Pan. Email: chaofenpannkust@gmail.com
Received: 14 May 2021; Accepted: 20 June 2021

Abstract: As global supply chains become more developed and complicated, supplier quality has become increasingly influential on the competitiveness of businesses during the Covid-19 pandemic. Consequently, supplier selection is an increasingly important process for any business around the globe. Choosing a supplier is a complex decision that can result in lower procurement costs and increased profits without increasing the cost or lowering the quality of the product. However, these decision-making problems can be complicated in cases with multiple potential suppliers. Vietnam's textile and garment industry, for example, has made rapid progress in recent years but is still facing great difficulties as the supply of raw materials and machinery depends heavily on foreign countries. Therefore, it is extremely important for textile and garment manufacturing companies in Vietnam to implement an effective supplier evaluation and selection process. While multicriteria decision-making models are frequently employed to assist with supplier evaluation and selection problems, few of these models consider the problem under the condition of a fuzzy decision-making environment. The aim of this paper is to create a hybrid MCDM model using the Fuzzy Analytical Hierarchy Process (FAHP) model and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to assist the supplier selection process in the garment industry in a fuzzy decision-making environment. In this study, the FAHP method is used to evaluate the performance and the weight of each criterion. TOPSIS is then used to rank all potential suppliers. The proposed model is then applied to a real-world case study to demonstrate both the process of calculation as well as its real-world applicability. The results from the case study provide empirical evidence that the model is feasible. The proposed approach can also be used in combination with other MCDM models to better support decision makers and can be modified to be applied in similar supplier selection processes for different industries.

Keywords: MCDM model; FAHP; fuzzy theory; TOPSIS; garment industry; covid-19

1  Introduction

The textile and garment industry of Vietnam sets an annual export target of 33.5 billion USD. To focus on investment in restructuring the internal branch, application of advanced technologies to gradually balance stages, improve productivity and product quality; accommodate production shift in regions; strengthen cooperation, joint venture and linkage between domestic textile and garment enterprises, domestic enterprises and foreign investment; and exploit traditional markets in parallel to the exploration of new markets. The dependence on imported raw materials and machinery for the textile and dyeing stages is a challenge to the sustainable development of Vietnam's textile and garment industry, especially as it interfaces with the global textile value chain. In recent years, businesses have considered implementation of supply chain management (SCM) to be an important issue affecting a company's productivity and efficiency. SCM has become a competitive strategy to connect companies with suppliers and distributors within an interagency system [1]. The supply chain is a system of organizations, people, activities, information and resources related to the transfer of products or services from a manufacturer to its customer [2]. Managing a supply chain puts a focus on continuous improvement to meet customer demand, reduce costs and increase profitability for the business. Since the onset of the Covid-19 pandemic, however, global supply chains have been greatly disturbed, with prolonged periods of demand uncertainty and supply shortage. Thus, supply evaluation and selection processes have become increasingly important during the pandemic, especially for an import-dependent industry such as garment and textile manufacturing in Vietnam.

The selection of one or more suppliers is one of the pressing issues along the supply chain because supplier quality directly affects the performance of the organization at cheaper prices in the corresponding quantities for a limited time. One of the most essential functions to reduce raw material costs is selecting suppliers [1]. Supplier selection is a complex decision-making process which involves multiple criteria. Multicriteria decision-making methods, such as Analytic Hierarchy Process (AHP), Analytic Network Process (ANP), Fuzzy Analytic Network Process (FANP), Data Envelopment Analysis (DEA), among others, are frequently applied to support the decision-making processes [3].

Since Saaty introduced the Analytical Hierarchy Process (AHP) in 1977, the method has become a commonly used quantitative approach to supplier selection [3–11] and supplier performance evaluation [12–13]. The Analytic Network Process (ANP) can also be applied to the same type of multicriteria decision making problems as AHP [14–16]. This approach is more practical because the internal and external relationships between the criteria are simultaneously considered in order to establish the relationships between the clusters [17].

In this study, we present the use of the FAHP and TOPSIS methods to solve supply chain management decision-making problems. Priorities between the criteria, recorded as weightings, are obtained from the FAHP model, after which the TOPSIS model is used to rank all potential suppliers. The proposed model is then applied to a real-world case study to demonstrate its accurate calculation process and real-world applicability.

2  Literature Review

Many studies in the past decade have focused on supplier evaluation and problems in selection. While supplier selection processes are becoming an increasingly important topic in SMC, their role in modern supply chain practices is only partially explored in the literature.

In this body of research, the supplier selection decision-making problem is commonly solved using quantitative methods and mathematical modelling [18]. In Dickson's study, for example, several different MCDM models are employed to support a supplier selection process [19]. Decision support models for supplier selection processes are also built around a set of criteria (Pi and Low) [20]. Timmerman proposed a single objective weighted linear model in which suppliers are rated on several criteria and in which these ratings are combined into a single score [21]. Pearson and Ellram identified the common supplier selection criteria used by procurement managers in electronics firms [22]. Asemi and Asemi developed a MCDM model using Fuzzy AHP and Fuzzy TOPSIS. This proposed model was then used to support a steel company with its supplier evaluation and selection processes [23]. Wang et al. [24] introduced a MCDM method using Fuzzy ANP and VIKOR methods for supplier selection in the plastics industry. Their proposed model used criteria from the Supply Chain Operation Reference model, which is widely used by organizations to evaluate the operational performance of their supply chains. Chakraborty et al. [25] introduced a decision support tool using AHP, Fuzzy Logic and Artificial Neural Network (ANN) for supplier selection problems. Badi et al. [26] proposed a supplier selection model for the steel manufacturing industry using the combination of Grey-MARCOS methods.

Ghorbani et al. [27] introduced a novel decision-making method using the Kano model and a fuzzy MCDM model, which is built using the FAHP and FTOPSIS methods. Stević et al. [28] proposed an MCDM model based on the MARCOS method. This particular model was developed to support sustainable supplier evaluation and selection processes within the private health care sector. Wang et al. [29] introduced a fuzzy MCDM model by employing Triple Bottom Line Approaches, Fuzzy AHP, and TOPSIS. This model provides a robust and effective method to the sustainable supplier selection problem for companies operating within the garment industry. Wu et al. [30] introduced a Fuzzy MCDM model to solve the fishmeal supplier selection problem in aquacultural production under the specific condition of maintaining sustainability criteria. This model was developed using the entropy method in combination with the VIKOR method. Govidan et al. [31] developed a hybrid MCDM model for socially responsible supplier selection. The model was created using fuzzy Delphi, DEMATEL-ANP and PROMETHEE methods. Ghorabaee et al. [32] introduced a novel MCDM model based on the extended WAPAS method with interval type-2 fuzzy sets. Chen et al. [33] proposed a fuzzy approach to the supplier selection problem in supply chain management using TOPSIS in combination with fuzzy set theory. Yucesan et al. [34] suggested a method to solve the green supplier selection problem by employing the Best-Worst method and Interval Type-2 Fuzzy TOPSIS method. Liao et al. [35] introduced a MCDM model for solving the supplier selection problem, which is based on AHP, goal programming, and Taguchi loss function. Dweiri et al. [36] developed a decision support system for the automotive industry using the AHP method.

As supply chains have increased in complexity, many mathematical models have been employed to support supplier evaluation and selection processes. Talluri et al. [37], Ng et al. [38], Guneri et al. [39] proposed a solution to this problem by using linear programming; integer linear programming was proposed in studies by Chaundry et al. [40] and Rosenthal et al. [41]; integer non-linear programming [42]; multi-objective programming [43–45]; goal programming [46,47]; and data envelopment analysis [48]. Hamdan et al. [49] developed a supplier selection and order allocation (SS/OA) decision support system with environmental performance criteria by employing AHP, Fuzzy TOPSIS and goal programming. Jia et al. [50] introduced an approach for the sustainable SS/OA problem; their suggested method is based on goal programming. Moghaddam [51] introduced a method to solve the SS/OA problem using a hybrid Monte Carlo simulation in combination with goal programming. Erdem et al. [52] proposed a decision support system for the SS/OA problem. The system, developed based on AHP and goal programming, was tested in a real-life environment and has since received positive feedback. Aktar Demirtas et al. [53] introduced an approach to the order allocation problem in a multi-period inventory sizing environment. The suggested approach is based on the ANP method and Archimedean Goal Programming (AGP). Wey et al. [54] developed a novel approach to the transportation infrastructure project selection based on the Fuzzy Delphi method, ANP and Zero-One Goal Programming. Nazari-Shirkouhi et al. [55] developed a two-phase fuzzy multi-objective linear programming (FMOLP) approach to the SS/OA problem. Govindan et al. [56] proposed an MCDM and MOLP method to support the green SS/OA process in their study of the paper manufacturing industry. Vahidi et al. [57] attempted to address the sustainable SS/OA problem with operational and disruption risks by introducing a mathematical programming model. The model is built on a hybrid SWOT-QFD framework and a programming model with a mixed sustainability and resilience function. Amin et al. [58] suggested an approach based on both a fuzzy SWOT analysis and fuzzy linear programming to address the SS/OA problem. Khoshfetrat et al. [59] attempted to approach the SS/OA problem under the condition of an uncertain decision-making environment in the automotive industry by developing a fuzzy multi-objective mathematical model. Hosseini et al. [60] developed an approach to the resilient SS/OA problem using mixed integer mathematical programming with disruptive events. Li et al. [61] introduced environmental and supply risks elements into a novel mathematical model to approach the SS/OA problem. You et al. [62] combined a fuzzy MCDM model and MOLP model to develop a decision support tool for the sustainable SS/OA problem. Mari et al. [63] developed an approach to the SS/OA problem with resilient criteria and under the condition of a fuzzy environment. The proposed approach is a fuzzy possibilistic MOLP model.

With the emergence of the Covid-19 pandemic, however, supply chains been globally distrupted, especially considering the increased uncertainty of supply that the pandemic has brought to bear on most industries [64,65]. In the present study, we develop a mathematical approach to support the supplier evaluation and selection process of the garment and textile manufacturing industry. The proposed approached is based on the FAHP and TOPSIS methods. The proposed model is then applied to a real-world case study to demonstrate its calculation process and real-world applicability.

3  Methodology

3.1 Research Development

The research process is carried out according to the main steps as shown in Fig. 1.

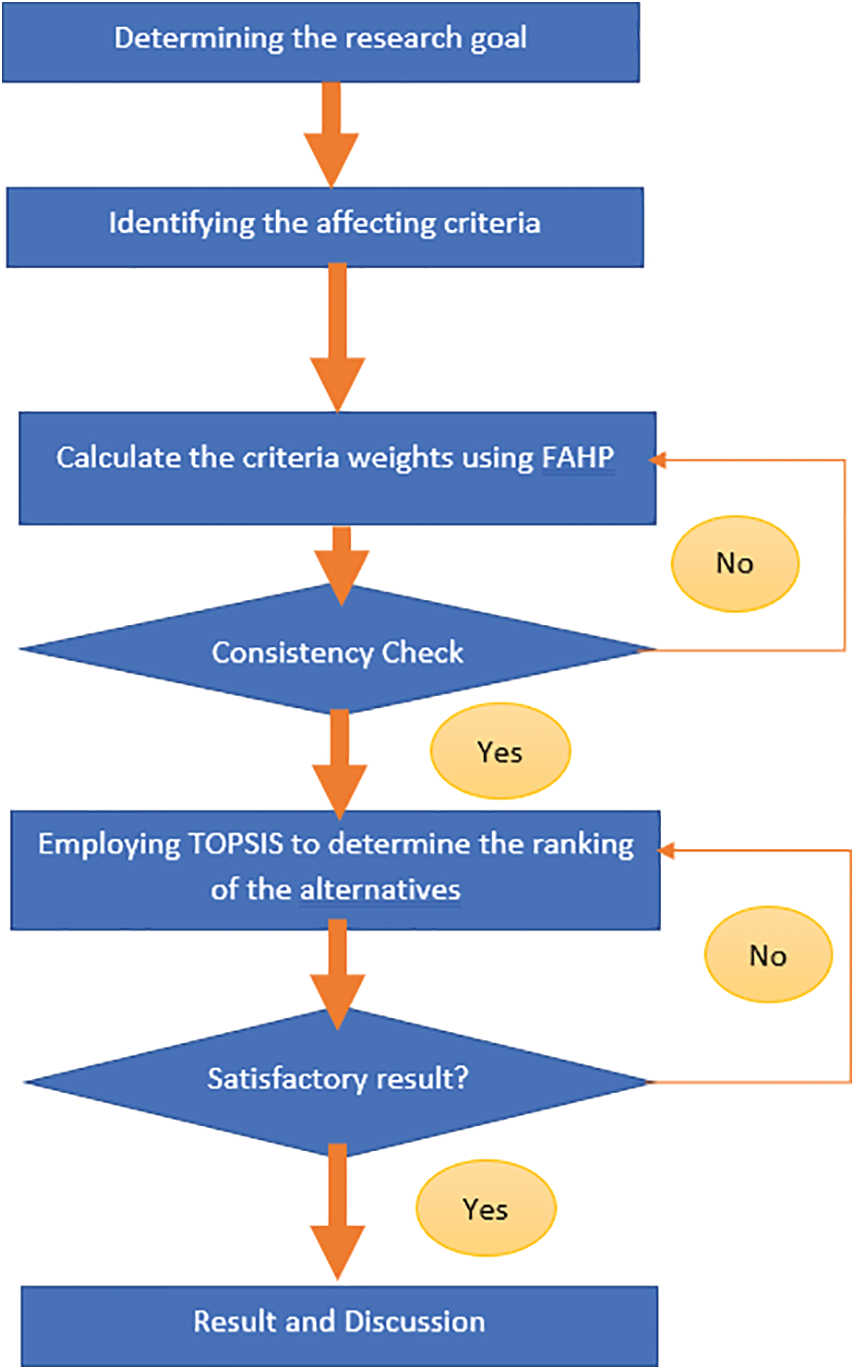
Figure 1: Research process

3.2 Methodology

3.2.1 Fuzzy Analytic Hierarchy Process

Fuzzy set theory was developed by Zadeh (1965) [66] to represent the uncertain and vagueness of human language. The theory allows mathematical operators to be performed in the fuzzy domain. A fuzzy set is defined as a class of objects with continuous grades of membership and characterized by its membership function. The membership function assigns each object in the set with a membership degree, which ranges between one and zero.

While there are many forms of fuzzy numbers, triangular fuzzy numbers are employed in this research due to their efficiency and ease of use [67–71]. It is defined in Fig. 2.

μ(x)={x−ab−a,a≤x≤bc−xc−b,b≤x≤c0,otherwise(1)

If a = b = c, the fuzzy number A~becomes a real number. Therefore, real numbers are considered as special fuzzy numbers [72].

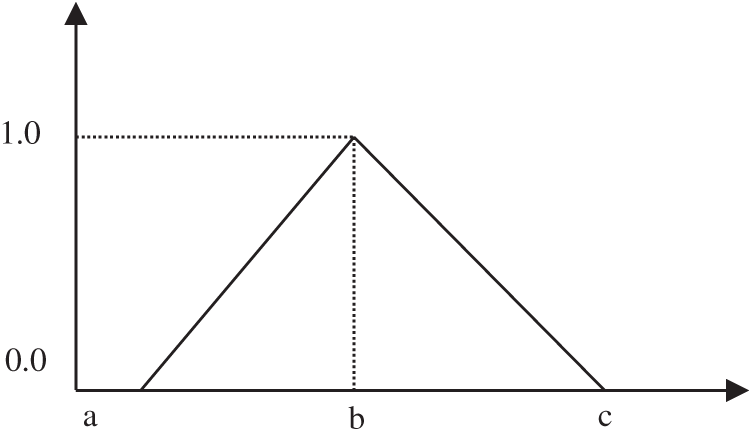
Figure 2: Triangular fuzzy number

The implementation of the Fuzzy AHP model consists of four stages as follows according to Buckley [73]:

Stage 1: Building the Fuzzy AHP model

The decision maker compares the criteria and alternative based on Fig. 3:

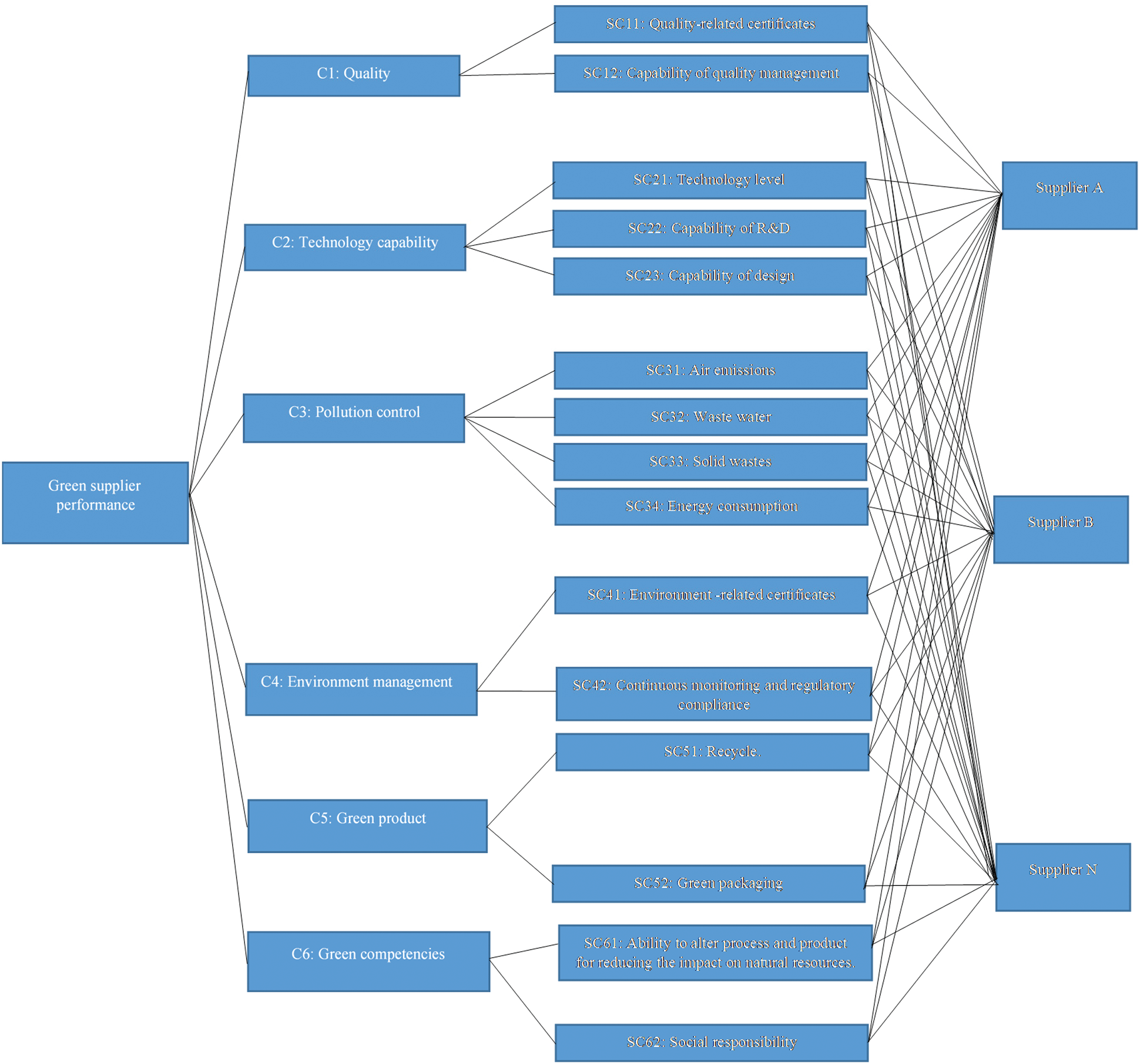
Figure 3: Fuzzy AHP model

Stage 2: Creating the pairwise comparison matrix

A pairwise comparison matrix is created using fuzzy numbers. The matrix is represented as follows:

Ak~=[a11k~a12k~⋯a1nk~a21k~a22k~⋯a2nk~⋯⋯⋯⋯an1k~an2k~⋯annk~](2)

where Ak~is the pairwise comparison matrix of the fuzzy elements and annk~ is the triangular fuzzy mean value.

Should there be more than one decision maker, the preferences of each expert (annk~) are averaged and (a~ij) is determined as in Eq. (3):

a~ij=∑k=1K⁡annk~K(3)

Stage 3: Based on the average preferences, the pair-wise contribution matrix will then be updated as displayed in Eq. (4).

Stage 4: Based on the study by Buckley [71], the geometric mean of the comparison values that have been fuzzified for each criterion is determined using Eq. (5). The values of gi~ are triangular values.

gi~=(∏j=1n⁡a~ij)1/n,i=1,2,…,n(4)

Stage 5: The fuzzified weights for each criterion can be determined in Eq. (5) by combining the following three minor stages:

Stage 5a: Determine the vector summation of each gi~.

Stage 5b: Determine the inverse power of summation vector. Replace the fuzzified triangular and sort into ascending order.

Stage 5c: Determine the fuzzified weight by multiplying each with its inverse vector.

w~i=g~i⊗(g1~⊗g2~⊗…⊗gn~)−1=(lwi,mwi,uwi)(5)

Stage 6: Because w~i are triangular numbers that are still fuzzified, the defuzzification process must be used with the Centre of Area method as used in the study by Chou et al. [74]; its method is shown in Eq. (6):

Yi=lwi+mwi+uwi3(6)

Stage 7: Even when Yi is a normal number, normalizing it is still required using Eq. (7):

Zi=Yi∑i=1n⁡Yi(7)

These seven stages are used to determine the normalized weights for both criteria and alternatives. From these results, the highest scoring alternative is presented to the decision maker as the best alternative to choose.

3.2.2 The Technique for Order of Preference by Similarity to Ideal Solution Model

TOPSIS is a multi-criteria decision analysis method, that was originally developed by Hwang et al. [75] in 1981 with further developments by Yoon [76] in 1987 and Hwang and subsequently by Lai and Liu in 1993 [77]. The TOPSIS process is carried out as follows:

Step 1: Create an evaluation matrix consisting of m alternatives and n criteria. With the intersection of each alternative and criteria given as xij, we therefore arrive at the matrix (xij)mxn.

Step 2: The matrix (xij)mxn is then normalized to form the matrix:

R=(rij)mxnusing the normalization method

rij=xij∑k=1m⁡xkj2, i = 1, 2,…, m; j = 1, 2,…, n

Step 3: Calculate the weighted normalized decision matrix:

where wj=Wj∑k=1n⁡Wk,j = 1, 2,…, n so that ∑i=1n⁡wj=1, and Wj is the original weight given to the indicator vj,j = 1, 2,…, n

Step 4: Determine the worst alternative (Aw)and the best alternative (Ab):

Step 5: Calculate the L2- distance between the target alternative i and the worst condition Aw:

as well as distance between the target alternative i and the worst condition Ab:

Step 6: Calculate the similarity to the worst condition:

siw=1 if and only if the alternative solution has the best condition; and

siw=0 if and only if the alternative solution has the worst condition.

Step 7: Rank the alternatives according to siw (i=1,2,…,m)

4  Case Study

To test the effectiveness of the FAHP-TOPSIS model, the implementation of hybrid model to select a sewing machine supplier was implemented in two phases, first using FAHP to calculate the weight of all criteria and then using the TOPSIS model to rank potential suppliers.

4.1 Fuzzy Analytical Hierarchy Process Model

Summary results from the FAHP model are presented in Tab. 1:

4.2 The Technique for Order of Preference by Similarity to Ideal Solution Model

After using the FAHP model to evaluate criteria, TOPSIS model will be developed to rank suppliers, a result as the following shown in Tabs. 2–4.

5  Discussion

In the current global business climate, the uncertainty inherent to both the supply and demand sides of a given supply chain have increased substantially due to the Covid-19 pandemic. For this reason, it is extremely important for companies to develop effective supplier evaluation and selection processes when selecting a supply chain. For garment and textile manufacturers in Vietnam, this prodcess is even more paramount to their survival, as they are heavily dependent on offshore suppliers in China. In this study, we developed a supplier evaluation and selection model based on the FAHP and TOPSIS models. With a set of 6 criteria and 15 sub-criteria, which were developed based on relevant literature in addition to industry experts’ reviews, this model allows decision makers to evaluate potential suppliers comprehensively. The choice of FAHP and TOPSIS methods also allows for increased applicability in the model, as the methods are easy to understand and widely available in decision-making support software.

The model is then applied to a real-world case study to demonstrate its calculation step validity and overall feasibility as a practical solution to the emergent supplier choice problem. In the case study, we considered nine potential suppliers and evaluated their performance based on the proposed 6 criteria and 15 sub-criteria. The model suggests that the optimal supplier is supplier A7 with a performance score of 0.7371, followed by A2 (0.6271) and then A5 (0.5184). Through this study, we successfully created a hybrid MCDM model using Fuzzy AHP and the TOPSIS model to assist the supplier selection process in the garment industry. Results from the case study show that the model is in fact a feasible one. The model can also be used in combination with other MCDM models to better support the decision-maker.

6  Conclusion

Selection of the garment industry's suppliers is crucial to decision-makers managing supply chains. Careful selection of suppliers in the garment industry is a top concern in this field. It is important for garment supply chains to have robust and effective supplier selection processes. However, these processes tend to be based on the decision-makers’ experiences, which are often incomplete or inaccurate, and are therefore ineffective. This study aimed to create a robust and effective supplier selection model by using a Fuzzy Analytical Hierarchy Process (FAHP) Model and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to assist the supplier selection process in the garment industry under the condition of a fuzzy decision-making environment. In this study, we used the FAHP method to evaluate the performance and weight of the selected criteria: we determined that FAHP is the appropriate method for evaluating and making multi-criteria decisions in cases where the decision-making process involves a large number of criteria that can be interdependent of one another. Next, we used the TOPSIS method to rank potential suppliers. This research provides businesses in the garment industry an effect tool to support their decision-making processes. Future research can be developed based upon the proposed approach using different MDCD methods, such as FANP or WASPAS. Comparison studies can also be conducted to evaluate the performance of existing supplier selection and evaluation models during and after the Covid-19 pandemic.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. Bozarth and R. Handfield, Introduction to Operations and Supply Chain Management, Global Edition, Harlow: Pearson Education Canada, 2015. [Google Scholar]

 2.  W. Ho, X. Xu and P. Dey, “Multi-criteria decision making approaches for supplier evaluation and selection: A literature review,” European Journal of Operational Research, vol. 202, no. 1, pp. 16–24, 2010. [Google Scholar]

 3.  G. Barbarosoglu and T. Yazgac, “An application of the analytic hierarchy process to the supplier selection problem,” Production and Inventory Management Journal, vol. 38, no. 1, pp. 14–21, 1997. [Google Scholar]

 4.  F. Çebi and D. Bayraktar, “An integrated approach for supplier selection,” Logistics Information Management, vol. 16, no. 6, pp. 395–400, 2003. [Google Scholar]

 5.  S. Ghodsypour and C. O'Brien, “A decision support system for supplier selection using an integrated analytic hierarchy process and linear programming,” International Journal of Production Economics, vol. 56,–vol. 57, pp. 199–212, 1998. [Google Scholar]

 6.  K. Bhutta and F. Huq, “Supplier selection problem: A comparison of the total cost of ownership and analytic hierarchy process approaches,” Supply Chain Management: An International Journal, vol. 7, no. 3, pp. 126–135, 2002. [Google Scholar]

 7.  R. Mohanty and S. Deshmukh, “Use of analytic hierarchic process for evaluating sources of supply,” International Journal of Physical Distribution & Logistics Management, vol. 23, no. 3, pp. 22–28, 1993. [Google Scholar]

 8.  R. Narasimhan, “An analytical approach to supplier selection,” Journal of Purchasing and Materials Management, vol. 19, no. 4, pp. 27–32, 1983. [Google Scholar]

 9.  R. Nydick and R. Hill, “Using the analytic hierarchy process to structure the supplier selection procedure,” International Journal of Purchasing and Materials Management, vol. 28, no. 2, pp. 31–36, 1992. [Google Scholar]

10. C. Weber, J. Current and W. Benton, “Vendor selection criteria and methods,” European Journal of Operational Research, vol. 50, no. 1, pp. 2–18, 1991. [Google Scholar]

11. S. Yahya and B. Kingsman, “Vendor rating for an entrepreneur development programme: A case study using the analytic hierarchy process method,” Journal of the Operational Research Society, vol. 50, no. 9, pp. 916, 1999. [Google Scholar]

12. R. Fung and C. Wong, “Supplier environmental performance evaluation using AHP,” in Proc.-6th ISAHP 2001 Berne, Switzerland, pp. 111–118, 2021. [Google Scholar]

13. R. Handfield, S. Walton, R. Sroufe and S. Melnyk, “Applying environmental criteria to supplier assessment: A study in the application of the analytical hierarchy process,” European Journal of Operational Research, vol. 141, no. 1, pp. 70–87, 2002. [Google Scholar]

14. A. Agarwal and R. Shankar, “Analyzing alternatives for improvement in supply chain performance,” Work Study, vol. 51, no. 1, pp. 32–37, 2002. [Google Scholar]

15. J. Sarkis and R. Sundarraj, “Hub location at digital equipment corporation: A comprehensive analysis of qualitative and quantitative factors,” European Journal of Operational Research, vol. 137, no. 2, pp. 336–347, 2002. [Google Scholar]

16. J. Sarkis and S. Talluri, “A model for strategic supplier selection,” Journal of Supply Chain Management, vol. 38, no. 1, pp. 18–28, 2002. [Google Scholar]

17. C. Chyu and Y. Fang, “A hybrid fuzzy analytic network process approach to the new product development selection problem,” Mathematical Problems in Engineering, vol. 2014, pp. 1–13, 2014. [Google Scholar]

18. J. Scott, W. Ho, P. Dey and S. Talluri, “A decision support system for supplier selection and order allocation in stochastic, multi-stakeholder and multi-criteria environments,” International Journal of Production Economics, vol. 166, pp. 226–237, 2015. [Google Scholar]

19. G. Dickson, “An analysis of vendor selection systems and decisions,” Journal of Purchasing, vol. 2, no. 1, pp. 5–17, 1966. [Google Scholar]

20. W. Pi and C. Low, “Supplier evaluation and selection via taguchi loss functions and an AHP,” International Journal of Advanced Manufacturing Technology, vol. 27, no. 5–6, pp. 625–630, 2005. [Google Scholar]

21. E. Timmerman, “An approach to vendor performance evaluation,” Journal of Purchasing and Materials Management, vol. 22, no. 4, pp. 2–8, 1986. [Google Scholar]

22. J. Pearson and L. Ellram, “Supplier selection and evaluation in small versus large electronics firms,” Journal of Small Business Management, vol. 33, no. 4, pp. 53–65, 1995. [Google Scholar]

23. A. Asemi and A. Asemi, “Intelligent MCDM method for supplier selection under fuzzy environment,” International Journal of Information Science and Management, no. S.1, pp. 33–40, 2014. [Google Scholar]

24. C. Wang, V. Nguyen, J. Chyou, T. Lin and T. Nguyen, “Fuzzy multicriteria decision-making model (MCDM) for raw materials supplier selection in plastics industry,” Mathematics, vol. 7, no. 10, pp. 981, 2019. [Google Scholar]

25. S. Nallusamy, D. Sri Lakshmana Kumar, K. Balakannan and P. Chakraborty, “MCDM tools application for selection of suppliers in manufacturing industries using AHP, fuzzy logic and ANN,” International Journal of Engineering Research in Africa, vol. 19, pp. 130–137, 2015. [Google Scholar]

26. I. Badi and D. Pamucar, “Supplier selection for steelmaking company by using combined grey-marcos methods,” Decision Making: Applications in Management and Engineering, vol. 3, no. 2, pp. 37–48, 2020. [Google Scholar]

27. M. Ghorbani, S. Mohammad Arabzad and A. Shahin, “A novel approach for supplier selection based on the kano model and fuzzy MCDM,” International Journal of Production Research, vol. 51, no. 18, pp. 5469–5484, 2013. [Google Scholar]

28. Ž Stević, D. Pamučar, A. Puška and P. Chatterjee, “Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to compromise solution (MARCOS),” Computers & Industrial Engineering, vol. 140, pp. 106231, 2020. [Google Scholar]

29. C. Wang, C. Yang and H. Cheng, “A fuzzy multicriteria decision-making (MCDM) model for sustainable supplier evaluation and selection based on triple bottom line approaches in the garment industry,” Processes, vol. 7, no. 7, pp. 400, 2019. [Google Scholar]

30. T. Wu, C. Chen, N. Mao and S. Lu, “Fishmeal supplier evaluation and selection for aquaculture enterprise sustainability with a fuzzy MCDM approach,” Symmetry, vol. 9, no. 11, pp. 286, 2017. [Google Scholar]

31. K. Govindan, M. Shankar and D. Kannan, “Supplier selection based on corporate social responsibility practices,” International Journal of Production Economics, vol. 200, pp. 353–379, 2018. [Google Scholar]

32. M. K. Ghorabaee, E. Zavadskas, M. Amiri and A. Esmaeili, “Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets,” Journal of Cleaner Production, vol. 137, pp. 213–229, 2016. [Google Scholar]

33. C. Chen, C. Lin and S. Huang, “A fuzzy approach for supplier evaluation and selection in supply chain management,” International Journal of Production Economics, vol. 102, no. 2, pp. 289–301, 2006. [Google Scholar]

34. M. Yucesan, S. Mete, F. Serin, E. Celik and M. Gul, “An integrated best-worst and interval type-2 fuzzy TOPSIS methodology for green supplier selection,” Mathematics, vol. 7, no. 2, pp. 182, 2019. [Google Scholar]

35. C. Liao and H. Kao, “Supplier selection model using taguchi loss function, analytical hierarchy process and multi-choice goal programming,” Computers & Industrial Engineering, vol. 58, no. 4, pp. 571–577, 2010. [Google Scholar]

36. F. Dweiri, S. Kumar, S. Khan and V. Jain, “Designing an integrated AHP based decision support system for supplier selection in automotive industry,” Expert Systems with Applications, vol. 62, pp. 273–283, 2016. [Google Scholar]

37. S. Talluri and R. Narasimhan, “Vendor evaluation with performance variability: A max–min approach,” European Journal of Operational Research, vol. 146, no. 3, pp. 543–552, 2003. [Google Scholar]

38. W. Ng, “An efficient and simple model for multiple criteria supplier selection problem,” European Journal of Operational Research, vol. 186, no. 3, pp. 1059–1067, 2008. [Google Scholar]

39. A. Guneri, A. Yucel and G. Ayyildiz, “An integrated fuzzy-lp approach for a supplier selection problem in supply chain management,” Expert Systems with Applications, vol. 36, no. 5, pp. 9223–9228, 2009. [Google Scholar]

40. S. Chaudhry, F. Forst and J. Zydiak, “Vendor selection with price breaks,” European Journal of Operational Research, vol. 70, no. 1, pp. 52–66, 1993. [Google Scholar]

41. E. Rosenthal, J. Zydiak and S. Chaudhry, “Vendor selection with bundling,” Decision Sciences, vol. 26, no. 1, pp. 35–48, 1995. [Google Scholar]

42. S. Ghodsypour and C. O'Brien, “The total cost of logistics in supplier selection, under conditions of multiple sourcing, multiple criteria and capacity constraint,” International Journal of Production Economics, vol. 73, no. 1, pp. 15–27, 2001. [Google Scholar]

43. C. Weber and L. Ellram, “Supplier selection using multi-objective programming: A decision support system approach,” International Journal of Physical Distribution & Logistics Management, vol. 23, no. 2, pp. 3–14, 1993. [Google Scholar]

44. Z. Gao and L. Tang, “A multi-objective model for purchasing of bulk raw materials of a large-scale integrated steel plant,” International Journal of Production Economics, vol. 83, no. 3, pp. 325–334, 2003. [Google Scholar]

45. D. Kannan, R. Khodaverdi, L. Olfat, A. Jafarian and A. Diabat, “Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain,” Journal of Cleaner Production, vol. 47, pp. 355–367, 2013. [Google Scholar]

46. B. Karpak, R. Kasuganti and E. Kumcu, “Multi-objective decision-making in supplier selection: An application of visual interactive goal programming,” Journal of Applied Business Research, vol. 15, no. 2, pp. 57, 2011. [Google Scholar]

47. C. Chang, H. Chen and Z. Zhuang, “Integrated multi-choice goal programming and multi-segment goal programming for supplier selection considering imperfect-quality and price-quantity discounts in a multiple sourcing environment,” International Journal of Systems Science, vol. 45, no. 5, pp. 1101–1111, 2013. [Google Scholar]

48. A. Hatami-Marbini, S. Hekmat and P. Agrell, “A strategy-based framework for supplier selection: A grey PCA-DEA approach,” Operational Research, vol. 20, no. 1, pp. 1–35, 2020. [Google Scholar]

49. S. Hamdan and A. Cheaitou, “Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach,” Computers & Operations Research, vol. 81, pp. 282–304, 2017. [Google Scholar]

50. R. Jia, Y. Liu and X. Bai, “Sustainable supplier selection and order allocation: Distributionally robust goal programming model and tractable approximation,” Computers & Industrial Engineering, vol. 140, pp. 106267, 2020. [Google Scholar]

51. K. Moghaddam, “Supplier selection and order allocation in closed-loop supply chain systems using hybrid monte carlo simulation and goal programming,” International Journal of Production Research, vol. 53, no. 20, pp. 6320–6338, 2015. [Google Scholar]

52. A. Erdem and E. Göçen, “Development of a decision support system for supplier evaluation and order allocation,” Expert Systems with Applications, vol. 39, no. 5, pp. 4927–4937, 2012. [Google Scholar]

53. E. Aktar Demirtas and O. Ustun, “Analytic network process and multi-period goal programming integration in purchasing decisions,” Computers & Industrial Engineering, vol. 56, no. 2, pp. 677–690, 2009. [Google Scholar]

54. W. Wey and K. Wu, “Using ANP priorities with goal programming in resource allocation in transportation,” Mathematical and Computer Modelling, vol. 46, no. 7–8, pp. 985–1000, 2007. [Google Scholar]

55. S. Nazari-Shirkouhi, H. Shakouri, B. Javadi and A. Keramati, “Supplier selection and order allocation problem using a two-phase fuzzy multi-objective linear programming,” Applied Mathematical Modelling, vol. 37, no. 22, pp. 9308–9323, 2013. [Google Scholar]

56. K. Govindan and R. Sivakumar, “Green supplier selection and order allocation in a low-carbon paper industry: Integrated multi-criteria heterogeneous decision-making and multi-objective linear programming approaches,” Annals of Operations Research, vol. 238, no. 1–2, pp. 243–276, 2015. [Google Scholar]

57. F. Vahidi, S. Torabi and M. Ramezankhani, “Sustainable supplier selection and order allocation under operational and disruption risks,” Journal of Cleaner Production, vol. 174, pp. 1351–1365, 2018. [Google Scholar]

58. S. Amin, J. Razmi and G. Zhang, “Supplier selection and order allocation based on fuzzy SWOT analysis and fuzzy linear programming,” Expert Systems with Applications, vol. 38, no. 1, pp. 334–342, 2011. [Google Scholar]

59. S. Khoshfetrat, M. Rahiminezhad Galankashi and M. Almasi, “Sustainable supplier selection and order allocation: A fuzzy approach,” Engineering Optimization, vol. 52, no. 9, pp. 1494–1507, 2019. [Google Scholar]

60. S. Hosseini, N. Morshedlou, D. Ivanov, M. Sarder, K. Barker and A. Khaled, “Resilient supplier selection and optimal order allocation under disruption risks,” International Journal of Production Economics, vol. 213, pp. 124–137, 2019. [Google Scholar]

61. F. Li, C. Wu, L. Zhou, G. Xu, Y. Liu and S. Tsai, “A model integrating environmental concerns and supply risks for dynamic sustainable supplier selection and order allocation,” Soft Computing, vol. 25, no. 1, pp. 535–549, 2020. [Google Scholar]

62. S. You, L. Zhang, X. Xu and H. Liu, “A New integrated multi-criteria decision making and multi-objective programming model for sustainable supplier selection and order allocation,” Symmetry, vol. 12, no. 2, pp. 302, 2020. [Google Scholar]

63. S. Mari, M. Memon, M. Ramzan, S. Qureshi and M. Iqbal, “Interactive fuzzy multi criteria decision making approach for supplier selection and order allocation in a resilient supply chain,” Mathematics, vol. 7, no. 2, pp. 137, 2019. [Google Scholar]

64. L. Fonseca and A. Azevedo, “COVID- 19: Outcomes for global supply chains,” Management & Marketing. Challenges for the Knowledge Society, vol. 15, no. 1, pp. 424–438, 2020. [Google Scholar]

65. A. Verbeke, “Will the COVID-19 pandemic really change the governance of global value chains,” British Journal of Management, vol. 31, no. 3, pp. 444–446, 2020. [Google Scholar]

66. L. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

67. A. Lee, “A fuzzy supplier selection model with the consideration of benefits, opportunities, costs and risks,” Expert Systems with Applications, vol. 36, no. 2, pp. 2879–2893, 2009. [Google Scholar]

68. A. Lee, H. Kang, C. Hsu and H. Hung, “A green supplier selection model for high-tech industry,” Expert Systems with Applications, vol. 36, no. 4, pp. 7917–7927, 2009. [Google Scholar]

69. A. Lee, H. Kang and C. Chang, “Fuzzy multiple goal programming applied to TFT-lCD supplier selection by downstream manufacturers,” Expert Systems with Applications, vol. 36, no. 3, pp. 6318–6325, 2009. [Google Scholar]

70. H. Kang and A. Lee, “Priority mix planning for semiconductor fabrication by fuzzy AHP ranking,” Expert Systems with Applications, vol. 32, no. 2, pp. 560–570, 2007. [Google Scholar]

71. C. Cheng, “Evaluating weapon systems using ranking fuzzy numbers,” Fuzzy Sets and Systems, vol. 107, no. 1, pp. 25–35, 1999. [Google Scholar]

72. M. Dehghani, M. Esmaeilian and R. Tavakkoli-Moghaddam, “Employing fuzzy ANP for green supplier selection and order allocations: A case study,” International Journal of Economy, Management and Sciences, vol. 8, no. 2, pp. 565–575, 2013. [Google Scholar]

73. J. Buckley, “Fuzzy hierarchical analysis,” Fuzzy Sets and Systems, vol. 17, no. 3, pp. 233–247, 1985. [Google Scholar]

74. S. Chou and Y. Chang, “The implementation factors that influence the ERP (enterprise resource planning) benefits,” Decision Support Systems, vol. 46, no. 1, pp. 149–157, 2008. [Google Scholar]

75. C. Hwang and K. Yoon, Multiple Attribute Decision Making, New York: Springer-Verlag, 1981. [Google Scholar]

76. K. Yoon, “A reconciliation among discrete compromise solutions,” Journal of the Operational Research Society, vol. 38, no. 3, pp. 277–286, 1987. [Google Scholar]

77. C. Hwang, Y. Lai and T. Liu, “A new approach for multiple objective decision making,” Computers & Operations Research, vol. 20, no. 8, pp. 889–899, 1993. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.