DOI:10.32604/cmc.2022.020491

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020491 |  |
| Article |
Indoor Air Quality Control Using Backpropagated Neural Networks
1International Information Technology University, Almaty, Kazakhstan
2Al-Farabi Kazakh National University, Almaty, Kazakhstan
3Abai Kazakh National Pedagogical University, Almaty, Kazakhstan
4University of International Business, Almaty, Kazakhstan
5College of Computing & Informatics, Tenaga National University, Kuala Lumpur, Malaysia
6L. N. Gumilyov Eurasian National University, Nur-Sultan, Kazakhstan
*Corresponding Author: Aigerim Altayeva. Email: aikosha1703@gmail.com
Received: 26 May 2021; Accepted: 12 July 2021
Abstract: Providing comfortable indoor air quality control in residential construction is an exceedingly important issue. This is due to the structure of the fast response controller of air quality. The presented work shows the breakdown and creation of a mathematical model for an interactive, nonlinear system for the required comfortable air quality. Furthermore, the paper refers to designing traditional proportional integral derivative regulators and proportional, integral, derivative regulators with independent parameters based on a backpropagation neural network. In the end, we perform the experimental outputs of a suggested backpropagation neural network-based proportional, integral, derivative controller and analyze model results by applying the proposed system. The obtained results demonstrated that the proposed controller can provide the required level of clean air in the room. The proposed developed model takes into consideration international Heating, Refrigerating, and air conditioning standards as ASHRAE AND ISO. Based on the findings, we concluded that it is possible to implement a proposed system in homes and offer equivalent indoor air quality with continuous mechanical ventilation without a profuse amount of energy.
Keywords: Air quality; indoor air; PID; backpropagation; math model; controller
Given the catastrophic level of urban air pollution and the even lower indoor air quality, we are forced to breathe air with a high concentration of life-threatening substances. Moreover, this problem does not depend on the place of residence, it is equally relevant for both a country house and a city apartment.
Spending most of our lives in homes where there are no natural mechanisms for purifying the air, we are forced to purify it with our lungs as its pollution continuously occurs. A person inhales up to 24 kg of air per day, which is at least 16 times more than the amount of water consumed per day [1].
A modern city dweller spends 90% of his time indoors. According to ecologists, the air in the house is 4–6 times dirtier and 8–10 times more toxic than street air. About 10% of infectious diseases and colds are acquired outside the walls, and 90%-indoors [2]. To restore the comfort of the room, reduce the humidity of the air, remove all solid particles from it and open it to fresh air. In short, to provide good air for your family, all living rooms in it must have good ventilation. In cases where the room layout is complex, this process requires human interference. Ventilation systems play an essential role in ensuring high indoor air quality. Ventilation air effectively removes internal dirt from the premises.
The quality of air in buildings is regulated by the parameters of the effects of endogenous and exogenous factors, which are usually determined by the conditions of comfort and health for human life. Providing a healthy air condition is challenging as multi-functional, and technically complicated mechanisms are utilized, making it challenging to keep indoor air quality acceptable.
However, research on air quality control (AQC) mechanisms can be considered as multiple-input multiple-output (MIMO) challenges [3], as it works in conjunction with interconnected variables to recovery sets of final values. Besides, these systems are influenced by a group of specific parameters from the user's side, passenger movements, and external environmental parameters all of which can alter their normal operations. Therefore, AQC issues are considered multi-criteria problems that are described with complicated analytic calculations.
Even though standard PID controllers have reasonable answers, they cannot wholly control the indeterminacy of AQC systems’ dynamics, which are described by their specific rules and variables [4,5]. Since fuzzy logic controllers (FLC) do not need mathematical modeling, they operate like the vital selection to conventional controllers [6,7].
This research paper is described as follows: appropriate literature was examined, indicating methods of control and existing methods of monitoring the prospects; Section 3 a mathematical model that shows indoor air quality is demonstrated; Section 4 describes the design process of backpropagation neural network (BPNN) based PID controller for air quality monitoring and also explains proposed techniques, in Section 5 we demonstrate simulation outcomes, and results of model performed in our laboratory during the research. At the end of the paper, we discuss further work.
Highlights of this research are the following: Firstly, the proposed work demonstrates the deconstruction and construction of a mathematical model for an interactive, nonlinear system that provides the desired agreeable air quality. Secondly, the paper discusses applying a backpropagation neural network (BPNN) to create proportional, integral, derivative (PID) regulators with independent parameters. Finally, we apply the proposed system to the experimental outputs of a proposed BPNN based PID controller and analyze model outcomes. The proposed model shows its efficiency in residential buildings where outdoor environmental factors are minimal to building constructions. However, during the model development, we did not consider working offices, where participation of outdoor parameters (when windows or doors open all time) is high.
Proportional-integral-differential (PID) control is the most common mathematical algorithm. It is used to control automated systems of modern industrial and commercial applications. Essentially, these three parameters of the proportional, integral, and derivative are collected using a sensor and then used to adjust the control element, which changes the output of the process to achieve the desired result [8]. This feedback mechanism can be applied to simple operations, for example, regulating the temperature in a house with a thermostat, or to more complex ones, such as building a tracking and stabilization system onboard an airplane.
While PID control is often used because of its adaptability in a wide range of applications and operating conditions, several common problems arise in the process of configuring PID.
Since complex variables must be precisely configured to achieve optimal performance of the managed system, the configuration process can take a lot of time and erroneous attempts. The difficulty may arise in the fact that the settings for a particular system may differ depending on the priorities of the system [9].
PID control algorithms have long been considered the industry standard for control automation [10]. They remain so today, despite certain shortcomings in the configuration process. Recently, functions such as automatic and adaptive settings have been used more often, which are aimed at reducing the setup time and can often independently achieve the correct settings for a given operation. In recent studies, machine learning methods are used to independently achieve the correct parameters. For example, intelligent controllers, optimized by the use of evolutionary algorithms were developed for the control of the subsystems of an intelligent building [11]. The combination of machine learning, fuzzy control, and evolutionary algorithms culminated in the so-called Computational Intelligence (CI), which is currently being used in architecture. Some sophisticated control methods have integrated fuzzy adaptive control [12–15], optimum comfort control [16], and minimum-power comfort control [17] to address the nonlinear characteristic of comfort parameters, computation, time delay, and system uncertainty. A back-propagation algorithm-based direct neural network controller has been developed and effectively used in hydronic heating systems [18].
In Japan [19], neural networks have been widely utilized in commercial goods such as air conditioners, electric fans, and so forth. To further fine-tune the equipment to the customers’ tastes, a system of two neural networks has been integrated into an air conditioner. Using only sensor inputs, one of the two neural networks calculates the value of the air quality rate. However, this is not always the best option for a particular user. This output is further corrected by the other neural network. This neural network may be trained by the user.
ML methods have been used to model predictive control (MPC) for energy efficiency and interior environment improvement in buildings in last state-of-the-art research. Ferreira et al. [20] used an MPC controller in conjunction with an ANN-based building model to manage the HVAC system in a federal establishment to optimize interior comfort and power consumption. When compared to a traditional hysteresis controller, Bünning et al. [21] installed an MPC controller with a random-forests-based building model in an apartment to regulate room air temperature and observed a 24.9 percent reduction in cooling energy usage. When compared to the original control, Merabet et al. [22] installed an MPC controller with a data-driven building model in an HVAC test facility to improve HVAC energy efficiency and reported an average of 1.5 MWh of energy savings. The trials in the aforementioned research, on the other hand, were only conducted for a limited period, ranging from hours to days. The majority of prior research in the literature on MPC with an ML-based construction model has relied on simulations. Smarra et al. [23] created an MPC controller based on a random-forest-based building model, which was shown to have similar performance to an MPC based on a perfectly-known physics-based building model via simulations. Huang et al. [24] evaluated an MPC controller with a physics-based construction model using an ANN-based airport building model. The results of their simulations indicated a 5%–18% decrease in HVAC energy usage. Chen et al. [25] used an ANN-based building model to create an MPC controller for hybrid ventilation buildings. In their simulations, the MPC controller outperformed a rule-based controller in terms of thermal comfort. Reynolds et al. [26] created an MPC controller for scheduling heating set points in a building based on an ANN-based architectural model. According to their calculations, the MPC controller saved 27% more energy than traditional control. Afram et al. [27] used an ANN-based building model to create an MPC controller for a residential building, and their simulations revealed an energy-saving potential of 6–73 percent. Experiments that might assess MPC's effectiveness using a machine learning-based construction model over a lengthy period of time are currently missing.
3 Mathematical Model for Determining Indoor Air Quality (CO2)
In our work, we get CO2 as a detector of the air contaminant. By managing the CO2 to an acceptable level, it is also possible to control other air pollutants to acceptable levels.
Fig. 1 illustrates enclosing structures with a compulsory fresh air filtering process. The corresponding values describing the volumetric airflow rate in the indoor and outdoor air, as well as the carbon dioxide concentration, are the following.
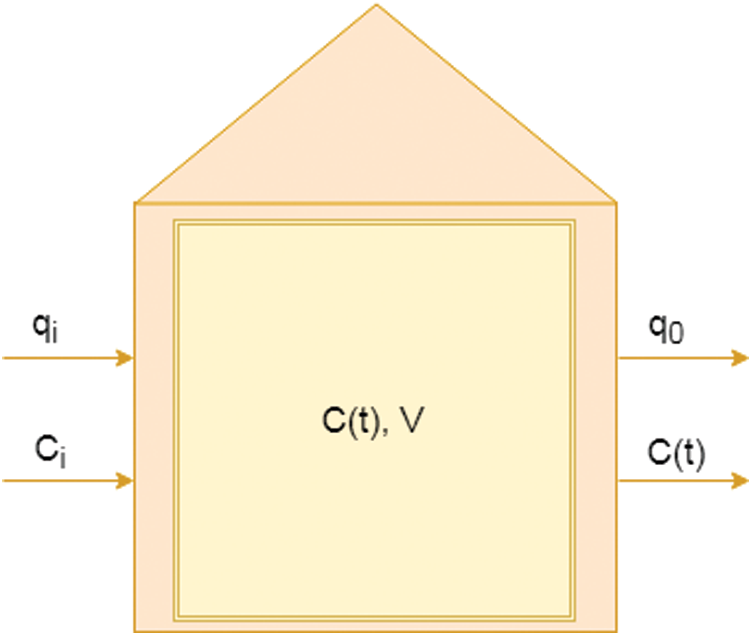
Figure 1: Mass balance conception for the mathematical model
The differential alignment, which manages the formation and dissolution of carbon dioxide, based on a variety of balance considerations, is expressed as
qi is the volume flow of fresh air via the filter; q0 is the volume flow rate of air leaked out; V is the indoor air volume; C is the indoor CO2 concentration at time t; C0 is the indoor CO2 concentration at time t0, and S is the rate of formation of CO2.
For the volume of indoor air inside, Eq. (1) can be rewritten as
For simplicity's sake coefficients K0 and K1:
Substituting Eq. (3) into Eq. (2) gives
The limits of integration in Eq. (4) are from C0 to C concentration and t0 to t time. Here C—determines the concentration of CO2 at time t, C0—determines the concentration of CO2 at the initial moment of time t0. The following expression is formed from (4)
Thus,
Rearranging Eq. (6) leads to
And
Substituting Eq. (3) into Eq. (8) gives the illative equation that characterizes the generation and decomposition of CO2:
When a leak from a building, q0, is equal to the volume of fresh air, qi, Eq. (9) will be rewritten as the following equation:
Eq. (10) will be considered later in connection with experiments that lead to CO2 generation due to the high occupancy rate and decomposition of CO2 after residents leave the building.
The survey of indoor air contaminants’ characteristics for overall control and air quality management is a compound problem [28–29]. It was offered that measuring and research of indoor CO2 mass can be used to realize IAQ and ventilation productivity. The severances in managing the IAQ because of time detentions and measuring errors [30]. To reach optimal method efficiency in the space of rapid replication time, system durability, interposition opposition, and small overshoots, a NN PID controller based on the backpropagation algorithm with a weight update algorithm is proposed.
4.1 Configuration of Neural Network and PID Based Control
The NN PID controller combines conventional and NN controllers that combine the PID controller's superiority and the NN network.
Fig. 2 exemplifies the architecture of a NN PID control comprising the nonlinear prediction mode land the NN PID controller, where r—is define the installation input, G(S)—is define the managed entity, y—is determine the real output, u—defines the monitoring variable, y—is define the prognosis of
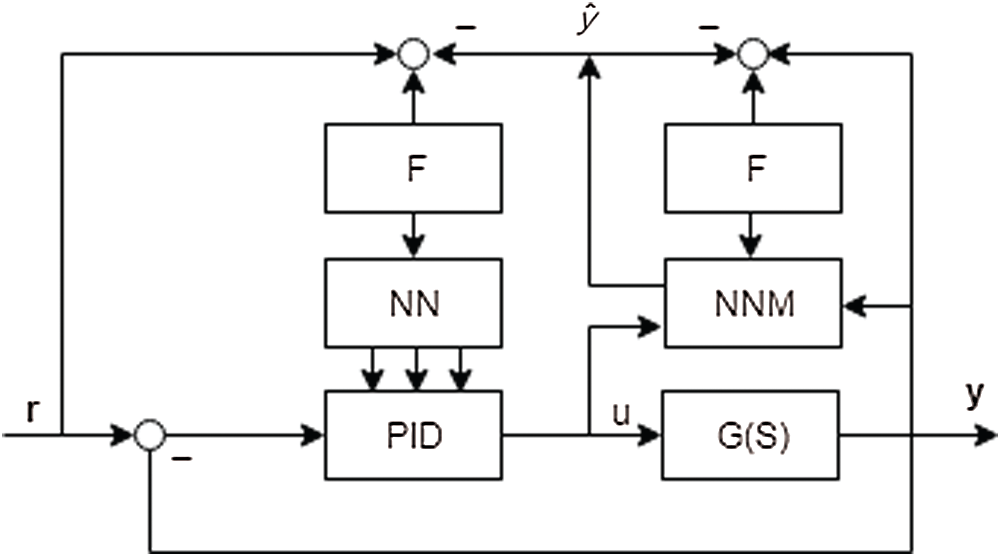
Figure 2: Neural Network PID Control System
The neural network in Fig. 2 is justified on the system status and adjusts the PID controller's arguments to get the best option possible of a determined productivity index. As soon as the neural network is put together in a particular learning algorithm, it is feasible such the output prognosis or variation is utilized to figure out the manage weight or regulate the NN values. But to get the result of the system prediction is so hard to get that the traditional method concludes the controller task's formation and the solution's prediction. In this way, the correct output can be instead of a forecast output for determining an NN's managed weight [31–34].
4.2 Neural Network PID Controller
Let the fault be defined as
where kp, ki, and kd are the proportional, integral, and derivative coefficients. Besides, the derivative profit of the PID regulator must be fixed. Eq. (14) can be rewritten as:
In Eq. (14)
Fig. 3 shows the NN module used to accommodate the strengthening of the PID controller, applying the adaptive way with the metering data u(k), y(k), and r(k). In our study, the layers of the BPNN used have M input neurons, three output neurons (kp, ki, and kd), and Q hidden neurons. The results of the BPNN define the three arguments of the PID controller.
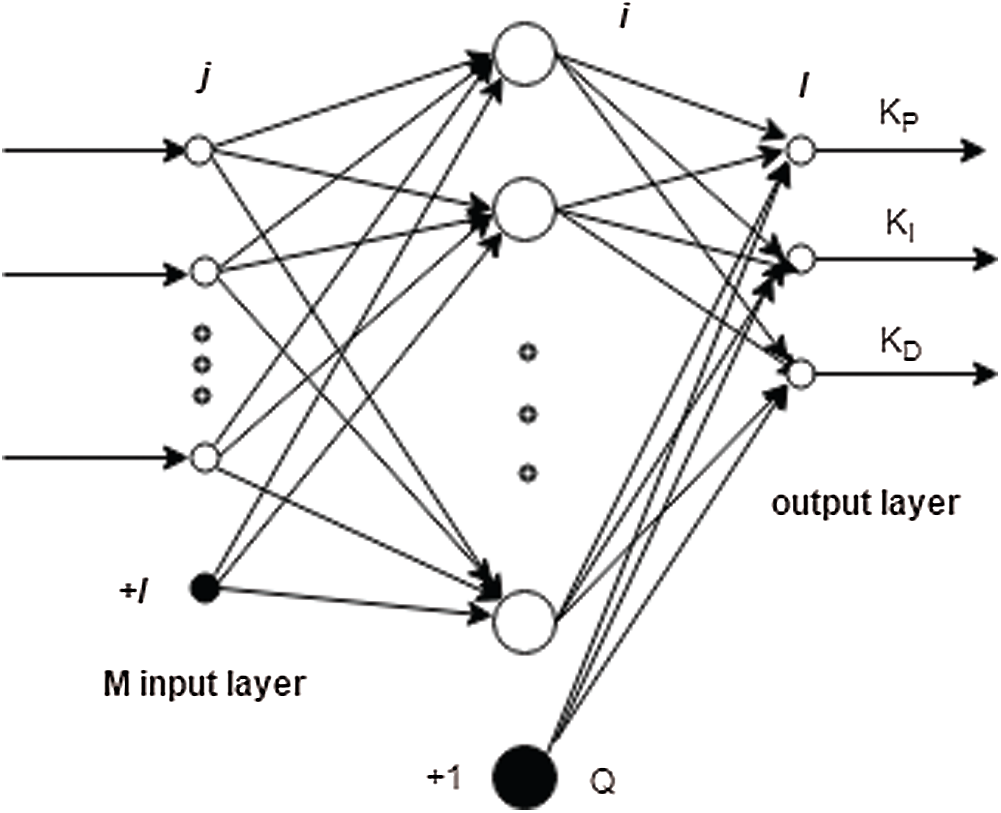
Figure 3: Neural Network module
Express as the output of BPNN input layer neurons are:
where
where
where
Based on the gradient way by utilizing the BP method, to lessen the productivity of index function J is signifying as:
And
where m is the learning rate and is the smoothing factor
In (18)
Therefore:
The hidden layers weights update:
And
This method suggested how the life-cycle controls system being a nonlinear system [39]. For the air-conditioning for variable-frequency method, the managed object is assumed to be a nonlinear system:
where y(k) is output, and u(k) is input at time k, relatively, ny, and nu, the methods of {y} and {u}, relatively.
By considering the prognosis of
The hidden layers of input and output are expressed as:
The result of the output layer can be written as follows:
The backward learning of the BPNN model is done by the BP learning algorithm modifying the weights and valve values and making the target function Jy a minimum:
The weight is modified by:
where m is defined as the speed of training, a is a smoothing coefficient, and both are in (0,1).
The activation function's derivative can be written as:
So,
Through the above BPNN PID analysis, it can be as follows
a) Select the BPNN configuration: define the input and hidden neurons M and Q, describe each layer's weight
b) Find
c) Standardize input parameters:
d) Based on Eqs. (24), (25), and (28), the forward calculation of BPNN is performed, and the regulated arguments of PID kp(k), ki(k), kd(k) are output.
e) Based on Eq. (11), u(k) is calculated.
f) Eqs. (23)–(25) are used to find
g) Using Eq. (29), the weights of the hidden and output layers are modified.
h) By using (30),
i) Eqs. (19) and (20) are applied to update the weights of output and hidden layers.
Apply increment operation to k, after return to the step b)
Fig. 4 demonstrates flowchart of PID control using BPNN model. The following steps are described in Fig. 4.
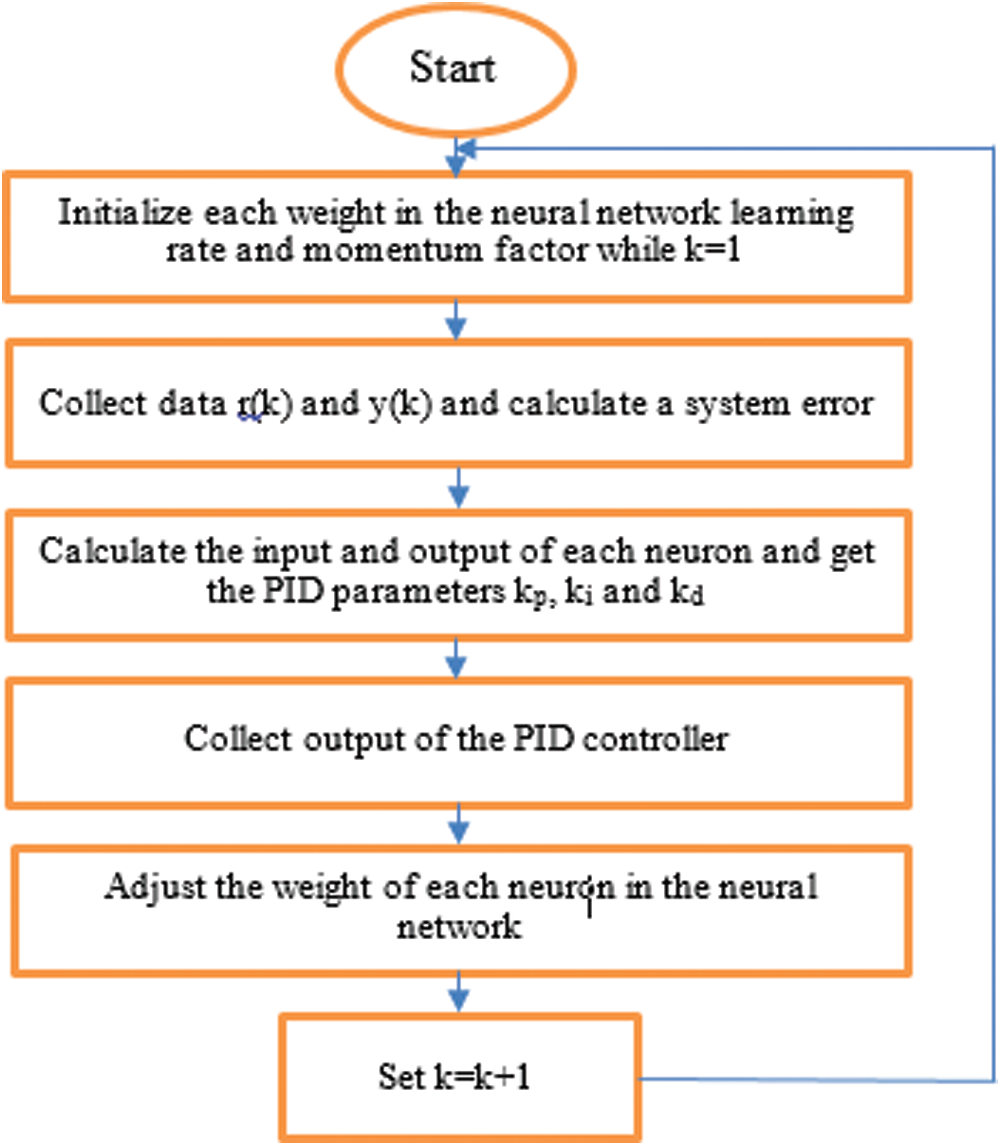
Figure 4: Flowchart of BPNN PID Controller
1)Initialize every weight in the NN
Assemble the r(k), y(k), and computation of error:
To get the PID arguments kp, ki, and kd, determine every neuron's inputs and outputs.
4)Calculate the Output.
5)Training in an online form. To implement your adaptive adjustment of the parameters PID ke, kI, and kd, regulate every neuron's weight in NN utilizing the algorithm of backpropagation.
6)Perform the k = k + 1 and return to rule 1).
Indoor environment air quality is investigated by using an advanced control technique based on a BPNN. As said earlier, by using a fuzzy logic-based controller, the system controls CO2 concentration inside the room. The experiments were executed from September 2020 until the end of February 2021. The concentration of CO2 is approximately 300–400 ppm outdoor. The succeeding list shows the steps to prepare for the experiment:
• The air conditioning system is utilized to provide the room with fresh air.
• A carbon dioxide sensor is used to determine CO2 concentration.
• As suggested, a fuzzy-based PID controller controlled the working ability of the air conditioner.
• The permissible over the limit of CO2 level is defined as 1000 ppm.
• Operating(working) hours are between 9.00 and 18.00
To simulate the real situation, opening the window or doors continually, occupation of the experimental room with people, or space (when people go out), are also considered during experiments. CO2 concentration levels may change and affect the controller's work and comfort when considering the situations listed above. Furthermore, folks may come back to the workplace and leave the office earlier or later than the established working hours.
CO2 is not made when there is no air-conditioning space because it is an air pollutant related to accommodations. This means that, when the working day begins, the level of CO2 in the room is similar to the levels of outdoor CO2. Therefore, after 9.00, depending on the occupation of the office, CO2 levels start to increase. Thus, when the first employer comes to work, the CO2 controller must be starting its work.
Fig. 5 illustrates CO2 level changes during one working day in January 2021. We can see that, when the working day started, the CO2 concentration level was low, at about 9.00 it rises sharply due to employers coming to work, and then, due to the controller's work, it fell to less than 1000 ppm. During lunchtime, starting from 13:00 and lasting until 14:00, there was a slight decrease to 600 ppm with a window open. After 14:00, as people return to work, CO2 concentration increased immediately, followed by a comparatively steady-state level. After 18:00, when the employees left, the CO2 concentration level decreased.
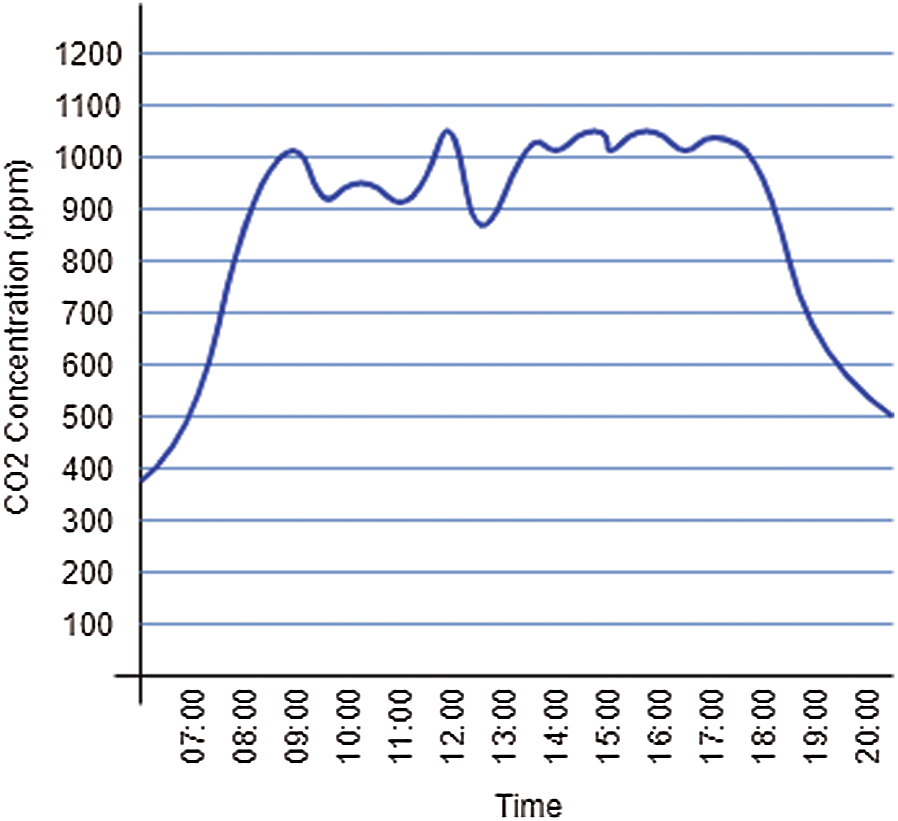
Figure 5: Indoor CO2 concentration level monitored in January 2021
Fig. 6 indicates the average monthly internal value of CO2 within the experiment, starting from September 2020 until February 2021. The red line represents the average monthly value of CO2 inside the room within labor time from 9:00 to 18:00, and they change among 850–930 ppm. They are approximately 125–60 ppm lower than the original CO2 value. The blue line indicates the importance of internal average monthly CO2 regulated after the management operation transmitted to a stable state. In normal conditions, the intermediate monthly CO2 level in the room is between 940–1000 ppm. Consequently, the CO2 maintains at an allowable level inside the room, and the stable small faults, meaning that within the laboring day when the controller is working, no over ventilation.
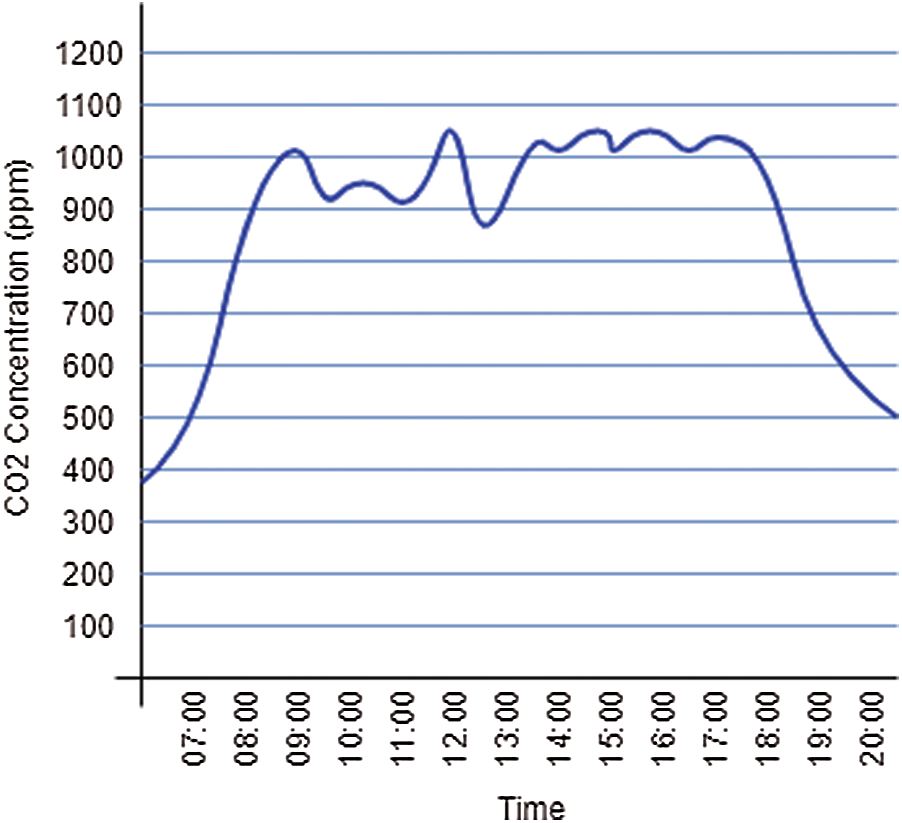
Figure 6: Average monthly internal value of CO2
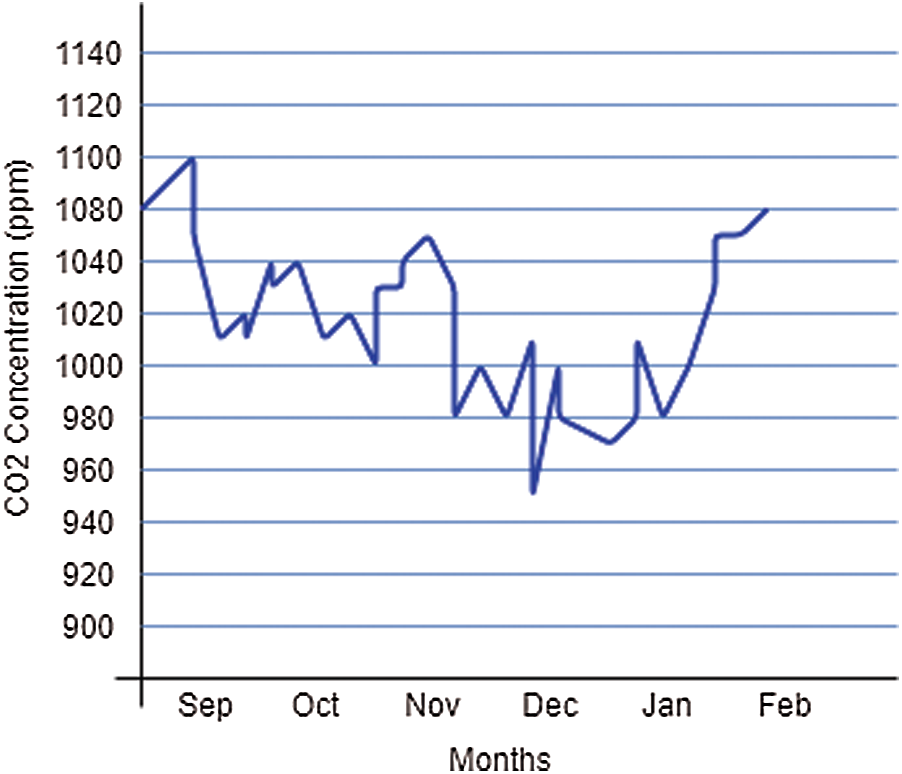
Figure 7: Indoor CO2 concentration level monitored for six months
The level of CO2 in the room must be monitored, unlike the level of relative humidity and temperature, which should be regulated within a given range. It behaves when the air conditioning region is open or free [41]; the CO2 concentration in the room is diminished; this achieved the lower setting. In this case, the CO2 concentration meanings of indoor are apportioned in a comparative diapason. The standard deviation is not appropriate for the conception of the productivity of IAQ control in the room. Therefore, the inside temperature is generally used to study the controller. The level of the maximum monthly internal CO2 value is shown in Fig. 7. Thus, according to the study results, the highest value for every day is 1100 parts ppm. This level, which does not harm the human body, does not persist for an extended period [42].
Traditional PID control achieves greater performance and higher control accuracy in heating, ventilation, and air conditioning systems when the PID control parameters, percentage gain, integral time, differential time, and sampling period, are adjusted and calibrated. There are certain drawbacks, such as a greater overshoot and a longer reaction time. PID parameter optimization and tuning need a particular math model, and if the PID controlled system is used in an HVAC system, parameter tuning necessitates a mix of theory and experimentation.
In an HVAC system, fuzzy control may minimize overshoot and cut reaction time, improving operating performance. However, a static mistake may occur in a fuzzy control system at times. The steady-state performance index isn't quite good enough, and the control accuracy isn't quite there.
The hybrid control switches between PID and fuzzy control depending on the threshold amount. The hybrid fuzzy-PID control shows both the benefit and the flaw at the same time. Individual control in an HVAC system is inferior to hybrid fuzzy-PID control.
The threshold amount in hybrid fuzzy-PID control is critical to the HVAC system's performance. The region of error and output, as well as experiments and other factors, should all be considered when selecting a threshold valve. In such cases, the use of machine learning has its advantages. Using internal and external parameters, machine learning can predict the necessary PID parameters and will be ready in advance to adjust the parameters. In our study, we used neural networks of backpropagation to predict and quickly adjust parameters.
The suggested approach has been proven to be effective in residential structures when outside environmental influences are limited. However, we did not include functioning offices in the model since they have many outside characteristics (windows or doors open all the time). In further, we are planning to expand our research by applying two more changes. Firstly, we are going to adapt our math model and machine learning model for adjusting PID parameters for office building air quality control by considering the high involvement of outdoor parameters. Secondly, we are going to develop a model for control three comfort parameters as temperature, humidity, and air quality.
The relevance of the work is determined by the need to improve the comfort of residential premises, which includes the improvement of their air quality. At present, taking into account energy-efficient work to ensure a comfortable building's comfortable climate attracts a lot of interest and attention. To get maximum correctness in monitoring the comfort parameters, mathematical models are explored. With the help of a developed mathematical model, a PID controller has been designed, which will give high accuracy and fast response when used using neural network algorithms.
The proposed BPNN PID regulator's effectiveness was demonstrated in experiments. Comfortable meanings inside the room corresponded to the international comfort standards, as indicated by ASHRAE and ISO. We'll use the presence detector and GPU's learning system to improve the system and get more reliable results.
In PID regulation, because complicated variables must be properly set for the controlled system to operate at its best, the configuration procedure may take a long time and result in many failed attempts. The issue may emerge as a result of the fact that the settings for a given system may vary based on the system's priorities.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Jo, B. Jo, J. Kim, S. Kim and W. Han, “Development of an IoT-based indoor air quality monitoring platform,” Journal of Sensors, vol. 2020, pp. 1–14, 2020. [Google Scholar]
2. S. Sun, X. Zheng, J. Villalba-Díez and J. Ordieres-Meré, “Indoor air-quality data-monitoring system: Long-term monitoring benefits,” Sensors, vol. 19, no. 19, pp. 1–18, 2019. [Google Scholar]
3. B. Omarov, A. Altayeva and Y. Cho, “Smart building climate control considering indoor and outdoor parameters,” Lecture Notes in Computer Science, vol. 10244, pp. 412–422, 2017. [Google Scholar]
4. G. Marques, J. Saini, M. Dutta, P. Singh and W. Hong, “Indoor air quality monitoring systems for enhanced living environments: A review toward sustainable smart cities,” Sustainability, vol. 12, no. 10, pp. 1–21, 2020. [Google Scholar]
5. M. Benammar, A. Abdaoui, S. Ahmad, F. Touati and A. Kadri, “A modular IoT platform for real-time indoor air quality monitoring,” Sensors, vol. 18, no. 2, pp. 1–18, 2018. [Google Scholar]
6. X. Liu, R. Jayaratne, P. Thai, T. Kuhn, I. Zing et et al., “Low-cost sensors as an alternative for long-term air quality monitoring,” Environmental Research, vol. 185, pp. 1–11, 2020. [Google Scholar]
7. U. Jaimini, T. Banerjee, W. Romine, K. Thirunarayan, A. Sheth et al., “Investigation of an indoor air quality sensor for asthma management in children,” IEEE Sensors Letters, vol. 1, no. 2, pp. 1–4, 2017. [Google Scholar]
8. S. DeVito, G. DiFrancia, E. Esposito, S. Ferlito, F. Formisano et al., “Adaptive machine learning strategies for network calibration of IoT smart air quality monitoring devices,” Pattern Recognition Letters, vol. 136, pp. 264–271, 2020. [Google Scholar]
9. Y. Song, S. Wu and Y. Yan, “Development of self-tuning intelligent PID controller based on 115 for indoor Air quality control,” International Journal of Emerging Technology and Advanced Engineering, vol. 3, no. 11, pp. 283–290, 2013. [Google Scholar]
10. D. Ibaseta, J. Molleda, F. Díez and J. Granda, “Indoor Air quality monitoring sensor for the Web of things,” in Multidisciplinary Digital Publishing Institute Proceedings, vol. 2, no. 23, pp. 1466, 2018. [Google Scholar]
11. E. Maddalena, Y. Lian and C. Jones, “Data-driven methods for building control—A review and promising future directions,” Control Engineering Practice, vol. 95, pp. 104211, 2020. [Google Scholar]
12. A. Abdo-Allah, T. Iqbal and K. Pope, “Modeling, analysis, and design of a fuzzy logic controller for an ahu in the sj carew building at memorial university,” Journal of Energy, vol. 2018, pp. 1–10, 2018. [Google Scholar]
13. J. Ahn, “Abatement of the increases in cooling energy use during a period of intense heat by a network-based adaptive controller,” Sustainability, vol. 13, no. 3, pp. 1353, 2021. [Google Scholar]
14. F. Behrooz, N. Mariun, M. Marhaban, M. Mohd Radzi and A. Ramli, “Review of control techniques for HVAC systems—Nonlinearity approaches based on fuzzy cognitive maps,” Energies, vol. 11, no. 3, pp. 495, 2018. [Google Scholar]
15. A. Shah, H. Nasir, M. Fayaz, A. Lajis and A. Shah, “A review on energy consumption optimization techniques in IoT based smart building environments,” Information, vol. 10, no. 3, pp. 108, 2019. [Google Scholar]
16. D. Fischer, J. Bernhardt, H. Madani and C. Wittwer, “Comparison of control approaches for variable speed air source heat pumps considering time variable electricity prices and PV,” Applied Energy, vol. 204, pp. 93–105, 2017. [Google Scholar]
17. D. Enescu, “A review of thermal comfort models and indicators for indoor environments,” Renewable and Sustainable Energy Reviews, vol. 79, pp. 1353–1379, 2017. [Google Scholar]
18. H. Shahnazari, P. Mhaskar, J. House and T. Salsbury, “Modeling and fault diagnosis design for HVAC systems using recurrent neural networks,” Computers & Chemical Engineering, vol. 126, pp. 189–203, 2019. [Google Scholar]
19. T. Lewis and P. Denning, “Learning machine learning,” Communications of the ACM, vol. 61, no. 12, pp. 24–27, 2018. [Google Scholar]
20. P. Ferreira, A. Ruanoa, S. Silva, E. Conceiçãoa, “Conceicao neural networks based predictive control for thermal comfort and energy savings in public buildings,” Energy and Buildings, vol. 55, pp. 238–251, 2012. [Google Scholar]
21. F. Bünning, B. Huber, P. Heer, A. Aboudonia and J. Lygeros, “Experimental demonstration of data predictive control for energy optimization and thermal comfort in buildings,” Energy and Buildings, vol. 211, pp. 109792, 2020. [Google Scholar]
22. G. Merabet, M. Essaaidi, M. Haddou, B. Qolomany, J. Qadir et al., “Intelligent building control systems for thermal comfort and energy-efficiency: A systematic review of artificial intelligence-assisted techniques,” Renewable and Sustainable Energy Reviews, vol. 144, pp. 110969, 2021. [Google Scholar]
23. F. Smarra, A. Jain, T. de Rubeis, D. Ambrosini, A. D'Innocenzo et al., “Data-driven model predictive control using random forests for building energy optimization and climate control,” Applied Energy, vol. 226, pp. 1252–1272, 2018. [Google Scholar]
24. H. Huang, L. Chen and E. Hu, “Model predictive control for energy-efficient buildings: An airport terminal building study,” in 11th IEEE Int. Conf. on Control & Automation, Taichung, Taiwan, pp. 1025–1030, 2014. [Google Scholar]
25. J. Chen, G. Augenbroe and X. Song, “Lighted-weighted model predictive control for hybrid ventilation operation based on clusters of neural network models,” Automation in Construction, vol. 89, pp. 250–265, 2018. [Google Scholar]
26. J. Reynolds, Y. Rezgui, A. Kwan and S. Piriou, “A zone-level, building energy optimisation combining an artificial neural network, a genetic algorithm, and model predictive control,” Energy, vol. 151, pp. 729–739, 2018. [Google Scholar]
27. A. Afram, F. Janabi-Sharifi, A. Fung and K. Raahemifar, “Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system,” Energy and Buildings, vol. 141, pp. 96–113, 2017. [Google Scholar]
28. M. Jia, R. Srinivasan, R. Ries and G. Bharathy, “A framework of occupant behavior modeling and data sensing for improving building energy simulation,” in Proc. of the Sym. on Simulation for Architecture and Urban Design, Delft, The Netherlands, pp. 15, 2018. [Google Scholar]
29. F. Oliveira and A. Ukil, “Energy efficiency in variable speed centrifugal chiller systems driven by synchro-nous reluctance motors,” in 2018 IEEE Innovative Smart Grid Technologies-Asia, Singapore, pp. 340–344, 2018. [Google Scholar]
30. H. Nehrir and K. Dehghanpour, “Agent-based microgrid power management and microgrid-based resilient distribution system,” in 2018 IEEE Power & Energy Society General Meeting, Portland, OR, USA, pp. 1–4, 2018. [Google Scholar]
31. G. Marques and R. Pitarma, “Indoor air quality monitoring for enhanced healthy buildings,” in Indoor Environmental Quality, Rijeka, Croatia, pp. 29–43, 2018. [Google Scholar]
32. R. Weyers, J. Jang-Jaccard, A. Moses, Y. Wang, M. Boulic et al., “Low-cost indoor air quality (IAQ) platform for healthier classrooms in New Zealand: Engineering issues,” in 2017 4th Asia-Pacific World Congress on Computer Science and Engineering, Mana Island, Fiji, pp. 208–215, 2017. [Google Scholar]
33. H. Zhang, R. Srinivasan and V. Ganesan, “Low cost, multi-pollutant sensing system using raspberry pi for indoor air quality monitoring,” Sustainability, vol. 13, no. 1, pp. 1–15, 2021. [Google Scholar]
34. M. Vukmirovic, A. Salaj and A. Sostaric, “Challenges of the facilities management and effects on indoor Air quality. case study “Smelly buildings” in Belgrade, Serbia,”Sustainability, vol. 13, no. 1, pp. 1–16, 2021. [Google Scholar]
35. P. Wargocki and D. Wyon, “Ten questions concerning thermal and indoor air quality effects on the performance of office work and schoolwork,” Building and Environment, vol. 112, pp. 359–366, 2017. [Google Scholar]
36. P. Babu and G. Suthar, “Indoor air quality and thermal comfort in green building: A study for measurement, problem and solution strategies,” Lecture Notes in Civil Engineering, vol. 60, pp. 139–146, 2020. [Google Scholar]
37. I. Gruicin, M. Ionascu and M. Popa, “A solution for Air quality monitoring and forecasting,” in 2018 IEEE 12th Int. Sym. on Applied Computational Intelligence and Informatics, pp. 503–508, 2018. [Google Scholar]
38. R. Sangi and Müller, “A novel hybrid agent-based model predictive control for advanced building energy systems,” Energy Conversion and Management, vol. 178, pp. 415–427, 2018. [Google Scholar]
39. S. Jangid, S. Sharma and S. Sharma, “Allergic patient centered air quality monitoring embedded system model,” in 2018 8th Int. Conf. on Cloud Computing, Data Science & Engineering (ConfluenceNoida, India, pp. 376–382, 2018. [Google Scholar]
40. W. Li, C. Koo, S. Cha, T. Hong and J. Oh, “A novel real-time method for HVAC system operation to improve indoor environmental quality in meeting rooms,” Building and Environment, vol. 144, pp. 365–385, 2018. [Google Scholar]
41. Y. Wang, J. Kuckelkorn, D. Li and J. Du, “A novel coupling control with decision-maker and PID controller for minimizing heating energy consumption and ensuring indoor environmental quality,” Journal of Building Physics, pp. vol. 43, vol. 1, pp. 22–45, 2019. [Google Scholar]
42. A. Dai, X. Zhou and X. Liu, “Design and simulation of a genetically optimized fuzzy immune PID controller for a novel grain dryer,” IEEE Access, vol. 5, pp. 14981–14990, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |