DOI:10.32604/cmc.2022.017682

| Computers, Materials & Continua DOI:10.32604/cmc.2022.017682 |  |
| Article |
Mechanical Properties of All MoS2 Monolayer Heterostructures: Crack Propagation and Existing Notch Study
1Institiute of Structural Mechanics, Bauhaus-Universität Weimar, Weimar, 99423, Germany
2Department of Computer Engineering, King Saud University, Riyadh, Saudi Arabia
3Mechanical Engineering Department, Islamic Azad University, North Tehran Branch, Iran
*Corresponding Author: Timon Rabczuk. Email: timon.rabczuk@uni-weimar.de
Received: 07 February 2021; Accepted: 02 April 2021
Abstract: The outstanding thermal, optical, electrical and mechanical properties of molybdenum disolphide (MoS2) heterostructures make them exceptional candidates for an extensive area of applications. Nevertheless, despite considerable technological and academic interest, there is presently a few information regarding the mechanical properties of these novel two-dimensional (2D) materials in the presence of the defects. In this manuscript, we performed extensive molecular dynamics simulations on pre-cracked and pre-notched all-molybdenum disolphide (MoS2) heterostructure systems using ReaxFF force field. Therefore, we study the influence of several central-crack lengths and notch diameters on the mechanical response of 2H phase, 1T phase and composite 2H /1T MoS2 monolayers with different concentrations of 1T phase in 2H phase, under uniaxial tensile loading at room temperature. Our ReaxFF models reveal that larger cracks and notches decrease the strength of all 2D MoS2 single-layer heterostructures. Additionally, for all studied crack and notch sizes, 2H phase of MoS2 films exhibits the largest strength. Maximum tensile stress of composite 2H/1T MoS2 nanosheet with different concentrations are higher than those for the equivalent 1T phase, which implies that the pre-cracked composite structure is remarkably stronger than the equivalent 1T phase. The comparison of the results for cracked and notched all-MoS2 nanosheet heterostructures reveal that the load bearing capacity of the notched samples of monolayer MoS2 are higher than the cracked ones.
Keywords: Molybdenum disulphide (MoS2); molecular dynamics simulations; uniaxial tension; cracks; notches
Molybdenum disulphide (MoS2) is well known for its various applications in industry and recently, its two-dimensional (2D) forms which are parts of the large family of so-called transition metal dichalcogenide (TMD), have attracted growing attention in high strength nanocomposites and in the nano-electronic technology. Like graphite, molybdenum disulfide crystals are composed of atomic layers with hexagonal lattices held together by van der waals forces. Even though MoS2 crystals exist in nature, its purification is difficult and expensive. On the other hand, natural gas and crude oil are sources of large amount of sulfur because they contain hydrogen sulphide (H2S). Chemical companies produce pure MoS2 crystals via the reaction of hydrogen sulphide with molybdenum oxide [1]. There are several methods to prepare single-layer forms of MoS2 including mechanical and chemical exfoliation of bulk crystals by peeling off the layers of MoS2 into 2D layers and vapour-phase growth of large-scale 2D monolayer MoS2 sheets [2]. In a recent method, Mo layers react with H2S and form large-areas of MoS2 monolayers [3]. Mono-layer MoS2 structures show extraordinary prospects for applications in flexible electrical and optical nanodevices for which mechanical stability is crucial [4,5]. One advantage of MoS2 over graphene includes its direct-bandgap, i.e., quasi-two-dimensional semiconducting behavior, while graphene is classified as a semi-metal, an electrically conducting metal. Another interesting property of MoS2 is its polymorphism characteristic. The electrical characteristics of single-layer MoS2 significantly depends on the S atoms locations. Experimental approaches show that extra tuning of the electrical properties of MoS2 monolayers by the fabrication of mono-layer heterostructures is possible. A monolayer MoS2 sheet has triple atomic planes with different atomic stacking sequences, in which a close-packed of molybdenum (Mo) is encompassed by two atomic layers of close-packed sulfur (S), as shown in Fig. 1. There exists three natural or synthetic polytypes of MoS2 sheets, depending on (1) the coordination of sulphur atoms with respect to the central molybdenum atom and (2) the stacking order of each layer. The semi-conducting (2H) phase which is the original structure of this material, 2D atomic layers of MoS2 sheets indicate a hexagonal lattice and an (Stop-Mo-SBot) ABA atomic stacking sequence (as depicted in Fig. 1a). Moreover, the metallic (1T) phase exhibits an atomic stacking sequence of (Stop-Mo-SBot) ABC, where the S atoms on the bottom are located in the hollow center of the hexagonal lattice. Both 2H and 1T structures have a 30° angle of symmetry. The loading angles of 0 and 30° are generally known as armchair and zigzag directions, respectively as illustrated in Fig. 1b. In addition to the aforementioned 2H and 1T phases, there are samples of 2H/1T heterostructures. The letter T stands for trigonal, and H for hexagonal structures. Amazingly, laboratory findings validate the probability of production of MoS2 heterostructure composed of semiconducting and metallic phases in a mono-layer configuration as shown in Fig. 1c [6]. In order to guarantee that nanomaterials and nanodevices manufactured from monolayer MoS2 sheets maintain their structural integrity throughout service life, it is required to obtain a basic knowledge of the mechanical behavior of monolayer MoS2 nanosheets under different loading conditions. Several authors have studied 2H phase of MoS2 sheets both experimentally and theoretically [7–15]. Experimentally fabricated MoS2 membranes will always contain different types of defects and impurities in their atomic lattices. For instance, crystal growth arising throughout the chemical vapor deposition (CVD) fabrication of monolayer MoS2 causes the formation of grain boundaries with different types of defects [16,17]. MoS2 nanosheets may also contain several atomic impurities like oxygen [18,19].
Cracks, holes and notches are among the most popular defects appearing in structures [20–25]. Initial flaws or fractures play a prominent role in two-dimensional materials impacting their mechanical behavior. Meanwhile, experimental studies on the materials at the nanoscale size are complex and expensive. Conversely, numerical approaches and computer simulations have been developed to get a better understanding on the nanomaterial behavior [26]. In order to evaluate the influence of defects and impurities on mechanical behavior of MoS2 films, ReaxFF reactive molecular dynamic simulation seems to be valuable choice. It worth mentioning that, in nonreactive force fields, molecules are formed through atomic static bonds that do not allow bond formations. This limitation prevents applying classical molecular dynamics (MD) methods to simulate chemical reactions. For the purpose of overcoming this limitation in MD simulation, the reactive force field (denoted ReaxFF) is employed [27]. A detailed description of the ReaxFF formulation can be found in the original work [28]. ReaxFF allows continuous bond-forming/breaking by replaced explicit bonds with bond orders. This method treats each atom as a separate body, which leads to the reformation of bond structures at every time-step [27]. This concept of dynamic bonding with charge redistribution together is the major difference between classical and reactive MD methods. In order to estimate and prevent mechanical failure caused by cracks and notches, it is necessary to understand the failure properties of monolayer MoS2. However, the failure behavior of MoS2 nanosheet is more complicated than those of graphene and other graphene-like materials which have planar surfaces with single-layer atomic structures. Bao et al. [29], conducted MD simulations to investigate the propagation of nanocracks in large sheets of 2H-MoS2 monolayer by using the Stillinger-Webber (SW) potential. In this work, the cracks were predefined by deleting some atoms in the nanosheet.
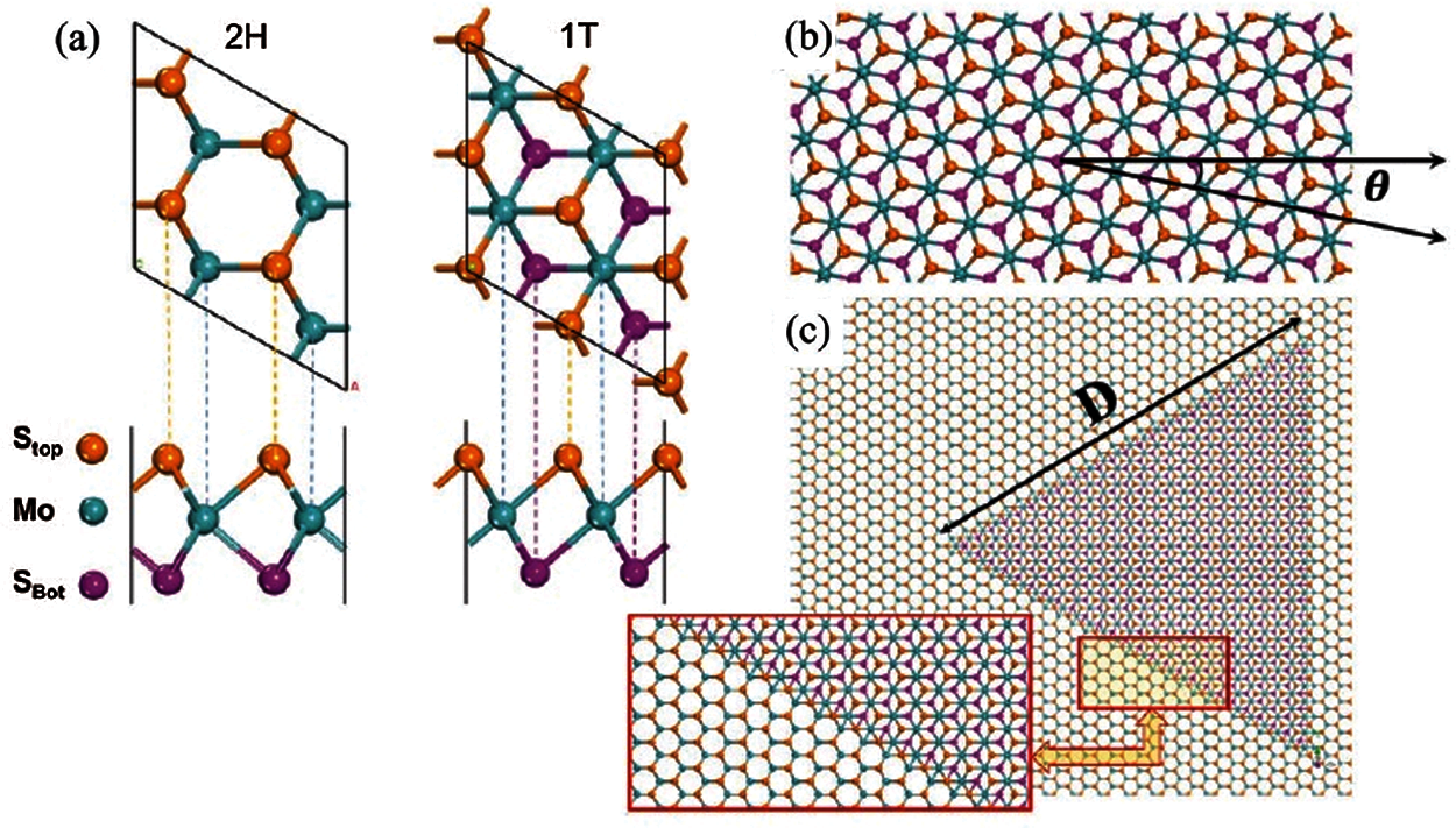
Figure 1: (a) MD representation of 2H and 1T mono-layered MoS2 phases on the basal plane and their related side view. The 2H structure represents a hexagonal lattice with threefold symmetry, whereas in 1T structure the underlying sulfur atom (SBot) is located in the void space at the center of the 2H hexagonal lattice. (b) Schematic illustration of 1T nonosheet where θ = 0 is the armchair direction. (c) A triangular domain of 1T phase inside the 2H phase which represents the periodic atomistic model ([6])
This research focuses on fracture of all phases of single-layer MoS2. We therefore extended the studies in [6] and performed MD simulations using the ReaxFF force field [30]. Section 2 describes the research methodology. Section 3 presents different types of defects in the nanosheet which are studied in this research. Section 4 discusses MD modeling and ReaxFF reactive force field. Section 5 presents the results of investigated mechanical response of all phases of molybdenum disulfide (MoS2) nanosheet with initial center nano-cracks and notches. Section 6 discusses the conclusions.
2 Description of the Research Methodology
The main objective of this research is to investigate the fracture properties (maximum tensile stress and fracture strain) and also crack and notch propagation of all aforementioned phases of MoS2 single-layer structures with various pre-existing crack and notch shape defects. Therefore, we conduct ReaxFF based molecular dynamics (MD) simulations and study the effect of different nano-crack sizes (lengths) and nano-notch sizes (diameters) on the single-layer MoS2 mechanical and failure response, predicting the macroscopic maximum tensile stress and fracture strain under uniaxial tension. We employ the approach discussed in our previous study [31] to generate initial cracks by disconnecting the interaction between atoms located at the crack edge.
3 Molybdenum Disulfide (MoS2) Nanosheet with Defects
The focus of this study is to computationally predict the mechanical behavior of MoS2 films containing nano-defects via MD calculations. We therefore extract the max. tensile stress and strain-at-fracture and model the crack and notch propagation in aforementioned 2D materials for several crack lengths and notch diameters at room temperature. To assess the effect of the crack and notch sizes on the mechanical properties of MoS2 structure, we created center crack and notch in the MoS2 nanosheet as depicted in Fig. 2, “L” denoting the side length of the nanosheet while “k” refers to a variable defining the initial crack length and notch diameter. Tensile loading is in the armchair direction of the nanosheet, which is perpendicular to the crack orientation. Two regions were defined at the left and the right sides of the crack location so that the coincident edges of the regions fall on the crack location as illustrated in Fig. 2c. Then, the interactions between atoms located at this edge are restricted by employing the “neigh-modify” command in LAMMPS.
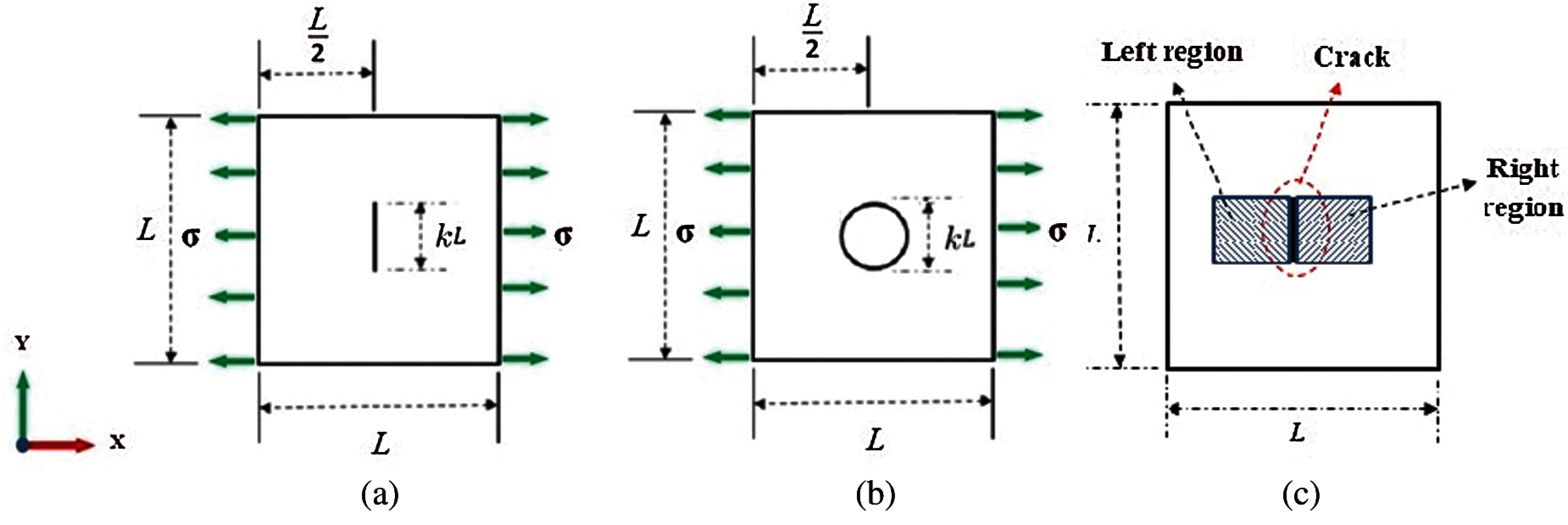
Figure 2: The nanosheet with a pre-defect located at the center of the nanosheet. (a) crack-shape defect (b) notch-shape defect. (c) Defining two regions to create a line crack in the nanosheet model
The results of MD modeling for pristine MoS2 nanosheets reveal that the elastic response of MoS2 phases depends on the loading direction. Along the armchair direction MoS2 exhibits a higher rigidity than in zigzag direction [6]. Thus, we load both 2H and 1T phases of the pre-cracked nanosheets in armchair direction. We study samples of pre-cracked single-layer 2H/1T heterostructures where the 1T phase inside 2H phase indicates a triangular geometry with a characteristics edge length, defined by “D” [6]. We consider different composite structures with specified characteristic sizes and concentrations of 1T phase inside 2H. According to experimental observations [32], three different grain boundaries of “α”, “β” and “γ” can be formed between the 2H and 1T phases. We follow the method used by Mortazavi et al. [6] and only consider the “β” grain boundary, which commonly exists in chemically grown polycrystalline MoS2 films [16]. All atomistic samples are assumed to be periodic along the planar direction avoiding the influence of free atoms on the boundaries. We employed a developed ReaxFF bond-order-dependent potential energy for introducing the atomic interaction of MoS2 presented in [30], in our MD simulations, which is a popular choice for such systems [33,34]. The atomic system energy (Esystem) in ReaxFF is additively decomposed into several partial energy contributions given by [28]:
where, Ebond, Eval, Etor, Eover, Eunder, Elp, EvdW and ECoulombic, represent the bond energy, valence-angle, torsion-angle, over-coordinate, under-coordinate, lone pair, non-bonded van der Waals and coulomb contribution, respectively. The parameters of the ReaxFF potential are obtained by a quantum mechanical (QM) dataset which introduces bond dissociation and valence angle bending in different molecules and also the energy of formation and the state of condensed-phases equations of crystalline MoS2 nanomaterials [30]. All simulations were done with the open-source software LAMMPS (Large-Scale Atomic/Molecular Massively Parallel Simulator) [35]. The post-processing was done with OVITO [36]. In order to estimate the fracture properties of all phases of MoS2 films, we first constructed models with different nanosheet sizes and obtained similar results which showed we have a concurrent multiscale method. Therefore, we select final models consisting of around 22,000 atoms with planar dimensions of about 25 nm × 25 nm and apply periodic boundary conditions in both planar directions. The time increment in all simulations is fixed at 0.25 fs. First, energy minimization was performed with a 10-6 stopping tolerance for energy. Then, the uniaxial loading condition is applied by increasing the periodic box size along the loading direction by a constant engineering strain rate of 109 s-1. Before subjecting the samples to uniaxial tension, the structures were relaxed and equilibrated to zero stress at room temperature taking advantage of the Nose-Hoover barostat and thermostat (NPT). This was done with damping parameters for 100 fs and 50 fs for the pressure and temperature, respectively. To apply the uniaxial load, the stress on the other two directions should remain small throughout the deformation procedure. As the atoms are in contact with vacuum along the nanosheet thickness orientation, the normal stress is insignificant. Moreover, the periodic simulation box along the width of the MoS2 nanosheet was kept at zero stress in the mentioned direction via the NPT approach. At every time step, the applied engineering strain rate was multiplied with the step time. The extracted values of the stresses and strains were averaged during each time interval of 250 fs.
The models were loaded in tension and the extracted uniaxial stress-strain results for defective MoS2 nanosheets are depicted on several graphs in order to calculate mechanical properties of MoS2 films. In the calculation of stresses, we choose the structure volume using a thickness of 6.1
5.1 Strain Rate Effect on Pristine Nanosheet
The strain rate is an effective factor influencing the strength of materials. We know that because of the enormous amount of computational costs, MD simulations cannot capture strain rates as they often occur in engineering applications. However, some researches have been done to extract the mechanical behavior under quassi-static conditions [37,38]. Commonly, the tensile strength of nanosheets increases with strain rate. Increasing strain rate decreases the relaxation time and makes it too short for atomic bonds to rotate and rearrange under stress and consequently, the tensile strength and strain-at-failure increases [39,40]. In this section we investigate the effect of different strain rates on the mechanical responses of the pristine MoS2 nanosheets. The tensile tests were performed for 2H phase and 1T phase of MoS2 material and also 2H/1T composite MoS2 structure with 5% concentration of 1T phase inside 2H phase at room temperature with strain rates ranging from 108 to 1010 s-1. Let us first consider a pristine 2H MoS2 nanosheet. The curves on Fig. 3a show the stress-strain response in armchair orientation. Obviously, for low strain rates of 108 and 109 s-1, the results converge against a curve. For high strain rate of 1010 s-1, first the results approximately converge against the other two curves until the strain of around 0.23 but it shows different pattern for high strains. Our results for 108 s-1 strain rate predict an ultimate stress of 25.8 GPa and the elastic modulus of 265.6 GPa which are in fair agreement to the results in [6]. The stress-strain curve of 1T-MoS2 nanosheet can be found in Fig. 3b. With reference to this figure, for low strain rates of 108 and 109 s-1, the results approximately converge against a similar curve. This behavior is more pronounced for strains less than 0.15. The curve for high strain rate of 1010 s-1 is above the other two curves which shows higher results. The maximum tensile stress and corresponding failure strain for 108 s-1 strain rate are 9.9 GPa and 0.18 respectively, which are very close to the results reported in [6]. Finally, the stress-strain curves of the 2H/1T hetero-structures of MoS2 films in armchair loading direction are depicted in Fig. 3c. This composite structure is made of the 1T phase with a domain size of 6 nm and with a concentration of 5%. The max. stress and corresponding failure strain in armchair direction for 108 s-1 strain rate are 19.36 GPa and 0.196, respectively which meet the results reported in [6]. Therefore, as the accuracy of the results for pristine nanosheets are verified, we conduct the same procedure to investigate the effects of pre-cracks and existing notches on the mechanical response of the equivalent MoS2 films. The failure properties of the aforementioned phases of MoS2 material which are obtained from Figs. 3a–3c are summarized and compared in Fig. 4, which include ultimate tensile strength, Young’s modulus and strain-at-failure of MoS2 nanosheets as a function of strain rate for different phases, as illustrated in Figs. 4a–4c respectively. As the strain rate increases, the ultimate tensile strength and strain at failure indicate an increasing trend. However, the strain rate effect on the mechanical properties of 1T phase of MoS2 nanosheet is more significant than 2H phase and hetero-structure.
5.2 Mechanical Response of the Sample with Initial Center Nano-crack
Fracture is a phenomenon with size effects and the crack length influences the mechanical properties of the nanosheet. As mentioned before, we use ReaxFF reactive MD modeling and estimate the fracture properties of monolayer MoS2 nanosheets with initial center cracks under mode I loading condition in armchair direction. We created MD models with side length of 25.0 nm simulation box size consisting of around 22000 individual atoms. We consider several pre-crack lengths including L/6, L/3 and L/2 where L is the length of the square graphene-like MoS2 monolayer.
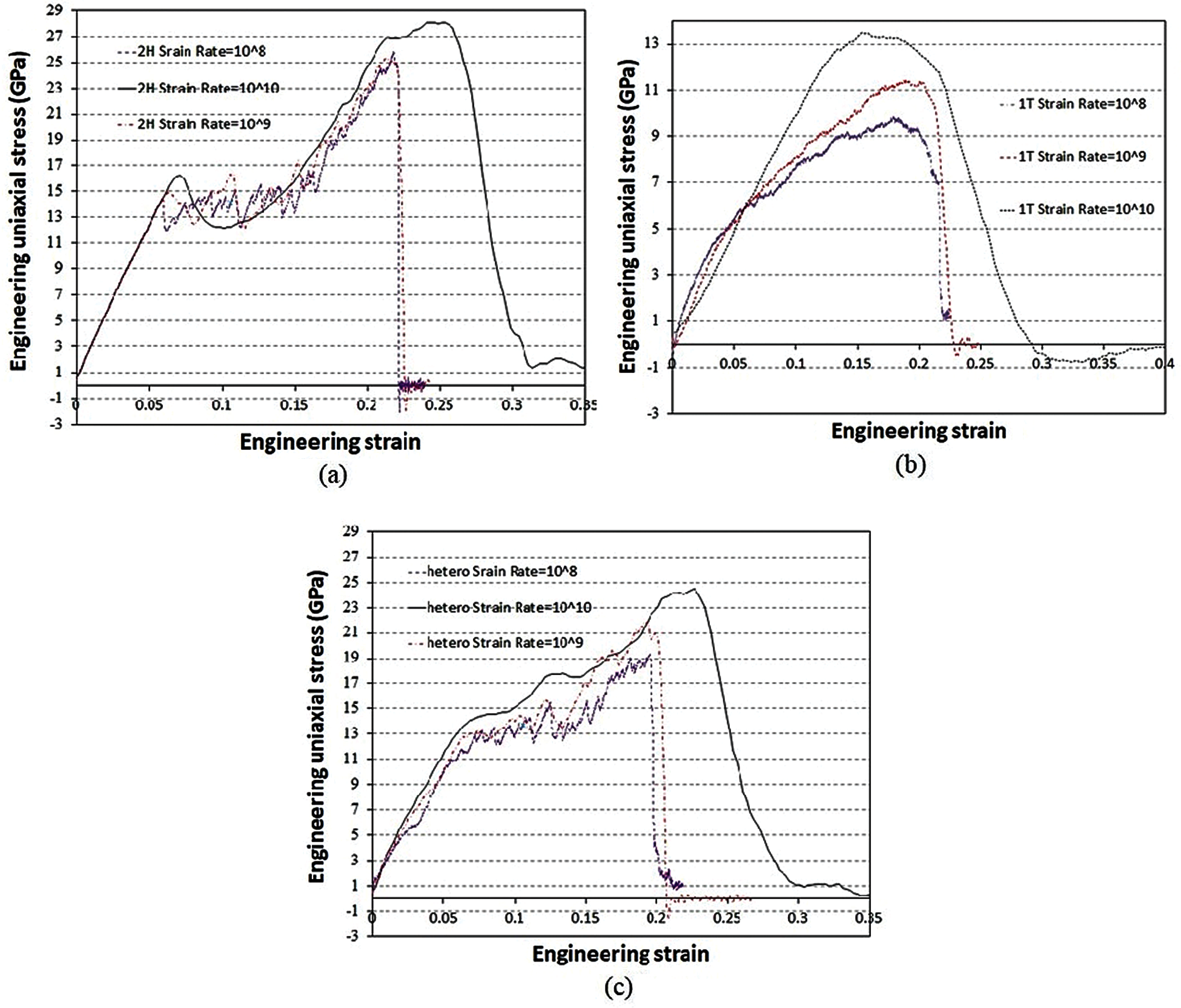
Figure 3: Tensile stress-strain response of pristine MoS2 nanosheet in armchair orientation. (a) 2H-phase of MoS2 (b) 1T-phase (c) 2H/1T hetero-structure for a concentration of 5% of the 1T phase inside 2H
5.2.1 Semiconducting (2H) MoS2 Nanosheets Results
Fig. 5 depicts the 2H phase of single-layer MoS2 film with a center crack size of L/3 at different time steps and associated strain values. Additionally, strains at each stage are shown on each picture which is 0.104 at the end of the crack propagation process of the whole length. As can be seen, for 2H phase MoS2 nanosheet, first the crack opens by increasing uniaxial tensile strain. Then by increasing crack-driving force, the crack rapidly grows perpendicular to the loading direction throughout the nanosheet. Following the nanosheet failure, the bonds between atoms are ruined and larger deformation araise. Stress concentration areas can be distinguished near the tip of the crack. We compare the results of our MD modeling for the 2H-MoS2 nanosheets subjected to different crack lengths of L/6, L/3 and L/2 where L is 25 nm. The related stress-strain curves are depicted in Fig. 6a. We also show the max. tensile stress for crack-free MoS2 nanosheet (0L). For L/6, L/3 and L/2 crack sizes, the max. tensile stresses are 13.42 GPa, 10.11 GPa and 7.79 GPa respectively and comparing them with crack-free MoS2 nanosheets, which exhibits a max. tensile stress of 25.8 GPa, shows the crack significantly decreases the max. tensile stress of 2D MoS2 material, i.e., the reductions are around 48%, 61% and 70% for L/6, L/3 and L/2 crack sizes, respectively. Also, Figs. 6b and 6c illustrate and compare the max. tensile stress and strain-at-fracture of the 2H-MoS2 nanosheet for the aforementioned crack sizes. Obviously, increasing the crack length, has a weakening effect on tensile strength of 2H MoS2 nanosheet. Additionally, strain-at-fracture decreases for larger crack sizes. According to Fig. 6b, a sudden reduction in the max. tensile stress is observed in the 2H-MoS2 models with crack sizes less than L/6, while larger crack sizes showed approximately a linear trend. Also, according to Fig. 6c a sudden decrease in strain-at-fracture is distinguished in samples with crack sizes less than L/6, while for larger crack sizes the decrease was very slow. It can be implied that the crack length nonlinearly influences fracture properties of MoS2 nanosheet.
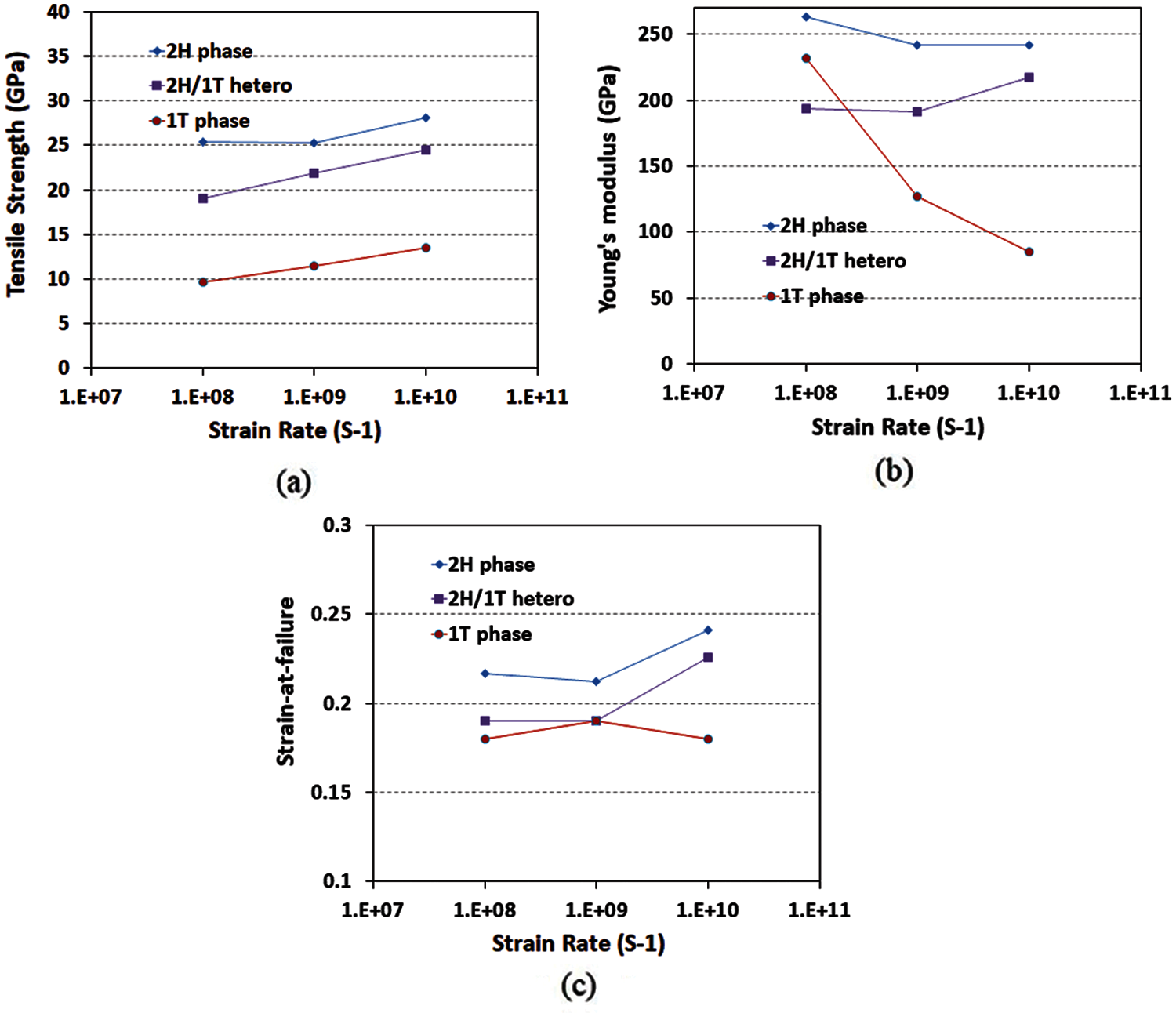
Figure 4: Failure properties of all defect-free MoS2 nanosheet hetero-structures. (a) Ultimate tensile strength, (b) Axial strain at ultimate tensile strength (c) Young’s modulus as a function of strain rate
Figure 5: Crack propagation stages (a--i) in a MoS2 nanosheets with simulation box size of 25 nm × 25 nm including the crack of length L/3 imposed to the room temperature (300 K)
5.2.2 Metallic (1T) MoS2 Nanosheets Results
In this section, we derive our effort to compare the results of MD modeling for 1T-MoS2 structure subjected to different crack lengths including L/6, L/3 and L/2 where L is 25 nm. Fig. 7a shows the related stress-strain curves for each crack length of 1T MoS2 monolayer. Additionally, max. tensile stress and strain-at-fracture of 1T phase structure for the aforementioned crack lengths are depicted on Figs. 7b and 7c respectively. In order to better evaluation of the crack effect, the max. tensile stress for crack-free 1T-MoS2 nanosheet (0L) is also presented. As expected, the max. tensile stress of 2D 1T-MoS2 material decreases under the effect of crack-shape defects. Obviously, crack length increase, has a weakening effect on the max. tensile stress of 1T-MoS2 structure, as the max. stress values decrease significantly by increasing the crack size. Max. tensile stresses for L/6, L/3 and L/2 crack sizes are 9.49 GPa, 7.42 GPa and 6.13 GPa respectively which are around 17%, 35% and 46% below the pristine 1T-MoS2 sample, respectively. Obviously, strain-at-fracture decreases for larger crack sizes of 1T-MoS2 nanosheet. As an example, based on Fig. 7c, for a crack size as half of the nanosheet length (L/2), fracture strain is 0.114 which is around 42% less than pristine 1T phase nanosheet.
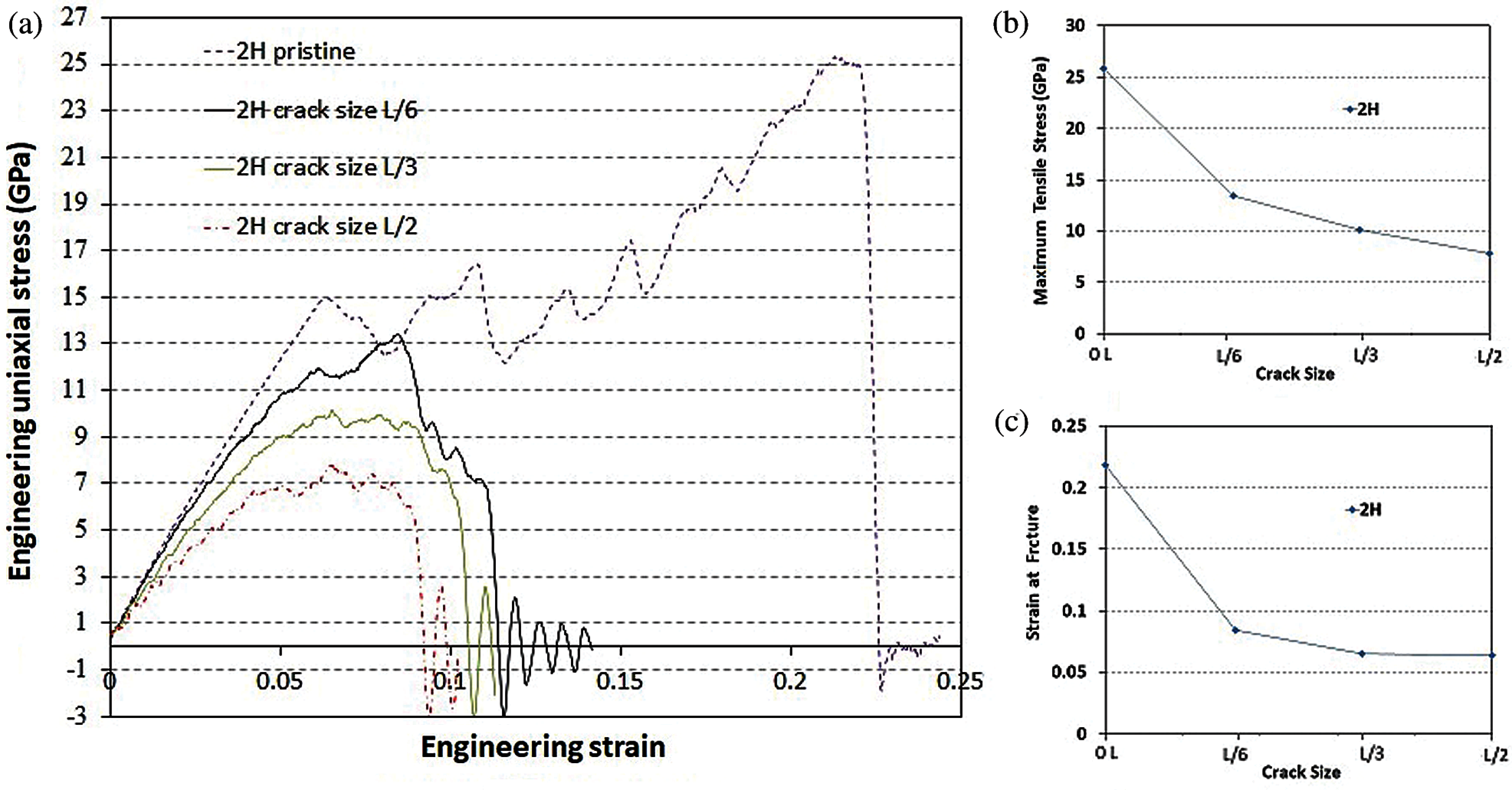
Figure 6: Crack size effect on fracture properties of 2H phase monolayer MoS2 nanosheet. (a) Plot of stress-strain diagrams. (b) Maximum tensile stress. (c) Engineering axial strain at fracture
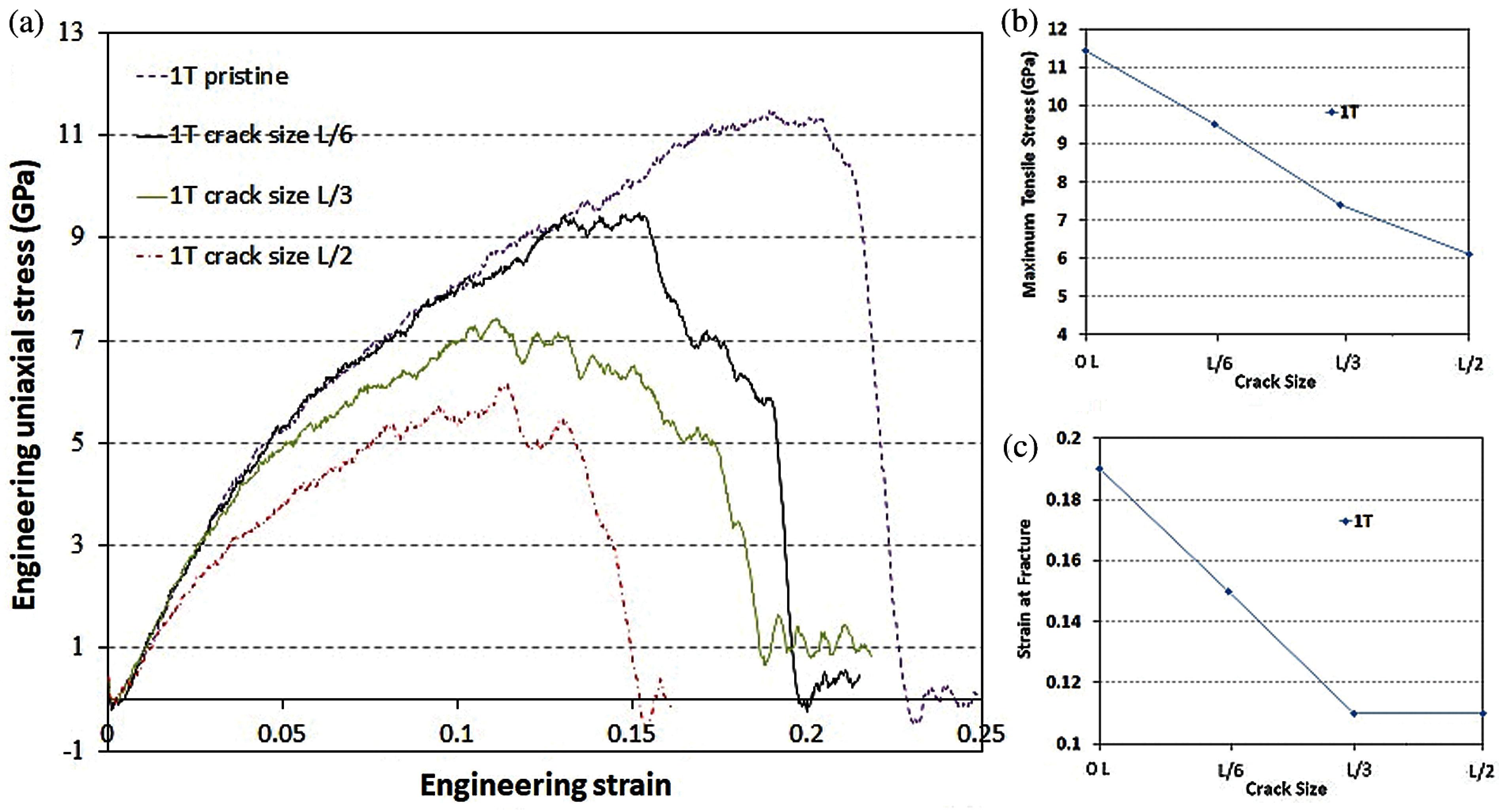
Figure 7: Crack size effect on fracture properties of 1T phase monolayer MoS2 nanosheet. (a) Plot of stress-strain diagrams. (b) Maximum tensile stress. (c) Engineering axial strain at fracture
5.2.3 2H/1T MoS2 Heterostructure Results
In this section, we use numerical simulations to evaluate the mechanical properties and to predict fracture geometry of 2H/1T singlelayer MoS2 heterostructures and investigate fracture initiation and crack propagation path in different samples of the nanosheet. It is likely the fracture properties (max. tensile stress) of 2H/1T heterostructures to be higher than that of the defective 1T phase and lower than defective 2H phase. This prediction is according to the fact that the results for the max. tensile stress of the defective 1T phase are almost half of that of the 2H phase. Figs. 8a–8c show the related stress-strain curves for each crack length of composite 2H/1T MoS2 monolayer with 5%, 10% and 15% concentrations respectively. Our results for different 1T concentrations of 2H/1T MoS2 heterostructure and three crack sizes are summarized in Fig. 9. Max. tensile stresses of 2H/1T MoS2 heterostructure for the previously mentioned crack lengths are compared on Fig. 9a. With respect to making a comparison with the pre-cracked samples, the max. tensile stress for crack-free MoS2 nanosheet (0L) is also presented. As expected, the max. tensile stress of two dimensional composite 2H/1T MoS2 heterostructure decreases under the effect of crack-shape defects. Obviously, crack length increase, has a weakening effect on max. tensile stress of composite 2H/1T MoS2 heterostructure, as the max. stress values drop significantly by increasing the crack size. With reference to Fig. 9a, a sharp reduction in the max. tensile stress is observed in all composite 2H/1T MoS2 heterostructure with crack sizes less than L/6, while larger crack sizes showed approximately a linear trend. Additionally, according to Fig. 9b, an approximately sudden decrease in strain-at-fracture is distinguished in samples with crack sizes less than L/6, while for larger crack sizes the decreases were very slow.
5.3 The Effect of Pre-existing Notch on the Mechanical Response
Finally we investigate the effect of notch shaped defects on the mechanical behavior of the MoS2 nanosheet. The impact of the notch on mechanical properties highly depends on the location of the notch in the samples. Furthermore, fracture is a phenomenon with size effects and the notch diameter influences mechanical properties of the 2D material. Therefore, we investigate notches located in the center of the nanosheet where their diameter range are L/6, L/3 and L/2. These sizes are selected similar to the length of previously studied cracks, enabling a comparison between these two kinds of defects. The existence of notch leads to a decrease in the max. tensile stress and strain-at-fracture compared to the samples without pre-existing notch. The obtained stress-strain curves for the samples with pre-existing notches in the 2H phase MoS2 nanosheet have been shown in Fig. 10a. With reference to Fig. 10b, a sudden reduction in the max. tensile stress is observed in 2H phase MoS2 models with notch sizes less than L/6, while larger notch sizes showed approximately a linear trend. As it can be seen in this figure, the max. tensile stress drops by 42%, 47% and 61% for samples with L/6, L/3 and L/2 of notch sizes, respectively. Fig. 11a illustrates the obtained stress-strain curves for the samples with pre-existing notches in 1T-MoS2 nanosheet. According to Fig. 11b, the max. tensile stress drops by 18%, 39% and 45% for samples with L/6, L/3 and L/2 of notch sizes, respectively.
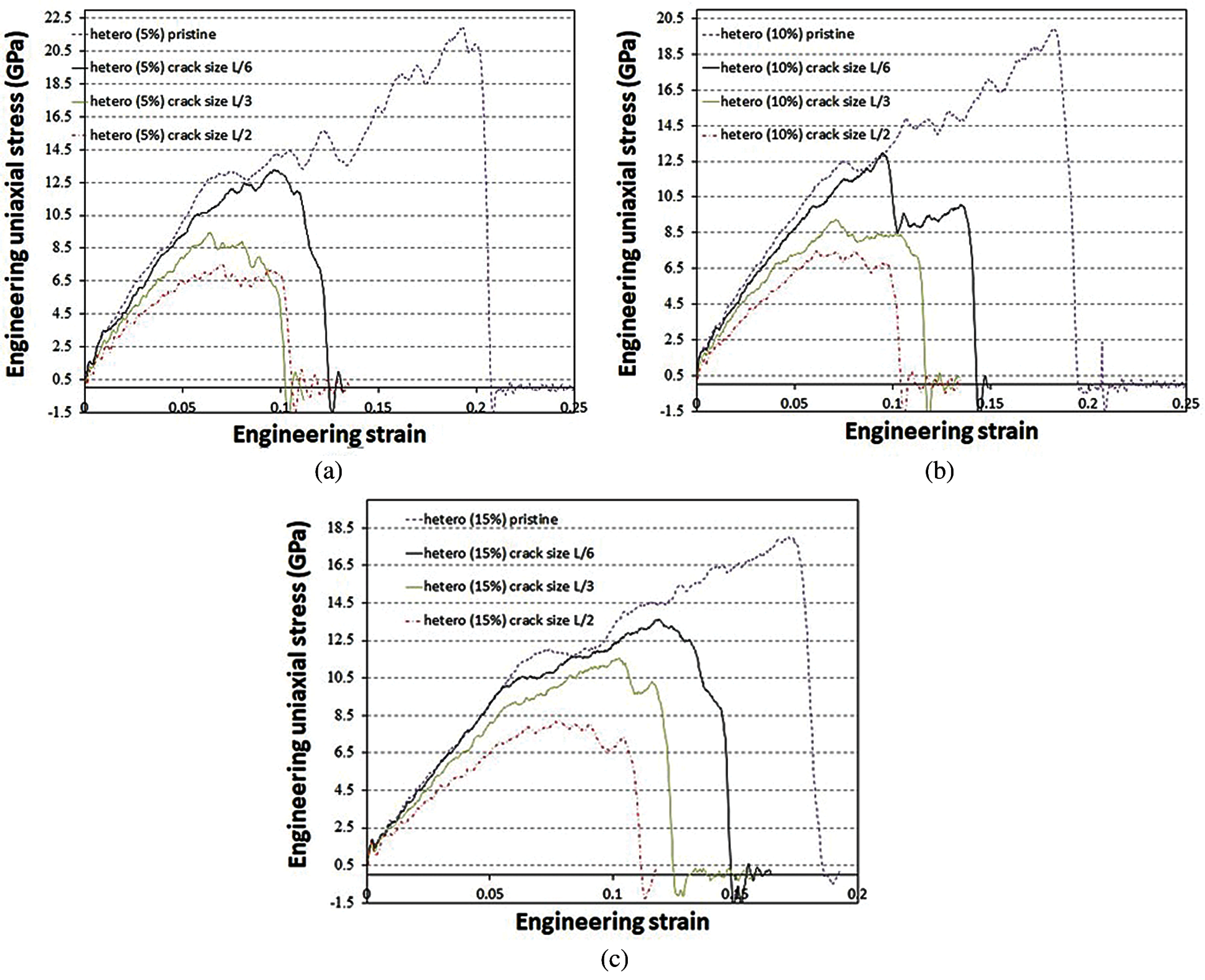
Figure 8: Plot of stress-strain diagrams to investigate crack size effect on single-layer MoS2 heterostructures under uniaxial loading at room temperature (a) for concentrations of 5% (b) for concentrations of 10% (c) for concentrations of 15%
In the next step we explore 2H/1T MoS2 heterostructures. Figs. 12a–12c illustrate the stress-strain curves for the samples with notches in the structures with 5%, 10% and 15% concentration of 1T phase in 2H phase, respectively. Fig. 13 summarizes our results for the fracture mechanics properties of the above mentioned different concentrations and three notch sizes. Max. tensile stresses of 2H/1T MoS2 heterostructure for the previously mentioned notch diameters are compared on Fig. 13a. With respect to further estimating the effect of the existing notches in the nanosheet, the max. tensile stress for notch-free MoS2 nanosheet (0L) is also presented. As expected, the max. tensile stress of the 2D composite 2H/1T MoS2 heterostructure decreases under the effect of notch defects. Obviously, notch diameter increase, has a weakening effect on max. stress of composite 2H/1T MoS2 heterostructure, as the max. stress values drop significantly by increasing the notch size. Additionally, among the three mentioned studied composite samples, for 10% concentration model a drop in the max. tensile stress and fracture strain is more pronounced compared to the defect-free specimen.
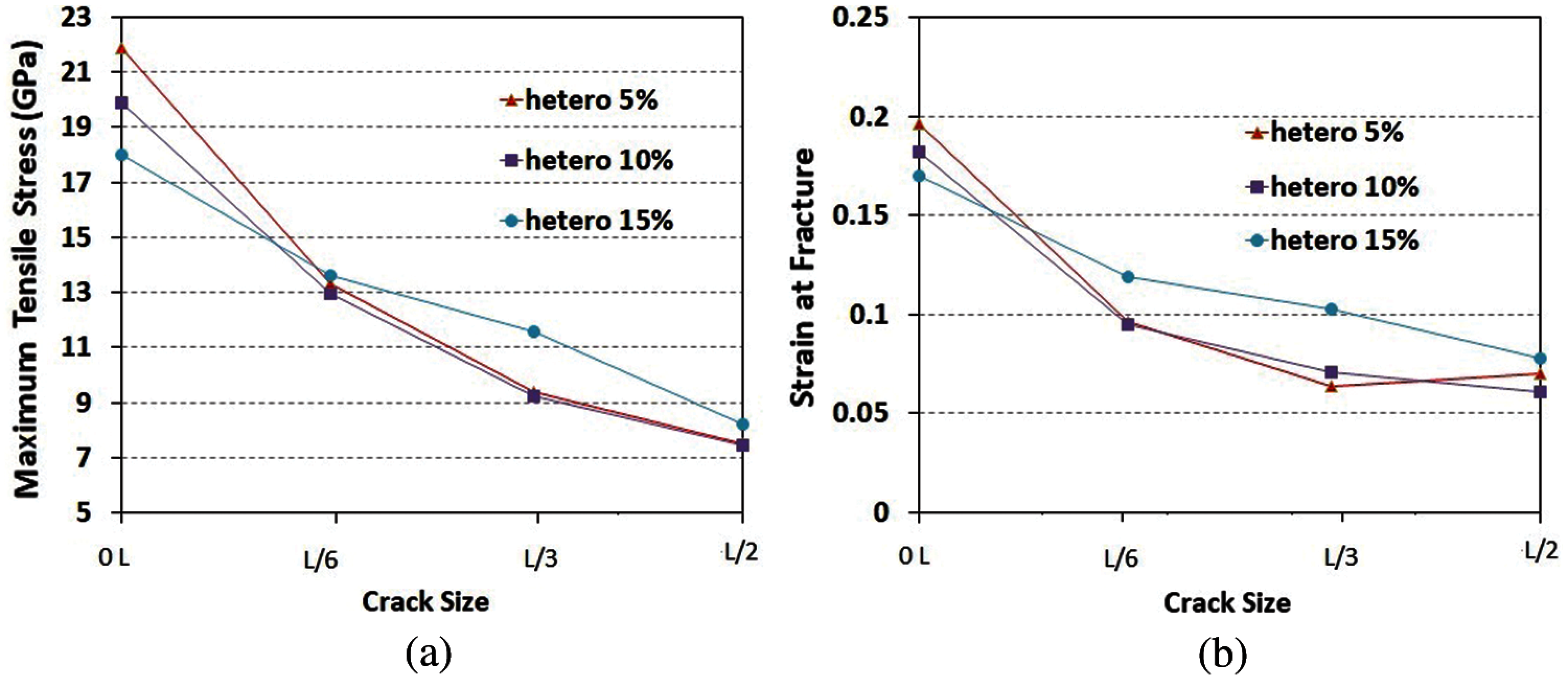
Figure 9: Fracture properties of monolayer MoS2 heterostructures including different crack sizes and for concentrations of 5%, 10% and 15%. (a) Max. tensile stress (b) Engineering axial strain at fracture
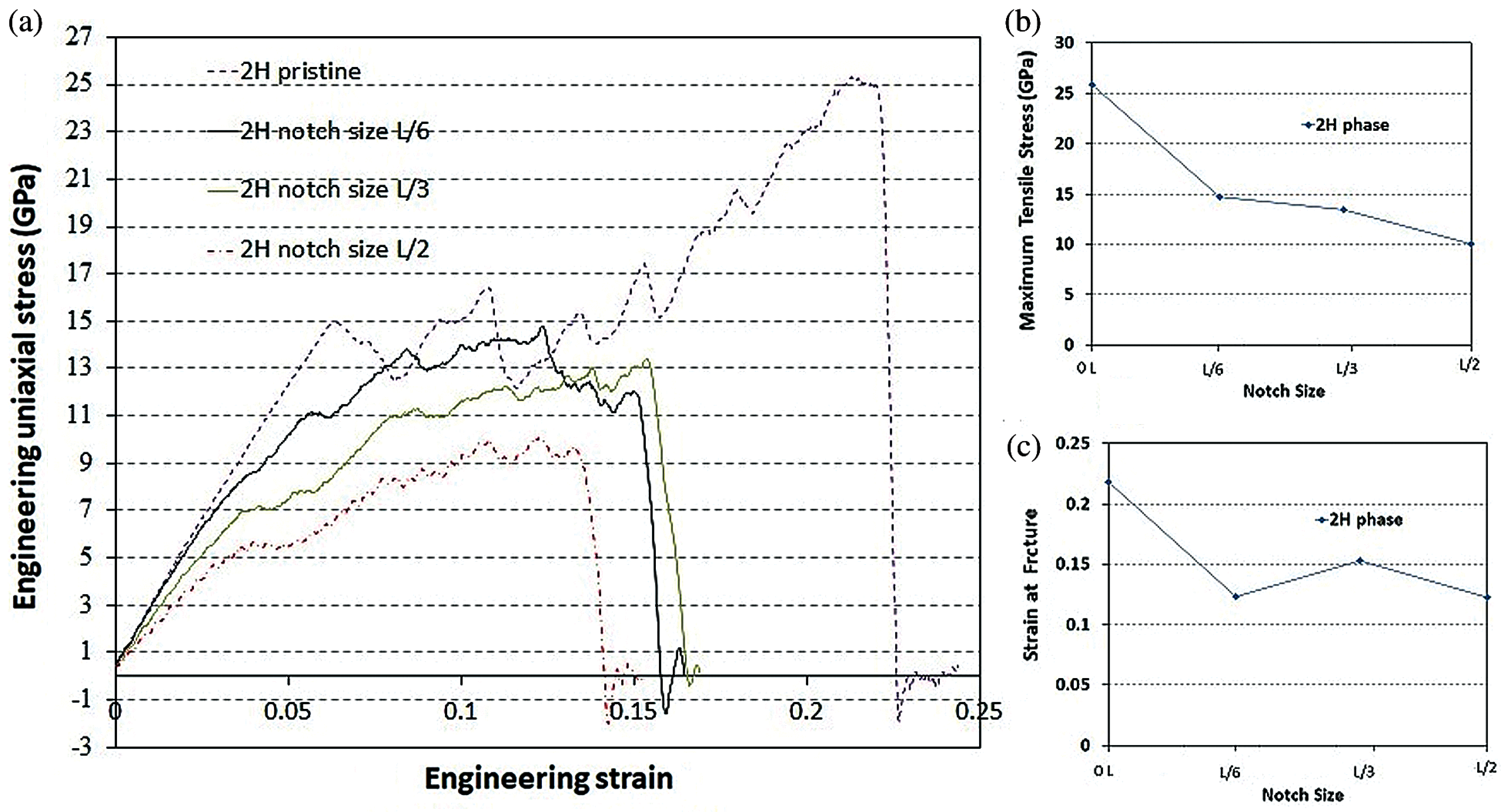
Figure 10: Notch size effect on fracture properties of 2H phase monolayer MoS2 nanosheet. (a) Plot of stress-strain diagrams. (b) Maximum tensile stress. (c) Engineering axial strain at fracture
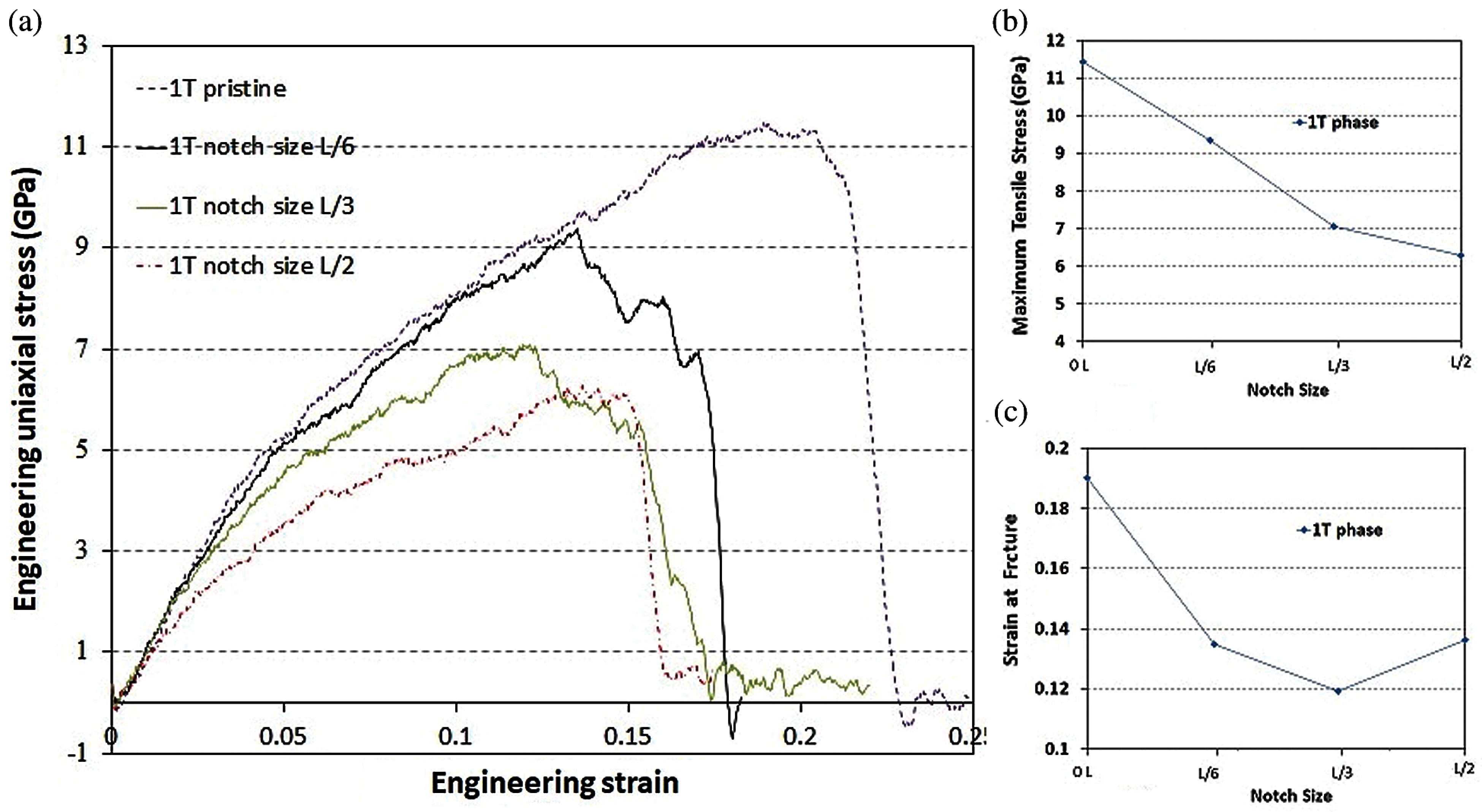
Figure 11: Notch size effect on fracture properties of 1T phase monolayer MoS2 nanosheet. (a) Plot of stress-strain diagrams. (b) Maximum tensile stress. (c) Engineering axial strain at fracture
5.4 Comparing the Results of All Pre-cracked and Notched MoS 2 nanosheet heterostructures
In order to compare fracture properties of all monolayer MoS2 nanosheet heterostructures in the presence of defects, we show all the obtained ReaxFF MD results for pre-cracks and pre-notches in Figs. 14 and 15, respectively. With reference to these figures, for all studied crack and notch sizes, 2H-MoS2 films has larger max. stress. Also, for this phase a drop in max. stress and fracture strain is more pronounced compared to the defect-free specimen. The lowest max. stress belongs to 1T phase. The results for 2H/1T MoS2 heterostructure with different concentrations are below the equivalent 2H phase but higher than 1T phase. However, max. tensile stress of cracked and notched nanosheets of 1T phase is well below both single-layer 2H and all studied 2H/1T composite structures of MoS2. According to Fig. 14a, for the MoS2 samples of 2H phase, hetero (5%), hetero (10%), hetero (15%) and 1T phase, shifting the samples from crack-free to having L/6 initial center crack, leads to a large drop in the max. tensile stress by 48%, 39%, 35%, 24% and 17%, respectively. For the aforementioned phases, when the initial center crack length increases from L/6 to L/3 a decrease in max. tensile stress of 25%, 29%, 29%, 15% and 22% is observed, respectively. Also, according to Fig. 14b, for the samples of 2H phase, hetero (5%), hetero (10%), hetero (15%) and 1T phase, a pronounced drop in fracture strain is observed. The strain-at-fracture is reduced by 61%, 51%, 48%, 30% and 20% compared to the defect-free samples, respectively. A drop of 23%, 34%, 25%, 16% and 20% in strain-at-fracture also occurs when initial crack length is increased from L/6 to L/3. With respect to the results (Fig. 15a), for the MoS2 samples of 2H phase, hetero (5%), hetero (10%), hetero (15%) and 1T phase at room temperature, shifting the samples from pristine to having L/6 pre-existing center notch, lead to a large drop in the max. tensile stress by 43%, 17%, 34%, 21% and 18%, respectively. A drop in max. tensile stress of 9%, 40%, 24%, 8% and 24% is observed when the pre-existing center notch diameter increases from L/6 to L/3, respectively.
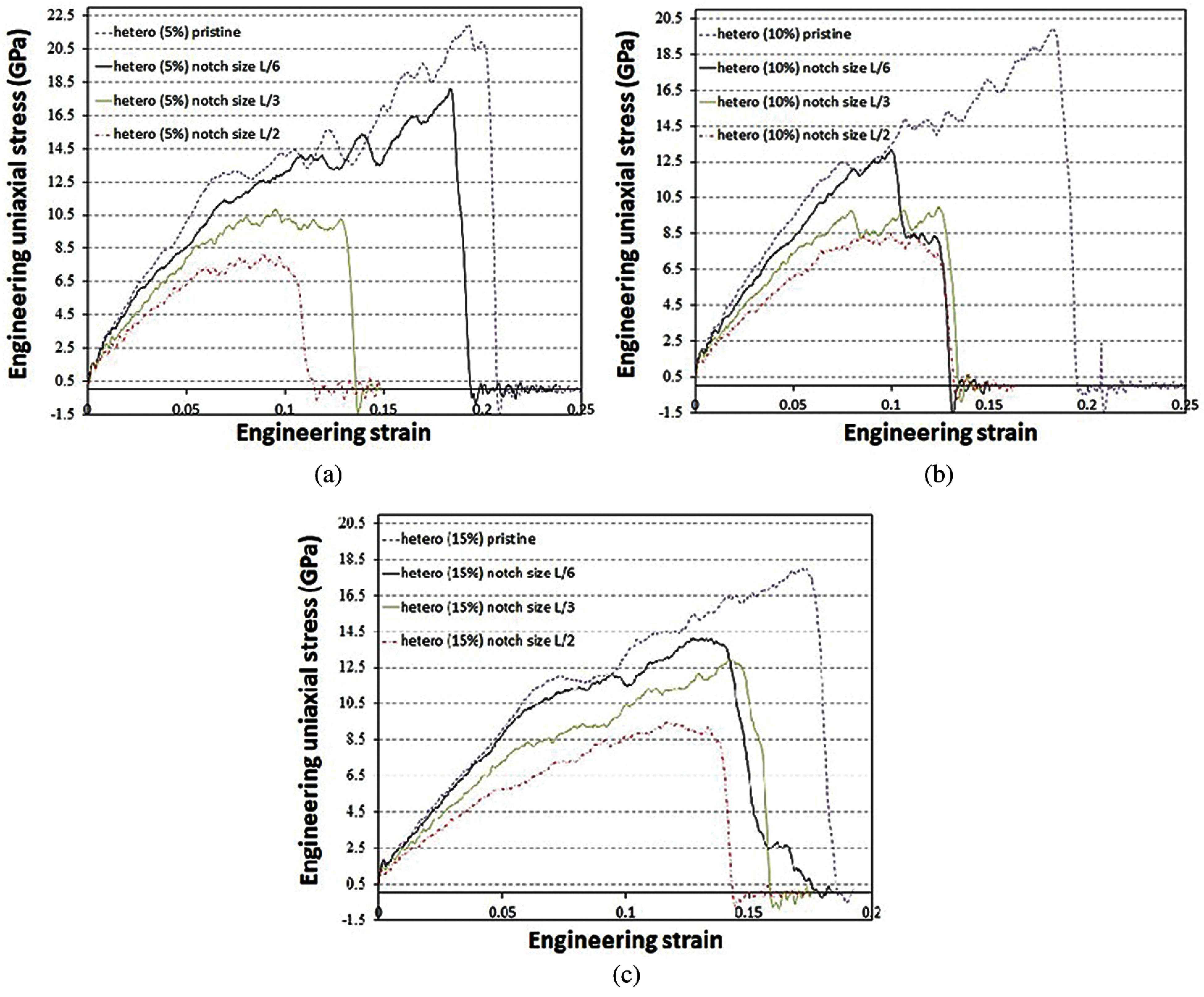
Figure 12: Plot of stress-strain diagrams to investigate notch size effect on single-layer MoS2 nanosheet heterostructure models (a) 5% concentration of 1T phase (b) 10% concentration of 1T phase (c) 15% concentration of 1T phase
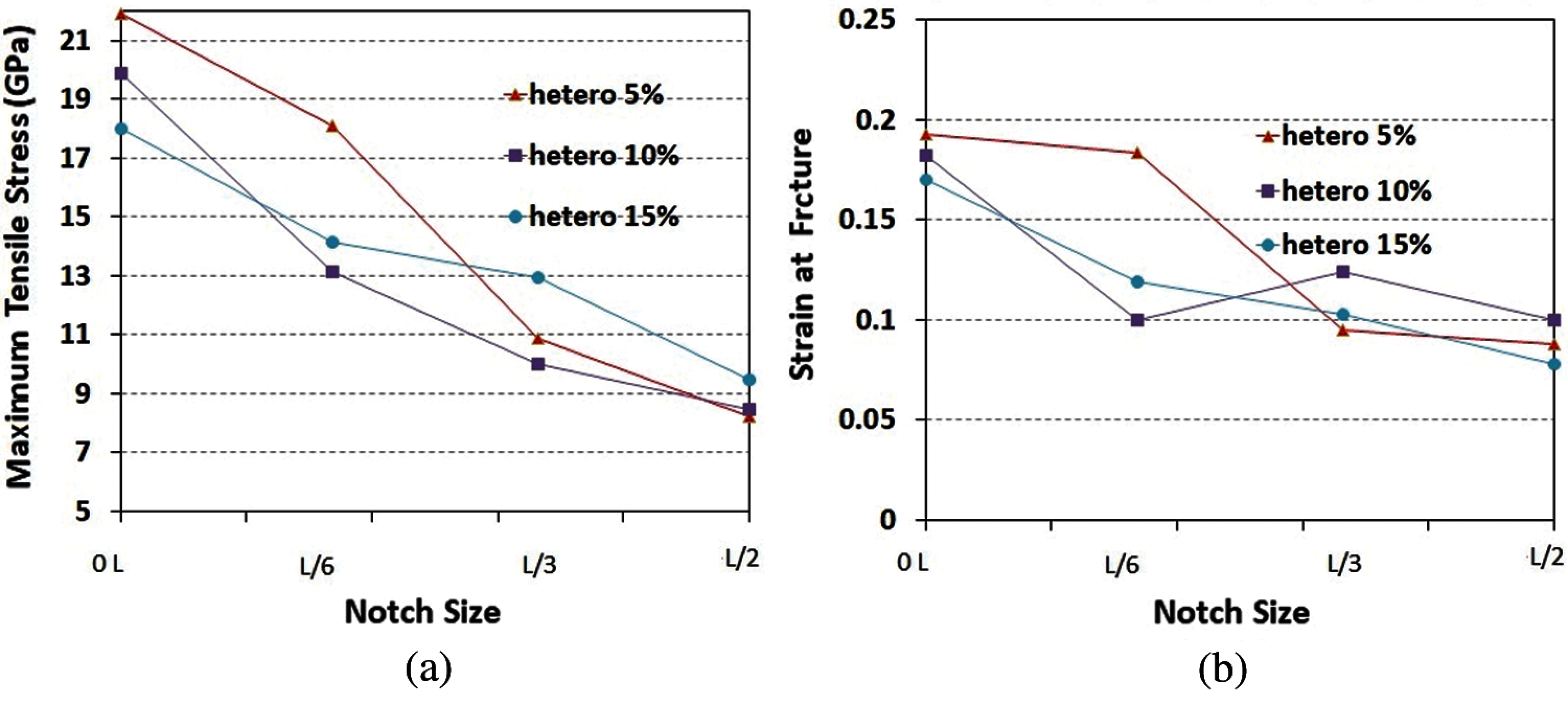
Figure 13: Fracture properties of MoS2 nanosheet heterostructures including different notch sizes and for concentrations of 5%, 10% and 15%. (a) Maximum tensile stress (b) Strain at fracture
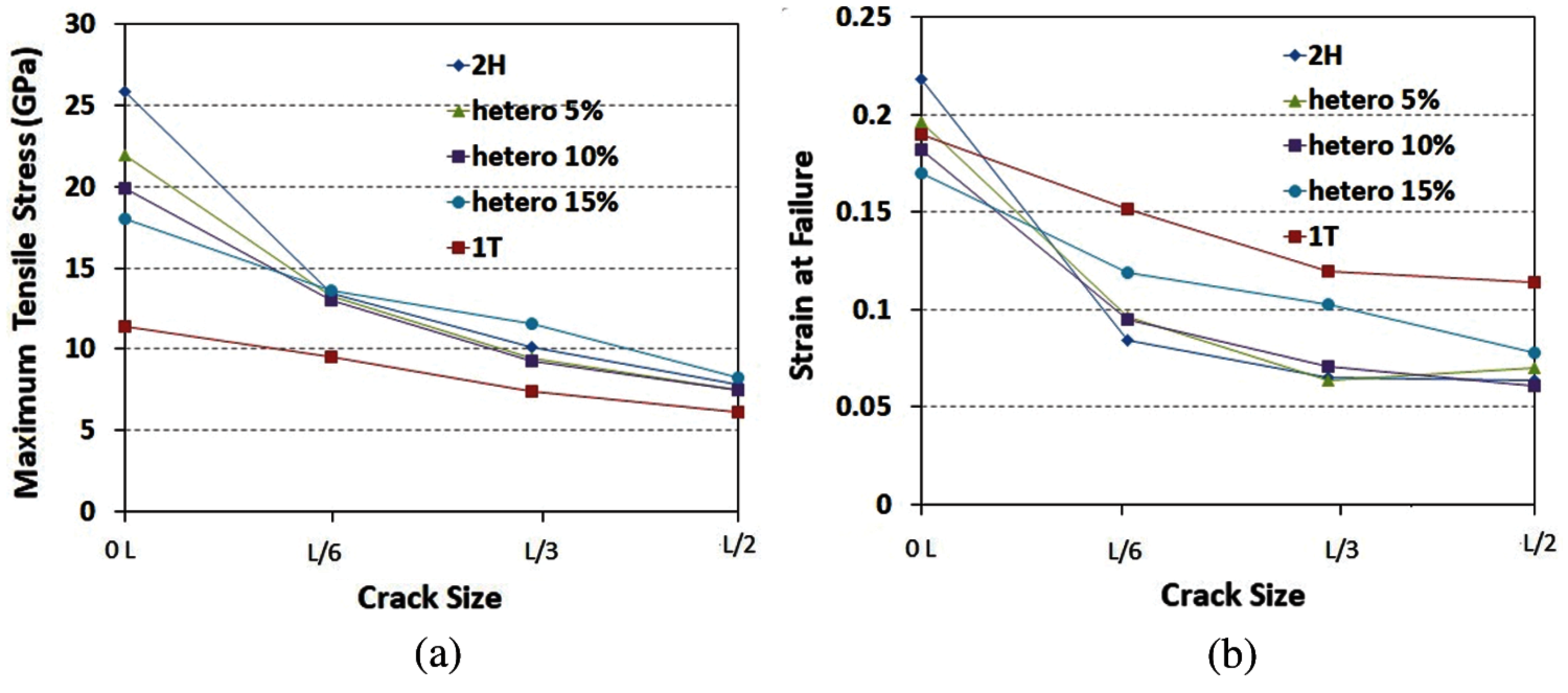
Figure 14: Fracture properties of all phases of monolayer MoS2 nanosheet including different crack sizes (a) Maximum tensile stress (b) Engineering axial strain at fracture
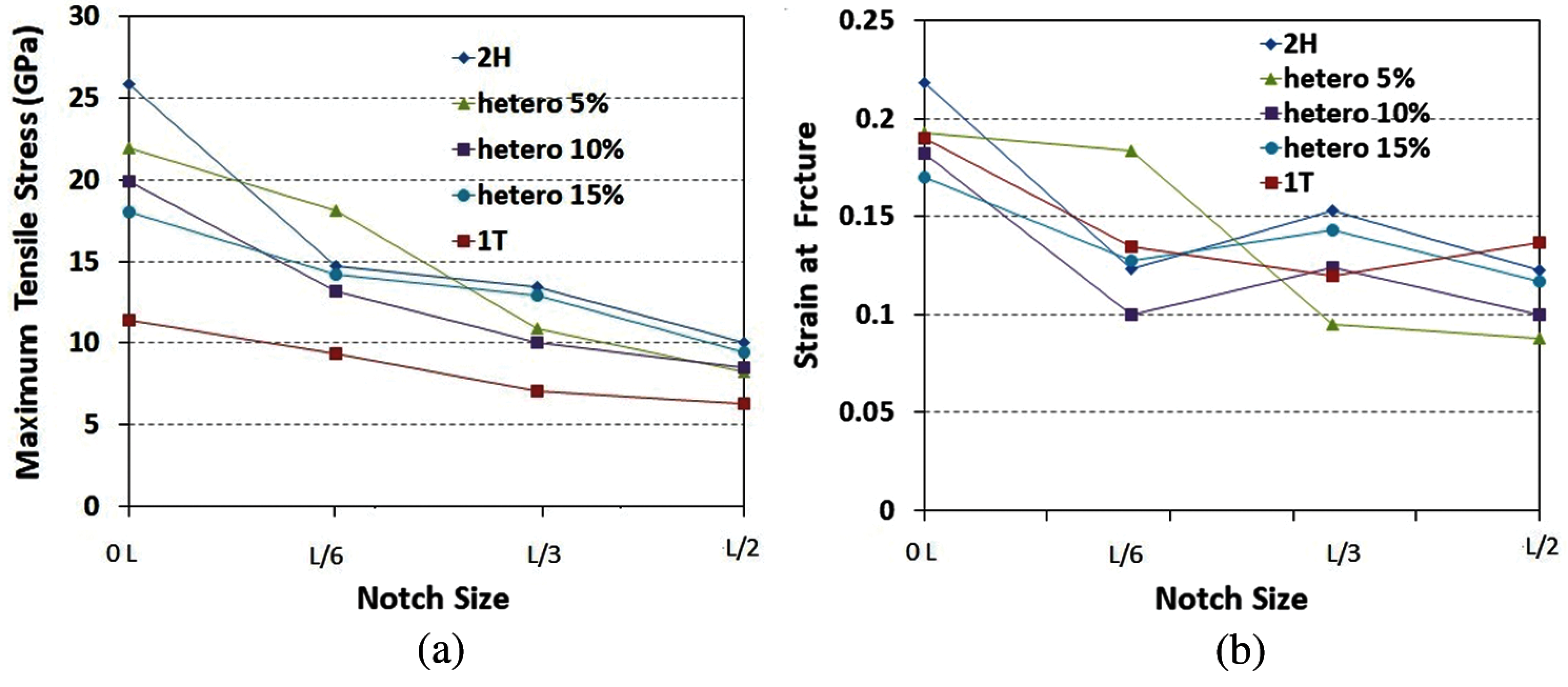
Figure 15: Fracture properties of all phases of monolayer MoS2 nanosheet including different notch sizes (a) Maximum tensile stress (b) Engineering axial strain at fracture
Fig. 16 shows the fracture properties versus defect size for pre-cracked and their corresponding values for pre-notched samples of monolayer 2H MoS2 material. The comparison of the results for cracked and notched 2H-MoS2 nanosheet shows that the max. stress and fracture strain of the notched samples are higher than the samples with crack. Therefore, the load bearing capacity of the notched samples of 2H-MoS2 nanosheets are higher than the cracked ones. Additionally, for 1T-MoS2 models, the comparison of results for cracked and notched samples with identical crack length and notch diameter indicates that the max. stress and strain-at-fracture of the notch and crack samples are close and therefore load bearing capacity of both cases are almost identical (see Figs. 17a and 17b). According to Fig. 18 for all studied composite 2H/1T heterostructures with 5%, 10% and 15% concentrations of 1T phase inside 2H phase, the max. stress and fracture strain of the notch samples are higher than the samples with crack.
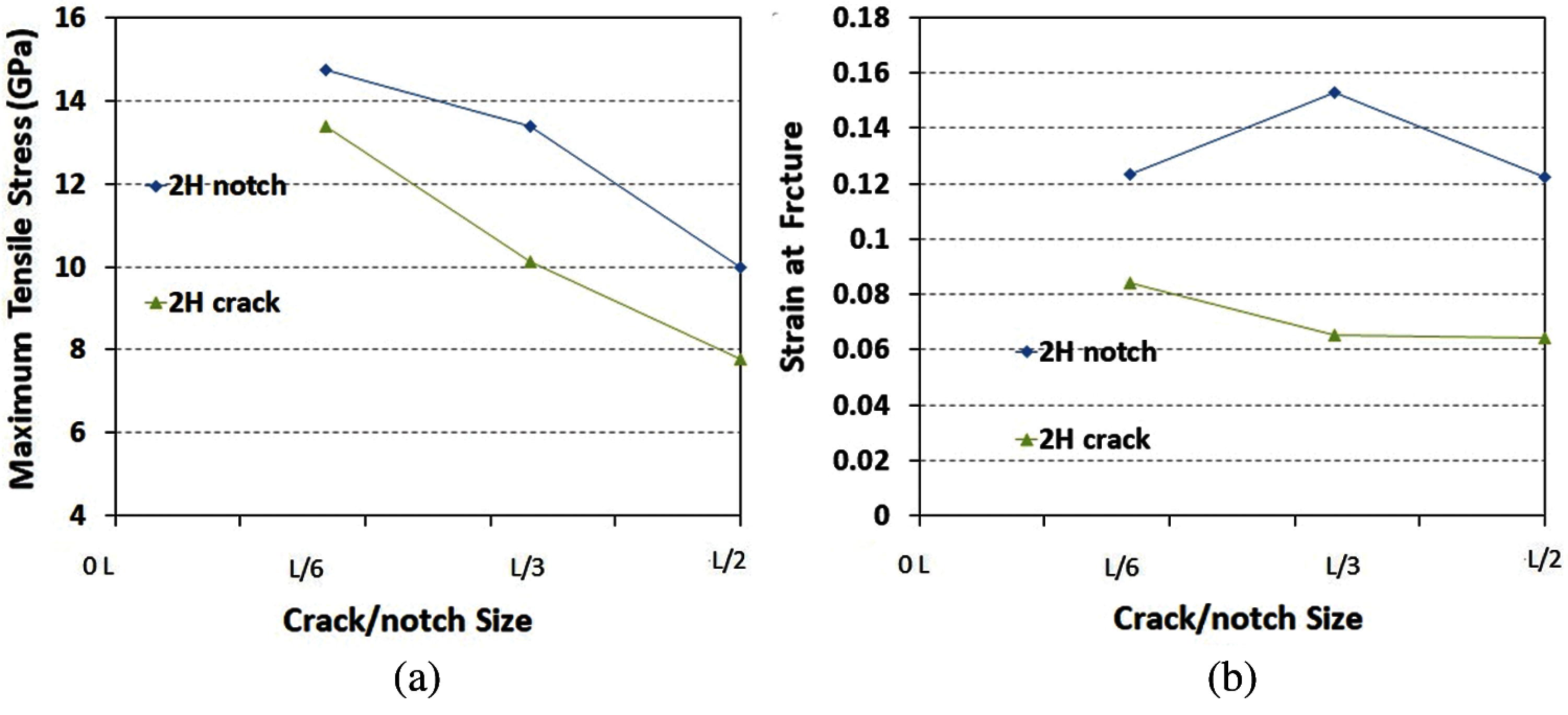
Figure 16: Comparison between 2H phase of monolayer MoS2 nanosheets containing pre-crack and pre-notch defects (a) Maximum tensile stress (b) Engineering axial strain at fracture
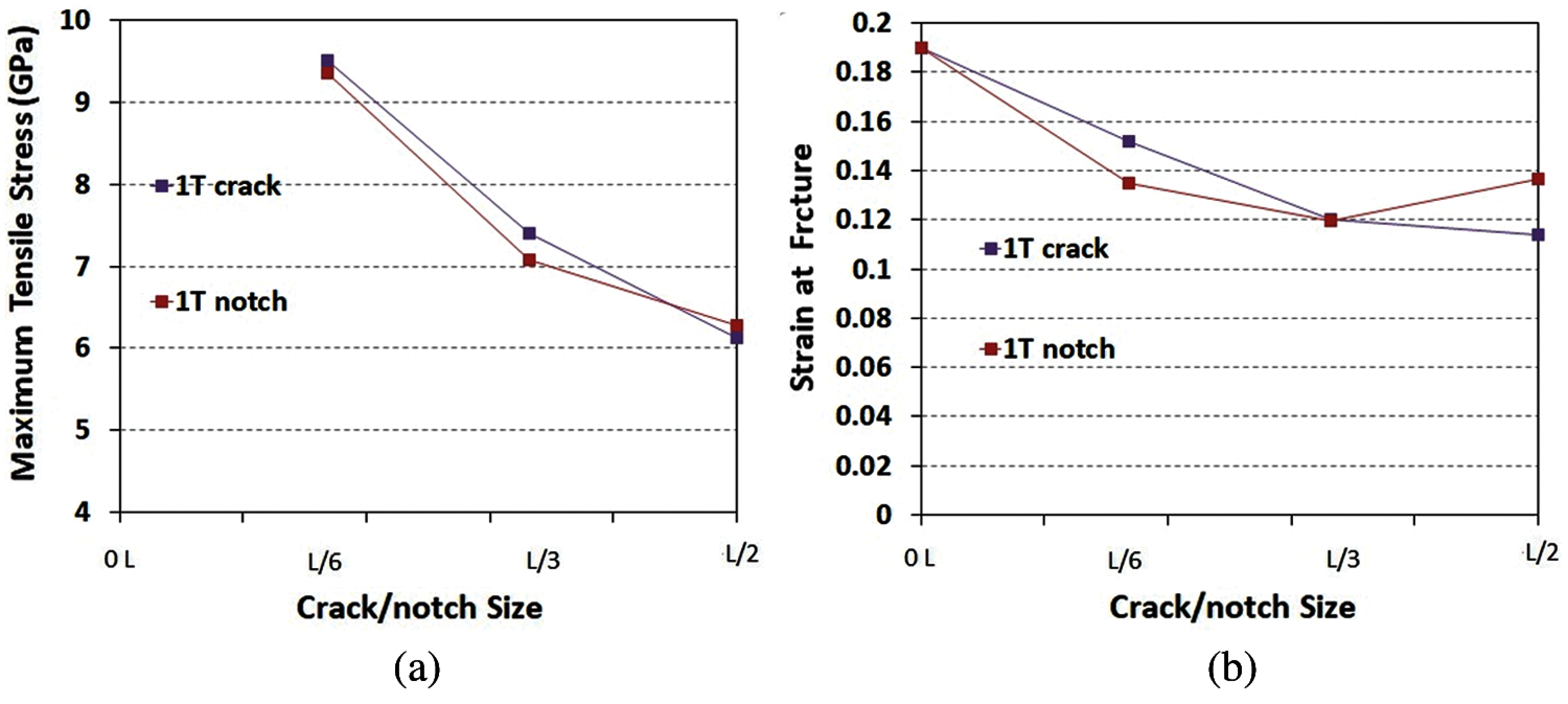
Figure 17: Comparison between 1T phase of monolayer MoS2 nanosheets containing pre-crack and pre-notch defects (a) Maximum tensile stress (b) Engineering axial strain at fracture
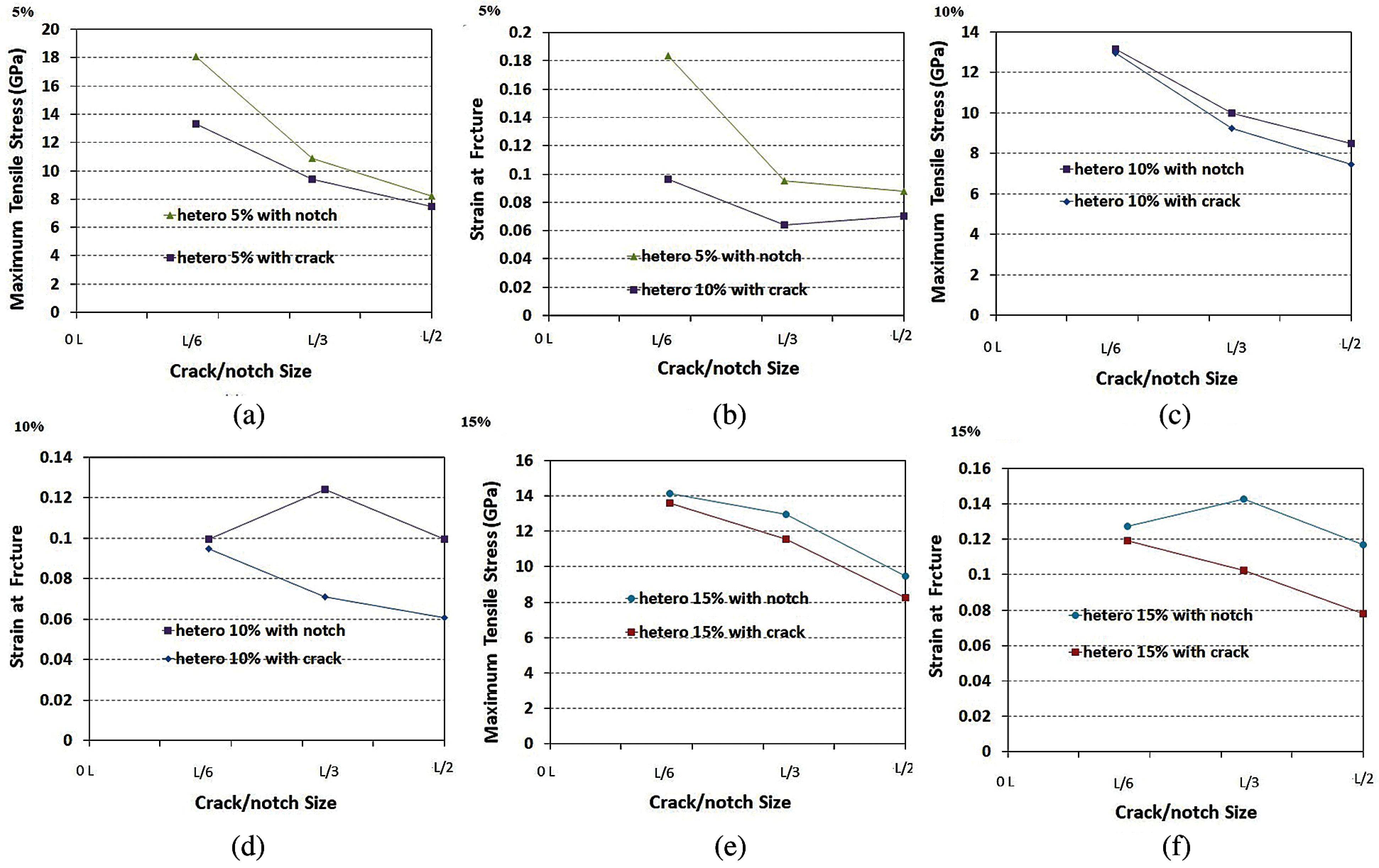
Figure 18: Comparison between composite MoS2 nanosheets with different concentrations containing pre-crack and pre-notch defects (a) Max. tensile stress for nanosheets with 5% concentration. (b) Engineering axial strain at fracture for nanosheets with 5 % concentration (c) Max. tensile stress for nanosheets with 10% concentration (d) Strain at fracture for nanosheets with 10% concentration (e) Max. tensile stress for samples with 15% concentration (f) Strain at fracture for nanosheets with 15 %
In the present contribution we used tensile loading simulations by performing MD calculations to predict the mechanical response of all phases of MoS2 single-layer heterostructures and studied the response of defective MoS2 mono-layers, where defects were assumed to be center-cracks and notches. To this goal realistic atomistic models were simulated with specified concentration and domain size for the metallic phase inside the semiconducting. The molecular dynamic simulations were performed for different crack lengths and notch diameters including, L/6, L/3 and L/2 all located at the center of the nonosheet. Our predictions based on a parameterized ReaxFF potential for the mechanical properties of the defective MoS2 monolayes, showed that MoS2 films subjected to crack and notch shape defects have significantly lower ultimate tensile strength compared to their pristine material. Our molecular dynamic (MD) modeling results confirm that the fracture is a phenomenon with size effect and the crack size and notch diameter non-linearly influence fracture properties of all-MoS2 heterostructures. For all studied crack and notch sizes, an increasing crack length and notch diameter, decreases the ultimate tensile strength of the monolayer MoS2 material as well as the Young’s modulus. Furthermore, according to our classical molecular dynamics simulations, semi-conducting (2H) phase of MoS2 films has the largest strength. Fracture properties of all studied concentrations of composite 2H/1T MoS2 nanosheet are higher than those for the equivalent metallic (1T) phase. We can imply that the pre-cracked and pre-notched composite MoS2 structure is remarkably stronger than equivalent metallic (1T) phase. Also, they are remarkably strong and flexible materials, even in the presence of the defects. This study provides valuable result for employing all strong, flexible MoS2 films for several industrial applications e.g., in nanodevices and as reinforcement of polymeric materials.
Acknowledgement: The first author would like to give a special thanks to Dr. Bohayra Mortazavi for providing a wealth of helpful advice and guidance related to the area of molecular dynamics simulation.
Funding Statement: The authors extend their appreciation to the Distinguished Scientist Fellowship Program (DSFP) at King Saud University for funding this work.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. H. Bhuiyan, “Synthesis of molybdenum (iv) sulphide: I. reaction of hydrogen sulphide with molybdenum (vi) oxide in the presence of ammonium chloride,” Journal of Chemical Technology and Biotechnology, vol. 28, no. 11, pp. 745–750, 1978. [Google Scholar]
2. I. Song, C. Park and H. C. Choi, “Synthesis and properties of molybdenum disulphide: From bulk to atomic layers,” RSC Advances, vol. 5, no. 10, pp. 7495–7514, 2015. [Google Scholar]
3. I. Song, C. Park, M. Hong, J. Baik, H. J. Shin et al., “Patternable large-scale molybdenium disulfide atomic layers grown by gold-assisted chemical vapor deposition,” Angewandte Chemie Inter- national Edition, vol. 53, no. 5, pp. 1266–1269, 2015. [Google Scholar]
4. V. Giacometti, B. Radisavljevic, A. Radenovic, J. Brivio and A. Kis, “Single-layer MoS2 transistors,” Nat. Nanotechnol, vol. 6, pp. 147–150, 2011. [Google Scholar]
5. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, “Electronics and optoelectronics of two-dimensional transition metal dichalcogenides,” Nature nanotechnology, vol. 7, no. 11, pp. 699–712, 2012. [Google Scholar]
6. B. Mortazavi, A. R. Ostadhossein, T. Rabczuk and A. C. T. V. Duin, “Mechanical response of all-MoS2 single-layer heterostructures: A reax investigation,” Physical Chemistry Chemical Physics, vol. 18, no. 34, pp. 23695–23701, 2012. [Google Scholar]
7. S. Bertolazzi, J. Brivio and A. Kis, “Stretching and breaking of ultrathin MoS2,” ACS Nano, vol. 5, no. 12, pp. 9703–9709, 2011. [Google Scholar]
8. A. C. Gomez, M. Poot, G. A. Steele, H. S. J. Van der Zant, N. Agrait et al., “Mechanical properties of freely suspended semiconducting graphene-like layers based on MoS2,” Nanoscale Research Letters, vol. 7, no. 1, pp. 1–4, 2012. [Google Scholar]
9. M. Hasanian, B. Mortazavi, A. R. Ostadhossein, T. Rabczuk and A. C. T. V. Duin, “Hydrogenation and defect formation control the strength and ductility of MoS2 nanosheets,” Extreme Mechanics Letters, vol. 22, pp. 157–164, 2018. [Google Scholar]
10. J. Zhao, J. W. Jiang and T. Rabczuk, “Temperature-dependent mechanical properties of single-layer molybdenum disulphide: Molecular dynamics nanoindentation simulations,” Applied Physics Letters, vol. 103, no. 23, pp. 231913, 2013. [Google Scholar]
11. J. O. Joswig, T. Lorenz, T. B. Wendumu, S. Gemming and G. Seifert, “Optics, mechanics, and energetics of two-dimensional MoS2 nanostructures from a theoretical perspective,” Accounts of Chemical Research, vol. 48, no. 1, pp. 48–55, 2015. [Google Scholar]
12. C. Ataca, M. Topsakal, E. Akturk and S. J. T. J. Ciraci, “A comparative study of lattice dynamics of three-and two-dimensional MoS2,” Journal of Physical Chemistry C, vol. 115, no. 33, pp. 16354–16361, 2011. [Google Scholar]
13. K. Q. Dang and D. E. Spearot, “Effect of point and grain boundary defects on the mechanical behavior of monolayer MoS2 under tension via atomistic simulations,” Journal of Applied Physics, vol. 116, no. 1, pp. 13508, 2014. [Google Scholar]
14. J. L. Feldman, “Elastic constants of 2H-MoS2 and 2H-NbSe2 extracted from measured dispersion curves and linear compressibilities,” Journal of Physics and Chemistry of Solids, vol. 37, no. 12, pp. 1141–1144, 1976. [Google Scholar]
15. T. Lorenz, J. O. Joswig and G. Seifert, “Stretching and breaking of monolayer MoS2- an atomistic simulation,” 2D Materials, vol. 1, no. 1, pp. 11007, 2014. [Google Scholar]
16. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi et al., “Intrinsic structural defects in monolayer molybdenum disulfide,” Nano Letters, vol. 13, no. 6, pp. 2615–2622, 2013. [Google Scholar]
17. S. Najmaei, Z. L. W. Zhou, X. Zou, G. Shi, S. Lei et al., “Vapour phase growth and grain boundary structure of molybdenum disulphide atomic layers,” Nature Materials, vol. 12, no. 8, pp. 754–759, 2013. [Google Scholar]
18. S. Ross and A. Sussman, “Surface oxidation of molybdenum disulfide,” Journal of Physical Chemistry, vol. 59, no. 9, pp. 889–892, 1955. [Google Scholar]
19. K. C. Santosh, R. C. Longo, R. M. Wallace and K. Cho, “Surface oxidation energetics and kinetics on MoS2 monolayer,” Journal of Applied Physics, vol. 117, no. 13, pp. 135301, 2017. [Google Scholar]
20. R. K. H. Zahedi, P. Alimouri, H. K. H. Zahedi and M. Shishesaz, “Investigating peak stresses in fitting and repair patches of buried polyethylene gas pipes,” Frontiers of Structural and Civil Engineering, vol. 14, no. 1, pp. 147–168, 2020. [Google Scholar]
21. R. K. H. Zahedi and P. Alimouri, “Finite element model updating of a large structure using multi-setup stochastic subspace identification method and bees optimization algorithm,” Frontiers of Structural and Civil Engineering, vol. 13, no. 4, pp. 965–980, 2019. [Google Scholar]
22. R. K. H. Zahedi, “Application of the finite element method for evaluating the stress distribution in buried damaged polyethylene gas pipes,” Underground Space, vol. 4, no. 1, pp. 59–71, 2019. [Google Scholar]
23. R. K. H. Zahedi and M. Shishesaz, “Application of a finite element method to stress distribution in buried patch repaired polyethylene gas pipes,” Underground Space, vol. 4, no. 1, pp. 48–58, 2019. [Google Scholar]
24. R. K. H. Zahedi and P. Alimouri, “Finite element analysis to the effect of thermo-mechanical loads on stress distribution in buried polyethylene gas pipes jointed by electrofusion sockets, repaired by PE patches,” Energies, vol. 11, no. 10, pp. 2818, 2018. [Google Scholar]
25. R. K. H. Zahedi P. Alimouri, H. Nguyen-Xuan and T. Rabczuk, “Crack detection in a beam on elastic foundation using differential quadrature method and the Bees algorithm optimization,” in Proc. Of the Int. Conf. on Advances in Computational Mechanics, Vietnam, Springer, Phu Quoc, pp. 439–460, 2017. [Google Scholar]
26. K. M. Hamdia and T. Rabczuk, “Key parameters of fracture toughness of particles/polymer nanocomposites; sensitivity analysis via XFEM modeling approach,” in In proc. Fracture, Fatigue and Wear (FFW 2018Singapore, Springer, pp. 41–51, 2012. [Google Scholar]
27. H. M. Aktulga, S. Pandit, A. Van Duin and A. Y. Grama, “Reactive molecular dynamics: numerical methods and algorithmic techniques,” SIAM Journal on Scientific Computing, vol. 34, no. 1, pp. C1–C23, 2012. [Google Scholar]
28. A. C. V. Duin, S. Dasgupta, F. Lorant and W. A. Goddard, “ReaxFF: A reactive force field for hydrocarbons,” J. Phys. Chem, vol. 105, pp. 9396–9409, 2001. [Google Scholar]
29. H. Bao, Y. Huang, Z. Yang, Y. Sun, Y. Bai et al., “Molecular dynamics simulation of nanocrack propagation in single-layer MoS2 nanosheets,” Journal of Physical Chemistry C, vol. 122, no. 2, pp. 1351–1360, 2017. [Google Scholar]
30. A. R. Ostadhossein, A. Rahnamoun, Y. Wang, P. Zhao, S. Zhang et al., “ReaxFF reactive force-field study of molybdenum disulfide (MoS2),” Journal of Physical Chemistry Letters, vol. 8, no. 3, pp. 631–640, 2017. [Google Scholar]
31. R. Khademi Zahedi, A. H. N. Shirazi, P. Alimouri, N. Alajlan and T. Rabczuk, “Mechanical properties of graphene-like BC3; a molecular dynamics study,” Computational Materials Science, vol. 168, no. 1, pp. 1–10, 2019. [Google Scholar]
32. Y. C. Lin, D. O. Dumcenco, Y. S. Huang and K. Suenaga, “Atomic mechanism of the semiconducting-to-metallic phase transition in single-layered MoS2,” Nature Nanotechnology, vol. 9, no. 5, pp. 391, 2014. [Google Scholar]
33. M. D. M. Islam, A. R. Ostadhossein, O. Borodin, A. T. Yeates, W. W. Tipton et al., “ReaxFF molecular dynamics simulations on lithiated sulfur cathode materials,” Physical Chemistry Chemical Physics, vol. 17, no. 5, pp. 3383–3393, 2015. [Google Scholar]
34. K. Yoon, A. R. Ostadhossein and A. C. T. V. Duin, “Atomistic-scale simulations of the chemomechanical behavior of graphene under nanoprojectile impact,” Carbon, vol. 99, no. 5696, pp. 58–64, 2016. [Google Scholar]
35. S. Plimpton, “Fast parallel algorithms for short-range molecular dynamics,” Journal of Computational Physics, vol. 117, no. 1, pp. 1–19, 1995. [Google Scholar]
36. A. Stukowski, “Visualization and analysis of atomistic simulation data with ovito- the open visualization tool,” Modelling and Simulation in Materials Science and Engineering, vol. 18, no. 1, pp. 015012, 2010. [Google Scholar]
37. R. Abadi, R. Uma, P. Raahul, M. R. Izadifar and T. Rabczuk, “The effect of temperature and topological defects on fracture strength of grain boundaries in single-layer polycrystalline boron-nitride nanosheet,” Computational Materials Science, vol. 123, pp. 86–99, 2017. [Google Scholar]
38. N. Vu-Bac, M. A. Bessa, T. Rabczuk and W. K. Liu, “A multiscale model for the quasi-static thermo-plastic behavior of highly cross-linked glassy polymers,” Macromolecules, vol. 48, no. 18, pp. 6713–6723, 2015. [Google Scholar]
39. T. Han, Y. Luo and C. Wang, “Effects of temperature and strain rate on the mechanical properties of hexagonal boron nitride nanosheets,” Journal of Physics D: Applied Physics, vol. 47, no. 2, pp. 025303, 2014. [Google Scholar]
40. Z. Yang, Y. Huang, F. Ma, Y. Sun, X. Yunjin et al., “Temperature and strain-rate effects on the deformation behaviors of nano-crystalline graphene sheets,” European Physical Journal B, vol. 88, no. 5, pp. 197, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |