DOI:10.32604/cmc.2022.020338

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020338 |  |
| Article |
Analytic Beta-Wavelet Transform-Based Digital Image Watermarking for Secure Transmission
1Department of Computer Engineering, College of Computers and Information Technology, Taif University, P.O. 11099, Taif, 21944, Saudi Arabia
2Department of Electrical Engineering, Faculty of Engineering, Menoufia University, Shebin El-Kom, 32511, Egypt
3Department of Information Technology, College of Computers and Information Technology, Taif University, P.O. 11099, Taif, 21944, Saudi Arabia
*Corresponding Author: Hesham Alhumyani. Email: h.alhumyani@tu.edu.sa
Received: 20 May 2021; Accepted: 26 July 2021
Abstract: The rapid development in the information technology field has introduced digital watermark technologies as a solution to prevent unauthorized copying and redistribution of data. This article introduces a self-embedded image verification and integrity scheme. The images are firstly split into dedicated segments of the same block sizes. Then, different Analytic Beta-Wavelet (ABW) orthogonal filters are utilized for embedding a self-segment watermark for image segment using a predefined method. ABW orthogonal filter coefficients are estimated to improve image reconstruction under different block sizes. We conduct a comparative study comparing the watermarked images using three kinds of ABW filters for block sizes 64 × 64, 128 × 128, and 256 × 256. We embed the watermark using the ABW-based image watermarking method in the 2-level middle frequency sub-bands of the ABW digital image coefficients. The imperceptibility and robustness of the ABW-based image watermarking method image is evaluated based on the Peak Signal to Noise Ratio (PSNR) and Correlation coefficient values. From the implementation results, we came to know that this ABW-based image watermarking method can withstand many image manipulations compared to other existing methods.
Keywords: Watermarking; ABW; median filtering; JPEG compression; PSNR
Data security becomes an essential issue in the digital world with the rapid growth of digital images and Internet technology accompanied by many security threats on the Internet. For this purpose, many image encryption technologies have emerged and proposed. The existing image encryption technologies use a simple structure and a small key space to reduce the time cost and complexity of algorithms and meet the requirements image information security [1]. Image encryption requires high fidelity of the original image due to its sensitivity to the image information [2]. Otherwise, people can easily modify the image content because of the fast advancement in image processing techniques. Therefore, we should focus on the capability of the proposed schemes to be more sensitive to detect any modifications [3]. Most existing approaches are based on scrambling or on information theory in the spatial domain [4]. The limit of this domain resides in the vulnerability to statistical attack [5]. A second family technique uses the chaotic systems where the pixel location is changed by using a 2D chaotic map [6]. These techniques suffer significantly from the sensitivity to the initial and external parameters [7]. The frequency-domain encryption algorithms use some common transforms like discrete cosine transform (DCT), discrete Fourier transform (DFT), and discrete wavelet transform (DWT) to transform the images from spatial to frequency domain first and then get the frequency coefficients and change their positions through those specific rules [8]. The frequency-based approach has strong initial value sensitivity and robust against external attacks [9]. In contrast, the wavelet transform has a low computational complexity that can effectively save the computational cost and reduce the loss of image information in the decryption operation. Nowadays, simplifying the access to digital content has facilitated hacking of image, audio, and video, which can be tampered with and copied. The owner of digital products is threatened severely by the tampered copyright. Therefore, digital watermarking technology is suggested as an effective method to protect copyright authentication and product tracking [10,11]. The protections of different digital contents often require different watermarking algorithms [12].
To enhance the adaptive ability of image watermarking, we proposed the utilization of a new wavelet family named Beta Wavelet family for proposing an efficient image watermarking scheme. The main contribution of the proposed algorithm is as follows: It uses Beta wavelet family to tune many parameters related to the Beta function [13] like order and support parameters and the classical parameters of wavelets like dilation and translation to improve coefficients approximation that achieves the specific goals of detection and verification. This work exploits the ABW advantages to design a robust watermarking approach for protection and verification processes.
The rest of the paper is organized as follows: Section 2 presents the mathematical background of the parametric Beta Wavelets proposed in the schemas of protection and verification of the encrypted images. Section 3 exhibits the proposed schemes in both protection and verification steps. The results analysis is presented in Section 4. Section 5 concludes the paper with future trends.
Image protection and verification have been investigated in the literature. Some of cryptosystems and digital watermarking approaches are proposed to help pushing efforts accordingly. The researchers [14] proposed a content-based image verification cryptosystem for insecure communication channels. First, they transferred the original image into frequency domain using DCT, and they used the mid frequency sub-band for watermarking. Second, the marked image is then encrypted using the chaotic baker map for additional security.
The authors in [15] utilized the dual DCT and chaotic baker mapping to obtain an efficient image cryptosystem. First, they applied the DCT transformed on the red, green, and blue planes of the input image, where each plane was handled independently. Second, they shuffled the DCT coefficients of each plane using chaotic bake mapping. Finally, they applied the inverse DCT and merged the three planes to obtain the encrypted image.
Another paper [16] utilized Fractional Fourier Transform (FrFT) and chaotic logistic mapping to produce secure optical encryption scheme. First, it shuffled and modulated each color channel of the original image using 2D logistic map and random mask, respectively. Second, it transformed the resulted shuffled image of the red, blue, green channels using optical-based FrFT. Again, it shuffled and modulated the transformed images using 2D logistic map and another random mask. Finally, it applied the inverse FrFT and obtained the cipher image.
Authors in [17] presented a multilayer protection scheme for medical images. They watermarked the Electronic Patient Record (EPR) in the original image containing essential health information. They compressed and encrypted the EPR using Huffman algorithm and Quantum logistic map, respectively. Then, they obtained hash value using SHA-256 and embedded it into the image for authentication purposes. After that, they applied the Lifting Wavelet Transform (LWT) on the resulting image's planes. The modified EPR and hash value were to be stored into the different LWT frequency bands, resulting in Watermarked Medical Image (WMMI). Each color layer of the WMMI image permuted using Arnold transformation and then compressed using a lossless Huffman scheme. Finally, they utilized the LWT (HH and LH) frequency bands to embed the resulted WMMI.
Another paper [18] proposed a double fragile watermark system based on diffusion watermark and authentication watermark to protect image integrity. Diffusion watermarking is composed of a cover image and two random sequences. Furthermore, the authors used the diffusion operations, 3D Arnold transformation, and DNA coding to confront chosen cover-image attacks. They utilized the resulted watermark image using DNA encoding to obtain the authentication watermark and cover images. For more security, the authors considered the Latin square permutation and double-layered embedding to perform scrambling to the authentication watermark.
The authors in [19] proposed an image verification scheme by exploiting double-random phase encoding (DRPE) incorporating chaotic mapping. Its proposed generated mask is produced using an image-based chaotic Lorenz system instead of a conventional random-based mask. For verification and authentication, after encrypting the original image using the new proposed DRPE, it is compared with the encrypted reference image in a database by calculating the peak-to-correlation energy.
Technical literature [20] presented a new transmission and integrity verification framework. This framework is robust and reliable for verifying the integrity of HEVC frames transmitted through insecure communication channels. Firstly, the transmitted HEVC frames are divided into a number of blocks with specific block size. The article used a discrete transform for watermarks self-embedding among blocks depending on a predefined mechanism. The suggested schema demonstrates the suitability of the proposed transmission framework for different multimedia cybersecurity applications.
In [21], the authors proposed a crypto-based algorithm that provides confidentially, authenticity, and integrity for the pixel data and the header data of DICOM files to secure medical image exchanges over public networks. They applied strong cryptographic primitives utilizing internally generated security data, such as encryption keys, hashing codes, and digital signatures. They used strong cryptographic primitives, utilizing internally generated encryption keys, such as encryption keys, hashing codes, and digital signatures to provide the required security services.
The authors of [22] proposed a new joint watermarking/encryption algorithm to verify the reliability of medical images in encrypted and spatial domains. Their algorithm combines a substitutive watermarking algorithm, the quantization index modulation (QIM) with a block cipher algorithm, and an Advanced Encryption Standard (AES). The proposed solution gives access to the image integrity outcomes and their origins, although they are stored encrypted.
Beta Wavelet (BW) is a family of wavelets derived from beta function under certain conditions. Unlike other wavelet forms, BW can be generated based on a proper selection of beta function parameters. The beta distribution is given as follows [13]:
where
Indeed, the beta function holds some properties as follows:
1. Beta distribution at the boundary of interval [
2. Beta distribution at the centroid,
3. Evaluation of the derivative of the beta function with respect to x at
4.
5. The second derivative of the beta function is given as follows:
where
Generally, the nth derivative of the beta function is given as the following:
with
The last property is crucial because the beta function's derivative is the essence of beta wavelets. Based on Eq. (5), when (n = 0) the result is identical to that one in Eq. (1), which represents beta distribution. However, when (n > 0), the beta function takes different wavelet shapes based on derivative order. For instance, Fig. 1 shows the form of beta function in the first raw, the second raw represents the first derivative of such function, and the third raw depicts the second derivative. Beta function and its generated wavelets achieve three characteristics, localization, oscillation, and admissibility. The proof of these properties is left for the reader in [5].

Figure 1: Beta function and its derivatives
Orthogonal multiresolution analysis is a powerful tool to create the basis of orthogonality. Multiresolution can be generated from interpolating scaling functions such as beta wavelet to ease the estimation of wavelet filter coefficients. To illustrate that, assume compact support wavelet in the interval [−N/2, N/2], and it is given as:
Let the interpolation scaling function is defined as follows:
Hence, Eq. (6) becomes
From Eq. (8), filter coefficients
Generally, the other coefficients that construct filter g can be computed with the same procedure for each sample as follows:
Eventually, the wavelets are orthogonal, and the filter is a quadrature mirror filter if any sample of g creates an orthogonal base on
4 The Proposed Image Watermarking Method
In this section, we study the suggested ABW-based image watermarking method in detail. The proposed method is with the potential of image integrity, verification, and tamper detection. It has two modules, watermark embedding module, and verification module. The two modules are explored and explained in detail. The Proposed ABW-based image watermarking method might be considered a fragile self-embedding watermarking process. It depends on segment-based self-watermarking instead of employing external watermarks.
4.1 Protection Module of the Suggested ABW-Based Image Watermarking Method
The protection module of the suggested method is explored stepwise as follows, considering three different Analytic Beta-Wavelet (ABW) orthogonal filters.
(a) Split the input image, f, into two equal sub-images, f1 and f2. Again, split the resulting parts into different non-overlapping segments. In our work, we try the block size of 64 × 64, 128 × 128, and 256 × 256. For example, given the original image of size (256 × 256), when splitting into two equal sub-images (f1, f2), their size will be (128 × 256) each. Each sub-image is then divided into 8 × 8 non-overlapped blocks. Therefore, the number of blocks per sub-image is (128 × 256)/(8 × 8) = 512.
(b) Apply ABW transform to each block in the sub-image f1 starting from the upper-left corner block.
(c) Embed the row and column of each block in sub-image f1 into the row and column of the corresponding transformed block in sub-image f2.
(d) Apply inverse ABW transform to each block in sub-image f1 starting from the upper-left corner block.
(e) Apply ABW transform to each block in sub-image f2, and repeat steps 3 and 4 for such an image.
(f) Recompose the resulted two sub-images to obtain the block-based watermarked image.
4.2 The Verification Module of the Proposed Method
The process of verification module can be digested in the following steps:
(a) Receive the watermarked image.
(b) Split the watermarked image, z, into two equal sub-images, z1 and z2. Again, split the resulting parts into different non-overlapping segments. In our work, we try the block size of 64 × 64, 128 × 128, and 256 × 256.
(c) Apply ABW transform to each block in the sub-image z1 starting from the upper-left corner block.
(d) Embed the row and column of each block in the transformed sub-image z1 into the row and column of the corresponding block in sub-image z2.
(e) Apply inverse ABW transform to each block in sub-image z1 starting from the upper-left corner block.
(f) Apply ABW transform to each block in sub-image z2, and repeat steps 4 and 5 for such an image.
(g) Recompose the resulted two sub-images to obtain the extracted image.
5.1 Experiments Setup and Dataset
We used four standard and widely used images to assess the performance and robustness of the beta wavelets in watermarking and forgery detection. These images are Barbara, Male, Cameraman, and Baboon, as shown in Fig. 2. The four images used in the experiments have different histograms, evident from Fig. 2, which depict the variation of the results on these images.

Figure 2: The standard images used in experiments with their histograms
5.2 Watermarking Using Beta Wavelets
The watermark is embedded into images by applying the safeguard method to the beta wavelets approximation coefficients at level 2. The non-sampled wavelet decomposition scheme is used in the experiments to preserve the quality of both the watermarked and the retrieved images.
The authors in [13] generated different bi-orthogonal beta wavelet filters and compared them to traditional wavelet families, such as Daubechies and Morlet wavelets. They tested such beta wavelets in an image compression application. Bi-orthogonal wavelets are less phase distortion, and they support symmetrical and exact reconstruction than orthogonal wavelet filters. Bi-orthogonal wavelets have two sets of scaling filters, and hence wavelet filters. No prior experiment with beta wavelets for image watermark has been carried out in the literature. The performance of those filters with different Filter orders in the image's watermark is checked and compared with two wavelets in this article: Daubechies (db2) and discrete Meyer wavelets.
Consequently, along with the Daubechies (db2) and discrete Meyer (dmey) wavelets, 17 bi-orthogonal beta wavelet filters with different filter orders are generated and applied to the Barbara image with block sizes of 64 × 64, 128 × 128, and 256 × 256. The results of this study are provided in Tab. 1. The performance of the BWT is assessed using visual inspection under two evaluation metrics: PSNR, and Correlation coefficient. Given two images I1 and I2, the equations of these measures are:
where
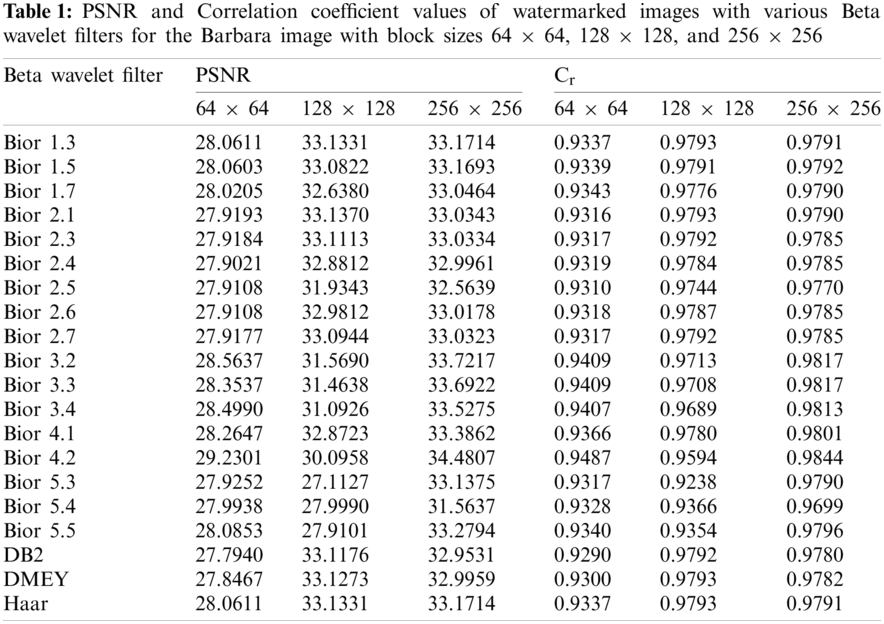
The findings in Tab. 1 show that the beta wavelet filter’s behavior differs depending on the PSNR and Cr values for the same image across the three block sizes. As shown in Tab. 1, the best performance of each filter out of the three block sizes is highlighted with a bolded font. The bior1.3 filter, for example, has better PSNR with 256 × 256 blocks than other block sizes, while its Cr coefficient has the best value with 128 × 128 blocks. For both PSNR and Cr, the bior2.3 filter shows the best results with the same block size. The PSNR and Cr coefficients for the bior4.2 filter, on the other hand, indicate that the block size 256 × 256 produces the best results as compared to other block sizes. This filter, bior4.2, also has the best values of all the beta and common wavelet families tested in this study. Comparing the biorthogonal beta filters in this paper with the wavelets Haar, db2, and dmey allows us to use them in watermarking simulation experiments, as shown in the following section. Due to the difficulty of testing all filters systematically in the following experiments, only three beta filters, bior1.3, bior2.3, and bior4.2, are chosen to represent the remaining beta filters, each of which has two possible performance measure variants.
5.3 Evaluation of Watermark Embedding
As mentioned in the previous section, the performance of the three selected beta wavelet filters bior1.2, bior2.3, and bior4.2 is investigated further as the experiments progress. The quality measures of the four images when inserting the watermark using the safeguard procedure with beta wavelets under block size of 256 × 256 is shown in Fig. 3.

Figure 3: Protection process visual results of the original and watermarked images with Beta Wavelet for the four tested images of block size 256 × 256
The plots in Fig. 4A show that when changing the block size, the performance of all filters varies. Bior4.2 has the best performance with the 64 × 64 block size, while the other two filters have relatively close MSE measurements. Increasing the block size to 128 × 128 dramatically improves the results of the first two filters, while slightly enhancing the error measure for the bior4.2, except for the Baboon image. The error in the Baboon image increases with 128 × 128 block size compared to the 64 × 64 block size for the bior4.2 filter. Applying the beta wavelet filters to images with different characteristics and different histograms may affect their output; the Baboon image is an example. All filters have far better outcomes with the 256 × 256 block size than other block sizes.
Tab. 1 and Fig. 4A clearly show that the performance measurements of the 256 × 256 block sizes outperform those of the 64 × 64 and 128 × 128 block sizes. Although the bior4.2 beta wavelet with block size 256 × 256 produces the best results, the bior1.3 and bior2.3 filters have comparable results, with the bior1.3 filter slightly outperforming the latter. The same behavior is repeated for the PSNR measure for the three beta wavelet filters as shown in Fig. 4B. The plots in Fig. 5C indicate that the Cr for the Baboon image has less performance compared to the other images used in the experiment for all filters. Although there are a lot of details in the Baboon image, most of these details are sporadic. Therefore, much of the energy for this image is based on the approximation coefficients that are subjected to the watermark at level 2 in this paper. The Baboon image displays less immunity to distortion when we attempt to extract it from the watermarked image. The visual quality of the watermarking process of the three biorthogonal filters and their effect on the tested images are shown in Fig. 3. The associated block-correlation provides the quality change assessment for each block on the images.
In this experiment, the images are extracted using the verification process with the Beta wavelet for block sizes 256 × 256, 128 × 128, and 64 × 64 without any attack. This method aims to ensure that the images are obtained from its watermarked version with minimal degradation. Again, the quality of the extracted images is measured by three metrics: PSNR, and Cr. Also, the extracted images are shown in each of the following Figs. 5–7, next to the original copy to visually assess the effect of the watermarking and extraction processes.
Tab. 2 indicates the performance of the three previously selected beta wavelet filters for all images based on the three different block sizes 64 × 64, 128 × 128, and 256 × 256. Similar to the outcome of the previous experiments, almost in all cases, performance indicators show that the 256 × 256 block size outperformed the block sizes 64 × 64 and 128 × 128. Also, the bior4.2 filter has the best results on 256 × 256 block size against all other filters with various block sizes when applied to the four tested images.
The block correlation plots shown in the Figs. 5–7 next to the extracted images indicate good results for 256 × 256 and 128 × 128 block sizes for all filters performed well as expected. However, block correlation measure is dropped in Cameraman image when dividing the image into a small number of blocks. For the 64 × 64 block size, all correlation coefficients (Cr) have a fluctuating behavior. Cameraman results show the worst case where the Cr alternate between zero to higher values closer to one. This behavior is due to the large dark areas found in the image and the nonuniform intensity distribution, evident from its histogram, which affects the image extraction. On the contrary, the Baboon image has the best stable readings due to its lack of these large dark areas. The same happens for the Barbara and Male images with most blocks that do not have large dark spots.

Figure 4: (A) MSE of watermarked images using the safeguard procedure with beta wavelet filters for block sizes 64 × 64, 128 × 128, and 256 × 256 applied to all images. (B) PSNR of watermarked images using the safeguard procedure with beta wavelet filters for block sizes 64 × 64, 128 × 128, and 256 × 256 applied to all images. (C) Cr of watermarked images using the safeguard procedure with beta wavelet filters for block sizes 64 × 64, 128 × 128, and 256 × 256 applied to all images


Figure 5: Verification process visual results of the original and extracted images with Beta wavelet for the four tested images of block size of 256 × 256
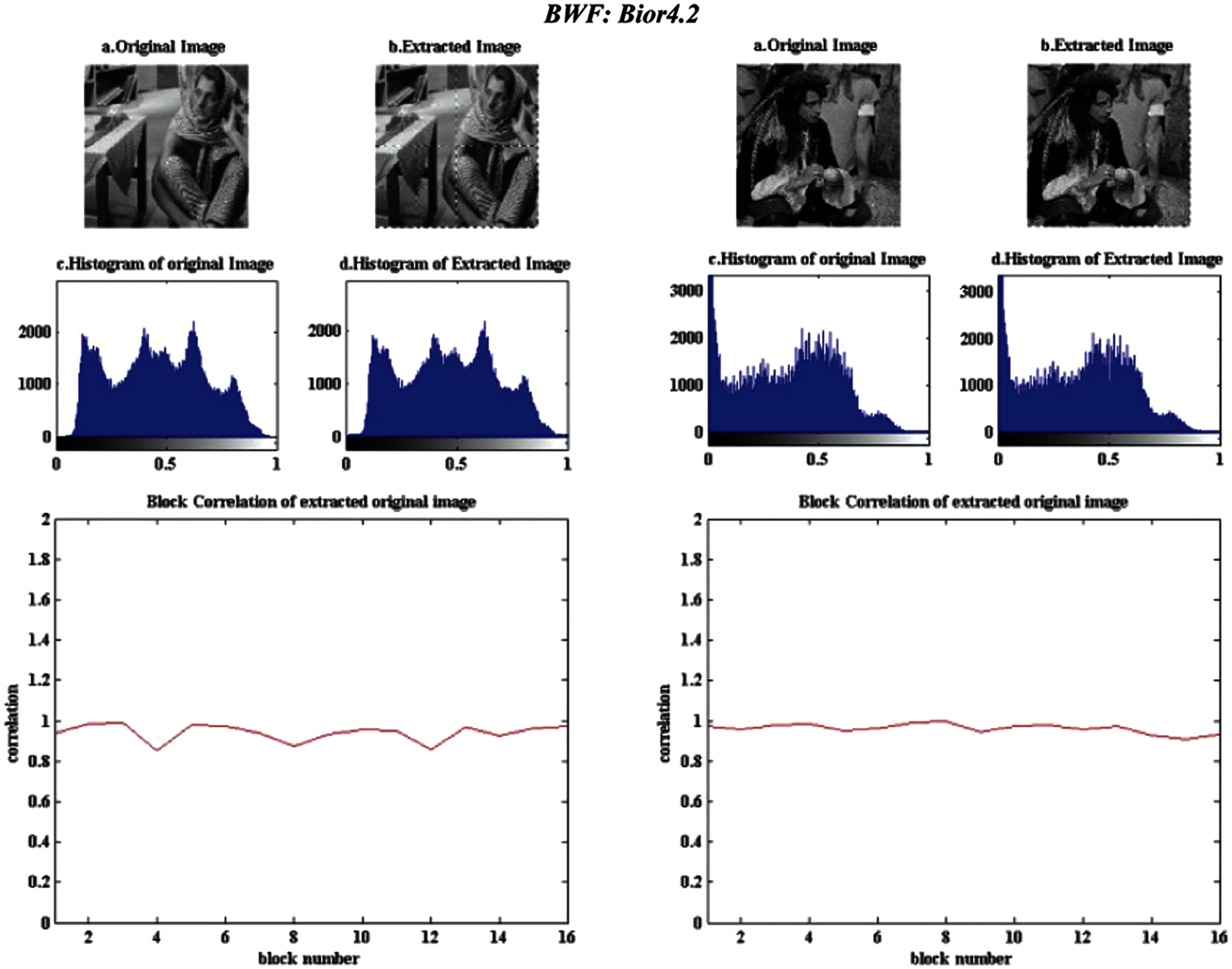

Figure 6: Verification process visual results of the original and extracted images with Beta wavelet for the four tested images of block size of 128 × 128


Figure 7: Verification process visual results of the original and extracted images with Beta wavelet for the four tested images of block size of 64 × 64
The paper presented an efficient ABW-based image watermarking protection and verification framework. The proposed ABW-based image integrity verification framework applied a certain ABW orthogonal filter for embedding internal segment-based watermarks into other segments of the transmitted image. Three different ABW orthogonal filters are examined in the proposed ABW-based image integrity verification framework. Simulation tests demonstrated that the possibility of watermark protection and verification using the suggested ABW-based image watermarking framework. Additionally, the proposed method provided a high robustness against multimedia attacks. Also, tampering and forgery detection simulations indicate superior results. The test results also indicated the high sensitivity of the suggested ABW-based image watermarking framework to detect different types of image tampering, although the received tampered image appeared to be visually not manipulated. Finally, we showed that the proposed method can be applied to provide a confidential image communication and detect any forensic operations.
Acknowledgement: The authors would like to thank the Deanship of Scientific research, Taif University Researches Supporting Project number (TURSP-2020/216), Taif University, Taif, Saudi Arabia for supporting this scientific research work.
Funding Statement: This research was funded by Deanship of Scientific Research, Taif University Researches Supporting Project number (TURSP-2020/216), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. F. An and J. Liu, “Image encryption algorithm based on adaptive wavelet chaos,” Journal of Sensors, vol. 2019, pp. 1–12, 2019. [Google Scholar]
2. X. Wu and W. Sun, “High-capacity reversible data hiding in encrypted images by prediction error,” Signal Processing, vol. 104, pp. 387–400, 2014. [Google Scholar]
3. D. Singh and S. Singh, “Effective self-embedding watermarking scheme for image tampered detection and localization with recovery capability,” Journal of Visual Communication and Image Representation, vol. 38, pp. 775–789, 2016. [Google Scholar]
4. L. Zeng, X. Zhang, L. Chen, Z. Fan and Y. Wang, “Scrambling-based speech encryption via compressed sensing,” EURASIP Journal on Advances in Signal Processing, vol. 2012, no. 257, pp. 1–12, 2012. [Google Scholar]
5. B. Stoyanov and G. Nedzhibov, “Symmetric key encryption based on rotation-translation equation,” Symmetry, vol. 12, no. 1, pp. 1–12, 2020. [Google Scholar]
6. A. Arab, M. J. Rostami and B. Ghavami, “An image encryption method based on chaos system and AES algorithm,” The Journal of Supercomputing, vol. 75, no. 10, pp. 6663–6682, 2019. [Google Scholar]
7. A. Mishra, A. Gupta and D. Rao, “Analysing the parameters of chaos based image encryption schemes,” World Applied Programming, vol. 1, no. 5, pp. 294–299, 2011. [Google Scholar]
8. O. S. Faragallah, A. Afifi, H. S. El-Sayed, M. Alzain, J. Al-Amri et al., “Efficient HEVC integrity verification scheme for multimedia cybersecurity applications,” IEEE Access, vol. 8, pp. 167069–167089, 2020. [Google Scholar]
9. K. Ramani, E. Prasad, S. Varadarajan and A. Subramanyam, “A robust watermarking scheme for information hiding,” in Proc. 16th Int. Conf. on Advanced Computing and Communications, Chennai, India, pp. 58–64, 2008. [Google Scholar]
10. A. Akter and M. A. Ullah, “Digital image watermarking based on DWT-DCT: Evaluate for a new embedding algorithm,” in Proc. ICIEV, Dhaka, Bangladesh, pp. 1–6, 2014. [Google Scholar]
11. M. Khan, A. Kushwaha and T. Verma, “A new digital image watermarking algorithm based on image interlacing, DWT, DCT,” in Proc. ICIC, Pune, India, pp. 885–890, 2015. [Google Scholar]
12. B. Sridhar and C. Arun, “An interlacing technique-based blind video watermarking using wavelet,” International Journal of Computer and Information Engineering, vol. 9, no. 6, pp. 1479–1482, 2015. [Google Scholar]
13. C. Ben Amar, M. Zaied and A. Alimi, “Beta wavelets: Synthesis and application to lossy image compression,” Advances in Engineering Software, vol. 36, no. 7, pp. 459–474, 2005. [Google Scholar]
14. S. Nassar, N. Ayad, H. Kelash Hala, S. El-Sayed, A. M. El-Bendary et al., “Content verification of encrypted images transmitted over wireless AWGN channels,” Wireless Personal Communications, vol. 88, no. 3, pp. 479–491, 2016. [Google Scholar]
15. O. Faragallah, H. El-sayed, A. Afifi and W. El-Shafai, “Efficient and secure opto-cryptosystem for color images using 2D logistic-based fractional Fourier transform,” Optics and Lasers in Engineering, vol. 137, pp. 106333, 2021. [Google Scholar]
16. H. Alhumyani, “Efficient image cipher based on baker map in the discrete cosine transform,” Cybernetics and Information Technologies, vol. 20, no. 1, pp. 68–81, 2020. [Google Scholar]
17. S. Dhall and S. Gupta, “Multilayered highly secure authentic watermarking mechanism for medical applications,” Multimedia Tools and Applications, vol. 80, pp. 18069–18105, 2021. [Google Scholar]
18. X. Gong, L. Chen and F. Yu, “A secure image authentication scheme based on dual fragile watermark,” Multimedia Tools and Applications, vol. 79, no. 25, pp. 18071–18088, 2020. [Google Scholar]
19. S. holami, K. Jaferzadeh and S. Shin, “An efficient image-based verification scheme by fusion of double random phase encoding and dynamic chaotic map,” Multimedia Tools and Applications, vol. 78, pp. 25001–25018, 2019. [Google Scholar]
20. Z. Liu, “Comparative evaluations of image encryption algorithms,” Ph.D. dissertation, Auckland University of Technology, New Zealand, 2018. [Google Scholar]
21. A. Al-Haj, “Providing integrity, authenticity, and confidentiality for header and pixel data of DICOM images,” Journal of Digital Imaging, vol. 28, no. 2, pp. 179–187, 2015. [Google Scholar]
22. D. Bouslimi, G. Coatrieux and C. Roux, “A joint watermarking/encryption algorithm for verifying medical image integrity and authenticity in both encrypted and spatial domains,” in Proc. Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, pp. 8066–8069, 2011. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |