Computers, Materials & Continua DOI:10.32604/cmc.2022.021186
Article

Graph Transformer for Communities Detection in Social Networks

G. Naga Chandrika1, Khalid Alnowibet2, K. Sandeep Kautish3, E. Sreenivasa Reddy4, Adel F. Alrasheedi2 and Ali Wagdy Mohamed5,6,*

1Department of Computer Science and Engineering, ANU College of Engineering and Technology, Guntur,522510, India
2Statistics and Operations Research Department, College of Science, King Saud University, Riyadh, 11451, Kingdom of Saudi Arabia
3LBEF Campus, Kathmandu, 44600, Nepal
4Department of Computer Science and Engineering, ANU, Guntur, 522510, India
5Operations Research Department, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, 12613, Egypt
6Wireless Intelligent Networks Center (WINC), School of Engineering and Applied Sciences, Nile University, Giza, 12588, Egypt
*Corresponding Author: Ali Wagdy Mohamed. Email: aliwagdy@gmail.com
Received: 26 June 2021; Accepted: 13 August 2021

Abstract: Graphs are used in various disciplines such as telecommunication, biological networks, as well as social networks. In large-scale networks, it is challenging to detect the communities by learning the distinct properties of the graph. As deep learning has made contributions in a variety of domains, we try to use deep learning techniques to mine the knowledge from large-scale graph networks. In this paper, we aim to provide a strategy for detecting communities using deep autoencoders and obtain generic neural attention to graphs. The advantages of neural attention are widely seen in the field of NLP and computer vision, which has low computational complexity for large-scale graphs. The contributions of the paper are summarized as follows. Firstly, a transformer is utilized to downsample the first-order proximities of the graph into a latent space, which can result in the structural properties and eventually assist in detecting the communities. Secondly, the fine-tuning task is conducted by tuning variant hyperparameters cautiously, which is applied to multiple social networks (Facebook and Twitch). Furthermore, the objective function (cross-entropy) is tuned by L0 regularization. Lastly, the reconstructed model forms communities that present the relationship between the groups. The proposed robust model provides good generalization and is applicable to obtaining not only the community structures in social networks but also the node classification. The proposed graph-transformer shows advanced performance on the social networks with the average NMIs of 0.67 ± 0.04, 0.198 ± 0.02, 0.228 ± 0.02, and 0.68 ± 0.03 on Wikipedia crocodiles, Github Developers, Twitch England, and Facebook Page-Page networks, respectively.

Keywords: Social networks; graph transformer; community detection; graph classification

1  Introduction

The concept of networks is widely used in various disciplines, such as social networks, protein to protein interactions, knowledge graphs, recommendation systems, etc. The social network analysis is studied due to the development of big data techniques, where the communities are categorized into groups based on their relationship. In biological networks, interconnectivity among protein molecules can result in similar protein-protein interactions which may depict similar functionality. In general, a community is a collection of the closely related entity in terms of the similarity among individuals. With the increase of social media utility, social network mining becomes one of the crucial topics in both industry and academia. With the growth of the network topology, the complexity of information mining increases. Therefore, it is challenging to detect and segregate the communities by analyzing individual clusters [1]. Moreover, it is also a sophisticated task to understand the topological properties of a cluster in a network as well as the information that they carry simultaneously. The graphs (networks) community detection refers to collecting a set of closely related nodes based on either the spatial location of nodes or topological characteristics. Hence, understanding the network behavior in detail is the key to mine information for detecting appropriate communities.

A variety of works study how to detect the communities in large-scale networks such as deep walk [2], skip-gram with negative sub-sampling [3], and matrix factorization methods [4,5]. However, with the advance of deep learning, the encoder-decoder structures are utilized to be a stacked autoencoder and preserve the proximities, which can achieve great performance. It can also provide a solution for image reconstruction in computer vision and language translation NLP. Hence, this paradigm is important for graph neural networks (GNN), and the graph autoencoder can provide an encoder and a decoder. The graph is represented by mapping the encoder into a latent space. Furthermore, the decoder reconstructs the latent representations to generate the new graph with varying embedding structures. Various researchers have focused on this direction. Some of them utilize transformers to improve the embedding quality of the model, considering the equivalent relationship with the encoder. The embedding feature vector is created by tuning the parameters rigorously optimally. In this paper, we aim to provide a robust solution by cautiously considering every constraint in detail. The graph transformer is implemented in Section 4.

2  Related Work

Deep Neural Network for graph representations (DNGR) [6] utilizes a stacked autoencoder [7] for finding patterns in the community by encoding a graph to the Positive Point-wise Mutual Information (PPMI) matrix. The procedure is initiated with the stacked denoising autoencoders in largely connected networks. Subsequently, structural deep network embedding (SDNE) [8] imparts stacked autoencoders for preserving the node proximities. The first-order and the second-order proximities are preserved together by providing two objective functions for encoder and decoder separately. The objective function for the encoder preserves the first-order node proximity.

Lenc←∑u,v∈E⁡Au,v‖encoder(xu)−encoder(xv)‖2,(1)

where xu=Au.

Ldec←∑u∈V⁡‖decoder(encoder(xu)−xn)⊙Cu‖2,(2)

where

However, DNGR and SDNE only preserve the topological information and fail to extract the information regarding the nodes’ attributes. To solve this problem, graph autoencoders in [9] import a graph convolutional network to leverage the information capturing ability of nodes.

Z←encode(X,A)=Graph−Convolution(ReLu(Graph−conv(A,X,θ1)),θ2)(3)

where Z represents the graph embedding space. Then the decoder tries to extract the information on the relationship of nodes from Z by reconstructing an adjacency matrix, i.e.,

A^u,v←decode(Zx,Zv),(4)

where

Note that the reconstruction of the adjacency matrix may cause overfitting of the model. To this end, researchers make efforts to detect communities through either understanding the structural properties of the nodes or extracting information from underlying relationships among nodes.

The above-mentioned research introduces the auto-encoder and encoder-decoder architecture to learn representations in a graph structure. Similarly, in the language processing, especially for the sequence transduction task, a Long Short-Term Memory (LSTM) architecture has been developed for the machine translation task [10]. Moreover, the neural machine translation (NMT) attracts attention from researchers since it can greatly improve the translation accuracy [11]. A variety of local and global attention paradigms are introduced to investigate the attention layers in NMT [12]. It is demonstrated that the attention in NMT is a deterministic factor for performance improvement. In addition, the transformer is proposed for NMT, which has a similar encoder-decoder architecture and is self-attention [13].

Besides the neural sequence transduction tasks, the transformers tend to provide numerous other applications, such as pre-trained machine translation [14], ARM to text-generation [15], and document classification [16]. Furthermore, the transformers can provide advanced performance in large-scale image recognition [17] and object detection in 3D videos [18]. It is even widely utilized in the domain of graph neural networks. Hu et al. [19] are motivated by the transformers and propose a heterogeneous graph transformer architecture for extracting complex networks variances from the node and edge dependent parameters. An HG Sampling algorithm is proposed to train the mini-batch samples in the large-scale academic dataset named Open Academic Graph (OAG), of which heterogeneous transformer is able to rise the baseline performance from 9% to 19% in the paper-filed classification task.

Some research focuses on designing models which provide hardware acceleration to fasten the training of the large-scale network. Auten et al. [20] provide a unique proposition to improve the performance of graph neural networks with Central Processing Unit (CPU) clusters instead of Graphical Processing Units (GPU). The authors consider some standard benchmark models, and the proposed architecture for computing the factorization can improve the performance of graph traversal greatly. Jin et al. [21] study a graph neural network named Pro-GNN, which learns the community structures underlying a network by defending against adversarial attacks. The model is able to tackle the problem of perturbations in large-scale networks. It presents high performance for some of the standard datasets, such as Cora, Citeseer, Pubmed, even though the perturbation rate is high. Ma et al. [22] investigate a graph neural network that can learn the representations dynamically, i.e., DyGNN. They address the problem of static graphs and propose a dynamic GNN model that performs well on both link prediction and node classification. Compared with the benchmark models, the DyGNN model shows better performance on link prediction with UCI and Epinions datasets. Moreover, for the case training ratios vary from 60–100% on the Epinions dataset, the model outperforms the individual models. El-Kenawy et al. [23] propose a modified binary Grey Wolf Optimizer (GWO) algorithm for selecting the optimal subset of features. It utilizes the Sandia frequency shift (SFS) technique, where the diffusion process is based on the Gaussian distribution method. In this way, the values can be converted to binary by sigmoid. Eid et al. [24] propose a new feature selection approach based on the Sine Cosine algorithm which obtains unassociated characteristics and optimum features. In 2021, El-Kenawy et al. [25] propose a method for disease classification based on the Advanced Squirrel Search Optimization algorithm. They employ a Convolutional Neural Network model with image augmentation for feature selection. However, most of the state-of-the-art models are focusing on specific domains. It means they cannot represent heterogeneous graphs information and are suitable for static graphs with deep neural networks.

3  Motivation

This work is inspired by the transformers, which is applicable to various domains. The contributions of this paper are summarized as follows.

1.    Firstly, the transformer is applied to downsample the first-order proximities of the graph into a latent space, which can preserve the structural properties and eventually assist in detecting the communities.

2.    The fine-tuning task is conducted by tuning various hyperparameters cautiously, which can be widely competent on multiple social networks, e.g., Facebook and Twitter. In addition, the objective function, i.e., cross-entropy, is tuned by L0 regularization.

3.    Finally, the learned representations are employed for node classification, which can be applicable to general scenarios.

4  Methodology

In this section, we aim to introduce the implementation of methodology and the process involved in this paper. The process is illustrated in Fig. 1, including (a) definitions of the basic notations and the related terms; (b) implementation of the graph-transformer for both graph clustering and classification tasks; (c) discussions on the insights of transformers in detail which present the self-attention mechanism, and residual connectivity with its relative connection to GNN for detecting communities by using the first-order proximity.

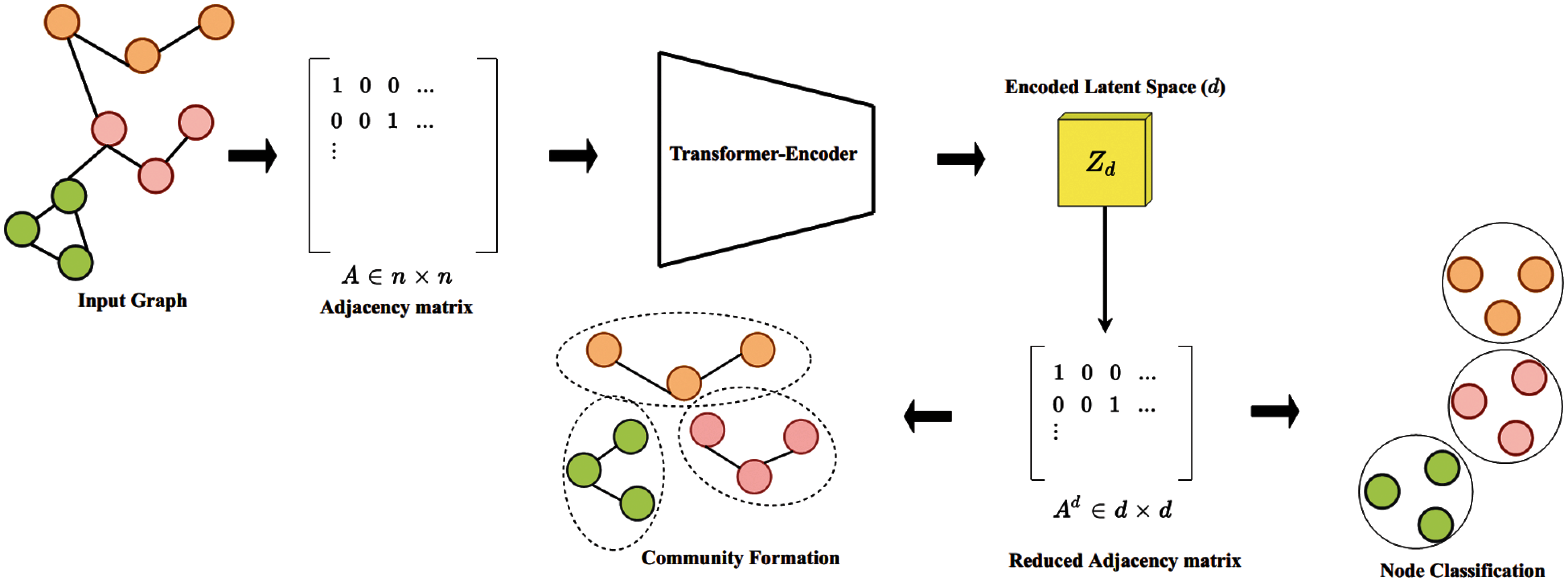
Figure 1: The model diagram of the proposed model

4.1 Notations and Definitions

Here, the required definitions and notations in the paper are described as follows.

Graph A graph is a collection of nodes and their relative connectivity. G <V, E> is used to denote a graph, where the pair < V, E > is a collection of nodes and edges. V ∈ v1, v2,…, vn represents the set of nodes, while E ∈ e1, e2,…, ekis the set of edges.

First-Order Proximity The first-order proximity determines the relationship between two specific nodes in the given graph G. Specifically, if an edge exists between the node pair (vi , vj), the first-order proximity is equal to w; otherwise, it is set to 0, i.e., null. Note that w depends on the connectivity of nodes in the given graph. If the edge of the graph is weighted, w will denote the edge weight; otherwise, it is regarded as 1.

Adjacency Matrix A square matrix is constructed according to the first-order proximity of nodes in the given graph and is represented as A. The value of the first-order proximity is placed by checking individual node pairs. In this way, a complete set of node pair samples is selected.

4.2 The Graph-Transformer

In this sub-section, the transformer and its internal working principle are explained first. The graph structures of the first-order proximity are subsequently learned. The transformers are guided with self-attention which has an encoder and a decoder structure. The encoder part consists of two attention blocks. One is a multi-head intra-attention network, and the other is a position-wise fully-connected feed-forward network. These two blocks are sequentially connected with multiple units. Each layer has a definite set of residual connections and successive layer normalization to overhaul covariate shifts in recurrent neural networks [26,27]. Fig. 2 demonstrates the internal working of the transformer.

A1,A2,A3←Attn(A1,A2,A3)←σ1(A1.A2Tdk12)(5)

where σ1(xi)←exi∑k⁡exk, and dkis the scaling coefficient. When the product increases exponentially, the activations tend to explode, which results in small gradients. Hence, the scaling factor dk12 is substantially used to avoid the case occurs.

MH−Attn(A1,A2,A3)←[c1,c2,c3]W0,(6)

where ci←Attn(A1WiA1,A2WiA2,A3WiA3). WiA1WiA2andWiA3 are the parametric projection matrices, and we have

FFNS(S)←f(ReLU(f(S))),(7)

where S is an input to the feed-forward neural network layer as mentioned in Fig. 2.

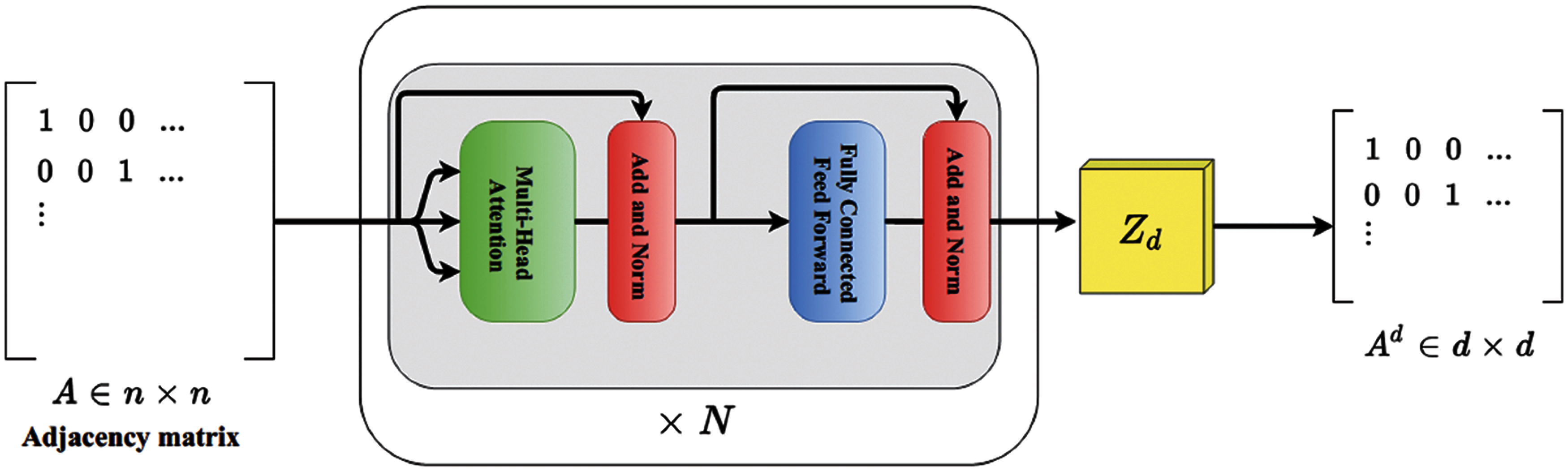
Figure 2: The internal working model diagram of the transformer

Eq. (7) represents the linear transformation of the input x, i.e., densely connected neurons. ReLU is an activation function to push the feed to the next layer, i.e., ReLU(S)←max(0,S). f is a tunable feed-forward neural network with a weight matrix W and bias b, i.e., f(S)←S.W+b. The FFNS is the same at different positions, while the parametric weights vary from layer to layer. In this way, the weighted combination of the entire neighborhood is obtained which is equivalent to summary the information from different connected inputs, as shown in Fig. 3. The densely connected networks are beneficial to compute new feature representation across the input space. The information is successively iterated for N times, and the weights are successively updated to achieve the minimal loss. As the residual connections can improve the gradient flow over the network without degradation [13], the positional information is carried. In addition, the self-attention layers introduce the similarity of different information, it thus can carry the first-order proximities. The provided attention is permutation invariant. It means that, even though the positional order is changed, the required information can be extracted. The gating interaction is provided when the information is succeeded to the subsequent layers. Note that the residual connections in the architecture carry the information about the position which attracts attention to the required regions, i.e., the region of interests. In this case, the positional embeddings can be obtained based on adjacency matrix, which carries structural proximities and leads to self-attention by iterations. The self-attention presents the relatively similarity between two data points.

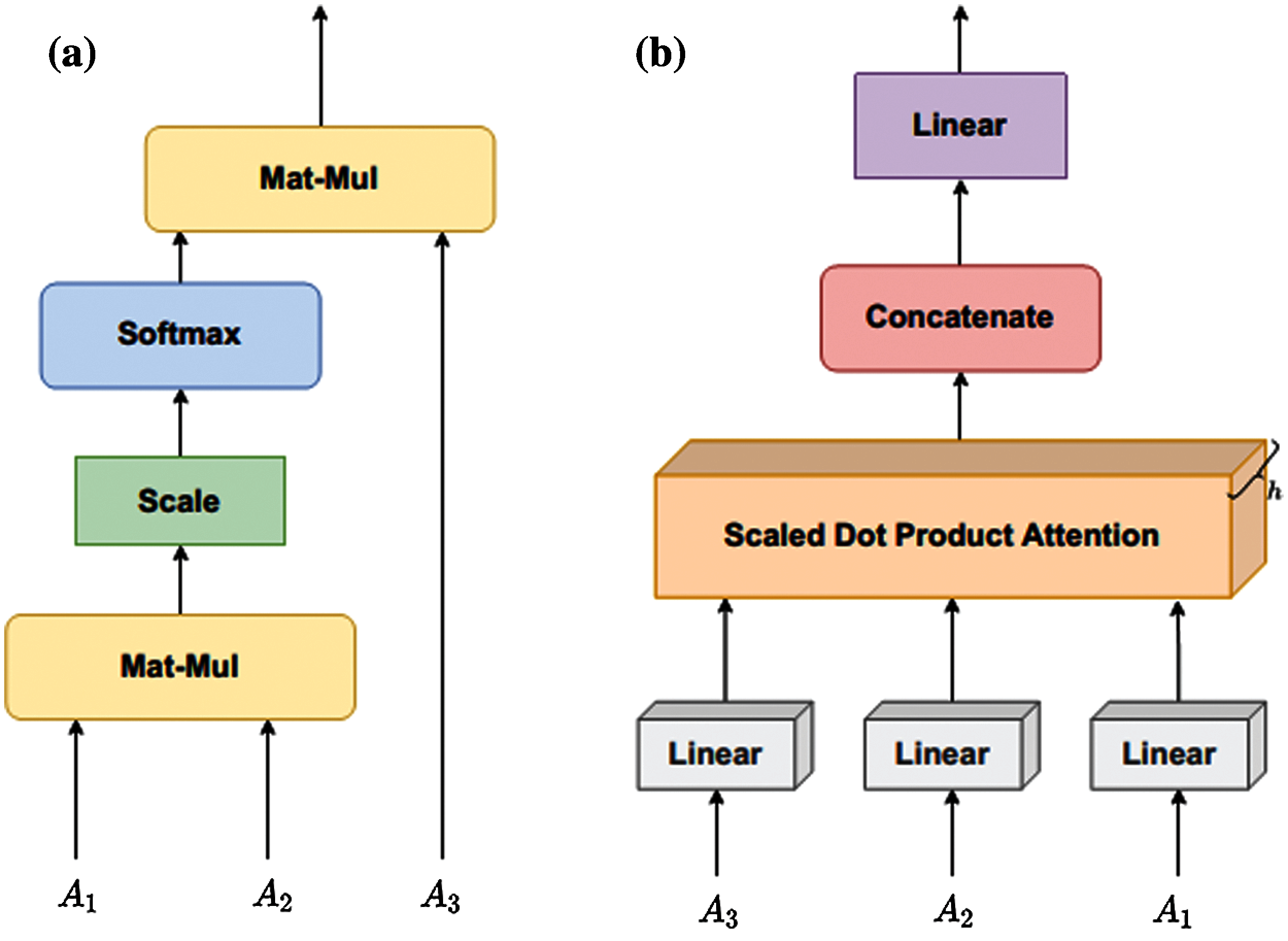
Figure 3: The information flow of the proposed model. (a) Scaled dot product attention (b) Multi head attention

4.3 Fine-Tuning of the Graph-Transformer

In this sub-section, the parameter settings are introduced for the graph transformer, as well as the corresponding tuning process.

1.    The individual attention layers and their layer partitions are illustrated in Fig. 3, where h in Fig. 3b denotes the number of the attention heads utilized and is set to 2.

2.    To obtain the structure, the adjacency matrix is the input of the graph-transformer and positional encoding, as shown in Figs. 2 and 3. It is constructed by query, key, and value. Note that the embeddings here are generic, and the whole first-order proximity is derived from the latent space.

3.    The hidden layers for each attention head are set to 2. The dimension of the transformer model is decreased to 128, where the shape of the adjacency matrix is reduced from n × n to n × 128. n represents the number of nodes in the given graph G.

4.    The number of attention heads is set to 2. For appropriate regularization, the graph-transformer dropout [kk] and layer normalization layers are added, where the drop rate is set to 50% for effective generalization during the testing phase.

5.    The objective function for evaluating the loss is categorical cross-entropy. And the Adam optimizer is involved with an initial learning rate of 4.5 × 10−5. Note that the learning is multiplied by 0.9 after a certain number of iterations (≈ 10 epochs). Since the model can reach convergence, no further increment in the learning rate is required.

The above-mentioned parameters are tuned internally in the network, and the objective function is regularized with a cautious optimization.

Objective Function Optimization It is known that A is sparse, if the sparse matrix is reconstructed without appropriate regularization. It can mislead the reconstruction of the matrix and result in a number of zeros in the matrix. To solve the problem, we introduce an appropriate penalty on neural networks. Generally, Ridge (L1) or Lasso (L2) can be utilized directly into the neural networks, as they have differentiable gradients. Here, L0 is selected which is beneficial to achieve convergence quickly. It can also solve the issue that the differentiable regularization techniques incur shrinkage of the sampled parameters.

R(θ)←1N(∑j=1N⁡L(h(Xj;θ)))+Λ∥θ0∥,(8)

where

θ is the dimension of the parametric factor, Λ is a weighting agent for the regularization, and L(.) is the objective (loss) function for the task. In this way, based on L0 regularization, the objective function will be optimized, which can obtain the rigorous outcome with high generalization [28].

5  Experiments

5.1 Datasets

To evaluate the proposed methodology, a set of vertex-level algorithms with the ground truth of communities are considered. The statistics of datasets are listed in Tab. 1. The ground-truth of communities in the datasets can assist in both community detection and graph classification. Moreover, the collaboration network, web network, and social networks in the datasets are considered. The raw adjacency matrix is constructed with available nodes and edges. The networks considered are acquired from the publicly available resources [29,30].

5.2 Community Detection

In this sub-section, whether the structure is preserved by the embeddings of the graph-transformer is investigated first. To this end, the latent space embeddings are evaluated with the standard graph clustering metrics. Normalized Mutual Information (NMI) [31] is chosen to be the standard metric for the cluster quality evaluation, due to its improvement on the relative normalized mutual information. The library of Karate Club [32] is utilized as a benchmark, which can obtain fast and reliable reproducible results with consistency.

The evaluation procedure is comparatively different from the proposed method. Firstly, a set of nodes are trained on the graph transformer. Only 50% of the nodes are trained in the network and the remaining ones are used for testing. The results are obtained over 10-times repetitive experiments, of which the mean deviations are shown in Tab. 2.

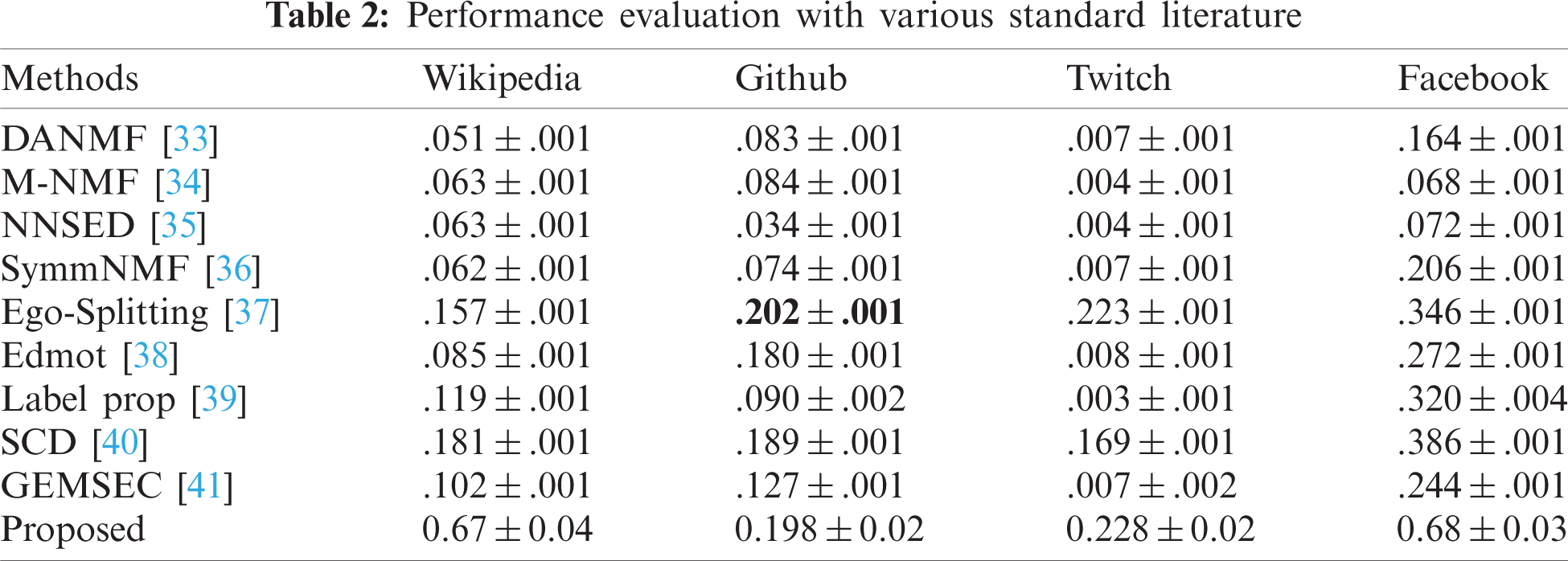
A set of standard models for community detection algorithms are utilized to validate the work. The first five models in Tab. 2 [33–37] are proposed for overlapping communities, whereas the remaining methods are designed for non-overlapping communities. It is observed that the proposed graph-transformer tends to have effective outcomes for the datasets. The results present the resilience of the model which can balance the performance of different communities appropriately. The average NMIs for Wikipedia crocodiles, Github Developers, Twitch England, and Facebook Page-Page networks are 0.67 ± 0.04, 0.198±0.02, 0.228 ± 0.02, and 0.68 ± 0.03, respectively. Furthermore, the NMIs of the testing sets for different networks are studied and shown in Fig. 4.

5.3 Graph Classification

Subsequently, the latent node embeddings of graph-transformer are investigated for node classification. Due to the availability of ground truth labels for the individual networks, the task is evaluated as similar as the clustering problem. The nodes are equally divided into two sets for training and test, respectively. The training convergence is studied accordingly. It is observed that, in most of the scenarios, the model can converge very fast and obtain the optimal accuracy within about 10 epochs. To present the learning ability of the graph-transformer, the accuracy and loss curves are illustrated in Fig. 5. The accuracy and loss values on node classification for the selected networks are listed in Tab. 3.

6  Drawbacks

This section aims to illustrate the drawbacks of the proposed work. Firstly, in some intricate scenarios, reducing dimensions can be problematic. Small data with higher sparsity can mislead the predictability, as the small-scale data cannot draw inferences generically. As a result, the dimensionality should not be selected for the case with small data samples. Secondly, the proposed work mainly focuses on undirected, homogeneous, and unweighted graphs. Thirdly, the method shall be fine-tuned to a specific dataset, as the constructed adjacency matrix varies with different network structures. It means that the problems of dynamically evolving networks cannot be solved, since an increasing number of nodes leads to the incensement of the adjacency matrix dimensions, in terms of width and length.

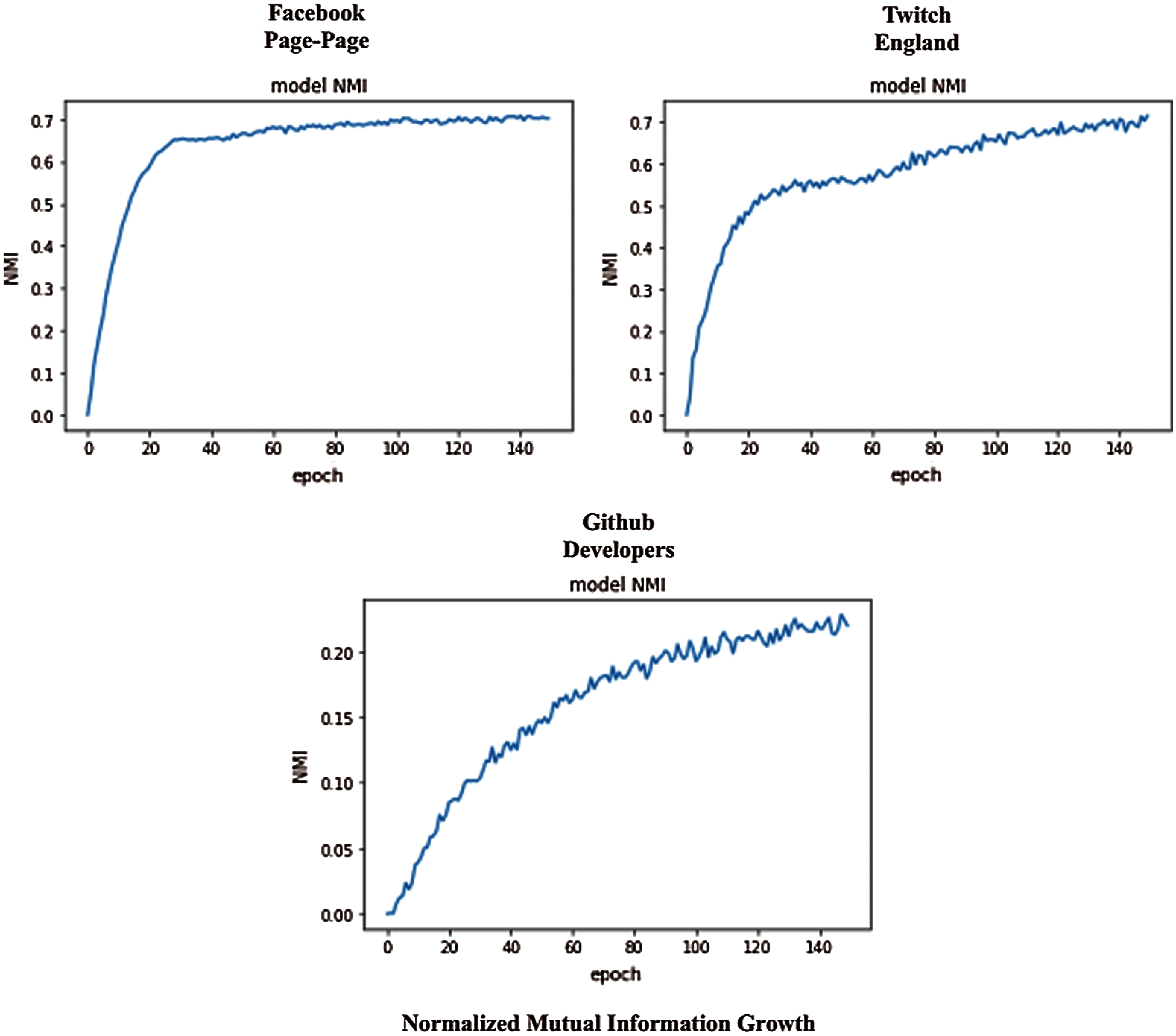
Figure 4: NMI growth (Test) for the selected networks with several epochs

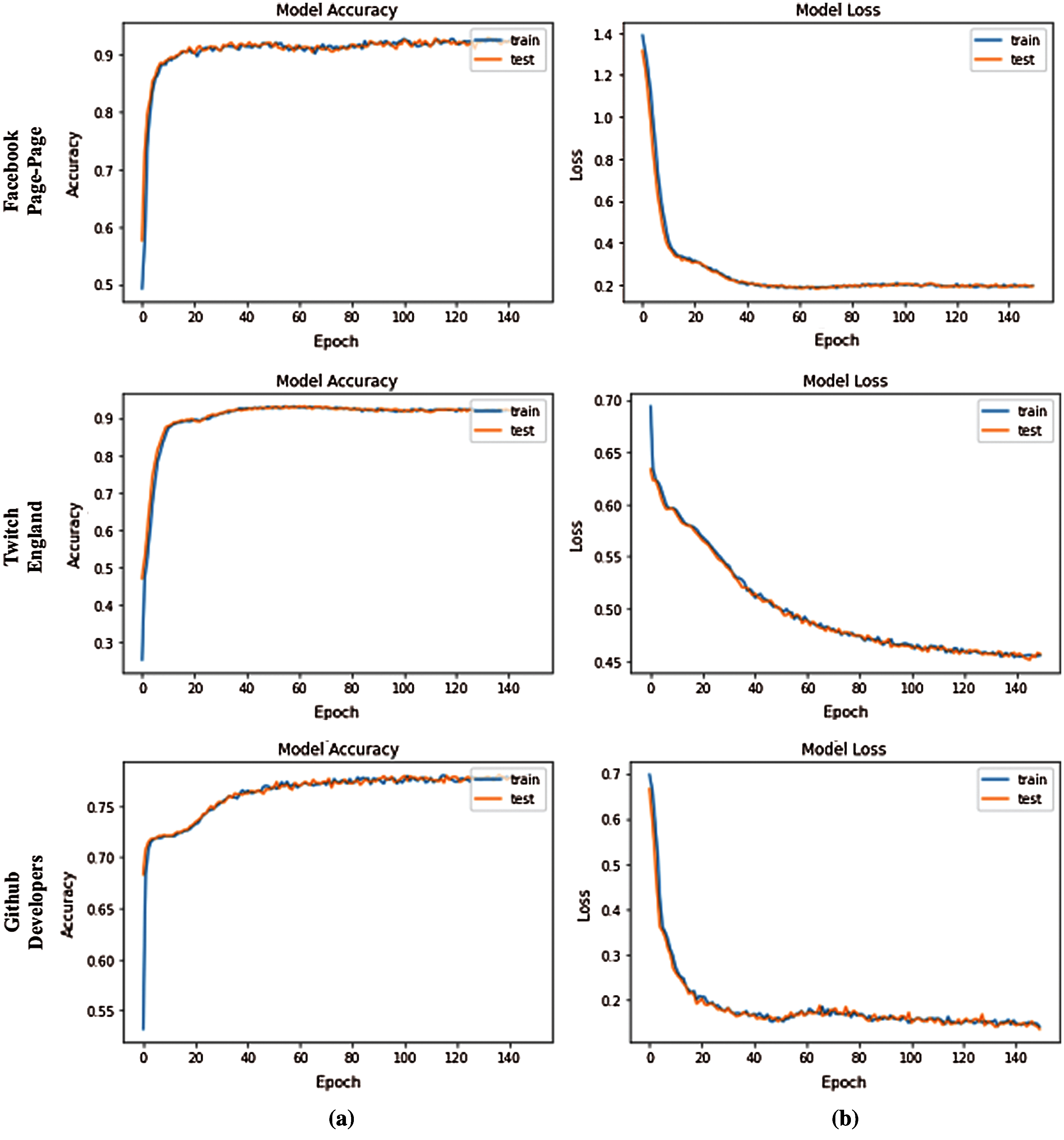
Figure 5: The individual accuracy plot and the loss decay plot of the networks. (a) Accuracy plots (b) Loss plots

Hence, it is recommended to build a very small model or a naive model for the unseen samples. The parametric weights are required to be dealt with carefully. It means that the specified attention layers should be added to extract temporal patterns, and the parameters are required to be tuned based on the real-life network.

7  Conclusion

It is possible to improve the performance by using various dimensionality reduction techniques, especially for the graph-transformer techniques. The attention heads and self-attention mechanisms are important with a balanced criterion. The structure of the complete graph can be captured with the assistant of the local patterns, which leads to the communities containing the global and local structural patterns. The objective function obliges to provide appropriate learning through stochastic optimization.

It is observed that, even on variant tasks, the proposed method can outperform the existing task invariant domain. Hence, the objective function can provide a domain invariant characterization with higher generalization. The proposed mechanism tends to have advanced performance on social network data for both detecting communities and node classification.

Acknowledgement: The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number RSP-2021/305, King Saud University, Riyadh, Saudi Arabia.

Funding Statement: The research is funded by the Researchers Supporting Project at King Saud University (Project# RSP-2021/305).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Palla, I. Derenyi, I. Farkas and T. Vicsek, “Uncovering the overlapping community structure of complex networks in nature and society,” Nature, vol. 435, no. 7043, pp. 814–818, 2005. [Google Scholar]

 2.  B. Perozzi, R. Al-Rfou and S. Skiena, “Deepwalk: Online learning of social representations,” in Proc. of the 20th ACM SIGKDD, New York, NY, USA, pp. 701–710, 2014. [Google Scholar]

 3.  T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado and J. Dean, “Distributed representations of words and phrases and their compositionality,” in Proc. of the 26th Int. Conf. on Neural Information Processing Systems, Red Hook, NY, USA, vol. 2, pp. 3111–3119, 2013. [Google Scholar]

 4.  P. Goyal and E. Ferrara, “Graph embedding techniques, applications, and performance: A survey,” Knowledge-Based Systems, vol. 151, pp. 78–94, 2018. [Google Scholar]

 5.  D. Cai, X. He, J. Han and T. S. Huang, “Graph regularized nonnegative matrix factorization for data representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 8, pp. 1548–1560, 2010. [Google Scholar]

 6.  S. Cao, W. Lu and Q. Xu, “Deep neural networks for learning graph representations,” in Proc. of the Thirtieth AAAI Conf. on Artificial Intelligence, Phoenix, Arizona, pp. 1145–1152, 2016. [Google Scholar]

 7.  P. Vincent, H. Larochelle, I. Lajoie, Y. Bengio and P. A. Manzagol, “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion,” Journal of Machine Learning Research, vol. 11, no. 110, pp. 3371–3408, 2010. [Google Scholar]

 8.  D. Wang, P. Cui and W. Zhu, “Structural deep network embedding,” in Proc. of the 22nd ACM SIGKDD, New York, NY, USA, pp. 1225–1234, 2016. [Google Scholar]

 9.  T. N. Kipf and M. Welling, “Variational graph auto-encoders,” in NIPS Workshop on Bayesian Deep Learning, Barcelona, Spain, 2016. [Google Scholar]

10. I. Sutskever, O. Vinyals and Q. V. Le, “Sequence to sequence learning with neural networks,” In Advances in Neural Information Processing Systems, Montreal, Quebec, Canada, pp. 3104–3112, 2014. [Google Scholar]

11. D. Bahdanau, K. Cho and Y. Bengio, “Neural machine translation by jointly learning to align and translate,” in Proc. of 3rd Int. Conf. on Learning Representations, San Diego, CA, USA, pp. 1–6, 2015. [Google Scholar]

12. M. T. Luong, H. Pham and C. D. Manning, “Effective approaches to attention-based neural machine translation,” in Proc. of the 2015 Conf. on Empirical Methods in Natural Language Processing, Lisbon, Portugal, pp. 1412–1421, 2015. [Google Scholar]

13. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones et al., “Attention is all you need,” In Advances in Neural Information Processing Systems, Long Beach, California, United States, pp. 5998–6008, 2017. [Google Scholar]

14. J. Devlin, M. W. Chang, K. Lee and K. Toutanova, “BERT: Pre-training of deep bidirectional transformers for language understanding,” In Proc. of the 2019 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, pp. 4171–4186, 2019. [Google Scholar]

15. T. Wang, X. Wan and H. Jin, “AMR-to-text generation with graph transformer,” Transactions of the Association for Computational Linguistics, vol. 8, pp. 19–33, 2020. [Google Scholar]

16. H. Zhang and J. Zhang, “Text graph transformer for document classification,” in Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing, Online, pp. 8322–8327, 2020. [Google Scholar]

17. A. Dosovitskiy, L. Beyer, A. Kolesnikov, D. Weissenborn, X. Zhai et al., “An image is worth 16x16 words: Transformers for image recognition at scale,” in Int. Conf. on Learning Representations, Vienna, Austria, pp. 1–21, 2021. [Google Scholar]

18. J. Yin, J. Shen, G. Chenye, D. Zhou and R. Yang, “Lidar-based online 3D video object detection with graph-based message passing and spatiotemporal transformer attention,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 11495–11504, 2020. [Google Scholar]

19. Z. Hu, Y. Dong, K. Wang and Y. Sun, “Heterogeneous graph transformer,” in Proc. of the Web Conf. 2020, Taiwan, pp. 2704–2710, 2020. [Google Scholar]

20. A. Auten, M. Tomei and R. Kumar, “Hardware acceleration of graph neural networks,” in Proc. of 2020 57th ACM/IEEE Design Automation Conf., San Francisco, CA, USA, pp. 1–6, 2020. [Google Scholar]

21. W. Jin, Y. Ma, X. Liu, X. Tang, S. Wang et al., “Graph structure learning for robust graph neural networks,” in Proc. of the 26th ACM SIGKDD, New York, NY, USA, pp. 66–74, 2020. [Google Scholar]

22. Y. Ma, Z. Guo, Z. Ren, J. Tang and D. Yin, “Streaming graph neural networks,” in Proc. of the 43rd Int. ACM SIGIR Conf. on Research and Development in Information Retrieval, Xi‘an, China, pp. 719–728, 2020. [Google Scholar]

23. E. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

24. M. M. Eid, E. S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in Proc. of 2021 National Computing Colleges Conf., Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

25. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. H. Alrahmawy, M. EI-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]

26. J. Xu, X. Sun, Z. Zhang, G. Zhao and J. Lin, “Understanding and improving layer normalization,” in Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, pp. 4383–4393, 2019. [Google Scholar]

27. J. L. Ba, J. R. Kiros and G. E. Hinton, “Layer normalization,” in Neural Information Processing Systems–Deep Learning Symposium, Barcelona, Spain, pp. 1–14, 2016. [Google Scholar]

28. C. Louizos, M. Welling and D. P. Kingma, “Learning sparse neural networks through L0 regularization,” in Sixth International Conference on Learning Representations, Vancouver Canada, pp. 1–11, 2018. [Google Scholar]

29. J. Leskovec and A. Krevl, “SNAP datasets: Stanford large network dataset collection,” Ann Arbor, MI, USA, 2014. [Online]. Available: http://snap.stanford.edu/data. [Google Scholar]

30. B. Rozemberczki, C. Allen and R. Sarkar, “Multi-scale attributed node embedding,” Journal of Complex Networks, vol. 9, no. 2, 2021. cnab014, https://doi.org/10.1093/comnet/cnab014. [Google Scholar]

31. N. X. Vinh, J. Epps and J. Bailey, “Information theoretic measures for clustering's comparison: Is a correction for chance necessary?,” in Proc. of the 26th Annual Int. Conf. on Machine Learning-ICML’09, New York, NY, USA, pp. 1073–1080, 2009. [Google Scholar]

32. B. Rozemberczki, O. Kiss and R. Sarkar, “Karate club: An API oriented open-source python framework for unsupervised learning on graphs,” in Proc. of the 29th ACM Int. Conf. on Information and Knowledge Management, Ireland, pp. 3125–3132, 2020. [Google Scholar]

33. J. Yang and J. Leskovec, “Overlapping community detection at scale: A nonnegative matrix factorization approach,” in Proc. of the Sixth ACM Int. Conf. on Web Search and Data Mining, ACM, Rome, Italy, pp. 587–596, 2013. [Google Scholar]

34. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy et al., “Scipy 1.0-fundamental algorithms for scientific computing in python,” Nat Methods, vol. 17, pp. 261–272, 2020. https://doi.org/10.1038/s41592-019-0686-2. [Google Scholar]

35. B. Rozemberczki and R. Sarkar, “Characteristic functions on graphs: Birds of a feather, from statistical descriptors to parametric models,” in Proc. of the 29th ACM Int. on Conf. on Information and Knowledge Management-CIKM’20, Ireland, pp. 1325–1334, 2020. [Google Scholar]

36. D. Kuang, C. Ding and H. Park, “Symmetric nonnegative matrix factorization for graph clustering,” in Proc. of the 2012 SIAM Int. Conf. on Data Mining, California, USA, pp. 106–117, 2012. [Google Scholar]

37. A. Epasto, S. Lattanzi and R. PaesLeme, “Ego-splitting framework: From non-overlapping to overlapping clusters,” in Proc. of the 23rd ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Halifax, NS, Canada, pp. 145–154, 2017. [Google Scholar]

38. P. Z. Li, L. Huang, C. D. Wang and J. H. Lai, “Edmot: An edge enhancement approach for motif-aware community detection,” in Proc. of the 25th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, Anchorage, AK, USA, pp. 479–487, 2019. [Google Scholar]

39. U. N. Raghavan, R. Albert and S. Kumara, “Near linear time algorithm to detect community structures in large-scale networks,” Physical Review E, vol. 76, vol. 76, no. 3, pp. 1–11, 2007. [Google Scholar]

40. A. Prat-Perez, D. Dominguez-Sal and J. L. Larriba-Pey, “High quality, scalable and parallel community detection for large real graphs,” in Proc. of the 23rd Int. Conf. on World Wide Web, Seoul, Korea, pp. 225–236, 2014. [Google Scholar]

41. B. Rozemberczki, R. Davies, R. Sarkar and C. Sutton, “GEMSEC: Graph embedding with self clustering,” in Proc. of the 2019 IEEE/ACM Int. Conf. on Advances in Social Networks Analysis and Mining, Vancouver, Canada, pp. 65–72, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.