Computers, Materials & Continua DOI:10.32604/cmc.2022.021724
Article

Beamforming Performance Analysis of Millimeter-Wave 5G Wireless Networks

Omar A. Saraereh* and Ashraf Ali

Deparment of Electrical Engineering, Engineering Faculty, The Hashemite University, Zarqa, 13133, Jordan
*Corresponding Author: Omar A. Saraereh. Email: eloas2@hu.edu.jo
Received: 12 July 2021; Accepted: 13 August 2021

Abstract: With the rapid growth in the number of mobile devices and user connectivity, the demand for higher system capacity and improved quality-of-service is required. As the demand for high-speed wireless communication grows, numerous modulation techniques in the frequency, temporal, and spatial domains, such as orthogonal frequency division multiplexing (OFDM), time division multiple access (TDMA), space division multiple access (SDMA), and multiple-input multiple-output (MIMO), are being developed. Along with those approaches, electromagnetic waves’ orbital angular momentum (OAM) is attracting attention because it has the potential to boost the wireless communication capacity. Antenna electromagnetic radiation can be described by a sum of Eigen functions with unique eigenvalues, as is well known. In order to address such issues, the millimeter-wave (mmWave) communication is proposed which is considered as one of the potential technology for 5G wireless networks. The intrinsic feature of all electromagnetic waves is OAM. The OAM beams’ unique qualities have led to a slew of new uses. Broadband OAM generators, on the other hand, have gotten very little attention, especially in the mmWave frequency band. The use of OAM in conjunction with mmWave can reduce the beam power loss, enhance the received signal quality, and hence increase the system capacity. The transmitter and receiver antennas must be coaxial and parallel to achieve precise mode detection. The proposed mmWave integrated with OAM system model is discussed in this study. The channel model is created using the channel transition characteristics. The simulation results demonstrate that the proposed system model is a good way to boost the system capacity.

Keywords: Antennas; beamforming; radiation pattern; mmwave; optimization

1  Introduction

With the explosive growth in the number of mobile devices, the demand for spectrum resources in wireless communications is rapidly increasing. According to Cisco's annual Internet forecast in 2017, the global data traffic will exceed 330 trillion terabytes in 2020, of which mobile devices will account for 73% of the total traffic [1–4]. How to greatly increase the capacity of the communication system to cope with the demand for traffic growth is imminent. However, the traditional use of spectrum resources below 3 GHz has become saturated, and the spectrum utilization rate has also become saturated [5]. Approaching Shannon's limit, it is a drop in the bucket to increase the system capacity only on the existing authorized frequency bands. Therefore, it is imperative to expand the new spectrum resources. The use of millimeter- wave (mmWave) frequency band communication can break through the bottleneck of the lack of available spectrum resources and meet the needs of future mobile data services [6–8]. At the same time, mmWave wireless communication technology has the advantages of extremely wide bandwidth and easy miniaturization. In addition, the 60 GHz mmWave also has the advantage of not requiring authorization [9–14]. Therefore, the millimeter-wave wireless communication technology is expected to become one of the key technologies of 5G communication, especially suitable for high-speed, large-capacity communication [15,16].

Although the mmWave frequency band provides abundant bandwidth resources, compared with the traditional frequency band, the ordinary plane electromagnetic wave has a very high path loss in this frequency band, which seriously affects the system capacity [17–21]. In recent years, the information carrying ability of electromagnetic waves with orbital angular momentum (OAM) (also known as vortex electromagnetic waves) exhibited in the mmWave frequency band due to the vortex shape of the wavefront has attracted more and more attention [22–25]. The phase function of the OAM is ejlϕ, where l is the number of topological charges, which is used to represent the OAM mode. Theoretically, the number of modes is infinite, which means that infinite-dimensional Hilbert space can be formed (high-dimensionality). At the same time, the OAM beams with different modes are orthogonal to each other (orthogonality) [26–34].

Therefore, applying the OAM modal characteristics to wireless communication can theoretically achieve a higher transmission rate. In [35], the authors achieved a total transmission rate of 32 Gbit/s and a spectrum utilization rate of 16 bits/s/Hz in the 60 GHz mmWave frequency band under line-of-sight (LoS) conditions. The experimental results show that, performing OAM multiplexing communication in this frequency band can reduce the power loss during beam propagation, increase the transmission distance, and reduce the size of the transceiver. Reference [36] proposed a mmWave communication system based on the OAM spatial modulation, which has greatly improved the energy efficiency as compared with OAM-MIMO system and has better robustness to mmWave path attenuation.

The OAM mmWaves are distributed in a spiral shape, which makes it impossible to receive signal energy in the main direction like ordinary plane waves. If it is not received in a specific direction, a considerable part of the energy cannot be captured by the receiving end [37]. Limited by the energy radiation characteristics of the OAM wave, the authors in [38] pointed out for the first time that when the uniform circular array (UCA) at both ends of the transmitter and receiver is aligned with the concentric coaxial height, the OAM mmWave system can provide the same performance as the multiple input multiple output (MIMO) system. However, when there is a slight tilt angle between the transmitting and receiving antenna arrays, it will seriously affect the accuracy of the receiving end modal detection, and the performance of the OAM mmWave system will be seriously reduced. In [39], the authors used the channel model of MIMO to study the channel model and capacity of the OAM mmWave communication system when the angle is shifted, thus verifying the above results. However, in this model, the UCA's multi-antenna system is used to generate the OAM mmWaves. The analysis process is based on the traditional MIMO transmission model, which takes into account the path attenuation between the transmitting and receiving antenna elements, but does not involve multiple OAM mmWave signals. The establishment and analysis of the transmission model is also not applicable to other antenna systems that generate the OAM mmWaves. In addition, this method only models the channel when the transceiver antennas are coaxial but there is an angular offset. This model is not suitable for the scenario where the transceiver antennas are parallel and non-coaxial. Therefore, how to establish a more universal OAM mmWave system channel model has important research significance.

When the OAM is used for wireless communication transmission, once the channel environment is disturbed, the energy of the OAM mode will be transferred with a certain probability, and the crosstalk between the modes will occur. Reference [40] used light waves to conduct the experiments in a wireless environment, and obtained the energy distribution of the transition due to turbulence. Based on this modal transition characteristic, this paper models the signal at the receiving end as a superposition of OAM mmWave signals of different paths, and derives the distribution of modal migration under the lateral axis offset of the transceiver through theoretical analysis, and models the system channel as multiple discrete memoryless channel model.

The remaining of this paper is arranged as follows. Section 2 establishes the transmission model of the OAM mmWave communication system. Section 3 models the channel based on the modal migration characteristics of the OAM mmWave, and derives the lateral axis offset of the transmitter and receiver. Section 4 analyzes the simulation results. Finally, the conclusion and summarizes the full text.

2  System Model

The OAM mmWave system studied in this paper is shown in Fig. 1. It contains multiple transceiver antenna pairs for generating and receiving different OAM mmWave signals. Each link transmitting end transmits a single OAM mode, then there are multiple mutually orthogonal OAM modes in the system, which can increase the system capacity.

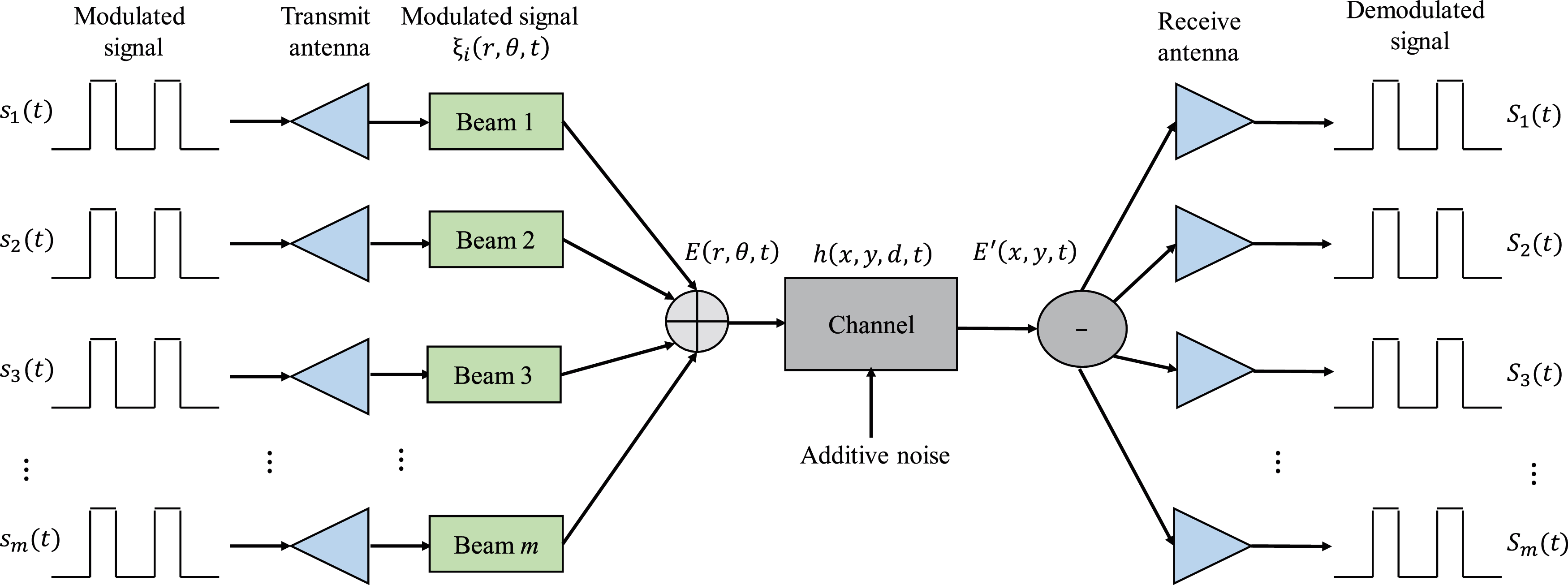
Figure 1: Proposed system model

Specifically, when a link is allocated to use mode li, the plane wave that originally carries information is modulated by the spatial phase of the corresponding parameter to become a vortex mmWave with |li| topological charges, where the positive and negative of li represent the spin direction of the beam, we assume that li is a positive integer (clockwise), then the mmWave carrier signal containing the OAM mode li generated by the transmitter can be expressed as

Φli(r,θ,t)=Uli(r,θ)ej(ωst+φs(t))(1)

Among them, ωs and φs(t) are the frequency and instantaneous phase of the OAM mmWave, respectively. Uli(r,θ) represents the OAM mode li generated by the antenna array, and its expression is

Uli(r,θ)=Rli(r)ejliθ(2)

where r and θ respectively represent the radius and azimuth angle of the OAM beam in polar coordinates, and ejliθ is the spatial phase of the OAM mmWave, which causes the vortex phase. Rli(r) represents the amplitude of the OAM mmWave, where the amplitude of the OAM mmWave in the Laguerre-Gaussian mode is

Rli(r)=c(r2w0)liLp|li|(2r2w02)exp⁡(−r2w02)(3)

where w0 is the zero-order Gaussian waist radius. L(⋅) is the associated Laguerre polynomial. li represents the transmitted OAM mode, and p represents the radial mode. c=2p!/(π(p+|l|)!w02) represents the normalization constant, when considering p=0

Rli(r)=c(r2w0)liexp⁡(−r2w02)(4)

The OAM mmWave modulated signal carrying data information at the transmitting end is

ξi(r,θ,t)=Psi(t)Uli(r,θ)ej(ωst+φs(t))(5)

Among them, P is the transmission power of the system, and si(t) is the modulated signal. Therefore, the transmitted signal E(r,θ,t) before entering the transmission channel in Fig. 1 can be regarded as a linear superposition of m-channel OAM mmWave signals

E(r,θ,t)=∑i=1m⁡ξi(r,θ,t)(6)

In the OAM mmWave communication system, the signal at the receiving end may be affected by factors such as atmospheric turbulence, antenna gain, path attenuation, and additive noise. Its mathematical expression is the convolution of the transmitted signal and the transfer function.

E′(r,θ,t)=E(r,θ,t)⊗h(r,θ,d,t)+n(t)(7)

where d represents the distance between the receiving and sending ends, that is, the path length. ⊗ represents convolution, n(t) represents additive white Gaussian noise in the channel. At the receiving end, the beams of each mode can be separated only through the corresponding inverse phase control and spatial filtering, and the mmWave signals containing different OAM modes are received at the receiving end through different receiving antennas. Using the natural quadrature characteristics of the OAM beam to demodulate and recover the signal information Si(t) of each channel, the mathematical expression of the demodulation process is as follows

Si′(t)=⟨Φli′(r,θ,t)∣E′(r,θ,t)⟩=∑i,i′=1m⁡si(t)⟨Φli′(r,θ,t)∣Φli(r,θ,t)⊗h(r,θ,d,t)⟩+ni(t).Φli′(r,θ,t)(8)

where ⟨⋅|⋅⟩ represents the inner product, and ni(t) represents the additive white Gaussian noise of the i-th subchannel.

3  Channel Modeling and Capacity Analysis

The OAM theoretically has an infinite number of orthogonal states, and we use this feature to establish multiple sub-channels between the transmitter and receiver for transmission. In the actual transmission process, additional consideration must be given to the modal transition caused by atmospheric turbulence and the offset of transmission and reception. Mode transfer means that during the transmission of OAM modes, the energy of a certain mode may be partly obtained by the transfer of other modes, and part of its own energy may also leak to other modes. At this time, although the signals received by the receiving end are still orthogonal to each other, they have produced varying degrees of distortion. That is to say, the original single-channel sub-channel transmission carries a single-mode OAM mmWave signal. Due to the influence of modal energy migration, the mmWave signal detected by the receiving end does not only carry the single-mode OAM, but with a certain The probability of taking a different modal value, which mistakenly restores it to a mmWave signal superimposed by multiple modalities. Therefore, in mathematical expression, the received distorted OAM mmWave signal can be regarded as the superposition of multiple mutually orthogonal OAM modes

E′(r,θ,t)=∑i′=1m⁡αli′(t)Uli′(r,θ)+n(t)(9)

Among them, αli′(t) is the distortion coefficient related to factors such as atmospheric turbulence, transmission and reception offset, antenna gain and path attenuation. This article focuses on the derivation of the distortion coefficient in the case of the transmission and reception offset.

The modal migration of OAM in the case of lateral offset is shown in Fig. 2. In the case of no distortion, the signal transmitted by each sub-channel only contains a single OAM mode li, that is, the signal receiving and sending ends of the channel use the same mode for transmission and detection respectively, as shown by the solid arrow in Fig. 2. Once the transverse axis shift occurs at both ends of the OAM mmWave system, the energy between the modes will migrate, as shown by the dashed arrow in Fig. 2. Where γii′ represents the sub-signal between the receiving and sending modes in the actual transmission.

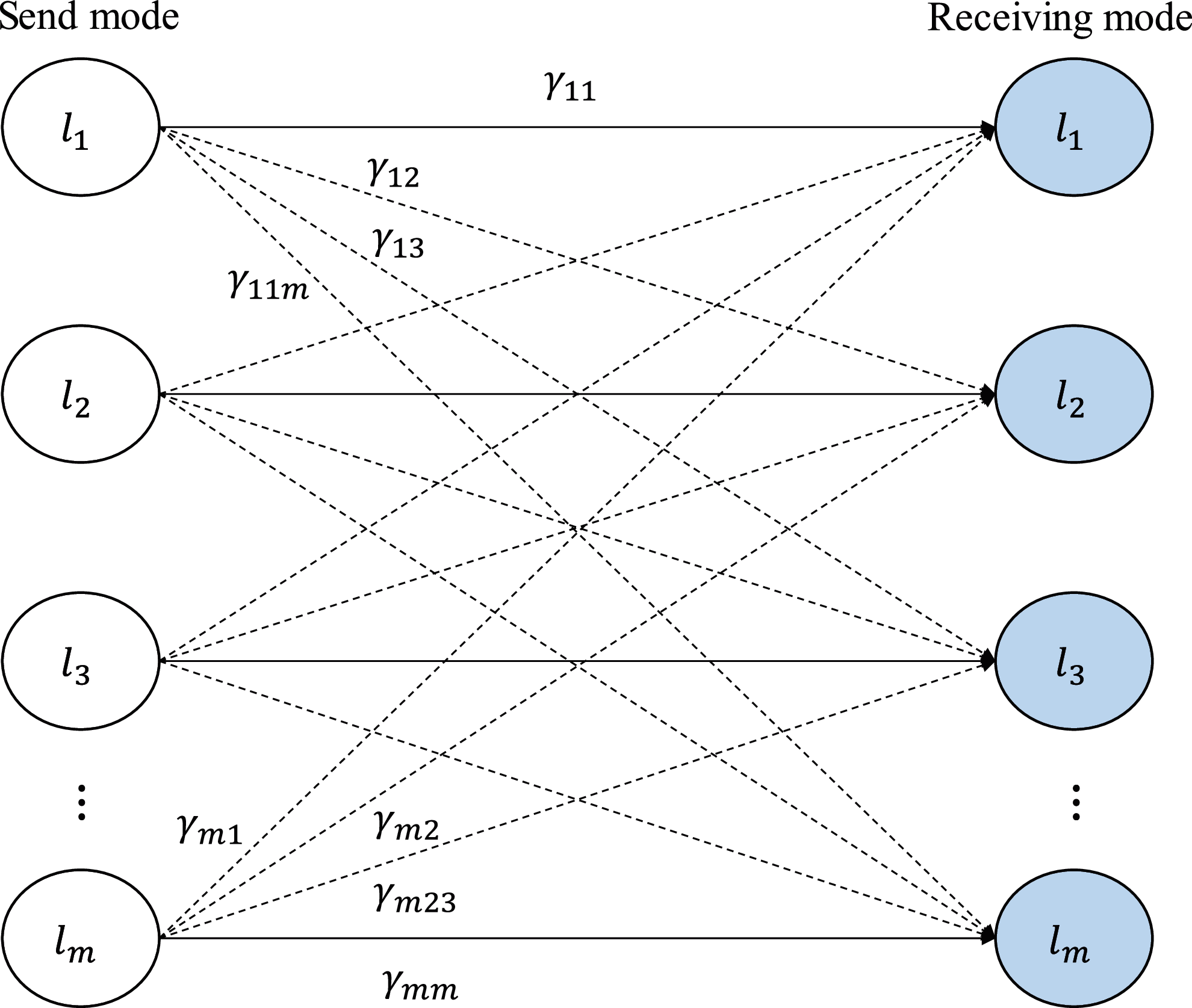
Figure 2: Illustration of transitions in energy

Channel characteristic coefficient, that is, the channel characteristic coefficient when the mode of the transmitting end is li and the receiving end is changed to the mode li. At this time, each signal may become no longer pure, which will cause the accuracy of the receiving end to be greatly limited. In theory, the distribution of potential interference signals caused by modal transitions will restrict the upper limit of the capacity of the OAM mmWave communication system. This makes the channel model of this system different from the traditional wireless fading model. It is necessary to consider the path attenuation between the transmitting and receiving ends and the distribution characteristics of the transition mode during offset.

Assuming that the entire system is in an atmospheric turbulence environment, the transmitter antenna generates mmWave signals with OAM mode, and the Laguerre Gaussian beam can be used to characterize the space and phase characteristics of the pure OAM mode mmWave, as shown in Eq. (3). Fig. 3 shows the geometric model of the transverse axis offset of the antennas at the receiving and transmitting ends in the Cartesian coordinate system. The coordinate origin O represents the antenna axis of the transmitting end, and the Z-axis represents the direction in which the beam axis points when the axis of the receiving end is aligned. The actual position of the axis of the receiving end is laterally shifted in the O′Z′ direction. Therefore, O′O′ in Fig. 3 represents the lateral axis offset of the transmitting and receiving ends. x0 and y0 are the relative displacements of the transmitting and receiving antennas in the x-axis and y-axis directions, causing crosstalk between OAM modes. In actual transmission, the displacement is a variable that changes with time t, namely x0(t) and y0(t).

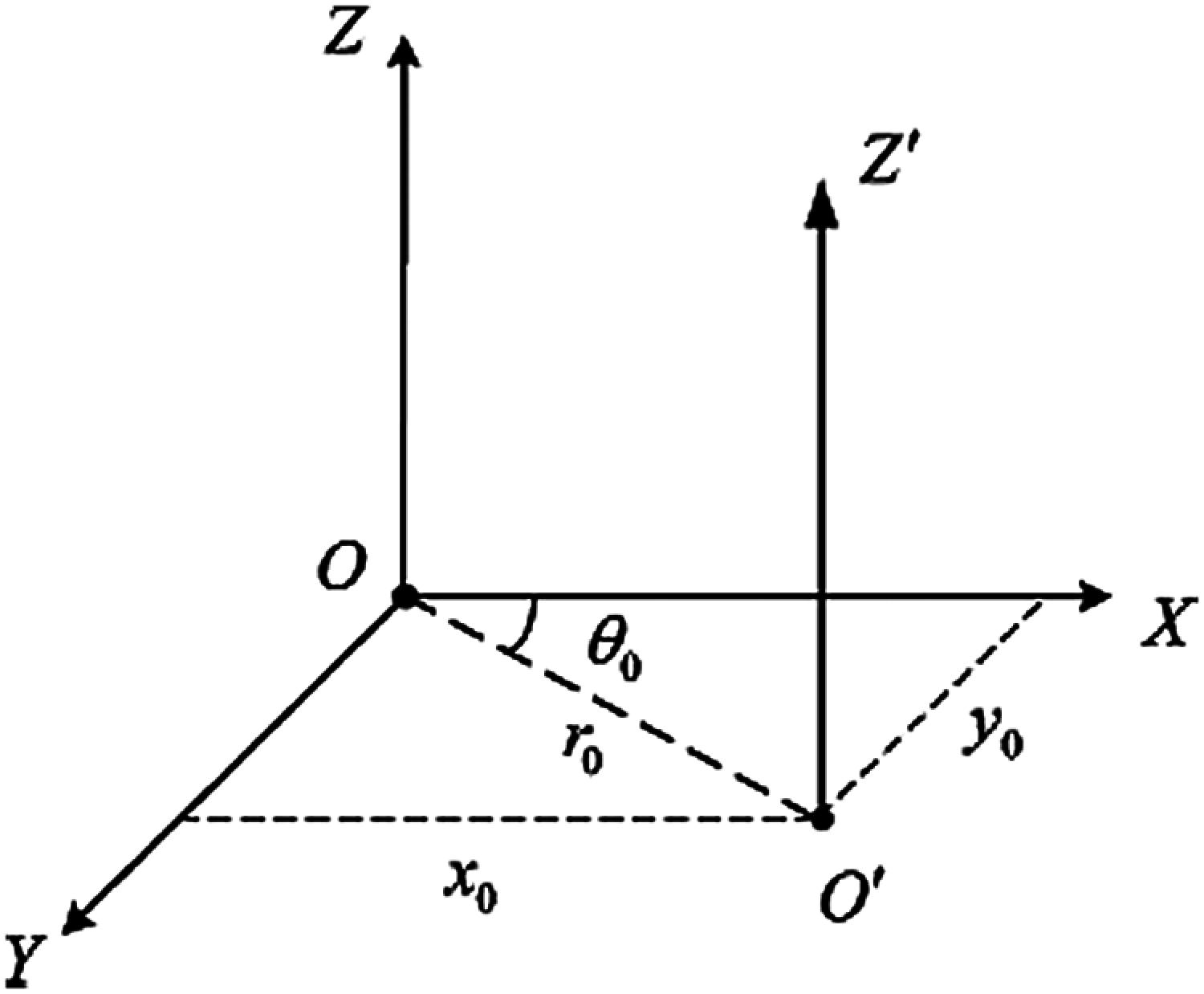
Figure 3: Tx-Rx antennas model in the coordinates

The expression of the transfer function h(x,y,d,t) in this case is as follows

h(x,y,d,t)=Bλ4πde−jkdδ(x−x0(t),y−y0(t))(10)

where B is the antenna gain coefficient, λ is the wavelength, k2π/λ is the wave number, and δ(⋅) is the Dirac function.

In order to show the situation of the transceiver offset more intuitively, a set of polar coordinate parameters r0 and θ0 are given to indicate the degree of offset between the transceiver devices, where r0 represents the distance of the lateral axis offset, that is, the length of OO′ indicates the offset angle θ0 between the antenna axis of the transmitting and receiving end, and satisfies x0=r0cos⁡θ0, y0=r0sin⁡θ0. Therefore, the transfer function in Eq. (10) can be converted to the form in polar coordinates and substituted into Eq. (7), and the OAM mmWave signal at the receiving end can be obtained as

E′(r,θ,t)=E(r,θ,t)⊗Bλ4πde−jkdδ(rcos⁡θ−r0(t)cos⁡θ0(t),rsin⁡θ−r0(t)sin⁡θ0(t))+n(t)(11)

Combining the above equation with Eq. (9), we can get the power correlation coefficient (distortion coefficient) between different modes at the receiving end as

αli′(t)=⟨Uli′(r,θ)∣E′(r,θ,t)⟩=∫02π⁡∫0∞⁡Uli′∗(r,θ)E′(r,θ,t)rdrdθ(12)

This coefficient reflects the distribution characteristics of OAM modal migration. Further substituting Eqs. (2) and (7) into the integrand function expression in the above formula, the expression of αli′(t) can be obtained

{αli′(t)=Bλ4πde−jkdP∑i,i′=1m⁡si(t)∬Uli′(r1,θ1)Uli′∗(r2,θ2)dxdyr1=(x−x0(t))2+(y−y0(t))2θ1=arctan⁡(y−y0(t)x−x0(t))r2=x2+y2,θ2=arctan⁡(yx)(13)

The channel characteristics are independent of the frequency and instantaneous phase of the modulation signal si(t) and OAM mmWave, that is, αli′(t)=∑i,i′=1m⁡γii′(t)si(t)ej(ωst+φs(t)), the general expression of the channel characteristic coefficient γii′(t) can be obtained

γii′(t)=Bλ4πde−jkdP∬​Uli′(r1,θ1)Uli′*(r2,θ2)dxdy (14)

In the same way, substituting Eq. (2) into the integrand in the above formula, the specific mathematical expression can be obtained

∑n=0li⁡Clin(−r0)li−n(j)li′−n+1Mli′+n+12,li′−n2(−r022w02)(2w02)li′+n+12Γ(li′−n+1)(15)

where Jv(⋅) is a Bessel function of order v, Γ(⋅) is a gamma function, Mλ,μ(⋅) is a Whittaker function, and Clin represents a combination of n elements from 0 to li different elements. Then, the modulated signal carried on the mmWave signal with the OAM mode of li′ received by the receiving end is Si′(t)=∑i=1m⁡γii′(t)si(t)+ni(t). Among them, the channel characteristic coefficient γii′ constitutes the channel transmission matrix H, which is expressed as follows

H=[γ11(t)γ12(t)⋮γ1m(t)γ21(t)γ22(t)⋮γ2m(t)⋯⋯⋮⋯γm1(t)γm2(t)⋮γmm(t)](16)

In order to derive the capacity of the OAM mmWave communication system, firstly, the channel matrix needs to be subjected to singular value decomposition (SVD). The specific expression is as follows

H=ULVH(17)

Both U and V are unitary matrices of order m×m, L is a diagonal matrix and L=diag\; (λ1,\; λ2,…,λr), the order of the elements of the diagonal matrix is λ1≥λ2≥…≥λr permutation, where λi(i=1,2,…,r) is the singular value of the channel matrix H,r=rank(H).

In the previous part, we established a system model with m OAM modes at both the receiving and transmitting ends, so the final channel transmission matrix order is m×m. Assuming that the transmit power of each link is equal, the total channel capacity of the OAM mmWave system is the sum of the capacities of the sub-channels, and its expression is as follows

C=∑i=1m⁡log2(1+λiPiσn2)(18)

4  Simulation Results

The numerical results of the channel capacity of the OAM system under the given parameters are given below. In the simulation, it is assumed that the transmitting end power P= 1W, and the power is allocated to each sub-channel in an evenly distributed manner, that is, the power of each channel is equal. Other default simulation parameter settings are as follows: Carrier frequency f= 60 GHz, antenna gain coefficient B=105, zero-order Gaussian waist radius w0= 0.001 m, the distance between the transmitting antenna and the receiving antenna is 30 m, and the bandwidth is 20 MHz.

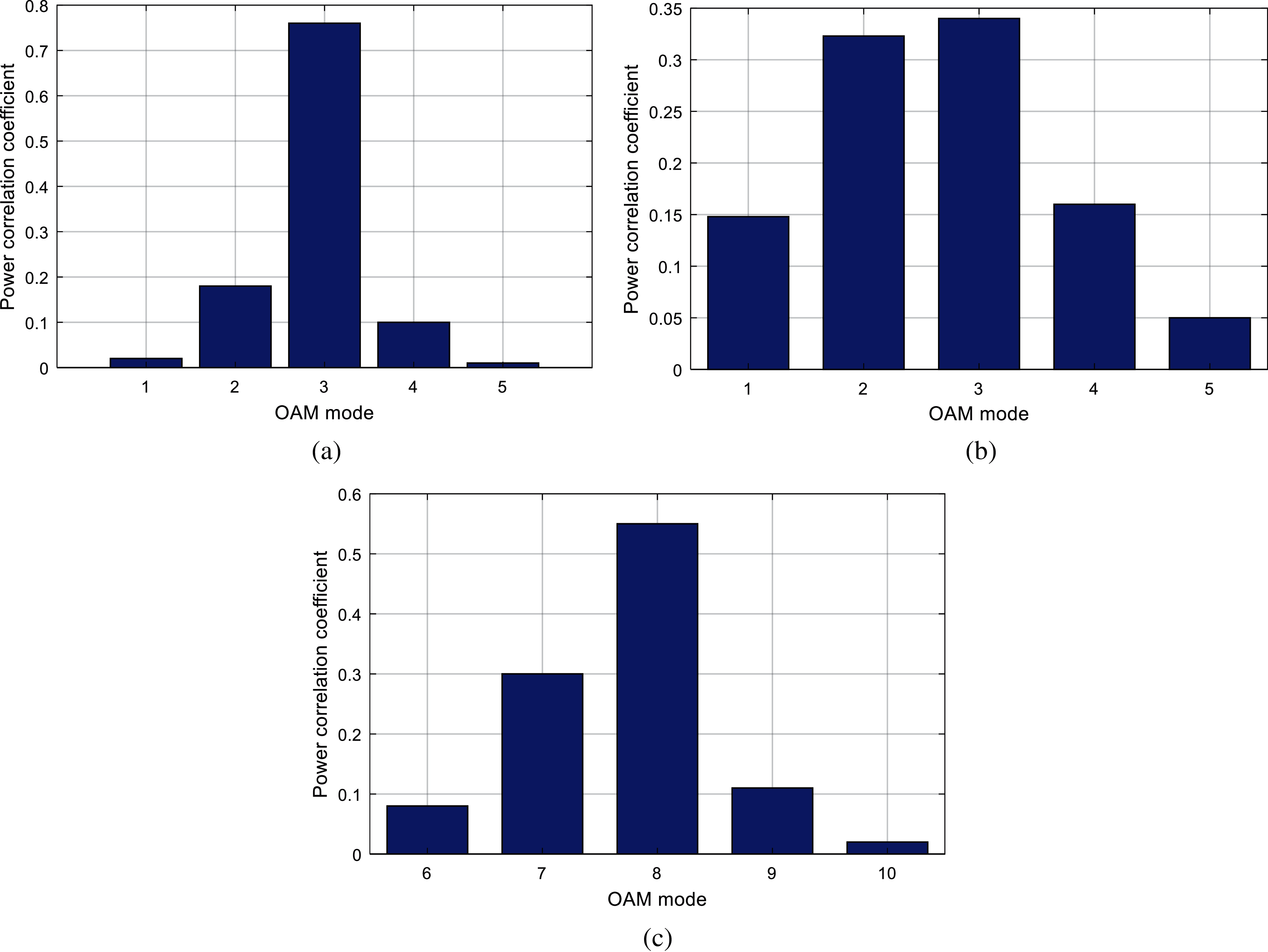
Figure 4: Comparison of power distribution (a) r=1mm,l=3 (b) r=5mm,l=3 (c) r=1mm,l=8

As mentioned above, the physical meaning of the channel characteristic coefficient γii′ in Eq. (15) is the amount of power transfer from mode li (transmitting end) to mode li′ (receiving end). Therefore, combining the matrix distribution in Eq. (16), take all the elements of a column and take the modulus respectively, that is, the power of the initial mode corresponding to the column to be transferred to the other modes is obtained by the residual power value carried by itself, and after the normalization of the calculation results. Fig. 4 shows the OAM modal power distribution. The simulation results show that when different initial transmission modes are interfered by lateral axis offsets at different distances, different energy transfers will occur between OAM modes. Figs. 4a to 4c shows that, when the same initial transmission mode is selected, due to the existence of the lateral axis offset, the OAM beam with l≠0 will have a beam emission effect during the transmission process. The mmWave signal beam energy of the carried mode will leak into the neighboring and the energy of the mode is higher than that of the non-adjacent modes, which means that the probability of transition and crosstalk between adjacent modes is the highest. The greater the offset distance, the more severe the energy leakage between the modes, and the error of the modal detection at the receiving end will also increase sharply. In addition, it can be found that, when the initial transmission mode is large, the energy leakage to other modes is greater, and the probability of detecting the original mode at the receiving end will decrease, indicating that the ability to resist the lateral axis deviation is poor. This is because the divergence angle of the OAM beam increases as the value of l becomes larger, that is, the divergence becomes stronger and stronger. Therefore, between different modes of the mode group with larger l, the mode will occur due to the lateral offset. The transfer probability of the state energy will inevitably be higher, which will cause the energy leakage of its modal to be more serious.

Fig. 5 shows the curve of the capacity of the traditional MIMO mmWave system and the OAM mmWave system as a function of the signal-to-noise ratio (SNR) under the ideal channel. We can see that the capacity of the two systems increases with the increase of the signal-to-noise ratio. At the same time, under the same SNR, the capacity of a 4-mode OAM mmWave communication system is greater than that of a 4 × 4 MIMO (the number of transmitting antennas and receiving antennas are 4). The capacity of a 2-mode OAM mmWave communication system is greater than that of a 2 × 2 MIMO mmWave communication system. From this result, it can be seen that the performance of OM mmWave communication in terms of system transmission rate is better than the traditional MIMO mmWave system.

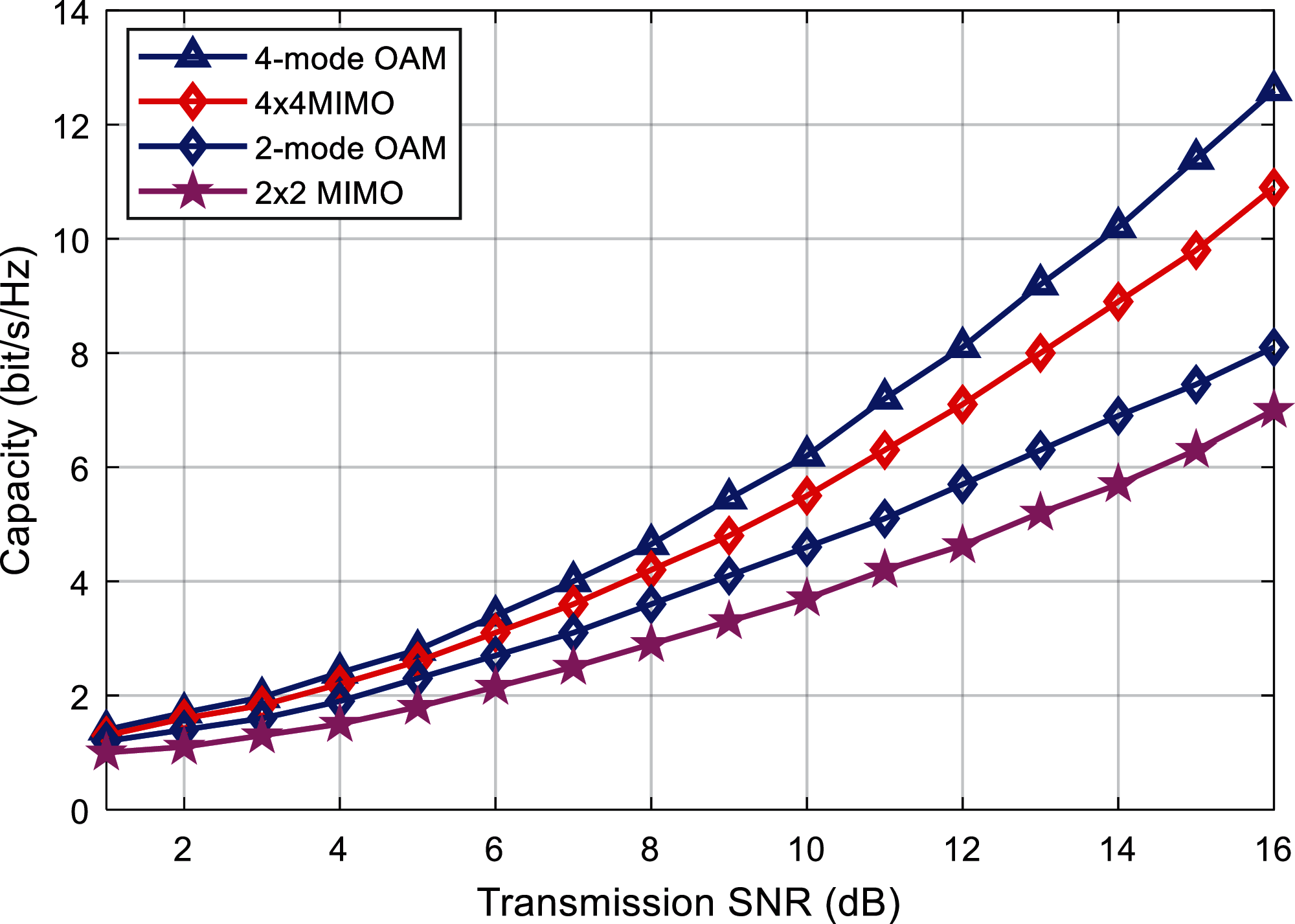
Figure 5: Capacity comparison of the proposed and existing algorithms

Fig. 6 shows the relationship between the system capacity and the transmission SNR for a given number of different modes. The selected 8-mode group is {l = 1, 2,…, 8}, and the 4-mode group is {l = 1, 2,…, 4}. It can be seen that for different modal numbers, the system capacity increases with the increase of the SNR, and the greater the number of modalities, the larger the system capacity. Set the offset distance to 1 mm. At this time, due to the transition and crosstalk between modes, the system capacity is significantly reduced. For example, when there is an offset, the system capacity of the 8-mode system is about 8.2 bits/s/Hz with a 15 dB SNR. This value is even smaller than the system capacity (about 12.6 bit/s/Hz) of the 4-mode system with the same SNR and no offset. Therefore, the lateral axis offset of the antennas at the receiving and transmitting ends will significantly reduce the performance of the OAM mmWave system. The alignment of the OAM mmWave transmission and reception is a problem that cannot be ignored.

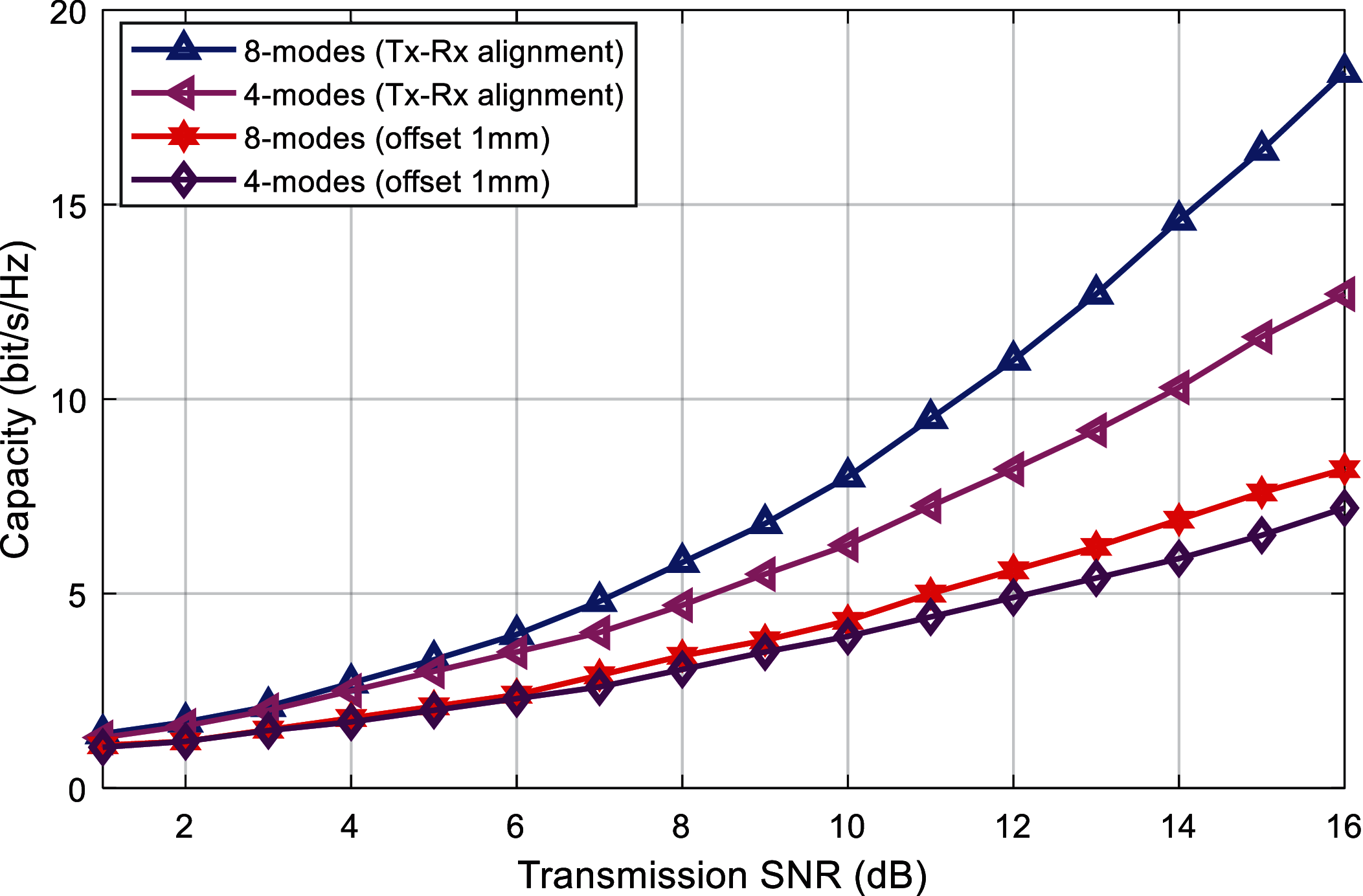
Figure 6: Capacity comparison in the on and off-axis alignment

Fig. 7 specifically depicts the specific relationship between the system capacity and the lateral offset distance under different number of modes. The given transmission SNR is 30 dB, and the selected 8-mode groups are {l = 1, 2 ,…, 8}, 4 modal group is {l = 1, 2, 3, 4}, and the 2 modal group is {l = 1, 2}. It can be found that with the increase of the lateral offset distance of the transmitting and receiving end, the probability of energy leakage between modes increases due to the modal migration, so the system capacity shows a significant decline trend. Taking the 8-mode as an example, when the lateral offset is 1 mm, the system capacity is about 24 bit/s/Hz, but when the lateral offset is increased to 5 mm, the capacity drops sharply to about 10 bit/s/Hz. It can be seen that the OAM is very sensitive to the lateral offset, and the existence of the lateral offset severely limits the performance of the OAM mmWave system. At the same time, when the offset reaches a certain distance, the system capacity will no longer decrease. This means that when the offset between the receiving and sending ends exceeds a certain limit, the interference distribution between modes will tend to a steady state, and the system capacity will no longer decrease. It is worth mentioning that when the offset distance is greater than 3 mm, the system capacity of the 8-mode and the 4-mode are both smaller than the system capacity of the 2-mode. This shows that the larger the number of modes, the more obvious the system performance will decrease as the offset distance increases. As there are more modes, the probability of modal migration is greater, and crosstalk between modes is more likely to occur.

Figs. 8 and 9 shows the relationship curve between the combination selection method of different modes and the system capacity. From the perspective of the system capacity, the power distribution of the OAM mode and the initial transmission mode and offset given in Fig. 4 are verified. Take the 4-mode group as an example, the given offset distance is 1 mm. In Fig. 8, three different OAM modal combination schemes are specifically considered with different mode intervals Δl respectively. The modal groups are {l = 1, 2, 3, 4}, {l = 1, 3, 5, 7}, {l = 1, 4, 7, 10}, and the corresponding modal interval is Δl = 1, 2, 3. From the simulation results, it can be found that under the same offset distance, the greater the modal interval, the lower the probability of energy leakage between modals, so the possibility of crosstalk between modals is reduced, and the system capacity is also greater.

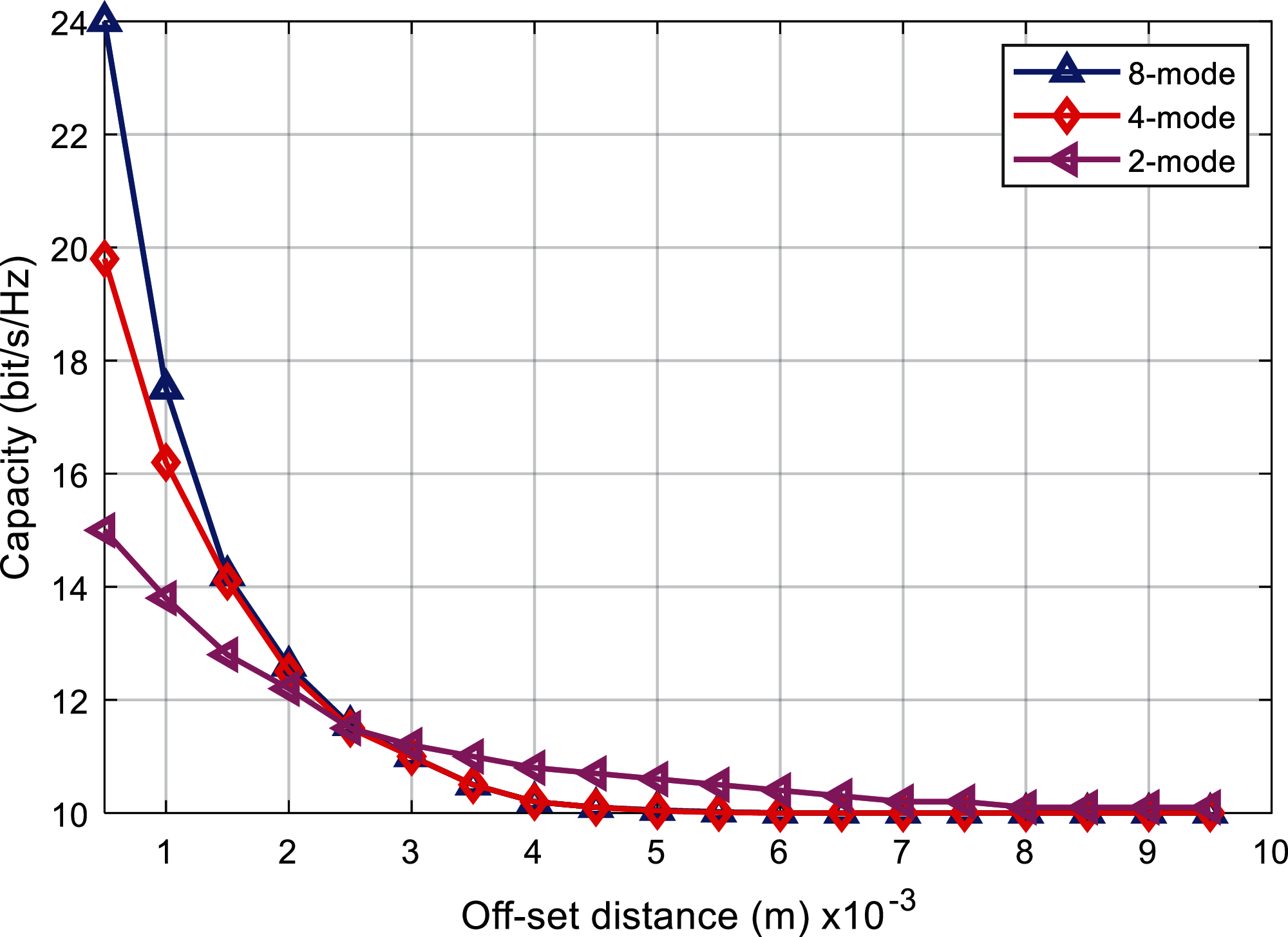
Figure 7: Comparison of capacity and offset distance for fixed SNR

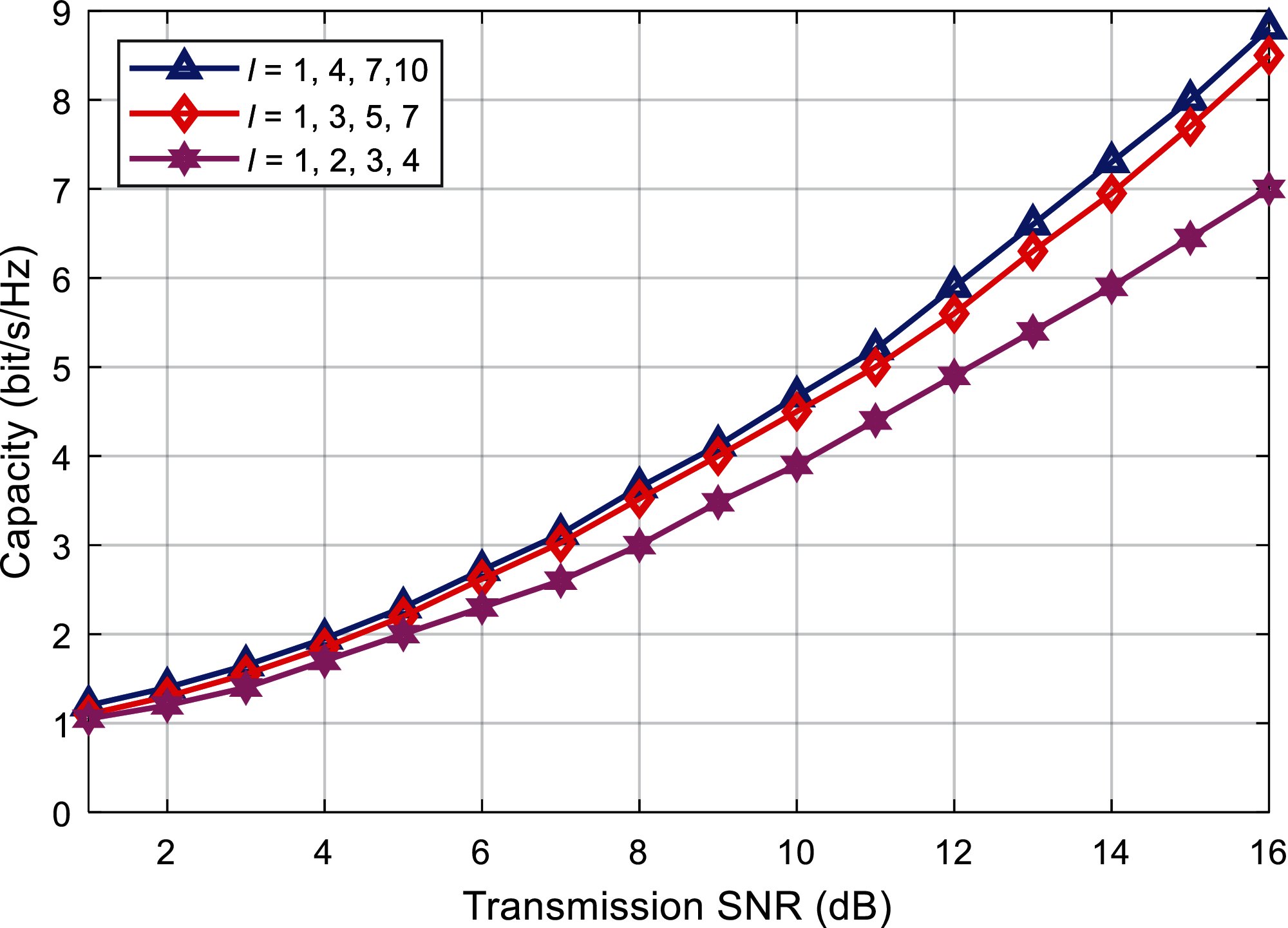
Figure 8: Capacity comparison against different modal intervals (Δl=1,2,3)

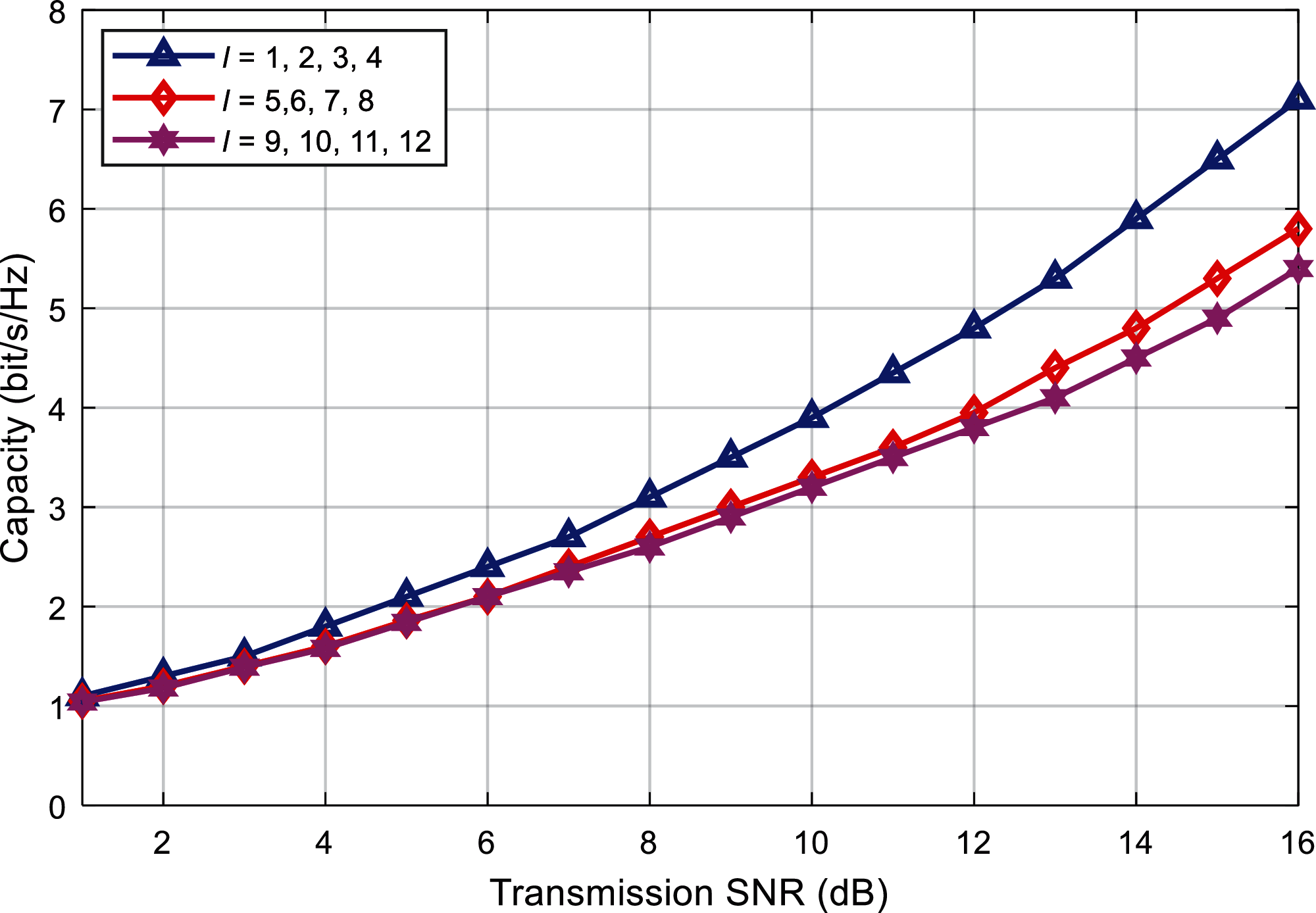
Figure 9: Capacity comparison with single modal interval

Fig. 9 depicts the relationship curve between different modal groups and system capacity when the modal interval is constant. Given the modal interval Δl = 1, the selected different modal groups {l = 1, 2, 3, 4}, {l = 5, 6, 7, 8}, {l = 9, 10, 11, 12}. It can be seen that, under the same offset distance, when the value of l is larger, the divergence of the OAM beam is stronger, and the energy transfer between modes is more serious at this time, so the system capacity is relatively small.

In summary, it is concluded that, the proposed method provides a feasible solution to solve the beamforming alignment problem with effective analysis and results. The results show that, the proposed technique provides improved results as compared with existing works which makes it a better candidate to be deployed in mmWave OAM environment.

5  Conclusion

In this paper, an OAM mmWave communication system is established, and for the situation that the antennas at both ends of the transceiver have a lateral axis offset when transmitting signals, combined with the modal migration characteristics of the OAM mmWave, the system is modeled and the theory is derived. The modal power distribution under the offset constructs the system channel transmission matrix. Based on the matrix, the system capacity is analyzed. The experimental simulation results show that the system capacity shows a downward trend as the offset distance increases, and eventually stabilize. The larger the number of modes, the more obvious the downward trend of system capacity. In addition, when transmitting and receiving offsets, when the system selects a modal group with a smaller modal value and a modal group with a larger modal interval, the system capacity is larger, that is, it is less affected by the offset at this time. This provides a feasible idea for improving the system capacity in the offset scenario. At the same time, future research work can also focus on the design of the axis offset calibration scheme to further optimize the system performance.

Acknowledgement: The authors would like to thank the editors and reviewers for their review and recommendations.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. A. Alhameed, I. Elfergani and J. Rodriguez, “Recent technical developments in energy-efficient 5G mobile cells: Present and future,” Computers, Electronics, vol. 9, no. 4, pp. 1–4, 2020. [Google Scholar]

 2.  S. L. Mohadmmed, M. H. Alsharif, S. K. Gharghan, I. Khan and M. Albreem, “Robust hybrid beamforming scheme for millimeter-wave massive mimo 5G wireless networks,” Symmetry, vol. 11, no. 11, pp. 1–18, 2019. [Google Scholar]

 3.  H. Zhang, B. Mao, Y. Han, Z. Wang, Y. Yue et al., “Generation of orbital angular momentum modes using fiber systems,” Applied Sciences, vol. 9, no. 5, pp. 1–17, 2019. [Google Scholar]

 4.  Z. Wang, J. Tu, S. Gao, Z. Li, C. Yu et al., “Transmission and generation of orbital angular momentum modes in optical fibers,” Photonics, vol. 8, no. 7, pp. 1–15, 2021. [Google Scholar]

 5.  C. H. Garcia, J. Vieira, J. T. Mendonca, L. Rego, J. S. Roman et al., “Generation and applications of extreme-ultraviolet vortices,” Photonics, vol. 4, no. 2, pp. 1–19, 2017. [Google Scholar]

 6.  A. M. Yao and M. J. Padgett, “Orbital angular momentum: Origins, behavior and applications,” Advances in Optics and Photonics, vol. 3, no. 2, pp. 161–204, 2011. [Google Scholar]

 7.  M. Liebmann, A. Treffer, M. Bock, U. Wallrabe and R. Grunwald, “Ultrashort vortex pulses with controlled spectral gouy rotation,” Applied Sciences, vol. 10, no. 12, pp. 1–13, 2020. [Google Scholar]

 8.  S. Alemaishat, O. A. Saraereh, I. Khan, S., H. Affes, X. Li et al., “An efficient precoding scheme for millimeter-wave massive mimo systems,” Electronics, vol. 8, no. 9, pp. 1–15, 2019. [Google Scholar]

 9.  O. A. Saraereh, I. Khan, B. M. Lee and A. Al-Bayati, “Modeling and analysis of wearable antennas,” Electronics, vol. 8, no. 1, pp. 1–12, 2018. [Google Scholar]

10. C. Wang, Y. Yao, J. Yu and X. Chen, “3d beam reconfigurable THz antenna with graphene-based high impedance surface,” Electronics, vol. 8, no. 11, pp. 1–21, 2019. [Google Scholar]

11. S. E. Hosseininejad, M. Neshat, R. Dana, M. Lemme, P. H. Bolivar et al., “Reconfigurable THz plasmonic antenna based on few-layer graphene with high radiation efficiency,” Nanomaterials, vol. 8, no. 8, pp. 1–18, 2018. [Google Scholar]

12. C. Lee and J. Jeong, “THz cmos on-chip antenna array using defected ground structure,” Electronics, vol. 9, no. 7, pp. 1–14, 2020. [Google Scholar]

13. F. Zhao, C. Zhu, W. Guo, J. Cong, C. Tee et al., “Resonant tunneling diode (RTD) terahertz active transmission line oscillator with graphene-plasma wave and two graphene antennas,” Electronics, vol. 8, no. 10, pp. 1–16, 2019. [Google Scholar]

14. S. Fajr, A. Rajawat and S. H. Gupta, “Design and optimization of THz antenna for onbody wban applications,” Optik, vol. 223, pp. 1–12, 2020. [Google Scholar]

15. S. Ullah, C. Ruan, T. Haq and X. Zhang, “High performance THz patch antenna using photonic band gap and defected ground structure,” Journal of Electromagnetic Waves and Applications, vol. 33, no. 15, pp. 1943–1954, 2019. [Google Scholar]

16. A. K. Geim and K. S. Novoselov, “The rise of graphene,” Nature Materials, vol. 6, no. 3, pp. 183–191, 2007. [Google Scholar]

17. J. Diaz and J. P. Carrier, “Microwave to THz properties of graphene and potential antenna applications,”“ in Ieee Int. Symp. on Antennas and Propagation (ISAPNagoya, Japan, pp. 239–242, 2012. [Google Scholar]

18. J. P. Carrier, M. Tamagone, J. G. Diaz and E. Carrasco, “Graphene antenna: Can integration and recofigurability compensate for the loss?,” in European Microwave Conf., Nuremberg, Germany, pp. 141–148, 2013. [Google Scholar]

19. X. Zhang, C. Ruan and J. Dai, “Reconfigurable antenna based on graphene at terahertz frequency,” in Progress in Electromagnetic Research Symposium (PIERSToyama, Japan, pp. 1–7, 2018. [Google Scholar]

20. M. Donelli, “A simple and efficient adaptive ISM-band antenna based on a reconfigurable optically driven parasitic structure,” Electronics, vol. 7, no. 2, pp. 1–13, 2018. [Google Scholar]

21. K. Payandehjoo and R. Abhari, “Investigation of parasitic elements for coupling reduction in multiantenna hand-set devices,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 24, no. 1, pp. 1–10, 2014. [Google Scholar]

22. Z. Li, Z. Du, M. Takahashi and K. Saito, “Reducing mutual coupling of MIMO antennas with parasitic elements for mobile terminals,” IEEE Transactions on Antennas and Propagation, vol. 60, no. 2, pp. 473–481, 2012. [Google Scholar]

23. I. Nadeem and D. Y. Choi, “Study on mutual coupling reduction technique for MIMO antennas,” IEEE Access, vol. 7, pp. 563–586, 2018. [Google Scholar]

24. S. Y. Zhu, Y. L. Li, K. M. Luk and S. W. Pang, “Compact high-gain si-imprinted THz antenna for ultrahigh speed wireless communications,” IEEE Transactions on Antennas and Propagation, vol. 68, no. 8, pp. 5945–5954, 2020. [Google Scholar]

25. M. S. Rabbani and H. G. Shiraz, “Fabrication tolerance and gain improvements of microstrip patch antenna at terahertz frequencies,” Microwave and Optical Technology Letters, vol. 58, no. 8, pp. 1819–1824, 2016. [Google Scholar]

26. S. Anand, D. S. Kumar, R. J. Wu and M. Chavali, “Graphene nanoribbon based terahertz antenna on polyimide substrate,” Optk, vol. 125, no. 19, pp. 5546–5549, 2014. [Google Scholar]

27. V. P. Gusynin, S. G. Sharapov and J. P. Carbotte, “Magneto-optical conductivity in graphene,” Journal of Physics, vol. 19, no. 2, pp. 231–241, 2007. [Google Scholar]

28. L. A. Falkovsky and S. S. Pershoguba, “Optical far-infrared properties of a graphene monolayer and multilayer,” Physical Review B, vol. 76, no. 15, pp. 1–17, 2007. [Google Scholar]

29. Y. M. Lin, K. A. Jenkins, A. V. Garcia, J. P. Small, D. B. Farmer et al., “Operation of graphene transistors at gigahertz frequencies,” Nano Letters, vol. 9, no. 1, pp. 422–426, 2009. [Google Scholar]

30. G. W. Hanson, “Dyadic green's functions for an anisotropic, non-local model of biased graphene,” IEEE Transactions on Antennas and Propagation, vol. 56, no. 3, pp. 747–757, 2008. [Google Scholar]

31. L. A. Falkovsky and S. S. Pershoguba, “Optical far-infrared properties of a graphene monolayer and multilayer,” Physical Review B, vol. 76, no. 15, pp. 1–19, 2007. [Google Scholar]

32. V. Ryzhii, A. Satou and T. Otsuji, “Plasma waves in two-dimensional electron-hole system in gated graphene heterostructures,” Journal of Applied Physics, vol. 101, no. 2, pp. 667–673, 2007. [Google Scholar]

33. L. A. Falkovsky, “Unusual field and temperature dependence of the hall effect in graphene,” Physical Review B, vol. 75, no. 3, pp. 1073–1085, 2007. [Google Scholar]

34. Z. K. Liu, Y. N. Xie, L. Geng, K. Pan and S. Pan, “Scattering of circularly polarized terahertz waves on a graphene nanoantenna,” Chinese Physics Letters, vol. 33, no. 2, pp. 3341–3352, 2016. [Google Scholar]

35. Y. Yan, L. Li, Z. Zhao, G. Xie, Z. Wang et al., “32-Gbit/s 60-gHz mmWave wireless communication using orbital angular momentum and polarization multiplexing,” in IEEE Int. Conf. on Communications (ICCKuala Lampur, Malaysia, pp. 1–6, 2016. [Google Scholar]

36. X. Ge, R. Zi, X. Xiong, Q. Li and L. Wang, “Mmwave communications with OAM-sM scheme for future mobile networks,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 9, pp. 2163–2177, 2017. [Google Scholar]

37. D. K. Nguyen, O. Pascal, J. Sokoloff, A. Chabory, B. Palacin et al., “Discussion about the link budget for electromagnetic wave with orbital angular momentum,” in European Conf. on Antennas & Propagation, The Hague, Netherlands, pp. 1117–1121, 2014. [Google Scholar]

38. A. Cagliero and R. Gaffoglio, “On the spectral efficiency limits of an OAM-based multiplexing scheme,” IEEE Antennas & Wireless Propagation Letters, vol. 16, no. 99, pp. 900–903, 2017. [Google Scholar]

39. N. Y. Zhang, W. Feng and N. Ge, “On the restriction of utilizing orbital angular momentum in radio communications,” in IEEE 8th Int. Conf. on Communications and Networking in China (CHINACOMGuilin, China, pp. 271–275, 2013. [Google Scholar]

40. S. M. Zhao, L. Wang, L. Zou, L. Gong, W. Cheng et al., “Both channel coding and wavefront correction on the turbulence mitigation of optical communication using orbital angular momentum multiplexing,” Optics Communications, vol. 376, no. 4, pp. 92–98, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.