Computers, Materials & Continua DOI:10.32604/cmc.2022.012635
Article

Heat Transfer of Casson Fluid over a Vertical Plate with Arbitrary Shear Stress and Exponential Heating

Dolat Khan1, Gohar Ali1, Arshad Khan2 and Ilyas Khan3,*

1Department of Mathematics, City University of Science and Information Technology, Peshawar, 25000, Pakistan
2Institute of Computer Sciences and Information Technology, The University of Agriculture, Peshawar, Pakistan
3Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, 72915, Vietnam
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 30 June 2020; Accepted: 30 August 2020

Abstract: The basic objective of this work is to study the heat transfer of Casson fluid of non-Newtonian nature. The fluid is considered over a vertical plate such that the plate exhibits arbitrary wall shear stress at the boundary. Heat transfers due to exponential plate heating and natural convection are due to buoyancy force. Magnetohydrodynamic (MHD) analysis in the occurrence of a uniform magnetic field is also considered. The medium over the plate is porous and hence Darcy’s law is applied. The governing equations are established for the velocity and temperature fields by the usual Boussinesq approximation. The problem is first written in dimensionless form using some useful non-dimensional quantities and then solved. The exact analysis is performed and hence solutions via integral transform are established. The analysis of various pertinent parameters on temperature distribution and velocity field are reported graphically. It is found that pours medium permeability parameter retards the fluid motion whereas, velocity decreases with increasing magnetic parameter. Velocity and temperature decrease with increasing Prandtl number whereas the Grashof number enhances the fluid motion. Further, it is concluded from this study that the results obtained here are more general and in a limiting sense several other solutions can be recovered. The Newtonian fluid results can be easily established by taking the Casson parameter infinitely large i.e., when β→∞.

Keywords: Heat transfer; casson fluid; shear stress; natural convection

1  Introduction

Non-Newtonian fluids have various important industrial applications in many fields [1,2], due to which the researchers are paying attention to study the non-Newtonian fluids in their investigations. In literature many non-Newtonian fluids was investigated, one of them is Casson fluid. In 1959 the Casson have presented this fluid model. Oka [3] was the first researcher who used the Casson fluid model in tube problem. Casson fluids examples are blood, honey, soup, stuffs, jelly, artificial fibers, slurries, etc. Casson fluids have various industrial, engineering and medical applications [4]. The investigation of Casson fluid with magnetohydrodynamic (MHD) flow over a shrinking plate is reported by [5]. The comparison of heterogeneous–homogeneous reaction of Casson fluid is presented by [6]. After that transfer of heat analysis in Casson fluid is investigated by [7]. Recently, many researchers have investigated the Casson fluids in their papers. Some of them are [8–12]. In addition, Casson fluid with MHD free convection flow is investigated by [13], over a vertical plate. Some interesting articles related to free convection Casson fluid can be found in [14–17], and the references therein. The investigation of mass and heat transfer for Casson fluid with the effect of MHD on a stretching surface is investigated by [18]. The radiation analysis of MHD Casson fluid with free convection flow in a porous medium is examined by [19]. They also examined the influence of viscous dissipation for the same problem. Narahari et al. [20] and Seth et al. [21] studied Unsteady MHD free convection flow past through a vertical plate, while in [22] analyze a discussion on the similar solutions. Recently Mohamad et al. [23] examine the influence of wall shear stress for MHD Casson fluid through an Upright Plate in the existence of Porous Medium. The force applied per unit area by the wall in a way of local tangent plane on the fluid is known as wall shear stress [24]. The significant role of wall shear stress in the focal distribution of atherosclerotic lesions, endothelial homeostasis and much application in medical side [25,26]. Due to its application the researchers are attract to study the wall shear stress in their study. Rubbab et al. [27] examined the flow of natural convection of viscous fluid adjacent to a perpendicular plate that spread over a shear stress. he obtained the exact solution via Laplace transform. Furthermore, the influence MHD conjugate flow of wall shear stress through an inclined plate in a porous medium is investigated by [28]. Recently, the same author investigates the irreversibility analysis for MHD flow, with arbitrary shear stress through a perpendicular plate in the existence of porous medium [29]. However, up to date in the literature no one is studded the heat transfer of Casson fluid with arbitrary shear stress over a vertical plate and exponential heating.

The goal of this paper is to inspect the exact study of heat transfer of Casson fluid through a perpendicular plate with random shear stress at the bounding wall which at the same time executing exponential heating. The problem is solved for exact solution via integral transform of Laplace. The special cases are also derived from the general solution. The outcomes for temperature and velocity are schemed and discussed graphically.

2  Mathematical Development of Momentum Transfer and Heat Transfer

Unsteady Casson fluid with mixed convection is considered. The flow is due to the arbitrary shear stress and natural convection through an unbounded vertical plate. The plate is heated exponentially. y-axis is normal to the plate on x-axis.

At beginning the fluid as well as plate are at rest with constant temperature Θ∞. At t≥0, the temperature is upraised to Θ∞+Θw(1−ae−bt). Variable shear stress Ωf0(t) is applied to the fluid. The effect of viscous dissipation and convective terms of the velocity are considered as negligible. Keeping in mind the Boussinesq approximations and the boundary layer, the governing equations are formed as [20–22]:

∂u(y1,t)∂t=ν(1+1β)∂2u(y1,t)∂y12−σB02ρu(y1,t)−(1+1β)νφKu(y1,t)+gβΘ(Θ−Θ∞);y1, t>0, (1)

∂Θ(y1,t)∂t=kρcp∂2Θ(y1,t)∂y12;y1, t>0, (2)

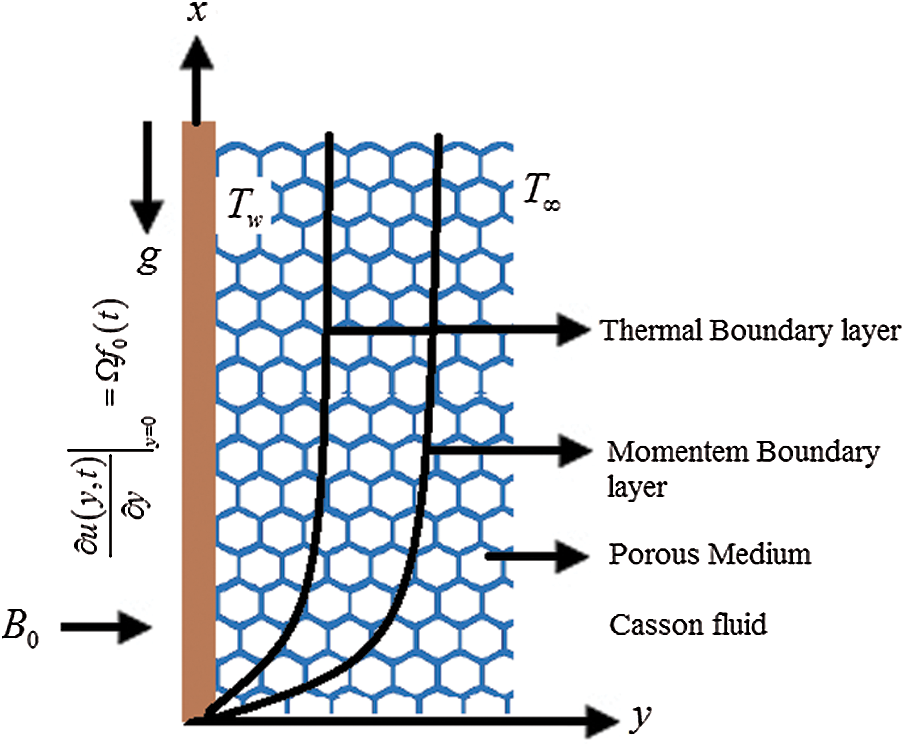
Figure 1: Physical model of the flow

The physical boundary conditions are:

u(y1,t)=0,Θ(y1,t)=Θ∞;t=0, y1≥0,∂u(y1,t)∂y1|y1=0=Ωf0(t),Θ(0,t)=Θ∞+Θw(1−ae−bt);t>0,u(y1,t)→0,Θ(y1,t)→Θ∞asy1→∞,}. (3)

where ν,β,ρ,σ,φ,k,βΘ,B0,g,Θ, cp and K are kinematic viscosity, Casson fluid parameter, density of fluid, electrical conductivity of the fluid, porosity, thermal conductivity of the fluid, Temperature expansion coefficient, magnetic parameter, gravitational acceleration, temperature profile, specific heat at constant temperature and permeability respectively. Also Ω,b>0 and a≥0 are constants.

The appropriate dimensionless variables are,

Into Eqs. (1)–(3), we get, for simplicity drop the * sign.

∂u(y1,t)∂t=(1+1β)∂2u(y1,t)∂y12−Hu(y1,t)+Grθ;y1, t>0, (4)

∂θ(y1,t)∂t=Pr∂2θ(y1,t)∂y12;y1, t>0, (5)

u(y1,t)=0,θ(y1,t)=θ∞;t=0, y1≥0,∂u(y1,t)∂y1|y1=0=Ωf(t),θ(0,t)=1−ae−bt;t>0,u(y1,t)→0,θ(y1,t)→0asy1→∞,}. (6)

where Gr=gβΘ(Θ−Θ∞)to32ν, M=σB02t0ρ, kp=νφt0K, c1=1+1β, H = c1kp + M, Pr=μcpk

kp, Pr Gr and M are pours medium permeability, Prandtl number, thermal Grashof number and magnetic parameter.

3  Problem Solution

By Laplace transform the exact solution of the Eqs. (4) and (5) under conditions (6) are:

θ(y1,t)=erfc(y1Pr2t)−2e−bt2{eiy1bPrerfc(y1Pr2t+ibt)+e−iy1bPrerfc(y1Pr2t−ibt)}, (7)

And the corresponding Nusselt number is obtained as

Nu=−∂θ(y1,t)∂y1|y1=0=Prπt(1+2e−bt)+2ibPrerf(ibt). (8)

and the velocity profile is

u(y1,t)=um(y1,t)+uc1(y1,t), (9)

where

um(y1,t)=−ΩB∫0tf(s−t)⋅e−c1s⋅e−y12B4sπsds, (10)

where

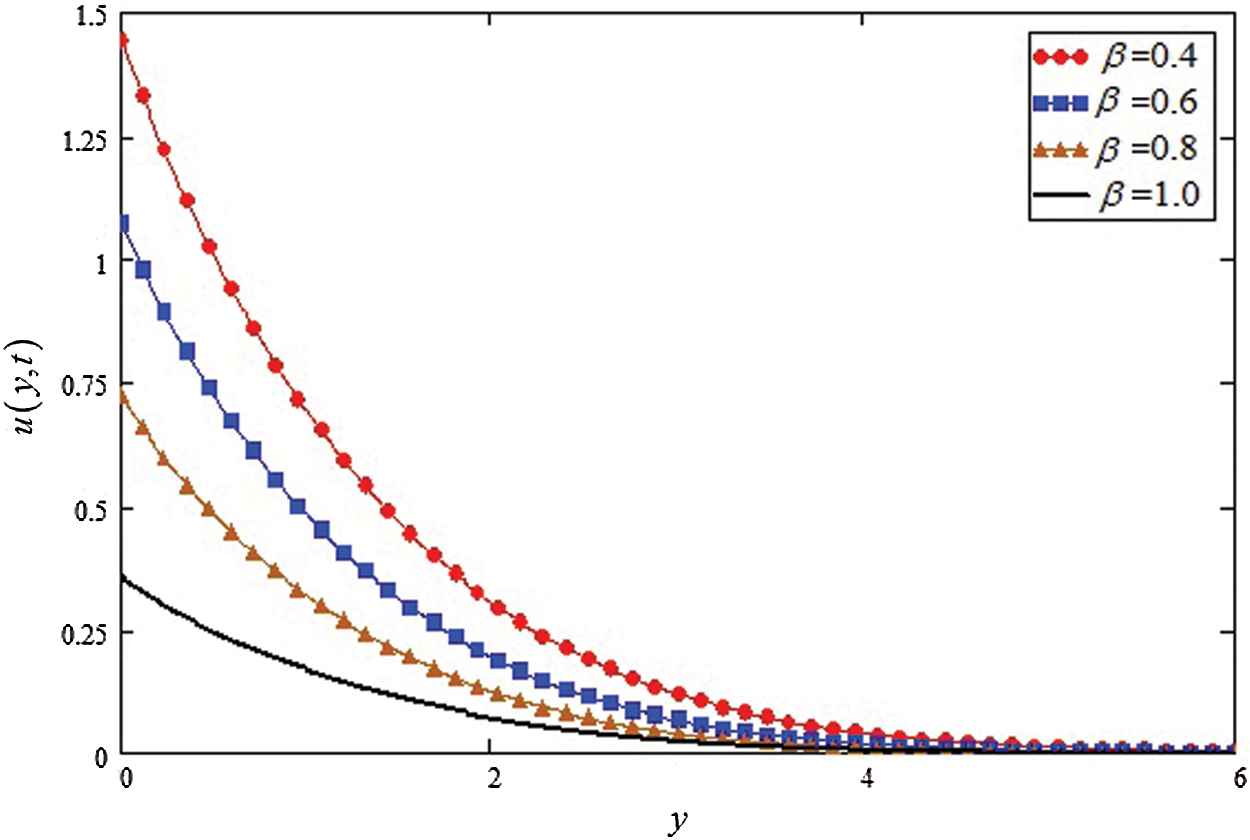
Figure 2: Influence of β on profile of velocity

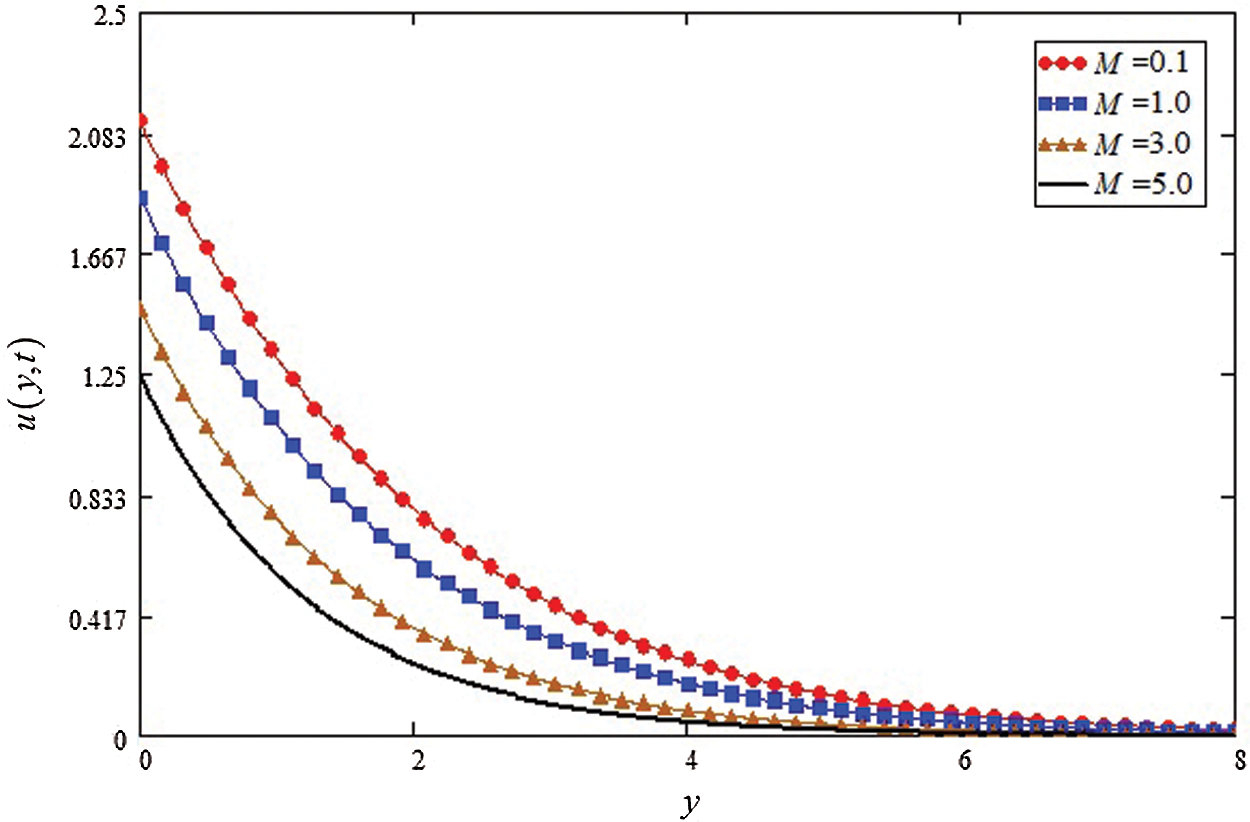
Figure 3: Influence of M on velocity profile

4  Graphical Discussion

The different physical parameters analysis for velocity and temperature is schemed graphically and discussed by using Mathcad-15 software. The influence of Casson parameter β is highlighted in Fig. 2, an increase in β values leads to decrease in velocity profile. It is because, for the large values of β decrease the velocity boundary layer thickness which make decrease velocity profile. The impact of magnetic parameter is shown in Fig. 3 for the greater value of M velocity profile is reduced, it is actually true the fact is that, increase of M mean to rise the Lorentz force which makes to decline the velocity of the fluids.

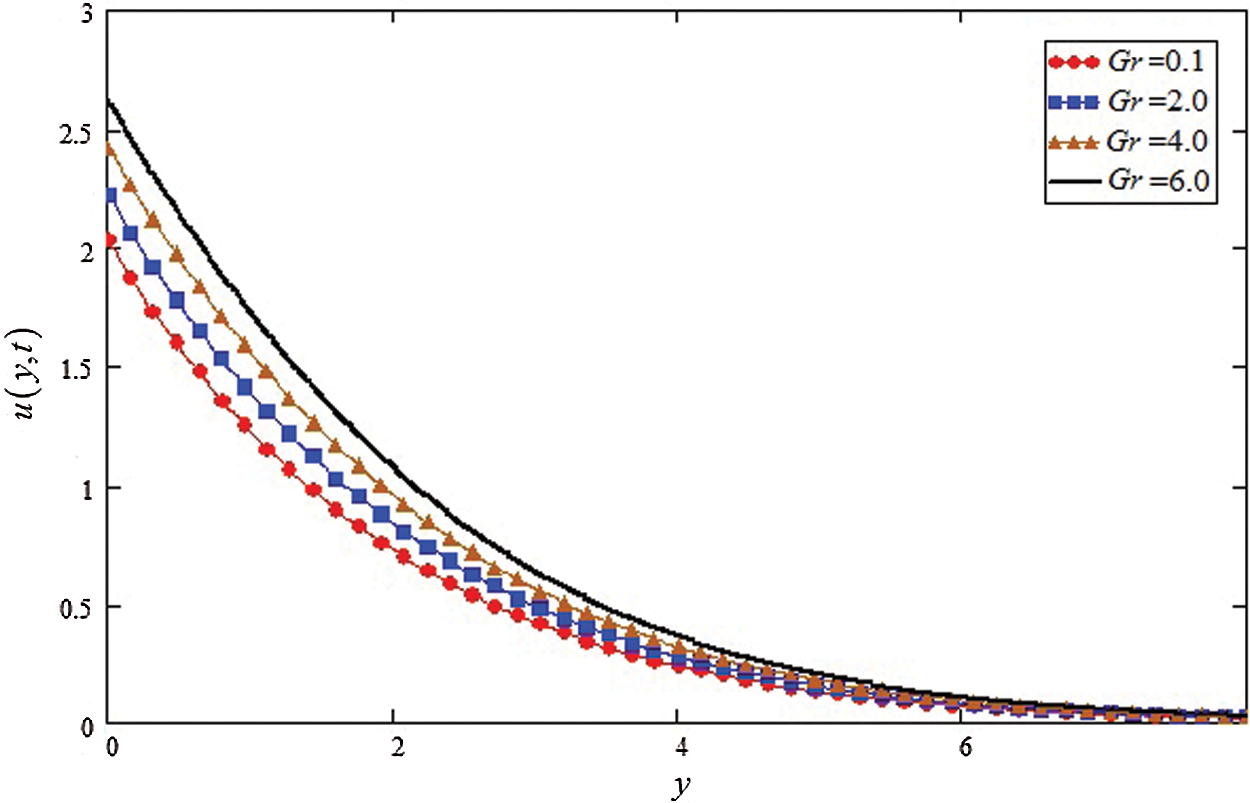
Figure 4: Influence of Gr on velocity profile

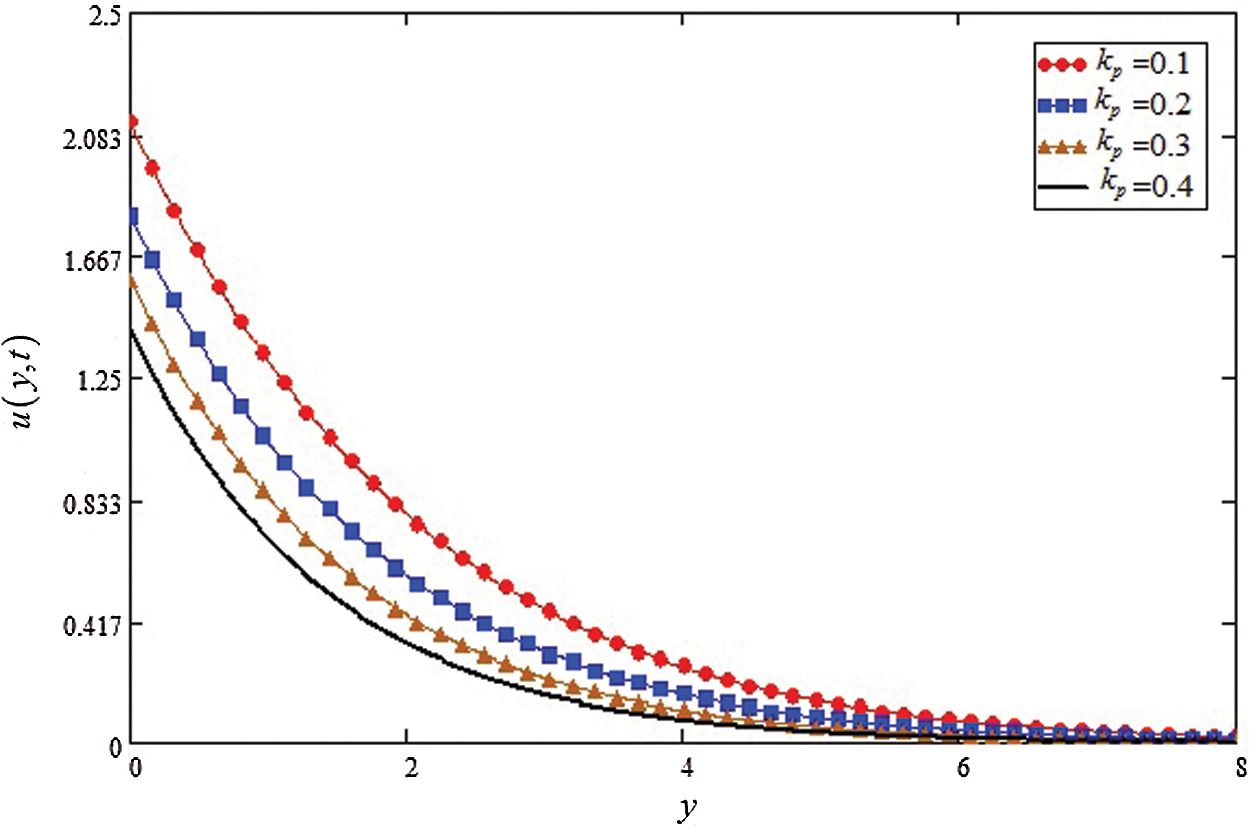
Figure 5: Influence of kp on velocity profile

The Gr effects on the velocity is show in Fig. 4, where an increase is detected in velocity for large values of Gr. In reality the buoyancy force is increase for greater values of Gr and decrease in viscose force, resulting the velocity profile is increase. Fig. 5 is highlighted the influence of kp on velocity, the decreasing effect on velocity is observed with the increasing of kp.

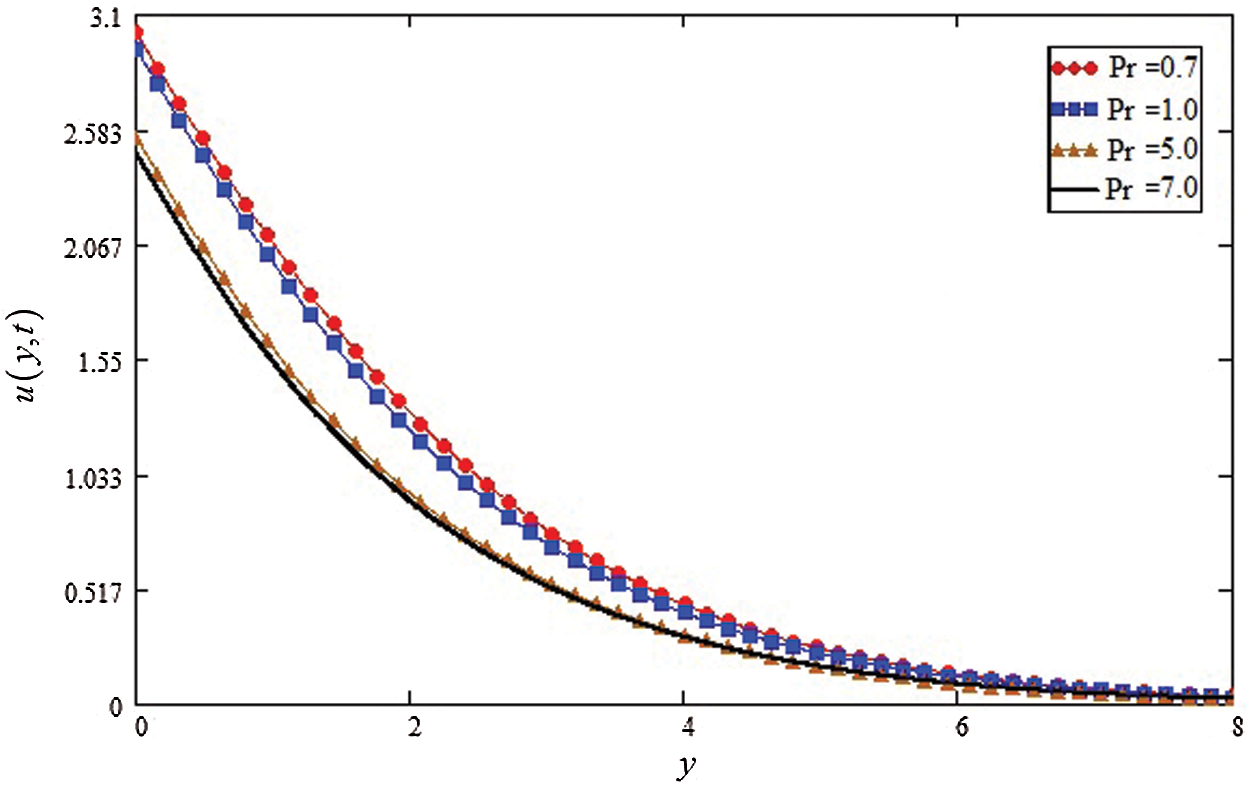
Figure 6: Influence of Pr on velocity profile

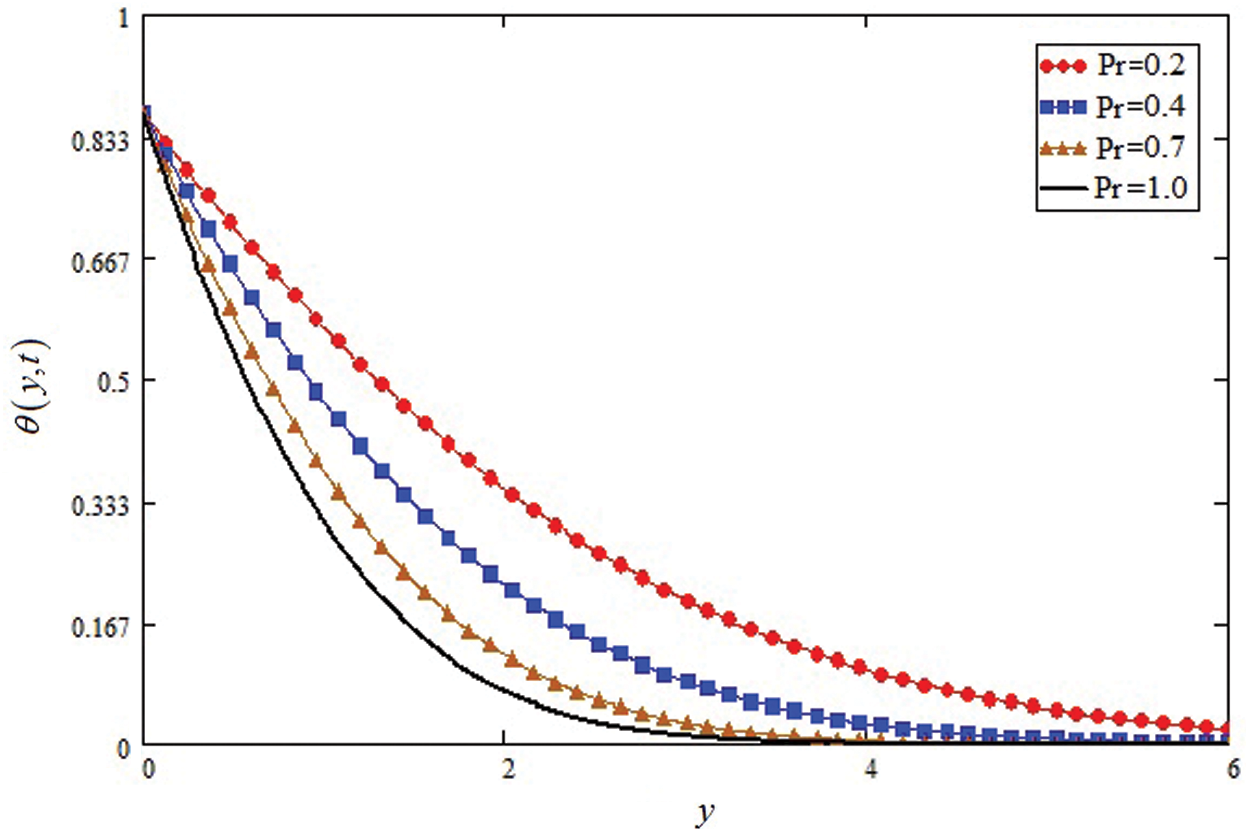
Figure 7: Influence of Pr on the temperature profile

Fig. 6 shows the influence of Pr on velocity profile, it is observed that increase of Pr, decrease the velocity profile. The influence of Pr is shown in Fig. 7 on temperature profile. The temperature profile is decrease for greater of Pr. Because the large values of Prandtl number decrease the fluid thermal conductivity and thickness of thermal boundary layer. Which makes to decrease the temperature as well as the velocity profile. The influence of β, M, Gr, Kp and Pr on velocity and temperature profile are identical to the results gained by [30].

5  Conclusions

The exact analysis for mixed convection Casson fluid is obtained. Where the plate exhibits arbitrary wall shear stress at the boundary over a vertical plate. Heat transfers because of exponential plate heating is also considered. The main equations with suitable initial and boundary condition is recognized for temperature and velocity. The Laplace technique is used to find the exact solution for velocity and temperature profile. The effects of different parameters are discussed graphically for temperature and velocity. The main conclusions are derived from this article are:

The embedded parameters β, M, kp, Pr is the source which leads to decline the velocity profile where the Gr is leads to rise the velocity of fluids.

•   The Pr is also the decreasing factor for temperature profile.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under Project Number (RGP-2019-6).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. J. Liao, “On the analytic solution of magnetohydrodynamic flows of non-newtonian fluids over a stretching sheet,” Journal of Fluid Mechanics, vol. 488, no. 1, pp. 189–212, 2003. [Google Scholar]

 2.  A. Aliseda, E. J. Hopfinger, J. C. Lasheras, D. M. Kremer, A. Berchielli et al., “Atomization of viscous and non-newtonian liquids by a coaxial, high-speed gas jet. Experiments and droplet size modeling,” International Journal of Multiphase Flow, vol. 34, no. 2, pp. 161–175, 2018. [Google Scholar]

 3.  S. Oka, “An approach to α unified theory of the flow behavior of time-independent non-newtonian suspensions,” Japanese Journal of Applied Physics, vol. 10, no. 3, pp. 287–291, 1971. [Google Scholar]

 4.  A. Khan, D. Khan, I. Khan, F. Ali, F. U. Karim et al., “MHD flow of sodium alginate-based casson type nanofluid passing through a porous medium with newtonian heating,” Scientific Reports, vol. 8, no. 1, pp. 8645, 2018. [Google Scholar]

 5.  S. Nadeem, R. U. Haq and C. Lee, “MHD flow of a casson fluid over an exponentially shrinking sheet,” Scientia Iranica, vol. 19, no. 6, pp. 1550–1553, 2012. [Google Scholar]

 6.  M. I. Khan, M. Waqas, T. Hayat and A. Alsaedi, “A comparative study of casson fluid with homogeneous-heterogeneous reactions,” Journal of Colloid and Interface Science, vol. 498, no. 6, pp. 85–90, 2017. [Google Scholar]

 7.  S. Mukhopadhyay and I. C. Mandal, “Boundary layer flow and heat transfer of a casson fluid past a symmetric porous wedge with surface heat flux,” Chinese Physics B, vol. 23, no. 4, pp. 44702, 2014. [Google Scholar]

 8.  F. Ali, N. A. Sheikh, I. Khan and M. Saqib, “Magnetic field effect on blood flow of casson fluid in axisymmetric cylindrical tube: A fractional model,” Journal of Magnetism and Magnetic Materials, vol. 423, no. 1, pp. 327–336, 2017. [Google Scholar]

 9.  Z. Shah, S. Islam, H. Ayaz and S. Khan, “Radiative heat and mass transfer analysis of micro polar nanofluid flow of casson fluid between two rotating parallel plates with effects of hall current,” Journal of Heat Transfer, vol. 141, no. 2, pp. 1–13, 2018. [Google Scholar]

10. I. Khan, M. Saqib and F. Ali, “Application of the modern trend of fractional differentiation to the MHD flow of a generalized casson fluid in a microchannel: Modelling and solution,” European Physical Journal Plus, vol. 133, no. 7, pp. 262, 2018. [Google Scholar]

11. R. S. Raju and K. Ramesh, “Study of grid independence of finite element method on MHD free convective casson fluid flow with slip effect,” AIP Conference Proceedings, vol. 1953, no. 1, pp. 140107, 2018. [Google Scholar]

12. R. Haq, S. Nadeem, Z. Khan and T. Okedayo, “Convective heat transfer and MHD effects on casson nanofluid flow over a shrinking sheet,” Open Physics, vol. 12, no. 12, pp. 862–871, 2014. [Google Scholar]

13. A. Khalid, I. Khan, A. Khan and S. Shafie, “Unsteady MHD free convection flow of casson fluid past over an oscillating vertical plate embedded in a porous medium,” Engineering Science and Technology, an International Journal, vol. 18, no. 3, pp. 309–317, 2015. [Google Scholar]

14. Q. Rubbab, D. Vieru, C. Fetecau, C. Fetecau and R. Planque, “Natural convection flow near a vertical plate that applies a shear stress to a viscous fluid,” PLoS One, vol. 8, no. 11, pp. 78352, 2013. [Google Scholar]

15. A. Khan, I. Khan, A. Khalid and S. Shafie, “Effects of arbitrary shear stress on unsteady free convection flow of casson fluid past a vertical plate,” Results in Physics, vol. 7, no. 1, pp. 3301–3306, 2017. [Google Scholar]

16. G. Mahanta and S. Shaw, “Soret and dufour effects on unsteady MHD free convection flow of casson fluid past a vertical plate embedded in a porous medium with convective boundary condition,” International Journal of Applied Engineering Research, vol. 10, no. 10, pp. 24917–24936, 2015. [Google Scholar]

17. I. Pop and M. Sheremet, “Free convection in a square cavity filled with a casson fluid under the effects of thermal radiation and viscous dissipation,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 27, no. 10, pp. 2318–2332, 2017. [Google Scholar]

18. C. S. K. Raju, N. Sandeep, V. Sugunamma, M. J. Babu and J. R. Reddy, “Heat and mass transfer in magnetohydrodynamic casson fluid over an exponentially permeable stretching surface,” Engineering Science and Technology, An International Journal, vol. 19, no. 1, pp. 45–52, 2016. [Google Scholar]

19. G. Makanda, S. Shaw and P. Sibanda, “Effects of radiation on MHD free convection of a casson fluid from a horizontal circular cylinder with partial slip in non-darcy porous medium with viscous dissipation,” Boundary Value Problems, vol. 2015, no. 1, pp. 1–14, 2015. [Google Scholar]

20. M. Narahari and L. Debnath, “Unsteady magnetohydrodynamic free convection flow past an accelerated vertical plate with constant heat flux and heat generation or absorption,” ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, vol. 93, no. 1, pp. 38–49, 2013. [Google Scholar]

21. G. S. Seth, R. Sharma and B. Kumbhakar, “Heat and mass transfer effects on unsteady MHD natural convection flow of a chemically reactive and radiating fluid through a porous medium past a moving vertical plate with arbitrary ramped temperature,” Journal of Applied Fluid Mechanics, vol. 9, no. 1, pp. 103–117, 2016. [Google Scholar]

22. J. H. Merkin, “A note on the similarity solutions for free convection on a vertical plate,” Journal of Engineering Mathematics, vol. 19, no. 3, pp. 189–201, 1985. [Google Scholar]

23. A. Q. Mohamad, I. Khan, L. Y. Jiann, A. Khan, M. R. Ilias et al., “Magnetohydrodynamic conjugate flow of casson fluid over a vertical plate embedded in a porous medium with arbitrary wall shear stress,” Journal of Nanofluids, vol. 6, no. 1, pp. 173–181, 2017. [Google Scholar]

24. D. Katritsis, L. Kaiktsis, A. Chaniotis, J. Pantos, E. P. Efstathopoulos et al., “Wall shear stress: Theoretical considerations and methods of measurement,” Progress in Cardiovascular Diseases, vol. 49, no. 5, pp. 307–329, 2007. [Google Scholar]

25. S. Chien, S. Li and J. Y. Shyy, “Effects of mechanical forces on signal transduction and gene expression in endothelial cells,” Hypertension, vol. 31, no. 1, pp. 162–169, 1998. [Google Scholar]

26. P. F. Davies, “Flow-mediated endothelial mechanotransduction,” Physiological Reviews, vol. 75, no. 3, pp. 519–560, 1995. [Google Scholar]

27. Q. Rubbab, D. Vieru, C. Fetecau and C. Fetecau, “Natural convection flow near a vertical plate that applies a shear stress to a viscous fluid,” PLoS One, vol. 8, no. 11, pp. 78352, 2013. [Google Scholar]

28. A. Khan, I. Khan, F. Ali and S. Shafie, “Effects of wall shear stress on MHD conjugate flow over an inclined plate in a porous medium with ramped wall temperature,” Mathematical Problems in Engineering, vol. 2014, no. 1, pp. 1–15, 2014. [Google Scholar]

29. A. Khan, I. Khan, F. Ali and S. Shafie, “A note on entropy generation in MHD flow over a vertical plate embedded in a porous medium with arbitrary shear stress and ramped temperature,” Journal of Porous Media, vol. 19, no. 2, pp. 175–187, 2016. [Google Scholar]

30. A. Hussanan, M. Z. Salleh, I. Khan and R. M. Tahar, “Heat transfer in magnetohydrodynamic flow of a casson fluid with porous medium and newtonian heating,” Journal of Nanofluids, vol. 6, no. 4, pp. 784–793, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.