DOI:10.32604/cmc.2022.020666

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020666 |  |
| Article |
Generating Type 2 Trapezoidal Fuzzy Membership Function Using Genetic Tuning
Centre for Research in Data Science, Department of Computer and Information Sciences, Universiti Teknologi PETRONAS, Perak, Malaysia
*Corresponding Author: Mohd Hilmi Hasan. Email: mhilmi_hasan@utp.edu.my
Received: 03 June 2021; Accepted: 19 August 2021
Abstract: Fuzzy inference system (FIS) is a process of fuzzy logic reasoning to produce the output based on fuzzified inputs. The system starts with identifying input from data, applying the fuzziness to input using membership functions (MF), generating fuzzy rules for the fuzzy sets and obtaining the output. There are several types of input MFs which can be introduced in FIS, commonly chosen based on the type of real data, sensitivity of certain rule implied and computational limits. This paper focuses on the construction of interval type 2 (IT2) trapezoidal shape MF from fuzzy C Means (FCM) that is used for fuzzification process of mamdani FIS. In the process, upper MF (UMF) and lower MF (LMF) of the MF need to be identified to get the range of the footprint of uncertainty (FOU). This paper proposes Genetic tuning process, which is a part of genetic algorithm (GA), to adjust parameters in order to improve the behavior of existing system, especially to enhance the accuracy of the system model. This novel process is a hybrid approach which produces Genetic Fuzzy System (GFS) that helps to enhance fuzzy classification problems and performance. The approach provides a new method for the construction and tuning process of the IT2 MF, based on the FCM outcomes. The result is compared to Gaussian shape IT2 MF and trapezoid IT2 MF generated by the classic GA method. It is shown that the proposed approach is able to outperform the mentioned benchmarked approaches. The work implies a wider range of IT2 MF types, constructed based on FCM outcomes, and an optimum generation of the FOU so that it can be implemented in practical applications such as prediction, analytics and rule-based solutions.
Keywords: Fuzzy inference system; membership function; genetic tuning; lateral adjustment; trapezoidal MF; fuzzy C means
The three main types of fuzzy membership function (MF) are Gaussian [1,2], triangular [3,4] and trapezoidal [5,6]. Each of the MFs has its own advantages and disadvantages, hence providing better performance than the other MFs in certain scenarios or applications. One way of constructing the MF is through data clustering using fuzzy C means (FCM). The limitation of FCM is that it generates Gaussian MF, instead of linear MFs such as triangular and trapezoidal. The previous work proposed the generation of trapezoidal MF for the interval type 2 (IT2) fuzzy inference system (FIS) [7]. This paper proposes the extension of the work which is to tune the IT2 trapezoidal MF so that it could produce improved accuracy.
The purpose of Genetic Algorithm (GA) as part of producing the FIS is to generate IT2 trapezoidal MF (referred as trapMF in this paper) by using the theory of genetic tuning and lateral adjustment [8]. It will be the continuation of the previous work [7] where FT1 trapMF is constructed through the theory of Gaussian distribution. To generate IT2 trapMF, UMF and LMF of the MF need to be identified to get the range of the FOU. In this section, the LMF is constructed to get the FOU range, while the parameters of the UMF is maintained. Genetic tuning process, which is part of GA, is the process of adjusting parameters to improve the behavior of existing system, especially to enhance the accuracy of the system model [9]. This process is a hybrid approach which produces Genetic Fuzzy System (GFS) that helps to enhance fuzzy classification problems and performance. In [9], a collaborative tuning based on ignorance function and lateral adjustment is performed to improve the fuzzy rule based classification system. Ignorance functions are also famously used to generate Interval Value Fuzzy Sets (IVFS) which is the general type of fuzzy IT2. The methodology used in this research is the modified adaptation of techniques in the IVFS performance enhancement, to specifically suit trapMF.
In GFS, the concept of weak ignorance function is introduced. It is used to evaluate or measure the uncertainty of membership values [9]. A definition in [10] implies that a value of 0.5 corresponds to the complete lack of knowledge of the expert on the membership of an element to a class. In [10] the five axioms are justified. Bijections are used to construct IT2 where their amplitude is proportional to weak ignorance function having the maximum ignorance degree for initial membership degree = 0. Thus, a bijection h : [0, 1] → [0.5, 1] so that h(0) = 0.5 and h(1) = 1 is employed.
The composed MFs are usually obtained by a normalization process and they remain the same during the rule based construction process [9]. This indicates that the MFs are not properly adapted to the context of each variable which may limit the performance of the global rule set [9]. A post-processing tuning step is often used to overcome this problem. The tuning provides a variation in the shape of the MFs with the main aim is to find the best global configuration for them. The previous work in [11] had carry out the tuning step for the amplitude of the support of UMF which manages the ignorance that each IT2 represents.
Tuning process in GFS is commonly applied to improve the performance of fuzzy model. It introduces an alterations of MF shapes to improve global interaction which induces better cooperation among rules [12,13]. Thus, the real aim of tuning is to find the best global configurations of the MF [14]. Based on this goal, the research methodology takes a new direction which is using the tuning process to directly construct trap IT2, instead of using it as a post processing steps after constructing the rules for the fuzzy sets. In this way, the best range for MF amplitude is obtained, and it reduces the steps of getting the best model with better result in term of its accuracy. This has become the aim of this paper. The proposed approach will provide practical implications through IT2 FIS implementation in the areas including health prediction and classification [15], computer and network security [16], image processing and security [17], rule-based solutions and many others.
The tuning steps will involve a simultaneous step of adjusting the amplitude with varying range, by moving only two parameters (left and right) of trapMF. At the same time, lateral adjustment based on 2-tuples fuzzy linguistic representation of the MF is also performed, where the trapMF parameters are adjusted to the left or right position based on varying range in order to achieve better adaptation of the fuzzy partitions. In order to prove the enhancement in term of performance of this methodology, the result of the fuzzy modeling through FIS will be compared with the generic tuning of trapMF whereby it follows the initial situation of genetic weak ignorance tuning [18]. It also uses triangular MF to show the initial lateral adjustment where the horizontal parameters, which exists only for trapMF, are not counted.
This paper is structured as follows; next section contains literature review, the explanation of FIS which becomes the research methodology is presented in Section 3, while results and discussion are contained in Section 4. The paper ends with conclusion in Section 5 in which the research is summarized as well as some future works are outlined.
The modification of the LMF amplitude of trapMF is based on ignorance function [9] represented by parameter W in this paper. The interval in which W can vary is [0, 0.5] where the situation without ignorance, W = 0 and W = 0.5 for maximum ignorance. The degree of ignorance will be increased from the initial value W = 0.05 until 0.5. Variation of degree of ignorance is depicted in Fig. 1.
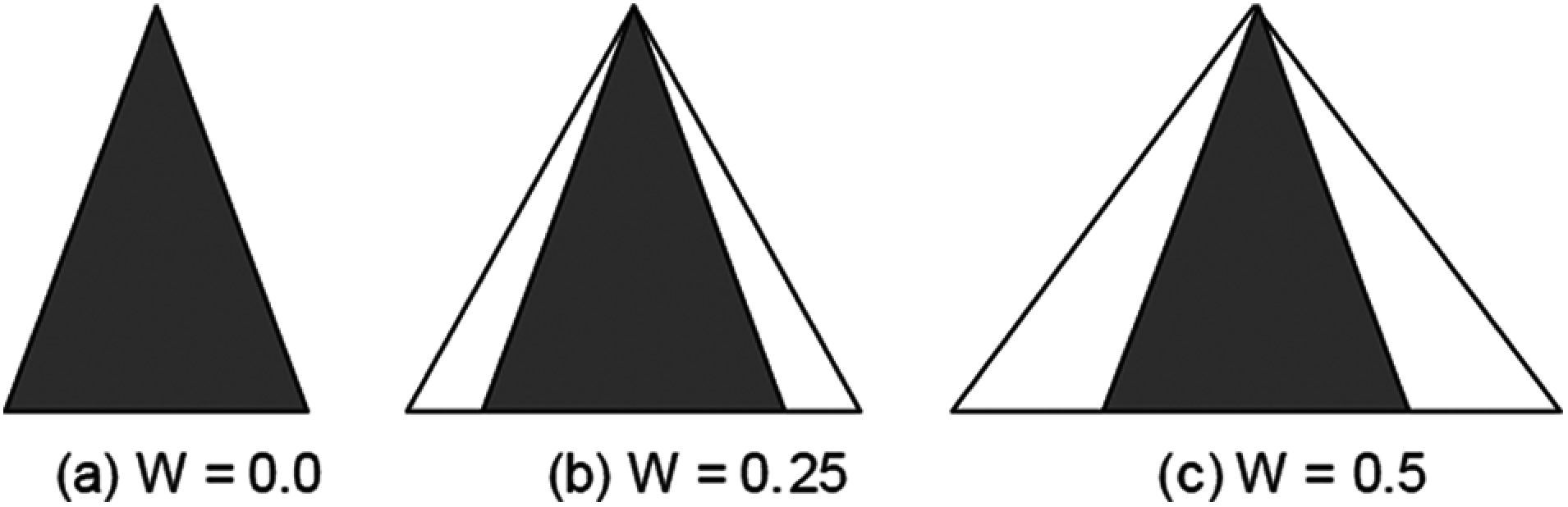
Figure 1: Parameter values representation in the genetic weak ignorance tuning. (a) No ignorance. (b) Initial situation. (c) Maximum ignorance [9]
The approximation of the genetic weak tuning in trapMF is initialized with the parameters for UMF. The equation of the straight line between parameter b and c is ignored due to the fact that the amplitude and lateral approximation only involve the intervals between parameter a to b, and parameter c to d. The calculation for c to d (straight vertical line of trapMF) will be similar since the MF involved in symmetrical. UMF and LMF of the interval are consistent with the following situation:
• Total certainty (W = 0): UMF and LMF values are the same.
• Maximum uncertainty (W = 0.5): Huge absence of information which causes the amplitude of UMF to be twice the amplitude of LMF.
Based on the above situation, the initial value set for W is 0.05 to test for any changes of amplitude. As mentioned, bijections are used for the constructions of IT2 so the amplitude is proportional to the weak ignorance function where degree of ignorance is considered maximum when the membership degree is 0. Specifically, we employ the following formula (Eq.(1)):
The initial FT1 trapMF is built first from the previous section, which is represented by the MF representation below:
In order to calculate the range of FOU for IT2 trapMF, the proposition in [9] is modified to suit with the trapezoidal shapes, whereby the parameters obtained from FT1 trapMF is combined with ignorance function, which is proportional to the MF amplitude. Fig. 2 shows the example of amplitude applied in FT1 trapMF to construct the IT2.
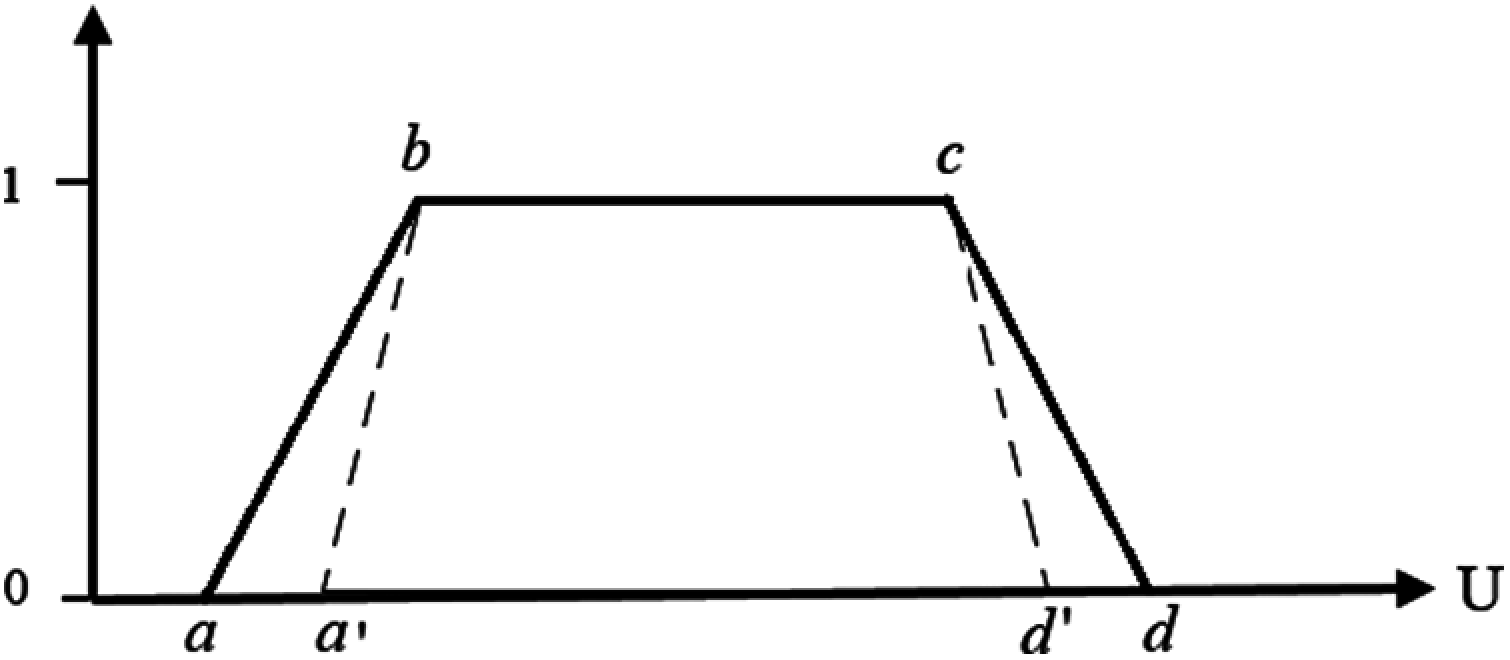
Figure 2: Amplitude tuning for IT2 trapMF
Based on Fig. 2, the amplitude is adjusted for the LMF of the FT1 trapMF at point (a′, b) and (c, d′). Since the trapMF is symmetrical, calculation for point (c, d′) will be the same except for the change of operator. Considering A is the amplitude of point (a, b) which is obtained from construction of trapMF, a complete algorithm to get the amplitude is:
Obtain each cluster center and sigma:
Point a = aCenter − aSigma ∗ 2
Point d = dCenter + dSigma ∗ 2
Point (a, b):
A =
a′ = Point a − W (Point d − Point a), where W > 0.
W is the parameter used for amplitude tuning to measure the certainty; W = 0 for total certainty, and 0.5 to be the maximum uncertainty. It can also be called weak tuning.
From A, the equation for amplitude of straight line (a′, b) named B is:
B =
In order to achieve the best possible range of FOU through this weak tuning, a range of parameter W is prepared to test for its accuracy. Tab. 1 shows the range of parameter W for the trapMF amplitude accuracy testing. This range will soon be used together for MF lateral adjustments since the methodology will be combined.

In [19], the symbolic translation of a linguistic term is a number within the interval [−0.5, 0.5] which expresses the domain of a label when it is moving between two lateral labels. The lateral displacement can be extended in the construction of MF, where the tuning of the support amplitude of MF is performed [10]. The displacement is a slight movement to the left/right of the original MF.
The adjustment is performed by considering two parameters, α and β, which represents the lateral displacement and the amplitude variation. Next, each label can be represented by a 3-tuple (s, α, β). α is a value within the interval [−0.5, 0.5]. β is also a number within the interval. It allows to reduce or increase the support amplitude until 50% of its initial size [19].
Fig. 3 illustrates the lateral and variation of amplitude for label S in symmetrical trap MFs. Due to similar linear parameter on the left and right side on the symmetrical triangular MF, the same adjustment can be applied to trapMF. Label S′ can be represented as the 3-tuple (S, α, β). The support for this label, FLs2, is computed in Eq. (3):
where lS and rS are respectively the right and the left extreme of the support of S, and FLS is the size of the support of S [19].
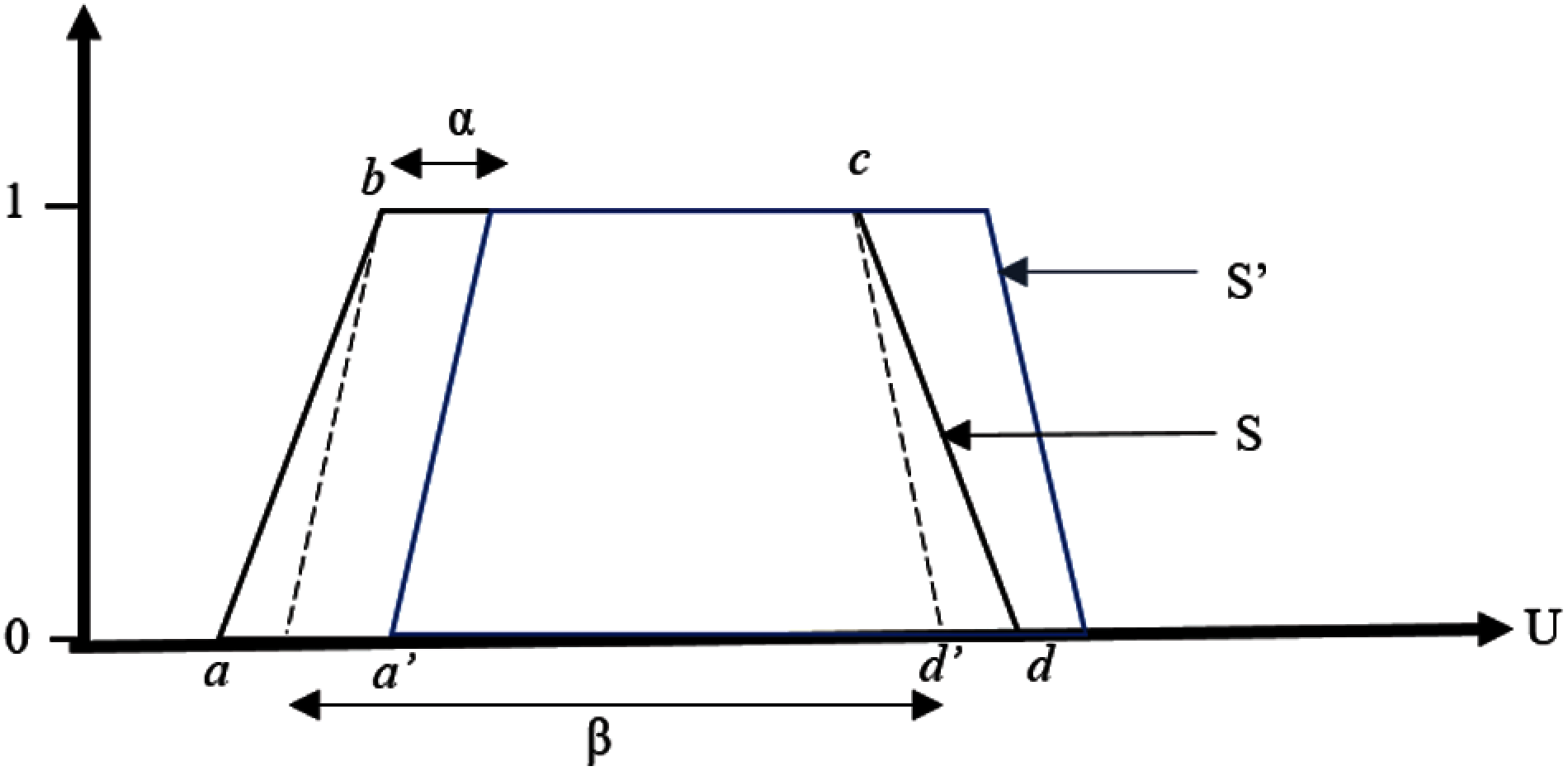
Figure 3: Original lateral displacement and amplitude variation of the linguistic label S
To show the enhancement of the tuning method, the lateral adjustment is modified so that it has similar range with the applied amplitude, to ensure better stability and accuracy of the MF. Hence, the proposition of the alignment of amplitude and lateral adjustment of the IT2 trapMF is α = (d − a) − β. To ensure the validity of the amplitude and lateral adjustment cooperation, testing is done with both original adjustment with the new proposed adjustment. Fig. 4 shows the lateral displacement and amplitude variation in this research.
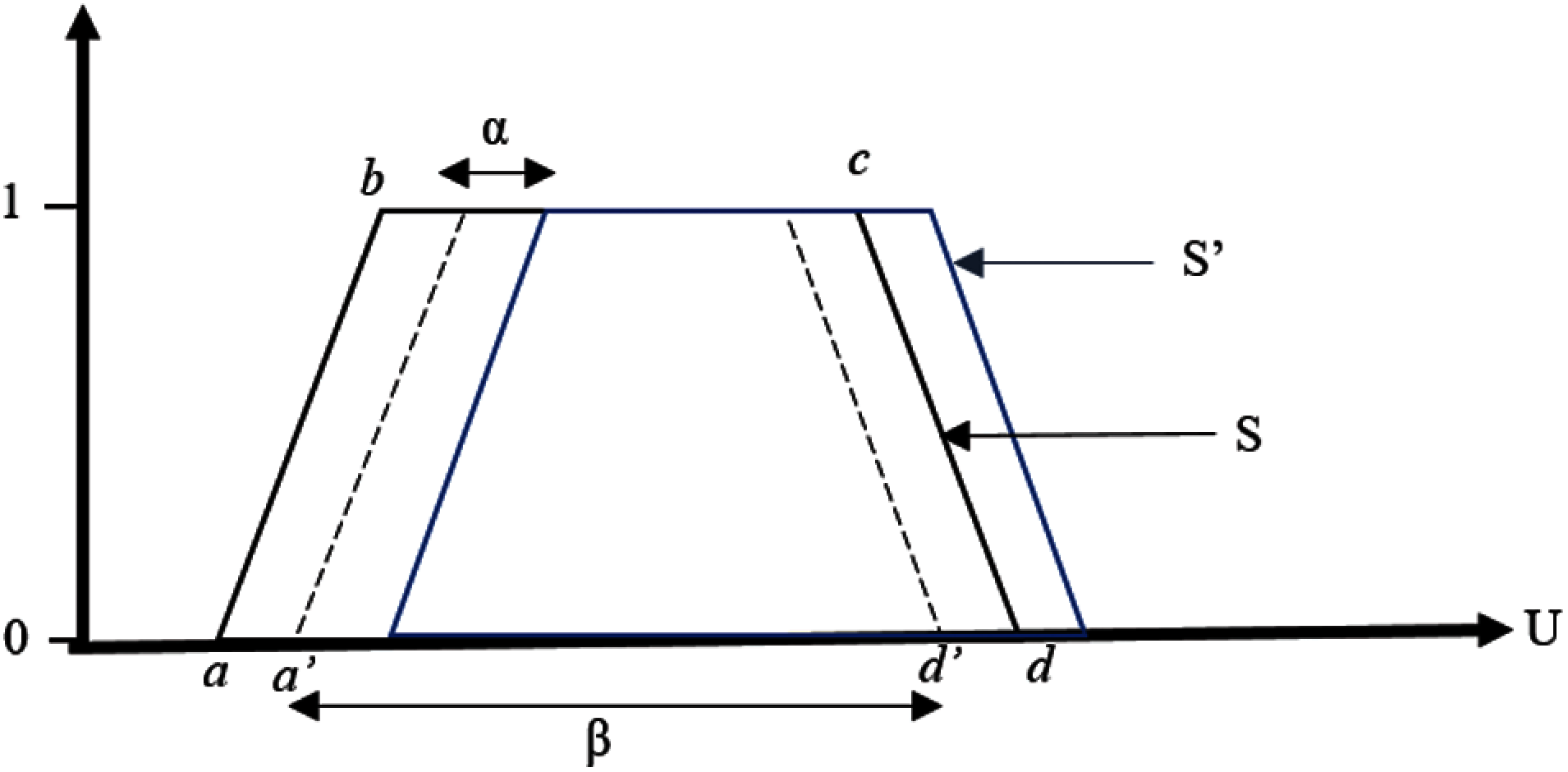
Figure 4: Proposed lateral displacement and amplitude variation
Based on Tab. 1, the initial value set for W is 0.05 to test for any changes of amplitude. Hence, the novelty of this approximation is where the adjustment of weak tuning has direct synergy with theoretical calculation of lateral tuning. While lateral tuning by theory is applied to shift MF to left or right, it is now used for parameter adjustments together with weak tuning. The motivation of this cooperation is the risk of the model to reach sub-optimal result. The cooperative approximation will fully utilize the characteristics of genetic tuning which leads to better performance of FSs in term of accuracy, specifically for trapMF IT2.
Based on the Gaussian output, the parameter center, c and sigma σ, mathematical model to construct fuzzy type 1 (FT1) trapMF is performed, as explained in [7]. Next, evaluation of the proposed method is done using a function called \texttt{evalmf()} in Matlab Fuzzy Logic Tool. Algorithm 1 shows the construction of FT1 trapMF after obtaining the Gaussian output for FIS:

FIS process in Algorithm 1 is repeated to generate IT2 trap FCM. Center, c and sigma, σ generated from the Gaussian output produce the UMF of the IT2 trap MF with four parameters a, b, c and d as described in [7]. Fig. 5 shows the FT1 trapMF produced by the proposed method. Afterward, LMF is generated based on the UMF and FOU. The LMF is constructed based on genetic weak tuning used to tune MFs. The parameters obtained from FT1 trapMF is combined with ignorance function, which is proportional to the MF amplitude. Fig. 6 shows the continuation of fuzzy inference process with FCM to complete the IT2 trapMF.
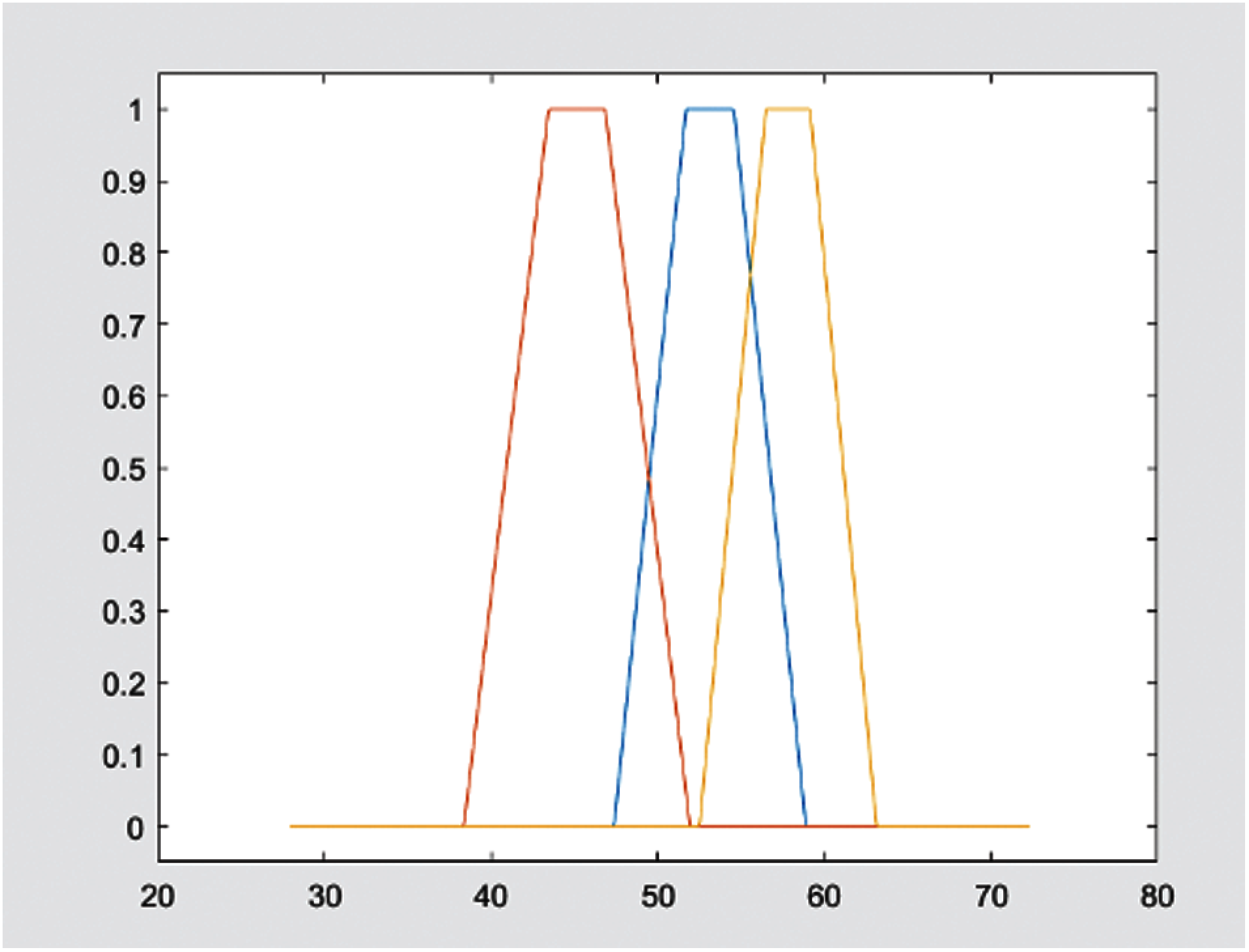
Figure 5: FT1 trapMF
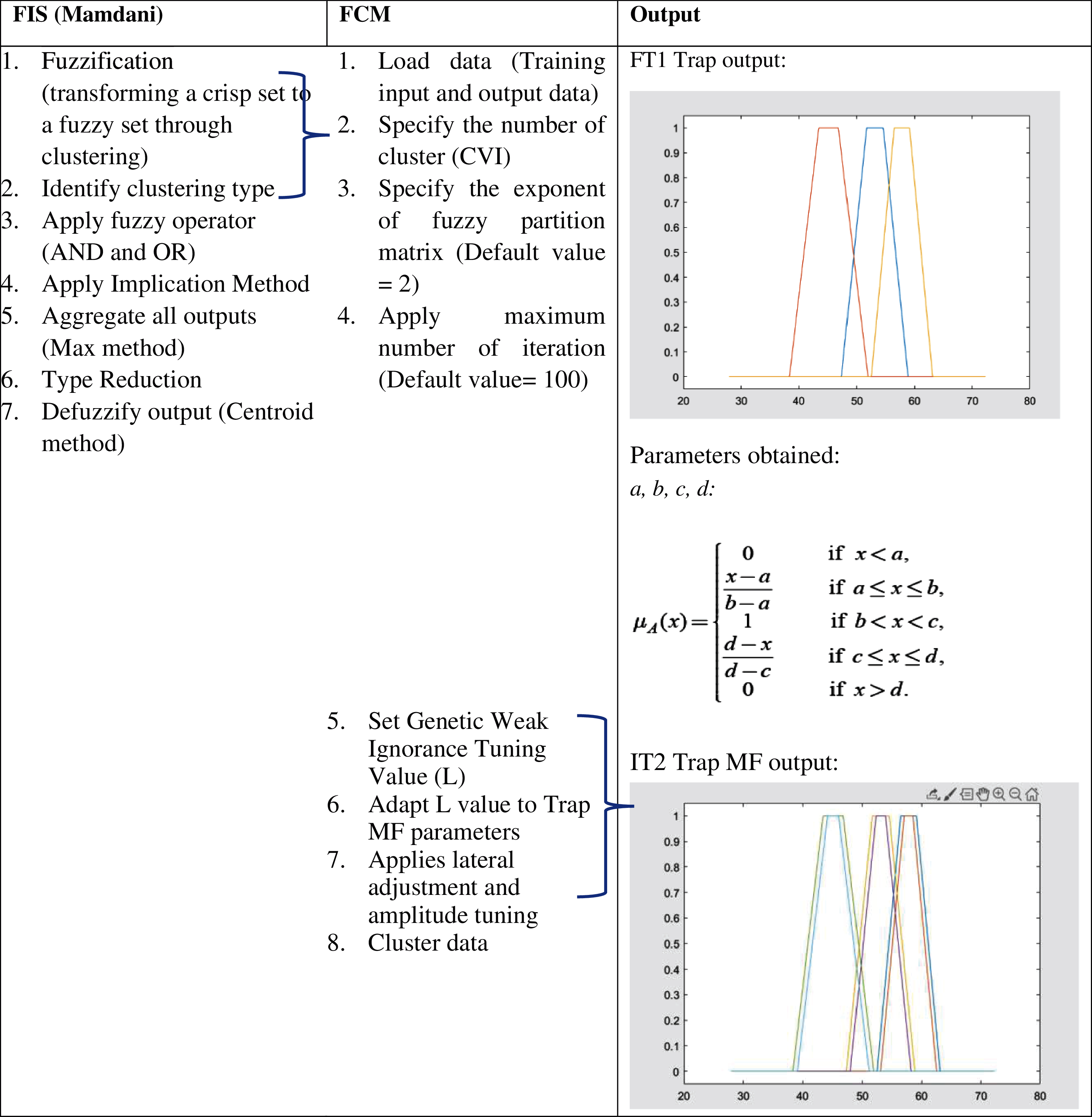
Figure 6: Fuzzy inference process with FCM for IT2 trapMF
Based on Fig. 6, fuzzification process determines the correlating degree of membership for UMF and LMF from the rule antecedent which generates two fuzzy values. Next, fuzzy operators are applied where the maximum value is obtained from the UMF and the minimum value is obtained from LMF [20]. In the implication phase, the rule firing will clip and scale the UMF and LMF of the output to produce the output fuzzy sets. Similar to FIS model for FT1 trapMF, max operator is used for aggregation phase which produces the final aggregated fuzzy output. The distinct phase in IT2 FIS is the type reduction. In order to generate the final crisp output, the aggregated fuzzy set is reduced to FT1 fuzzy set, which is the range with lower (CL) and upper limit (CR). It is frequently referred as the IT2 centroid, which is based on Eq. (4) [21]:
where
N = output variables
Xi = ith output value
μumf = UMF
μlmf = LMF
L and R = switch points estimated by type reduction method.
To estimate the values for CL and CR, iterative type-reduction methods are used [20]. For this research, Enhanced Iterative Algorithm with Stop Condition (EIASC) is used due to its significant improvement in performance compared to other methods [20,22–24].
The approximation of the genetic weak tuning in trapMF is initialized with the parameters for UMF. The equation of the straight line between parameter b and c is ignored due to the fact that the amplitude and lateral approximation only involve the intervals between parameter a to b, and parameter c to d. The calculation for c to d (straight vertical line of trapMF) will be similar since the MF involved in symmetrical. Algorithm 2 summarizes the construction IT2 trapMF after obtaining the FT1 trapMF output for FIS:

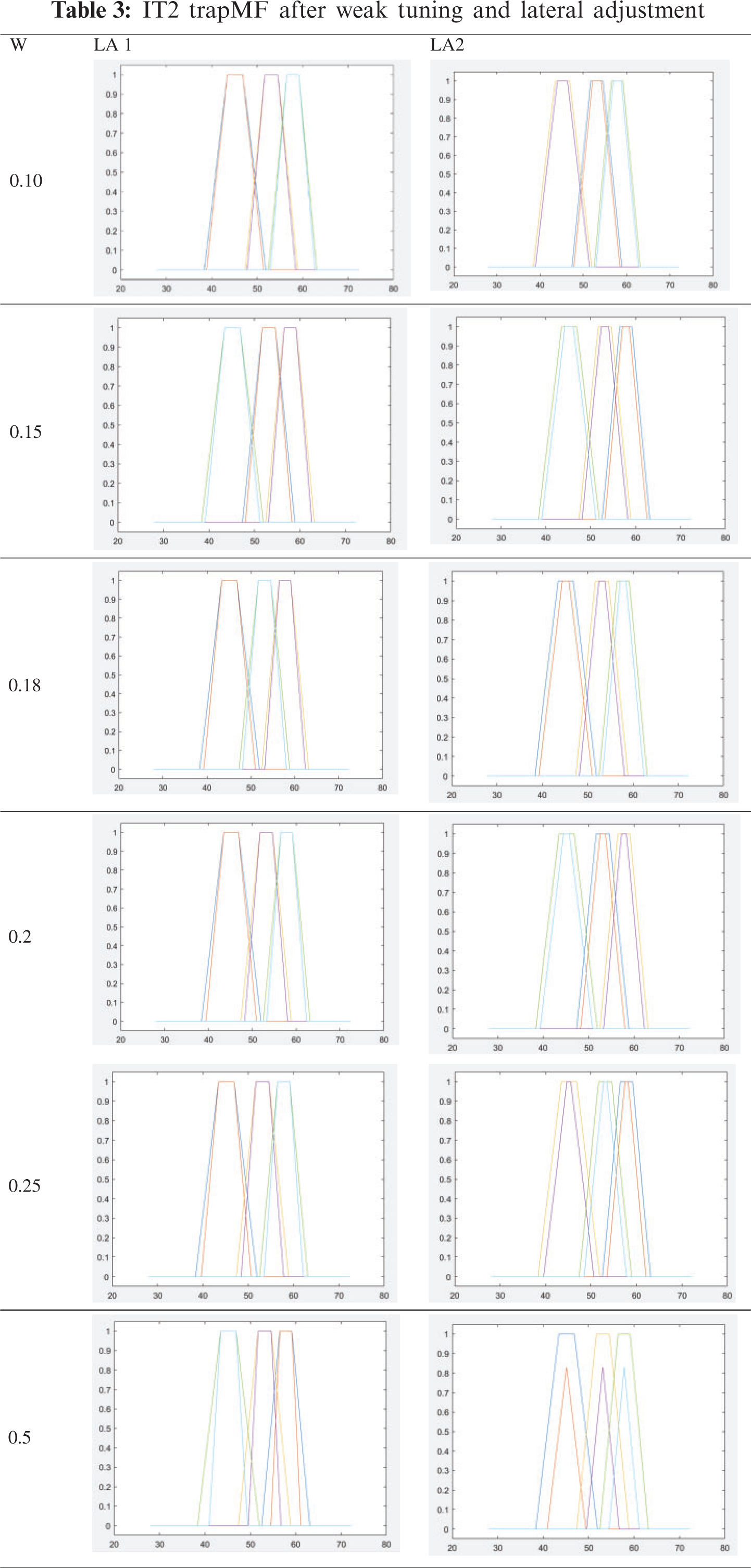
For the purpose of testing the theory, the same dataset to generate FT1 trapMF from Gaussian output is used to ensure the continuation of research objective, which is to generate IT2 trapMF from FCM. The total of six datasets, (QoS, Iris, Abalone, HCV, BirchSet, Europe), which are popular among benchmark datasets are prepared to test for result accuracy [25–29]. Tab. 1 shows the range of W parameter used for weak tuning, with trapMF parameters involved for lateral adjustments. Two types of lateral adjustment are tested in this research, LA1 where parameter a and b of trapMF are adjusted and LA2 where all four trapMF parameters, a, b, c and d are affected in the lateral adjustments.
First amplitude parameter W 0.05 is performed in all datasets, and according to result, IT2 trapMF is failed to be generated as the number of uncertainties becomes close 0, with values of UMF and LMF are the same except for very slight difference. Fig. 7 shows the generated trapMF with W = 0.05 for both lateral adjustment 1 (LA1) and 2 (LA2). No further testing is done for this parameter value.
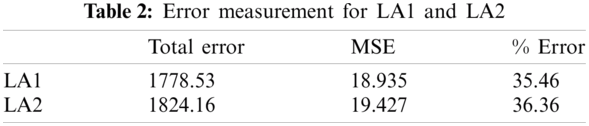
Since this method comes from GA components, further evaluation of the output is performed using MSE to test for accuracy of FIS using the IT2 trapMF. The MSE is measured to identify the best W value for IT2 trapMF and which lateral adjustment is better suited to construct a more accurate MF. Tab. 2 summarizes the error measurement for both LA 1 and LA2.
From the error measurements, it is proven that genetic weak tuning can be used to construct IT2 trapMF, with the cooperation of lateral adjustment. Tab. 2 indicates that less error is obtained through L1, where the adjustment adapted in the weak tuning is more accurate for parameter a and d of the trapMF. Tab. 3 shows that by increasing the weak tuning until maximum ignorance W = 5 (not shown in Tab. 3) will decrease the accuracy of the model. Hence, the optimum value of W which successfully construct good interval for IT2 trapMF can be observed through the MF input values. W = 0.15 is considered to be optimum since it produces the least error, but further study on different size of dataset might result in different optimum W.
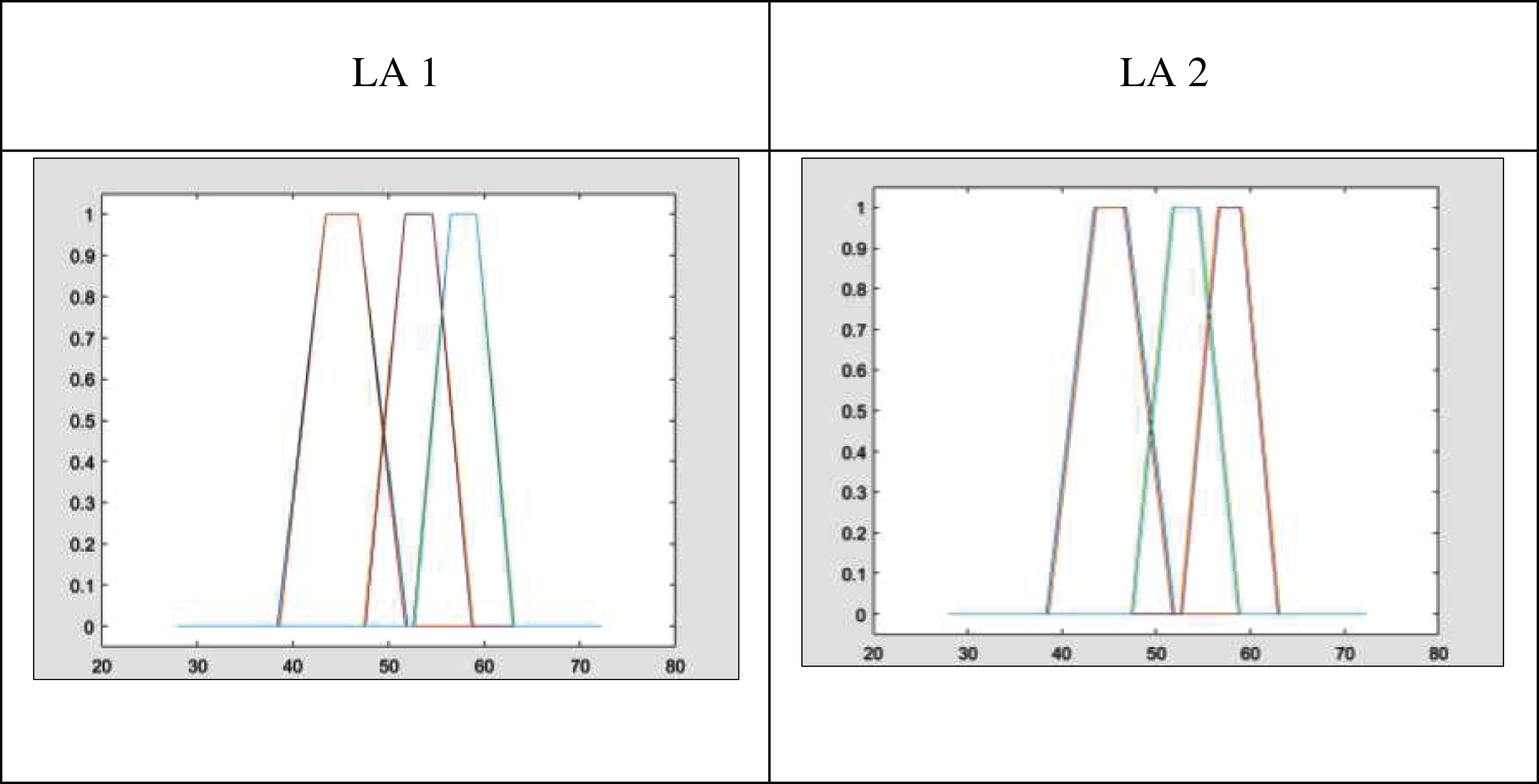
Figure 7: IT2 trapMF with W = 0.05.
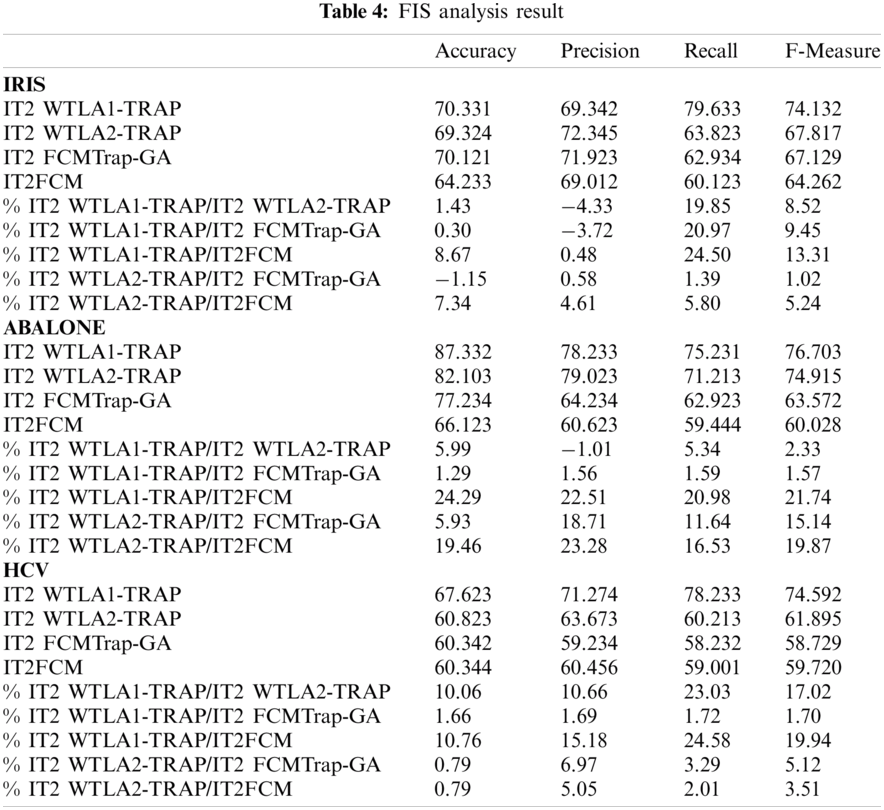
In this section, the proposed method that construct IT2 Trap for FCM using both tuning methods is implemented in FIS. The output of FIS is then evaluated against the other FIS with input MFs from classic IT2FCM and trapezoidal input MFs optimized using GA (IT2 FCMTrap-GA). The proposed algorithm with the discussed two tuning methods are named IT2WTLA1-TRAP and IT2WTLA2-TRAP respectively.
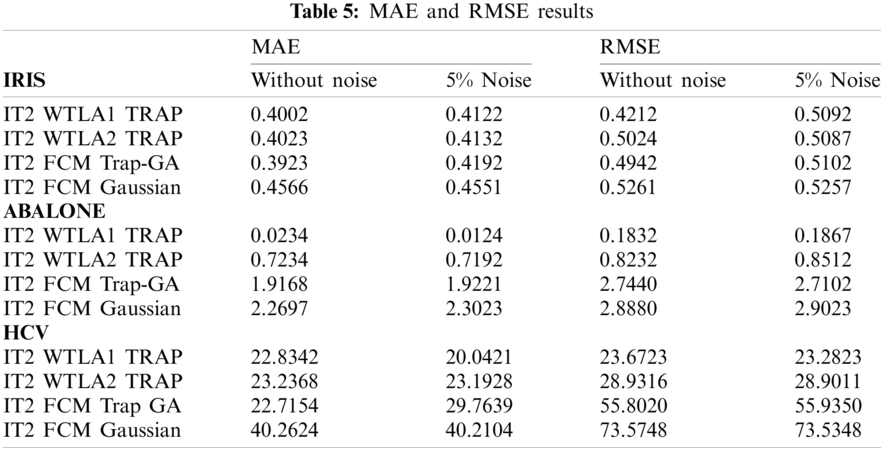
Accuracy of the FIS are measured through several evaluation metrics, which are Classification accuracy, Precision, Recall, F-Measure. Confusion matrix is used to obtain the evaluation metrics. Other evaluation measurements to measure the performance are Mean Absolute Error (MAE) and Root Mean Square Error (RMSE).
Different tuning in the proposed method also being evaluated against each other to identify which tuning method has better performance. As for example, the calculation to get the percentage of difference is described in Eq. (5):
Referring to Tab. 4, the improvement of performance for the proposed algorithm is evident. In the tables, negative (−) values indicate lower values (lower performance) for the evaluation metrics. For example, in Iris dataset, IT2FCMtrap-GA has 1.15% higher accuracy than IT2 WTLA2-TRAP. The small difference in percentage shows less impact of performance evaluation since IT2 WTLA1-TRAP shows improvement in accuracy by 0.3% and 8.67% compared to IT2FCMtrap-GA and IT2FCM respectively. Looking at average performance for dataset Iris, IT2 WTLA1-TRAP has good improvement in term of accuracy compared to IT2 WTLA2-TRAP and the other two algorithms. Abalone and HCV datasets show promising performance for both IT2 WTLA1-TRAP and IT2 WTLA2-TRAP. IT2 WTLA1-TRAP has slightly lower values by 4.33% and 1.01% compared to IT2 WTLA2-TRAP for Iris and Abalone dataset, respectively. The precision performs better in dataset HCV with 10.66% higher precision. Tab. 5 shows the results of MAE and RMSE for all datasets. Shaded cells in the table indicate the lowest value. Cells with lighter shades indicate second lowest value. Two sets of datasets are evaluated: datasets without noise and datasets with 5% noise. Based on the results, IT2 WTLA1 TRAP obtains the lowest value of both RMSE and MAE by about 83.3% from all the values compared in the evaluation. IT2 WTLA1 TRAP achieves stronger performance by having all lower values compared to IT2 WTLA2 TRAP. This indicates the best tuning method for the proposed algorithm is IT2 WTLA1 TRAP. In overall observation, IT2 WTLA2 TRAP has promising performance whereby it achieves 75% lower MAE and RMSE values compared to IT2 FCM Trap-GA and IT2 FCM Gaussian. It is also proven that IT2 WTLA1 TRAP and IT2 WTLA2 TRAP are executing well even with noise. Both methods attain good performance with 5% noise with minimal decline of performance. As an example, MAE value for WTLA1 TRAP has increased value (less performance) between 1.2% and 14%. For RMSE, declined performance are between 0.2% and 17%.
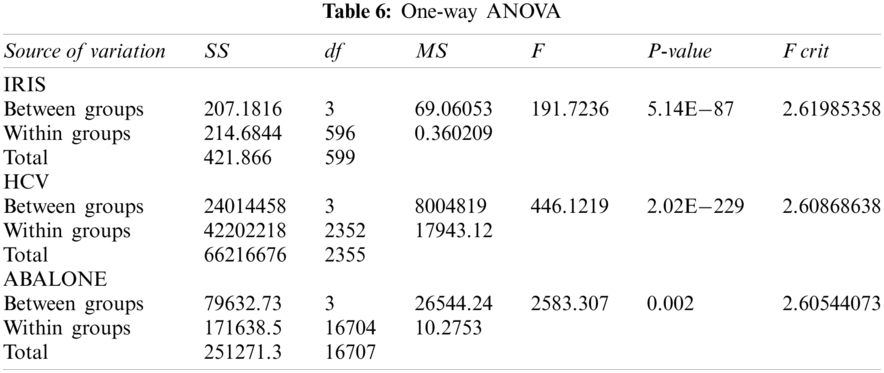
Statistical test is carried out after obtaining all results to further analyze the significance of the experiment results. One-way analysis of variance or ANOVA (Tab. 6) is utilized to identify whether there is any statistically significant dissimilarity between the means of independent labels or groups. From Tab. 6, it is proven that the null hypothesis is rejected based on higher F Values as compared to F Critical values for all datasets. In addition, p value less than 0.05 is achieved which indicates that the test is statistically significant different.
In this paper, we presented a method to generate IT2 trapMF by using approximation of genetic weak tuning and lateral adjustment. The UMF is initially prepared, and the LMF is approximated by the combination of the two elements of genetic algorithm. The result shows that it successfully generates symmetrical trapMF with minimum W value of 0.10. From the results, it shows that weak tuning and lateral adjustment with two lower limit a and upper limit d of trapMF is more accurate than involving all four parameters of trapMF. The contribution of this work includes providing alternative IT2 MFs, constructed based on FCM outcomes, that can be used especially in the event that Gaussian MF is not performing well. Furthermore, the proposed approach provides an optimum way to construct the trapMF. By having more options of MFs, IT2 FIS can be applied to a wider range of practical applications such as prediction, analytics and rule-based solutions. However, further study on optimum W value can be done to generate different shapes of MF, either symmetrical or asymmetrical. Based on the forecasting results, it shows that it gives better performance in term of accuracy as compared to other methods. Another limitation of this work is that the proposed method is only tested on mamdani FIS. Furthermore, amplitude tuning, and lateral adjustments performed to construct IT2 Trap MF are applied simultaneously; separate execution of the two algorithms was not investigated.
There are several areas of improvement that can be incorporated in the present work and can be further extended. The possible future directions are discussed as follows:
(1) Different genetic tuning methods other than amplitude and lateral adjustments can be explored to assist on IT2 MF constructions for different shapes of MFs.
(2) Investigations on single amplitude tuning or lateral adjustments to construct IT2 trapMF with larger range without limited to weak ignorance function.
(3) Introducing a method that can heuristically produce the correct trapezoidal shapes given any types of data. The improvement in term of accuracy or precision, for example, can be further explored.
(4) Optimizing IT2 FIS results through the application of other than GA in MF generation processes.
(5) Investigating of the IT2 MFs generated by FCM being applied in the general fuzzy type 2 FIS. The performance effects in various general fuzzy type 2 applications can be further explored.
Acknowledgement: The research is carried out under the funding of the Fundamental Research Grant Scheme, granted by the Ministry of Higher Education, Malaysia, and Yayasan Universiti Teknologi PETRONAS, granted by Universiti Teknologi PETRONAS.
Funding Statement: The works presented in this paper are part of an ongoing research funded by the Fundamental Research Grant Scheme (FRGS/1/2018/ICT02/UTP/02/1); a grant funded by the Ministry of Higher Education, Malaysia and the Yayasan Universiti Teknologi PETRONAS grant (015LC0-274 and 015LC0-311).
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. Rubio and O. Castillo, “Interval type-2 fuzzy clustering for membership function generation,” in 2013 IEEE Workshop on Hybrid Intelligent Models and Applications (HIMASingapore, pp. 13–18, 2013. [Google Scholar]
2. J. E. Rodríguez-Sánchez, M. G. Orozco-del-Castillo, A. Rodríguez-Castellanos, R. Ávila-Carrera and C. Valle-Molina, “A fuzzy inference system applied to estimate the error in the recovery of the Green’s function by means of seismic noise correlations,” Journal of Geophysics and Engineering, vol. 15, pp. 2110–2123, 2018. [Google Scholar]
3. K. A. Ahmad, S. L. S. Abdullah, O. Mahmod and M. A. Bakar, “Induction of membership function and fuzzy rules for Harumanis classification,” Journal of Fundamental and Applied Sciences, vol. 10, no. 1S, pp. 1202–1215, 2018. [Google Scholar]
4. U. Ghani, I. Bajw and A. Ashfaq, “A fuzzy logic based intelligent system for measuring customer loyalty and decision making,” Symmetry, vol. 10, no. 12, pp. 1–19, 2018. [Google Scholar]
5. P. Pancardo, J. A. Hernández-Nolasco and F. Acosta-Escalante, “A fuzzy logic-based personalized method to classify perceived exertion in workplaces using a wearable heart rate sensor,” Mobile Information Systems, vol. 2018, pp. 1–7, 2018. [Google Scholar]
6. I. Subbotin, “Trapezoidal fuzzy logic model for learning assessment,” 2014. [Online]. Available: https://www.researchgate.net/publication/263582488_Trapezoidal_Fuzzy_Logic_Model_for_Learning_As- https://sessment. [Google Scholar]
7. J. Tyagi and N. Verma, “Optimization of fuzzy C means clustering using genetic algorithm for an image,” International Journal of Computer Applications, vol. 121, no. 17, pp. 29–32, 2015. [Google Scholar]
8. S. H. Khairuddin, M. H. Hasan and M. A. Hashmani, “Integration of cluster centers and gaussian distributions in fuzzy c-means for the construction of trapezoidal membership function,” Mathematics and Statistics, vol. 8, no. 5, pp. 559–565, 2020. [Google Scholar]
9. J. Sanz, A. Fernández, H. Bustince and F. Herrera, “A genetic tuning to improve the performance of fuzzy rule-based classification systems with interval-valued fuzzy sets: Degree of ignorance and lateral position,” International Journal of Approximate Reasoning, vol. 52, no. 11, pp. 751–766, 2011. [Google Scholar]
10. R. Alcalá, J. Alcalá-Fdez, M. J. Gacto and F. Herrera, “Rule base reduction and genetic tuning of fuzzy systems based on the linguistic 3-tuples representation,” Soft Computing, vol. 11, no. 5, pp. 401–419, 2007. [Google Scholar]
11. J. A. Sanz, A. Fernández, H. Bustince and F. Herrera, “Improving the performance of fuzzy rule-based classification systems with interval-valued fuzzy sets and genetic amplitude tuning,” Information Sciences, vol. 180, no. 19, pp. 3674–3685, 2010. [Google Scholar]
12. J. Qin and X. Lew, “Type-2 fuzzy sets and its extensions,” Type-2 Fuzzy Decision-Making Theories, Methodologies and Applications, pp. 1–11, 2019. [Google Scholar]
13. S. Guillaume, “Designing fuzzy inference systems from data: An interpretability-oriented review,” IEEE Transactions on Fuzzy Systems, vol. 9, no. 3, pp. 426–443, 2001. [Google Scholar]
14. A. Kowalczyk and A. Pelikant, “Implementation of automatically generated membership functions based on grouping algorithms,” in EUROCON, 2007—The Int. Conf. on Computer as a Tool, Warsaw, Poland, 2007. [Google Scholar]
15. P. N. Srinivasu, J. G. SivaSai, M. F. Ijaz, A. K. Bhoi, W. Kim et al., “Classification of skin disease using deep neural networks with MobileNet V2 and LSTM,” Sensors, vol. 21, no. 8, pp. 2852, 2021. [Google Scholar]
16. R. Panigrahi, S. Borah, A. K. Bhoi, M. F. Ijaz, M. Pramanik et al., “A consolidated decision tree-based instrution detection system for binary and multiclass imbalanced datasets,” Mathematics, vol. 9, no. 7, pp. 751, 2021. [Google Scholar]
17. J. Tamang, J. D. D. Nkapkop, M. F. Ijaz, P. K. Prasad, N. Tsafack et al., “Dynamical properties of ion-acoustic waves in space plasma and its application to image encryption,” IEEE Access, vol. 9, pp. 18762–18782, 2021. [Google Scholar]
18. F. Gomide, Uncertain rule-based fuzzy logic systems: Introduction and new directions. Cham, Switzerland: Springer International Publishing, 2003. [Google Scholar]
19. R. Alcalá, J. Alcalá-Fdez and F. Herrera, “A proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection,” IEEE Transactions on Fuzzy Systems, vol. 15, no. 4, pp. 616–635, 2007. [Google Scholar]
20. D. Wu and M. Nie, “Comparison and practical implementation of type-reduction algorithms for type-2 fuzzy sets and systems,” in 2011 IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2011Taipei, Taiwan, 2011. [Google Scholar]
21. J. M. Mendel, H. Hagras, W. W. Tan, W. W. Melek and H. Ying, Introduction to type-2 fuzzy logic control: Theory and applications. Hoboken, New Jersey, USA: Wiley-IEEE Press, 2014. [Google Scholar]
22. C. E. Celemin and M. A. Melgarejo, “A proposal to speed up the computation of the centroid of an interval type-2 fuzzy set,” Advances in Fuzzy Systems, vol. 2013, pp. 1–18, 2013. [Google Scholar]
23. W. E. Sari, O. Wahyunggoro, S. Fauziati and A. I. Cahyadi, “State of charge estimation of lithium polymer battery using ANFIS and IT2FLS,” in Proc.—2016 2nd Int. Conf. on Science and Technology-Computer, ICST 2016, Yogyakarta, Indonesia, 2017. [Google Scholar]
24. C. Chen, R. John, J. Twycross and J. M. Garibaldi, “A direct approach for determining the switch points in the Karnik–Mendel algorithm,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 2, pp. 1079–1082, 2018. [Google Scholar]
25. R. A. Fisher, “The use of multiple measurements in taxonomics problems,” Annals of Human Genetics, vol. 7, no. 2, pp. 87–193, 1936. [Google Scholar]
26. W. Nash, T. L. Sellers, S. R. Talbot, A. J. Cawthorn and W. B. Ford, “The Population Biology of Abalone (_Haliotis_ species) in Tasmania. I. Blacklip Abalone (_H. rubra_) from the North Coast and Islands of Bass Strait,” Sea Fisheries Division, Technical Report No. 48, 1994. [Google Scholar]
27. G. Hoffmann, A. Bietenbeck, R. Lichtinghagen and F. Klawonn, “Using machine learning techniques to generate laboratory diagnostic pathways—A case study,” Journal of Laboratory and Precision Medicine, vol. 3, no. 6, pp. 1–10, 2018. [Google Scholar]
28. T. Zhang, R. Ramakrishnan and M. Livny, “BIRCH: A new data clustering algorithm and its applications,” Data Mining and Knowledge Discovery, vol. 1, pp. 141–182, 1997. [Google Scholar]
29. P. Fränti, M. Rezaei and Q. Zhao, “Centroid index: Cluster level similarity measure,” Pattern Recognition, vol. 47, no. 9, pp. 3034–3045, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |