Computers, Materials & Continua DOI:10.32604/cmc.2022.021847
Article

An Optimized Algorithm for CR-MIMO Wireless Networks

Imran Khan1, Fahd N. Al-Wesabi2, Marwa Obayya3, Anwer Mustafa Hilal4, Manar Ahmed Hamza4, Mohammed Rizwanullah4, Fahad Ahmed Al-Zahrani5, Hirofumi Amano6 and Samih M. Mostafa7,*

1Department of Electrical Engineering, University of Engineering & Technology, Peshawar, Pakistan
2Department of Computer Science, King Khalid University, Muhayel Aseer, KSA
3Department of Biomedical Engineering, College of Engineering, Princess Nourah bint Abdulrahman University, Saudi Arabia
4Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
5Computer Engineering Department, Umm Al-Qura University, Mecca, 24381, Saudi Arabia
6Research Institute for Information Technology, Kyushu University, Fukuoka, 819-0395, Japan
7Computer Science-Mathematics Department, Faculty of Science, South Valley University, Qena, 83523, Egypt
*Corresponding Author: Samih M. Mostafa. Email: samih_montser@sci.svu.edu.eg
Received: 16 July 2021; Accepted: 17 August 2021

Abstract: With the rapid development of wireless communication technology, the spectrum resources are increasingly strained which needs optimal solutions. Cognitive radio (CR) is one of the key technologies to solve this problem. Spectrum sensing not only includes the precise detection of the communication signal of the primary user (PU), but also the precise identification of its modulation type, which can then determine the a priori information such as the PU’ service category, so as to use this information to make the cognitive user (CU) aware to discover and use the idle spectrum more effectively, and improve the spectrum utilization. Spectrum sensing is the primary feature and core part of CR. Classical sensing algorithms includes energy detection, cyclostationary feature detection, matched filter detection, and so on. The energy detection algorithm has a simple structure and does not require prior knowledge of the PU transmitter signal, but it is easily affected by noise and the threshold is not easy to determine. The combination of multiple-input multiple-output (MIMO) with CR improves the spectral efficiency and multi-path fading utilization. To best utilize the PU spectrum while minimizing the overall transmit power, an iterative technique based on semidefinite programming (SDP) and minimum mean squared error (MMSE) is proposed. Also, this article proposed a new method for max-min fairness beamforming. When compared to existing algorithms, the simulation results show that the proposed algorithms perform better in terms of total transmitted power and signal-to-interference plus noise ratio (SINR). Furthermore, the proposed algorithm effectively improved the system performance in terms of number of iterations, interference temperature threshold and balance SINR level which makes it superior over the conventional schemes.

Keywords: Cognitive radio; spectrum utilization; bandwidth; primary user

1  Introduction

With the rapid growth in demand for wireless communication services, available spectrum resources have become increasingly scarce, and basically all the available spectrum resources have been licensed to specific user groups. However, the united states federal communications commission (FCC) conducted a large number of actual measurements on the efficiency of wireless spectrum usage and found that at any given moment, the spectrum resources used by consumers only account for 2% to 6% of all available spectrum resources [1–6]. Therefore, the reason for the “scarcity” of wireless spectrum resources is not the scarcity of the spectrum resources itself, but that the spectrum utilization is too low. Therefore, wireless networks are facing serious problems of relative “shortage” and “waste” of spectrum resources. The root cause of these problems lies in the contradiction that the centralized static network is difficult to adapt to the dynamic changes of the environment and avoiding or eliminating the interference to the primary user (PU), while ensuring the normal communication of the secondary user (SU) [7–11]. An effective method is to use the beamforming technology for interference control, which well solves the coexistence problem of the PU and the cognitive user (CU) [2–4]. This is because the beamforming technology is a spatial interference suppression technology [8–15], which can adaptively adjust the antenna array pattern according to the changes in the environment, and align the main beam at the desired signal with zero trapping or the low sidelobe is aligned with the interference signal, which has the characteristics of suppressing interference, improving the signal transmission quality and increasing the spectrum utilization. By selecting the optimal beamforming weight vector at the transmitting and receiving end, the communication quality of the SU can be optimized while suppressing the interference to the primary user, and the normal communication between the CU and the PU can be ensured in the same frequency band [16]. One of the effective methods to solve these problems is cognitive radio (CR) technology [17–18]. CR is a new intelligent wireless communication technology. Its emergence has changed the way in which the spectrum resources are used exclusively by PU, allowing unlicensed users (SU) with cognitive radio functions to use it. The wireless communication environment performs interactive sensing and automatically changes its own transmission and reception parameters, and dynamically reuses the authorized spectrum resources without causing interference to the PU, thereby significantly improving the spectrum utilization [19–25].

In recent years, with the continuous deepening of CR technology research, researches on the beamforming algorithms under the cognitive environment continues to emerge. Literature [26–29] studied the standard form and solution of the optimization problem of beamforming in the downlink under different objective functions and constraints. These methods can basically be summarized into two categories. The first one is the beamforming algorithm based on convex optimization. The other is to obtain the optimal weight vector through an iterative algorithm. Literature [30–33] studied the beamforming problem in the multi-cast transmission. This type of problem can generally be transformed into a quadratic constrained quadratic programming (QCQP) problem, which is non-convex. Through corresponding transformation of the QCQP problem and relaxation of the constraint conditions, a positive semidefinite programming (SDP) problem is formed using the interior point method to obtain the optimal solution. The scenarios studied in the literature [26–33] are configured with multiple antennas at the transmitting end and a single antenna at the receiving end. If multiple antennas are configured at the transmitting and receiving end at the same time, the system performance will inevitably be improved. Literature [34–36] studied the beamforming problem in MIMO networks. It uses the dual characteristics of the signal-to-interference and noise ratio (SINR) in the uplink-downlink to divide a non-convex optimization problem into several convex optimization problems. But this method is only suitable for the optimization problem of minimizing the transmission power.

This paper studies the beamforming algorithms under different optimization objectives in a MIMO CR environment, and considers two types of optimization problems. 1) Under the condition that the communication quality requirements of the CUs are met and the interference to the PU is less than the threshold value, the total transmission power is minimized. In this paper, using positive SDP and MMSE criterion, a MIMO cognitive beamforming algorithm that minimizes the transmission power is proposed. Compared with the existing algorithms, the transmission power is reduced and the system performance is improved. 2) Maximize the minimum cognitive user SINR under the condition that the interference to the PU is less than the threshold and the total transmit power is limited. As we all know, in the MIMO cognitive network, there are multiple CUs. To ensure that each user has a fair chance to communicate normally, the balance of the cognitive network is also an important issue at this time. However, the author has consulted many domestic and foreign literature, and the article on the issue of equalization in MIMO cognitive networks has not been reported. Therefore, a beamforming algorithm of SINR equalization is proposed to ensure that every user has a fair chance to perform normal operations. The scenario studied in this paper is to configure multiple antennas at both the transmitting and receiving end, and the corresponding weight vectors needs to be obtained at the same time. This is a bottleneck problem to be solved. To this end, first fix the weight vector of the receiving end and assign an initial value to it, so that the original problem is transformed into a downlink beamforming optimization problem, and then the SDP and interior point method is used to obtain the weight vector of the transmitting end. Then, fix the weight vector of the transmitting end, and use the MMSE criterion to further obtain the weight vector of the receiving end. After continuous loop iteration, until the objective function converges, the weight vector of the optimal beamforming is finally obtained. The simulation results show that the proposed algorithm has better performance and can effectively solve the MIMO cognitive wireless network beamforming issues.

In the text, bold uppercase, bold lowercase and normal lowercase letters represent matrix, row vector and scalar respectively; (⋅)H means conjugate transpose of matrix or vector; E{⋅} means to take expectation; rank(⋅) and Tr(⋅) respectively represent the rank of the matrix and the trace of the matrix; ∥⋅∥ represents the Euclidian norm of the vector; εmax(A) represents the eigenvector corresponding to the largest eigenvalue of matrix A; I represents the identity matrix.

2  System Model

Consider a multi-user cognitive MIMO communication system. The CU communicates with the PU in the same frequency spectrum, and the CU adopts an underlay access method based on interference temperature. Here, the concept of interference temperature [37] is similar to noise temperature. It is defined in the receiving RF front end of a wireless device and is used to measure the amount of interference received by the receiver in a certain geographical location and frequency band. Its mathematical expression is Ti=I(fc,B)/kB. Among them I(fc,B) means that the center frequency is fc, and the bandwidth is the average interference power received by the receiver in the B band and k=1.38×10−23J/K is the Boltzmann constant.

As shown in Fig. 1, the system includes a main network and a cognitive network. The cognitive network includes a transmitting base station and K number of SUs. The base station is configured with Ns antennas, and the k-th user is configured with Mk antennas. The main network includes a transmitting base station with Np antennas and a PU with Mp antennas. The signal xs∈CK×1 sent from the cognitive base station is

xs=Tss (1)

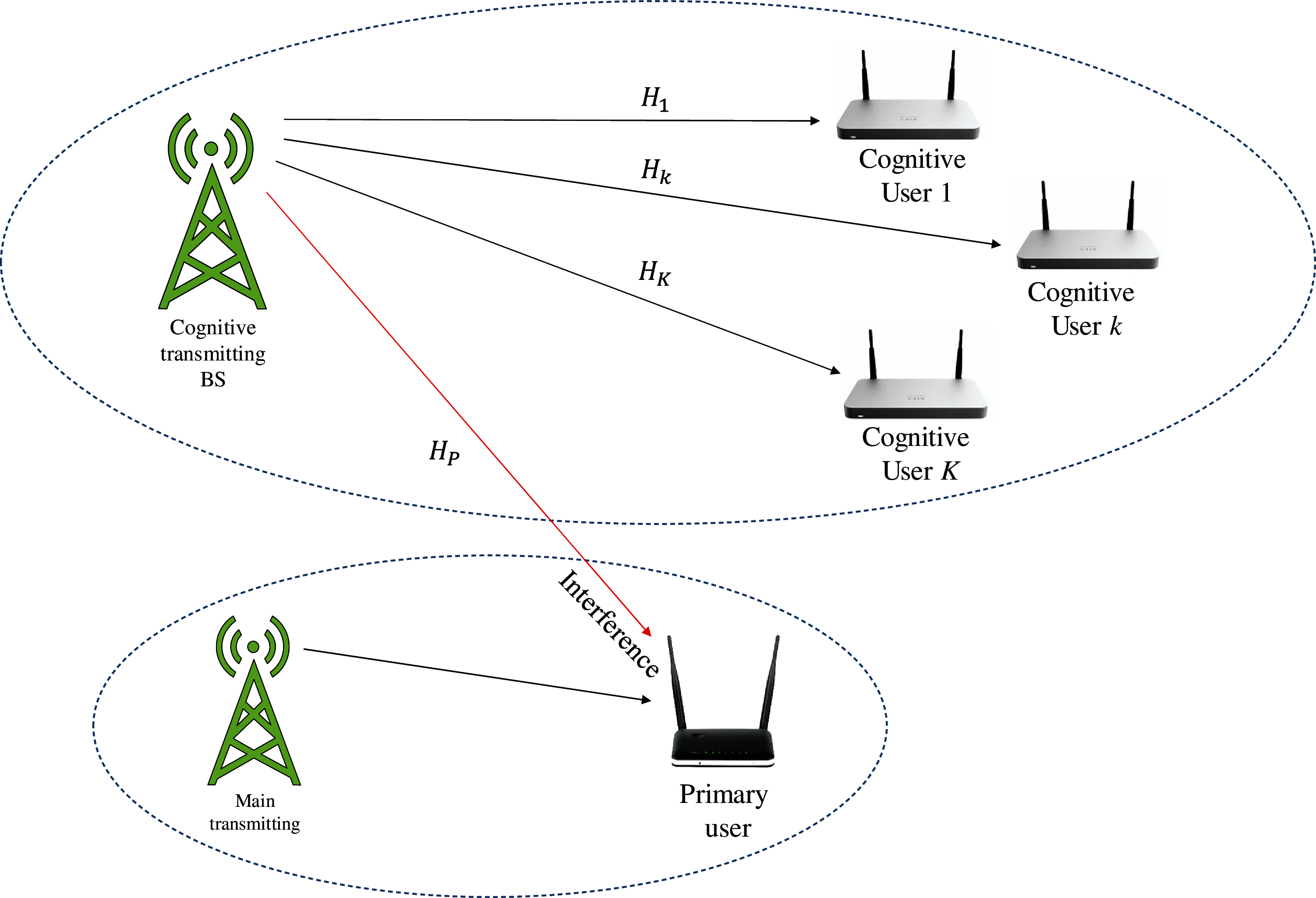
Figure 1: Proposed system model

Here, s=[s1…sk…sK], where sk(E{|sk|2}=1) represents the signal sent to the k-th SU, Ts=[t1…tk…tK] means the k-th SU is in the weighting vector of the transmitter. Then, the signal received by the k-th SU is

yk=rkH(Hkxk+nk) (2)

Among them, rk∈CMk×1 is the normalized receiving end weight vector, that is, ∥rk∥F2=1, Hk∈CMk×Ns represents the channel between the cognitive transmitting base station and the k-th SU, nk∼CN(0,σn2I) represents the additive circular symmetric Gaussian white noise with a variance of σn2. In this paper, the interference of the PU to the CU is ignored [38]. Then the SINR of the k-th SU is

SINRk=E{|rkHHktksk|2}E{∑j=1,j≠kK|rkHHktjsj|2+|rkHnk|2}

=|rkHHktk|2∑j=1,j≠kK|rkHHktj|2+σk2 (3)

At the same time, the signal sent from the cognitive base station to the SU will cause interference to the PU, and the interference received by the PU is expressed as

INT=E{∑k=1K|rpHHptksk|2}=∑k=1K|rpHHptk|2 (4)

Among them, Hp∈CMp×Ns is the channel between the cognitive base station and the PU, and rp∈CMp×1(∥rp∥F2=1) is the weight vector of the PU receiving end. Because the main network rarely cooperates with the cognitive network, the PU reception weight vector is defined only by the main network channel. In addition, it is assumed that the reception weight vector rp of the PU, the channel Hp between the cognitive base station and the PU, and the interference temperature of the PU are all known. Under this system model, two types of optimization problems are studied: minimum transmit power and SINR equalization.

3  Minimum Transmit Power Optimization

The optimization goal of this section is to minimize the transmission power while ensuring that the communication quality of the SU reaches the given standard, and the interference to the PU is less than the given threshold. At this point, the problem can be described as

tkmin∑k=1K∥tk∥F2

subject to:

∑k=1K|rPHHptk|2≤β,k=1,…,K

|rPHHptk|2∑j=1,j≠kK|rkHHktj|2+σk2≥αk (5)

Among them, αk represents the minimum SINR that the k-th SU needs to meet, and β is the maximum interference threshold that the PU can tolerate. The first constraint in Eq. (5) indicates that the interference caused by the cognitive network to the PU must be less than β, and the second constraint indicates that each SU must meet its minimum SINR requirement.

It can be seen from Eq. (5) that there are two sets of variables in the problem to be optimized, and it is very difficult to solve them at the same time. This paper uses the method of distributed solution [39–41] to fix one set of variables to obtain another set of unknown value of the variable, and then find the value of the previous set of variables, and iterate alternately until the optimal solution is obtained. Here, first fix the receiving end weight vector rk and assign a set of initial values to it, so that the problem in Eq. (5) turns into a downlink MISO beamforming optimization problem.

According to aHb=Tr(baH), aHbbHa=Tr(bbHaaH) and Tr(AB)=Tr(BA), Eq. (5) can be transformed into

min∑k=1KTr(Tk)

subject to:

Tr(RkTk)−αk∑j≠kTr(RkTk)≥αkσk2

∑k=1KTr(RpTk)≤β

Tk≽0,rank(Tk)=1,k=1,…,K (6)

Among them, Tk=tktkH, Rk=HkHrkrkHHk, Rp=HpHrprpHHp, A≽0 means that matrix A is a positive semi-definite matrix. In Eq. (6), except for the constraint condition rank(Tk), the objective function and other constraint conditions are all linear expressions about Tk, and they are all convex functions. Therefore, the constraint condition is relaxed, and the non-convex constraint condition rank(Tk)=1 is removed (also increasing the range of feasible solutions to the problem), and the expression is

min∑k=1KTr(Tk)

subject to:

Tr(RkTk)−αk∑j≠kTr(RkTk)≥αkσk2

∑k=1KTr(RpTk)≤β

Tk≽0,k=1,…,K (7)

The above formula is a convex problem. More precisely, it is a positive SDP problem [42]. Using the MATLAB-based CVX (convex linear programming system) toolbox, this type of optimization problem can be solved [43].

Conclusion 1: It can be seen from the above constraints conditions that, compared with Eq. (6), the Eq. (7) only lacks the constraint condition of rank(Tk)=1. If the rank of the solution T^k is 1, then the optimization problem of Eq. (7) has the same solution as Eq. (6). When rank(T^k)=1, then T^k=t^kt^kH is the optimal solution in Eq. (5).

Therefore, this article use CVX to solve Eq. (7) and verify the rank of its solution T^k. According to conclusion 1, when rank(Tk)=1, then T^k=t^kt^kH, t^k is the optimized value of the problem in Eq. (5).

When rank(T^k)>1, then T^k is only the lower bound of the optimal solution in problem in Eq. (6) and not the complete optimal solution. Therefore, using the random search method, a feasible solution that satisfies the constraint condition of Eq. (5) can be generated from T^k.

Assuming rank(T^k)=l, perform singular value decomposition on T^k

T^k=U∑UH (8)

Among them, the matrix U is a unitary matrix composed of eigenvectors of T^k,Σ is a diagonal matrix, the diagonal elements are the eigenvalues of T^k, and the diagonal elements are arranged in a monotonous decreasing order. When j>l, ∑(j,j)=0, the feasible solution of Eq. (5) can be expressed as

t^k=UΣ1/2vk,k=1…K (9)

Among them, vk is a complex Gaussian random vector with a mean value of 0 and a variance of 1. However, the t^k generated by Eq. (9) is not necessarily feasible, and may not satisfy a certain constraint in Eq. (5), so t^k needs to be scaled accordingly. In this article, first multiply t^k by a coefficient α>1, and the expression is

α=k=1,…,Kmaxαk(∑j=1,j≠kK|rkHHktj|2+σk2)|rkHHktk|2>1 (10)

In this way, a new weight vector t^k=αt^k is generated, which can satisfy the SINR constraint condition in Eq. (5). It’s also worth notable whether the PU interference constraint is met at this point. If the new weight vector violates the interference constraint, it will be discarded and a new round of random search will be started. Finally, t^k satisfies all the constraints of Eq. (5) and has the smallest objective function value which is the optimal solution.

So far, by fixing the weight vector of the receiving end, a downlink MISO cognitive network beamforming problem is formed. Using positive SDP and variable relaxation methods, the optimal beamforming weight vector tk of the transmitting end is obtained. For the beamforming weight vector at the receiving end, this article uses the MMSE criterion and then uses the previously obtained tk, which can be expressed as

rk=(∑j=1KHktjtjHHkH+σk2I)Hktk (11)

According to this expression, the optimization problem in Eq. (5) can be solved optimally through the following two steps: 1) Initialize rk, apply SDP to optimize the beamforming weight vector tk at the transmitting end in the downlink; 2) According to Eq. (11), the weight vector rk of the receiving end is obtained. Therefore, this paper designs an iterative algorithm. In the n-th iteration, the value of rk(n−1) remains unchanged, and the beamforming weight vector of problem in Eq. (5) is solved optimally under the premise of satisfying the corresponding constraints tk(n). Then keep tk(n) unchanged and use Eq. (11) to update the receiving end weight vector rk(n). The algorithm continues to iterate until the objective function converges. Based on the above analysis, the proposed algorithm steps are summarized as follows.

4  SINR Balanced Beamforming Optimization

In a cognitive MIMO network, there are multiple CUs. To ensure that each user can communicate normally, the fairness of the cognitive network becomes more important at this time. This section studies the SINR equalization problem of MIMO cognitive networks, which can be expressed as

minimizemink=1,…,K|rkHHktk|2∑j=1,j≠kK|rkHHktj|2+σk2

subject to:

∑k=1K|rpHHptk|2≤β,k=1,…,K

∑k=1K∥tk∥F2≤Pmax,∥tk∥F2≥0 (12)

Among them, β is the threshold of PU interference temperature, and Pmax is the maximum transmit power. By adding a variable t, Eq. (12) can be equivalent to

k=1,…,Kmaxt

Subject to:

|rkHHktk|2∑j=1,j≠kK|rkHHktj|2+σk2≥t

∑k=1K|rpHHptk|2≤β,k=1,…,K

∑k=1K∥tk∥F2≤Pmax,∥tk∥F2≥0 (13)

Similarly, according to aHb=Tr(baH),  Tr(AB)=Tr(BA), aHbbHa=Tr(bbHaaH) and relax the constraint conditions (remove the constraint condition rank(Tk)=1, Eq. (13) can be transformed into

k=1,…,Kmaxt

Subject to:

Tr(RkTk)−t∑j≠kTr(RkTk)≥tσk2

∑k=1KTr(RpTk)≤β

∑k=1KTr(Tk)≤Pmax

Tk≽0,k=1,…,K (14)

It can be found that Eq. (14) is a convex-like problem. When t is given any value, Eq. (14) is transformed into a convex problem. Therefore, for any given value, if

Find Tk

Subject to:

Tr(RkTk)−t∑j≠kTr(RkTk)≥tσk2

∑k=1KTr(RpTk)≤β

∑k=1KTr(Tk)≤Pmax

Tk≽0,rank(Tk)=1,k=1,…,K (15)

There is a feasible solution, that is, when t takes this value, the corresponding Tk can be found to satisfy the constraint in the above formula.

Conclusion 2: Let tmax be the maximum value of t in the optimization problem of Eq. (14). For any given value t, if there is a feasible solution to the optimization problem in Eq. (15), then tmax≥t can be obtained. Conversely, if the optimization problem in Eq. (15) has no feasible solution, that is, when t takes this value, the constraints in the optimization problem of Eq. (14) cannot be satisfied, so tmax<t. According to conclusion 2, by assigning a value to t, it is judged whether there is a feasible solution to the problem in Eq. (15), and the binary search algorithm is used to determine the value range of tmax. Assuming that the problem in Eq. (13) has a feasible solution, a value interval of [l,u] is selected in advance, and this interval contains the optimal solution tmax of the problem. Let t = (l+u)/2, if the optimization problem in Eq. (15) has a feasible solution, then update l=t. On the contrary, update u=t, and then update the value of t. After multiple loop iterations, until the value interval of t is small enough, the optimal solution tmax of the optimization problem in Eq. (13) can be obtained. The steps of the binary search method are summarized below in Algorithm 2. In step 1, the threshold limits for the optimal solution is defined. In step 2, the maximum value of time interval is determined. In step 3, the feasible solution of Eq. (15) is obtained. In step 4, the optimal solution is determined by l and u. Finally, step 5 stops the process if u−l<ε.

When the maximum value of t is obtained, it is substituted into Eq. (14). At this time, the problem Eq. (14) is transformed into a convex problem, and the CVX toolbox is also used to solve the optimal solution T^k. If rank(T^k), a random search algorithm is required. Based on the above analysis, the algorithm is summarized as follows.

5  Simulation Results

This section uses the Monte Carlo simulation to verify the proposed beamforming optimization algorithm in the MIMO CR network. The system parameters in the main network and the cognitive network are as follows. The number of antennas of the transmitting base station is 4, the number of antennas of the receiving end is 2, the number of CUs in the system is 2 or 3, and the number of PUs is 1. Different user channels are statistically independent of each other, and each channel is an independent and identically distributed Rayleigh fading channel composed of complex Gaussian random variables with zero mean and unit variance. In the simulation, the proposed algorithm is compared with the algorithms proposed in [35] and [41]. All values are the average of 1000 Monte Carlo experiments.

5.1 Transmit Power Optimization

Experiment 1 compared the minimum transmit power under different SNR requirements. In order to fully study the influence of various factors on the transmit power in the simulation, not only the two cases of interference temperature β = 1 dB and β = 2 dB are considered, but also the number of different cognitive users K = 2 and K = 3 are selected. It can be seen from Fig. 2 that, with the continuous increase in the demand for SINR, the transmission power continues to increase. In other words, more power is needed to improve the performance of the system. Under the same SINR requirement, the greater the number of users, the greater the power required. When the user’s SINR demand increases, the transmission power grows rapidly, showing an exponential growth trend. At the same time, it can be seen from Fig. 2 that, when the interference temperature of the PU increases, the required transmit power decreases. This feature is more obvious in Experiment 3.

Experiment 2 tested the performance of the algorithm when there are different numbers of CUs. The performance comparison of the algorithms in the two scenarios of K = 3 and K = 2 is shown in Figs. 3 and 4. Analyze the example of K = 3 without losing generality. Three CUs and one PU communicate in the system using the same frequency spectrum, and the primary user’s interference temperature is β=1 dB. It can be seen from Fig. 3, that the performance of the proposed algorithm is much better than the other two algorithms. This advantage is more pronounced when the user’s communication quality criteria are higher. For example, when the SINR requirement α = 10 dB, the transmission power of the proposed and references [35,41] algorithms are 4 dBW, 6 dBW and 12 dBW. When α = 14 dB, the transmit power of the three algorithms becomes 11, 16 and 33 dBW.

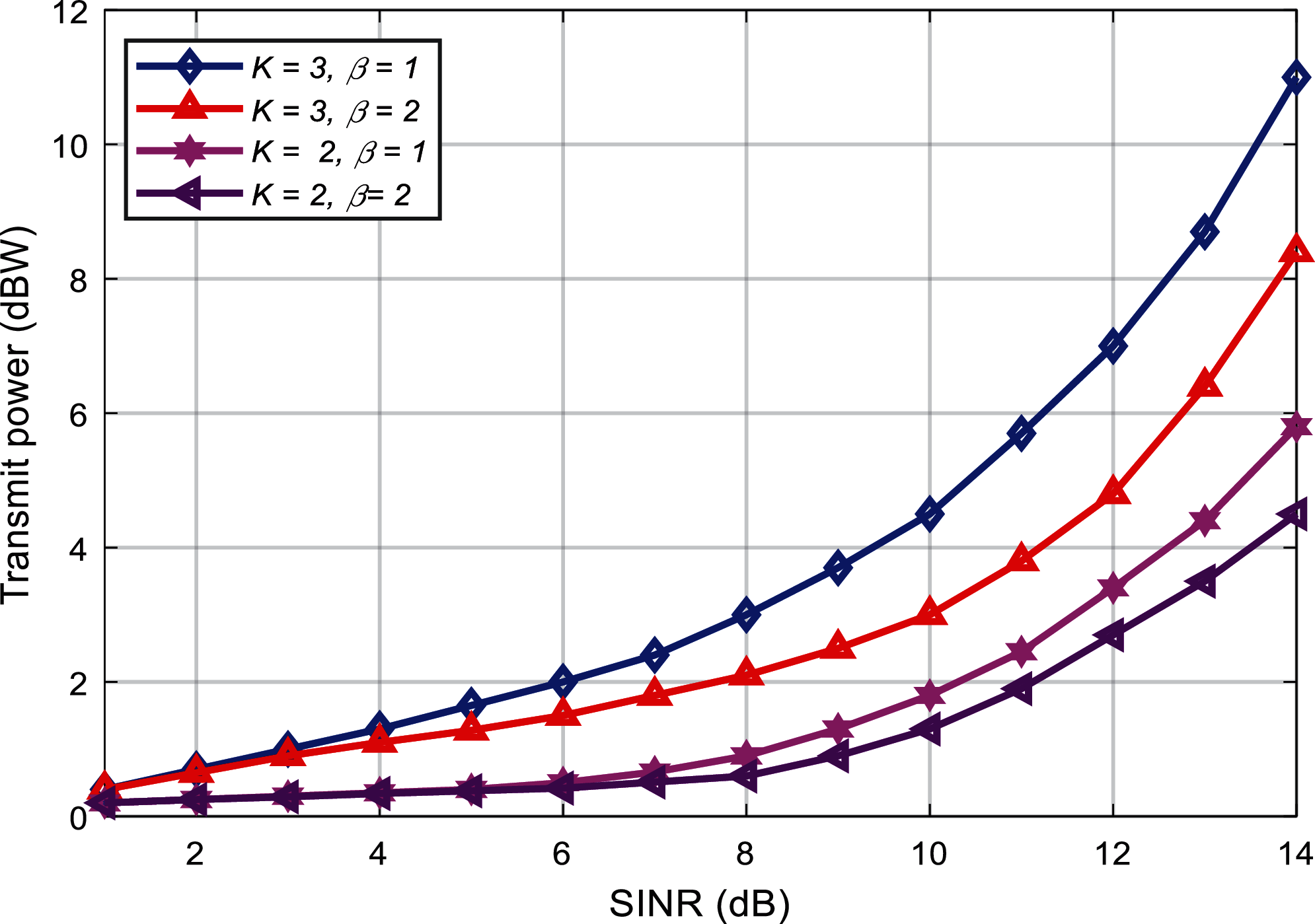
Figure 2: The impact of user SINR requirements on transmit power

Since the reference [35] algorithm considers a system model with multiple antennas at the transmitter and single antenna at the receiving end, this article and reference [41] algorithm also configure multiple antennas at the receiving end. Diversity and combination of signals can significantly improve the system performance and reduce the transmit power.

Figure 3: Comparison of the minimum transmit power of the algorithms under K = 3 and different SINR requirements

Therefore, the performance of the proposed algorithm and the reference [41] algorithm is better than the reference [35] algorithm. For non-convex problems, SDR (semidefinite relaxation) method is generally adopted to convert the non-convex problems into convex problems and then solve them. From the analysis in Section 3, it can be seen that the solution obtained by this method may only be a feasible solution to the original problem, not necessarily the global optimal solution. The reference [41] algorithm uses the dual characteristics of uplink-downlink to convert the original problem into two SDR problems, and the solution obtained by iteration is approximated twice. However, the algorithm proposed in this paper only needs to solve one SDR problem, so the solution obtained is only approximated once. After many iterations, the performance advantage of the proposed algorithm is reflected.

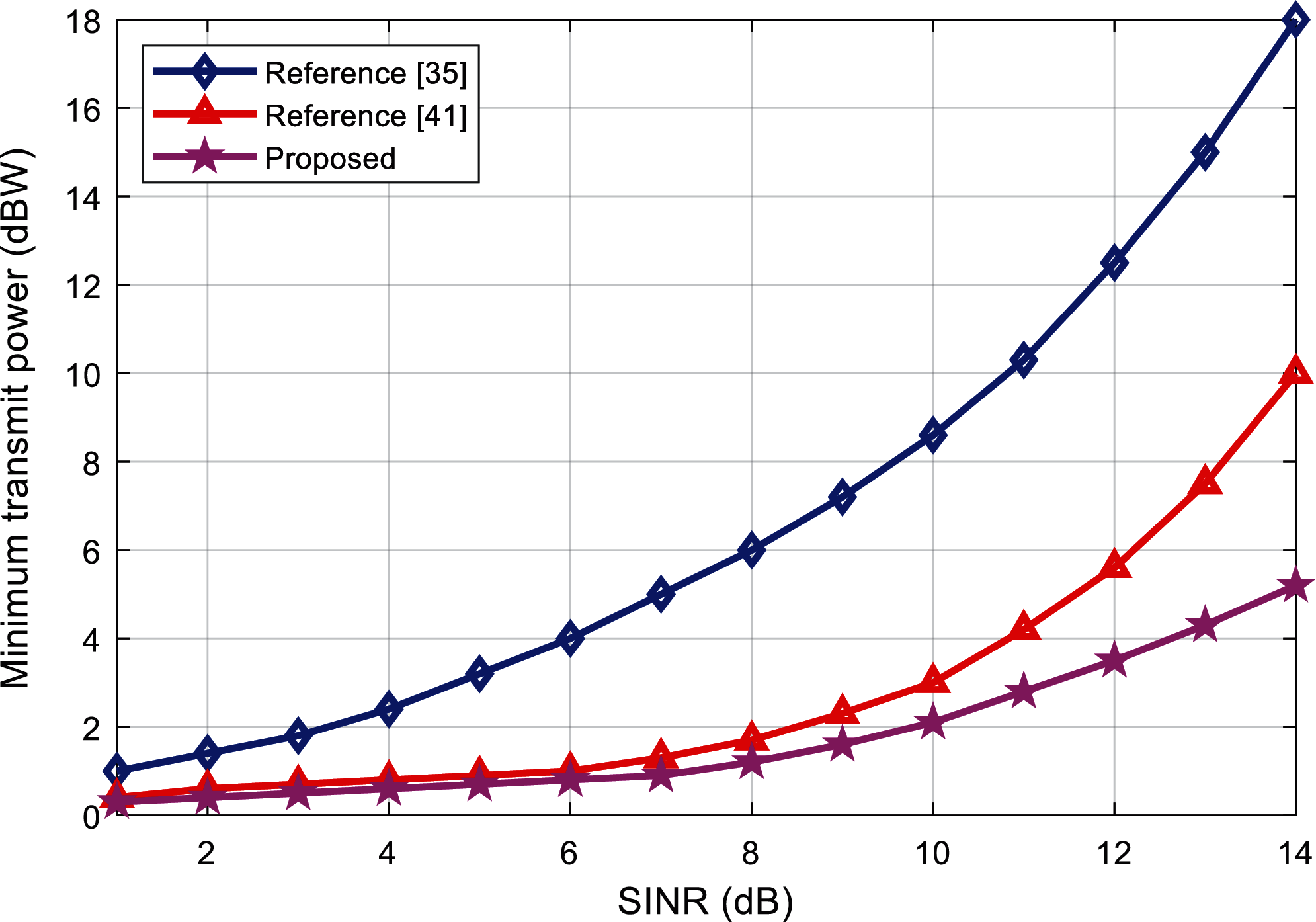
Figure 4: Comparison of the minimum transmit power of the algorithms under K = 2 and different SINR requirements

Experiment 3 compares the transmit power of the algorithms at different interference temperatures. In this paper, the SINR requirement is fixed at α = 12 dB. It can be observed from Fig. 5 that, under the same SNR requirement, the higher the interference temperature of the PU, the lower the transmit power. The smaller the number of users, the smaller the transmission power. Under the same conditions, the transmission power of the proposed algorithm is less than that of the other two algorithms. At the same time, it is also noticed that with the increase of interference temperature β, the transmit power of the reference [35] algorithm changes very obviously, while the transmit power of the proposed algorithm changes slightly, which shows that the multi-antenna beamforming technology is used at the transmitting and receiving end at the same time can well control the interference to the PU.

Figure 5: The influence of the PU interference temperature on the transmit power

5.2 SINR Balanced Beamforming

Experiment 4 gives the SINR equalization level under different transmit powers. It can be seen from Fig. 6 that the SINR equalization level increases with the increase of the transmission power, and when the transmission power is small, the SINR increases significantly. At the same time, the higher the interference temperature, the greater the SINR. The main factor that affects the SINR is the number of users, because as the number of users increases, the interference in the small area will continue to increase, thereby reducing the user’s SINR. It can be seen from Fig. 6 that, when P = 10 dBW and β = 1 dB, the SINR of K = 2 has a performance gain of 3 dB compared with K = 3. When the interference temperature β = 3 dB, Fig. 7 demonstrates the performance comparison between the proposed algorithm and the reference [35] algorithm. It has been discovered that the proposed algorithm outperforms the existing algorithm.

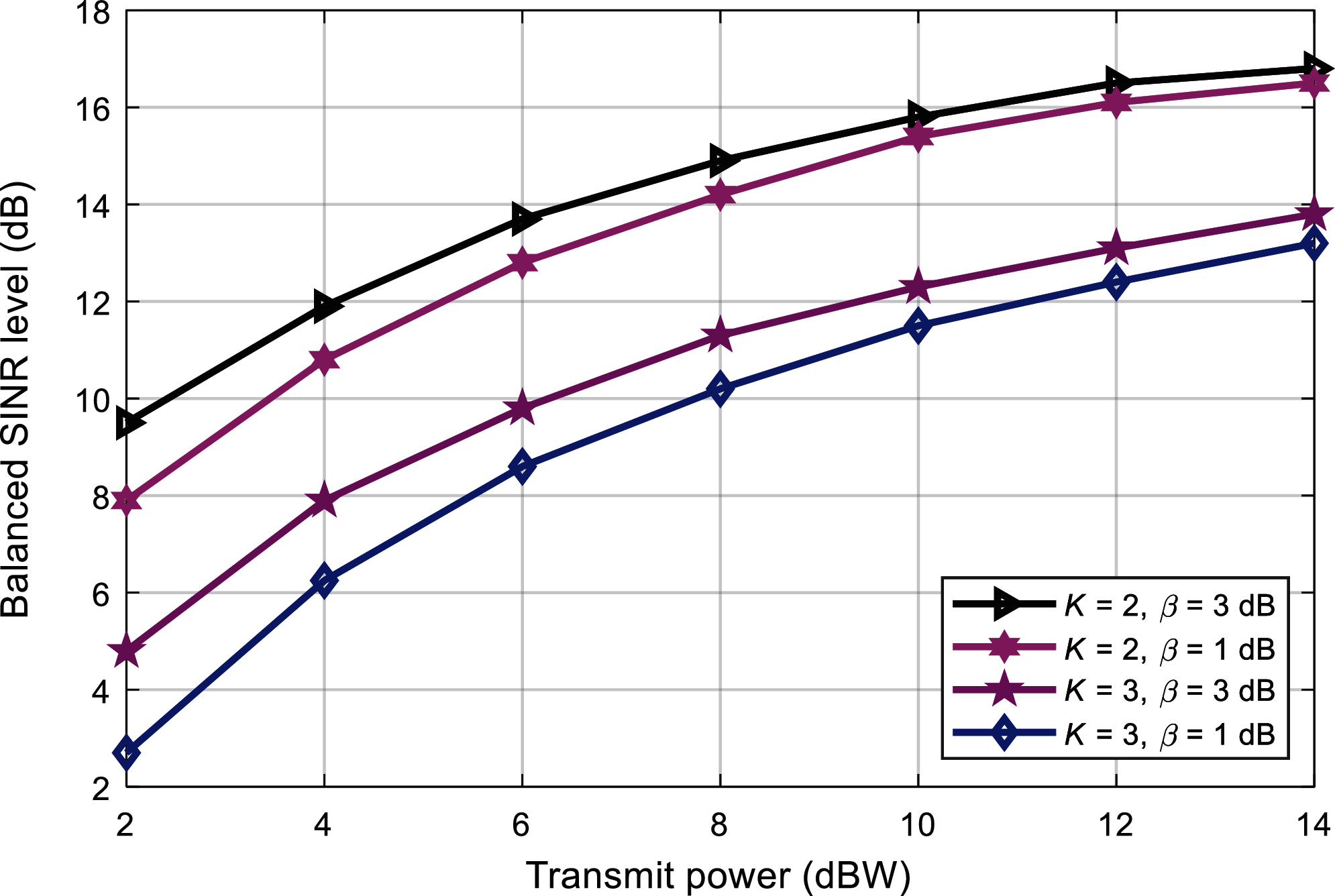
Figure 6: The influence of transmit power on the balanced SINR level

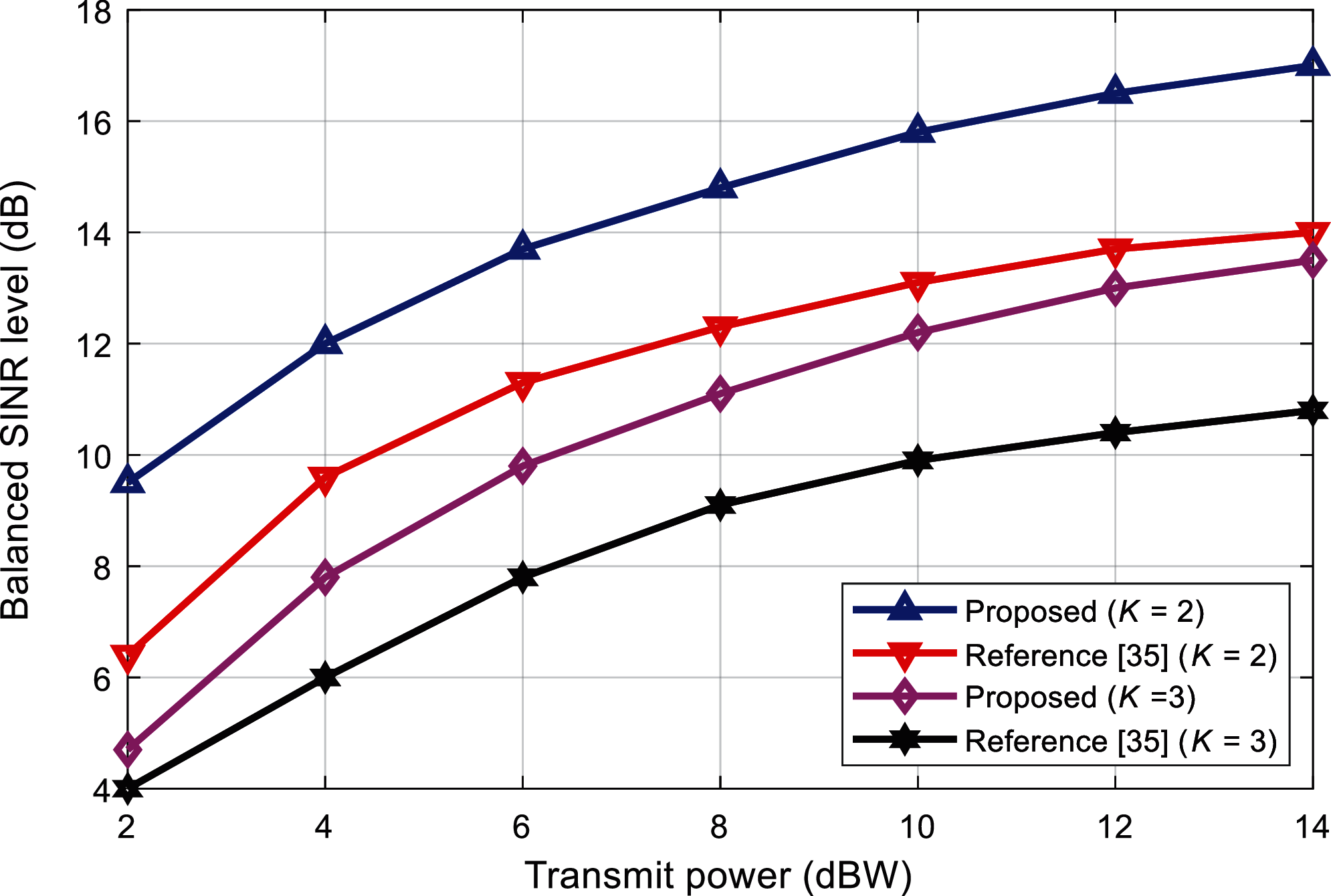
Figure 7: Comparison of the balanced SINR level of the algorithms under different transmit power

Experiment 5 further studied the relationship between the interference temperature β and the equilibrium level of SINR under different conditions. It can be seen from Fig. 8 that as the interference temperature increases, the SINR equalization level ratio continues to increase, but when β > 3, the improvement of the SINR becomes slow. It can also be seen from Fig. 8 that the number of users will affect the performance of the system. The greater the number of users, the worse the system performance.

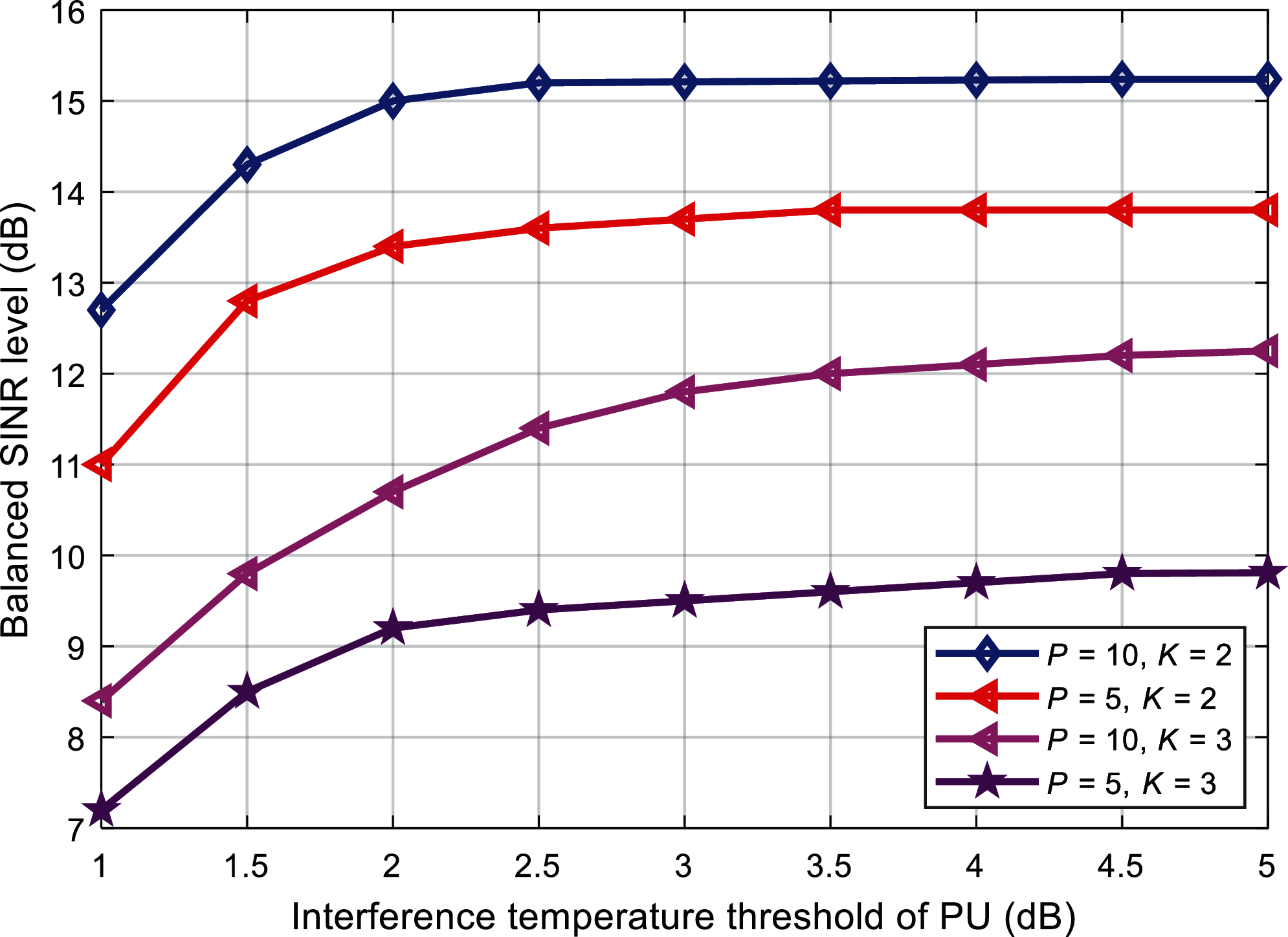
Figure 8: The influence of the PU interference temperature on the balanced SINR level

5.3 Algorithm Complexity and Convergence Analysis

In addition to performance, it is also necessary to analyze the complexity of the algorithm. This paper proposes corresponding algorithms to solve the two types of beamforming problems of minimizing the transmit power and SINR equalization. The ideas of the two algorithms are basically similar. The transmit power algorithm is analyzed as an example. The convex optimization method is adopted for this paper. The reference [35] algorithm is aimed at the beamforming problem of the MISO cognitive network. It only needs to optimize the beamforming weight vector at the transmitting end and there is no iterative process. As a result, the problem’s solution can be found by solving the SDR problem once. The proposed algorithm, like the reference [41] algorithm, uses an iterative method to discover the best beamforming solution with the least amount of transmit power. The SDP and MMSE algorithms must be executed once in each iteration by the new algorithm. Compared with the SDP algorithm, the complexity of the MMSE algorithm and random search is lower, so the computational complexity is mainly reflected in the SDP algorithm. According to [44], the complexity of the SDP algorithm is O(nSDP0.5(mSDPnSDP3+mSDP2nSDP2+mSDP3)), where mSDP represents the number of constraint conditions, and nSDP represents the semi-definite cone dimension. Specific to the Eqs. (7)–(11) in this article, mSDP=K+1,nSDP=Ns+K+1. The reference [41] algorithm uses the dual characteristics of the uplink-downlink to decompose the original problem into two convex problems. Therefore, in each iteration, the reference [41] algorithm needs to run the SDP algorithm twice. In summary, the calculation complexity of the above three algorithms is equivalent, and in each iteration, the calculation amount of the reference [41] algorithm is higher than that of the proposed algorithm.

Experiment 6 compares the convergence performance of three different algorithms. Set the system parameters as K = 3, α = 12 dB, β = 1 dB. In this paper, similar to [17], the initial value of the weighting vector at the receiving end is selected as rk(0)=εmax(HkHkH), and the algorithm stops when the difference between the minimum transmit power obtained by two consecutive iterations is less than the given threshold. By iteratively updating the weight vectors of the transmitting and receiving ends, and pointing the antenna patterns to each other, it can be ensured that the transmission power is reduced until the algorithm converges without degrading the system performance. It can be seen from Fig. 9 that the proposed algorithm requires approximately 28 iterations to converge, the reference [41] algorithm requires 22 iterations, and reference [35] algorithm does not require iteration. Since the calculation amount of the proposed algorithm in each iteration is lower than that of the reference [35] algorithm, the running time of the entire algorithm is shorter. The running time of the proposed algorithm, the reference [41] algorithm and reference [35] algorithm were counted with the tic command in MATLAB and they were t = 7.0779s, t = 10.0587s and t = 0.1987s, respectively.

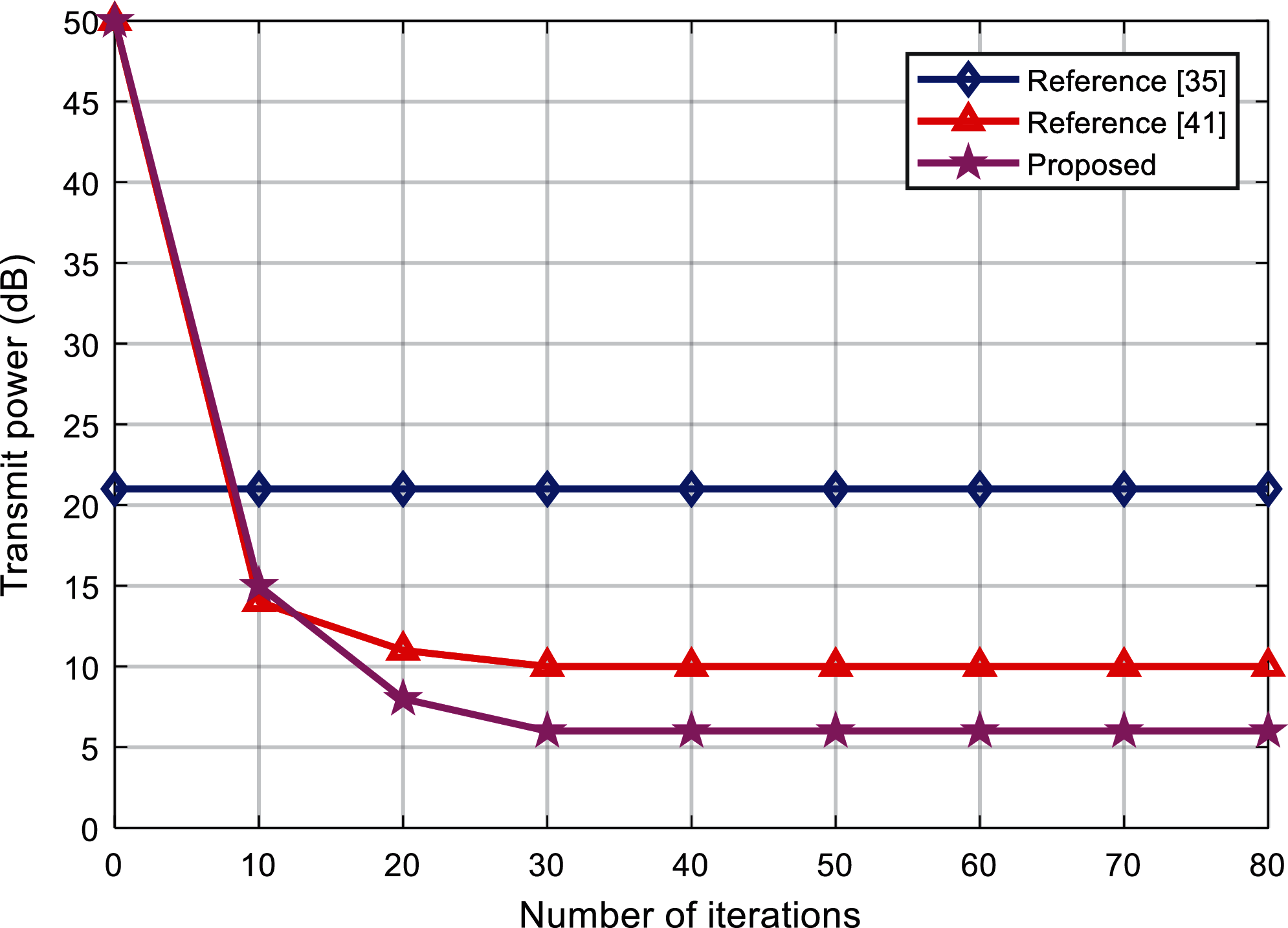
Figure 9: The influence of the number of iterations on the transmit power

6  Conclusion

This article analyzes the problem of joint transceiver beamforming in MIMO wireless cognitive systems.

For the two types of beamforming problems of minimizing transmit power and SINR equalization, corresponding beamforming algorithms are proposed. Numerical simulation results prove that the proposed algorithm can effectively reduce the transmission power of the system while avoiding excessive interference to the primary user, and greatly improve the balanced SINR level. The next step is to study the feasibility and robustness of the proposed algorithm under imperfect channel conditions. At the same time increase the number of users in the system, and further study the impact of the number of users on system performance.

Acknowledgement: This project was supported financially by the Academy of Scientific Research and Technology (ASRT), Egypt, Grant No. (6475), (ASRT) is the 2nd affiliation of this research.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 2/209/42). This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-Track Path of Research Funding Program.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Amjad, M. H. Rehmani and S. Mao, “Wireless multimedia cognitive radio networks: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 20, no. 2, pp. 1056–1103, 2018. [Google Scholar]

 2.  M. Amjad, F. Akhtar, M. H. Rehmani, M. Reisslein and T. Umer, “Full-duplex communication in cognitive radio networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 19, no. 4, pp. 2158–2191, 2017. [Google Scholar]

 3.  A. Nasser, H. A. H. Hassan, J. A. Chaaya, A. Mansour and K. C. Yao, “Spectrum sensing for cognitive radio: Recent advances and future challenges,” Sensors, vol. 21, no. 7, pp. 1–24, 2021. [Google Scholar]

 4.  J. Zhang, L. Liu, M. Liu, Y. Yi, Q. Yang et al., “MIMO spectrum sensing for cognitive radio-based internet of things,” IEEE Internet of Things Journal, vol. 7, no. 9, pp. 8874–8885, 2020. [Google Scholar]

 5.  T. Alam, S. R. Thummaluru and R. K. Chaudhary, “Integration of MIMO and cognitive radio for sub-6 GHz 5G applications,” IEEE Antennas and Wireless Propagation Letters, vol. 18, no. 10, pp. 2021–2025, 2019. [Google Scholar]

 6.  L. Zhang, Y. Wang, W. Tao, Z. Jia, T. Song et al., “Intelligent reflecting surface aided MIMO cognitive radio systems,” IEEE Transactions on Vehicular Technology, vol. 69, no. 10, pp. 11445–11457, 2020. [Google Scholar]

 7.  X. Zhao, S. Riaz and S. Geng, “A reconfigurable MIMO/UWB antenna for cognitive radio applications,” IEEE Access, vol. 7, pp. 46739–46747, 2019. [Google Scholar]

 8.  S. R. Thummaluru, M. Ameen and R. K. Chaudhary, “Four-port MIMO cognitive radio system for midband 5G applications,” IEEE Transactions on Antennas and Propagation, vol. 67, no. 8, pp. 5634–5645, 2019. [Google Scholar]

 9.  M. Mohammadi and S. M. Andargoli, “Resource allocation algorithm for downlink MIMO-OFDMA based cognitive radio networks in spectrum underlay scenario,” IET Communications, vol. 14, no. 11, pp. 1811–1820, 2020. [Google Scholar]

10. Y. Liu, X. Zhao, H. Zhou, Y. Zhang and T. Qiu, “Low-complexity spectrum sensing for MIMO communication systems based on cyclostationary,” EURASIP Journal on Advances in Signal Processing, vol. 29, pp. 1–14, 2019. [Google Scholar]

11. R. Ahmed, Y. Chen and B. Hassan, “Optimal spectrum sensing in MIMO-based cognitive radio wireless sensor network (CR-WSN) using GLRT with noise uncertainty at low SNR,” AEU-International Journal of Electronics and Communications, vol. 136, no. 7, pp. 997–1008, 2021. [Google Scholar]

12. Y. Ashraf, F. Newagy and I. Hafez, “Performance evaluation of cooperative and non-cooperative MIMO cognitive radio networks,” IET Communications, vol. 13, no. 20, pp. 3588–3594, 2019. [Google Scholar]

13. F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communication under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 1, no. 1, pp. 1–9, 2019. [Google Scholar]

14. T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–14, 2019. [Google Scholar]

15. K. Bakht, F. Jameel, Z. Ali, W. U. Khan, I. Khan et al., “Power allocation and user assignment scheme for beyond 5G heterogeneous networks,” Wireless Communications and Mobile Computing, vol. 7, pp. 1–9, 2019. [Google Scholar]

16. S. L. Mohammed, M. H. Alsharif, S. K. Gharghan, I. Khan and M. Albreem, “Robust hybrid beamforming scheme for millimeter-wave massive MIMO 5G wireless networks,” Symmetry, vol. 11, no. 11, pp. 1–16, 2019. [Google Scholar]

17. W. Shahjehan, A. Riaz, I. Khan, A. S. Sadiq, S. Khan et al., “Bat algorithm-based beamforming for mmwave massive mimo systems,” International Journal of Communication Systems, vol. 33, no. 2, pp. 845–904, 2020. [Google Scholar]

18. Q. Alsafasfeh, O. A. Saraereh, A. Ali, L. Al-Tarawneh, I. Khan et al., “Efficient power control framework for small-cell heterogeneous networks,” Sensors, vol. 20, no. 5, pp. 1–14, 2019. [Google Scholar]

19. R. M. Narayanan, R. K. Pooler, A. F. Martone, K. A. Gallagher and K. D. Sherbondy, “The spectrum analysis solution (SAS) system: Theoretical analysis, hardware design and implementation,” Sensors, vol. 18, no. 2, pp. 1–22, 2018. [Google Scholar]

20. K. Kotobi, P. B. Mainwaring, C. S. Tucker and S. G. Bilen, “Data-throughput enhancement using data mining-informed cognitive radio,” Electronics, vol. 4, no. 2, pp. 1–19, 2015. [Google Scholar]

21. S. Haykin, “Cognitive-radio: Brain-empowered wireless communications,” IEEE Journal on Selected Areas in Communications, vol. 23, no. 2, pp. 201–220, 2005. [Google Scholar]

22. A. Goldsmith, A. S. Jafar, I. Maric and S. Srinivasa, “Breaking spectrum gridlock with cognitive radios: An information theoretic perspective,” Proc. of the IEEE, vol. 97, no. 5, pp. 894–914, 2009. [Google Scholar]

23. L. Zhang, Y. C. Liang and Y. Xin, “Joint beamforming and power allocation for multiple access channels in cognitive radio networks,” IEEE Journal on Selected Areas in Communications, vol. 26, no. 1, pp. 38–51, 2008. [Google Scholar]

24. G. Zhao, J. Ma, Y. Li, T. Wu, Y. H. Kwon et al., “Spatial spectrum holes for cognitive radio with directional transmission,” in IEEE Global Telecommunications Conf., New Orleans, USA, pp. 1–5, 2008. [Google Scholar]

25. T. Yoo and A. Goldsmith, “On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming,” IEEE Journal on Selected Areas in Communications, vol. 24, no. 3, pp. 528–541, 2006. [Google Scholar]

26. M. Schubert and H. Boche, “Solution of the multiuser downlink beamforming problem with individual SINR constraints,” IEEE Transactions on Vehicular Technology, vol. 53, no. 1, pp. 18–28, 2004. [Google Scholar]

27. D. J. Costello, “Fundamentals of wireless communication,” IEEE Transactions on Information Theory, vol. 55, no. 2, pp. 919–920, 2009. [Google Scholar]

28. Z. H. Qaisar, M. Irfan, T. Ali, A. Ahmad, G. Ali et al., “Effective beamforming technique amid optimal value for wireless communication,” Electronics, vol. 9, no. 11, pp. 1–18, 2020. [Google Scholar]

29. X. Fu, J. Wang and S. Li, “Joint power management and beamforming for base stations in cognitive radio systems,” in Proc. of the 6th Int. Symp. on Wireless Communication Systems (ISWCSSiena, Italy, pp. 403–407, 2009. [Google Scholar]

30. N. D. Sidiropoulos, T. N. Davidson and Z. Q. Luo, “Transmit beamforming for physical-layer multicasting,” IEEE Transactions on Signal Processing, vol. 54, no. 6, pp. 2239–2251, 2006. [Google Scholar]

31. K. T. Phan, S. A. Vorobyov, N. D. Sidiropoulos and C. Tellambura, “Spectrum sharing in wireless networks via QoS-aware secondary multicast beamforming,” IEEE Transactions on Signal Processing, vol. 57, no. 6, pp. 2323–2335, 2009. [Google Scholar]

32. A. H. Phan, H. D. Tuan, H. H. Kha and D. T. Ngo, “Nonsmooth optimization for efficient beamforming in cognitive radio multicast transmission,” IEEE Transactions on Signal Processing, vol. 60, no. 6, pp. 2941–2951, 2012. [Google Scholar]

33. M. Beko, “Efficient beamforming in cognitive radio multicast transmission,” IEEE Transactions on Wireless Communications, vol. 11, no. 11, pp. 4108–4117, 2012. [Google Scholar]

34. H. Du, T. Ratnarajah, M. Pesavento and C. B. Papadias, “Joint transceiver beamforming in MIMO cognitive radio network via second-order cone programming,” IEEE Transactions on Signal Processing, vol. 60, no. 2, pp. 781–792, 2012. [Google Scholar]

35. Q. Liu and C. W. Chen, “Joint transceiver beamforming design and power allocation for multiuser MIMO systems,” in Proc. of the IEEE Int. Conf. on Communications (ICCOttawa, Canada, pp. 3867–3871, 2012. [Google Scholar]

36. M. Codreanu, A. Tolli, M. Juntti and M. L. Aho, “Joint design of Tx-Rx beamformers in MIMO downlink channel,” IEEE Transactions on Signal Processing, vol. 55, no. 9, pp. 4639–4655, 2007. [Google Scholar]

37. X. Zhu, L. Shen and T. P. Yum, “Analysis of cognitive radio spectrum access with optimum channel reservation,” IEEE Communication Letters, vol. 11, no. 4, pp. 304–306, 2007. [Google Scholar]

38. J. Lee, H. Wang, J. G. Andrews and D. Hong, “Outage probability of cognitive relay networks with interference constraints,” IEEE Transactions on Wireless Communications, vol. 10, no. 2, pp. 390–395, 2011. [Google Scholar]

39. K. R. Kumar and F. Xue, “An iterative algorithm for joint signal and interference alignment,” in Proc. of the IEEE Int. Symp. on Information Theory (ISITAustin, Texas, USA, pp. 2293–2297, 2010. [Google Scholar]

40. K. Gomadam, V. R. Cadambe and A. S. Jafar, Approaching the Capacity of Wireless Networks through Distributed Interference Alignment. New Orleans, USA: IEEE Global Telecommunications Conference, pp. 1–6, 2008. [Google Scholar]

41. M. Pesavento, D. Ciochina and A. B. Gershman, “Iterative dual downlink beamforming for cognitive radio networks,” in Proc. of the 5th Int. Conf. on Cognitive Radio Oriented Wireless Networks & Communications (CROWNCOMCannes, France, pp. 1–5, 2010. [Google Scholar]

42. Z. Q. Luo and W. Yu, “An introduction to convex optimization for communications and signal processing,” IEEE Journal on Selected Areas in Communications, vol. 24, no. 8, pp. 1426–1438, 2006. [Google Scholar]

43. Y. Yan, H. Wang, X. Shen, B. Leng and S. Li, “Efficient convex optimization for energy-based acoustic sensor self-localization and source localization in sensor networks,” Sensors, vol. 18, no. 5, pp. 1–22, 2018. [Google Scholar]

44. M. S. Lobo, L. Vandenberghe, S. Boyd and H. Lebret, “Application of second-order cone programming,” Linear Algebra and its Applications, vol. 284, no. 1, pp. 193–228, 1998. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.