DOI:10.32604/cmc.2022.021917

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021917 |  |
| Article |
Deep Deterministic Policy Gradient to Regulate Feedback Control Systems Using Reinforcement Learning
1Department of Electrical & Computer Engineering, COMSATS University Islamabad, Lahore Campus, 54000, Pakistan
2Department of Electrical Engineering, Government College University, Lahore, 54000, Pakistan
3Industrial Engineering Department, College of Engineering, King Saud University, P.O. Box 800, Riyadh, 11421, Saudi Arabia
4Department of Information and Communication Engineering, Yeungnam University, Gyeongsan, 38541, Korea
*Corresponding Author: Muhammad Shafiq. Email: shafiq@ynu.ac.kr
Received: 19 July 2021; Accepted: 07 September 2021
Controlling feedback control systems in continuous action spaces has always been a challenging problem. Nevertheless, reinforcement learning is mainly an area of artificial intelligence (AI) because it has been used in process control for more than a decade. However, the existing algorithms are unable to provide satisfactory results. Therefore, this research uses a reinforcement learning (RL) algorithm to manage the control system. We propose an adaptive speed control of the motor system based on depth deterministic strategy gradient (DDPG). The actor-critic scenario using DDPG is implemented to build the RL agent. In addition, a framework has been created for traditional feedback control systems to make RL implementation easier for control systems. The RL algorithms are robust and proficient in using trial and error to search for the best strategy. Our proposed algorithm is a deep deterministic policy gradient, in which a large amount of training data trains the agent. Once the system is trained, the agent can automatically adjust the control parameters. The algorithm has been developed using Python 3.6 and the simulation results are evaluated in the MATLAB/Simulink environment. The performance of the proposed RL algorithm is compared with a proportional integral derivative (PID) controller and a linear quadratic regulator (LQR) controller. The simulation results of the proposed scheme are promising for the feedback control problems.
Keywords: Feedback control systems; reinforcement learning; artificial intelligence
Reinforcement learning is a leading neural network method used to train and process intelligent decisions to optimize a control system. It allows agents/bots to learn through trial and error search by interacting with the environment using a reward function. In recent years, RL has played a vital role by making significant contributions to process control. An extensive literature survey led us to conclude that the existing algorithms cannot handle the control problems entirely and accurately. Therefore, it is exciting to use model-free RL for model-free optimal control in the continuous domain. Different controllers are used In the process industry, including proportional controllers, prediction-based controllers, and model predictive controllers (MPC). The shortcomings in the classic controller design are 1) designing a controller requires careful analysis of process dynamics, which is a time-consuming design process. 2) PID, fuzzy logic controller and MPC, need to design an abstract mathematical model. 3) pre-defined control laws are required to meet design standards. 4) the controller usually requires continuous maintenance. We have designed a universal controller to overcome the prescribed shortcomings. This controller can accurately learn the feedback control law from the data. We have introduced RL algorithm into the control system performed as an effective method to make the controller proficient in automatic learning. Since RL methods are model-free, they use Actor-Critic (AC) scenarios to learn closed-loop control laws directly through collaboration with factories or systems without prominent model recognition. We have considered a 2D MIMO system for testing the proposed RL-based algorithm. Most of the existing methods use traditional P, PI, and PID for inspection, facilitating comparative analysis of testing and verification. Moreover, proportional integral derivative (PID) has been selected because of its low price and easy implementation in a linear system. In addition, a linear quadratic regulator (LQR) is also used as an optimal control regulator to track the reference point better. The application of RL requires a simulator for exploration and action simulation for learning. The most common RL simulators are OpenAI Gym based on Python, a deep-thinking control suite based on Python and MuJoCo engines, and a unified machine-learning agent for unified game engines. The key contributions of this paper are summarized as follows:
• A server (using Python) and a client (Simulink-based framework) are developed to implement RL algorithms as Markov Decision Processes (MDP) by taking advantage of RL in control systems.
• We have designed and implemented a reusable architecture to set the RL algorithm as a direct adaptive model-free optimal controller for modeling and control the system environment.
• Moreover, the proposed architecture has been tested on Single Input Single Output (SISO) direct current motor speed control and two-dimensional motion of Multiple Input Multiple Output (MIMO) systems. In addition, we have analyzed the performance of the proposed algorithm using a (PID) controller and (LQR).
The structure of this paper is as follows. In Section 2, the literature review has been summarized. Section 3 illustrates the control algorithm and the proposed system. Moreover, Section 4 presents the simulation results for the proposed approach. In the last section, the conclusions of this work are drawn.
In the existing literature, neural networks and deep learning have extensively used RL to solve control problems [1]. In 2015, the Google DeepMind team proposed a deep reinforcement learning algorithm-Deep Q Network (DQN) [2], which insists on its recognition and hegemony in Atari 2600 [3], StarCraft, Go [4] and other games. In [5], the author focused on these algorithms, namely A3C, DDPG, and D4PG, and used the Actor-Critic (AC) method to learn closed-loop control laws directly from collaboration with factories or systems without prominent model recognition. In [6], the motion space problem has been resolved by using a DDPG algorithm as a replay buffer. In [7], the authors proposed an RL algorithm to optimize the tracking and control of a completely unknown nonlinear system. We can find an actor-critic framework based on the DDPG algorithm in [8], which facilitates tracking stability by adapting to uncertainty and interference. In [9–11], the authors have developed a DDPG algorithm to improve accuracy that performs better than PID controllers. Moreover, authors in [12] have proposed a push-pull converter and a fuzzy logic-based maximum power point tracking (MPPT) algorithm to ensure that the total amount of incident energy is extracted. In [13], the author combines strategy-based and value-based methods in a non-policy and stable model-free deep learning algorithm.
In further, [14] proposed a deep RL algorithm based on near-end Actor-Critic for feedback control applications. A prototype model is also designed to monitor the climatic parameters and light intensity in a greenhouse environment that comprises of a sensor network-based (SN) node and a Raspberry Pi-based embedded system (ES) [15]. A framework to optimize the training process and performance improvement has been proposed in [16,17] using m-out-of-n bootstrapping and aggregating multiple DDPGs for experimental verification. However, most RL tasks make iterative training data, which runs counter to the assumption of the independent and identical distribution of training samples, so it becomes challenging to learn the optimal strategy. We propose a universal controller, which can accurately learn feedback control laws from data, and requires marginal adjustments for different application areas, namely linear/nonlinear, deterministic/random System, SSISO/MIMO, to set point tracking and monitoring issues.
For the Model-free RL continuous (infinite) action and continuous (infinite) state-space, actor-critic methods are best suited to optimize the continuous domain. The actor
3.1 Deep Deterministic Policy Gradient (DDPG)
DDPG is an actor-critic method for continuous action space proposed by [25] that uses deterministic policy gradients to adjust NN and experience replay. It is an off-strategy algorithm based on a value function, and it learns the function by deriving the optimal strategy. Moreover, DDPG algorithm provides stable learning because it has a target value and a learning strategy. Therefore, exploration and learning remain separated. The prescribed method requires an AC architecture and learning algorithms to deal directly with more complex problems and massive networks. Fig. 1 illustrates some conditions of the DDPG algorithm since it is a model-free reinforcement-learning model that needs many training sets or more simulation time to find the best strategy for solving complex problems.

Figure 1: DDPG algorithm [25]
3.2 Proposed Reinforcement Learning SIMULINK Framework
In this paper, the adaptive speed control of the DC motor system (based on the DDPG algorithm) has been proposed. A communication scenario implemented to build the RL agent is presented in Fig. 2. Moreover, the reward function is defined under the assumption that the speed control error of the DC motor can be tracked. The state is limited in which the RL agent can act according to the optimal strategy by obtaining the maximum reward function while keeping the tracking error close to zero. This self-learning algorithm is far superior to the fixed parameters of PID. The RL preprocessing is the first part of the system, as shown in Fig. 2. It writes the state of the factory into a file on the Python RL server and waits for it to be written into the operation file. Its state and actions are passed to the next block. If it is the first step of a plot, the system’s initial state is also set in it.
Additionally, the system takes the actions given by the RL model for the current time step in the plant block. It further updates the system state and propagates the new state. It needs to be covered to use different devices. In this study, the device model is a DC motor, and the device block of the DC motor model must be updated. The reward Gen block adopts the previous state, newly updated state, and further take actions to give rewards in the last state. The RL post-processing writes the new status and rewards into the file read by the RL server. Data storage and memory blocks are used as global variables for data persistence between blocks. The basic structure of an RL Server code is similar to the pseudo-code required to change the setup parameters while creating model and updating the model in code template.
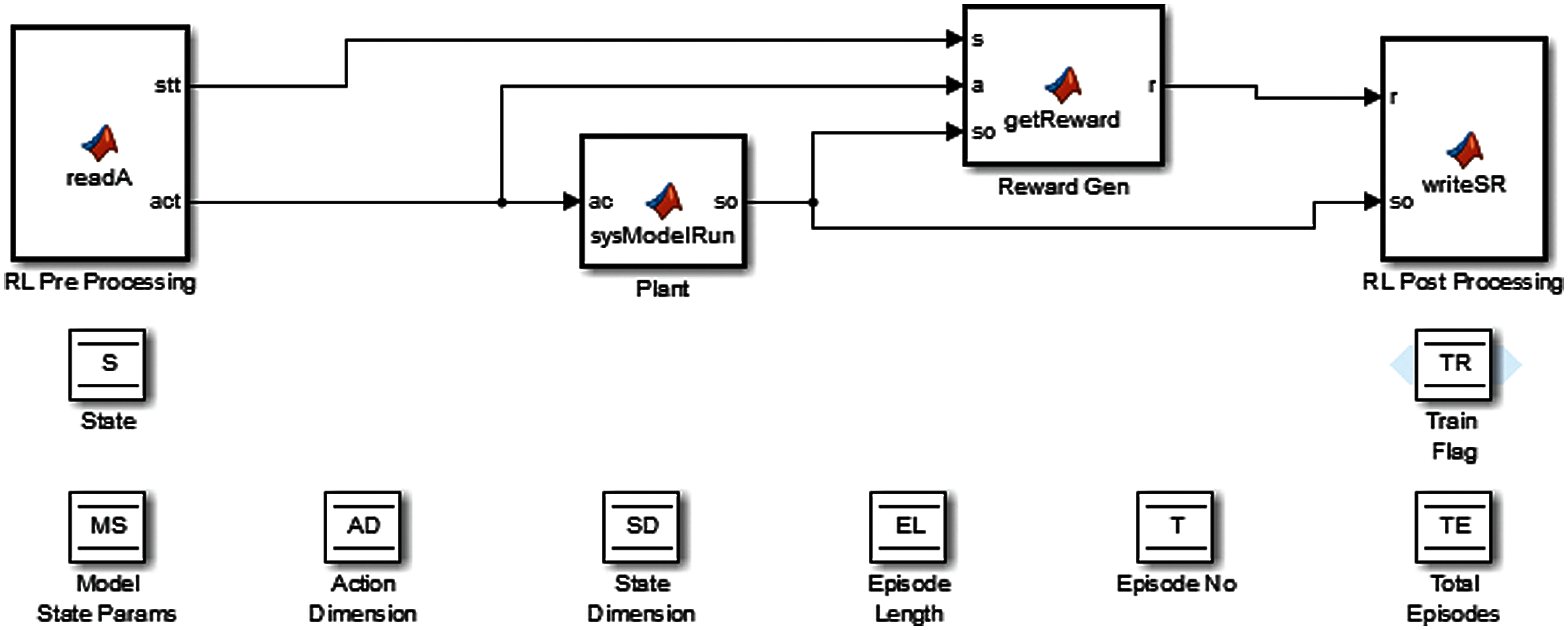
Figure 2: Simulink model architecture
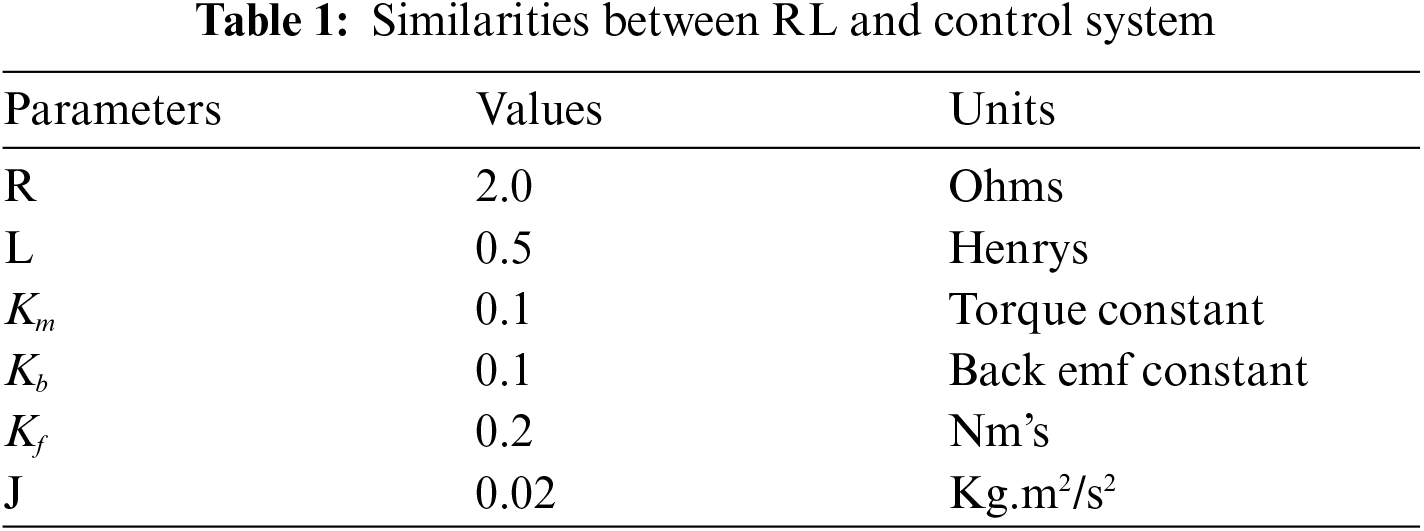
The design requirement of the proposed scheme is to create an RL framework that meets the required speed of DC motor that should be 50 rpm/sec to minimize errors and create ease in using the control system in RL. Therefore, the 50 rpm/s is provided to the system to reduce error in the direction of the optimal value. Tab. 1 lists the DC motor parameters.
The MIMO system chosen for the DDPG experiment is a simple 2D motion. A two-degree-of-freedom (2-DOF) system must move along the x-axis and y-axis to reach the reference x and y states by treating the error only as of the RL model’s state. The length of the action vector is 2, the delta x in the range [–1, 1] is added to the position x, and the delta y in the range [–1, 1] is added. It uses the 2D state [x, reference(x)] and [y, reference(y)] as the MS, and the 2D state [error] as the S. It is achieved by creating an architecture that integrates the MDP used in RL into the traditional feedback control system [26]. Since the work of the motor involves continuous action space, an algorithm is needed to obtain satisfactory results for the continuous action space. The DDPG meets this prerequisite because it requires a straightforward actor-critic architecture and learning algorithm, which is easy to implement and suitable for scalability. Therefore, it has been selected for the testing of the RL algorithm. In addition, DDPG is also ideal for continuous action spaces. The success of the RL algorithm depends on the formation of rewards. If the reward function is adequately formulated, these rewards are further used to guide the RL controller (agent) and help the agent learn the best strategy to obtain the most significant reward signal. We implement and investigate the proposed system with MATLAB, Python, and libraries named TensorFlow, Numpy, and Matplotlib.
3.4 Reinforcement Learning and Control Systems
System learning strategy behavior is essential for linking RL with the control system. The policy observes the environment and takes action to accomplish the given task in the best way. This operation is similar to the function performed by the controller in the control system. Fig. 3 represents the closed-loop diagram of RL that can be implemented in terms of a closed-loop control system. In this implemented scheme, we have used an environment (considered as a plant), an agent (equivalent to the controller) to calculate action

Figure 3: RL-based closed-loop system
We have conducted simulations to check the proposed RL algorithm performance by testing SISO system at 50 rpm DC motor speed. Moreover, different training sets and rewards are used in simulations that show the algorithm applies to more training sets. In addition, the error has been regarded as a state between the target output (50 RPM) and the actual speed.
Training the model requires a different number of episodes and further tests the trained model to check whether the algorithm has learned an excellent optimal strategy or needs more episodes to train. In Tab. 2, we have shown the similarities between RL and the control system. While Tab. 3 presents the parameters of training data, including length of state vector, length of action vector, number of steps in each episode, and number of episodes in the system model. Initially, a smaller amount of training has been performed on available data to check if the agent can learn the best strategy in these training sets or needs more training sets to learn the best strategy.


The training of the system has been done by setting the last line (mode) of configuration file to 1 and setting the number of episodes as needed. Additionally, Python RL Server has been executed in the Simulink model (Run). Initially, ten training sets are selected to train the learning agent. The simulation results of the trained system are shown in Fig. 4 and the list of parameters used to train SISO system on ten sets are listed in Tab. 4.

Figure 4: Training of DDPG for ten episodes (SISO system) and its reward
The testing has been done by setting the last line (mode) of the configuration file to 0 and setting the number of episodes (4th line) if required. Use more episodes for training and less for testing if needed. The minimum training episodes required by the proposed DDPG algorithm are three (03) as the reward function is directly linked with the number of training episodes. If the number of training sets increases, the agent will have more time to explore the environment by learning the best strategy that provides positive rewards to obtain the desired output. With a small number of training sets, the agent may not realize the best strategy due to a lack of exploration time.

Since the proposed system is suitable for high-dimensional problems, the training set should be arranged according to the problem formulation. In Fig. 4, the x-axis shows the number of training sets and the y-axis indicates the rewards obtained on these training sets. It is observed that the agent received 20 rewards in 10 training sessions that can be further verified from Fig. 5. The test graph clearly shows minimized agent’s error. Moreover, Tab. 3 lists the test parameters of the learning algorithm on the SISO system. In Fig. 5, the x-axis represents the number of steps in each episode, while the y-axis represents the performance of DDPG (SISO system). In further, it is used to evaluate errors in displaying the learning strategy graph. According to the prescribed strategy, it considers the required SISO system speed error.

Figure 5: Testing of DDPG system
Fig. 5 also shows that the learning algorithm does not minimize the error because the training time of the algorithm to learn the optimal strategy is limited. Hence, it is unable to identify optimally. Therefore, rerunning the simulation with a more significant number of training steps allows exploring an ideal policy. Tab. 5 lists the parameters chosen to train the system at 50 episodes. The model has been trained again for more episodes by entering parameters in the configuration file. The x-axis in Fig. 6 shows the learning curve segments, while y-axis represents the rewards for 50 segments. Moreover, Fig. 6 illustrates that by increasing the training sets, the proposed algorithm obtain more rewards. The configuration parameter are reset in configuration file by changing its (configuration file) mode to 0 for testing. In Fig. 7, x-axis shows the number of steps in each episode, and the y-axis carries the error assessment.
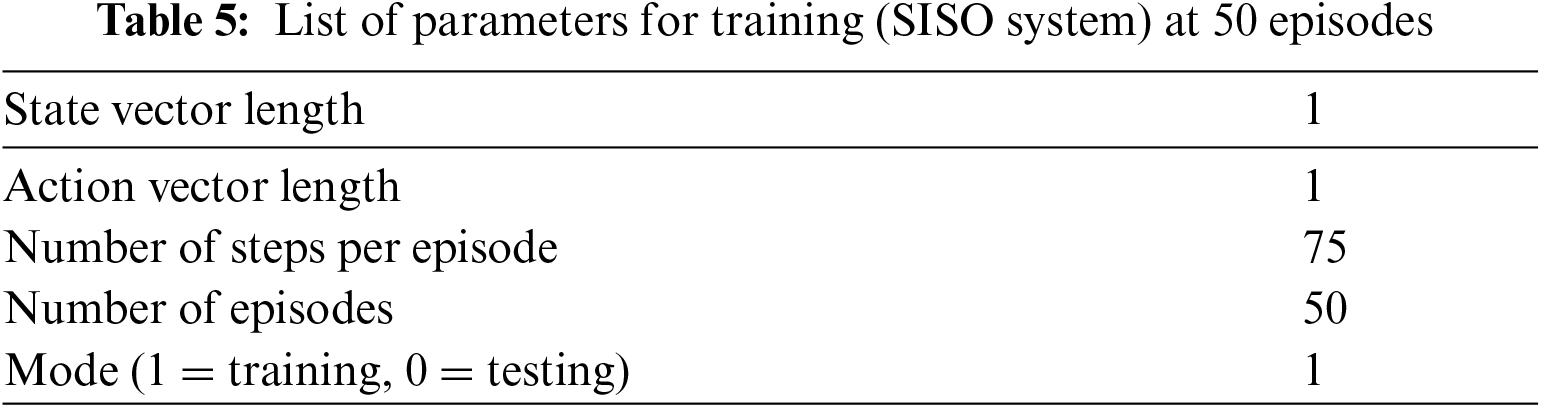

Figure 6: Training of DDPG for 50 episodes (SISO system) and its reward

Figure 7: Testing performance of DDPG (SISO system) for evaluating the error
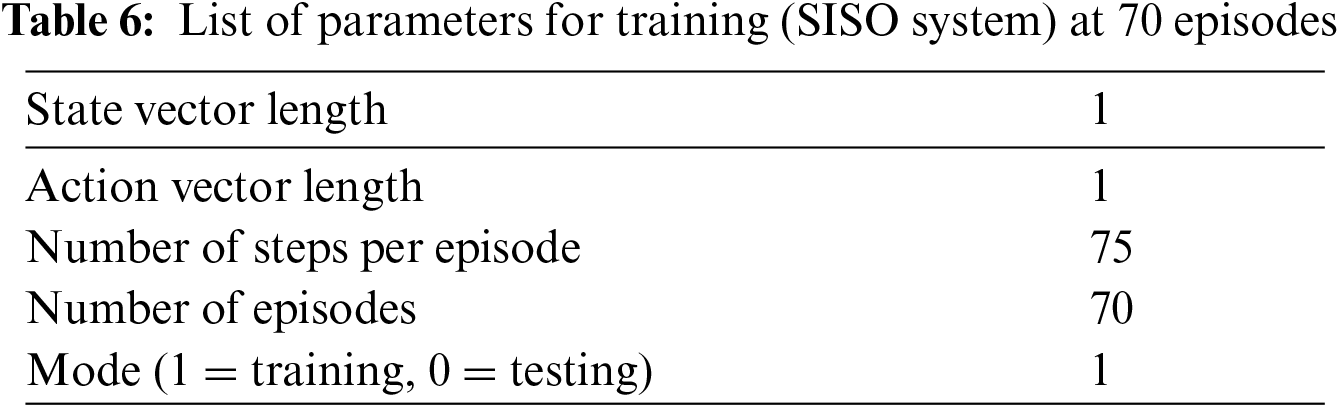
Fig. 7 further shows by increasing training sets, the algorithm explores the environment through learning and obtaining positive rewards that minimize the error. Next, the parameters of 70 training sets are considered and a similar pattern is followed. Tab. 6 shows the list of parameters used to train 70 sets in SISO system.
In Fig. 8, the x-axis shows the learning curve segment, and the y-axis shows the reward for 70 training segments. As the training sets are increased algorithm learns more and the reward also increases. The trained SISO based algorithm has been implemented by resetting parameters in the configuration file by keeping test mode as 0. In Fig. 9, x-axis shows the steps, and y-axis indicates the 70 sets of error evaluations of the trained model.

Figure 8: Training of DDPG for 70 episodes (SISO system) and its reward

Figure 9: Testing the performance of DDPG (SISO system) for evaluating the error
Fig. 9 shows how the learning algorithm learns the best strategy because it minimizes the error to approximately zero. Tab. 7 illustrates approximately zero error by increasing the system’s training set that validates the proposed algorithm and proved it an optimal approach to maximize the reward.
The different number of sets are used to train DDPG and the performance matrix has been checked. We have opted 70 training sets to train the system. The parameters shown in Tab. 8 are used to train 70 sets of the MIMO system. Moreover, the x-axis in Fig. 10 shows learning curve episodes and the y-axis illustrating rewards for 70 episodes.
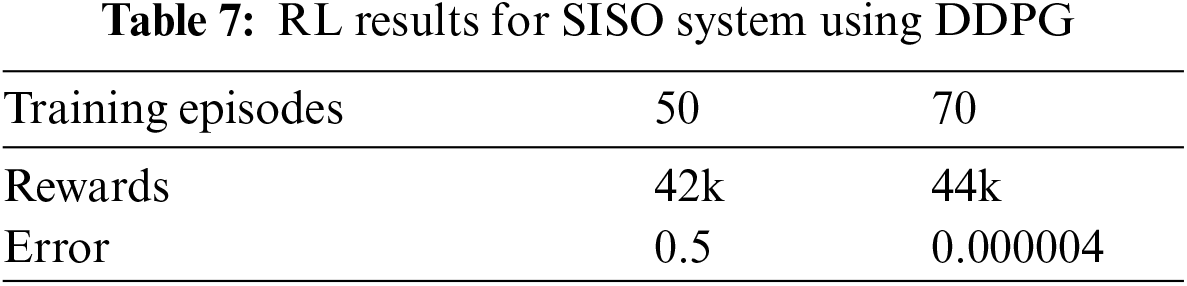

Yet again, Fig. 10 illustrated that the algorithm obtained more rewards by increasing the training sets. The learned algorithm on the MIMO system uses Tab. 9 in the configuration file that again sets the configuration mode file to 0.
The x-axis in Fig. 11 represents the steps and the y-axis presents the error evaluation of the trained model for 70 episodes. The said figure also shows that the algorithm would learn more by receiving positive rewards and minimizing the error by increasing training episodes.

Figure 10: Training of DDPG for 70 episodes (MIMO system) and rewards


Figure 11: Evaluating error of MIMO system
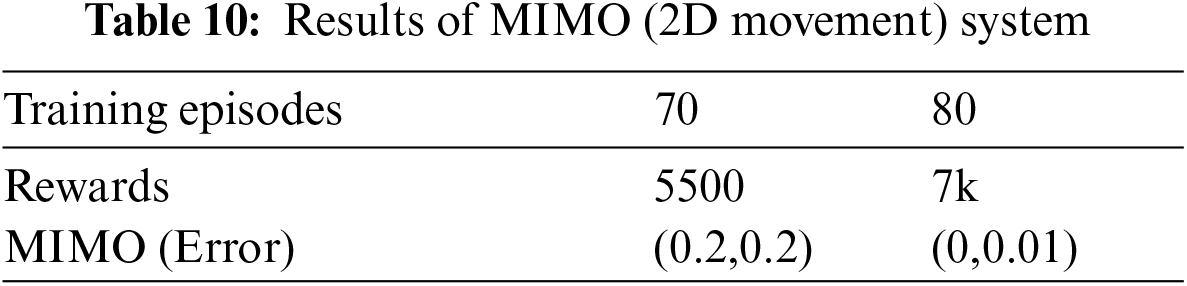
The x-axis in Fig. 12 shows the learning curve episodes and y-axis represents the rewards for 80 episodes. Fig. 12 also indicates that the algorithm is learning positively by receiving rewards.

Figure 12: Training of DDPG for 80 episodes and evaluation of error of MIMO system (a) DDGP system (b) MIMO systems
In Fig. 13, x-axis illustrates the steps and y-axis indicates the error evaluation. It depicts the algorithm finally finds the best strategy to maximize the reward function by setting the error to 0. Tab. 10 shows the result of the MIMO system.

Figure 13: PID response to SISO system
4.3 Proportional Integral Derivative Controller (PID)
The PID system consists of three primary proportional integral differential coefficients. These coefficients are adjusted to obtain the best response. It is widely used as a control loop feedback controller in control system problems. The closed-loop control system gets a stable design under the set point or desired value [27]. For motor speed control using PID as the controller, please set the following PID parameters given in Tab. 11.
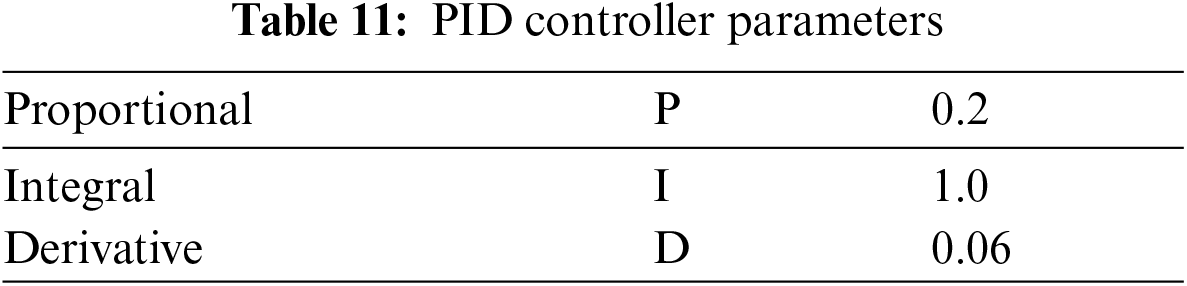
As given in the close loop diagram, suppose that the proposed plant is a motor. Desired value (50 RPM) is given to the system. Hence, the controller may reduce the error in the direction of optimal value. Moreover, its performance is measured by plotting the graph of actual and desired speed in the workspace. Fig. 13 shows PID results using SISO system (DC motor) while the time has been demonstrated on x-axis, and y-axis shows desired speed, actual speed, error, and control input.
4.4 Linear Quadratic Regulator (LQR)
LQR provides design techniques for practical feedback systems. It uses the state feedback method for controller design. Fig. 14 illustrates the result of LQR on DC motor while x-axis shows time, and y-axis represents the desired speed, actual speed, error, and control input.

Figure 14: LQR response to SISO system
The simulation results of PID and LQR on the SISO (DC motor) system show that the proposed RL algorithm (DDPG) performance is almost as good as PID and LQR. The summary of the results for control system controllers and DDPG for error minimization between the desired and actual speed of the motor is given in Tab. 12.

The findings of proposed DDPG study are significant, however it has some limitations while improving performance. Since the presented model is a model-free RL model that requires many training sets and more simulation time to find the best strategy of solving complex problems. It is an off-policy algorithm in which the agent can be explored independently of the learning algorithm. Therefore, the DDPG is considered more suitable for high-dimensional continuous action space.
This paper proposes a DDPG algorithm for setpoint tracking (minimizing errors) in the continuous domain on SISO and MIMO systems. The proposed algorithm has been validated through software architecture executed using python 3.6 and simulation using MATLAB/Simulink. It includes a framework for synchronous communication between Python (running as a server platform) and Simulink (a client platform) programs allowing direct control of any plant. The comparative analysis between DDPG, PID and LQR controllers confirms the efficacy of the proposed system as the tracking error of DDPG is measured as 0.000004 where the PID and LQR are remained at 0.0004 and 0.11, respectively. Furthermore, the results inferred that RL performs well in the control process. However, the performance of AC algorithms (i.e., DDPG) can be further improved by increasing the number of training sets. By increasing the training time, the algorithm would learn the best strategy to maximize the performance of the system. The proposed method has been tested on linear systems, and it can be further extended to nonlinear systems in the future.
Acknowledgement: The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP-2021/387), King Saud University, Riyadh, Saudi Arabia.
Funding Statement: This work was supported by the King Saud University in Riyadh, Saudi Arabia, through the Researchers Supporting Project Number (RSP-2021/387).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Y. Lecun, Y. Bengio and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015. [Google Scholar]
2. V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou et al., “Playing Atari with deep reinforcement learning. New York,ArXiv preprint, arXiv:1312.5602, 2013. [Google Scholar]
3. V. Mnih, K. Kavukcuoglu, D. Silver, A. Rusu, J. Veness et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015. [Google Scholar]
4. D. Silver, A. Huang, C. Maddison, A. Guez, A. Sifre et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, no. 7587, pp. 484–489, 2016. [Google Scholar]
5. K. Arulkumaran, M. Deisenroth, M. Brundage and A. Bharath, “A brief survey of deep reinforcement learning. New York,ArXiv preprint arXiv:1708.05866, 2017. [Google Scholar]
6. T. Lillicrap, J. Hunt, A. Pritzel, N. Heess, T. Erez et al., “Proximal policy optimization algorithms learning. New York, ArXiv preprint arXiv:1509.02971, 2015. [Google Scholar]
7. H. Jiang, H. Zhang, Y. Luo and J. Wang, “Optimal tracking control for completely unknown nonlinear discrete-time Markov jump systems using data-based reinforcement learning method,” Neurocomputing, vol. 194, no. 9, pp. 176–182, 2016. [Google Scholar]
8. M. Gheisarnejad and M. Khooban, “An intelligent non-integer PID controller-based deep reinforcement learning: Implementation and experimental results,” IEEE Transactions on Industrial Electronics, vol. 68, no. 4, pp. 3609–3618, 2021. [Google Scholar]
9. R. Yu, Z. Shi, C. Huang, T. Li and Q. Ma, “Deep reinforcement learning based optimal trajectory tracking control of autonomous underwater vehicle,” in Proc. CCC, Dalain, China, pp. 4958–4965, 2017. [Google Scholar]
10. A. Hassan, A. Rehman, N. Shabbir, S. Hassan, M. Sadiq et al., “Impact of inertial response for the variable speed wind turbine,” in Proc. ICEET, Lahore, Pakistan, pp. 1–6, 2019. [Google Scholar]
11. P. Chen, Z. He, C. Chen and J. Xu, “Control strategy of speed servo systems based on deep reinforcement learning,” Algorithms, vol. 11, no. 5, pp. 65, 2018. [Google Scholar]
12. R. Asif, A. Rehman, S. Rehman, J. Arshad, J. Hamid et al., “Design and analysis of robust fuzzy logic maximum power point tracking based isolated photovoltaic energy system,” Engineering Reports, vol. 2, no. 9, pp. 1–16, 2020. [Google Scholar]
13. W. Shi, S. Song and C. Wu, “Soft policy gradient method for maximum entropy deep reinforcement learning. New York,ArXiv preprint arXiv:1909.03198, 2019. [Google Scholar]
14. Y. Wang, K. Velswamy and B. Huang, “A novel approach to feedback control with deep reinforcement learning,” IFAC-PapersOnLine, vol. 51, no. 18, pp. 31–36, 2018. [Google Scholar]
15. J. Arshad, R. Tariq, S. Saleem, A. Rehman, H. Munir et al., “Intelligent greenhouse monitoring and control scheme: An arrangement of Sensors, Raspberry Pi based Embedded System and IoT platform,” Indian Journal of Science and Technology, vol. 13, no. 27, pp. 2811–2822, 2020. [Google Scholar]
16. J. Wu and H. Li, “Deep ensemble reinforcement learning with multiple deep deterministic policy gradient algorithm,” Mathematical Problems in Engineering, vol. 2020, no. 6, pp. 1–12, 2020. [Google Scholar]
17. R. Sutton and G. Barto, Finite Markov Decision Processes in Reinforcement Learning, 1st ed., vol. 1. London, UK: The MIT Press, pp. 37–43, 2017. [Google Scholar]
18. K. Vijay and N. Tsitsiklis, “Actor-critic algorithms,” Control and Optimization, vol. 42, no. 4, pp. 1143–1166, 2003. [Google Scholar]
19. T. Lillicrap, J. Hunt, A. Pritzel, N. Heess, T. Erez et al., “Continuous control with deep reinforcement learning. New York,ArXiv preprint arXiv:1509.02971, 2015. [Google Scholar]
20. J. Schulman, S. Levine, P. Abbeel, M. Jorda and P. Moritz, “Trust region policy optimization,” in Proc. ICML, Lille, France, pp. 1–9, 2015. [Google Scholar]
21. J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, “Proximal policy optimization algorithms. New York,ArXiv preprint arXiv:1707.06347, 2017. [Google Scholar]
22. Z. Wang, V. Bapst, N. Heess, V. Mnih, R. Munos et al., “Sample efficient actor-critic with experience replay. New York,ArXiv preprint arXiv:1611.01224, 2016. [Google Scholar]
23. M. Andrychowicz, F. Wolski, A. Ray, J. Schneider, R. Fong et al., “Hindsight experience replay,” in Advances in Neural Information Processing System (NIPS), Amazon, 2017. [Google Scholar]
24. Z. Wang, T. Schaul, M. Hessel, H. Hasselt and M. Lanctot, “Dueling network architectures for deep reinforcement learning,” in Proc. ICML, New York, USA, pp. 1–9, 2016. [Google Scholar]
25. T. Lillicrap, J. Hunt, A. Pritzel, N. Heess, T. Erez et al., “Continuous control with deep reinforcement learning,” in Proc. ICLR, San Juan, Puerto Rico, pp. 1–14, 2016. [Google Scholar]
26. S. Spielberg, R. Gopaluni and P. Loewen, “Deep reinforcement learning approaches for process control,” in Proc. AdCONIP, Taipei, Taiwan, pp. 201–206, 2017. [Google Scholar]
27. K. Cheon, J. Kim, M. Hamadache and D. Lee, “On replacing PID controller with deep learning controller for DC motor system,” Journal of Automation and Control Engineering, vol. 3, no. 6, pp. 452–456, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |