DOI:10.32604/cmc.2022.021987

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021987 |  |
| Article |
Hyperuricemia Prediction Using Photoplethysmogram and Arteriograph
1Department of Electrical, Electronic and Systems, Faculty of Engineering and Built Environment, Universiti Kebangsaan Malaysia, Bangi, 43600, Malaysia
2Department of Physiology, Faculty of Medicine, Universiti Kebangsaan Malaysia, Cheras, 56000, Malaysia
3Department of Medicine, Faculty of Medicine, Universiti Kebangsaan Malaysia, Cheras, 56000, Malaysia
4Family Medicine Department, Faculty of Medicine, Universiti Kebangsaan Malaysia, Cheras, 56000, Malaysia
*Corresponding Author: Nazrul Anuar Nayan. Email: nazrul@ukm.edu.my
Received: 22 July 2021; Accepted: 23 August 2021
Abstract: Hyperuricemia is an alarming issue that contributes to cardiovascular disease. Uric acid (UA) level was proven to be related to pulse wave velocity, a marker of arterial stiffness. A hyperuricemia prediction method utilizing photoplethysmogram (PPG) and arteriograph by using machine learning (ML) is proposed. From the literature search, there is no available papers found that relates PPG with UA level even though PPG is highly associated with vessel condition. The five phases in this research are data collection, signal preprocessing including denoising and signal quality indexes, features extraction for PPG and SDPPG waveform, statistical analysis for feature selection and classification of UA levels using ML. Adding PPG to the current arteriograph able to reduce cost and increase the prediction performance. PPG and arteriograph data were measured from 113 subjects, and 226 sets of data were collected from the left and right hands of the subjects. The performance of four types of ML, namely, artificial neural network (ANN), linear discriminant analysis (LDA), k-nearest neighbor (kNN), and support vector machine (SVM) in predicting hyperuricemia was compared. From the total of 98 features extracted, 16 features of which showed statistical significance for hyper and normouricemia. ANN gives the best performance compared to the other three ML techniques with 91.67%, 95.45%, and 94.12% for sensitivity, specificity, and accuracy, respectively. Features from PPG and arteriograph able to be used to predict hyperuricemia accurately and noninvasively. This study is the first to find the relationship of PPG with hyperuricemia. It shows a significant relation between PPG signals and arteriograph data toward the UA level. The proposed method of UA prediction shows its potential for noninvasive preliminary assessment.
Keywords: PPG; arteriograph; second derivative of PPG; hyperuricemia; ML
Cardiovascular disease (CVD) contributed approximately 18.6 million deaths globally in 2019; it increases to approximately 53.7% from 1990 [1]. This finding may be attributed to the escalation of obesity, diabetes, hypertension, dyslipidemia, and hyperuricemia [2]. According to a study by Touserkani et al. [3 and Lee et al. 4], the risk of CVD mortality was associated significantly with high uric acid (UA) level for males and females. Even though the elevation of UA level as an independent risk factor of CVD risk still remains debatable, a study from Chang et al. [5] showed that UA level is associated significantly with cardiovascular risk.
Hyperuricemia, a high UA level condition, is >420 μmol/L for males and >360 μmol/L for females [6]. Purine-rich food, such as red meat, internal organs of animals, and few types of seafood, may elevate UA level. Excessive UA leads to accumulation of monosodium urate crystals around joint and kidney and causes kidney stones and gouty arthritis. Currently, the gold standard in measuring UA level is through micro-invasive blood test, which causes discomfort and difficulty in continuous monitoring.
The significant association between elevated UA level and escalated CVD risk may be mediated by increased arterial stiffness [7]. Few studies on measuring arterial stiffness noninvasively have been conducted. The gold standard measurement of arterial stiffness is through carotid–femoral pulse wave velocity (cf-PWV). UA was found to be significantly correlated with cf-PWV in hypertension patients [8]. A study on the correlation between UA and brachial-ankle pulse wave velocity (ba-PWV) was controversial [9,10]. However, a cross-sectional study from Japan population has shown a significant association between ba-PWV and UA with a p-value of less than 0.05 [11,12]. In addition to ba-PWV, machine learning (ML) is a promising tool in prediction and classification, especially in various applications in a clinical setup. ML approaches have been used in predicting UA level with sociodemographic characteristics, clinical measurements, and dietary information as the inputs [4,13,14]. Performance was measured in terms of area under the curve (AUC), root mean square error (RMSE), sensitivity (Se), and specificity (Sp). Ichikawa et al. [13] showed performance of 0.796, 0.752, and 0.819 for AUC, Se, and Sp, respectively, by using gradient-boosting decision tree for Japan population. A study from Korea showed that when using naïve Bayes, the highest Se (0.73) was obtained, and random forest classification produced the highest balanced classification rate (0.68) [4]. The boosted decision tree also showed the least RMSE of 0.03 for the Bangladesh population [14].
Photoplethysmogram (PPG) has become a promising technique in physiological parameter analysis because it responds to changes in blood volume. This technique may also provide beneficial information on the cardiovascular system. PPG has been widely used in measuring heart rate, blood pressure [15] and respiration rate [16]. However, the PPG signal morphology is easily influenced by age, gender, and pathophysiological changes, such as blood oxygen saturation, heart rate, blood pressure, cardiac output, and respiration [17,18]. A study on man with CVD risk found significant relationship between PPG morphology and lipid profile with onset to systolic peak as the significant feature [19]. In addition to raw PPG data, second derivative of PPG (SDPPG) was brought along because it can easily be quantified depending on the delicate changes in the PPG contour [20]. The idea of applying the first derivative to the PPG (FDPPG) waveform was started by Ozawa in 1972. The SDPPG was applied to simplify the interpretation and understanding of the original PPG waveform [21]. Fig. 1 shows the raw, first derivative, and second derivative of PPG waveform recorded from the present study. Inoue et al. [22] proposed that SDPPG waveform is an independent predictor of cardiovascular mortality. In addition, a study on relating fiducial point from SDPPG waveform has also been conducted to detect myocardial infarction; the accuracy (Acc) of 95.40% [23] and 90.60% [24] are acceptable. The morphological features of SDPPG are closely related to vessel conditions [25]; thus, the association of UA and PPG can be investigated as UA affects vessel condition, such as arterial stiffness. UA has been long associated with arterial stiffness [26]. Various types of equipment in analyzing pulse wave have been introduced, such as complior, sphygmoCor, and arteriograph [27]. This noninvasive equipment has been validated and compared with invasive technique [28–30]. Complior and sphygmoCor rely on tonometric method, and arteriograph is based on oscillometric method. According to Horváth et al. [30], arteriograph output were closely correlated with invasive measurement. In addition, the position of the cuff for the arteriograph is much simpler than the complior and sphygmoCor devices [27,31]. Recent studies using arteriograph showed that PWV produces a significant p-value (<0.001) for healthy males and females [32]. In addition, studies from Jekell and Kahan used arteriograph as a monitoring device for hypertensive patients. Arteriograph was compared with sphygmoCor (which is the gold standard); they produce similar values of PWV [33]. A similar study on hypertension and normotensive subjects found a significant p-value on PWV value [34].
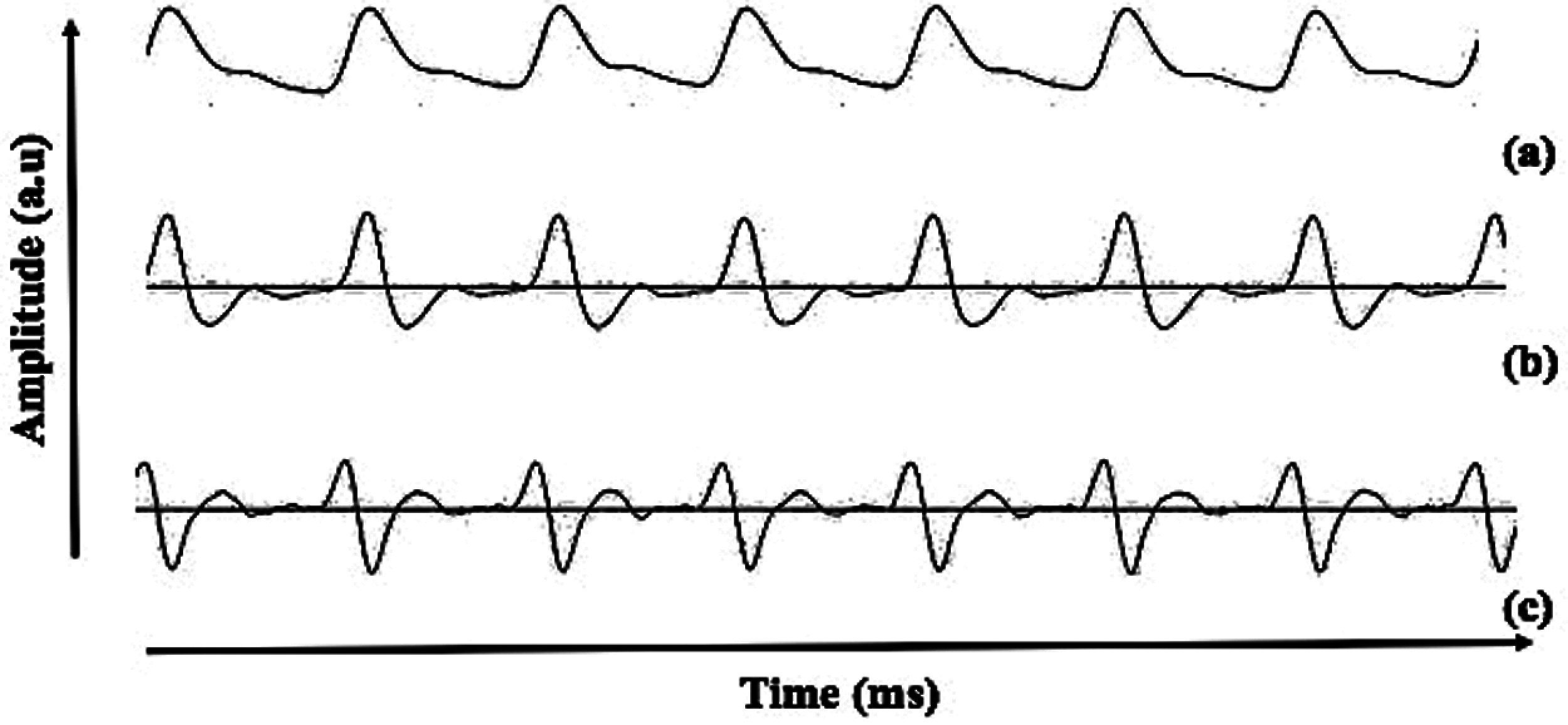
Figure 1: Description of the (a) PPG, (b) FDPPG and (c) SDPPG waveform recorded in the present study
A novel PPG-based method is proposed to establish the utility of the PPG signal morphology and arteriograph output for UA classification, i.e., hyperuricemia and normouricemia with the aid of ML techniques; artificial neural network (ANN), linear discriminant analysis (LDA), k-nearest neighbor (kNN), and support vector machine (SVM). The use of PPG signal provides simple yet reliable implementation on home monitoring applications to enable preliminary UA level prediction at home non- invasively. To the best of our knowledge, this study on arteriograph and PPG-based association regarding UA level is the first. In the proposed method, output and features from arteriograph, PPG, and SDPPG signals are extracted to develop a UA prediction model using the ML algorithm.
The brief block diagram of the proposed UA prediction technique is shown in Fig. 2. The proposed prediction model can be divided into five major sections, as follows: (I) PPG and arteriograph data acquisition; (II) preprocessing and selection of the good quality signal; (III) fiducial point detection from the PPG and SDPPG signal followed by feature extraction; (IV) feature selection of the input to the ML process using the most significant p-value from statistical analysis; (V) classification of hyperuricemia and normouricemia using the best performance of classifier in terms of Se, Sp, and Acc.
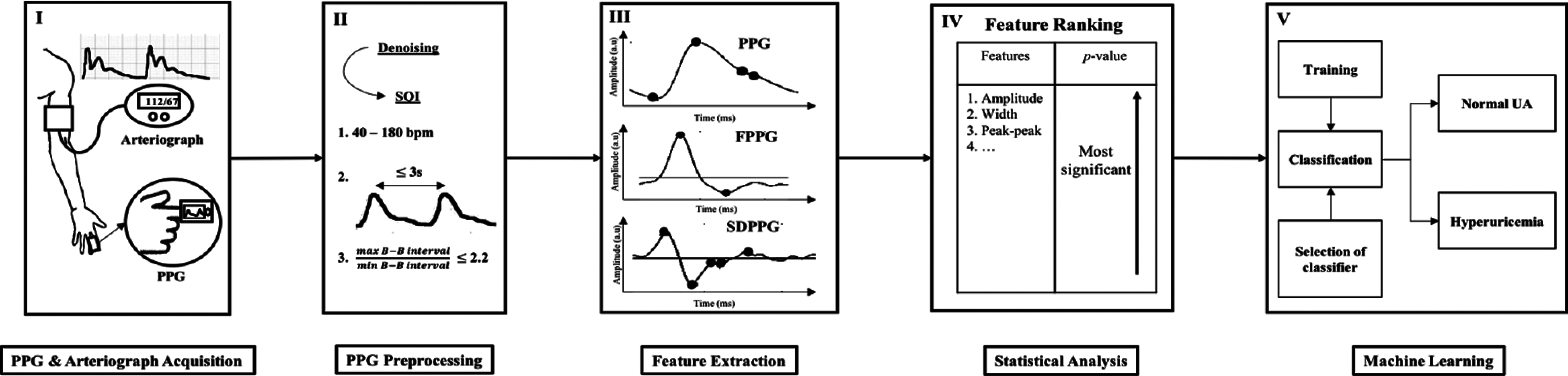
Figure 2: Block diagram of methodology consisting of 5 phase: I. data acquisition, II. preprocessing, III. feature extraction, IV. feature ranking and V. ML for classifying normal and high UA level
2.1 PPG and Arteriograph Data Acquisition
This study was approved by The Research and Ethics Committee of the Hospital Universiti Kebangsaan Malaysia with a registration number of UKM.PPI.800-1/2/21. The study population consisted of 113 nonsmoking subjects (60 men and 53 women) with age ranging from 19–80 years old (mean ± standard deviation, 37.1 ± 13.4 years); they participated in the data collection process at the UKM Medical Center (UKMMC), UKMMC’s primary care clinic, and university health centre, UKM. A total of 16.81% of the subjects had hypertension, 14.16% had hypercholesterolemia, 6.19% had diabetes, and the remaining 62.84% does not have any CVD risk factors based on the questionnaire provided for subjects.
Participants submitted their informed consent prior to the data collection process. Subjects arrived for the data collection in the morning after fasting overnight for the blood test. A random fasting blood test was required to gauge the individual’s UA level. A questionnaire, which consisted of the health status of the subjects, was provided. The weight, height, arm circumference, and distance between suprasternal notch (jugulum, jug) and pubic bone (symphysis, sy) were measured prior to the arteriographs’ protocol assessment. Arm circumference was measured and recorded for better selection of cuff size. The velocity of the PWV value is measured in m/s given the jug-sy measurement.
Arteriograph (TensioMed Ltd., Hungary) is a cuff-based oscillometry device that requires a cuff to be placed at the upper hand in measuring pulse wave. Every subject should be rested in a supine position for 10 mins before the arteriograph measurement is recorded. The subjects should avoid speaking and muscle movements, which may result in measurement failure. The measurement process was repeated three times for each arm, and the mean of these output was used for the next phase. Tab. 1 shows the explanation of hemodynamic output measured by the arteriograph (P1: Amplitude of the early (forward) systolic wave, P2: Amplitudes of the late (backward) systolic wave, R: Correlation coefficient). At the first cuff inflation, the systolic blood pressure (SBP) and diastolic blood pressure (DBP) were measured. The cuff was overinflated at 35–40 mmHg above the subject’s SBP for pulse wave configuration. The pulse wave produced was a combination of early and late systolic peaks. During systole, the blood volume ejected into the aorta resulted in pulse wave (early systolic peak). Then, this pulse wave was reflected at the bifurcation of the aorta when it propagates through periphery (late systolic peak). The early, late systolic, and diastolic waves were decomposed using arteriograph software, and the onset and peaks of the waves were determined [35].
The pulse oximeter (CMS50D+, Contec, China) with sampling frequency of 100 Hz was placed at the index finger of subjects for the PPG measurement from both hands for 10 mins each. It was placed at the opposite arm from the arteriograph-cuffed arm during the recording. Our preliminary result showed no PPG pulse from the pulse oximeter once the arteriograph is inflated. This finding may be due to the flow condition that stopped due to the occlusion in the brachial artery that prevented blood flow in the artery for better detection of late systolic wave to determine Aix and SPBao [30].
2.2 Preprocessing and Signal Quality Indexing
PPG signal preprocessing algorithm consists of baseline and high-frequency removal and signal quality indices (SQI). All PPG data were processed offline in MatLAB (The Mathworks Inc., USA). In this step, a fast Fourier transform technique was used as a band-pass filter with a cut-off frequency of 0.5–10.0 Hz. Based on the collected PPG signals, a frequency above 10 Hz was considered high-frequency noise and that below 0.5 Hz was attributed to baseline wander. Amplitude offset was found using the filtering process. To overcome this problem, auto-offsetting was used to bring back any y-axis below zero value to a positive value. It was performed by offsetting the signal by the difference between zero-amplitude and the largest negative value.
Then, the filtered PPG signal undergoes SQI in determining the reliable signals. This step is crucial because only high-quality signal is processed for the next phase. This type of signals is referred to as stable signal within a period of time, in which the three conditions proposed by Orphanidou et al. [36] are fulfilled, as follows: (1) the extrapolated 10 s PPG signal must be between 40 and 180 bpm, (2) the PPG pulse-peak gap must not exceed 3 s to avoid missing more than one beat, and (3) the ratio of maximum and minimum beat–beat interval within a sample must be less than 2.2. Fig. 3 shows that the poor quality PPG signal was described in red color, and the blue color indicates the good quality signal based on conditions previously described.
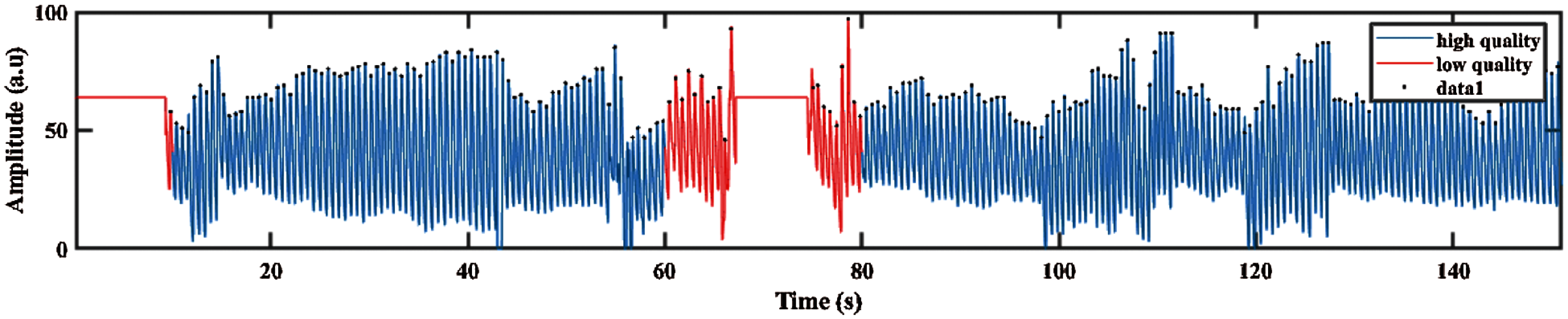
Figure 3: PPG signal with good and poor quality defined in blue and red color signal respectively
The good quality of PPG signals undergoes first and second differentiations, resulting in FDPPG and SDPPG, respectively. Fig. 4 shows the PPG signal and their derivative of first and second derivations. The FDPPG and SDPPG represent the velocity and acceleration of blood, respectively. Delineator [37] and bp_annotate [38] algorithms were applied to detect the fiducial points in the PPG signals. These points are pulse onset, systolic peak, dicrotic notch, and diastolic peak, as shown in Fig. 4a. Both algorithms were compared manually in detecting fiducial points toward our PPG data. Delineator algorithm shows accurate detection of onset and systolic peak, and bp_annotate provides better detection of notch and diastolic peak. The determination of pulse onset related to zero-crossing point prior to maximum inflection and systolic peak was defined as the zero-crossing point after inflection [37]. Maximum and minimum inflection points are represented in blue dotted line in Fig. 4c respectively. The dicrotic notch is the minimum of the subtraction of the signal and the straight line from systole to diastole [38]. For the diastolic peak, the minimum of the second derivative of the time series following the dicrotic notch relative to a window of radius systolic–systolic peak (median heartbeat interval calculated from the onset) is divided by 5 s.
The SDPPG consists of five waves and divided into systole region (a, b, c, and d waves) and diastole region (e wave). SDPPG waves were detected by adapting the algorithm proposed in [23] with some modification to improve ‘a’ and ‘e’ wave detection. The first and second derivatives of PPG signal are derived using the following equations: interval calculated from the onset divided by 5 s around itself. The first and second derivative of PPG signal are derived using the following Eqs. (1) and (2):
where y(t), y(t – 1), and y(t + 1) are the present sample, previous, and next sample, respectively. The maximum and minimum peaks from FDPPG were determined for references in detecting all SDPPG waves, as shown in Fig. 4b. For maximum peak identification, all positive peaks and the first peak obtained prior to systolic peak and after onset. The minimum peak is defined from all the negative peaks and peaks found after the maximum peak and before half of the current cycle duration. After maximum and minimum peak determination, five waves, namely, wave ‘a’, ‘b’, ‘c’, ‘d’, and ‘e’ from the SDPPG waveform were then extracted, as shown in Fig. 4c. The first positive peak prior to the maximum peak of FDPPG considered as the ‘a’ wave, which can be easily located using the maximum peak location in SDPPG. This approach was different from [23] that used threshold for the determination of the most significant peak. It can result in false peak detection due to the low amplitude of the maximum peak. The ‘b’ wave was defined from all negative peaks and the first negative peak that occurred after the zero-crossing of the ‘a’ wave. The ‘c’ wave was determined at the first positive peak prior to ‘d’ wave, and ‘d’ wave is the first negative peak prior to the ‘e’ wave; otherwise, ‘c’, ‘d’, and ‘e’ waves were merged into a single wave. Finally, ‘e’ wave lies within the minimum peak and local extreme peak in FDPPG given its maximum range, prior to the dicrotic notch detected in the PPG signal compared with [23]. Hence, finding the local extreme peak is a complicated process. Tab. 2 shows the features used in the proposed method (O: Onset, S: Systolic, N: Dicrotic notch, D: Diastolic, R: Peak ratio, A: Amplitude difference, T: Peak interval, J: Jerk, RCT: Relative crest time).
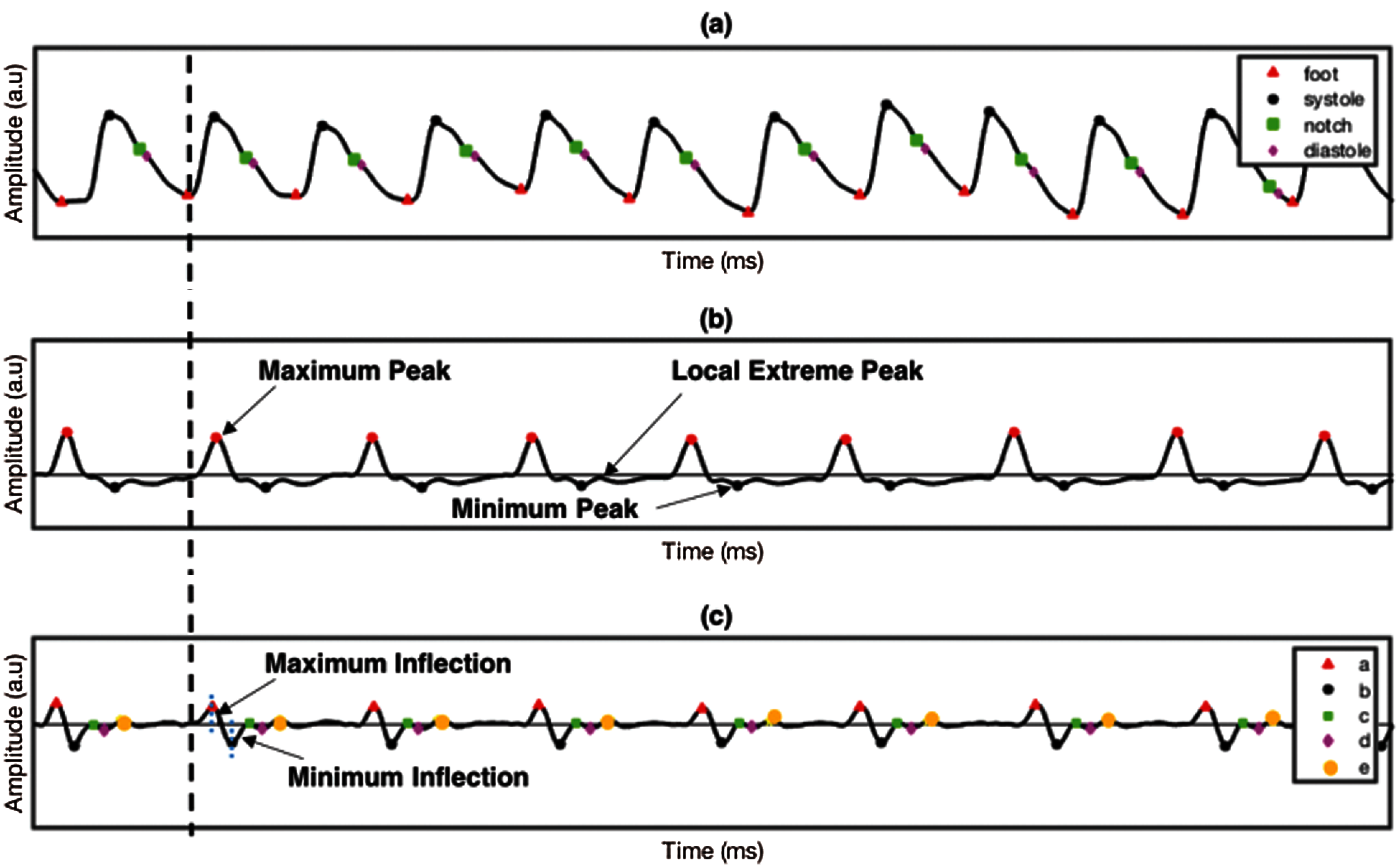
Figure 4: PPG signal and its derivatives (a) PPG, (b) FDPPG and (c) SDPPG
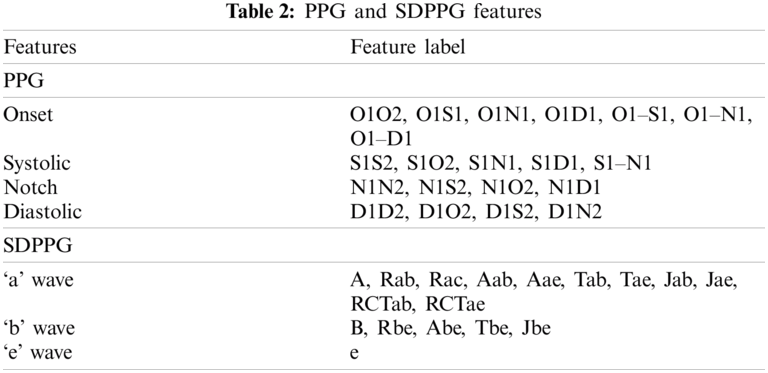
Twenty features can be extracted from PPG pulse consisting of two domain time (16 features) and amplitude (4 features) domain, as shown in Fig. 5a. The number ‘2’ indicates features from the next PPG pulse. For SDPPG, 17 features can be extracted on the basis of five waves from SDPPG after removing ‘c’ and ‘d’ waves because, for some signals, the ‘c’, ‘d’, and ‘e’ waves were merged into one wave (‘e’ wave) due to the high heart rate [38] bring to previous. Hence, features related to ‘c’ and ‘d’ waves were excluded because they result in non-accurate value of both features. Jerk is the accelerated volume change per unit time. It can be measured from the absolute height of two respective waves with the corresponding time interval, as summarized in Eq. (3). The relative crest time (RCT) feature is the ratio of extracted interval compared with the pulse width. Fig. 5b shows features that are available in the SDPPG pulse.
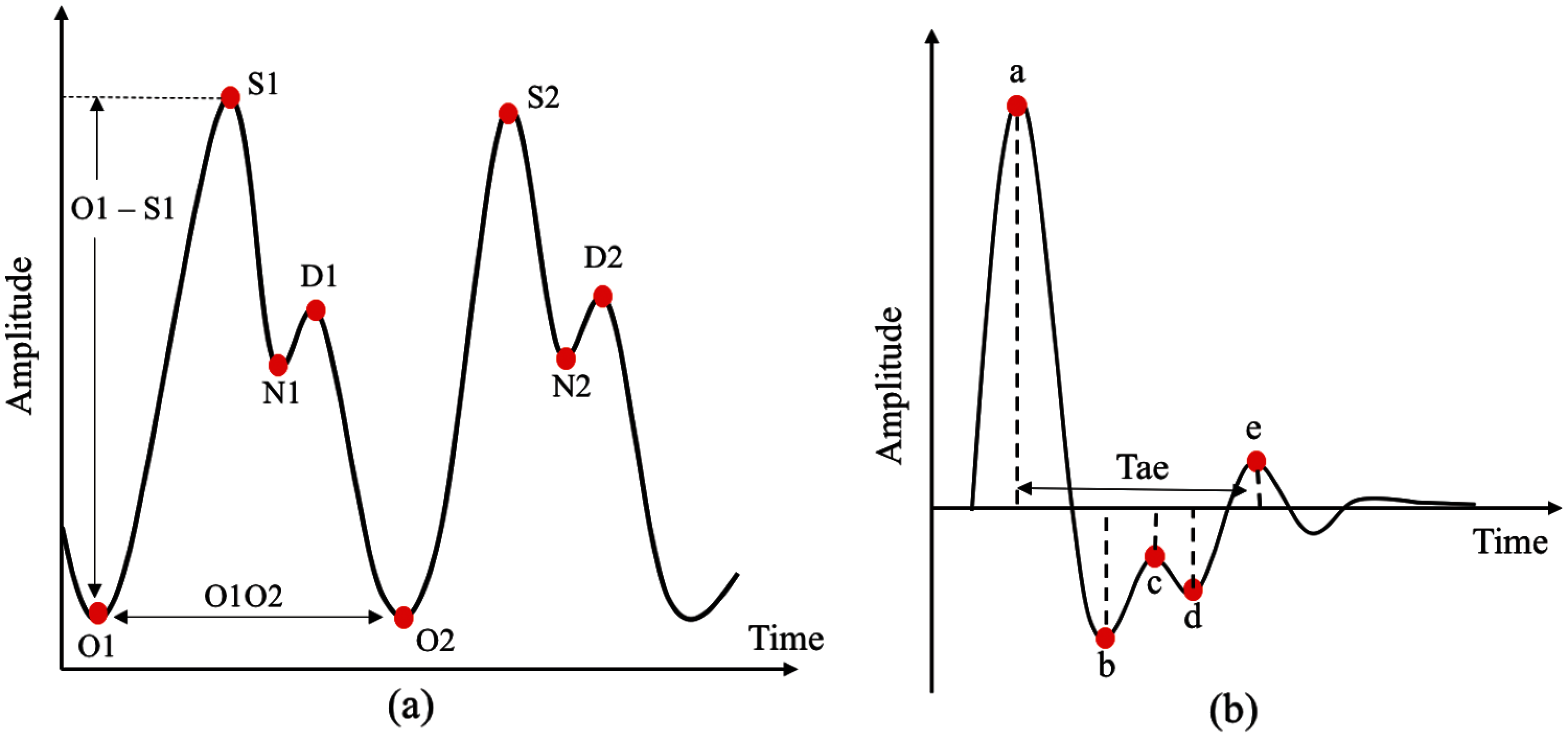
Figure 5: Features available in PPG and SDPPG pulses (a) time and amplitude domain features in PPG pulses and (b) features extracted in SDPPG pulses
A total of 98 features were obtained from PPG, SDPPG, and arteriograph from the left and right hands. These features were divided as follows: 40 from PPG, 34 from SDPPG, and 24 from arteriograph’s output. A descriptive statistics of the features (mean ± SD) in ranking the features based on the p-value was applied using SPSS software. The normality of all features was assessed using the Shapiro–Wilk test, Q–Q plot, and equality of variance using Levine’s test. Shapiro–Wilk technique was preferable because of good power properties over a wide range of asymmetric distribution compared with the Kolmogorov–Smirnov for normality test [39]. Non-normally distributed features undergo Mann–Whitney U test to find the significant difference between two groups, hyperuricemia and normouricemia. Independent t-test was performed for normally distributed features. The features were then sorted by the least to the highest p-value with confidence interval of 95%. This step enhances the accuracy rate of the classifiers [40]. Significant features (p < 0.05) were used as the inputs for ML classification.
The final phase of the proposed method is to design an effective decision boundary for the classification of two different groups of normouricemia (control) and hyperuricemia (case). The respective features were divided randomly for training and test data with ratio of 70 and 30, respectively. UA level greater than 360 μmol/L for women and 420 μmol/L for male was under the case group, and UA level lower than those values was categorized as control group. ANN, LDA, kNN, and SVM were used to investigate which ML techniques produced better performance in classifying control and case group. The selection of these 4 types of ML is due to their wide application in the study of CVD prediction [41–46].
ANN is a very capable ML technique given that neural networks are data-driven self-adaptive methods [47]. ANN is composed of an input, hidden, and output layers. The input layer consists of neurons that represent different features. A three-layer feed-forward network was used with Levernberg–Marquadt training algorithm and log-sigmoid transfer function at the first and second hidden layers, respectively. The number of hidden neurons was set to 1–15 at each layer. The purelin transfer function was used at the output layer, and the outputs of control and case group were set to ‘0’ and ‘1’, respectively. The LDA technique allows transformation of features into a low-dimensional space that maximizes the ratio between-class to the within-class variance [48]. Three steps in transforming into a low-dimensional space are as follows: (1) calculate the separability between different classes, (2) calculate the distance between the mean and the samples of each class, and (3) construct the low-dimensional space that maximizes the calculation in step 1 and minimizes that in step 2. kNN identifies the similarities between the training inputs (control and case group). Each neighbor is set with a weight age to allow the nearer neighbors to contribute more than the distant ones to the average [49]. Euclidean distance of five neighbors was applied to determine the nearest neighbor of the test data corresponding to the control or case group. The SVM technique uses the hyperplane decision boundary to maximize the distance from the hyperplane to the nearest training data point [50]. The linear and nonlinear quadratic function kernels were used to find the linear and nonlinear relations, respectively, of the selected input to the corresponding groups.
Performance evaluation of four different types of ML used Se, Sp, and Acc. The details of performance evaluators in Eqs. (4)–(6) are as follows:
where TP = number of hyperuricemia accurately detected as case group, TN = number of normouricemia accurately identified as control group, FN = number of hyperuricemia inaccurately detected as control group, and FP = number of normouricemia inaccurately detected as case group.
This section evaluates the performance of the proposed UA level prediction based on the features and output from PPG, SDPPG, and arteriograph through several types of ML techniques.
Patient’s demographics are described in Tab. 3 (L: Left hand, R: Right hand). A total of 113 subjects were divided into control and case groups, which consist of 72 and 41, respectively. A total of 226 sets of PPG data were recorded with a duration of 10 min per data. Only PPG and SDPPG signals undergo signal analysis given that arteriograph produces parametric form of measurement, which is not signal-based. High-quality signals based on SQI process proceed to the next phase, which is feature extraction. A total of 40 features were extracted from the left and right hands of the PPG signal based on onset, systolic peak, dicrotic notch, and diastolic peak. For the SDPPG feature, given that ‘c’, ‘d’, and ‘e’ waves merge, any features that contain ‘c’ and ‘d’ waves are discarded to obtain accurate feature values. The total features after reduction of ‘c’ and ‘d’ waves is 17. The features are excluded for the next phase, which is feature ranking, because of the limited sample size. Fig. 6 shows an example of merged ‘c’ and ‘d’ waves.
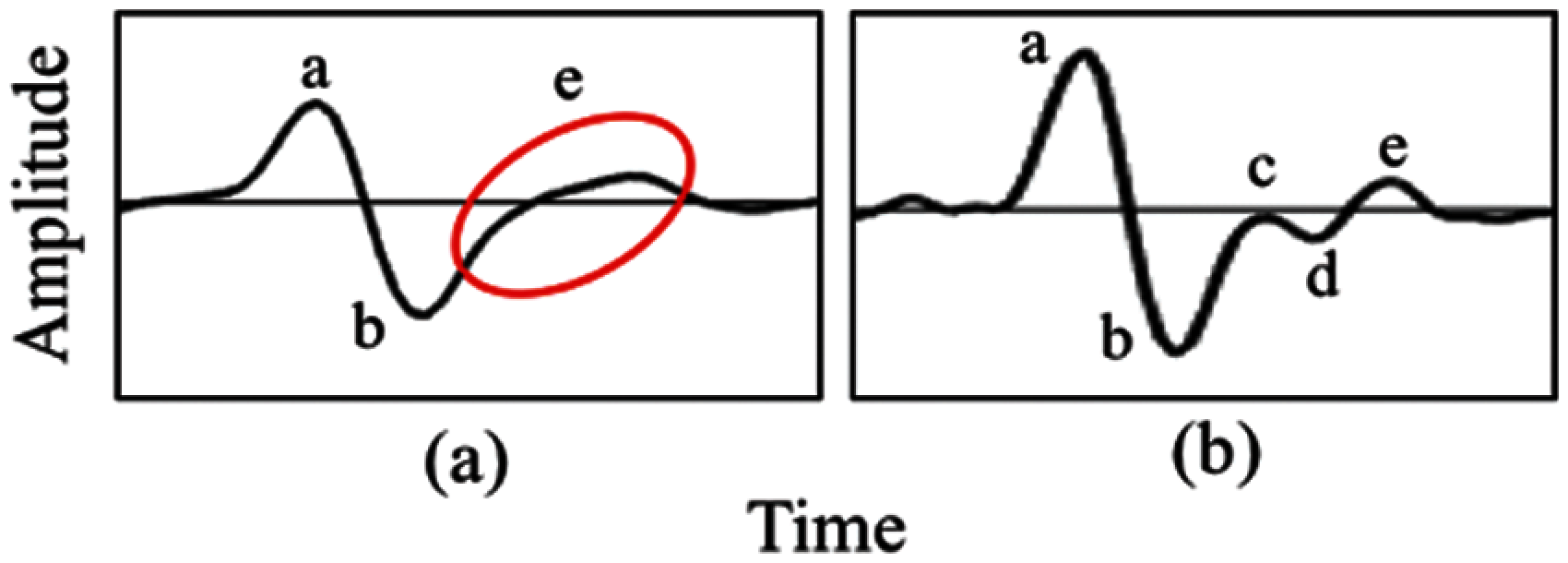
Figure 6: Comparison from (a) merge ‘c’, ‘d’ and ‘e’ into ‘e’ wave (b) presence of ‘c’, ‘d’ and ‘e’ wave
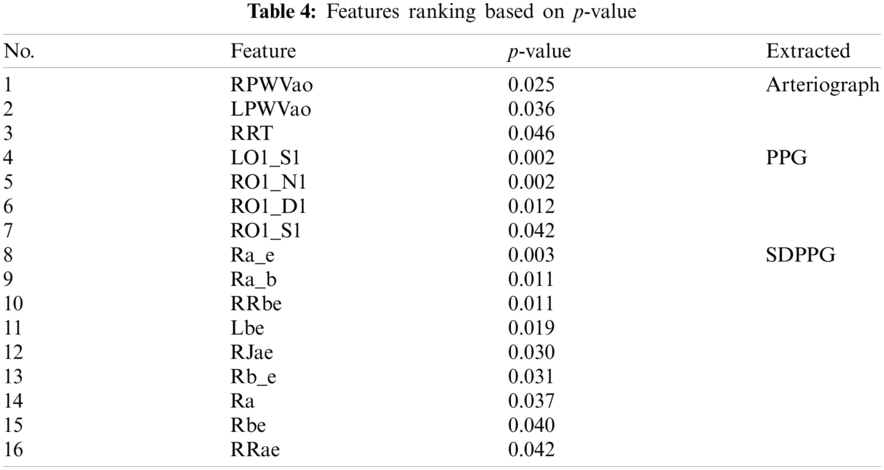
Statistical analyses were performed using t-test (independent samples t-test) and Mann–Whitney U test for normal and non-normally distributed data. This type of t-test compared the mean between two groups, and the Mann–Whitney U test or Wilcoxon rank sum test is an alternative for nonparametric analysis, comparing median between two groups. Among the 98 features, 16 features with significant p-value < 0.05 are fed as the inputs for ML algorithm, as shown in Tab. 4. Arteriograph produced three significant features, as follows: LPWVao (0.036), RPWVao (0.025), and RRT (0.046). The four significant features from PPG include LO1_S1 (0.002), RO1_S1 (0.042), RO1_N1 (0.002), RO1_D1 (0.012). The highest number of significant features is 9 from SDPPG, namely, Lbe (0.019), RRae (0.042), RRbe (0.011), Rbe (0.040), Ra_b (0.011), Ra_e (0.003), Ra (0.037), RJae (0.030), and Rb_e (0.031).
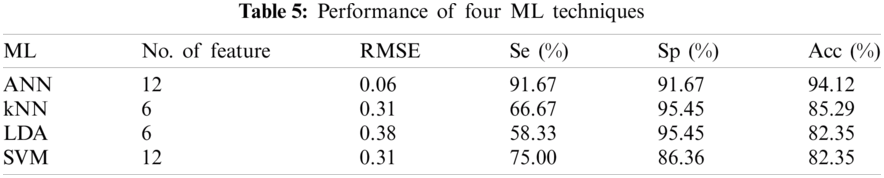
The performance of the four classifiers was evaluated using RMSE, Se, Sp, and Acc. Different numbers of features provide different performance results. Tab. 5 shows the performance summary of the result using different types of ML techniques. The number of features from Tab. 4 is sorted from greatest to least significant p prior to feeding into the ML algorithm. All MLs use five-fold cross-validation and 16 features as the inputs. SVM compared four types of kernel functions, namely, linear, radial basis function, and third- and fourth-order polynomial. Linear kernel functions produced better performance than other kernel functions using six features. The LDA ML uses two different types of discriminants, which are linear and quadratic. Quadratic discriminants only require six features compared with linear type but obtain the same performance result. For kNN ML, the maximum number of neighbor is set to 100, and the best number of neighbor is 7–13 using six features that produce the same best performance for that neighbor. The least amount of neighbor was selected for the final comparison with other ML techniques. The ANN produced better performance than the three other ML techniques. Hidden layers one and two were set to 30. Random data division was used as the target. It was divided into three groups using random indexes (train, validation and test). Levenberg-Marquardt training function and the performance were expressed in terms of mean square error. For the training computation mode, MEX algorithm was used. The epoch number was set at 1000 and the algorithm has converged at a performance of 0.00. The threshold gradient and MU value were set at (

Data had been collected from normouricemia and those with hyperuricemia subjects. PPG and arteriograph techniques were used to correlate UA level noninvasively. Significant association was obtained between the level of UA to the extracted features from PPG and arteriograph. A total of 37.16% of the subjects have comorbidities, such as hypertension, hypercholesterolemia, and diabetes. Out of 37.16%, 16.42% come from control group and the remaining, 20.74% come from case group. This can be said that subjects with high uric acid level does not necessarily have comorbidities and similarly with normal uric acid level. These subjects were also included given that such comorbidities may be difficult to neglect because several studies proved the significant association among hyperuricemia and hypertension [51], hypercholesterolemia [52], and diabetes [53]. The PPG signals may represent many physiological processes within cardiovascular system [54], and arteriograph was used in measuring oscillometric PWV parameter [30]. Tab. 4 shows that the left and right hands of the PWV parameter showed significant relation with high and normal UA which similar as reported in [11,12]. The PPG features showed that the onset to the systolic peak of left hand (LO1_S1) and onset to the dicrotic notch of the right hand (RO1_N1) of PPG in time domain is the most significant compared the three other fiducial points. Applying the SDPPG added more significant features than only using raw PPG signal and arteriograph. However, the relationship between each significant PPG and SDPPG features may be further studied in accordance with PWV parameter, which was related to UA level [55]. This study is the first to use PPG, and it has shown significant differences between hyperuricemia and normouricemia subjects.
Studies on UA only focused on PWV parameters with arterial stiffness [9–12]. Several studies also predicted the UA level by using the ML method, but with only the sociodemographic, clinical parameter, and dietary information as the input [4,13,14]. Tab. 7 shows the performance comparison using different ML techniques by other researchers in relation with UA (NA: Not available). Ichikawa et al. [13] proposed the ML approach from the medical records including body mass index, blood pressure, and blood screening test to identify high risk hyperuricemia patients for reducing medical costs; they showed a promising result. Lee et al. [4] compared conventional logistic regression with several types of ML, such as discriminant analysis, kNN, naïve Bayes, SVM, decision tree, and random forest classification as the hyperuricemia estimation method. However, their study is limited to an expensive self-paid health check-up program, in which the generalization of the results is limited to other population. Sampa et al. [14] introduced the ML approach using medical records with addition of dietary information. However, they focused on the RMSE values compared with other performance of ML. In addition, the population was from a group of employees who work in a corporate setting [14].
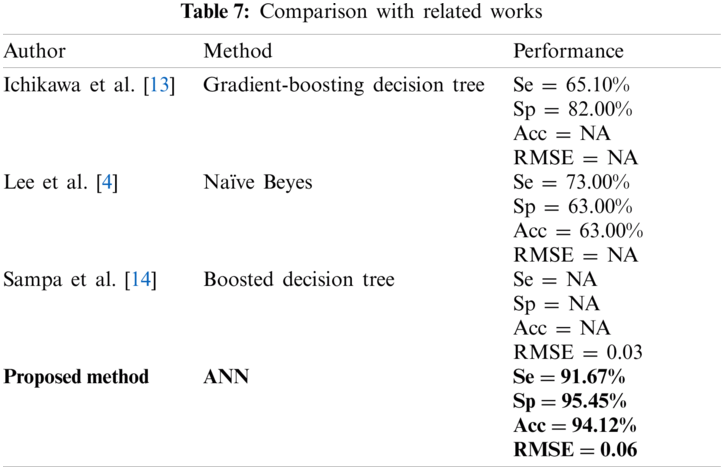
We compared four types of ML algorithm, namely, ANN, LDA, kNN, and SVM to predict hyperuricemia using PPG and arteriograph data. We found that ANN produced better performance than the other ML used in previous studies [4,12,13].
A hyperuricemia prediction method was proposed using multiple PPG and SDPPG features, which were extracted from a low-cost pulse oximeter, in addition to arteriograph output. The analysis result showed that 16 out of 98 features and output were significantly correlated with UA level with p-value less than 0.05. The result was discussed from the viewpoint of noninvasive technique in assessing UA level. This work demonstrated the first study in relating UA with PPG features, and ANN was applied for hyperuricemia prediction and produced 91.67%, 95.45%, and 94.12% for Se, Sp, and Acc.
The limitation of the study was the number of subjects, particularly hyperuricemia patients. In addition, the complete five waves should be detected because SDPPG waveform contains abundant information regarding vascular health. Some subjects merged ‘c’, ‘d’, and ‘e’ waves and caused reduction in features because features that contained ‘c’ and ‘d’ waves should be eliminated for better quality of features in the ML phase. Elgendi et al. developed an algorithm that can detect ‘c’, ‘d’, and ‘e’ waves simultaneously in SDPPG signals with promising results [56].
For future work, manual jug-sy measurement that was used in PWV calculation can be replaced by automated measurement. Secondly, age and gender matching between case and control groups can be done for better comparison as the morphology of PPG signal can be easily effected by age, especially SDPPG [57]. Multiscale principal component analysis used in [58] can then be applied to compare with the traditional denoising method with cascade forward neural network as classifier. This method proved to achieve 100% classification accuracy with small training samples. In addition, additional data must be collected with robust detection of SDPPG wave, especially ‘c’, ‘d’, and ‘e’ waves, in which the performance of the developed hyperuricemia prediction model can be improved. Direct relationship between PPG parameter with PWV can be further explored for hyperuricemia prediction using only PPG morphology for cost effectiveness.
Acknowledgement: Authors would like to thank those who contributed to this article and give some valuable comments.
Funding Statement: This work was supported by the Ministry of Higher Education Malaysia under Grant FRGS1/2019/TK04/UKM/02/4.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. A. Roth, G. A. Mensah, C. O. Johnson, G. Addolorato, E. Ammirati et al., “Global burden of cardiovascular diseases and risk factors, 1990–2019: Update from the GDB, 2019 study,” Journal of the American College of Cardiology, vol. 76, no. 25, pp. 2982–3021, 2020. [Google Scholar]
2. M. R. Mora, I. O. G. Estevez, M. E. C. Irigoyen, R. Bojalil, H. P. Gonzalez et al., “Hyperuricemia on admission predicts short-term mortality due to myocardial infarction in a population with high prevalence of cardiovascular risk factors,” Revista de Investigación Clinica, vol. 69, no. 5, pp. 247–253, 2017. [Google Scholar]
3. M. F. Touserkani, E. Tamilia, F. Coughlin, S. Hammond, E. R. Atrache et al., “Photoplethysmographic evaluation of generalized tonic-clonic seizures,” Epilepsia, vol. 61, no. 8, pp. 1606–1616, 2020. [Google Scholar]
4. S. Lee, E. K. Choe and B. Park, “Exploration of machine learning for hyperuricemia prediction models based on basic health checkup tests,” Journal of Clinical Medicine, vol. 8, no. 2, pp. 172, 2019. [Google Scholar]
5. C. C. Chang, C. H. Wu, L. K. Liu, R. H. Chou, C. S. Kuo et al., “Association between serum uric acid and cardiovascular risk in nonhypertensive and nondiabetic individuals: The Taiwan I-Lan Longitudinal Aging Study,” Scientific Reports, vol. 8, no. 1, pp. 1–6, 2018. [Google Scholar]
6. X. Zhang, Q. Meng, J. Feng, H. Liao, R. Shi et al., “The prevalence of hyperuricemia and its correlates in Ganzi Tibetan Autonomous Prefecture, Sichuan Province,” China Lipids in Health Disease, vol. 17, no. 1, pp. 1–10, 2018. [Google Scholar]
7. M. Canepa, F. Viazzi, J. B. Strait, P. Ameri, R. Pontremoli et al., “Longitudinal association between serum uric acid and arterial stiffness: Results from the Baltimore longitudinal study of aging,” Hypertension, vol. 69, no. 2, pp. 228–235, 2017. [Google Scholar]
8. J. Liu, K. Wang, H. Liu, H. Zhao, X. Zhao et al., “Relationship between carotid-femoral pulse wave velocity and uric acid in subjects with hypertension and hyperuricemia,” Endocrine Journal, vol. 66, no. 7, pp. 629–636, 2019. [Google Scholar]
9. Y. J. Lim, W. G. Kwack, Y. S. Lee, K. B. Hahm and Y. K. Kim, “Increased pulse wave velocity reflecting arterial stiffness in patients with colorectal adenomas,” Journal of Clinical Biochemistry and Nutrition, vol. 47, no. 3, pp. 261–265, 2010. [Google Scholar]
10. U. Bae, J. Y. Shim, H. R. Lee and J. Y. Shin, “Serum carcinoembryonic antigen level is associated with arterial stiffness in healthy Korean adult,” Clinical Chimica Acta, vol. 415, no. 1, pp. 286–289, 2013. [Google Scholar]
11. S. Nagano, M. Takahashi, N. Miyai, M. Oka, M. Utsumi et al., “Association of serum uric acid with subsequent arterial stiffness and renal function in normotensive subjects,” Hypertension Research, vol. 40, no. 6, pp. 620–624, 2017. [Google Scholar]
12. F. Luo and C. Zhuo, “Association between uric acid and brachial-ankle pulse wave velocity: Secondary analysis of data from a cross-sectional study,” Scientific Reports, vol. 10, no. 1, pp. 1–8, 2020. [Google Scholar]
13. D. Ichikawa, T. Saito, W. Ujita and H. Oyama, “How can machine-learning methods assist in virtual careening for hyperuricemia? A healthcare machine-learning approach,” Journal of Biomedical Informatics, vol. 64, no. 1, pp. 20–24, 2016. [Google Scholar]
14. M. B. Sampa, M. N. Hossain, M. R. Hoque, R. Islam, F. Yokota et al., “Blood uric acid prediction with machine learning: Model development and performance comparison,” JMIR Medical Informatics, vol. 8, no. 10, pp. e18331, 2020. [Google Scholar]
15. M. H. Chowdhury, M. N. I. Shuzan, M. E. Chowdhury, Z. B. Mahbub, M. M. Uddin et al., “Estimating blood pressure from the photoplethysmogram signal and demographic features using machine learning techniques,” Sensors, vol. 20, no. 11, pp. 3127, 2020. [Google Scholar]
16. N. A. Nayan, R. Jaafar and N. S. Risman, “Development of respiratory rate estimation technique using electrocardiogram and photoplethysmogram for continuous health monitoring,” Bulletin of Electrical Engineering and Informatics, vol. 7, no. 3, pp. 487–494, 2018. [Google Scholar]
17. J. Allen, “Photoplethysmography and its application in clinical physiological measurement,” Physiological Measurement, vol. 28, no. 3, pp. R1, 2007. [Google Scholar]
18. Q. Yousef, M. B. I. Reaz and M. A. M. Ali, “The analysis of PPG morphology: Investigating the effects of aging on arterial compliance,” Measurement Science Review, vol. 12, no. 6, pp. 266–271, 2012. [Google Scholar]
19. R. M. S. Raifana, K. Chellappan, O. Norsuhana, M. M. N. Noranita and A. Amilia, “Finger photoplethysmograph as a monitoring device for LIPID profile in men with cardiovascular risk,” Journal of Theoretical and Applied Information Technology, vol. 95, no. 6, pp. 1225–1235, 2017. [Google Scholar]
20. M. Elgendi, R. R. Fletcher, I. Norton, M. Brearley, D. Abbott et al., “Frequency analysis of photoplethysmogram and its derivatives,” Computer Methods and Programs in Biomedicine, vol. 122, no. 3, pp. 503–512, 2015. [Google Scholar]
21. K. Takazawa, N. Tanaka, M. Fujita, O. Matsuoka, T. Saiki et al., “Assessment of vasoactive agents and vascular aging by the second derivative of photoplethysmogram waveform,” Hypertension, vol. 32, no. 2, pp. 365–370, 1998. [Google Scholar]
22. N. Inoue, H. Kawakami, H. Yamamoto, C. Ito, S. Fujiwara et al., “Second derivative of the finger photoplethysmogram and cardiovascular mortality in middle-aged and elderly Japanese women,” Hypertension Research, vol. 40, no. 2, pp. 207–211, 2017. [Google Scholar]
23. A. Chakraborty, D. Sadhukhan, S. Pal and M. Mitra, “Automated myocardial infarction identification based on interbeat variability analysis of the photoplethysmographic data,” Biomedical Signal Processing and Control, vol. 57, no. 6, pp. 101747, 2020. [Google Scholar]
24. N. Mahri, K. B. Gan, R. Meswari, M. H. Jaafar and M. A. M. Ali, “Utilization of second derivative photoplethysmographic features for myocardial infarction classification,” Journal of Medical Engineering & Technology, vol. 41, no. 4, pp. 298–308, 2017. [Google Scholar]
25. M. Liu, L. M. Po and H. Fu, “Cuffless blood pressure estimation based on photoplethysmography signal and its second derivative,” International Journal of Computer Theory and Engineering, vol. 9, no. 3, pp. 202, 2017. [Google Scholar]
26. H. H. Kang, K. B. Won, R. Heo, D. Han and H. J. Chang, “Independent association of serum uric acid levels with arterial stiffness in the absence of established cardiovascular disorders,” International Journal of Clinical Practise, vol. 75, no. 3, pp. e13720, 2021. [Google Scholar]
27. M. Ring, M. J. Eriksson, G. Nyberg and K. Caidahl, “Importance of software version for measurement of arterial stiffness: Arteriograph as an example,” PLoS One, vol. 13, no. 5, pp. e0197019, 2018. [Google Scholar]
28. T. Pereira, J. Maldonado, R. Coutinho, E. Cardoso, M. Laranjeiro et al., “Invasive validation of the complior analyse in the assessment of central artery pressure curves: A methodological study,” Blood Pressure Monitoring, vol. 19, no. 5, pp. 280–287, 2014. [Google Scholar]
29. M. G. Schultz, D. S. Picone, M. K. Armstrong, J. A. Black, N. Dwyer et al., “Validation study to determine the accuracy of central blood pressure measurement using the Sphygmocor Xcel cuff device,” Hypertension, vol. 76, no. 1, pp. 244–250, 2020. [Google Scholar]
30. I. G. Horvath, A. Nemeth, Z. Lenkey, N. Alessandri, F. Tufano et al., “Invasive validation of a new oscillometric device (Arteriograph) for measuring augmentation index, central blood pressure and aortic pulse wave velocity,” Journal of Hypertension, vol. 28, no. 10, pp. 2068–2075, 2010. [Google Scholar]
31. N. A. Jatoi, A. Mahmud, K. Bennett and J. Feely, “Assessment of arterial stiffness in hypertension: Comparison of oscillometric (Arteriographpiezoelectronic (Complior) and tonometric (SphygmoCor) techniques,” Journal of Hypertension, vol. 27, no. 11, pp. 2186–2191, 2009. [Google Scholar]
32. I. Juganaru, C. T. Luca, A. I. Dobrescu, O. Voinescu, M. Puiu et al., “A non-invasive, easy to use medical device for arterial stiffness,” Revista de Chimie, vol. 70, no. 2, pp. 642–645, 2019. [Google Scholar]
33. A. Jekell and T. Kahan, “The usefulness of a single arm cuff oscillometric method (Arteriograph) to assess changes in central aortic blood pressure and arterial stiffness by antihypertensive treatment: Results from the Doxazosin-Ramipril Study,” Blood Pressure, vol. 27, no. 2, pp. 88–98, 2018. [Google Scholar]
34. S. Gökaslan, Ç. Ö. Gökaslan, E. Demirel and S. Çelik, “Role of aortic stiffness and inflammation in the etiology of young-onset hypertension,” Turkish Journal of Medical Sciences, vol. 49, no. 6, pp. 1748–1753, 2019. [Google Scholar]
35. D. Echeverri, A. Pizano, J. Cabrales and K. Moreno, “Validation of central and peripheral non-invasive hemodynamic variables using an oscillometric method,” High Blood Pressure & Cardiovascular Prevention, vol. 25, no. 1, pp. 65–77, 2018. [Google Scholar]
36. C. Orphanidou, T. Bonnici, P. Charlton, D. Clifton, D. Vallance et al., “Signal-quality indices for the electrocardiogram and photopelthysmogram: Derivation and applications to wireless monitoring,” IEEE Journal of Biomedical and Health Informatics, vol. 19, no. 3, pp. 832–838, 2014. [Google Scholar]
37. B. N. Li, M. C. Dong and M. I. Vai, “On an automatic delineator for arterial blood pressure waveforms,” Biomedical Signal Processing and Control, vol. 5, no. 1, pp. 76–81, 2010. [Google Scholar]
38. A. Laurin, “Implementation of a feature detection algorithm for arterial blood pressure,” 2020. [Online]. Available: https://mathworks.com/matlabcentral/fileexchange/60172-bp_annotate. [Google Scholar]
39. M. Elgendi, “Detection of c, d, and e waves in the acceleration photoplethysmogram,” Computer Methods and Programs in Biomedicine, vol. 117, no. 2, pp. 125–136, 2014. [Google Scholar]
40. B. W. Yap and C. H. Sim, “Comparison of various types of normality tests,” Journal of Statistical Computation and Simulation, vol. 81, no. 12, pp. 2141–2155, 2011. [Google Scholar]
41. M. Llamedo and J. P. Martinez, “An automatic patient-adapted ECG heartbeat classifier allowing expert assistance,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 8, pp. 2312–2320, 2012. [Google Scholar]
42. W. Yang, Y. Si, D. Wang and B. Guo, “Automatic recognition of arrhythmia based on principal component analysis network and linear support vector machine,” Computers in Biology and Medicine, vol. 101, no. 9765, pp. 22–32, 2018. [Google Scholar]
43. C. G. Nayak, G. Seshikala, U. Desai and S. G. Nayak, “Identification of arrhythmia classes using machine-learning techniques,” International Journal of Biology and Biomedicine, vol. 1, pp. 48–53, 2016. [Google Scholar]
44. H. J. Leach, D. P. O’Connor, R. J. Simpson, H. S. Rifai, S. K. Mama et al., “An exploratory decision tree analysis to predict cardiovascular disease risk in African American women,” Health Psychology, vol. 35, no. 4, pp. 397–402, 2016. [Google Scholar]
45. S. Chabchoub, S. Mansouri and R. B. Salah, “Detection of valvular heart diseases using impedence cardiography ICG,” Biocybernetics and Biomedical Engineering, vol. 38, no. 2, pp. 251–261, 2018. [Google Scholar]
46. T. Mar, S. Zaunseder, J. P. Martinez, M. Llamedo and R. Poll, “Optimization of ECG classification by means of feature selection,” IEEE Transactions on Biomedical Engineering, vol. 58, no. 8, pp. 2168–2177, 2011. [Google Scholar]
47. C. A. Kumar, M. P. Sooraj and S. Ramakrishnan, “A comparative performance evaluation of supervised feature selection algorithms on microarray datasets,” in 7th Int. Conf. on Advances in Computing & Communications, Cochin, India, pp. 209–217, 2017. [Google Scholar]
48. L. Berus, S. Klancnik, M. Brezocnik and M. Ficko, “Classifying Parkinson’s disease based on acoustic measures using artificial neural networks,” Sensors, vol. 19, no. 1, pp. 16, 2019. [Google Scholar]
49. F. Pan, G. Song, X. Gan and Q. Gu, “Consistent feature selection and its application to face recognition,” Journal of Intelligent Information Systems, vol. 43, no. 2, pp. 307–321, 2014. [Google Scholar]
50. J. Abdulridha, O. Batuman and Y. Ampatzidis, “UAV-based remote sensing technique to detect citrus canker disease utilizing hyperspectral imaging and machine learning,” Remote Sensing, vol. 11, no. 11, pp. 1373, 2019. [Google Scholar]
51. Z. Soumaya, B. D. Taoufiq, N. Benayad, K. Yunus and A. Abdelkrim, “The detection of Parkinson disease using the genetic algorithm and SVM classifier,” Applied Acoustics, vol. 171, no. 1, pp. 107528, 2021. [Google Scholar]
52. W. Shi, H. Wang, Y. Zhou, Y. Sun and Y. Chen, “Synergistic interaction of hyperuricemia and hypertension on reduced eGFR: Insights from a general Chinese population,” Postgraduate Medicine, vol. 132, no. 3, pp. 263–269, 2020. [Google Scholar]
53. A. Ali, R. Whittall, M. E. Babar, T. Hussain and S. E. Humphries, “Genetics of LDLR Gene in Pakistani Hypercholesterolemia Families,” International Journal of Pharma Medicine and Biological Sciences, vol. 8, no. 4, pp. 143–146, 2019. [Google Scholar]
54. J. Liu, L. Tao, Z. Zhao, Y. Mu, D. Zou et al., “Two-year changes in hyperuricemia and risk of diabetes: A five-year prospective cohort study,” Journal of Diabetes Research, vol. 2018, no. 10010, pp. 1–7, 2018. [Google Scholar]
55. S. L. O. Martin, A. M. Carek, C. S. Kim, H. Ashouri, T. O. Inan et al., “Weighing scale-based pulse transit time is a superior marker of blood pressure than conventional pulse arrival time,” Scientific Reports, vol. 6, no. 1, pp. 1–8, 2016. [Google Scholar]
56. P. Rebora, A. Andreano, N. Triglione, E. Piccinelli, M. Palazzini et al., “Association between uric acid and pulse wave velocity in hypertensive patients and in the general population: A systematic review and meta-analysis,” Blood Pressure, vol. 22, no. 4, pp. 220–231, 2020. [Google Scholar]
57. K. Pilt, R. Ferenets, K. Meigas, L. G. Lindberg, K. Temitski et al., “New photoplethysmographic signal analysis algorithm for arterial stiffness estimation,” The Scientific World Journal, vol. 2013, no. 4, pp. 1–9, 2013. [Google Scholar]
58. M. T. Sadiq, X. Yu, Z. Yuan and M. Z. Aziz, “Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform,” Electronic Letters, vol. 56, no. 25, pp. 1367–1369, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |