DOI:10.32604/cmc.2022.022260

| Computers, Materials & Continua DOI:10.32604/cmc.2022.022260 |  |
| Article |
Optimal Cooperative Spectrum Sensing Based on Butterfly Optimization Algorithm
1Department of Electronics Engineering, Korea Polytechnic University, 15073, Gyeonggi-do, Korea
2Department of Electronics, University of Peshawar, 25120, Pakistan
3Department of Electrical Engineering, Mirpur University of Science of Technology, AJ&K, 10250, Pakistan
4Department of Electrical Engineering, International Islamic University, Islamabad 44000, Pakistan
*Corresponding Author: Junsu Kim. Email: junsukim@kpu.ac.kr
Received: 01 August 2021; Accepted: 02 September 2021
Abstract: Since the introduction of the Internet of Things (IoT), several researchers have been exploring its productivity to utilize and organize the spectrum assets. Cognitive radio (CR) technology is characterized as the best aspirant for wireless communications to augment IoT competencies. In the CR networks, secondary users (SUs) opportunistically get access to the primary users (PUs) spectrum through spectrum sensing. The multipath issues in the wireless channel can fluster the sensing ability of the individual SUs. Therefore, several cooperative SUs are engaged in cooperative spectrum sensing (CSS) to ensure reliable sensing results. In CSS, security is still a major concern for the researchers to safeguard the fusion center (FC) against abnormal sensing reports initiated by the malicious users (MUs). In this paper, butterfly optimization algorithm (BOA)-based soft decision method is proposed to find an optimized weighting coefficient vector correlated to the SUs sensing notifications. The coefficient vector is utilized in the soft decision rule at the FC before making any global decision. The effectiveness of the proposed scheme is compared for a variety of parameters with existing schemes through simulation results. The results confirmed the supremacy of the proposed BOA scheme in both the normal SUs’ environment and when lower and higher SNRs information is carried by the different categories of MUs.
Keywords: Internet of Things; cognitive radio network; butterfly optimization algorithm; particle swarm optimization; malicious users; genetic algorithm
Exponential growth in mobile devices and rising demand of data rates pose challenges to mobile network operators [1]. The 5G broadband systems are anticipated to deliver huge contents to the users over highly reliable wireless links. In addition to increased throughput, 5G systems are expected to provide lower latency and outage probability, higher spectral efficiency, and lower infrastructure deployment costs. The extensive use of cognitive radio (CR), software defines radio (SDR), and software defined networking are the main features that distinguish the 5G from previous mobile communication generations [2,3]. The fast technological development in 5G mobile broadband, Internet of Things (IoT), Big Data, Cloud Computing and SDR, has made those technologies one after another and created strong interdependence among one another. IoT introduces a new era of pervasive computing and communication by empowering physical objects to see, hear, think, and conversate to swap information for coordinate decisions [3–7]. Wireless communication technologies emerge as a cost-effective solution to provide essential inter-connectivity between IoT enabled devices and accessibility to remote users [8]. Big data generated by IoT devices will be largely computed and stored using Cloud which further requires high bit rate and low latency offered by 5G for faster and cost-effective transmission of data [4,9]. Radio frequency spectrum scarcity has emerged as one of the major challenges with the unprecedented growth in the number of devices connected in the IoT [10].
The researchers argue that in IoT, along with the connectivity, the objects should have the cognitive capability to learn and understand the environment by themselves. This entails the need to develop a new paradigm, named cognitive Internet of Things (CIoT) to empower the current IoT with Intelligence [5]. Similarly, the scarcity of the frequency spectrum in IoT paradigm is another significant challenge. Introduction of cognitive radio network (CRN) and CR in IoT enabled devices can improve the efficiency of the spectrum [11]. The integration of CR in IoT networks, has shown considerably better performance in radio frequency spectrum control and management to optimize the scare spectrum resources as compared to traditional communication technologies. Furthermore, the studies suggest that the benefits of IoT without cognitive skills such as CR and intelligence is unsound [8].
In the CRN, secondary users (SUs) perform spectrum sensing to dynamically access the primary users’ (PUs) channel when the PU is not active [5,12]. The SU vacates the channel when PU becomes active to avoid any interference to the PU. The wireless channel properties of the multipath fading and shadowing create ambiguities in the individual SU sensing. Thus, to tackle these challenges, it is more appropriate to utilize cooperative spectrum sensing (CSS) [13–15]. In the centralized CSS, a central base station, such as fusion center (FC) receives sensing information from the SUs in the hard or soft modes for final decision about the presence or absence of PU [16,17]. The hard decision fusion (HDF) often employs logical AND, logical OR, and majority voting schemes [18–20]. In the soft decision fusion (SDF) schemes, such as maximum gain combining (MGC), equal gain combining (EGC), and Kullback-Leibler (KL) divergence, SUs forward soft sensing reports to FC [21–24]. Influenced by certain motives, malicious users (MUs) intrude into the CSS networks. The security threats and protection of CSS from the malicious users (MUs) are currently the major concern for researchers [25–27]. The work in [28–30] examined defensive mechanisms to reduce the presence of Byzantine attacks, jamming attacks, and primary user emulation attackers (PUEA). In [20] and [31], authors focused on the optimization of detection and false alarm probabilities of the SUs using particle swarm optimization (PSO) and genetic algorithm (GA) for the centralized CSS.
Individual SUs in CSS, report from distinct geographical locations observe distinct Rayleigh fading effects. Therefore, it is unfair to weight their sensing reports equally at the FC. Contrary to above mentioned studies who dealt the normal and MUs statistics in a similar manner, this work allocates weights to the sensing data considering the reliability of SU by utilizing butterfly optimization algorithm (BOA). The BOA is considered effective among the various optimization classes to best estimate the PU activity. The BOA is a nature-inspired global optimization algorithm that was inspired by the behavior of butterflies to find food/mating partners using their senses, sight, taste, and smell. The main contributions of this paper itemized as follows:
• A centralized CSS is inspected in the normal users and MUs environment when sensing data is reposted to the FC. The working norms of the MUs’ considered in the proposed work is the yes always (YA), no always (NA), and opposite always (OA), and opposite random (OR). The BOA governs the optimum weighting coefficient vector for the normal SUs and various classes of MUs’ along with a dynamic (adaptive) threshold in contrast to the static threshold adjustment schemes investigated in [20,23,28,31].
• The coefficient vectors determined by the proposed BOA-based SDF scheme are further employed in the SDF scheme at the FC to get concluding remarks of the channel availability. In this the received sensing reports of the normal and MUs are adjusted with the help of the optimum coefficient vector and matched with the BOA identified optimum threshold.
• Simulation outcomes of the error probabilities are collected at multiple variations of: (1) sensing samples; (2) population size of the optimization algorithms; (3) algorithm iterations; (4) total number of cooperative SUs. The results validated the improvement in, sensing response of the CSS with minimum sensing error, high detection, and low false alarms for the proposed BOA-based SDF scheme in comparison with the MGC-SDF, PSO-SDF, and GA-SDF schemes.
The rest of the paper is organized as follows. In Section 2, the system model of the paper is presented. In Section 3, the BOA-based SDF scheme is elaborated. Section 4 evaluates the suggested and conventional schemes through simulations. Finally, conclusion is furnished in Section 5. Tab. 1 comprises of the acronyms used in the paper. Algorithm of the BOA-based SDF is shown in Tabs. 2 and 3 shows the simulation parameters.


The system model adopts a CSS consisting of a PU, normal SUs, MUs, and a common FC as shown in Fig. 1. The objective in the model is to adopt an appropriate detection scheme that resembles the actual PU conditions at the FC.
The local sensing users in Fig. 1 perform their sensing responsibility and report their findings to the FC for final decision. The PU’s activity in the sensing channel is characterized with the binary testing hypothesis at the individual SUs as
where
In Fig. 1, the YA MUs’ reports higher energy values to the FC irrespective of the actual PU channel occupancy [28]. The YA presence in the CSS drastically lessens data rate of the normal SUs. On the other hand, the NA always reports low energy signals to the FC that creates interference for the PUs’. The OA users persistently report signals to the FC that always negate the PU activity, hence, their contribution results in reduce SUs data rate and increased interference for the PU. While the OR act as OA with probability
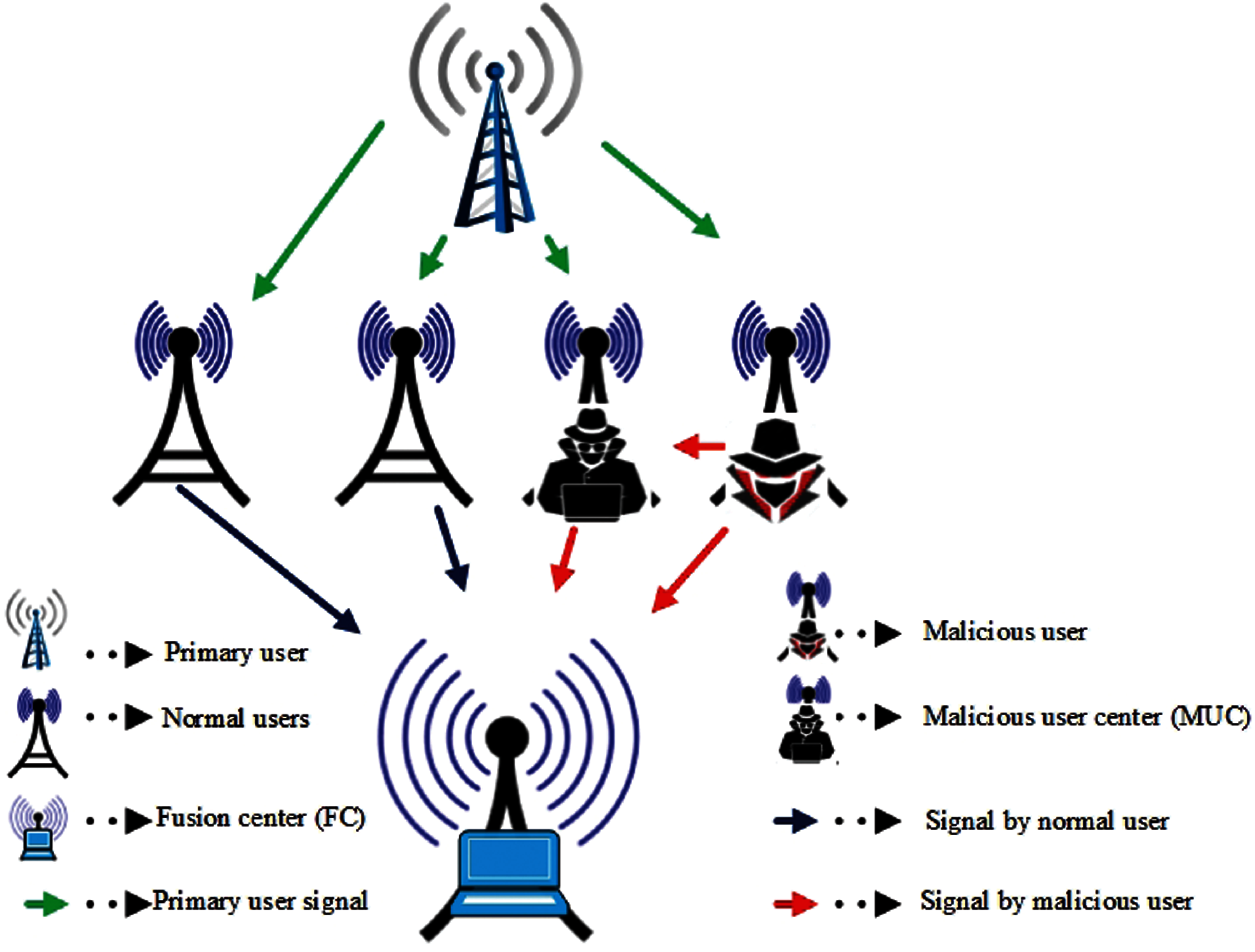
Figure 1: System model
The sensing energy conveyed to FC by the
where
In the given CSS model, the FC takes its global decision by combining soft energy reports with optimum weighting coefficient vector
where
In the above the variances of
A model of the proposed CSS scheme retaining the weighted SDF to reduce the impacts of abnormal sensing is shown in Fig. 2.
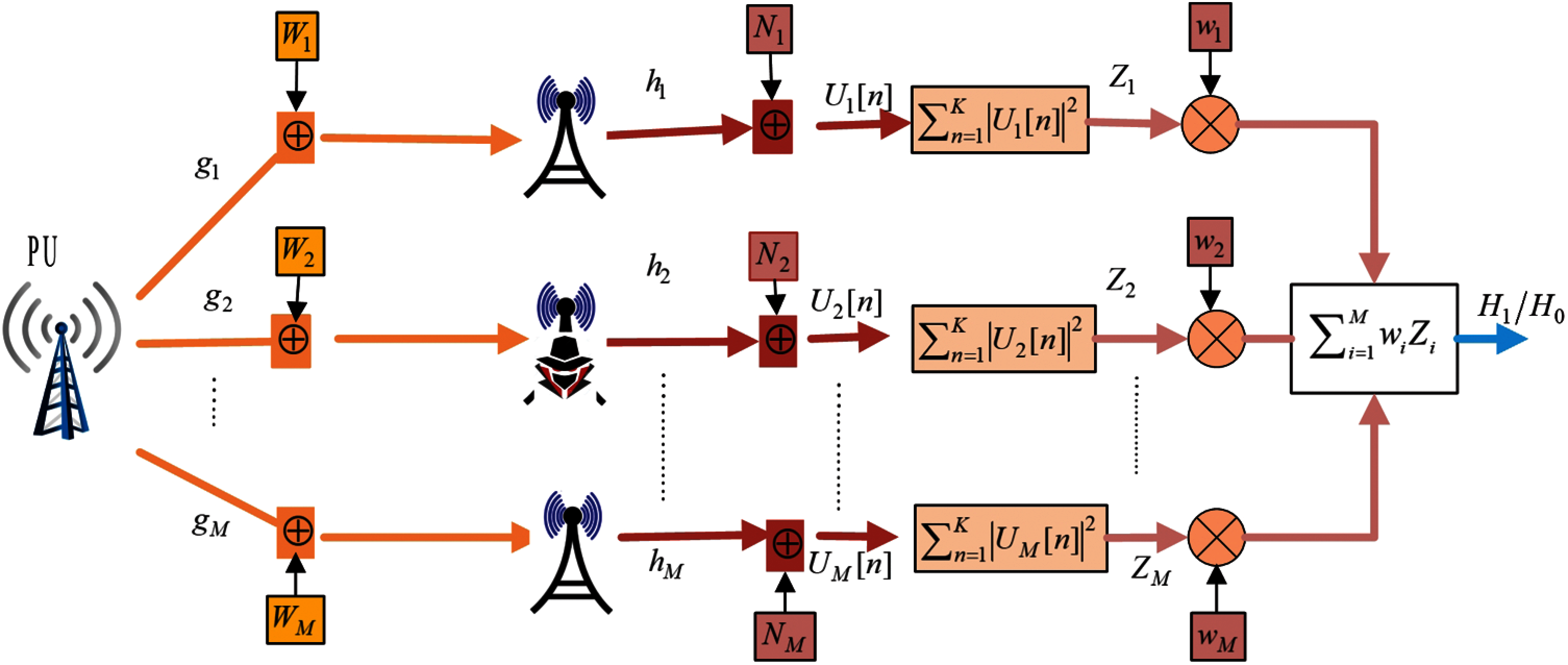
Figure 2: Weighted CSS scheme
The selection of the optimal coefficient vector
In these equations, the diagonalization practice is specified by
In Eq. (12), the false alarm
In Eq. (12), it is evident that the error probability is exceptionally subject to the selection of the weighting coefficient vector
2.2 Butterfly Optimization Algorithm
Nature-inspired optimization algorithms have got a high interest in various disciplines of engineering, where real-world problems are expressed as optimization problems. These optimization problems require enormous computational complexity that is difficult to solve using traditional methods [33]. This motivation directs researchers to the use of optimization methods to produce better results with lower computational complexity. Most of the time, the nature-inspired optimization algorithms can discover optimum solutions to the complex problems, however, the optimum solutions are not always guaranteed. The two general procedures to optimize a function are to either follow mathematical programming or metaheuristic methods [34]. Some of the commonly used metaheuristic algorithms till now are PSO, GA, BOA, firefly algorithm, surrogate optimization, tabu search, gravitational search, ant colony optimization, and many more [34,35].
In recent times, Arora introduced BOA as a promising metaheuristic algorithm, which is inspired by the butterfly’s food searching movements. The studies demonstrate that the BOA has superior results when compared with some other metaheuristic algorithms [36]. In the BOA, butterflies perform optimization and work as search agents. The butterflies can smell or sense the fragrance of the food and flower through their sense receptors also called chemoreceptors. These chemoreceptors are scattered over the butterfly’s body parts such as antennae, palps, and legs. A fragrance with intensity is generated when the butterflies change their residence. Further, the objective function decides the butterfly’s stimulus intensity. The fragrance of some intensity is assumed to be generated by every butterfly that is sensed by all other butterflies in the territory. This emitted fragrance is then correlated with butterfly fitness. Hence, the butterfly fitness varies accordingly, whenever the butterfly tries to move from one position to the other in a search space. A collective social data network is formed as the propagated fragrance is sensed by the butterflies [33]. When a butterfly senses some high intense fragrance emitted by other butterfly that will move towards the high intensity fragrance butterfly in the region. This phase of the BOA is named as the global search phase. However, when the butterfly is not able to sense high-intensity fragrance than its own, a random walk is performed and this is the local search phase of the BOA [33,35].
The BOA’s main strength lies in its fragrance modulating mechanism. To know fragrance modulation, it is first important to realize how any sense is processed by the stimulus of a living organism. The sensing basic concepts are dependent on three vital parameters such as power exponent (
3 Proposed BOA-Based SDF Scheme
This section illustrates the proposed BOA-based SDF scheme in the participation of the MUs’ to discover the optimum coefficient vector and threshold adjustments. The FC resolves the global decision by employing this weighted SDF approach to settle the PU channel detection based on the SUs’ sensing data.
The proposed BOA-SDF scheme consists of the following steps, while sensing the PU spectrum, such as (1) Initialization phase (2) Iteration phase (3) Final Phase [37].
3.1 Phase 1: Initialization Phase
The number of butterflies in the proposed work are fixed to
Similarly, the switching probability
The suitability of the coefficient vectors is based on
In the second phase of this algorithm, i.e., the iteration phase, algorithm gets several iterations to grasp the desired objective. The butterflies in the given solution space try to move to a distinct position and their fitness values are measured. The algorithm first computes butterflies’ fitness on different positions in the solution space. Then these butterflies cause fragrance as follows
where
Likewise, the local search phase is as follows
where
3.3 Phase 3: Stopping Criteria
The BOA repeats step 2 if the fitness functions (i.e., minimum
A general flowchart of the proposed BOA-based SDF scheme is shown in Fig. 3 followed by its algorithm in Tab. 2.
4 Numerical Evaluation and Discussions
In this section, we verify the performance of the proposed BOA-based SDF scheme in contrast to some other conventional schemes. The number of SUs in the CRN are set to 10 and 14 in this portion of the simulations. Out of the total SU, 4 of them are assumed as YA, NA, OA, and RO malicious. In the simulation, SNRs is kept at an average of −13.5 and −11.5 dB while determining sensing error. The 1
The proposed scheme results are evaluated in simulations and compared with the conventional PSO-SDF, GA-SDF, and MGC-SDF schemes. Furthermore, the results are distributed into 4 different scenarios as in Tab. 3 to indorse the proposed scheme reliability. Scenario 1 discusses the error probability results collected at different number of SUs in the CSS with retained values of the SNRs for the SUs, algorithm iterations, population size, and sensing samples. In a similar way the error probability outcomes are shown for the increase in number of iterations in scenarios 2. Here the total number of SUs, SNRs, population size, and sensing samples parameters are kept constant. In scenario 3, the changing sensing samples effects on the collection of error probabilities are investigated, while keeping the SUs, SNRs, algorithm iterations, and population size as constants. Finally, scenario 4 tests the effectiveness of the proposed scheme in terms of the error probabilities estimated against the increasing algorithm population size.
The graphical illustrations of scenario 1 are composed at the involvement of the normal NUs environment, lower SNRs subsidized by MU’s in CSS, and higher SNRs sensing contribution from MU’s. The average SNR values in respect of all users are kept at −13.5 dB with 270 sensing samples in each iteration. The population is 30 with total SUs varying from 10 to 22 users. In addition, the number of MUs are 4 that report sensing data along with the normally behaving users to the FC.
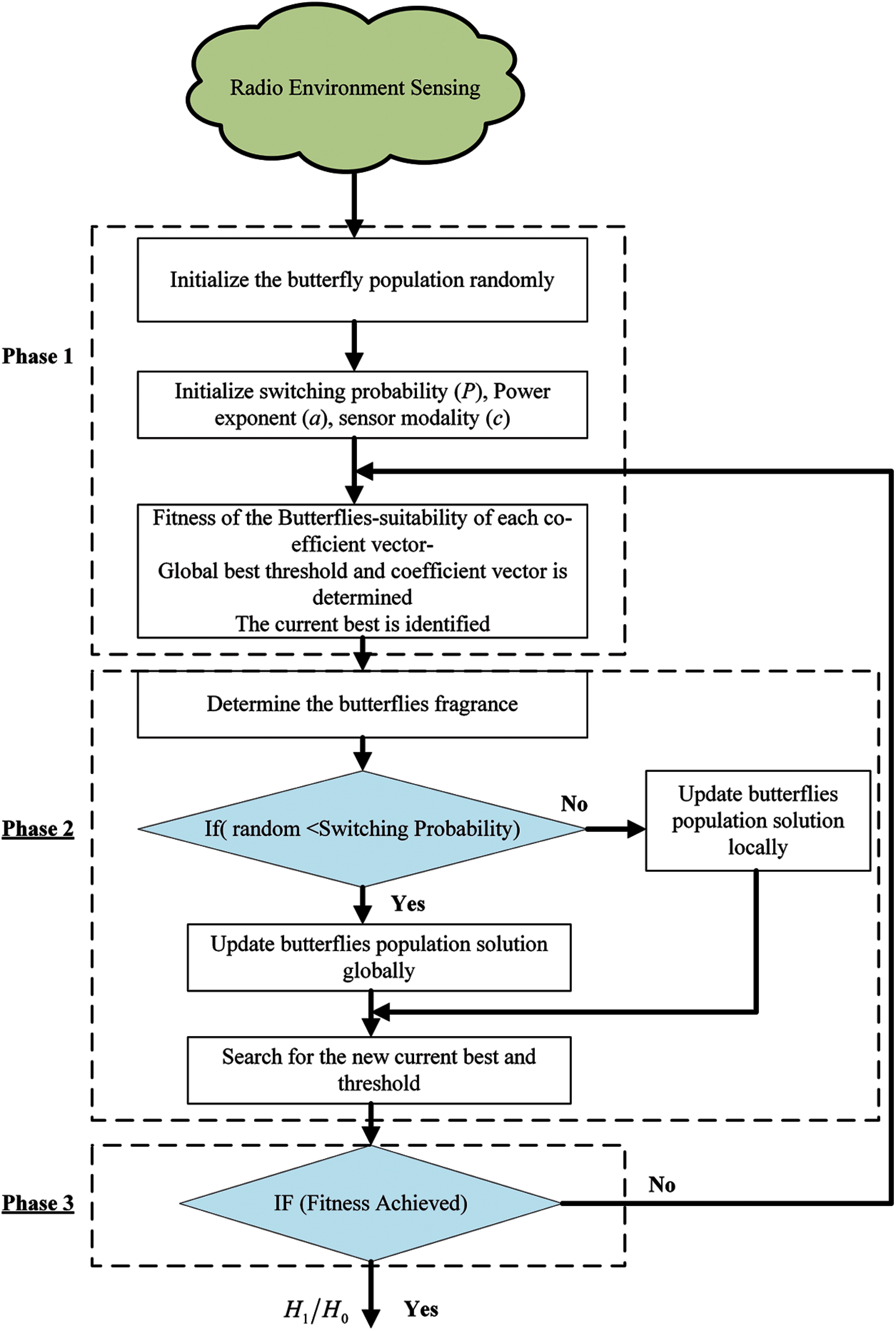
Figure 3: A flowchart of the proposed BOA-based SDF scheme
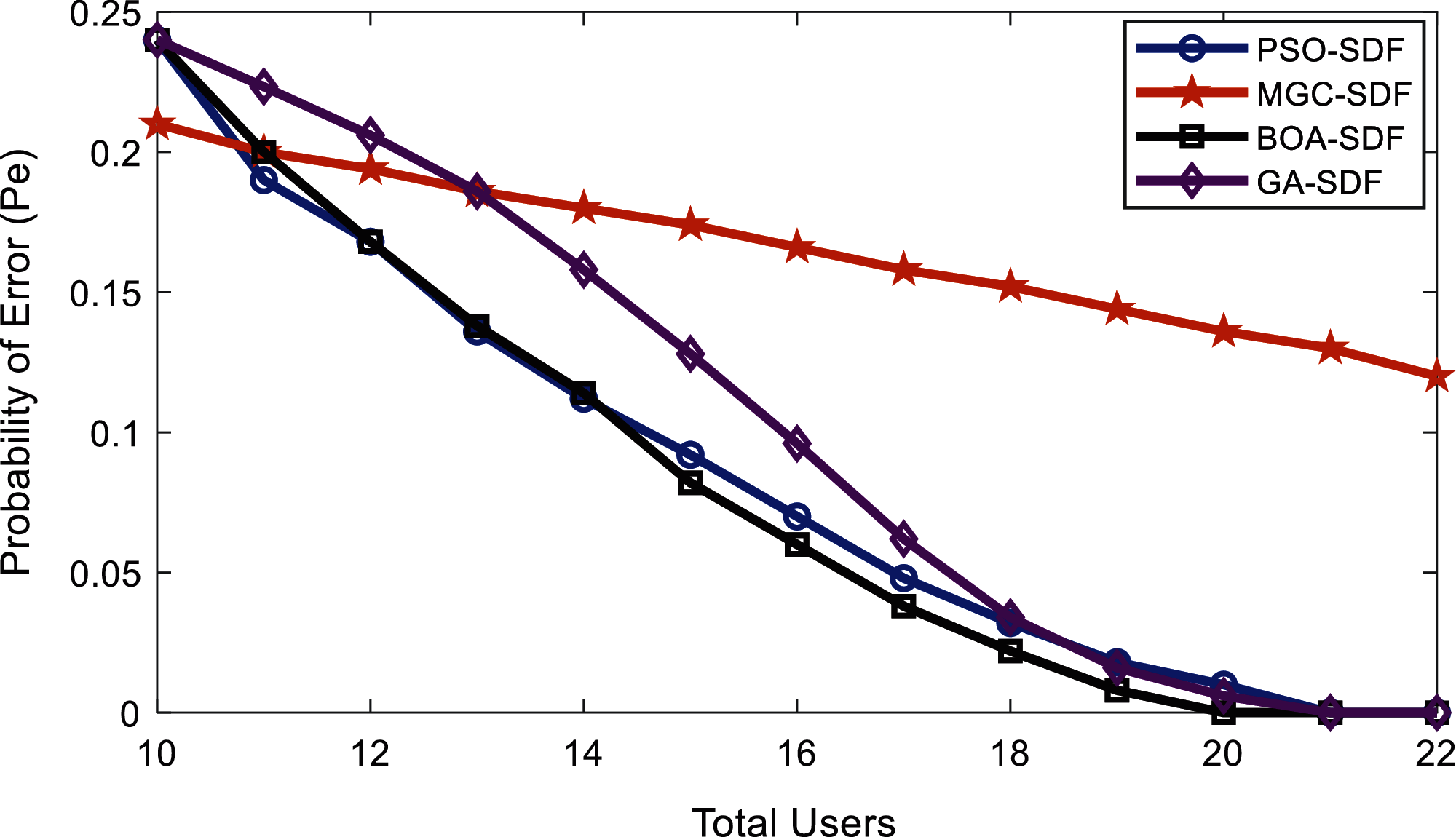
Figure 4: Error probability vs. number of cooperative users at normal users
In Fig. 4, results for different SDF schemes such as PSO-SDF, MGC-SDF, BOA-SDF, and GA-SDF are presented. The result in Fig. 4 indicated that the BOA scheme is outperforming all other schemes with minimum error probability as the number of users exceeds from 14 to 20. The MGC-SDF shows poor sensing results with a higher error probability than all other schemes. Similar, results are shown for cases in scenario 1 when MU’s participated in CSS of Figs. 5 and 6.
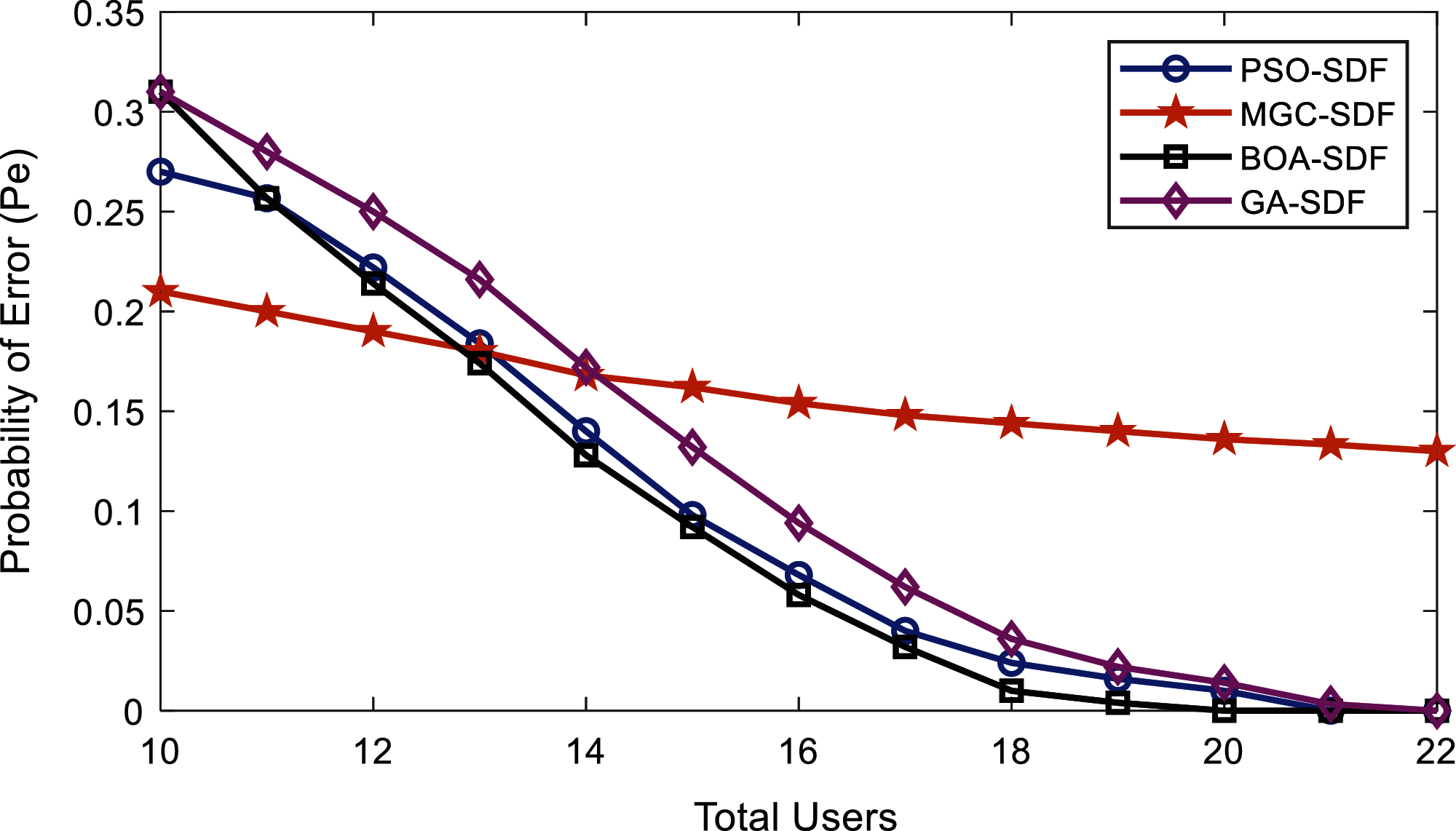
Figure 5: Error probability vs. number of cooperative users at lower SNRs by malicious
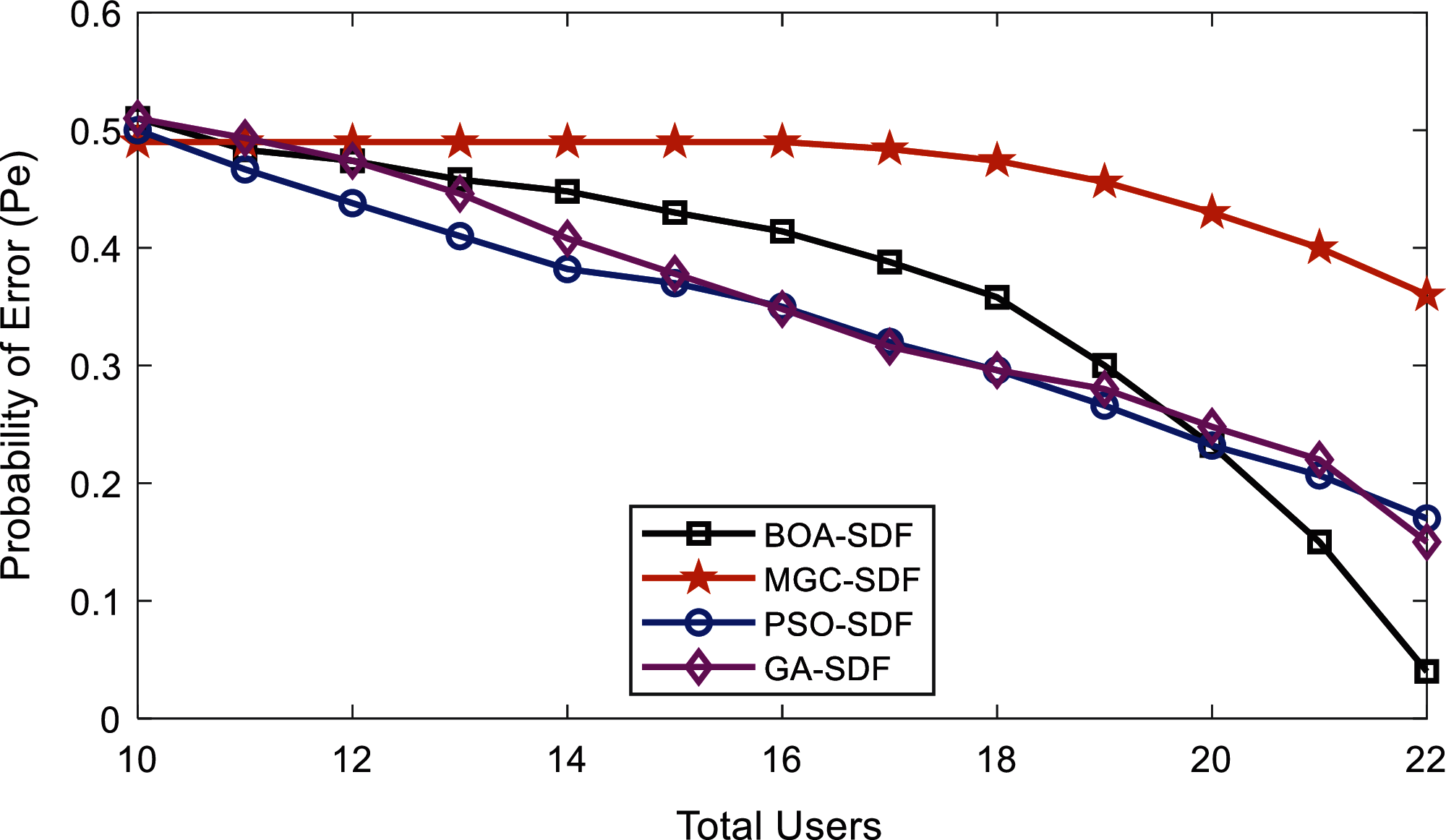
Figure 6: Error probability vs. number of cooperative users at higher SNRs by malicious
In Fig. 5, the MU’s behavior is purposely selected such that it reports low SNRs information in contrast with the normal behaving users. The proposed BOA-SDF is able to get the optimum sensing results as the number of cooperative users is increased from 14 to 20 in contrast with the other SDF schemes. Similarly, in Fig. 6 the results are collected from MUs’ and normal SUs under the same parameter settings with the assumption of high SNRs information contributed by the MUs’ to reduce the system performance. The BOA-SDF algorithm reduces the impact of these MUs’ and resulted in minimum sensing error out of all SDF schemes. The MGC-SDF scheme in this case performed poorly when MU’s participated in sensing.
In scenario 2, the simulation parameters are selected with 14 cooperative users, fixed average SNRs at −11.5 dB, 20 population size and 270 sensing samples. The algorithm iterations in this case are kept changing from 50 to 110. The results in Figs. 7–9 are obtained in this case when only normal users, low SNRs assignment to the MU’s, and high SNRs assignment to the MU’s.
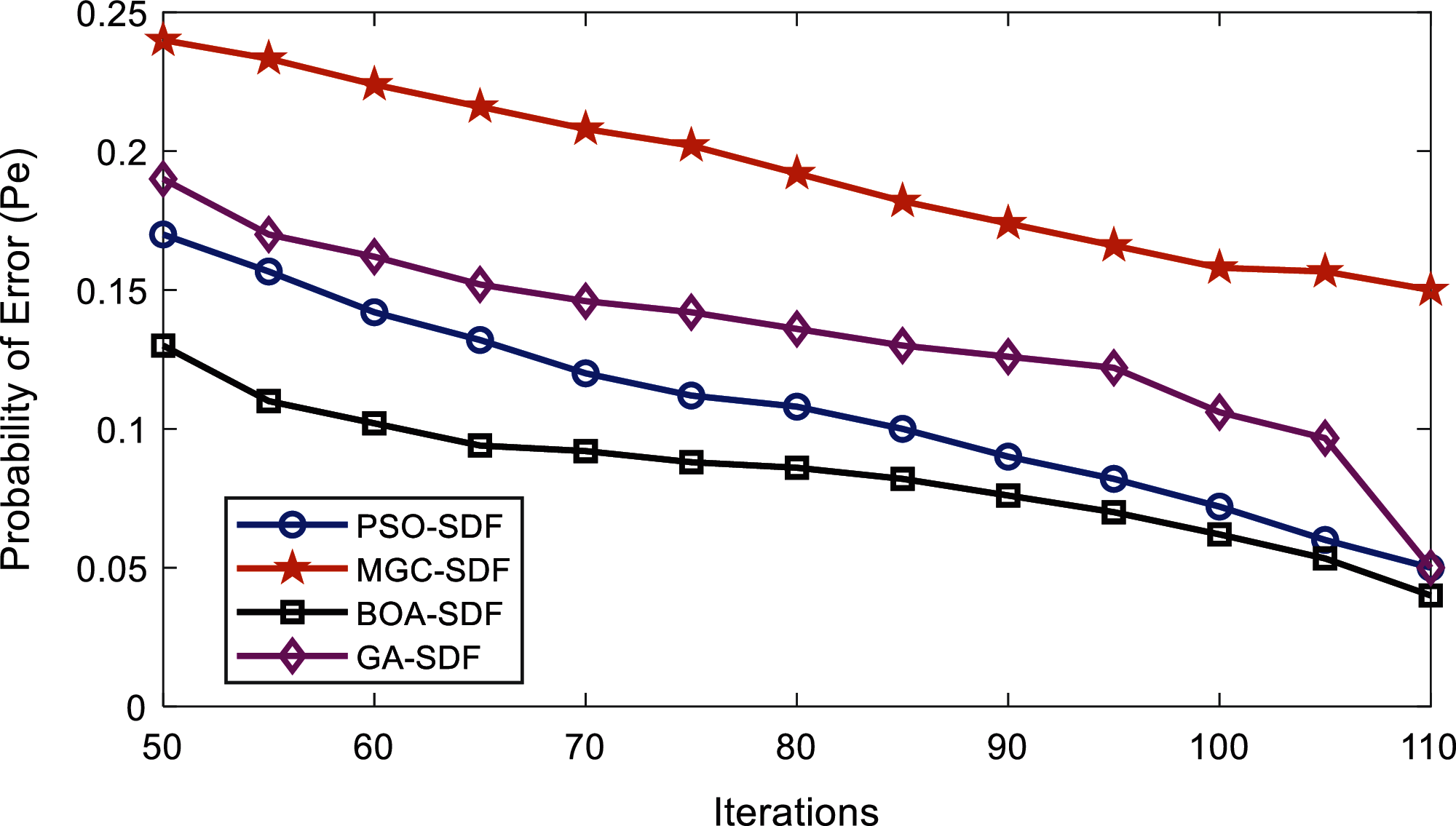
Figure 7: Error probability vs. algorithm iterations at normal users
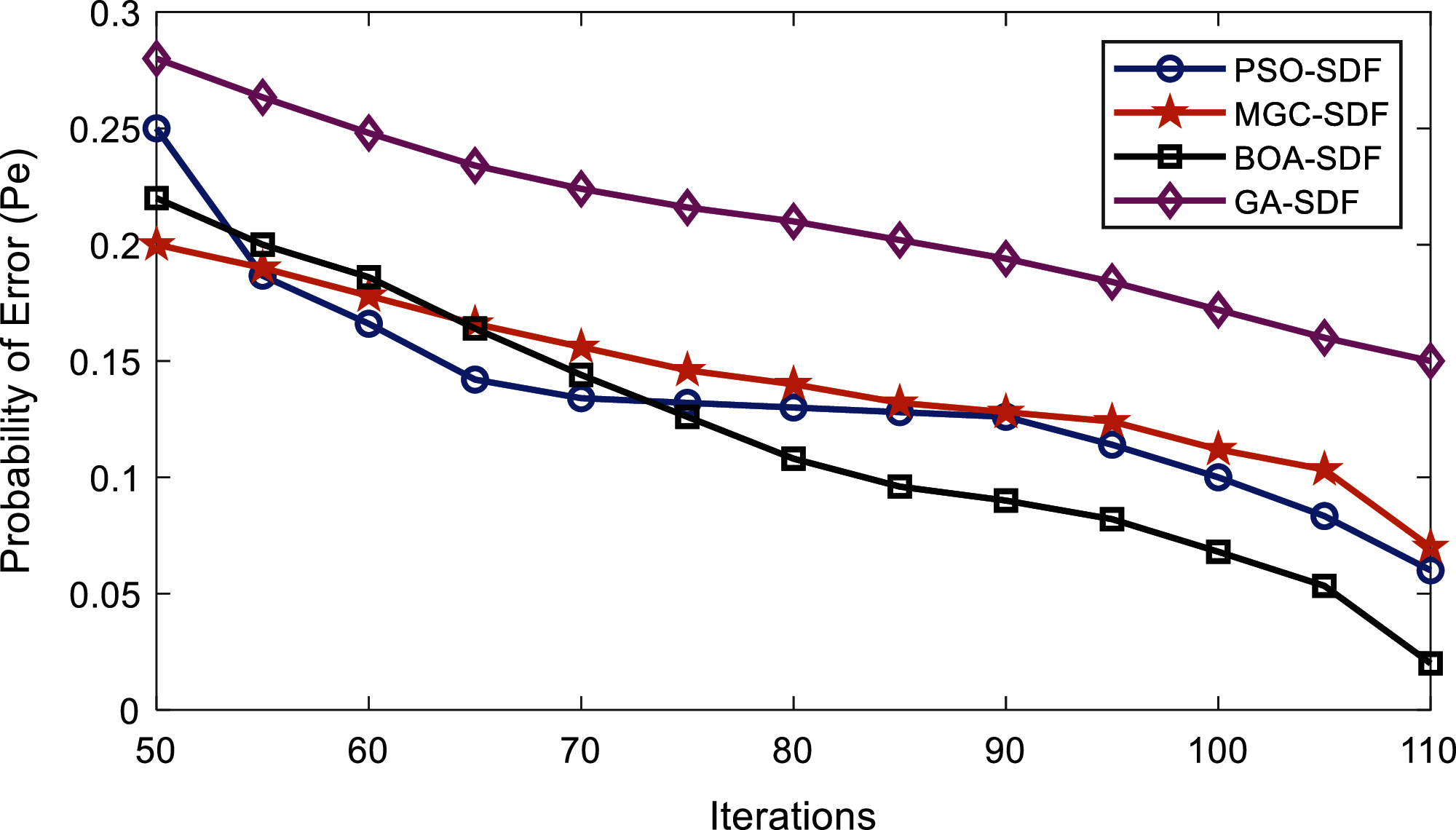
Figure 8: Error probability vs. algorithm iterations at lower SNRs by malicious
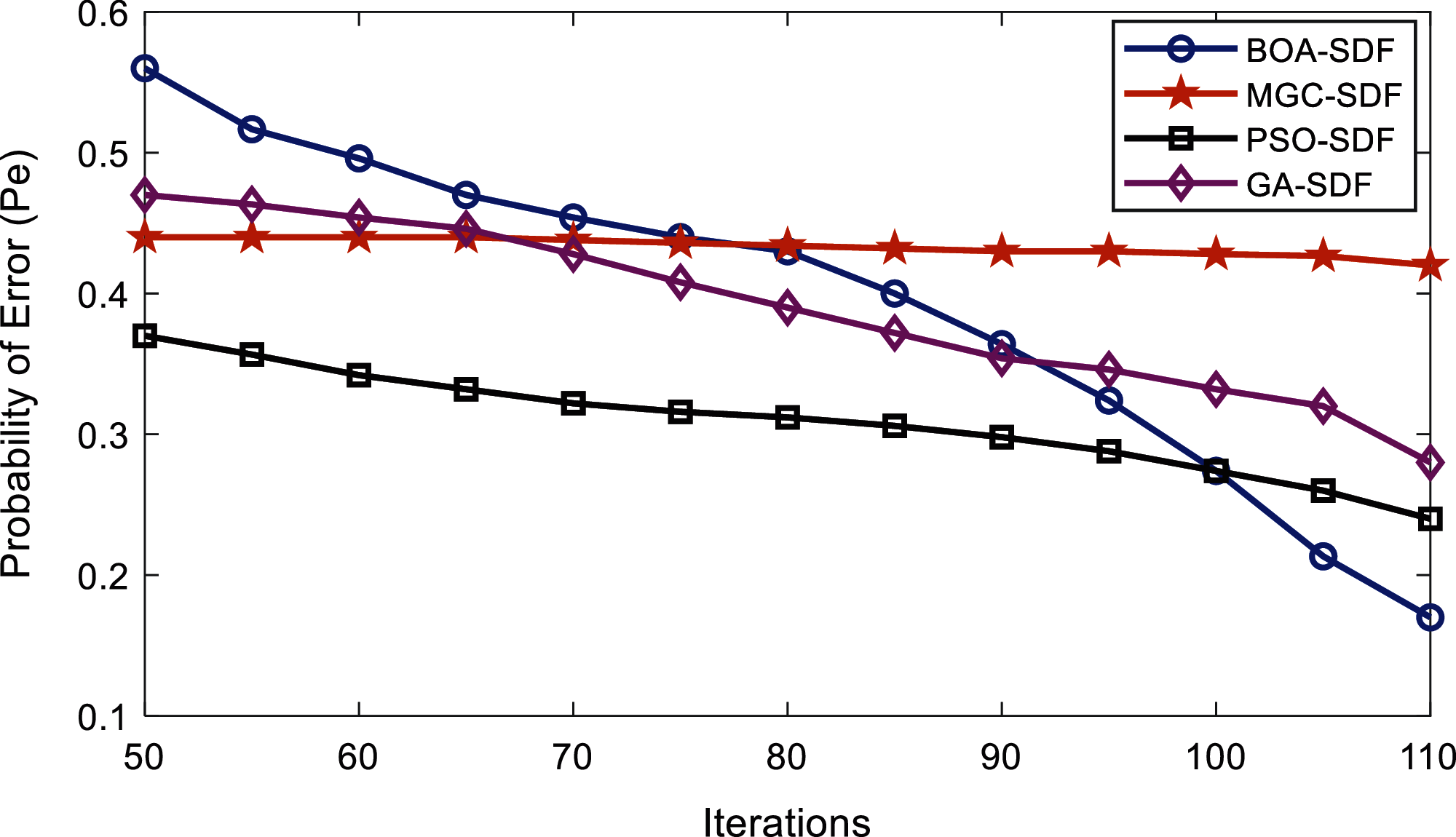
Figure 9: Error probability vs. iterations at higher SNRs by malicious
In Fig. 7, the results are drawn for PSO-SDF, MGC-SDF, BOA-SDF, and GA-SDF under the participation of the normal users. Fig. 7 shows that the MGC-SDF results have poor sensing performance by delivering high error probability followed by the GA-SDF, and PSO-SDF. The proposed BOA-SDF scheme has achieved better sensing results with minimum sensing error. BOA-SDF shows the best performance at iteration range by providing a minimum error probability of 0.13 at the iteration of 50 and that reduces to the lowest error probability of 0.04 as the number of iterations exceed to 110, which is the minimum in all other SDF schemes.
In Fig. 8, the results of error probabilities against the increasing number of iterations are investigated when high SNRs are assigned to the MU’s. In this part, the GA-SDF result in poor sensing performance by giving maximum error probability, followed by the PSO-SDF with an error probability of 0.25. Similarly, the MGC-SDF begins with an error probability of 0.2 and at the end of 110 iterations its error probability reduces to 0.07. The proposed BOA-SDF indicates the best performance when the number of iterations exceeds 75. The BOA-SDF scheme error probability at the 75 iterations is 0.126 and further gets down to 0.02 at the 110-iteration level to beat all other schemes.
In Fig. 9 the BOA-SDF scheme shows the best results at all algorithm iterations. It is visible from the results in Fig. 9 that at 110 the error probability is 0.17 which is the minimum error probability of all other SDF schemes.
In this scenario, the error probability results are shown for the increasing number of sensing samples varying in the range 270–335. Here the total number of the SUs are 14 with an average SNRs as −11.5 dB. The algorithm population size is kept as 20 with total 50 iterations. All other parameters are retained as identical to get the results in Figs. 10–12.
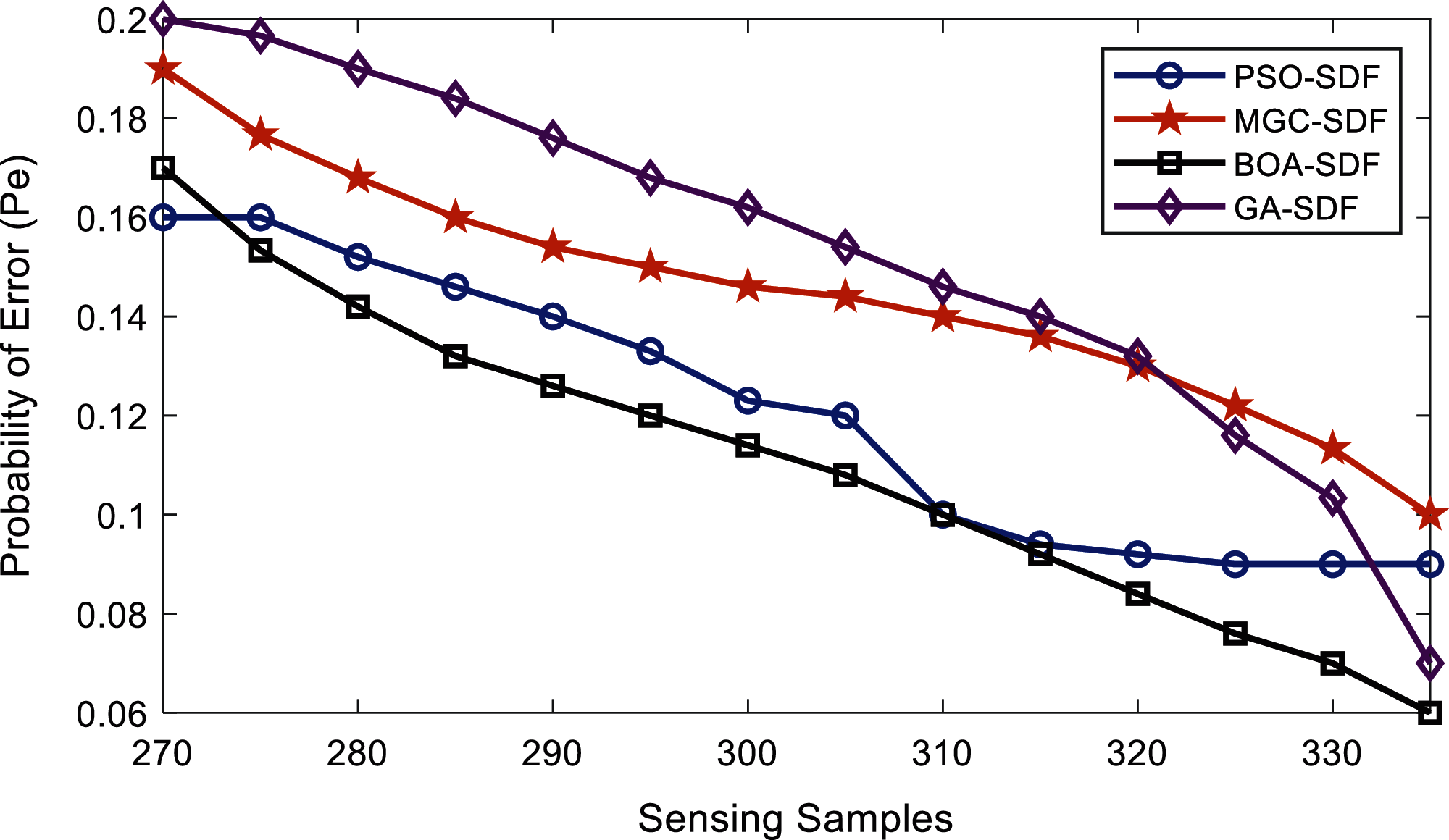
Figure 10: Error probability vs. sensing samples at normal users
In Fig. 10, the GA-SDF results are poor among all with maximum error probability while sensing PU. MGC-SDF and PSO-SDF-based combination schemes also has minimum accuracy in sensing as compared with the proposed BOA-SDF schemes. The starting error probability of BOA-SDF is 0.17 at 270 sensing samples that further gets down as the number of samples is increased. This improvement in terms of the error probability is noticeable at 335 sensing samples, where the BOA-SDF scheme error probability reduces to 0.06 at 335 sensing samples.
In Fig. 11, the proposed BOA-SDF scheme and PSO-SDF schemes have similar sensing results in this case, while the MGC-SDF and GA-SDF schemes’ performance is poor. As the sensing samples exceed 310, the proposed BOA-SDF dominate PSO-SDF results.
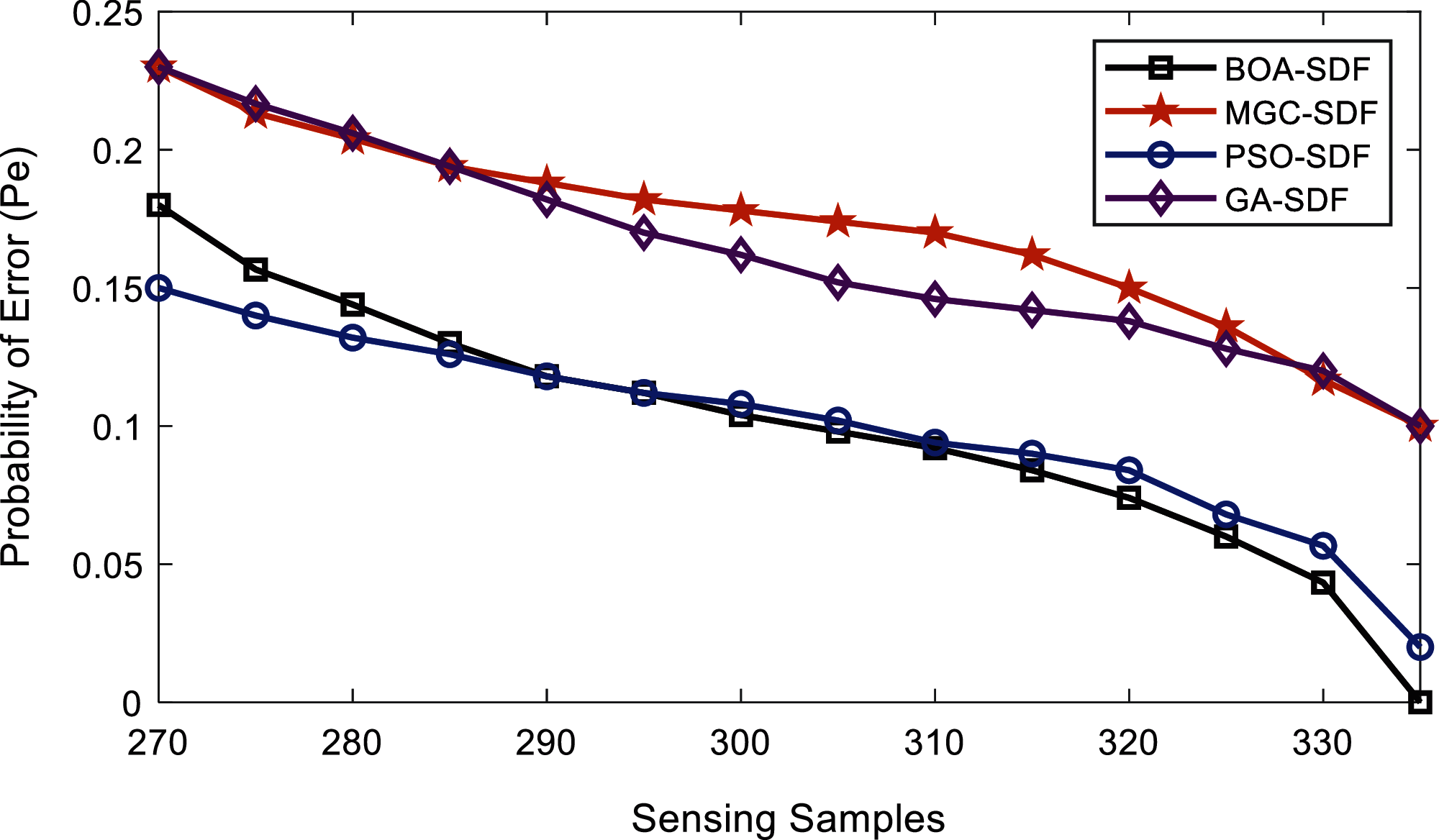
Figure 11: Error probability vs. sensing samples at lower SNRs by malicious
In Fig. 12, BOA-SDF shows improved sensing results with minimum sensing error. At the beginning of 270 sensing samples, BOA-SDF has a maximum error probability of 0.53. As the sensing samples exceeds 310 outstanding results are achieved by the proposed scheme with minimum sensing error of 0.23 at 335 samples in comparison with all others.
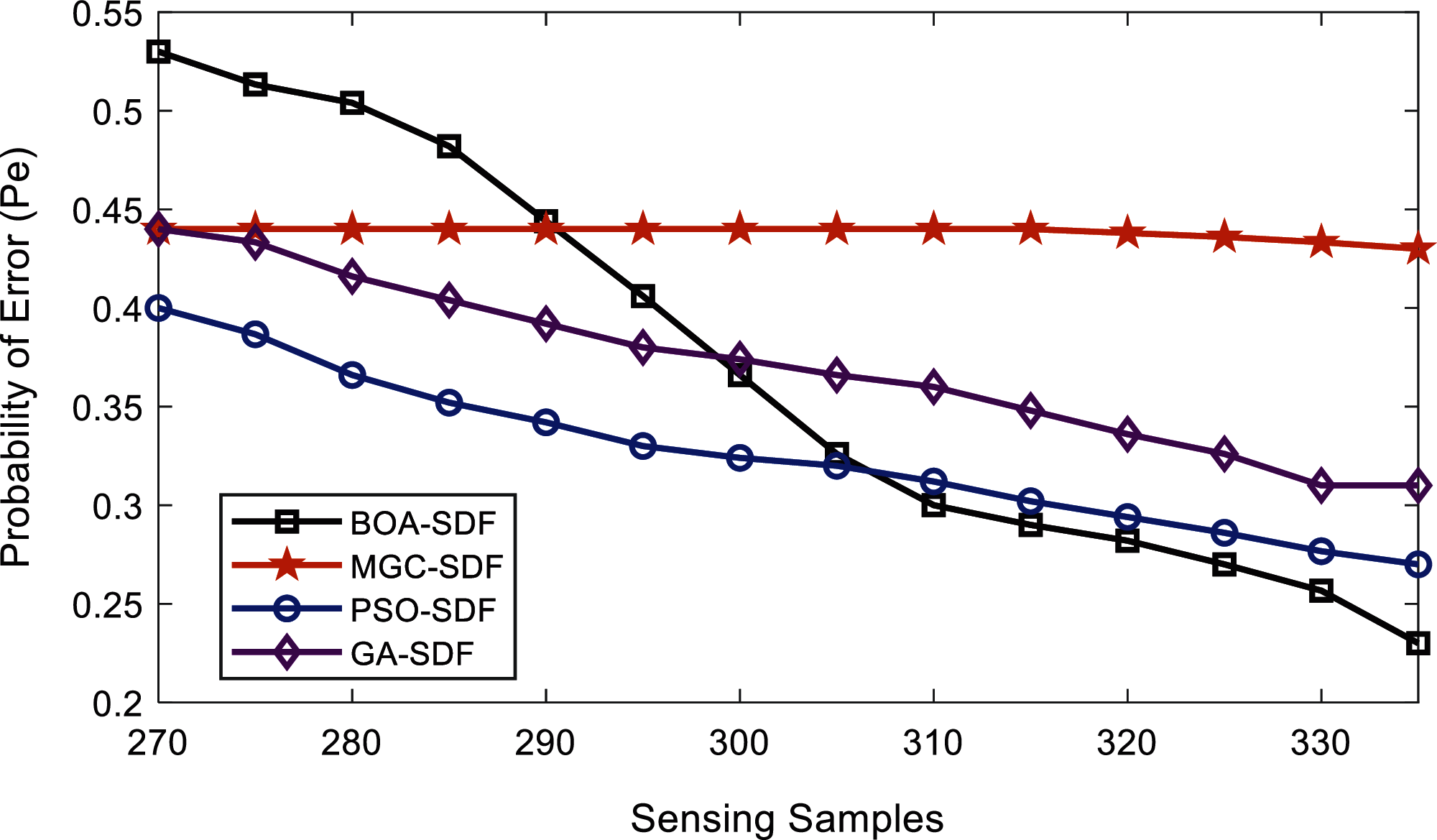
Figure 12: Error probability vs. sensing samples at higher SNRs by malicious
This scenario discusses the results of error probability against population size ranging from 20 to 80. The SDF scheme results are collected in this case to investigate the performance by keeping the total number of cooperative users fixed at 14, average SNRs −11.5 dB, sensing iterations 50, and fixed sensing samples as 270.
In Fig. 13, as the algorithm population increases error probability of the SDF schemes reduces. The error probability of the MGC-SDF is the maximum of all i.e., 0.25 when the population size is 20. As the population size approaches 80, MGC-SDF error probability reduces to 0.14. The GA-SDF achieves accurate sensing performance with an error probability of 0.18 in the beginning that reduces to 0.08 as the population is increased to 80. In this scenario, the results of the PSO-SDF and the proposed BOA-SDF are closer until 75. The result shows that as population size exceeds 75, BOA-SDF outcomes in a minimum sensing error of 0.01 at 80. Whereas, the PSO-SDF has its error probability of 0.05 at a population size of 80.
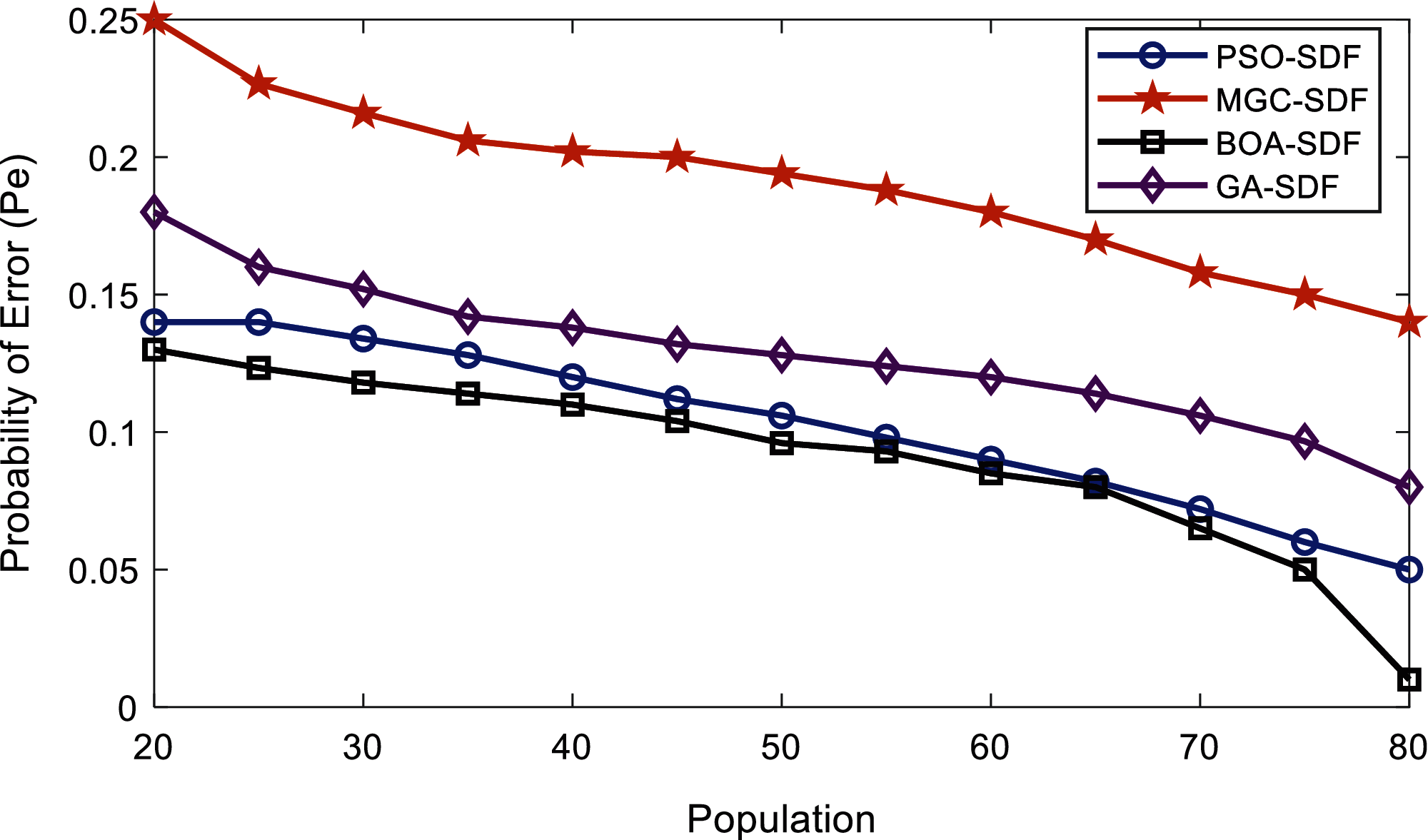
Figure 13: Error probability vs. algorithm population at normal users
The result in Fig. 14 shows that error probabilities of the proposed scheme reduce as the population size exceeds 50. The proposed scheme has a minimum error probability of 0.04 among all other schemes as the population size increases to 80.
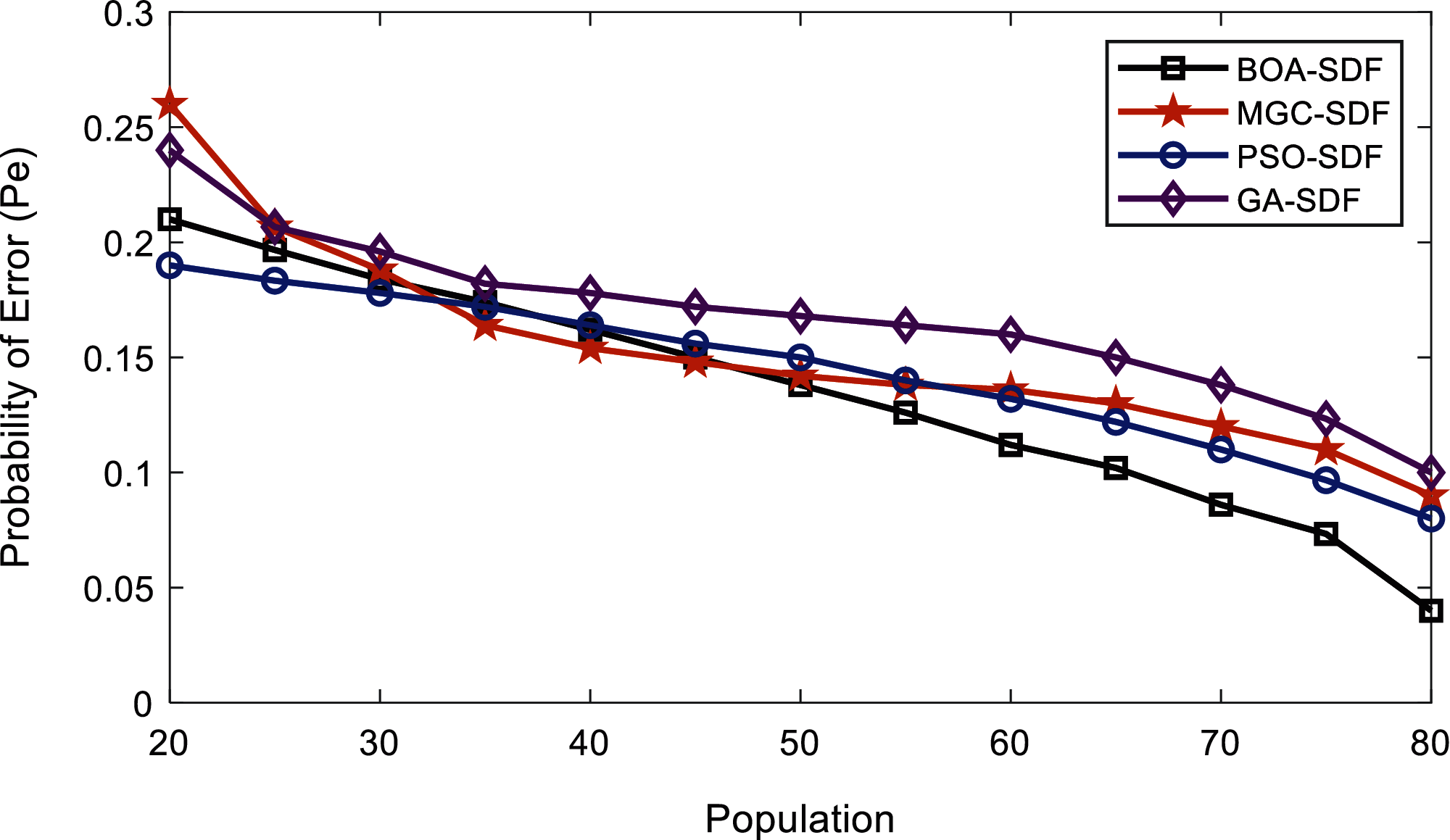
Figure 14: Error probability vs. algorithm population at lower SNRs by malicious
In Fig. 15 as high SNRs are assigned to the MUs, the MGC-SDF show reduced sensing performance with high sensing error. The proposed BOA-SDF scheme has better sensing reliability than the PSO-SDF, MGC-SDF, and GA-SDF schemes with error probabilities of 0.34 at population 20 that further gets down to 0.24 as the population rises to 80.
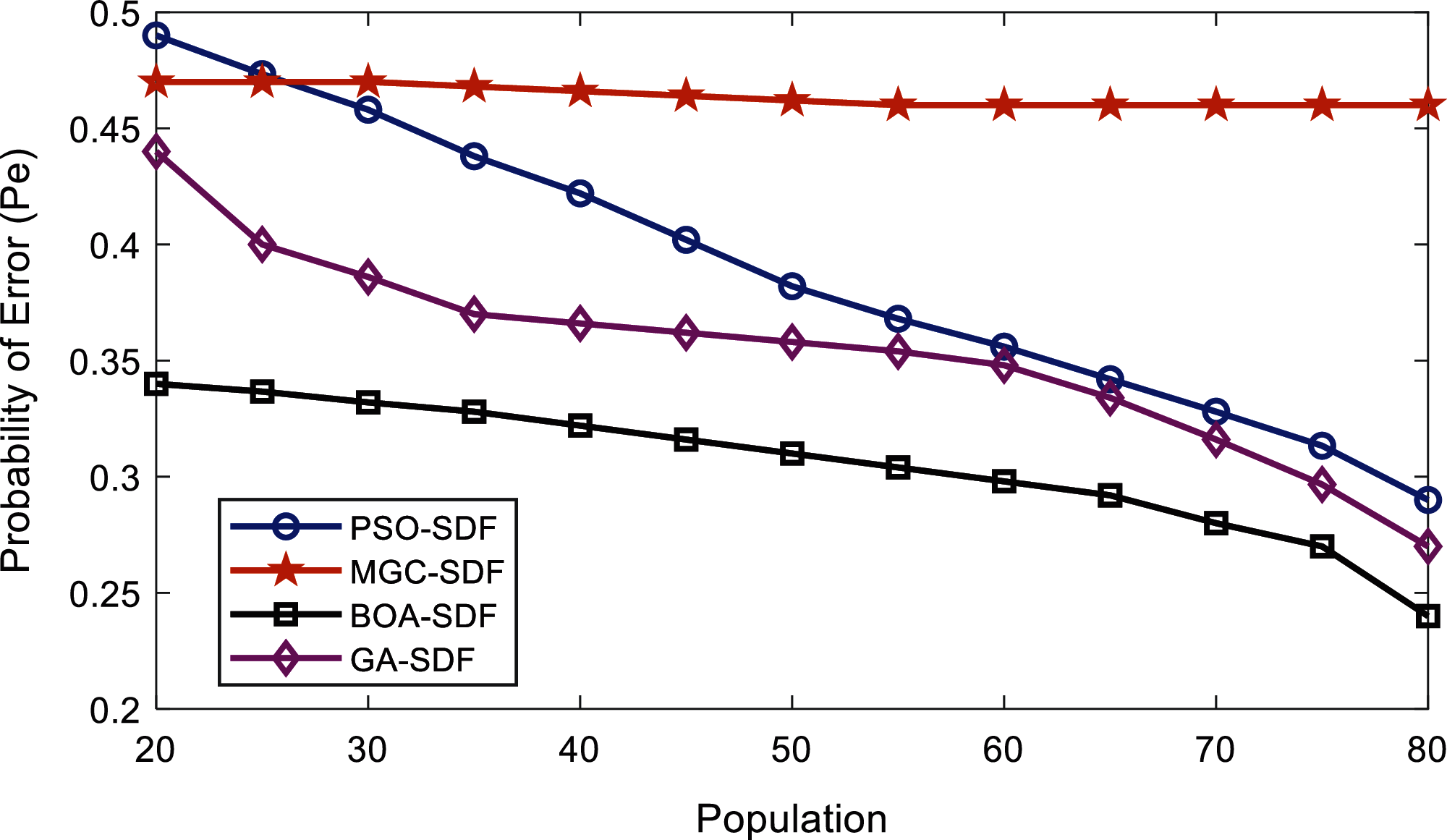
Figure 15: Error probability vs. algorithm population at higher SNRs by malicious
The integration of CR with the IoT is anticipated to expand the devices connectivity and services in future. The CR increases spectrum utilization by getting accurate sensing information through the SUs’ cooperation. Although CSS can sense the PU spectrum opportunities more reliably, the deceitful sensing data stated by the MU’s in the CSS can essentially influence the FC decision. This paper proposed a BOA-based SDF scheme to determine a coefficient vector against SUs’, while making a global decision at the FC. The weighting coefficient vector in the proposed BOA-SDF scheme support in the PU channel identification with high detection, minimum false alarm and low error probabilities through the assignment of high weights to the normal SUs sensing in comparison with the MUs.
The simulation results at different SUs, average SNRs, and sensing samples confirm that the proposed BOA-based SDF essentially outperforms the traditional MGC-SDF, PSO-SDF and GA-SDF schemes.
Funding Statement: This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2016R1C1B1014069) and in part by the National Research Foundation of Korea (NRF) funded by the Korea government (MIST) (No. 2021R1A2C1013150).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. T. Q. Duong and N. S. Vo, “Editorial: Wireless communication and network for 5G and beyond,” Mobile Networks and Applications, vol. 24, no. 2, pp. 443–446, 2019. [Google Scholar]
2. J. Ali and B. H. Roh, “An effective hierarchical control plane for software-defined networks leveraging TOPSIS for end-to-end QoS class-mapping,” IEEE Access, vol. 8, pp. 88990–89006, 2020. [Google Scholar]
3. R. Chavez-santiago, M. Szydelvo, A. Kliks, F. Foukalas, Y. Haddad et al., “5G, the convergence of wireless communication,” Wireless Personal Communication, vol. 83, no. 3, pp. 1617–1642, 2015. [Google Scholar]
4. B.-S. P. Lin, F. J. Lin and L.-P. Tung, “The role of 5G mobile broadband in the development of IoT, big data, cloud and SDN,” Communication and Networks, vol. 8, no. 1, pp. 9–21, 2016. [Google Scholar]
5. Q. Wu, G. Ding and Y. Xu, “Cognitive internet of things: A new paradigm beyond connection,” IEEE Internet of Things Journal, vol. 1, no. 2, pp. 129–143, 2014. [Google Scholar]
6. J. Ali and B. H. Roh, “Quality of service improvement with optimal software-defined networking controller and control plane clustering,” Computers Materials & Continua, vol. 67, no. 1, pp. 849–875, 2021. [Google Scholar]
7. A. Al-Fuqaha, M. Guizani, M. Mohammadi, M. Aldhari and M. Ayyash, “Internet of things: A survey on enabling technologies, protocols, and applications,” IEEE Communication Survey and Tutorial, vol. 17, no. 4, pp. 2347–2376, 2015. [Google Scholar]
8. A. A. Khan, M. H. Rehmani and A. Rachedi, “When cognitive radio meets the internet of things?,” in Proc. IEEE Int. Wireless Communications & Computing Conf. (IWCMCPaphos, Cyprus, pp. 469–474, 2016. [Google Scholar]
9. W. Ejaz, A. Anpalagan, M. A. Imran, M. Jo, M. Naeem et al., “Internet of things (IoT) in 5G wireless communication,” IEEE Access, vol. 4, pp. 10310–10314, 2016. [Google Scholar]
10. F. A. Awin, Y. M. Alginahi, E. A. Raheem and K. Tepe, “Technical issues on cognitive radio based internet of things: A survey,” IEEE Access, vol. 7, pp. 97887–97908, 2019. [Google Scholar]
11. S. Chatterjee, R. Mukherjee, S. Ghosh, D. Gosh, S. Gosh et al., “Internet of things and cognitive radio-issues and challenges,” in 2017 4th Int. Conf. on Opto-Electronics and Applied Optics (OptronixKolkata, India, pp. 1–4, 2017. [Google Scholar]
12. Y. Arjoune and N. Kaabouch, “A comprehensive survey on spectrum sensing in cognitive radio networks: Recent advances, new challenges, and future research direction,” Sensors, vol. 19, no. 1, pp. 126, 2019. [Google Scholar]
13. A. Ranjan, Anurag and B. Singh, “Design and analysis of spectrum sensing in cognitive radio based on energy detection,” in Proc. IEEE Int. Conf. on Signal and Information Processing (IConSIPNanded, India, pp. 1–5, 2016. [Google Scholar]
14. I. Ilyas, S. Paul, A. Rahman and R. K. Kundu, “Comparative evaluation of cyclo- stationary detection based cognitive spectrum sensing,” in Proc. 2016 IEEE 7th Annual Ubiquitous Computing, Electronics & Mobile Communication Conf. (UEMCONNew York, NY, USA, pp. 1–7, 2016. [Google Scholar]
15. I. F. Akilidz, B. F. Lo and R. Balakrishnan, “Cooperative spectrum sensing in cognitive radio networks: A survey,” Physical Communication, vol. 4, no. 1, pp. 40–62, 2011. [Google Scholar]
16. D. Cabric, S. M. Mishra and R. W. Brodersen, “Implementation issues in spectrum sensing for cognitive radios,” in Conf. Record of the Thirty-Eighth Asilomar Conf. on Signals, Systems and Computers, Pacific Grove CA, USA, pp. 772–776, 2004. [Google Scholar]
17. N. Gul, M. S. Khan, J. Kim and S. M. Kim, “Robust spectrum sensing via double-sided neighbor distance based on genetic algorithm in cognitive radio networks,” Mobile Information Systems, vol. 2020, pp. 1–10, 2020. [Google Scholar]
18. D. Lee, “Adaptive random access for cooperative spectrum sensing in cognitive radio networks,” IEEE Transactions on Wireless Communications, vol. 14, no. 2, pp. 831–840, 2015. [Google Scholar]
19. Y. He, J. Xue and T. Ratnarajah, “On the performance of cooperative spectrum sensing in random cognitive radio networks,” IEEE Systems Journal, vol. 12, no. 1, pp. 881–892, 2016. [Google Scholar]
20. N. Gul, I. M. Qureshi, A. Elahi and I. Rasool, “Defense against malicious users in cooperative spectrum sensing using genetic algorithm,” International Journal of Antennas and Propagation, vol. 2018, pp. 1–11, 2018. [Google Scholar]
21. D. Hamza, S. Member, S. Aïssa, S. Member and G. Aniba, “Equal gain combining for cooperative spectrum sensing in cognitive radio networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 8, pp. 4334–4345, 2014. [Google Scholar]
22. R. Biswas, J. Wu and X. Du, “Mitigation of the spectrum sensing data falsifying attack in cognitive radio networks,” in Proc. ICC, 2019 - 2019 IEEE Int. Conf. on Communications (ICCShanghai, China, pp. 1–6, 2019. [Google Scholar]
23. N. Gul, I. M. Qureshi, A. Omar, A. Elahi and M. S. Khan, “History based forward and feedback mechanism in cooperative spectrum sensing including malicious users in cognitive radio network,” PLOS One, vol. 12, no. 8, pp. e0183387, 2017. [Google Scholar]
24. N. Gul, I. M. Qureshi, S. Akbar, M. Kamran and I. Rasool, “One-to-many relationship based kullback leibler divergence against malicious users in cooperative spectrum sensing,” Wireless Communications and Mobile Computing, vol. 2018, no. 1, pp. 1–14, 2018. [Google Scholar]
25. M. Jenani, “Network security, a challenge,” International Journal of Advanced Networking and Applications, vol. 8, no. 5, pp. 120–123, 2017. [Google Scholar]
26. M. S. Khan, N. Gul, J. Kim, I. M. Qureshi and S. M. Kim, “A genetic algorithm-based soft decision fusion scheme in cognitive IoT networks with malicious users,” Wireless Communications and Mobile Computing, vol. 2020, no. 2, pp. 1–10, 2020. [Google Scholar]
27. I. S. Turbin, “Security threats in mobile cognitive radio networks,” in Proc. 2018 IEEE East- West Design & Test Symposium (EWDTSRussia, pp. 1–6, 2018. [Google Scholar]
28. N. Gul, I. M. Qureshi, A. Naveed, A. Elahi and I. Rasool, “Secured soft combination schemes against malicious-users in cooperative spectrum sensing,” Wireless Personal Communication, vol. 2019, no. 108, pp. 389–408, 2019. [Google Scholar]
29. H. A. B. Salmeh, S. Almajali, M. Ayyash and H. Elgala, “Spectrum assignment in cognitive radio networks for internet of things delay sensitive applications under jamming attack,” IEEE Internet of Things, vol. 5, no. 3, pp. 1904–1913, 2018. [Google Scholar]
30. Sh Lin, Ch Wen and W. A. Sethares, “Two-tier device based authentication protocol against PUEA attacks for IoT applications,” IEEE Transaction on Signal and Information Processing over Networks, vol. 4, no. 1, pp. 33–47, 2018. [Google Scholar]
31. N. Gul, M. S. Khan, S. M. Kim, M. St-Hilaire, I. Ullah et al., “Particle swarm optimization in the presence of malicious users in cognitive IoT networks with data,” Scientific Programming, vol. 2020, pp. 1–11, 2020. [Google Scholar]
32. M. Akbari, M. R. Manesh, A. A. Saleh and M. Ismail, “Improved soft fusion based cooperative spectrum sensing using particle swarm optimization,” IEICE Electronics Express, vol. 9, no. 6, pp. 436–442, 2012. [Google Scholar]
33. S. Arora, S. Singh and K. Yetilmezsoy, “A modified butterfly optimization algorithm for mechanical design optimization problems,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 40, no. 1, pp. 1–17, 2018. [Google Scholar]
34. S. A. Salem, “BOA: A novel optimization algorithm,” in Int. Conf. on Engineering and Technology, ICET, 2012 - Conf. Booklet”, Cairo, Egypt, pp. 1–5, 2012. [Google Scholar]
35. S. Arora and S. Singh, “Node localization in wireless sensor networks using butterfly optimization algorithm,” Arabian Journal for Science and Engineering, vol. 42, no. 8, pp. 3325–3335, 2017. [Google Scholar]
36. S. Arora and S. Singh, “An improved butterfly optimization algorithm with chaos,” Journal of Intelligent and Fuzzy Systems, vol. 32, no. 1, pp. 1079–1088, 2017. [Google Scholar]
37. Z. Quan, S. Cui and A. H. Sayed, “Optimal linear cooperation for spectrum sensing in cognitive radio network,” IEEE Journal of Selected Topics in Signal Processing, vol. 2, no. 1, pp. 28–40, 2008. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |