Computers, Materials & Continua DOI:10.32604/cmc.2022.022290
Research paper

Fed-DFE: A Decentralized Function Encryption-Based Privacy-Preserving Scheme for Federated Learning

Zhe Sun1, Jiyuan Feng1, Lihua Yin1,*, Zixu Zhang2, Ran Li1, Yu Hu1 and Chongning Na3

1Cyberspace Institute of Advanced Technology (CIAT), Guangzhou University, Guangzhou, China
2School of Electrical and Data Engineering, University of Technology Sydney, Sydney, Australia
3Zhejiang Lab, Hangzhou, China
*Corresponding Author: Lihua Yin. Email: yinlh@gzhu.edu.cn
Received: 02 August 2021; Accepted: 03 September 2021

Abstract: Federated learning is a distributed learning framework which trains global models by passing model parameters instead of raw data. However, the training mechanism for passing model parameters is still threatened by gradient inversion, inference attacks, etc. With a lightweight encryption overhead, function encryption is a viable secure aggregation technique in federation learning, which is often used in combination with differential privacy. The function encryption in federal learning still has the following problems: a) Traditional function encryption usually requires a trust third party (TTP) to assign the keys. If a TTP colludes with a server, the security aggregation mechanism can be compromised. b) When using differential privacy in combination with function encryption, the evaluation metrics of incentive mechanisms in the traditional federal learning become invisible. In this paper, we propose a hybrid privacy-preserving scheme for federated learning, called Fed-DFE. Specifically, we present a decentralized multi-client function encryption algorithm. It replaces the TTP in traditional function encryption with an interactive key generation algorithm, avoiding the problem of collusion. Then, an embedded incentive mechanism is designed for function encryption. It models the real parameters in federated learning and finds a balance between privacy preservation and model accuracy. Subsequently, we implemented a prototype of Fed-DFE and evaluated the performance of decentralized function encryption algorithm. The experimental results demonstrate the effectiveness and efficiency of our scheme.

Keywords: Decentralized function encryption; incentive mechanism; differential privacy; federated learning

1  Introduction

As a result of the rapid development of deep neural networks, data-driven artificial intelligence has been widely used in smart transportation [1,2], Internet of Things [3,4], smart grid [5,6] and financial applications [7,8]. Accuracy in data analytics depends not only on the volume of training data but also on the diversity of training data. However, the protection of data assets and user privacy makes it difficult for service providers to directly access data held by other data owners. Federated learning is a good way to leverage data from different owners to improve the accuracy of service models. Users use the same learning model structure as the server and only provide model parameters during the cooperative training process [9]. Federated learning prevents direct transmission of raw data, which is key privacy protection advance for cooperative training. Nonetheless, subsequent research has shown that an attacker can still reverse training data from gradients, infer users’ privacy attributes, or determine whether a member belongs to a certain privacy grouping [10].

To prevent gradient leakage, users can rely on homomorphic encryption, function encryption, and other cryptographic methods to encrypt local models, and service providers do not have direct access to the plaintext of individual gradients. Zhang et al. [11] proposed a distributed selective stochastic gradient descent algorithm combined with Paillier homomorphic encryption. In this scheme, a trusted third party (TTP) assigns keys to users and the server, and the server uses Paillier additive homomorphism to achieve secure gradient aggregation. To address the efficiency problem of homomorphic encryption algorithms, Xu et al. [12] proposed a secure aggregation scheme based on function encryption. Service providers can combine aggregation and decryption missions using functional decryption keys to improve the efficiency of gradient aggregation. Subsequently, Yin et al. [13] proposed a function-hiding function encryption method for protecting weighting parameters in the gradient aggregation. This method prevents attackers from performing inference attacks by combining the available weight parameters with background knowledge. Unfortunately, these schemes usually require a TTP to manage, generate, and distribute public and private keys. Driven by commercial interests, malicious service providers may conspire with third parties to steal users’ gradients.

Researchers often incorporate differential privacy into cryptographic methods to defend against inference attacks, such as attribute inference attacks and member inference attacks. Differential privacy is a privacy-preserving technique proven by rigorous mathematics. It prevents malicious attackers from inferring user privacy in the training data by adding carefully designed noise to the model. But this also has led to a decline in the accuracy of global models. The trade-off between privacy protection and model accuracy is key to the practical use of differential privacy in federated learning. Incentive mechanisms are an effective way to regulate conflict by rewarding users for submitting gradients with higher model accuracy. Common incentive mechanisms in federated learning include Stackelberg game-based methods [14,15] and auction-based methods [16]. Zhan et al. [14] simulate a Stackelberg game model between servers and users to optimize the global cost of servers while satisfying user benefits. Stackelberg game generally requires that one party to be the leader, so it is not appropriate for a status parity scenario. Unlike that, Zeng et al. [16] propose an incentive mechanism based on the auction model. They evaluate and reward users based on their reputation and past behavior. Most of these game theory-based mechanisms are oriented towards traditional unencrypted gradients, and the quantitative metrics involved are so different from those of secure aggregation algorithms. In the function encryption algorithm, the service provider can only decrypt the aggregated model, and thus cannot judge the quality of the local model uploaded by individual users. Individual users may become more selfish after the overall evaluation, unwilling to contribute high-quality models and parameters, or even uploading untrained models published by the server. There is still a gap between game theory and secure aggregation in federated learning.

In this paper, we propose a hybrid privacy-preserving framework for federated learning called Fed-DFE. It combines function encryption with differential privacy to prevent gradient leakage and inference attacks. Specifically, the keys are generated through users’ interaction with the server, removing the reliance on trusted third parties for traditional function encryption. Meanwhile, Fed-DFE introduces an incentive mechanism to avoid the low accuracy problem caused by excessive noise addition in differential privacy. Our main contributions include the following:

•   We design a decentralized multi-client function encryption algorithm (DMCFE). It does not require a TTP to manage, generate and assign keys, preventing collusion attacks by service providers and TTP.

•   We present an embedded incentive mechanism for function encryption. It models and evaluates the real parameters in federated learning that affect the quality of model services, and then uses the evaluation results as criteria for selecting participants.

•   We implement a prototype system of our proposed Fed-DFE. We evaluate the performance of DMCFE algorithm, and then analyze the impact of incentive mechanism parameters on the accuracy of federated learning model.

The rest of the paper is organized as follows: In Section 2, we review the related work. Then, we brief introduce the preliminaries of scheme and threat models in Section 3. In Section 4, we present the design details of the proposed Fed-DFE scheme. We provide security and privacy analyses in Section 5. The evaluations of experiments are described in Section 6. And we conclude the paper in Section 7.

2  Related Work

Federated Learning is an effective collaborative training architecture that has become a research hotspot for privacy preservation. In this section, we focus on the cryptography-based secure aggregation algorithm and incentive mechanism for federated learning.

2.1 Cryptography-Based Secure Aggregation Algorithm in Federated Learning

Federated learning effectively avoids the privacy leakage problem associated with sending raw data directly. However, recent studies indicate that malicious attackers can obtain privacy information of training data. To prevent user privacy leakage caused by sending models directly, researchers have proposed a variety of cryptography-based security aggregation schemes. Currently, the main cryptographic methods in federated learning include homomorphic encryption, secure multiparty computation, and functional encryption.

The characteristic of homomorphic encryption is that the result calculated on the plaintext is the equivalent to the decrypted result after calculated on the ciphertext. Therefore, it is widely applied to parameter aggregation on servers. Zhang et al. [11] proposed PEFL, a distributed machine learning privacy-preserving scheme based on homomorphic encryption. This scheme can perform computation directly using ciphertext to achieve secure aggregation. The PEFL method ensures that the server only gets the aggregated models and not the individual users’ models. However, directly using the paillier algorithm to encrypt the model causes huge communication and computation overhead.

Secure multiparty computation allows multiple users to jointly compute a convention result without revealing their input information. Bonawitz et al. [17] proposed to use a lightweight secret sharing technique to aggregate the user’s model. Secret sharing does not require complex operations, so it has reduced computation overhead compared to homomorphic encryption. But in the meanwhile, it reduces the security of model aggregation. Specifically, it requires secret parameters to be exchanged between two clients through a trusted channel. As user numbers increase, this can cause a huge communication overhead between users.

Different from the above, function encryption is a lightweight secure aggregation algorithm with acceptable security. Xu et al. [12] first applied function encryption to a horizontal federated learning scenario. They confirm through extensive experiments that function encryption can effectively reduce the computational overhead. However, this scheme is only applicable when all the user weights are equal. Contrarily, a malicious attacker can infer sensitive attributes from a specific user’s weights. To solve the above problem, Yin et al. [13] proposed a multi-input function encryption scheme that can hide the user weight information to protect the users’ model parameters. In this scheme, a TTP assigns keys to the user and the server, but each user individually sends the aggregation weights to the TTP. As a result, the server is completely unaware of the user’s weight information. This scheme can effectively avoid malicious servers from stealing users’ privacy through the weights. However, there is also a TTP in the above functional encryption algorithm. Federated learning is difficult to satisfy this assumption during practical application. Motivated by profits, service providers may collude with TTP to execute complicit attacks.

In this paper, we design a secure aggregation algorithm based on decentralized multi-client function encryption, and try to solve the problem of collusion by removing the TTP.

2.2 Incentive Mechanism in Federated Learning

Cryptography-based secure aggregation can prevent malicious attackers from stealing individual parameters and private information. However, researchers demonstrated [18] that malicious attackers can still execute inference attacks through published aggregated models or service interfaces. Consequently, researchers commonly combine cryptographic methods and differential privacy [19] to address the various privacy attacks. When applying differential privacy in federation learning, we need to add noise to the model parameters. Excessive noise can significantly reduce the global model accuracy or even cause it not to converge. As a result, some researchers encourage users to contribute high-quality parameters through the incentive mechanism [14].

To find the optimal solution that can adjust user privacy and global model accuracy, researchers have tried to design incentive mechanisms by using Game theory. Zhan et al. [14] proposed a two-part game model based on Stackelberg game. The scheme goal is to reach the Nash equilibrium of the model by maximizing each node’s reward, while minimizing the parameter server’s total reward. Based on these system states in each iteration round, the server and nodes will adjust their respective strategies in the game model to obtain the rewards. In addition, Khan et al. [20] also constructed an incentive mechanism model for service providers and participants in federated learning. This model incentivizes devices to participate in federated learning through the Stackelberg game. To address the problem of reluctance to actively participate in federated learning. Zeng et al. [16] proposed a federated learning incentives mechanism based on multidimensional auctions. In this model, the server acts as a seller to send bid requests, and all users participate in the bidding. Finally, all winning users will reach a Nash equilibrium to maximize their respective benefits. However, the above scheme has only conducted numerical simulation experiments, and there is a gap from the practical training process in federated learning.

The other researchers have made efforts to apply incentive mechanisms in a realistic scenario in federated learning. They have concretely combined incentives with realistic scenarios by using real indicators to measure users’ contributions. Kang et al. [21] proposed an incentive mechanism that uses the mobile devices’ reputation as an indicator to measure contribution. The scheme manages the reputation of mobile devices through alliance chain. The scheme offers higher rewards to users who provide high quality locally trained models in federated learning. Besides, Weng et al. [22] proposed a blockchain-based incentive mechanism. Users will get rewards for successfully creating a new block during the training process. Since the effective implementation of incentive mechanism is closely related to realistic scenarios. Neither of the above schemes can directly apply to security aggregation scenarios in federated learning. To build practical incentive mechanisms for cryptographic methods, we need to tightly integrate user evaluation indicators and cryptographic schemes.

In this paper, we design an embedded incentive mechanism which closely integrates with function encryption. With our incentive mechanism, the server can avoid excessive privacy-preserving by adjusting the reward.

3  Preliminaries

In this section, we first briefly introduce definitions of decentralized function encryption algorithms and differential privacy. And then we describe our threat models and motivations.

3.1 Decentralized Multi-Client Functional Encryption

Function encryption is a new encryption method that is different from traditional public key encryption system. For the inner product function f, the ciphertext x is encrypted by the plaintext c with an encryption key. Users can use the function decryption key dky to decrypt and calculate f(x), but they cannot get any information about the plaintext c. In function encryption, there is only one encryptor to encrypt its own plaintext vector, which cannot satisfy the needs of practical application.

The multi-client function encryption scheme solves the problem. The scheme divides the high-dimensional vector into n sub-vectors x1,x2,…,xn. And each user holds one of the sub-vectors and encrypts its own sub-vector xi separately to obtain its own ciphertext ci=Encrypt(xi). The decryptor can only obtain the computation result of the function f(x1,x2,…,xn) by decryption key dky. However, the multi-client function encryption algorithm generally requires a trusted third party to manage and generate the master secret key msk.

It is difficult to find a fully trusted third party to perform key management and distribution tasks in practical applications. Trusted third party may also collude with the decryptor which will cause the decryptor to obtain the client’s plaintext. Therefore, to prevent a trusted third party from conspiring with the decryptor, we introduce decentralized multi-client function encryption algorithm [23]. In this algorithm, each user generates a partial decryption key. All users send the partial decryption key to the decryptor, and the decryptor combines all partial decryption keys to generate the decryption key dky.

3.2 Differential Privacy

Differential privacy is a privacy-preserving mechanism that minimizes the recognition probability of data records by adding noise. ε is called the privacy budget or privacy loss, which describes the privacy-preserving level of random algorithm M on adjacent datasets D and D′. The higher the value of ɛ, the lower the privacy-preserving level.

Definition 1. Differential privacy. Given the N users, each user has its own dataset, given an algorithm M for the dataset and its domain Dom(M) and range Ran(M). If the algorithm obtains the same output result S∗(S∗ belongs to the range of Ran(M)) on adjacent datasets D and D′(D and D′ belong to the domain Dom(M)) satisfies the following inequality, then the algorithm M satisfies (ε,δ)-differential privacy. δ represents the probability of plain ε-differential privacy.

Pr[M(D)=S∗]≤eε⋅Pr[M(D′)=S∗]+δ (1)

Deep learning model accuracy substantially depends on the quality of the training data, and adding perturbations directly to the training data may reduce the model quality greatly. Therefore, Abadi et al. [24] proposed adding noise that conforms to differential privacy algorithms in deep learning models to protect model privacy. The main noise mechanisms in differential privacy include: Gaussian noise, Laplace mechanism, and Exponential mechanisms. Considering the properties of neural network models, researchers typically choose the Gaussian noise mechanism as the typical noise addition mechanism. Definition 2 illustrates the Gaussian noise mechanism.

Definition 2. Gaussian noise mechanism. f:D→R is a certain real-valued function, when f satisfies the differential privacy mechanism by adding noise, Sf represent the f′ sensitivity. The definition of Sf is the maximum absolute distance |f(d)−f(d′)|, where d and d′ are the adjacent datasets. Finally, the Gaussian noise mechanism is defined as follows:

M(d)≜f(d)+N(0,Sf2⋅σ2) (2)

where N(0,Sf2⋅σ2) is the Gaussian distribution with mean 0 and standard deviation Sfσ.

The most typical application of Gaussian noise mechanism differential privacy in deep learning is Differentially Private SGD Algorithm, which is based on the basic combination theorem and composability of differential privacy. The algorithm can also track and accumulate privacy loss during the execution of the combined mechanism.

To avoid relying on servers to add noise, researchers have proposed local differential privacy (LDP). According to the LDP mechanism, the user will add noise to the local model instead of the server. In our Fed-DFE, we use the LDP parameters as an important component of the incentive mechanism. Our scheme can encourage users to provide high quality models while preserving the local models’ privacy.

3.3 Motivation and Our Basic Ideas

The federated learning process suffers primarily from two privacy threats. One is the inversion of the user’s training data by the transmitted gradients. Another is to infer whether privacy attributes are contained in the training data or whether a certain sample is included in the training dataset.

To prevent gradient inversion attacks, we introduce a function encryption algorithm to prevent an individual user’s gradient from being obtained by the server. Each user encrypts its own model and uploads it to the server. The server can only extract the plaintext of the aggregated results, but not the plaintext of individual gradients or any intermediate results. Homomorphic encryption algorithm first performs ciphertext computation to obtain the aggregated result, and then decrypts the aggregated result. In contrast, function encryption obtains the plaintext of the aggregation result by directly computing the decryption key and the ciphertext of individual gradients. It reduces the number of intermediate steps and thus increases efficiency. However, most function encryption algorithms in federation learning rely on TTP to assign keys [12]. If the TTP colludes with a server, the server can obtain the key for each user and can thus decrypt the ciphertext of any user’s gradient. In this paper, we utilize a decentralized multi-client encryption function via user-server interaction, where users can generate their own keys based on the interaction’s content. The user’s key is no longer available to any party except the user itself, thus solving the problem of collusion.

Differential privacy makes it difficult for an attacker to infer users’ privacy attributes by adding noise to the gradient. However, in practice, large amounts of excessive noise often cause a sharp drop in the accuracy of the aggregation model. To prevent users from adding noise that far exceeds their needs, researchers usually design incentive mechanisms to encourage users to submit more contributing gradients. In this paper, we design an incentive mechanism that is deeply integrated with function encryption. We use the auction model as an example to discuss how to use the intermediate parameters in function encryption as evaluation indicators for incentives. We also used experiments to evaluate the effectiveness of our chosen parameters in real-world federal learning. We hope that these works can serve as a reference for different game theories applied in federated learning, so as to find a balance between privacy protection and model accuracy.

4  Our Fed-DFE Scheme

In this section, we first overview our proposed Fed-DFE. Then we separately describe the details of decentralized multi-client function encryption (DMCFE), local differential privacy, and incentive mechanism involved in Fed-DFE.

4.1 System Architecture

Our Fed-DFE scheme includes both users and service provider. The users are responsible for training the model on the local dataset and uploading the parameters; And the service provider is responsible for aggregating the parameters and updating the global model. They collaborate to train a global model without compromising user privacy.

We denote a series of users as P={P1,P2,…,Pn}, and the service provider as SP. The workflow of Fed-DFE is shown in Fig. 1. (1) The SP first releases the initial model, master public key, and testing dataset. (2) Each user can generate its own encryption key based on master public key and its local information. It is impossible for anyone else to obtain a user’s key, thus avoiding the problem of collusion. (3) The users select appropriate privacy budgets and noise parameters according to their own privacy-preserving requirements. Individual users train local models with local differential privacy (LDP) mechanism against inference attacks. (4) Before uploading local models, users submit their testing accuracy to the SP. (5) SP selects participating users through the embedded incentive mechanism. (6) All the selected users encrypt the local models and upload them to SP. (7) They also generate and upload partial decryption keys that contain the weights of the aggregation parameters. (8) All partial decryption keys are combined into a function decryption key. (9) The SP executes secure aggregation of encrypted model through function decryption key.

4.2 DMCFE for Fed-DFE

In our proposed Fed-DFE, we modify the DMCFE algorithm to be suitable for secure aggregation in federated learning. The DMCFE algorithm includes Setup, Encrypt, DKeyGenShare, DKeyComb, and Decrypt algorithms. The Setup algorithm generates their respective private key ski, encryption key eki and master public key mpk for all users. Then, each user independently executes the Encrypt and DKeyGenShare algorithms, which respectively encrypt the local model and generate the partial decryption key dky→,i. Finally, SP performs the DKeyComb and Decrypt algorithm to generate the function decryption key dky→, and uses dky→ to decrypt the global model through Decrypt algorithm. We then describe the steps of DMCFE algorithm in one iteration of federated learning:

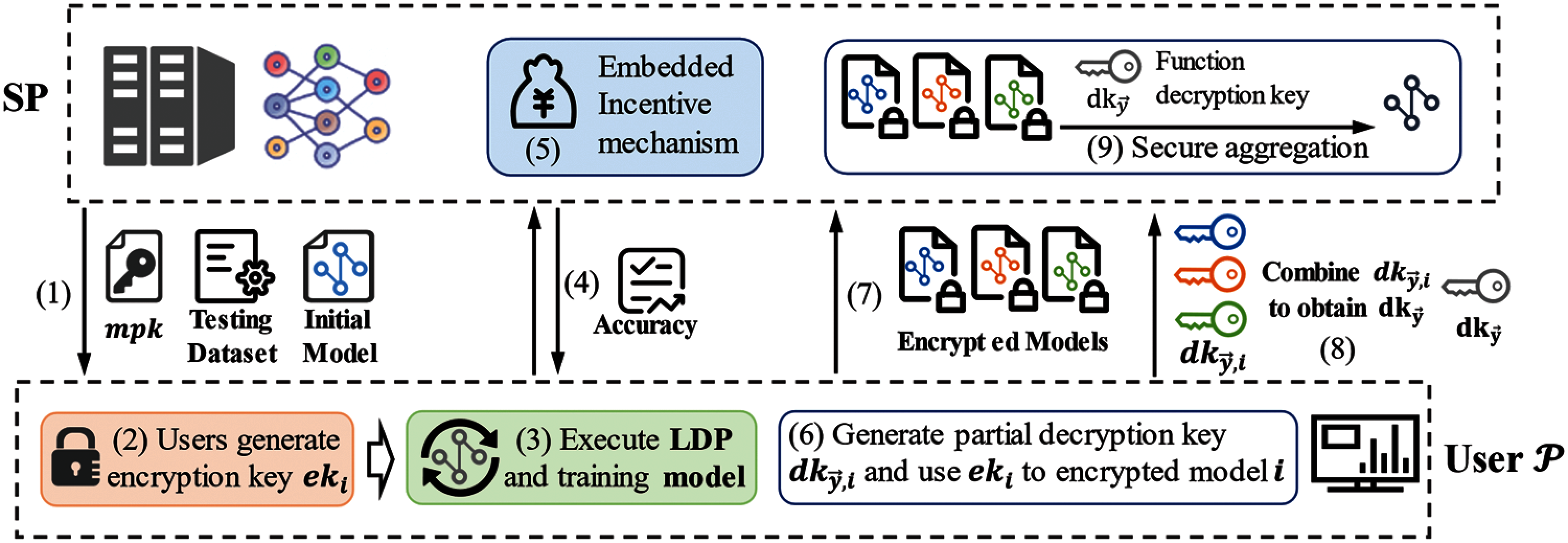
Figure 1: System architecture of Fed-DFE

Step 1. Initialize model and distribute mpk: Prior to iteration training, SP separately generates the initial model, scoring rules, and master public key (mpk). Among them, the structure of the initial model is the same as the user’s local model. We construct scoring rules based on the corresponding model. Generally, we use the classification model accuracy as the scoring rule for the incentive mechanism. In addition, SP also generates the master public key (mpk) according random number λ. Finally, SP sends the initialized model, the mpk and the scoring rules to each user.

Step 2. Execute Setup protocol: Each user generates own encryption key eki using the master public key mpk, and all users interact with each other to generate Ti(∑inTi=0). Then, each user generates the respective private key ski by Ti and the encryption key eki.

Step 3. Encrypt model: After training the local model xi, each user encrypts the local model xi to obtain the encrypted model [ci]1, using their respective encryption key eki and the Label delivered by SP.

Step 4. Generate partial decryption key: Each user generates the partial decryption key dky→,i using the private key ski and the weights y→ of the inner product function Fy→(x→)=⟨x→,y→⟩. Then, each user sends the partial decryption key dky→,i and encrypted model [ci]1 to SP.

Step 5. Generate function decryption key: SP receives partial decryption key dky→,i and encrypted model [ci]1 from all users. Then SP combines all the partial decryption key dky→,i to obtain the function decryption key dky→, and the function decryption key dky→ can aggregate model without decrypting the user’s encrypted model [ci]1.

Step 6. Execute model secure aggregation: SP calculates the discrete logarithm to directly obtain the aggregation result α, using the function decryption key dky→, the encrypted model [ci]1, and the Label.

We integrate the DMCFE algorithm into the training process of federated learning. Each user encrypts the local model using the Encrypt algorithm in DMCFE. SP executes secure aggregation directly through the Decrypt algorithm and function decryption key dky→. Differing from traditional function encryption, the DMCFE algorithm does not rely on TTP in the whole process. Thus, it avoids the collusion problem of SP and TTP. In the following, Algorithm 1 further illustrates the computational details of the DMCFE algorithm.

4.3 Local Differential Privacy for Fed-DFE

In our proposed Fed-DFE, to allow local users to freely choose the appropriate level of privacy preserving, we design a local differential privacy based on Gaussian noise mechanism. according to the privacy preserving requirement, each user can independently determine noise parameters and privacy budget in the Gaussian noise mechanism. Then, users also can use moment accountant method [24] to track privacy loss of local model. Compared to the standard combination theorem [25], this method considers the specific noise distribution in a specific situation. It can more accurately calculate the privacy loss that occurs in the differential privacy.

Specifically, the privacy loss c(o;M,aux,d,d′) at the outcome o∈R of mechanism M be defined as c(o;M,aux,d,d′)≜logPr[M(aux,d)=o]Pr[M(aux,d′)=o], where d and d′ are the adjacent datasets, and aux is the auxiliary input. To continuously apply the differential privacy mechanism in each model update, we define λth moment αM(λ;aux,d,d′)≜logEo∼M(aux,d)[exp⁡(λc(o;M,aux,d,d′))] for λ≤32. To ensure that differential privacy guarantees of M, we take the maximum bound of αM(λ;aux,d,d′) as the moment bound αM(λ)≜maxaux,d,d′αM(λ;aux,d,d′).

Theorem. Tail bound. For any ε>0, the mechanism M satisfies the (ϵ,δ)-differential privacy for

δ=minλexp⁡(αM(λ)−λε) (3)

Finally, according to Eq. (3), we use the standard Markov inequality to convert the moment bound αM(λ) into tail bound that satisfies the (ϵ,δ)-local differential privacy and represents the privacy loss. δ is a fixed threshold; if the privacy loss calculated by moments accountant method reaches this threshold, it means that the probability of the user model leaking privacy becomes too high and the training will stop.

LDP provides a flexible privacy-preserving mechanism for local users. Each user can decide for itself the privacy-preserving budget and the noise parameter. Users often subjectively choose to overestimate the privacy budget in practice, which reduces global model accuracy. Thus, the researchers introduce incentive mechanisms in the LDP that can encourage users to select appropriate privacy budgets.

4.4 Incentives Mechanism for Fed-DFE

It is easy to obtain public parameters for evaluating user contribution in incentive mechanism of traditional federated learning. However, the data is no longer readable when Fed-DFE encrypts the model parameters, making the implementation of the traditional incentive mechanism difficult. Accordingly, we design an incentive mechanism for function encryption. It models and evaluates the real parameters affecting the accuracy of the model. We define the utility functions of the server and the user separately and perform a simple analysis of how the Nash equilibrium is finally reached.

We assume that all users are rational in our incentive mechanism. They have a lower limit of acceptable privacy protection pri_. Before local model is uploaded to the server, users perform LDP with the appropriate privacy budget budg and noise parameters nois to suit their privacy protection requirements pri(budg,nosi)≥pri_. The user evaluates the model accuracy Acc of LDP on the test dataset and uploads Acc to the server as a bid. The server selects the k users with the highest accuracy to participate in federated learning and rewards the selected users. The specific steps are shown in the Fig. 2.

(1) During the iteration of federated learning, the server issues an initial model to each user. Meanwhile, the server publishes a public test dataset to assess the quality of local models.

(2) After receiving the initial model and the test dataset, each user selects its own privacy budget budg and noise parameters nosi of LDP to protect the local model based on their data quality, data distribution characteristics, and privacy protection requirements. The user adjusts the privacy-preserving parameters so that the privacy-preserving local model gets the appropriate accuracy Acc on the test dataset and sends it to the server for bidding. The user’s utility function is

Utilit y use r i ={ reward(Ac c i )−risk(pri(buge, nosi)), use r i  is one of top−k users 0, elsewise (4)

where reward(Acc) is the reward from the SP, and risk(pri(buge,nosi)) is the risk cost of user privacy exposure.

(3) After SP receives bids from all users and selects the k users with the highest accuracy rate to participate in federated learning. SP assigns aggregation weights based on user accuracy and distributes aggregation weights along with the list of selected users.

(4) The user interacts with other users to generate the partial decryption key. The partial decryption key contains information about the weight of each user in model aggregation. The user then sends the partial decryption secret key and the encrypted model to the server.

(5) SP combines all the partial decryption keys to generate a function decryption key. The function decryption key is used to perform operations with the encrypted model to obtain the plaintext of the aggregated model. SP then evaluates the aggregated model on a test dataset. If the accuracy of aggregated model meets the requirements, SP will pay a reward to the users who participated in the training. The utility function of the server is

UtilitySP=profit(Accglobal)−∑i=1krewardi (5)

where profit(Accglobal) is profits from global accuracy improvement, and rewardi is the reward of useri.

(6) If the accuracy of the model is much lower than expected, it is possible that some users are passing off a low-accuracy model as a high-accuracy model. SP will drop this training and mark the users who participated. Malicious users accumulate more marks and a poorer reputation over the long term. In later tasks, SPs can ban the participation of users with low reputation. In addition, some researchers have used zero-knowledge proofs to bind the accuracy of encrypted models [26]. These methods can also prevent the falsification problem of contributions. However, since this is more distantly related to incentives, we will not describe it in detail in this paper.

To get more rewards, users improve the accuracy of their local models as much as they can while satisfying their privacy protection lower limit. On the other hand, SPs reduce the total expenses while the accuracy of the global model meets its target requirements, thus avoiding an unrestricted thirst for data. Through multiple iterations, both the server and the user can find the most appropriate policy for themselves and thus reach a Nash equilibrium.

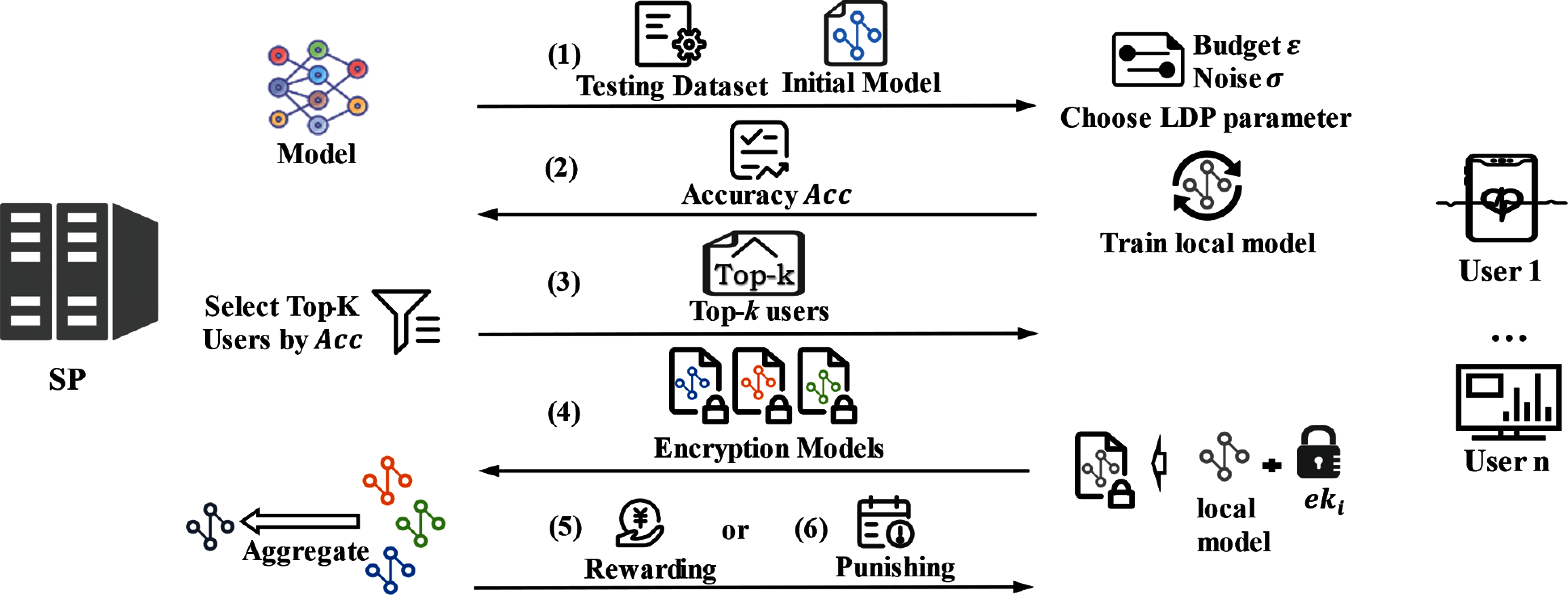
Figure 2: The incentives mechanism for Fed-DFE

5  Security and Privacy Analysis

In this section, we conduct security and privacy analysis on the proposed scheme.

5.1 Security Analysis of Fed-DFE

To prevent gradient inversion attacks, researchers typically utilize cryptographic methods to encrypt their models in federated learning. Function encryption has attracted a wide attention for its high-efficiency and security properties [12]. It only allows SP to obtain the aggregated gradient, but not the individual gradient. However, traditional functional encryption methods, such as Inner Product Function Encryption (IPFE), Multi Input Function Encryption (MIFE), and Function Hiding Multi Input Encryption (FHMIE), require a TTP to generate, distribute and manage the keys. Malicious SP may collude with TTP through a secret trade of benefits. Through the collusion attack, the malicious SP can obtain key parameters that do not belong to it, or even obtain the user’s key directly. With the keys, it is easy for the malicious SP to crack the user’s encrypted gradient and reverse the user’s privacy.

To prevent collusion attacks, we utilize a decentralized multi-client function encryption algorithm. In this algorithm, the SetUp protocol in Algorithm 1 is executed interactively by the users to replace the TTP in traditional function encryption. Each user generates encryption keys s→i←Zp2(i∈[n]) and parameters Ti←Zp2×2(∑i∈[n]Ti=0). Next, users utilize ski=(s→i,Ti) as the private key, and they compute the partial decryption key dky→,i:=([d→i]2) by using the weight yi of the inner product function Fy→(x→)=⟨x→,y→⟩. Then, SP combines all the partial decryption keys dky→,i:=([d→i]2) to obtain dky→:=(y→,∑i∈[n][d→i]2). The DMCFE scheme decentralizes the authority of generating keys to all users. Thus, the DMCFE ensures the security of the keys, and also prevents malicious TTP and SP from executing collusion attacks.

Rather than simply allowing multiple users to generate keys, DMCFE requires adherence to a parameter exchange protocol between users. The parameter exchange protocol is based on the Decisional Diffie-Hellman assumption, the DDH assumption means that, in a prime-order group G←GGen(1λ), for the following distributions

{([a],[r],[ar])|a,r←Zp}and{([a],[r],[s])|a,r,s←Zp} (6)

there is no probabilistic polynomial-time (PPT) adversary can distinguish them with non-negligible advantage [22]. Therefore, decentralized does not reduce the security of function encryption.

5.2 Privacy Analysis of Fed-DFE

Function encryption prevents the server or a third party from obtaining the plaintext of individual gradients and effectively resists the gradient inversion attack. Nevertheless, the attacker can still execute inference attacks on the aggregated model, combined with background knowledge. After adding the noise of Gaussian distribution N(0,Sf2⋅σ2) using differential privacy, we need to calculate the probability that the privacy loss exceeds the privacy budget by the formula δ=minλexp⁡(αM(λ)−λε), where ε denotes the privacy budget, αM(λ) denotes the privacy loss, and δ denotes the threshold value. When the result of minλexp⁡(αM(λ)−λε) exceeds the threshold δ, it means that the model with added noise can make the attacker unable to distinguish the presence of privacy attributes. However, users often set more strict differential noise for subjective reasons, resulting in unnecessary degradation of global model accuracy.

In practice, researchers often use the incentives to encourage users to submit high-quality model gradients, that is, appropriate reductions of differential privacy noise. In this process, we provide each user with a utility function Utilityuseri=reward(Acci)−risk(pri(buge,nosi)). Users can compare the reward SP provides with the cost of privacy leakage risk, and then decide whether to reduce the privacy protection noise. It is worth noting that if the reward is increased infinitely, will there be a problem of users not adding differential privacy noise? For this reason, we have established the assumption that users are rational. They will set a differential privacy noise floor for themselves pri_, and will not participate in the federated learning when the noise is lower than the actual privacy requirement pri(budg,nosi)<pri_. In reality, these regulations can be prescribed by laws and policies that enable SPs and users to optimize model accuracy within certain privacy-preserving rules.

6  Experiment and Analysis

In this section, we discuss the experimental results and evaluate the performance of the incentive mechanism.

6.1 System Setup

We implemented a prototype of federated learning. The prototype is developed based on TensorFlow and its architecture is similar to [21]. We deploy SP on a server that includes 2×Hygon-C86-7159, 236G DDR, 5T SSD, and Linux Centos 7 OS. We conducted experiments on the MNIST dataset, which consists of 60,000 training examples and 10,000 testing examples. The size of each image is 28 ∗ 28. We separated the MNIST into 100 sub-datasets to simulate the corresponding users. Under the setting of different users, we studied the influence of the incentive mechanism on the performance of federated learning. We apply a CNN model with 6 neural network layers. Its structure includes: 2 Convolutional layers, 2 Maxpooling layers, 1 Dense layer, and 1 Logits layer. In the performance of DMCFE, our baseline is the classical inner product function encryption scheme. In the performance of incentive mechanism, our baseline is the federated learning based on local differential privacy without incentive mechanism.

6.2 Performance of the DMCFE

We implement the DMCFE algorithm in Fed-DFE and evaluate its performance in different numbers of users. And then, we compared the overhead of other function encryption algorithms with DMCFE algorithm in one time encryption and decryption process. Our comparison schemes include Inner Product Function Encryption (IPFE), Multi Input Function Encryption (MIFE), Function Hiding Multi Input Encryption (FHMIE), Function Hiding Inner Product Encryption (FHIPE) and Decentralizing Inner-Product Functional Encryption (DIPFE). Tab. 1 shows the overhead of various encryption algorithms under different size of users. The overhead of the encryption algorithm includes overall encryption overhead (Enc) and decryption overhead (Dec). Among all comparative cryptography algorithms, the decryption overhead of MIFE and FHIPE is even 2 times higher than other algorithms. While the number of users reached 40, the decryption overhead of MIFE and FHIPE algorithms reached 3.618s and 3.773s, respectively. In decentralized schemes, the Dec of DIPFE and DMCFE is close, but the DMCFE maintains lower Enc. By comparison, the decryption overhead of our DMCFE algorithm only takes up 0.699s.

Fig. 3 visualizes the encryption and decryption overheads of different encryption algorithms. Generally, model encryption process is performed independently by users in federated learning, thus the overhead increases linearly as the number of users. Different from the encryption process, the decryption process is generally performed by the SP, the growth trend of the decryption overhead is more significant. Among all the algorithms, the FHIPE algorithm has the least encryption overhead, but its decryption overhead is higher than others. Since the inner product of the DMCFE is calculated by using pairings to solve the discrete logarithm problem. Our DMCFE algorithm has a slightly higher encryption overhead than FHIPE, however, both its decryption overhead is lower than all other algorithms. Thus, it still has a great advantage over other algorithms in overall overhead.

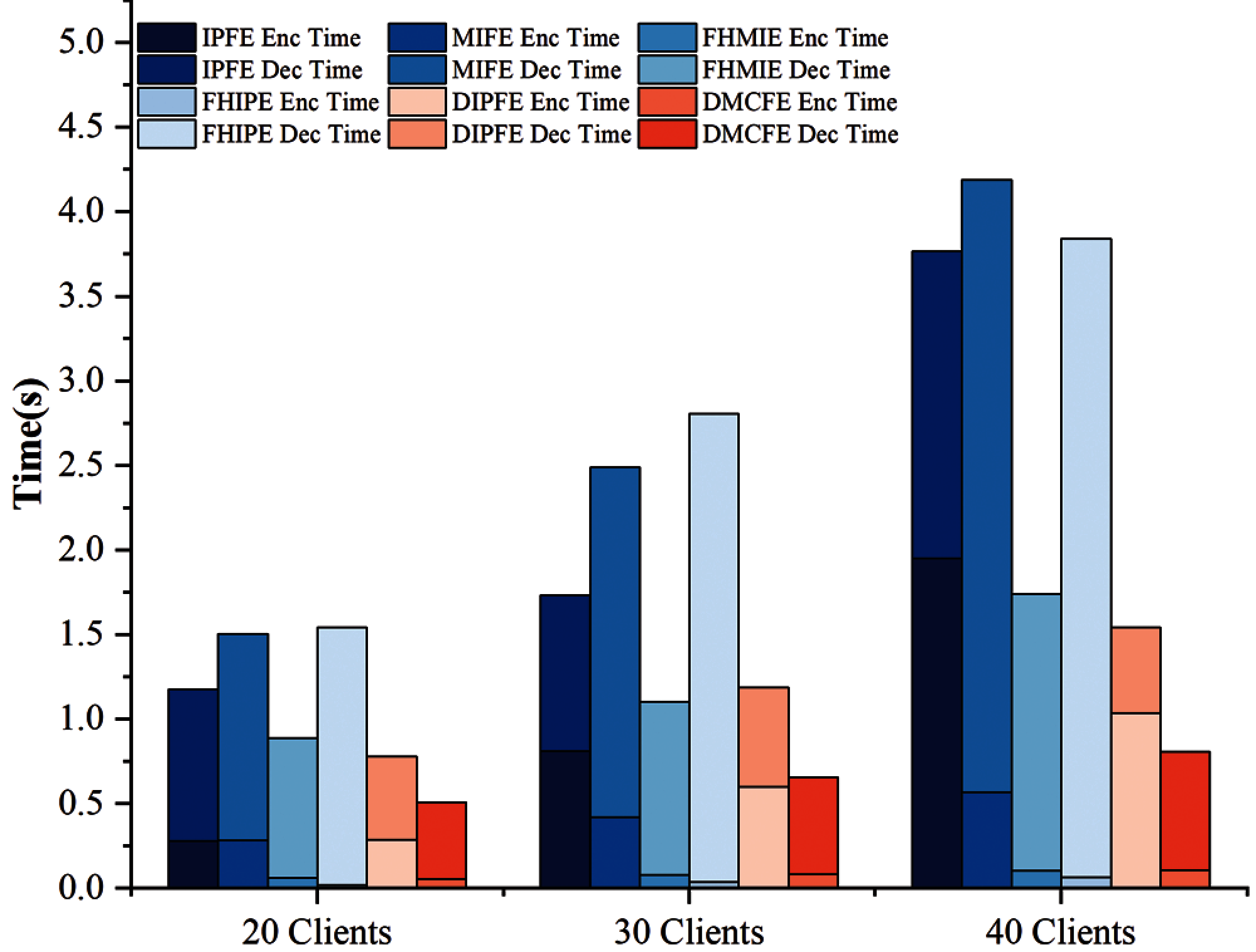
Figure 3: The overhead of different encryption algorithms

6.3 Performance of Incentive Mechanism

To verify the effect of the incentive mechanism, we conduct experiments with different privacy budgets (eps) and different noise parameters under the size of 20, 30, and 40 users, respectively. We set each user to hold the same sample number, which can exclude the effect of additional factors. The elements that impact our incentive mechanisms include local model accuracy, privacy budget, noise parameter. Among these, local model accuracy is obtained by users training on the test samples. Next, we observe the effect of privacy budget and noise parameters on incentive mechanisms separately.

6.3.1 The Impacts of Privacy Budget

The privacy budget is an important parameter in differential privacy, which is used to accumulate the privacy loss incurred during iterative training. A smaller privacy budget means a stricter privacy guarantee, and smaller privacy budget reduces global model accuracy. We adjust the moment accountant method to LDP mechanism to accumulate the privacy loss of each user. The impact of privacy budget on the model accuracy is shown in Tab. 2. We use Non-Fed-DFE to indicate the baseline, which means without applying the incentive mechanism scheme. In Non-Fed-DFE, with the privacy budget of 50 and the noise parameter of 1, the global model accuracy can only reach 95.48% when 20 users. After we utilize the incentive mechanism in Fed-DFE, we allow all users to randomly select own privacy budget from the privacy budget range 36--45. It means Fed-DFE uses a stricter privacy guarantee than Non-Fed-DFE. To ensure that experimental results are only affected by the privacy budget, all users set the same noise parameter. In the size of 20, 30, and 40 users, our experimental results are higher than the baseline Non-Fed-DFE. For 20 users, the model accuracy is up to 97.86%. We also set the step size to 5 and stepwise decrease the privacy budget range to 21--30. At different privacy budget ranges, we separately test the model accuracy.

Fig. 4 visualizes the trends of model accuracy across the different privacy budget ranges for 20, 30, and 40 users. In the case of 20 and 30 users, the model accuracy is consistently higher than the Non-Fed-DFE, regardless of the privacy budget range. Since in differential privacy theory, a smaller privacy budget means tighter privacy protection. As the number of clients increases and the privacy budget decreases, the quality of the user’s model becomes worse. Therefore, for 40 users, the model accuracy is still higher than the baseline when the privacy budget range drops to 26--35. The experimental results indicate that our incentive mechanism is effective, and the selected users provide high-quality models.

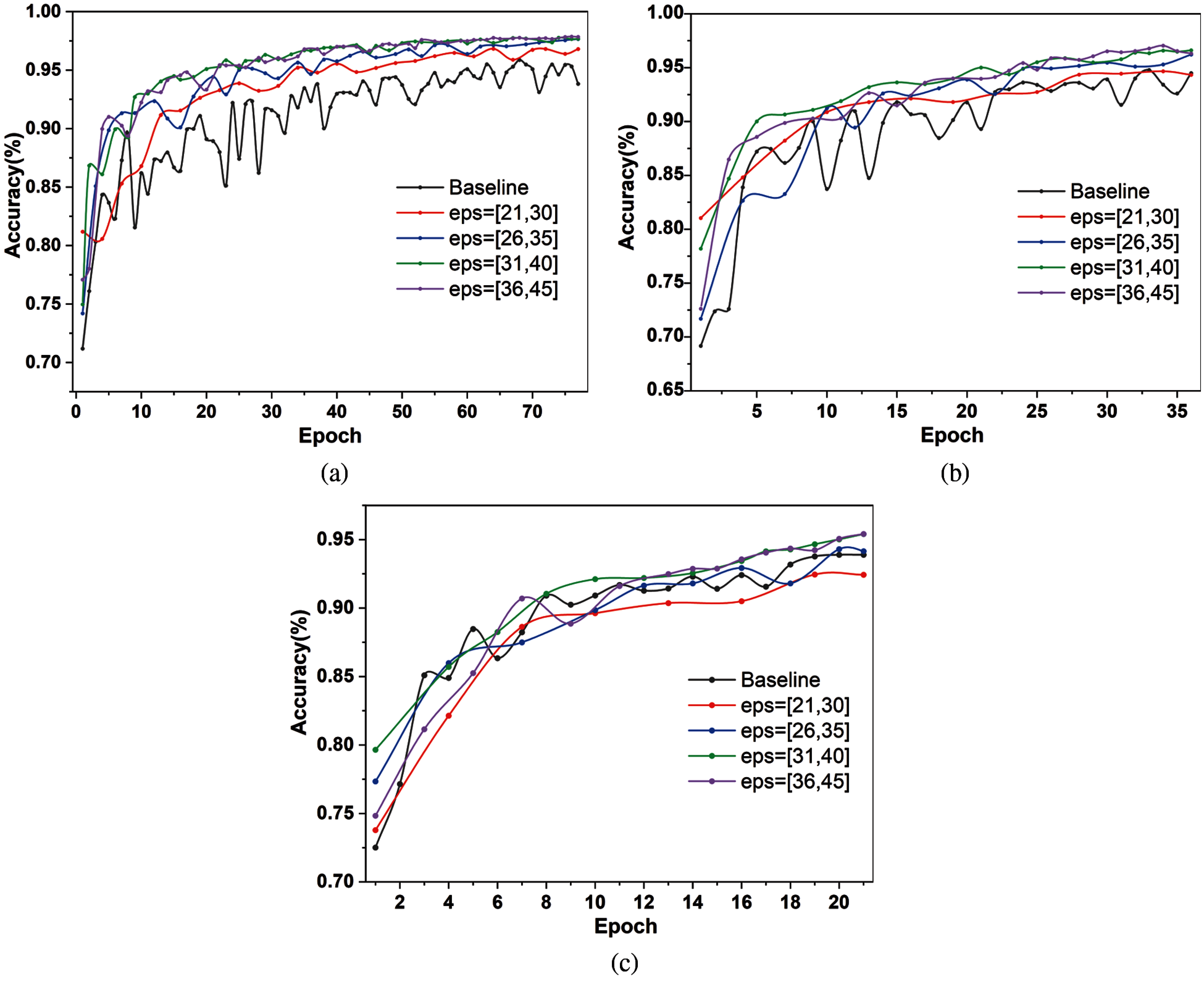
Figure 4: The accuracy of model when varying privacy budget range. (a) For 20 users. (b) For 30 users. (c) For 40 users

6.3.2 The Impacts of Noise Parameter

In differential privacy, we adjust the amount of noise added to the model by the noise parameter σ. For a fixed number of users and privacy budget, the smaller the noise parameter, the smaller the range of data perturbation caused by adding noise. To evaluate the impact of the noise parameter σ on the model accuracy, we specify the same privacy budget for each user. It means that model accuracy is only affected by the noise parameter in the incentive mechanism. By stepwise decreasing the range of noise parameter σ, we observe the trend in model accuracy change. In the case of 20 and 30 users, the experimental results are shown in Tab. 3. With 30 users and the privacy budget of 45, our Fed-DFE greatly improves the model accuracy up to 96.77%. Meanwhile, noise parameter σ is significantly being reduced by up to 10%.

We first study the effect of the noise parameter when the number of users is 40. As shown in Fig. 5a, we specify the privacy budget as 35, and observe the trend of model accuracy by varying the range of noise parameters. By analyzing our utility function, users usually choose smaller noise parameters to provide high-quality models in exchange for rewards. When the noise parameter ranges were 0.9--0.99 and 0.86--0.95, the model accuracy with the incentive machine is higher than the baseline. This means that our incentive mechanism encourages users to choose smaller noise parameters. To verify the effect of the incentive mechanism on the noise parameters under different privacy budgets. Figs. 5b and 5c show the trends for privacy budgets of 40 and 45, respectively. With the above two privacy budgets, the final model accuracy is still higher than baseline. This proves that our incentive mechanism can effectively improve the model accuracy.

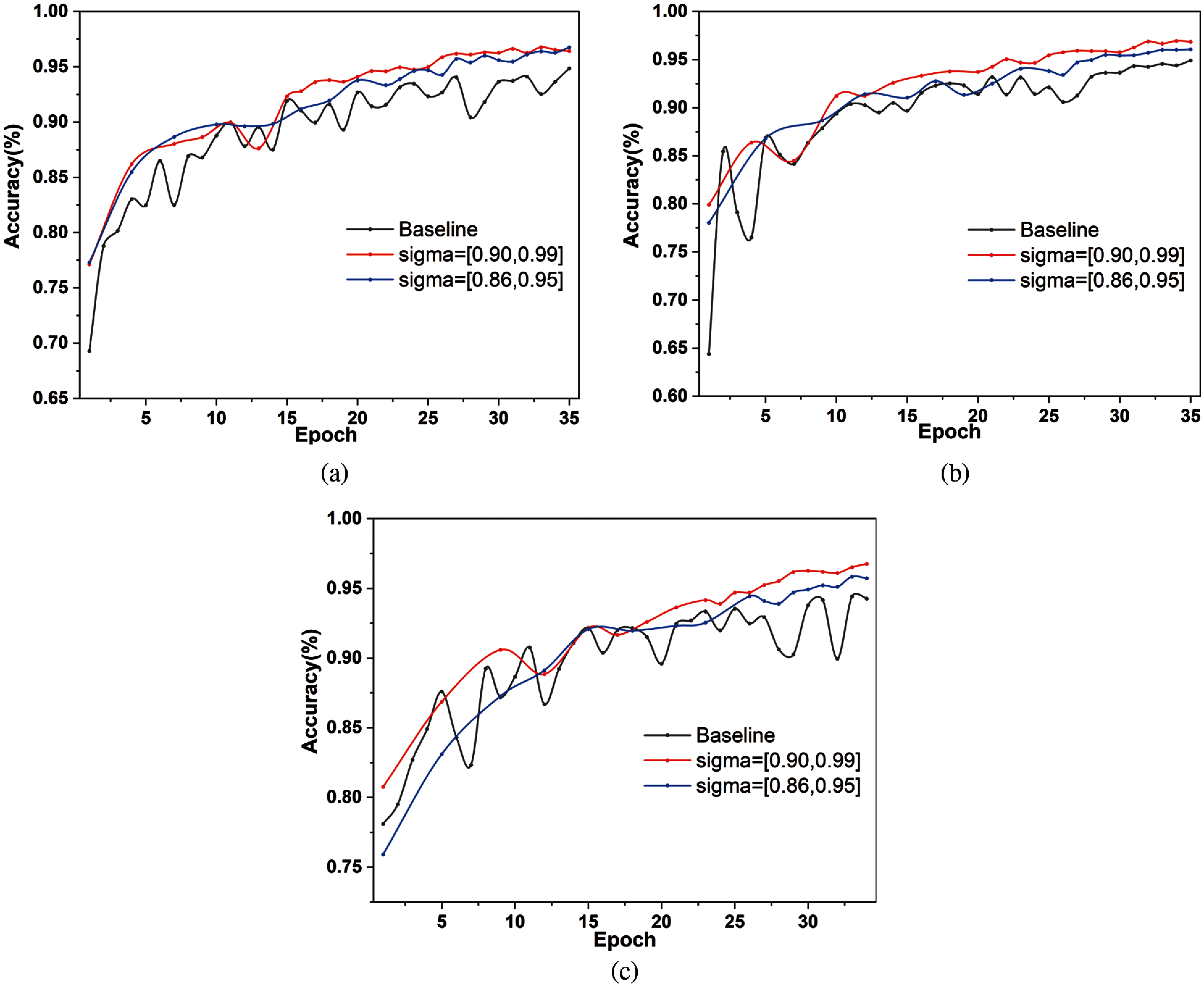
Figure 5: The accuracy of model when varying noise parameter in 40 users. (a) with eps = 35. (b) with eps = 40. (c) with eps = 45

Then, we further verify the effectiveness of our incentive mechanism in the case of 30 users. As show in Fig. 6, we only adjust the number of users to 30 and set the other parameters the same as in Fig. 5. Regardless of the privacy budget, the final model accuracy with the incentive mechanism is higher than the baseline. By conducting experiments with different numbers of user and different privacy budgets, we indicate that our incentive mechanism is effective in encouraging users to improve the model quality.

Figure 6: The accuracy of model when varying noise parameter in 30 users. (a) with eps = 35. (b) with eps = 40. (c) with eps = 45

7  Conclusion

In this paper, we designed, implemented, and evaluated a privacy-preserving federated learning scheme, termed Fed-DFE, which integrated function encryption, local differential privacy and incentive mechanisms. It could help users prevent gradient leakage and improve the accuracy of the global model. Specifically, we generated keys through the interaction between the server and users, which is an alternative to the method generated by TTP in traditional function encryption. Each user’s secret key is managed on its own, avoiding the problem of collusion between TTP and the server. Further, we designed an embedded incentive mechanism for function encryption and local differential privacy, which could find a trade-off between privacy protection and model accuracy. We conducted experiments to evaluate the performance of the decentralized function encryption, and the impact of our chosen parameters on the incentive mechanism.

Funding Statement: This work was supported in part by the National Key R&D Program of China (No. 2018YFB2100400), in part by the National Natural Science Foundation of China (No. 62002077, 61872100), in part by the China Postdoctoral Science Foundation (No. 2020M682657), in part by Guangdong Basic and Applied Basic Research Foundation (No. 2020A1515110385), in part by Zhejiang Lab (No. 2020NF0AB01), in part by Guangzhou Science and Technology Plan Project (202102010440).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Li, G. Sun, H. He, Y. Jiang, R. Sui et al., “Gender forecast based on the information about people who violated traffic principle,” Journal on Internet of Things, vol. 2, no. 2, pp. 65–73, 2020. [Google Scholar]

 2.  S. Su, Z. Tian, S. Liang, S. Li, S. Du et al., “A reputation management scheme for efficient malicious vehicle identification over 5G networks,” IEEE Wireless Communications, vol. 27, no. 3, pp. 46–52, 2020. [Google Scholar]

 3.  J. Park and S. Kim, “Noise cancellation based on voice activity detection using spectral variation for speech recognition in smart home devices,” Intelligent Automation & Soft Computing, vol. 26, no. 1, pp. 149–159, 2020. [Google Scholar]

 4.  Z. Tian, X. Gao, S. Su, J. Qiu, X. Du et al., “Evaluating reputation management schemes of internet of vehicles based on evolutionary game theory,” IEEE Transactions on Vehicular Technology, vol. 68, no. 6, pp. 5971–5980, 2019. [Google Scholar]

 5.  Z. Liu, X. Qiu, S. Zhang, S. Deng and G. Liu, “Service scheduling based on edge computing for power distribution IoT,” Computers, Materials & Continua, vol. 62, no. 3, pp. 1351–1364, 2020. [Google Scholar]

 6.  P. Xia, A. Xu and T. Lian, “Analysis and prediction of regional electricity consumption based on BP neural network,” Journal of Quantum Computing, vol. 2, no. 1, pp. 25–32, 2020. [Google Scholar]

 7.  O. B. Sezer and A. M. Ozbayoglu, “Financial trading model with stock bar chart image time series with deep convolutional neural networks,” Intelligent Automation & Soft Computing, vol. 26, no. 2, pp. 323–334, 2020. [Google Scholar]

 8.  E. Qi and M. Deng, “R&D investment enhance the financial performance of company driven by big data computing and analysis,” Computer Systems Science and Engineering, vol. 34, no. 4, pp. 237–248, 2019. [Google Scholar]

 9.  A. Li, Y. Duan, H. Yang, Y. Chen and J. Yang, “TIPRDC: Task-independent privacy-respecting data crowdsourcing framework for deep learning with anonymized intermediate representations,” in Proc. of the 26th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining (KDD’20Virtual Event, CA, USA, pp. 824–832, 2020. [Google Scholar]

10. Z. Wang, M. Song, Z. Zhang, Y. Song, Q. Wang et al., “Beyond inferring class representatives: User-level privacy leakage from federated learning,” in Proc. of IEEE Conf. on Computer Communications (IEEE INFOCOMParis, France, pp. 2512–2520, 2019. [Google Scholar]

11. J. Zhang, B. Chen, S. Yu and H. Deng, “PEFL: A privacy-enhanced federated learning scheme for big data analytics,” in Proc. of 2019 IEEE Global Communications Conf. (GLOBECOMWaikoloa, HI, USA, pp. 1–6, 2019. [Google Scholar]

12. R. Xu, N. Baracaldo, Y. Zhou, A. Anwar and H. Ludwig, “HybridAlpha: An efficient approach for privacy-preserving federated learning,” in Proc. of the 12th ACM Workshop on Artificial Intelligence and Security (AISec’19London, United Kingdom, pp. 13–23, 2019. [Google Scholar]

13. L. Yin, J. Feng, H. Xun, Z. Sun and X. Cheng, “A privacy-preserving federated learning for multiparty data sharing in social IoTs,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 3, pp. 2706–2718, 2021. [Google Scholar]

14. Y. Zhan, P. Li, Z. Qu, D. Zeng and S. Guo, “A learning-based incentive mechanism for federated learning,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 6360–6368, 2020. [Google Scholar]

15. Z. Sun, L. Yin, C. Li, W. Zhang, A. Li et al., “The QoS and privacy trade-off of adversarial deep learning: An evolutionary game approach,” Computers & Security, vol. 96, no. 6, pp. 101876, 2020. [Google Scholar]

16. R. Zeng, S. Zhang, J. Wang and X. Chu, “Fmore: An incentive scheme of multi-dimensional auction for federated learning in MEC,” in Proc. of 2020 IEEE 40th Int. Conf. on Distributed Computing Systems (ICDCSSingapore, Singapore, pp. 278–288, 2020. [Google Scholar]

17. K. Bonawitz, V. Ivanov, B. Kreuter, A. Marcedone, H. B. McMahan et al., “Practical secure aggregation for privacy-preserving machine learning,” in Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security (CCS’17Dallas, Texas, USA, pp. 1175–1191, 2017. [Google Scholar]

18. K. Ganju, Q. Wang, W. Yang, C. A. Gunter and N. Borisov, “Property inference attacks on fully connected neural networks using permutation invariant representations,” in Proc. of the 2018 ACM SIGSAC Conf. on Computer and Communications Security (CCS’18Toronto, Canada, pp. 619–633, 2018. [Google Scholar]

19. S. Truex, N. Baracaldo, A. Anwar, T. Steinke, H. Ludwig et al., “A hybrid approach to privacy-preserving federated learning,” in Proc. of the 12th ACM Workshop on Artificial Intelligence and Security (AISec’19London, United Kingdom, pp. 1–11, 2019. [Google Scholar]

20. L. U. Khan, S. R. Pandey, N. H. Tran, W. Saad, Z. Han et al., “Federated learning for edge networks: Resource optimization and incentive mechanism,” IEEE Communications Magazine, vol. 58, no. 10, pp. 88–93, 2020. [Google Scholar]

21. J. Kang, Z. Xiong, D. Niyato, S. Xie and J. Zhang, “Incentive mechanism for reliable federated learning: A joint optimization approach to combining reputation and contract theory,” IEEE Internet of Things Journal, vol. 6, no. 6, pp. 10700–10714, 2019. [Google Scholar]

22. J. Weng, J. Weng, J. Zhang, M. Li, Y. Zhang et al., “Deepchain: Auditable and privacy-preserving deep learning with blockchain-based incentive,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 5, pp. 2438–2455, 2021. [Google Scholar]

23. J. Chotard, E. D. Sans, R. Gay, D. H. Phan and D. Pointcheval, “Decentralized multi-client functional encryption for inner product,” in Int. Conf. on the Theory and Application of Cryptology and Information Security (ASIACRYPT 2018Brisbane, Queensland, Australia, pp. 703–732, 2018. [Google Scholar]

24. M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov et al., “Deep learning with differential privacy,” in Proc. of the 2016 ACM SIGSAC conf. on computer and communications security (CCS’16Vienna, Austria, pp. 308–318, 2016. [Google Scholar]

25. C. Dwork and A. Roth, “The algorithmic foundations of differential privacy,” Foundations and Trends in Theoretical Computer Science, vol. 9, no. 3--4, pp. 211–407, 2014. [Google Scholar]

26. Y. Lu, X. Huang, Y. Dai, S. Maharjan and Y. Zhang, “Blockchain and federated learning for privacy-preserved data sharing in industrial IoT,” IEEE Transactions on Industrial Informatics, vol. 16, no. 6, pp. 4177–4186, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.