DOI:10.32604/cmc.2022.015378

| Computers, Materials & Continua DOI:10.32604/cmc.2022.015378 |  |
| Article |
Research on Optimization of Random Forest Algorithm Based on Spark
1Hebei University of Economics and Business, Shijiazhuang, 050061, China
2Griffith University, Brisbane, 4222, Australia
*Corresponding Author: Zhanfeng Zhang. Email: zhzf_cs@163.com
Received: 18 November 2020; Accepted: 04 March 2021
Abstract: As society has developed, increasing amounts of data have been generated by various industries. The random forest algorithm, as a classification algorithm, is widely used because of its superior performance. However, the random forest algorithm uses a simple random sampling feature selection method when generating feature subspaces which cannot distinguish redundant features, thereby affecting its classification accuracy, and resulting in a low data calculation efficiency in the stand-alone mode. In response to the aforementioned problems, related optimization research was conducted with Spark in the present paper. This improved random forest algorithm performs feature extraction according to the calculated feature importance to form a feature subspace. When generating a random forest model, it selects decision trees based on the similarity and classification accuracy of different decision. Experimental results reveal that compared with the original random forest algorithm, the improved algorithm proposed in the present paper exhibited a higher classification accuracy rate and could effectively classify data.
Keywords: Random forest; spark; feature weight; classification algorithm
The rapid development of the Internet has led to the continuous generation of different types of data in various industries. As such, the question of how to obtain valuable information from the massive data through data mining has become a focus of attention. As a classification algorithm in data mining, the random forest algorithm [1], is widely used in credit evaluation {[2–4]}, image classification [5,6], text classification [7], among others. This can be attributed to it being better at avoiding over-fitting without being sensitive to noise values. Research into the random forest algorithm, have mainly focused on the relationship between the classification interval of the classifier and the analysis of its generalization ability, while proposing a random forest pruning algorithm based on the classification interval weighting [8]. Further, an interval weighted voting method was advanced [9], and a weighted random sampling was used to filter out features with minimal information in the selection process [10]. In order to select the important features for decision tree splitting, weights were assigned to feature values and subspaces were constructed according to the mean of the weights, thereby improving the classification effect of the algorithm [11].
As a memory-based distributed computing platform, Spark has significantly poweful computational efficiency, and the high parallelism of the random forest algorithm also means that the algorithm is quite suitable for integration into the Spark platform for parallel computing as a means to increase the computing speed of the algorithm and increase data processing efficiency.
Several scholars have conducted research related to the random forest algorithm based on Spark. A method relying on similarity calculations and feature similarity graphs was proposed to optimize the performance of random forest from the perspective of feature selection [12]. Additionally, a random forest algorithm based on rough set theory was also considered [13]. Here, this algorithm calculated the importance of attributes based on a discernibility matrix and selected the first several attributes with the highest importance to form the feature subspace. Related research has also been conducted on randoms forest while processing high-dimensional data, and a hierarchical subspace implementation was proposed to provide a solution for the issue where random forest algorithms cannot distinguish feature correlation when processing high-dimensional data [14].
In the present study, founded on the Spark framework, the feature subspace generation of the random forest algorithm was used as a starting point, and the feature subspace generation was optimized to achieve the purpose of optimizing the random forest algorithm.
The main research conducted for the present paper includes the following parts:
a. Theoretical research on the random forest algorithm
b. Research on optimizing the feature subspace of the random forest algorithm
c. Parallel implementation of the random forest algorithm based on Spark.
As a distributed computing and processing platform similar to Hadoop, Spark uses the concept of Shuffle to implement distributed computing. Hence, Spark differs from Hadoop in that calculations are performed based on memory and the intermediate output and results from tasks are saved in the memory, thereby saving a significant amount of disc access overhead and effectively improving the efficiency of data reading and writing.
The basic ecosystem of Spark is shown in Fig. 1.
As shown in Fig. 1, the Spark ecosystem primarily includes:
Spark SQL: primarily used for data query analysis and processing;
Spark Streaming: primarily used for stream computing;
Spark MLlib: primarily used for machine learning;
Spark GraphX: primarily used for graph computing.
The components above and Apache Spark form the Spark ecosystem.
The most basic data structure is Resilient Distributed Dataset (RDD) and is the most fundamental operational unit in Spark [15]. This data set has a certain scalability and supports parallel processing. RDD adopts a delay computing system and supports two operations: conversion and action. The calculation will only proceed when there is an absolute necessity for the results to be returned to the RDD. This lazy operation mode also effectively improves calculation efficiency. In addition, Spark provides users with richer and simpler operations, including creation operations, conversion operations, control operations, and mobile operations to allow developers to fully utilize these operators to operate on RDD. Due to the high computing efficiency inherent in Spark, the application research for Spark is considerably extensive, including large-scale text analysis [16], large-scale data mining [17], etc.

Figure 1: Spark ecosystem
The random forest algorithm is an ensemble algorithm that utilizes decision trees as the classifiers, and in this algorithm, the random forests are composed of multiple decision trees. As a classifier, the decision tree is similar to an inverted tree structure. Starting from the root node, the nodes are split according to the split rules until the decision tree is generated. In the decision tree, the leaf node is generated by splitting the data sample according to a certain attribute, which represents a class label, and the path from the root node to the leaf node represents a certain decision process [18].
A decision tree has the characteristics inherent in a simple model and easily implemented, yet it is prone to defects, such as over-fitting and the inability to guarantee the global optimum when classifying. Therefore, stemming from the characteristics of the decision tree algorithm, the random forest algorithm was created. The random forest algorithm combines multiple decision trees to improve classification accuracy for the algorithm and avoid phenomena such as over-fitting [19].
The random forest algorithm is primarily concerned with solving the over-fitting phenomenon and optimal issues that easily occur when a single decision tree is classified. The principal reasons for solving these problems are as follows:
(a) The random forest algorithm obtains a sample subset through random replacement sampling to ensure the randomness and diversity of the training samples of the decision tree.
(b) The random forest algorithm provides optional feature attributes for node splitting by randomly extracting feature subsets, ensuring the difference of varieties of decision trees in the generation process.
(c) When the random forest algorithm classifies the final result, the final result is selected by combining multiple decision trees to vote, thereby preventing the algorithm from encountering local optimal and over-fitting problems.
3 Analysis of the Random Forest Algorithm
The advantages inherent to the random forest algorithm are notably due to the randomness of the decision tree training subset generated during the training process and the randomness of the decision tree feature subspace. This is why the classification accuracy of the decision tree and the differences between different decision trees are integral to the classifier, as has a significant impact on the quality of performance. To ensure the classification effects of the classifiers, the effectiveness and diversity of the training subset and feature subspace must be ensured to guarantee the classification strength of the decision tree and the differences between varieties of decision trees.
Feature subspace generation is a major step in the random forest algorithm. Meanwhile, the decision tree strength of the random forest algorithm and the difference between decision trees are also related to feature subspace generation. Although findings have been concluded that smaller feature subspaces lead to the greater the randomness and greater differences between decision trees, this will evoke less effective information and reduce the classification accuracy rate. Conversely, larger feature subspaces lead to more effective information a stronger classification effect for the decision tree. However, this will reduce the differences between decision trees and affect the classification accuracy of the algorithm.
On the other hand, due to the different classification capabilities of different decision trees, when performing random forest ensemble, fair voting will affect the overall classification effect of random forests. Due to this, the classification results should be treated differently for decision trees being exported with different classification effects.
To summarise, in the present study, for the purposes of ensuring the classification accuracy of the random forest algorithm while simultaneously ensuring the stability of the random forest algorithm, the feature importance was calculated, the features were distinguished, and then the feature subspace was generated based on the feature importance. This method could not only improve the classification strength of the decision tree, but also improve the overall classification effect inherent in the algorithm. Concurrently, the feature extraction with a weaker classification effect could be added to ensure the differences between different decision trees and the classification ability of the algorithm. Furthermore, when performing random forest model integration, different weights were assigned to decision trees with different classification strengths to increase the result weights of decision trees with strong classification abilities and improve the overall classification accuracy of the algorithm.
4 Improved Random Forest Algorithm W-RF
Regarding the traditional random forest algorithm, how classification accuracy influences redundant feature algorithms is not considered when forming the feature subspace, and the classification strengths of different decision trees are not distinguished. Therefore, a weighted random forest (W-RF) algorithm is proposed in the present paper. In this section, several pivotal parts of the W-RF algorithm will be described in detail: feature importance calculation, feature subspace generation, and decision-tree weight calculation.
4.1 Feature Subspace Generation Strategy Based on Feature Importance
In the node splitting stage of decision tree training, the traditional random forest algorithm is utilized to randomly extract several features from the data set to form a feature subspace and select a feature from the feature subspace for node splitting. To that end, feature subspace effectiveness must be ensured. Firstly, the features need to be distinguished. The Relief-F algorithm is a feature selection algorithm, and feature selection is performed by calculating the feature weight in the classification. The feature weight is measured by the differences between the neighboring points of the features of the same type and the neighboring points of different types. If a small difference is presented in a feature between samples of the same type and a large difference between samples of different types, this indicates that the distinguishing ability of the feature is high; otherwise, this indicates that the distinguishing ability of the feature is low. In the present study, the feature weight of the Relief-F algorithm was converted into feature importance for feature distinction.
The specific calculation process involved:
A sample Xi belonging to category C in the data set S was randomly selected. First, the k nearest neighbor samples in similar samples to Xi were found and recorded as Hj (j = 1, 2, 3,…, k), and then the k neighbor samples were extracted as Fdj (j = 1, 2, 3,…, k) from samples differing from Xi in the category sample set where d represents a different class from the class C that Xi belongs to, and the distance between Xi and Hj and Fdj was calculated. This process was repeated m times to obtain the feature importance of feature A.
The importance calculation method of feature A is shown in Eq. (1).
In Eq. (3), Pd is the proportion of class d samples in the data set. The calculation method is shown in Eq. (4).
After the feature importance W of all the features was calculated, the features could be sorted, and then the strong and weak features could be distinguished according to the importance of those features.
Once the importance of all the features was calculated, the features were classified, that is, a higher importance for a feature meant higher category relevance during classification and conversely, a lower importance for a feature meant lower category relevance during classification. Taking this into account, two disjoint feature sets could be obtained. Specifically, the feature set was divided into strong correlation features NS and weak correlation features NW according to the threshold
Upon distinguishing between strong and weak correlation features NS and NW, for the purpose of ensuring the effectiveness and differences of feature subspace when extracting features to form feature subspace, the traditional random forest algorithm was not utilized to randomly extract features in the present study. Instead, stratification extracting features were used to form a feature subspace generation method to ensure the effectiveness and difference of the decision tree.
When performing hierarchical extraction, the proportion of strong and weak related features is related to the importance of strong and weak related features, which is specifically expressed as: assuming that there are Sub features in the feature subspace, then the strong correlation feature in the feature subspace number NumNS is:
Among them, SNS is the proportion of the importance of the strong correlation feature in the importance of all features, and the calculation method is shown in Eq. (9).
The random forest algorithm is an integration of multiple decision trees. The construction process of each decision tree is independent of each other, and the classification ability of the formed decision tree is different, thus, a decision tree with poor classification ability will affect the classification accuracy of the random forest algorithm.
For the aforementioned reason, in the present study, the decision tree combination process in the random forest algorithm was improved. According to the decision trees formed based on the weight feature subspace, the classification weight values of different decision trees were obtained by calculating the prediction classification accuracies for each decision tree. This was to enhance the influence of decision trees with strong classification abilities in the integration process, and weaken the influence of decision trees with poor classification abilities in the integration process, thereby improving the classification ability of the random forest algorithm.
Conversely, to avoid an increase in similar decision trees in the obtained random forest model, the similarity of decision trees was calculated in the present study. By calculating the similarity between different decision trees, the decision trees were distinguished. Among the higher decision tree group, the decision tree with higher classification accuracy was selected for random forest model integration to improve the model effect.
To summarize, the calculation category of the final classification is shown in Eq. (10), where wi represents the classification weight of the i decision tree, and F represents the final classification category of a sample.
4.3 Improving the Random Forest Algorithm Process
The core ideas of the improved algorithm are as shown in Tab. 1.

Once the classifier completed its related tasks, evaluating the classification effect was a crucial part of the experiment. In evaluating the classification effect, the confusion matrix is a significantly useful tool. Taking two classifications as an example, the confusion matrix is shown in Tab. 2.

In the confusion matrix, TP represents the number of samples that originally belonged to category 0 and were correctly classified as category 0 by the classifier, while FP represents the number of samples that originally belonged to category 1 but were incorrectly classified as category 0 by the classifier. FN represents the number of samples that originally belonged to category 0 but were incorrectly classified into Class 1 by the classifier, while TN represents the number of samples that originally belonged to Class 1 and were correctly classified into Class 1 by the classifier.
The evaluation indicators for classifiers were primarily divided into the aforementioned categories. The indicator used in the present article was the classification accuracy rate, which is a common indicator in classifier evaluation. The specific calculation method is shown in Eq. (11).
In the present study, multiple data sets were tested to compare and verify, and the classification accuracy of different data sets before and after the algorithm was improved under different numbers of decision trees, as shown in Fig. 2.
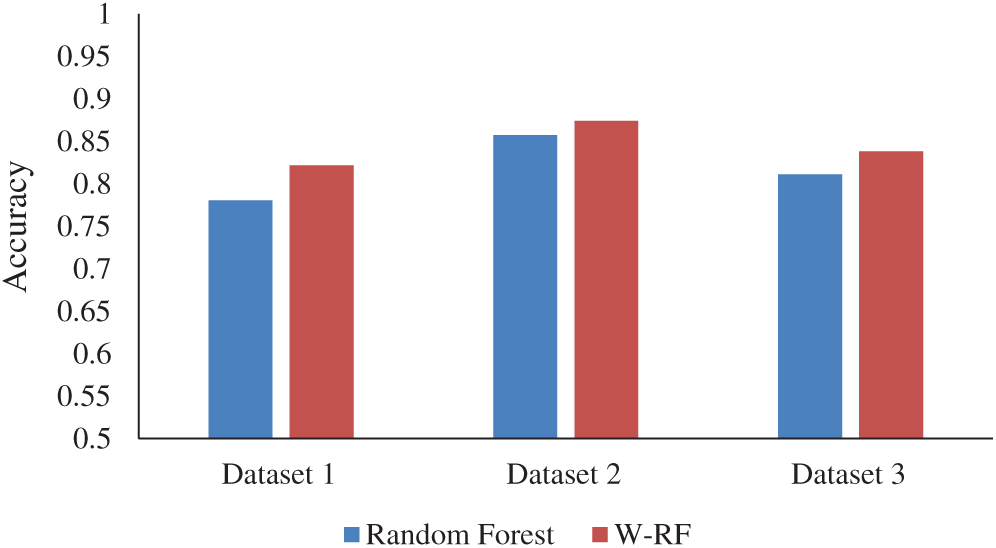
Figure 2: Classification accuracy rate
As shown in Fig. 2, the experimental results reveal that under the same parameters, the optimized random forest algorithm proposed in the present paper exhibited a significant improvement in classification accuracy when compared with the random forest algorithm before optimization. Meanwhile, in the case of different feature dimension data sets, as the feature dimension of the data sets increased, although the classification accuracy would gradually decrease, the improved algorithm proposed in the present paper demonstrated a clearer effect that improved the classification accuracy. Hence, an observation can be made from Fig. 2 that indicates that optimized random forest algorithm proposed exhibited better results on data sets with higher feature dimensions than the random forest algorithm before optimization.
Subsequently, for the present study, algorithm acceleration effect verification was conducted in the Spark cluster environment to verify whether the algorithm exhibited a positive parallelization acceleration performance. The verification standard is the speedup ratio, which is used to describe the reduction effect of the running time of the parallel algorithm. The calculation method is shown in Eq. (12).
In Eq. (12), T1 represents the running time of the algorithm under a single node, and Tn represents the running time of the algorithm in parallel computing on n nodes. The speedup change of the algorithm is shown in Fig. 3.
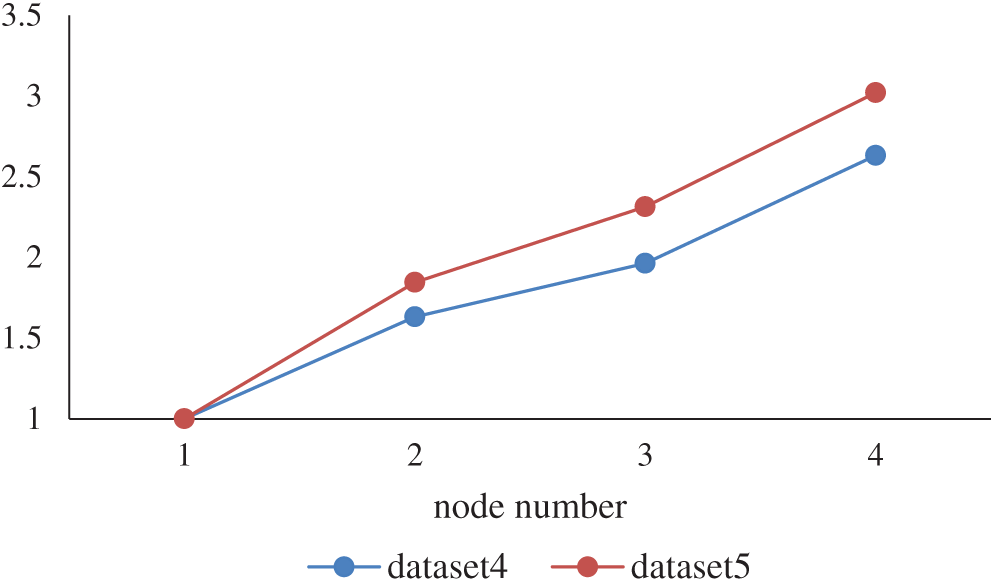
Figure 3: Speedup ratio
Fig. 3 evidently shows that as the number of working nodes in the Spark cluster increased, the algorithm speedup ratio also increased. This demonstrates that the algorithm had a positive parallelization effect, and from looking at the data volume from different data sets, dataset 5 was larger than dataset 4, indicating that the algorithm had a better speedup ratio when the amount of data increased. Hence, the parallelisation of optimization algorithms based on Spark could effectively conduct big data analysis and processing.
Further, the CreditData data sets were utilized in the present study to conduct credit evaluation applications, and the manner for averaging the experimental results for multiple experiments was compared. The results are shown in Fig. 4.
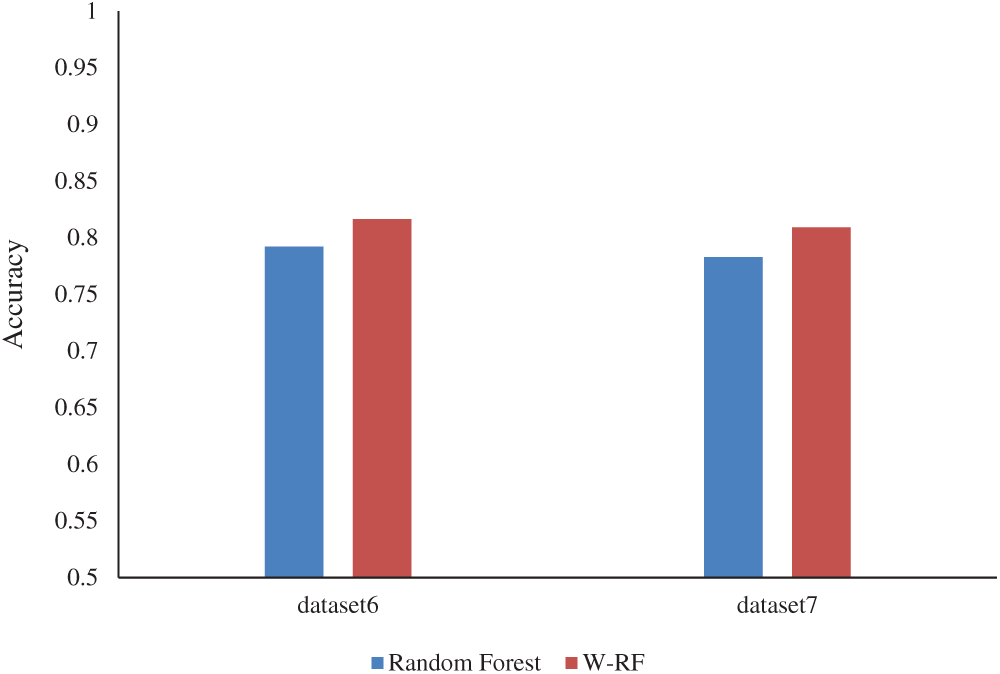
Figure 4: Application results in the credit field
An observation can be made in Fig. 4 that compared with the random forest algorithm before optimization, the classification accuracy of the optimized random forest algorithm proposed in the present paper exhibited a significantly improvement in applying data sets in the field of credit evaluation, and could be effectively applied to the field of credit evaluation.
In attempting to overcome the problems of the random forest algorithm, in the present study, strong correlation features were distinguished from weak features by calculating feature weights, and stratified sampling was used to obtain feature subspaces to improve the classification effects of random forest algorithms. In addition, when the random forest performed decision tree integration, this was performed according to the classification accuracy and similarity of the decision tree, and then the optimized random forest algorithm was implemented in parallel in the Spark platform. Finally, the performance of the algorithm was compared and analyzed through a classification performance experiment, the results of which reveal how effective the algorithm improvement was. However, not enough consideration was given to the imbalance of data in the present study. In future research, the primary focuses will be calculating the degree of data balance and how to ensure the efficiency in algorithm classification and reduce the time complexity while improving the classification effect.
Acknowledgement: The author(s) received no specific help from somebody other than the listed authors for this study.
Funding Statement: This paper is partially supported by the Social Science Foundation of Hebei Province (No. HB19JL007), and the Education technology Foundation of the Ministry of Education (No. 2017A01020).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. Breiman, “Random forests,” Machine Learning, vol. 45, no. 1, pp. 5–32, 2001. [Google Scholar]
2. H. C. Wu and Y. T. Wu, “Evaluating credit rating prediction by using the KMV model and random forest,” Kybernets, vol. 45, no. 10, pp. 1637–1651, 2017. [Google Scholar]
3. M. Hiroyuki and U. Yasushi, “Credit risk evaluation in power market with random forest,” in ICSMC, Montreal, Canada, pp. 3737–3742, 2007. [Google Scholar]
4. X. Zhang, Y. Yang and Z. R. Zhou, “A novel credit scoring model based on optimized random forest,” in CCWC, Las Vegas, America, pp. 60–65, 2018. [Google Scholar]
5. B. C. Ko, J. W. Gim and J. Y. Nam, “Cell image classification based on ensemble features and random forest,” Electronics Letters, vol. 47, no. 11, pp. 638–639, 2011. [Google Scholar]
6. B. X. Xu, Y. M. Ye and L. Nie, “An improved random forest classifier for image classification,” in ICIA, Shenyang, China, pp. 795–800, 2012. [Google Scholar]
7. Z. Peng, L. J. Wang and H. Guo, “Parallel text categorization of random forest,” Computer Science, vol. 45, no. 12, pp. 148–152, 2018. [Google Scholar]
8. Z. G. Li, “Several research on random forest improvement,” M. S. Theses, Xiamen University, China, 2018. [Google Scholar]
9. M. Robnik-Sikonja, “Improving random foresrs,” in ECML, Pisa, Italy, pp. 359–370, 2004. [Google Scholar]
10. D. Amaratunga, J. Cabrera and Y. S. Lee, “Enriched random forests,” Bioinformatics, vol. 24, no. 18, pp. 2010–2014, 2008. [Google Scholar]
11. X. Wang, “The research on random forest and its parallelization oriented to unbalanced high-dimensional data,” M. S. Theses, Liaoning University, China, 2016. [Google Scholar]
12. Y. S. Luo, “Research on parallel text classification algorithm base on random forest and Spark,” M. S. Theses, Southwest Jiaotong University, China, 2016. [Google Scholar]
13. Z. H. Niu, “Research on random forest classification algorithm based on Spark distributed platform,” M. S. Theses, Civil Aviation University of China, China, 2017. [Google Scholar]
14. T. Y. Hu, “Research on parallelization and optimization of random forest classification algorithm based on Spark,” M. S. Theses, Qilu University of Technology, China, 2019. [Google Scholar]
15. A. Svyatkovskiy, K. Imai, M. Kroeger and Y. Shiraito, “Large-scale text processing pipeline with Apache Spark,” in 2016 IEEE Int. Conf. on Big Data, Washington, America, pp. 3928–3935, 2016. [Google Scholar]
16. P. Liu, H. H. Zhao, J. Y. Teng, Y. Y. Yang, Y. F. Liu et al., “Parallel naive bayes algorithm for large-scale Chinese text classification based on Spark,” Journal of Central South University, vol. 26, no. 1, pp. 1–12, 2019. [Google Scholar]
17. M. Last and M. Roizman, “Avoiding the look-ahead pathology of decision tree learning,” International Journal of Intelligent Systems, vol. 28, no. 10, pp. 974–987, 2013. [Google Scholar]
18. Y. Zhang and J. Cao, “Decision tree algorithms for big data analysis,” Computer Science, vol. 43, no. S1, pp. 374–379, 2016. [Google Scholar]
19. X. L. Li, “The study and application of feature selection algorithms based on relief,” M. S. Theses, Dalian University of Technology, China, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |